ROC Calculation for Burst Traffic Packet Detection—An Old Problem, Newly Revised

Abstract

Burst traffic radio systems use short signal bursts, which are prepended with an a priori known preamble sequence. The burst receivers exploit these preamble sequences for burst start detection. The process of burst start detection is commonly known as Packet Detection (PD), which employs preamble sequence cross-correlation and threshold detection. One major figure of merit for PD performance is the so-called ROC—receiver operating characteristics. ROC describes the trade-off between the probability of missed detection vs. the probability of false alarm. This article describes how to calculate the ROC for specified preamble sequences by deriving the probability density function (PDF) of the cross-correlation metric. We address this long-standing problem in the context of LEO (low Earth orbit) satellite systems, where differentially modulated PN (pseudo-noise) sequences are used for packet detection. For this particular class of preamble signals, the standard Ricean PDF assumption no longer holds and needs to be revised accordingly within this article.

1. Introduction

Recent low-Earth orbit (LEO) satellite systems utilize burst traffic uplink signals, where the satellite receiver exploits a known preamble sequence to perform packet detection. Packet detection means detecting the presence of the uplink signal and estimating the ideal packet start time instant. The LEO satellite system Starlink, for instance, uses OFDM (orthogonal frequency division multiplexing) uplink bursts, whereas the preamble is a conventional single-carrier differentially modulated PSK (phase shift keying) sequence [1]. Burst traffic LEO satellite receivers use a cross-correlator, which is linked with a threshold detector. The threshold detector declares a valid burst start if the cross-correlation metric exceeds a given threshold T. In order to define the threshold value T, the so-called receiver operating characteristics (ROC [2]) need to be derived. ROC describes the trade-off between the probability of missing the packet start and the probability of a false alarm event. Both probabilities can be controlled by the threshold value T, which is used in the packet detector. In order to derive the ROC, time-consuming Monte Carlo simulations must be performed. This corresponds to the problem mentioned in the title. For each newly developed receiver, engineers need to derive an ROC to find an appropriate threshold value T. In this article, we revisit this long-standing in the context of LEO satellite receivers and derive an analytical solution for the ROC. The analytical ROC derivation allows for skipping time-consuming Monte Carlo simulations. Instead, the ROC is numerically calculated for a wide range of system parameters by means of the analytical solutions provided in this article.

Related Work and Contribution

Burst start detection using a priori known preamble sequences is a long-standing task in digital receivers. Burst start detection is applied in various wireless applications, independently of their data rate or technical context. Authors in [3,4] refer to NB-IoT (narrow-band Internet of Things) receivers. Authors in [5] explain burst start detection in WiMAX (Worldwide Interoperability of Microwave Access) 802.16e downlink receivers, which only uses the repetitive nature of the WiMAX preamble. This blind auto-correlation approach exploits performance penalties compared to the cross-correlation approach discussed in this article. Authors in [6] refer to cross-correlation-based burst start detection in optical networks, which relies on a deterministic received power and therefore does not fit into the wireless LEO application discussed here. Authors in [7] describe cross-correlation-based burst start detection in the context of UWB (ultra-wide band) radar applications. For all the mentioned references and applications, the trade-off between the probability of false alarm and the probability of miss detection is described as a function of the threshold value T. In most cases, the ROC was derived from time-consuming Monte Carlo simulations. Only a few authors, such as [8,9], mention the computational complexity of burst start detection systems, including digital power normalization circuits. However, computational complexity is outside the scope of this article since it typically requires assumptions to be made about the underlying computation platform (CPU, FPGA, etc.). Since our aim is to derive the PDF of the cross-correlator metric, computational complexity issues for cross-correlation and threshold detection are not considered here.

The ROC can be calculated numerically if the probability density function (PDF) of the cross-correlator metric is known. Such an analytic ROC calculation approach is the scope of this article, as it allows for quick ROC and threshold derivations without time-consuming Monte Carlo simulations. Many authors describe the probability density function of the cross-correlation metric at the actual packet start by means of a Ricean PDF [10] or Rayleigh PDF [7]. The Ricean or Rayleigh PDF appears to be a standard assumption in AWGN (additive white Gaussian noise) channels, which applies well to classical CAZAC (constant amplitude zero autocorrelation) [11] or PN sequence types, as long as an automatic gain control (AGC) is neglected in the receiver. Authors in [7,10] typically assume normalized received signal power, which easily allows for simplified but inaccurate PDF derivations. Moreover, many authors do not explain how the normalized power assumption of the received signal is achieved in practice. Hence, our aim is to derive a PDF of the cross-correlation metric under the impact of real-world AGC. Such a real-world AGC will never perfectly achieve normalized signal power at the cross-correlator input. Instead, real-world AGC circuits will cause the received signal power to fluctuate randomly around the given power target. These stochastic power fluctuations will be part of the PDF derivations in this article.

Common literature on burst start detection only derives ROC for CAZAC or PN-type preamble sequences. In LEO satellite communications, however, differentially modulated PN sequences are a Doppler-robust alternative to the classical CAZAC or PN preamble sequence types. Hence, our contribution in this article is threefold:

• We derive the PDF of the cross-correlation metric for different preamble sequence types, including differentially encoded PN sequences.
• We show that the standard Ricean PDF assumption should not be used for differentially encoded PN sequences. In addition, we demonstrate that the AGC will have a considerable impact on the PDF shape, which also limits the usage of the Ricean assumption for non-differentially modulated preamble types.
• We will illustrate how to perform ROC calculation under realistic AGC conditions and under high carrier frequency offset, which is typical for LEO satellite communications.

The article is structured as follows: In Section 2, we introduce the baseband signal model and explain the major differences between CAZAC, bipolar modulated PN sequences, and differentially modulated PN sequences. Section 2 also introduces the cross-correlation operation performed in the packet detector. Section 3 will explain the ROC concept and will introduce the probability of false alarm and the probability of packet detection. We derive the PDF for the cross-correlation metric in Section 4. Finally, we show how to parametrize the PDF with respect to AGC settings in Section 5. Then, we will introduce the concept of BCM (best common metric) in Section 6. BCM is used to describe the ROC with a single real-valued number. We conclude in Section 7.

2. Signal Model and Cross-Correlation

2.1. Baseband Signal Model

We define $y\left[k\right]$ as the received complex baseband symbol at time instant k when the preamble sequence $x_p$ of length L is transmitted:

$$y\left[k\right]=x_p\left[k\right]e^{j2\pi \nu k}{e}^{j2\pi \mathsf{\Delta }\varphi }+n\left[k\right]\mathrm{with}0\le k\le L-1.$$

(1)

Without loss of generality, we assume that $k=0$ denotes the first symbol time instant of the received preamble sequence. Moreover, we explicitly assign the symbol time instant $k=k_0=L-1$ when the preamble is fully received, and the burst start detector shall declare burst detection. The variable $\nu$ denotes the carrier frequency offset (CFO) normalized to the symbol rate, whereas $\mathsf{\Delta }\varphi$ represents a static phase error. The additive white Gaussian noise (AWGN) signal is represented by the complex sample $n\left[k\right]$. We assume an uncolored AWGN, where the real and imaginary parts of $n\left[k\right]$ are assumed to be mutually statistically independent random variables. We further assume zero-mean noise signals, i.e., $E\left\{n\right[k\left]\right\}=0$ and ${E\left\{\right|n\left[k\right]|}^2\}={\sigma }_n^2$. Since we assume signal representation in the complex baseband after ADC (analog-to-digital conversion), all signal variables are assumed unitless. We introduce ${\sigma }_x^2$ and ${\sigma }_n^2$ as useful signal power and noise power, respectively. We can now define the signal-to-noise ratio (SNR) $\gamma$ as follows:

$$\gamma ={\displaystyle \frac{{\sigma }_x^2}{{\sigma }_n^2}}.$$

(2)

Note that the signal model of Equation (1) does not contain channel fading coefficients, as they are often used in terrestrial wireless mobile communications. Here, we explicitly do not model random channel fading since we assume an LOS (line of sight) channel. This is a standard assumption in LEO satellite communications due to the directional antennas of the ground station equipment.

Without loss of generality, we assume that ${\sigma }_x^2=1$. More specifically, we assume that all sequence elements $x_p\left[k\right]$ are mapped on the unit circle of the complex number plane, i.e., ${|x_p\left[k\right]|}^2={\sigma }_x^2=1$, which holds for all sequence types regarded in this article.

2.2. Preamble Signal Types

There is a vast literature on types of preamble sequences that show preferable properties for packet detection and CFO estimation. The basic principles behind preamble detection come from classical radar applications. Typically, the burst receiver uses cross-correlation in order to estimate the burst start and coarse CFO. Generally, there are two types of preamble sequences:

• Chirp signals and CAZAC (constant amplitude zero auto-correlation) sequences [12] with $x_p\left[k\right]\in \mathbb{C}$;
• Bipolar BPSK (binary phase-shift keying)-modulated pseudo noise (PN) sequences with $x_p\left[k\right]\in \{-1,1\}$ [13].

CAZAC sequences are complex-valued and are used, for instance, in chirp spread spectrum systems, as described in [10]. In LEO satellite systems, for instance, CAZAC sequences are used in [14,15,16] as preamble and for symbol spreading.

Figure 1 shows a standard cross-correlator used for burst start detection. The cross-correlator implements the following equation to generate the complex-valued metric $m\left[k\right]$ at symbol time instant k:

$$m\left[k\right]={\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}y[k-l]x_p^{*}[L-l-1].$$

(3)

Let us define the burst-start time instant $k_0$ at which the preamble sequence is fully received. The aim of the packet detector is to detect the cross-correlation metric $m\left[k_0\right]$ at the threshold detector as follows:

$${\left|m\left[k_0\right]\right|}^2\ge T,$$

(4)

where T represents the provided threshold. The major difference between CAZAC and bipolar BPSK PN sequences is their ambiguity function [14]. CAZAC sequence cross-correlators are much more robust against high CFO than BPSK PN sequences. This important issue shall be illustrated in the following small example: let us consider a preamble sequence $x_p$ of length $L=1023$. Figure 2 shows the cross-correlation metric $|m\left[k_0\right]{|}^2$ for a BPSK-modulated PN sequence. Notably, the correlation peak gets lower at even small CFO values. More precisely, $|m\left[k_0\right]{|}^2$ depends on the CFO and sequence length, as shown in [3], where the equation accounts for the time-varying phase rotation:

$$\mathrm{bipolar}\mathrm{PN}\mathrm{Sequences}:{\left|m\left[k_0\right]\right|}^2\propto {\left|{\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}{e}^{j2\pi \nu l}\right|}^2.$$

(5)

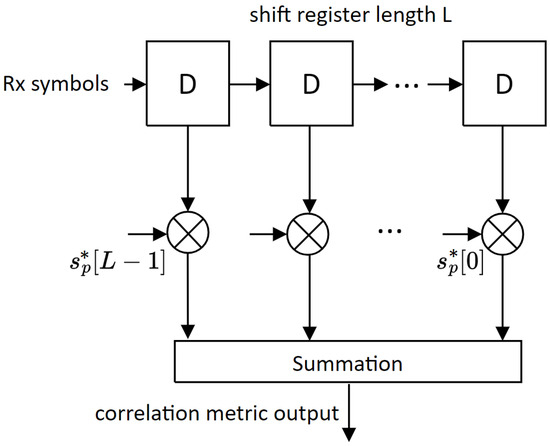
Figure 1. Shift register-based cross-correlator used for burst-start detection.

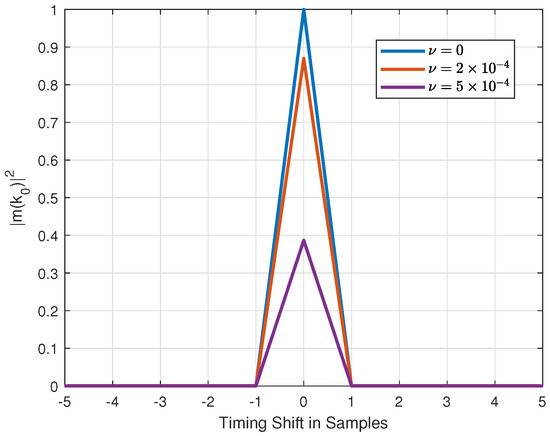
Figure 2. M-sequence cross-correlation with different CFO, L = 1023.

As an alternative to PN sequences, CAZAC sequences can be used, which are more robust against even high CFO values. One specific CAZAC sequence type is the Frank–Zhadoff–Chu (FZC) sequence [17,18], which is widely used in mobile wireless communications. The most prominent property of FZC sequences, as shown in Figure 2 and Figure 3, is that the correlation-peak magnitude does not degrade much even under high CFO. However, a time-delay shift of the correlation peak is observable, which depends on the CFO. This behavior is fully displayed in Figure 4, where the ambiguity function of the FZC sequence is shown. The ambiguity function shows the uncertainty of the correlation peak regarding CFO and time delay. This behavior is, for instance, used for CFO estimation and packet detection in LEO satellite systems, as it is described in [14,19]. Here, two complementary (conjugate complex) FZC subsequences are used to jointly estimate burst start and CFO. This, however, means that two FZC subsequences need to be transmitted as preamble. PN sequence-based preambles, instead, are only formed from a single sequence.

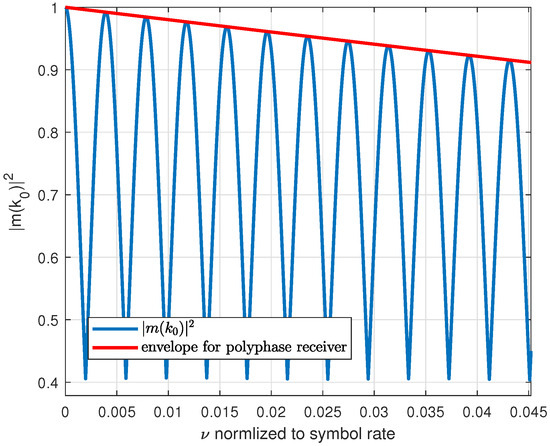
Figure 3. FZC sequence cross-correlation vs. CFO, L = 255.

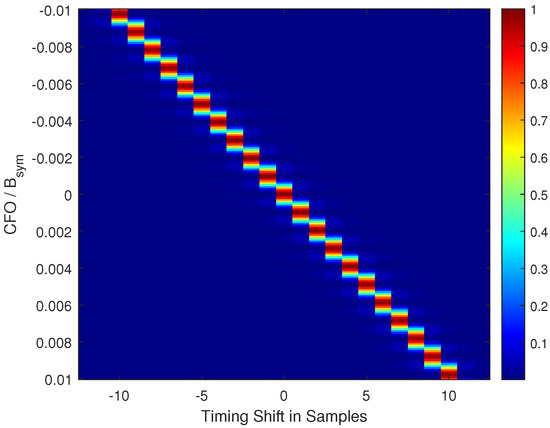
Figure 4. Ambiguity function of the FZC sequence, L = 1023.

Authors in [19] report that the uncertainty behavior of CAZAC sequences can lead to strong attenuation of $|m\left[k_0\right]{|}^2$ under specific CFO conditions, which is depicted in Figure 3.

These problems, however, are no longer observable in multi-rate receivers, as outlined in Section 2.4, which applies signal oversampling, where cross-correlation is performed on each polyphase. Hence, we have strong reasons to model the CAZAC cross-correlation metric $m\left[k_0\right]$, which is attenuated by CFO according to the envelope depicted in Figure 3 as follows, where the derivation can be found in [3,19]:

$$\mathrm{FZC}\mathrm{sequences}:{\left|m\left[k_0\right]\right|}^2\propto {\left(1-\nu \right)}^2.$$

(6)

The attenuation of FZC sequences, however, is much lower than the one observed for PN sequences, as shown in Equation (5).

Concerning the processing complexity of the cross-correlator, it is becoming evident that complex-valued CAZAC sequences require the use of multiple complex multipliers in the cross-correlator. This limits the use of CAZAC sequences, especially in LEO satellite receivers, due to their high computational effort. BPSK-modulated PN sequences, however, do not require multipliers at all, because the multiplication of sequence elements (1 or −1) can be substituted by simple ADD and SUB operations.

2.3. Differentially Modulated PN Sequences

There is an alternative sequence type that combines the simple correlator design of the BPSK-modulated PN sequences and the CFO robustness of CAZAC sequences: differentially modulated BPSK PN sequences. Let us consider a binary bipolar BPSK-modulated preamble sequence $x_p\left[k\right]$ of length L. Let us further define a binary bipolar BPSK-modulated M-sequence $s_p\left[k\right]$ of length $L-W$. The integer value $W\ll L$ parametrizes the differential modulation and is assigned as the differential modulation distance. Since $s_p\left[k\right]$ is defined to be an M-sequence, it shows preferable autocorrelation properties that are exploited in the burst-receiver packet detection. We call $x_p\left[k\right]$ a differentially modulated preamble sequence if it applies that

$$x_p\left[k\right]x_p^{*}[k-W]=s_p\left[k\right],\forall k=W:L-1.$$

(7)

When ignoring AWGN noise, it becomes evident how differential demodulation eliminates both the constant phase error and the time-varying phase offset, yielding

$$y\left[k\right]y^{*}[k-W]=s_p\left[k\right]e^{j2\pi \nu W},$$

(8)

where the time-varying phase offset due to the CFO now translates into a single complex number. This complex number shows a phase that is proportional to the CFO.

The differentially demodulated signal, according to Equation (8), is fed into the packet detector cross-correlator as depicted in Figure 5, yielding

$$m\left[k\right]={\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}y[k-l]y^{*}[k-l-W]s_p^{*}[L-W-l-1],$$

(9)

where $m\left[k\right]$ again denotes the complex-valued cross-correlation metric at the packet detector output. Note that the differential demodulator in Figure 5 uses the conjugate complex (∗) delayed signal. As already explained in the previous subsection, we define the packet-start time index as $k_0$, at which the packet detector declares a valid burst start.

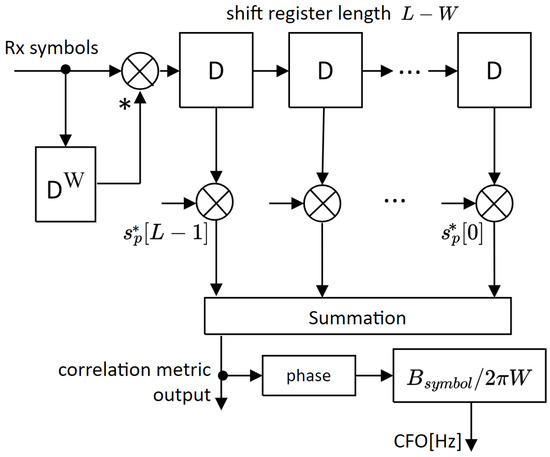
Figure 5. Differential shift register-based cross-correlator used for burst-start detection and CFO estimation.

2.4. Oversampling and Polyphase Timing

In most burst traffic receivers, the packet detector not only estimates the frame start but also derives the symbol clock timing. The symbol clock timing can be considered as finding the polyphase component of an oversampled received signal, which provides ISI (inter-symbol interference)-free demodulation. Within this article, all sequences are defined in the so-called symbol space, i.e., their respective timing instant k represents the symbol clock $T_{symbol}$. Conversely, the receiver uses an oversampling factor $N_{OS}\in \mathbb{N}$ from which the sample clock $T_{sample}$ is derived by $N_{OS}·T_{sample}=T_{symbol}$. Symbol clock timing can be derived if multiple cross-correlators are used in parallel. Each cross-correlator uses one polyphase component of the oversampled received signal, according to Figure 6.

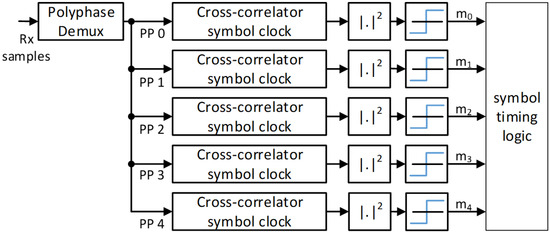
Figure 6. Parallel cross-correlator structure for polyphase timing estimation, $N_{OS}=5$.

In the course of this article, we denote the perfect timing instance $k_0$ as the symbol clock index at which the preamble sequence is fully received. Without mentioning this again, we inherently assume that $k_0$ refers to the polyphase component that exhibits the strongest correlation peak, according to Figure 6.

3. The ROC Concept

3.1. Basic Concept

Burst traffic LEO satellite receivers use a cross-correlator, which is linked to a threshold detector [2]. The threshold detector declares a valid burst start if the cross-correlation metric exceeds a given threshold T. In this respect, the threshold needs to be optimized according to the following targets:

• The threshold shall be high enough in order to avoid random noise to fire a burst detection event. This would result in a so-called false alarm, where $P_{FA}$ denotes the probability of false alarm accordingly.
• The threshold shall be low enough in order to ensure that even weak cross-correlation peaks of the incoming preamble sequence are still being detected. If the threshold detector misses a valid packet start, this results in a miss-detection event. The miss-detection probability represents the variable $P_{miss}$.

Hence, the system designer needs to define the threshold T such that it achieves a viable compromise between the probability of false alarm and the probability of miss-detection. In ROC, both probabilities are typically displayed in one diagram, as shown in Figure 7.

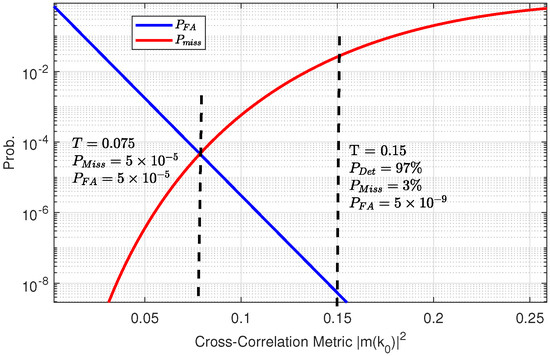
Figure 7. ROC example, BPSK PN Sequence, L = 127, SNR = 0 dB.

The probability of miss detection $P_{miss}$ depends on the PDF of $|m\left[k_0\right]{|}^2$, i.e., at the ideal burst-start time instant $k_0$. Hence, we define $f_{M,k_0}\left(m\right)$ as the PDF of the random variable $|m\left[k_0\right]{|}^2$ accordingly, from which we can calculate $P_{miss}$ by

$$P_{miss}={\int }_{-T}^T{f}_{M,k_0}\left(m\right)\mathrm{d}m.$$

(10)

The probability of false alarm, $P_{FA}$, in turn, depends on the PDF of ${\left|m\left[k\right]\right|}^2$ in the case where only noise $n\left[k\right]$ is received. In this case, we define the PDF of ${\left|m\left[k\right]\right|}^2$ as $f_{M,n}\left(m\right)$, from which we can calculate $P_{FA}$ as follows:

$$P_{FA}=1-{\int }_{-T}^T{f}_{M,n}\left(m\right)\mathrm{d}m.$$

(11)

Many authors, such as [19], model the RV $\left|m\right[k_0\left]\right|$ as Ricean distributed, which allows for closed-form solutions of Equations (10) and (11). However, we will show in the course of this article that the Ricean assumption does not hold for practical burst receivers, which apply an AGC for power normalization. Moreover, the Ricean PDF shall not be used to model the PDF $f_{M,k_0}\left(m\right)$ for differentially modulated PN sequences. We will address these issues in Section 4, where we derive the non-Ricean PDF $f_{M,k_0}\left(m\right)$ accordingly.

3.2. Power Normalization and AGC

Let us consider an arbitrary signal scaling in the digital receiver using the real-valued scaling factor c:

$$y\left[k\right]=c·x_p\left[k\right]e^{j2\pi \nu k}{e}^{j2\pi \mathsf{\Delta }\varphi }+c·n\left[k\right].$$

(12)

This scaling factor makes the cross-correlation metric $|m\left[k_0\right]{|}^2$ to be proportional to $c^2$:

$${\left|m\left[k_0\right]\right|}^2\propto c^2{\sigma }_x^2.$$

(13)

Hence, any signal scaling will result in an adaptation of T, depending on $c^2$, in order to achieve the required ROC performance. This is, however, impractical and forces the system designer to normalize the cross-correlation metric to the power ${\sigma }_y^2$ of the received signal:

$$m^{\prime }\left[k\right]={\displaystyle \frac{{\left|m\left[k\right]\right|}^2}{{\sigma }_y^2}}.$$

(14)

At high SNR, this yields the normalized cross-correlation metric at the packet-start time instant $k_0$, which no longer depends on the scaling factor, because:

$$m^{\prime }\left[k_0\right]={\displaystyle \frac{|m\left[k_0\right]{|}^2}{{\sigma }_y^2}}\approx {\displaystyle \frac{c^2{\sigma }_x^2}{{\sigma }_y^2}}\approx 1\mathrm{with}{\sigma }_y^2\approx c^2{\sigma }_x^2.$$

(15)

Hence, power normalization, according to Equation (15), allows setting a single threshold value T irrespective of the actual signal power ${\sigma }_y^2$. It can be shown that the power normalization in the case of differentially modulated PN sequences shall be done differently from Equation (15), according ot the following rule:

$$m^{\prime }\left[k\right]={\displaystyle \frac{{\left|m\left[k\right]\right|}^2}{{\sigma }_y^4}}.$$

(16)

4. PDF Derivation of the Cross-Correlation Metric

In this section, the PDF $f_{M,k_0}\left(m\right)$ is derived for CAZAC and PN sequences in Section 4.1. For differentially modulated PN sequences, the PDF is derived in Section 4.3. In both subsections, we assume that no AGC and power normalization are applied, i.e., that the signal scaling factor c = 1. We will later add the effects of AGC and signal scaling to the PDF parameters in Section 5.

4.1. PDF for CAZAC and PN Sequences

We like to derive $f_{M,k_0}\left(m\right)$ and again consider the cross-correlation equation

$$m\left[k\right]={\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-1}y[k-l]x_p^{*}[L-W-l-1],$$

(17)

where we assume that only a simple AGWN signal model (without CFO and phase error) is present:

$$y\left[k\right]=x_p\left[k\right]+n\left[k\right].$$

(18)

Substituting Equation (18) into Equation (17) yields

$$\begin{array}{c}\hfill m\left[k_0\right]={\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}x[k_0-l]x_p^{*}[L-l-1]\\ \hfill +{\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}n[k_0-l]x_p^{*}[L-l-1].\end{array}$$

(19)

The first part of Equation (19) turns into the following constant value:

$${\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}x[k_0-l]x_p^{*}[L-l-1]={\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}{\sigma }_x^2=1.$$

(20)

The second part of Equation (19) turns into a complex zero-mean Gaussian RV:

$${\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}n[k_0-l]x_p^{*}[L-l-1]\to \mathrm{CN}\left(0,{\displaystyle \frac{{\sigma }_n^2}{L}}\right).$$

(21)

Now, it is becoming evident that the correlation metric $m\left[k_0\right]$ follows a complex Gaussian with

$$m\left[k_0\right]=1+n^{\prime }\to \mathrm{CN}\left(1,{\displaystyle \frac{{\sigma }_n^2}{L}}\right),$$

(22)

where we decompose $n^{\prime }=n_r+j·n_q$, and both real and imaginary parts are equally powered i.i.d Gaussian RVs:

$$n_r,n_q\to \mathrm{N}\left(0,{\displaystyle \frac{{\sigma }_n^2}{2L}}\right).$$

(23)

The cross-correlation metric is fed into the threshold detector after ${|.|}^2$ operation:

$${\left|m\left[k_0\right]\right|}^2={\left(1+n_r\right)}^2+n_q^2.$$

(24)

The first part $r={\left(1+n_r\right)}^2$ of Equation (24) can be modeled as a non-central chi-square distributed random variable with one degree of freedom [20], which has the following PDF:

$$f_R\left(r\right)={\displaystyle \frac{1}{2\sqrt{2\pi r{\sigma }_1^2}}}{e}^{-{\displaystyle \frac{r+a^2}{2{\sigma }_1^2}}}\left(e^{\sqrt{{\displaystyle \frac{r{a}^2}{{\sigma }_1^4}}}}+e^{-\sqrt{{\displaystyle \frac{r{a}^2}{{\sigma }_1^4}}}}\right).$$

(25)

The variable $a^2$ denotes the non-centrality parameter, which is $a^2=1$. We defined ${\sigma }_1^2={\displaystyle \frac{{\sigma }_n^2}{2L}}$ as the variance of $n_r$. The second part $n_q^2$ of Equation (24) is a central chi-square random variable because $n_q$ is a zero-mean Gaussian [20]. Hence, the PDF of $q=n_q^2$ is

$$f_Q\left(q\right)={\displaystyle \frac{1}{2\sqrt{2\pi q{\sigma }_2^2}}}{e}^{-{\displaystyle \frac{q}{2{\sigma }_2^2}}}.$$

(26)

We defined ${\sigma }_2^2={\displaystyle \frac{{\sigma }_n^2}{2L}}$ as the variance of $n_q$. According to Equation (24), both PDF $f_R\left(r\right)$ and $f_Q\left(q\right)$ need to be convolved to obtain $f_{M,k_0}\left(m\right)$. In [20], a series expression is provided as follows:

$$\begin{array}{c}\hfill f_{M,k_0}\left(m\right)={\displaystyle \frac{1}{2{\sigma }_1^2}}\left({\displaystyle \frac{{\sigma }_1^2}{{\sigma }_2^2}}\right)e^{-{\displaystyle \frac{m+a^2}{2{\sigma }_1^2}}}\\ \hfill ·\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }(0.5+n)}{n!\mathsf{\Gamma }\left(0.5\right)}}{\left({\displaystyle \frac{\sqrt{m}\left({\sigma }_2^2-{\sigma }_1^2\right)}{a{\sigma }_2^2}}\right)}^n{\mathrm{I}}_n\left({\displaystyle \frac{a\sqrt{m}}{{\sigma }_1^2}}\right).\end{array}$$

(27)

When assuming that both ${\sigma }_1^2=\mathrm{E}\left\{|n_r{|}^2\right\}$ and ${\sigma }_2^2=\mathrm{E}\left\{|n_q{|}^2\right\}$ are equal, then the PDF in Equation (27) simplifies and can be interpreted as the squared version of the well-known Ricean PDF, which is commonly used by many authors, such as [19]. Figure 8 shows an example PDF for a PN sequence of length $L=127$ under an SNR of $\gamma$ = 0 dB, where the analytical PDF is compared with a PDF from a Matlab Monte Carlo simulation.

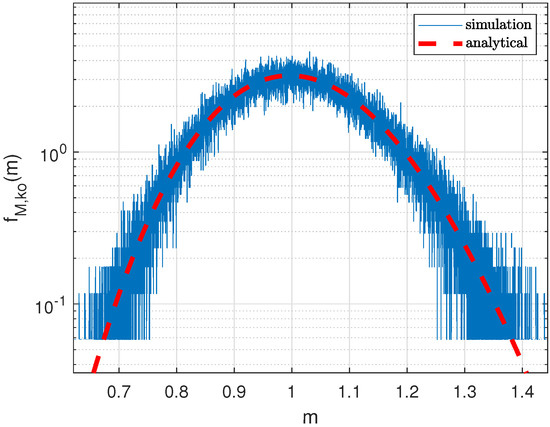
Figure 8. PDF bipolar PN Sequence, L = 127, SNR = 0 dB.

We strongly recommend using the series expression of the PDF according to Equation (27) instead of the simpler Ricean PDF. This is because we will show that ${\sigma }_1^2\ne {\sigma }_2^2$, which makes the Ricean PDF no longer applicable. There are two reasons that make ${\sigma }_1^2\ne {\sigma }_2^2$:

• Differentially modulated PN sequences are used in packet detection;
• AGC: The power normalization of Equations (15) and (16) uses an estimate of the received signal power ${\widehat{\sigma }}_y^2$, where ${\widehat{\sigma }}_y^2\ne {\sigma }_y^2$.

In these practically relevant cases, we hence need to calculate the ROC with the PDF provided in Equation (27) instead of using the simpler Ricean PDF. In practice, we recommend calculating the series in Equation (27) up to $n=4$ in order to yield accurate results. Let’s extend the simple AWGN signal model towards a static phase error:

$$y\left[k\right]=x_p\left[k\right]e^{j2\pi \mathsf{\Delta }\varphi }+n\left[k\right].$$

(28)

The PDF, according to Equation (27), is formulated to comply with the simple AWGN signal model. We now extend the signal model towards amplitude scaling and phase rotation. A static phase error is known not to change the PDF $f_{M,k_0}\left(m\right)$ because $\left|e^{j2\pi \mathsf{\Delta }\varphi }\right|=1$. The time-varying phase error due to CFO, however, has an impact on the PDF. This is because the non-centrality parameter $a^2$ depends on the CFO and the sequence length, which is based on Equation (5):

$$\mathrm{bipolar}\mathrm{PN}\mathrm{sequences}:a^2={\left|{\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}{e}^{j2\pi \nu ł}\right|}^2.$$

(29)

Figure 9 shows the accuracy of the PDF even under a strong CFO for a bipolar PN sequence of length $L=127$ at $\gamma$ = 0 dB.

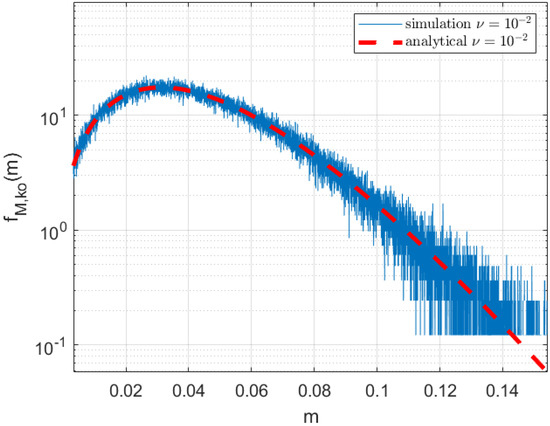
Figure 9. PDF bipolar PN Sequence, $\nu$ = ${10}^{-2}$, L = 127, $\gamma$ = 0 dB.

For FZC (CAZAC) sequences, the non-centrality parameter $a^2$ can be written as follows using Equation (6):

$$\mathrm{FZC}\mathrm{sequences}:a^2={(1-\nu )}^2.$$

(30)

4.2. PDF Parameters Under Channel Attenuation and Signal Scaling

In typical scenarios, two-channel attenuation factors need to be considered, which require extending the baseband signal model further:

$$y\left[k\right]=c·h·x_p\left[k\right]e^{j2\pi \mathsf{\Delta }\varphi }+c·n\left[k\right].$$

(31)

Here, the channel gain h denotes the signal attenuation at the receiver side, and c represents the arbitrary signal scaling due to the number format of the digital receiver. The SNR can be defined accordingly:

$$\gamma ={\displaystyle \frac{c^2{h}^2{\sigma }_x^2}{c^2{\sigma }_n^2}}={\displaystyle \frac{h^2{\sigma }_x^2}{{\sigma }_n^2}}.$$

(32)

Hence, the arbitrary signal scaling factor c does not impact the SNR. The channel gain h, however, directly determines the SNR. Without loss of generality, we assume that ${\sigma }_x^2=1$ and that $h^2=1$, where the entire SNR scaling is covered within the variable ${\sigma }_n^2$. If we use the relationship that the received power is equal to ${\sigma }_y^2=c^2+c^2{\sigma }_n^2$, we can now write the variance SNR-dependent as follows:

$${\sigma }_1^2={\sigma }_2^2={\displaystyle \frac{1}{2L\left(1+\gamma \right)}}.$$

(33)

The non-centrality parameter $a^2$ can also be defined as SNR-dependent. For bipolar PN sequences, the parameter $a^2$ depends on the CFO and the sequence length, which is based on Equation (5):

$$a^2={\left|{\displaystyle \frac{1}{L}}\sum _{l=0}^{L-1}{e}^{j2\pi \nu ł}\right|}^2{\displaystyle \frac{\gamma }{1+\gamma }}.$$

(34)

Since CAZAC sequences’ cross-correlation is not impaired by CFO, we can reuse Equation (6) and write:

$$a^2={(1-\nu )}^2{\displaystyle \frac{\gamma }{1+\gamma }}.$$

(35)

4.3. PDF for Differentially Modulated PN Sequences

The PDF $f_{M,K_0}\left(m\right)$ for differentially modulated PN sequences can be derived by recalling the following cross-correlation operation

$$m\left[k\right]={\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}y[k-l]y^{*}[k-l-W]s_p^{*}[L-W-l-1].$$

(36)

As in Section 4.1, we start with the following simple AWGN channel model:

$$y\left[k\right]=x_p\left[k\right]+n\left[k\right].$$

(37)

If we substitute Equation (37) into Equation (36), we obtain

$$\begin{array}{c}\hfill m\left[k\right]={\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}{s}_p[k-l]s_p^{*}[L-l-1]\\ \hfill +{\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}n[k-l]n^{*}[k-W-l]s_p^{*}[L-l-1]\\ \hfill +{\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}x[k-l]n^{*}[k-W-l]s_p^{*}[L-l-1]\\ \hfill +{\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}n[k-l]x^{*}[k-W-l]s_p^{*}[L-l-1].\end{array}$$

(38)

In the case of perfect timing ($k=k_0$), the first part of Equation (38) turns into a constant value:

$${\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}{s}_p[k_0-l]s_p^{*}[L-l-1]={\sigma }_s^2=1.$$

(39)

Equivalent to Section 4.1, we can now formulate $m\left[k_0\right]$ as a Gaussian RV:

$$m\left[k_0\right]=1+n^{\prime }.$$

(40)

However, the PDF and variance of $n^{\prime }$ cannot be formulated as easily as was done before for bipolar PN sequences or CAZAC sequences. The reason is the complexity of the resulting noise term $n^{\prime }$. Let’s analyze $n^{\prime }$ a little closer. At first, we define that the differentially PN sequences are bipolar (BPSK)-modulated:

$$s_p\left[k\right]\in \left\{-1,1\right\}\forall k,$$

(41)

$$x_p\left[k\right]\in \left\{-1,1\right\}\forall k.$$

(42)

We can hence conclude that

$$x_p\left[k\right]·s_p\left[k\right]\in \left\{-1,1\right\}\forall k.$$

(43)

In the next step, we assume that the first noise term in Equation (38) is statistically independent from the residual noise terms and forms an independent complex Gaussian:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{L-W}}\sum _{l=0}^{L-W-1}n[k-l]n^{*}[k-W-l]s_p^{*}[L-l-1]\\ \hfill \to \mathrm{CN}\left(0,{\displaystyle \frac{{\sigma }_n^4}{L-W}}\right).\end{array}$$

(44)

This assumption, however, is not entirely true. Nonetheless, it shows in practice that this assumption leads to accurate PDF results over a large parameter space. The variance of the residual noise terms in Equation (38) is calculated in Appendix A. Finally, we yield the following complex Gaussian model for $m\left[k_0\right]$:

$$m\left[k_0\right]=1+n^{\prime }\to \mathrm{CN}\left(1,{\displaystyle \frac{2{\sigma }_n^2+{\sigma }_n^4}{L-W}}\right).$$

(45)

We now reformulate Equation (45) as follows:

$$m\left[k_0\right]=1+n_r+j·n_q.$$

(46)

The most important observation is that both variances ${\sigma }_{n_r}^2$ and ${\sigma }_{n_q}^2$ are no longer equal, and the simple Ricean PDF can no longer be used for differentially modulated PN sequences, as already outlined in Section 4.1:

$${\sigma }_{n_r}^2={\displaystyle \frac{2\left(2{\sigma }_n^2+{\sigma }_n^4\right)}{3\left(L-W\right)}}\mathrm{and}{\sigma }_{n_q}^2={\displaystyle \frac{1\left(2{\sigma }_n^2+{\sigma }_n^4\right)}{3\left(L-W\right)}}.$$

(47)

Applying power normalization

$$m^{\prime }\left[k\right]={\displaystyle \frac{{\left|m\left[k\right]\right|}^2}{{\sigma }_y^4}}$$

(48)

We finally can derive the PDF parameters $a^2$, ${\sigma }_1^2$, and ${\sigma }_2^2$ as SNR-dependent variables:

$$a^2={\left({\displaystyle \frac{\gamma }{\gamma +1}}\right)}^2,$$

(49)

$${\sigma }_1^2={\displaystyle \frac{2\left(2\gamma +1\right)}{3{\left(\gamma +1\right)}^2(L-W)}}\mathrm{and}{\sigma }_2^2={\displaystyle \frac{1\left(2\gamma +1\right)}{3{\left(\gamma +1\right)}^2(L-W)}}.$$

(50)

The CFO no longer impacts $a^2$ due to the differential demodulation before cross-correlation which leads to the accurate PDF as depicted in Figure 10.

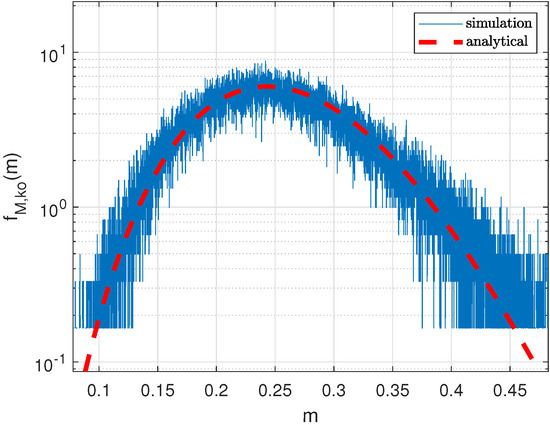
Figure 10. PDF of the differentially modulated PN sequence, W = 8, L = 135, $\gamma$ = 0 dB.

5. PDF Parametrization Depending on AGC Settings

As already explained in Section 3.2, power normalization is required in order to define a threshold value T independent from actual signal power ${\sigma }_y^2$. In this section, we will explain that the PDF parametrization highly depends on the assumptions made regarding AGC (automatic gain control). The reason behind this is that ${\sigma }_y^2$ is an unknown zero-mean random variable that needs to be estimated by AGC on the receiver side (using Bessel correction, which ensures an unbiased variance estimation):

$${\widehat{\sigma }}_y^2={\displaystyle \frac{1}{L+L_{AGC}-1}}\sum _{l=0}^{L+L_{AGC}-1}{\left|y[k-l]\right|}^2.$$

(51)

Hence, the AGC uses $L+L_{AGC}$ symbols to estimate ${\sigma }_y^2$. If $L_{AGC}$ is high, it follows that ${\widehat{\sigma }}_y^2\to {\sigma }_y^2$ because Equation (51) is an unbiased estimator. In this case, the PDF parameters $a^2$, ${\sigma }_1^2$, and ${\sigma }_2^2$ can be used for ROC calculation as already derived.

5.1. $L_{AGC}=0$ Non-Differentially Modulated Sequences

One important corner case is $L_{AGC}=0$, where the AGC power normalization is only derived from the length L of received preamble symbols. The correlation metric, hence, can be expressed as

$$m^{\prime }\left[k_0\right]={\displaystyle \frac{{\left|m\left[k_0\right]\right|}^2}{\frac{1}{L-1}{\sum }_{l=0}^{L-1}{\left|y[k-l]\right|}^2}}.$$

(52)

In the case of Equation (52), the PDF parameters $a^2$, ${\sigma }_1^2$, and ${\sigma }_2^2$ appear inaccurate, and the PDF deviates from the Matlab Monte Carlo simulation. Hence, we need to rework the PDF for $L_{AGC}=0$. There is one solution: the correlation metric problem of Equation (52) was described in [21] in the context of seismic statistics and earthquake detection. The authors of [21] derived the PDF $f_{M,k_0}\left(m\right)$ in a close form as a Beta distribution:

$$f_{M,k_0}(m,\alpha ,\beta )={\displaystyle \frac{\mathsf{\Gamma }(\alpha +\beta )}{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{m}^{\alpha +1}{(1-m)}^{\beta -1}.$$

(53)

Both parameters $\alpha$ and $\beta$ are the non-centrality parameters of the Beta distribution. The authors of [21] derived closed-form expressions for both $\alpha$ and $\beta$, which cannot be applied directly to our cross-correlation problem due to various reasons. For instance, the seismic earthquake detection problem in [21] does not match our complex baseband signal model, and so forth. Hence, we need to derive closed-form expressions for $\alpha$ and $\beta$ using a heuristic computer search and obtain the following equations:

$$\alpha =\sqrt{a}·\gamma ·L\mathrm{and}\beta ={\displaystyle \frac{\alpha }{\gamma }}=\sqrt{a}·L.$$

(54)

Here, the parameter a denotes the square root of the non-centrality parameter derived in Equations (34) and (35). Figure 11 shows a good accuracy between the Beta PDF and the simulation result for a CFO $\nu =0$.

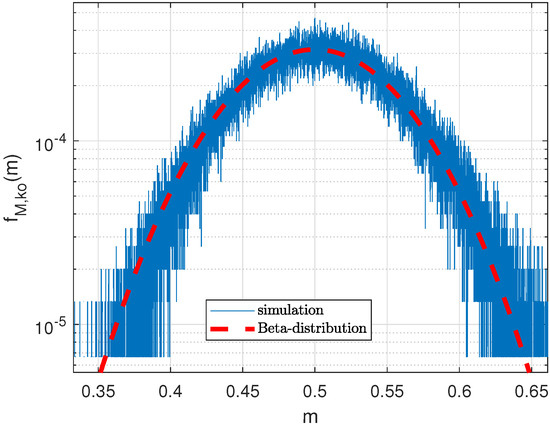
Figure 11. Beta PDF bipolar PN sequence, L = 127, $\gamma$ = 0 dB, $\nu =0$.

For moderate CFO values, however ($\nu ={10}^{-3}$), the Beta distribution shows inaccuracies, as depicted in Figure 12.

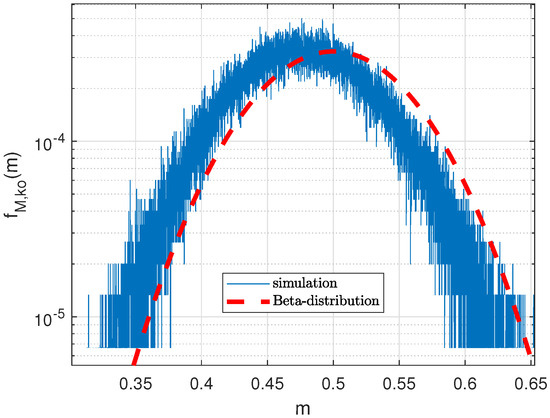
Figure 12. Beta PDF bipolar PN sequence, L = 127, $\gamma$ = 0 dB, $\nu ={10}^{-3}$.

Hence, we can conclude that the Beta PDF shows accurate results for non-differential modulated preamble sequences (bipolar PN, CAZAC) under low CFO. For high CFO, as it is present in LEO satellite communication, however, we need to focus on modifications of the PDF parameters $a^2$, ${\sigma }_1^2$, and ${\sigma }_2^2$. Results show that the non-centrality parameter $a^2$ does not need to be modified for $L_{AGC}=0$. The variances ${\sigma }_1^2$ and ${\sigma }_2^2$, however, need to be modified, where the following equation was heuristically found by computer search and appears valid over a large parameter space:

$${\sigma }_{1,2}^2={\displaystyle \frac{p}{5L(\gamma +1)\sqrt{\gamma +1}}}.$$

(55)

For ${\sigma }_1^2$ parameter $p=0.9$ and for ${\sigma }_2^2$ parameter $p=0.1$. Figure 13 shows accurate results of the modified variance values even for high CFO values.

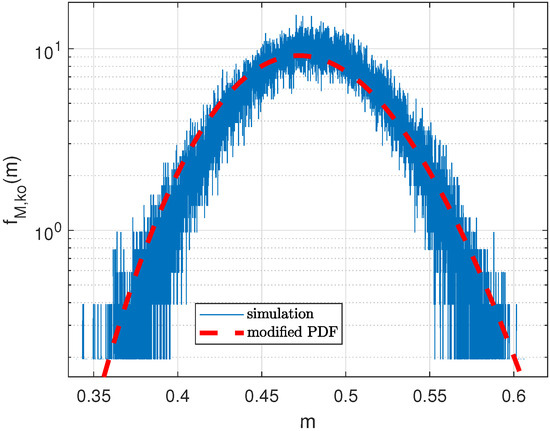
Figure 13. Modified PDF bipolar PN sequence, L = 127, $\gamma$ = 0 dB, $\nu ={10}^{-3}$.

5.2. $L_{AGC}>0$ Non-Differentially Modulated Sequences

In many burst traffic systems, the preamble is prepended by a dedicated AGC training field (see, for instance, IEEE 802.11 WLAN [13]). In such cases, the power estimation is done over $L+L_{AGC}$ symbols. The lower $L_{AGC}$, the more the PDF converges towards the modified parameter space shown in the last Section 5.1. Conversely, the higher $L_{AGC}$, the more the PDF converges towards the unmodified case derived in Section 4.2. This trade-off is depicted in Figure 14, where both modified and non-modified PDFs are compared for $L_{AGC}=50$.

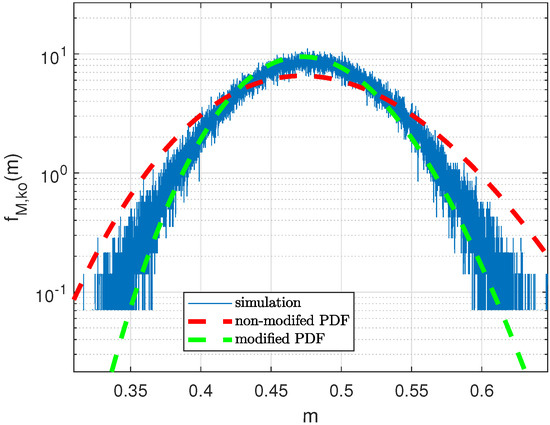
Figure 14. Comparison of modified PDF and non-modified PDF bipolar PN sequence, L = 127, $\gamma$ = 0 dB, $L_{AGC}=50$.

Hence, the choice of PDF parameters depends on the specific use case. In any case, the non-modified PDF parameters provide a worst-case model, which should be used in ROC calculations for typical $L_{AGC}>50$.

5.3. $L_{AGC}\ge 0$ Differentially Modulated Sequences

For differentially demodulated PN sequences, the power normalization is performed using the following equation for a given $L_{AGC}$

$$m^{\prime }\left[k_0\right]={\displaystyle \frac{{\left|m\left[k_0\right]\right|}^2}{{\left(\frac{1}{L+L_{AGC}-1}{\sum }_{l=0}^{L+L_{AGC}-1}{\left|y[k-l]\right|}^2\right)}^2}}.$$

(56)

For the corner-case $L_{AGC}=0$, we recommend using a modified parameter set, as already explained in Section 5.1. Again, the non-centrality parameter $a^2$ does not need to be modified and can be used from Equation (49). The variances ${\sigma }_1^2$ and ${\sigma }_2^2$, however, need to be modified, where the following equation was heuristically found by computer search and appears valid over a large parameter space:

$${\sigma }_{1,2}^2={\displaystyle \frac{p(2\gamma +1)}{(L-W){(\gamma +1)}^2\sqrt{\gamma +1}}}.$$

(57)

For ${\sigma }_1^2$ parameter $p=2/3$ and for ${\sigma }_2^2$ parameter $p=1/3$. As already explained in the previous Section 5.2, the non-modified PDF parameters provide a worst-case performance bound for ROC calculation. In cases with low $L_{AGC}\le 50$, we recommend using the modified PDF instead, which achieves more accurate results.

6. Best Common Metric of ROC

In order to calculate the ROC, we need to derive the probability of false alarm, $P_{FA}$:

$$P_{FA}=1-{\int }_{-T}^T{f}_{M,n}\left(m\right)\mathrm{d}m,$$

(58)

where $f_{M,n}\left(m\right)$ denotes the PDF of the cross-correlation metric if only noise is received. In such a case, the cross-correlation metric is a complex Gaussian random variable; hence, $f_{M,n}\left(m\right)$ can be expressed as an exponential PDF:

$$f_{M,n}\left(m\right)={\displaystyle \frac{1}{{\sigma }^2}}{e}^{-{\displaystyle \frac{m}{{\sigma }^2}}}.$$

(59)

If only noise is received, we can conclude that ${\sigma }_y^2={\sigma }_n^2$. Due to power normalization, the variance ${\sigma }^2$ of Equation (59) becomes independent of the actual noise power ${\sigma }_n^2$. For non-differentially modulated preamble sequences (bipolar PN, CAZAC), we can write:

$${\sigma }^2={\displaystyle \frac{1}{L}}.$$

(60)

For differentially modulated PN sequences, we can write:

$${\sigma }^2={\displaystyle \frac{1}{L-W}}.$$

(61)

As the ROC illustrates the trade-off between $P_{miss}$ and $P_{FA}$ as a pair of function graphs, it appears impractical for packet detection engineering and sequence design. The reason is that both functions $P_{miss}\left(T\right)$ and $P_{FA}\left(T\right)$ depend on the threshold value, and engineers like to optimize T regarding a scalar optimization criterion. Hence, we introduce the concept of BCM—best common metric. BCM can be used to map the entire ROC curves to one single performance value, which simplifies threshold optimization in burst traffic systems. The $BCM$ is defined as

$$BCM=\max \left\{P_{FA}\left(T_{BCM}\right),P_{miss}\left(T_{BCM}\right)\right\},$$

(62)

where the BCM threshold value $T_{BCM}$ is defined as

$$T_{BCM}=arg\underset{T}{min}\left\{\max \left\{P_{FA}\left(T\right),P_{miss}\left(T\right)\right\}\right\}.$$

(63)

Hence, the BCM is defined as the probability value of the cross-section of $P_{miss}$ and $P_{FA}$ at threshold value $T_{BCM}$. This is depicted in Figure 15.

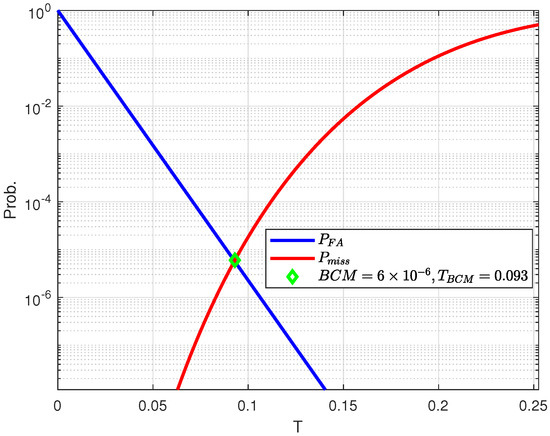
Figure 15. BCM of the differentially modulated PN sequence, L = 131, $\gamma$ = 0 dB, $W=4$.

For reference, we list BCM values for typical use cases obtained from LEO satellite communications for differentially modulated PN sequences in Table 1 and for non-differentially modulated sequences (CAZAC, PN) in Table 2. Note that a higher L allows the cross-correlator to accumulate more signal energy, which shows preferable performance, especially for differentially modulated PN sequences in Table 1. Conversely, larger L decreases robustness against CFO in non-differentially modulated sequences, according to Table 2.

Table 1. BCM table for typical LEO parameters, diff. modulated PN-seq.

$\mathit{\gamma }$ [dB]	L	W	$\mathit{B}\mathit{C}\mathit{M}$	${\mathit{T}}_{\mathit{B}\mathit{C}\mathit{M}}$
−8	1027	4	$2·{10}^{-3}$	0.006
−8	2051	4	$1·{10}^{-5}$	0.006
−5	1027	4	$3·{10}^{-8}$	0.02
−5	519	8	$1·{10}^{-4}$	0.02
−5	515	4	$1·{10}^{-4}$	0.02
−3	263	8	$1·{10}^{-4}$	0.03
−3	259	4	$9·{10}^{-5}$	0.04
−3	519	8	$2·{10}^{-8}$	0.03
−3	515	4	$1·{10}^{-8}$	0.03
0	135	8	$7·{10}^{-6}$	0.08
0	131	4	$5·{10}^{-6}$	0.08
3	67	4	$7·{10}^{-6}$	0.19

Table 2. BCM table for typical LEO parameters, CAZAC and PN Seq.

$\mathit{\gamma }$ [dB]	L	CFO	$\mathit{B}\mathit{C}\mathit{M}$	${\mathit{T}}_{\mathit{B}\mathit{C}\mathit{M}}$
−13	1023	$4·{10}^{-4}$	$3·{10}^{-4}$	0.01
−13	1023	$1·{10}^{-4}$	$1·{10}^{-7}$	0.01
−13	1023	$1·{10}^{-5}$	$5·{10}^{-8}$	0.01
−8	511	$1·{10}^{-3}$	$1·{10}^{-4}$	0.02
−8	511	$1·{10}^{-5}$	$1·{10}^{-8}$	0.04
−8	255	$1·{10}^{-3}$	$1·{10}^{-4}$	0.03
−8	255	$1·{10}^{-5}$	$2·{10}^{-5}$	0.04
−5	255	$2·{10}^{-3}$	$3·{10}^{-4}$	0.03
−5	255	$1·{10}^{-3}$	$2·{10}^{-7}$	0.06
−5	127	$3·{10}^{-3}$	$2·{10}^{-3}$	0.05
−5	127	$1·{10}^{-3}$	$7·{10}^{-5}$	0.08
−3	127	$5·{10}^{-3}$	$3·{10}^{-2}$	0.03
−3	127	$1·{10}^{-3}$	$1·{10}^{-6}$	0.10
−3	100	$1·{10}^{-3}$	$2·{10}^{-5}$	0.11
−3	100	$1·{10}^{-4}$	$1·{10}^{-5}$	0.11
0	63	$5·{10}^{-3}$	$2·{10}^{-4}$	0.14
0	63	$1·{10}^{-3}$	$5·{10}^{-6}$	0.18
0	63	$1·{10}^{-4}$	$3·{10}^{-6}$	0.18

7. Conclusions

In this article, we derived the PDF of the cross-correlation metric for different preamble types in burst traffic radio systems. We are able to show that the standard Ricean PDF assumption should not be used for differentially encoded PN sequences. In addition, we are able to show that the AGC will have a considerable impact on the PDF shape, which further limits the usage of the Ricean PDF. As an alternative, we derived a PDF in the form of a series expansion that covers most of the practical use cases: high CFO, different preamble types, inaccurate AGC, and arbitrary SNR. We illustrate how to perform ROC calculations through a newly introduced concept of BCM—best common metric. BCM can be used to map the entire ROC curves to one single performance value, simplifying threshold optimization in burst traffic systems.