Hybrid Wavelet–CNN Fault Diagnosis Method for Ships’ Power Systems
Abstract
:1. Introduction
2. Related Works
3. System Description
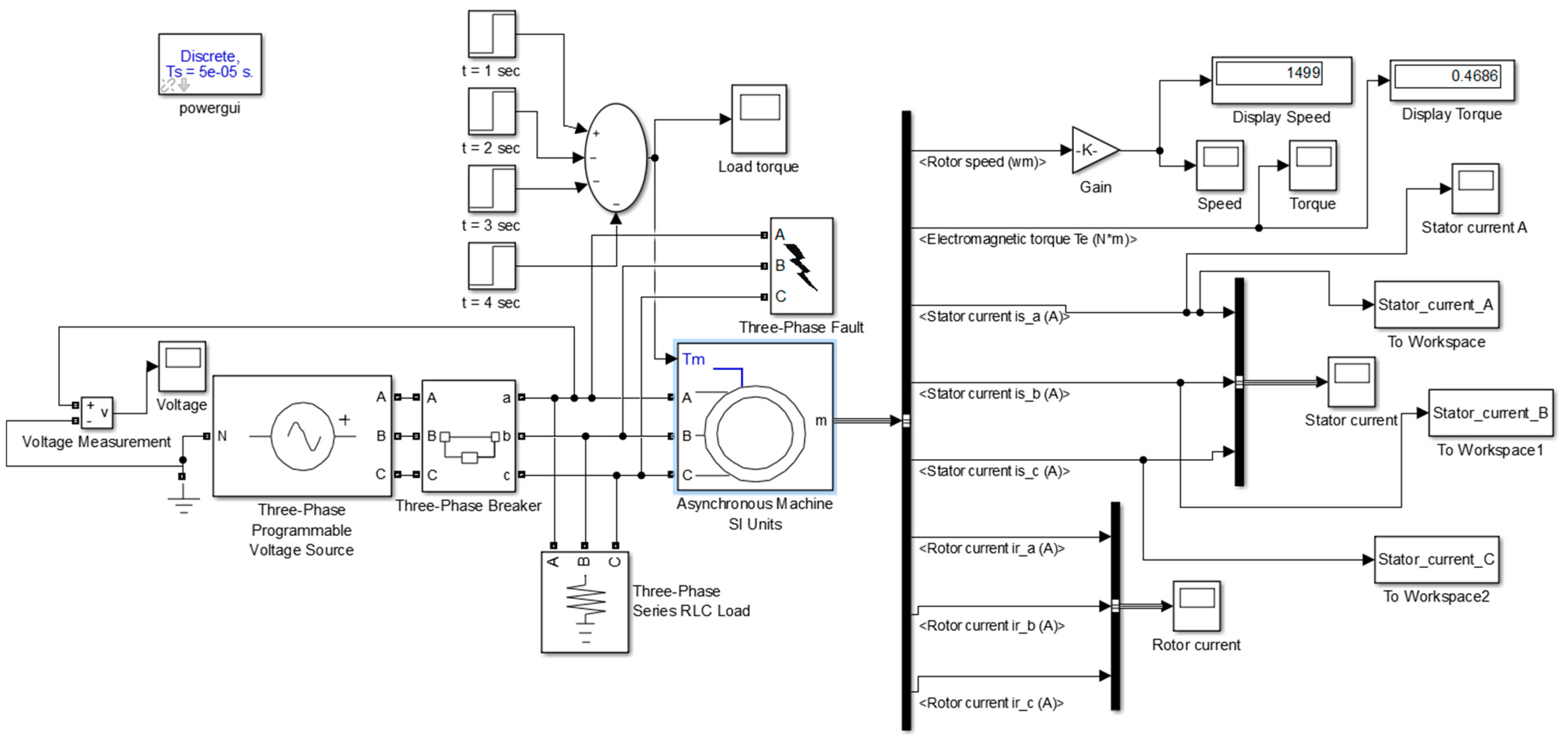
3.1. Description of Simulation Model
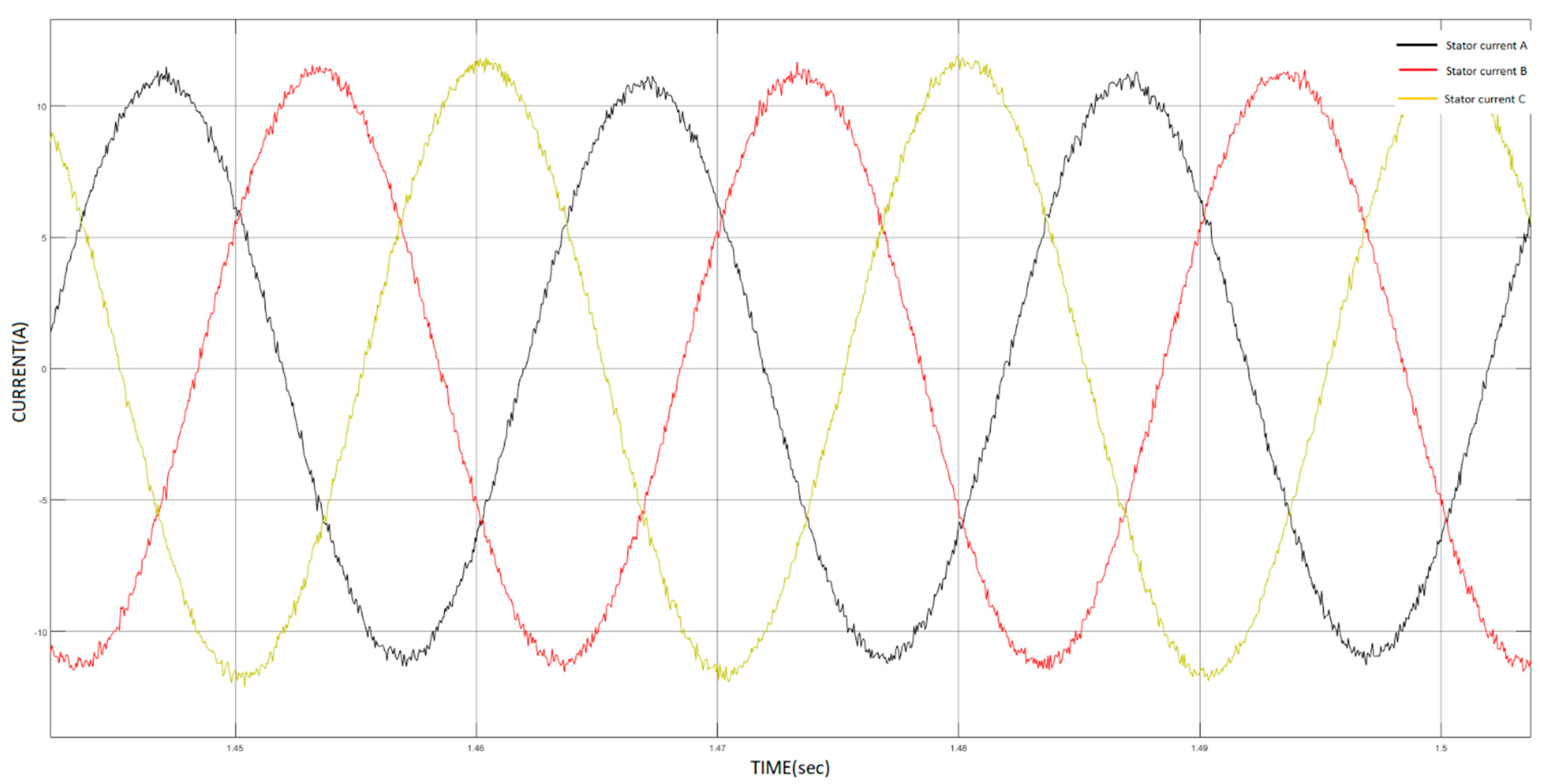
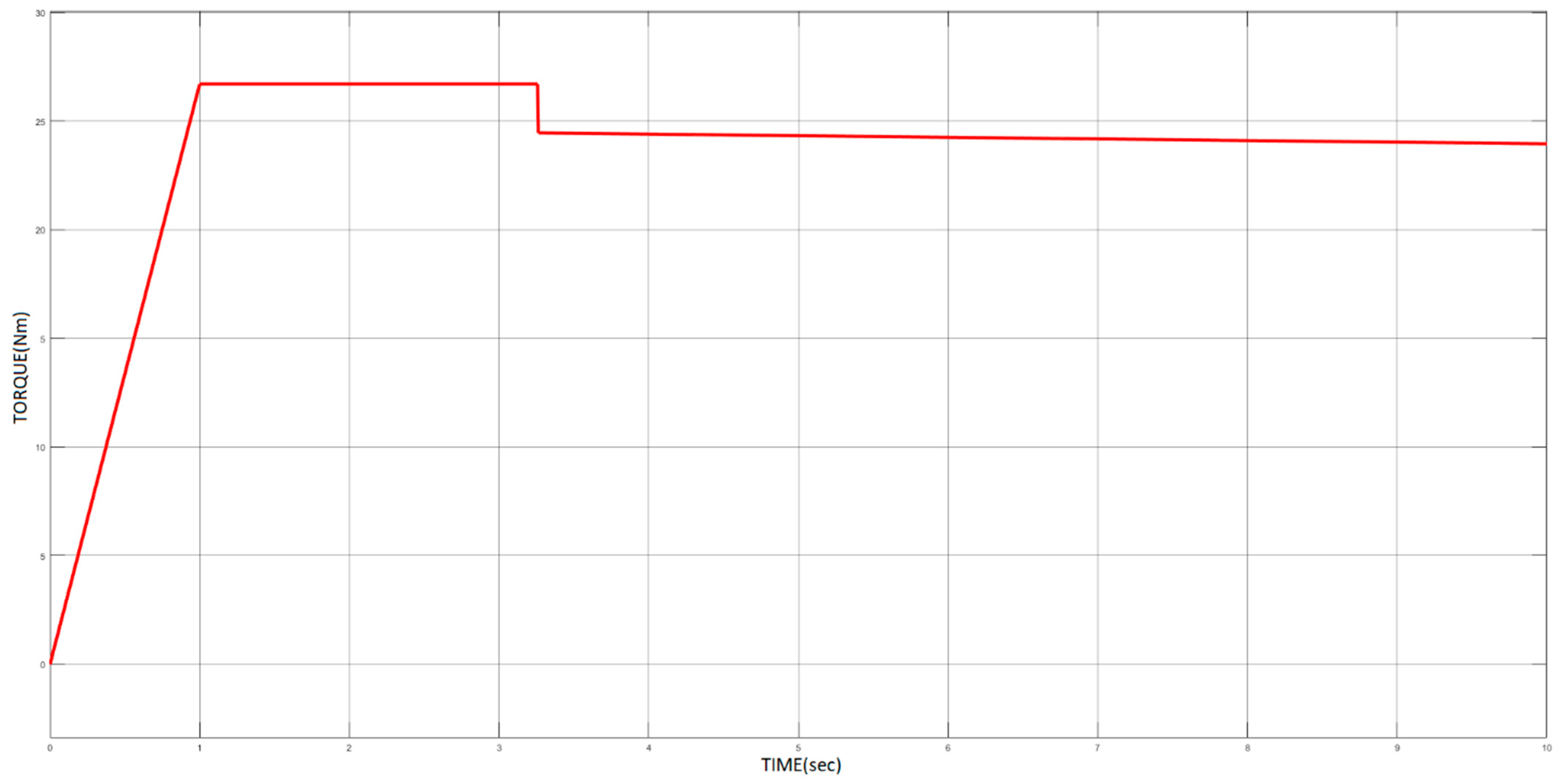
3.2. Running the Simulation
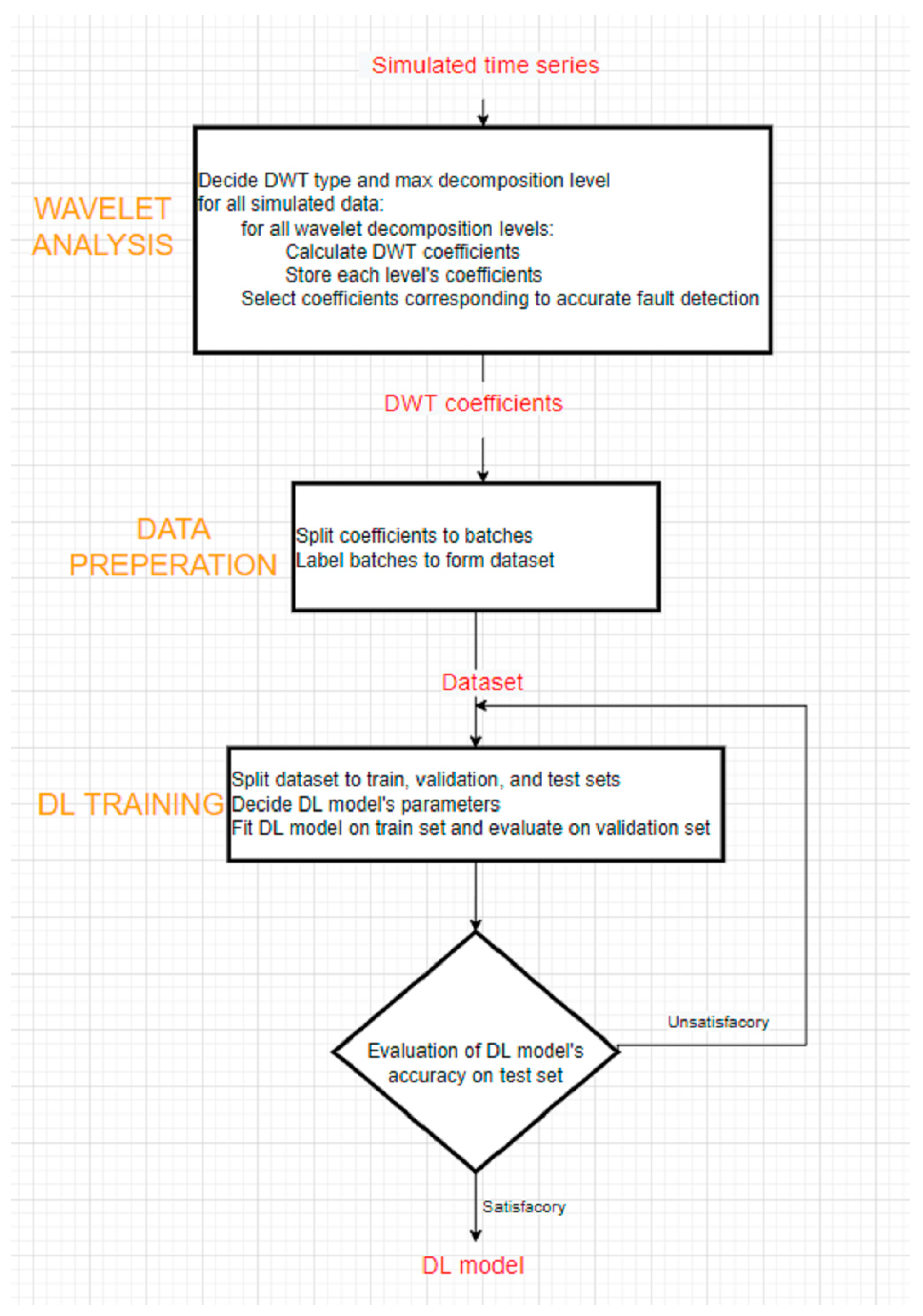
4. Research Methodology
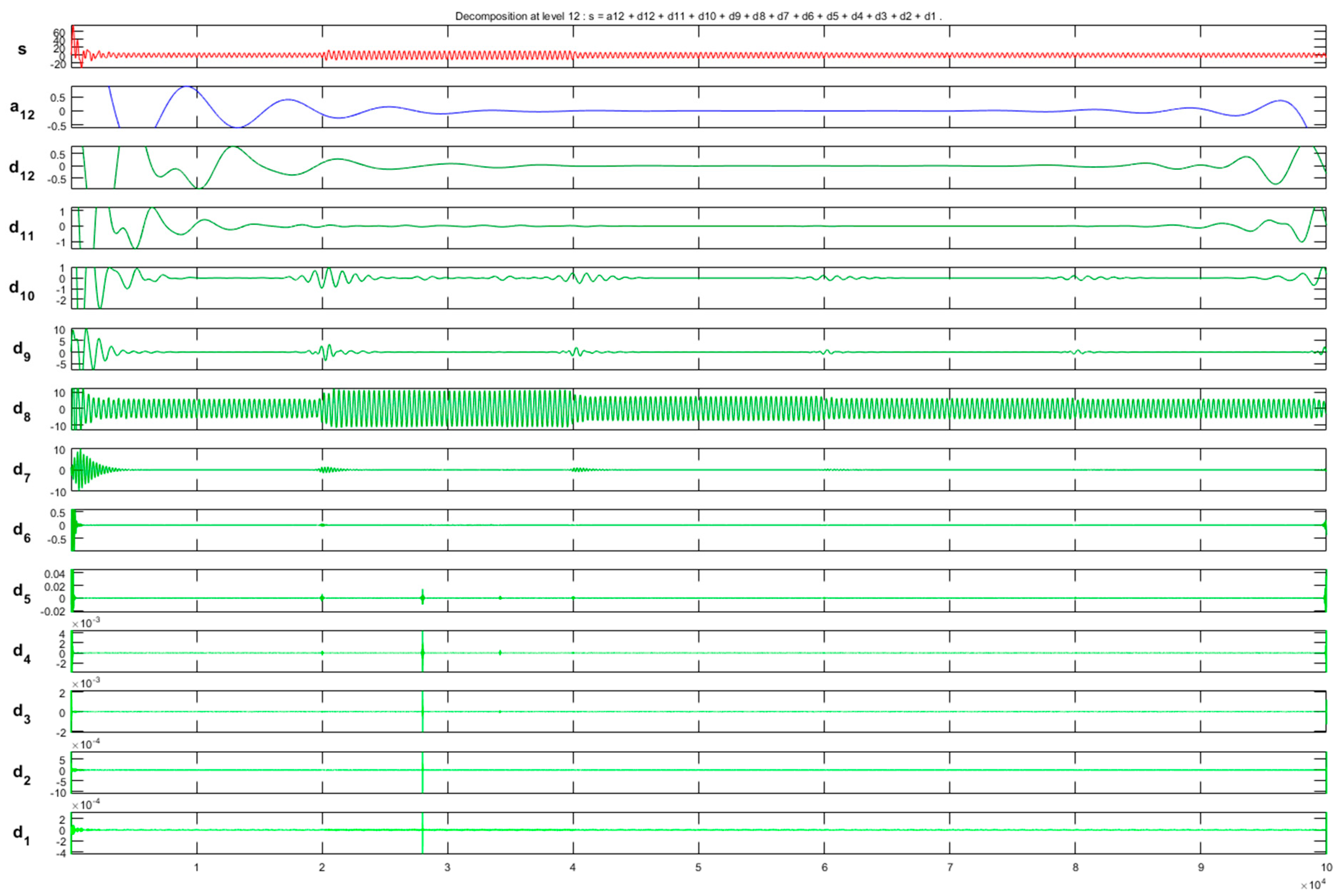
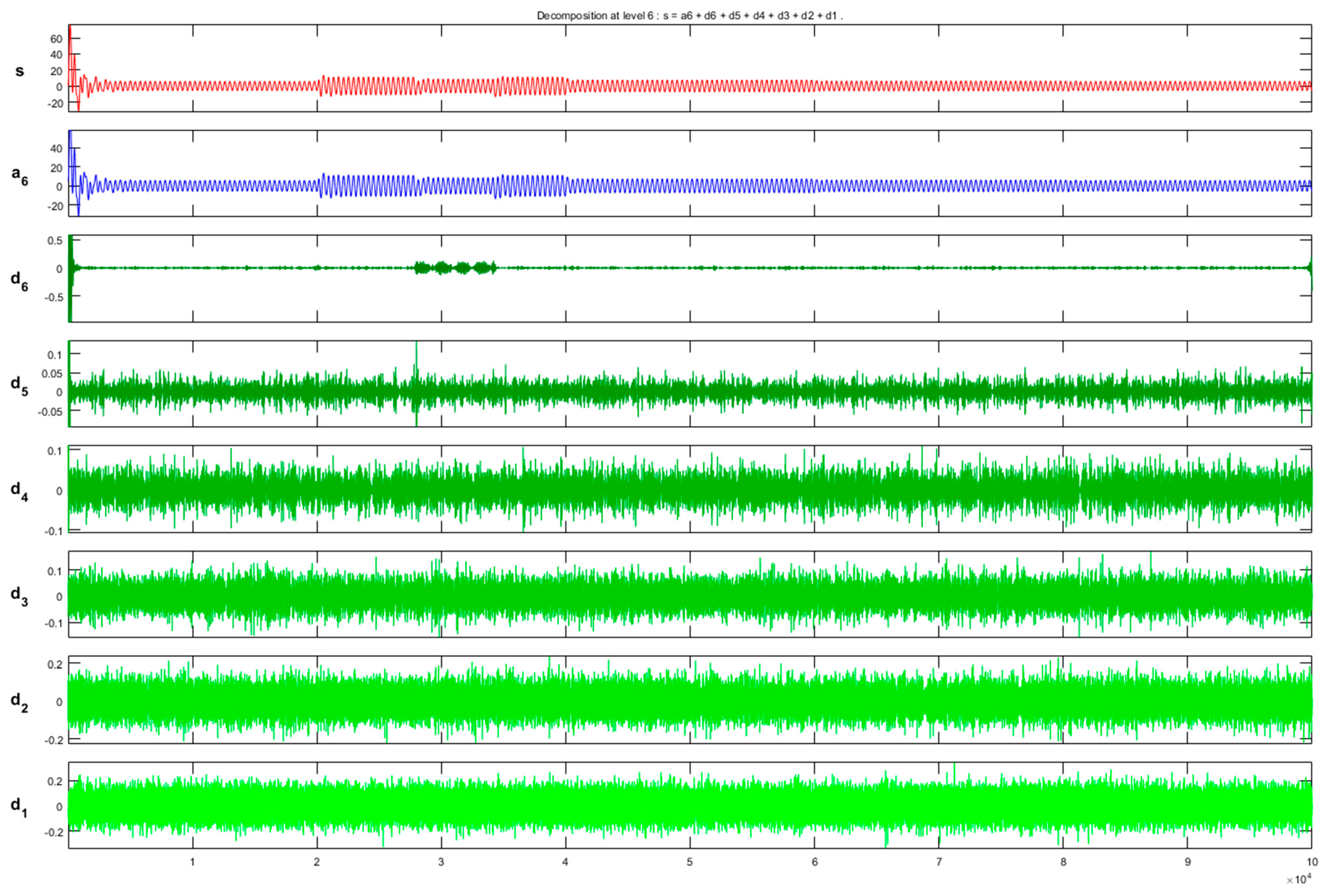
4.1. Discrete Wavelet Analysis
4.2. Convolutional Neural Networks
4.3. Hybrid Discrete Wavelet–CNN Method
5. Results
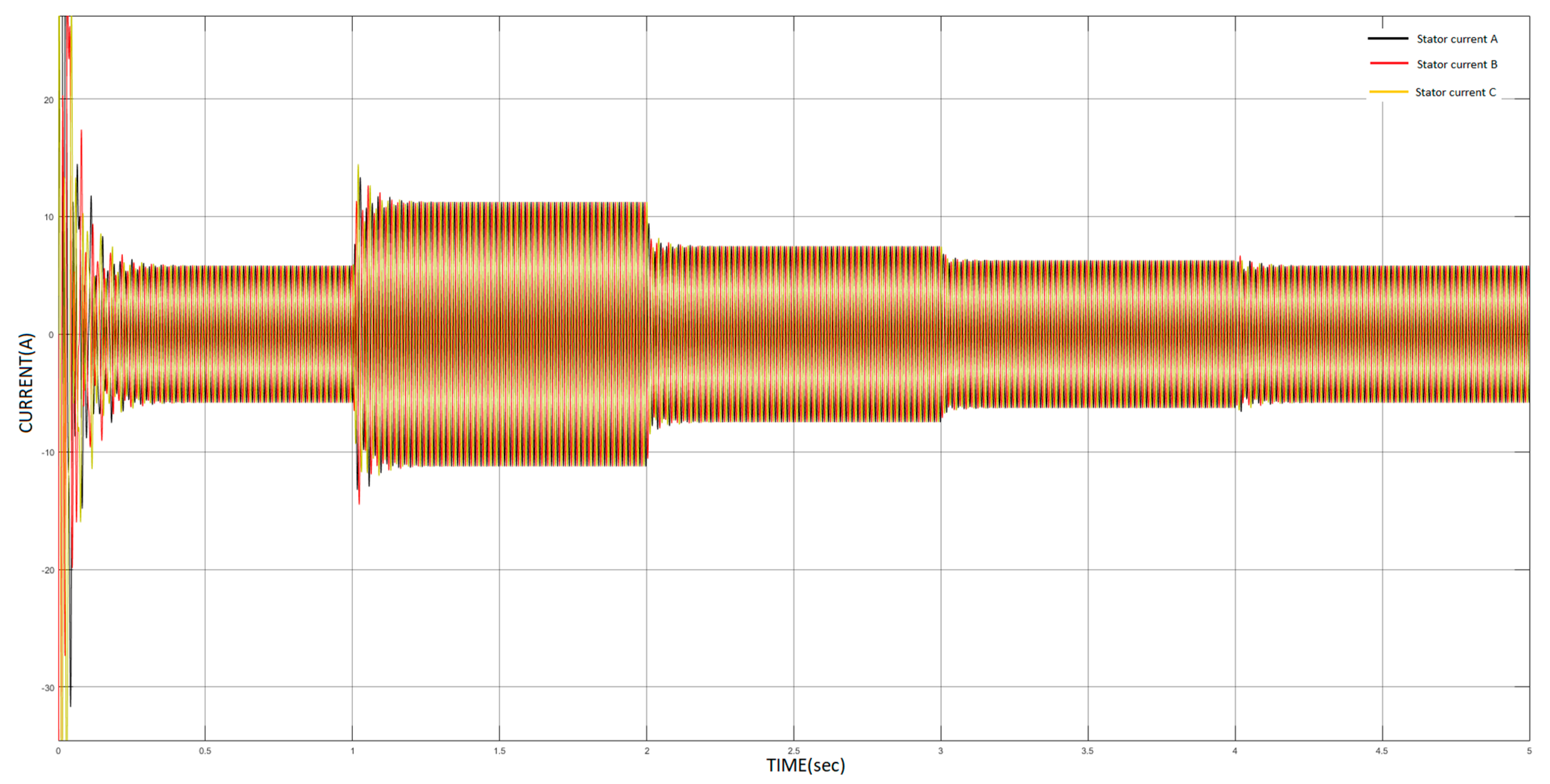
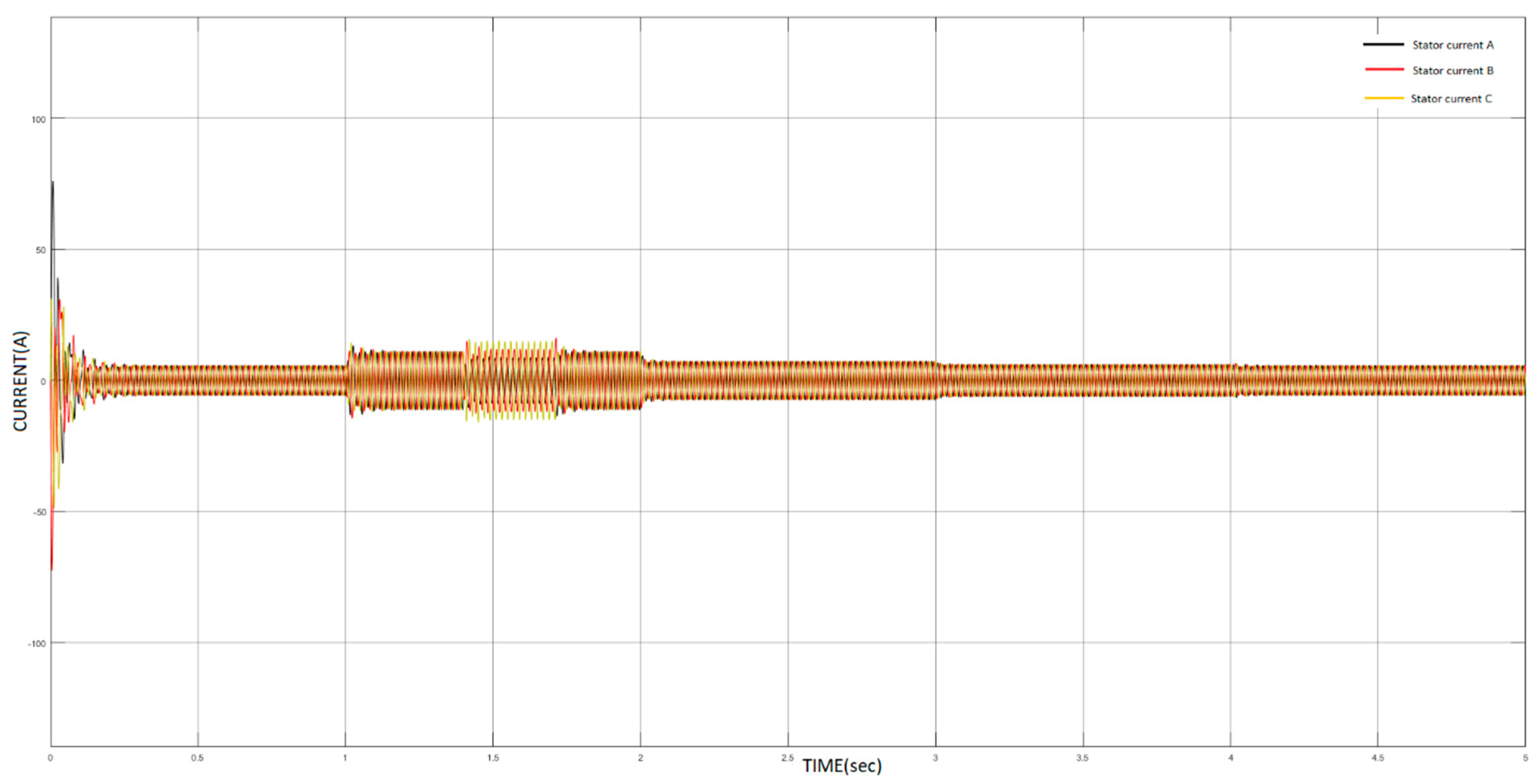
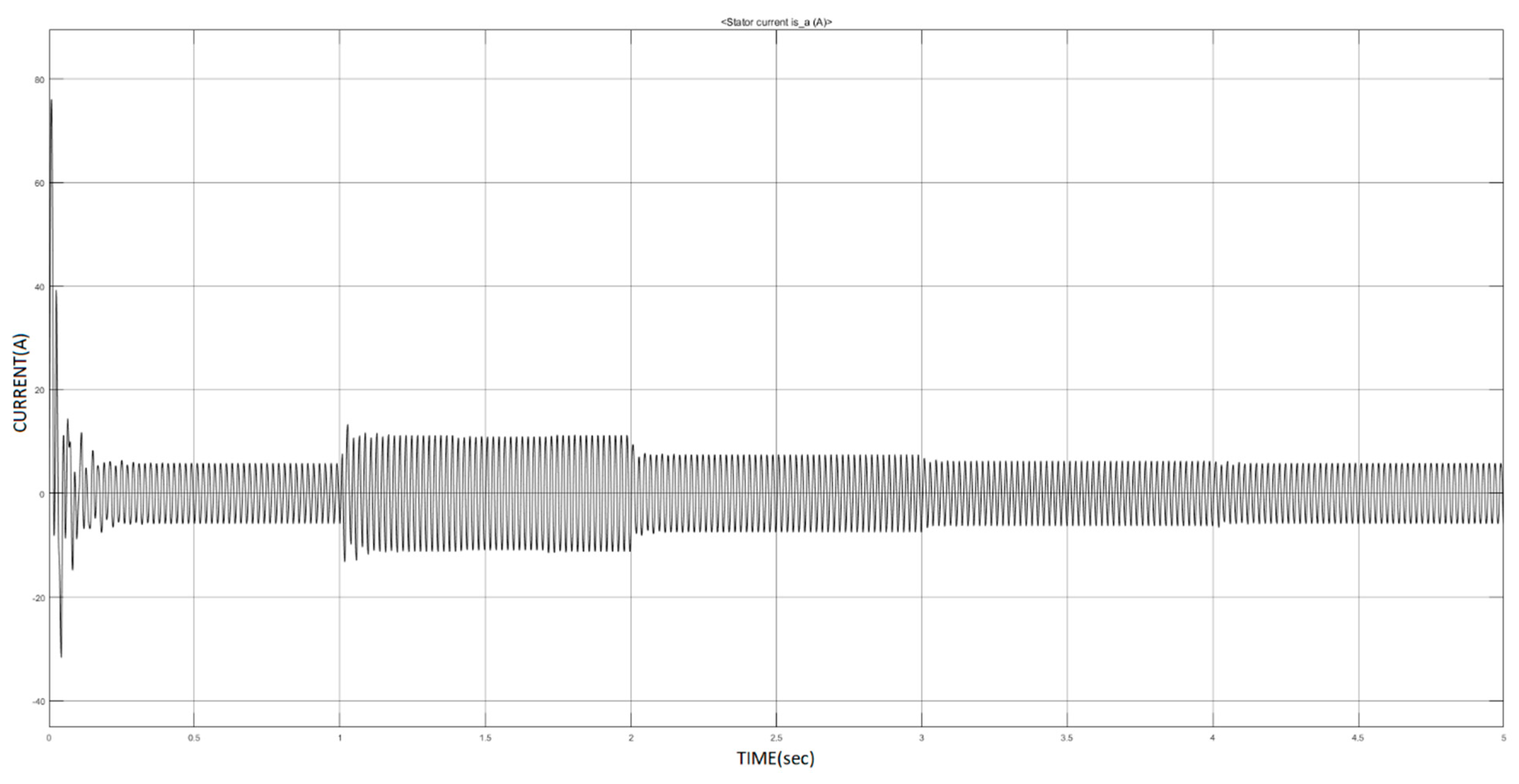
5.1. Descriptive Analysis
5.2. Hybrid Discrete Wavelet–CNN Model
5.2.1. Training Parameters
- Epochs = 100.
- Batch size = 4.
- Learning rate = 0.001.
- Optimizer = ADAM.
- Dataset split = 70%, 15%, 15%.
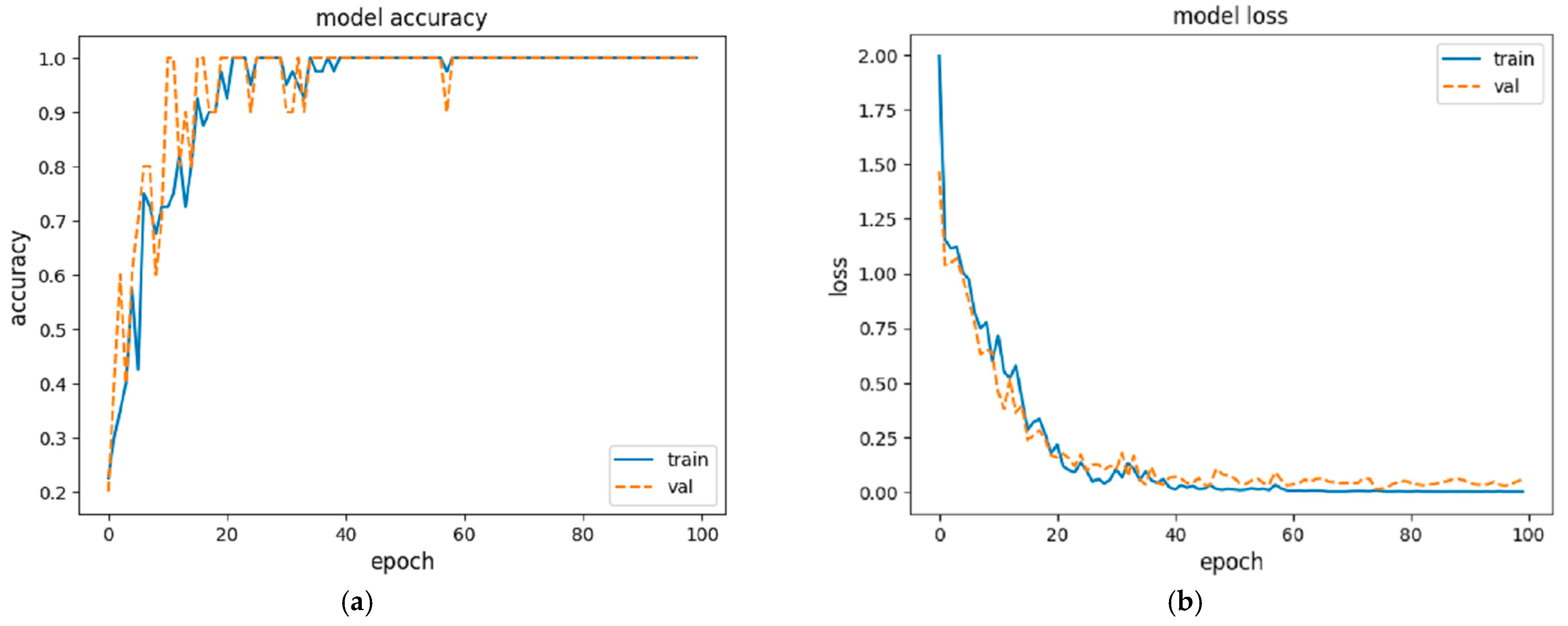
5.2.2. Results
5.3. Discussion
6. Conclusions
- It can automatically and effectively classify faults related to short circuits even in indistinguishable cases where white noise and load changes occur.
- It can drastically reduce both the training time and the data volume employed for training the neural network while maintaining competitive accuracy. Therefore, the proposed method could be considered a data compression method as well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Albrecht, P.F.; Appiarius, J.C.; McCoy, R.M.; Owen, E.L.; Sharma, D.K. Assessment of the Reliability of Motors in Utility Applications—Updated. IEEE Power Eng. Rev. 1986, PER-6, 31–32. [Google Scholar] [CrossRef]
- Singh, G.K.; Al Kazzaz, S.A.S. Induction machine drive condition monitoring and diagnostic research—A survey. Electr. Power Syst. Res. 2003, 64, 145–158. [Google Scholar] [CrossRef]
- Karmakar, S.; Chattopadhyay, S.; Mitra, M.; Sengupta, S. Induction Motor and Faults. In Induction Motor Fault Diagnosis. Power Systems; Springer: Singapore, 2016; pp. 7–28. [Google Scholar] [CrossRef]
- Mortazavizadeh, S. A Review on Condition Monitoring and Diagnostic Techniques of Rotating Electrical Machines. Phys. Sci. Int. J. 2014, 4, 310–338. [Google Scholar] [CrossRef]
- Laamari, Y.; Allaoui, S.; Bendaikha, A.; Saad, S. Fault Detection Between Stator Windings Turns of Permanent Magnet Synchronous Motor Based on Torque and Stator-Current Analysis Using FFT and Discrete Wavelet Transform. Math. Model. Eng. Probl. 2021, 8, 315–322. [Google Scholar] [CrossRef]
- Theodoropoulos, P.; Spandonidis, C.C.; Fassois, S. Use of Convolutional Neural Networks for vessel performance optimization and safety enhancement. Ocean Eng. 2022, 248, 110771. [Google Scholar] [CrossRef]
- Spandonidis, C.; Theodoropoulos, P.; Giannopoulos, F.; Galiatsatos, N.; Petsa, A. Evaluation of deep learning approaches for oil & gas pipeline leak detection using wireless sensor networks. Eng. Appl. Artif. Intell. 2022, 113, 104890. [Google Scholar] [CrossRef]
- Theodoropoulos, P.; Spandonidis, C.C.; Giannopoulos, F.; Fassois, S. A Deep Learning-Based Fault Detection Model for Optimization of Shipping Operations and Enhancement of Maritime Safety. Sensors 2021, 21, 5658. [Google Scholar] [CrossRef]
- Jayaswal, P.; Wadhwani, A.K. Application of artificial neural networks, fuzzy logic and wavelet transform in fault diagnosis via vibration signal analysis: A review. Aust. J. Mech. Eng. 2009, 7, 157–171. [Google Scholar] [CrossRef]
- Verma, A.K.; Nagpal, S.; Desai, A.; Sudha, R. An efficient neural-network model for real-time fault detection in industrial machine. Neural Comput. Appl. 2021, 33, 1297–1310. [Google Scholar] [CrossRef]
- Duan, L.; Hu, J.; Zhao, G.; Chen, K.; Wang, S.X.; He, J. Method of inter-turn fault detection for next-generation smart transformers based on deep learning algorithm. High Volt. 2019, 4, 282–291. [Google Scholar] [CrossRef]
- Ashfaq, H.; Quadri, M.N. Fault Current Detection of Three Phase Power Transformer Using Wavelet Transform. J. Eng. Res. Appl. 2013, 3, 1444–1454. [Google Scholar]
- Hussain, M.; Soother, D.K.; Kalwar, I.H.; Memon, T.D.; Memon, Z.A.; Nisar, K.; Chowdhry, B.S. Stator winding fault detection and classification in three-phase induction motor. Intell. Autom. Soft Comput. 2021, 29, 869–883. [Google Scholar] [CrossRef]
- Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, J.; Duan, L.; Cheng, W. A multi-scale convolution neural network for featureless fault diagnosis. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 65–70. [Google Scholar] [CrossRef]
- Agrawal, P.; Jayaswal, P. Diagnosis and Classifications of Bearing Faults Using Artificial Neural Network and Support Vector Machine. J. Inst. Eng. Ser. C 2020, 101, 61–72. [Google Scholar] [CrossRef]
- Yan, X.; She, D.; Xu, Y. Deep order-wavelet convolutional variational autoencoder for fault identification of rolling bearing under fluctuating speed conditions. Expert Syst. Appl. 2023, 216, 119479. [Google Scholar] [CrossRef]
- Attallah, O.; Ibrahim, R.A.; Zakzouk, N.E. Fault diagnosis for induction generator-based wind turbine using ensemble deep learning techniques. Energy Rep. 2022, 8, 12787–12798. [Google Scholar] [CrossRef]
- Mansour, R.F.; Alabdulkreem, E.; Eid, H.F.; K, S.; Khan, M.A.R.; Kumar, A. Fuzzy logic based on-line fault detection and classification method of substation equipment based on convolutional probabilistic neural network with discrete wavelet transform and fuzzy interference. Optik 2022, 270, 169956. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault identification of hydraulic pump using deep adaptive normalized CNN and synchrosqueezed wavelet transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Othman, M.M.; Alrifaey, M.; Bo, R.; Ang, C.K. Classification of faults in grid-connected photovoltaic system based on wavelet packet transform and an equilibrium optimization algorithm-extreme learning machine. Meas. J. Int. Meas. Confed. 2022, 197, 111338. [Google Scholar] [CrossRef]
- Allan, O.A.; Morsi, W.G. A new passive islanding detection approach using wavelets and deep learning for grid-connected photovoltaic systems. Electr. Power Syst. Res. 2021, 199, 107437. [Google Scholar] [CrossRef]
- Venkatesh, S.N.; Jeyavadhanam, B.R.; Sizkouhi, A.M.; Esmailifar, S.; Aghaei, M.; Sugumaran, V. Automatic detection of visual faults on photovoltaic modules using deep ensemble learning network. Energy Rep. 2022, 8, 14382–14395. [Google Scholar] [CrossRef]
- Esfetanaj, N.N.; Nojavan, S. The Use of Hybrid Neural Networks, Wavelet Transform and Heuristic Algorithm of WIPSO in Smart Grids to Improve Short-Term Prediction of Load, Solar Power, and Wind Energy. In Operation of Distributed Energy Resources in Smart Distribution Networks; Elsevier: Amsterdam, The Netherlands, 2018; pp. 75–100. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A Review of Wavelet Analysis and Its Applications: Challenges and Opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Cordeiro, J.R.; Raimundo, A.; Postolache, O.; Sebastião, P. Neural Architecture Search for 1D CNNs—Different Approaches Tests and Measurements. Sensors 2021, 21, 7990. [Google Scholar] [CrossRef]

| Block Name | Parameter | Value |
|---|---|---|
| Three-phase squirrel-cage IM (4 kW, 400 V, 50 Hz, 1430 rpm) | Stator resistance | 1.4050 Ω |
| Rotor resistance | 1.3590 Ω | |
| Stator inductance | 0.005839 H | |
| Rotor inductance | 0.005839 H | |
| Pole pairs | 2 | |
| Friction factor | 0.002985 N m s | |
| Inertia | 0.0131 J/kg m² | |
| Mutual Inductance | 0.1722 H | |
| Three-phase block of fault | Fault resistance | 0.1 Ω |
| Ground resistance | 0.01 Ω | |
| Snubber resistance | 106 Ω |
| Duration (s) | Load Torque (Nm) | Rotational Speed (rpm) |
|---|---|---|
| 0–1 | 0 | 1499 |
| 1–2 | 26.72 | 1434 |
| 2–3 | 13.36 | 1468 |
| 3–4 | 6.68 | 1484 |
| 4–5 | 0 | 1499 |
| Threshold | d5 | Many d | Indistinguishable | Unrecognizable |
|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
| Phase A | Phase B | Phase C |
|---|---|---|
| 0.01137 | 0.012 | 0.019 |
| Monitoring Parameter | Type | Intensity R (Ω) | Level |
|---|---|---|---|
| Current of Phase A | A–B | 0.1 | 1 |
| A–G | 0.1 | 1 | |
| A–C | 0.1 | 1 | |
| B–C | 0.1 | 2 | |
| B–G | 0.1 | 1 | |
| C–G | 0.1 | 1 | |
| A–B | 1.0 | 1 | |
| A–G | 1.0 | 3 | |
| A–B | 5.0 | 3 | |
| A–G | 5.0 | 4 | |
| Current of Phase B | A–B | 0.1 | 1 |
| A–G | 0.1 | 1 | |
| A–C | 0.1 | 3 | |
| B–C | 0.1 | 1 | |
| B–G | 0.1 | 1 | |
| C–G | 0.1 | 1 | |
| A–B | 1.0 | 1 | |
| A–G | 1.0 | 5 | |
| A–B | 5.0 | 3 | |
| A–G | 5.0 | 5 | |
| Current of Phase C | A–B | 0.1 | 3 |
| A–G | 0.1 | 3 | |
| A–C | 0.1 | 1 | |
| B–C | 0.1 | 1 | |
| B–G | 0.1 | 1 | |
| C–G | 0.1 | 1 | |
| A–B | 1.0 | 5 | |
| A–G | 1.0 | 4 | |
| A–B | 5.0 | 5 | |
| A–G | 5.0 | 5 |
| Monitoring Parameter | Type | Intensity R (Ω) | Level |
|---|---|---|---|
| Current of Phase A | A–B | 0.1 | 1 |
| A–G | 0.1 | 1 | |
| Current of Phase B | A–B | 0.1 | 1 |
| A–G | 0.1 | 3 | |
| Current of Phase C | A–B | 0.1 | 3 |
| A–G | 0.1 | 3 |
| Monitoring Parameter | Type | Intensity R (Ω) | Level |
|---|---|---|---|
| Current of Phase A | A–B | 0.1 | 1 |
| A–G | 0.1 | 4 | |
| Current of Phase B | A–B | 0.1 | 1 |
| A–G | 0.1 | 5 | |
| Current of Phase C | A–B | 0.1 | 4 |
| A–G | 0.1 | 4 |
| Monitoring Parameter | Type | Intensity R (Ω) | Level |
|---|---|---|---|
| Current of Phase A | A–B | 5.0 | 2 |
| A–G | 5.0 | 4 | |
| Current of Phase B | A–B | 5.0 | 3 |
| A–G | 5.0 | 5 | |
| Current of Phase C | A–B | 5.0 | 5 |
| A–G | 5.0 | 4 |
| Monitoring Parameter | Type | Intensity R (Ω) | Level |
|---|---|---|---|
| Current of Phase A | A–B | 0.1 | 1 |
| A–G | 0.1 | 3 | |
| Current of Phase B | A–B | 0.1 | 1 |
| A–G | 0.1 | 3 | |
| Current of Phase C | A–B | 0.1 | 3 |
| A–G | 0.1 | 4 |
| Layer | Number | Parameters |
|---|---|---|
| Conv1D | 2 | Filters = 64, kernel size = 3, activation = ReLU. |
| Dropout | 1 | Rate = 0.5. |
| MaxPooling1D | 1 | Pool size = 2. |
| Flatten Dense 1 | 1 1 | - Units = 100, activation = ReLU. |
| Dense 2 | 1 | Units = 3, activation = softmax. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paraskevopoulos, D.; Spandonidis, C.; Giannopoulos, F. Hybrid Wavelet–CNN Fault Diagnosis Method for Ships’ Power Systems. Signals 2023, 4, 150-166. https://doi.org/10.3390/signals4010008
Paraskevopoulos D, Spandonidis C, Giannopoulos F. Hybrid Wavelet–CNN Fault Diagnosis Method for Ships’ Power Systems. Signals. 2023; 4(1):150-166. https://doi.org/10.3390/signals4010008
Chicago/Turabian StyleParaskevopoulos, Dimitrios, Christos Spandonidis, and Fotis Giannopoulos. 2023. "Hybrid Wavelet–CNN Fault Diagnosis Method for Ships’ Power Systems" Signals 4, no. 1: 150-166. https://doi.org/10.3390/signals4010008
APA StyleParaskevopoulos, D., Spandonidis, C., & Giannopoulos, F. (2023). Hybrid Wavelet–CNN Fault Diagnosis Method for Ships’ Power Systems. Signals, 4(1), 150-166. https://doi.org/10.3390/signals4010008






