Abstract
The Fokas method (also known as the unified transform method) is used to investigate acoustic scattering by thin, infinite grating by extending the methodology to apply to spatially periodic domains. Infinite grating is used to model a perforated screen, a material of interest in aeroacoustics and noise reduction. Once the method is established, its numerical results are verified against the Wiener–Hopf (WH) technique, which has solved the problem only for a special case. A key benefit of the novel approach is that the scatterer, modelled as an infinitely repeating unit cell consisting of a thin, rigid plate, can take any length. This is in contrast to the WH method, where the plate length is restricted to half the width of the unit cell (for this method, no such restriction exists). The numerical method is an over-sampled collocation method of the integral equation resulting from applying the Fokas method: the global relation. The only increase in complexity in adapting the Fokas method to more complicated cell geometries is a higher number of terms in the global relation. The proportion of energy transmitted and reflected by the grating structure is assessed for varying incident wave angles, frequencies, and plate lengths.
1. Introduction
Acoustic scattering by periodic gratings is motivated, in part, by an interest in manipulating noise emission from turbulence–structure interactions. For example, turbulence–aerofoil interaction noise is a large contributor to overall broadband jet noise and environmental sound pollution concerns [1]. Some engineering research aims to investigate the properties of fluid structures and whether they may be specially chosen to reduce noise production, creating novel devices known as metamaterials. These artificial materials are engineered to perform a highly specific function. Acoustic metamaterials are inspired by photonic crystals and are designed to control sound waves by manipulating parameters of the medium or boundary, such as densities, permeabilities, and pressure differences [2,3] in order to achieve desired effects. The effect explored in this work is the ability to redirect or trap sound waves within a structure, leading to the possession of band gaps to act as filters for certain frequencies of sound [4,5]. Moreover, experimental work has shown that the introduction of porosity in otherwise rigid surfaces decreases sound propagation into the far field [6,7,8]. Overall, this forms the basis of this work’s mathematical interest in acoustic scattering by infinite, periodic arrays of screens (a grating in two dimensions) of varying lengths and spacings.
Acoustic scattering, governed by the Helmholtz equation,
an equation for the time-harmonic acoustic pressure p, has a rich literature for both analytical and numerical advances. Gratings, which in this work are understood to be permeable structures, give rise to mixed boundary value problems (BVPs), where the boundary condition changes discontinuously to that of the material (for example, zero-normal velocity on a rigid surface) to a continuity condition across the zero-streamline. A famous example of a mixed BVP in acoustic scattering is the Sommerfeld half-plane diffraction problem [9]. Here, there is only one point at which the boundary condition changes; therefore, the exact solution is achieved using the Wiener–Hopf (WH) technique [10]. This method has formed the standard for acoustic scattering problems using complex methods. Another closely related family of problems involve acoustic wedge diffraction [11]. These also involve scattering by faces where the boundary condition may change at the corner and are applicable to both acoustic and elastic waves [12,13].
In situations where there are multiple points at which the boundary condition changes, the WH method produces a matrix equation for which a desired matrix factorisation is often difficult to compute. Indeed, for perforated screen grating (for which there are infinitely many such points), the WH method is applied by reducing it to a periodic problem formulated in a unit cell and produces a matrix equation [14,15], for which a closed-form analytic expression of the matrix factorisation is only found when the plate length and the gap length (the spacing between two neighbouring plates) are equal. As well as the method being difficult to generalise for differing ratios of hole size and spacing, if we were to consider gratings with, say, multiple holes of different sizes within one period window, the dimension of the matrix Wiener–Hopf equation would only grow larger and even more difficult to wield. This lack of easy generalisability to more boundary conditions prompts us to explore alternative methods.
Another classical family of techniques popular in fluid dynamics are boundary element methods (BEMs). These are robust in that they are compatible with many kinds of boundaries, particularly those exhibiting mixed boundary conditions. The solution to the boundary-value problem (BVP) is expressed in terms of a boundary integral equation (BIE) via Green’s identities. This reduces the problem to that of the values of the solution and its normal derivative only on the boundaries of the domain, that is, its Dirichlet and Neumann values, respectively. Often, as only one of these values is known a priori, the bulk of the problem is shifted to finding a suitable Dirichlet-to-Neumann (DtN) map, for which there is currently no general procedure and is specific to the problem. A semi-analytical BEM was developed in [16] for two-dimensional infinite grating. The quasi-periodic Green’s function was computed using images as an infinite sum of point sources. As is typical for BEMs, a singular integral equation is formed for the unknown jump in the solution across the rigid screen, which is solved using a polynomial expansion. This technique also extends into three dimensions [17].
The approach put forth in this work is related to the above boundary integral methods, providing an analogue of their procedures in spectral space. In this sense, it can be seen as a fusion of Fourier transform methods (of which the WH method is based) and Green’s identity representations. The method, based on the unified transform method (commonly also known as the Fokas method [18]), produces a BIE in spectral space linking the Dirichlet and Neumann values of the solution, giving an alternative characterisation of the DtN map. Hence, this paper serves as an extension of the Fokas method to spatially periodic domains with mixed boundary conditions. For periodic rough surfaces, i.e., surfaces described by a continuous periodic function, a similar method was developed independently, with these problems being discussed in [19,20,21,22]. Moreover, an extensive review of acoustic scattering in continuous periodic media is available in [23]. The main novelty put forth in this work is that the periodic surface considered here has discontinuous boundary conditions, allowing it to be modelled as a perforated screen. Therefore, sharp-edge diffraction must be accounted for at the point where the boundary condition changes from Neumann (the plate condition) to Dirichlet (a continuity condition).
The Fokas method is a novel boundary integral technique for solving integrable partial differential equations. It serves as a unified method for linear and non-linear initial-boundary value problems (IBVPs), with connections to multiple classical PDE techniques by its formulation of the so-called global relation, a spectral analogue of Green’s identity coupling transforms of known and unknown boundary values [24]. Literature specific to elliptic equations emerged in [25,26]. Certain simplifications are shown to arise when these equations are considered in convex polygons [27]. Numerical implementations of the method are successful, leading to solutions that achieve spectral accuracy [28,29,30]. Lastly, the Fokas method has shown promising results when applied to acoustic scattering problems in unbounded domains [31].
In this work, we focus on the application of the Fokas method’s global relation to the Helmholtz equation in two dimensions to the unit cell problem. While the canonical problem will be formulated under the assumption of a rigid screen, a large advantage of the Fokas method is its applicability to a large set of boundary conditions. The novel method, as an advantage over classical Green’s integral techniques, produces a non-singular integral equation in spectral space in terms of integral transforms of the known and unknown boundary data (the global relation). Analytically manipulating the global relation using symmetries of the domain (if they exist) allows one to then explicitly express the solution in terms of known boundary values only.
The layout of the rest of the paper is as follows. The grating problem is conceptualised, formally stated, and non-dimensionalised in Section 2 with a formulation in the unit cell. The radiation condition is discussed. In Section 3, the Fokas method for the Helmholtz equation is reviewed and applied to the grating problem. The global relations (that is, the integral equation coupling Dirichlet and Neumann boundary values of the scattered pressure) are derived and reduced to a single integral equation of two unknown equations. The discretisation of the spectral parameter is found in Section 3.2.2. In Section 4, the numerical method to approximately solve the integral equation is formulated, where it is reduced to an over-sampled linear system by approximating the unknown functions as series expansions in appropriate basis functions. The endpoint singularities are discussed. These approximate solutions are then fed back into Green’s integral representation in Section 5 to obtain an expression for the full pressure in the form of a modal decomposition. Lastly, results are plotted and discussed in Section 6.
2. Statement of the Diffraction Grating Problem
We consider a homogeneous acoustic medium in with sound speed and an infinite screen, perforated periodically, occupying the plane of in dimensional coordinates . Grating is represented by an infinite tessellation of a unit cell . In the cell, a rigid plate occupies , where . There is a pressure wave incident from above of the form , where is a wavenumber, is the angle of incidence, and is a constant with units of pressure. As this is a linear problem, the time-harmonic term is henceforth suppressed. The scattered acoustic pressure field, denoted as the total field with the incident wave subtracted, , satisfies the Helmholtz Equation (1) with along with the relevant boundary condition on the scattering surface.
In this paper, we assume the plate to be a sound-hard surface, but the method is not restricted by the choice of boundary condition. To ensure consistency with the periodicity of the domain, a periodicity condition is also imposed. Indeed, the incident wave satisfies . This quasi-periodicity condition is therefore inherited by and, by continuity, its x-derivative. Lastly, an appropriate radiation condition must be discussed. Because the scattering surface is of infinite extent in the -axis, the traditional two-dimensional Sommerfeld radiation condition does not hold; therefore, its one-dimensional variant is used instead. This is equivalent to the assumptions of Rayleigh [32], further expanded on by Kirsch [33], that state that any two-dimensional acoustic wave under such quasi-periodic conditions may be decomposed into a linear combination of incoming, outgoing, and evanescent plane waves in the form of Bloch modes [34]. This is the Rayleigh expansion radiation condition (RERC). Let be the dimensionalised Laplacian. The boundary-value problem satisfied by is described below.
Problem (2) is non-dimensionalised via a typical length L and typical pressure . Under this rescaling, the transformed unit cell has a width of 1 with a plate length of , as illustrated in Figure 1. The equivalent boundary-value problem for is
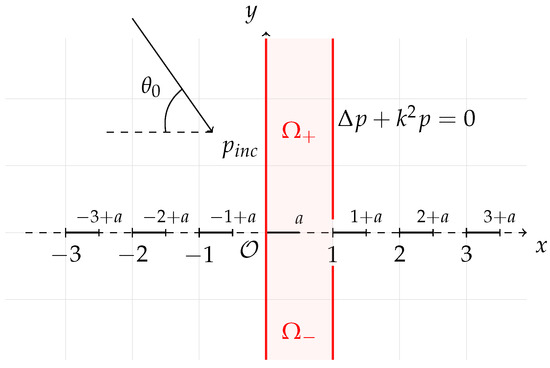
Figure 1.
Geometry of the non-dimensionalised problem (3). The wave is incident from above. Grating at consists of thin plates of length a spaced equally apart. The unit cell is the shaded region of unit width.
The non-dimensionalised incident wave is . In order to apply the Fokas method to the doubly-infinite unit cell, is split into convex subdomains [35]. The method is applied in each subdomain separately and recombined afterwards. The subdomains we will consider, as highlighted in Figure 1, are the upper and lower half-strips, and . In this grating problem, the boundary condition changes discontinuously from an inhomogeneous Neumann condition to a zero Dirichlet condition (from deducing the oddness of the scattered field). Implicitly imposing a finite pressure condition on the corners and 1, a sufficiently regular solution exists with a singularity no worse than the square root [35].
The RERC is imposed under this framework by requiring that, for sufficiently large y, the form for the scattered field p is as follows [33]:
where are arbitrary complex constants, , and such that . Hence, p is a linear combination of plane waves of wavenumber k, which all satisfy the same quasi-periodicity relation. The modes satisfying the inequality
are waves propagating to and are finitely many. All the other modes in the expansion are evanescent waves that decay exponentially and whose influence is not communicated to the far field.
3. The Fokas Method
3.1. Integral Formulation
In this subsection, we review the derivation of the global relation of the Fokas method, specific to the Helmholtz Equation (1) in the interior of a convex polygon . We start by applying Green’s second identity to p and v, where v is a solution to the adjoint equation (in this case, also the Helmholtz equation).
As per convention, is understood to be the derivative in the normal direction pointing outward from , and s is the arclength parametrisation of . The novelty of the Fokas method comes from the choice of v. Indeed, the ingenuity of the Fokas method comes from the choice of a particular solution v. Rather than a tailored Green’s function, we choose a one-parameter family of solutions of the form , where is a free parameter. Using this form for v in (6), we obtain the Cartesian coordinate global relation
where is the outward normal vector to . In the literature, the global relation (7) is also expressed in complex coordinates where it takes a simpler form. Indeed, for and , where the free parameter is replaced with an equivalent . Then, we obtain the following formulation of the global relation for the Helmholtz equation.
The above form for the global relation also comes with some restrictions for the domain. Strictly speaking, the convexity of is assumed to ensure the uniqueness of the novel integral representation [25] (or the “inverse transform”). However, it was shown in [28] that this is not a restrictive requirement. Non-convex domains may be considered without a large loss of numerical accuracy by decomposing the domain into convex sub-polygons and applying appropriate interface conditions on the artificial boundaries. A full algebraic detail of the derivation of the global relation, along with rigorous discussion on so-called fundamental k-forms relating to the following analysis, is available in [18] (Part III) and [36].
We remark that (8) represents many equations for any in the complex plane for bounded . For unbounded domains, is restricted to regions of the complex plane where the exponential takes the negative real part to ensure convergence of the integrals. Hence, the relation is valid for so that . The constraints on that produce a valid global relation are particularly important, as the numerical solution of the DtN map induced by the global relation relies on a (pseudo-) spectral collocation method [31]. Therefore, by choosing a subset of , we can extract a finite system for our unknown boundary value functions, and thus begins the procedure of solving the DtN map. Once the unknown boundary values are determined, either analytically or numerically, the full solution p in the interior of may then be found either by the classical solution formula via the associated fundamental solution, or the solution formula associated with the Fokas method itself.
3.2. Global Relation of the Unit Cell
3.2.1. Convex Decomposition
The global relation for the unit cell of the grating problem (3) is derived by decomposing the full domain into two half-strips, including with a shared boundary at , as depicted in Figure 1. Although, for this specific problem, the scattered field is known to be odd, the procedure is detailed in both halves of the strip to demonstrate the applicability of the method to problems where such symmetries do not exist.
We begin by applying the global relation (8) to the truncated upper half-strip , where is arbitrarily large. Explicitly, we have
The first term is the transform of the boundary values at , equivalently (with ). The second and third terms are the transforms of the boundary values for the vertical boundaries of the unit cell, corresponding to and , , respectively. Lastly, the fourth term is the transform of the boundary values at the artificial boundary , the contribution from which we will show tends to zero as . Indeed, substituting the RERC form for p into the final term, the quantity we are interested in is
Restricting consideration to such that provides exponential decay of all terms, regardless of whether the m-th mode of p is propagating or evanescent. This domain corresponds to
The unit circle may also be included by introducing dissipation to the system by writing , where is small and taken to zero at the end of the analysis. The equivalent analysis also applies to the global relation in the truncated lower half-strip , where the required constraint is now , i.e.,
This difference in the domains of validity of the global relations also highlights why the doubly infinite unit cell had to be decomposed in this way. Hence, for in the appropriate regions of the complex plane, we are able to take the limit, and we have the hlfollowing global relations for each half-strip:
In order to be able to combine the two global relations, they must be defined for the same values , requiring a procedure analogous to symmetry relations analysed in the classical unified transform method [18]. We note that the domains are symmetries of each other and related through the transform . Hence, applying this transform to one of the global relations will allow it to be valid in the opposing region. Before doing this, however, we exploited the periodicity of the problem to obtain a great simplification of the method.
3.2.2. Quasi-Periodic Collocation Points
In this subsection, a specific discretisation of parameters is found to impose upon global relations. Up to this point, the parameter is still free to be chosen as we wish, provided it is in the continuous regions for each integral equation. We fix the choice of as follows. First, we use the quasiperiodicity condition in (10a,b) so that the second and third integrals become one. The global relations read
We choose such that the prefactor of the second term vanishes. That is, we consider the global relation evaluated only for discrete values of , satisfying
Interestingly, we have the relation . This sequence for is multi-valued: solving the quadratic equation gives two values for each n. The choice of square root is fixed by considering the radiation condition and reconciling the points inside their respective domains for each global relation. Indeed, the corresponding representation for is
Denote to be the branch of that lies in and to be the branch of that lies in . Importantly, this means we have and . Imposing these sequences on our global relations (10a) and (10b), they simplify to the following equations:
The two global relations (13a,b) are now combined to produce a single integral equation to be solved. Firstly, we use the aforementioned symmetry transform to bring both integrals under consideration of the same discretisation of . Indeed, for , the reciprocal value is an element of the sequence and vice versa. Hence, we apply this map to the parameters in (13b) so that it equivalently reads
The sum of Equations (13a) and (14) is as follows:
where we now see the emergence of the important quantity , the pressure jump across . It now remains to separate the integration over the two intervals and , substitute the boundary conditions, and evaluate any known terms. We arrive at the final integral equation characterising the DtN map using the Fokas method. This equation couples two unknown boundary values: the pressure jump across the plate and the pressure gradient in the space beside the plate. The aim of the following section is to solve this integral equation for the pressure jump in order to formulate a representation for the scattered pressure field.
4. Numerical Implementation
4.1. Approximate Global Relation and Choice of Basis Functions
The approximate solution to the generalised Dirichlet-to-Neumann (DtN) map generated by the global relation (16), first discussed in [37], is found via a collocation method based on the complex parameter . The unknown functions are the pressure jump across the rigid plate and the pressure gradient on the zero-streamline:
which can be approximated by a truncated series expansion of N basis functions, each reducing the problem of two unknown functions to complex series coefficients. Following [28], we choose the Legendre polynomials, , as the basis functions in our series expansions of the unknown functions. These are preferred due to their easy-to-compute Fourier transform, which is given by
where is the modified Bessel function of the first-kind with index . The basis functions undergo an affine transform to fit to the desired intervals of the unknown functions; the composite Fourier transform for defined by
is used to compact notation. Hence, we seek solutions for the unknown functions in the following approximate form:
Substituting (19) into (16) gives a countable set of equations for the unknown complex coefficients and .
where we used the equivalence . For the final collocative step, we choose M numbers to evaluate (20) at, according to (11) and (12). Provided , this results in an overdetermined linear system of size for the unknowns of the form , where and
4.2. Correcting for Endpoint Singularities
While a basis of orthogonal polynomials produces powerful results in terms of spectral rates of convergence, for problems involving endpoint and corner singularities, their performance suffers. Ultimately, a basis of smooth functions can never accurately fit into singular behaviour. From considering the physics of plate scattering problems, it is a priori known that the pressure jumps across a plate exhibits a square-root-type singularity approach to the tip of the plate. We further expect the pressure gradient to exhibit an inverse square-root singularity in response. Because of this, the inherent exponential convergence of a Legendre polynomial basis is reduced to algebraic convergence for [35].
To remedy the convergence of the method, we are able to supplement any suitable basis with one or more global singular functions that capture the correct endpoint behaviour. For the pressure jump , the square-root behaviour is captured by using a Chebyshev-type basis, , defined by
This has the corresponding finite range Fourier transform
where is the first-kind Bessel function of index j. A similar expression for the composite Fourier transform exists in the form of (18). Next, for the pressure gradient across the aperture , we approximate it using an expansion of Legendre polynomials, supplemented by two inverse square roots. Explicitly, we seek an improved solution of the form
These singular functions have finite range Fourier transforms given in terms of the error function:
These alternative ansatzes may be used to produce an equivalent linear system for its series coefficients that is more accurate to the physical constraints of the problem.
4.3. Conditioning and Limiting Parameter Values
Although choosing collocation points for a square system of equations is sufficient, least-squares oversampling has been shown to dramatically decrease condition numbers of collocation methods, facilitating more accurate numerical computation [38]. In the limit , the grating tends to that of one with infinitesimally small gaps between rigid plates. The effect of such grating is naturally anticipated to only be felt at high frequencies, where viscosity would also become significant, making this problem out of the scope of the acoustical considerations of this paper. Indeed, for moderate frequencies such as those in the audible range, the results of [39] investigating the effects of small holes on bounded scatterers may be extrapolated to the infinite case by modelling the number of holes to also tend to infinity at the same or faster rate as the size of the holes tends to zero. As such, it is expected that the grating behaves as if it were rigid, and the waves are expected to be totally reflected from the surface.
On the other hand, represents the limit of acoustic scattering by colinear point scatterers. This scenario has been considered for wedge-like configurations of scatterers using the WH technique in [40]. In the small plate length limit, the acoustical behaviour of the plate becomes that of a point scatterer, which scatters sound in such a way that can be approximated by a Hankel function, i.e., waves produced by a point source. Therefore, the scattered field we expect to see would no longer be a combination of plane waves but radially propagating waves in two dimensions. This is also the rationale behind approaches such as Foldy’s method [41].
For a treatment using the Fokas method, we can look at this limit from a different perspective: for a moderately sized a with a comparatively large incoming wavelength , the resulting problem can also be approximated as a grating of point scatterers that are positioned very close together [42]. Since the numerical Fokas method encounters no problems in the numerical integration of moderate values of a, this formulation of the limit can be used to produce illustrative results. For geometries in which the point scatterers are placed further apart, the width of the unit cell itself (which in this paper has been normalised to 1) can be introduced as an independent parameter.
5. Reconstructing the Full Solution
5.1. Green’s Identity
The whole solution to the scattering problem (3) is now reconstructed using the found boundary values obtained using the Fokas method in Section 3. A wholly analytical solution using this method is possible via an ‘inverse’ transform utilising complex integral techniques and specially chosen integration contours [43] (Chapter 12). In this paper, however, the chosen reconstruction method is that of the Green’s identity integral representation. Due to the geometry of the unit cell in the grating problem being a simple semi-infinite strip, Green’s function is known and easy to compute. Indeed, for the grating problem (3), its fundamental solution in is the quasi-periodic two-dimensional Green’s function, denoted . This solution for the Helmholtz equation in a periodic domain was analysed extensively in [44,45]. It is defined as an infinite combination of periodically spaced point sources on the x-axis:
where is the first-kind Hankel function. Green’s function satisfies the quasi-periodicty conditions in both x and (for the coordinate, the phase shift is ). Using Green’s second identity, the solution is
This expression is an infinite sum of a slowly decaying function and hence is slowly converging. For the purposes of numerical computation, it is advantageous to consider using its equivalent spectral formulation [46], an infinite sum of the Bloch modes with wavevectors .
hence, differentiating and evaluating at gives
This form is preferred for its exponential decay for non-zero y for certain values of . Indeed, most of the contribution to the value of the sum is concentrated in terms within a neighbourhood of , where is real and the terms are modal. Lastly, the exponential term in x is identified with the Fourier transform of the Legendre polynomial. This gives the following expression for the pressure (23):
5.2. Effective Reflection and Transmission Coefficients
The scattered pressure (26) can be decomposed into propagating and evanescent modes with amplitudes that can be determined. The modal representation of (26) in is
From this, we see that the scattered pressure exists as a combination of propagating and evanescent waves. Indeed, the propagating modes correspond to those m-terms for which is real, i.e., those which satisfy (5). For a given incident angle , this expression can be used to obtain the cut-on and cut-off frequencies for the problem: the wavenumbers k at which a certain term (mode) switches from being an evanescent wave that is trapped near the structure to a propagating wave. Let m satisfy the inequality (5) that lies in the interval . Then, the propagating part of the solution in , is
Similarly, the transmitted wave, i.e., , is
The modes that propagate in are determined by the same inequality (5); therefore, the propagating part of the solution in , , is
Crucially, we have the equivalence . Denoting , the total field is expressed in all space as follows:
In order to investigate the effect of the grating on the incident wave, we analyse the proportion of energy reflected and transmitted by the structure. Let be the acoustic intensity, where is the acoustic particle field velocity, linked to the pressure via for a homogeneous acoustic medium with unit density and wave speed. The time-averaged energy flux of the grating is therefore given by the following divergence integral:
where the time-averaging is understood to be over one period window . Applying this energy integral to our computed pressure (26), after some algebraic manipulation [47], we obtain the following forms for the reflected and transmitted energy flux of the periodic structure.
Note that we include only the propagating modes of the pressure field because we are interested in the far-field effect of the grating on the incident sound wave. Evanescent modes are ‘trapped’ within the grating, and their influence is not communicated to larger distances from the structure. These, as they are defined by the inequality (5), exist in “band-gap”-like configurations. They can suddenly switch from being evanescent to propagating with changes in frequency and play an important role in the noise reduction effect of acoustic gratings. As will be discussed further in the conclusion, the Fokas method can also be applied to stacks of gratings, for which evanescent modes are an important emergence in imposing the relevant continuity conditions across the grating [48]. Now, we normalise the expressions by the incident energy . Hence, we have the following three expressions:
6. Results
In Section 4, we found an approximate solution to the global relation (16) using a spectral collocation method. The unknown functions are approximated using either a smooth Legendre polynomial basis or bases tailored to the edge singularities of the problem. The found pressure jump is then used to reconstruct the full solution to the grating problem (3) using Green’s integral representation (26). Given the robustness of the MATLAB backslash solver \, the series coefficients (19) are easily obtained to an accuracy close to , decreasing up to machine precision of as the number of collocation points is increased. All numerical experiments were run on a 3.2 GHz Apple M1 processor in MATLAB.
Figure 2a plots the solutions and on their respective intervals using the tailored bases of Section 4.2, showing the expected singularity structure that emerges within the unit cell. Figure 2b compares the endpoint behaviour of computed using a smooth Legendre basis with no added singular functions versus one that does. The Legendre polynomial basis on its own is not sufficient to solve for the values close to the endpoints for moderate numbers of terms N with suitable accuracy.
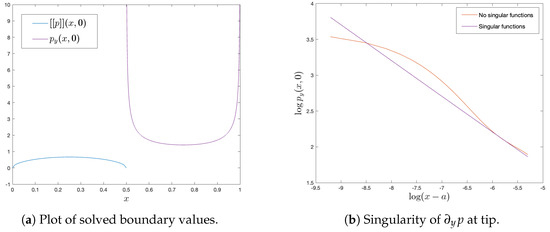
Figure 2.
.
Next, the periodic Fokas method of this paper (referred to as PFM) is validated against the equivalent problem as solved using the Wiener–Hopf (WH) technique by Erbaş and Abrahams in [14]. We benchmark against the WH method as it is a classical and effective method for thin-plate acoustic scattering problems [49]. The case considered by the WH method is restricted to , for which a closed-form factorisation of the matrix WH kernel exists and is found by reducing it to a size of . We consider the rates of energy reflection and transmission (30) of the grating. After adjusting for differences in scales between the novel method and the WH method (simply due to a difference in defining the geometry of the unit cell and non-dimensionalising quantities), Figure 3 depicts the superposition of the proportion of reflected energy as computed by both methods. For the periodic Fokas method, the values used were and and chosen such that any increases would lead to no changes in the quality of the figure within the orders of magnitude we are interested. The plots are shown to be in excellent agreement, showing the periodic Fokas method as a much simpler alternative than the matrix WH method for acoustic scattering by grating.
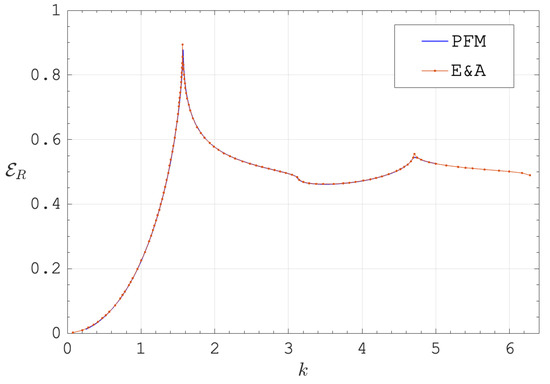
Figure 3.
as calculated by the Wiener–Hopf method by Erbaş and Abrahams (E&A) overlaid with the same problem computed using the periodic Fokas method (PFM). , , , .
Furthermore, Figure 4 expands upon the validation of the PFM by showing the behaviour of and when , as the wavenumber k varies, for several angles of incidence . These results also agree with the WH technique of [14]. The characteristic peaks and dips for each are clearly defined, and the largest proportion of energy that is reflected occurs for normal incidence ().
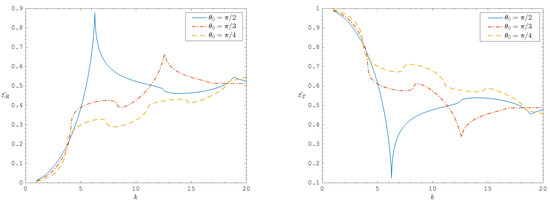
Figure 4.
Energy reflected and transmitted from the periodic structure for and as k varies.
The advantage of the PFM is its ability to be applied to gratings that are currently not easily considered by the WH technique. Namely, those that are constructed of non-equal plate lengths and plate spacings, i.e., . To this end, Figure 5 and Figure 6 all depict energy plots for and as k varies, for different angles of incidence . In each figure, the addition of extra propagating modes to the sums (30) as k increases is made apparent by the spikes in energies. Indeed, the m-terms included in the sums are those defined by (5), which give rise to cut-on and cut-off frequencies. When such a threshold is passed as k increases, a new mode switches from being evanescent to propagating, which is what causes the sudden peaks and dips in the figures. The effect of on the cut-off frequencies is also apparent by the differing locations of the peaks for each . This is also shown in Figure 6, where is an almost-grazing incident wave that shows no propagating reflected mode.
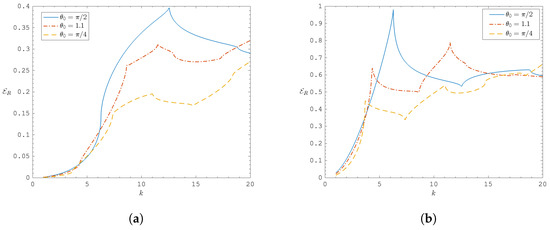
Figure 5.
against k for (a) and (b).
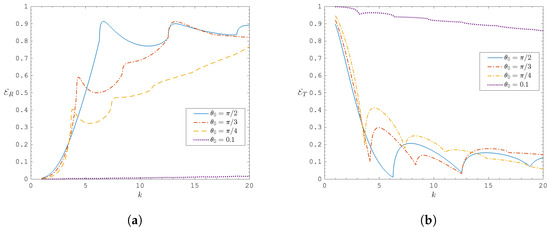
Figure 6.
(a) and (b) against k for .
Next, we discuss and expand upon an observation found in [14,47] as wavenumber k increases. For large k, in the case, the proportion of energy reflected by the structure, approaches . Similarly, for , it approaches and, respectively, for and . As expected, this is because, at small wavelengths, most of the incident wave is either fully reflected by the rigid parts of the structure or fully passes through the gaps in the structure without interacting with the edges. The part of the field that is diffracted by the edges is small. This leads to a total reduction in the loss of energy from being ‘trapped’ within the structure in the form of evanescent waves, also corroborated by the values of the cut-off frequencies in the large k limit.
Lastly, Figure 7 shows the scattering pattern of the total acoustic field (that is, the solution to (3) added to the incident wave for two different incident waves and two different plate lengths. For both we are able to observe that diffraction into the region below the grating increases as the gap size increases and the incident angle decreases, which is consistent with the discussion above.
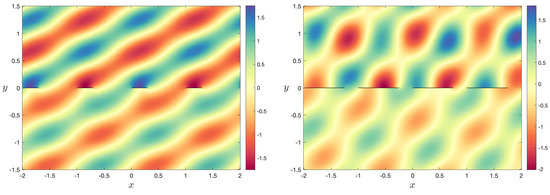
Figure 7.
Total field in the non-dimensional plane when with (left) and (right).
Verification Using Homogenised Compliance
One application of the analysis performed in this paper is finding the effective compliance of a homogenised surface exhibiting the same acoustical behaviour as the grating in a limiting configuration of parameters. In this section, an effective interface condition is found in the regime where the wavelength is small compared to the period of the grating, and the length of the aperture is small compared to the length of the plate. In the notation of this paper, this corresponds to the parameter , where is small and . Using the effective compliance parameter derived by Leppington [50] and Lamb [51], we seek to verify our results against the homogenised interface condition:
where . A unit amplitude plane wave of the form in (2), normally incident on a homogeneous surface with the above boundary condition, induces a scattered field with reflection and transmission coefficients R and T given by
For large wavelengths, i.e., small wavenumbers k, the inequality (5) implies only the mode of (27) propagate; hence, we evaluate the zero-order reflection and transmission coefficients and , respectively. Figure 8 shows that the error between the reflection coefficient as computed by the unified transform and the effective compliance generated in [50] is of the same order as the small parameter . This provides a strong foundation to explore avenues of homogenisation via equivalent compliance parameters popular in application, such as the Rayleigh conductivity [52], as well as a route to homogenising more complicated grating structures, as can be considered by the unified transform.
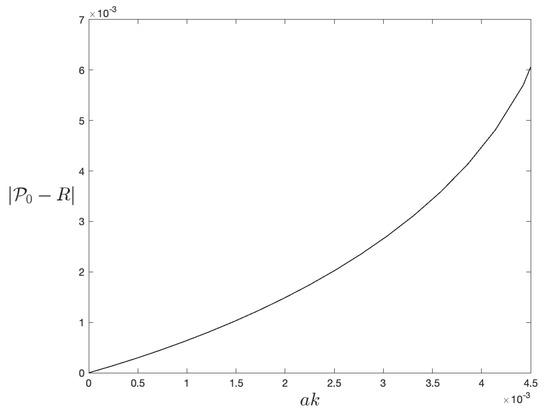
Figure 8.
vs. the error in the small aperture limit for a normal incidence wave.
7. Conclusions
This paper presents an extension to the Fokas method, also called the unified transform method, to periodic domains, in particular, to gratings representing perforated screens exhibiting a discontinuous change in boundary condition. The extended method is capable of tackling a wider range of problems efficiently, which could not be done with the Fokas method before, such as acoustic gratings, multi-layered lattices, and periodic rough surfaces with discontinuous boundary conditions [53,54]. Furthermore, it is a computationally and algebraically simple method for problems that were previously approached with more difficult methods such as WH.
The central idea for the periodic method is to take advantage of the fact that is a free parameter along with the quasi-periodicity condition to remove the influence of the vertical artificial boundaries of the unit cell. Then, an expansion of the unknown boundary values in terms of a Legendre series is used in conjunction with the collocation method in the spectral coordinate. This leads to an accurate numerical scheme for the series coefficients found by solving an overdetermined linear system. Over-sampling the system by using more collocation points M than basis functions N and solving the resulting linear system via a least squares approach shows to improve conditioning.
The new approach recreates the existing solution obtained via existing methods, such as the Wiener–Hopf technique, in the case of equal plate and gap spacings (corresponding to in the nomenclature of this paper). Crucially, a great advantage of the Fokas method is that it is not restricted to this single value of a. As such, a wide range of grating sizes have been analysed. From the engineering point of view, gratings with varying gap lengths lend themselves to the investigation of more complex metamaterial building blocks, which often comprise multiple scales. Furthermore, considering a noise reduction application, this method can be easily employed for frequency-targeting noise reduction, for which a specific a-value can be determined to minimise or maximise the energy flux through the structure.
The specific choice of spectral parameters (11) in this paper is in further contrast to non-periodic scattering problems also investigated using the Fokas method, such as in [31]. In non-periodic problems, the collocation parameter is free to be chosen in either the entire or some region of the complex plane. The resulting numerical method employs a selection of collocation points chosen on a semi-random basis. Indeed, for such problems, the acoustic domain is some unbounded convex polygon (e.g., the upper half-plane or quarter plane). The Fokas method applied to these geometries results in a continuous subset of the complex plane in which the global relation evaluated at in that region is valid. Therefore, any numerical discretisation involving points from this subset is permissible. For extra details on the motivation of the collocation points in the non-periodic case, the reader is referred to [55].
Owing to the periodic structure of the perforated screen, the quasi-periodicity of the solution is reminiscent of Bloch waves and the Floquet–Bloch theory of waves propagating in periodic media or governed by periodic differential equations [34]. For the lattice structures usually encountered in these types of problems, the scattered wave decomposition is often seen as a multi-pole expansion, which is distinct from the plane wave expansion used in this paper [56]. Importantly, Bloch waves share the property of propagating waves being governed by an inequality (5), giving rise to a discrete set of propagating modes. This explains the “band-gap”-like structure seen in energy diagrams [57], as it is linked to the evanescence we discuss next.
Moreover, this work shows how the Helmholtz scattering problem is solved using the Fokas method in a unit cell exterior to a bounded scatterer, which here takes the form of a finite plate. A property emerging uniquely from the periodic geometry is the existence of evanescent waves (or surface waves) in the modal decomposition of the scattered field. The effect of these surface waves can be maximised by considering geometries that consist of stacked gratings [53]. This is increasingly promising as the periodic Fokas method is not limited to the simple geometry present in this grating problem: the global relation can indeed be applied to any unit cell, for example, multiple plates of varying sizes within a unit cell or stacked gratings or rotated plates. Future work will focus on the method being applied to these stacked gratings as well as different boundary conditions, such as elastic plate scattering. The main obstacle in this setting would be a robust numerical implementation of such a method. However, this paper provides groundwork for these avenues of research.
Author Contributions
Conceptualisation, writing—review and editing, S.B.N. and L.J.A.; methodology, software, validation, writing—original draft preparation, S.B.N.; supervision, L.J.A. All authors have read and agreed to the published version of the manuscript.
Funding
S.B.N. acknowledges support from the EPSRC Studentship EP/T517847/1 grant number 2602427. L.J.A. acknowledges support from the EPSRC Early Career Fellowship EP/P015980/1.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Mahashabde, A.; Wolfe, P.; Ashok, A.; Dorbian, C.; He, Q.; Fan, A.; Lukachko, S.; Mozdzanowska, A.; Wollersheim, C.; Barrett, S.R.; et al. Assessing the environmental impacts of aircraft noise and emissions. Prog. Aerosp. Sci. 2011, 47, 15–52. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, P. Sound Absorption Structures: From Porous Media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Smith, M.J.A. Wave Propagation Through Periodic Structures in Thin Plates. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2013. [Google Scholar]
- Geyer, T.F.; Sarradj, E.; Fritzsche, C. Nature-inspired porous airfoils for sound reduction. In Nature-Inspired Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 119, pp. 355–370. [Google Scholar] [CrossRef]
- Ayton, L.J.; Colbrook, M.J.; Geyer, T.F.; Chaitanya, P.; Sarradj, E. Reducing aerofoil-turbulence interaction noise through chordwise-varying porosity. J. Fluid Mech. 2021, 906, A1. [Google Scholar] [CrossRef]
- Chaitanya, P.; Joseph, P.; Chong, T.P.; Priddin, M.J.; Ayton, L.J. On the noise reduction mechanisms of porous aerofoil leading edges. J. Sound Vib. 2020, 485, 115574. [Google Scholar] [CrossRef]
- Palleja-Cabre, S.; Chaitanya, P.; Joseph, P.; Kim, J.W.; Priddin, M.J.; Ayton, L.J.; Geyer, T.F.; Chong, T.P. Downstream porosity for the reduction of turbulence-aerofoil interaction noise. J. Sound Vib. 2022, 541, 117–324. [Google Scholar] [CrossRef]
- Crighton, D.G.; Dowling, A.P.; Williams, J.E.F.; Heckl, M.; Leppington, F.G. Modern Methods in Analytical Acoustics; Springer: London, UK, 1992. [Google Scholar] [CrossRef]
- Noble, B. Methods Based on the Wiener-Hopf Technique; Pergamon Press: Oxford, UK, 1958. [Google Scholar] [CrossRef]
- Daniele, V.G.; Lombardi, G. Scattering and Diffraction by Wedges 1: The Wiener-Hopf Solution—Theory; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Chehade, S.; Kamta Djakou, A.; Darmon, M.; Lebeau, G. The spectral functions method for acoustic wave diffraction by a stress-free wedge: Theory and validation. J. Comput. Phys. 2019, 377, 200–218. [Google Scholar] [CrossRef]
- Chehade, S.; Darmon, M.; Lebeau, G. 2D elastic plane-wave diffraction by a stress-free wedge of arbitrary angle. J. Comput. Phys. 2019, 394, 532–558. [Google Scholar] [CrossRef]
- Erbaş, B.; Abrahams, D.I. Scattering of sound waves by an infinite grating composed of rigid plates. Wave Motion 2007, 44, 282–303. [Google Scholar] [CrossRef]
- Erbaş, B. Scattering of Waves in Ducts and by Periodic Structures. Ph.D. Thesis, Univeristy of Manchester, Manchester, UK, 2002. [Google Scholar]
- Achenbach, J.D.; Li, Z.L. Reflection and transmission of scalar waves by a periodic array of screens. Wave Motion 1986, 8, 225–234. [Google Scholar] [CrossRef]
- Leppington, F.G.; Levine, H. Reflexion and transmission at a plane screen with periodically arranged circular apertures or elliptical apertures. J. Fluid Mech. 1973, 61, 109–127. [Google Scholar] [CrossRef]
- Fokas, A.S. A Unified Approach to Boundary Value Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Nicholls, D.P.; Tammali, V. A high-order perturbation of surfaces (HOPS) approach to Fokas integral equations: Vector electromagnetic scattering by periodic crossed gratings. Appl. Numer. Math. 2016, 101, 1–17. [Google Scholar] [CrossRef]
- Arens, T.; Chandler-Wilde, S.N.; DeSanto, J.A. On Integral Equation and Least Squares Methods for Scattering by Diffraction Gratings. Commun. Comput. Phys. 2006, 1, 1010–1042. [Google Scholar]
- Chandler-Wilde, S.N.; Langdon, S. Acoustic scattering: High frequency boundary element methods and unified transform methods. arXiv 2014, arXiv:1410.6137. [Google Scholar]
- DeSanto, J.A. Exact boundary integral equations for scattering of scalar waves from perfectly reflecting infinite rough surfaces. Wave Motion 2008, 45, 918–926. [Google Scholar] [CrossRef]
- Desanto, J. Spectral Methods for Gratings. In Gratings: Theory and Numeric Applications; Popov, E., Ed.; AMU (PUP): Marseille, France, 2012; pp. 3.1–3.38. Available online: www.fresnel.fr/numerical-grating-book (accessed on 5 August 2024).
- Fokas, A.S. A unified transform method for solving linear and certain nonlinear PDEs. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1997, 453, 1411–1443. [Google Scholar] [CrossRef]
- Spence, E.A. Boundary Value Problems for Linear Elliptic PDEs. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2010. [Google Scholar]
- Ashton, A.C.L. Elliptic PDEs with constant coefficients on convex polyhedra via the unified method. J. Math. Anal. Appl. 2015, 425, 160–177. [Google Scholar] [CrossRef]
- Fokas, A.S.; Kapaev, A.A. On a transform method for the Laplace equation in a polygon. IMA J. Appl. Math. 2003, 68, 355–408. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Fokas, T.S.; Hashemzadeh, P. A Hybrid Numerical-Analytical Technique for Elliptic PDEs. SIAM J. Sci. Comput. 2019, 41, A1066–A1090. [Google Scholar] [CrossRef]
- Smitheman, S.A.; Spence, E.A.; Fokas, A.S. A spectral collocation method for the Laplace and modified Helmholtz equations in a convex polygon. IMA J. Numer. Anal. 2009, 30, 1184–1205. [Google Scholar] [CrossRef]
- Hashemzadeh, P.; Fokas, A.S.; Smitheman, S.A. A numerical technique for linear elliptic partial differential equations in polygonal domains. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140747. [Google Scholar] [CrossRef] [PubMed]
- Colbrook, M.J.; Ayton, L.J.; Fokas, A.S. The unified transform for mixed boundary condition problems in unbounded domains. Proc. A 2019, 20180605. [Google Scholar] [CrossRef]
- Strutt, J.W. The Theory of Sound; Dover Publications: New York, NY, USA, 1945. [Google Scholar] [CrossRef]
- Kirsch, A. Diffraction by periodic structures. In Inverse Problems in Mathematical Physics; Päivärinta, L., Somersalo, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 87–102. [Google Scholar] [CrossRef]
- Figotin, A.; Kuchment, P. Band-Gap Structure of Spectra of Periodic Dielectric and Acoustic Media. I. Scalar Model. SIAM J. Appl. Math. 1996, 56, 68–88. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Flyer, N.; Fornberg, B. On the Fokas method for the solution of elliptic problems in both convex and non-convex polygonal domains. J. Comp. Phys. 2018, 374, 996–1016. [Google Scholar] [CrossRef]
- Ashton, A.C. The Fundamental k-Form and Global Relations. Symmetry Integr. Geom. Methods Appl. 2008, 33, 1–15. [Google Scholar] [CrossRef]
- Fulton, S.; Fokas, A.; Xenophontos, C. An analytical method for linear elliptic PDEs and its numerical implementation. J. Comput. Appl. Math. 2004, 167, 465–483. [Google Scholar] [CrossRef]
- Maierhofer, G.; Huybrechs, D. An analysis of least-squares oversampled collocation methods for compactly perturbed boundary integral equations in two dimensions. J. Comput. Appl. Math. 2022, 416, 114500. [Google Scholar] [CrossRef]
- Challa, D.P.; Mantile, A.; Sini, M. Characterization of the acoustic fields scattered by a cluster of small holes. Asymptot. Anal. 2020, 118, 235–268. [Google Scholar] [CrossRef]
- Nethercote, M.A.; Kisil, A.V.; Assier, R.C. Diffraction of Acoustic Waves by a Wedge of Point Scatterers. SIAM J. Appl. Math. 2022, 82, 872–898. [Google Scholar] [CrossRef]
- Foldy, L.L. The Multiple Scattering of Waves. I. General Theory of Isotropic Scattering by Randomly Distributed Scatterers. Phys. Rev. 1945, 67, 107–119. [Google Scholar] [CrossRef]
- Linton, C.M.; Martin, P.A. Semi-Infinite Arrays of Isotropic Point Scatterers. A Unified Approach. SIAM J. Appl. Math. 2004, 64, 1035–1056. [Google Scholar] [CrossRef]
- Fokas, A.; Kaxiras, E. Modern Mathematical Methods for Scientists and Engineers; WORLD SCIENTIFIC (EUROPE): Singapore, 2023. [Google Scholar] [CrossRef]
- Linton, C. The Green’s Function for the Two-Dimensional Helmholtz Equation in Periodic Domains. J. Eng. Math. 1998, 33, 377–401. [Google Scholar] [CrossRef]
- Heins, A.E. The Green’s Function for Periodic Structures in Diffraction Theory with an Application to Parallel Plate Media, I. J. Math. Mech. 1957, 6, 401–426. [Google Scholar] [CrossRef][Green Version]
- Linton, C.M.; Evans, D.V. The Radiation and Scattering of Surface Waves by a Vertical Circular Cylinder in a Channel. Philos. Trans. Phys. Sci. Eng. 1992, 338, 325–357. [Google Scholar] [CrossRef]
- Heins, A.E.; Baldwin, G.L. On the diffraction of a plane wave by an infinite plane grating. Math. Scand. 1954, 2, 103–118. [Google Scholar] [CrossRef][Green Version]
- Mansuripur, M. Classical Optics and Its Applications; Cambridge University Press: Cambridge, UK, 2009; pp. 387–403. [Google Scholar] [CrossRef]
- Priddin, M. Scattering by Porous Aerofoil Adaptations. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2022. [Google Scholar]
- Leppington, F.G. The effective compliance of perforated screens. Mathematika 1977, 24, 199–215. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Howe, M.S. Acoustics of Fluid-Structure Interactions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Meylan, M.H.; Smith, M.J. Perforated grating stacks in thin elastic plates. Wave Motion 2017, 70, 15–28. [Google Scholar] [CrossRef]
- Desanto, J.; Erdmann, G.; Hereman, W.; Misra, M. Theoretical and computational aspects of scattering from periodic surfaces: One-dimensional transmission interface. Waves Random Media 2001, 11, 425–453. [Google Scholar] [CrossRef]
- Fornberg, B.; Flyer, N. A numerical implementation of Fokas boundary integral approach: Laplace’s equation on a polygonal domain. Proc. R. Soc. A 2011, 467, 2983–3003. [Google Scholar] [CrossRef]
- Tymis, N.; Thompson, I. Scattering by a semi-infinite lattice and the excitation of Bloch waves. Q. J. Mech. Appl. Math. 2014, 67, 469–503. [Google Scholar] [CrossRef][Green Version]
- Kuchment, P. Floquet Theory for Partial Differential Equations; Birkhäuser Basel: Basel, Switzerland, 1993. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).