Computational and Theoretical Investigation of Acoustical and Vibrational Properties of Rigid Thin Material
Abstract
1. Introduction
2. Theory of the Vibrational Behavior of Waves in Rigid Thin Materials
2.1. Deflection of Rigid Thin Materials
2.2. Acoustic Radiation Efficiency from Rigid Thin Materials
3. COMSOL Simulation of Fiberglass Materials
4. Comparison of Computational Simulations and Analytical Results of Vibrated Materials
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Szilard, R. Theory and Analysis of Plates. In Classical and Numerical Methods; Prentice-Hall: Englewood, NJ, USA, 1974. [Google Scholar]
- Leissa, A.W. The free vibration of rectangular plates. J. Sound Vib. 1973, 1, 257–293. [Google Scholar] [CrossRef]
- Young, D. Vibration of rectangular plates by the Ritz method. J. Appl. Mech. 1950, 17, 448–453. [Google Scholar] [CrossRef]
- Theodorakopoulos, D.D.; Beskos, D.E. Flexural vibration of poroelastic plates. Acta Mech. 1994, 103, 191–203. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of elastic wave propagation in a fluid saturated porous solid. Part I-low frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of elastic wave propagation in a fluid saturated porous solid. Part 2-higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Leclaire, P.; Cummings, A.; Horoshenkov, K.V. Transverse vibration of a thin rectangular porous plate saturated by a fluid. J. Sound Vib. 2001, 247, 1–18. [Google Scholar] [CrossRef]
- Leclaire, P.; Horoshenkov, K.V.; Swift, M.J.; Hothersall, D.C. The vibration response of a clamped rectangular porous plate. J. Sound Vib. 2001, 217, 19–31. [Google Scholar] [CrossRef]
- Aygun, H.; Attenborough, K. Predicted effects of fluid loading on the vibration of elastic porous plates. Acta Acoust. United Acust. 2007, 93, 284–289. [Google Scholar]
- Aygun, H.; Attenborough, K. Sound absorption by clamped poroelastic plates. J. Acoust. Soc. Am. 2008, 124, 1550–1556. [Google Scholar] [CrossRef]
- Davies, H.G. Low frequency random excitation of water-loaded rectangular plates. J. Sound Vib. 1971, 15, 107–126. [Google Scholar] [CrossRef]
- Pope, L.D.; Leibowitz, R.C. Intermodal coupling coefficients for a fluid-loaded rectangular plate. J. Acoust. Soc. Am. 1974, 56, 408–414. [Google Scholar] [CrossRef]
- Gomperts, M.C. Radiation from rigidly baffled rectangular panels with general boundary conditions. Acustica 1974, 30, 320–327. [Google Scholar]
- Gomperts, M.C. Sound radiation from baffled, thin, rectangular plates. Acustica 1977, 37, 93–102. [Google Scholar]
- Berry, A. A general formulation for the sound radiation from rectangular, baffled plates with arbitrary boundary conditions. J. Acoust. Soc. Am. 1990, 88, 2792–2802. [Google Scholar] [CrossRef]
- Berry, A. A new formulation for the vibrations and sound radiation of fluid-loaded plates with elastic boundary conditions. J. Acoust. Soc. Am. 1994, 96, 889–901. [Google Scholar] [CrossRef]
- Atalla, N.; Nicolas, J. A new tool for predicting rapidly and rigorously the radiation efficiency of plate-like structures. J. Acoust. Soc. Am. 1994, 95, 3369–3378. [Google Scholar] [CrossRef]
- Foin, O.; Nicolas, J.; Atalla, N. An efficient tool for predicting the structural acoustic and vibration response of sandwich plates in light or heavy fluid. Appl. Acoust. 1999, 57, 213–242. [Google Scholar] [CrossRef]
- Sandman, B.E. Motion of a three-layered elastic-viscoelastic plate under fluid loading. J. Acoust. Soc. Am. 1975, 57, 1097–1107. [Google Scholar] [CrossRef]
- Nelisse, H.; Beslin, O.; Nicolas, J. Fluid–structure coupling for an unbaffled elastic panel immersed in a diffuse field. J. Sound Vib. 1996, 198, 485–506. [Google Scholar] [CrossRef]
- Nelisse, H.; Beslin, O.; Nicolas, J. A generalized approach for the acoustic radiation from a baffled or unbaffled plate with arbitrary boundary conditions, immersed in a light or heavy fluid. J. Sound Vib. 1998, 211, 207–225. [Google Scholar] [CrossRef]
- McCann, F.; Aygun, H. Structural and acoustical performance of recycled glass bead panels. J. Constr. Build. Mater. 2020, 258, 119581. [Google Scholar]
- Singh, B.N.; Hota, R.N.; Dwivedi, S.; Jha, R.; Ranjan, V.; Rehak, K. Analytical investigation of sound radiationfrom functionally graded thin plates based onelemental raditor approach and phsycialneutral surface. J. Appl. Sci. 2022, 12, 7707. [Google Scholar] [CrossRef]
- Ziao, X.; Tao, J.; Sun, H.; Sun, Q. Modeling of Acoustic Vibration Theory Based on a Micro Thin Plate System and Its Control Experiment Verification. J. Sustain. 2022, 14, 14900. [Google Scholar]
- Liu, C.W.; Kam, T.Y. Free Vibration of Rectangular Composite Cantilever Plate and Its Application in Material Degradation Assessment. J. Appl. Sci. 2023, 13, 5101. [Google Scholar] [CrossRef]
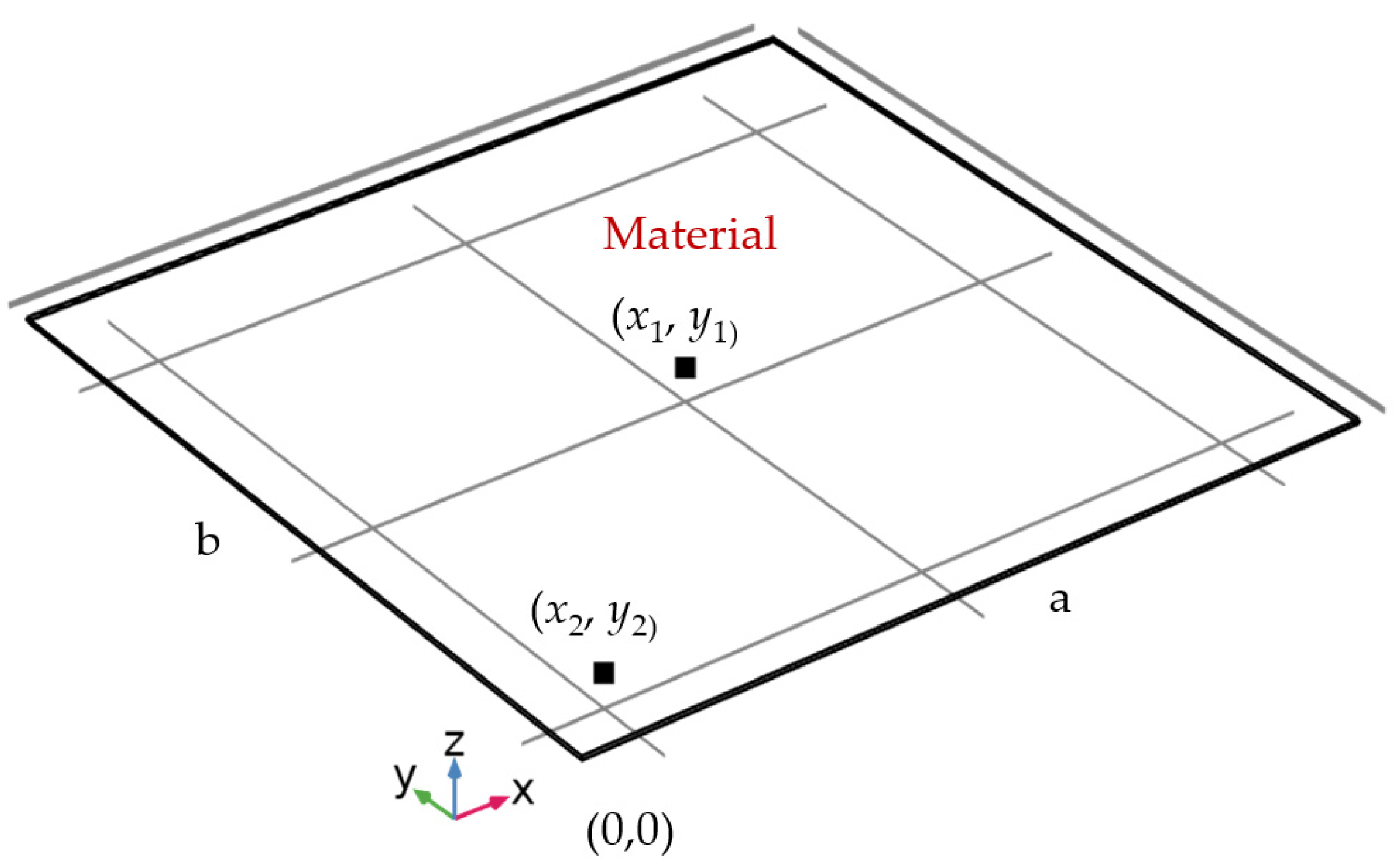
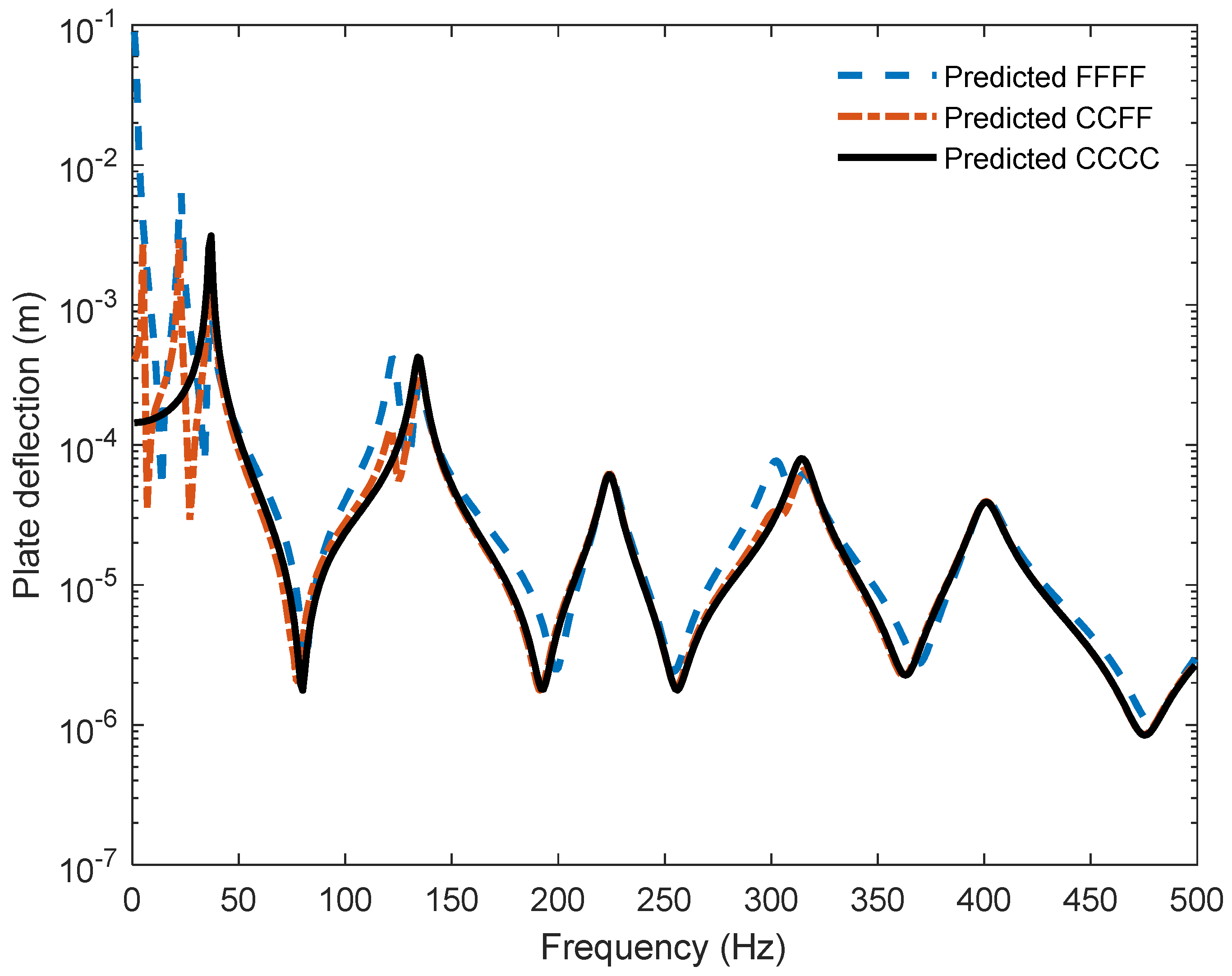
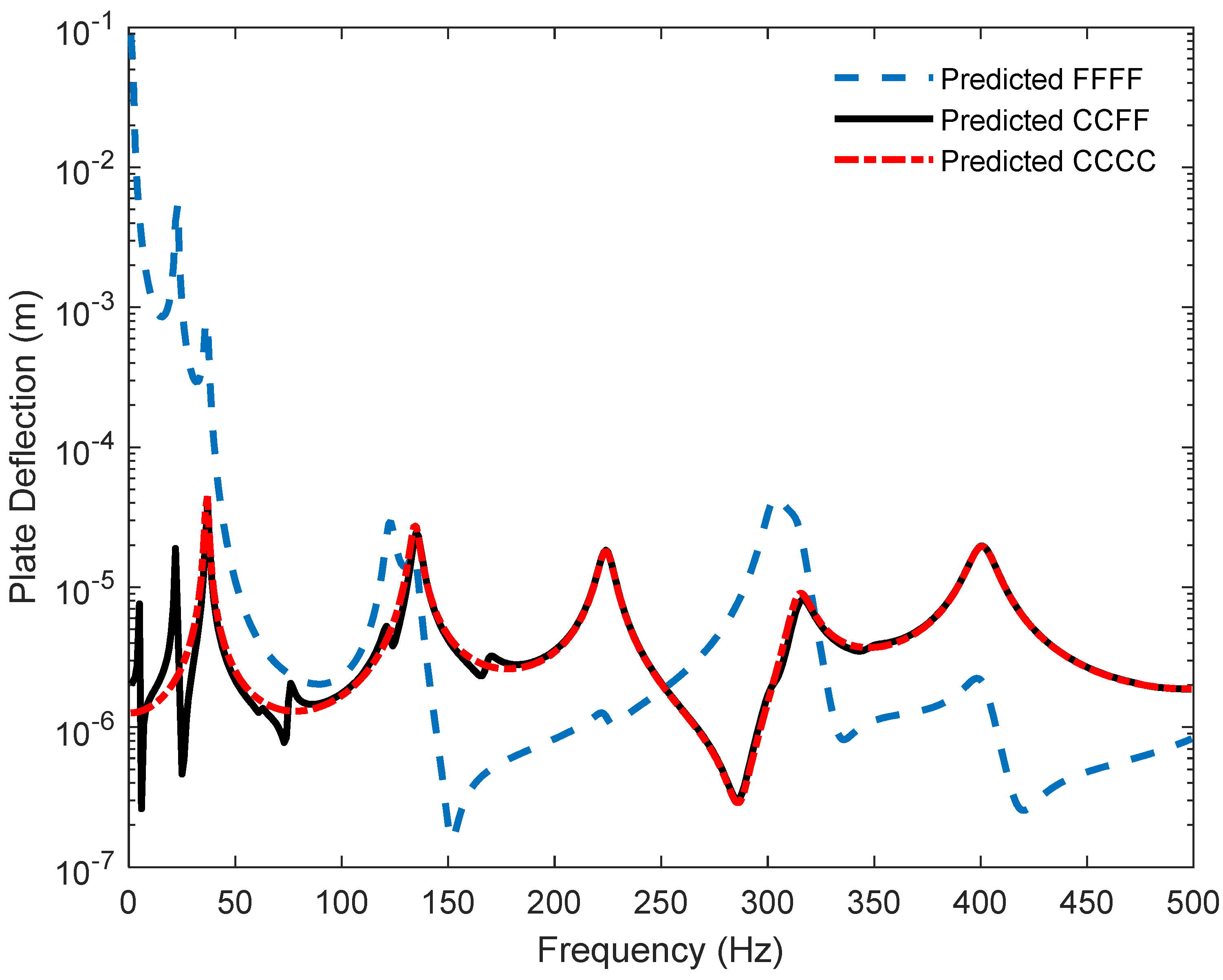
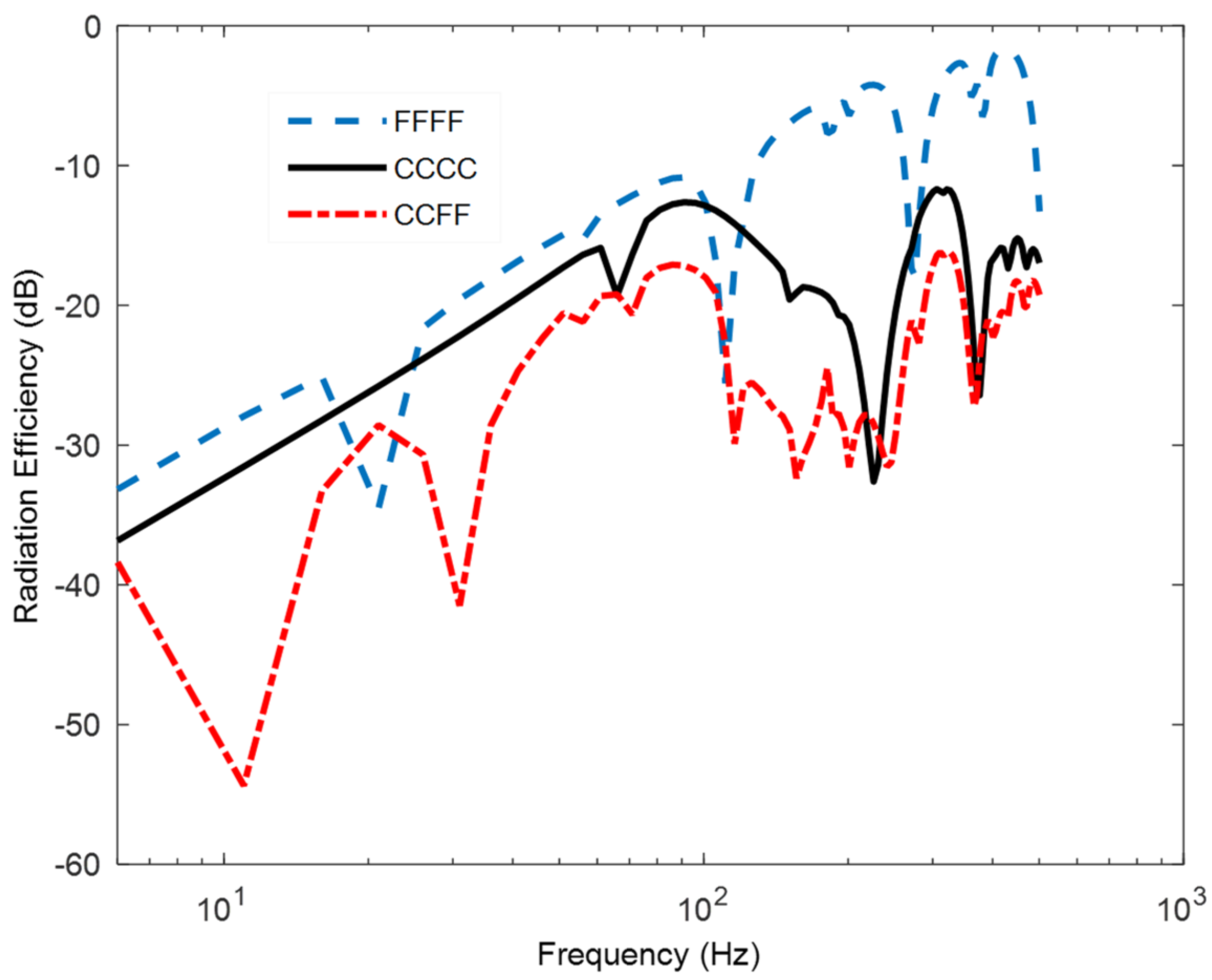
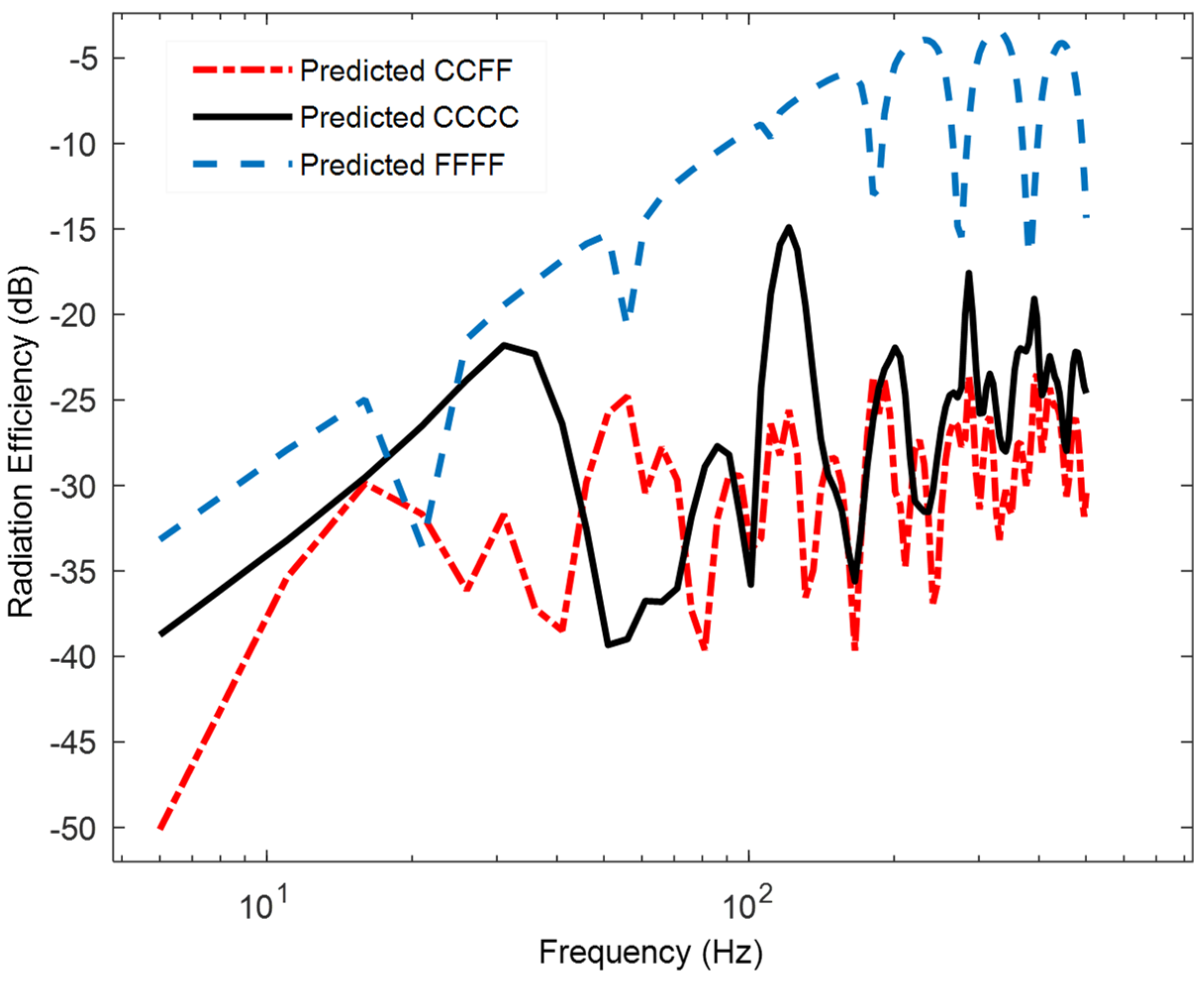

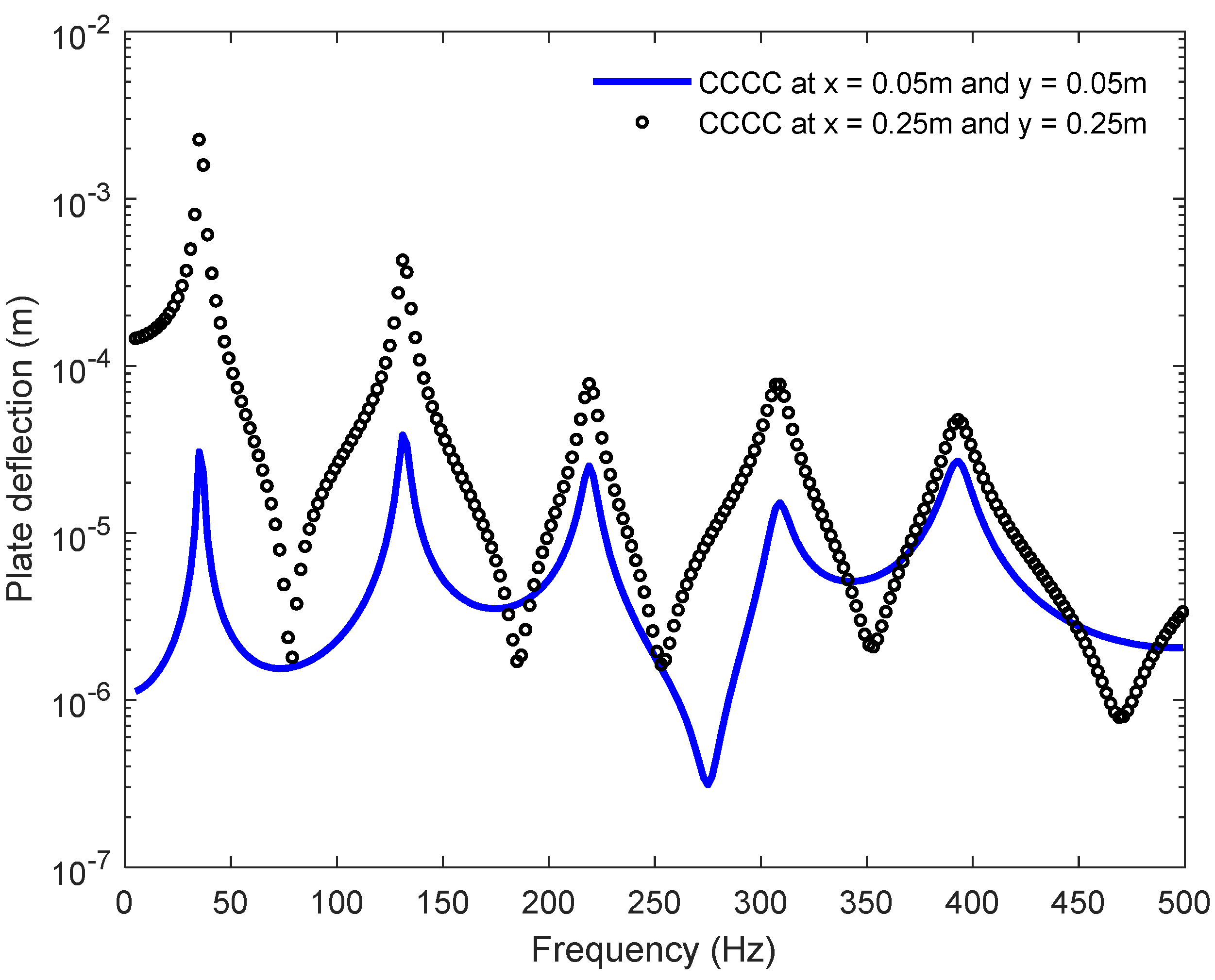
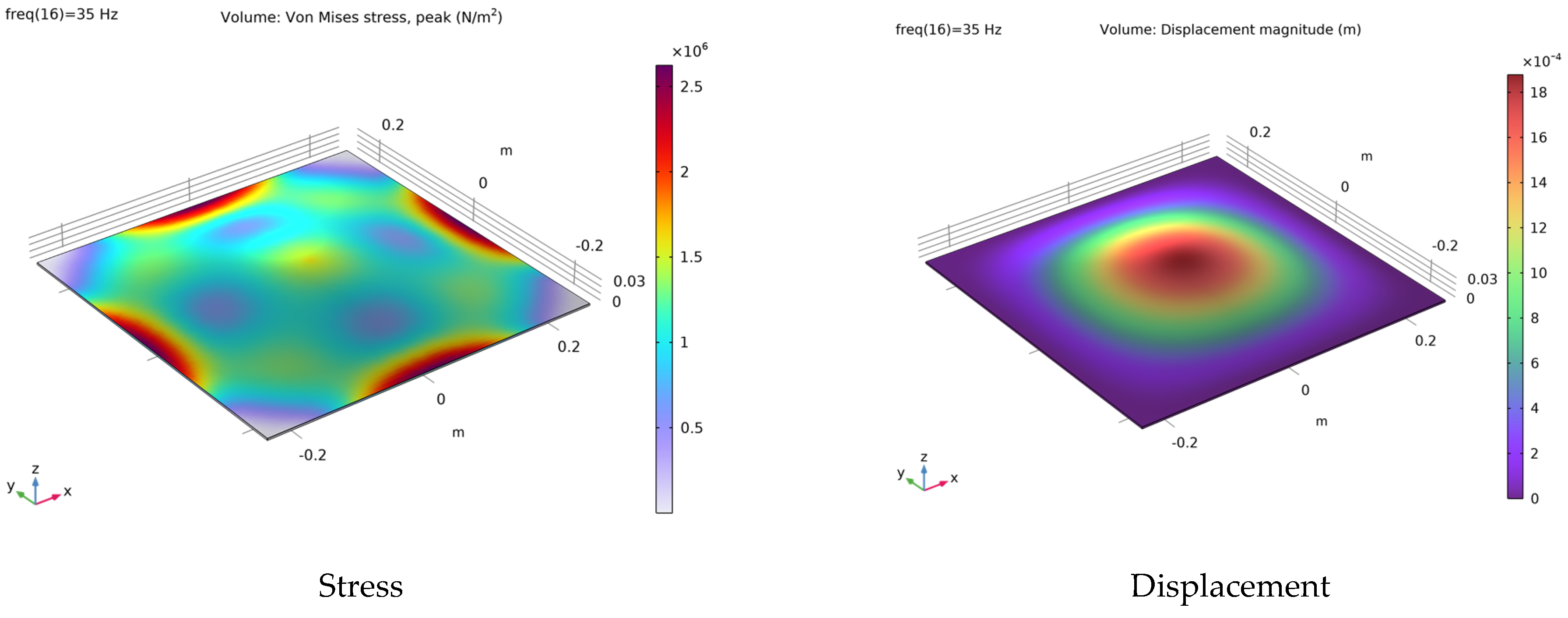
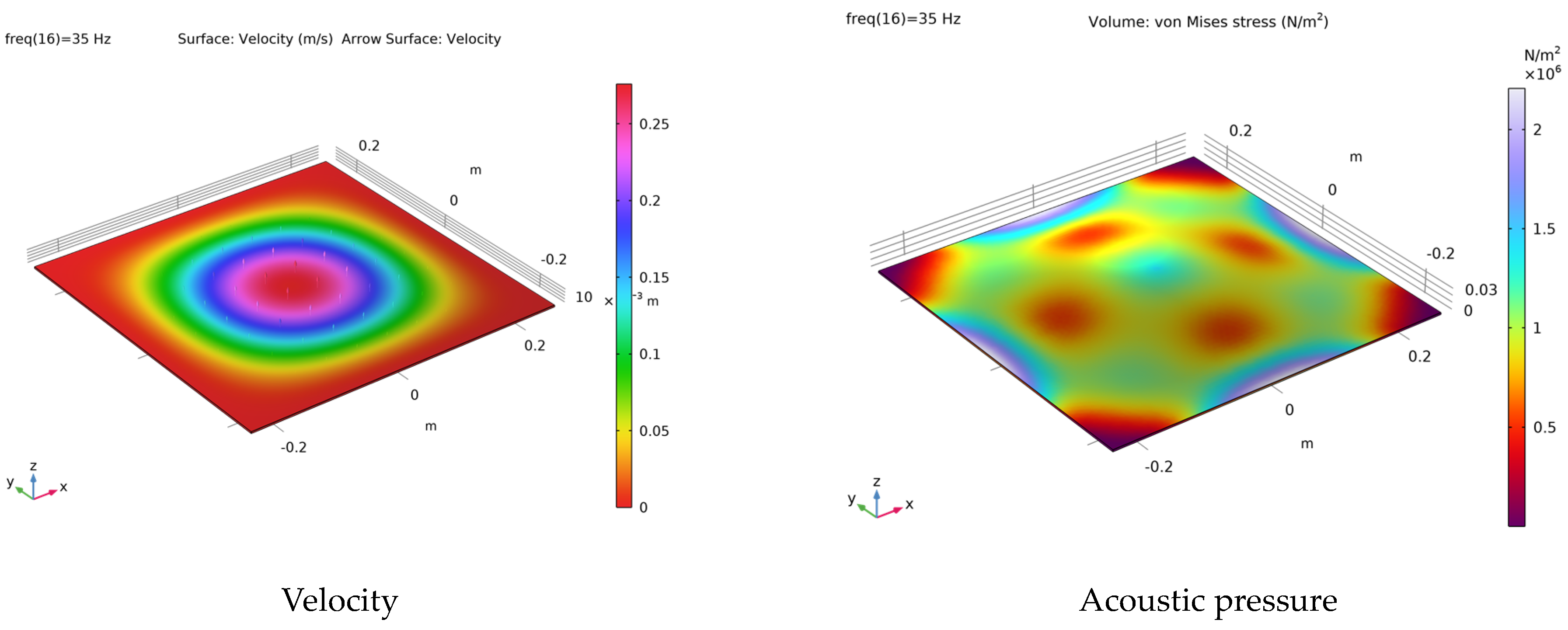
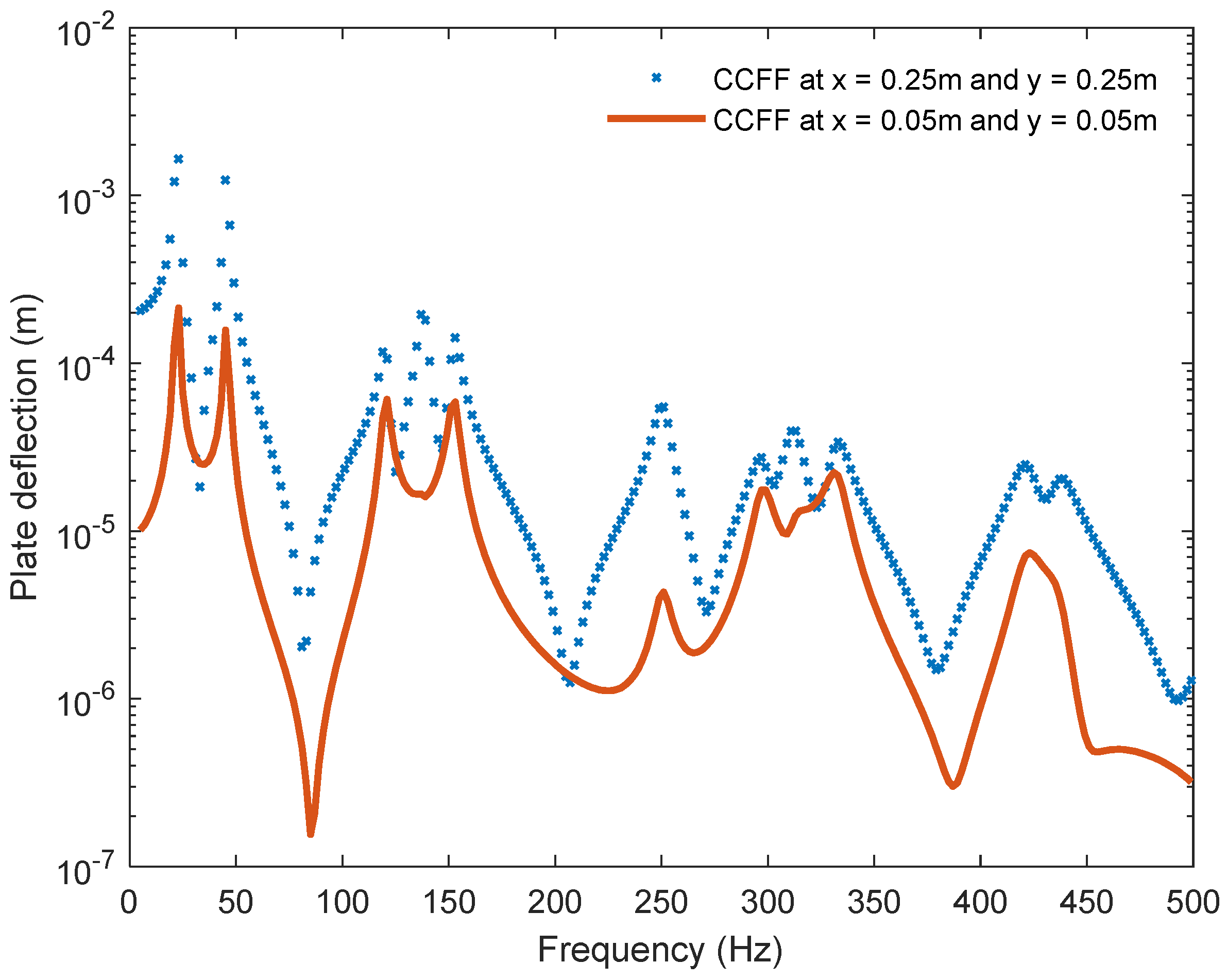
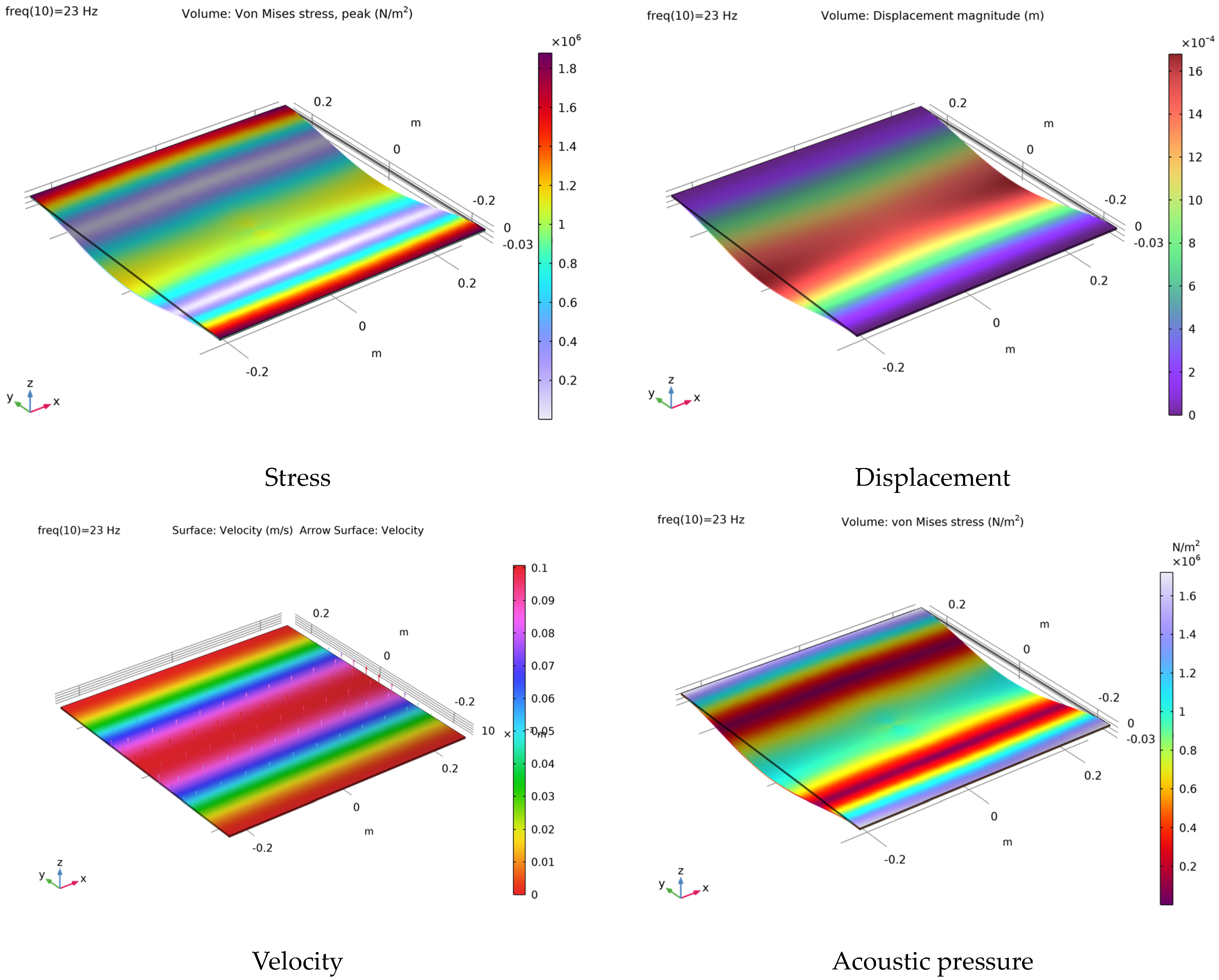
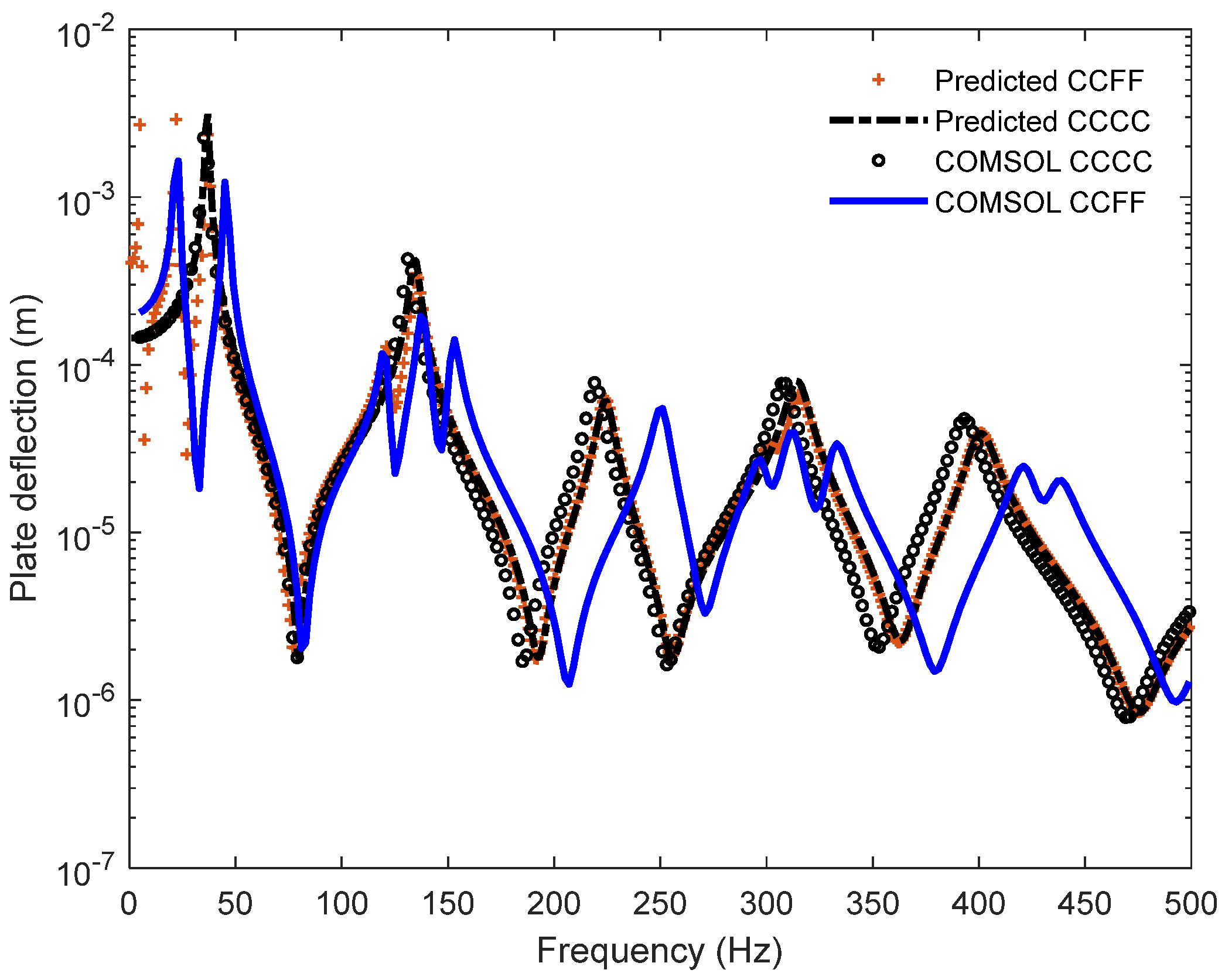
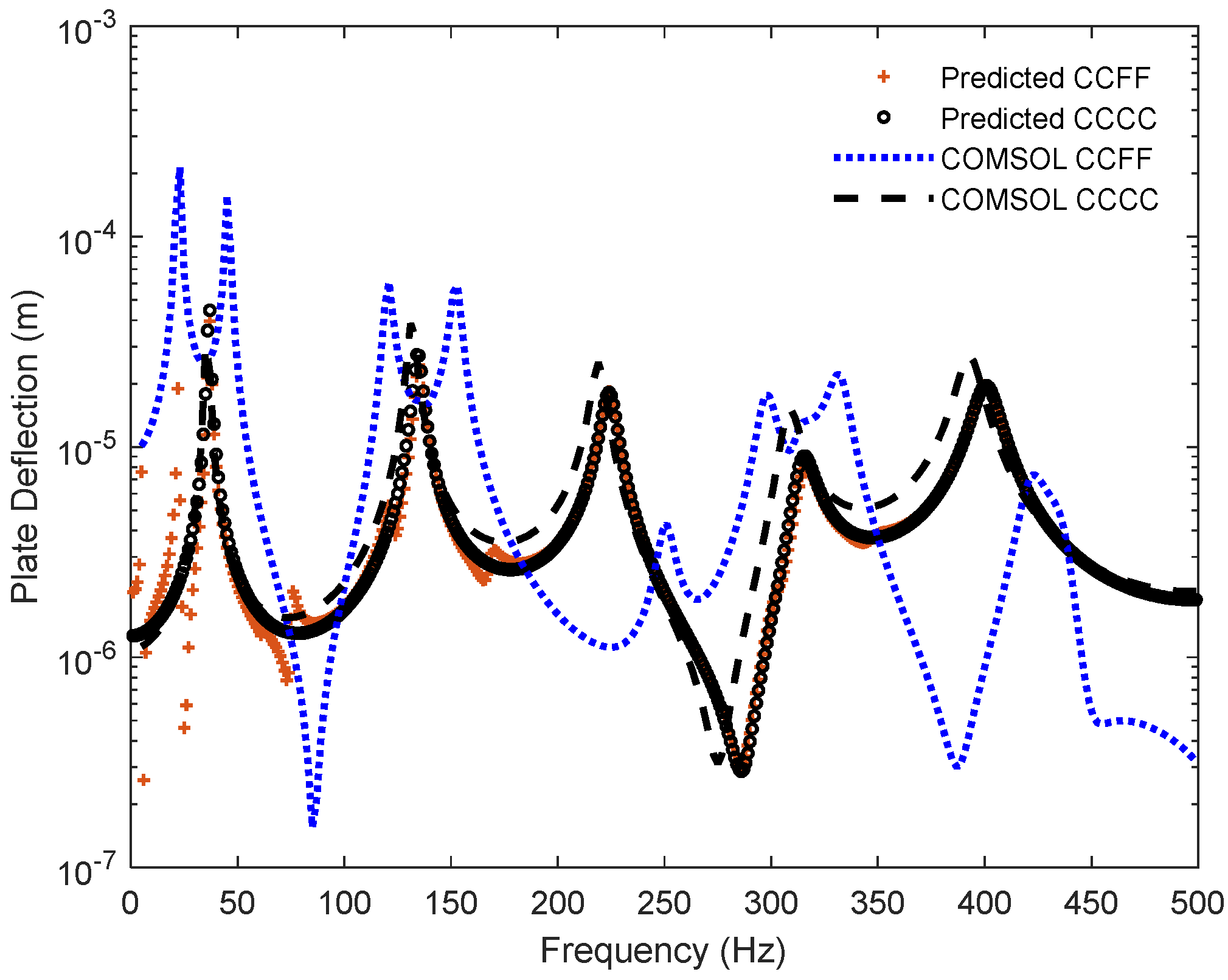
| Length (cm) | Width (cm) | Depth (mm) | Solid Density (kg/m3) | Elastic Modulus (GPa) | Loss Factor | Poisson Ratio |
|---|---|---|---|---|---|---|
| 50 | 50 | 2.5 | 1600 | 7.489 | 0.03 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aygun, H. Computational and Theoretical Investigation of Acoustical and Vibrational Properties of Rigid Thin Material. Acoustics 2024, 6, 83-96. https://doi.org/10.3390/acoustics6010005
Aygun H. Computational and Theoretical Investigation of Acoustical and Vibrational Properties of Rigid Thin Material. Acoustics. 2024; 6(1):83-96. https://doi.org/10.3390/acoustics6010005
Chicago/Turabian StyleAygun, Haydar. 2024. "Computational and Theoretical Investigation of Acoustical and Vibrational Properties of Rigid Thin Material" Acoustics 6, no. 1: 83-96. https://doi.org/10.3390/acoustics6010005
APA StyleAygun, H. (2024). Computational and Theoretical Investigation of Acoustical and Vibrational Properties of Rigid Thin Material. Acoustics, 6(1), 83-96. https://doi.org/10.3390/acoustics6010005







