Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models
Abstract
1. Introduction
2. Background
2.1. Nature of the Near-Field Environment and How It Evolves over Time
- Host rock—in addition to determining, in part, the nature of the groundwater at repository depth, the nature of the host rock also determines the relative importance of the engineered and natural barriers in the overall safety assessment. For low-permeability sedimentary host rock (clay, shale, and limestone), the container is a relatively minor contributor to overall safety since the transport of radionuclides through the geosphere is slow. In contrast, fractured crystalline rocks do not provide the same degree of radionuclide retardation and the use of long-lived containers, supported by robust long-term corrosion predictions, is common;
- Repository location—in all but one national program, the repository is to be located in the saturated zone 300–1000 m beneath the water table. Groundwaters at this depth are invariably anoxic, so the only available O2 is trapped in the repository sealing materials at closure. The one exception is the proposed DGR at Yucca Mountain, Nevada which is located in the vadose (unsaturated) zone located 300–400 m below the surface (Following submission of the construction license application by the U.S. Department of Energy in 2008, the Yucca Mountain Program was suspended and has essentially ceased. However, based on the Nuclear Waste Policy Act (amended in 1987), the HLW/SF repository at Yucca Mountain, Nevada is still the only designated HLW/SF repository site in the U.S.). Although the supply of atmospheric O2 to the repository might be restricted, it is prudent to assume that the disposal drifts are essentially aerated at all times. This, in turn, impacts the choice of container material, the nature of the likely corrosion processes, and the nature of the predictive models that are required;
- Buffer—the choice of buffer material immediately around the container (and, to some degree, that of the backfill material in the tunnels) affects the near-field chemical environment at the container surface, as well as the extent of microbial activity (both bentonite and cementitious backfill suppress near-field microbial activity). Bentonite buffer also limits the rate of supply of reactants to the container surface. In contrast, the absence of backfill will make microbial activity more likely, as well as allow advective transport of species to and away from the container;
- Container temperature—the maximum container temperature in most national programs is limited by the design of the repository to ≤100 °C in order to prevent damage to the backfill material. For the high-temperature operating mode (HTOM) repository layout at Yucca Mountain, the elevated near-field temperature was deliberately designed to prevent aqueous corrosion processes during the initial period of highest radiogenic activity. Even in DGRs in the saturated zone, there will be an initial period of unsaturated conditions around the container which must be accounted for in the lifetime prediction;
- γ-radiation dose rate—the maximum γ-dose rate depends on a number of factors, including the nature of the waste, the container loading, and the duration of interim storage, as well as the container design. Although the expected γ-dose rates are small in comparison to in-reactor dose rates, many national programs assess the extent of radiation-induced corrosion (RIC), both experimentally and through the use of predictive models;
- Groundwater chemistry—the salinity of the groundwater (characterised in Table 1 by the associated Cl− ion concentration) varies from site to site and often, for a given site, with depth. While useful as a broad indicator of the “corrosiveness” of a given location, the container is not in contact with the groundwater itself if a bentonite or cementitious backfill is used. Instead, the container is contacted by the porewater, the composition of which may be quite different from that of the groundwater. A prime example of the modification of the near-field environment by the backfill is the highly alkaline porewater in cement backfill which imparts passivity to the carbon steel overpack of the Belgian Supercontainer and impacts not only the nature of the resulting corrosion processes but also the types of models used to predict the long-term behaviour;
- Microbial activity—as noted above, the use of bentonite or cement backfill precludes near-field microbial activity. Thus, predictive models are based on the possibility of remote microbial activity and the subsequent transport of aggressive metabolic byproducts to the container surface. For un-backfilled repository designs, microbial activity is possible at the container surface, which comes with the challenge of predicting the extent of microbiologically influenced corrosion (MIC) underneath a biofilm;
- Mechanical loads—although the current review does not address purely mechanical failure modes, the nature (tensile, compressive, and shear) and magnitude of the residual and applied stresses on the container affect certain joint mechanical–corrosion degradation mechanisms.
| Country | Waste Type | Host Rock | Repository Location a | Buffer b | Max. Container Temperature (°C) | Max. γ-Radiation Dose Rate (Gy/h) | Groundwater [Cl−] (mg/L) | Notes |
|---|---|---|---|---|---|---|---|---|
| Belgium | HLW (SF) * | Boom clay | Saturated | Cementitious | <100 | 25 | 27 | |
| Canada | SF | Granite Shale/limestone | Saturated | Bentonite | 100 | 3 | 34,300 200,000 | 1 |
| China | HLW | Granite | Saturated | Bentonite | <100 | - | 1155 | |
| Czechia | SF | Granite | Saturated | Bentonite | <100 | 0.5 | TBD | 2 |
| Finland | SF | Granite | Saturated | Bentonite | <100 | 0.17–0.34 | 16,000 | |
| France | HLW (SF) * | Clay | Saturated | None (HLW) | <100 | <10 | 2000 | |
| Germany | HLW/SF | Salt | Saturated | Crushed salt | 200 | <1 | 300,000 | 3 |
| Japan | HLW | Generic | Saturated | Bentonite | 100 | 0.03 | TBD | 4 |
| Spain | SF | Granite, Clay | Saturated | Bentonite | 100 | _ | 6550 | 5 |
| Sweden | SF | Granite | Saturated | Bentonite | <100 | 0.2 | 6900 | |
| Switzerland | HLW/SF | Opalinus clay | Saturated | Bentonite | 150 | 0.1–0.2 | 3450 | |
| Taiwan | SF | Crystalline | Saturated | Bentonite | <100 | <1 | 50 | 6 |
| UK | HLW (SF) * | Generic | Saturated | TBD | 100? | 0.03–0.3 | TBD | 7 |
| USA | SF/HLW | Tuff | Unsaturated | None | 200–220 | <1 | 7 | 8 |
2.2. Container Materials and Designs
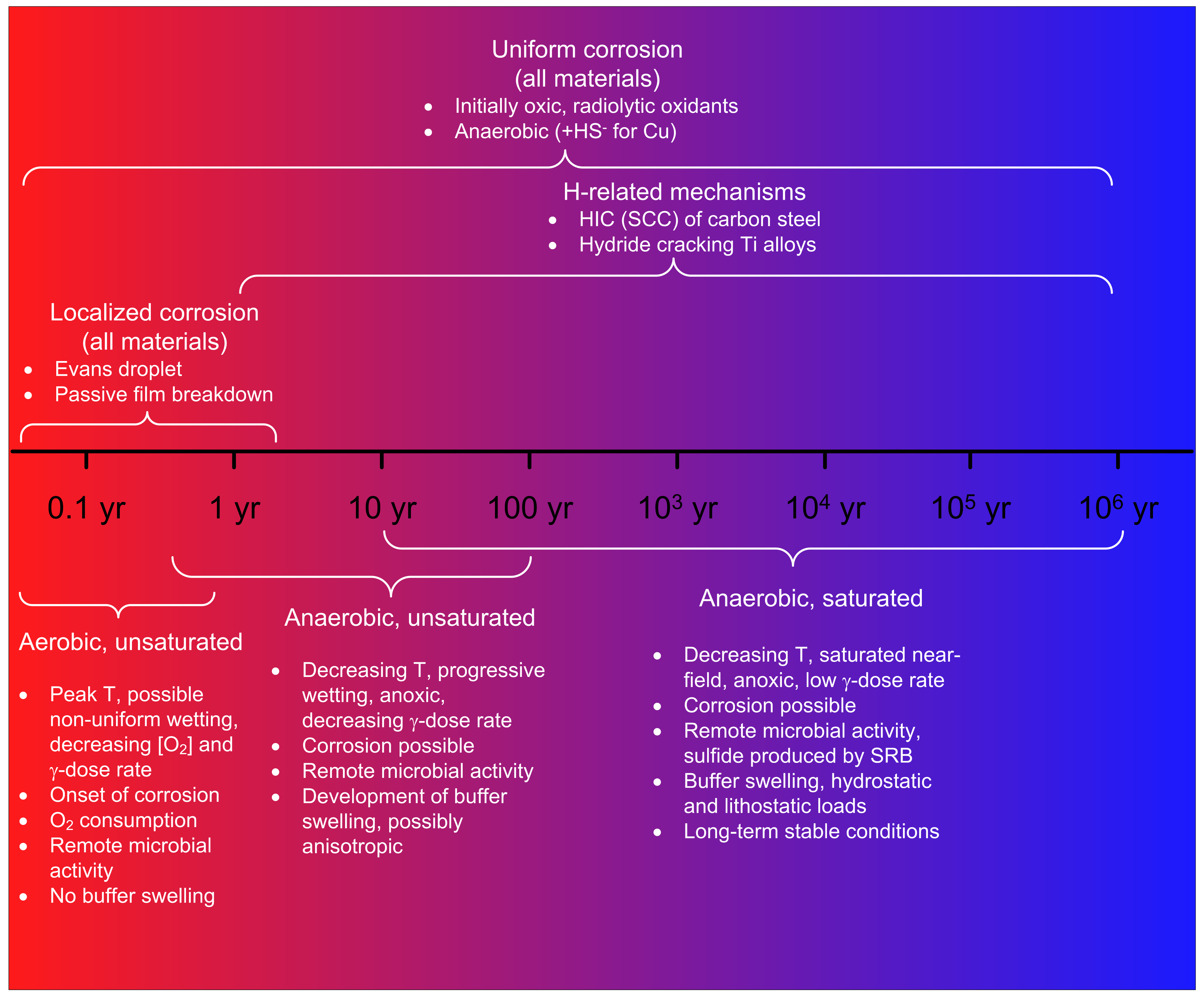
2.3. Evolution of the Corrosion Behaviour and the Implications for Lifetime Prediction
- An initial aerobic, unsaturated phase;
- A subsequent anaerobic, unsaturated phase;
- A long-term anaerobic, saturated phase.
3. Process Models
3.1. Uniform Corrosion
3.1.1. Empirical
3.1.2. Reactive Transport

- Reaction (1):
- annihilation of a cation vacancy () along with a metal atom (m) at the metal–film (barrier layer) interface resulting in the formation of a metal cation on the cation lattice (MM) and a vacancy in the metal phase (Vm);
- Reaction (2):
- generation of cation interstitials () at the metal–film interface;
- Reaction (3):
- generation of oxygen vacancies at the metal–film interface;
- Reaction (4):
- generation of cation vacancy and dissolved metal ion (Mδ+(aq)) at the film–solution (precipitated outer layer) interface
- Reaction (5):
- annihilation of metal interstitials at the film–solution (precipitated outer layer) interface
- Reaction (6):
- annihilation of oxygen vacancies at the film–solution (precipitated outer layer) interface and the formation of oxygen ions in an anion site (OO)
- Reaction (7):
- dissolution of the barrier layer oxide (MOχ/2) at the film–solution (precipitated outer layer) interface
3.1.3. Mass Transport
- Corrosion of copper in O2-free H2O based on the assumption that the interfacial dissolved H2 concentration is equivalent to that reported experimentally [43].
3.1.4. Electrochemical
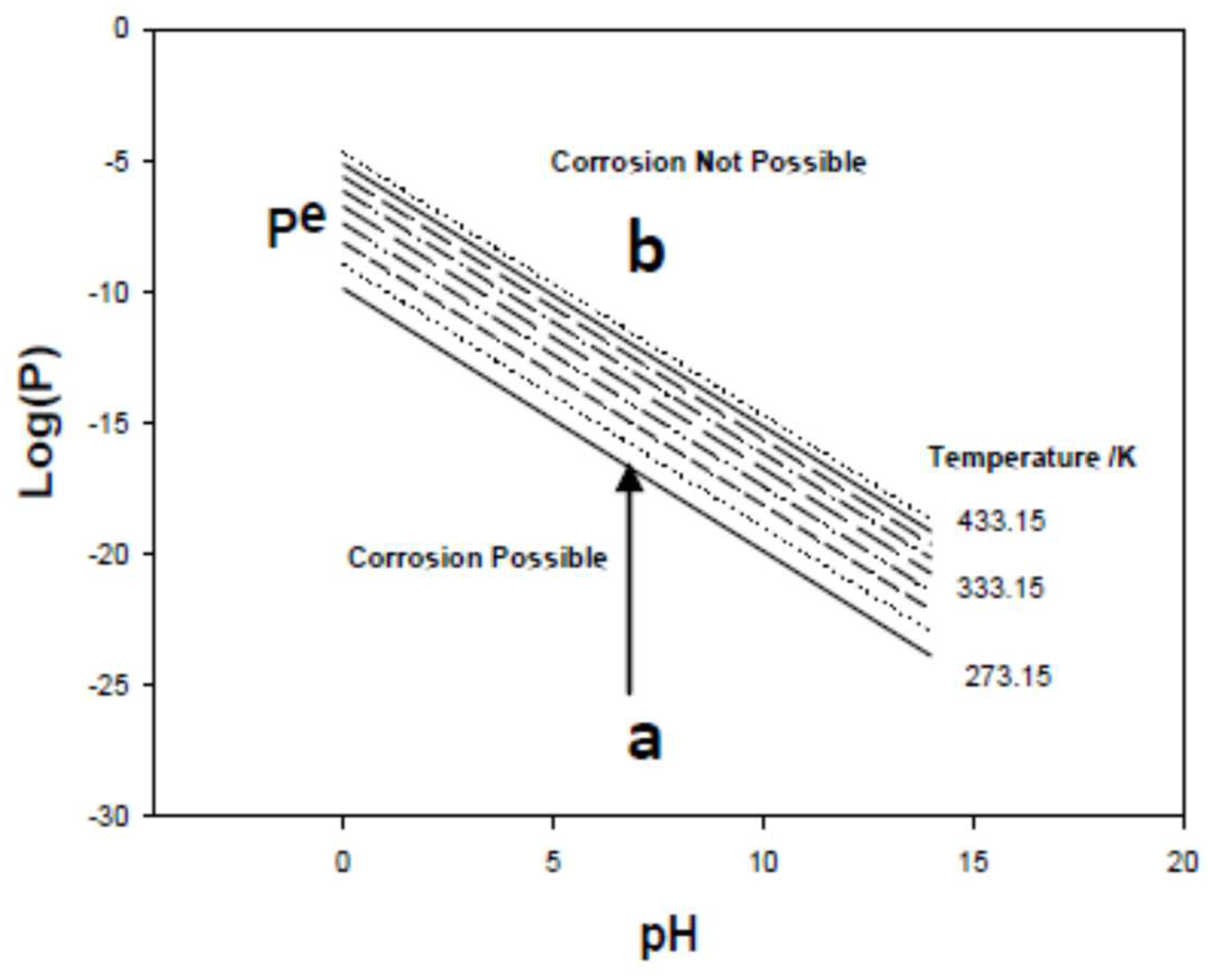
3.1.5. Thermodynamic
3.1.6. Current Status of the Process Modelling of Uniform Corrosion
3.2. Localised Corrosion
3.2.1. Requirement for Passivation
| Approach | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Requirement for passivation | Period of susceptibility based on ability to sustain passive current density for carbon steel [97]. Suitable pH, [Cl−], [SO42−], [HCO3−] and temperature for passivation of copper [98] | Establishes a period of time for which localised corrosion is of concern, which is typically a small fraction of the required service life. | - |
| Empirical | Pitting factor for copper [3] and carbon steel [10,99]. Extreme value analysis of maximum pit depth for copper [100] and carbon steel [101]). Time-dependent crevice propagation for Ti-Grade 2 [8]. Surface roughening factor of copper [16]. | Conceptually simple. In the case of archaeological analogue samples and data from long-term in situ experiments, the exposure periods can exceed the duration of the oxic phase in the repository. | Limited mechanistic basis. Typically requires a large database. Environmental conditions for buried objects are different from those in the DGR. Material used in long-term exposure tests is often different from container alloy. Extrapolation beyond the length of the exposure periods and to containers with a larger surface area than the specimens that form the database can be challenging. |
| Reactive transport | Propagation of crevice corrosion for carbon steel [102]. Initiation of crevice corrosion for Ni and Ti alloys [103]. Pit propagation for copper [104,105]. Atmospheric corrosion stainless steel [106] Initiation, propagation, stifling of pitting on carbon steel in cementitious backfill [107]. | Can provide additional mechanistic insight. Applicable to all phases of pit/crevice corrosion; initiation, propagation, stifling. | Difficult to define the cathode–anode surface area ratio. In some cases, no attempt to couple anode and cathode. Limited treatment of cathodic reduction of H+ inside occluded region. Difficult to predict shape of corroded region inside a pit or crevice. |
| Electrochemical | Pit initiation and period of propagation based on comparison of ECORR to film breakdown and repassivation potential for Alloy 22 [9,108] and copper [98]. | Mechanistically based and, although most current modelling relies on empirical measurements of the critical potentials, these too can be predicted deterministically. | Critical potentials dependent on method of measurement and many experimental variables. |
| Stochastic | Pitting of passive alloys [109,110,111] | Addresses variability and uncertainty inherent to localised corrosion. | Lack of mechanistic basis. |
| Decision tree | Localised corrosion of Alloy 22 due to dust deliquescence [112]. | Questions that form the decision tree are generally mechanistically based. | Less valuable if the answers to the question are qualitative. |
| Rules-based | Cellular automata model for carbon steel [113]. | Rules can be mechanistically based. | Coupling of processes occurring on different spatial scales can be difficult, e.g., mass transport on the scale of metres and corrosion on the scale of μm. |
3.2.2. Empirical

3.2.3. Reactive Transport
3.2.4. Electrochemical
3.2.5. Stochastic
3.2.6. Decision Tree
3.2.7. Rule Based
3.2.8. Current Status of the Process Modelling of Localised Corrosion
3.3. Environmentally Assisted Cracking
3.3.1. Stress-Corrosion Cracking
| Approach | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Limited propagation (SCC) | Slip-dissolution model for Alloy 22 [158] Limited O2 flux for aerobic SCC mechanisms for copper [159] | Mechanistically based. Avoids the need to demonstrate immunity over an extended period of time. | Large experimental database required. |
| Non-susceptibility (SCC) | Decision-tree analysis [154,155] Stress relief of fabrication stresses for carbon steel [5] Specification of steel grade with optimum chemical and microstructural properties [152,153] | Structure of decision tree is mechanistically based. Some evidence from pipeline operating experience to support benefits of stress reduction and improved material specification for steel | Relies heavily on empirical evidence |
| Threshold criterion (HIC) | Threshold [HABS] for onset of fast fracture for Ti alloys [160,161] Threshold hydride-layer thickness for crack initiation for Ti alloys [12,13,162] Threshold [HABS] for crack growth for carbon steel dependent on stress-intensity factor [20,26] | Conservative because of assumption of fast crack growth following initiation, except for hydride-layer thickness of Nakayama et al. [12,13,162]. | Prediction of [HABS] for Ti alloys depends on hydrogen pick-up ratio which can be difficult to predict, especially in the event of crevice corrosion and/or for Pd-containing grades. |
| Non-susceptibility (HIC) | Low strength of selected grades of carbon steel are immune to HIC [5,10] | Extensive industrial experience from oil and gas industry. | No direct evidence for long-term exposure to repository environments. |
3.3.2. Hydrogen- and Hydride-Induced Cracking
3.3.3. Current Status of the Process Modelling of the EAC of HLW/SF Containers
3.4. Microbiologically Influenced Corrosion
3.4.1. Empirical
3.4.2. Mass-Balance Approaches
3.4.3. Reactive Transport Models
- 1D representation of the buffer, backfill, and host rock, with all materials treated as equivalent porous media;
- diffusive mass transport of reactants and products but not of microbes, which were deemed to be immobile in the compacted bentonite buffer;
- organotrophic and lithotrophic reduction of sulphate using organic carbon (represented by acetate) and H2, respectively, as electron donors;
- Monod kinetics to describe the rate of microbial reactions;
- death, or alternatively the dormancy, of microbes due to desiccation (low water activity) or irradiation, with recycling of a fraction of the dead cell material;
- corrosion of the copper container based on the assumption of a sulphide-transport limited corrosion process;
- precipitation of mackinawite FeS as a sink for sulphide;
- spatial and temporal variation of temperature.
- aerobic respiration;
- organotrophic and lithotrophic denitrification;
- nitrogen fixation;
- nitrosofication;
- nitrification;
- ammonia oxidation;
- fermentation;
- organotrophic and lithotrophic Fe(III) reduction;
- organotrophic and lithotrophic sulphate reduction.
3.4.4. Mass Transport
3.4.5. Current Status of the Process Modelling of the MIC of HLW/SF Containers
3.5. Radiation-Induced Corrosion
- neutron- and/or γ-irradiation could embrittle the material, rendering the container more susceptible to fracture, especially cast iron and carbon steel;
- the production of radiolytic oxidants could increase the rate of uniform corrosion;
- ennoblement of ECORR by radiolytic oxidants could increase the probability of the initiation of localised corrosion of passive materials;
- radiolysis could produce species that induce localised corrosion or EAC, such as ammonia or nitrite which are SCC agents for copper;
- the absorption of hydrogen could lead to embrittlement of various container materials.
3.5.1. Empirical
3.5.2. Uncoupled Radiolysis Models
| Approach | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Empirical | Effective G-value for radiolytic oxidants for carbon steel [5]. Dose rate limit for significant effect of irradiation [11,30,31,201] | Concept of a “threshold” dose rate is useful for engineering purposes | The definition of “significant” depends on the container material, as well as on the experimental methodology and duration. |
| Bulk radiolysis (uncoupled) | Humid air radiolysis model (HARM) for copper [197]. RIC mixed-potential model for copper [202] | Mechanistically based. Computationally simpler to uncouple radiolysis reactions from interfacial processes. | Assumes steady-state concentrations of radiolysis products are not affected by interfacial reactions. |
| Bulk radiolysis (coupled) | Thin-layer mixed-potential model (TLMPM) [203] Coupled corrosion-bulk radiolysis model for copper [204,205] Copper corrosion model for radiation-induced corrosion (CCM-RIC) [206] | Yield of radiolysis products takes into account their interfacial consumption. Mechanistically rigorous approach. | Some software requires that the interfacial reaction be “homogenized“, i.e., that the heterogenous process be converted to a homogeneous reaction. Interfacial rate constants may be difficult to obtain, especially for radical species. |
3.5.3. Coupled Radiolysis Models
3.5.4. Current Status of the Process Modelling of the RIC of HLW/SF Containers
3.6. Joint Mechanical–Corrosion Degradation Models
3.6.1. Environmentally Assisted Cracking
3.6.2. Effect of the Formation of Expansive Corrosion Products
3.6.3. Fracture Mechanics
3.6.4. Current Status of the Process Modelling of Joint Mechanical–Corrosion Effects
3.7. Miscellaneous Corrosion Models
- thermodynamic analysis of the effects of phosphorus and sulphur on the properties and structure of pure copper and the implications for the creep behaviour [218];
- calculation of bulk and surface properties of Cu(I) sulphides using the interface Green’s function method [219];
- density functional theory (DFT) and linear response theory calculations of the stability of various Cu-H-O species that have been proposed to be formed during the corrosion of copper in O2-free H2O [220];
- DFT calculations of copper vacancy diffusivity in a Cu2S film in support of PDM characterization of the film [224].
- CALPHAD (calculation of phase diagrams) calculations of the temperature-time-transformation (TTT) and the possible thermal ageing of various Ni-Cr-Mo alloys for the Yucca Mountain program. Phase transformation could impact the localised corrosion behaviour of the alloy [225];
- Model for predicting the possibility of the separation of solutes due to the flow of electrolytes over the surface of a waste package in an unsaturated environment. The model addresses the question of whether the composition of the surface electrolyte in an evaporating droplet (and, crucially, the ratio of the concentration of aggressive ions such as Cl− to that of inhibitive ions such as NO3−) will vary circumferentially around the waste-package surface due to solute solubility differences as the drip moves over the surface under the effects of gravity [226];
- Calculation of the time-dependent internal pressure due to hydrogen diffusion through the wall of a carbon steel container during the long-term anaerobic phase. Internal pressurisation offsets the compressive load from the buffer swelling and hydrostatic pressures, but will also lead to an increased risk of hydrogen-induced cracking due to internal or embedded flaws [227];
- The use of multiple models to determine the number and timing of canister failures due to earthquakes and shear across deposition holes in a KBS-3-type repository in crystalline rock [228].
3.8. Ancillary Models
4. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Generic reactive transport model for copper or steel containers in a saturated repository | Reactive transport | 2D cartesian or axisymmetric cylindrical reactive transport model with electrochemical boundary conditions. Assumes film-free container surface. Includes effects of sulphate reduction to sulphide and radiolytic oxidants. Not applied to a specific repository system due to cancellation of basalt project in the U.S. | [255] |
| Mixed-potential model for carbon steel in bentonite buffer | Reactive transport | Mixed-potential model for the uniform corrosion of carbon steel in compacted bentonite buffer in a DGR in granitic host rock. The anodic dissolution of Fe as Fe2+ was coupled to the cathodic reduction of O2 (assumed to be under transport control) and of H2O (assumed to be kinetically controlled). The production and consumption of radiolytic oxidants were also considered. Model used to predict a steady-state ECORR value and a conservative corrosion rate at an assumed constant temperature of 90 °C. The reduction in corrosion rate due to precipitated corrosion products was not taken into account. Also used for assessment of corrosion of carbon steel for disposal in marine sediment. | [5,6] |
| Point defect model (PDM) | Reactive transport | General framework for the prediction of the growth and breakdown of passive films. Applied to a number of HLW/SF container corrosion issues (see below). | [33,34,35] |
| Mixed-potential model for copper in O2-containing Cl− environments | Electrochemical | Analytical mixed-potential model for copper validated against experimental data covering five orders of magnitude variation in mass-transfer coefficient, three orders of magnitude in [O2], and one order of magnitude in [Cl−]. Subsequently implemented using COMSOL. | [44,45] |
| Copper corrosion model (CCM) | Reactive transport | Mixed-potential model based on coupling of interfacial electrochemical reactions to mass-transport, redox, adsorption/desorption, and precipitation/dissolution reactions occurring in highly compacted bentonite buffer. Model assumes initially aerated, Cl− dominated conditions. Effects of thermal and saturation transients included. | [39,40,77,78,83] |
| CAMEO | Reactive transport | 3D cylindrical geometry of copper canister in deposition hole with assumption that corrosion rate is determined by either the rate of transport of oxidants (O2 or HS−) towards or of corrosion products (CuCl2−) away from the container. | [256] |
| Threshold corrosion product spalling thickness | Analytical | Time-dependent decrease in corrosion rate due to build up of protective corrosion product affected by assumed spalling of corrosion products on carbon steel container in an un-backfilled disposal tunnel. | [257] |
| Uniform corrosion of carbon steel in bentonite | Mixed-potential model | Coupled interfacial electrochemical kinetics for Fe dissolution and O2 and H2O reduction with O2 transport in bentonite | [46] |
| CUPRS | Electrochemical | Mixed-potential model for copper in O2-containing Cl− environments. Based on model of [44] | [93] |
| Steel–clay interaction models | Reactive transport | Geochemical models focussed on the prediction of alteration of the clay barrier due to reactions with dissolved Fe. Generally based on a thermodynamic speciation code coupled to a transport model. However, with the exception of the study of Marty et al. [38], the corrosion rate is an input parameter and is not predicted by the codes. | [36,37,38,87,88,258,259] |
| General corrosion model (GCM) and accumulated damage model (ADM) for Alloy 22 | Reactive transport | Based on the PDM for prediction of barrier layer thickness and Butler–Volmer expressions for the cathodic reactions (reduction of O2 and/or H2O). Model predicts ECORR, corrosion rate, and transpassive dissolution potential. Application of model to predict transients in passive film growth on Alloy 22 | [28,58,61,62] |
| Long-term passivity of Alloy 22 | Reactive transport | Mechanistic model for the long-term passive dissolution of Alloy 22 based on an extension of the PDM. Conclude that dissolution of alloy is congruent provided diffusivities for the alloying elements are similar. Periodic film spalling should not drastically increase the corrosion rate. Therefore, long-term prediction based on the extrapolation of empirical corrosion rates is justified. | [260] |
| Uniform corrosion of carbon steel | Empirical | Arrhenius temperature-dependent fit to empirical data for oxic and anaerobic conditions in compacted clay or clay–water systems | [116] |
| Wet–dry cycle atmospheric corrosion | Reactive transport | Atmospheric corrosion of iron during a wet–dry cycle. | [261] |
| Diffusion Poisson coupled model (DPCM) | Reactive transport | Based on the point defect model but with the potential profile within the barrier oxide layer explicitly calculated based on the Poisson equation | [41,69,262,263,264] |
| Low-temperature oxidation model | Empirical and reactive transport | Simple empirical and advanced reactive transport models for predicting the extent of dry oxidation of carbon steel containers at repository-relevant temperatures | [265,266] |
| Transport model for the uniform corrosion of carbon steel | Reactive transport | 1D cylindrical reactive transport model for the corrosion of carbon steel in bentonite buffer. Corrosion rate assumed to be determined by the rate of transport of dissolved Fe2+ away from the container surface. Sorption of Fe2+ by bentonite was the only reaction considered. Corrosion rate depends on solubility of assumed corrosion product. | [91] |
| Uniform corrosion rate of copper and carbon steel | Empirical | Power-law time-dependent corrosion rates for Cu and carbon steel derived from experiments in bentonite slurry | [267] |
| Uniform corrosion Alloy 22 | Empirical | Uniform corrosion rate derived from mass-loss results from 5-year exposure tests and assumed to be temperature dependent but constant over time. Rates independent of solution chemistry. | [9,32] |
| Corrosion potential model for Alloy 22 | Empirical | Empirical fit to long-term ECORR measurements expressed as a function of T, pH, [Cl−] and [NO3−]. For use with ERCREV relationship to determine if crevice corrosion initiates. | [9,32] |
| Uniform corrosion Ti Grade 7 | Empirical | Uniform corrosion rate derived from mass-loss results from 2.5- and 5-year exposure tests and assumed to be independent of temperature and constant over time. Rates independent of solution chemistry. | [9] |
| Diffusion-limited corrosion model for carbon steel | Reactive transport | Interfacial dissolution of Fe under anaerobic conditions described by an equilibrium expression with Fe2+ and H2 as corrosion products. Corrosion rate is then determined by the flux of Fe2+ and/or H2 away from the container surface, with equilibrium corrosion product concentrations calculated using PHREEQC. Corrosion rate decreases with decreasing effective diffusivity. | [268] |
| Copper sulphide model (CSM) | Reactive transport | Extension of the copper corrosion model (CCM) to include the effects of sulphide present either in the groundwater or generated by sulphate-reducing bacteria (SRB) activity. Based on the assumption of the formation of a porous Cu2S corrosion-product film. | [70,71,72,76,79,80,190,191,192] |
| Mixed-potential model for predicting H2 generation in ONDRAF/NIRAS supercontainer | Reactive transport | Mixed-potential model to predict the evolution of the consumption of initial O2 and the subsequent generation of H2 within the cementitious backfill due to corrosion of the carbon steel container and stainless steel envelope | [269] |
| Corrosion domain and volt-equivalent diagrams | Thermodynamic | Assessment of the thermodynamic driving force for corrosion of copper in pure water and in the presence of sulphur species and other ligands. | [47,48,270] |
| Uniform corrosion of carbon steel | Empirical | Assumption of a constant corrosion rate based on empirical data. | [11,30,31,254] |
| Point defect model for copper in presence of sulphide | Reactive transport | Application of PDM to passivation of copper by sulphide and development of a mixed-potential model for the prediction of ECORR | [65,271] |
| Uniform corrosion of carbon steel in anoxic environments in presence of corrosion-product film | Coupled chemical equilibrium and mass-transport model | Effect of bilayer oxide film on corrosion rate of carbon steel in anoxic environments. Model accounts for H2O diffusion through film and film dissolution at the film–solution interface. | [42] |
| Steel corrosion model (SCM) | Reactive transport | 1D reactive transport model for carbon steel corrosion under anoxic conditions, solved using a mixed-potential model for the boundary conditions on the container surface. Model accounts for the development of a mixed bentonite–corrosion-product layer, as well as the production and periodic release of H2. | [73,81,272,273] |
| Oxide growth on copper during friction stir welding (FSW) | Empirical | Estimation of amount of oxygen incorporated into an FSW during welding based on expected thermal profile and empirical copper oxidation data. | [274] |
| Effect of precipitated porous corrosion products on carbon steel | Reactive transport | 1D finite element model to predict the effect of precipitated FeCO3 on the time-dependent corrosion rate of carbon steel. Considered both a constant porosity and variable porosity corrosion-product layer, with the latter in better agreement with experimental data. Effect of conductive corrosion-product layer also considered. | [74,75] |
| PDM for steel in cementitious environments | Reactive transport | Coupling PDM with Butler–Volmer expressions for the cathodic reaction (H2 evolution) constitutes a mixed-potential model from which the corrosion rate and ECORR can be determined. Model also used to demonstrate the irreversibility of the passive state for carbon steel in the cementitious environment, | [60,63] |
| Copper corrosion in pure O2-free H2O | Mass transport, empirical | What-if calculations for the corrosion of copper in pure H2O based on (a) temperature-dependent corrosion rate derived from the proposed literature rates or (b) mass transport of H2 away from canister surface. | [43] |
| Extent of copper corrosion based on results from large-scale in situ tests | Empirical | Regression analysis of extent of copper corrosion as a function of temperature and buffer thickness from large-scale in situ tests. | [275] |
| Corrosion of copper at high Cl− concentration | Coupled thermodynamic speciation–mass transport | PHREEQC thermodynamic speciation code used to predict equilibrium-dissolved Cu concentration, which was then used as a source concentration in simplified mass-transport expressions to predict the corrosion rate as a function of pH, [Cl−], T, and mass-transfer coefficient | [49,92] |
| Anaerobic corrosion of carbon steel in bentonite | Reactive transport | Model based on observations from various bench-scale and in situ experiments. Fractures in bentonite can occur as a result of desiccation due to H2O consumption in the corrosion reaction. Oxygen is assumed to be immobile but reacts with Fe2+ diffusing away from the corroding interface. Precipitation of corrosion products results in decoration of fractures in bentonite with Fe(II)/Fe(III) and, ultimately, clogging of the pore structure. | [276] |
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Pitting factor for copper | Empirical | Ratio of the deepest penetration (measured from the original surface) to the mean depth of penetration. Thus, a pitting factor of 1 represents uniform corrosion. Pitting factors typically determined from long-term exposure of archaeological or anthropogenic objects to near-surface burial conditions. | [3] |
| Pit propagation rate for carbon steel | Empirical | Time-dependent pit depth expression based on electrochemically grown pits in Cl−/HCO3− environments. | [277] |
| Period of passivation of carbon steel | Electrochemical | Maximum duration for which carbon steel is deemed to be passive and, therefore, susceptible to localised corrosion is defined as the period that the flux of oxidants (initially trapped O2 and/or oxidising radiolysis products) is sufficient to sustain the passive current density. | [97,278,279] |
| Extreme value analysis (EVA) of pit depths for carbon steel | Statistical analysis of empirical data | EVA of laboratory pit depths fitted to limited and unlimited distribution functions to predict time dependence of maximum probable pit depth on container. | [5,128] |
| Propagation of pitting or crevice corrosion of carbon steel | Reactive transport | 1D or 2D finite-element model of chemistry inside and dissolution rate within an occluded pit or crevice as a function of external electrode potential and crevice dimensions. Propagation assumed not to be limited by external cathode. | [102,125,126,127] |
| Model for large-scale corrosion cells | Reactive transport | Reactive transport model for predicting localised corrosion due to long-range electrochemical cells, as might develop due to differential aeration or spatial variations in current/potential behaviour of the (steel) substrate. Such long-range cells tend to result in surface roughening rather than discrete pits. | [280] |
| Pit or crevice chemistry and electrochemical potential model | Reactive transport | Coupled speciation, transport, and electrochemical model for the prediction of the evolution of the chemistry and potential distribution within the occluded region. | [281] |
| Crevice corrosion initiation time | Reactive transport | Prediction of initiation for crevice corrosion of titanium and stainless steels based on time to establish a critical pH within the crevice. Effect of crevice length and gap found to be important. | [103,144,145] |
| Damage function analysis (DFA) | Deterministic | General deterministic approach to predicting corrosion damage. Applied to the pitting of Alloy 22 using the point defect model for determining passivity breakdown, deterministic models for cavity growth, and the assumption of delayed repassivation. | [59,282,283] |
| Model for the initiation of crevice corrosion | Reactive transport | Development of the earlier model for crevice propagation, with initiation determined by the time to establish critical pH, [Cl−], and potential within the crevice. | [132] |
| Stochastic pitting models | Stochastic, Monte Carlo | Stochastic models for predicting the initiation time, survival probability, and pit-depth distribution. Time to container failure and the time dependence of the number of through-wall pits can also be predicted. | [109,110,111] |
| Extreme value analysis (EVA) of pit depths on copper | Statistical analysis of empirical data | EVA of empirical pit depth data from long-term buried corrosion study and Bronze Age archaeological artefacts. Time dependence of location parameter permitted extrapolation in time for prediction of probability of maximum pit depth as a function of time. | [100] |
| Extreme value analysis (EVA) of pit depths for carbon steel | Statistical analysis of empirical data | EVA of maximum and average corrosion depths on galvanostatically polarised specimens. Derived a maximum pit depth–average corrosion depth ratio for any one of 20,000 containers. | [101,120] |
| Crevice corrosion initiation model for Fe-Ni-Cr-Mo alloys | Reactive transport | Prediction of chemistry and distribution of potential within crevice for Type 316L stainless steel and Alloy 825. Initiation based on time for pH, [Cl−], and potential to result in depassivation of surface inside crevice. | [130] |
| Crevice corrosion propagation model for Ti Grade 2 | Probabilistic, empirical | Rate of crevice corrosion based on empirical measurements and treated as temperature dependent. | [7,8,123] |
| Use of repassivation potential as a criterion for the initiation of localised corrosion | Electrochemical | Definition of the electrochemical criterion for the initiation of localised corrosion (in the form of either pitting or crevice corrosion); ECORR ≥ ERP/ERCREV. Repassivation potential is argued to be a more conservative criterion for initiation than the film breakdown potential. | [108,146,147] |
| Pitting of carbon steel in compacted bentonite | Electrochemical | Maximum pit depth predicted based on duration of pitting and maximum pit growth rate. Duration of pitting equated to length of time that the O2 flux can sustain the passive current density. Pit growth rate based on Sharland localised corrosion model and empirical pit growth expression | [46] |
| Pitting of carbon steel | Reactive transport | Reactive transport model of pit propagation in carbon steel. Pit kinetics dependent on assumed cathode size. | [133] |
| Crevice chemistry model for Alloy 22 | Reactive transport | Prediction of the evolution of the chemistry inside a crevice on Alloy 22 as a function of crevice geometry. Predicted decrease of pH in crevice insufficient to lead to crevice initiation, especially in combination with the decrease in potential within the crevice. | [131] |
| Environmental conditions for passivation of carbon steel | Empirical | Based on active or passive characteristics of voltammograms measured in compacted bentonite | [10] |
| Equilibrium-mass transport model for pitting of copper | Reactive transport | Pit propagation model based on the need to prevent pit stifling by precipitation of corrosion products within the pit. Equilibrium calculations of dissolved species coupled with transport expressions determine the rate of removal of oxidised copper from pit. Assumes pit propagation is anodically limited. | [104,105,134] |
| Stochastic localised corrosion model | Rule based | Generic rule-based model for predicting passivation and evolution from uniform to localised corrosion. | [284] |
| Depth-dependent pitting factor for carbon steel | Empirical | Pitting factor decreases with increasing depth of uniform corrosion | [116] |
| Critical potential for initiation and repassivation of passive alloys | Based on the concept of a critical electrochemical potential that must be exceeded for the initiation of pitting or crevice corrosion. Pit or crevice stifling occurs below the repassivation potential | Crevice corrosion of Ti alloys Crevice corrosion Alloy 22 | [9,12,148,285] |
| Extreme value analysis (EVA) of pit depths | Statistical analysis of empirical data | Carbon steel | [12,286] |
| Propagation of crevice corrosion of iron | Electrochemical-based reactive transport | Prediction of chemical conditions and potential distribution within an occluded region and the conditions under which precipitation and, hence, crevice stifling might occur. | [129] |
| Cathodic limitation of crevice corrosion under atmospheric conditions | Electrochemical | Analytical expressions for the extent of coupling between an external cathode and an occluded pit or crevice under atmospheric conditions. Initially developed for stainless steel, subsequently applied by Payer and Kelly to the case of the crevice corrosion of Alloy 22 under dust deposits. Model provides conditions of crevice dimensions and electrolyte conductivity (related to salt loading and RH) under which pits will either propagate or stifle. | [124,142,143] |
| Localised corrosion of Alloy 22 under dust deposit | Decision tree | Analysis of the possibility of crevice corrosion of Alloy 22 due to deliquescence of soluble minerals in a dust layer deposited on a waste package | [112,149] |
| Localised corrosion of Alloy 22 due to seepage drips | Decision tree | Crevice corrosion requires that (i) seepage drips contact waste-package surface (no thermal or capillary barrier, drip shield failed), (ii) the composition of seepage water leads to development of aggressive aqueous phase after evaporation, (iii) a crevice exists, and (iv) conditions are sufficiently oxidising. | [150] |
| Crevice corrosion of Alloy 22 | Empirical | Model accounts for initiation, propagation, and stifling of crevice corrosion of Alloy 22. Initiation based on the ECORR ≥ ERCREV criterion, with the value of ERCREV dependent on temperature and [Cl−] and the inhibitive effects of NO3−, CO32−, and SO42−. Propagation based on empirical time-dependent penetration depth. Empirical expression for ECORR. Monte Carlo simulations run to account for variability and uncertainty. | [117] |
| Crevice corrosion under porous deposit | Reactive transport | General model for prediction of crevice initiation and propagation for a metal covered by a permeable layer, such as a dust layer on a HLW/SF container in an open disposal tunnel | [135] |
| Crevice corrosion initiation for Alloy 22 | Empirical | Empirical expression for the crevice repassivation potential ERCREV as a function of T, [Cl−], and [NO3−]. ERCREV used as a conservative indicator of crevice initiation. | [9,32] |
| Surface roughening factor for copper | Empirical | Localised corrosion of copper under repository conditions takes the form of surface roughening rather than discrete pits, and is consistent with the non-permanent spatial separation of anodic and cathodic processes. Treated in lifetime predictions as an allowance of 50–100 μm. | [15,16] |
| Crevice chemistry model for Alloy 22 | Reactive transport | Model for predicting the development of the chemistry inside and outside an occluded region, but link to either the initiation or propagation of crevice corrosion not stated. | [287] |
| Cellular automata (CA) model for surface roughening of carbon steel | Rule based | CA approach for pitting and surface roughening of carbon steel. Extended to include a probabilistic treatment of the probability of the transitions between different states. | [113,151] |
| Critical potential for initiation and repassivation of passive alloys | Based on the concept of a critical electrochemical potential that must be exceeded for the initiation of pitting or crevice corrosion. Pit or crevice stifling occurs below the repassivation potential | Attempt to apply literature expressions for pitting and repassivation potentials to bentonite pore-water solutions. Correlation fails because copper not passive in bentonite pore water | [288,289] |
| Atmospheric pitting corrosion of stainless steel | Reactive transport | Reactive transport model for the pitting of stainless steel in contact with a thin electrolyte layer representative of atmospheric conditions. The extent to which the external cathode can couple to the anodically dissolving pit due to the limited conductivity of the thin electrolyte layer is taken into account in the model. | [106] |
| Passivity breakdown of Cu2S films | Reactive transport | Determination of the effect of chloride ions and elevated temperatures on the breakdown of passive Cu2S films and interpretation using the point defect model | [64,65] |
| Dissolution of oxide particles in copper friction stir welds | Reactive transport | Finite-element model for the dissolution of Cu2O particles embedded in the surface of FSW based on the assumption of chemical equilibrium between the oxide and dissolved Cu(I) species | [136] |
| Pit repassivation model | Reactive transport | Deterministic model for predicting pit repassivation based on the concept that there exists a critical pit propagation rate (and, hence, a critical coupling current between internal anode and external cathode) necessary to maintain aggressive conditions within the pit. Applied to the case of the pitting of the carbon steel overpack for the Belgian Supercontainer concept. | [137] |
| Pitting of carbon steel in alkaline cementitious porewater | Reactive transport | Application of the PDM and DFA to predict the initiation (incubation time and critical potential), propagation, and stifling of pits on Belgian Supercontainer. | [107] |
| Effect of chloride ions on passivity breakdown of carbon steel in alkaline solutions | Reactive transport | Use of PDM to predict the effect of [Cl−] on the breakdown potential of passive films on carbon steel in simulated cementitious pore water solutions. No passivity breakdown for [NaCl] ≤ 1 mol/L. | [138] |
| Environmental conditions for passivation of copper | Machine learning | Machine-learning algorithms applied to empirical electrochemical database to predict conditions of T, pH, [Cl−], [SO42−], [HCO3−] for passivation of Cu as a prerequisite condition for pitting | [98,114] |
| Probabilistic pitting model for copper under aerobic, saturated conditions | Electrochemical/Machine Learning | Pit initiation based on requirement for a passive surface and exceeding a critical potential, with propagation based on empirical growth law. Probabilistic model accounts for variability and uncertainty in repository environmental conditions | [98,114] |
| Model Name or Brief Description | Model type | Description | Reference(s) |
|---|---|---|---|
| Hydrogen degradation (embrittlement and/or hydrogen-induced cracking) of carbon steel | Empirical | Excluded based on the use of a relatively low-strength grade of carbon steel with limited empirical susceptibility to effects of absorbed H. | [5,10] |
| Stress-corrosion cracking (SCC) of carbon steel | Empirical | Excluded based on the proposed use of stress relief to reduce the residual stress to less than 50% of the yield strength. | [5] |
| Limited propagation model for SCC of copper | Empirical | For aerobic forms of SCC of Cu (e.g., in NO2− solutions), rate of crack propagation determined as a function of applied anodic current density. Under repository conditions, corresponding current density is due to flux of oxidant (O2) to the container surface, from which the rate of crack growth as a function of time can be estimated. | [159] |
| Critical absorbed hydrogen concentration for HIC of Ti alloys | Empirical | Based on empirical threshold of absorbed H concentration for the loss of fracture toughness of Ti alloys and the assumption that a defect of appropriate size, location, and orientation will be subject to a sufficient tensile load that the fracture toughness will exceed. | [160] |
| Critical hydride-layer thickness HIC of Ti alloys (Ti-H-iT model) | Empirical | Cracks propagate due to the repeated fracturing of Ti hydrides when the hydride layer reaches a critical thickness of approximately 10 μm. Hydride-layer thickness is proportional to the square root of time and the corrosion current density. Threshold charge density below which no cracks are observed experimentally. Crack depth approximately 50% of thickness of hydride based on empirical data. | [13,162] |
| Copper corrosion model for stress-corrosion cracking (CCM-SCC) | Reactive transport | Modified version of the CCM to include the prediction of the interfacial pH. Used in conjunction with the CCM-MIC to predict the time dependence of the interfacial concentration of SCC agents (nitrite, ammonia, acetate), of ECORR and the interfacial pH, the latter two parameters then compared with potential and pH at which SCC of copper has been observed empirically. CCM suite of models based on active dissolution of surface instead of passive, as required for SCC. | [156,157] |
| Slip dissolution model for SCC of Alloy 22 | Empirical | Crack initiation and propagation model based on the requirements of a threshold stress for crack initiation and a threshold stress-intensity factor KISCC for crack growth. Crack growth rate a function of KI. | [158] |
| SCC of copper | Decision-tree analysis | Logical basis for reasoned argument to exclude possibility of SCC of copper. Each prerequisite environmental, material, and stress-related condition must be met for SCC to be possible. Applied to SCC under aerobic and anaerobic, saturated and unsaturated near-field conditions. | [154,155] |
| Stress-corrosion cracking (SCC) of carbon steel | Empirical | Excluded based on the absence of suitable environmental conditions and/or of cyclic loading found necessary to support crack growth in anaerobic near-neutral pH environments. | [290] |
| HIC Ti Grade 7 | Probabilistic | Based on concept of a threshold absorbed H concentration above at which fast fracture occurs and the time-dependent absorption of H due to uniform corrosion. Under oxic conditions, only a fraction of the total cathodic current is supplied by H2 reduction and only a fraction of the resulting H is absorbed. | [161,165,166] |
| Hydrogen degradation of copper | Transport | Model developed to predict H2 bubble formation during electrochemical charging of OFP copper. For H charging rates typical of anaerobic corrosion in the repository (1 nm/yr), effects of absorbed H would be minimal. | [291,292] |
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Maximum extent of sulphidation by SRB | Mass balance | Mass-balance calculation of the maximum amount of FeS that could be produced based on the stoichiometry of organotrophic sulphate reduction and the assumption that organic carbon is the limiting factor, and on the assumption of 100% bioavailable organic matter in the bentonite buffer. | [5] |
| Nutrient and energy balance analysis | Mass and energy balance | Analysis of the inventory of nutrients and potential energy sources in the repository, leading to a calculation of the maximum microbial population | [171] |
| Radiation-induced microbial-depleted zone | Empirical | Creation of “sterilized” zone around container due to reduction in microbial population due to γ-irradiation of buffer material and empirical radiation-sensitivity of indigenous microbes. | [293] |
| Microbial activity model (MAM) | Reactive transport | Monod kinetics used to describe rates of organotrophic and lithotrophic sulphate reduction by SRB under repository conditions, and the reaction of the sulphide with Fe(II) and the copper container. | [174] |
| Copper corrosion model for microbiologically influenced corrosion (CCM-MIC) | Reactive transport | Extended version of the CCM to include various forms of microbial activity, including aerobic respiration, denitrification, nitrogen fixation, nitrosofication, ammonia oxidation, fermentation, iron reduction, and sulphate reduction. Microbial activity described using Monod kinetics. Limitations on the rate of microbial activity based on (i) the availability of electron donors and acceptors, (ii) water activity, (iii) temperature, (iv) redox potential | [172,173,185,294] |
| MIC of copper | Reactive transport | 2D model of fracture intersecting deposition hole for the KBS-3 system, with assumed first-order reduction of sulphate to sulphide. Fraction of sulphide swept away in flowing groundwater, with remainder causing corrosion of the canister. No other sink for sulphide considered. | [295] |
| MIC of Alloy 22 | Empirical | Multiplication factor for MIC based on electrochemical corrosion rates measured with and without microbes indigenous to Yucca Mountain (determined at ambient temperature with added organic nutrient). The MIC enhancement factor fMIC is a uniform distribution between values of 1 and 2. | [9,32] |
| Suppression of microbial activity by cementitious backfill | Empirical | Evidence that while SRB may remain viable after prolonged exposure to alkaline conditions similar to those in a cementitious backfill, the microbes are not active. | [182] |
| Suppression of microbial activity by highly compacted bentonite | Empirical | Based on empirical observations that the ability to cultivate microbes from highly compacted bentonite (HCB) diminishes with increasing buffer density, with indications of a threshold HCB dry density of approximately 1600 kg/m3 for complete suppression of microbial activity. The physiological cause of this apparent threshold is not known but is likely to be due to one or more of the following factors: (i) low water activity aW, (ii) high swelling pressure, and/or (iii) lack of physical space. | [169,170,180,181] |
| Sulphide transport model | Mass transport | 1D, 2D, and 3D sulphide transport models based on assumed constant sulphide source and zero-concentration boundary condition at copper surface to simulate a transport-limited corrosion reaction. Extended to consider the temporal and spatial variation of the near-field saturation and temperature. | [89,179,194,195,196] |
| Sulphide transport and reactive transport models for copper containers in a Nagra repository | Reactive transport | Two sulphide transport models were used to estimate the extent of corrosion of a copper-coated container for the Nagra repository design and for various backfill properties. In the simpler model, the sulphide flux was estimated based on the flux of sulphate subject to solubility control by an iron sulphide phase; equivalent to assuming fast sulphate reduction kinetics dependent only on the availability of the electron acceptor. For the second, more complex, model, the rate of sulphide production was explicitly calculated based on Monod kinetics (as in the UBSM, see below). | [176,177,186,187] |
| Assessment of damage under biofilm for copper and carbon steel | Empirical | Empirical determination of localised damage under a biofilm in the presence of sulphate-reducing bacteria. Carbon steel exhibits pitting and little uniform corrosion, whereas copper exhibits both forms of corrosion. Damage can be expressed in terms of a pitting factor. | [296] |
| Amphos21 sulphide model | Reactive transport | Reactive transport model for the production, transport, and consumption of microbially produced sulphide and the consequences for container corrosion. Transport based on interlayer bentonite pore-water model. | [175] |
| University of Bern Sulphide Model (UBSM) | Reactive transport | 1D, 2D, and 3D reactive transport models for the production, transport, and consumption of sulphide due to remote microbial activity by SRB. Corrosion rate determined based on the assumption of sulphide transport control. 2D and 3D models permit the effect of the spatial relationship between the sulphide source (typically the excavation damaged zone around the rock openings) and the sulphide sink (i.e., the canister) to be determined. | [176,177,188,189] |
| Effect of SRB on corrosion of copper containers | Reactive transport | Reactive transport model for the effect of sulphate reduction by SRB based on assumed first-order kinetics for the sulphate reduction reaction. Sulphate reduction rate assumed to be a function of bentonite density. No limitation due to the availability of electron donors. No attenuation of sulphide flux by reaction with ferrous or ferric species. | [297] |
| INER Sulphide Model (ISM) | Reactive transport | COMSOL-based 1D, linear reactive transport model for the production, transport, and consumption of sulphide due to organotrophic and lithotrophic SRB. Microbial activity described by Monod kinetics. | [178] |
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Extent of radiation-induced corrosion (RIC) of copper canisters | Uncoupled bulk radiolysis model | Net production of oxidants equated to the rate of diffusive loss of reductants (H2) away from canister surface. Concentration of H2 calculated based on bulk radiolysis model for H2O containing 5 mg/L Fe2+. Corrosion rate assumed to be controlled by rate of production of oxidants. | [4] |
| Radiolysis effect on iron-base materials | Empirical | Semi-empirical model based on fitting experimental corrosion rates to conceptual model for competing production and consumption reactions for radiolytic species. | [199] |
| Effective G-value | Empirical | The overall yield of radiolytic oxidants (the effective G-value) was calculated from empirical data based on the enhancement of the rate of corrosion in the presence of radiation. The effective radiolytic yield was then used as an input to a reactive transport, mixed-potential model. | [5] |
| Effective G-value | Uncoupled bulk radiolysis model | An effective G-value of 2.13 molecules/100 eV was defined assuming an average valence of 2 for the radiolytic oxidants. This effective G-value appears to include contributions from both the primary species (OH•, H2O2) and secondary species (O2, O2−, HO2). | [97] |
| Thin-layer mixed-potential model (TLMPM) | Reactive transport, coupled bulk radiolysis model | Fully-coupled radiolysis–interfacial electrochemical reactive transport model for radiation-induced uniform corrosion in thin adsorbed H2O layer. Coupled with passive current-potential expressions for Types 304L and 316L stainless steel and oxygen-free copper, aluminium bronze, and 70:30 Cu:Ni. | [203] |
| Dose rate limit | Empirical | Argument that effects of γ-radiolysis are insignificant below a given dose rate. Based on the review of Shoesmith and King [200] who reported no observable effect for dose rates of the order of 1–10 Gy/h. Subsequently adopted by others with varying dose rate limits between 1 Gy/h and 25 Gy/h. | [11,30,31,200,201] |
| Humid air radiolysis model (HARM) | Uncoupled bulk radiolysis model-corrosion damage | HARM bulk radiolysis model used to predict yield of HNO3 due to radiolysis of humid air, which was then assumed to dissolve into a droplet of arbitrary diameter from a volume of air of arbitrary size leading to corrosion of the copper substrate | [197,209] |
| Uncoupled mixed-potential model for copper | Uncoupled bulk radiolysis–mixed-potential model | Anodic dissolution of copper coupled to cathodic reduction of H2O2. Yield of H2O2 calculated from simplified bulk radiolysis model. | [202] |
| Coupled corrosion–bulk radiolysis model for copper | Coupled corrosion–bulk radiolysis model | RIC model based on a bulk radiolysis model for H2O with O2 as the species supporting oxidation of the Cu. Interfacial reaction incorporated as a homogeneous reaction between Cu and O2. Model subsequently extended by Jonsson [205] to examine the effect of groundwater species, such as chloride, sulphide, dissolved Fe, bicarbonate, dissolved O2, and dissolved organic matter. | [204,205] |
| Radiolysis of moist air inside canister | Uncoupled bulk radiolysis model | Radiolysis model for humid air/Ar gas phase inside canister due to entrainment of liquid H2O in defected spent fuel assemblies. While not a corrosion model as such, predictions do highlight the possibility of the formation of NH3, a potential SCC agent for copper. Ammonia only produced once O2 has been consumed. | [208] |
| Copper corrosion model for radiation-induced corrosion (CCM-RIC) | Reactive transport, coupled bulk radiolysis model | Fully-coupled radiolysis/interfacial electrochemical reactive transport model for radiation-induced uniform corrosion of copper. The effects of oxide interfaces (clay particles and on container surface) on the effective radiolytic yield taken into account. Reactions between oxidising and reducing radiolysis products and structural Fe(II)/Fe(III) in octahedral lattice sites, as well as reactions between radiolysis products and accessory minerals in the bentonite clay also considered. | [206] |
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Development of stress due to corrosion of inner vessel of advanced cold process canister (ACPC) | Analytical | Calculation of the hoop stress in the copper outer barrier due to the formation of expansive corrosion products from the corrosion of the inner carbon or cast steel vessel. | [212,213] |
| Consolidation stress due to formation of expansive corrosion products | Analytical | The formation of carbon steel corrosion products with a volume greater than that of the corroded Fe is assumed to lead to a load on the container, after accounting for the effects of consolidation of the buffer and creep of the host rock (if any). Resulting stress depends on buffer thickness, but is predicted to be of the order of 1 MPa to >20 MPa. | [10] |
| Assessment of effect of surface-breaking flaws | Fracture mechanics | Effect of surface-breaking flaws on the possibility of SCC of copper containers due to stress concentration or intensification by notch-like and crack-like flaws, respectively. | [298] |
| Consequences of seismic activity and/or rockfall on waste-package integrity | Finite element model | Impact damage of waste packages by falling rocks or by collisions due to seismically induced ground motion could induce plastic deformation and residual stresses, which would then render the waste packages susceptible to SCC. | [9] |
| Structural integrity of closure weld of carbon steel HLW container | Fracture mechanics | Fracture mechanics assessment of the critical flaw size for an assumed defect in weld material susceptible to uniform corrosion but not SCC or HIC | [19] |
| Structural integrity of carbon steel container containing defects | Fracture mechanics | Application of the failure-assessment diagram (FAD) approach to a defected carbon steel container subjected to internal and external mechanical loads and time-dependent reduction in wall thickness due to corrosion and degradation of fracture toughness due to hydrogen absorption. | [20] |
| Modelling of physically constrained systems | Mechanical | Prediction of time-dependent porosity of carbon steel corrosion-product layer in cementitious backfill constrained at the inner and outer boundaries, as in the Belgian Supercontainer concept. Model predicts that corrosion ceases as porosity of outer corrosion-product layer is reduced to zero. | [215] |
| Probabilistic canister breaching model (PCBM) | Fracture mechanics | Based on the same general principles as the model of King et al. [20], but run probabilistically to account for variability and uncertainty in the values of the different input parameters. Model used to predict the distribution of breaching times for a carbon steel canister in a DGR in Opalinus Clay. | [26] |
| Model Name or Brief Description | Model Type | Description | Reference(s) |
|---|---|---|---|
| Assessment of effect of environmental uncertainties on predicted container lifetime | stochastic | Study addresses the question of how well the evolution of environmental conditions needs to be known in order to predict container lifetimes with a given scatter. | [299] |
| Hydrogen production from advanced cold process canister (ACPC) | Analytical | Assessment of the rate and extent of H2 generation from the corrosion of carbon steel inner vessel of ACPC in the event of a through-wall defect in the outer copper corrosion barrier. | [300] |
| Effect of defect interactions in copper | Atomistic | Effect of P and S (and Ag) impurities on properties and structure of pure copper studied using first principles thermodynamic calculations. Results are useful for understanding the effects of P and S on creep properties. | [218] |
| Surface properties of digenite | Atomistic | Calculation of bulk and surface properties of copper(I) sulphides using the interface Green’s function method. Digneite Cu2-δS found to contain stable cation vacancies and high cation mobility, consistent with the ionic nature of digenite | [219] |
| Phase stability of Ni alloys | CALPHAD (calculation of phase diagrams) | Temperature–time–transformation (TTT) assessment of the thermal ageing of various Ni-Cr-Mo alloys for the Yucca Mountain program. Phase transformation could impact the localised corrosion behaviour of the alloy. | [225] |
| Flow separation processes on waste-package surface | Reactive transport | Model for predicting the possibility of the separation of solutes due to the flow of electrolyte over the surface of a waste package in an unsaturated environment. The model addresses the question of whether the composition of the surface electrolyte in an evaporating droplet (and, crucially, the ratio of the concentration of aggressive ions such as Cl− to that of inhibitive ions such as NO3−) will vary circumferentially around the waste-package surface due to solute solubility differences as the drip moves over the surface under the effects of gravity. | [226] |
| Hydrogen accumulation inside steel canister | Mass transport | Calculation of the time-dependent internal pressure due to H diffusion through the wall of a carbon steel canister due to the generation of hydrogen on the external surface of the canister during the long-term anaerobic phase. Internal pressurisation will offset the compressive load from the buffer swelling and hydrostatic pressures, but will also lead to an increased risk of hydrogen-induced cracking due to internal or embedded flaws. | [227] |
| Quantum-mechanical calculations of stability of Cu-H-O species | Atomistic | Density functional theory and linear response theory calculations of the stability of various Cu-H-O species have been proposed to be formed during the corrosion of copper in O2-free H2O. | [220] |
| Density functional theory (DFT) model of the sulphidation of Cu2O | Atomistic | DFT model of the conversion of Cu2O to Cu2S by sulphide, including an assessment of the relative reactivities of different crystal planes and different sulphide species | [221,222,223] |
| Diffusivity of copper vacancies in copper sulphide film | Atomistic | DFT calculations of copper vacancy diffusivity in Cu2S film in support of PDM characterization of film. | [224] |
| Consequences of canister failure due to seismic activity | Multiple | Use of multiple models to determine the number and timing of canister failures due to earthquakes and shear across deposition holes in a KBS-3 type repository in crystalline rock in Taiwan. A total of five canisters are predicted to fail, with the first failure after 230,000 yr. | [228] |
References
- Posiva. Canister Evolution; Working Report WR-2021-06; Posiva Oy: Eurajoki, Finland, 2021. [Google Scholar]
- Ondraf/Niras. A Review of Corrosion and Material Selection Issues Pertinent to Underground Disposal of Highly Active Nuclear Waste in Belgium: A Report for ONDRAF/NIRAS Prepared by the Corrosion Study Panel; Technical Report NIROND 2004-02; Ondraf-Niras: Brussels, Belgium, 2004. [Google Scholar]
- Swedish Corrosion Institute. Copper as Canister Material for Unreprocessed Nuclear Waste—Evaluation with Respect to Corrosion; Technical Report KBS TR-90; Kärnbränslesäkerhet: Stockholm, Sweden, 1978. [Google Scholar]
- Swedish Corrosion Institute. Corrosion Resistance of a Copper Canister for Spent Fuel; Technical Report KBS 83-24; Kärnbränsleförsörjning AB/Avdelning KBS: Stockholm, Sweden, 1983. [Google Scholar]
- Marsh, G.P.; Taylor, K.J. An assessment of carbon steel containers for radioactive waste disposal. Corros. Sci. 1988, 28, 289–320. [Google Scholar] [CrossRef]
- Marsh, G.P.; Harker, A.H.; Taylor, K.J. Corrosion of carbon steel nuclear waste containers in marine sediment. Corrosion 1989, 45, 579–589. [Google Scholar] [CrossRef]
- Shoesmith, D.W.; Ikeda, B.M.; LeNeveu, D.M. Lifetime prediction for titanium nuclear waste containers. In Life Prediction of Corrodible Structures; Parkins, R.N., Ed.; NACE International: Houston, TX, USA, 1994; Volume I, pp. 484–496. [Google Scholar]
- Shoesmith, D.W.; Ikeda, B.M.; LeNeveu, D.M. Modeling the failure of nuclear waste containers. Corrosion 1997, 53, 820–829. [Google Scholar] [CrossRef]
- DOE (United States Department of Energy DOE). Yucca Mountain Repository License Application; Technical Report DOW/RW-0573; US Department of Energy: Washington, DC, USA, 2008. [Google Scholar]
- JNC. H-12: Project to Establish the Scientific and Technical Basis for HLW Disposal in Japan, Porting Report 2, Repository Design and Engineering Technology; Technical Report JNC TN1410 2000-003; Japan Nuclear Cycle Development Institute: Tokyo, Japan, 2000. [Google Scholar]
- Ogawa, Y.; Suzuki, S.; Kubota, S.; Deguchi, A. Re-evaluation of the required thickness of the carbon steel overpack for high-level radioactive waste disposal in Japan based on the latest scientific and engineering knowledge. Corros. Eng. Sci. Technol. 2017, 52, 204–209. [Google Scholar] [CrossRef]
- Nakayama, G.; Nakamura, N.; Fukaya, Y.; Akashi, M.; Ueda, H. Assessment of crevice corrosion and hydrogen-induced stress-corrosion cracks in titanium-carbon steel composite overpack for geological disposal of high-level radioactive waste. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 25; pp. 373–394. [Google Scholar]
- Nakayama, G.; Murakami, K.; Akashi, M. Assessment of crevice corrosion and hydrogen induced stress corrosion cracks of Ti-Pd alloys for HLW overpack in deep underground water environments. Mat. Res. Soc. Symp. Proc. 2003, 757, 771–778. [Google Scholar] [CrossRef]
- Diomidis, N.; King, F. Development of Copper Coated Canisters for the Disposal of SF and HLW in Switzerland; Technical Report NTB 20-01; Nagra: Wettingen, Switzerland, 2022. [Google Scholar]
- King, F.; Lilja, C.; Pedersen, K.; Pitkänen, P.; Vähänen, M. An Update of the State-of-the-Art Report on the Corrosion of Copper under Expected Conditions in a Deep Geologic Repository; Technical Report SKB TR-10-67; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010. [Google Scholar]
- King, F.; Lilja, C.; Vähänen, M. Progress in the understanding of the long-term corrosion behaviour of copper canisters. J. Nucl. Mater. 2013, 438, 228–237. [Google Scholar] [CrossRef]
- Hall, D.S.; Behazin, M.; Binns, W.J.; Keech, P.G. An evaluation of corrosion processes affecting copper-coated nuclear waste containers in a deep geological repository. Progr. Mater. Sci. 2021, 118, 100766. [Google Scholar] [CrossRef]
- SKB. Corrosion Calculations Report for the Safety Assessment SR-Site; Technical Report SKB TR-10-66; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010. [Google Scholar]
- Asano, H.; Nakamura, A.; Kobayashi, M. Long term integrity of overpack closure weld for HLW geological disposal. Part 1—Prediction and evaluation method for structural integrity of weld joint. Corros. Eng. Sci. Technol. 2011, 46, 165–170. [Google Scholar] [CrossRef]
- King, F.; Burt, D.; Ganeshalingam, J.; Gardner, P.; Sanderson, D.; Watson, S.; Padovani, C. Coupled analysis of mechanical- and corrosion-related degradation of carbon steel spent fuel container. Corros. Eng. Sci. Technol. 2014, 49, 442–4591. [Google Scholar] [CrossRef]
- Posiva, S.K.B. The Integrated Sulfide Project—Summary Report. A Collaboration Project 2014–2018; Technical Report 09; Posiva Oy: Eurajoki, Finland; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2021. [Google Scholar]
- SRG (Scientific Review Group). An Evaluation of the Environmental Impact Statement on Atomic Energy of Canada Limited’s Concept for the Disposal of Canada’s Nuclear Fuel Waste; Report of the Scientific Review Group; Advisory to the Nuclear Fuel Waste Management and Disposal Concept Environmental Assessment Panel; Canadian Environmental Assessment Agency: Ottawa, ON, Canada, 1995. [Google Scholar]
- Duquette, D.J.; Latanision, R.M.; Di Bella, C.A.W.; Kirstein, B.E. Corrosion issues related to disposal of high-level nuclear waste in the Yucca Mountain repository—Peer reviewers’ perspective. Corrosion 2009, 65, 272–280. [Google Scholar] [CrossRef]
- King, F. Predicting the lifetimes of nuclear waste containers. JOM 2014, 66, 526–537. [Google Scholar] [CrossRef]
- King, F.; Kolář, M.; Briggs, S.; Behazin, M.; Keech, P.; Diomidis, N. Review of the modelling of corrosion processes and lifetime prediction for HLW/SF containers—Part 2. Performance assessment models. Corros. Mater. Degrad. 2024. to be published. [Google Scholar]
- King, F.; Wu, H.; Diomidis, N. Probabilistic Canister Breaching Model (PBCM) for Carbon Steel Canisters in a Deep Geological Repository in Opalinus Clay; Technical Report; Nagra: Wettingen, Switzerland, to be published.
- Féron, D.; Macdonald, D.D. Prediction of long term corrosion behaviour in nuclear waste systems. Mat. Res. Soc. Symp. Proc. 2006, 932, 351. [Google Scholar] [CrossRef]
- Macdonald, D.D. The Holy Grail: Deterministic prediction of corrosion damage thousands of years into the future. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 6; pp. 75–90. [Google Scholar]
- Macdonald, D.D. The role of determinism in the prediction of corrosion damage. Corros. Mater. Degrad. 2023, 4, 212–273. [Google Scholar] [CrossRef]
- Crusset, D.; Deydier, V.; Necib, S.; Gras, J.-M.; Combrade, P.; Féron, D.; Burger, E. Corrosion of carbon steel components in the French high-level waste programme: Evolution of disposal concept and selection of materials. Corros. Eng. Sci. Technol. 2017, 52, 17–24. [Google Scholar] [CrossRef]
- Diomidis, N.; Johnson, L.H. Materials options and corrosion-related considerations in the design of spent fuel and high-level waste disposal canisters for a deep geological repository in Opalinus Clay. JOM 2014, 66, 461–470. [Google Scholar] [CrossRef]
- Sandia. General Corrosion and Localized Corrosion of Waste Package Outer Barrier; Technical Report ANL-EBS-MD-000003 REV 03C; Sandia National Laboratories: Las Vegas, NV, USA, 2007. [Google Scholar]
- Macdonald, D.D. The Point Defect Model for the passive state. J. ElectroChem. Soc. 1992, 139, 3434–3449. [Google Scholar] [CrossRef]
- Macdonald, D.D. Passivity: The key to our metals-based civilization. Pure Appl. Chem. 1999, 71, 951–978. [Google Scholar] [CrossRef]
- Macdonald, D.D. The history of the Point Defect Model for the passive state: A brief review of film growth aspects. Electrochim. Acta 2011, 56, 1761–1772. [Google Scholar] [CrossRef]
- Bildstein, O.; Trotognon, L.; Perronnet, M.; Jullien, M. Modelling iron-clay interactions in deep geological disposal conditions. Phys. Chem. Earth 2006, 31, 618–625. [Google Scholar] [CrossRef]
- Samper, J.; Lu, C.; Montenegro, L. Reactive transport model of interactions of corrosion products and bentonite. Phys. Chem. Earth 2008, 33, S306–S316. [Google Scholar] [CrossRef]
- Marty, N.C.M.; Fritz, B.; Clément, A.; Michau, N. Modelling the long term alteration of the engineered bentonite barrier in an underground radioactive waste repository. Appl. Clay Sci. 2010, 47, 82–90. [Google Scholar] [CrossRef]
- King, F.; Kolář, M. Prediction of the lifetimes of copper nuclear waste containers under restrictive mass-transport and evolving redox conditions. In Proceedings of CORROSION95; NACE International: Houston, TX, USA, 1995; paper 425. [Google Scholar]
- King, F.; Kolář, M.; Maak, P. Reactive-transport model for the prediction of the uniform corrosion behaviour of copper used fuel containers. J. Nucl. Mater. 2008, 379, 133–141. [Google Scholar] [CrossRef]
- Bataillon, C.; Bouchon, F.; Chainias-Hillairet, C.; Desgranges, C.; Hoareau, E.; Marin, F.; Perrin, S.; Tupin, M.; Talnadier, J. Corrosion modelling of iron based alloy in nuclear waste repository. Electrochim. Acta 2010, 55, 4451–4467. [Google Scholar] [CrossRef]
- Shibata, T.; Watanabe, M.; Taniguchi, N.; Shimizu, A. Modelling of carbon steel corrosion under oxygen depleted environment. Corros. Eng. Sci. Technol. 2014, 49, 435–441. [Google Scholar] [CrossRef]
- Hedin, A.; Johansson, A.J.; Lilja, C. Copper corrosion in pure water—Scientific and post-closure safety aspects. In Proceedings of the International High-Level Radioactive Waste Management Conference, Charlotte, NC, USA, 9–13 April 2017; American Nuclear Society: La Grange Park, IL, USA, 2017; pp. 559–567. [Google Scholar]
- King, F.; Litke, C.D.; Quinn, M.J.; LeNeveu, D.M. The measurement and prediction of the corrosion potential of copper in chloride solutions as a function of oxygen concentration and mass-transfer coefficient. Corros. Sci. 1995, 37, 833–851. [Google Scholar] [CrossRef]
- King, F.; Briggs, S. Development and Validation of a COMSOL Version of the Copper Corrosion Model; Technical Report NWMO-TR-2022-08; Nuclear Waste Management Organization: Toronto, ON, Canada, 2023. [Google Scholar]
- Honda, A.; Taniguchi, N.; Ishikawa, H.; Hoch, A.R.; Porter, F.M.; Sharland, S.M. A modelling study for long-term life prediction of carbon steel overpack for geological isolation of high-level radioactive waste. In Proceedings of the International Symposium on Plant Aging and Life Prediction of Corrodible Structures, Sapporo, Japan, 15–18 May 1995; Shoji, T., Shibata, T., Eds.; NACE International: Houston, TX, USA, 1997; pp. 217–227. [Google Scholar]
- Macdonald, D.D.; Sharifi-Asl, S. Is Copper Immune to Corrosion When in Contact with Water and Aqueous Solutions? Technical Report SSM 2011:09; Strålsäkerhetsmyndigheten: Stockholm, Sweden, 2011. [Google Scholar]
- Macdonald, D.D.; Sharifi-Asl, S. Volt Equivalent diagrams as a means of displaying the electrochemical thermodynamics of the sulfur-water system. Corros. Sci. 2014, 81, 102–109. [Google Scholar] [CrossRef]
- Lilja, C.; King, F.; Puigdomenech, I.; Pastina, B. Speciation of copper in high chloride concentrations, in the context of corrosion of copper canisters. Mater. Corros. 2021, 72, 293–299. [Google Scholar] [CrossRef]
- Hesketh, J.; Haynes, H.; Reddy, B.; Rance, A.; Padovani, C.; Diomidis, N. Carbon steel corrosion in a bentonite buffer: A comparison between in-situ exposure and lab-based experiment. Mater. Corros. 2023, 74, 1728–1745. [Google Scholar] [CrossRef]
- Diomidis, N.; King, F. The corrosion of radioactive waste disposal canisters based on in situ tests. In Nuclear Corrosion: Research, Progress and Challenges; Ritter, S., Ed.; European Federation of Corrosion, Number 69; Woodhead Publishing: Duxford, UK, 2020; Chapter 10; pp. 371–389. [Google Scholar]
- Neff, D.; Dillmann, P.; Descostes, M.; Beranger, G. Corrosion of iron archaeological artefacts in soil: Estimation of the average corrosion rates involving analytical techniques and thermodynamic calculations. Corros. Sci. 2006, 48, 2947–2970. [Google Scholar] [CrossRef]
- Hélie, M.; Desgranges, C.; Perrin, S. Prediction of corrosion behaviour of HLW containers in the framework of the French interim storage concept. Nucl. Technol. 2006, 155, 120–132. [Google Scholar] [CrossRef]
- Ahn, T.; Jung, H.; He, X.; Pensado, O. Understanding long-term corrosion of Alloy 22 container in the potential Yucca Mountain repository for high-level nuclear waste disposal. J. Nucl. Mater. 2008, 379, 33–41. [Google Scholar] [CrossRef]
- Kojima, Y.; Hioki, T.; Tsujikawa, S. Simulation of the state of carbon steel n years after disposal with n years of corrosion product on its surface in a bentonite environment. Mat. Res. Soc. Symp. Proc. 1995, 353, 711–718. [Google Scholar] [CrossRef]
- Taniguchi, N. Effect of magnetite as a corrosion product on the corrosion of carbon steel overpack. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 28; pp. 424–438. [Google Scholar]
- Macdonald, D.D. On the existence of our metals-based civilization. I. Phase-space analysis. J. ElectroChem. Soc. 2006, 153, B213–B224. [Google Scholar] [CrossRef]
- Macdonald, D.D. On the tenuous nature of passivity and its role in the isolation of HLNW. J. Nucl. Mater. 2008, 379, 24–32. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Engelhardt, G.; Jayaweera, P.; Priyantha, N.; Davydov, A. The deterministic prediction of localised corrosion damage to Alloy C-22 HLNW canisters. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 8; pp. 104–117. [Google Scholar]
- Lu, P.; Kursten, B.; Macdonald, D.D. Deconvolution of the partial anodic and cathodic processes during the corrosion of carbon steel in concrete pore solution under simulated anoxic conditions. Electrochim. Acta. 2014, 143, 312–323. [Google Scholar] [CrossRef]
- McMillion, L.G.; Sun, A.; Macdonald, D.D.; Jones, D.A. General corrosion of Alloy 22: Experimental determination of model parameters from electrochemical impedance spectroscopy data. Metall. Mater. Trans. A 2005, 36A, 1129–1141. [Google Scholar] [CrossRef]
- Urquidi-Macdonald, M.; Macdonald, D.D. Transients in the growth of passive films on high level nuclear waste canisters. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 12; pp. 165–178. [Google Scholar]
- Lu, P.; Sharifi-Asl, S.; Kursten, B.; Macdonald, D.D. The irreversibility of the passive state of carbon steel in the alkaline concrete pore solution under simulated anoxic conditions. J. ElectroChem. Soc. 2015, 162, C572–C581. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Mao, F.; Dong, C.; Sharifi-Asl, S. Measurements of Parameter Values for Predicting Corrosion Phenomena on Copper in Swedish HLNW Repositories. Phase IV: Impact of Chloride Ion on the Passivity and Pitting of Copper; Technical Report SSM 2016:30; Strålsäkerhetsmyndigheten: Stockholm, Sweden, 2016. [Google Scholar]
- Mao, F.; Dong, C.; Sharifi-Asl, S.; Lu, P.; Macdonald, D.D. Passivity breakdown on copper: Influence of chloride ion. Electrochim. Acta. 2014, 144, 391–399. [Google Scholar] [CrossRef]
- Huttunen-Saarivirta, E.; Ghanbari, E.; Mao, F.; Rajala, P.; Carpén, L.; Macdonald, D.D. Kinetic properties of the passive film on copper in the presence of sulfate-reducing bacteria. J. ElectroChem. Soc. 2018, 165, C450–C460. [Google Scholar] [CrossRef]
- Martino, T.; Chen, J.; Guo, M.; Ramamurthy, S.; Shoesmith, D.W.; Noël, J.J. Comments on E. Huttunen-Saarivirta et al. Kinetic Properties of the Passive Film on Copper in the Presence of Sulfate-Reducing Bacteria. J. ElectroChem. Soc. 2019, 166, Y13–Y16. [Google Scholar] [CrossRef]
- Huttunen-Saarivirta, E.; Rajala, P.; Carpén, L.; Wang, J.; Liu, F.; Ghanbari, E.; Mao, F.; Dong, C.; Yang, J.; Sharifi-Asl, S.; et al. Response to “Comments on E. Huttunen-Saarivirta et al.; ‘Kinetic Properties of the Passive Film on Copper in the Presence of Sulfate-Reducing Bacteria” by T. Martino, J. Chen, M. Guo, S. Ramamurthy, D.W. Shoesmith, and J.J. Noël. J. ElectroChem. Soc. 2019, 166, Y17–Y26. [Google Scholar] [CrossRef]
- Bataillon, C. Application of the Point Defect Model to modelling the corrosion of iron based canisters in geological repository. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 11; pp. 154–164. [Google Scholar]
- King, F.; Kolář, M.; Vähänen, M. Reactive-transport modelling of the sulphide-assisted corrosion of copper nuclear waste containers. In Sulphur-Assisted Corrosion in Nuclear Disposal Systems; Kursten, B., Féron, D., Druyts, F., Eds.; European Federation of Corrosion; Maney Publishing: Leeds, UK, 2011; Chapter 9; Volume 59, pp. 152–164. [Google Scholar]
- King, F.; Kolář, M.; Vähänen, M.; Lilja, C. Modelling the long-term corrosion behaviour of copper canisters in a KBS-3 repository. Corros. Eng. Sci. Technol. 2011, 46, 217–222. [Google Scholar] [CrossRef]
- King, F.; Kolář, M.; Puigdomenech, I.; Pitkänen, P.; Lilja, C. Modeling microbial sulfate reduction and the consequences for corrosion of copper canisters. Mater. Corros. 2021, 72, 339–347. [Google Scholar] [CrossRef]
- King, F.; Kolář, M.; Keech, P.G. Simulations of long-term anaerobic corrosion of carbon steel containers in Canadian deep geological repository. Corros. Eng. Sci. Technol. 2014, 49, 455–460. [Google Scholar] [CrossRef]
- Mohamed-Said, M.; Vuillemin, B.; Oltra, R.; Trenty, L.; Crusset, D. One-dimensional porous electrode model for predicting the corrosion rate under a conductive corrosion product layer. J. ElectroChem. Soc. 2017, 164, E3372–E3385. [Google Scholar] [CrossRef]
- Mohamed-Said, M.; Vuillemin, B.; Oltra, R.; Trenty, L.; Crusset, D. Predictive modelling of the corrosion rate of carbon steel focusing on the effect of the precipitation of corrosion products. Corros. Eng. Sci. Technol. 2017, 52, 178–185. [Google Scholar] [CrossRef]
- King, F. Mixed-Potential Modelling of the Corrosion of Copper in the Presence of Sulphide; Working Report, WR 2007-63; Posiva Oy: Eurajoki, Finland, 2008. [Google Scholar]
- King, F.; Kolář, M. A numerical model for the corrosion of copper nuclear waste containers. Mat. Res. Soc. Symp. Proc. 1996, 412, 555–562. [Google Scholar] [CrossRef]
- King, F.; Kolář, M. The Copper Container Corrosion Model Used in AECL’s Second Case Study; Technical Report 06819-REP-01200-10041-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2000. [Google Scholar]
- King, F.; Kolář, M. Copper Sulfide Model (CSM)—Model Improvements, Sensitivity Analyses, and Results from the Integrated Sulfide Project Inter-Model Comparison Exercise; Technical Report TR-18-08; Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2019. [Google Scholar]
- King, F.; Kolář, M. Lifetime predictions for nuclear waste disposal containers. Corrosion 2019, 75, 309–323. [Google Scholar] [CrossRef]
- King, F.; Kolář, M. Theory Manual for the Steel Corrosion Model Version 1.0; Technical Report NWMO-TR-2009-07; Nuclear Waste Management Organization: Toronto, ON, Canada, 2009. [Google Scholar]
- King, F.; Chen, J.; Qin, Z.; Shoesmith, D.; Lilja, C. Sulphide-transport control of the corrosion of copper canisters. Corros. Eng. Sci. Technol. 2017, 52, 210–216. [Google Scholar] [CrossRef]
- King, F.; Kolář, M.; Shoesmith, D.W. Modelling the effects of porous and semi-permeable layers on corrosion processes. In Proceedings of the CORROSION96, Denver, CO, USA, 24–29 March 1996; NACE International: Houston, TX, USA, 1996. paper 380. [Google Scholar]
- Liu, M.; Kwon, B.; Kang, P.K. Machine learning to predict effective reaction rates in 3D porous media from pore structural features. Sci. Rep. 2022, 12, 5486. [Google Scholar] [CrossRef] [PubMed]
- Le Traon, C.; Aquino, T.; Bouchez, C.; Maher, K.; Le Borgne, T. Effective kinetics driven by dynamic concentration gradients under coupled transport and reaction. Geochim. Cosmochim. Acta 2021, 306, 189–209. [Google Scholar] [CrossRef]
- Manaka, M. Comparison of rates of pyrite oxidation by dissolved oxygen in aqueous solution and in compacted bentonite. J. Mineral. Petrol. Sci. 2009, 104, 59–68. [Google Scholar] [CrossRef]
- Lu, C.; Samper, J.; Fritz, B.; Clement, A.; Montenegro, L. Interactions of corrosion products and bentonite: An extended multicomponent reactive transport model. Phys. Chem. Earth 2011, 36, 1661–1668. [Google Scholar] [CrossRef]
- Ngo, V.V.; Delalande, M.; Clément, A.; Michau, N.; Fritz, B. Coupled transport-reaction modelling of the long-term interaction between iron, bentonite and Callovo-Oxfordian claystone in radioactive waste confinement systems. Appl. Clay Sci. 2014, 101, 430–443. [Google Scholar] [CrossRef]
- Rashwan, T.L.; Asad, M.A.; Molnar, I.L.; Behazin, M.; Keech, P.G.; Krol, M.M. Exploring the governing transport mechanisms of corrosive agents in a Canadian deep geological repository. Sci. Total Environ. 2022, 828, 153944. [Google Scholar] [CrossRef] [PubMed]
- Giroud, N.; Tomonaga, Y.; Wersin, P.; Briggs, S.; King, F.; Vogt, T.; Diomidis, N. On the fate of oxygen in a spent fuel emplacement drift in Opalinus Clay. Appl. GeoChem. 2018, 97, 370–378. [Google Scholar] [CrossRef]
- Vokál, A.; Lukin, D.; Vopálka, D. Carbon steel canister performance assessment: Iron transfer study. Mat. Res. Soc. Symp. Proc. 2006, 932, 877–884. [Google Scholar] [CrossRef]
- King, F.; Puigdomenech, I.; Lilja, C. Effect of High Groundwater Chloride Concentration on the Corrosion of Copper Canisters; Working Report WR-2021-10; Posiva Oy: Eurajoki, Finland, 2021. [Google Scholar]
- Honda, A.; Taniguchi, N.; Ishikawa, H.; Kawasaki, M. A modelling study of general corrosion of copper overpack for geological isolation of high-level radioactive waste. Mat. Res. Soc. Symp. Proc. 1999, 556, 911–918. [Google Scholar] [CrossRef]
- Qin, Z.; Daljeet, R.; Ai, M.; Farhangi, N.; Noël, J.J.; Ramamurthy, S.; Shoesmith, D.; King, F.; Keech, P. The active/passive conditions for copper corrosion under nuclear waste repository environment. Corros. Eng. Sci. Technol. 2017, 52, 45–49. [Google Scholar] [CrossRef]
- Nakayama, G.; Fukaya, Y.; Akashi, M. The effects of carbonate-bicarbonate concentration on empirical corrosion diagrams of mild steel as a material of geological disposal package for high level nuclear wastes. Mat. Res. Soc. Symp. Proc. 1997, 451, 567–572. [Google Scholar] [CrossRef]
- Taniguchi, N.; Honda, A.; Ishikawa, H. Experimental investigation of passivation behavior and corrosion rate of carbon steel in compacted bentonite. Mat. Res. Soc. Symp. Proc. 1998, 506, 495–501. [Google Scholar] [CrossRef]
- Marsh, G.P.; Taylor, K.J.; Sharland, S.M.; Tasker, P.W. An approach for evaluation the general and localised corrosion of carbon-steel contains for nuclear waste disposal. Mat. Res. Soc. Symp. Proc. 1987, 84, 227–238. [Google Scholar] [CrossRef]
- Briggs, S.; Lilja, C.; King, F. Probabilistic model for pitting of copper canisters. Mater. Corros. 2021, 72, 308–316. [Google Scholar] [CrossRef]
- Féron, D.; Crusset, D.; Gras, J.-M. Corrosion issues in the French high-level nuclear waste program. Corrosion 2009, 65, 213–223. [Google Scholar] [CrossRef]
- King, F.; LeNeveu, D. Prediction of the lifetimes of copper nuclear waste containers. In Proceedings of the Topical Meeting on Nuclear Waste Packaging. Focus 91, Las Vegas, NV, USA, 29 September–2 October 1991; American Nuclear Society: La Grange Park, IL, USA, 1992; pp. 253–261. [Google Scholar]
- Akashi, M.; Fukuda, T.; Yoneyama, H. A corrosion localization assessment of the mild steel used for nuclear waste package. Mat. Res. Soc. Symp. Proc. 1990, 176, 525–532. [Google Scholar] [CrossRef]
- Sharland, S.M.; Tasker, P.W. A mathematical model of crevice corrosion and pitting corrosion—I. The physical model. Corros. Sci. 1988, 28, 603–620. [Google Scholar] [CrossRef]
- Watson, M.K.; Postlethwaite, J. Numerical simulation of crevice corrosion of stainless steels and nickel alloys in chloride solutions. Corrosion 1990, 46, 522–530. [Google Scholar] [CrossRef]
- Taxén, C. Pitting Corrosion of Copper. An Equilibrium—Mass Transport Study; Technical Report SKB TR-02-22; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2002. [Google Scholar]
- Taxén, C. Pitting Corrosion of Copper. Further Model Studies; Technical Report SKB TR-02-23; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2002. [Google Scholar]
- Krouse, D.; Laycock, N.; Padovani, C. Modelling pitting corrosion of stainless steel in atmospheric exposure to chloride containing environments. Corros. Eng. Sci. Technol. 2014, 49, 521–528. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Qiu, J.; Sharifi-Asl, S.; Yang, J.; Engelhardt, G.R.; Xu, Y.; Ghanbari, E.; Xu, A.; Saatchi, A.; Kovalov, D. Pitting of carbon steel in the synthetic concrete pore solution. Mater. Corros. 2021, 72, 166–193. [Google Scholar] [CrossRef]
- Dunn, D.S.; Cragnolino, G.A.; Sridhar, N. An electrochemical approach to predicting long-term localized corrosion of corrosion-resistant high-level waste container materials. Corrosion 2000, 56, 90–104. [Google Scholar] [CrossRef]
- Henshall, G.A. Stochastic models for predicting pitting corrosion damage of HLRW containers. In Proceedings of the Topical Meeting on Nuclear Waste Packaging. Focus 91, Las Vegas, NV, USA, 29 September–2 October 1991; American Nuclear Society: La Grange Park, IL, USA, 1992; pp. 225–232. [Google Scholar]
- Henshall, G.A. Stochastic modelling of the influence of environment on pitting corrosion damage of radioactive-waste containers. Mat. Res. Soc. Symp. Proc. 1995, 353, 679–686. [Google Scholar] [CrossRef]
- Henshall, G.A. A phenomenological approach to simulating the evolution of radioactive-waste container damage due to pitting corrosion. Mat. Res. Soc. Symp. Proc. 1996, 412, 613–619. [Google Scholar] [CrossRef]
- Apted, M.; King, F.; Langmuir, D.; Arthur, R.; Kessler, J. The unlikelihood of localized corrosion of nuclear waste packages arising from deliquescent brine formation. JOM 2005, 57, 43–48. [Google Scholar] [CrossRef]
- Di Caprio, D.; Vautrin-Ul, C.; Stafiej, J.; Chaussé, A.; Féron, D.; Bidiali, J.P. Cellular automata approach for morphological evolution of localised corrosion. Corros. Eng. Sci. Technol. 2011, 46, 223–227. [Google Scholar] [CrossRef]
- Briggs, S.; Lilja, C.; King, F. Probabilistic Model for the Pitting of Copper Canisters under Aerobic, Saturated Conditions; Technical Report SKB TR-20-01; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2020. [Google Scholar]
- Wang, L. Near-Field Chemistry of a HLW/SF Repository in Boom Clay—Scoping Calculations Relevant to the Ercontainer Design; Technical Report SCK•CEN-ER-17; SCK•CEN: Boeretang, Belgium, 2006. [Google Scholar]
- Foct, F.; Gras, J.-M. Semi-empirical model for carbon steel corrosion in long term geological nuclear waste disposal. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 7; pp. 91–102. [Google Scholar]
- Dunn, D.S.; Pensado, O.; Pan, Y.-M.; Yang, L.T.; He, X. Modeling corrosion processes for Alloy 22 waste packages. Mat. Res. Soc. Symp. Proc. 2006, 932, 271. [Google Scholar] [CrossRef]
- Bresle, A.; Saers, J.; Arrhenius, B. Studies in Pitting Corrosion on Archaeological Bronzes. Copper; Technical Report SKB TR-83-05; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1983. [Google Scholar]
- Romanoff, M. Underground Corrosion; NACE International: Houston, TX, USA, 1989. [Google Scholar]
- Fukuda, T.; Akashi, M. A Gumbel distribution model for assessing the general corrosion propagation of mild steel used for nuclear waste disposal package. In Life Prediction of Corrodible Structures; Parkins, R.N., Ed.; NACE International: Houston, TX, USA, 1994; Volume I, pp. 419–428. [Google Scholar]
- Johnson, L.H.; King, F. The effect of the evolution of environmental conditions on the corrosion evolutionary path in a repository for spent fuel and high-level waste in Opalinus Clay. J. Nucl. Mater. 2008, 379, 9–15. [Google Scholar] [CrossRef]
- SKB. Post-Closure Safety for the Final Repository for Spent Nuclear Fuel at Forsmark. Fuel and Canister Process Report, PSAR version; Technical Report SKB TR-21-02; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2022. [Google Scholar]
- He, X.; Noël, J.J.; Shoesmith, D.W. Crevice corrosion damage function for grade-2 titanium of iron content 0.078 wt% at 95C. Corros. Sci. 2005, 47, 1177–1195. [Google Scholar] [CrossRef]
- Payer, J.H.; Kelly, R.G. Perspectives on localized corrosion in thin layers of particulate. Mat. Res. Soc. Symp. Proc. 2007, 985, 801. [Google Scholar] [CrossRef]
- Sharland, S.M. The theoretical evaluation of localised corrosion in radioactive waste canisters. Mat. Res. Soc. Symp. Proc. 1987, 84, 283–293. [Google Scholar] [CrossRef]
- Sharland, S.M. A mathematical model of crevice corrosion and pitting corrosion—II. The mathematical solution. Corros. Sci. 1988, 28, 621–630. [Google Scholar] [CrossRef]
- Sharland, S.M.; Jackson, C.P.; Diver, A.J. A finite-element model of the propagation of corrosion crevices and pits. Corros. Sci. 1989, 29, 1149–1166. [Google Scholar] [CrossRef]
- Sharland, S.M.; Naish, C.C.; Taylor, K.J.; Marsh, G.P. An experimental and modelling study of the localized corrosion of carbon steel overpacks for the geological disposal of radioactive waste. In Life Prediction of Corrodible Structures; Parkins, R.N., Ed.; NACE International: Houston, TX, USA, 1994; Volume I, pp. 402–418. [Google Scholar]
- Mousson, J.-L.; Vuillemin, B.; Oltra, R.; Crusset, D.; Santarini, G.; Combrade, P. Modelling of the propagation of crevice corrosion. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems, Proceedings of the 2nd International Workshop, Nice, France, 14–15 September 2004; Crusset, D., Féron, D., Gras, J.-M., Macdonald, D.D., Eds.; Andra Science and Technology Series: Châtenay-Malbry, France, 2004; pp. 180–186. [Google Scholar]
- Sridhar, N.; Cragnolino, G.; Pennick, H.; Torng, T.Y. Application of a transient crevice corrosion model to the prediction of performance of high-level nuclear waste container materials. In Life Prediction of Corrodible Structures; Parkins, R.N., Ed.; NACE International: Houston, TX, USA, 1994; Volume I, pp. 429–453. [Google Scholar]
- Farmer, J.C.; McCright, R.D.; Estill, J.C.; Gordon, S.R. Development of integrated mechanistically-based degradation-mode models for performance assessment of high-level waste containers. Mat. Res. Soc. Symp. Proc. 1999, 556, 855–862. [Google Scholar] [CrossRef]
- Sharland, S.M. A mathematical model of the initiation of crevice corrosion in metals. Corros. Sci. 1992, 33, 183–201. [Google Scholar] [CrossRef]
- Hoch, A.R.; Honda, A.; Porter, F.M.; Sharland, S.M.; Taniguchi, N. Development of mathematical models for long-term prediction of corrosion behaviour of carbon steel overpacks for radioactive waste disposal. Mat. Res. Soc. Symp. Proc. 1997, 465, 683–690. [Google Scholar] [CrossRef]
- Taxén, C. Pitting corrosion of copper. Equilibrium-mass transport limitations. Mat. Res. Soc. Symp. Proc. 2000, 608, 103–108. [Google Scholar] [CrossRef]
- Engelhardt, G.R.; McMillion, L.G.; Macdonald, D.D. A mathematical model for crevice corrosion under porous deposits. J. Nucl. Mater. 2008, 379, 48–53. [Google Scholar] [CrossRef]
- Björck, M.; Taxen, C.; Vuoristo, T.; Elger, R.; Zavalis, T.; Wikström, L.; Sparr, M. Embedded oxide particles in Friction Stir Welds; Technical Report Posiva SKB Report 10; Posiva Oy: Eurajoki, Finland; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2019. [Google Scholar]
- Engelhardt, G.; Macdonald, D.D. Monte-Carlo simulation of pitting corrosion with a deterministic model for repassivation. J. ElectroChem. Soc. 2020, 167, 013540. [Google Scholar] [CrossRef]
- Qiu, J.; Zhu, Y.; Xu, Y.; Li, Y.; Mao, F.; Wu, A.; Macdonald, D.D. Effect of chloride on the pitting corrosion of carbon steel in alkaline solutions. J. ElectroChem. Soc. 2022, 169, 031501. [Google Scholar] [CrossRef]
- Shoesmith, D.W.; Noël, J.J. Corrosion of titanium and its alloys. In Shreir’s Corrosion, 4th ed.; Cottis, R.A., Graham, M.J., Lindsay, R., Lyon, S.B., Richardson, J.A., Scantlebury, J.D., Stott, F.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 3, Chapter 3.10; pp. 2042–2052. [Google Scholar]
- Chen, Z.Y.; Kelly, R.G. Computational modelling of bounding conditions for pit size on stainless steel in atmospheric environments. J. ElectroChem. Soc. 2010, 157, C69–C78. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cui, F.; Kelly, R.G. Calculations of the cathodic current delivery capacity and stability of crevice corrosion under atmospheric conditions. J. ElectroChem. Soc. 2008, 155, C360–C368. [Google Scholar] [CrossRef]
- Agarwal, A.S.; Landau, U.; Shan, X.; Payer, J.H. Modeling the effects of crevice former, particulates, and the evolving surface profile in crevice corrosion. ECS Trans. 2007, 3, 459–471. [Google Scholar] [CrossRef]
- Payer, J.H.; Shan, X.; Agarwal, A.S.; Landau, U. Crevice corrosion damage evolution in high temperature brines. ECS Trans. 2008, 11, 39–53. [Google Scholar] [CrossRef]
- Watson, M.K.; Postlethwaite, J. Numerical simulation of crevice corrosion: The effect of the crevice gap profile. Corros. Sci. 1991, 32, 1253–1262. [Google Scholar] [CrossRef]
- Heppner, K.L.; Evitts, R.W.; Postlethwaite, J. Effect of the crevice gap on the initiation of crevice corrosion in passive metals. Corrosion 2004, 60, 718–728. [Google Scholar] [CrossRef]
- Dunn, D.S.; Sridhar, N.; Cragnolino, G.A. Long-term prediction of localized corrosion of Alloy 825 in high-level nuclear waste repository environments. Corrosion 1996, 52, 115–124. [Google Scholar] [CrossRef]
- Sridhar, N.; Dunn, D.; Cragnolino, G. The use of repassivation potential in predicting the p[performance of high-level nuclear waste container materials. Mat. Res. Soc. Symp. Proc. 1995, 353, 663–670. [Google Scholar] [CrossRef]
- Dunn, D.S.; Pensado, O.; Brossia, C.S.; Cragnolino, G.A.; Sridhar, N.; Ahn, T.M. Modelling corrosion of Alloy 22 as a high-level radioactive waste canister material. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 15; pp. 208–224. [Google Scholar]
- Bryan, C.; Jarek, R.; Wolery, T.; Shields, D.; Sutton, M.; Hardin, E.; Barr, D. Evaluation of the corrosivity of dust deposited on waste packages at Yuca Mountain, Nevada. Mat. Res. Soc. Symp. Proc. 2006, 932, 1061. [Google Scholar] [CrossRef]
- Payer, J.H. The proposed Yucca Mountain repository from a corrosion perspective. Mat. Res. Soc. Symp. Proc. 2006, 932, 341. [Google Scholar] [CrossRef]
- Pérez-Brokate, C.F.; di Caprio, D.; Féron, D.; de Lamare, J.; Chaussé, A. Probabilistic cellular automata model of generalised corrosion, transition to localised corrosion. Corros. Eng. Sci. Technol. 2017, 52, 186–193. [Google Scholar] [CrossRef]
- Andra. Dossier D’autorisation de Creation de L’installation Nucléaire de base (INB) Cigéo. Pièce 7. Version Préliminaire du Rapport de Sûreté. Partie III Démonstration de Sûreté; Volume 8 La Demonstration de Sûreté après Fermeture; Technical Report CG-TE-D-NTE-AMOA-SR0-0000-21-0007/A; Agence nationale pour la gestion des déchets radioactifs: Châtenay-Malabry, France, 2022. [Google Scholar]
- Bulidon, N.; Deydier, V.; Bumbieler, F.; Duret-Thual, C.; Mendibide, C.; Crusset, D. Stress corrosion cracking susceptibility pf P285NH and API 5L X65 steel grades in the high-level radioactive waste repository cell concept. Mater. Corros. 2021, 72, 154–165. [Google Scholar] [CrossRef]
- Maak, P.; King, F. A model for predicting stress corrosion cracking of copper containers in a deep geological repository. Mat. Res. Soc. Symp. Proc. 2006, 932, 837–843. [Google Scholar] [CrossRef]
- King, F. Assessment of the Stress Corrosion Cracking of Copper Canisters; Working Report, WR-2021-11; Posiva Oy: Eurajoki, Finland, 2021. [Google Scholar]
- King, F.; Kolář, M. Theory Manual for the Copper Corrosion Model for Stress Corrosion Cracking of Used Fuel Disposal Containers CCM-SCC.0; Technical Report 06819-REP-01300-10095-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2004. [Google Scholar]
- King, F.; Kolář, M. Preliminary Assessment of the Stress Corrosion Cracking of Used Fuel Disposal Containers Using the CCM-SCC.0 model; Technical Report 06819-REP-01300-10103-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2005. [Google Scholar]
- Andresen, P.L.; Gordon, G.M.; Lu, S.C. The stress-corrosion-cracking model for high-level radioactive-waste packages. JOM 2005, 57, 27–30. [Google Scholar] [CrossRef]
- King, F.; Litke, C.D.; Ikeda, B.M. The stress corrosion cracking of copper nuclear waste containers. Mat. Res. Soc. Symp. Proc. 1999, 556, 887–894. [Google Scholar] [CrossRef]
- Shoesmith, D.W.; Noël, J.J.; Hardie, D.; Ikeda, B.M. Hydrogen Absorption and the Lifetime Performance of Titanium Nuclear Waste Containers; Technical Report AECL-11770, COG-97-035-I; Atomic Energy of Canada Limited: Pinawa, Manitoba, 1997. [Google Scholar]
- Qin, Z.; Shoesmith, D.W. Failure model and Monte Carlo simulations for titanium (grade-7) drip shields under Yucca Mountain repository conditions. J. Nucl. Mater. 2008, 379, 169–173. [Google Scholar] [CrossRef]
- Nakayama, G.; Fukaya, Y.; Akashi, M.; Sawa, S.; Kanno, T.; Owada, H.; Otsuki, A.; Asano, H. Hydrogen-induced stress corrosion crack initiation and propagation in titanium alloys in deep underground environments. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems, Proceedings of the 2nd International Workshop, Nice, France, 14–15 September 2004; Crusset, D., Féron, D., Gras, J.-M., Macdonald, D.D., Eds.; Andra Science and Technology Series: Châtenay-Malbry, France, 2004; pp. 35–44. [Google Scholar]
- Sandia. Stress Corrosion Cracking of Waste Package Outer Barrier and Drip Shield Materials; Technical Report ANL-EBS-MD-000005 REV 04; Sandia National Laboratories: Las Vegas, NV, USA, 2007. [Google Scholar]
- SKB. Plementary Information on Canister Integrity Issues; Technical Report SKB TR-19-15; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2019. [Google Scholar]
- Hua, F.; Mon, K.; Paathi, P.; Gordon, G.; Shoesmith, D. A review of corrosion of titanium grade 7 and other titanium alloys in nuclear waste repository environments. Corrosion 2005, 61, 987–1003. [Google Scholar] [CrossRef]
- Hua, F.; Mon, K.; Paathi, P.; Gordon, G.; Shoesmith, D. Modeling the hydrogen-induced cracking of titanium alloys in nuclear waste repository environments. JOM 2005, 57, 20–26. [Google Scholar] [CrossRef]
- King, F. Microbiologically influenced corrosion of nuclear waste containers. Corrosion 2009, 65, 233–251. [Google Scholar] [CrossRef]
- Marciales, A.; Peralta, Y.; Haile, T.; Crosby, T.; Wolodko, J. Mechanistic microbiologically influenced corrosion modelling—A review. Corros. Sci. 2019, 146, 99–111. [Google Scholar] [CrossRef]
- Masurat, P.; Eriksson, S.; Pedersen, K. Microbial sulphide production in compacted Wyoming bentonite MX-80 under in situ conditions relevant to a repository for high-level radioactive waste. Appl. Clay Sci. 2010, 47, 58–64. [Google Scholar] [CrossRef]
- Stroes-Gascoyne, S.; Hamon, C.J.; Maak, P.; Russell, S. The effects of the physical properties of highly compacted smectitic clay (bentonite) on the culturability of indigenous microorganisms. Appl. Clay Sci. 2010, 47, 155–162. [Google Scholar] [CrossRef]
- Stroes-Gascoyne, S. The Potential for Microbial Life in a Canadian High-Level Nuclear Fuel Waste Disposal Vault: A Nutrient and Energy Source Analysis; Technical Report AECL-9574; Atomic Energy of Canada Limited: Pinawa, Manitoba, 1989. [Google Scholar]
- King, F.; Kolář, M.; Stroes-Gascoyne, S. Theory Manual for the Microbiological Copper Corrosion Model CCM-MIC.0; Technical Report 06819-REP-01200-10091-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2002. [Google Scholar]
- King, F.; Kolář, M.; Stroes-Gascoyne, S. Preliminary Simulations of the Long-Term Activity of Microbes in a Deep Geologic Repository Using CCM-MIC.0 and the Implications for Corrosion of Copper Containers; Technical Report 06819-REP-01200-10104-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2003. [Google Scholar]
- King, F.; Kolář, M.; Stroes-Gascoyne, S.; Bellingham, P.; Chu, J.; Dawe, P.V. Modelling the activity of sulphate-reducing bacteria and the effects on container corrosion in an underground nuclear waste disposal vault. Mat. Res. Soc. Symp. Proc. 1999, 556, 1167–1174. [Google Scholar] [CrossRef]
- Idiart, A.; Coene, E.; Bagaria, F.; Román-Ross Birgersson, M. Reactive Transport Modelling Considering Transport in Interlayer Water. New Model, Sensitivity Analyses and Results from the Integrated Sulfide Project Inter-Model Comparison Exercise; Technical Report SKB TR-18-07; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2019. [Google Scholar]
- Pękala, M.; Alt-Epping, P.; Wersin, P. 3D and 1D Dual-Porosity Reactive Transport Simulations—Model Improvements, Sensitivity Analyses, and Results from the Integrated Sulfide Project Inter-Model Comparison Exercise; Working Report, WR-2018-31; Posiva Oy: Eurajoki, Finland, 2019. [Google Scholar]
- Pekala, M.; Wersin, P.; Cloet, V.; Diomidis, N. Reactive transport calculations to evaluate sulphide fluxes in the near-field of a SF/HLW repository in the Opalinus Clay. Appl. GeoChem. 2019, 100, 169–180. [Google Scholar] [CrossRef]
- Hung, C.-C.; Briggs, S.; Yu, Y.-C.; Wu, Y.-C.; King, F. Reactive transport model for the production, transport, and consumption of sulfide in a spent nuclear fuel deep geological repository in crystalline rock. Mater. Corros. 2023, 74, 1848–1860. [Google Scholar] [CrossRef]
- Briggs, S.; Krol, M. Diffusive Transport Modelling of Corrosion Agents through the Engineered Barrier System in a Deep Geological Repository for Used Nuclear Fuel; Technical Report NWMO-TR-2018-06; Nuclear Waste Management Organization: Toronto, ON, Canada, 2018. [Google Scholar]
- Pedersen, K. Analysis of copper corrosion in compacted bentonite clay as a function of clay density and growth conditions for sulfate-reducing bacteria. J. Appl. Microbiol. 2010, 108, 1094–1104. [Google Scholar] [CrossRef]
- Stroes-Gascoyne, S.; Hamon, C.J.; Maak, P. Limits to the use of highly compacted bentonite as a deterrent for microbiologically influenced corrosion in an nuclear fuel waste repository. Phys. Chem. Earth 2011, 36, 1630–1638. [Google Scholar] [CrossRef]
- Aerts, S. Effect of Geochemical Conditions on Bacterial Activity; Technical Report SCK•CEN-ER-75; Belgian Nuclear Research Centre SCK•CEN: Boeretang, Belgium, 2009. [Google Scholar]
- Haynes, H.M.; Bailey, M.T.; Lloyd, J.R. Bentonite barrier materials and the control of microbial processes: Safety case implications for the geological disposal of radioactive waste. Chem. Geol. 2021, 581, 120353. [Google Scholar] [CrossRef]
- Taborowski, T.; Bengtsson, A.; Chukharkina, A.; Blom, A.; Pedersen, K. Bacterial Presence and Activity in Compacted Bentonite; Technical Report, Microbiology in Nuclear Waste Disposal (MIND); Deliverable D2.4, v2; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- King, F.; Kolář, M. Consequences of Microbial Activity for Corrosion of Copper Used Fuel Containers—Analyses Using the CCM-MIC.0.1 Code; Technical Report 06819-REP-01300-00120-R00; Ontario Power Generation Nuclear Waste Management Division: Toronto, ON, Canada, 2006. [Google Scholar]
- Cloet, V.; Pekala, M.; Smith, P.; Wersin, P.; Diomidis, N. An Evaluation of Sulphide Fluxes in the Near Field of a HLW Repository; Technical Report NTB 17-04; Nagra: Wettingen, Switzerland, 2017. [Google Scholar]
- Pekala, M.; Smith, P.; Wersin, P.; Diomidis, N.; Cloet, V. Comparison of models to evaluate microbial sulphide generation and transport in the near field of a SF/HLW repository in Opalinus Clay. J. Contam. Hydrol. 2020, 228, 103561. [Google Scholar] [CrossRef]
- Ma, J.; Pekala, M.; Alt-Epping, P.; Pastina, B.; Maanoja, S.; Wersin, P. 3D modelling of long-term sulfide corrosion of copper canisters in a spent nuclear fuel repository. Appl. GeoChem. 2022, 146, 105439. [Google Scholar] [CrossRef]
- Ma, J.; Alt-Epping, P.; Patina, B.; Niskanen, M.; Salonen, T.; Wersin, P. Development of a 2D model for rapid estimation of sulfide corrosion of copper canisters in a spent nuclear fuel repository. Mater. Corros. 2023, 74, 1823–1833. [Google Scholar] [CrossRef]
- King, F.; Kolář, M. Modelling the Long-Term Corrosion Behaviour of Copper Canisters in a KBS-3 Repository (Copper Sulfide Model Version 1.1); Working Report WR-2021-12; Posiva Oy: Eurajoki, Finland, 2021. [Google Scholar]
- King, F.; Kolář, M. Copper Sulfide Model for the Safety Case for the Operating Licence Application (CSM-SC-OLA); Working Report WR-2023-XX; Posiva Oy: Eurajoki, Finland, 2023. [Google Scholar]
- King, F.; Ma, J.; Alt-Epping, P.; Wersin, P.; Kolář, M. Benchmarking of University of Bern Sulfide Model (UBSM) and Copper Sulfide Model Used in the Safety Case SC-OLA; Working Report, WR-2023-05; Posiva Oy: Eurajoki, Finland, 2023. [Google Scholar]
- Posiva. Sulfide Fluxes and Concentrations in the Spent Nuclear Fuel Repository at Olkiluoto—2021 Update; Working Report WR-2021-07; Posiva Oy: Eurajoki, Finland, 2021. [Google Scholar]
- Briggs, S.; McKelvie, J.; Keech, P.; Sleep, B.; Krol, M. Transient modelling of sulphide diffusion under conditions typical of a deep geological repository. Corros. Eng. Sci. Technol. 2017, 521, 200–203. [Google Scholar] [CrossRef]
- Briggs, S.; McKelvie, J.; Sleep, B.; Krol, M. Multi-dimensional transport modelling of corrosive agents through a bentonite buffer in a Canadian deep geological repository. Sci. Total Environ. 2017, 599–600, 348–354. [Google Scholar] [CrossRef]
- Briggs, S.; McKelvie, J.; Krol, M. Temperature dependent sulphide transport in highly compacted bentonite. In Proceedings of the International High-Level Radioactive Waste Management Conference, Charlotte, NC, USA, 9–13 April 2017; American Nuclear Society: La Grange Park, IL, USA, 2017; pp. 317–321. [Google Scholar]
- Morco, R.P.; Jospeh, J.M.; Hall, D.S.; Medri, C.; Shoesmith, D.W.; Wren, J.C. Modelling of radiolytic production of HNO3 relevant to corrosion of a used fuel container in deep geologic repository environments. Corros. Eng. Sci. Technol. 2017, 52, 141–147. [Google Scholar] [CrossRef]
- Farnan, I.; King, F.; Roberts, D.; Smith, V.; Swanton, S.; Thetford, R. Effects of Ionising Radiation of Engineered Barrier System Performance; Technical Report; NDA Report no. RWM/Contr/19/041; Radioactive Waste Management: Oxfordshire, UK, 2019. Available online: https://webarchive.nationalarchives.gov.uk/ukgwa/20200401140306/https:/rwm.nda.gov.uk/publication/effects-of-ionising-radiation-on-engineered-barrier-system-performance/ (accessed on 18 April 2023).
- Westerman, R.E.; Nelson, J.L.; Pitman, S.G.; Kun, W.L.; Basham, S.J.; Moak, D.P. Evaluation of iron-base materials for waste package containers in a salt repository. Mat. Res. Soc. Symp. Proc. 1984, 26, 427–436. [Google Scholar] [CrossRef]
- Shoesmith, D.W.; King, F. The Effects of Gamma Radiation on the Corrosion of Candidate Materials for the Fabrication of Nuclear Waste Packages; Technical Report AECL-11999; Atomic Energy of Canada Limited: Pinawa, Manitoba, 1999. [Google Scholar]
- Kursten, B.; Macdonald, D.D.; Smart, N.R.; Gaggiano, R. Corrosion issues of carbon steel radioactive waste packages exposed to cementitious materials with respect to the Belgian ercontainer concept. Corros. Eng. Sci. Technol. 2017, 52, 11–16. [Google Scholar] [CrossRef]
- King, F.; Behazin, M. A review of the effect of irradiation on the corrosion of copper-coated used fuel containers. Corros. Mater. Degrad. 2021, 2, 678–707. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Urquidi-Macdonald, M. Thin-layer mixed-potential model for the corrosion of high-level nuclear waste canisters. Corrosion 1990, 46, 380–390. [Google Scholar] [CrossRef]
- Soroka, I.; Chae, N.; Jonsson, M. On the mechanism of γ-radiation-induced corrosion of copper in water. Corros. Sci. 2021, 182, 109279. [Google Scholar] [CrossRef]
- Jonsson, M. Exploring the impact of groundwater constituents and irradiation conditions on radiation-induced corrosion of copper. Radiat. Phys. Chem. 2023, 211, 111048. [Google Scholar] [CrossRef]
- Behazin, M.; Briggs, S.; King, F. Radiation-induced corrosion model for copper-coated used fuel containers. Part 1. Validation of the bulk radiolysis submodel. Mater. Corros. 2023, 182, 109279. [Google Scholar] [CrossRef]
- Joseph, J.M.; Choi, B.S.; Yakabuskie, P.; Wren, J.C. A combined experimental and model analysis on the effect of pH and O2(aq) on γ-radiolytically produced H2 and H2O2. Radiat. Phys. Chem. 2008, 77, 1009–1020. [Google Scholar] [CrossRef]
- Henshaw, J.; Spahiu, K. Radiolysis Calculations of Air, Argon and Water Mixtures in a KBS-3 Canister; Technical Report SKB TR-21-11; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2021. [Google Scholar]
- Morco, R.P. Gamma-Radiolysis Kinetics and Its Role in the Overall Dynamics of Materials Degradation. Ph.D. Thesis, Western University, London, ON, Canada, 2020. [Google Scholar]
- Wu, M.; Beahzin, M.; Nam, J.; Keech, P. Internal Corrosion of Fused Fuel Container; Technical Report NWMO-TR-2019-02; Nuclear Waste Management Organization: Toronto, ON, Canada, 2019. [Google Scholar]
- Carver, M.B.; Hanley, D.V.; Chaplin, K.R. MAKSIMA-CHEMIST. A Program for Mass Action Kinetics Simulation by Automatic Chemical Equation Manipulation and Integration Using Stiff Techniques; Technical Report AECL-6413; Atomic Energy of Canada Limited: Chalk River, ON, Canada, 1979. [Google Scholar]
- Hoch, A.R.; Sharland, S.M. Assessment Study of the Stresses Induced by Corrosion in the Advanced Cold Process Canister; Technical Report SKB TR-94-13; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1993. [Google Scholar]
- Bond, A.E.; Hoch, A.R.; Jones, G.D.; Tomczyk, A.J.; Wiggin, R.M.; Worraker, W.J. Assessment of a Spent Fuel Disposal Canister. Assessment Studies for a Copper Canister with Cast Steel Inner Component; Technical Report SKB TR-97-19; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1997. [Google Scholar]
- Smart, N.R.; Rance, A.P.; Fennell, P.A.H. Expansion Due to the Anaerobic Corrosion of Iron; Technical Report SKB TR-06-41; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2006. [Google Scholar]
- Engelhardt, G.R.; Kursten, B.; Macdonald, D.D. Corrosion of carbon steel in physically constrained locations in high level nuclear waste isolation systems. Corros. Sci. 2020, 177, 108974. [Google Scholar] [CrossRef]
- Patel, R.; Punshon, C.; Nicholas, J.; Bastid, P.; Zhou, R.; Schneider, C.; Bagshaw, N.; Howse, D.; Hutchinson, E.; Asano, R.; et al. Canister Design Concepts for Disposal of Spent Fuel and High Level Waste; Technical Report NTB 124-06; Nagra: Wettingen, Switzerland, 2012. [Google Scholar]
- BS 7910:2019; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures. British Standards Institute: London, UK, 2019.
- Korzhavyi, P.A.; Abrikosov, I.A.; Johansson, B. Theoretical investigation of the defect interactions in dilute copper alloys intended for nuclear waste containers. Mat. Res. Soc. Symp. Proc. 1999, 556, 895–902. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Abrikosov, I.A.; Johansson, B. Theoretical study of bulk and surface properties of digenite Cu2-δS. Mat. Res. Soc. Symp. Proc. 2000, 608, 115–120. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Johansson, B. Thermodynamic Properties of Copper Compounds with Oxygen and Hydrogen from First Principles; Technical Report SKB TR-10-30; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010. [Google Scholar]
- Stenlid, J.H.; Johansson, A.J.; Leygraf, C.; Brinck, T. Computational analysis of the early stage of cuprous oxide sulphidation: A top-down process. Corros. Eng. Sci. Technol. 2017, 52, 50–53. [Google Scholar] [CrossRef]
- Stenlid, J.H.; dos Santos, E.C.; Arán-Ais, R.M.; Bagger, A.; Johansson, A.J.; Cuenya, B.R.; Rossmeisl, J.; Pettersson, L.G.M. Uncovering the electrochemical interface of low-index copper surfaces in deep groundwater environments. Electrochim. Acta 2020, 362, 137111. [Google Scholar] [CrossRef]
- Stenlid, J.H.; dos Santos, E.G.; Johansson, A.J.; Pettersson, L.G.M. Properties of interfaces between copper and copper sulphide/oxide films. Corros. Sci. 2021, 183, 109313. [Google Scholar] [CrossRef]
- Kong, D.; Xu, A.; Dong, C.; Mao, F.; Xiao, K.; Li, X.; Macdonald, D.D. Electrochemical investigation and ab initio computation of passive film properties on copper in anaerobic sulphide solutions. Corros. Sci. 2017, 116, 34–43. [Google Scholar] [CrossRef]
- Turchi, P.E.A.; Kaufman, L.; Liu, Z.-K. Stability and aging of candidate alloys for the Yucca Mountain Project: CALPHAD results. Mat. Res. Soc. Symp. Proc. 2003, 757, paper II4.3. [Google Scholar] [CrossRef]
- Hall, D.; Walton, J. Conceptual model for low separation processes affecting waste package environment, Yucca Mountain, Nevada. Appl. GeoChem. 2006, 21, 859–869. [Google Scholar] [CrossRef]
- Turnbull, A. A Review of the Possible Effects of Hydrogen on Lifetime of Carbon Steel Nuclear Waste Canisters; Technical Report NTB 09-04; Nagra: Wettingen, Switzerland, 2009. [Google Scholar]
- Yu, Y.-C.; Chen, C.-J.; Chung, C.-C.; Ni, C.-F.; Lee, I.-H.; Wu, Y.-C.; Lin, T.-Y. A multimodel framework for quantifying flow and advective transport controlled by earthquake-induced canister failures in a reference case for radioactive waste geological disposal. Energies 2023, 16, 5081. [Google Scholar] [CrossRef]
- Birgersson, M.; Karnland, O. Ion equilibrium between montmorillonite interlayer space and an external solution—Consequences for diffusional transport. Geochim. Cosmochim. Acta 2009, 73, 1908–1923. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Porewater chemistry in compacted re-saturated MX-80 bentonite. J. Contam. Hydrol. 2003, 61, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Wersin, P. Geochemical modelling of bentonite porewater in high-level waste repositories. J. Contam. Hydrol. 2003, 61, 405–422. [Google Scholar] [CrossRef]
- Wersin, P.; Curti, E.; Appelo, C.A.J. Modelling bentonite-water interactions at high solid/liquid ratios: Swelling and diffuse double layer effects. Appl. Clay Sci. 2004, 26, 249–257. [Google Scholar] [CrossRef]
- Berner, U.R. Evolution of pore water chemistry during degradation of cement in a radioactive waste repository environment. Waste Manage. 1992, 12, 201–219. [Google Scholar] [CrossRef]
- BSC (Bechtel SAIC Company). In-Drift Precipitates/Salts Model; Technical Report for U.S. Department of Energy; NV, USA, ANL-EBS-MD-000045 REV 02; Bechtel SAIC Company: Las Vegas, NV, USA, 2004. [Google Scholar]
- BSC (Bechtel SAIC Company). Analysis of Dust Deliquescence for FEP Screening; Technical Report for U.S. Department of Energy; ANL-EBS-MD-000074 REV 01; Bechtel SAIC Company: Las Vegas, NV, USA, 2005. [Google Scholar]
- Sandia. Engineered Barrier System: Physical and Chemical Environment; Technical Report ANL-EBS-MD-000033 REV 06; Sandia National Laboratories: Las Vegas, NV, USA, 2007. [Google Scholar]
- Guo, R. Coupled Thermal-Mechanical Modelling of a Deep Geological Repository Using the Horizontal Tunnel Placement Method in Sedimentary Rock Using CODE_BRIGHT; Technical Report NWMO-TR-2010-22; Nuclear Waste Management Organization: Toronto, ON, Canada, 2010. [Google Scholar]
- Guo, R. Thermal Modelling of a Mark II Container; Technical Report NWMO-TR-2015-06; Nuclear Waste Management Organization: Toronto, ON, Canada, 2015. [Google Scholar]
- Guo, R. Thermal Response of a Mark II Conceptual Deep Geological Repository in Crystalline Rock; Technical Report NWMO-TR-2016-03; Nuclear Waste Management Organization: Toronto, ON, Canada, 2016. [Google Scholar]
- Samper, J.; Zheng, L.; Montenegro, L.; Fernández, A.M.; Rivas, P. Coupled thermo-hydro-chemical models of compacted bentonite after FEBEX in situ test. Appl. GeoChem. 2008, 23, 1186–1201. [Google Scholar] [CrossRef]
- Åkesson, M.; Kristensson, O.; Börgesson, L.; Dueck, A.; Hernelind, J. THM Modelling of Buffer, Backfill and Other System Components; Technical Report SKB TR-10-11; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010. [Google Scholar]
- Ariani, I. Dose Rate Analysis to Port Radiolysis Assessment of Used CANDU Fuel; Technical Report NWMO-TR-2022-02; Nuclear Waste Management Organization: Toronto, ON, Canada, 2022. [Google Scholar]
- Gutiérrez, M.M.; Caruso, S.; Diomidis, N. Effects of materials and design on the criticality and shielding assessment of canister concepts for the disposal of spent nuclear fuel. Appl. Radiat. Isotopes 2018, 139, 201–208. [Google Scholar] [CrossRef]
- Sidborn, M.; Neretniks, I. Modelling of biochemical processes in rocks: Oxygen depletion by pyrite oxidation—Model development and exploratory simulations. Mat. Res. Soc. Symp. Proc. 2003, 757, II11.5. [Google Scholar] [CrossRef]
- Yang, C.; Samper, J.; Molinero, J.; Bonilla, M. Modelling geochemical and microbial consumption of dissolved oxygen after backfilling a high level radioactive waste repository. J. Contam. Hydrol. 2007, 93, 130–148. [Google Scholar] [CrossRef]
- Jonsson, M.; Emilsson, G.; Emilsson, L. Mechanical Design Analysis for the Canister; Technical Report Posiva SKB Report 04; Posiva Oy: Eurajoki, Finland; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2018. [Google Scholar]
- Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions, 2nd ed.; NACE International: Houston, TX, USA, 1974. [Google Scholar]
- Puigdomenech, I.; Taxén, C. Thermodynamic Data for Copper. Implications for the Corrosion of Copper under Repository Conditions; Technical Report SKB TR-00-13; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2000. [Google Scholar]
- Protopopoff, E.; Marcus, P. Potential-pH diagrams for sulfur and hydroxyl adsorbed on copper surfaces in water containing sulfides, sulfites or thiosulfates. Corros. Sci. 2003, 45, 1191–1201. [Google Scholar] [CrossRef]
- Protopopoff, E.; Marcus, P. Potential-pH diagrams for hydroxyl and hydrogen adsorbed on copper surfaces. Electrochim. Acta 2005, 51, 408–417. [Google Scholar] [CrossRef]
- Frankel, G.S.; Sridhar, N. Understanding localized corrosion. Mater. Today 2008, 11, 38–44. [Google Scholar] [CrossRef]
- Liu, C.; Kelly, R.G. A review of the application of finite element method (FEM) to localized corrosion modelling. Corrosion 2019, 75, 1285–1299. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, D.D.; Engelhardt, G.R. A brief review of determinism in the prediction of localized corrosion damage. Zeit. Phys. Chem. 2012, 226, 871–888. [Google Scholar] [CrossRef]
- Pospiskova, I.; Dobrev, D.; Kouril, M.; Stoulil, J.; Novikova, D.; Kotnour, P.; Matal, O. Czech national programme and disposal concept. Corros. Eng. Sci. Technol. 2017, 52, 6–10. [Google Scholar] [CrossRef]
- Walton, J.C.; Sagar, B. A corrosion model for nuclear waste containers. Mat. Res. Soc. Symp. Proc. 1987, 84, 271–282. [Google Scholar] [CrossRef]
- Worgan, K.; Apted, M.; Sjöblom, R. Performance analysis of copper canister corrosion under oxidizing or reducing conditions. Mat. Res. Soc. Symp. Proc. 1995, 353, 695–702. [Google Scholar] [CrossRef]
- Lee, J.H.; Atkins, J.E.; Dunlap, B. Incorporating of “corrosion-time” and effects of corrosion-product spalling in waste package degradation simulation in the potential repository at Yucca Mountain. Mat. Res. Soc. Symp. Proc. 1997, 465, 1075–1082. [Google Scholar] [CrossRef]
- Trotignon, L.; Faure, M.-H.; Cranga, M.; Peycelon, H. Numerical simulation of the interaction between granitic groundwater, engineered clay barrier and iron canister. Mat. Res. Soc. Symp. Proc. 1999, 556, 599–606. [Google Scholar] [CrossRef]
- Gondolli, J.; Dobrev, D.; Klajmon, M.; Mendoza, A.; Černoušek, T.; Kouřil, M.; Stoulil, J. Corrosion Products—Final Report; Technical Report 329/2018/ENG; SÚRAO: Prague, Czech Republic, 2018. [Google Scholar]
- Pensado, O.; Dunn, D.S.; Cragnolino, G.A. Long-term extrapolation of passive behavior of Alloy 22. Mat. Res. Soc. Symp. Proc. 2003, 757, 42. [Google Scholar] [CrossRef]
- Hœrlé, S.; Mazaudier, F. A contribution to the modelling of atmospheric corrosion of iron. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 13; pp. 179–193. [Google Scholar]
- Bataillon, C.; Bouchon, F.; Chainais-Hillairet, C.; Fuhrman, J.; Hoaru, E.; Touzani, R. Numerical methods for the simulation of a corrosion model with moving oxide layer. J. Comput. Phys. 2012, 231, 6213–6231. [Google Scholar] [CrossRef]
- Chainais-Hillairet, C.; Bataillon, C. Mathematical and numerical study of a corrosion model. Numer. Math. 2008, 110, 1–25. [Google Scholar] [CrossRef]
- Martin, F.A.; Bataillon, C. Modelling of the evolution of iron passivity: Solving the moving boundary problem. Mat. Res. Soc. Symp. Proc. 2012, 1475, 275–280. [Google Scholar] [CrossRef]
- Desgranges, C.; Abbas, A.; Terlain, A. Model for low temperature oxidation during long term interim storage. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 14; pp. 194–207. [Google Scholar]
- Desgranges, C.; Bertrand, N.; Gauvain, D.; Terlain, A.; Poquillon, D.; Monceau, D. Model for low temperature oxidation during long term interim storage. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems, Proceedings of the 2nd International Workshop, Nice, France, 14–15 September 2004; Crusset, D., Féron, D., Gras, J.-M., Macdonald, D.D., Eds.; Andra Science and Technology Series: Châtenay-Malbry, France, 2004; pp. 170–179. [Google Scholar]
- Kim, S.S.; Chun, K.S.; Kang, K.C.; Baik, M.H.; Kwon, S.H.; Choi, J.W. Estimation of the corrosion thickness of a disposal container for high-level radioactive wastes in a wet bentonite. J. Ind. Eng. Chem. 2007, 13, 959–964. [Google Scholar]
- Peña, J.; Torres, E.; Turrero, M.J.; Escribano, A.; Martín, P.L. Kinetic modelling of the attenuation of carbon steel canister corrosion due to diffusive transport through corrosion product layers. Corros. Sci. 2008, 50, 2197–2204. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Urquidi-Macdonald, M.; Engelhardt, G.R.; Azizi, O.; Saleh, A.; Almazooqi, A.; Rosas-Camacho, O. Some important issues in electrochemistry of carbon steel in simulated concrete pore water. Part I—Theoretical issues. Corros. Eng. Sci. Technol. 2011, 46, 98–103. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Sharifi-Asl, S.; Engelhardt, G.R.; Urquidi-Macdonald, M. Issues in the Corrosion of Copper in a Swedish High Level Nuclear Waste Repository; Technical Report SSM 2012:11; Strålsäkerhetsmyndigheten: Stockholm, Sweden, 2012. [Google Scholar]
- Macdonald, D.D.; Sharifi-Asl, S.; Engelhardt, G.R. Issues in the Corrosion of Copper in a Swedish High Level Nuclear Waste Repository. Phase III. Role of Sulphide Ion in Anodic and Cathodic Processes—Research Report; Technical Report SSM 2014:57; Strålsäkerhetsmyndigheten: Stockholm, Sweden, 2014. [Google Scholar]
- King, F.; Kolář, M. Simulation of the Anaerobic Corrosion of Carbon Steel Used Fuel Containers Using the Steel Corrosion Model Version 1.0 (SCM V1.0); Technical Report NWMO-TR-2012-07; Nuclear Waste Management Organization: Toronto, ON, Canada, 2012. [Google Scholar]
- King, F.; Kolář, M.; Maak, P.; Keech, P. Simulation of the anaerobic corrosion of carbon steel used fuel containers and the impact of corrosion products on other barriers in the repository. In Proceedings of the CORROSION2013, Orlando, FL, USA, 17 March 2013; NACE International: Houston, TX, USA, 2013. paper 2735. [Google Scholar]
- Björck, M. Estimation of Oxide Growth on Joint Surfaces during FSW; Technical Memo, skb.1402837.doc; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2015; Available online: https://skb.se/wp-content/uploads/2015/05/1402837-Estimation-of-oxide-growth-on-joint-surfaces-during-FSW_2.pdf (accessed on 12 August 2019).
- Johansson, A.J.; Lilja, C.; Hedin, A. Corrosion of copper in repository-like field tests: Compilation and analysis of data. In Proceedings of the International High-Level Radioactive Waste Management, Knoxville, TN, USA, 14–18 April 2019; American Nuclear Society: La Grange Park, IL, USA, 2019; pp. 316–327. [Google Scholar]
- Leupin, O.X.; Smart, N.R.; Zhang, Z.; Stefanoni, M.; Angst, U.; Papafotiou, A.; Diomidis, N. Anaerobic corrosion of carbon steel in bentonite: An evolving interface. Corros. Sci. 2021, 187, 109523. [Google Scholar] [CrossRef]
- Marsh, G.P.; Taylor, K.J.; Bland, I.D.; Westcott, C.; Tasker, P.W.; Sharland, S.M. Evaluation of the localised corrosion of carbon steel overpacks for nuclear waste disposal in granite environments. Mat. Res. Soc. Symp. Proc. 1985, 50, 421–428. [Google Scholar] [CrossRef]
- Marsh, G.P. Predicting the long term corrosion of metal containers for nuclear waste disposal. Mat. Res. Soc. Symp. Proc. 1988, 112, 85–97. [Google Scholar] [CrossRef]
- Marsh, G.P.; Taylor, K.J.; Harker, A.H. The Kinetics of Pitting Corrosion of Carbon Steel Applied to Evaluating Containers for Nuclear Waste Disposal; Technical Report TR-91-62; Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 1991. [Google Scholar]
- Walton, J.C. Mathematical modelling of large-scale nonuniform corrosion: Coupling of corrosion, transport, and geochemical processes in nuclear waste isolation. Nucl. Chem. Waste Manag. 1988, 8, 143–156. [Google Scholar] [CrossRef]
- Walton, J.C. Theoretical modelling of crevice and pitting corrosion processes in relation to corrosion of radioactive waste containers. Mat. Res. Soc. Symp. Proc. 1990, 176, 509–516. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Urquidi-Macdonald, M. Corrosion damage function—Interface between corrosion science and engineering. Corrosion 1992, 48, 354–367. [Google Scholar] [CrossRef]
- Engelhardt, G.; Macdonald, D.D. Deterministic prediction of pit depth distribution. Corrosion 1998, 54, 469–479. [Google Scholar] [CrossRef]
- Roux, F.; Stafiej, J.; Chaussé, A.; Badiali, J.P. Numerical simulations of simple processes associated with corrosion, diffusion and formation of a passive layer. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 9; pp. 118–128. [Google Scholar]
- Lee, J.H.; Mon, K.G.; Longsine, D.E.; Bullard, B.E. An integrated stochastic model for long term performance of waste package for high level nuclear waste disposal. In Prediction of Long Term Corrosion Behaviour in Nuclear Waste Systems; Féron, D., Macdonald, D.D., Eds.; European Federation of Corrosion, Number 36; Maney: London, UK, 2003; Chapter 10; pp. 129–153. [Google Scholar]
- Taniguchi, N.; Suzuki, H.; Kawasaki, M.; Naito, M.; Kobayashi, M.; Takahashi, R.; Asano, H. Propagation behaviour of general and localised corrosion of carbon steel in simulated groundwater under aerobic condition. Corros. Eng. Sci. Technol. 2011, 46, 117–123. [Google Scholar] [CrossRef]
- Shukla, P.; Pabalan, R.; He, X. In-Crevice Chemistry Model Development for Nickel-Based Alloys and Analysis of Model Results in View of Literature Information; Technical Report Contract NRC-02-07-006; Center for Nuclear Waste Regulatory Analyses: San Antonio, TX, USA, 2011. Available online: https://www.nrc.gov/docs/ML1126/ML112640376.pdf (accessed on 9 March 2012).
- King, F.; Lilja, C. Localised Corrosion of Copper Canisters in Bentonite Pore Water; Technical Report TR-13-27; Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2013. [Google Scholar]
- King, F.; Lilja, C. Localised corrosion of copper canisters. Corros. Eng. Sci. Technol. 2014, 49, 420–424. [Google Scholar] [CrossRef]
- King, F. Overview of a Carbon Steel Container Corrosion Model for a Deep Geological Repository in Sedimentary Rock; Technical Report NWMO-TR-2007-01; Nuclear Waste Management Organization: Toronto, ON, Canada, 2007. [Google Scholar]
- Martinsson, Å.; Sandström, R. Hydrogen depth profile in phosphorus-doped, oxygen-free copper after cathodic charging. J. Mater. Sci. 2012, 47, 6768–6776. [Google Scholar] [CrossRef]
- Sandström, R. Analysis of a MODEL for Hydrogen Bubble Nucleation and Growth in Copper; Technical memo, skb.1337317.doc; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2014; Available online: https://skb.se/wp-content/uploads/2015/05/1337317.pdf (accessed on 10 December 2017).
- King, F.; Stroes-Gascoyne, S. Microbially influenced corrosion of nuclear fuel waste disposal containers. In Proceedings of the International Conference of Microbially Influenced Corrosion, New Orleans, LO, USA, 8–10 May 1995; NACE International: Houston, TX, USA, 1995; pp. 35/1–35/14. [Google Scholar]
- King, F.; Kolář, M.; Stroes-Gascoyne, S.; Maak, P. Model for the microbiological corrosion of copper containers in a deep geologic repository. Mat. Res. Soc. Symp. Proc. 2004, 807, 811–816. [Google Scholar] [CrossRef]
- Sidborn, M.; Neretnieks, I. Corrosion of copper canisters through microbially mediated sulphate reduction. Mat. Res. Soc. Symp. Proc. 2006, 932, 261. [Google Scholar] [CrossRef]
- Dou, W.; Jia, R.; Jin, P.; Liu, J.; Chen, S.; Gu, T. Investigation of the mechanism and characteristics of copper corrosion by sulfate reducing bacteria. Corros. Sci. 2018, 144, 237–248. [Google Scholar] [CrossRef]
- Garcia-Hernandez, J.A.; Ponnambalam, K.; Sivaraman, M. Lifetime of used nuclear fuel containers affected by sulphate-reducing bacteria reactions inside the Canadian deep geological repository. Appl. Sci. 2021, 11, 7806. [Google Scholar] [CrossRef]
- King, F. The Effect of Discontinuities on the Corrosion Behaviour of Copper Canisters; Technical Report SKB TR-04-05; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2004. [Google Scholar]
- Williford, R.E. Uncertainties in container failure time predictions. Mat. Res. Soc. Symp. Proc. 1991, 212, 335–342. [Google Scholar] [CrossRef]
- Blackwood, D.J.; Hoch, A.R.; Naish, C.C.; Rance, A.; Sharland, S.M. Research on Corrosion Aspects of the Advanced Cold Process Canister; Technical Report SKB TR-94-12; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 1994. [Google Scholar]
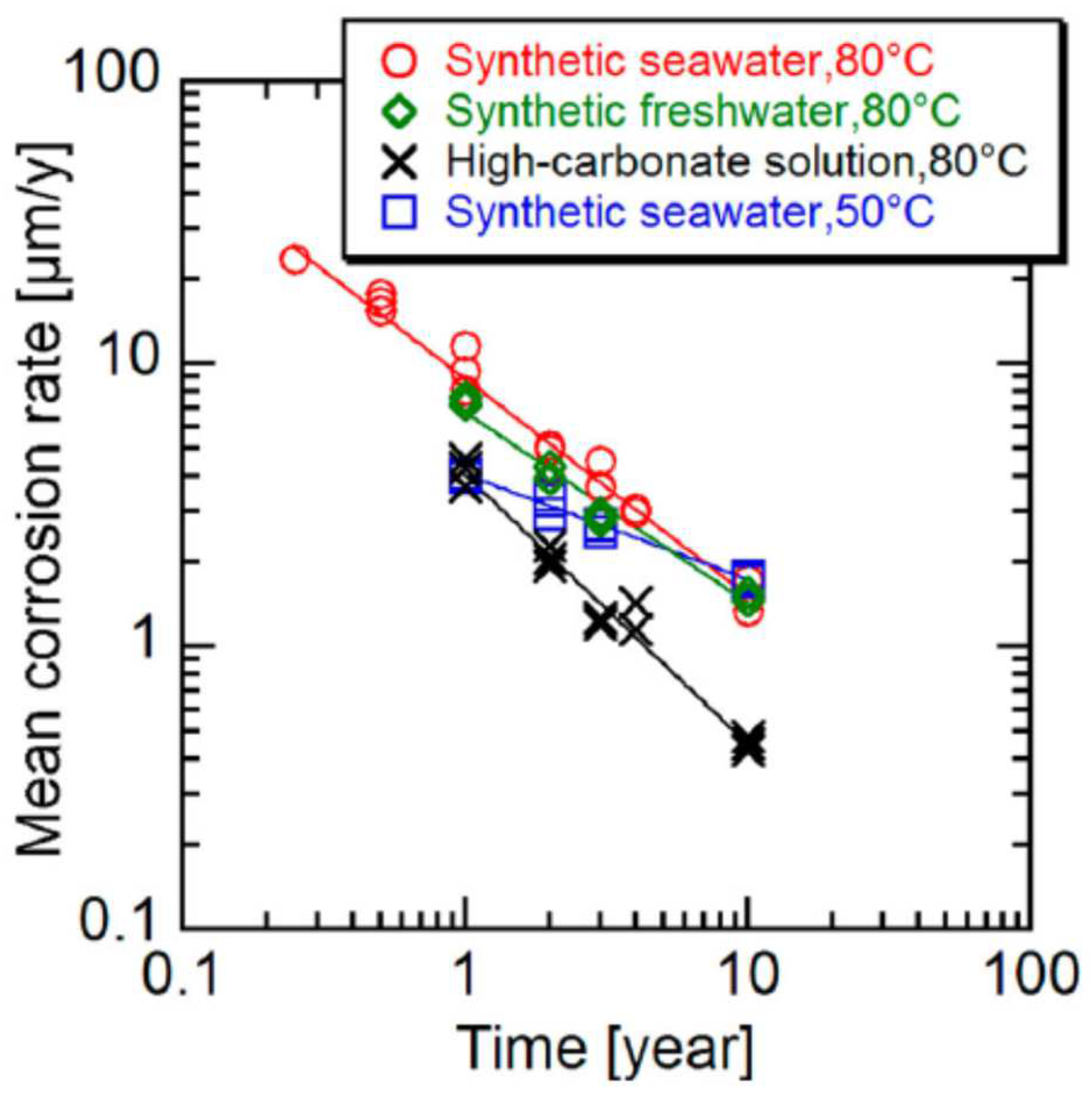


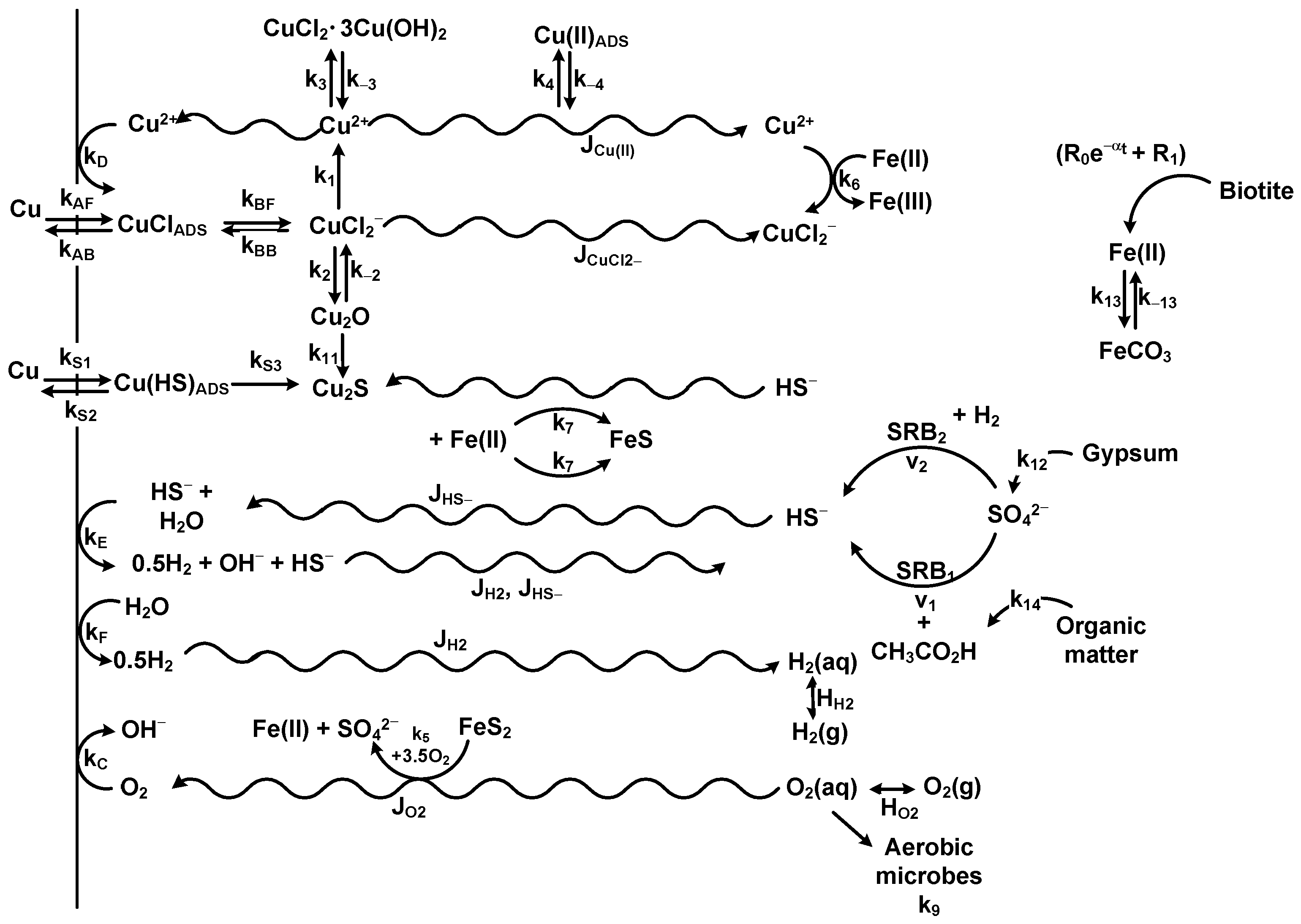


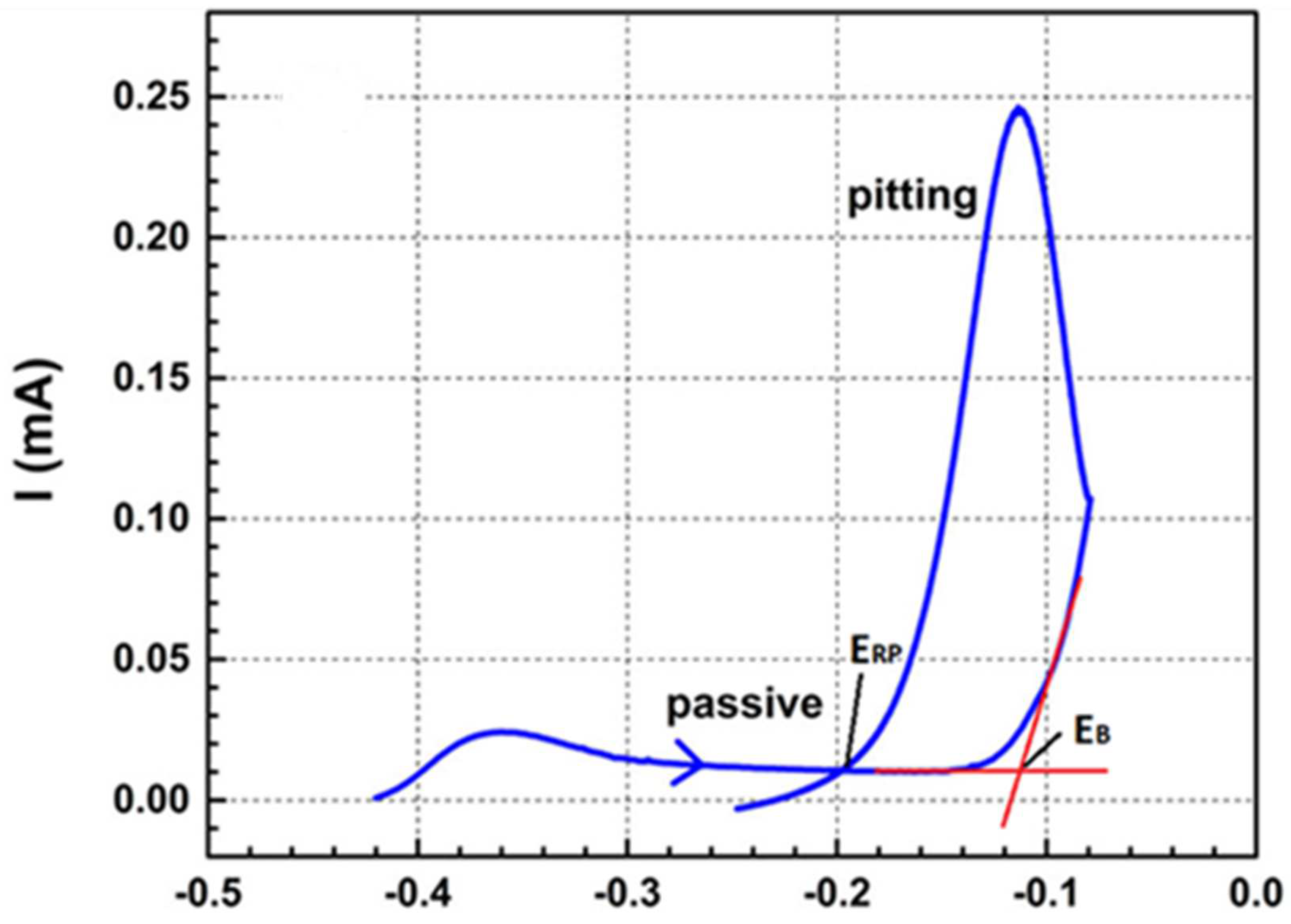

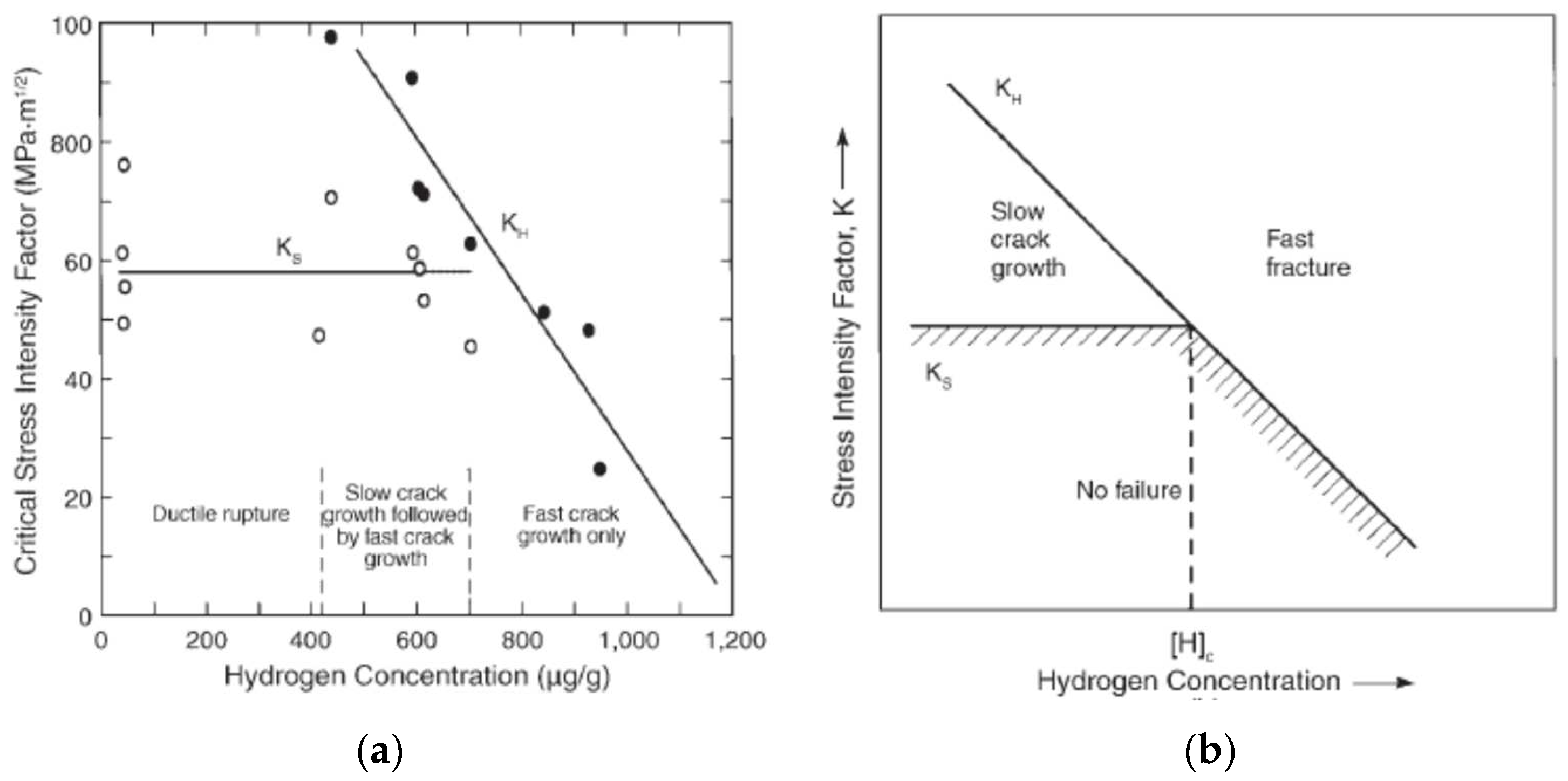
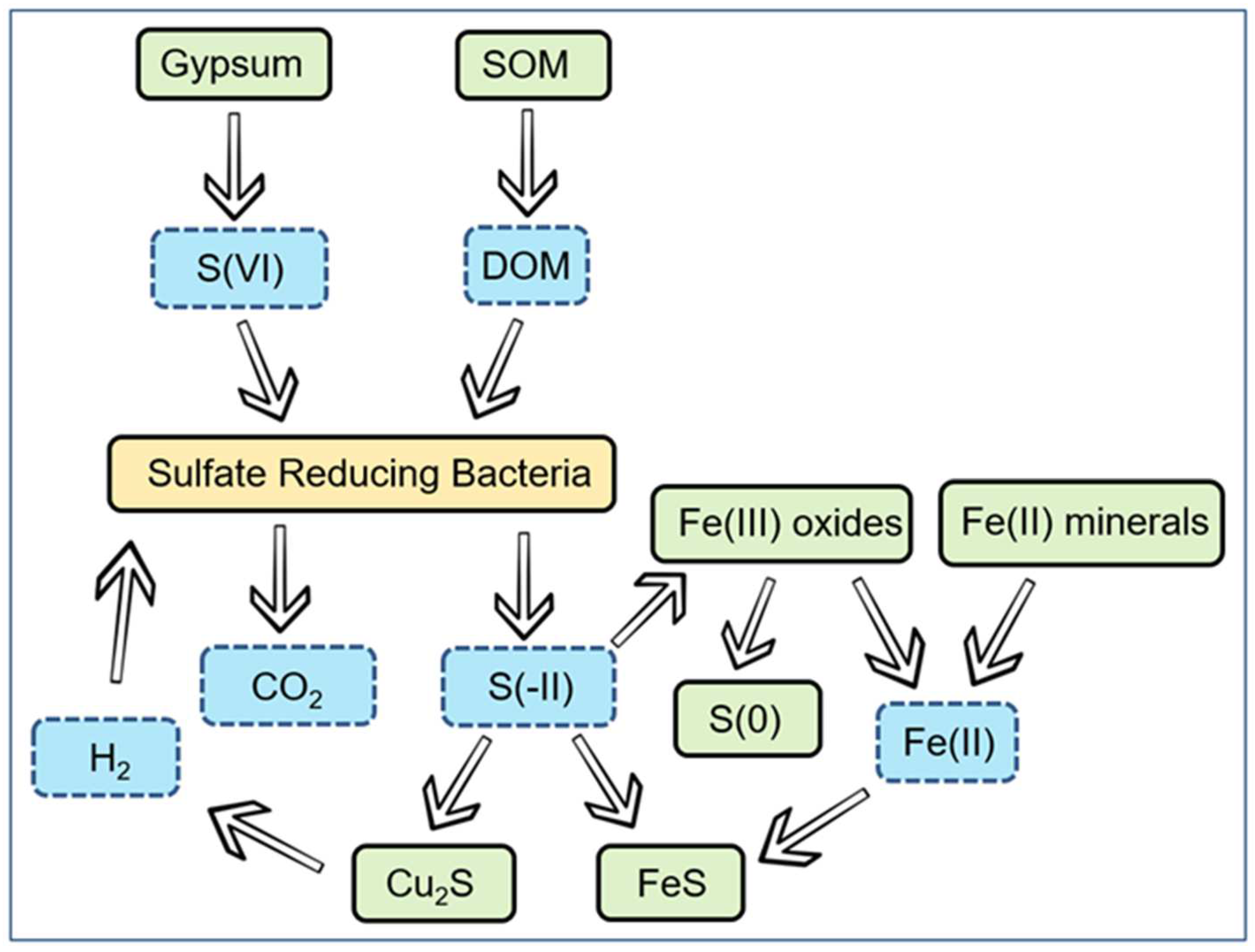
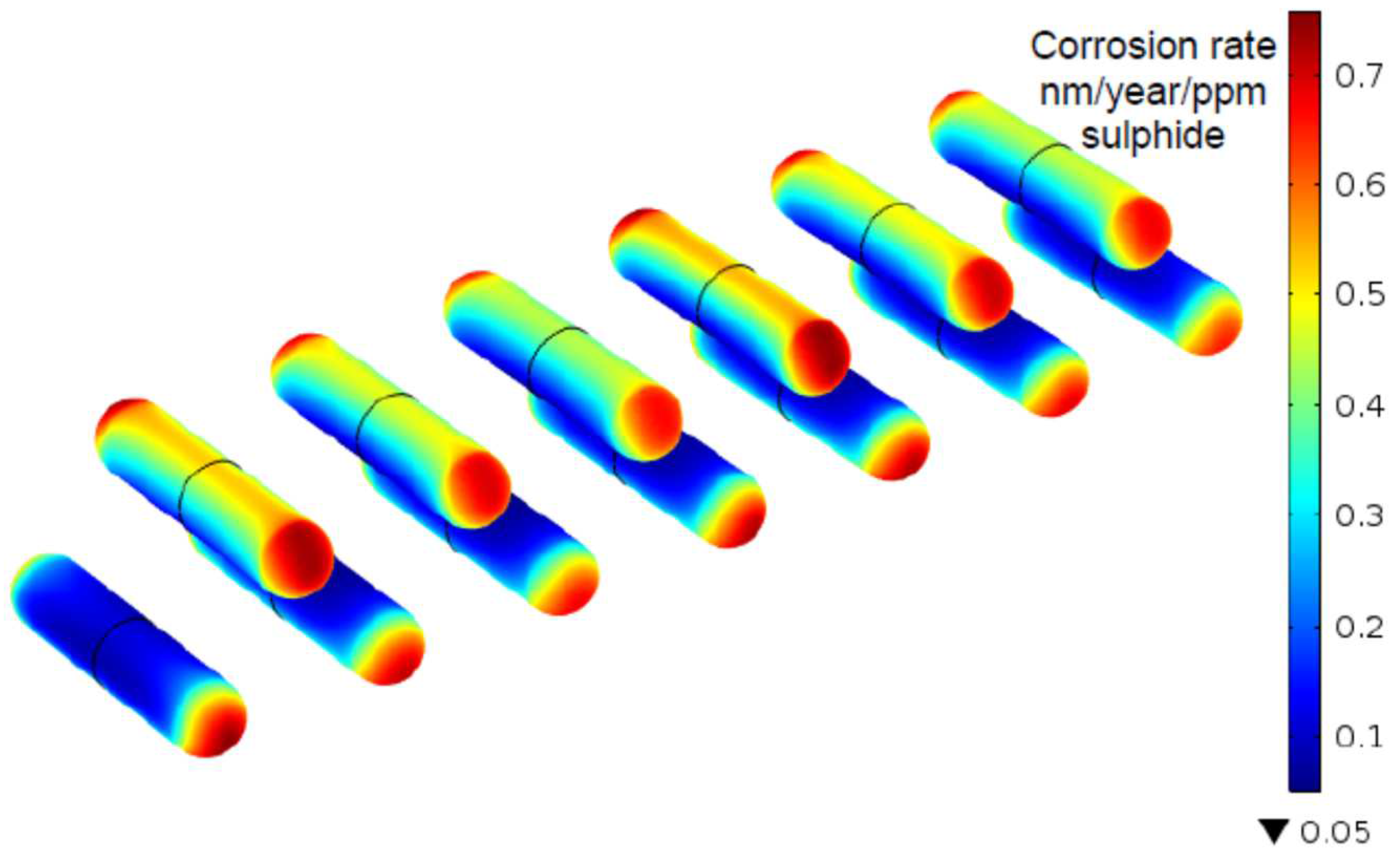
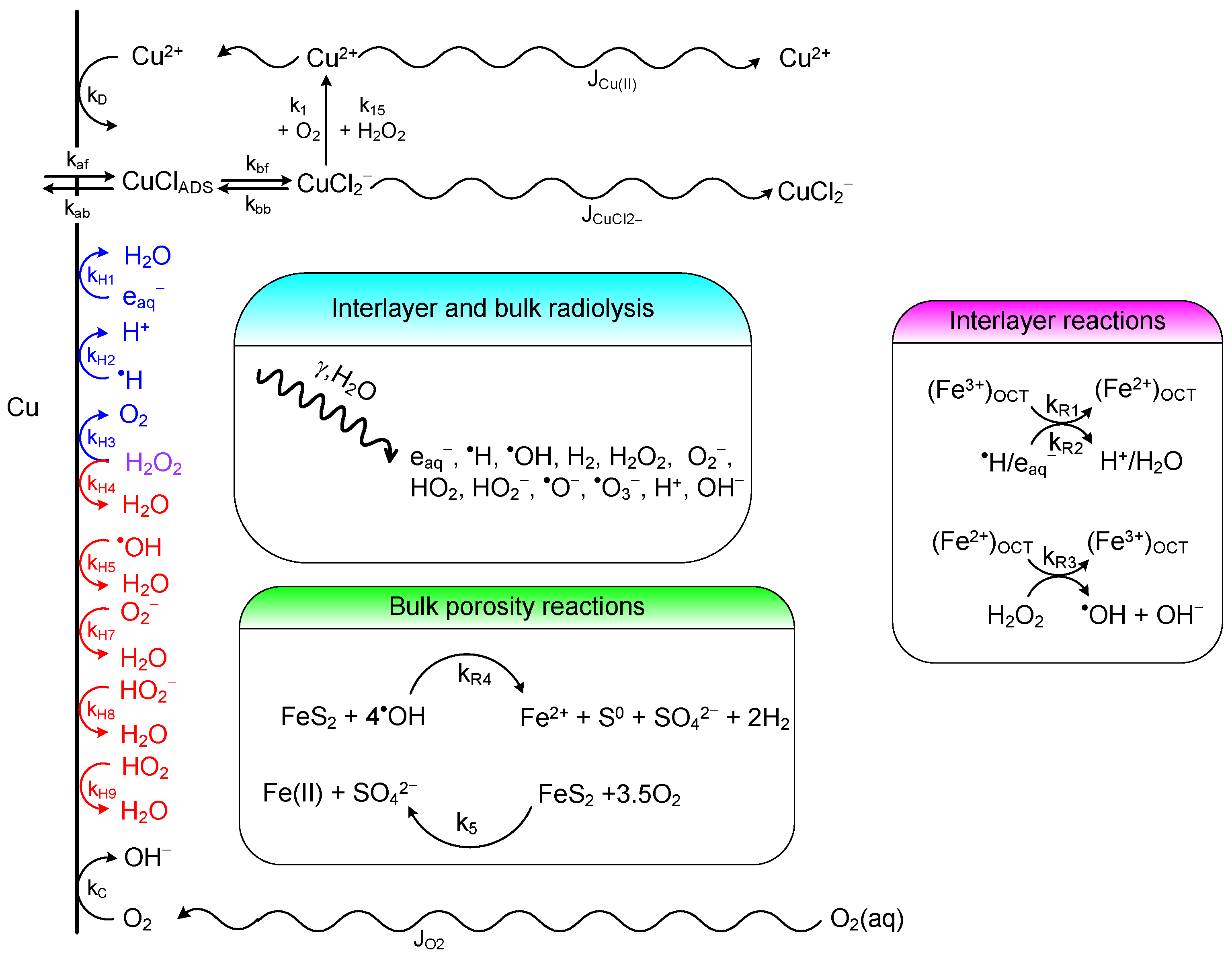


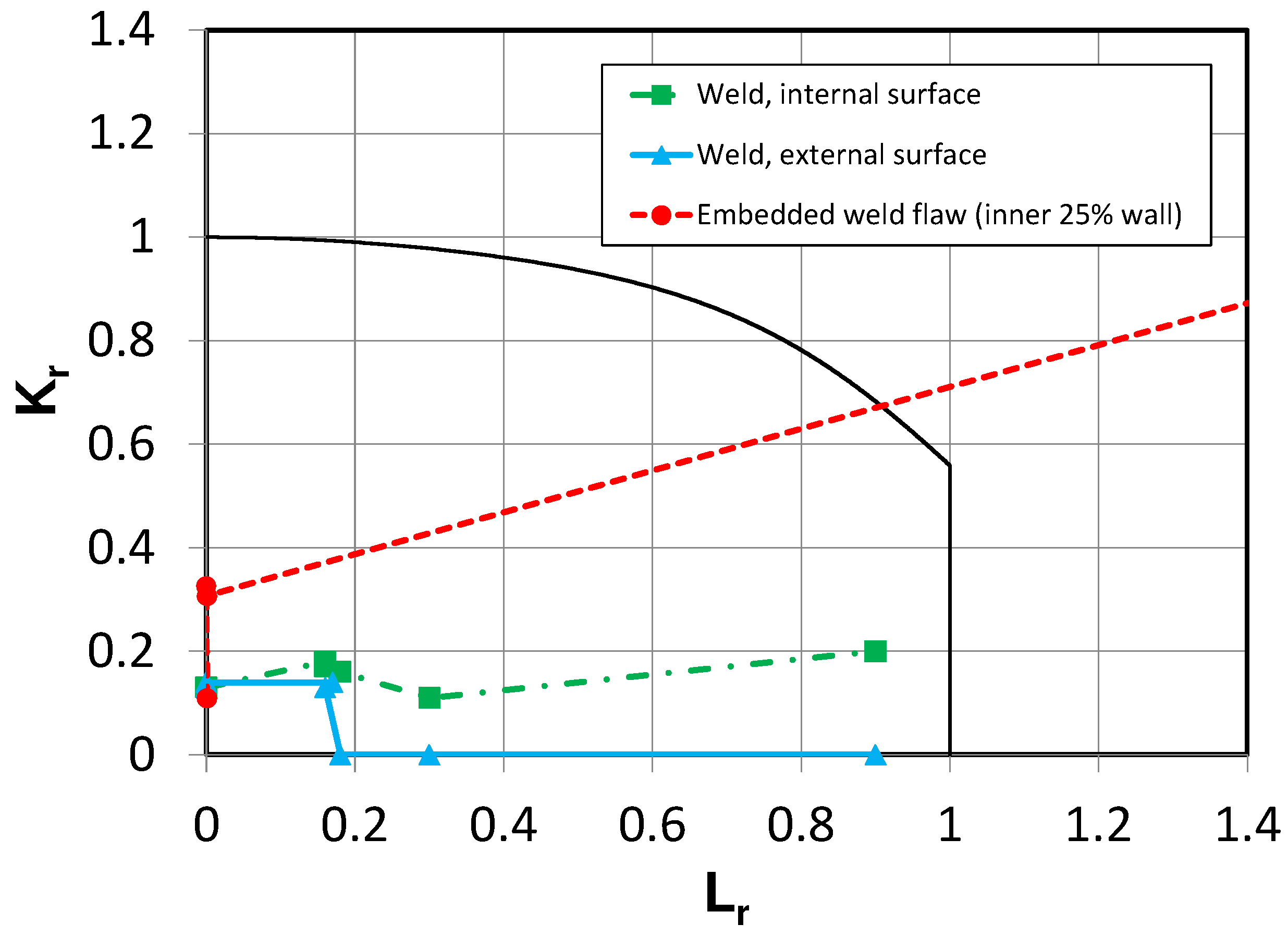
| Country | Waste Type | Reference Container Material(s) | Alternative Container Materials Considered |
|---|---|---|---|
| Belgium | HLW (SF) * | Carbon steel | AISI 316L hMo |
| Canada | SF | Copper | Carbon steel, Ti alloys |
| China | HLW | Carbon steel | Ti alloys, copper |
| Czechia | SF | Carbon steel outer, stainless steel inner | Copper, Ti alloys |
| Finland | SF | Copper, cast iron structural support | - |
| France | HLW (SF) * | Carbon steel | Undefined passive alloy, ceramics |
| Germany | HLW/SF | Carbon steel, Hastelloy C-4, Ti 99.8-Pd, pure copper | Inconel 625, Incoloy 825, Cu10Ni, Cu30Ni, cast steel, cast iron |
| Japan | HLW | Carbon steel | Ti alloys, copper |
| Spain | HLW/SF | Carbon steel | AISI 316L, Hastelloy C-22, oxygen-free copper |
| Sweden | SF | Copper, cast iron structural support | Ti alloy, ceramics |
| Switzerland | HLW/SF | Carbon steel | Copper |
| Taiwan | SF | Copper, cast iron structural support | - |
| UK | HLW (SF) * | - | Carbon steel, copper, Ti alloys, Ni-Cr-Fe alloys |
| USA | SF/HLW | Alloy 22, Ti-7 drip shield | Carbon steel, various Cu and Ni-Cr-Mo alloys |
| Copper alloys | Cu | P | S | H | O | ||||
| Oxygen-free high-conductivity OFHC | >99.99 | <0.0003 | - | - | <0.0005 | ||||
| Oxygen-free phosphorus deoxidised low residual P | 99.90 | 0.004–0.012 | - | - | - | ||||
| Oxygen-free with phosphorus OFP | >99.99 | 0.003–0.01 | <0.0012 | <0.00006 | Tens of ppm max. | ||||
| Ferrous alloys | Fe | Mn | Si | Cu | C | Other | |||
| Carbon steel | Balance | <1.65 | <0.60 | <0.60 | <2 | Cr, Ni, Mo, Ni, W, Zr (trace) | |||
| Low-carbon steel | Balance | <1.65 | <0.60 | <0.60 | 0.05–0.15 | Cr, Ni, Mo, Ni, W, Zr (trace) | |||
| Mild steel | Balance | <1.65 | <0.60 | <0.60 | 0.16–0.29 | Cr, Ni, Mo, Ni, W, Zr (trace) | |||
| Nodular cast iron | >90 | <4 | <0.05 | <6 | |||||
| Ni alloys | Ni | Cr | Fe | Mo | C | Si | Other | ||
| Alloy 825 | 36.0–46.0 | 19.5–23.5 | 24–40 | 2.5–3.5 | 0.05 | 0.5 | 1.5–3.0 Cu, 0.2 Al, 0.03 S | ||
| Alloy 22 | 56.0 | 22.0 | 3.0 | 13.0 | 0.015 | 0.08 | 3.0 W | ||
| Ti alloys | Ti | O | Pd | ||||||
| Grade 2 | Balance | 0.12 | |||||||
| Grade 7 | Balance | 0.12 | 0.15 | ||||||
| Grade 16 | Balance | 0.12 | 0.05 | ||||||
| Country | Reference Container Material(s) | Corrosion Processes Considered a |
|---|---|---|
| Belgium | Carbon steel | Uniform corrosion, SCC, localised corrosion, RIC |
| Canada | Copper | Uniform corrosion, localised corrosion, SCC, MIC, galvanic corrosion, RIC |
| China | Carbon steel | Uniform corrosion, localised corrosion, hydrogen embrittlement, RIC |
| Czechia | Carbon steel/stainless steel | Uniform corrosion, localised corrosion (carbon steel only), MIC, HIC, galvanic corrosion, RIC |
| Finland | Copper | Uniform corrosion, localised corrosion, SCC, MIC |
| France | Carbon steel | Uniform corrosion, MIC, SCC, HIC, RIC |
| Germany | TStE 355 C-steel | Uniform corrosion, pitting, SCC, IGA, RIC |
| Japan | Carbon steel | Uniform corrosion, localised corrosion, SCC, HIC, RIC |
| Spain | TStE 355 C-steel | Uniform corrosion, localised corrosion, SCC, IGA |
| Switzerland | Carbon steel | Uniform corrosion, localised corrosion, SCC, HIC |
| Sweden | Copper | Uniform corrosion, localised corrosion, SCC, MIC |
| Taiwan | Copper | Uniform corrosion, localised corrosion, SCC, MIC |
| USA | Alloy 22 Ti-7 drip shield | Uniform corrosion, crevice corrosion, SCC, MIC Uniform corrosion, HIC, SCC |
| Approach | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Empirical | Anaerobic corrosion of carbon steel [11,30,31]. Passive corrosion of Alloy 22 [9,32] | Conceptually simple. Conservative since the corrosion rate typically decreases with exposure time | Absence of any mechanistic basis. |
| Reactive transport | Point Defect Model [33,34,35] Steel–clay interaction model [36,37,38] Copper Corrosion Model (CCM) [39,40] Diffusion Poisson Coupled Model (DCPM) [41] | Mechanistically based. In some cases, provide additional information (e.g., ECORR values) that is useful for predicting the long-term corrosion performance. | May require a lot of input data. Models tend to be mathematically complex, necessitating some skill in development and interpretation. |
| Mass transport | Corrosion of carbon steel under anoxic conditions in presence of corrosion-product film [42] Copper corrosion in O2-free H2O [43] | As for reactive transport models, couple the interfacial reaction to the (transport) properties of the near-field. | Non-conservative if a diffusing species reacts, resulting in a steeper concentration gradient but is not accounted for in the model. |
| Electrochemical | Mixed-potential model for copper in O2-containing Cl− environments [44,45] Corrosion of carbon steel in bentonite [46] | Typically involve prediction of the corrosion potential ECORR which can provide additional insight. Inclusion of mass-transport effects provides link to near-field properties. | Can be overly conservative if protective properties of precipitated corrosion-product films are not taken into account. |
| Thermodynamic | Corrosion Domain and Volt Equivalent Diagrams [47,48] Corrosion of copper at high Cl− concentration [49] | Sound physical basis and necessary data are widely available. | Unless coupled to a mass-transport expression, only provides information about what reactions are possible, not the reaction kinetics. Correction for activity coefficients at high concentrations somewhat uncertain. |
| Approach | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Empirical | Suppression of microbial activity in highly compacted buffer material [169,170] Empirical corrosion rate for carbon steel that includes microbial effects [152] or enhancement factor for uniform corrosion of Alloy 22 [9] | Absence of microbial activity in buffer material obviates the need to predict corrosion under a biofilm. | Mechanistic basis required to support argument of suppression of microbial activity. Difficult to justify specific corrosion rates or enhancement factors. Empirical corrosion rates often measured in presence of added nutrients and/or under non-repository conditions, so relevance is questionable. |
| Mass balance | Mass-balance calculations for nutrients, electron acceptors, and energy [5,171]. | Establishes an upper limit to the extent of corrosion, assuming a closed system in which no additional electron acceptors or donors enter the system. | Prediction of maximum microbial population is not informative. No account taken for possible recycling of organic material. |
| Reactive transport | Copper Corrosion Model for MIC (CCM-MIC) [172,173,174]. Sulphide production, transport, and consumption models [175,176,177,178] | Mechanistically based and supported by analogues in nature. Allows optimization of repository design (for example, buffer density and mineralogical composition). Models available in 2D and 3D to assess multidimensional aspects. | Treatment of all possible microbial processes requires a large database of input values. |
| Transport | Sulphide transport model [89,179] | Extended to include effect of near-field re-saturation. Multidimensional models available to explore complex geometrical effects. | Based on an assumed source term (sulphide concentration). Absence of reactions in models, especially sinks for sulphide (Fe(II)/Fe(III)). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
King, F.; Kolàř, M.; Briggs, S.; Behazin, M.; Keech, P.; Diomidis, N. Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models. Corros. Mater. Degrad. 2024, 5, 124-199. https://doi.org/10.3390/cmd5020007
King F, Kolàř M, Briggs S, Behazin M, Keech P, Diomidis N. Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models. Corrosion and Materials Degradation. 2024; 5(2):124-199. https://doi.org/10.3390/cmd5020007
Chicago/Turabian StyleKing, Fraser, Miroslav Kolàř, Scott Briggs, Mehran Behazin, Peter Keech, and Nikitas Diomidis. 2024. "Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models" Corrosion and Materials Degradation 5, no. 2: 124-199. https://doi.org/10.3390/cmd5020007
APA StyleKing, F., Kolàř, M., Briggs, S., Behazin, M., Keech, P., & Diomidis, N. (2024). Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models. Corrosion and Materials Degradation, 5(2), 124-199. https://doi.org/10.3390/cmd5020007







