A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part II, Prediction of Corrosion Damage in Operating Reactors
Abstract
:1. Introduction
2. The Electrochemical Corrosion Potential (ECP)
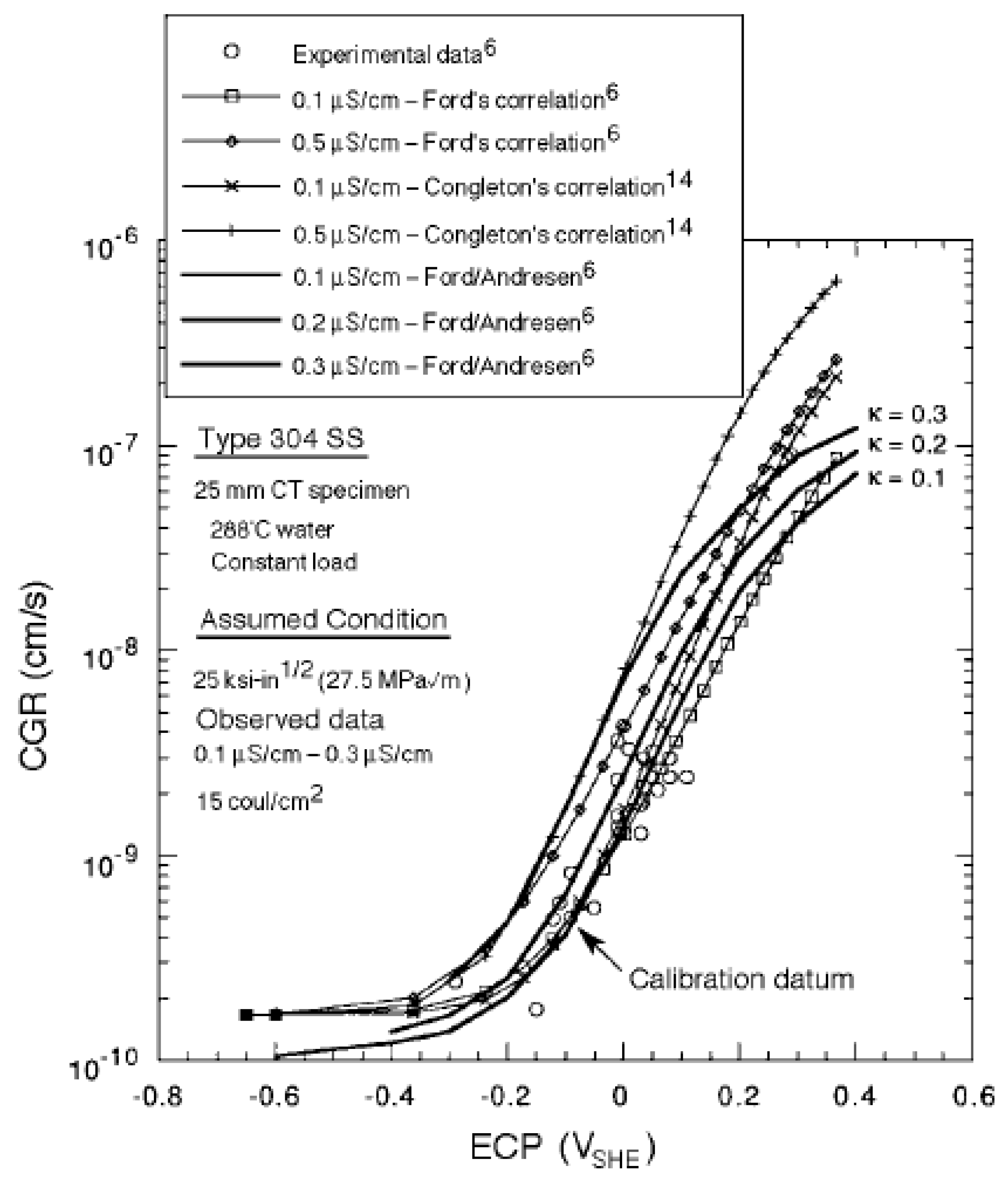
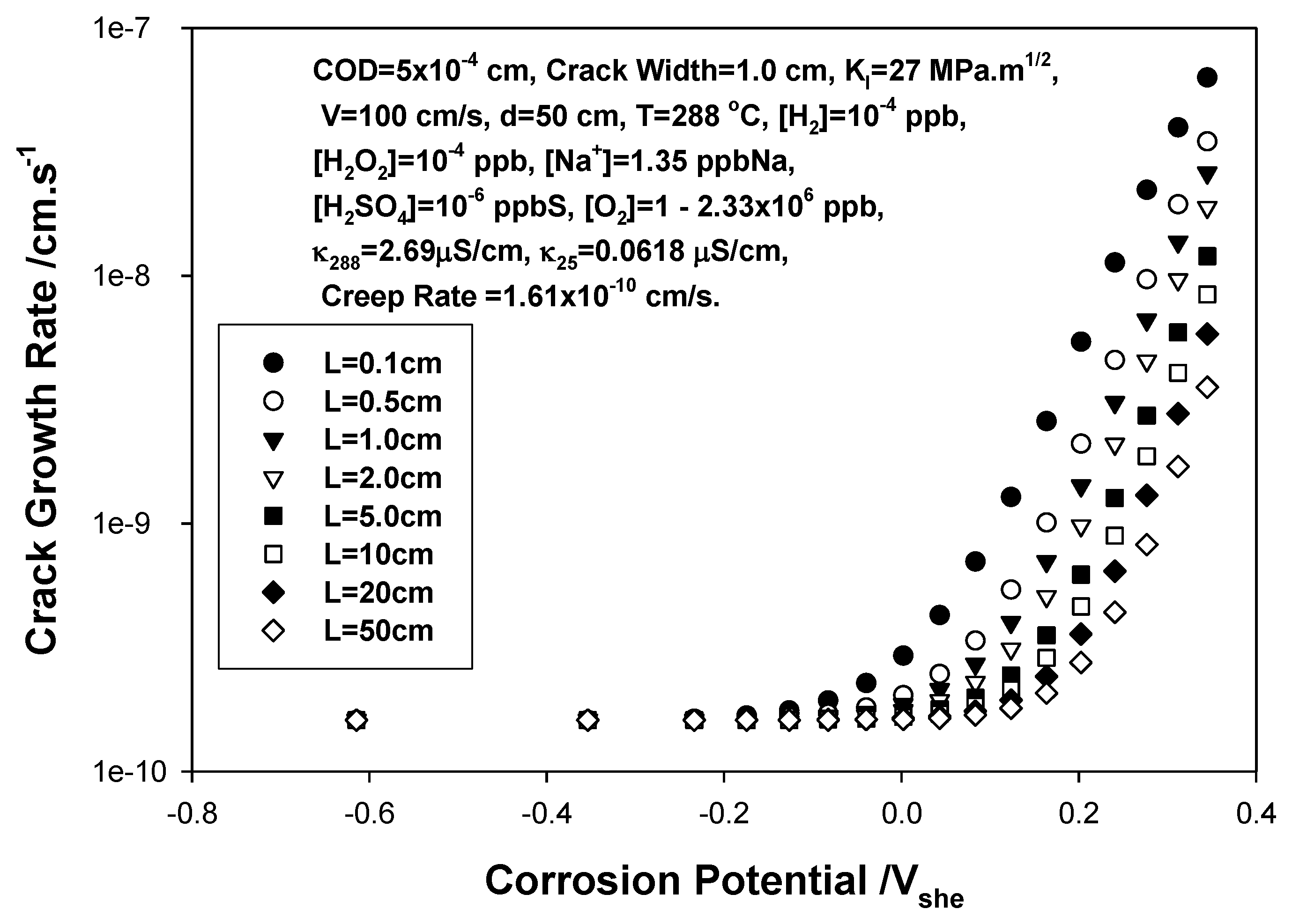
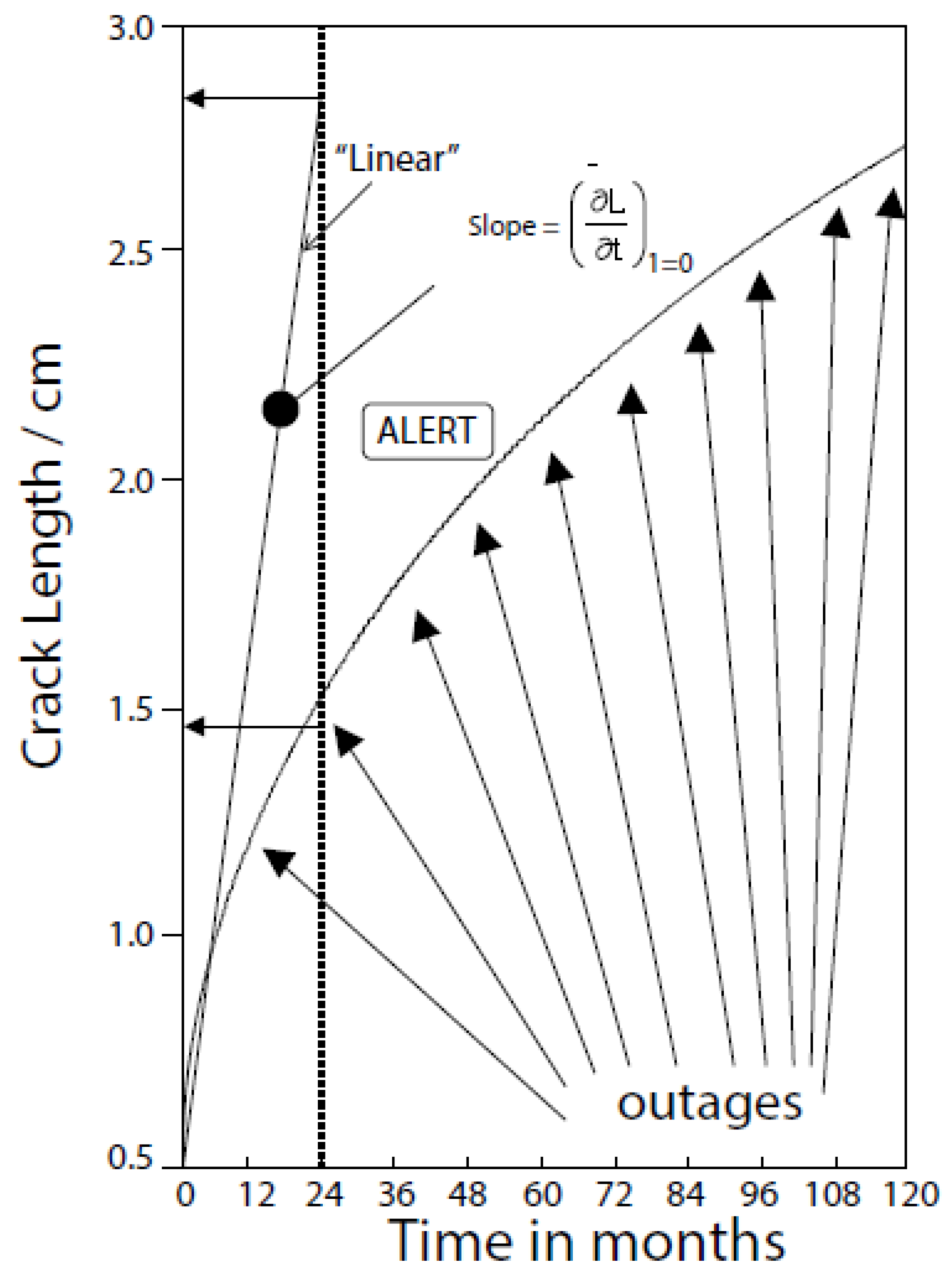
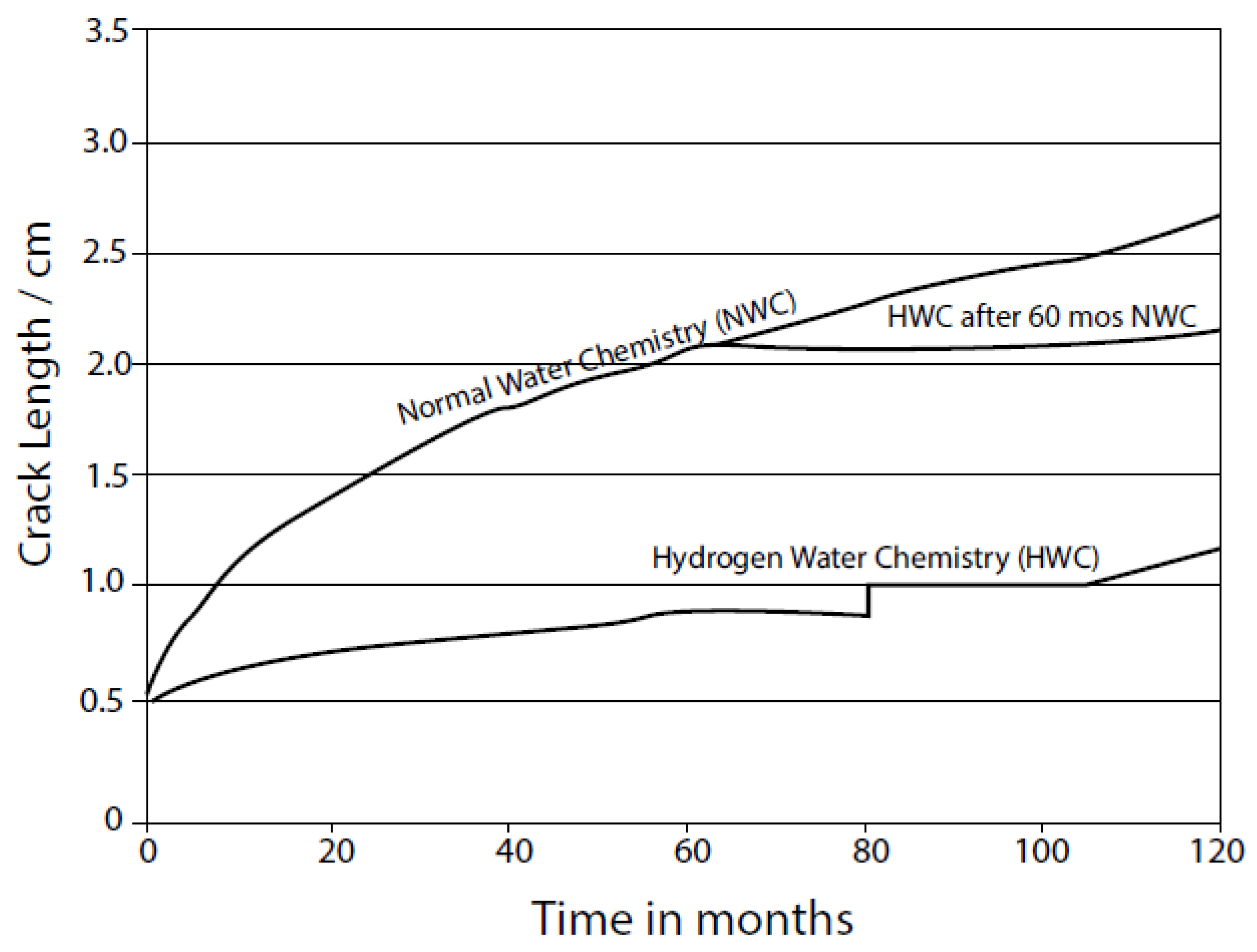
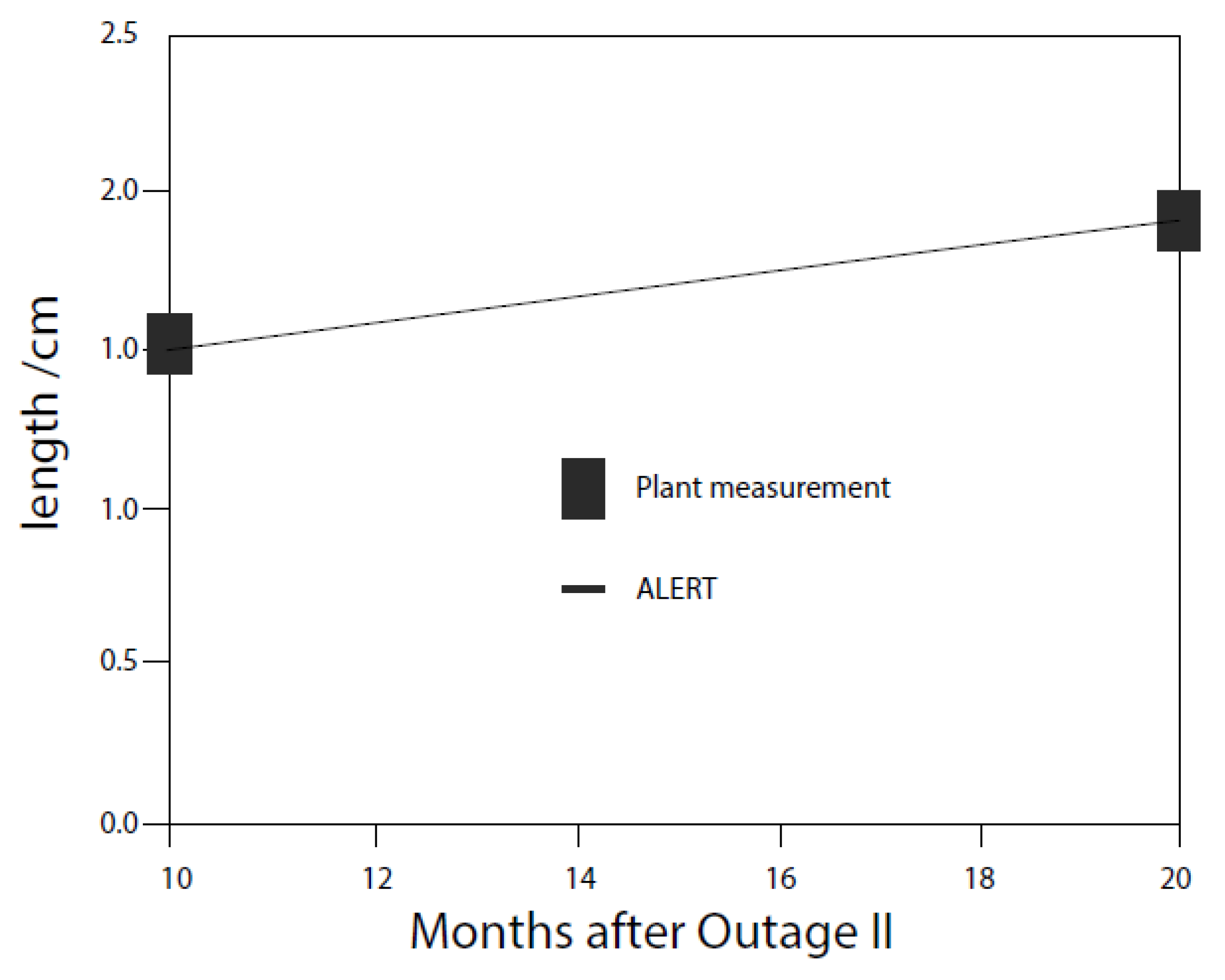
3. Calculation of Crack Growth Rate
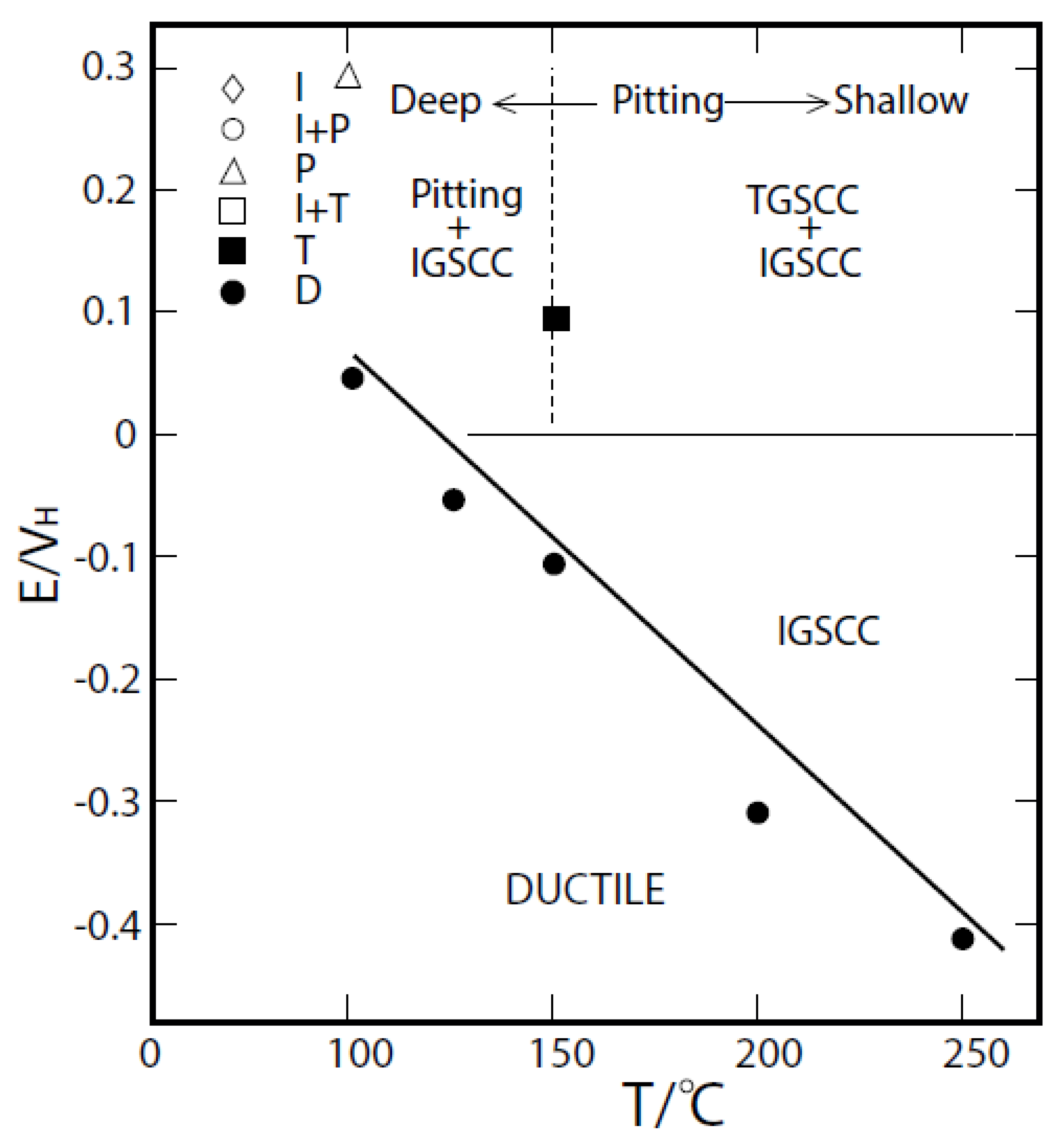
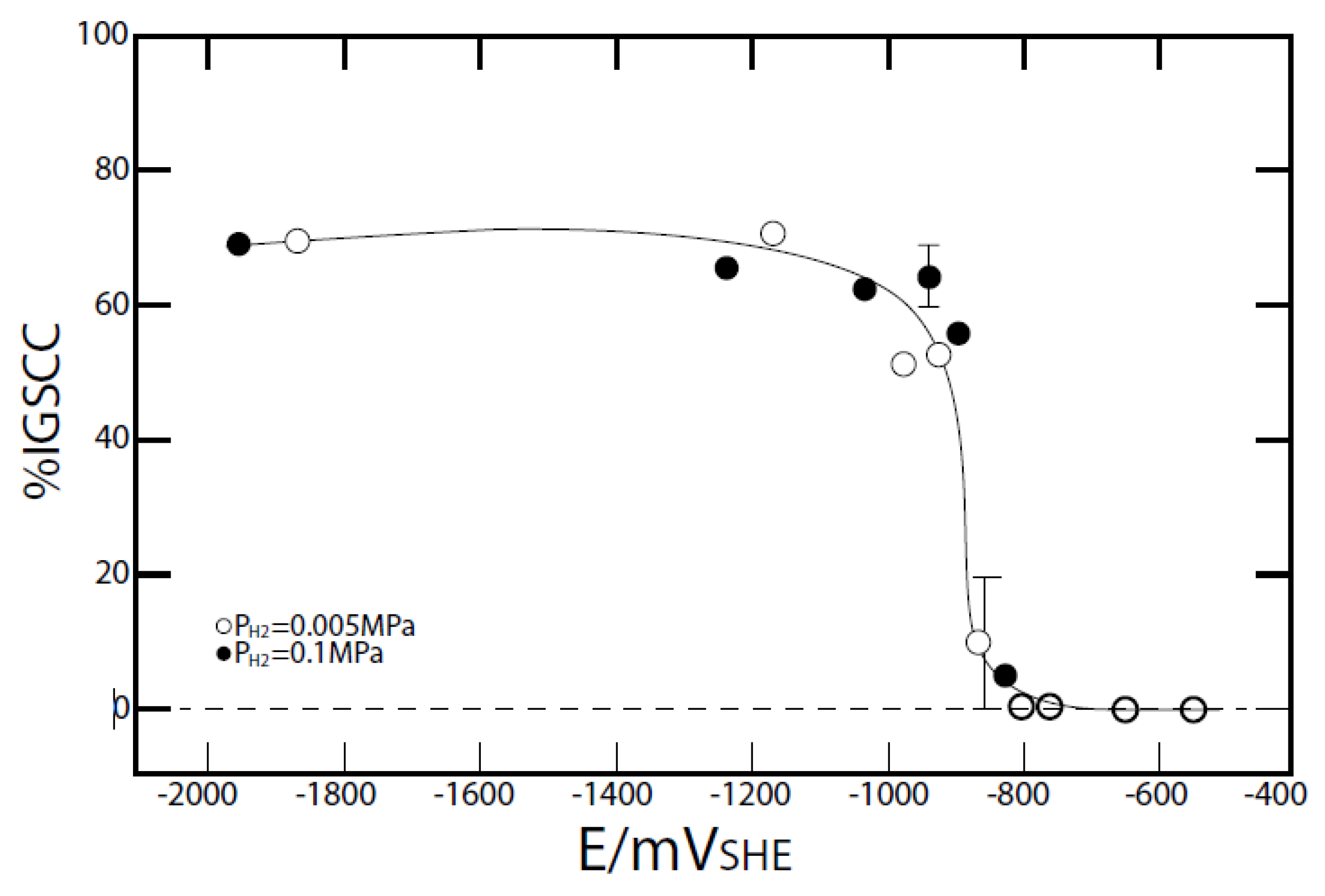
4. The Critical Potential
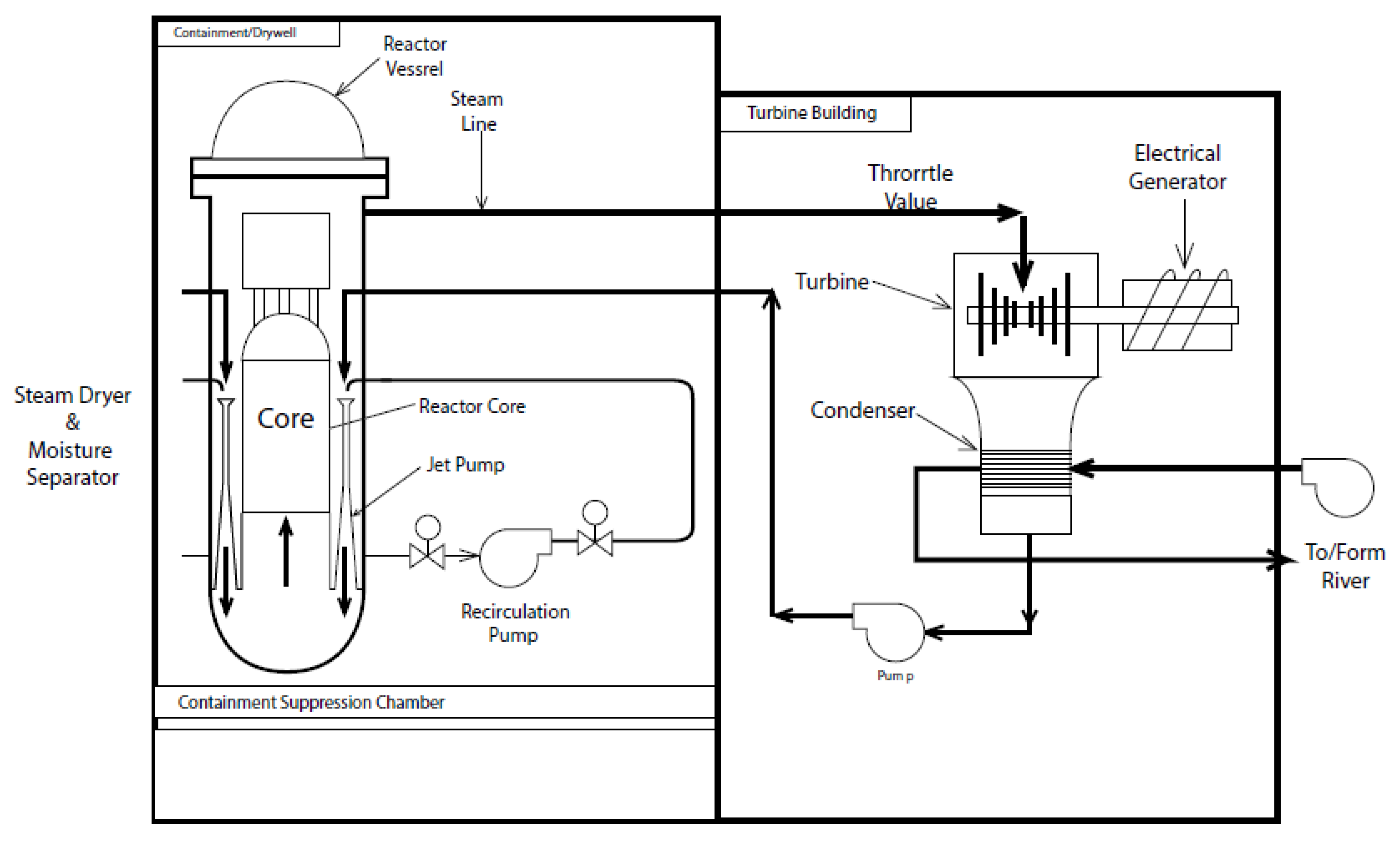
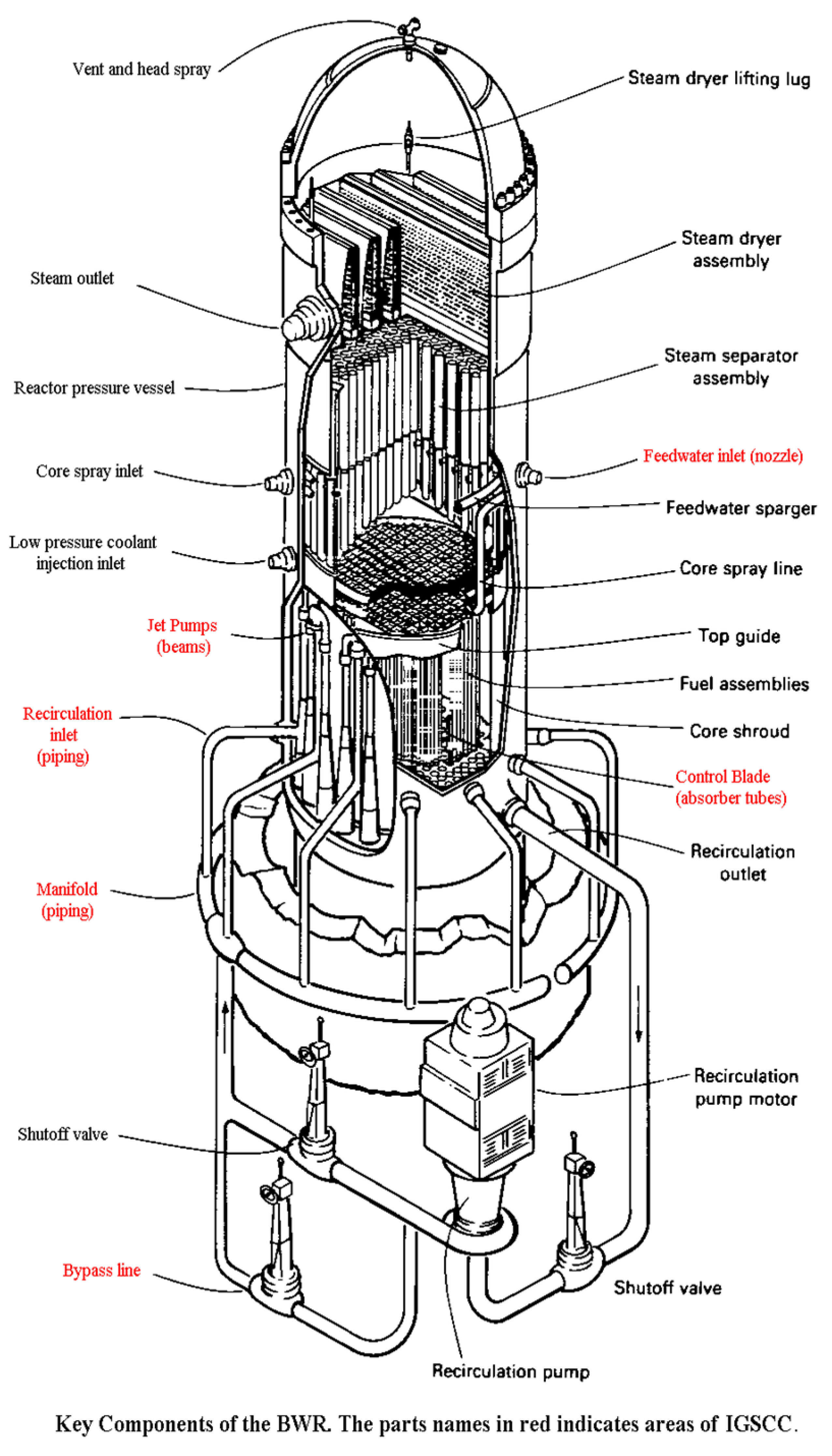
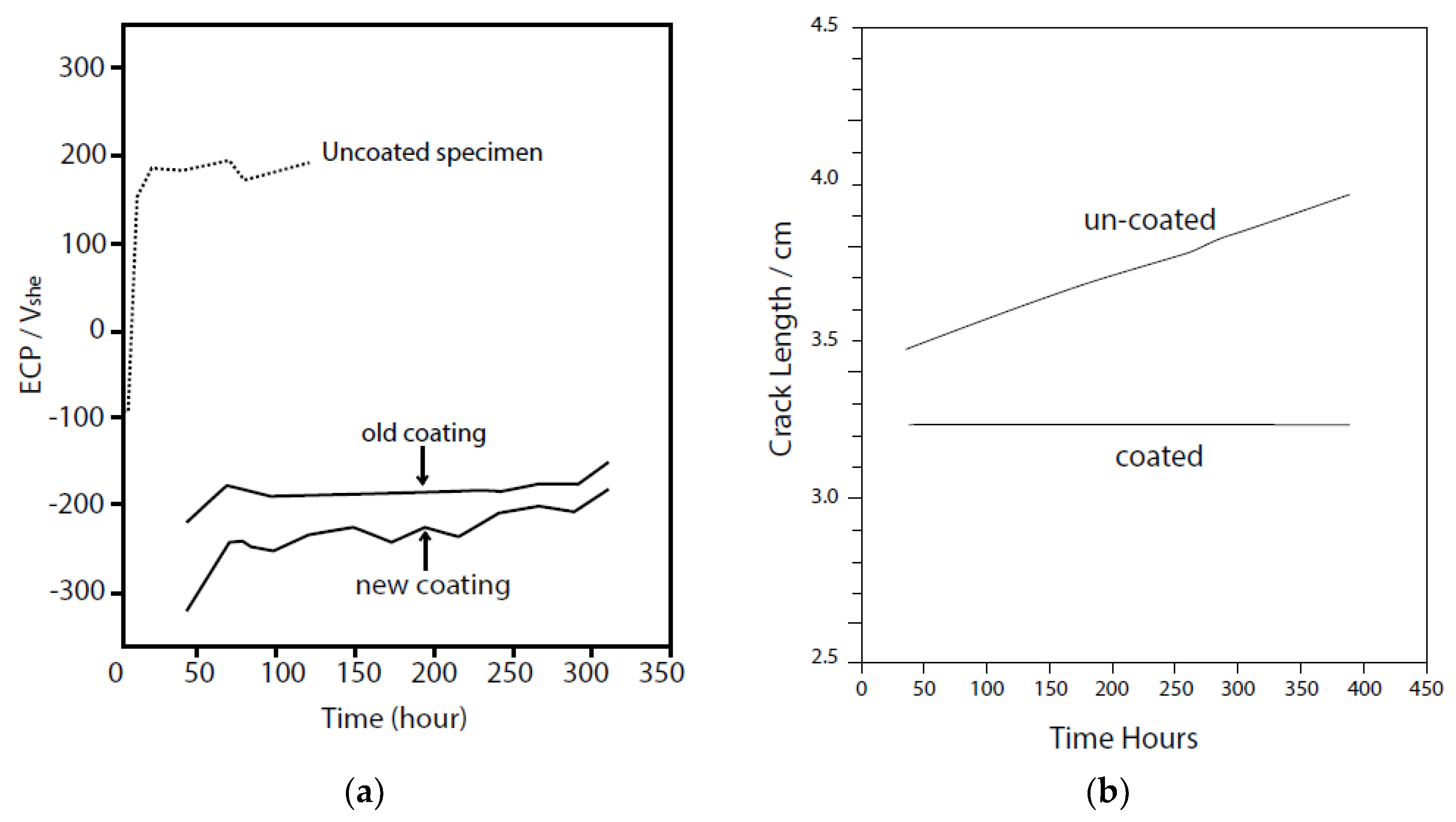
5. Boiling Water Reactors (BWRs)
5.1. The Anatomy of a BWR
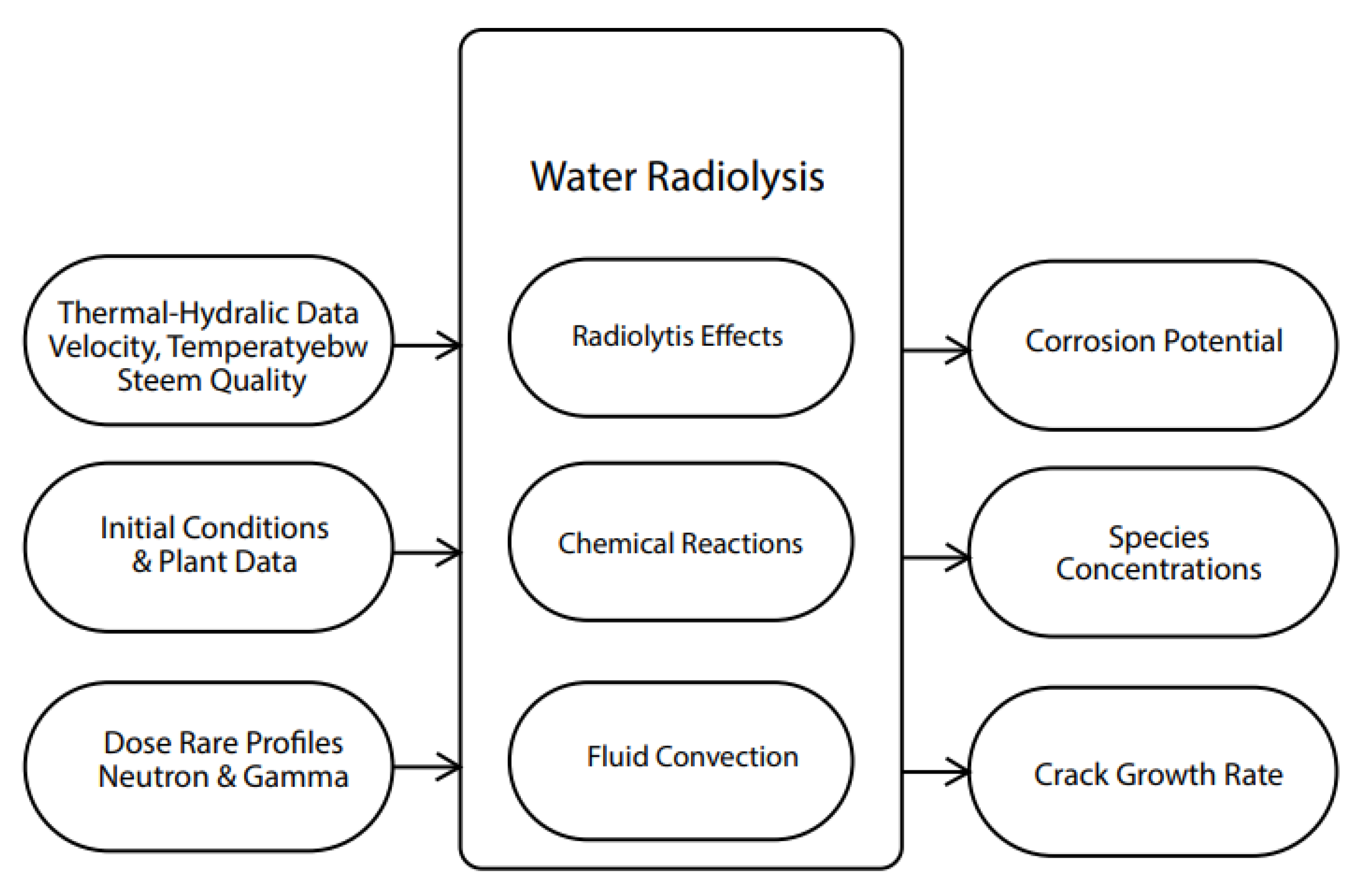
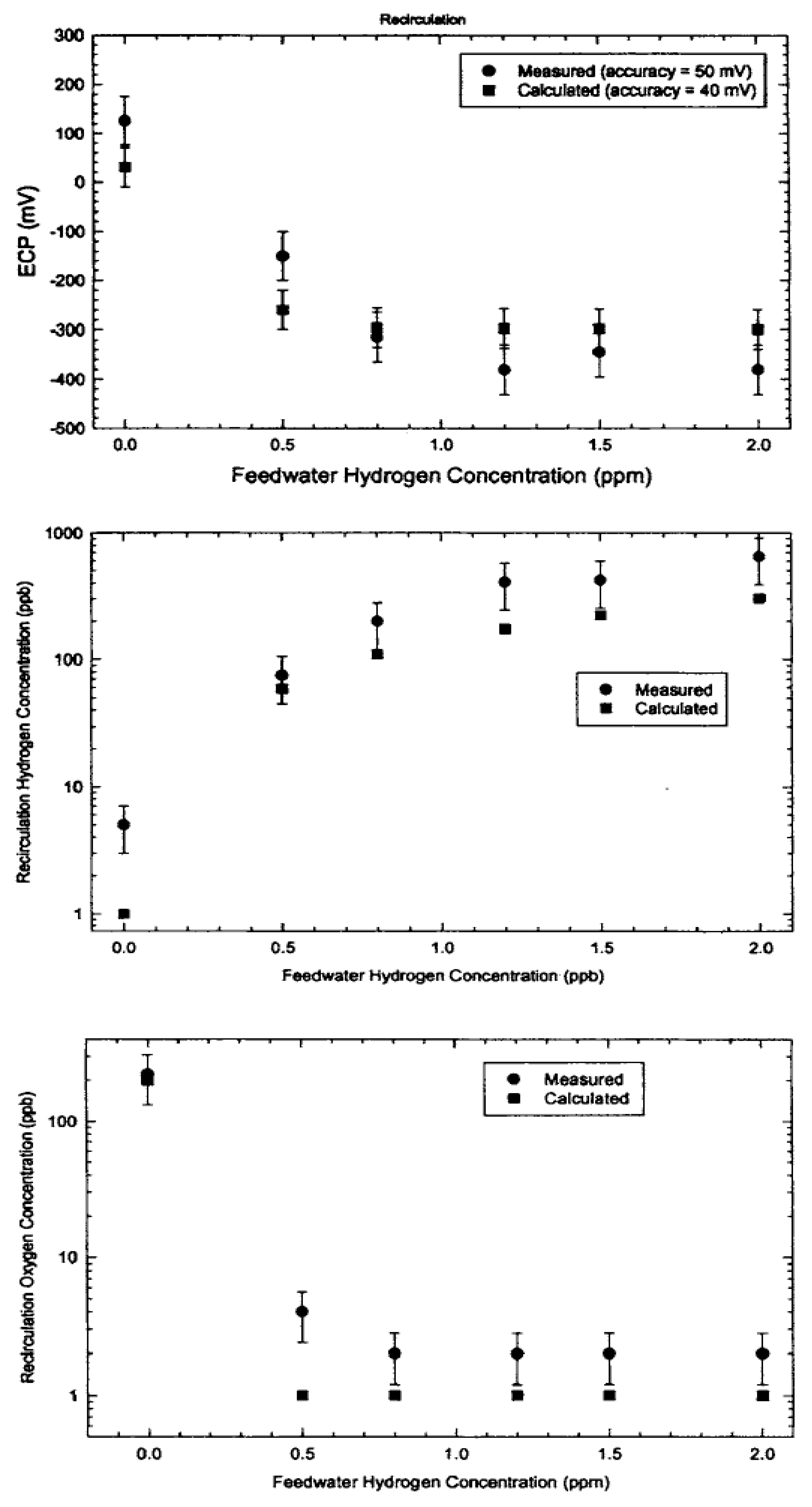
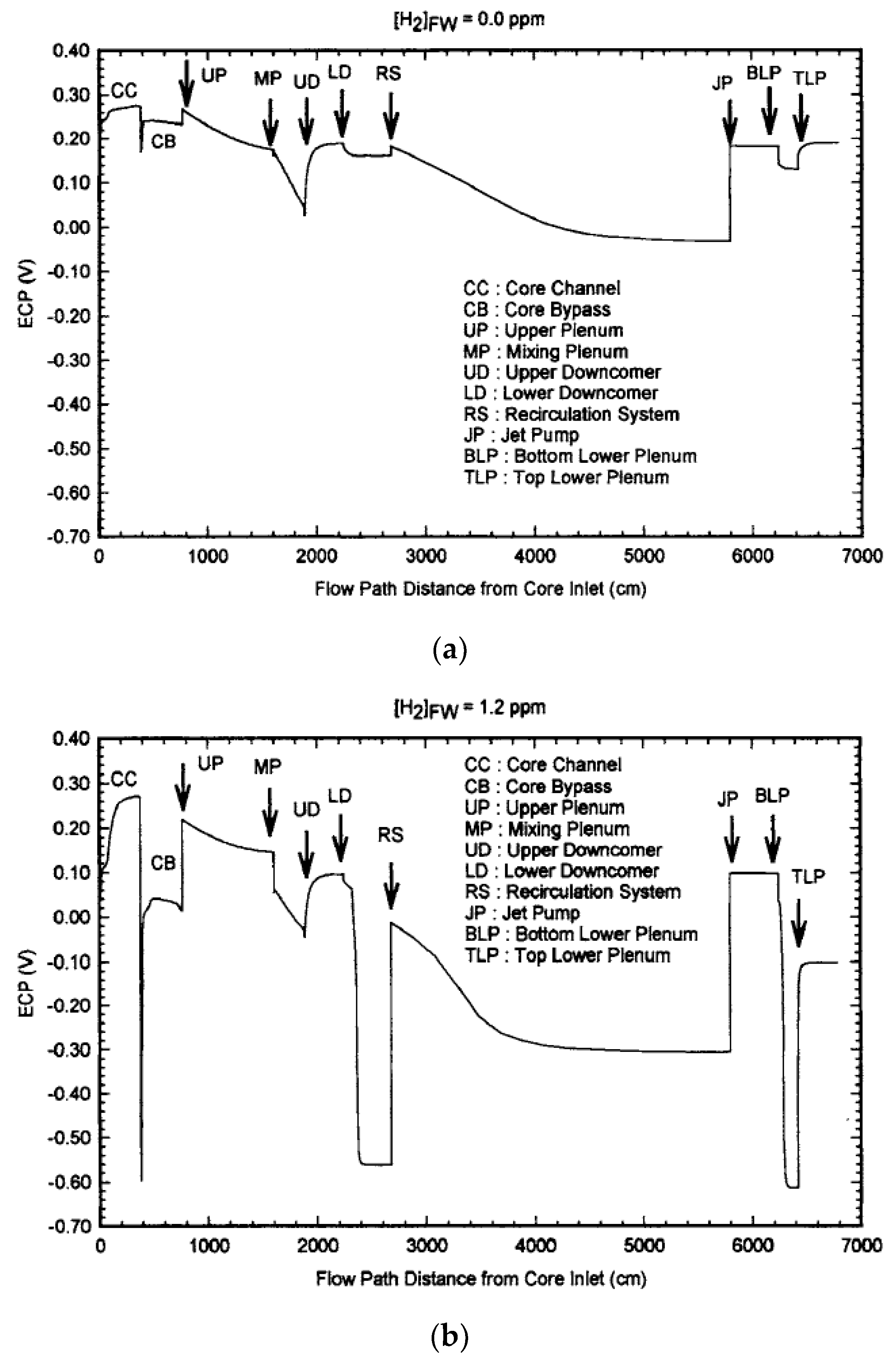
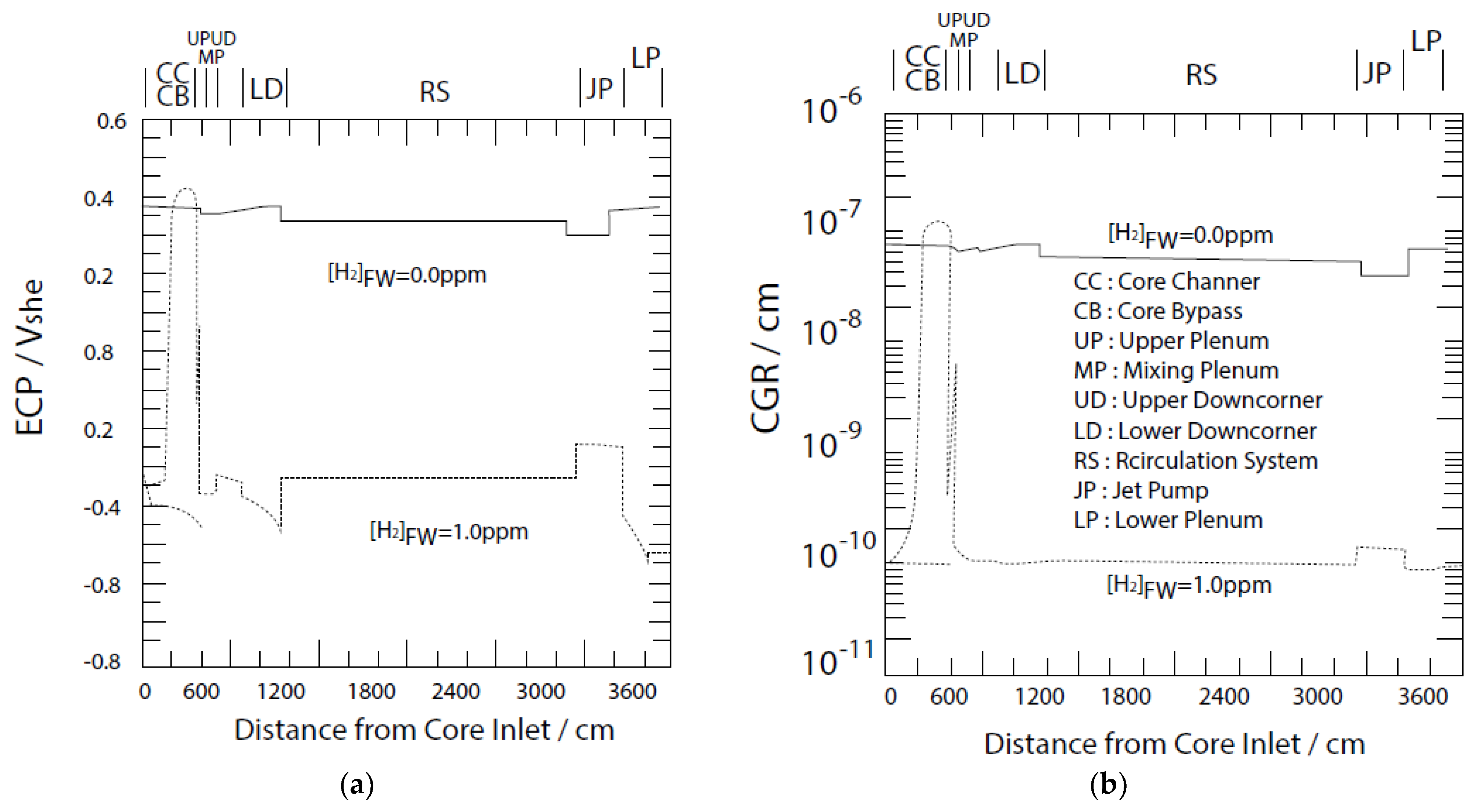
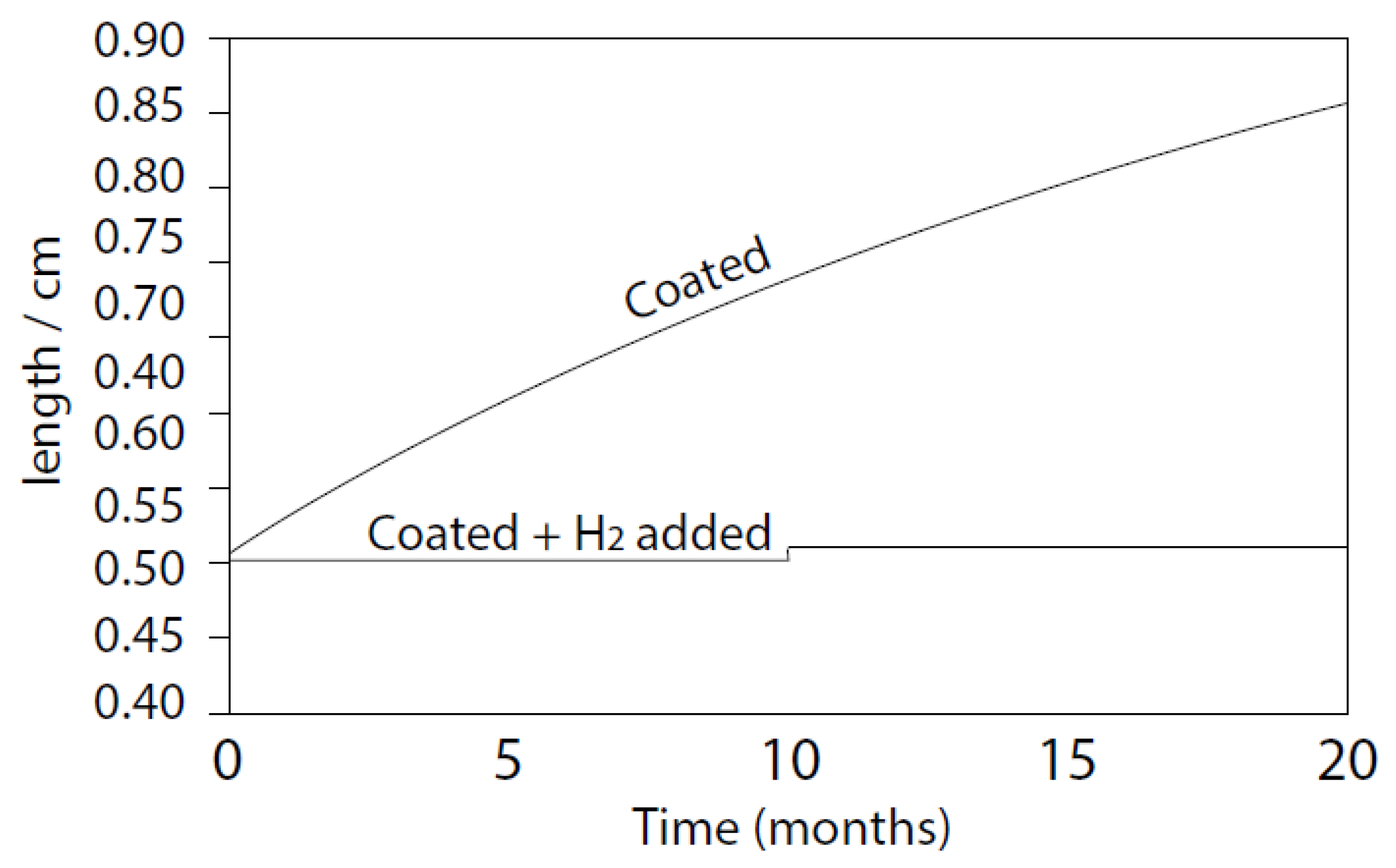
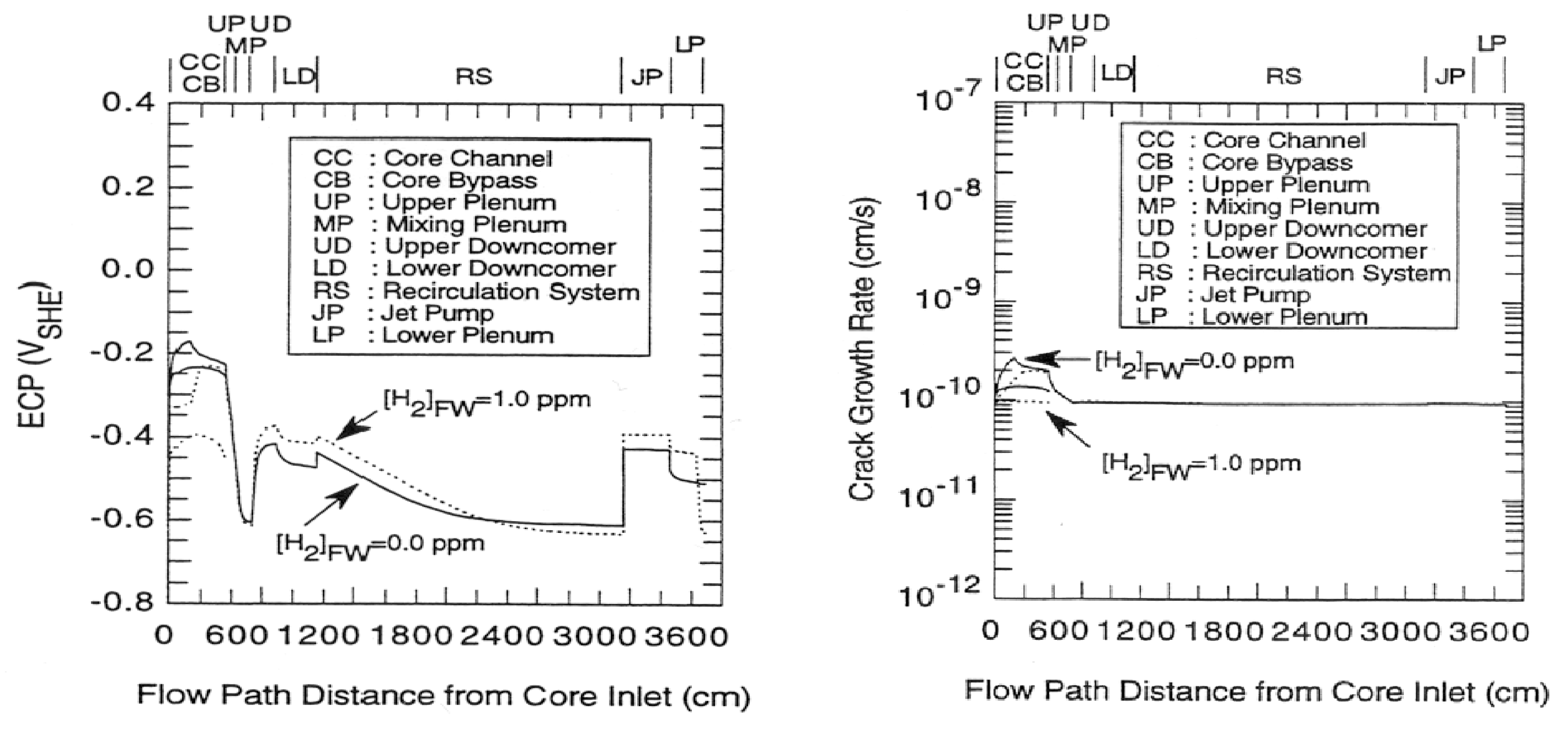
5.2. Radiolysis/ECP/CGR Modeling of BWR PHTSs
6. Pressurized Water Reactors (PWRs)
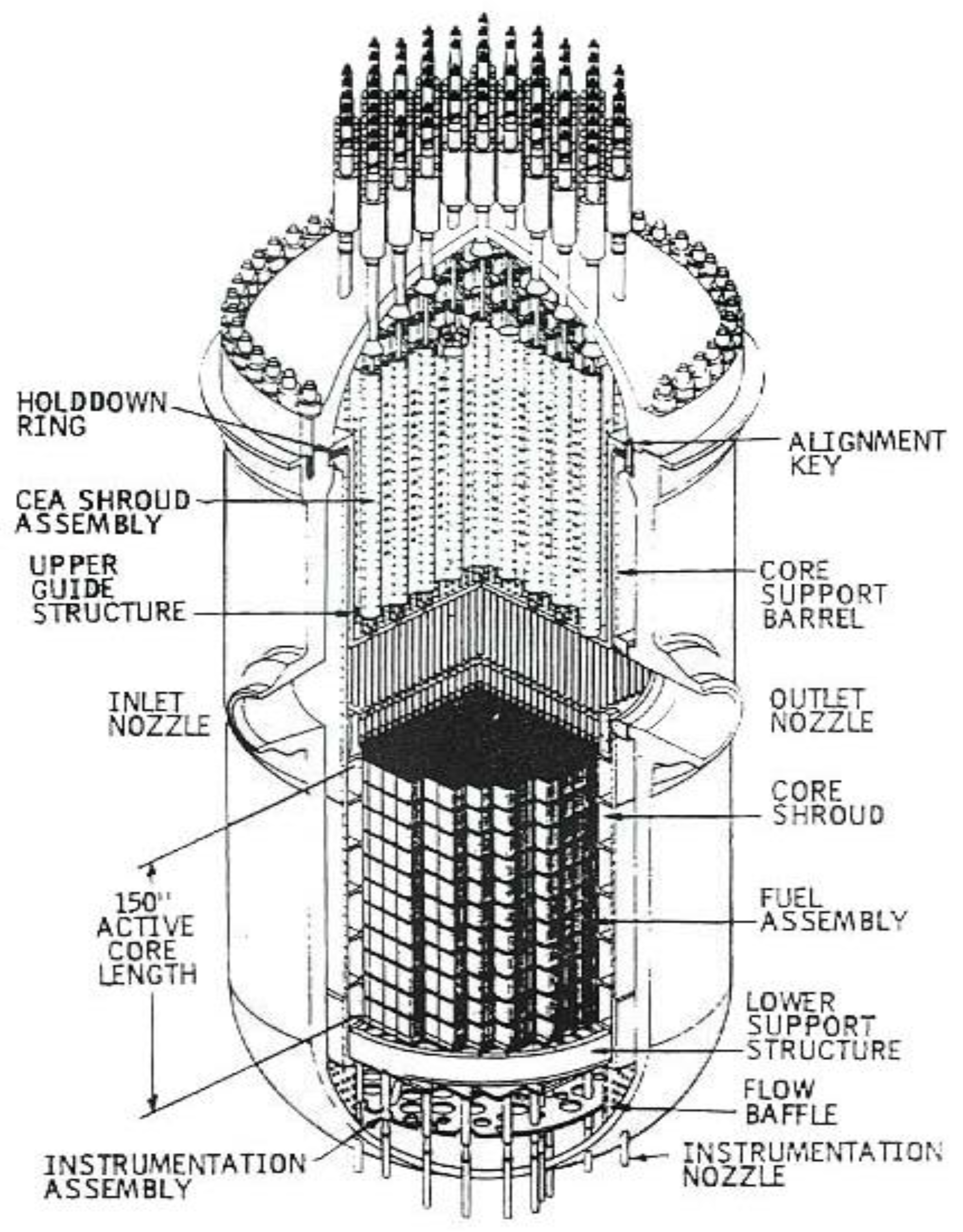
6.1. Anatomy of a PWR
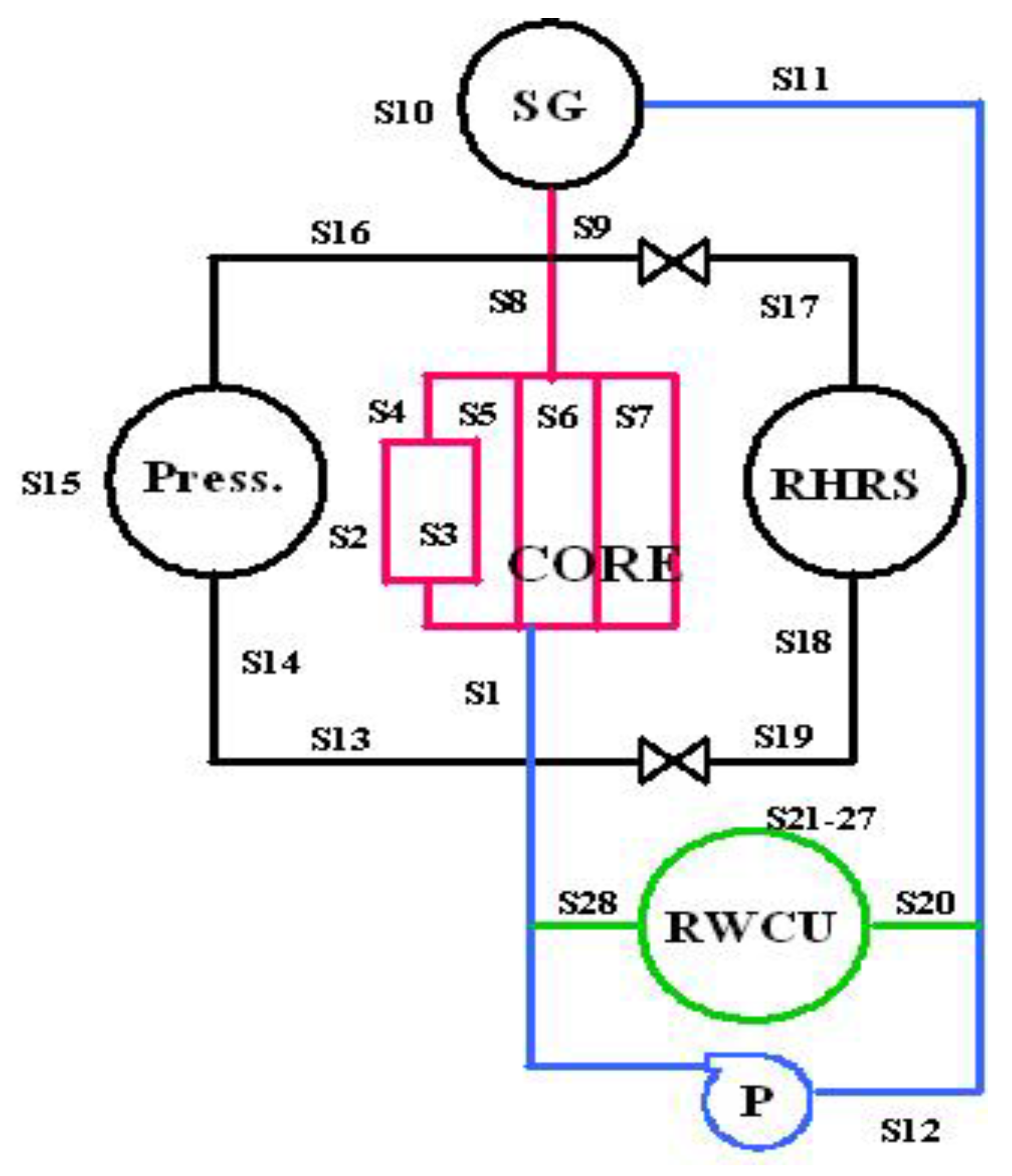
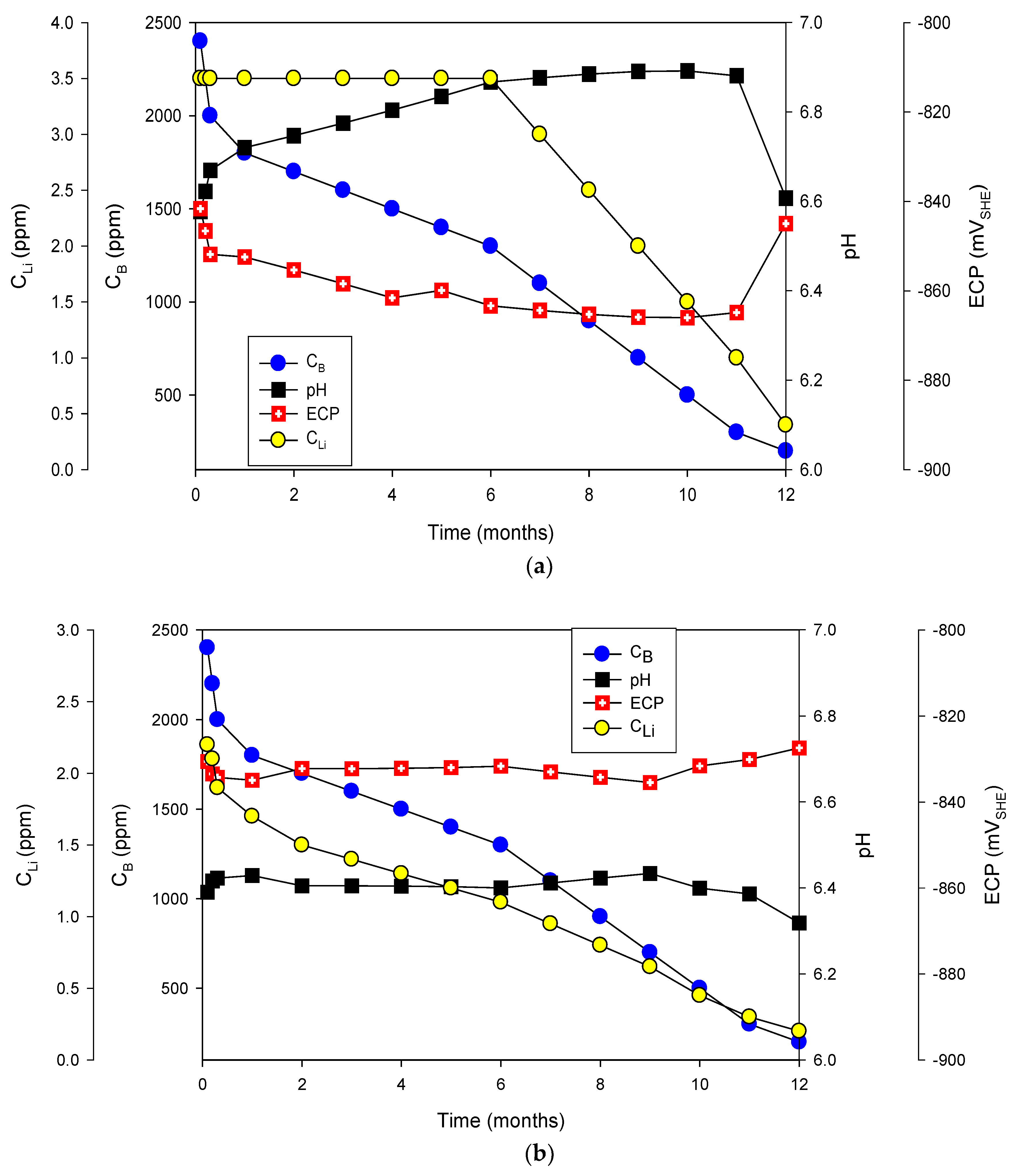
6.2. Radiolysis/ECP/CGR Modeling of PWR PHTSs
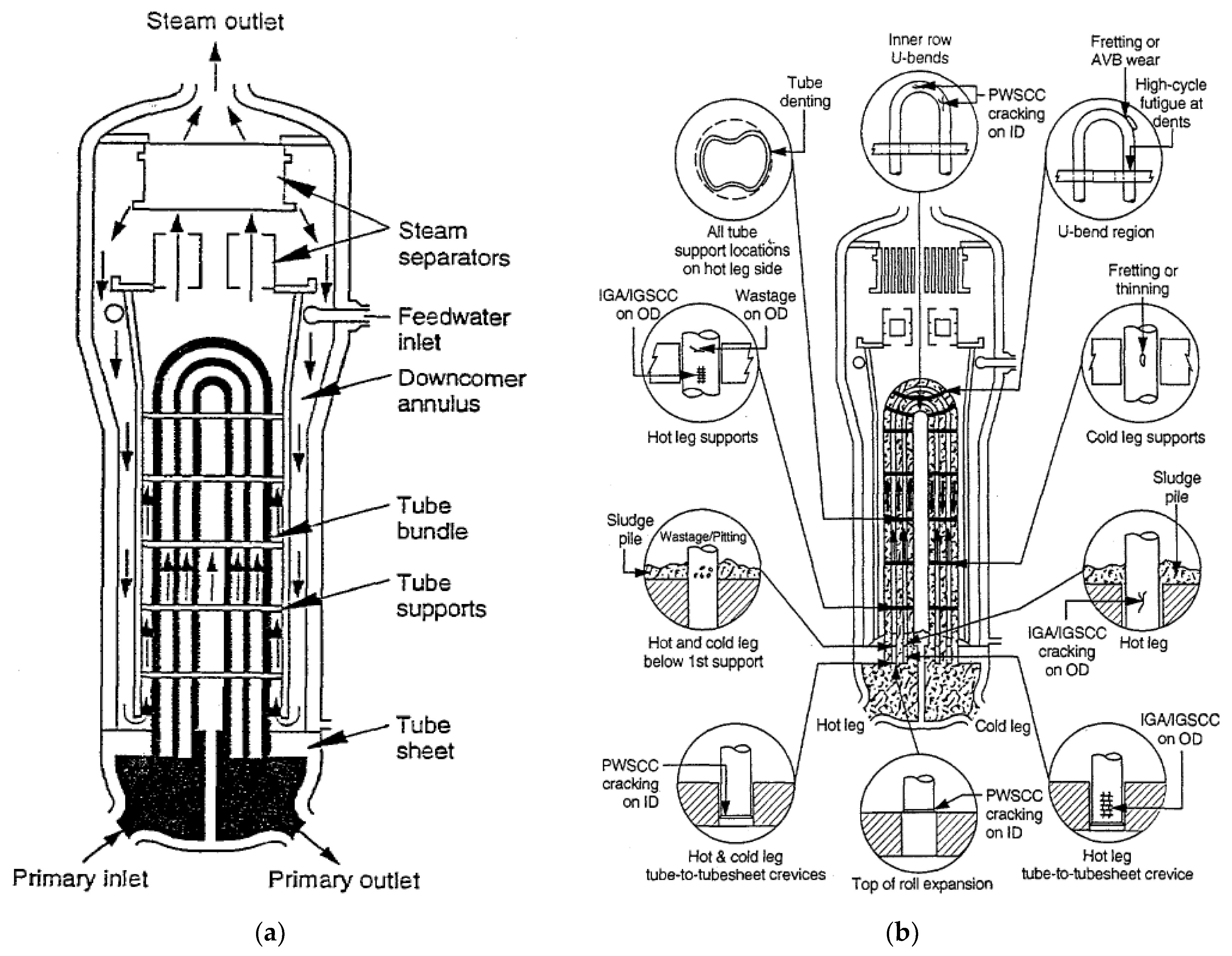
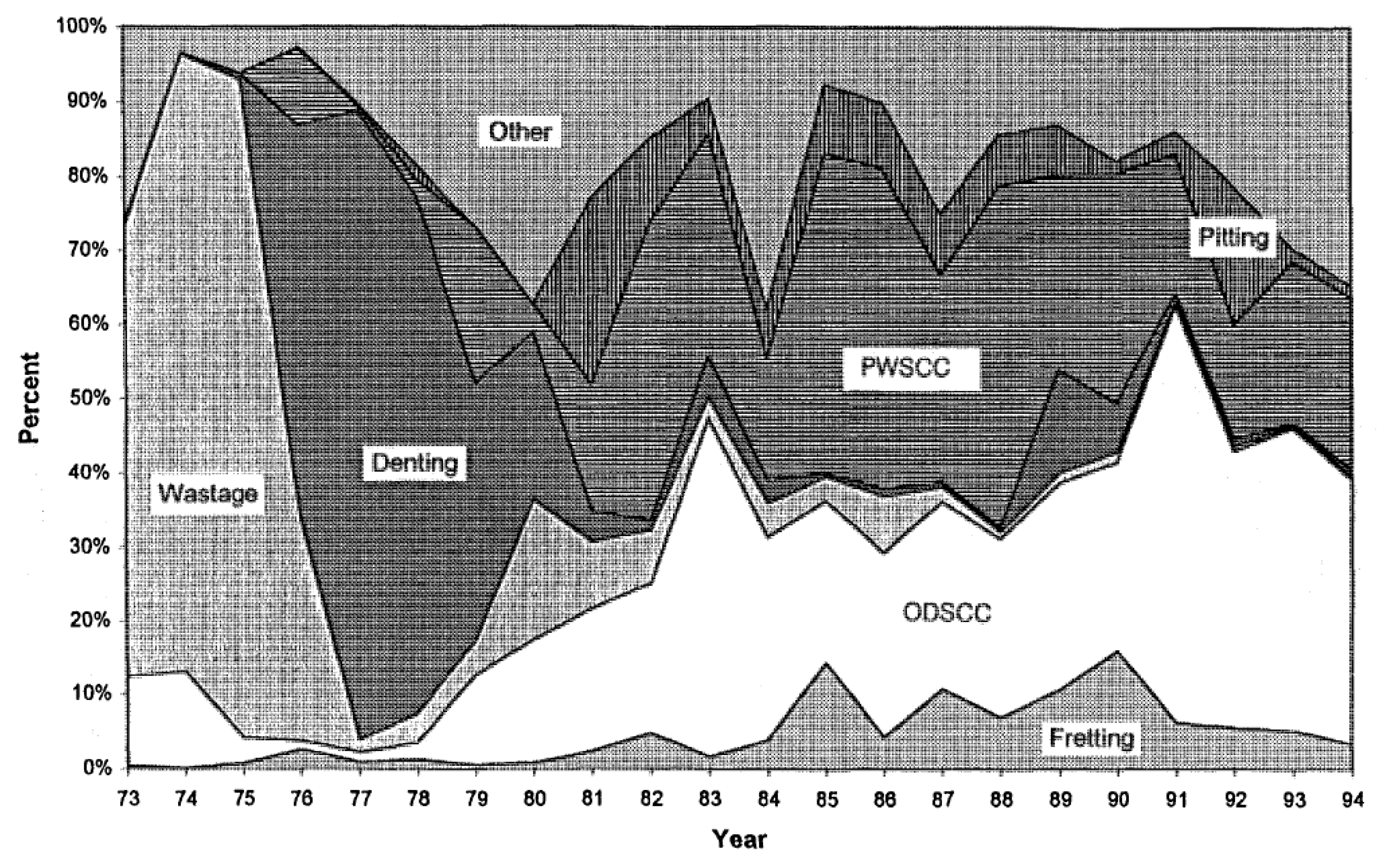
6.3. PWR Steam Generators
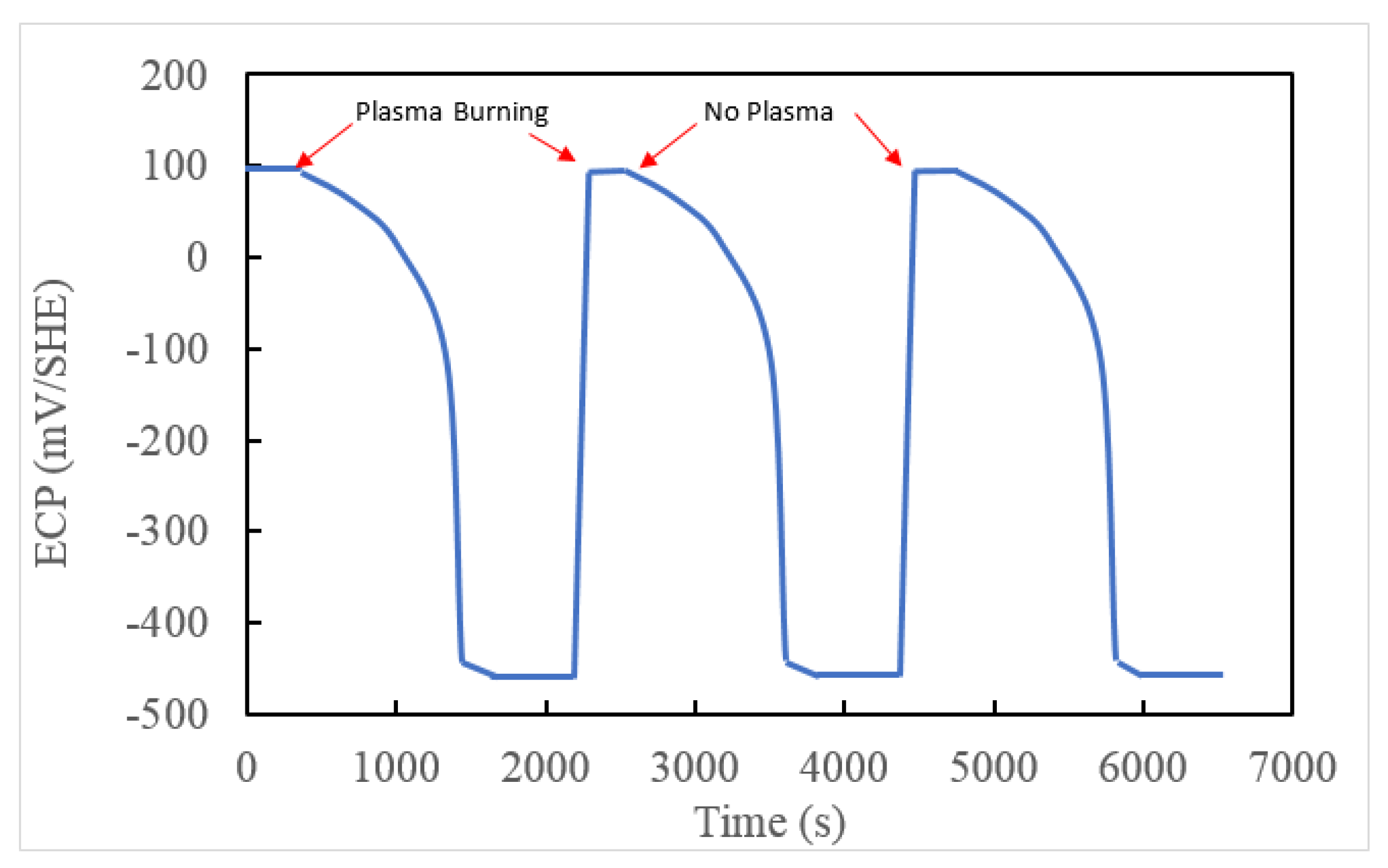
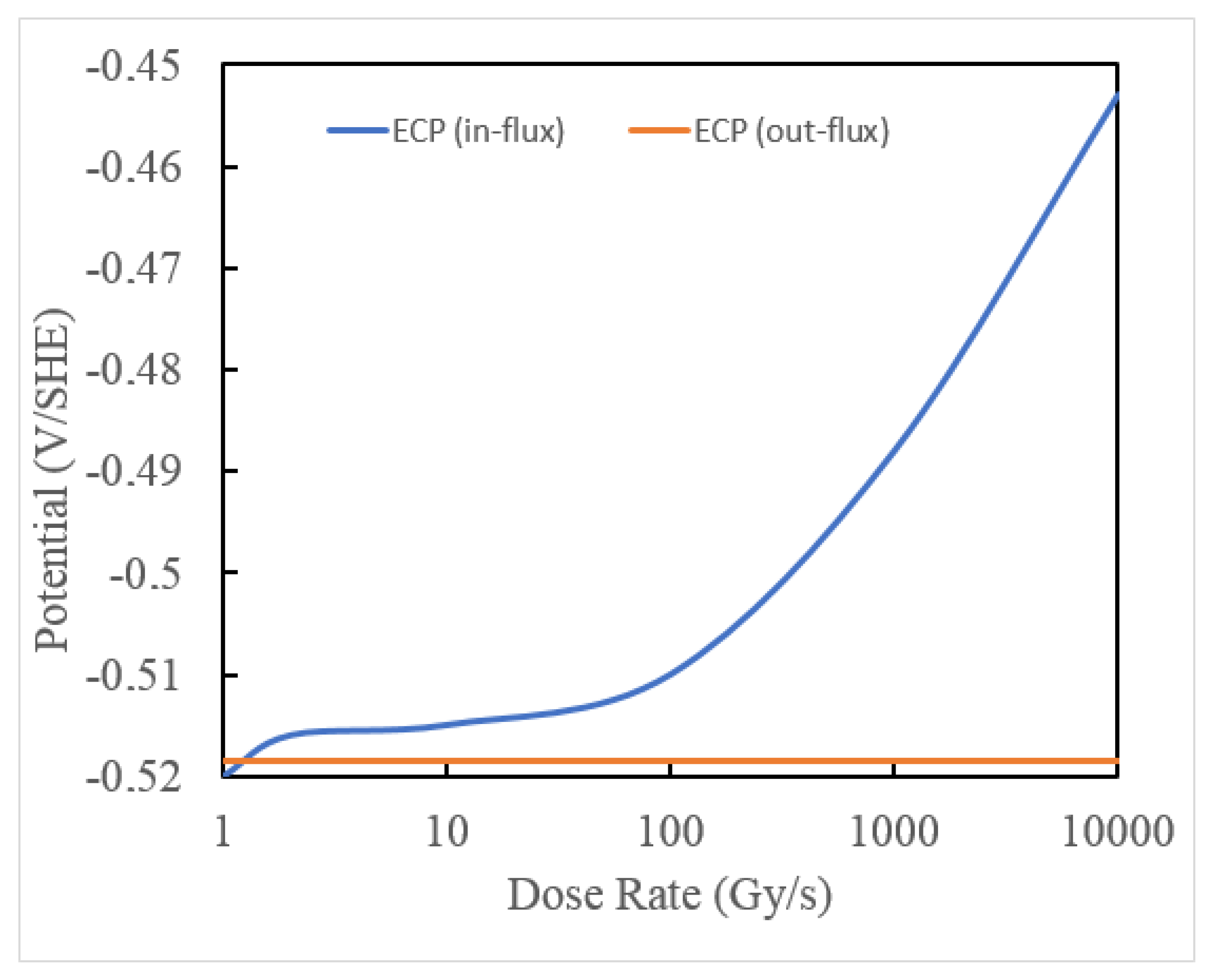
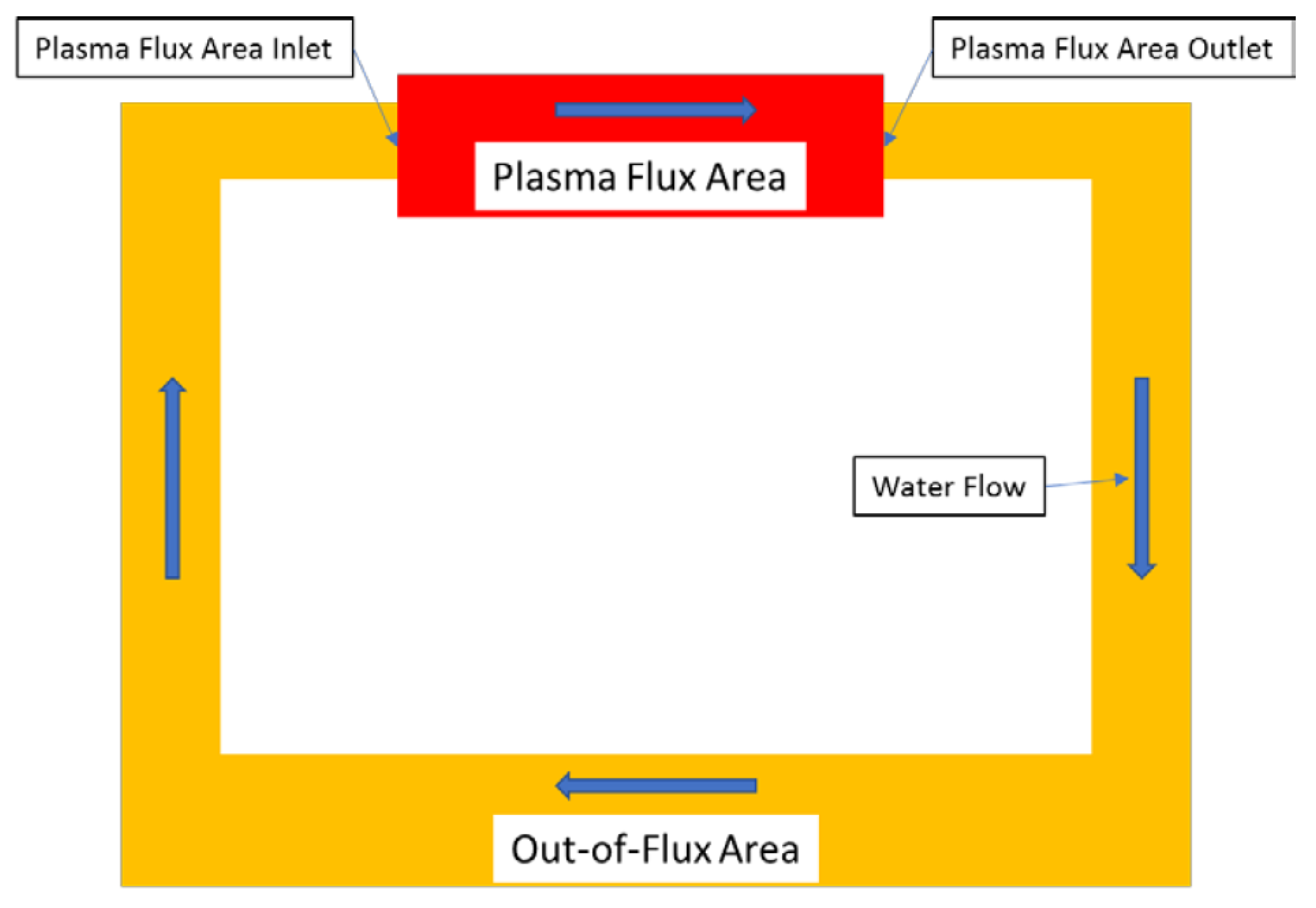
7. Predicted ECP and CGR in ITER PHTS
- Work carried out using a variant of the model/code (PWR_ECP) and the scoping calculations reported in [8,68,71] for PWR primary circuits indicates that under certain circumstances the ECP in the steam generators may become sufficiently negative that Alloy 600, a common steam generator tubing material, could suffer HIC (PWSCC). Thus, the work reported in [5] indicates that cracking of Alloy 600 in PWR primary circuits occurs at potentials that are more negative than a critical value of −835 mVshe. This critical potential is perilously close to the calculated ECP in the steam generators, particularly when using deoxygenated makeup water. The calculations of Bertuch et.al [4] and later by Kim [71] and Kim and Macdonald [68] suggest that the ECP may become more negative than −850 mVshe, which poses a threat to steam generator integrity. Accordingly, one of the authors (DDM) of this paper has argued for examination of a “low hydrogen” water chemistry [4], which would maintain the ECP at a value that is more positive than the critical value for HIC, but is less positive than the critical potential for IGSCC in Alloy 600 under all operational conditions. A hydrogen concentration of about 5 cc(STP)/kg(H2O) is estimated to be sufficiently low to avoid primary side cracking of steam generator tubes and yet is sufficiently high to “suppress radiolysis” to the extent that it needs to be done [4].
- Mass transport and the closely related activity transport phenomenon are fundamentally electrochemical in nature. Thus, to a significant extent, the movement of corrosion products around the primary circuits of both BWRs and PWRs is due to differential solubility of magnetite (Fe3O4), for example, induced by the variation in the ECP, coupled with hydrodynamic factors, as proposed in research reported in [8] and [69], among others. In the authors’ opinion, mass and activity transport phenomena in water-cooled nuclear reactors (WCNRs) can only be understood and predicted by first defining the electrochemistry of the primary heat transport circuits.
- It is not clear, yet, that activity transport will become an issue in ITER, but the potential for this phenomenon must be recognized in choosing materials for the PHTS. Thus, it is expected that many of the elements in the structural materials in the irradiation zone will be neutron activated. Corrosion will then produce CRUD (Chalk River Unidentified Products) that may deposit on out-of-plasma zone regions of the PHTS, thereby creating γ radiation fields in areas of the reactor that were not designed for the presence of such fields. Together with the contributions from 16N7 and 17N7, it is likely that significant man-REM issues will arise during the operation of ITER. Clearly, this issue must be explored, if we are to avoid the same issues that exist in fission reactors. Understanding and controlling the electrochemistry of the coolant circuit is key to managing this problem.
8. Summary and Conclusions
- We demonstrate, that the radiolytic generation of oxidizing radiolysis products, such as O2, H2O2, HO2−, and OH in molar excess over reducing species (H2, H, and O22−), some of which (H2) are preferentially stripped from the coolant upon boiling in a BWR PHTS, for example, renders the coolant oxidizing, thereby shifting the corrosion potential (ECP) in the positive direction to a value that is more positive than the critical potential (Ecrit = −0.23 Vshe at 288 °C) for Intergranular Stress Corrosion Cracking (IGSCC) in sensitized austenitic stainless steel (e.g., Type 304 SS) and other forms of corrosion (e.g., pitting and corrosion fatigue). This has led to a rash of IGSCC incidents in recirculation piping and internal components in operating BWRs over the past five decades that has exacted a great cost on the operators and electricity consumers, alike.
- In the case of PWRs, the primary circuits are pressurized with hydrogen to give a hydrogen concentration of 20 to 50 cm3/kgH2O (0.89 to 4.46 ppm), such that no sustained boiling occurs and the hydrogen suppresses the radiolysis of water, thereby inhibiting the formation of oxidizing radiolysis products of water. Thus, the ECP is dominated by the hydrogen electrode reaction (HER), although important deviations from the HER equilibrium potential have been noted. In any event, the ECP is displaced to approximately −0.85 Vshe, which if below the critical potential for IGSCC in sensitized stainless steels, but it is more negative than the critical potential for the hydrogen-induced cracking of mill-annealed Alloy 600. This has led to extensive, primary water stress corrosion cracking (PWSCC) of steam generator tubing and other components (e.g., control rod drive tubes) in PWRs that has also exacted a high cost on operators and power consumers.
- Although the ITER has yet to operate, the proposed chemistry protocol for the coolant places it close to a BWR operating on Normal Water Chemistry (NWC) without boiling or if hydrogen (approx. 80 ppb) is added, close to a BWR on Hydrogen Water Chemistry (HWC).
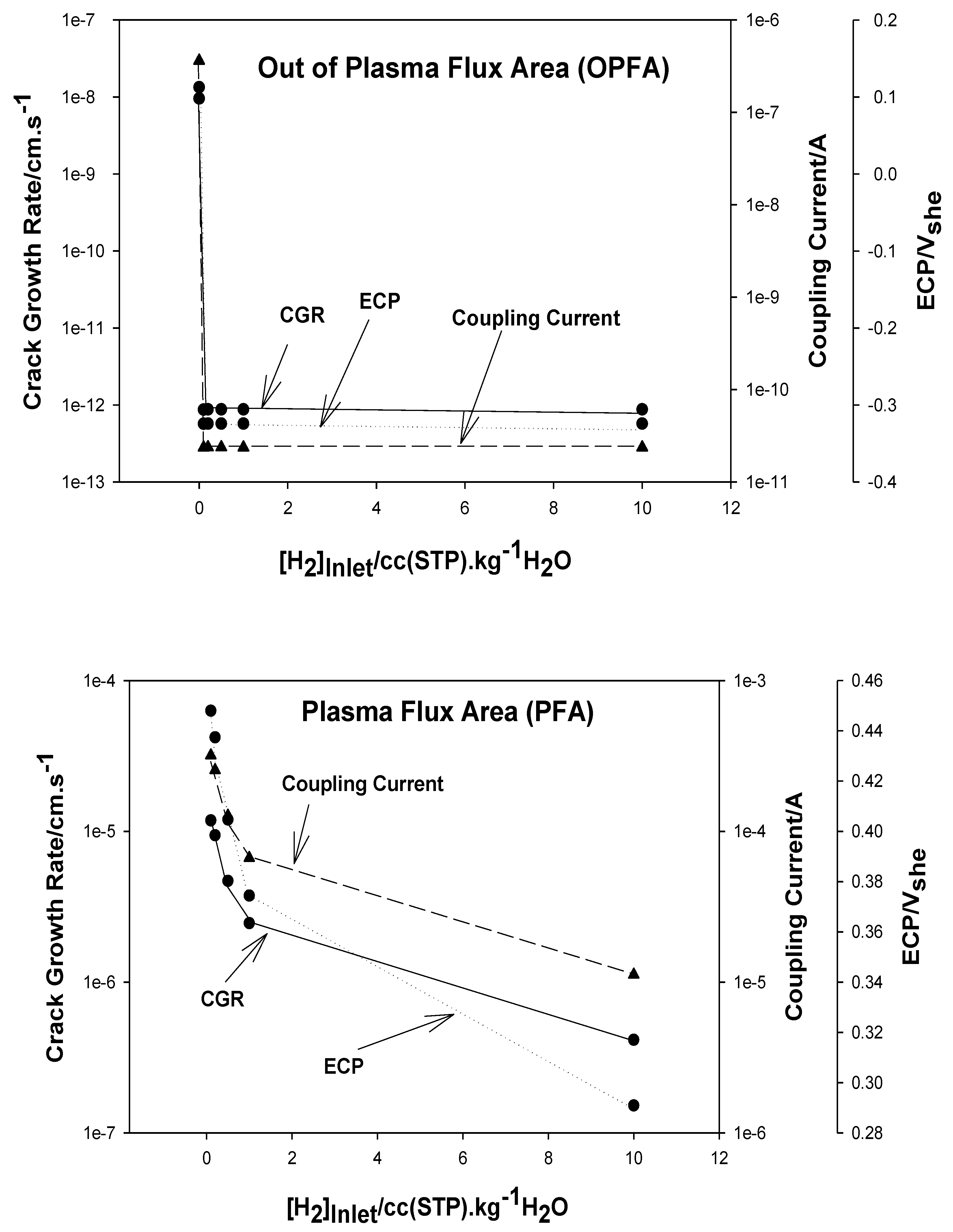
- In the current technology, the concentration of [H2] in the Plasma Flux Area (PFA) and in the Out of Plasma Flux Area (OPFA) is specified as 80 ppb [0.89 cc(STP)H2/KgH2O]. This level may be compared with 20–50 cc(STP) H2/KgH2O employed in a PWR primary coolant circuit and 500 ppb to 2000 ppb [5.5 to 22.2 cc(STP)H2/KgH2O] in a BWR operating on HWC. Hydrogen at the 80ppb level is predicted to reduce the ECP in the OPFA to −0.324 Vshe, which is sufficient to suppress the CGR below the practical, maximum level of 10−9 cm/s (0.315 mm/a) at which SCC is not a problem in a coolant circuit but, in the PFA, the ECP is predicted to be 0.380 Vshe, which gives a calculated standard CGR of 2.7 × 10−6 cm/s. This is more than three orders in magnitude greater that the desired maximum value. We recommend that the HWC issue in ITER be revisited to develop a protocol that is effective in suppressing both the ECP and the CGR in the PFA to levels that permit the operation of the IBED-PHTS in light of the experience gained in fission reactor technology.
- The key to managing the development of general and localized corrosion damage in fission and fusion reactor PHTS is exerting close control over the electrochemistry of the system to ensure that the ECP does not lie in a region where damaging corrosion processes occur.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Macdonald, D.D.; Engelhardt, G.R.; Petrov, A. A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part I, Assessment of Radiolysis Models. Corros. Mater. Degrad. 2022, 3, 470–535. [Google Scholar] [CrossRef]
- Petrov, A.; Macdonald, D.; Engelhardt, G. Assessment of Radiolysis in Tokamak Cooling Water System of ITER Fusion Reactor. In Proceedings of the 21st International Conference on Water Chemistry in Nuclear Reactor Systems, San Francisco, CA, USA, 9–14 September 2018; EPRI: Palo Alto, CA, USA, 2019; p. 3002016101. [Google Scholar]
- Stanbury, M. Reduction Potentials Involving Inorganic Free Radicals in Aqueous Solution. Adv. Inorg. Chem. 1989, 33, 69–138. [Google Scholar]
- Bertuch, A.; Pang, J.; Macdonald, D.D. The Argument for Low Hydrogen and Lithium Operation in PWR Primary Circuits. In Proceedings of the 7th International Symposium on Environmental Degradation of Materials in Nuclear Power Systems–Water Reactors, NACE International, Breckenridge, CO, USA, 6–10 August 1995; pp. 687–697. [Google Scholar]
- Totsuka, N.; Szklarska-Smialowska, Z. Effect of Electrode Potential on the Hydrogen-Induced IGSCC of Alloy 600 in an Aqueous Solution at 350 °C. Corrosion 1987, 43, 734. [Google Scholar] [CrossRef]
- Cragnolino, G.; Macdonald., D.D. Intergranular Stress Corrosion Cracking of Austenitic Stainless Steel at Temperatures Below 100 °C—A Review. Corrosion 1982, 38, 406–424. [Google Scholar] [CrossRef]
- Engelhardt, G.R.; Macdonald, D.D. Unpublished Data. 2021. [Google Scholar]
- Macdonald, D.D.; Urquidi-Macdonald, M. The Electrochemistry of Nuclear Reactor Coolant Circuits. In Encyclopedia of Electrochemistry; Bard, A.J., Stratmann, M., Eds.; Electrochemical Engineering; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2007; Volume 5, pp. 665–720. [Google Scholar]
- Indig, M.E.; Nelson, J.L. Electrochemical Measurements and Modeling Predictions in Boiling Water Reactors Under Various Operating Conditions. Corrosion 1991, 47, 202–209. [Google Scholar] [CrossRef]
- Macdonald, D.D. Viability of Hydrogen Water Chemistry for Protecting In-Vessel Components of Boiling Water Reactors. Corrosion 1992, 48, 194–205. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Hettiarachchi, S.; Lenhart, S.J. The thermodynamic viability of yttria-stabilized zirconia pH sensors for high temperature aqueous solutions. J. Solut. Chem. 1988, 17, 719–732. [Google Scholar] [CrossRef]
- Kriksunov, L.B.; Macdonald, D.D.; Millett, P.J. Tungsten/Tungsten Oxide pH Sensing Electrode for High Temperature Aqueous Environments. J. Electrochem. Soc. 1994, 141, 3002–3005. [Google Scholar] [CrossRef]
- Macdonald, D.D. The Point Defect Model for the Passive State. J. Electrochem. Soc. 1992, 139, 3434–3449. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Yang, J.; Fekete, B.; Balachov, I.; Spencer, B. Development and Integration of Light Water Reactor (LWR) Materials Corrosion Degradation Codes into Grizzly; DOE/NEUP, Award DE-NE0008541(2019); Idaho National Lab. (INL): Idaho Falls, ID, USA, 2019. [Google Scholar]
- Lu, P.; Sharifi-Asl, S.; Kursten, B.; Macdonald, D.D. The Irreversibility of the Passive State of Carbon Steel in the Alkaline Concrete Pore Solution under Simulated Anoxic Conditions. J. Electrochem. Soc. 2015, 162, C572–C581. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Qiu, J. Re-defining the kinetics of redox reactions on passive metal surfaces. J. Solid State Electrochem. 2020, 24, 2663–2677. [Google Scholar] [CrossRef]
- Bao, J.; Macdonald, D.D. Hydrogen Oxidation on Oxidized Platinum at Elevated Temperatures, Part I: The Tunneling Current. J. Electroanal. Chem. 2007, 600, 205–216. [Google Scholar] [CrossRef]
- Burns, W.G.; Moore, P.B. Water radiolysis and its effect upon in-reactor zircaloy corrosion. Radiat. Eff. 1976, 30, 233–242. [Google Scholar] [CrossRef]
- Yeh, T.K.; Macdonald, D.D.; Motta, A.T. Modeling Water Chemistry, Electrochemical Corrosion Potential and Crack Growth Rate in the Boiling Water Reactor Heat Transport Circuits-Part I: The DAMAGE-PREDICTOR Algorithm. Nucl. Sci. Eng. 1995, 121, 468–482. [Google Scholar] [CrossRef]
- Macdonald, D.D. Unpublished Data (2021).
- Balachov, I.; Engelhardt, G.R.; Macdonald, D.D. Deterministic Prediction of Damage in Boiling Water Reactors Due to Stress Corrosion Cracking. In Proceedings of Symposium on Critical Factors in Localized Corrosion; Electrochemical Society: Pennington, NJ, USA, 1999. [Google Scholar]
- Macdonald, D.D.; Balachov, I.; Engelhardt, G. Deterministic Prediction of Localized Corrosion Damage in Power Plant Coolant Circuits. Power Plant Chem. 1999, 1, 9–16. [Google Scholar]
- Lu, P.C.; Macdonald, D.D.; Urquidi-Macdonald, M.; Yeh, T.K. Theoretical Estimation of Crack Growth Rates in Type 304 Stainless Steel in BWR Coolant Environments. Corrosion 1996, 52, 768–785. [Google Scholar]
- Turnbull, A.; Thomas, J.G.N. A model of crack electrochemistry for steels in the active state based on mass transport by diffusion and ion migration. J. Electrochem. Soc. 1982, 129, 1412. [Google Scholar] [CrossRef]
- Gutman, E.M. An inconsistency in the film rupture model of stress corrosion cracking. Corros. Sci. 2007, 49, 2289–2303. [Google Scholar] [CrossRef]
- Manahan, M.; MacDonald, D.; Peterson, A. Determination of the fate of the current in the stress corrosion cracking of sensitized type 304SS in high temperature aqueous systems. Corros. Sci. 1995, 37, 189–208. [Google Scholar] [CrossRef]
- Ford, F.P.; Taylor, D.F.; Andresen, P.; Ballinger, R. Corrosion-Assisted Cracking of Stainless and Low-Alloy Steels in LWR Environments; Final Report, EPRI NP-5064M; Electric Power Research Institute: Palo Alto, CA, USA, 1987. [Google Scholar]
- Congleton, J.; Shoji, T.; Parkins, R.N. The stress corrosion cracking of reactor pressure vessel steel in high temperature water. Corros. Sci. 1985, 25, 633. [Google Scholar] [CrossRef]
- Peng, Q.; Kwon, J.; Shoji, T. Development of a fundamental crack tip strain rate equation and its application to quantitative prediction of stress corrosion cracking of stainless steels in high temperature oxygenated water. J. Nucl. Mater. 2004, 324, 52–61. [Google Scholar] [CrossRef]
- Hall, M. An alternative to the Shoji crack tip strain rate equation. Corros. Sci. 2008, 50, 2902–2905. [Google Scholar] [CrossRef]
- Gomez-Duran, M.; Macdonald, D.D. Stress corrosion cracking of sensitized Type 304 stainless steel in thiosulfate solution: I. Fate of the coupling current. Corros. Sci. 2003, 45, 1455–1471. [Google Scholar] [CrossRef]
- Liu, S.; Macdonald, D.D. Fracture of AISI 4340 Steel in Concentrated Sodium Hydroxide Solution. Corrosion 2002, 58, 835–845. [Google Scholar] [CrossRef]
- Macdonald, D.D. The Electrochemistry of IGSCC Mitigation in BWR Coolant Circuits. Power Plant Chem. 2002, 4, 329–335. [Google Scholar]
- Macdonald, D.D.; Urquidi-Macdonald, M. An Advanced Coupled Environment Fracture Model for Predicting Crack Growth Rates. Chapter 4—Control, Mitigation, and Prediction of Stress Corrosion Cracking. In Proceedings of the TMS Parkins Symposium on Fundamental Aspects of Stress Corrosion Cracking, Cincinnati, OH, USA, 20–24 October 1991; pp. 443–455. [Google Scholar]
- Macdonald, D.D.; Urquidi-Macdonald, M. A coupled environment model for stress corrosion cracking in sensitized type 304 stainless steel in LWR environments. Corros. Sci. 1991, 32, 51–81. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Vankeerberghen, M. Predicting Crack Growth Rate vs. Temperature-Behavior of Type 304 Stainless Steel in Dilute Sulfuric Acid Solutions. Corros. Sci. 2002, 44, 1425–1441. [Google Scholar]
- Andresen, P.L. Effects of Temperature on Crack Growth Rate in Sensitized Type 304 Stainless Steel and Alloy 600. Corrosion 1993, 49, 714–725. [Google Scholar] [CrossRef]
- Lin, L.F.; Cragnolino, G.; Szklarska-Smialowska, Z.; Macdonald, D.D. Stress Corrosion Cracking of Sensitized Type 304 Stainless Steel in High Temperature Chloride Solutions. Corrosion 1981, 37, 616–627. [Google Scholar] [CrossRef]
- Cragnolino, G.; Macdonald, D.D.; Park, H.C. Stress Corrosion Cracking of Sensitized Type 304 SS in Borate Solutions at Elevated Temperatures. In Proceedings of the International Conference on Environmental Degradation of Materials in Nuclear Power System-Water Reactors, Myrtle Beach, SC, USA, 22–25 August 1983; pp. 604–622. [Google Scholar]
- Boiling Water Reactor Systems. Reactor Concepts Manual, USNRC Technical Training Center 3-1 0400 (undated).
- Zinkle, S.J.; Was, G.S. Materials challenges in nuclear energy. Acta Mater. 2013, 61, 735–758. [Google Scholar] [CrossRef]
- Kenik, E. Radiation-induced segregation in irradiated Type 304 stainless steels. J. Nucl. Mater. 1992, 187, 239–246. [Google Scholar] [CrossRef]
- Burns, W.G.; Henshaw, J.; Goodball, J.A.B. The Radiation Chemistry of a Pressurized Water Reactor. The Effect of Added Hydrogen Based on a Simplified Modeling Approach; AEA Technology Report AEA RS 3478; AEA Technology, Inc.: Carlsbad, CA, USA, 1994. [Google Scholar]
- Burns, W.G.; Sims, H.E. Effect of radiation type in water radiolysis. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1981, 77, 2803–2813. [Google Scholar] [CrossRef]
- Ruiz, C.P.; Lin, C.C.; Robinson, R.; Burns, W.G.; Curtis, A.R. Model Calculations of Water Radiolysis in BWR Primary Coolant. In Proceedings of the International conference on water chemistry of nuclear reactor systems, Bournemouth, UK, 23–27 October 1989. [Google Scholar]
- Yeh, T.K.; Macdonald, D.D.; Motta, A.T. Modeling Water Chemistry, Electrochemical Corrosion Potential, and Crack Growth Rate in the Boiling Water Reactor Heat Transport Circuits-Part III: Effect of Reactor Power Level. Nucl. Sci. Eng. 1996, 123, 305–316. [Google Scholar] [CrossRef]
- Yeh, T.K.; Macdonald, D.D.; Motta, A.T. Modeling Water Chemistry, Electrochemical Corrosion Potential and Crack Growth Rate in the Boiling Water Reactor Heat Transport Circuits-Part II: Simulation of Operating Reactors. Nucl. Sci. Eng. 1996, 123, 295–304. [Google Scholar] [CrossRef]
- Yeh, T.K.; Macdonald, D.D. Predictions of Enhancing Hydrogen Water Chemistry for Boiling Water Reactors by General Catalysis and General Inhibition; Paper #124; Corrosion/96; NACE International: Houston, TX, USA, 1996; pp. 124/1–124/10. [Google Scholar]
- Yeh, T.K.; Macdonald, D.D. Effects of Power Level Change on the Development of Damage in Boiling Water Reactors under Hydrogen Water Chemistry; Paper # 126; Corrosion/96; NACE International: Houston, TX, USA, 1996; pp. 126/1–126/12. [Google Scholar]
- Macdonald, D.D.; Yeh, T.K. Modeling the Development of Damage in BWR Primary Coolant Circuits. In Proceedings of the 7th International Conference on Environmental Degradation of Materials in Nuclear Power Systems-Water Reactors; NACE International: Breckenridge, CO, USA, 1995; pp. 909–919. [Google Scholar]
- Ullberg, M.; Gott, K.; Lejon, J.; Granath, G. Advanced ECP model for BWRs. In Proceedings of the International Conference on Environmental Degradation of Materials in Nuclear Power Systems, Whistler, BC, Canada, 19–23 August 2007. [Google Scholar]
- Hiroki, A.; LaVerne, J.A. Decomposition of Hydrogen Peroxide at Water−Ceramic Oxide Interfaces. J. Phys. Chem. B 2005, 109, 3364–3370. [Google Scholar] [CrossRef]
- Lin, C.C.; Smith, F.R.; Ichikawa, N.; Baba, T.; Itow, M. Decomposition of hydrogen peroxide in aqueous solutions at elevated temperatures. Int. J. Chem. Kinet. 1991, 23, 971–987. [Google Scholar] [CrossRef]
- Hiroishi, D.; Ishigure, K. Poster 12. Homogeneous and heterogeneous decomposition of hydrogen peroxide in high-temperature water. Proc. Water Chem. Nucl. React. Syst. 1989, 5, 311–312. [Google Scholar] [CrossRef]
- Haines, R.I.; McCracken, D.R. Decomposition of Hydrogen Peroxide under Coolant Chemistry Conditions. Proc. Water Chem. Nucl. React. Syst. 1989, 5, 309–310. [Google Scholar]
- Lin, C.C.; Smith, F.R. Decomposition of Hydrogen Peroxide at Elevated Temperatures; Report NP-6733; Electric Power Research Institute: Washington, DC, USA, 1990. [Google Scholar]
- Blakeslee, J.A. ZEBRA—A Computer Code for the Steady-State Thermal Analysis of Light Water Cooled Nuclear Power Reactor. Master’s Thesis, Department of Nuclear Engineering, The Pennsylvania State University, State College, PA, USA, 1974. [Google Scholar]
- TRAC-BD1/MOD 1: An Advanced Best Estimate Computer Program for Boiling Water Reactor Transient; Idaho National Engineering Laboratory: Idaho Falls, ID, USA, 1992.
- TRAC-BF1/MOD1: An Advanced Best-Estimate Computer program for BWR Accident Analysis. TRAC-BD1/MODI User’s Manuals, Volume 1; Idaho National Engineering Laboratory: Idaho Falls, ID, USA, 1992.
- Balachov, I.; Macdonald, D.; Stellwag, B.; Henzel, N.; Kilian, R. Prediction of Materials Damage History From Stress Corrosion Cracking in Boiling Water Reactors. In Proceedings of the Proc. ASME/JSME Joint Press. Vess. Piping Conf., San Diego, CA, USA, 26–30 July 1998; Volume 376, pp. 101–109. [Google Scholar]
- Balachov; Macdonald, D.D.; Henzel, N.; Stellwag, B. Modeling and Prediction of Materials Integrity in Boiling Water Reactors. In Proceedings of the Eurocorr ’98, Utrecht, NL, USA, 28 September–1 October 1998. [Google Scholar]
- Zhou, X.; Macdonald, D.D.; Balachov, I. Enhancing the Operation of Boiling Water Reactors by Deterministic Simulation. In Proceedings of the Water Chemistry ‘98, 1998 JAIF international conference on water chemistry in nuclear power plants, Kashiwazaki, Japan, 13–16 October 1998. [Google Scholar]
- Macdonald, D.D.; Balachov, I. Modeling Noble Metal Coatings for Hydrogen Water Chemistry in BWRs. In Proceedings of the 9th International Symposium on Environmental Degradation of Material in Nuclear Power System-Water Reactors, Newport Beach, La Grange, IL, USA, 1–5 August 1999. [Google Scholar]
- Zhou, X.-Y.; Balachov, I.I.; Macdonald, D.D. The Effect of Dielectric Coatings on IGSCC in Sensitized Type 304 SS in High Temperature Dilute Sodium Sulfate Solution. Corros. Sci. 1998, 40, 1349–1362. [Google Scholar] [CrossRef]
- Hettiarachchi, S.; Law, R.J.; Miller, W.D.; Diaz, T.P.; Cowan, R.L. First application of NobleChemTM to an operating BWRs; Japan Atomic Industrial Forum, Inc.: Tokyo, Japan, 1998. [Google Scholar]
- Cohen, P. Water Coolant Technology of Power Reactors; Gordon and Breach Science Publishers, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Macdonald, D.; Engelhardt, G. Predictive Modeling of Corrosion. In Shreir’s Corrosion; Elsevier: Amsterdam, The Netherlands, 2010; Volume 2, pp. 1630–1679. [Google Scholar] [CrossRef]
- Kim, H.-S.; Macdonald, D.D. PWSCC of Mill-annealed Alloy 600 in PWR Primary Coolant Circuits. 2021; in preparation. [Google Scholar]
- Macdonald, D.D.; Mahaffy, J.H.; Pitt, J.S.; Urquidi-Macdonald, M. Electrochemical Model of Activity Transport in Pressurized Water Reactors. In Proceedings of the 13th International Conference on Nuclear Engineering, Paper ICONE13-50423, Beijing, China, 16–20 May 2005. [Google Scholar]
- Urquidi-Macdonald, M.; Pitt, J.; Macdonald, D.D. The impact of radiolytic yield on the calculated ECP in PWR primary coolant circuits. J. Nucl. Mater. 2007, 362, 1–13. [Google Scholar] [CrossRef]
- Kim, H.S. A Study for Modeling Electrochemistry in Light Water Reactors. Ph.D. Thesis, Department of Nuclear Engineering, Pennsylvania State University, State College, PA, USA, 2007. [Google Scholar]
- Elliot, J.; Bartels, D.M. The Reaction Set, Rate Constants and g-Values for the Simulation of the Radiolysis of Light Water over the Range 20 to 350 °C Based on Information Available in 2008; AECL Report, Nuclear Platform Research and Development 153-1 271 60-450-001; Atomic Energy of Canada Limited: Mississauga, ON, Canada, 2009. [Google Scholar]
- Garbett, K.; Henshaw, J.; Sims, H.E. Hydrogen and Oxygen Behaviour in PWR Primary Coolant. Proc. Water Chem. Nucl. React. Syst. 2000, 8, 85–92. [Google Scholar]
- Takiguchi, H.; Ullberg, M.; Uchida, A.S. Optimization of Dissolved Hydrogen Concentration for Control of Primary Coolant Radiolysis in Pressurized Water Reactors. J. Nucl. Sci. Tech. 2004, 41, 601–609. [Google Scholar] [CrossRef]
- Cristensen, H. Remodeling of the Oxidant Species During Radiolysis of High-temperature Water in a Pressurized Water Reactor. Nucl. Tech. 1995, 109, 373. [Google Scholar] [CrossRef]
- Pastina, B.; Isabey, J.; Hickel, B. The influence of water chemistry on the radiolysis of the primary coolant water in pressurized water reactors. J. Nucl. Mater. 1999, 264, 309–318. [Google Scholar] [CrossRef]
- Salter-Williams, M. Mass Transport of Magnetite in Pressurized Water Reactor Primary Circuits. Master’s Thesis, Department of Nuclear Eng., Pennsylvania State University, State College, PA, USA, 2000. [Google Scholar]
- Shi, J.; Fekete, B.; Wang, J.; Macdonald, D.D. Customization of the coupled environment fracture model for predicting stress corrosion cracking in Alloy 600 in PWR environment. Corros. Sci. 2018, 139, 58–67. [Google Scholar] [CrossRef]
- MacDonald, P.E.; Shah, V.N.; Ward, L.W.; Ellison, P.G. Steam Generator Tube Failures; NUREG/CR-6365 (INEL-95/0383); U.S. Nuclear Regulatory Commission: Washington, DC, USA, 1996. [Google Scholar]
- Peter, J.; Paine, N.; Ulla, E. Volume 1, The Steam Generator Owners Groups I and II. In Gustafsson, Editors, Steam Generator Reference Book; Revision 1; The Steam Generator Reliability Project and Electric Power Research Institute: Palo Alto, CA, USA, 1994. [Google Scholar]
- Wikman, S.; Molander, A.; Öijerholm, J.; Eskhult, J.; Törnblom, O. Recent Development and Qualification of Materials for the European Contribution to ITER. ITR/P1-53. In Proceedings of the 23rd IAEA Fusion Energy Conference, Daejon, Korea, 11–16 October 2010. [Google Scholar]
- Saji, G. Scientific Bases of Corrosion Control for Water-Cooled Fusion Reactors Such as ITER. In Proceedings of the 2012 20th International Conference on Nuclear Engineering Collocated with the ASME 2012 Power Conference ICONE20-POWER2012, Anaheim, CA, USA, 30 July–3 August 2012. [Google Scholar]
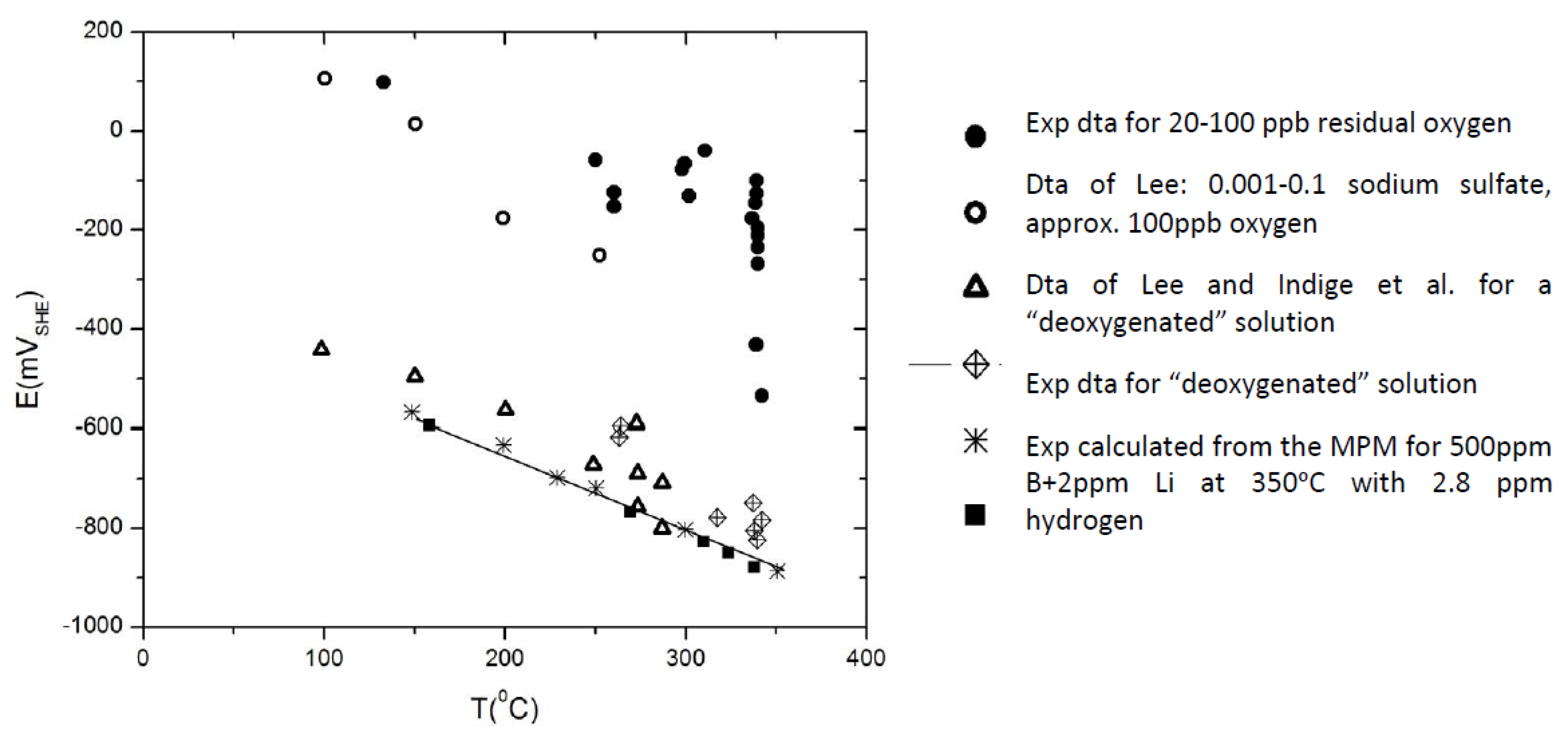
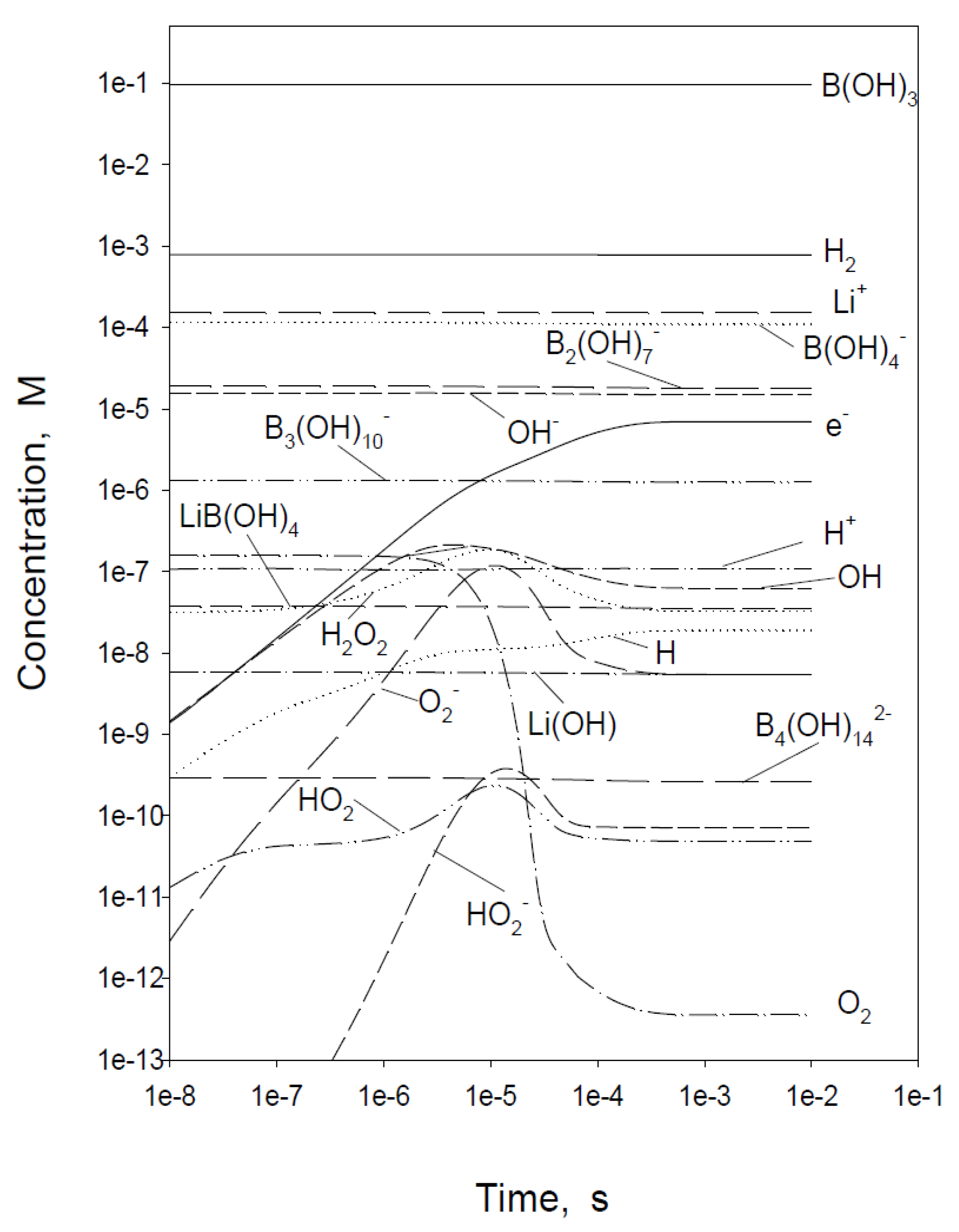


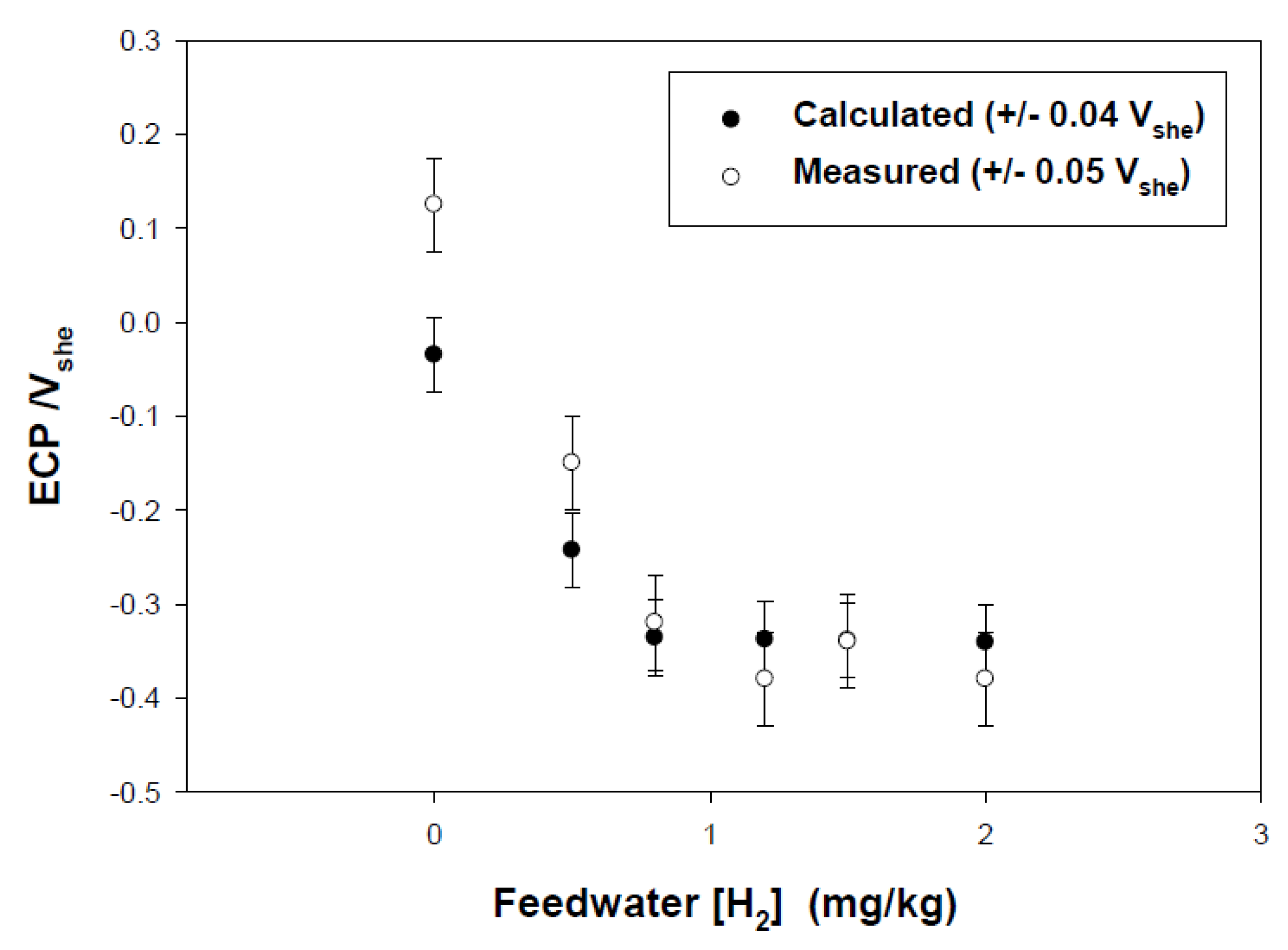

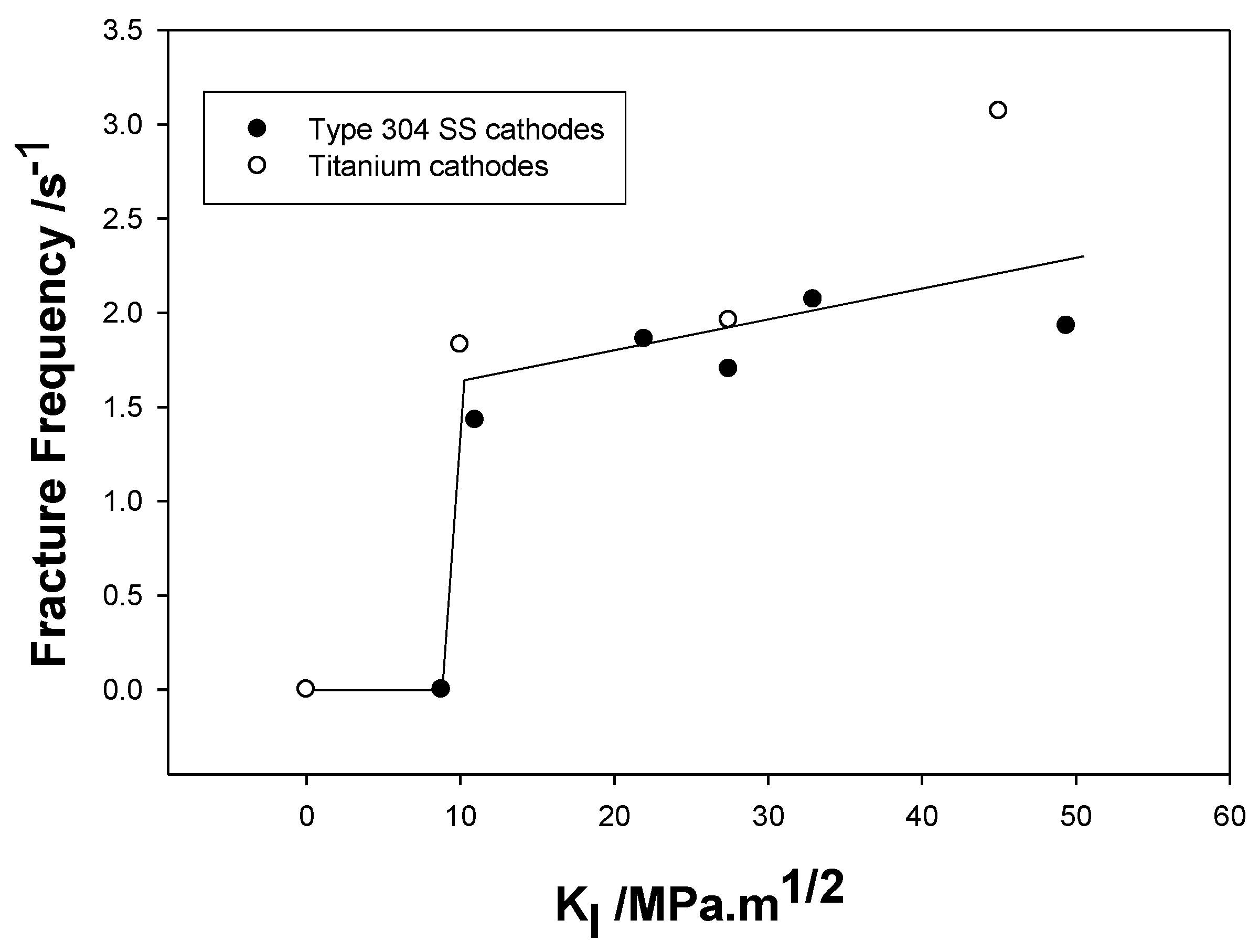







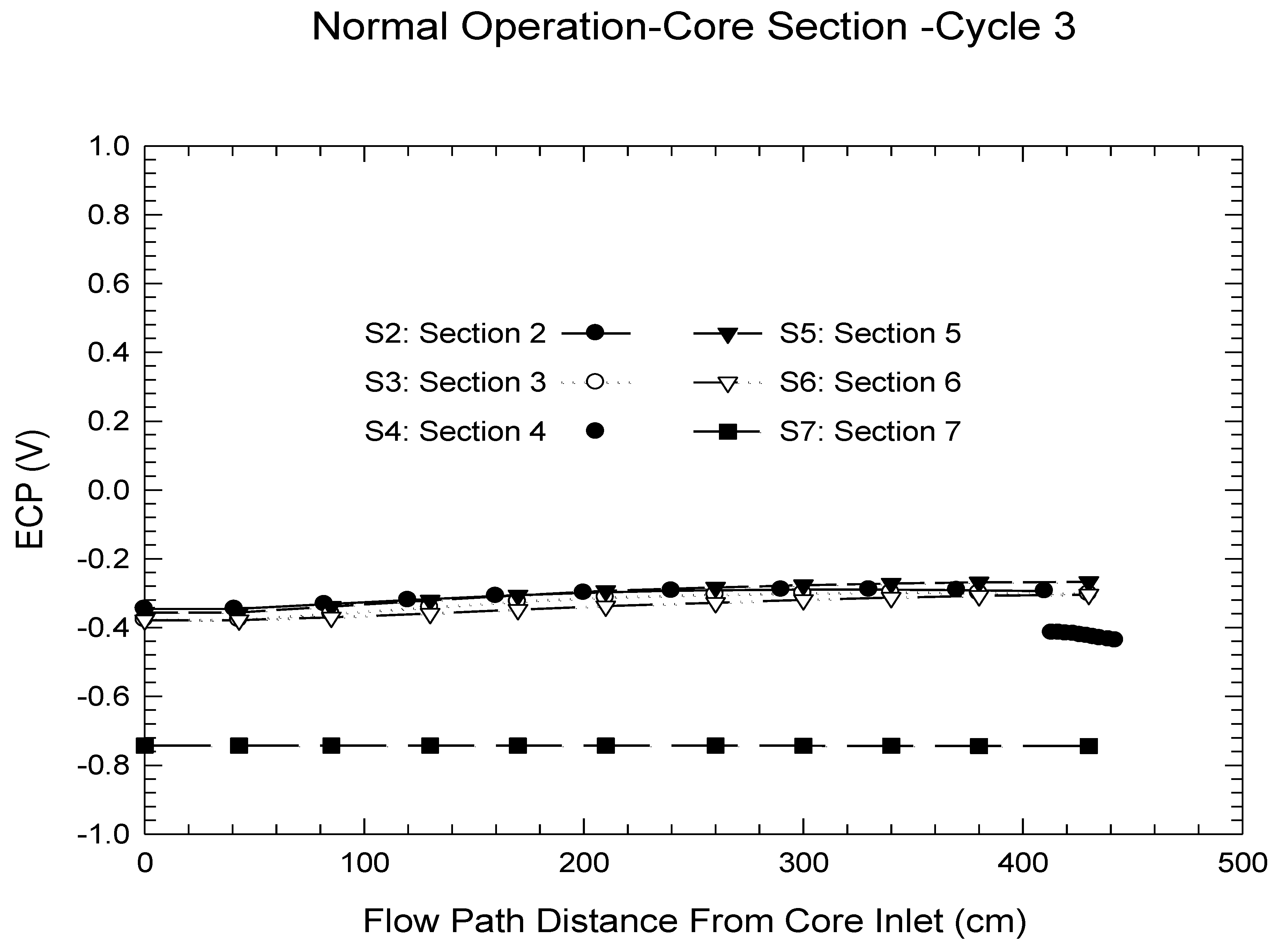
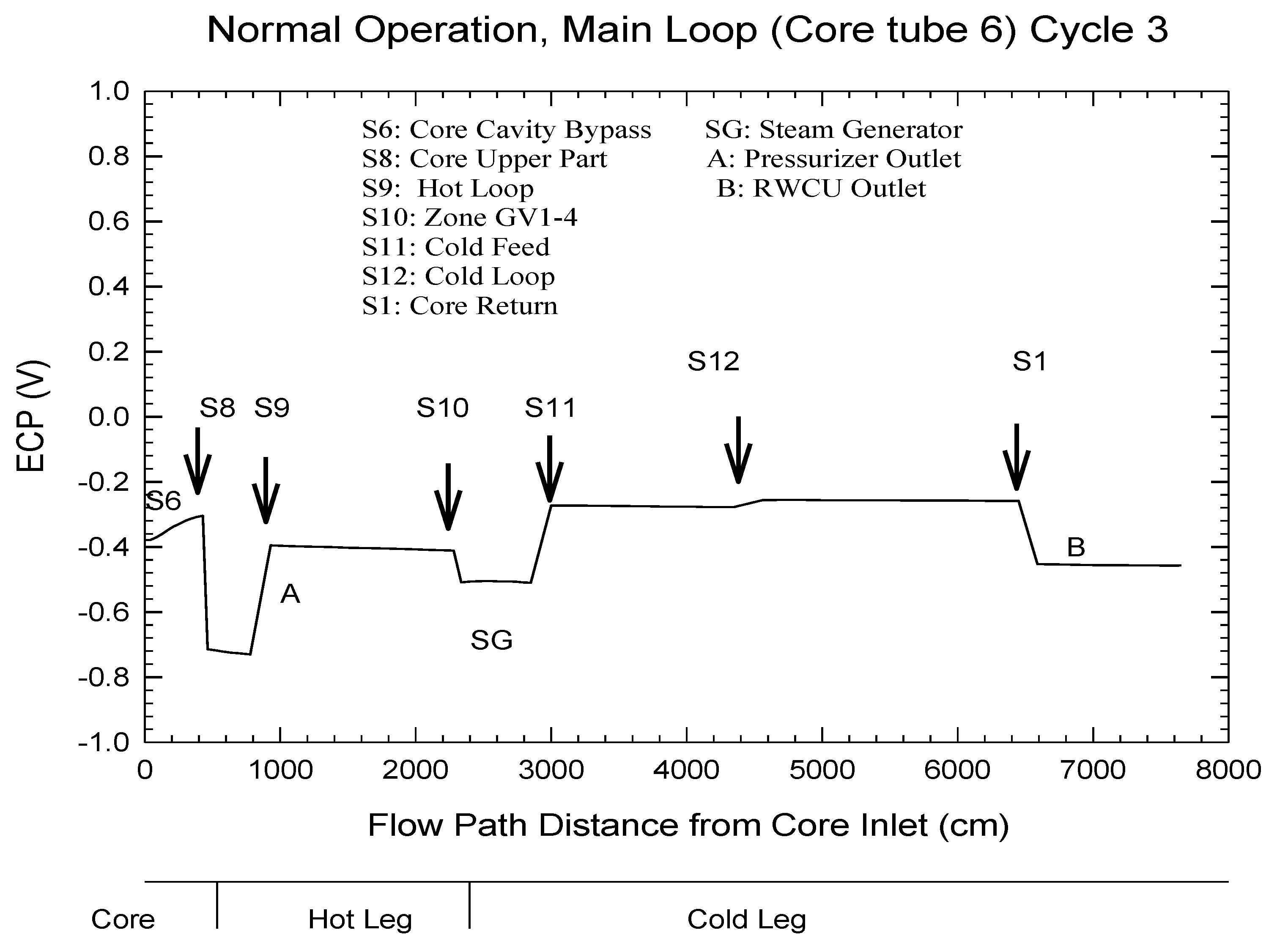
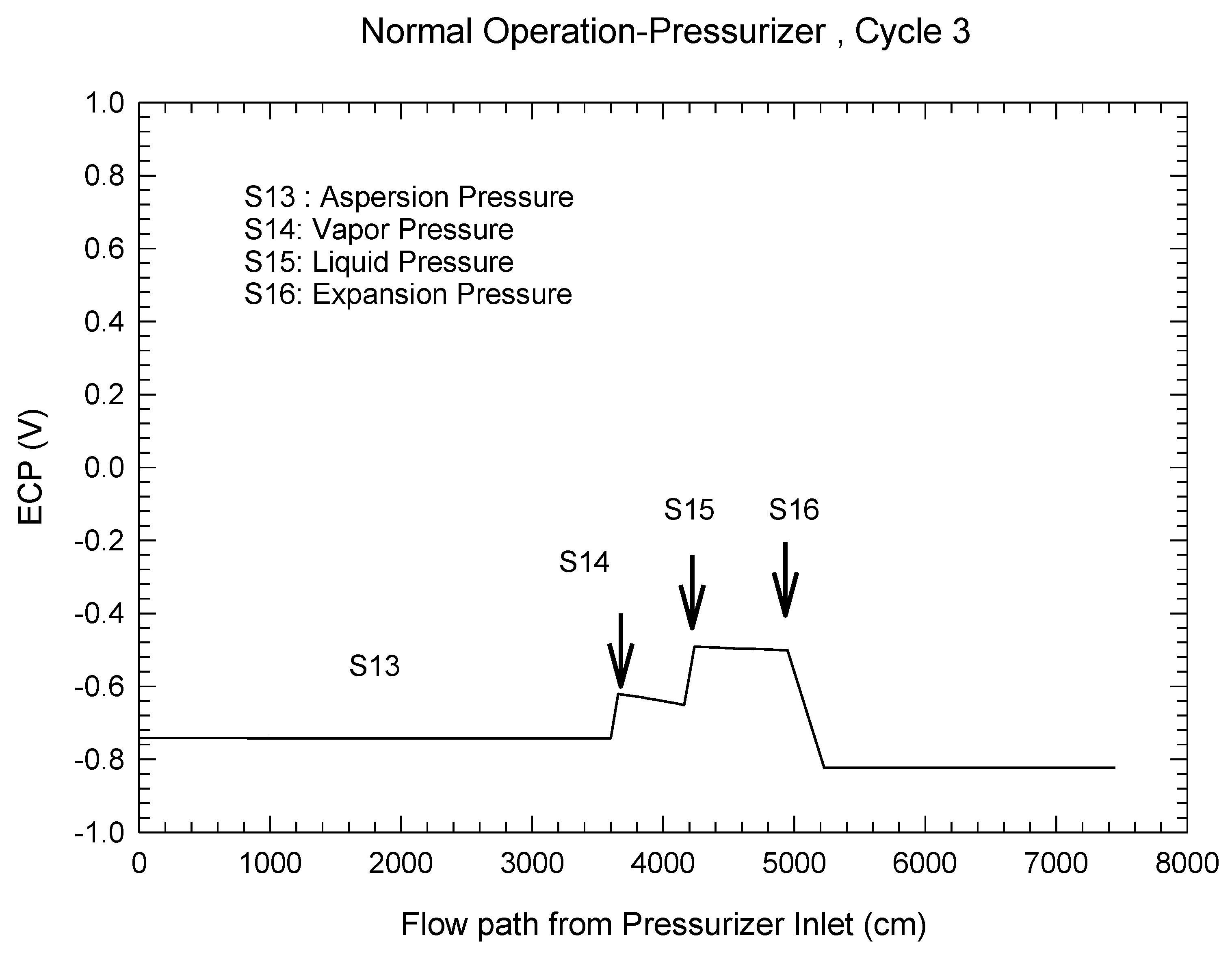
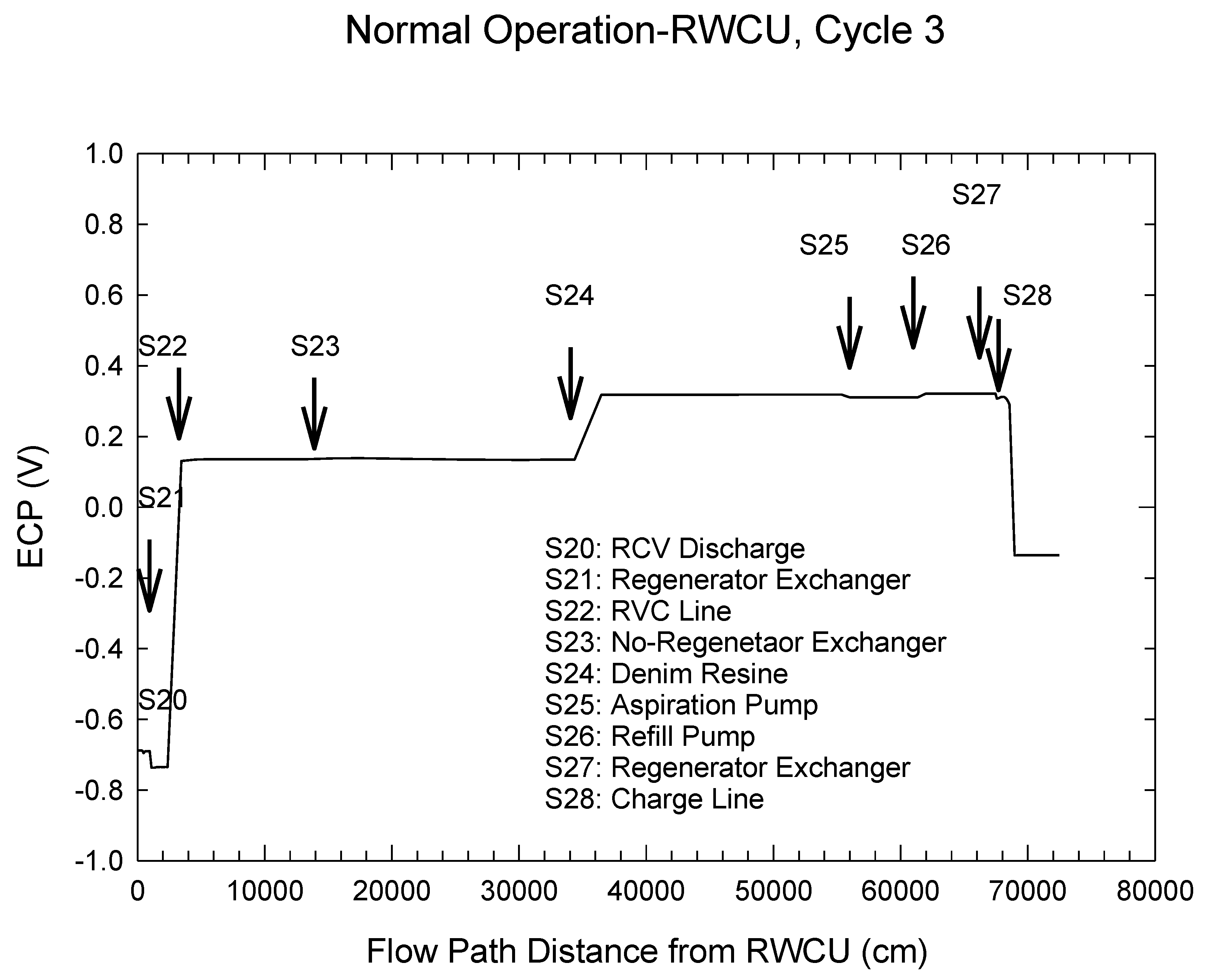


| Redox Couple | E0/Vshe | Redox Couple | E0/Vshe | Redox Couple | E0/Vshe |
|---|---|---|---|---|---|
| −2.87 | OH/H2O | 2.72 | H2O2/H2O | 1.77 | |
| H/H+ | −2.31 | H2/H+ | 0 | O−/H2O | 1.77 |
| H/H− | 0.05 | O2/H2O2 | 1.23 | O2/O2− | −0.16 |
| (O2, H+)/HO2 | 0.12 | O3/O3− | 0.83 | O2+/O2 | 3.2 |
| NH3+/NH3 | 2.13 | NH2/NH2− | 0.7 | NH2OH+/NH2OH | ≤1.26 |
| NO+/NO | 1.21 | NO2/NO2− | 1.04 | NO2+/NO2 | 1.51 |
| NO3−/NO32− | <−0.40 | NO3/NO3− | 2.5 | N2H4+/N2H4 | 0.01 |
| N3/N3− | 1.33 |
| Parameter/T °C | 25 | 50 | 100 | 150 | 200 | 250 | 288 | 300 |
|---|---|---|---|---|---|---|---|---|
| /Vshe | 0.16 | 0.13 | 0.05 | −0. 09 | −0.25 | −0.40 | −0.52 | −0.67 |
| /Vshe | 0.108 | 0.116 | 0.135 | 0.153 | 0.171 | 0.189 | 0.203 | 0.207 |
| /Vshe | 0.268 | 0.246 | 0.185 | 0.063 | −0.079 | −0.211 | −0.317 | −0.463 |
| /Vshe, Expt | −0.230 [9] | |||||||
| /Vshe | −0.086 | −0.108 | −0.138 | −0.170 | −0.190 | −0.195 | −0.200 | −0.342 |
| ECP (0.2 ppm O2)/Vshe | 0.118 | 0.134 | 0.140 | 0.119 | 0.074 | 0.010 | −0.056 | −0.070 |
| Property | Value | Comment |
|---|---|---|
| Temperature | 295 °C–330 °C | Typical |
| Pressure | 150 bar (2250 psi) | Typical |
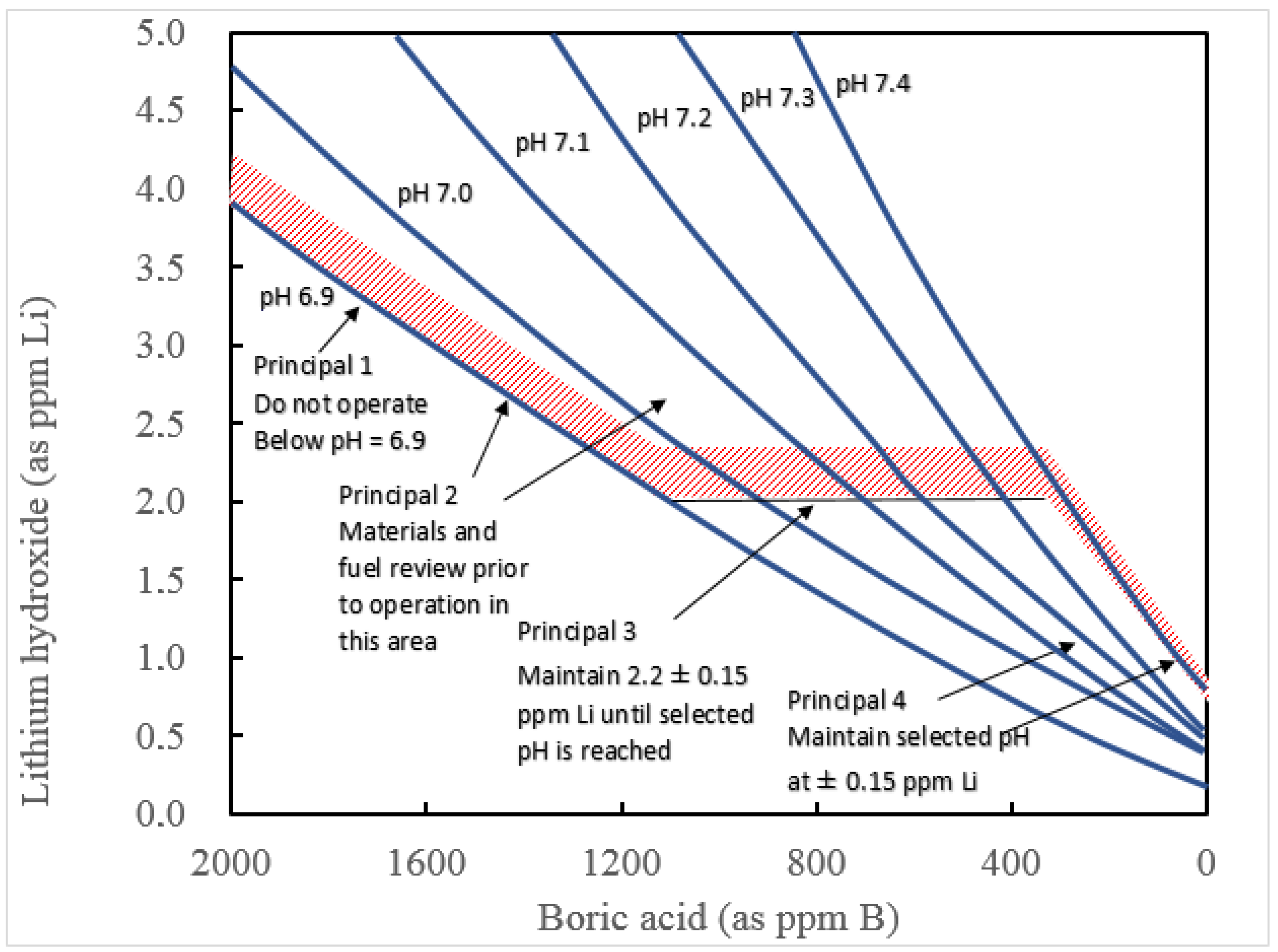
| Coolant composition | 4000–0 ppm B as boric acid, 4–1 ppm Li as lithium hydroxide, depending upon the burn-up of the fuel and the vendor | Li-B trajectory over a typical fuel cycle is shown in Figure 32 |
| Hydrogen concentration | 25–55 cc(STP [standard temperature and pressure])/kg(H2O) | Some noncommercial units operate with [H2] as high as 70 cc(STP)/kg(H2O) |
| Core channel dose rate | Typical | |
| γ-Photon | 3 × 105 Rad/s | |
| Neutron | 6 × 105 Rad/s | |
| α Particles | 3 × 105 Rrad/s | |
| Coolant Mass Flow Rate | 18,000 kg/s | Typical |
| Parameter | Value |
|---|---|
| Hydrogen, cc (STP)/kg | 1 |
| Oxygen, ppb | 10 |
| Cu2+, ppb | 10 |
| Cu+, ppb | 0 |
| Fe2+, ppb | 10 |
| Fe3+, ppb | 0 |
| N2, ppm | 2 |
| Temperature, °C | 98 |
| tL, s | 81.3 |
| Qn, W/cm3 | 3.2 |
| Qγ, W/cm3 | 4.3 |
| [H2]Input | [H2]Input | [H2]Input | [H2]ss | [O2]ss | [H2O2]ss | ECP | CGR |
|---|---|---|---|---|---|---|---|
| cc (STP)/kg H2O | M | ppb | ppb | ppb | ppb | Vshe | cm/s |
| 0 | 0 | 0 | 31.7524 | 144.8283 | 212.1415 | 0.4389 | 9.71 × 10−6 |
| 0.1 | 4.31 × 10−6 | 8.9229 | 21.6517 | 15.9027 | 212.4514 | 0.4480 | 1.18 × 10−5 |
| 0.2 | 8.61 × 10−6 | 17.8442 | 26.5881 | 4.1772 | 170.4914 | 0.4374 | 9.41 × 10−6 |
| 0.5 | 2.15 × 10−5 | 44.6146 | 48.101 | 0.5303 | 87.2583 | 0.4047 | 4.69 × 10−6 |
| 1 | 4.31 × 10−5 | 89.2292 | 90.4824 | 0.0925 | 48.5876 | 0.3744 | 2.46 × 10−6 |
| 10 | 4.37 × 10−4 | 892.2089 | 891.8567 | 6.38 × 10−4 | 20.9557 | 0.2909 | 4.14 × 10−6 |
| [H2]Input | [H2]Input | [H2]Input | [H2]ss | [O2]ss | [H2O2]ss | ECP | CGR |
|---|---|---|---|---|---|---|---|
| cc (STP)/kg H2O | M | ppb | ppb | ppb | ppb | Vshe | cm/s |
| 0 | 0 | 0 | 7.5569 | 70.5978 | 6.44 × 10−3 | 0.0981 | 1.34 × 10−8 |
| 0.1 | 4.31 × 10−6 | 8.9229 | 7.6366 | 1.17 × 10−6 | 5.85 × 10−4 | −0.3244 | 8.73 × 10−13 |
| 0.2 | 8.61 × 10−6 | 17.8442 | 17.2391 | 4.41 × 10−7 | 5.95 × 10−4 | −0.3241 | 8.78 × 10−13 |
| 0.5 | 2.15 × 10−5 | 44.6146 | 42.7094 | 2.71 × 10−7 | 5.95 × 10−4 | −0.3241 | 8.78 × 10−13 |
| 1 | 4.31 × 10−5 | 89.2292 | 86.7085 | 2.35 × 10−7 | 5.92 × 10−4 | −0.3242 | 8.77 × 10−13 |
| 10 | 4.37 × 10−4 | 892.2089 | 879.062 | 2.14 × 10−7 | 5.92 × 10−4 | −0.3242 | 8.77 × 10−13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macdonald, D.D.; Engelhardt, G.R. A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part II, Prediction of Corrosion Damage in Operating Reactors. Corros. Mater. Degrad. 2022, 3, 694-758. https://doi.org/10.3390/cmd3040038
Macdonald DD, Engelhardt GR. A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part II, Prediction of Corrosion Damage in Operating Reactors. Corrosion and Materials Degradation. 2022; 3(4):694-758. https://doi.org/10.3390/cmd3040038
Chicago/Turabian StyleMacdonald, Digby D., and George R. Engelhardt. 2022. "A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part II, Prediction of Corrosion Damage in Operating Reactors" Corrosion and Materials Degradation 3, no. 4: 694-758. https://doi.org/10.3390/cmd3040038
APA StyleMacdonald, D. D., & Engelhardt, G. R. (2022). A Critical Review of Radiolysis Issues in Water-Cooled Fission and Fusion Reactors: Part II, Prediction of Corrosion Damage in Operating Reactors. Corrosion and Materials Degradation, 3(4), 694-758. https://doi.org/10.3390/cmd3040038








