Monolayer Gas Adsorption on Graphene-Based Materials: Surface Density of Adsorption Sites and Adsorption Capacity
Abstract
:1. Introduction
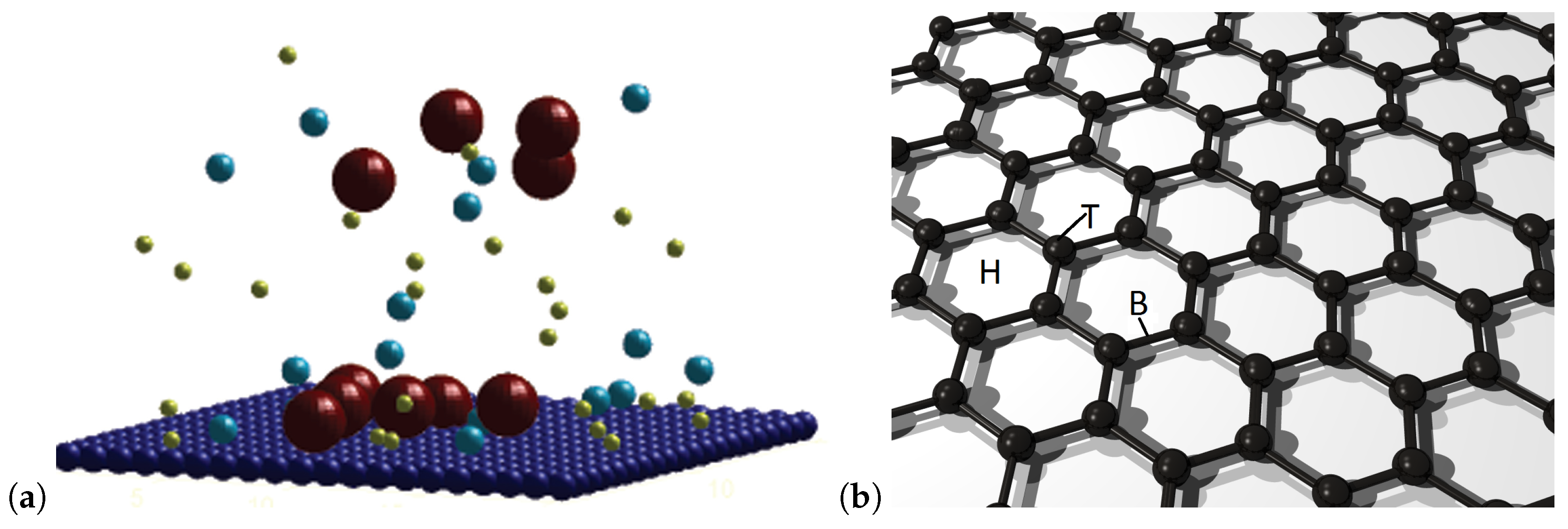
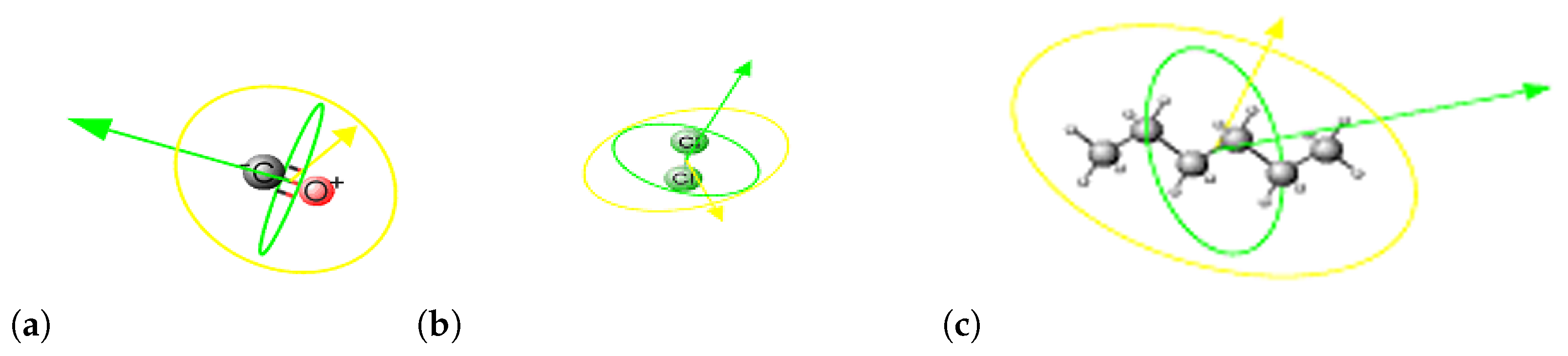
2. Methods
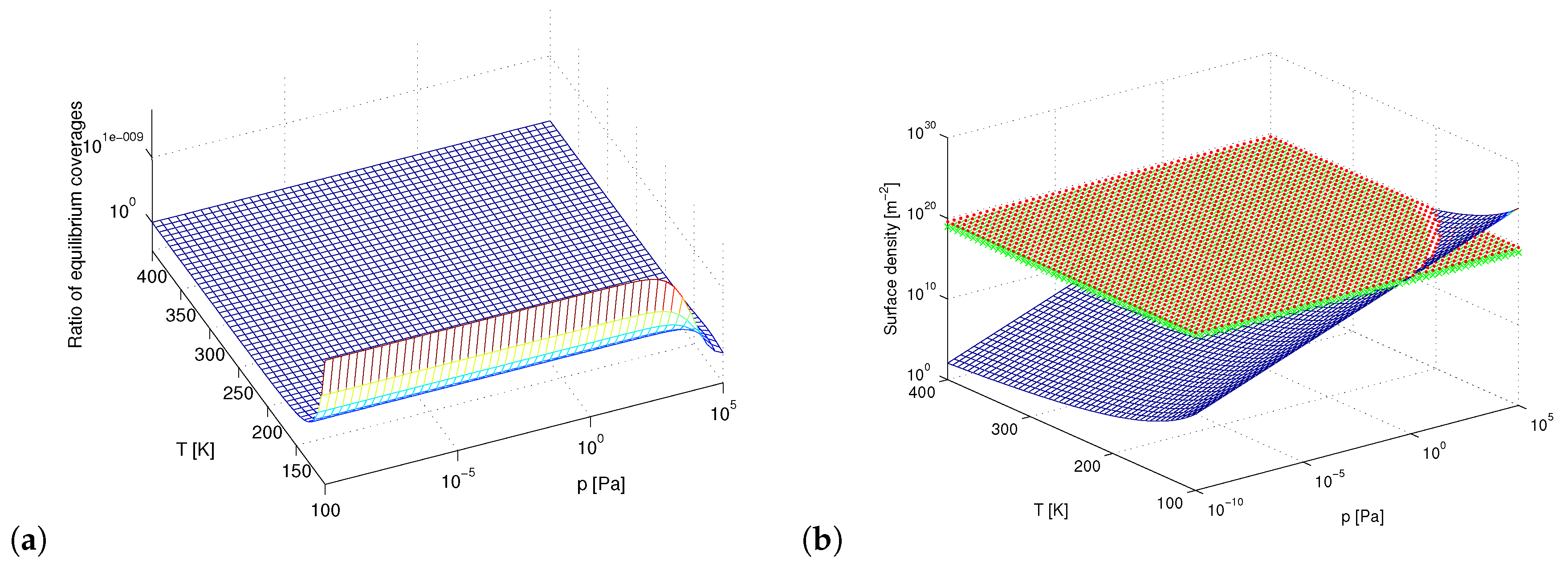
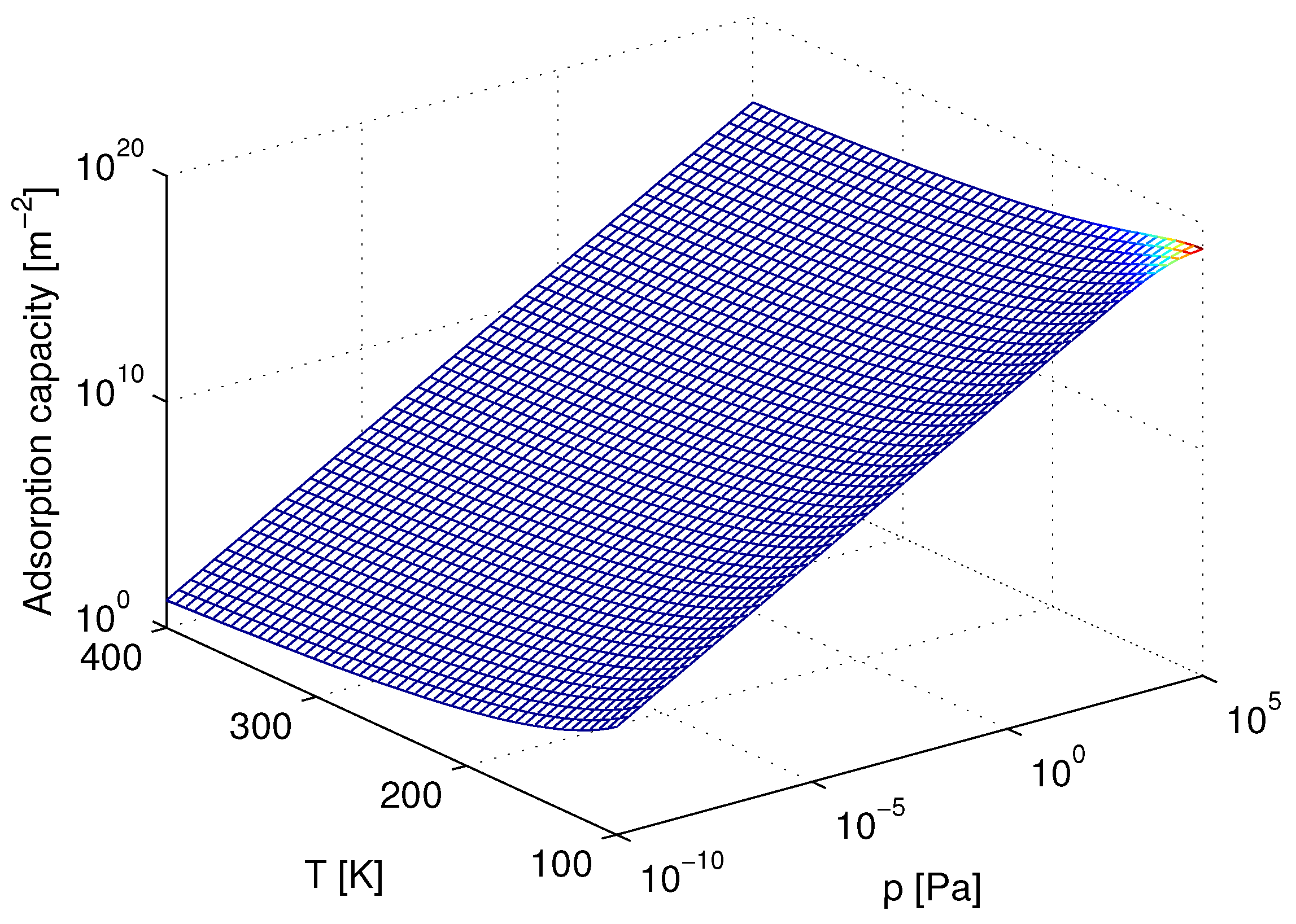
3. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdulhalim, I.; Zourob, M.; Lakhtakia, A. Surface plasmon resonance for biosensing: A mini-review. Electromagnetics 2008, 28, 214–242. [Google Scholar] [CrossRef]
- Tian, W.; Liu, X.; Yu, W. Research progress of gas sensor based on graphene and its derivatives: A review. Appl. Sci. 2018, 8, 1118. [Google Scholar] [CrossRef] [Green Version]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Djurić, Z.; Jokić, I.; Djukić, M.; Frantlović, M. Fluctuations of the adsorbed mass and the resonant frequency of vibrating MEMS/NEMS structures due to multilayer adsorption. Microelecron. Eng. 2010, 87, 1181–1184. [Google Scholar] [CrossRef]
- Lagergren, S.Y. Zur Theorie Der Sogenannten Adsorption Gelöster Stoffe. Zeitschr f Chem und Ind der Kolloide 1907, 2, 15. [Google Scholar] [CrossRef]
- Jakšić, O.; Jokić, I.; Jakšić, Z.; Mladenović, I.; Radulović, K.; Frantlović, M. The time response of plasmonic sensors due to binary adsorption: Analytical versus numerical modeling. Appl. Phys. A 2020, 126, 1–13. [Google Scholar] [CrossRef]
- Weinan, E. Principles of Multiscale Modeling; Cambridge University Press: London, UK, 2011; ISBN 9781107096547. [Google Scholar]
- González-Hernández, J.L.; Canedo, M.M.; Encinar, S. Application of a Robust Hybrid Algorithm (Neural Networks-AGDC) for the Determination of Kinetic Parameters and Discrimination among Reaction Mechanisms. MATCH Commun. Math. Comput. Chem. 2018, 79, 619–644. [Google Scholar]
- Kumar, G.P.; Malla, K.A.; Yerra, B.; Rao, K.S. Removal of Cu(II) using three low-cost adsorbents and prediction of adsorption using artificial neural networks. Appl. Water Sci. 2019, 9, 44. [Google Scholar] [CrossRef] [Green Version]
- Ullah, S.; Assiri, M.A.; Al-Sehemi, A.G.; Bustam, M.A.; Sagir, M.; Abdulkareem, F.A.; Raza, M.R.; Ayoub, M.; Irfan, A. Characteristically Insights, Artificial Neural Network (ANN), Equilibrium, and Kinetic Studies of Pb(II) Ion Adsorption on Rice Husks Treated with Nitric Acid. Intern. J. Environ. Res. 2020, 14, 43–60. [Google Scholar] [CrossRef]
- Anderson, R.; Rodgers, J.; Argueta, E.; Biong, A.; Gomez-Gualdron, D.A. Role of pore chemistry and topology in the CO2 capture capabilities of MOFs: From molecular simulation to machine learning. Chem. Mater. 2018, 30, 6325–6337. [Google Scholar] [CrossRef]
- Do, D.D.; Do, H.D.; Nicholson, D. Effects of surface structure and temperature on the surface mediation, layer concentration and molecular projection area: Adsorption of argon and nitrogen onto graphitized thermal carbon black. Adsorpt. Sci. Technol. 2007, 25, 347–363. [Google Scholar] [CrossRef] [Green Version]
- Jakšić, O.M.; Randjelović, D.V.; Jakšić, Z.S.; Čupić, Ž.D.; Kolar-Anić, L.Z. Plasmonic sensors in multi-analyte environment: Rate constants and transient analysis. Chem. Eng. Res. Des. 2014, 92, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Conti, S.; Cecchini, M. Accurate and efficient calculation of the desorption energy of small molecules from graphene. J. Phys. Chem. C 2015, 119, 1867–1879. [Google Scholar] [CrossRef]
- Leenaerts, O.; Partoens, B.; Peeters, F.M. Adsorption of H2O, NH3, CO, NO2, and NO on graphene: A first-principles study. Phys. Rev. B 2008, 77, 125416. [Google Scholar] [CrossRef] [Green Version]
- Casolo, S.; Løvvik, O.M.; Martinazzo, R.; Tantardini, G.F. Understanding adsorption of hydrogen atoms on graphene. J. Chem. Phys. 2009, 130, 054704. [Google Scholar] [CrossRef]
- Lee, G.; Lee, B.; Kim, J.; Cho, K. Ozone adsorption on graphene: Ab initio study and experimental validation. J. Phys. Chem. C. 2009, 113, 14225–14229. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Zhang, Y.; Shen, C.; Chai, Y. Adsorption of CO molecules on doped graphene: A first-principles study. AIP Adv. 2016, 6, 025317. [Google Scholar] [CrossRef]
- Lin, X.; Ni, J.; Fang, C. Adsorption capacity of H2O, NH3, CO, and NO2 on the pristine graphene. J. Appl. Phys. 2013, 113, 034306. [Google Scholar] [CrossRef]
- Kong, L.; Enders, A.; Rahman, T.S.; Dowben, P.A. Molecular adsorption on graphene. J. Phys. Cond. Matt. 2014, 26, 443001. [Google Scholar] [CrossRef]
- Jakšić, O. Parameters for modeling and analysis of adsorption kinetics and dynamics in adsorption based refractometric gas sensors. Mendeley Data 2020. [Google Scholar] [CrossRef]
- Jakšić, O. Parameters for adsorption of (CWA) chemical warfare agents and CWA simulants. Harvard Dataverse 2018. [Google Scholar] [CrossRef]
- Ulissi, Z.W.; Tang, M.T.; Xiao, J.; Liu, X.; Torelli, D.A.; Karamad, M.; Cummins, K.; Hahn, C.; Lewis, N.S.; Jaramillo, T.F.; et al. Machine-learning methods enable exhaustive searches for active bimetallic facets and reveal active site motifs for CO2 reduction. ACS Catal. 2017, 7, 6600–6608. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 32, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Neto, C.; Guinea, F.; Peres, N.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Mohan, V.B.; Lau, K.; Hui, D.; Bhattacharyya, D. Graphene-based materials and their composites: A review on production, applications and product limitations. Compos. Part B Eng. 2018, 142, 200–220. [Google Scholar] [CrossRef]
- Nag, A.; Arkadeep, M.; Mukhopadhyay, S.C. Graphene and its sensor-based applications: A review. Sens. Actuators A Phys. 2018, 270, 177–194. [Google Scholar] [CrossRef]
- Wu, Y.; Jianhua, Z.; Huang, L. A review of three-dimensional graphene-based materials: Synthesis and applications to energy conversion/storage and environment. Carbon 2019, 143, 610–640. [Google Scholar] [CrossRef]
- Rosli, N.N.; Ibrahim, M.A.; Ludin, N.A.; Mat-Teridi, M.A.; Sopian, K. A review of graphene based transparent conducting films for use in solar photovoltaic applications. Renew. Sustain. Energy Rev. 2019, 99, 83–99. [Google Scholar] [CrossRef]
- Lawal, A.T. Graphene-based nano composites and their applications: A review. Biosens. Bioelectr. 2019, 141, 111384. [Google Scholar] [CrossRef] [PubMed]
- Spasenović, M. Applications of Graphene. In Surface and Interface Science: Volume 10: Applications of Surface Science II; Wandelt, K., Ed.; Wiley-VCH: Weinheim, Germany, 2020. [Google Scholar] [CrossRef]
- Balog, R.; Jørgensen, B.; Nilsson, L.; Andersen, M.; Rienks, E.; Bianchi, M.; Fanetti, M.; Lægsgaard, E.; Baraldi, A.; Lizzit, S.; et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat. Mater. 2010, 9, 315–319. [Google Scholar] [CrossRef]
- Grimme, S.; Jens, A.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Chan, K.T.; Neaton, J.B.; Cohen, M.L. First-principles study of metal adatom adsorption on graphene. Phys. Rev. B 2008, 77, 235430. [Google Scholar] [CrossRef] [Green Version]
- Leenaerts, O.; Partoens, B.; Peeters, F.M. Water on graphene: Hydrophobicity and dipole moment using density functional theory. Phys. Rev. B 2009, 79, 235440. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Silvestrelli, P.L. Adsorption of rare-gas atoms and water on graphite and graphene by van der Waals-corrected density functional theory. J. Phys. Chem. C 2011, 115, 3695–3702. [Google Scholar] [CrossRef]
- Toth, J. Adsorption: Theory, Modeling, and Analysis; Surfactant Sciences Series; Marcel Dekker Inc: New York, NY, USA, 2002; Volume 107. [Google Scholar] [CrossRef]
- Pu, H.H.; Rhim, S.H.; Gajdardziksa-Josifovska, M.; Hirschmugl, C.J.; Weinert, M.; Chen, J.H. A statistical thermodynamics model for monolayer gas adsorption on graphene-based materials: Implications for gas sensing applications. RSC Adv. 2014, 4, 47481–47487. [Google Scholar] [CrossRef] [Green Version]
- Jakšić, O. ADmoND: MathWorks Matlab Package for simulation of monolayer adsorption processes in nano devices. Mendeley Data 2019. [Google Scholar] [CrossRef]
- Nakada, K.; Akira, I. DFT calculation for adatom adsorption on graphene. In Graphene Simulation; Gong, J.R., Ed.; IntechOpen: Rijeka, Croatia, 2011; pp. 1–20. [Google Scholar] [CrossRef] [Green Version]
- Jette, E.R.; Foote, F. Precision determination of lattice constants. J. Chem. Phys. 1935, 3, 605–616. [Google Scholar] [CrossRef]
- Jakšić, O.; Jakšić, Z.; Čupić, Ž.; Randjelović, D.; Kolar-Anić, L. Fluctuations in transient response of adsorption-based plasmonic sensors. Sens. Actuators B 2014, 190, 419–428. [Google Scholar] [CrossRef]
- Jakšić, O.; Jakšić, Z.; Rašljić, M.; Kolar-Anić, L. On Oscillations and Noise in Multicomponent Adsorption: The Nature of Multiple Stationary States. Adv. Math. Phys. 2019, 2019. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998; p. 15. [Google Scholar] [CrossRef]
- Yong, Y.K.; Vig, J.R. Resonator Surface Contamination—A Cause of Frequency fluctuations? IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1989, 36, 452–458. [Google Scholar] [CrossRef] [PubMed]
- Barakat, T.; Abodayeh, K.; Al-Dossary, O.M. Exact solutions for vibrational levels of the Morse potential via the asymptotic iteration method. Czech J. Phys. 2006, 56, 583–590. [Google Scholar] [CrossRef] [Green Version]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A.; Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ambrosetti, A.; Silvestrelli, P.L.; Tkatchenko, A. Physical adsorption at the nanoscale: Towards controllable scaling of the substrate-adsorbate van der Waals interaction. Phys. Rev. B. 2017, 95, 235417. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Silvestrelli, P.L. Hidden by graphene—Towards effective screening of interface van der Waals interactions via monolayer coating. Carbon 2018, 139, 486–491. [Google Scholar] [CrossRef] [Green Version]
- Ambrosetti, A.; Silvestrelli, P.L. Faraday-like screening by two-dimensional nanomaterials: A scale-dependent tunable effect. J. Phys. Chem. Lett. 2019, 10, 2044–2050. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Trends in the change in graphene conductivity upon gas adsorption: The relevance of orbital distortion. J. Phys. Chem. Lett. 2020, 11, 2737–2741. [Google Scholar] [CrossRef]
| Gas | CH | CO | N | A | O | CO |
|---|---|---|---|---|---|---|
| [49], p.1390 | 6.3 | 6.6 | 6.6 | 7.7 | 7.7 | 6.1 |
| our data | 6.52 | 7.15 | 7.5 | 7.08 | 7.34 | 6.52 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakšić, O.; Spasenović, M.; Jakšić, Z.; Vasiljević-Radović, D. Monolayer Gas Adsorption on Graphene-Based Materials: Surface Density of Adsorption Sites and Adsorption Capacity. Surfaces 2020, 3, 423-432. https://doi.org/10.3390/surfaces3030031
Jakšić O, Spasenović M, Jakšić Z, Vasiljević-Radović D. Monolayer Gas Adsorption on Graphene-Based Materials: Surface Density of Adsorption Sites and Adsorption Capacity. Surfaces. 2020; 3(3):423-432. https://doi.org/10.3390/surfaces3030031
Chicago/Turabian StyleJakšić, Olga, Marko Spasenović, Zoran Jakšić, and Dana Vasiljević-Radović. 2020. "Monolayer Gas Adsorption on Graphene-Based Materials: Surface Density of Adsorption Sites and Adsorption Capacity" Surfaces 3, no. 3: 423-432. https://doi.org/10.3390/surfaces3030031
APA StyleJakšić, O., Spasenović, M., Jakšić, Z., & Vasiljević-Radović, D. (2020). Monolayer Gas Adsorption on Graphene-Based Materials: Surface Density of Adsorption Sites and Adsorption Capacity. Surfaces, 3(3), 423-432. https://doi.org/10.3390/surfaces3030031









