Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces
Abstract
:1. Introduction
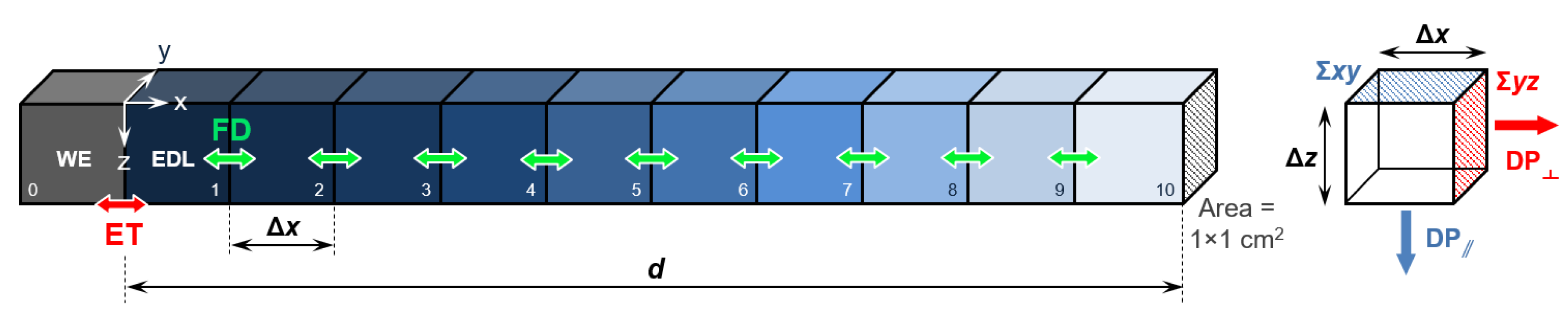
2. Methods: Stochastic Simulation Details
3. Results and Discussion
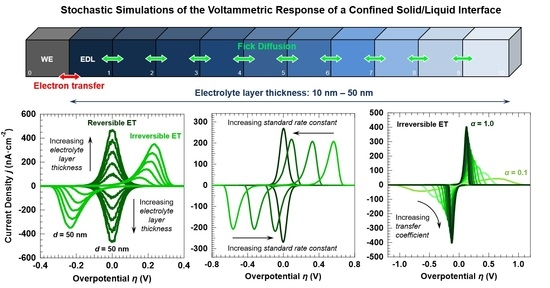
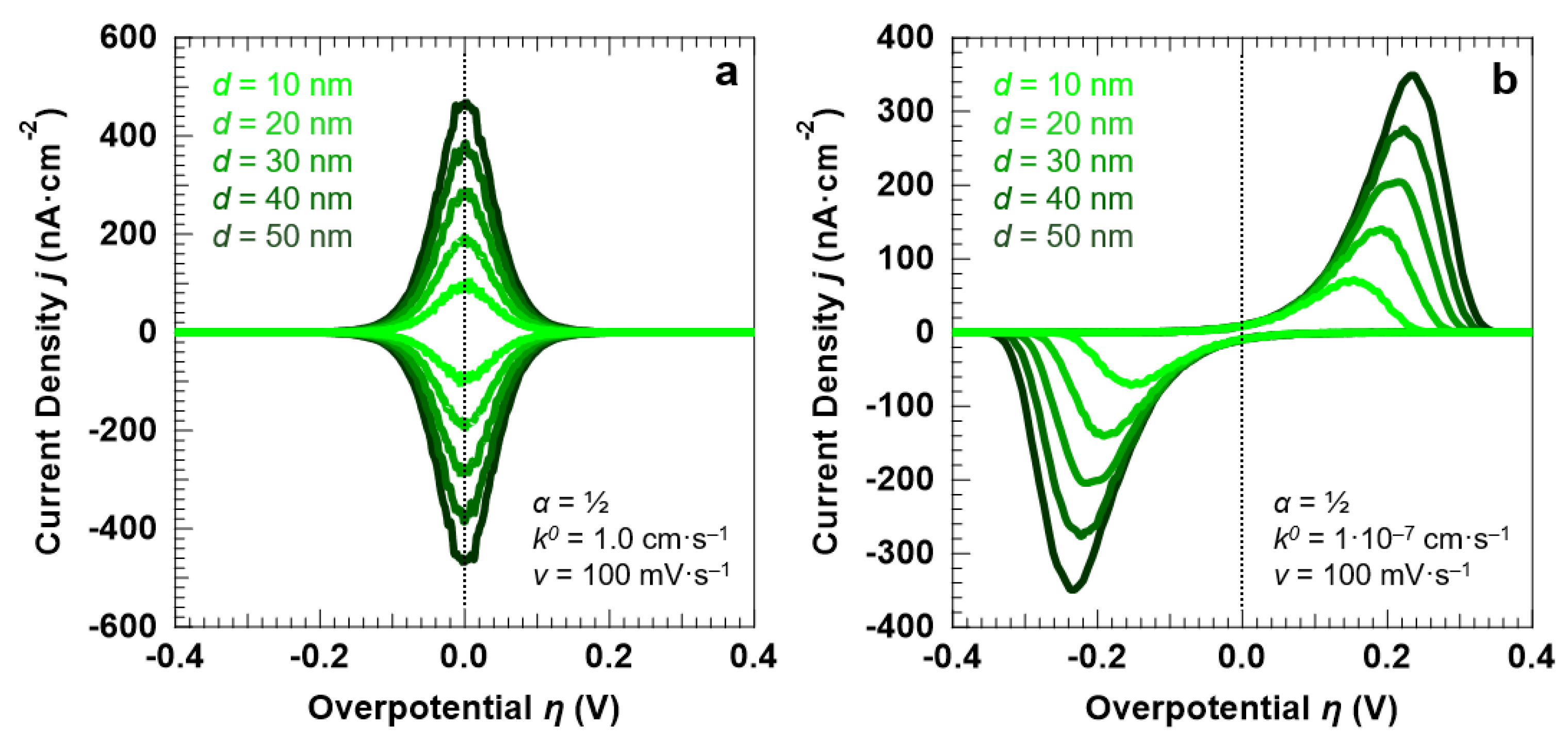
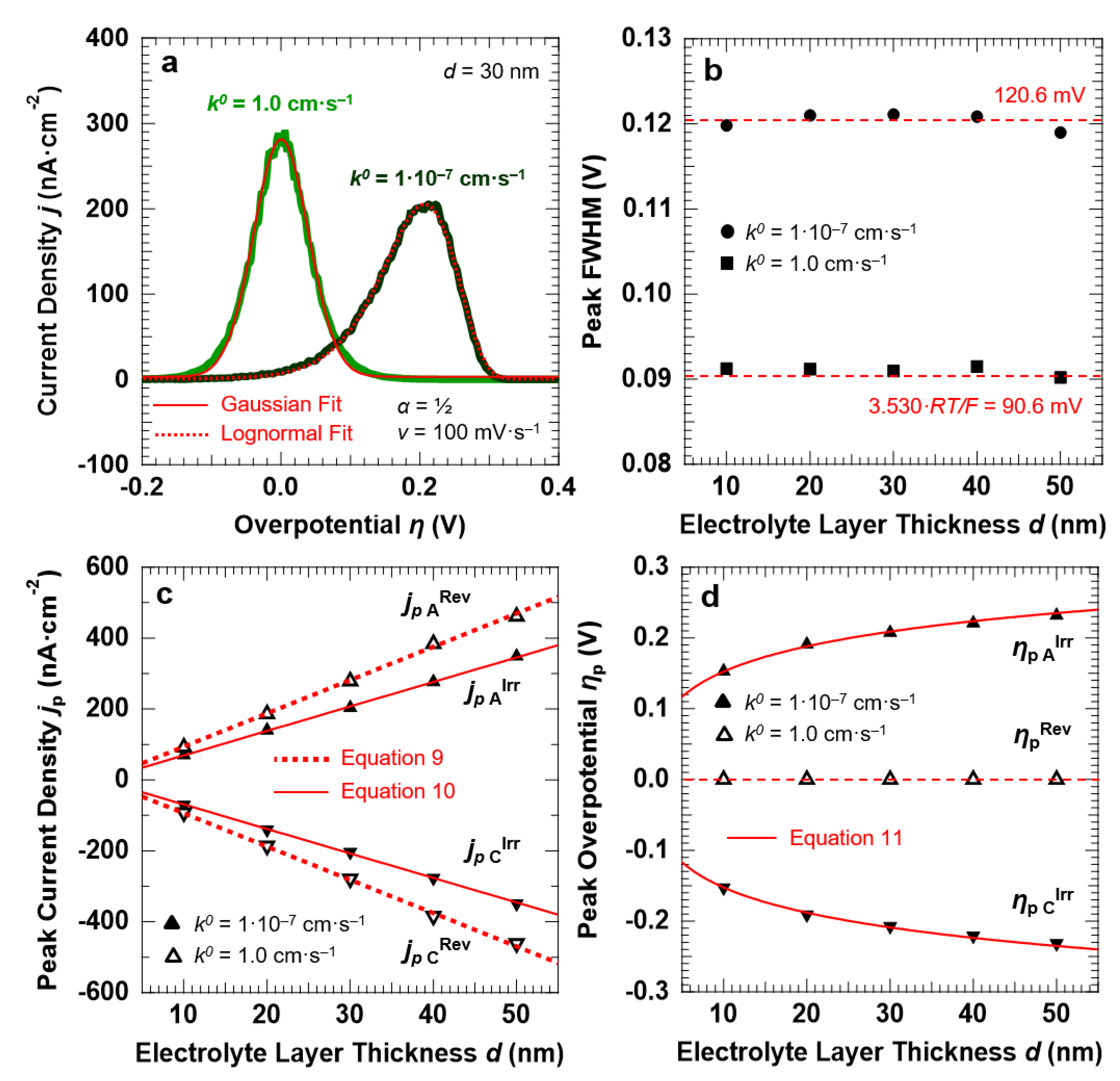
3.1. Voltammetric Response of the “Confined Interface” for a Symmetric (α = ½) ET as a Function of d (v = 100 mV·s−1)
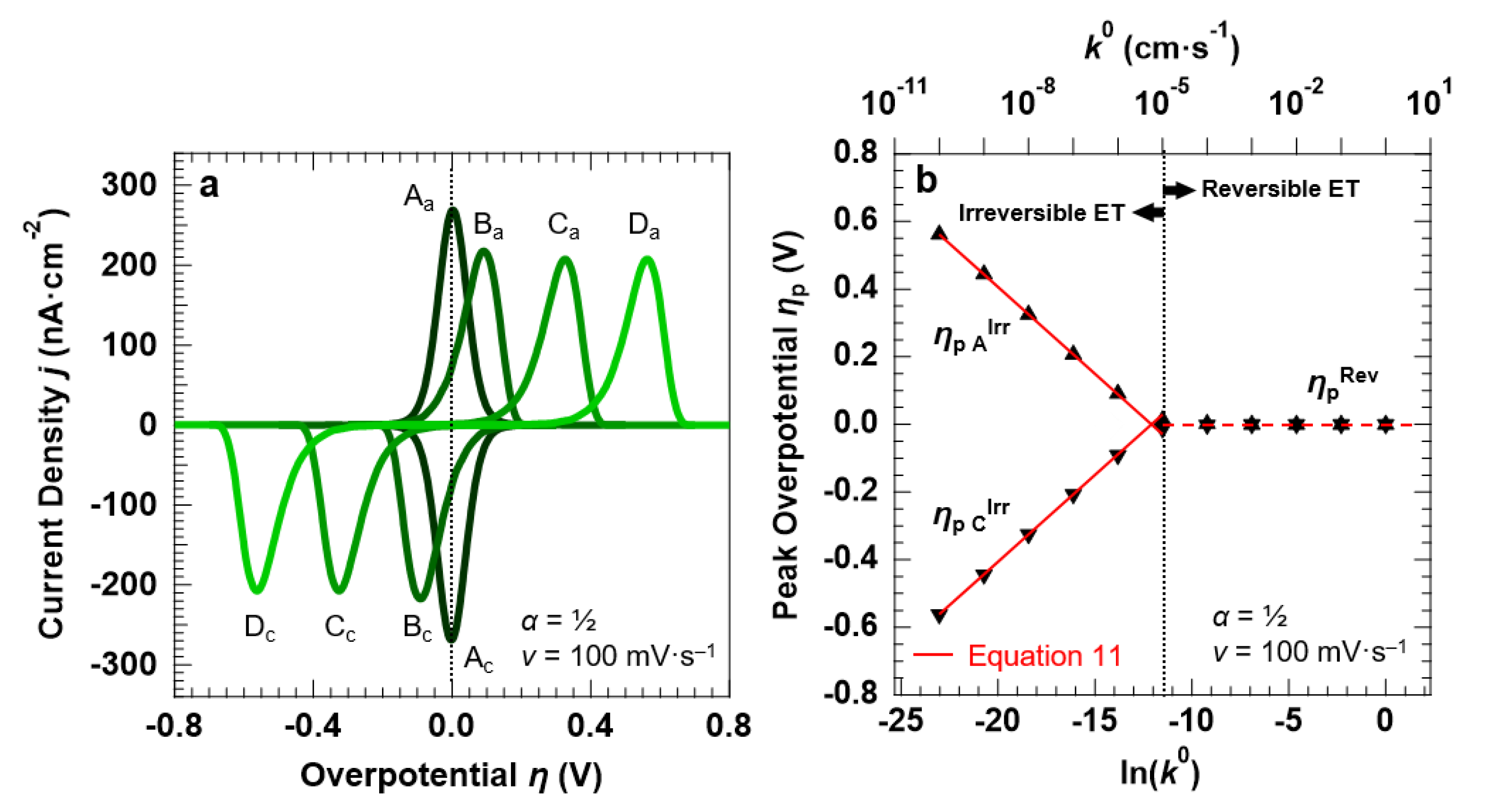
3.2. Voltammetric Response of the “Confined Interface” (d = 30 nm) for a Symmetric ET (α = ½) as a Function of k0
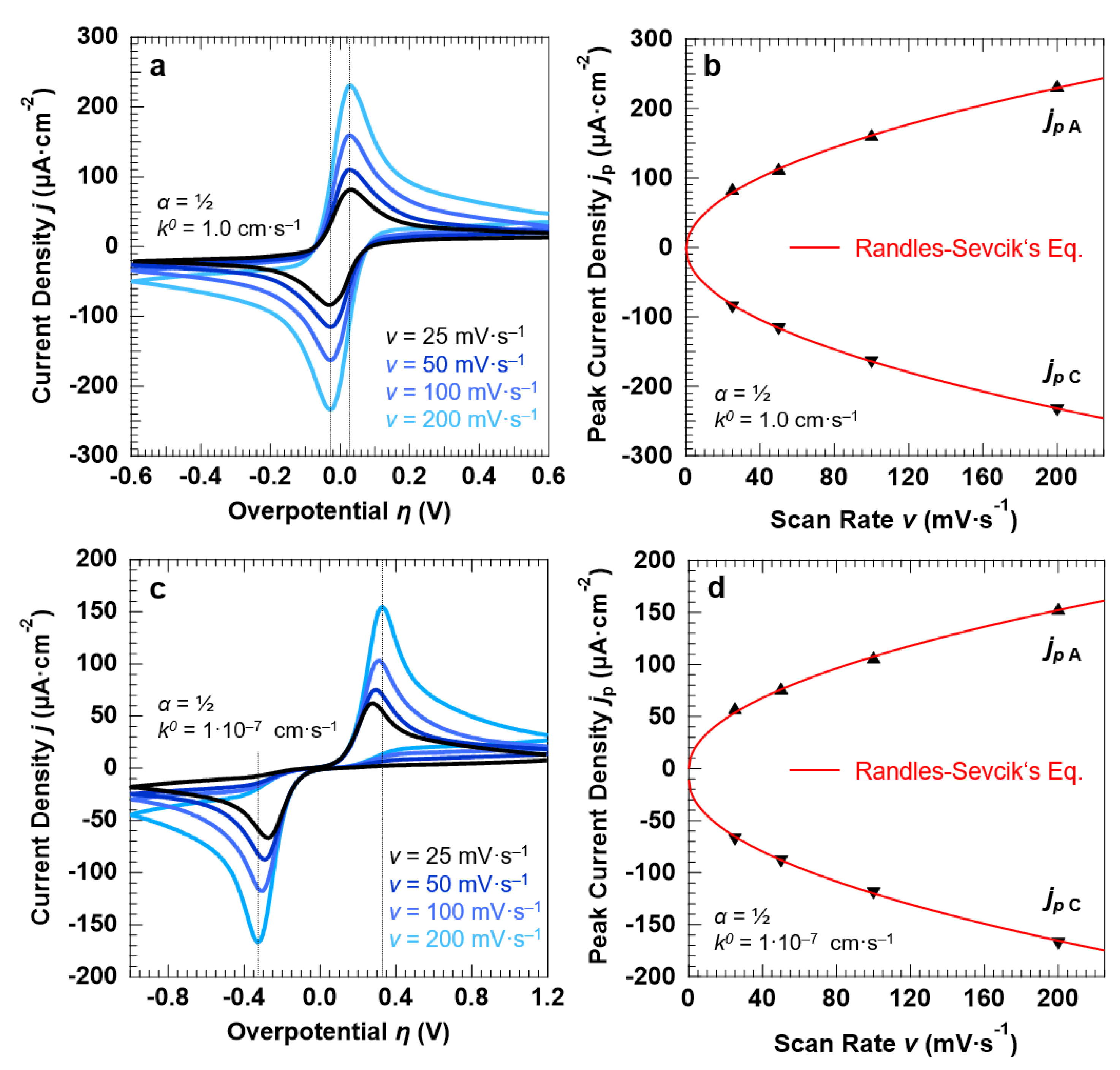
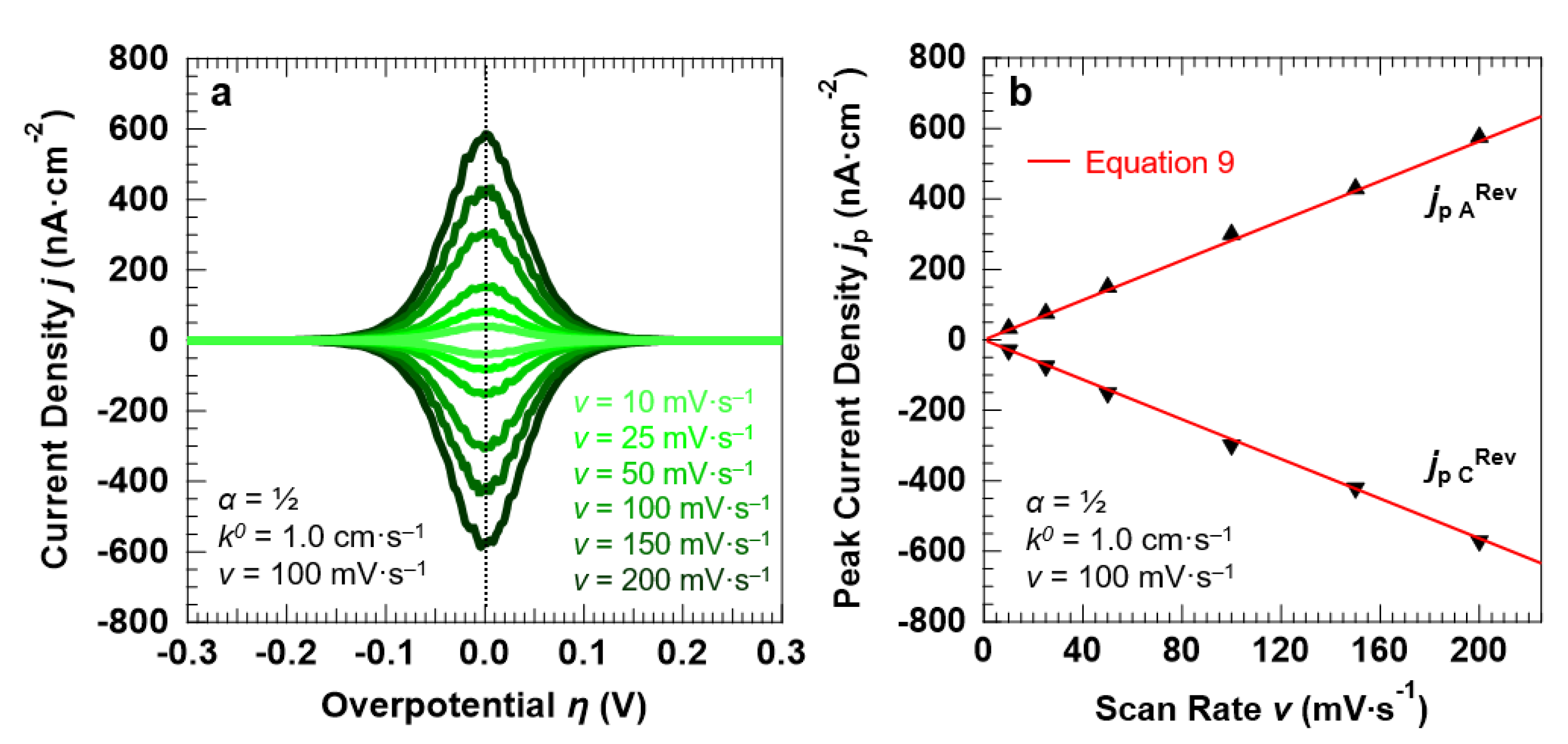
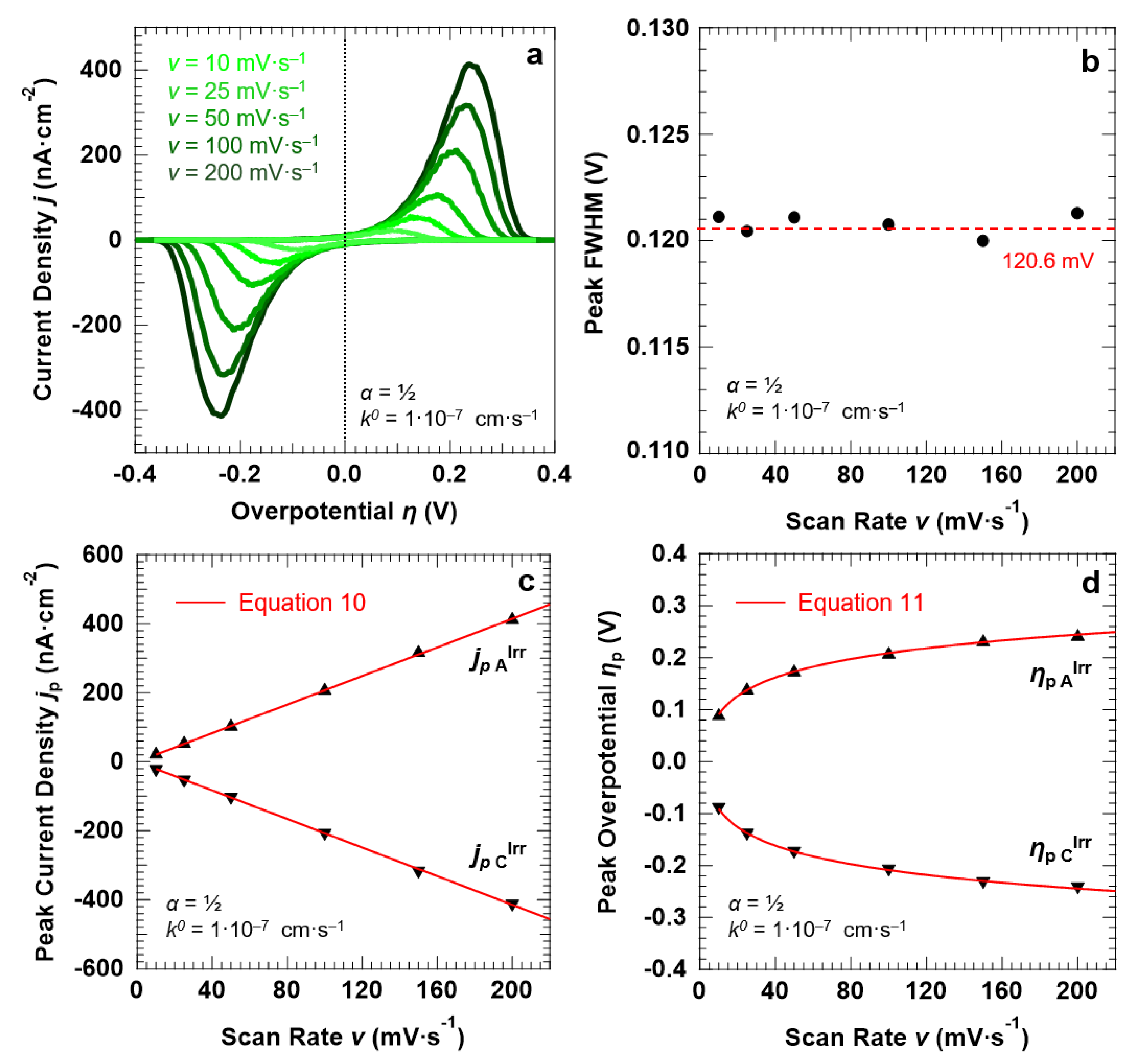
3.3. Voltammetric Response of the “Confined Interface” (d = 30 nm) for a Symmetric (α = ½) ET as a Function of v
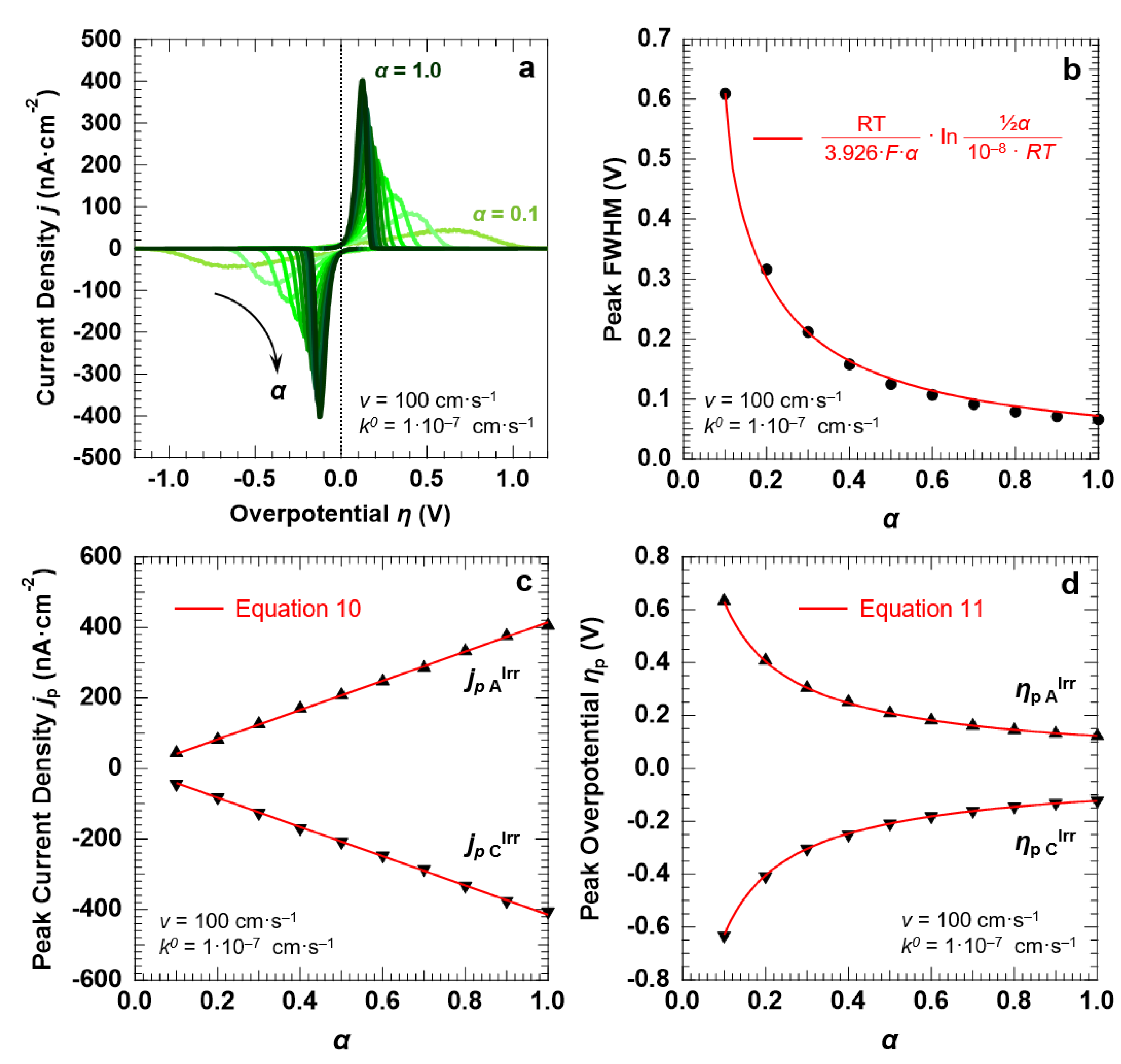
3.4. Voltammetric Response of the “Confined Interface” (d = 30 nm) for an Irreversible ET (k0 = 1.0 × 10−7 cm·s−1) as a Function of α
4. Conclusions
- We show that the electrochemical response of nanometer-sized interfaces can be described with the thin-layer voltammetry theory originally elaborated by Hubbard for liquid layer thicknesses spanning from tens to hundreds of micrometers. For both space scales, the common dominant factor is that the diffusion of reactants is confined to the direction orthogonal to the interface. This is in agreement with our recent experimental work where the oxygen evolution reaction (OER) was investigated on a poly crystalline Pt surface immersed in 1.0M KOH aqueous solution [32]. Under those conditions, the hydroxyl anions present in the solution were depleted from the thin liquid layer due to the ongoing oxidation to molecular oxygen, eventually causing the loss of potential control at the interface [32]. We concluded that the applied overpotential (~700 mV with respect to the thermodynamic water oxidation potential, +1.23 V vs. RHE) sustained an electrolyte consumption rate in the thin electrolyte layer that was not counterbalanced on the same time scale by the diffusion rate from the macroscopic liquid meniscus.
- We investigated the confined interface by simulating reversible and irreversible electron transfer processes as a function of the liquid layer thickness. For irreversible electron transfers, we find that the current density and the line shape of the voltammetric features are strongly dependent on the symmetry of the reactant and product free energy curves around the energy barrier. In addition, for both types of electron transfers, we observe that the current density is a linear function of the liquid layer thickness, and that the peak current density values are on the order of hundreds of nA·cm−2 at most. It is noteworthy to compare this value with the one experimentally retrieved using two different working electrode configurations, as reported in ref. [13]: the first preserved the usual “dip and pull” geometry [7,13], while in the second one the bottom part of the sample immersed in the electrolyte was masked to approximate the current density reached at the “confined interface” [13]. We determined a current density ratio between the two experimental configurations of about 3, with the current density for the “masked” working electrode reaching some hundreds of μA·cm−2 at most [13]. The discrepancy between this value and the one obtained in this work from the stochastic simulations can be easily explained in terms of the macroscopic liquid meniscus still present on the “masked” electrode, ensuring the necessary electrochemical continuity between the electrolyte layer on the sample and the bulk solution [13]. We use the capillary length as a “yardstick” to characterize the curvature of the meniscus, finding a value of about 4 mm for the liquid water/water vapor interface at r.t [47]. Therefore, although showing an expected decreasing trend when passing from a “bulk” to a “confined interface”, the current density values found in ref. [13] are dominated by the presence of the meniscus and do not capture the true properties of electrolyte layers with thicknesses limited to few tens of nanometers.
Funding
Acknowledgments
Conflicts of Interest
References
- Salmeron, M.; Schlögl, R. Ambient pressure photoelectron spectroscopy: A new tool for surface science and nanotechnology. Surf. Sci. Rep. 2008, 63, 169–199. [Google Scholar] [CrossRef] [Green Version]
- Crumlin, E.J.; Bluhm, H.; Liu, Z. In situ investigation of electrochemical devices using ambient pressure photoelectron spectroscopy. J. Electr. Spectr. Relat. Phenom. 2013, 190, 84–92. [Google Scholar] [CrossRef]
- Liu, X.; Yang, W.; Liu, Z. Recent progress on synchrotron-based in-situ soft X-ray spectroscopy for energy materials. Adv. Mater. 2014, 26, 7710–7729. [Google Scholar] [CrossRef] [PubMed]
- Crumlin, E.J.; Liu, Z.; Bluhm, H.; Yang, W.; Guo, J.; Hussain, Z. X-ray spectroscopy of energy materials under in situ/operando conditions. J. Elect. Spectr. Relat. Phenom. 2015, 200, 264–273. [Google Scholar] [CrossRef] [Green Version]
- Roy, K.; Artiglia, L.; van Bokhoven, J.A. Ambient Pressure Photoelectron Spectroscopy: Opportunities in Catalysis from Solids to Liquids and Introducing Time Resolution. Chem. Cat. Chem. 2018, 10, 666–682. [Google Scholar] [CrossRef]
- Lewerenz, H.-J.; Lichterman, M.F.; Richter, M.H.; Crumlin, E.J.; Hu, S.; Axnanda, S.; Favaro, M.; Drisdell, W.; Hussain, Z.; Brunschwig, B.S.; et al. Operando analyses of solar fuels light absorbers and catalysts. Electrochim. Acta 2016, 211, 711–719. [Google Scholar] [CrossRef] [Green Version]
- Favaro, M.; Abdi, F.F.; Crumlin, E.J.; Liu, Z.; van de Krol, R.; Starr, D.E. Interface science using ambient pressure hard X-ray photoelectron spectroscopy. Surfaces 2019, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Bluhm, H. Liquid/solid interfaces studied by ambient pressure HAXPES. In Hard X-ray Photoelectron Spectroscopy (HAXPES), 1st ed.; Woicik, J., Ed.; Springer: Cham, Switzerland, 2016; pp. 447–466. ISBN 978-3-319-24043-5. [Google Scholar]
- Axnanda, S.; Crumlin, E.J.; Mao, B.; Rani, S.; Chang, R.; Karlsson, P.G.; Edwards, M.O.M.; Lundqvist, M.; Moberg, R.; Ross, P.N.; et al. Using “tender” X-ray ambient pressure X-ray photoelectron spectroscopy as a direct probe of solid-liquid interface. Sci. Rep. 2015, 5, 9788. [Google Scholar] [CrossRef]
- Karslıoğlu, O.; Nemšák, S.; Zegkinoglou, I.; Shavorskiy, A.; Hartl, M.; Salmassi, F.; Gullikson, E.M.; Ng, M.L.; Rameshan, C.; Rude, B.; et al. Aqueous solution/metal interfaces investigated in operando by photoelectron spectroscopy. Faraday Discuss. 2015, 180, 35–53. [Google Scholar] [CrossRef] [Green Version]
- Favaro, M.; Jeong, B.; Ross, P.N.; Yano, J.; Hussain, Z.; Liu, Z.; Crumlin, E.J. Unravelling the electrochemical double layer by direct probing of the solid/liquid interface. Nat. Commun. 2016, 7, 12695. [Google Scholar] [CrossRef]
- Favaro, M.; Drisdell, W.S.; Marcus, M.A.; Gregoire, J.M.; Crumlin, E.J.; Haber, J.A.; Yano, J. An operando investigation of (Ni–Fe–Co–Ce)Ox system as highly efficient electrocatalyst for oxygen evolution reaction. ACS Catal. 2017, 7, 1248–1258. [Google Scholar] [CrossRef] [Green Version]
- Favaro, M.; Valero-Vidal, C.; Eichhorn, J.; Toma, F.M.; Ross, P.N.; Yano, J.; Liu, Z.; Crumlin, E.J. Elucidating the alkaline oxygen evolution reaction mechanism on platinum. J. Mater. Chem. A 2017, 5, 11634–11643. [Google Scholar] [CrossRef] [Green Version]
- Favaro, M.; Yang, J.; Nappini, S.; Magnano, E.; Toma, F.M.; Crumlin, E.J.; Yano, J.; Sharp, I.D. Understanding the oxygen evolution reaction mechanism on CoOx using operando ambient-pressure X-ray photoelectron spectroscopy. J. Am. Chem. Soc. 2017, 139, 8960–8970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shavorskiy, A.; Ye, X.; Karslıoğlu, O.; Poletayev, A.D.; Hartl, M.; Zegkinoglou, I.; Trotochaud, L.; Nemšák, S.; Schneider, C.M.; Crumlin, E.J.; et al. Direct mapping of band positions in doped and undoped hematite during photoelectrochemical water splitting. J. Phys. Chem. Lett. 2017, 8, 5579–5586. [Google Scholar] [CrossRef] [Green Version]
- Calvillo, L.; Fittipaldi, D.; Rüdiger, C.; Agnoli, S.; Favaro, M.; Valero-Vidal, C.; Di Valentin, C.; Vittadini, A.; Bozzolo, N.; Jacomet, S.; et al. Carbothermal Transformation of TiO2 into TiOxCy in UHV: Tracking Intrinsic Chemical Stabilities. J. Phys. Chem. C 2014, 118, 22601–22610. [Google Scholar] [CrossRef]
- Stoerzinger, K.A.; Favaro, M.; Ross, P.N.; Yano, J.; Liu, Z.; Hussain, Z.; Crumlin, E.J. Probing the Surface of Platinum during the Hydrogen Evolution Reaction in Alkaline Electrolyte. J. Phys. Chem. B 2018, 122, 864–870. [Google Scholar] [CrossRef] [Green Version]
- Gokturk, P.A.; Camci, M.T.; Suzer, S. Lab-based operando x-ray photoelectron spectroscopy for probing low-volatile liquids and their interfaces across a variety of electrosystems. J. Vac. Sci. Technol. A 2020, 38, 040805. [Google Scholar] [CrossRef]
- Novotny, Z.; Aegerter, D.; Comini, N.; Tobler, B.; Artiglia, L.; Maier, U.; Moehl, T.; Fabbri, E.; Huthwelker, T.; Schmidt, T.J.; et al. Probing the solid–liquid interface with tender x rays: A new ambient-pressure x-ray photoelectron spectroscopy endstation at the Swiss Light Source. Rev. Sci. Instrum. 2020, 91, 023103. [Google Scholar] [CrossRef]
- Starr, D.E.; Favaro, M.; Abdi, F.F.; Bluhm, D.; Crumlin, E.J.; van de Krol, R. Combined soft and hard X-ray ambient pressure photoelectron spectroscopy studies of semiconductor/electrolyte interfaces. J. Elect. Spectr. Relat. Phenom. 2017, 221, 106–115. [Google Scholar] [CrossRef] [Green Version]
- Velasco-Vélez, J.J.; Pfeifer, V.; Hävecker, M.; Wang, R.; Centeno, A.; Zurutuza, A.; Algara-Siller, G.; Stotz, E.; Skorupska, K.; Teschner, D.; et al. Atmospheric pressure X-ray photoelectron spectroscopy apparatus: Bridging the pressure gap. Rev. Sci. Instrum. 2016, 87, 053121. [Google Scholar] [CrossRef]
- Velasco-Vélez, J.J.; Pfeifer, V.; Hävecker, M.; Weatherup, R.S.; Arrigo, R.; Chuang, C.-H.; Stotz, E.; Weinberg, G.; Salmeron, M.; Schlögl, R.; et al. Photoelectron spectroscopy at the graphene-liquid interface reveals the electronic structure of an electrodeposited cobalt/graphene electrocatalyst. Angew. Chem. Int. Ed. 2015, 54, 14554–14558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rik, M.; Frevel, L.; Velasco-Vélez, J.J.; Plodinec, M.; Knop-Gericke, A.; Schlögl, R. The Oxidation of Platinum under Wet Conditions Observed by Electrochemical X-ray Photoelectron Spectroscopy. J. Am. Chem. Soc. 2019, 141, 6537–6544. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Velez, J.-J.; Mom, R.V.; Sandoval-Diaz, L.-E.; Falling, L.J.; Chuang, C.-H.; Gao, D.; Jones, T.E.; Zhu, Q.; Arrigo, R.; Roldan Cuenya, B.; et al. Revealing the Active Phase of Copper during the Electroreduction of CO2 in Aqueous Electrolyte by Correlating In Situ X-ray Spectroscopy and In Situ Electron Microscopy. ACS Energy Lett. 2020, 5, 2106–2111. [Google Scholar] [CrossRef] [PubMed]
- Lichterman, M.F.; Hu, S.; Richter, M.H.; Crumlin, E.J.; Axnanda, S.; Favaro, M.; Drisdell, W.; Hussain, Z.; Mayer, T.; Brunschwig, B.S.; et al. Direct observation of the energetics at a semiconductor/liquid junction by operando X-ray photoelectron spectroscopy. Energy Environ. Sci. 2015, 8, 2409–2416. [Google Scholar] [CrossRef] [Green Version]
- Kolb, D.M.; Hansen, W.N. Electroreflectance spectra of emersed metal electrodes. Surf. Sci. 1979, 79, 205–211. [Google Scholar] [CrossRef]
- Hansen, W.N. Electrode resistance and the emersed double layer. Surf. Sci. 1980, 101, 109–122. [Google Scholar] [CrossRef]
- Kolb, D.M.; Rath, D.L.; Wille, R.; Hansen, W.N. An ESCA study on the electrochemical double layer of emersed electrodes. Ber. Bunsenges. Phys. Chem. 1983, 87, 1108. [Google Scholar] [CrossRef]
- Siegbahn, H. Electron spectroscopy for chemical analysis of liquids and solutions. J. Phys. Chem. 1985, 89, 897–909. [Google Scholar] [CrossRef]
- Weingarth, D.; Foelske-Schmitz, A.; Wokaun, A.; Kötz, R. In situ electrochemical XPS study of the Pt/[EMIM][BF4] system. Electrochem. Comm. 2011, 13, 619–622. [Google Scholar] [CrossRef]
- Booth, S.G.; Tripathi, A.M.; Strashnov, I.; Dryfe, R.A.W.; Walton, A.S. The offset droplet: A new methodology for studying the solid/water interface using X-ray photoelectron spectroscopy. J. Phys. Condens. Matter 2017, 29, 454001. [Google Scholar] [CrossRef] [Green Version]
- Stoerzinger, K.A.; Favaro, M.; Ross, P.N.; Hussain, Z.; Liu, Z.; Yano, J.; Crumlin, E.J. Stabilizing the meniscus for operando characterization of platinum during the electrolyte-consuming alkaline oxygen evolution reaction. Top. Catal. 2018, 61, 2152–2160. [Google Scholar] [CrossRef] [Green Version]
- Favaro, M.; Abdi, F.F.; Lamers, M.; Crumlin, E.J.; Liu, Z.; van de Krol, R.; Starr, D.E. Light-induced surface reactions at the bismuth vanadate/potassium phosphate interface. J. Phys. Chem. B 2018, 122, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Kinetiscope Web Site. Available online: http://hinsberg.net/kinetiscope/index.html (accessed on 7 August 2020).
- Hubbard, A.T. Study of the kinetics of electrochemical reactions by thin-layer voltammetry: I. Theory. J. Electroanal. Chem. 1969, 22, 165–174. [Google Scholar] [CrossRef]
- Houle, F.A.; Hinsberg, W.D.; Morrison, M.; Sanchez, M.I.; Wallraff, G.; Larson, C.; Hoffnagle, J. Determination of coupled acid catalysis-diffusion processes in a positive-tone chemically amplified photoresist. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2000, 18, 1874. [Google Scholar] [CrossRef]
- Houle, F.A.; Hinsberg, W.D.; Sanchez, M.I. Kinetic Model for Positive Tone Resist Dissolution and Roughening. Macromolecules 2002, 35, 8591–8600. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2001; Appendix B; ISBN 13 978-0-471-04372-0. [Google Scholar]
- Wiegel, A.A.; Wilson, K.R.; Hinsberg, W.D.; Houle, F.A. Stochastic methods for aerosol chemistry: A compact molecular description of functionalization and fragmentation in the heterogeneous oxidation of squalane aerosol by OH radicals. Phys. Chem. Chem. Phys. 2015, 17, 4398–4411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, L.L. Molecular Thermodynamics of Electrolyte Solutions; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2008; Chapter 11; ISBN 13 978-981-281-418-0. [Google Scholar]
- Archer, G.G.; Wang, P. The Dielectric Constant of Water and Debye-Hückel Limiting Law Slopes. J. Phys. Chem. Ref. Data 1990, 19, 371–411. [Google Scholar] [CrossRef] [Green Version]
- Bauer, H.H. The electrochemical transfer-coefficient. J. Electroanal. Chem. Interf. Electrochem. 1968, 16, 419–432. [Google Scholar] [CrossRef]
- Salbeck, J. An electrochemical cell for simultaneous electrochemical and spectroelectrochemical measurements under semi-infinite diffusion conditions and thin-layer conditions. J. Electroanal. Chem. 1992, 340, 169–195. [Google Scholar] [CrossRef]
- Favaro, M.; Perini, L.; Agnoli, S.; Durante, C.; Granozzi, G.; Gennaro, G. Electrochemical behavior of N and Ar implanted highly oriented pyrolytic graphite substrates and activity toward oxygen reduction reaction. Electrochim. Acta 2013, 88, 477–487. [Google Scholar] [CrossRef]
- Favaro, M.; Agnoli, S.; Cattelan, M.; Moretto, A.; Durante, C.; Leonardi, S.; Kunze-Liebhäuser, J.; Schneider, O.; Gennaro, A.; Granozzi, G. Shaping graphene oxide by electrochemistry: From foams to self-assembled molecular materials. Carbon 2014, 77, 405–415. [Google Scholar] [CrossRef]
- Botasini, S.; Mendez, E. Limited Diffusion and Cell Dimensions in a Micrometer Layer of Solution: An Electrochemical Impedance Spectroscopy Study. Chem. Electro. Chem. 2017, 4, 1891–1895. [Google Scholar] [CrossRef]
- Boucher, E.A. Capillary phenomena: Properties of systems with fluid/fluid interfaces. Rep. Prog. Phys. 1980, 43, 497–546. [Google Scholar] [CrossRef]
| Potential Scan Rate v (mV·s−1) | Potential Sweep Duration Δt (s) for ΔV = 1.2 V | Diffusion Layer Thickness l (µm) for ΔV = 1.2 V |
|---|---|---|
| 25 | 48 | 930 |
| 50 | 24 | 660 |
| 100 | 12 | 465 |
| 200 | 6 | 330 |
| Liquid Electrolyte Layer Thickness d (nm) | Δx Element 1 (EDL) (nm) 1 | Δx Elements 2–10 (nm) |
|---|---|---|
| 10 | 2.88 | 0.79 |
| 20 | 2.88 | 1.90 |
| 30 | 2.88 | 3.01 |
| 40 | 2.88 | 4.12 |
| 50 | 2.88 | 5.24 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favaro, M. Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces. Surfaces 2020, 3, 392-407. https://doi.org/10.3390/surfaces3030029
Favaro M. Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces. Surfaces. 2020; 3(3):392-407. https://doi.org/10.3390/surfaces3030029
Chicago/Turabian StyleFavaro, Marco. 2020. "Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces" Surfaces 3, no. 3: 392-407. https://doi.org/10.3390/surfaces3030029
APA StyleFavaro, M. (2020). Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces. Surfaces, 3(3), 392-407. https://doi.org/10.3390/surfaces3030029