Machine Learning Forecasting of Direct Solar Radiation: A Multi-Model Evaluation with Trigonometric Cyclical Encoding
Abstract
1. Introduction
2. Methodology
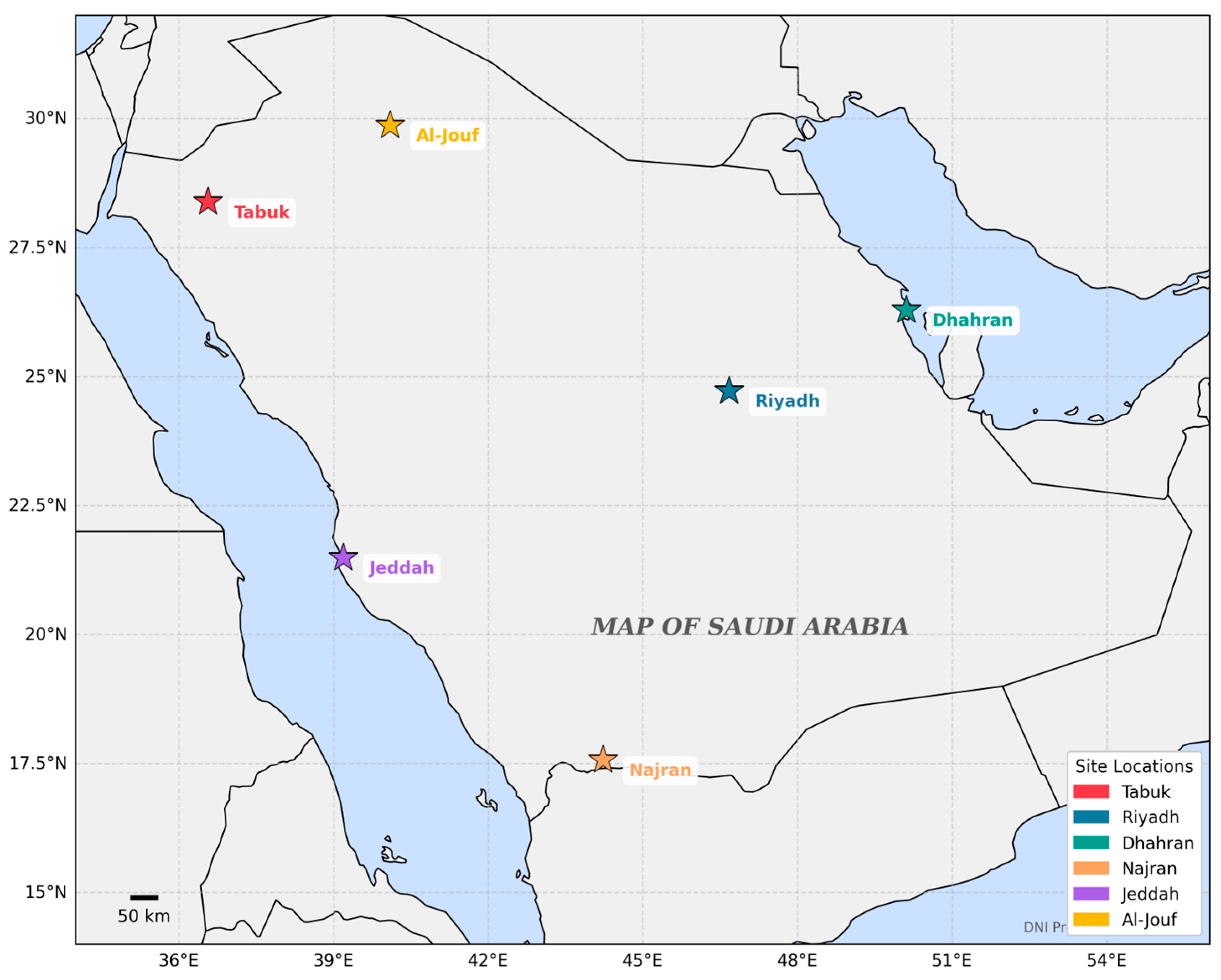
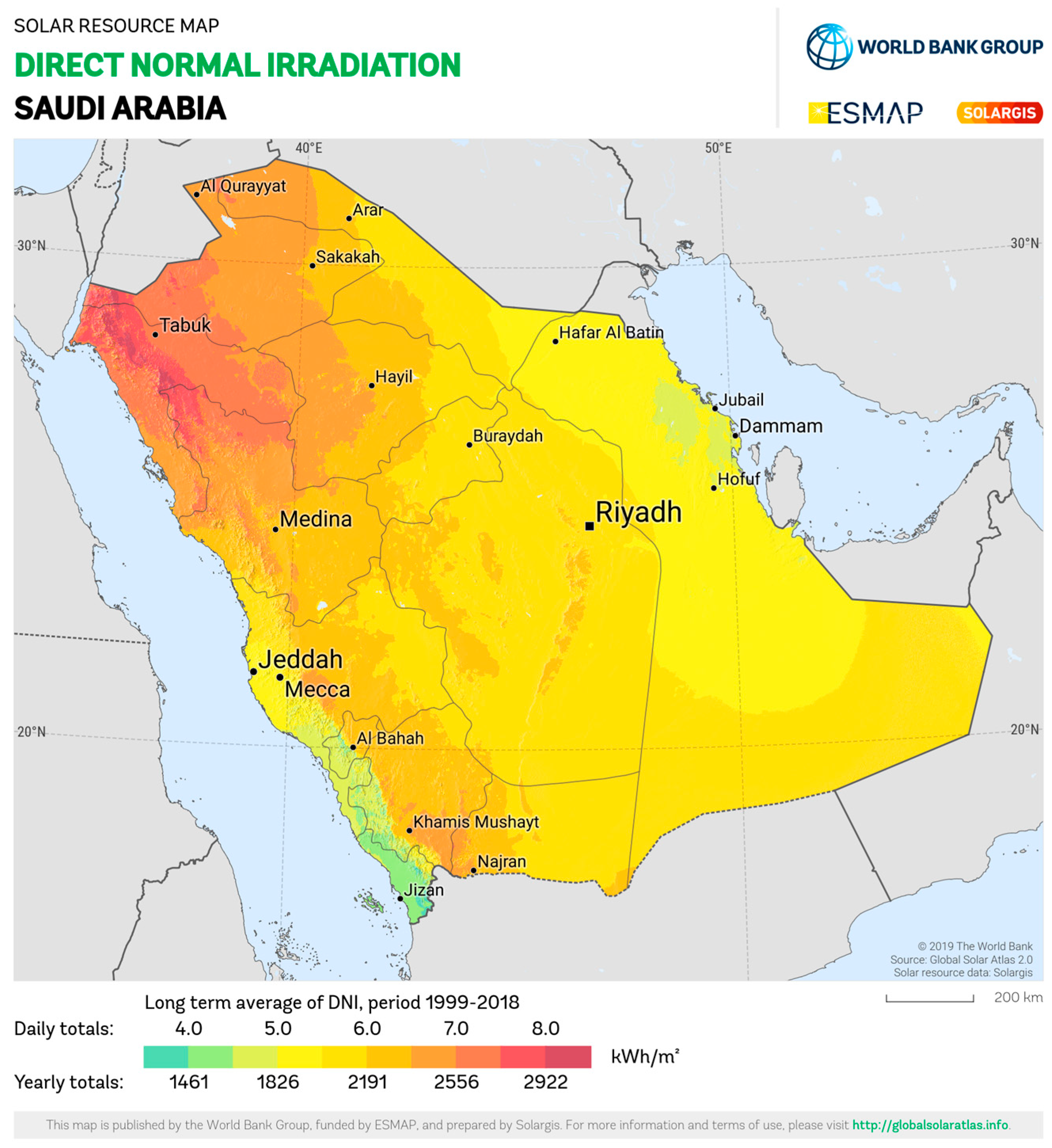
2.1. Case-Study Area Examination
2.2. Meteorological Data Overview
2.3. ML Algorithms
2.4. Hyperparameter Optimization
Deep Learning Model
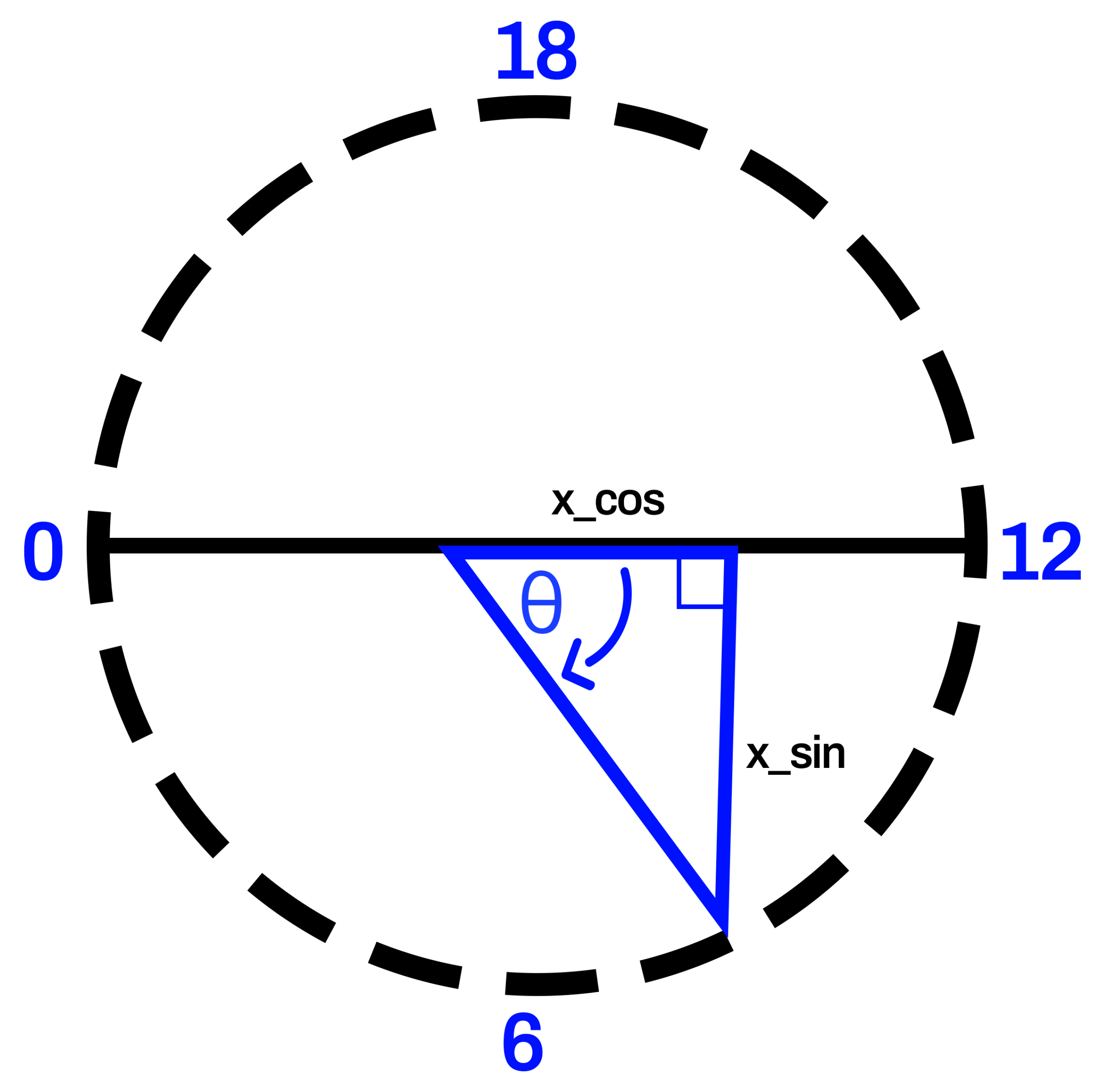
2.5. Trigonometric Cyclic Encoding (TCE)
2.6. Performance Metrics
3. Results
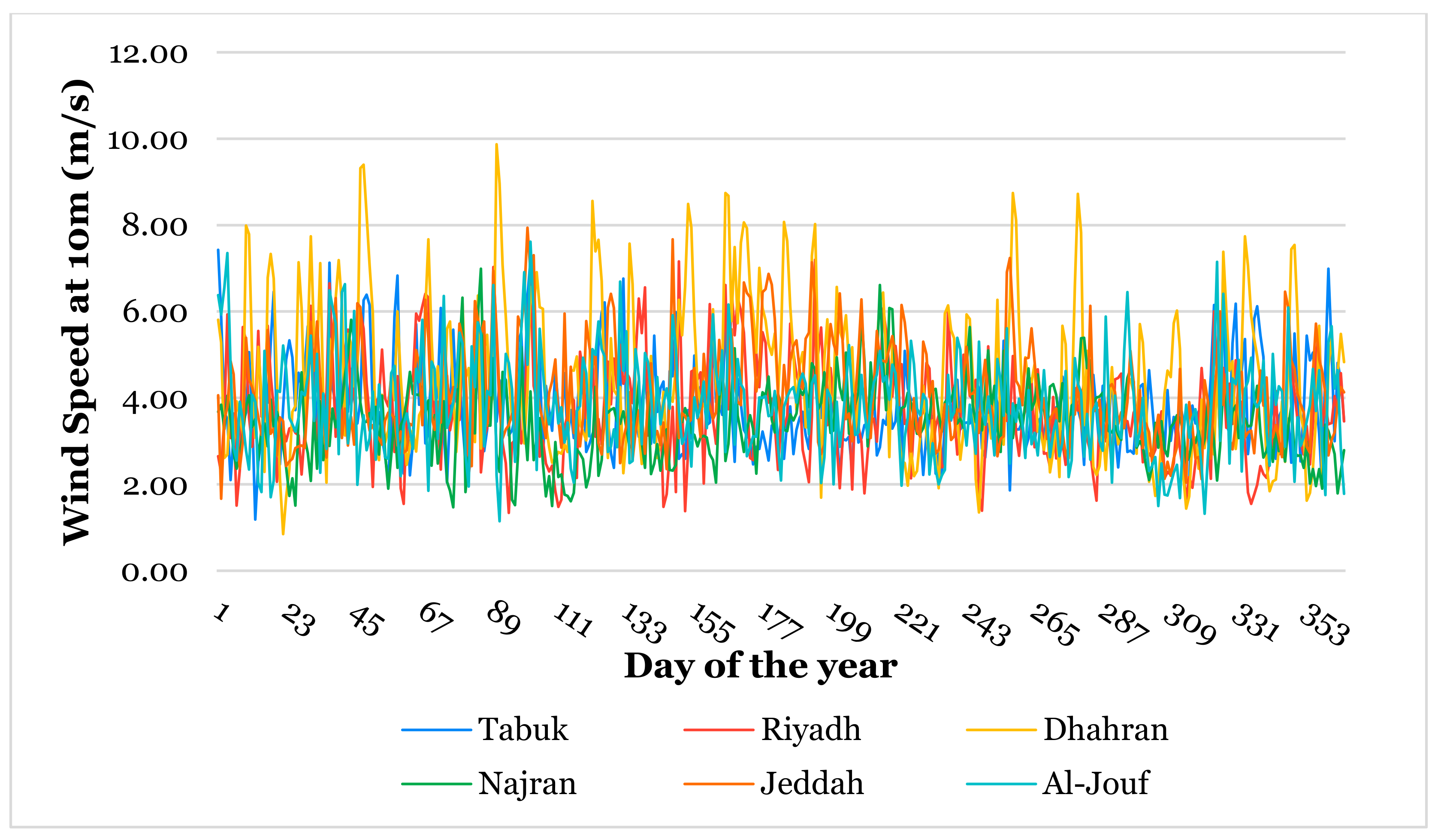
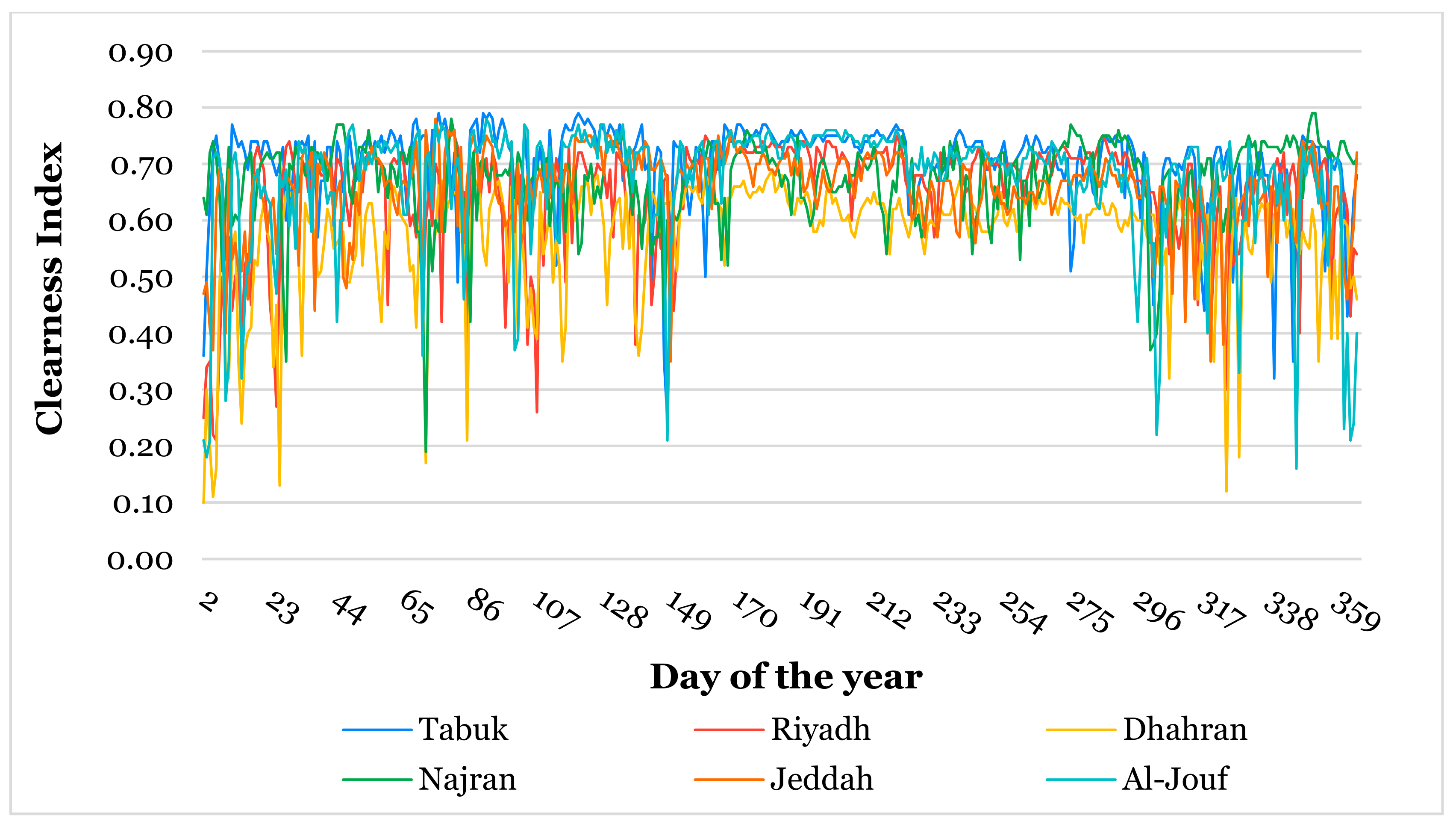
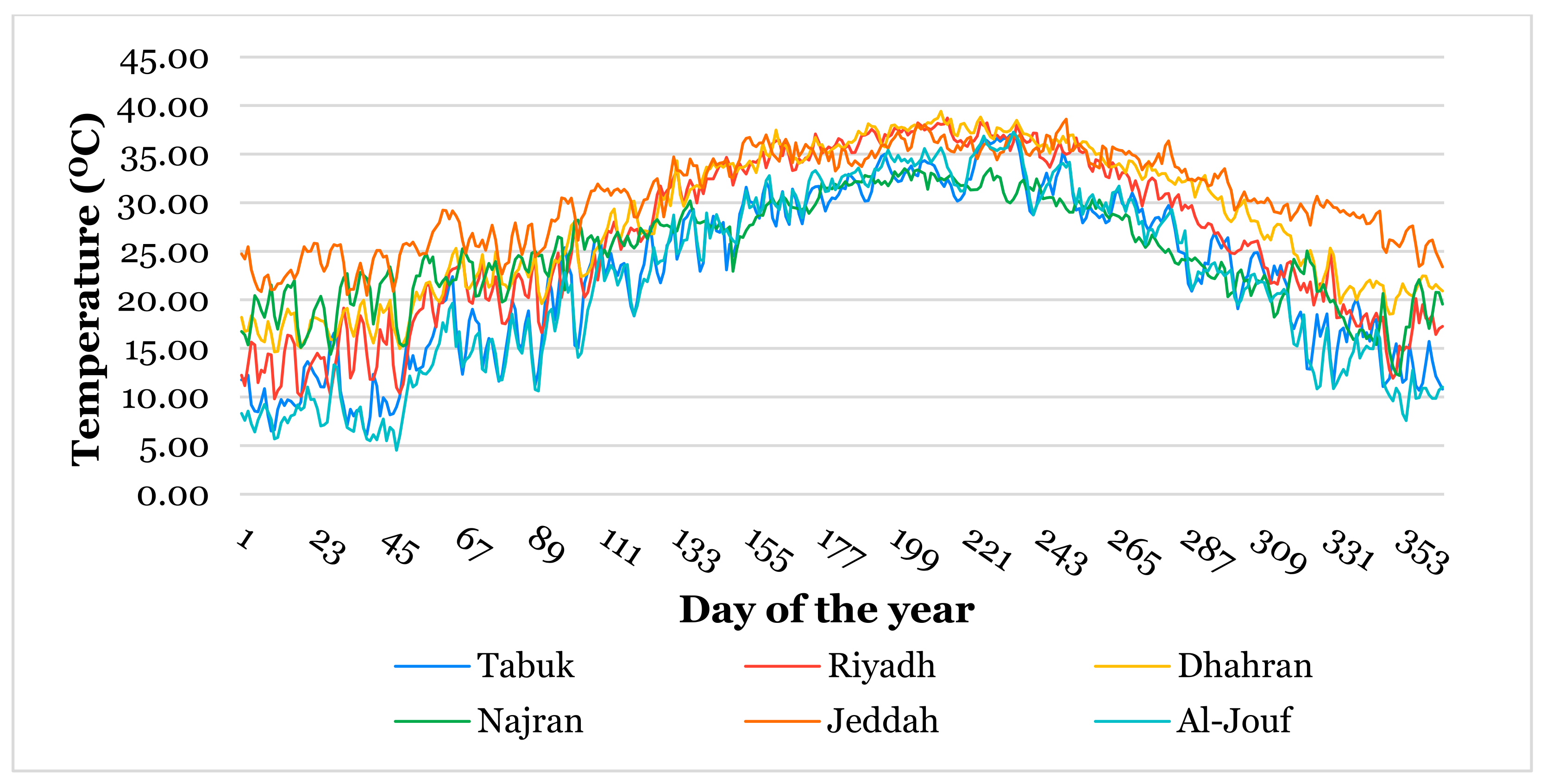
3.1. Temporal Patterns of DNI and Climatic Variables
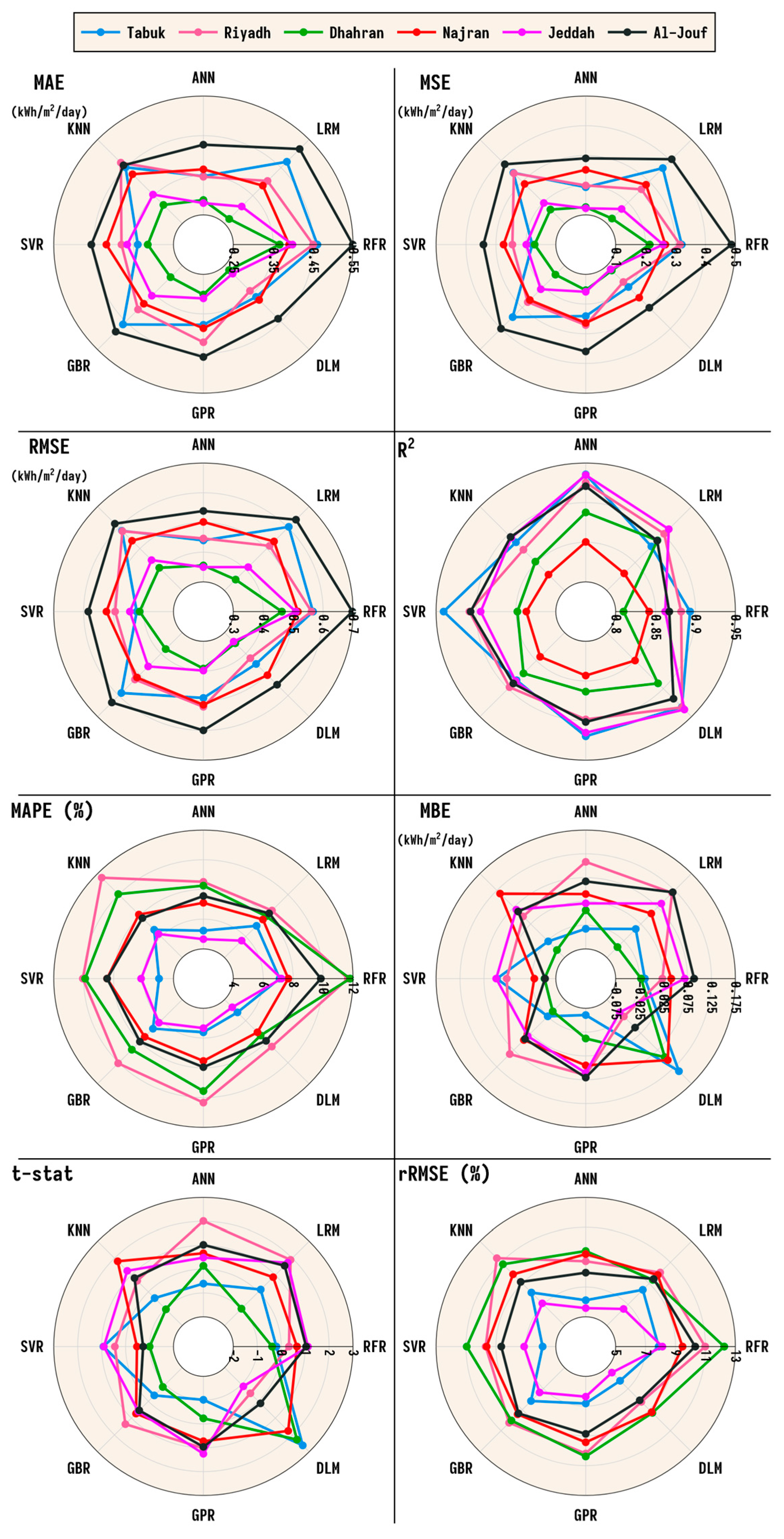
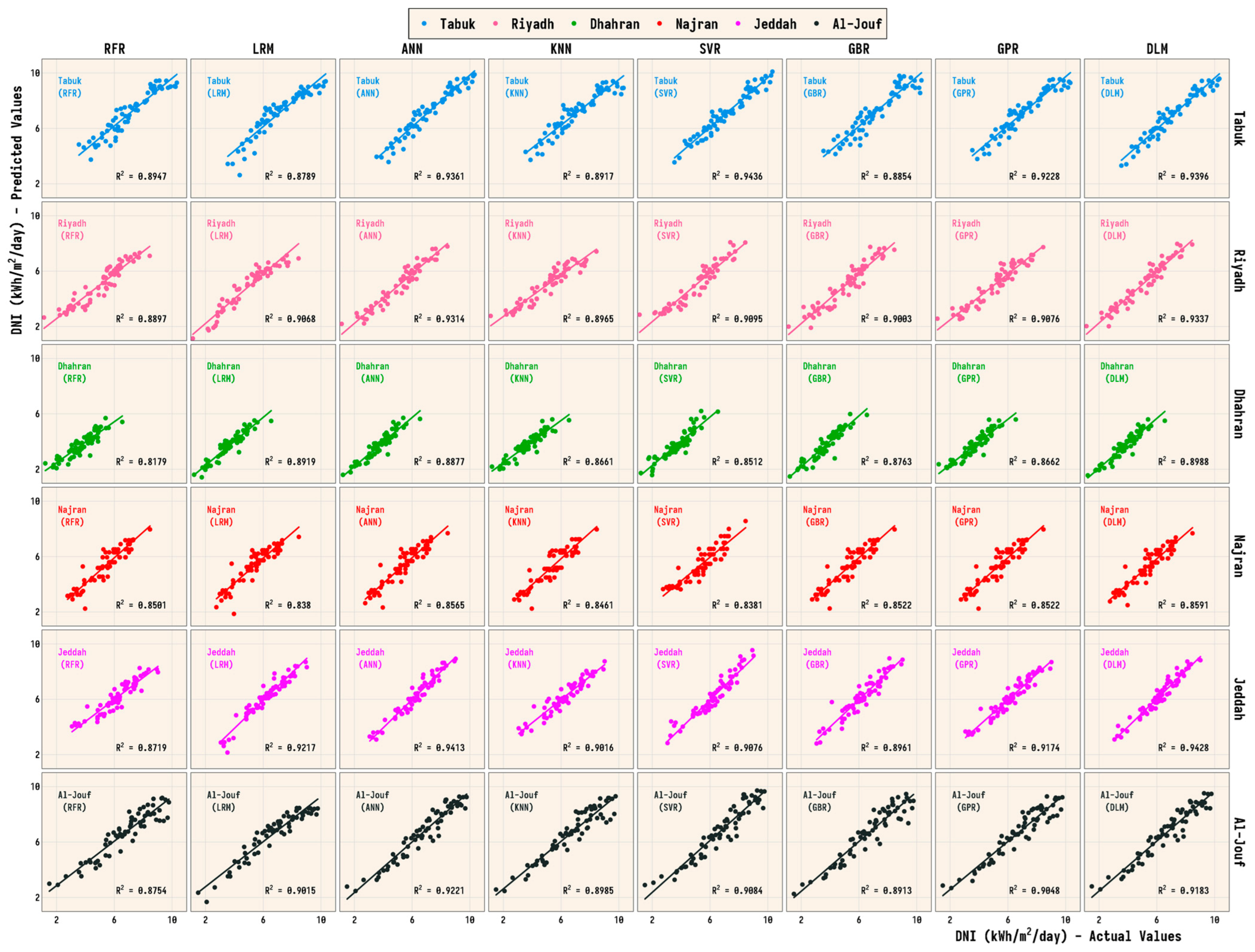
3.2. Model Performance Evaluation
3.2.1. Multi-Metric Evaluation
3.2.2. Multi-Site Evaluation
3.3. Temporal Performance Evaluation
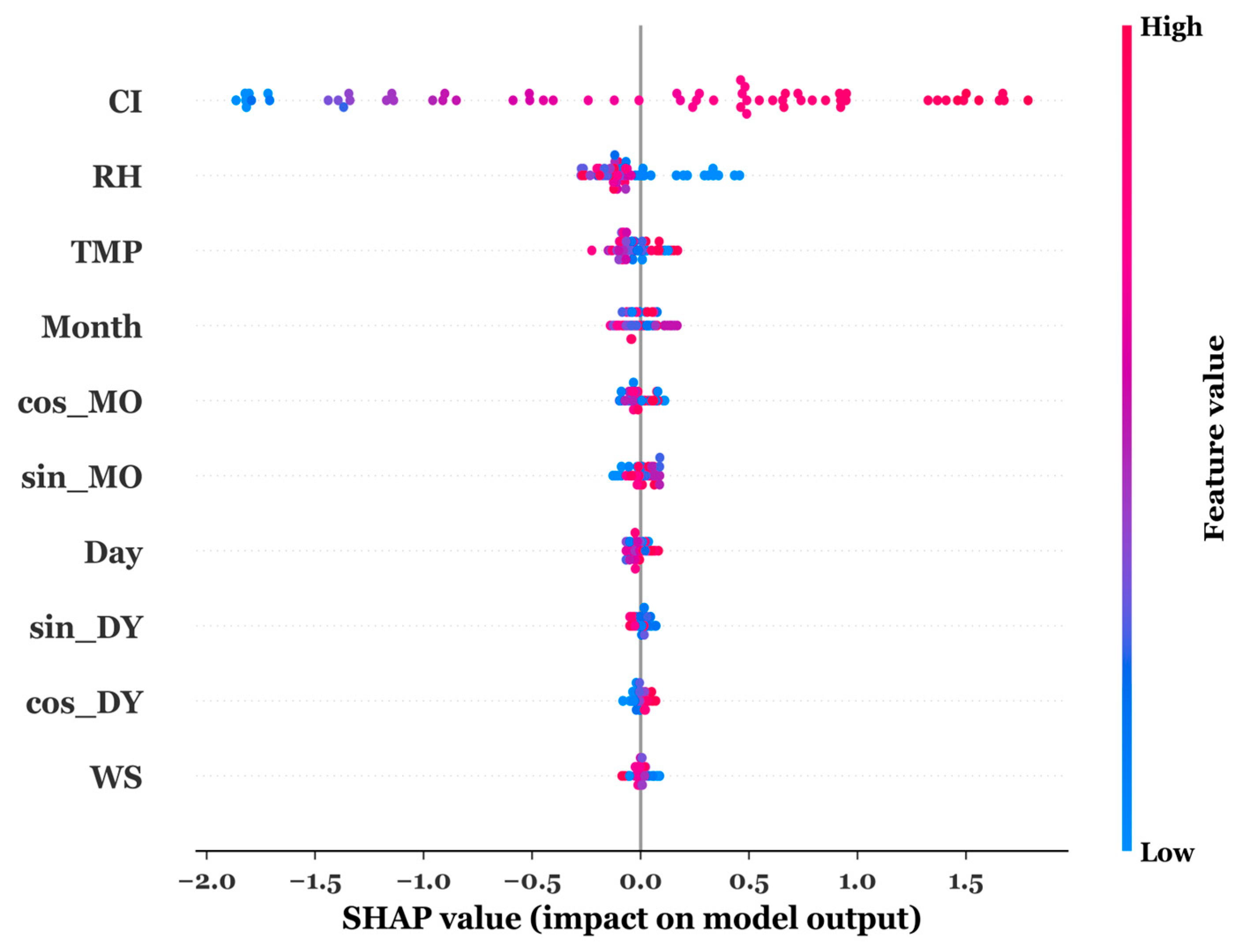
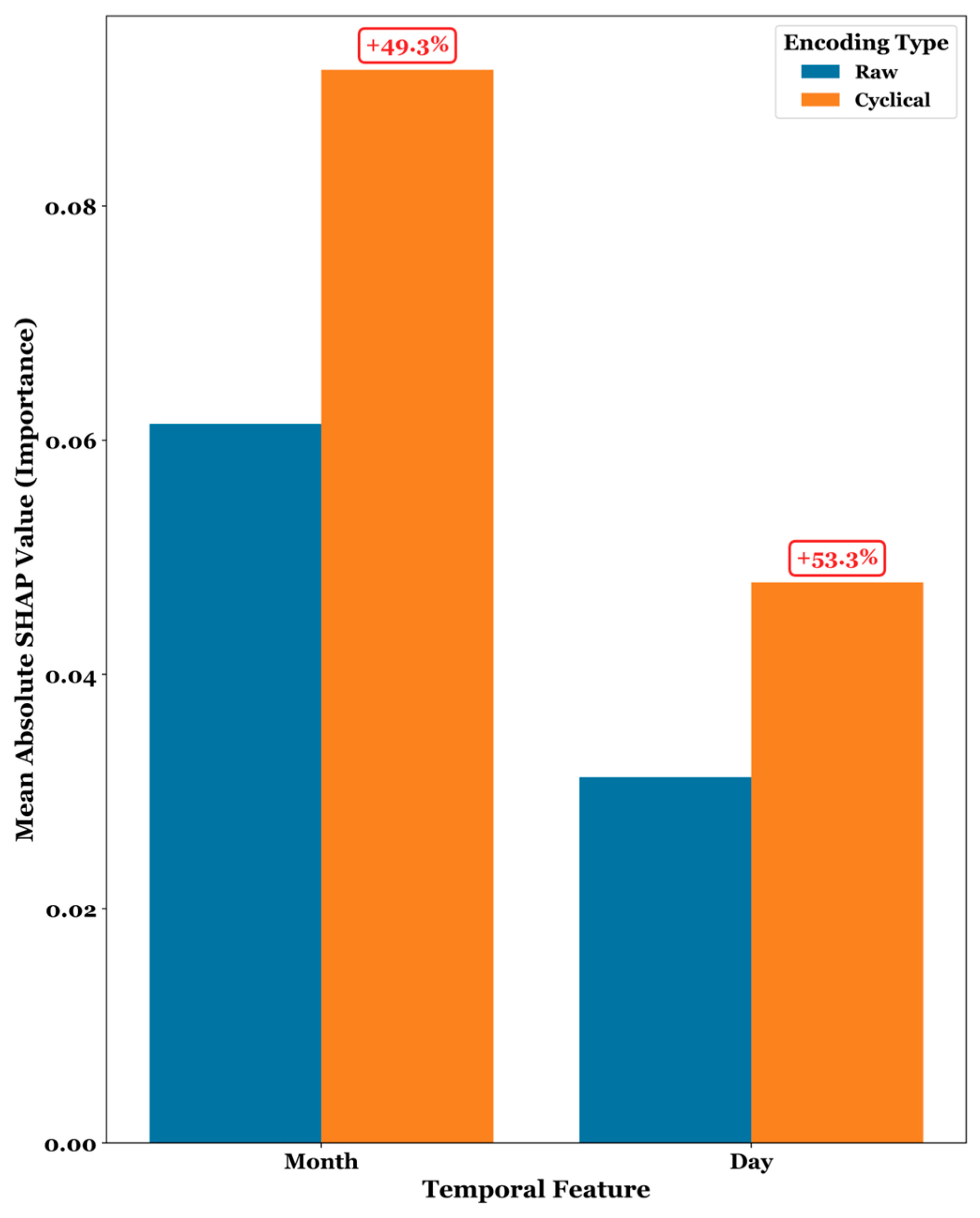
3.4. Impact of Trigonometric Cyclical Encoding (TCE)
4. Conclusions
- The Deep Learning (DNN) and Artificial Neural Network (ANN) models demonstrated superior and consistent performance across most locations, with DNN achieving the lowest RMSE (as low as 0.343 kWh/m2/day, in Jeddah) and ANN showing remarkable stability and low error rates (e.g., an MAPE of 7.10% in Najran).
- Model effectiveness was significantly influenced by geographical and climatic conditions. Support Vector Regression (SVR) excelled in specific arid inland regions like Riyadh and Tabuk, while other models, such as RFR and KNN, exhibited greater performance volatility.
- The implementation of Trigonometric Cyclical Encoding (TCE) for temporal features substantially enhanced model learning. A comparative analysis revealed that TCE increased the feature importance of temporal signals by over 49% for monthly cycles and 53% for daily cycles, enabling models to more effectively capture fundamental periodic patterns in solar radiation.
- Time-series and error analyses confirmed that ANN and DNN maintained the most stable prediction accuracy, particularly during high solar radiation seasons, whereas other models showed wider fluctuations.
Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADSSOA | Adaptive Dynamic Squirrel Search Optimization Algorithm |
| AI | Artificial Intelligence |
| CART | Classification And Regression Tree |
| DNI | Direct Normal Irradiance |
| DNN | Deep Neural Networks |
| DNR | Direct Normal Radiation |
| DSR | Direct Solar Radiation |
| DT | Decision Tree |
| FE | Feature Engineering |
| FS | Feature Selection |
| GA | Genetic Algorithm |
| GBM | Gradient Boosting Machine |
| GHI | Global Horizontal Irradiance |
| GPR | Gaussian Process Regression |
| GWO | Grey Wolf Optimizer |
| HHO | Harris Hawks Optimization |
| IEA | International Energy Agency |
| IRENA | International Renewable Energy Agency |
| KSA | Kingdom of Saudi Arabia |
| LR | Linear Regression |
| LSTNet | Learning Spectral Transformer Network |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| NASA | National Aeronautics and Space Administration |
| NLP | Natural Language Processing |
| POWER | Prediction of Worldwide Energy Resources |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| RF | Random Forest |
| RFE | Recursive Feature Elimination |
| RFR | Random Forest Regressor |
| RMSE | Root Mean Squared Error |
| R2 | R-squared |
| RTM | Referential Translation Machine |
| SDG | Sustainable Development Goal |
| SGDR | Stochastic Gradient Descent Regressor |
| SVR-BO | Support Vector Regression–Bayesian Optimization |
| TCE | Trigonometric Cyclic Encoding |
| UN | United Nations |
| XGBoost | Extreme Gradient Boosting |
References
- Margaritou, M.D.; Tzannatos, E. A multi-criteria optimization approach for solar energy and wind power technologies in shipping. FME Trans. 2018, 46, 374–380. [Google Scholar] [CrossRef]
- Bezari, S.; Bekkouche, S.M.E.A.; Benchatti, A. Investigation and Improvement for a Solar Greenhouse Using Sensible Heat Storage Material. FME Trans. 2020, 49, 154–162. [Google Scholar] [CrossRef]
- Rašuo, B.P.; Bengin, A.Č. Optimization of Wind Farm Layout. FME Trans. 2010, 38, 107–114. [Google Scholar]
- Rashid, L.B.; Musah, A.; Amoah, R.K. Technoeconomic Feasibility of Renewable Energy Systems for Sporting Stadiums. Int. J. Energy Res. 2025, 2025, 9701161. [Google Scholar] [CrossRef]
- Gojak, M.; Ljubinac, F.; Banjac, M. Simulation of solar water heating system. FME Trans. 2019, 47, 1–6. [Google Scholar] [CrossRef]
- Rašuo, B.; Dinulović, M.; Veg, A.; Grbović, A.; Bengin, A. Harmonization of new wind turbine rotor blades development process: A review. Renew. Sustain. Energy Rev. 2014, 39, 874–882. [Google Scholar] [CrossRef]
- Parezanovic, V.; Rasuo, B.; Adzic, M. Design of Airfoils for Wind Turbine Blades. 2006, 17–24. Available online: https://www.researchgate.net/publication/228608628_DESIGN_OF_AIRFOILS_FOR_WIND_TURBINE_BLADES (accessed on 18 June 2025).
- Stojicevic, M.; Jeli, Z.; Obradovic, M.; Obradovic, R.; Marinescu, G.C. Designs of solar concentrators. FME Trans. 2019, 47, 273–278. [Google Scholar] [CrossRef]
- Hussain, F.M.; Rehman, S.; Al-Sulaiman, F.A. Performance Analysis of a Solar Chimney Power Plant for Different Geographical Locations of Saudi Arabia. FME Trans. 2020, 49, 64–71. [Google Scholar] [CrossRef]
- Habtay, G.; Buzas, J.; Farkas, I. Heat Transfer analysis in the chimney of the indirect solar dryer under natural convection mode. FME Trans. 2020, 48, 701–706. [Google Scholar] [CrossRef]
- Jakoplić, A.; Franković, D.; Kirinčić, V.; Plavšić, T. Benefits of short-term photovoltaic power production forecasting to the power system. Optim. Eng. 2021, 22, 9–27. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Bayrakçı, H.C.; Demircan, C.; Keçebaş, A. The development of empirical models for estimating global solar radiation on horizontal surface: A case study. Renew. Sustain. Energy Rev. 2018, 81, 2771–2782. [Google Scholar] [CrossRef]
- Hissou, H.; Benkirane, S.; Guezzaz, A.; Azrour, M.; Beni-Hssane, A. A Novel Machine Learning Approach for Solar Radiation Estimation. Sustainability 2023, 15, 10609. [Google Scholar] [CrossRef]
- Solano, E.S.; Affonso, C.M. Solar Irradiation Forecasting Using Ensemble Voting Based on Machine Learning Algorithms. Sustainability 2023, 15, 7943. [Google Scholar] [CrossRef]
- Rehman, S.; Salman, U.T.; Mohandes, M.A.; Al-Sulaiman, F.A.; Adetona, S.; Alhems, L.M.; Baseer, M.A. Wind Speed Prediction Based on Long-Short Term Memory using Nonlinear Autoregressive Neural Networks. FME Trans. 2022, 50, 260–270. [Google Scholar] [CrossRef]
- Rehman, S.; Khan, S.A.; Alhems, L.M. The Effect of Acceleration Coefficients in Particle Swarm Optimization Algorithm with Application to Wind Farm Layout Design. FME Trans. 2020, 48, 922–930. [Google Scholar] [CrossRef]
- Mohandes, M.; Nuha, H.H.; Mugitama, S.A.; Rehman, S.; Al-Shailkhi, A. Global solar radiation prediction using machine learning approaches. Sigma J. Eng. Nat. Sci.—Sigma Mühendislik Ve Fen Bilim. Derg. 2025, 43, 1725–1736. [Google Scholar] [CrossRef]
- Chaibi, M.; Benghoulam, E.M.; Tarik, L.; Berrada, M.; El Hmaidi, A. Machine Learning Models Based on Random Forest Feature Selection and Bayesian Optimization for Predicting Daily Global Solar Radiation. Int. J. Renew. Energy Dev. 2022, 11, 309–323. [Google Scholar] [CrossRef]
- Bakır, H. Prediction of daily global solar radiation in different climatic conditions using metaheuristic search algorithms: A case study from Türkiye. Environ. Sci. Pollut. Res. 2024, 31, 43211–43237. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Zhu, C.; Zou, L.; Zhang, M.; Feng, L.; Cao, Q. Predicting surface solar radiation using a hybrid radiative Transfer–Machine learning model. Renew. Sustain. Energy Rev. 2023, 173, 113105. [Google Scholar] [CrossRef]
- Khafaga, D.S.; Alhussan, A.A.; Eid, M.M.; El-kenawy, E.-S.M. Improving solar radiation source efficiency using adaptive dynamic squirrel search optimization algorithm and long short-term memory. Front. Energy Res. 2023, 11, 1164528. [Google Scholar] [CrossRef]
- Zell, E.; Gasim, S.; Wilcox, S.; Katamoura, S.; Stoffel, T.; Shibli, H.; Engel-Cox, J.; Al Subie, M. Assessment of solar radiation resources in Saudi Arabia. Sol. Energy 2015, 119, 422–438. [Google Scholar] [CrossRef]
- Mohandes, M.; Khan, S.A.; Rehman, S.; Al-Shaikhi, A.; Liu, B.; Iqbal, K. GARM: A Stochastic Evolution based Genetic Algorithm with Rewarding Mechanism for Wind Farm Layout Optimization. FME Trans. 2023, 51, 575–584. [Google Scholar] [CrossRef]
- Živković, G.S.; Mirkov, N.S.; Dakić, D.V.; Erić, A.M.; Erić, M.D.; Rudonja, N.R. Numerical Simulation of Thermo-Fluid Properties and Optimisation of Hot Water Storage Tank in Biomass Heating Systems. FME Trans. 2010, 38, 63–70. [Google Scholar]
- Nadeem, T.B.; Ali, S.U.; Asif, M.; Suberi, H.K. Forecasting daily solar radiation: An evaluation and comparison of machine learning algorithms. AIP Adv. 2024, 14, 75010. [Google Scholar] [CrossRef]
- Hossain, M.K.; Arifuzzaman, M.; Seliaman, M.E.; Rahman, A.; Sarker, D.; Altammar, H. Ensemble Learning Algorithms for Solar Power Prediction in Saudi Arabia: A Data-Driven Approach. In Proceedings of the 2024 ASU International Conference in Emerging Technologies for Sustainability and Intelligent Systems (ICETSIS), Manama, Bahrain, 28–29 January 2024; pp. 1368–1372. [Google Scholar] [CrossRef]
- Hissou, H.; Benkirane, S.; Guezzaz, A.; Beni-Hssane, A.; Azrour, M. Advanced Prediction of Solar Radiation Using Machine Learning and Principal Component Analysis; Springer: Cham, Switzerland, 2024; pp. 201–207. [Google Scholar] [CrossRef]
- Villegas-Mier, C.; Rodriguez-Resendiz, J.; Álvarez-Alvarado, J.; Jiménez-Hernández, H.; Odry, Á. Optimized Random Forest for Solar Radiation Prediction Using Sunshine Hours. Micromachines 2022, 13, 1406. [Google Scholar] [CrossRef]
- Wang, S.; Ma, J. A novel GBDT-BiLSTM hybrid model on improving day-ahead photovoltaic prediction. Sci. Rep. 2023, 13, 15113. [Google Scholar] [CrossRef]
- Duan, J.; Zuo, H.; Bai, Y.; Chang, M.; Chen, X.; Wang, W.; Ma, L.; Chen, B. A multistep short-term solar radiation forecasting model using fully convolutional neural networks and chaotic aquila optimization combining WRF-Solar model results. Energy 2023, 271, 126980. [Google Scholar] [CrossRef]
- Rehman, S.; Mohandes, M. Splitting Global Solar Radiation into Diffuse and Direct Normal Fractions Using Artificial Neural Networks. Energy Sources Part A Recovery Util. Environ. Eff. 2012, 34, 1326–1336. [Google Scholar] [CrossRef]
- Tercha, W.; Tadjer, S.A.; Chekired, F.; Canale, L. Machine Learning-Based Forecasting of Temperature and Solar Irradiance for Photovoltaic Systems. Energies 2024, 17, 1124. [Google Scholar] [CrossRef]
- Dikmen, O. Predicting Solar Irradiance Using Machine Learning Approaches: The Case of Duzce, Turkey. Int. J. Adv. Nat. Sci. Eng. Res. 2024, 8, 133–145. [Google Scholar]
- Soleymani, S.; Mohammadzadeh, S. Comparative Analysis of Machine Learning Algorithms for Solar Irradiance Forecasting in Smart Grids. arXiv 2023, arXiv:2310.13791. [Google Scholar] [CrossRef]
- Mohandes, M.; Balghonaim, A.; Kassas, M.; Rehman, S.; Halawani, T.O. Use of radial basis functions for estimating monthly mean daily solar radiation. Sol. Energy 2000, 68, 161–168. [Google Scholar] [CrossRef]
- Rasuo, B.P.; Veg, A.D. Design, fabrication and verification testing of the wind turbine rotor blades from composite materials. In Proceedings of the ICCM International Conferences on Composite Materials, Kyoto, Japan, 9–13 July 2007; pp. 1–4. [Google Scholar]
- Dinulovic, M.; Trninic, M.; Rasuo, B.; Kozovic, D. Methodology for aeroacoustic noise analysis of 3-bladed h-Darrieus wind turbine. Therm. Sci. 2023, 27, 61–69. [Google Scholar] [CrossRef]
- Rašuo, B.; Bengin, A.; Veg, A. On Aerodynamic Optimization of Wind Farm Layout. Proc. Appl. Math. Mech. 2010, 10, 539–540. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep Reinforcement Learning: An Overview. In Proceedings of the SAI Intelligent Systems Conference (IntelliSys) 2016, London, UK, 21–22 September 2016; pp. 426–440. [Google Scholar] [CrossRef]
- Rohanian, O.; Jauncey, H.; Nouriborji, M.; Kumar, V.; Gonalves, B.P.; Kartsonaki, C.; Isaric Clinical Characterisation Group; Merson, L.; Clifton, D. Using Bottleneck Adapters to Identify Cancer in Clinical Notes under Low-Resource Constraints. arXiv 2022, arXiv:2210.09440. [Google Scholar] [CrossRef]
- Alabdulhadi, A.A.; Rehman, S.; Ali, A.; Shafiullah, M. Deep learning framework for wind speed prediction in Saudi Arabia. Neural. Comput. Appl. 2025, 37, 3685–3701. [Google Scholar] [CrossRef]
- Rehman, S.; Mohandes, M. Artificial neural network estimation of global solar radiation using air temperature and relative humidity. Energy Policy 2008, 36, 571–576. [Google Scholar] [CrossRef]
- Chauhan, V.K.; Zhou, J.; Lu, P.; Molaei, S.; Clifton, D.A. A brief review of hypernetworks in deep learning. Artif. Intell. Rev. 2024, 57, 250. [Google Scholar] [CrossRef]
- Uçak, K.; Günel, G.Ö. Adaptive stable backstepping controller based on support vector regression for nonlinear systems. Eng. Appl. Artif. Intell. 2024, 129, 107533. [Google Scholar] [CrossRef]
- Tahir, M.F.; Yousaf, M.Z.; Tzes, A.; El Moursi, M.S.; El-Fouly, T.H.M. Enhanced solar photovoltaic power prediction using diverse machine learning algorithms with hyperparameter optimization. Renew. Sustain. Energy Rev. 2024, 200, 114581. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.-H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Gurenko, V.V.; Bychkov, B.I.; Syuzev, V.V. An Approach to Simulation of Stationary and Non-stationary Processes in the Harmonic Basis. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Moscow, Russia, 26–29 January 2021; pp. 2664–2667. [Google Scholar] [CrossRef]
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A Survey of Forecast Error Measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar] [CrossRef]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLoS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef] [PubMed]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Application of functional deep belief network for estimating daily global solar radiation: A case study in China. Energy 2020, 191, 116502. [Google Scholar] [CrossRef]
- Yang, L.; Cao, Q.; Yu, Y.; Liu, Y. Comparison of daily diffuse radiation models in regions of China without solar radiation measurement. Energy 2020, 191, 116571. [Google Scholar] [CrossRef]
- Gouda, S.G.; Hussein, Z.; Luo, S.; Yuan, Q. Model selection for accurate daily global solar radiation prediction in China. J. Clean. Prod. 2019, 221, 132–144. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhang, F.; Bai, H.; Lu, X.; Xiang, Y. New combined models for estimating daily global solar radiation based on sunshine duration in humid regions: A case study in South China. Energy Convers. Manag. 2018, 156, 618–625. [Google Scholar] [CrossRef]
- Petrosian, O.; Zhang, Y. Solar Power Generation Forecasting in Smart Cities and Explanation Based on Explainable AI. Smart Cities 2024, 7, 3388–3411. [Google Scholar] [CrossRef]





| Ref. | Methodology | Key Findings | Limitations |
|---|---|---|---|
| [26] | Predicts daily global solar radiation data for 6 Pakistani cities | SVR achieves the best performance, with R2 values up to 0.99 | No FE; No feature selection reported |
| [27] | Ensemble ML algorithms for solar power prediction in Saudi Arabia | RF outperformed other models (MAE = 0.0141), (RMSE = 0.0211) | Limited to Dhahran Limited evaluation metrics |
| [28] | Multiple ML models (RF, GBM, LR, CART, and DT) | LR and RF achieved lowest nMAE (−0.144, −0.151) | Limited feature-selection methods |
| [29] | Compares RF with hyperparameter optimization to other ML models | 95.98% accuracy with optimized RF | Limited to Queretaro, Mexico; Focused on short-term predictions |
| [30] | Comparative analysis of BiLSTM-based LSTNet | RF-LSTNet performed best | Limited explanation of feature-selection process |
| [15] | Multiple ML algorithms (RF, XGBoost, and CatBoost) | Best performance with RF and CatBoost combination | Limited to Brazilian region |
| [31] | WRF Solar model | Superior performance compared to baseline models | Region-specific (Northwest China) |
| [21] | Comparison of six ML approaches | RTM-RF showed best performance (MAE 15.57 W/m2) | Limited to clear sky conditions |
| [19] | Comparison of 5 ML models with/without BO | SVR-BO performed best (RMSE = 0.4473 kWh/m2/day) | Single location study (Fez, Morocco); Limited feature set |
| [32] | Radial Basis Function Neural Network (RBF-NN) for DSR and DNR | DSR; MAPE = 1.6–9.3% DNR; MAPE= 0.49–41% | Relatively old dataset (1998–2002) |
| [33] | Review of ML techniques | Decision trees, RF, XGBoost, and SVM are effective ML models | Inadequate use of FE; Limited context for the KSA |
| [20] | Multiple metaheuristic algorithms (GBO, HHO, BMO, SCA, and HGSO) for distinct locations in Turkey | SCA best for Afyonkarahisar; GBO best for Ağrı | Limited input variables |
| [22] | ADSSOA-LSTM hybrid comparison with GA, PSO, and GWO | ADSSOA-LSTM achieved lowest RMSE (0.000388) | Limited feature exploration |
| [34] | Comparison of multiple ML algorithms | XGBoost showed highest performance | Single-location study |
| [35] | Comparison of next-gen ML algorithms | Random Forest outperformed other algorithms; MLP-ANN improved with feature selection | Limited to single application |
| Location | Region | Latitude (°N) | Longitude (°E) | Altitude (m) |
|---|---|---|---|---|
| Tabuk | Northern | 28.3835 | 36.5662 | 695 |
| Riyadh | Central | 24.7136 | 46.6753 | 630 |
| Dhahran | Eastern | 26.2869 | 50.1140 | 10 |
| Najran | Southern | 17.5656 | 44.2289 | 1742 |
| Jeddah | Western | 21.4858 | 39.1925 | 12 |
| Al-Jouf | Northern | 29.8679 | 40.1000 | 680 |
| Feature | Description | Unit |
|---|---|---|
| DT | Date | - |
| MO | Month | - |
| DY | Day | - |
| HR | Hour | hr |
| TMP | Temperature at 2 m | °C |
| RH | Relative Humidity at 2 m | % |
| CI | All-Sky Insolation Clearness Index | dimensionless |
| WS | Wind Speed at 10 m | m/s |
| DNI | All-Sky Surface Shortwave Downward Irradiance | kWh/m2/day |
| Algorithm | Strengths | Limitations | Use Case Fit | Ref. |
|---|---|---|---|---|
| RFR | Robust to overfitting, handles non-linearity well | Slow for large forests, less interpretable | Great for noisy or non-linear tabular data | - |
| LRM | Simple, fast, interpretable | Fails to capture non-linear patterns | Best for simple, linear relationships | - |
| ANN | Captures complex non-linear patterns | Needs tuning, prone to overfitting | Good for moderately complex patterns and flexible modelling | [43] |
| GPR | Probabilistic predictions, flexible | Computationally intensive | Useful when uncertainty estimates are important | - |
| KNN | Simple, no training phase | Sensitive to ‘k’ and scale of data | Useful for small datasets where local similarity matters | - |
| DNN | Learns hierarchical features, handles time patterns | Requires large amounts of data, slow to train | Best for large datasets and capturing complex temporal/spatial patterns | [40,42,44] |
| GBR | High accuracy, customizable | Slow training, risk of overfitting | Ideal for maximizing accuracy on structured data | - |
| SVR | Strong performance on smaller datasets | Poor scalability to large datasets | Works well for small to medium datasets with clear margins | [45] |
| Model | Hyperparameter | Optimization Range | Optimized Hyperparameters |
|---|---|---|---|
| GPR | kernel | 1.0 * RBF (length scale = 1.0), 1.0 * Matern (length scale = 1.0, nu = 1.5) | 1 ** 2 * Matern (length scale = 1, nu = 1.5) |
| alpha | 1 × 10−5, 1 × 10−3, 1 × 10−1 | 1 × 10−1 | |
| optimizer | fmin_l_bfgs_b | fmin_l_bfgs_b | |
| restarts | 3, 5 | 5 | |
| LRM | - | - | Default |
| RFR | estimators | 800, 1000, 1200, 1800 | 1800 |
| Max depth | None, 10, 20 | None | |
| Min samples split | 2, 4, 6 | 5 | |
| Min samples leaf | 1, 2, 3 | 2 | |
| Max features | 0.3, 0.5, sqrt, log2 | log2 | |
| KNN | neighbors | 3, 5, 7, 10 | 10 |
| weights | Uniform, Distance | Distance | |
| metric | euclidean, manhattan | manhattan | |
| GBR | estimators | 100, 200, 300 | 1000 |
| Learning rate | 0.01, 0.1, 0.2 | 0.03 | |
| Max depth | 3, 5, 7 | 6 | |
| Sub sample | 0.8, 1.0 | 0.9 | |
| Min samples split | 2, 5, 10 | 5 | |
| ANN | Hidden layer sizes | - | (128, 64, 32, 16) |
| activation | - | relu | |
| solver | - | adam | |
| alpha | - | 0.0001 | |
| Learning rate | - | Adaptive | |
| SVR | C | 1, 10, 50, 100 | 50 |
| epsilon | 0.01, 0.1, 0.2, 0.5 | 0.2 | |
| kernel | Linear, rbf | rbf | |
| gamma | Scale, Auto | Scale |
| Parameter | Value |
|---|---|
| Feature Selection | Top 3 features |
| Input Dimension | 3 (based on FS output) |
| Hidden Layers | 128, 64, 32, 16 |
| Activation Function | relu |
| Dropout Rate | 0.1 |
| Optimizer | adam |
| Loss Function | MSE |
| Evaluation Metric | MAE |
| Learning Rate Strategy | adaptive |
| Max Iterations (Epochs) | 1000 |
| Batch Size | 128, 64, 32, 16 |
| Early Stopping | Yes |
| Metrics | Mathematical Model | Description | Desired Output |
|---|---|---|---|
| MAE | Measures the mean magnitude of errors between predicted and actual values without considering their direction [49,50] | Closer to 0 is better | |
| MSE | Measures the mean squared differences between predicted and actual values, and penalises larger errors more heavily [49] | Closer to 0 is better | |
| RMSE | Square root of MSE, providing error measure in the same units as the target variable [51] | Closer to 0 is better | |
| Explains the variation in the target variable that is predictable from the input variable(s) [52] | Closer to 1 is better | ||
| MAPE | Expresses accuracy as a percentage, showing the mean absolute percent difference between predicted and actual values [51,53] | Closer to 0% is better | |
| MBE | Used to evaluate the bias of forecasting models [54] | Closer to 0 is better | |
| rRMSE | Derived from RMSE [51] | Closer to 0% is better |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, L.B.; Shuja, S.Z.; Rehman, S. Machine Learning Forecasting of Direct Solar Radiation: A Multi-Model Evaluation with Trigonometric Cyclical Encoding. Forecasting 2025, 7, 58. https://doi.org/10.3390/forecast7040058
Rashid LB, Shuja SZ, Rehman S. Machine Learning Forecasting of Direct Solar Radiation: A Multi-Model Evaluation with Trigonometric Cyclical Encoding. Forecasting. 2025; 7(4):58. https://doi.org/10.3390/forecast7040058
Chicago/Turabian StyleRashid, Latif Bukari, Shahzada Zaman Shuja, and Shafiqur Rehman. 2025. "Machine Learning Forecasting of Direct Solar Radiation: A Multi-Model Evaluation with Trigonometric Cyclical Encoding" Forecasting 7, no. 4: 58. https://doi.org/10.3390/forecast7040058
APA StyleRashid, L. B., Shuja, S. Z., & Rehman, S. (2025). Machine Learning Forecasting of Direct Solar Radiation: A Multi-Model Evaluation with Trigonometric Cyclical Encoding. Forecasting, 7(4), 58. https://doi.org/10.3390/forecast7040058








