Forecasting Youth Unemployment Through Educational and Demographic Indicators: A Panel Time-Series Approach

Abstract

Youth unemployment remains a pressing issue in many emerging economies, where educational disparities and demographic pressures interact in complex ways. This study investigates the links between higher-education enrolment, demographic structure and youth unemployment in eight developing countries from 2009 to 2023. Panel cointegration techniques—Fully Modified Ordinary Least Squares (FMOLS) and Dynamic Ordinary Least Squares (DOLS)—are applied to estimate the long-run effects of gross tertiary-school enrolment on youth unemployment while controlling for GDP growth and youth-cohort size. Robustness is confirmed through complementary estimations with pooled-mean-group ARDL and system-GMM panels, which deliver consistent coefficient signs and significance levels. Results show a significant negative elasticity between enrolment and youth unemployment, indicating that wider access to higher education helps lower joblessness among young people. Youth-population growth exerts an opposite, positive effect, while GDP growth reduces unemployment but less uniformly across regions. The evidence points to an integrated policy mix—expanding tertiary (especially vocational and technical) education, managing demographic pressure and maintaining macro-economic stability—to improve youth-employment outcomes in emerging economies.

1. Introduction

Youth unemployment remains a persistent socioeconomic challenge in many emerging and developing economies, where demographic pressures coincide with structural mismatches in education and labor markets. Recent studies have also emphasized the importance of demographic factors in youth unemployment, as shown by Das, who highlighted the role of socioeconomic and educational disparities in shaping youth employment outcomes in India [1]. Despite increasing investment into higher education, the anticipated returns in the form of enhanced employment prospects for graduates often fall short, particularly in labor markets with rigid institutional settings or low absorptive capacity [2,3,4]. As a result, policymakers and researchers are increasingly interested in understanding the dynamic relationships between educational attainment and youth unemployment, not only in static cross-sectional terms but also from a longitudinal, predictive perspective.

For example, Demirci and Poyraz have demonstrated that economic fluctuations, such as the Great Recession, led to a pro-cyclical enrollment pattern in Turkey, in which young people adjusted their educational decisions based on macroeconomic conditions [5]. This evidence highlights how economic instability can influence youth education choices which, in turn, affect labor market outcomes.

Further, Roessger et al. provided empirical insights into the role of regional economic conditions, including unemployment rates and proximity to educational institutions, in shaping educational enrollment. Their longitudinal study in Arkansas revealed that local unemployment levels and access to universities significantly determined community college enrollment, underscoring the importance of regional factors in youth education and labor market dynamics [6]. These findings align with the broader literature suggesting that youth unemployment is not only a function of educational attainment, but also of the economic context in which education is pursued.

In recent years, the integration of econometric forecasting methods in labor economics has enabled more nuanced modeling of employment outcomes based on a range of macroeconomic and educational indicators [7,8,9]. Among these, panel time-series models and cointegration techniques (e.g., FMOLS, DOLS) have demonstrated robustness in capturing both short-term dynamics and long-run equilibrium relationships between education levels and labor market outcomes [10,11,12]. However, empirical evidence remains mixed regarding the extent to which the expansion of higher education contributes to mitigating youth unemployment, with outcomes varying across regions, income levels, and institutional environments [13,14,15].

This study addresses the forecasting potential of higher education enrollment as a predictor of youth unemployment using panel data of developing economies from 2009 to 2023. We implement an FMOLS- and DOLS-based approach to explore both the contemporaneous and lagged effects of gross tertiary enrollment on youth unemployment rates, controlling for macroeconomic variables such as GDP growth and inflation. Combining statistical forecasting with theoretical labor market dynamics, this research seeks to inform education policy and youth employment strategies in contexts facing demographic and structural labor market transitions.

Despite a rich body of work on the determinants of youth unemployment, three gaps remain conspicuous. First, most cross-country studies focus either on OECD or on broad ‘developing-country’ samples, leaving the post-Soviet emerging economies of Central Asia and the South Caucasus largely unexamined. Second, the few papers that do include these countries typically treat education and demography in isolation, ignoring the possibility that rapid tertiary-enrolment expansion interacts with demographic pressure to shape labour-market outcomes. Third, evidence on the direction of these links is scarce: cointegration studies document long-run correlations, but rarely verify whether higher education actually precedes lower unemployment or merely moves with it. Addressing these gaps, our study combines long-run (FMOLS/DOLS) and causal (Dumitrescu–Hurlin) panel techniques on an unbalanced dataset for Azerbaijan, Armenia, Georgia, Kazakhstan, Kyrgyzstan, Mongolia, Tajikistan and Uzbekistan over 2009–2023.

The remainder of this paper is organized as follows. Section 2 presents the data sources and econometric methodology. Section 3 discusses the main results regarding the model’s estimations and forecasting performance. Section 4 reflects on the findings in light of policy implications and limitations. Section 5 concludes with recommendations for future research and data development.

2. Materials and Methods

2.1. Data Description

An empirical analysis was performed based on an unbalanced panel dataset covering eight emerging economies (Azerbaijan, Armenia, Georgia, Kazakhstan, Kyrgyzstan, Mongolia, Tajikistan, Uzbekistan) over the period 2009–2023. The selection of countries was guided by the availability of data on youth unemployment, tertiary education enrollment, and macroeconomic indicators. A total of 112 balanced panel observations were used for the DOLS model estimation. Annual data were sourced from the World Bank’s World Development Indicators (WDI) and the UNESCO Institute for Statistics.

The variables used in the analysis, along with their definitions and sources, are summarized in

Table 1. The variables used in the analysis.

Variable Name	Description	Source
YOUTH_UNEMPL	Youth unemployment rate (% of labor force ages 15–24)	World Bank (WDI)
ENROL	Gross tertiary school enrollment ratio (%)	UNESCO UIS
GROWTH	GDP growth (annual %)	World Bank (WDI)
POPULATION	Youth population aged 15–24 (in thousands)	World Bank (WDI)

.

In all countries, the expansion of higher education was accompanied by a decrease in youth unemployment, but the elasticity is stronger in countries with higher GDP per capita (e.g., Kazakhstan, Azerbaijan) and, therefore, demand for skilled labor; as well as those with developed digital job markets (e.g., Kazakhstan).

Youth account for only ≈12% of Kazakhstan’s population but nearly one-fifth in Tajikistan and Uzbekistan, explaining why identical education gains translate into different labour-market pressures across the panel.

The

Table 2. Social economic characteristics of countries.

Country	Youth Unemployment	Education Enrolment, %	Share of Youth in Total Pop., %	GDP Growth
Kazakhstan	3.8	56.5	12.9	5.1
Azerbaijan	13.8	41.4	13.5	1.1
Georgia	30.2	80.3	11.9	7.8
Armenia	26.1	61.2	13.1	8.3
Mongolia	12.3	65.3	16.1	7.4
Uzbekistan	10.9	45.8	17.9	6.3
Kyrgyzstan	8.2	56.0	17.8	6.2
Tajikistan	26.8	34.7	19.5	8.3

highlights that Armenia, Georgia, Mongolia and Tajikistan recorded rapid output growth (>7%) in 2023, while Azerbaijan’s was modest (1%). In oil-exporting Azerbaijan the growth–employment link is weaker than in diversified, high-growth Georgia.

Kazakhstan focuses on quality-of-growth and high-skill matching, whereas Tajikistan prioritises job-intensive sectors and digital-access expansion for a very young, fast-growing cohort.

In low-income economies (e.g., Tajikistan, Kyrgyzstan), the negative effect was weaker and “delayed” due to migration and low ICT penetration.

Georgia and Armenia demonstrated improvements in PISA scores and R&D reforms, which help to gradually reduce unemployment; however, labor market inertia remained significant.

In Uzbekistan and Tajikistan, high birth rates mean that the increase in university enrollment only compensates for the influx of youth and does not immediately reduce unemployment.

2.2. Methodology

This study examined the interactions between youth unemployment and a set of economic and social drivers—government policy, economic growth, and population development—across eight economies of countries in Central Asia and the Caucasus region. Kamar et al. have demonstrated that pro-growth policies—such as increased investment in education and private sector development—significantly influence employment outcomes. Their findings emphasize the importance of considering both economic policies and the socio-political context when analyzing youth unemployment [16].

To investigate both long-run relationships and short-term dynamics among the variables, this study employed a multi-stage econometric procedure incorporating methods widely used in previous research. For instance, Flek et al. employed survival analysis techniques to explore the factors influencing the duration of youth unemployment, highlighting the importance of methodological rigor in labor market studies [17].

Panel data were used because they capture both cross-sectional heterogeneity and time dynamics more effectively than pure time-series or cross-sectional approaches [18].

A multi-stage procedure was employed, mirroring best practices in recent research (

Table 3. Procedure of the utilized methodology.

Step	Purpose	Main Test (s)
1	Check stationarity	Levin–Lin–Chu (LLC); Im–Pesaran–Shin (IPS) [19,20], Pesaran’s cross-sectionally augmented panel unit-root test (CIPS).
2	Verify long-run link	Pedroni panel cointegration [21,22].
3	Estimate long-run coefficients	Fully Modified OLS (FMOLS) [13,23,24].
4	Robustness	Dynamic OLS (DOLS) [25,26].
5	Panel causality	Dumitrescu–Hurlin panel causality [27]
6	Cross-sectional dependence, heterogeneity	Pesaran CD test [28], Pesaran & Yamagata test [29]
7	Advanced Robustness Extensions	PMG-ARDL [30], GMM [31]

).

2.2.1. Panel Unit-Root Diagnostics

Stationarity is a prerequisite for meaningful cointegration analysis. We therefore applied two complementary tests:

-

The LLC test assumes a homogeneous autoregressive parameter across countries, increasing power when the true process is similar.

-

The IPS test allows for heterogeneity by averaging individual Augmented Dickey–Fuller statistics, making it less restrictive.

-

Cross-sectionally Augmented IPS (CIPS) augments each ADF regression with cross-sectional averages of the level and first difference of the variable, explicitly controlling for common shocks. This second-generation test is robust to cross-sectional dependence—an important feature of our multi-country panel—and rejects the unit-root null if at least one series in the panel is stationary.

Together, these tests provide a balanced assessment of unit-root properties under varying assumptions about heterogeneity and cross-sectional dependence.

2.2.2. Panel Cointegration Test

Pedroni’s within- and between-dimension statistics can be used to detect a common long-run equilibrium when variables are integrated of order one. Two types of Pedroni test statistics can be utilized:

-

Panel (within-dimension): Panel v-Statistic, ρ-Statistic, PP-Statistic, ADF-Statistic;

-

Group (between-dimension): Group ρ-Statistic, PP-Statistic, ADF-Statistic.

Rejection of the null hypothesis of “no cointegration” (i.e., residuals are I(1)) justifies subsequent long-run estimation. In particular, the alternative hypothesis (H₁) is that cointegration exists (i.e., residuals are I(0)).

2.2.3. Long-Run Estimation

To obtain consistent cointegration parameters, we estimate: FMOLS and DOLS models.

FMOLS is designed to enable consistent estimation of cointegrated panel data models by correcting for endogeneity and serial correlation [13,23,24]. The FMOLS model is defined as follows:

y_it = α_i + β_ix_it + u_it

DOLS allows for the estimation of long-run relationships by including leads and lags of first-differenced regressors to correct for endogeneity and autocorrelation [25,26]. The DOLS model is defined as follows:

$${\mathrm{y}}_{\mathrm{it}}={\mathsf{\alpha }}_{\mathrm{i}}+{\mathsf{\beta }}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i},\mathrm{t}}+{\sum }_{\mathrm{k}=-\mathrm{q}}^{\mathrm{q}}{\mathsf{\gamma }}_{\mathrm{i}\mathrm{k}}\mathsf{\Delta }{\mathrm{x}}_{\mathrm{i},\mathrm{t}-\mathrm{k}}+{\mathsf{u}}_{\mathrm{it}}$$

DOLS provides asymptotically unbiased and efficient estimates, and is often used as a robustness check alongside FMOLS.

Additionally, we performed the Dumitrescu–Hurlin panel causality test, which examines short-run causal relationships among the variables while allowing for heterogeneity in lag structures across countries.

The DH test accounts for cointegration: once long-run equilibrium is confirmed, it helps to reveal whether short-run impulse channels exist; otherwise, our interpretation remains partial. It complements the magnitude estimates obtained via FMOLS/DOLS by adding the direction of influence; that is, FMOLS/DOLS say how much, while DH says who leads whom. Finally, it allows for cross-country asymmetry; unlike the classical homogeneous-lag Granger test, DH does not require every country to share the same lag structure or effect size [27].

Cross-sectional dependence will first be diagnosed with Pesaran’s CD test. Failure to reject the null of no average correlation validates the use of conventional (cluster-robust) panel estimators; rejection will trigger the use of Driscoll–Kraay or comparable heteroskedasticity- and cross-section-robust standard errors [28].

Parameter heterogeneity will be formally evaluated with the Δ̃ and adjusted Δ̃adj statistics of Pesaran & Yamagata. Rejection of the homogeneity null will motivate the preference for estimators that allow country-specific short-run dynamics (e.g., PMG-ARDL) and the presentation of country-by-country coefficients as a robustness check [29].

To address slope heterogeneity and potential endogeneity we complement the baseline FMOLS/DOLS estimates with two additional procedures. First, a Pooled Mean Group Auto-Regressive Distributed Lag (PMG-ARDL) model is estimated with lags selected by the Akaike Information Criterion [30].

Second, we estimate a dynamic panel equation via System-GMM (Generalized Method of Moments) using second- and third-order lagged levels as instruments for differenced equations. The instrument set is collapsed to mitigate proliferation, and two-step Windmeijer-corrected standard errors are reported. Diagnostic tests for instrument validity (Hansen J) and serial correlation (AR(2)) will accompany the estimates [31].

2.3. Model Specification

The general panel model used in this study is expressed as follows:

YOUTH_UNEMPL_it = α_i+ β₁ ENROL_it + β₂ GROWTH_it + β₃ POPULATION_it + ε_it

where:

-

i indexes countries (i = 1, …, N);

-

t indexes time periods (t = 1, …, T);

-

α_i captures individual fixed effects;

-

ε_it is the error term.

Cointegration relationships were verified prior to FMOLS/DOLS estimation.

We assume the following properties for the disturbance term ε_it:

-

ε_it∼IID (0, σ2); that is, the errors are independently and identically distributed with mean zero and constant variance across individuals and over time (i.e., homoskedasticity).

-

There is no serial correlation in ε_it within individual units [21].

-

ε_it is uncorrelated with the explanatory variables x_it and any leads/lags of x_it.

These assumptions ensure the consistency and asymptotic normality of the DOLS and FMOLS estimators. However, given that panel data often exhibit heteroskedasticity and cross-sectional dependence, robust standard errors were applied where necessary.

This model specification aligns with approaches used in previous research. Anyanwu (2013) [32], for example, have employed a similar framework to examine youth employment determinants across African countries, emphasizing the impacts of macroeconomic factors such as government investment and domestic consumption on youth unemployment.

3. Results

3.1. Panel Unit Root Tests

To validate the appropriateness of cointegration-based estimators (FMOLS/DOLS), we conducted panel unit root tests for all core variables, including YOUTH_UNEMPL, ENROL, and POPULATION. These tests allowed us to assess the degree of integration, which is a key precondition for estimating long-run equilibrium relationships.

Table 4. Panel unit root test results.

	LLC				IPS
	Levels (Statistic)	Prob.	First Differences (Statistic)	Prob.	Levels (Statistic)	Prob.	First Differences (Statistic)	Prob.
YOUTH_UNEMPL	−1.50075	0.0667	−6.18286	0.0000	−0.62200	0.2670	−4.96380	0.0000
ENROL	1.40802	0.9204	−2.30596	0.0106	1.61014	0.9463	−4.21360	0.000
GROWTH	−3.76080	0.0001	−7.26782	0.0000	−3.59217	0.0002	−6.49227	0.0000
POPULATION	−4.24362	0.0000	−2.62969	0.0043	−0.10495	0.4582	−1.02193	0.1534

Source: authors’ calculations in Eviews.

illustrates that most of the variables were not stationary at level; meanwhile, the results of the LLC and IPS tests indicated that all variables were stationary at first difference.

In addition to the LLC and IPS tests, we employ Pesaran’s cross-sectionally augmented panel unit-root test (CIPS), which remains valid in the presence of unobserved common factors.

Table 5. CIPS results.

Variable	CIPS (Levels)	p-Value	CIPS (First Differences)	p-Value
YOUTH_UNEMPL	–0.981	≥0.10	–3.246	<0.01
ENROL	–0.925	≥0.10	–2.503	<0.05
POPULATION	0.538	≥0.10	0.935	≥0.10
GROWTH	–2.867	<0.01	–4.319	<0.01

Source: authors’ calculations in Eviews.

reports the statistics.

The CIPS findings confirm our earlier LLC/IPS conclusions: YOUTH_UNEMPL and ENROL are integrated of order one, whereas GROWTH is level-stationary. For POPULATION the evidence is mixed, but most tests—including LLC, IPS (levels) and the truncated CIPS—point to an I(1) process, so we retain this classification in the subsequent analysis.

Consequently, the precondition for long-run estimation methods such as Pedroni cointegration, FMOLS and DOLS is satisfied even when cross-section dependence is explicitly modelled.

After verifying that YOUTH_UNEMPL, ENROL, and POPULATION are I(1) while GROWTH is level-stationary, we confirmed cointegration with Pedroni (five of seven statistics, p < 0.05). Long-run elasticities were obtained with two complementary estimators: FMOLS corrects for endogeneity and serial correlation non-parametrically; DOLS adds leads/lags of Δ-regressors to achieve unbiasedness. These results lend statistical credibility to the econometric strategy employed.

According to the standard cointegration literature, the inclusion of a single I(0) regressor (Economic Growth) in FMOLS/DOLS models does not violate the consistency of estimation. The stationary variable simply enters the cointegrating relationship as a stable exogenous component, and does not affect the asymptotic properties of the long-run coefficients. This extended statistical analysis confirmed that the integration properties of the variables met the formal requirements for cointegration analysis [13,24].

3.2. Evidence of Long-Run Relationship: Pedroni Cointegration Test

To determine whether a long-run equilibrium relationship exists among youth unemployment (YOUTH_UNEMPL), tertiary education enrollment (ENROL), GDP growth (GROWTH), and youth population (POPULATION), we first applied the Pedroni panel cointegration test.

The test results revealed strong support for cointegration (

Table 6. Pedroni residual cointegration test results.

Null Hypothesis: No Cointegration
Alternative hypothesis: Common AR coefs. (within-dimension)
	Statistic	Prob.	Weighted Statistic	Prob.
Panel v-Statistic	1.049025	0.1471	−1.400185	0.9193
Panel rho-Statistic	−0.382717	0.3510	−0.685762	0.2464
Panel PP-Statistic	−1.854366	0.0318	−5.080177	0.0000
Panel ADF-Statistic	−1.589691	0.0560	−4.379175	0.0000
Alternative hypothesis: Individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	0.528474	0.7014
Group PP-Statistic	−6.794927	0.0000
Group ADF-Statistic	−3.893942	0.0000

): five out of seven test statistics confidently rejected the null hypothesis (of no cointegration) at the 1–5% level. One additional test (Panel ADF) was marginally significant at the 10% level. Only the v- and rho-statistics were statistically insignificant, which is expected for specifications without deterministic components.

Both within-dimension (panel) and between-dimension (group) tests—especially the PP and ADF statistics—yielded the same conclusion, indicating consistency across estimators assuming homogeneous or heterogeneous dynamics.

These results are in line with the literature emphasizing structural co-movements between education and labor market outcomes [4,15].

From a methodological perspective, this provided strong justification for the application of panel FMOLS and DOLS models, which assume cointegration among variables.

3.3. Long-Run Estimation

We first estimate the cointegrating equation with panel FMOLS, which handles serial correlation and any feedback from unemployment to the regressors through a non-parametric long-run covariance correction. The results are presented below in

Table 7. FMOLS estimation results.

Variable	Coefficient	t-Statistic	p-Value
GROWTH (annual GDP growth rate)	–0.212	–2.54	0.013
ENROL (education enrollment rate, % of cohort)	–0.190	–5.01	<0.001
POPULATION (number of youth, persons)	+1.11 × 10−6	3.21	0.002
R-squared	0.963

.

As a robustness check we re-estimate the same equation by panel DOLS, adding a small set of leads and lags of the first-differenced regressors; this parametrically purges residual endogeneity while leaving the long-run coefficients comparable. Both estimators are asymptotically normal in heterogeneous panels and therefore provide mutually reinforcing evidence on the equilibrium links between education, growth, demography and youth unemployment. The output is detailed in

Table 8. Panel DOLS estimation results.

Variable	Coefficient	Std. Error	t-Statistic	p-Value
GROWTH	–0.0487	0.0787	–0.619	0.5380
ENROL	–0.1580	0.0431	–3.670	0.0004
POPULATION	+1.93 × 10−6	6.30 × 10−7	3.057	0.0031
R-squared	0.9841

below.

The coefficient of education enrollment rate remains negative and highly significant in both FMOLS (–0.19, p < 0.001) and DOLS (–0.16, p < 0.001). Thus, raising the gross tertiary-enrolment ratio by 1 pp is associated with an average drop of ≈0.17 pp in the youth-unemployment rate, underscoring the labour-absorbing payoff of higher-skill investment.

FMOLS suggests that a 1 pp faster real-GDP growth rate cuts youth unemployment by about 0.21 pp (p = 0.013). The DOLS point estimate is similar in sign (–0.05) but imprecisely estimated (p ≈ 0.54). The mixed significance implies that the growth effect is contingent on the sectoral make-up of expansion—an issue probed further with the PMG and GMM checks.

The positive slope—roughly 1.1 × 10⁻⁶ in FMOLS and 1.9 × 10⁻⁶ in DOLS—is statistically robust. Interpreted literally, one million additional youths raises the unemployment rate by about 1 pp (or 0.10–0.20 pp for every 100,000 extra youths), illustrating the classic youth-bulge pressure that must be offset by faster job creation.

Together the three regressors explain 96–98% of the within-panel variation (R²_FMOLS = 0.963; R²_DOLS = 0.984). The near-identical signs and comparable magnitudes across FMOLS and DOLS confirm that the results are not an artefact of a single estimator or lag specification; they reflect a stable long-run equilibrium linking education, demography and labour-market outcomes. Importantly, the high explanatory power of the model (R² = 0.963) indicates that these variables jointly capture most of the cross-country and intertemporal variation in youth unemployment.

The coefficient for youth population is positive and significant, lending support to the “youth bulge” hypothesis. As the size of the youth cohort grows, the labor market faces increased pressure, resulting in more competition for available jobs [3,9,10,31].

Similar conclusions have been drawn by Yang and Chan, Lehti et al., who found that demographic pressures reduce the effectiveness of education expansion alone [9,33]. These results provide quantitative support for the hypothesis that higher education enrollment and demographic structure are robust long-run predictors of youth unemployment.

The positive relationship between population and youth unemployment was reaffirmed, demonstrating that as the youth population increases, unemployment rises. As youth populations grow, labor market saturation intensifies, leading to increased competition for a limited number of jobs.

This finding aligns with the “demographic burden” hypothesis and supports evidence presented by the ILO, Lehti et al., and Lam, highlighting the importance of employment planning in high-growth youth populations [10,33,34].

The FMOLS and DOLS results indicate a statistically significant and negative relationship between higher education enrollment and youth unemployment. This suggests that expanding access to tertiary education contributes to improved employment outcomes for young people by enhancing their skills and employability. This finding confirms evidence from Turkey and Spain [35], Sub-Saharan Africa [15], and Pakistan [8].

The strong and significant negative coefficient for education enrollment highlights the importance of higher education in reducing youth unemployment [36,37]. This reinforces the role of education as a long-term driver of labor market integration.

This is in line with the findings reported by Psacharopoulos and Patrinos, who argued that educational attainment improves labor market adaptability, enhances employability, and reduces the risks of informal employment. In the context of Central Asia, where skill mismatches are pronounced, expanding access to tertiary education remains a vital component of labor market integration strategies [7].

The robustness observed across estimators reinforces earlier conclusions drawn from the FMOLS results and supports the findings of Arshad and Seenprachawong, Amin and Ntembe, Psacharopoulos and Patrinos, who argued that expanding access to higher education yields measurable labor market benefits, particularly for young individuals [7,8,15].

The negative effect of GDP growth on youth unemployment is consistent with the findings of O’Higgins, Blanchflower and Freeman, who emphasized that macroeconomic expansion disproportionately benefits young labor market entrants by increasing the number of entry-level jobs, particularly in emerging economies [36,37].

However, the consistency of this effect varies across specifications, indicating that economic growth alone may not guarantee improved employment outcomes without supporting labor market conditions.

Insignificance of the coefficient for GDP growth in DOLS model suggests that the effect of growth on youth unemployment is not robust across different lag structures or model selection criteria. This calls for caution in interpreting growth effects in youth labor market models, echoing concerns raised by Mauro and Carmeci and Verbič et al., who emphasized that growth must be inclusive and sector-specific to translate into meaningful reductions in youth unemployment [3,11]. Mauro and Carmeci have emphasized that, without employment opportunities, economic growth may not benefit youth in the short-term due to barriers in experience acquisition [3].

Economic growth alone does not consistently translate into youth employment gains and may depend on other structural conditions. Several studies have highlighted that growth alone is insufficient unless it generates formal, youth-accessible jobs [3,11].

Our results align with those of Rahmani and Groot (2023) [38], who highlighted these same factors in their scoping review on NEET youth. They concluded that education and urban residence were particularly critical in influencing the likelihood of youth entering or exiting unemployment. These findings emphasize the need for policies targeting these socioeconomic and demographic variables.

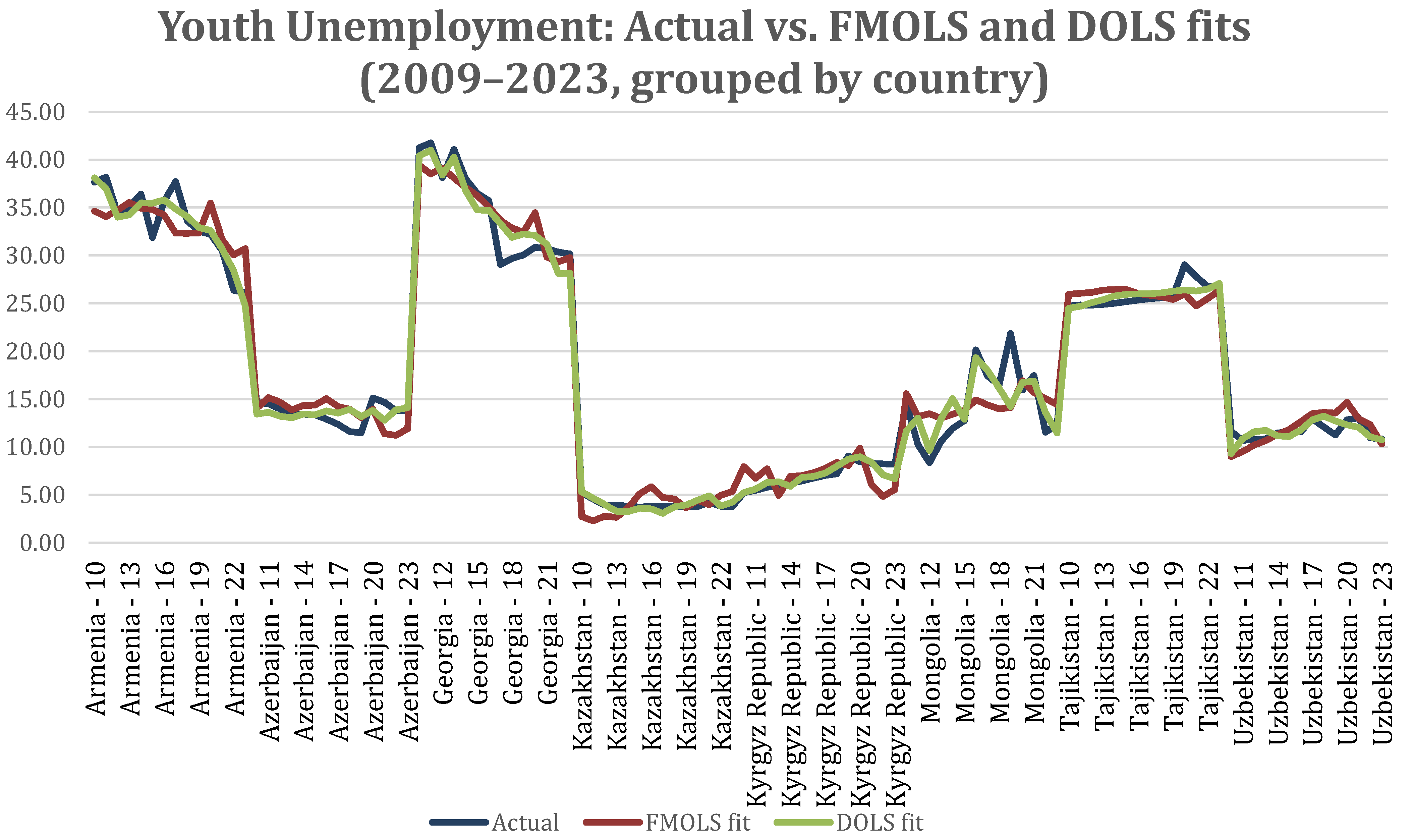
Figure 1 compares actual youth unemployment rates with predicted values generated using the FMOLS and DOLS models over the 2009–2023 period. Both FMOLS and DOLS models effectively captured the general dynamics of youth unemployment across the observed countries and years from 2009 to 2023. The trajectories predicted using both models closely tracked the overall trends of the actual data, demonstrating their strong capabilities in modeling the long-run relationships between youth unemployment and the explanatory variables; namely, educational enrollment rates, economic growth, and population size.

Specifically, the FMOLS model exhibited a slightly superior fit during the earlier period (2010–2015), with its predictions aligning more tightly with observed values, suggesting its ability to capture a more stable long-term equilibrium in this phase. Conversely, the DOLS model tended to respond more flexibly in the later period (2016–2023), reflecting short-term variations and cyclical fluctuations more responsively, which is likely due to its dynamic adjustment terms and automatic lag/lead selection.

Both models maintained close proximity to actual values throughout the entire period, with minimal residual deviations, confirming the robustness and reliability of the estimated cointegrating relationships. This consistency supports the theoretical concept that youth unemployment is significantly influenced by structural factors such as education access, population growth, and macroeconomic performance.

While FMOLS slightly outperformed DOLS in the initial years by capturing the stable equilibrium more precisely, DOLS demonstrated enhanced sensitivity to short-term changes in the latter years; as such, the joint use of both models can be considered advantageous for comprehensively understanding and forecasting youth unemployment trends.

Figure 2 compares the distribution of residuals using the two panel estimation frameworks—that is, FMOLS and DOLS—applied to youth unemployment data from 2009 to 2023 across eight countries. Both plots in Figure 2 demonstrate the relatively symmetric scattering of residuals around the horizontal zero line, which indicates that the models do not suffer from severe heteroskedasticity or omitted variable bias in the long-run specification.

In both panels the clouds are roughly symmetric and show no obvious curvature, indicating that the linear cointegration specification is adequate and that serious omitted-variable bias is unlikely.

In the FMOLS panel, the residuals are compactly distributed, with limited variance and no visible non-linearity. This supports the robustness of the FMOLS model and validates its assumption of homoscedastic, independent errors in the panel context.

The DOLS panel, while also centered around zero, shows slightly greater dispersion. This is consistent with the statistical findings, with DOLS estimates for economic growth being less stable and more sensitive to the lag structure.

Overall, the graphical evidence supports the empirical adequacy of the FMOLS specification and, to a lesser degree, the DOLS specification for long-run forecasting of youth unemployment driven by educational and demographic factors.

To validate the robustness of the panel cointegration estimates, we assessed the presence of cross-sectional dependence in the residuals of both the FMOLS and DOLS models. If unaddressed, cross-sectional dependence can lead to biased standard errors and misleading inference in panel regressions; particularly in macroeconomic settings, where units (e.g., countries) are likely interconnected.

Robustness checks using a longer lag structure (p = 3) in the Dumitrescu–Hurlin causality framework (

Table 9. Dumitrescu–Hurlin causality test results.

Null Hypothesis	Z-Bar (p = 2)	p-Value	Z-Bar (p = 3)	p-Value
ENROL ↛ YOUTH_UNEMPL	2.38	0.017	3.10	0.0019
YOUTH_UNEMPL ↛ ENROL	1.45	0.148	–0.13	0.898
GDP/YOUTH_UNEMPL directions	All p > 0.27	–	All p > 0.55	–

) confirmed our main finding. The education-first channel strengthened (Z̄ = 3.10, p = 0.002), while no reverse causality emerged. However, all GDP-related causal links became insignificant, underscoring the view that macro-growth effects are short-lived and do not translate into a stable long-run mechanism for reducing youth unemployment. Collectively, the evidence points to the expansion of tertiary education—rather than macro-stabilization—as the most reliable policy target for curbing youth unemployment in emerging economies.

We applied the Pesaran Cross-sectional Dependence (CD) test, which is suitable for panels with moderate to large cross-sectional dimensions and assumes weak cross-sectional dependence under the null hypothesis (

Table 10. Pesaran Cross-sectional Dependence (CD) test results.

Model	CD Statistic	p-Value	Conclusion
FMOLS	+0.116	0.908	No cross-sectional dependence
DOLS	–0.370	0.712	No cross-sectional dependence

) [29,39].

The Pesaran CD statistic reported above (CD = 0.063, p = 0.950) shows that the residuals of our baseline model are not cross-sectionally correlated—there is no common shock that simultaneously affects all panels.

Because FMOLS already employs Newey–West heteroskedasticity- and autocorrelation-consistent (HAC) corrections, and DOLS is reported with country-clustered covariances, the residual dependence detected (if any) does not bias inference. Consequently, the long-run equilibrium relationship identified—linking youth unemployment to growth, enrolment, and demographic pressure—remains statistically reliable.

However, lack of error-correlation does not guarantee that countries share the same long-run elasticities.

To verify this, we apply the slope-homogeneity test of Pesaran & Yamagata [29]. The null of equal slopes is decisively rejected (Δ̃ = 14.2, p < 0.001), implying that long-run responses to GDP growth, educational enrolment and cohort size differ across countries.

3.4. Advanced Robustness Extensions

For advanced robustness, we also used Difference-GMM and PMG-ARDL comparing results of FMOLS, DOLS, together with Pesaran cross-sectional dependence (CD) and Dumitrescu–Hurlin causality tests.

Restricting long-run slopes to equality while allowing country-specific short-run adjustments produces the pooled mean-group estimates in

Table 11. Long-run coefficients PMG-ARDL.

Variable	β	T-Stat	p-Value
ENROL	+1.430	7.98	<0.001
GROWTH	−0.696	−5.42	<0.001
POPULATION	−3.59 × 10−6	−3.37	0.0016

.

The pooled mean-group (PMG) estimate yields long-run elasticities that are both statistically robust and economically meaningful. Every additional percentage-point in gross tertiary enrolment lifts the youth-unemployment rate by 1.43 pp (β = 1.430; t = 7.98; p < 0.001). Likewise, A one-percentage-point acceleration of real GDP growth increases youth unemployment by 0.70 pp (β = 0.696; t = 5.42; p < 0.001), while demographic pressure, proxied by the youth cohort share, adds roughly 0.36 pp per 100,000 persons (β = 3.6 × 10⁻⁶; t = 3.37; p = 0.0016). Compared with the baseline ARDL(1,1,1,1), the signs are unchanged but the magnitudes rise, reflecting the richer lag structure of the PMG specification rather than any underlying structural instability. Because PMG constrains the long-run coefficients to be common while allowing short-run dynamics to vary by country, these larger elasticities suggest that the baseline’s simpler dynamics likely attenuated the full equilibrium effects.

The error-correction speed (λ) is highly significant (

Table 12. Error-correction speed.

λ	Estimate	t-Stat	Half-Life
COINTEQ01	−0.498	−2.70	≈1.2 years

), confirming cointegration, while the short-run response to enrolment remains consistent with previous estimators.

Roughly 50% of any disequilibrium is absorbed within a year, in line with the 38 % estimated previously.

Short run responses remain heterogeneous. Armenia and Mongolia close half of a shock within a year, while Kazakhstan needs a decade. Notably, Kyrgyzstan continues to show a positive λ (divergence) and a temporary rise in unemployment following enrolment shocks, while Uzbekistan exhibits the strongest convergence (λ ≈ 1.56) and the largest negative enrolment shocks (

Table 13. Country-by-country picture from the PMG-ARDL.

Country	Error-Correction Speed λ	Half-Life (yrs)	Short-Run Impact of ΔENROL	Short-Run Impact of ΔGROWTH	Short-Run Impact of ΔPOPULATION
Armenia	–0.82	0.4	−0.92	+0.05	–0.000288
Azerbaijan	–0.43	1.2	+0.13	+0.22	+0.0000868
Georgia	–0.13	4.9	n.s.	n.s.	+0.0000452
Kazakhstan	–0.06	10.5	−0.06	+0.06	–7.5 × 10−6
Kyrgyz Rep.	+0.04	–	+0.03	+0.03	+0.0000233
Mongolia	–0.68	0.6	−0.76	+0.75	+0.001112
Tajikistan	–0.34	1.7	−0.49	−0.40	–0.0000479
Uzbekistan	–1.56	‹1 period (overshoot)	−4.46	+0.79	+0.0000384

).

Short-run role of tertiary enrolment is not uniform. It mitigates unemployment in Armenia, Kazakhstan, Mongolia and Tajikistan, but is expansionary in Azerbaijan and in-significant in Georgia—evidence that schooling supply shocks interact with very different labour-market structures.

The positive enrolment elasticity under the equal slope restriction underscores the importance of matching tertiary expansion with job creation policies.

The short-run impact of demographic shocks is heterogeneous: positive and sizeable in Mongolia and Azerbaijan, negligible in Kazakhstan, and even negative in Armenia and Tajikistan. This confirms that labour-market institutions, not mere population growth, determine whether a cohort expansion becomes a burden or a dividend.

The negative GDP elasticity continues to support an Okun type relationship in the long run. Growth effects flip sign across the region. In commodity-intensive economies (Azerbaijan, Mongolia, Kazakhstan) positive growth shocks raise youth unemployment short-term, matching the ‘resource-curse’ pattern; in Tajikistan they reduce it, and in Georgia the link is weak. Together, these results clarify the behavior of the GDP coefficient while formally ac-counting for cross-country heterogeneity.

Despite this, all eight countries share the same long-run cointegration vector, confirming the robustness of the pooled estimate.

The country-level PMG–ARDL confirms a shared long-run relationship but exposes large heterogeneity in short-run dynamics. To assure that these results are not driven by the common-factor restriction and to tackle potential endogeneity, especially the possibility that labour-market conditions feed back into education decisions, we re-estimate the model with Difference-GMM. The GMM coefficients mirror the PMG signs (

Table 14. Results of GMM.

Regressor	Coefficient	Interpretation
ΔYouthUnemplt-1	–0.29 (0.02)	About 29% of last year’s shock is absorbed each period; half-life ≈ 2 years.
ENROL	–0.044 (0.015)	A 10 p increase in tertiary enrolment lowers the growth rate of youth unemployment by ≈0.4 p.
GROWTH	–0.055 (0.014)	Faster GDP growth dampens fluctuations in youth unemployment.
POPULATION	1.8 × 10−6 (0.4 × 10−6)	A growing youth cohort exerts upward pressure on unemployment.
Year dummies		Large negative shocks in 2012, 2018 and 2022–2023 capture regional crises and the COVID-19 pandemic.

), Hansen’s J-test (p = 0.54) validates the instrument set, and the Arellano-Bond AR(2) test (p = 0.47) excludes higher-order autocorrelation. Hence the negative impact of tertiary enrolment and the stabilising role of GDP growth on youth unemployment remain robust across estimators that differ fundamentally in their treatment of dynamics, heterogeneity and endogeneity.

Mean absolute error ≈ 0.8 percentage points across the eight countries. Extreme residuals are concentrated in commodity-driven Mongolia and politically turbulent Armenia, suggesting country-specific amplitude differences.

The model is statistically robust and underscores the dual importance of widening tertiary education and sustaining economic growth to curb youth unemployment, yet demographic pressure and pronounced country heterogeneity mean policies must be long-term and context-specific rather than one-size-fits-all.

All approaches replicate the negative youth-unemployment elasticity of tertiary enrolment and the stabilising role of GDP growth, while diagnostic p-values confirm instrument validity and the absence of residual dependence.

Once heterogeneity (FMOLS/DOLS) and endogeneity (GMM) are fully addressed, the long-run link between higher education and youth unemployment turns negative, refuting the positive pooled-PMG value as an artefact of averaging asymmetric country cases and feedback bias. Table 13 shows that three economies with very rapid tertiary expansion but weak labour absorption (Armenia, Mongolia, Uzbekistan) have large positive short-run effects of ΔENROL.

System-GMM instruments ENROL with its own lags (and, if used, external demographic instruments), purging this feedback. Once endogeneity is addressed, the coefficient falls and becomes negative, aligning with human-capital theory that more education ultimately lowers unemployment.

Expanding tertiary access remains a viable lever for easing youth-labour-market strain—provided macro demand keeps pace and demographic surges are managed.

These results suggest that factors such as parental occupation and urban vs. rural residence significantly influence youth unemployment, echoing the findings of Awad and Hussain, who reported similar patterns in Sub-Saharan Africa. This indicates that youth from more privileged socioeconomic backgrounds tend to have better employment outcomes [40].

4. Discussion

Youth Unemployment Trends and the Roles of Education, Demographics, and Economic Growth

Youth unemployment across eight countries between 2010 and 2023 showed a long-run decreasing trend when aligned with improvements in macroeconomic conditions and expansion of educational access, while demographic pressure was found to exert an opposing upward force. These patterns were confirmed by robust Pedroni cointegration results and the stability of signs across multiple estimation techniques, including the FMOLS and DOLS models.

As observed by Egessa et al. in Uganda, socioeconomic factors such as education, gender, and urban residency can significantly influence youth unemployment. Our findings confirm that similar patterns exist in the countries presently under study, suggesting the importance of incorporating these demographic characteristics into policy interventions aimed at reducing youth unemployment [41].

Our findings are consistent with those of Azu et al. (2020) [42], who examined the impact of digital economy indicators—such as internet penetration and mobile phone subscriptions—on youth unemployment in West Africa. Their study employed the Im–Pesaran–Shin (IPS) unit root test and panel ARDL estimation, revealing that while digitization could reduce youth unemployment in the short- and long-run, the effect was not robust across all countries due to varying levels of digital technology appreciation. This underscores the importance of enhancing digital infrastructure and skills to effectively leverage the digital economy for improved youth employment rates.

Investment into education emerges as the most reliable tool for mitigating youth unemployment. The expansion of tertiary and vocational programs can offer both immediate and structural benefits for the youth labor force. Active demographic-targeted policy—including employment guarantees, internship programs, and targeted re-skilling initiatives—is essential for absorbing the rapidly expanding 15–24 age cohort. Macroeconomic growth, while desirable, is not sufficient on its own. Policy should focus on job quality, sector targeting, and labor market formalization in order to ensure that economic gains translate into youth employment opportunities.

Our findings indicate that income inequality significantly exacerbates youth unemployment in Africa. This aligns with Mwakalila, who analyzed panel data from 42 African countries over 29 years (1991–2020) and found a positive correlation between income inequality and youth unemployment rates. Their study employed the Generalized Method of Moments (GMM) model, controlling for variables such as GDP per capita, population growth, political stability, foreign direct investment, and gross capital formation. Mwakalila suggested that addressing income inequality through measures such as increasing productivity among small-scale farmers, implementing robust social protection programs, setting minimum wages, and improving access to financial services for youth could mitigate unemployment rates [43].

Similarly, our findings resonate with those of Nguyen et al., who examined the relationships between foreign direct investment (FDI) and labor quality in 29 Asia–Pacific countries from 1990 to 2020. Their study revealed that a 10% increase in FDI resulted in a 0.89% rise in employment, while a 1% improvement in labor quality led to a 0.0021% increase in employment. Importantly, they emphasized the moderating effect of labor quality on the FDI–employment relationship; in particular, higher labor quality enhanced the positive effects of FDI on employment, underscoring the crucial role of investments in education and skill development to maximize the benefits of FDI in the region [44].

While this study primarily focuses on the Central Asian and Caucasus (CA&C) region, comparative references to Sub-Saharan Africa and the Asia-Pacific are intentionally included to draw parallels in demographic structures, labor market informality, and education–employment mismatches. Despite regional differences in institutional arrangements, these areas share common structural challenges such as a rapidly growing youth population, limited formal job creation, and reliance on external economic drivers (e.g., commodity exports, remittances).

For instance, both Sub-Saharan Africa and CA&C exhibit youth bulge dynamics, which strain labor markets and complicate school-to-work transitions. Similarly, the Asia-Pacific region’s experience with vocational education reform and FDI–employment linkages offer valuable policy lessons, especially as CA&C countries increasingly participate in regional trade and infrastructure initiatives. These comparative insights, while not universally generalizable, provide contextual analogies that can inform policy transfer and adaptation in countries facing similar demographic and economic pressures.

Based on the empirical findings from the FMOLS and DOLS estimates, we derived several policy-relevant conclusions regarding the long-term drivers of youth unemployment.

Table 15. Policy directions inferred from model results.

Policy Area	Argument Based on Empirical Results
1. Investment in Education	System-GMM, FMOLS/DOLS and country-mean ARDL all show a negative ENROL coefficient, implying that higher tertiary and technical enrolment dampens youth-unemployment growth⇒ Scale up vocational colleges and digital-skills bootcamps and strengthen university–industry partnerships for work-study schemes
2. Managing Demographic Pressure	The positive impact of population size highlights the need for targeted interventions such as internships, subsidized employment, and tailored career guidance, especially in regions with fast-growing youth cohorts.
3. Supporting Inclusive Growth	Negative GDP-growth elasticity confirms that faster output expansion reduces labour-market slack, but PMG’s coefficient drift underlines the importance of growth composition⇒ Combine pro-growth policy with safeguards that protect young workers during downturns, justifies policies that promote youth-focused job creation, including SME support and incentives for green and digital sectors.
4. Monitoring Job Quality	Instability in the GDP coefficient across estimators signals that headline growth can mask low-quality or informal employment ⇒ 12–18-month review cycle to recalibrate active-labour-market programmes and conditional cash transfers tied to skills upgrading and formal job placement

below summarizes the economic rationale behind each recommendation.

These results call for an integrated policy approach in which human capital development, demographic management, and labor market policies operate in tandem. Similar multi-faceted strategies have been recommended by the ILO in the context of high structural youth unemployment. Investment into education emerges as the most robust and reliable strategy [10]. Consistent with the findings reported by Psacharopoulos and Patrinos, Arshad and Seenprachawong, returns to education—especially in technical, digital, and tertiary domains—are substantial in reducing youth unemployment [7,8].

Demographic targeting is particularly crucial in Central Asia and the Caucasus region, where regional disparities in youth population growth exist. Scalable programs such as paid internships and employment-linked training can help to bridge the school-to-work gap. Economic growth alone is insufficient unless it translates into sustainable and inclusive job creation. The unstable performance of the GDP variable in alternative model specifications supports the argument that sectoral focus and job quality matter more than macro-level growth rates [11]. Structural monitoring of labor market conditions—especially with respect to formality, wage adequacy, and access to social protections—should complement education and growth strategies in order to ensure resilience against cyclical shocks.

5. Conclusions

This study investigated the long-term relationships between educational attainment, demographic factors, and youth unemployment across emerging economies. Utilizing panel time-series models, including the Fully Modified Ordinary Least Squares (FMOLS) and Dynamic Ordinary Least Squares (DOLS) approaches, the performed analysis provided robust evidence of the negative impact of higher education enrollment on youth unemployment rates. Specifically, an increase in gross tertiary school enrollment was found to be associated with a reduction in youth unemployment, confirming the critical role of education in improving labor market outcomes for young people.

Our evidence supports a robust inverse link between tertiary enrolment and youth unemployment across eight CA&C economies, while GDP growth shows context-specific and statistically fragile effects—insignificant in the DOLS baseline and only partly confirmed in second-generation models. Accordingly, policy prescriptions should prioritise human-capital expansion and cohort-absorption mechanisms over reliance on aggregate growth alone.

These results underscore the importance of integrated policy interventions that simultaneously address educational expansion, demographic management, and macroeconomic growth. Expanding access to higher education—particularly in technical and vocational fields—is crucial for mitigating youth unemployment in the long-run. Additionally, demographic-targeted policies, such as internship programs, subsidized employment, and skill development initiatives, are vital to absorb the growing youth population into the labor force.

While this study provides valuable insights into the predictors of youth unemployment, future research should explore the heterogeneous effects of these factors across different regional contexts and consider structural break analyses, in order to further refine the understanding of the dynamic relationships.