Distribution Prediction of Decomposed Relative EVA Measure with Levy-Driven Mean-Reversion Processes: The Case of an Automotive Sector of a Small Open Economy

Abstract

The paper is focused on predicting the financial performance of a small open economy with an automotive industry with an above-standard share. The paper aims to predict the probability distribution of the decomposed relative economic value-added measure of the automotive production sector NACE 29 in the Czech economy. An advanced Monte Carlo simulation prediction model is applied using the exact pyramid decomposition function. The problem is modelled using advanced stochastic process instruments such as Levy-driven mean-reversion, skew t-regression, normal inverse Gaussian distribution, and t-copula interdependencies. The proposed method procedure was found to fit the investigated financial ratios sufficiently, and the estimation was valid. The decomposed approach allows the reflection of the ratios’ complex relationships and improves the prediction results. The decomposed results are compared with the direct prediction. Precision distribution tests confirmed the superiority of the decomposed approach for particular data. Moreover, the Czech automotive sector tends to decrease the mean value and median of financial performance in the future with negative asymmetry and high volatility hidden in financial ratios decomposition. Scholars can generally use forecasting methods to investigate economic system development, and practitioners can obtain quality and valuable information for decision making.

1. Introduction

Predicting and measuring a sector’s or firm’s performance is a critical problem in planning and managing economic growth. A practically valuable group of performance measures is based on the economic profit term, or alternatively, the profit level after the deduction of an alternative cost of capital. In this case, market and accounting data are combined, and economic value added (EVA) is a practically useful financial performance measure. This measure is complex and reflects many factors and their interrelationships. Therefore, a decomposition approach can be fruitful.

A probability distribution forecast can give more valuable information in comparison to a point forecast. For instance, the authors of [1] state that the “density forecast especially provides a complete description of the uncertainty associated with a prediction and stands in contrast to a point forecast, which contains no description of the associated uncertainty”.

The automotive sector, with an above-standard share in the Czech economy, is an important economic segment influencing the effectiveness and performance of the national economy. The sector is designated 29 in the NACE categorisation—Manufacture of motor vehicles, trailers and semi-trailers. Sector share in the C-Manufacturing sector is significant and is as follows: assets, 25.44%; fixed assets, 24.80%; current assets, 27.45%; equity, 21.57%; debt, 28.86%; sales, 37.60%; cost, 39.10%; salaries, 29.51%; EBIT, 30.30%; and value added, 30.48%. With regard to production, other sectors are also connected. Therefore, the analysis and prediction of the performance measure of sector 29 constitute a very important problem.

This paper’s objective is to predict the relative EVA measure probability distribution of sector 29 in the Czech economy using advanced methods, including distribution precision testing. The proposed model and procedure consist of the following elements: (a) a decomposed financial performance measure, (b) forecasting via the Monte Carlo simulation method, (c) a mean reversion random process with NIG (normal inverse Gaussian) distribution, (d) modelling the statistical interdependencies with t-copula, and (e) testing the precision of distribution forecasting. To be more precise:

(a)

Approaches for measuring a sector’s performance have evolved and reflect the technical-economic type of economy, information possibilities, data reachability, and knowledge of economic systems management. Among performance indicators, traditional groups based on accounting profitability measures can be found, such as ROE, ROA, ROC, ROI, and RONA, as well as measures based on financial cash flow, such as CFROI, NPV, and CROGA. Researchers deal with various financial performance measures (see, e.g., [2,3]). The compromise between accounting and market data is the measures combining both data types, so economic value added (EVA) and refined economic value added (REVA) measures were developed. Three authors [4,5,6,7] have, for instance, applied EVA performance measures. A financial performance measure can be decomposed by the pyramid (DuPont) method in several financial ratios and simulated as their function with correlations, obtaining a more robust prediction (see [8,9,10,11,12,13]).

(b)

A crucial problem in financial decision making is achieving good financial forecasting, and researchers have verified various methods (see [14,15,16,17,18,19]). Interesting forecasting approaches were introduced in [20,21,22,23]. One of the forecasting approaches and conceptions is applying the simulation method with dependencies modelled by the copula function [24,25,26]. The generalised random processes are mean-reversion processes, e.g., [27,28].

(c)

The probability distributions of financial variables are asymmetric, with fat tails, leptokurtic distributions, jumps, and mean reversion. To model such variables, Levy distributions were proposed and verified. A suitable probability distribution for the modelling of financial ratios and electricity and energy prices is the so-called NIG distribution, coined by the author of [29]. The distribution parameters can be estimated by the likelihood method or the method of moments, and possible approaches have been described, e.g., [30,31,32,33]. Subsequently, for example, refs. [34,35,36,37,38] applied the NIG distribution in option valuation and value at risk prediction. The authors of [39] first proposed and verified the Levy-driven mean-reversion process, also known as the Levy-driven Ornstein–Uhlenbeck or non-Gaussian Ornstein–Uhlenbeck random processes. The first term is used in this paper exclusively because of the financial modelling background. Other researchers further analysed and developed this problem, e.g., [28,40,41,42,43,44,45,46]. Several authors [1,47,48,49,50,51,52] dealt with probability distribution forecasting for predicting uncertainty.

(d)

The procedures and advantages of disaggregated (multifactor) forecasting are described in [53,54,55]. A multifactor simulation needs to model dependencies, and copula functions can usually be used. Furthermore, refs. [19,20] are authors who have dealt with such a conception. The precision of the simulation and the number of replications (interactions) are investigated in, e.g., [25,56,57,58,59].

(e)

A particular problem in distribution forecasting is stating forecasting precision and choosing the more suitable probability distribution. Two conceptions exist, absolute and relative ones. The first one is based on the probability integral transform of the distribution and a comparison with the uniform distribution. The closer the uniform distribution, the better the forecasting distribution is (see [49,52,60,61]). The scoring method investigates the relative evaluation of two distributions, and a higher score means a better forecast distribution [47,62,63,64,65]. The statistical difference significance can be tested by a paired t-test.

This paper’s novelty lies in using the advanced prediction methods of the decomposed relative EVA measure of the Czech automotive NACE sector 29. Whereas prediction is based on the pyramid decomposition expressed by an exact mathematical function, the applied advanced stochastic processes (mean-reversion, skew t-regression, NIG distribution, t-copula) suitably reflect the behaviour and features of financial ratios. These characteristics are significant not only because of these reflections but also due to fundamental features such as economic and technical shocks (particularly COVID-19), shortages of spare parts and commodities, product transportation disorders, and military operations in the sector. With an above-standard share in the small open Czech economy, the automotive sector is also crucial for national economic performance and public finance. Furthermore, empirical verification and prediction are therefore desirable.

The paper is structured as follows: (i) a conceptual and methodological background description, (ii) a proposal and description of the applied decomposed methodology, (iii) a description of the compared direct (non-decomposed) methodology, (iv) input data, solution procedures and interpretation of the results, (v) probability distributions precision testing, and (vi) discussion and conclusion.

2. Methodology and Procedure Description

The relative EVA measure, $EVAr$, is decomposed on the pyramid decomposition basis on two levels. Firstly, the EVA is divided into $ROE$ and $r_e$; subsequently, $ROE$ is decomposed into $EAT/EBT,EBT/EBIT,EBIT/S,S/A,A/E$. Summarising $EVAr$ is expressed by the exact function of six basic influencing financial ratios:

$$EVAr=ROE-r_e=\frac{EAT}{EBT}·\frac{EBT}{EBIT}·\frac{EBIT}{S}·\frac{S}{A}·\frac{A}{E}-r_e,$$

(1)

where $ROE$ is a return on equity, $EAT$ is earnings after tax, $EAT$ is earnings before tax, $EBIT$ is earnings before interest and tax, $S$ is sales, $A$ is an asset value, $E$ is the equity value, and $r_e$ is the cost of equity capital. Therefore, performance is given by tax reduction, debt coverage, revenue profitability, asset turnover, financial leverage, and the equity cost of capital. The proposed decomposition is used in the analysis and prediction part.

2.1. Prediction of Performance Measure by Simulation

The primary goal is to predict a relative EVA measure distribution based on decomposition (1) using a simulation approach. Due to the Levy-driven mean-reversion process with an NIG distribution, particular ratios are supposed to develop along the way. The arithmetic Levy-driven mean-reversion (LDAMR) process is presented, e.g., in [42,46], and expressed in (2). The Levy-driven, one-factor Schwartz mean-reversion (LDSMR) process [44] is formulated in (3):

$$dx=a·\left(b-x\right)dt+dL,$$

(2)

$$\frac{dx}{x}=a·\left(b-\ln x\right)·dt+dL,$$

(3)

where $dx$ represents the changes in ratios, $a$ is the speed parameter, $b$ is the long-term equilibrium, $dt$ is the time interval, and $dL$ is the random NIG process.

The LDAMR process is suitable for ratios with positive or negative values. LDSMR is applicable only for positive financial ratio values, e.g., prices and turnovers. The solution to the equations are as follows:

$$x_t=x_{t-dt}·e^{-a·dt}+b·\left(1-e^{-a·dt}\right)+{\displaystyle \underset{s=t-dt}{\overset{t}{\int }}{e}^{-a·\left(t-s\right)}}·d{L}_s,$$

(4)

$$x_t=\exp \left\{\left[\ln \left(x_{t-dt}\right)·e^{-a·dt}\right]+\left[b·\left(1-e^{-a·dt}\right)\right]+{\displaystyle \underset{s=t-dt}{\overset{t}{\int }}{e}^{-a·\left(t-s\right)}}·d{L}_s\right\}.$$

(5)

The advantages of these processes are in their generalisation because, for $a=0$, the process is reduced in a Levy process and the exponential Levy process, respectively; for $b=0$, the process reduces in an arithmetic and exponential (geometric) Levy process, respectively.

Since the intention is to predict a relative EVA distribution, the stochastic integral with respect to the Levy process is simulated by a sum method, such as the Riemann–Stieltjes sum method (see, e.g., [34,66]):

$${\displaystyle \underset{s=t-dt}{\overset{t}{\int }}{e}^{-a·\left(t-s\right)}}·d{L}_s\approx {\displaystyle \sum _{j=1}^N{e}^{-a·\left(t-s_{j-1}\right)}}·\Delta L_{s_j},$$

(6)

where $s_j=t-dt+\Delta ·(j-1)$, $\Delta =dt/N$, and $\Delta L_{s_j}\approx NIG(\alpha ,\beta ,\Delta \delta ,\Delta \mu )$.

The approximate simulation formulas of processes (4) and (5) for $M$ steps are as follows:

$$x_{s_M}=x_{s_0}·e^{-a·(s_j)}+b·\left(1-e^{-a·s_j}\right)+{\displaystyle \sum _{j=1}^M{e}^{-a·\left(t-s_{j-1}\right)}}·\Delta L_{s_j},$$

(7)

$$x_{s_M}=\exp \left\{\ln \left(x_{s_0}\right)·e^{-a·(s_j)}+b·\left(1-e^{-a·s_j}\right)+{\displaystyle \sum _{j=1}^M{e}^{-a·\left(t-s_{j-1}\right)}}·\Delta L_{s_j}\right\}.$$

(8)

The applied estimation and simulation procedure steps of a decomposed conception

The estimations of the processes of the indices were obtained using Stata software (Version 15.1); for other operations, Matlab software (Version R2020b) was used.

(i)

Statistical estimation of Equations (2) and (3) using skew-t regression

An estimation of parameters $a$ and $b$ is carried out using the skew-t regression with parameters using the Stata function $skewtreg(\alpha ,\omega ,df)$, as in [67], where $\alpha$ is a shape parameter ($\alpha >0$ skewness to the right; $\alpha <0$ skewness to the left), $\omega >0$ is a scale parameter, and $df>0$ is the degree of freedom (the tails parameter). The choice of a suitable process, (2) or (3), is made based on the Akaike (AIC) and the Bayesian (BIC) information criterion values.

(ii)

Estimation of the chosen models regarding the NIG distribution parameters of the residuals

NIG distribution, including jumps and asymmetry, is parametrised as follows: $NIG(\alpha ,\beta ,\delta ,\mu )$, where $\alpha \ge 0$ is the tail heaviness, $\beta$ is skewness, $\mu$ is a location, $\delta >0$ is a scale parameter, and ${\alpha }^2>{\beta }^2$. The NIG distribution parameters are estimated using the method of moments (see, e.g., [32]).

(iii)

Estimation of the t-copula function

The t-copula function models the mutual interdependencies of the ratio residuals for a t-distribution with parameters of the correlation matrix $R$ and degree of freedom $v$ (see [18]).

(iv)

Simulation of the one scenario with N steps of the development of financial ratios and the following calculation of relative EVA

Financial ratios are simulated according to (7) or (8). Relative EVA is calculated using (1). The Matlab functions $copularnd$ and $niginv$ are applied to generate the random numbers of stochastic processes.

(v)

Repeating step (iv) for M scenarios, the result is one replication of the EVA distribution

(vi)

Replication (iteration) of step (v) r-times for a given precision

According to [56], the precision criterion of the distribution parameters (expected value, median, quantiles) is the relative confidence interval of a standard error, $d_r=\left(2·s_{{\overline{X}}_r}·t_{r-1}(\alpha /2)/\sqrt{r}·k\right)/{\overline{X}}_r\le 0.10$, where ${\overline{X}}_r$ and $s_{{\overline{X}}_r}$ are parameters (mean, quantiles) of the expected value and expected value standard error of the $r$ replications; $t_{r-1}(.)$ is the Student-t distribution with the significance $\alpha$; and $r-1$ is the degree of freedom. Furthermore, $k$ is a coefficient, with a mean value $k=1$ and for quantiles $p$ $k=p·(1-p)/\varphi (z(p))$ with $\varphi (·)$ and $z(p)$, respectively, equal to a density function. $p^{th}$ is the quantile of the standard normal distribution.

(vii)

Calculating the chosen parameters and graphical presentation of the results

Mean, medians, and quantile development values are tabulated, and the predicted relative EVA distribution is graphically presented.

2.2. The Evaluation of Forecast Prediction Precision

The absolute precision evaluation is based on probability integral transform (PIT), creating a random variable $z$. Following [60], $z_t=F_{t-1}(y_t)={\displaystyle \underset{-\infty }{\overset{y_t}{\int }}{f}_{t-1}(u)}du$, where $F_t$ is the distribution, $f_t$ is the density function, and $y_t$ is the real relative EVA. The variable is compared with uniform distribution $z_t\sim U\left(0,1\right)$. The closer the forecast distribution is to a uniform distribution, including statistical significance, the more suitable the distribution is for prediction. To verify its significance, the STATA Epps–Singleton Two-Sample Empirical Characteristic Function test is applied as in [68]. Here, hypothesis H0 states the distributions are identical, and HA states the distributions are not identical. The W2 statistics are calculated.

The relative precision conception compares two distributions using to any score measure. A suitable score approach for distribution $F$ is the logarithmic scoring rule, where, according to [63], $S_{}^L\left(f_{t-1},y_t\right)=\log \left(f_{t-1}\left(y_t\right)\right)$, and the whole score is $S_f^L=E\left(S_{}^L\left(f_{t-1},y_t\right)\right)=N^{-1}{\displaystyle \sum _{t=1}^N\log \left(f_{t-1}\left(y_t\right)\right)}$. The bigger the whole score is, the better the distribution. To test the significance of the difference (diff) of the two distributions $F$ and $G$, the STATA paired t-stat is calculated, $diff=E\left[\log \left(f_{t-1}\left(y_t\right)\right)-\log \left(g_{t-1}\left(y_t\right)\right)\right]$.

Hypothesis H0.

$diff=0$ and HA: $diff\ne 0$.

3. Results

The relative EVA measure decomposition is used to predict four quarters using a simulation procedure, including precision testing. A particular decomposition equation is introduced in (1). The applied methodology follows the procedures described in Section 2.1 and Section 2.2.

Furthermore, a direct (non-decomposed) EVA measure to predict four quarters using the simulation procedure is applied for comparison.

3.1. Input Data

The input data of the exact pyramid decomposition financial ratios are obtained quarterly and are calculated from MPO ČR (see [69]). The data of MPO ČR are obtained on a cumulative yearly basis every month. Therefore, the necessary transformation procedure for quarterly data is as follows: for flow data, two subsequent quarters are subtracted; for returns, the yearly returns are divided four times. Data are divided into two groups: in the sample and out of the sample. The first one is the period from 2007 to 2019 (

Table 1. Input quarter financial ratios data obtained quarterly, 1Q 2007–4Q 2019 (in the sample).

Quarter	Eat/EBT	EBT/EBIT	EBIT/S	S/A	A/E	re	EVAr
1	0.75014	0.95004	0.07881	0.47491	1.98257	0.02658	0.02630
2	0.75086	0.94867	0.07807	0.90783	2.02903	0.02538	0.07706
3	0.74061	0.94354	0.07396	1.30160	1.94837	0.02660	0.10446
4	0.74366	0.94023	0.07327	1.78199	1.92289	0.02566	0.14988
5	0.77734	0.94413	0.07794	0.44540	1.98827	0.02369	0.02697
6	0.77577	0.94586	0.08551	0.86450	2.00749	0.02551	0.08337
7	0.76879	0.93705	0.07759	1.27875	1.97374	0.02629	0.11477
8	0.75428	0.91863	0.06732	1.60054	1.98394	0.02617	0.12195
9	3.18631	−0.16599	0.01625	0.32793	2.16358	0.03535	−0.04145
10	0.81536	1.36320	0.05431	0.38117	2.12725	0.03816	0.01078
11	0.78156	1.08712	0.02851	0.35716	2.07487	0.03816	−0.02021
12	0.51225	0.97850	0.01080	0.40405	2.14607	0.03894	−0.03425
13	0.78997	1.10192	0.06197	0.41753	2.17226	0.03747	0.01146
14	0.79720	0.90460	0.08597	0.43299	2.17778	0.03231	0.02615
15	0.78066	1.29319	0.03556	0.36251	2.14857	0.03062	−0.00266
16	0.77958	1.18283	0.01240	0.42034	2.24465	0.03080	−0.02002
17	0.79540	1.07171	0.05844	0.43528	2.38018	0.03197	0.01964
18	0.81016	1.00998	0.06542	0.44084	2.29702	0.03086	0.02334
19	0.80254	1.59366	0.04524	0.38416	2.26978	0.03127	0.01918
20	0.78895	0.51720	0.03792	0.42881	2.41741	0.03023	−0.01419
21	0.79985	1.04540	0.06700	0.44184	2.45263	0.03389	0.02682
22	0.79481	0.82626	0.05999	0.42084	2.40768	0.02918	0.01074
23	0.79339	1.03788	0.04133	0.36101	2.25590	0.02895	−0.00123
24	0.79175	0.98847	0.02653	0.40537	2.26410	0.02850	−0.00944
25	0.78358	0.90614	0.05187	0.41812	2.18459	0.02436	0.00928
26	0.78903	0.83680	0.05464	0.43442	2.12970	0.02763	0.00574
27	0.80333	1.00609	0.05703	0.40554	2.09579	0.02303	0.01615
28	0.78411	0.97700	0.03392	0.44027	2.13028	0.02721	−0.00284
29	0.79993	0.87324	0.06610	0.46646	2.22686	0.02340	0.02456
30	0.80483	0.92038	0.06917	0.47099	2.14962	0.02395	0.02793
31	0.79859	0.83385	0.06575	0.43322	2.18257	0.02229	0.01911
32	0.80797	0.84079	0.05176	0.44778	2.23624	0.02045	0.01476
33	0.80349	0.97089	0.11268	0.46954	2.38048	0.01947	0.07878
34	0.80661	0.97800	0.07062	0.46676	2.28247	0.01993	0.03942
35	0.80506	0.95861	0.06289	0.42888	2.16827	0.01970	0.02543
36	0.80378	0.98388	0.04972	0.47314	2.09924	0.01962	0.01943
37	0.80539	0.86607	0.07405	0.47049	2.23160	0.01966	0.03457
38	0.81084	0.92645	0.08247	0.51032	2.17226	0.01846	0.05022
39	0.80621	1.02778	0.07186	0.41665	2.13081	0.01801	0.03485
40	0.81898	0.88190	0.06425	0.55275	2.06532	0.01735	0.03562
41	0.80230	0.96162	0.07472	0.52125	2.22759	0.01789	0.04905
42	0.80273	0.92573	0.07995	0.41421	2.08879	0.01757	0.03383
43	0.79929	0.92112	0.04366	0.48833	2.07591	0.01760	0.01499
44	0.80408	0.99536	0.05780	0.46164	2.23160	0.01940	0.02826
45	0.79745	0.97059	0.06132	0.48362	2.37538	0.02329	0.03123
46	0.80391	0.95780	0.06989	0.50216	2.33403	0.02379	0.03928
47	0.76634	0.90302	0.03822	0.41458	2.31449	0.02379	0.00158
48	0.79852	0.92980	0.03040	0.51344	2.24047	0.02353	0.00243
49	0.79214	0.97320	0.06131	0.47749	2.55076	0.02343	0.03414
50	0.80321	0.97833	0.05211	0.51524	2.45404	0.02394	0.02785
51	0.79190	0.95308	0.04275	0.45720	2.41447	0.02394	0.01168
52	0.79548	0.98283	0.03868	0.47719	2.35871	0.02343	0.01061

). The period finishes in 2019 because it marks the end of the pre-COVID-19 period. The last row of Table 1 contains the first real set of data used for prediction; in particular, the relative EVA is 1.0605%. The second group includes the prediction period and is shown in

Table 2. Input quarter financial ratios data obtained monthly (out of sample).

Month		Eat/EBT	EBT/EBIT	EBIT/S	S/A	A/E	re	EVAr
Beginning	Ending
1/2020	2/2019	0.79548	0.98283	0.03868	0.47719	2.35871	0.02343	0.01061
2/2020	1/2020	0.70667	0.85787	0.03911	0.46644	2.42099	0.02463	0.00214
3/2020	2/2020	0.73808	0.94020	0.03568	0.59935	2.37640	0.03882	−0.00355
4/2020	3/2020	0.78519	0.80588	0.04163	0.47701	2.31912	0.02593	0.00321
5/2020	4/2020	0.61353	0.59215	0.02147	0.72470	2.38058	0.03733	−0.02387
6/2020	5/2020	0.58124	0.63163	0.02013	0.77064	2.36644	0.05973	−0.04625
7/2020	6/2020	0.64582	0.55732	0.02281	0.76829	2.33867	0.03394	−0.01918
8/2020	7/2020	0.69266	0.70302	0.02797	0.73958	2.42558	0.02986	−0.00543
9/2020	8/2020	0.68537	0.74358	0.02644	0.92002	2.38921	0.03898	−0.00936
10/2020	9/2020	0.72912	0.67598	0.02909	1.22080	2.30392	0.03144	0.00889
11/2020	10/2020	0.58227	0.78497	0.03377	1.20068	2.66936	0.03699	0.01248
12/2020	11/2020	0.71838	0.83068	0.03191	1.40694	2.57366	0.04867	0.02029
1/2021	12/2020	0.63274	0.92568	0.02909	0.84507	2.24924	0.02332	0.00907
2/2021	1/2021	0.71838	0.94209	0.03165	1.31222	2.45315	0.04227	0.02669
3/2021	2/2021	0.53447	0.90599	0.03954	0.64222	2.42609	0.02407	0.00576

.

3.2. The Prediction Results of Relative Decomposed EVA Performance Measure by Simulation

In step (i), the skew-t regression is realised for all ratios, as well as for LDAMR and LDSMR models. The best models are chosen following the AIC and the BIC (see

Table 3. Estimated parameters of LDAMR and LDSMR models.

Variable	Eat/EBT		EBT/EBIT		EBIT/S
Model	LDSMR	LDAMR	LDSMR	LDAMR	LDSMR	LDAMR
Ln(x)	−0.541 ***		−0.581 ***		−1.069 ***
x		−0.995 ***		−1.338 ***		−0.728 ***
constant	−0.114 ***	0.801 ***	−0.029 ***	1.258 ***	−2.803 ***	0.059 ***
alpha	−1.050	−1.965	0.017	0.313	−0.607	−2.164
omega	0.00918	0.00815	0.02960	0.04846	0.27832	0.02047
df	0.89853	0.90846	0.84705	1.29175	1.59042	3.81904
LL	112.021	126.315	39.122	39.687	−38.228	130.651
chi2	18,000	250,000	84.363	257.752	40.380	66.421
p	0	0	0	0	0	0
BIC	−204.38	−232.97	−58.68	−59.72	96.12	−241.64
AIC	−214.04	−242.63	−68.24	−69.37	86.46	−251.30
a		0.9945541		1.3379895		0.7281569
b		0.8056467		0.9401605		0.0811942
Variable	S/A		A/E		re
Model	LDSMR	LDAMR	LDSMR	LDAMR	LDSMR	LDAMR
Ln(x)	−0.567 ***		−0.181 **		−0.028
x	0	−0.474 ***		−0.209 **		−0.037
constant	−0.436 ***	0.216 ***	0.099	0.364 **	−0.122	0.001
alpha	−0.267	−0.017	4.826	4.621	0.321	0.204
omega	0.06734	0.03453	0.05878	0.12619	0.04628	0.00109
df	3.49384	6.92404	17.63702	14.06937	2.01174	1.71258
LL	42.827	77.310	97.033	57.209	58.271	243.776
chi2	23.471	13.011	7.874	10.515	0.551	0.894
p	0	0	0.005	0.001	0.458	0.345
BIC	−66.85	−135.81	−174.41	−94.76	−96.88	−467.89
AIC	−75.65	−144.62	−184.07	−104.42	−106.54	−477.55
a		0.4749463	0.1808063			0.0367403
b		0.4538435	0.5453796			0.0146380

Legend: ** and *** denote significance at 5% and 1%, respectively.

). The estimated parameters are statistically significant. Furthermore, parameter $\alpha$ shows the asymmetry of the distributions on the left or right side; nothing equals zero, meaning symmetry is maintained. Four ratios are left-skewed, and two are right-skewed, showing non-positive tendencies. The parameters $\omega$ illustrate a scale which is not high. The parameters $df$ are small, confirming the fat tails of distributions. The empirical results confirm a correct regression model choice and financial ratio features. The last two rows present estimated parameters $a$ and $b$, including the selected best models. The empirical results show that all the best models are of the LDAMR (arithmetic) type, except for the ratio A/E model, which is of the LDSMR (Schwartz) type.

Step (ii) consists of estimating the NIG distribution parameters of the residuals. Parameters are estimated using the method of moments (see, e.g., [32]), where the Matlab $nigpar$ function is used. The results are presented in

Table 4. NIG residuals distribution parameters of the chosen ratio models.

Model Ratios		α	β	μ	δ
Eat/EBT	LDAMR	11.1	−10.267	0.0084	0.001
EBT/EBIT	LDAMR	202.3	201.861	−0.1447	0.0057
EBIT/S	LDAMR	104.6	15.0765	−0.0147	0.0426
S/A	LDAMR	64.5961	14.1858	−0.0229	0.1003
A/E	LDSMR	105.2	104.37	−0.0694	0.0062
re	LDAMR	12.9	12.3956	−0.0002	0.0087
EVA direct	LDAMR	51.3976	14.7134	−0.0034	0.0518

. The estimated parameters indicate heaviness $\alpha$, high skewness $\beta$, a location close to zero $\mu$, and a not large scale $\delta$. The NIG distributions adequately fit the data.

In step (iii), the parameters of the t-copula function from residuals are estimated. The Matlab function $copulafit$ was used for parameter estimation as the average of the one million simulations, particularly the degree of freedom $v=3.4583$.

Table 5. The correlation matrix of the residuals.

R	Eat/EBT	EBT/EBIT	EBIT/S	S/A	A/E	re
Eat/EBT	1	−0.2435	0.6426	−0.0029	−0.8151	−0.4035
EBT/EBIT	−0.2435	1	−0.1462	−0.1772	0.2115	0.3274
EBIT/S	0.6426	−0.1462	1	0.217	−0.6158	−0.3574
S/A	−0.0029	−0.1772	0.217	1	−0.0078	0.1567
A/E	−0.8151	0.2115	−0.6158	−0.0078	1	0.4517
re	−0.4035	0.3274	−0.3574	0.1567	0.4517	1

displays the correlation matrix $R$.

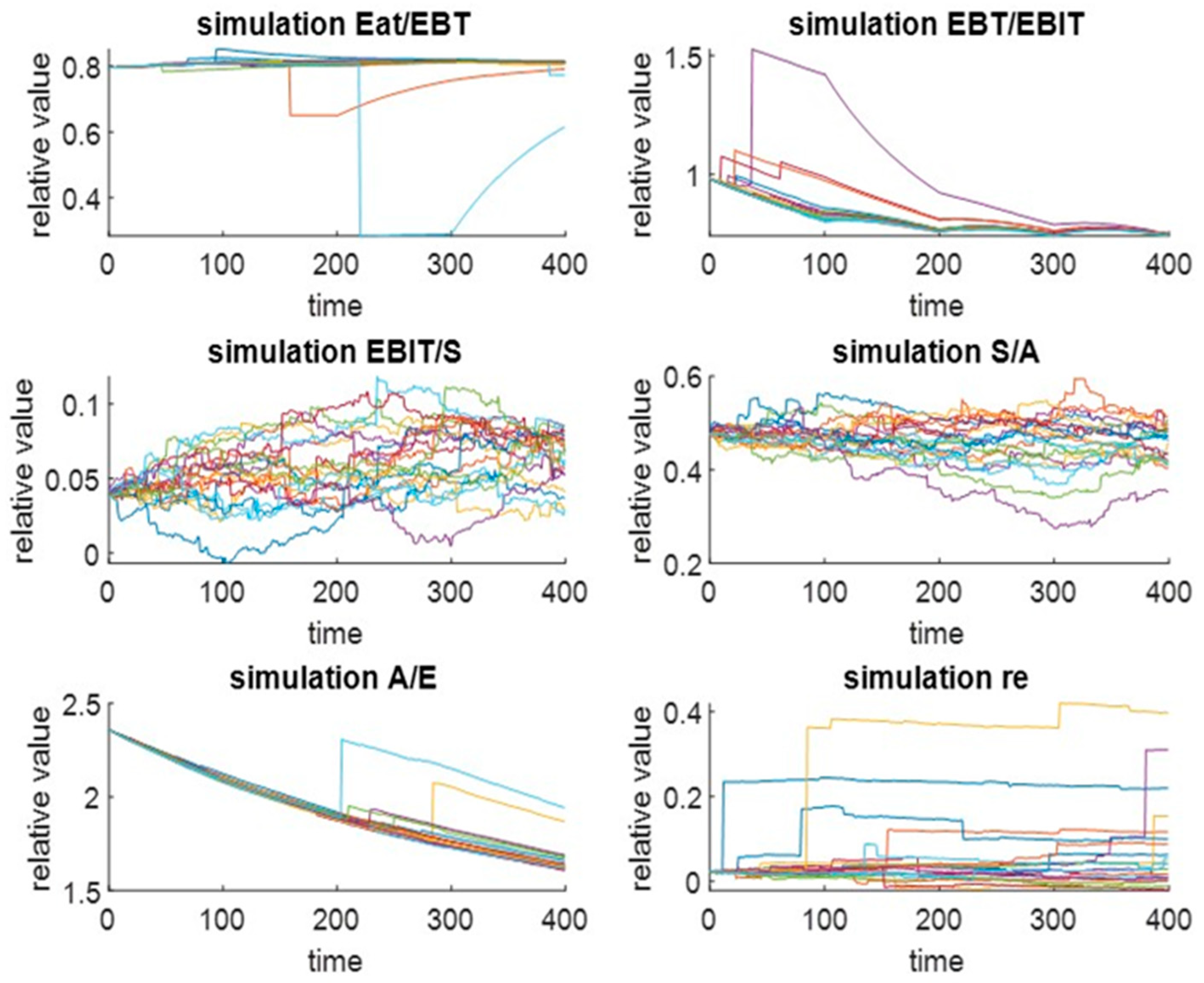
Steps (iv) and (v) encompass the simulation of six particular ratios and the relative EVA measure’s calculation—400 steps were used in one scenario for the year with 10⁶ scenarios. The special Matlab functions $copularnd$ and $niginv$ reflecting the t-copula function were utilised to generate random numbers and simulations. A presentation of 20 scenarios (colored), including their interdependencies, is shown in Figure 1, where asymmetry, fat tails, and jumps are apparent and verified. Likewise, every ratio demonstrates a different and unique distribution shape. Furthermore, the distribution of the relative EVA measure for one replication is illustrated in Figure 2 with decreasing distribution quantiles and negative asymmetry.

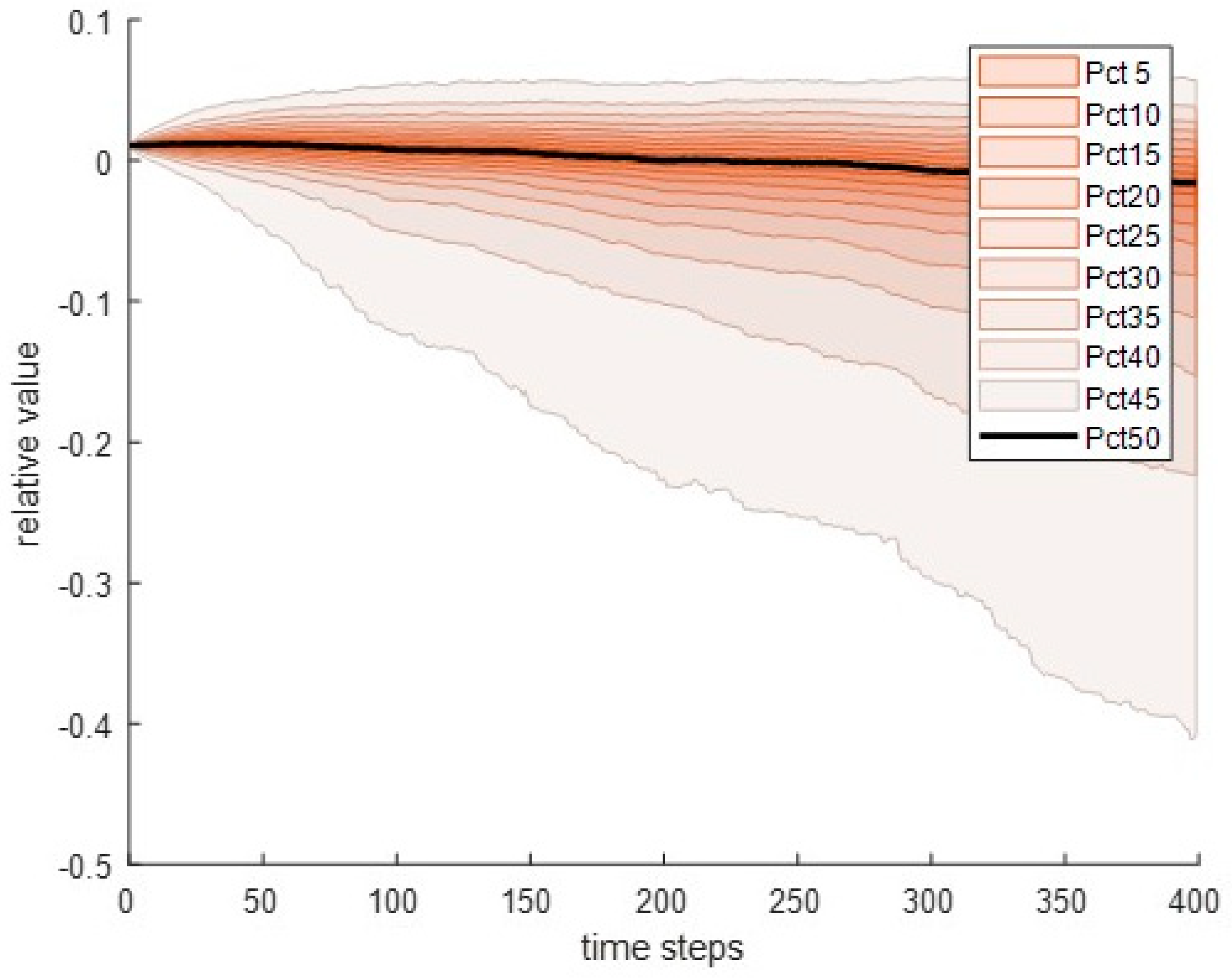
Step (vi) consists of the replication of step (v) 110 times due to the relative confidence interval of a standard error being less than 0.1. The results are shown in

Table 6. Quarterly prediction results of relative EVA measure in %.

Quarter		I. Q			II. Q
Parameter		${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
$Mean$		−0.898	0.231	9.578	−2.787	0.178	2.376
$Median(·)$		0.468	0.056	0.897	−0.062	0.060	7.271
Quantiles (%)	95	4.402	0.028	0.005	4.833	0.036	0.006
	90	3.300	0.030	0.018	3.508	0.036	0.020
	80	2.208	0.035	0.067	2.173	0.041	0.078
	70	1.527	0.041	0.158	1.313	0.045	0.205
	60	0.970	0.048	0.347	0.606	0.051	0.597
	50	0.468	0.056	0.897	−0.062	0.060	7.271
	40	−0.053	0.069	9.066	−0.770	0.073	0.673
	30	−0.643	0.088	0.813	−1.645	0.099	0.358
	20	−1.485	0.128	0.358	−3.047	0.162	0.222
	10	−3.570	0.284	0.156	−7.143	0.405	0.111
	5	−8.293	0.740	0.075	−16.235	0.826	0.043
Quarter		III. Q			IV. Q
Parameter		${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
$Mean$		−5.803	0.174	1.119	−7.570	0.398	1.960
$Median(·)$		−1.122	0.073	0.486	−1.875	0.172	0.681
Quantiles (%)	95	4.670	0.045	0.008	4.688	0.103	0.018
	90	3.192	0.046	0.028	3.080	0.104	0.066
	80	1.658	0.049	0.123	1.382	0.113	0.341
	70	0.633	0.055	0.514	0.212	0.126	3.532
	60	−0.247	0.062	1.779	−0.812	0.144	1.254
	50	−1.122	0.073	0.486	−1.875	0.172	0.681
	40	−2.125	0.093	0.307	−3.145	0.218	0.490
	30	−3.522	0.129	0.217	−5.008	0.306	0.362
	20	−6.137	0.213	0.145	−8.582	0.496	0.241
	10	−14.425	0.443	0.060	−19.332	0.994	0.101
	5	−30.395	0.757	0.021	−38.508	1.649	0.036

for the mean value and quantiles, including the standard error and the parameter of preciseness. The predicted probability distribution development is presented in Figure 3.

Apparently, the precision of distribution parameters is commonly less than 10% and mostly less than 5%.

3.3. The Prediction Results of Relative Direct EVA Performance Measure by Simulation

The direct approach is simplified by comparing the decomposition approach (Section 3.1) in forecasting using only one measure and not using interdependencies. In step (i), the skew-t regression is realised for the direct relative EVA measure for the LDAMR and LDSMR models. The best model selected according to the AIC and the BIC is the LADMR model (see

Table 7. The estimated parameters of LDAMR and LDSMR models for direct EVA.

Model	LDSMR	LDAMR
Variable	EVA	EVA
Ln(x)	−0.195	0
x	0	−0.706 ***
constant	−1.072 *	0.007
alpha	0.604	0.537
omega	0.62002	0.02032
df	1.54496	2.28416
LL	−65.996	105.743
chi2	14.663	14.663
p	0	0
BIC	150.68	−191.83
AIC	141.99	−201.49
a		0.7060
b		0

Legend: * and *** denote significance at 10% and 1%, respectively.

). Moreover, parameter $\alpha$ shows the right skewness of the direct relative EVA distribution, and parameter $df$ confirms the existence of fat tails. The value of parameter $\omega$ demonstrates a smaller scale.

In step (ii), the parameters of the NIG distribution residuals of the direct relative EVA are estimated by the method of moments, as in, e.g., [32], applying the Matlab $nigpar$ function (see Table 4). The estimated parameters indicate lower heaviness $\alpha$, high skewness $\beta$, a location close to zero $\mu$, and a small scale $\delta$.

The last step (iii) involves a simulation of the direct relative EVA measure using 400 steps in one scenario for a year with 10⁵ scenarios. The Matlab function $copularnd$ is used to generate random numbers and simulations. In step (iv), step (iii) is replicated ten times, and the distribution of the direct relative EVA is obtained due to the relative confidence interval of a standard error being determined to be less than 0.1 (see the results in

Table 8. Quarterly prediction results of direct relative EVA measure in %.

Quarter		I. Q			II. Q
Parameter		${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
$Mean$		1.727	0.003	0.253	2.057	0.003	0.187
$Median(·)$		1.495	0.002	0.041	1.837	0.005	0.084
Quantiles (%)	95	7.624	0.010	0.004	8.521	0.009	0.003
	90	5.976	0.007	0.008	6.806	0.006	0.006
	80	4.242	0.004	0.013	4.938	0.003	0.008
	70	3.136	0.003	0.023	3.711	0.001	0.008
	60	2.263	0.002	0.026	2.721	0.004	0.036
	50	1.495	0.002	0.041	1.837	0.005	0.084
	40	0.753	0.002	0.084	0.978	0.003	0.086
	30	−0.023	0.004	3.936	0.082	0.001	0.352
	20	−0.919	0.005	0.079	−0.967	0.004	0.059
	10	−2.201	0.005	0.016	−2.422	0.004	0.012
	5	−3.327	0.010	0.009	−3.659	0.005	0.004
Quarter		III. Q			IV. Q
Parameter		${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	$\mathit{S}{\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
$Mean$		2.225	0.002	0.123	2.307	0.004	0.264
$Median(·)$		2.000	0.006	0.081	2.086	0.005	0.066
Quantiles (%)	95	8.826	0.008	0.003	8.912	0.009	0.003
	90	7.078	0.007	0.007	7.183	0.005	0.005
	80	5.173	0.002	0.005	5.276	0.004	0.012
	70	3.924	0.002	0.011	4.026	0.006	0.035
	60	2.912	0.004	0.036	3.008	0.007	0.059
	50	2.000	0.006	0.081	2.086	0.005	0.066
	40	1.119	0.006	0.135	1.192	0.005	0.109
	30	0.191	0.006	0.747	0.258	0.005	0.456
	20	−0.879	0.007	0.120	−0.816	0.003	0.060
	10	−2.373	0.004	0.011	−2.323	0.006	0.020
	5	−3.645	0.009	0.007	−3.599	0.007	0.006

and Figure 4). The precision of the distribution in all parameters is less than 5%.

3.4. The Evaluation of Predictive Precision of EVAr Distribution Forecasts

The precision evaluation is focused on a one-quarter prediction. Firstly, quarterly predicted distributions for particular months are estimated using a simulation procedure stemming from the estimated models’ parameters. The parameters of the decomposed EVA are presented in Table 3, Table 4 and Table 5 and those for the direct EVA in Table 4 and Table 7. One simulation represents 10⁶ scenarios, and 80 replications are applied. The resulting distribution quantiles, including relative precision, are show in

Table 9. Monthly quarter prediction results of decomposed relative EVA measure in %.

Month		3/2020		4/2020		5/2020		6/2020
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		−0.898	9.578	−2.216	1.192	−2.799	1.665	−2.285	1.126
Medr (Q)		0.468	0.897	−0.084	7.266	−0.890	1.978	−0.151	3.743
Quantiles (%)	95	4.402	0.005	3.807	0.357	3.352	0.693	3.730	0.333
	90	3.300	0.018	2.734	0.390	2.201	0.840	2.659	0.366
	80	2.208	0.067	1.670	0.536	1.038	1.535	1.597	0.511
	70	1.527	0.158	0.990	0.870	0.289	5.374	0.920	0.855
	60	0.970	0.347	0.435	2.036	−0.322	5.020	0.366	2.219
	50	0.468	0.897	−0.084	7.266	−0.890	1.978	−0.151	3.743
	40	−0.053	9.066	−0.627	1.763	−1.479	1.373	−0.693	1.496
	30	−0.643	0.813	−1.278	1.089	−2.168	1.173	−1.343	0.986
	20	−1.485	0.358	−2.258	0.922	−3.165	1.184	−2.322	0.869
	10	−3.570	0.156	−5.003	1.071	−5.716	1.610	−5.067	1.046
	5	−8.293	0.075	−11.605	1.456	−11.779	2.459	−11.676	1.443
Month		7/2020		8/2020		9/2020		10/2020
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		−3.301	1.533	−5.392	0.888	−2.836	1.795	−2.120	1.959
Medr (Q)		−1.370	0.862	−3.467	0.329	−0.910	1.332	−0.129	8.026
Quantiles (%)	95	2.731	0.867	0.712	3.311	3.254	0.768	4.242	0.527
	90	1.612	1.174	−0.423	4.422	2.122	0.935	3.066	0.575
	80	0.489	3.351	−1.567	1.030	0.982	1.743	1.871	0.804
	70	−0.232	6.975	−2.304	0.686	0.249	6.737	1.097	1.324
	60	−0.821	2.059	−2.906	0.565	−0.351	4.963	0.463	3.232
	50	−1.370	0.862	−3.467	0.329	−0.910	1.332	−0.129	8.026
	40	−1.941	1.111	−4.051	0.512	−1.491	1.478	−0.743	2.501
	30	−2.613	1.042	−4.736	0.550	−2.174	1.273	−1.463	1.579
	20	−3.594	1.126	−5.729	0.671	−3.165	1.291	−2.501	1.347
	10	−6.159	1.641	−8.290	1.143	−5.726	1.761	−5.126	1.583
	5	−12.263	2.600	−14.378	2.074	−11.817	2.687	−11.396	2.233
Month		11/2020		12/2020		1/2021		2/2021
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		−2.477	1.479	−0.746	5.072	−0.575	7.322	−0.591	7.761
Medr (Q)		−0.496	1.858	1.183	0.905	1.301	0.947	1.178	1.180
Quantiles (%)	95	4.300	0.448	6.579	0.372	6.986	0.418	7.638	0.415
	90	3.033	0.504	5.177	0.373	5.515	0.416	5.985	0.419
	80	1.722	0.765	3.702	0.439	3.961	0.482	4.218	0.501
	70	0.866	1.482	2.731	0.568	2.935	0.616	3.045	0.663
	60	0.161	8.249	1.930	0.816	2.088	0.874	2.077	0.987
	50	−0.496	1.858	1.183	0.905	1.301	0.947	1.178	1.180
	40	−1.175	1.418	0.415	4.565	0.493	4.393	0.261	9.384
	30	−1.965	1.058	−0.470	4.900	−0.432	6.047	−0.779	3.798
	20	−3.080	0.983	−1.687	1.915	−1.693	2.151	−2.164	1.891
	10	−5.725	1.232	−4.371	1.610	−4.390	1.774	−4.939	1.710
	5	−11.956	1.841	−10.425	2.033	−10.290	2.245	−10.505	2.281

and

Table 10. Monthly quarter prediction results of direct relative EVA measure in %.

Month		3/2020		4/2020		5/2020		6/2020
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		1.727	0.253	1.301	0.171	1.018	0.219	1.358	0.176
Medr (Q)		1.495	0.041	1.061	0.157	0.778	0.214	1.117	0.160
Quantiles (%)	95	7.624	0.004	7.146	0.206	6.863	0.214	7.203	0.143
	90	5.976	0.008	5.508	0.172	5.225	0.181	5.568	0.105
	80	4.242	0.013	3.788	0.122	3.505	0.132	3.845	0.160
	70	3.136	0.023	2.691	0.118	2.408	0.132	2.748	0.175
	60	2.263	0.026	1.824	0.160	1.541	0.189	1.882	0.185
	50	1.495	0.041	1.061	0.157	0.778	0.214	1.117	0.160
	40	0.753	0.084	0.328	0.632	0.045	4.562	0.387	0.834
	30	−0.023	3.936	−0.440	0.478	−0.723	0.291	−0.384	1.054
	20	−0.919	0.079	−1.335	0.269	−1.618	0.222	−1.276	0.316
	10	−2.201	0.016	−2.609	0.217	−2.892	0.196	−2.550	0.190
	5	−3.327	0.009	−3.737	0.216	−4.020	0.201	−3.674	0.197
Month		7/2020		8/2020		9/2020		10/2020
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		0.012	9.801	−1.105	0.202	0.248	0.466	0.925	0.241
Medr (Q)		−0.227	0.461	−1.344	0.124	0.009	9.976	0.688	0.238
Quantiles (%)	95	5.867	0.211	4.740	0.310	6.094	0.182	6.768	0.181
	90	4.222	0.129	3.103	0.306	4.457	0.119	5.129	0.148
	80	2.498	0.155	1.382	0.334	2.733	0.149	3.410	0.131
	70	1.400	0.253	0.286	1.111	1.638	0.211	2.313	0.126
	60	0.538	0.413	−0.582	0.501	0.774	0.235	1.450	0.204
	50	−0.227	0.461	−1.344	0.124	0.009	9.976	0.688	0.238
	40	−0.962	0.227	−2.077	0.100	−0.723	0.317	−0.047	5.154
	30	−1.730	0.179	−2.846	0.074	−1.494	0.194	−0.815	0.388
	20	−2.624	0.097	−3.741	0.096	−2.390	0.125	−1.707	0.256
	10	−3.898	0.128	−5.015	0.113	−3.664	0.131	−2.986	0.222
	5	−5.012	0.183	−6.142	0.131	−4.779	0.177	−4.103	0.247
Month		11/2020		12/2020		1/2021		2/2021
Parameter		${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$	${\mathit{E}}_{\mathit{r}}$	${\mathit{d}}_{\mathit{r}}$
Er (Q)		0.733	0.236	1.641	0.149	1.817	0.110	2.203	0.093
Medr (Q)		0.496	0.312	1.403	0.197	1.576	0.115	1.965	0.092
Quantiles (%)	95	6.573	0.195	7.480	0.184	7.672	0.177	8.043	0.202
	90	4.943	0.142	5.845	0.099	6.023	0.146	6.408	0.130
	80	3.223	0.167	4.125	0.109	4.302	0.105	4.697	0.089
	70	2.125	0.161	3.028	0.117	3.203	0.099	3.594	0.119
	60	1.258	0.234	2.165	0.185	2.340	0.103	2.730	0.119
	50	0.496	0.312	1.403	0.197	1.576	0.115	1.965	0.092
	40	−0.239	1.028	0.670	0.616	0.842	0.327	1.227	0.201
	30	−1.008	0.289	−0.096	3.417	0.078	3.725	0.463	0.638
	20	−1.905	0.159	−0.990	0.364	−0.816	0.383	−0.435	0.868
	10	−3.181	0.197	−2.271	0.296	−2.090	0.248	−1.712	0.419
	5	−4.301	0.176	−3.387	0.345	−3.209	0.362	−2.830	0.278

.

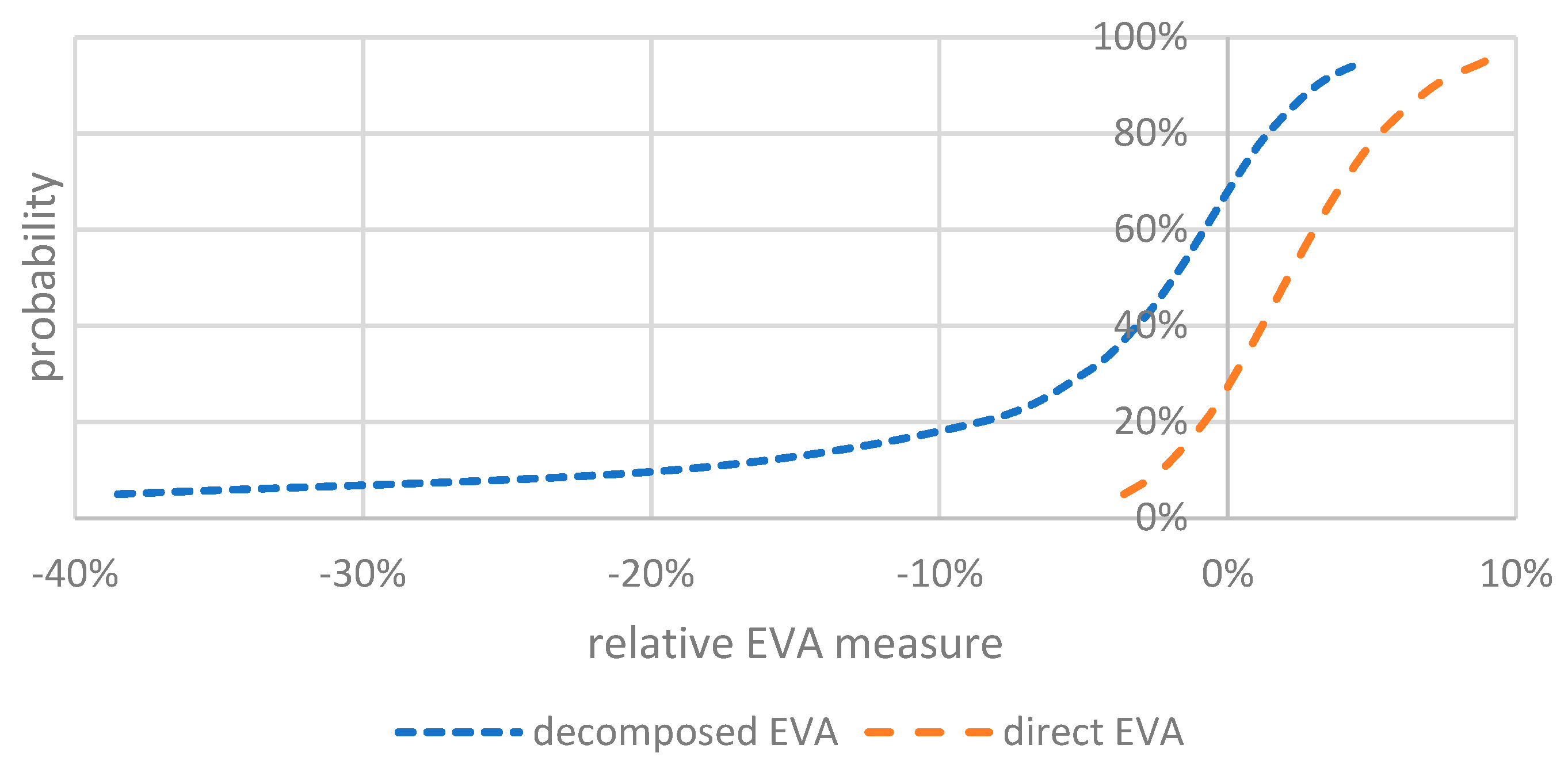
The precision of the forecasted distribution was verified by the absolute and relative tests comparing the decomposed and direct EVA predicted distribution. The STATA esftest test, as in [68], was applied for the absolute test. For decomposed EVA, the W2 statistic is 2.492, with a significance of 0.6461, and for direct EVA, the W2 statistic is 2.669, with a significance of 0.61459. The H0 hypothesis was confirmed in both cases. Lower values affirm that the decomposed EVA coincides more with a uniform distribution and is more suitable. The relative test is evaluated using the logarithmic scoring rule, and STATA paired t-test. The score of the decomposed EVA is −1.9788, and the score of the direct EVA is −2.0718 (see

Table 11. Monthly quarter prediction testing parameters of relative EVA measure in %.

Month	EVA Real	EVA Decomposed			EVA Direct
	y	Ft−1(yt)	ft−1(yt)	log(ft−1(yt))	Gt−1(yt)	gt−1(yt)	log(gt−1(yt))
3/2020	0.3210	47.1784	1.9194	−1.7168	34.4329	1.2887	−1.8899
4/2020	−2.3873	19.5304	0.4796	−2.3191	11.7439	0.4440	−2.3526
5/2020	−4.6252	14.2753	0.1059	−2.9752	4.6234	0.0751	−3.1241
6/2020	−1.9183	24.1251	0.4796	−2.3191	14.9605	0.7800	−2.1079
7/2020	−0.5430	64.7137	1.6949	−1.7709	45.7012	1.1161	−1.9523
8/2020	−0.9356	85.5211	1.1876	−1.9253	55.3575	0.7800	−2.1079
9/2020	0.8890	78.7295	1.9920	−1.7007	61.3347	1.3477	−1.8704
10/2020	1.2483	71.9514	1.7953	−1.7459	57.3554	1.3477	−1.8704
11/2020	2.0288	82.3402	1.4684	−1.8331	68.8856	1.3021	−1.8854
12/2020	0.9071	46.4045	1.9920	−1.7007	43.2295	1.3477	−1.8704
1/2021	2.6688	66.8581	0.9158	−2.0382	63.8094	1.1455	−1.9410
2/2021	0.5757	43.4305	1.9920	−1.7007	31.4751	1.2887	−1.8899
Average	score			−1.9788			−2.0718

). So, a bigger value means that the decomposed EVA forecasts the probability distribution better. The value of the STATA paired t-statistic is 2.5099, with a significance of 0.029. Therefore, hypothesis H0 is not confirmed, and the estimated forecasting models of EVA differ. Consequently, the decomposed model, when compared, is better as well.

4. Discussion and Conclusions

The relative EVA (Section 3.1) shows that the mean value decreases and so does the median. The quarterly forecast decreased from a starting value of 1.0605% for the mean value to −7.570%, and the median value decreased to −1.875%. The median looks more stable compared to the expected value, even with the same negative trend. The characteristics are huge and include negatively skewed quantile intervals. This is caused, among other things, by considering the interdependencies of ratios under the asymmetry of financial ratios and jumps. This phenomenon is hidden in relations among decomposed financial ratios.

The results of direct relative EVA distribution prediction (Section 3.2) show and confirm the historical behaviour of the measure. The median slightly increases to 2.086%, and the mean value is 2.307%. Quantiles are almost symmetrically distributed, with positive skewness. This approach does not include the possibility of using the hidden relations of the system behaviour in the prediction.

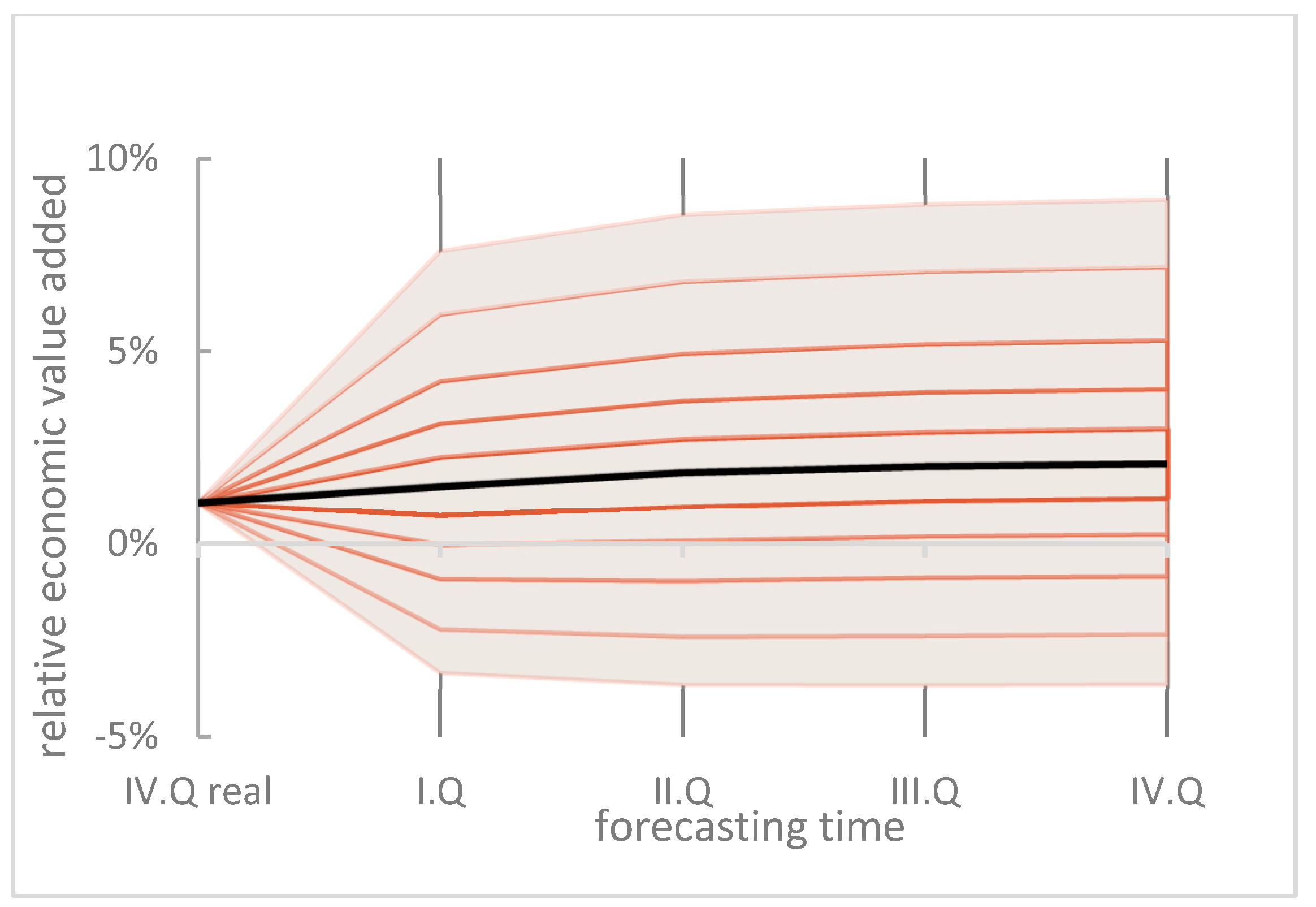
A comparison of the predicted distributions is apparent in Table 6 and Table 7, and a graphical comparison for the fourth quarter is demonstrated in Figure 5.

The comparison of the decomposed and direct relative EVA one-quarter prediction (Section 3.3) was tested using absolute and relative tests. The absolute test showed that the distribution prediction for the decomposed EVA is more accurate in comparison with the direct EVA. Similarly, the relative scoring logarithm test and the paired t-statistic confirmed the better accuracy of the decomposed EVA. Both applied tests verified the superiority of the decomposed EVA forecast model in the particular data case.

The proposed and applied probability distribution decomposition forecasting method is a more adequate and precise approach allowing the prediction of complete uncertainty compared to point prediction.

The proposed innovative advanced forecasting simulation method was verified as a proper conception for the problem of modelling and reflecting empirical data. The LDAMR and LDSMR processes sufficiently fit the chosen financial ratios, and the skew t-regression estimation was valid. The Monte-Carlo simulation of the NIG distribution with a t-copula adequately serves for a decomposed relative EVA distribution prediction, including its precision. It was shown that the direct relative EVA distribution prediction captures the historical behaviour of the complex measure only superficially and simplistically. Therefore, the direct EVA approach is unsuitable for predicting complex, synthetic, and risk measures, such as an EVA indicator. The EVA measure can be explained by reflecting the complexity and comprehensiveness of particular indicators, including their relationship phenomena hidden in financial performance.

The empirical results were verified, proving that the mean value and median of the decomposed relative EVA of the Czech automotive production sector tends to decrease in the future, with negative asymmetry and high volatility hidden in the decomposition of the financial ratios. The median is more stable in comparison to the mean value, even with a negative trend. The applied model led to huge volatility, with extreme values. This volatility is caused, among other things, by considering the ratios’ interdependencies and jumps. This phenomenon is hidden in the empirical historical data and in the relations among exact pyramid-decomposed financial ratios, and it looks both realistic and interesting.

The prediction of the decomposed relative EVA confirms that the sector is exposed to some fundamental structural changes. It is influenced by the limited qualified workers’ capacity, the efficiency of production, and industry competition. The sector is also affected by economic shocks caused by regulatory ecological measures, competitiveness, and substantial technological changes. New phenomena not considered in the model are pandemics, military attacks, and the shortage of spare parts and input material sources.

Further research can be devoted to developing other pyramid decomposition, Levy model types, copula functions, parameter estimations, and simulation approaches. Time series can be prolonged, and crisis periods can be included in them. For comparison, the financial performance of other sectors can also be analysed and predicted.