Improving Hotel Room Demand Forecasts for Vienna across Hotel Classes and Forecast Horizons: Single Models and Combination Techniques Based on Encompassing Tests

Abstract

The present study employs daily data made available by the STR SHARE Center covering the period from 1 January 2010 to 31 January 2020 for six Viennese hotel classes and their total. The forecast variable of interest is hotel room demand. As forecast models, (1) Seasonal Naïve, (2) Error Trend Seasonal (ETS), (3) Seasonal Autoregressive Integrated Moving Average (SARIMA), (4) Trigonometric Seasonality, Box–Cox Transformation, ARMA Errors, Trend and Seasonal Components (TBATS), (5) Seasonal Neural Network Autoregression (Seasonal NNAR), and (6) Seasonal NNAR with an external regressor (seasonal naïve forecast of the inflation-adjusted ADR) are employed. Forecast evaluation is carried out for forecast horizons h = 1, 7, 30, and 90 days ahead based on rolling windows. After conducting forecast encompassing tests, (a) mean, (b) median, (c) regression-based weights, (d) Bates–Granger weights, and (e) Bates–Granger ranks are used as forecast combination techniques. In the relative majority of cases (i.e., in 13 of 28), combined forecasts based on Bates–Granger weights and on Bates–Granger ranks provide the highest level of forecast accuracy in terms of typical measures. Finally, the employed methodology represents a fully replicable toolkit for practitioners in terms of both forecast models and forecast combination techniques.

1. Introduction

1.1. Motivation

With an average annual growth rate of +4.9% from 2018 to 2019, bednights in European cities grew more than twice as fast as bednights at the national level of the EU-28 countries over the same period [1]. The Austrian capital, Vienna, ranked eighth in terms of bednights out of 119 European cities with 18.6 mn bednights in 2019, which corresponded to a growth of +7.0% from 2018 to 2019 [1]. The current COVID-19 pandemic notwithstanding, these figures make the Austrian capital one of the most popular city destinations of Europe, for leisure and business travelers alike. Despite the increase in Airbnb and similar types of non-traditional accommodation in the city [2], the vast majority of tourists to Vienna stay in one of its 422 hotels with their 34,250 rooms (data as of 2019; [3]).

Accurate hotel room demand forecasts (particularly daily forecasts) are crucial for successful hotel revenue management (e.g., for revenue-maximizing pricing) in a fast-paced and competitive industry [4,5,6,7,8]. Besides their hotel’s absolute performance, (revenue) managers are typically also interested in the relative performance of their hotel with respect to the relevant peer group (also known as the competitive set; [9]) within or beyond the same destination: other hotels from the same hotel class, those that cater to the same type of travelers [10], or those belonging to the same hotel chain [11,12]. Therefore, daily hotel room demand data that are aggregated per hotel class constitute a particularly worthwhile data source for hotel room demand forecasting. Another advantage of aggregated data per hotel class is that these do not suffer from the lack of representativity that individual hotel-level data would.

The data for this study were generously made available by the STR SHARE Center (https://str.com/training/academic-resources/share-center (accessed on 26 November 2021)) in March 2020 and consist of the daily raw data from seven Trend Reports for Vienna for the period from 1 January 2010 to 31 January 2020 ($T=3683$) for the hotel classes ‘luxury’ (17 properties as of 31 January 2020), ‘upper upscale’ (31 properties), ‘upscale’ (54 properties), ‘upper midscale’ (76 properties), ‘midscale’ (58 properties), and ‘economy’ (142 properties). STR undertakes this classification primarily according to the hotels’ ADR (https://str.com/data-insights/resources/faq (accessed on 26 November 2021)). The Trend Reports also contain the hotel class ‘all’ (378 properties), i.e., the total of the aforementioned hotel classes. This corresponds to a coverage of approximately 90% of the 422 hotels operating in Vienna in 2019 [3].

Apart from conforming with the characteristics of the data (i.e., weekly and annual seasonal as well as other patterns in the daily data), all candidate forecast models have been selected based on the principles of parsimony and feasibility, so that practitioners (e.g., a revenue manager working in a particular hotel; [5]) can easily and in a timely manner produce and use them by employing mostly automated routines. Sorokina et al. [13] arrive at a similar conclusion. Sensibly, the creation and evaluation of one-day-ahead forecasts should be achievable in the course of one day; thereby, ruling out forecast models such as the Seasonal Autoregressive Integrated Moving Average model with an external regressor (SARIMAX; [14]) that are associated with an excessive computational burden. These principles also rule out complex recurrent neural network models such as the Long Short-Term Memory (LSTM) model [15] or the deep learning method proposed by Law et al. [16], which, in turn, has shown better predictive performance than neural network models or Support Vector Machines (SVM) for the case of Macau. Similar results have been found for the Kernel Extreme Learning Machine (KELM) proposed by Sun et al. [17] that has been successfully applied to data for Beijing.

Consequently, the Seasonal Naïve, the Error Trend Seasonal (ETS) model [18,19], the Seasonal Autoregressive Integrated Moving Average (SARIMA) model [14], the Trigonometric Seasonality, Box–Cox Transformation, ARMA Errors, Trend and Seasonal Components (TBATS) model [20], the Seasonal Neural Network Autoregression (Seasonal NNAR) model [21], and a variant of the latter model, the Seasonal NNAR model with an external regressor [21] were selected. As an external regressor, the seasonal naïve (i.e., 365-days-ahead) forecast of the inflation-adjusted Average Daily Rate (ADR), an important realized price measure in hotel revenue management [22,23], has been employed. In more general terms, own price has long been identified as one of the most important economic drivers of tourism demand [24].

As long as different forecast models contain different and useful information, combining them with different forecast combination techniques has been shown to yield even more accurate predictions [25]. To avoid any detrimental impact of underperforming forecast models, the two-step forecast combination procedure suggested by Costantini et al. [26] is employed. Step 1 of this procedure consists of a forecasting encompassing test [27,28]. Only those models surviving these forecast encompassing tests are considered for forecast combination in step 2 of the procedure in terms of the subsequent forecast combination techniques. These techniques also follow the aforementioned principles of parsimony and feasibility. Thus, they represent five “classical” techniques that have proven to be effective in a variety of empirically relevant forecasting situations [29,30,31,32]. These are the mean and the median forecast [28,33], regression-based weights [34], Bates–Granger weights [35], and Bates–Granger ranks [36].

1.2. Related Literature

Accurate demand forecasts are the basis of most business decisions in the tourism industry [24]. Tourism products and services are described as highly perishable because (leisure) tourism demand is highly sensitive to external shocks such as natural or human-made disasters [37]. For instance, the lost revenue from an unsold hotel room cannot be regenerated. Moreover, accurate hotel room demand forecasts are important for planning (e.g., staff scheduling, renovation periods) or balancing overbookings with “no shows” given limited capacities [38]. Therefore, improving the accuracy of tourism demand forecasts is consistently near the top of the agenda for both academics and industry practitioners. This continuous interest has also resulted in two tourism forecast competitions to date [39,40], the latest one specifically focuses on forecasting tourism demand amid the COVID-19 pandemic: three teams have taken part in this competition, producing and evaluating forecasts for three different world regions, notably Africa [41], Asia and the Pacific [42], and Europe [43]. Specifically, during the COVID-19 pandemic, hybrid scenario forecasting (i.e., different quantitative forecasting scenarios coupled with expert judgment) has proven worthwhile [44].

Concerning tourism demand forecasting in general, Athanasopoulos et al. [45] evaluate the predictive accuracy of five hierarchical forecast approaches applied to domestic Australian tourism data. Using data from Hawaii, Bonham et al. [46] employ a vector error correction model to forecast tourism demand. Kim et al. [47] evaluate a number of univariate statistical models in producing interval forecasts for Australia and Hong Kong. In addition to using data from Hong Kong, Song et al. [48] develop and evaluate a time-varying parameter structural time series model. Andrawis et al. [49] explore the benefits of forecast combinations for tourism demand for Egypt. Gunter and Önder [50] assess various uni- and multivariate statistical models to forecast monthly tourist arrivals to Paris from various source markets. Athanasopoulos et al. [51] employ bagging (i.e., bootstrap aggregation) to improve the forecasting of tourism demand for Australia. Li et al. [52] use the Baidu index as a web-based leading indicator to forecast tourist volume within principal component analysis and neural network approaches. Finally, Panagiotelis et al. [53] employ Australian tourism flow data to empirically demonstrate their theoretical conclusion that bias correction before forecast reconciliation leads to higher predictive accuracy compared to using only one of these two approaches.

Pertaining to hotel room demand forecasting in particular, Rajopadhye et al. [6] employ the classical Holt–Winters exponential smoothing model. Haensel and Koole [4] forecast both single bookings as well the aggregate booking curve based on daily data. Google search engine data are used as web-based leading indicators by Pan et al. [54] to predict hotel room demand. Teixeira and Fernandes [55] explore the predictive ability of different neural network models in comparison to univariate statistical models. Song et al. [56] show that hybrid approaches (i.e., a combination of statistical models and expert judgment) improve the forecast accuracy of hotel room demand forecasts for Hong Kong. Yang et al. [57] analyze the predictive ability of the traffic volume of the website of a destination management organization, another web-based leading indicator, for estimating hotel room demand. Guizzardi and Stacchini [58] investigate the usefulness of information on tourism supply in forecasting hotel arrivals. Pereira [5] investigates the ability of the TBATS model to accommodate multiple seasonal patterns simultaneously. Different Poisson mixture models are used by Lee [59] to improve short-term forecast accuracy. In addition, Guizzardi et al. [60] use ask price data from online travel agencies as a leading indicator for daily hotel room demand forecasting. Finally, only a few further tourism and hotel room demand forecasting studies based on daily data have been published to date, with the publications by Ampountolas [61], Bi et al. [62], Chen et al. [63], Schwartz et al. [64] and Zhang et al. [65,66] representing some noteworthy exceptions.

This short review of exemplary studies does not claim to be complete. However, it can be concluded that numerous quantitative forecast models (i.e., uni- and multivariate statistical models, machine learning models and, more recently, hybrids of these two), as well as forecast combination and aggregation techniques, have been applied to generate point, interval, and density forecasts in the ample tourism demand forecasting literature. Their precision has been evaluated using different forecast accuracy measures and statistical tests of superior predictive accuracy for a variety of destinations, source markets, sample periods, data frequencies, forecast horizons, and tourism demand measures. Jiao and Chen [67] or Song et al. [68] can be consulted for recent comprehensive reviews of this literature, as a more detailed review of the tourism forecasting literature lies beyond the scope of this study. However, these recent comprehensive reviews confirm the conventional wisdom yielded by earlier studies that there is no single best tourism demand forecast model able to produce tourism demand forecasts characterized by superior forecast accuracy on all occasions [69,70].

Besides past realizations of the tourism demand measure to allow for habit persistence, economic drivers of tourism demand such as own and competitor’s prices, tourist incomes, marketing expenditures, etc., and dummy variables capturing one-off events have been employed as predictors of tourism demand in multivariate forecast models [24]. For Vienna, with the exception of Smeral [71], almost all published tourism demand forecasting studies to date have been dedicated to web-based leading indicators as predictors, while employing monthly tourist arrivals aggregated at the city level as their tourism demand measure [72,73,74,75].

Therefore, the first contribution of this study lies in the first-time use of more disaggregated hotel class data with a daily frequency and an economic predictor—seasonal naïve forecast of the inflation-adjusted ADR—as an external regressor in one of the forecast models for this important European city destination. This also allows for the evaluation of one-day-ahead and one-week-ahead hotel room demand forecasts, which are crucial for hotel revenue management [5].

The second contribution is the thorough assessment of the accuracy of six forecast models and five forecast combination techniques in terms of four different forecast accuracy measures for seven hotel classes and four forecast horizons: daily, weekly, monthly, and quarterly, which correspond to different planning horizons in hotel revenue management, ranging from the aforementioned very short-term (one-day-ahead and one-week-ahead; [5]) to medium-term planning horizons. The relatively long sample period allows the evaluation of pseudo-ex-ante out-of-sample point forecasts based on rolling windows and at least 185 counterfactual observations (for $h=90$), thereby being more robust to potential structural breaks compared to expanding windows [76]. This makes the methodology and the results of this study relevant for the post-COVID-19 period: once the impact of this severe structural break has vanished and the tourism industry has recovered, tourism and hotel room demand forecasting for normal times will become feasible again.

The third contribution is based on the provision of a fully replicable forecasting toolkit for practitioners in terms of both forecast models and forecast combination techniques that are based on mostly automated routines and, therefore, respect the principles of parsimony and feasibility. This toolkit also enables revenue managers working in smaller (boutique) hotels that do not belong to an international hotel chain (i.e., without access to a professional revenue management system; [13,38]) to employ the proposed methodology on their own hotel-level dataset to easily create and use reliable hotel room demand forecasts and, in the following, benchmark their own hotel against the performance of other hotels from the relevant peer group.

The fourth contribution of this study lies in its use of the seasonal naïve forecast of the inflation-adjusted ADR as an external regressor, which makes (a) the forecast evaluation completely ex-ante and, thereby, attends to a recent call in the tourism demand forecasting literature for more ex-ante forecasting [77] and (b) avoids any impact of unrelated general price level changes. Moreover, this variable is employed within the Seasonal NNAR model with an external regressor [21], which has not been used regularly in tourism demand forecasting to date.

Finally, the fifth contribution of this research is the first-time application of the two-step forecast combination procedure suggested by Costantini et al. [26] in a hotel room demand forecasting setting. While having become more popular in general tourism demand forecasting research—beginning with the pioneering contribution by Fritz et al. [78], Song et al. [68] count 17 studies on tourism demand forecast combination in their recent review study covering 211 key papers published between 1968 and 2018—very few studies have employed any type of forecast combination in a hotel room demand forecasting context; the research by Song et al. [56], Fiori and Foroni [79], as well as Schwartz et al. [80] being notable exceptions.

The remainder of this study is structured as follows. Section 2 describes the data. Section 3 presents the employed forecast models and forecast combination techniques. Section 4 lays out the forecasting procedure and presents and discusses the forecast evaluation results. Section 5 draws some overall conclusions including managerial implications and limitations. Supporting tables are provided in Appendix A.

2. Data

The forecast variable of interest in the data made available by the STR SHARE Center is hotel room demand (i.e., the number of rooms sold per day by hotel class), while the seasonal naïve (i.e., 365-days-ahead) forecast of the ADR (in euros) is employed as the external regressor in one of the forecast models (see Section 3), thereby ensuring that the forecasts produced by this model are ex-ante. Given a time span of more than ten years, and to avoid any impact of unrelated general price level changes, the ADR has been inflation-adjusted using Austria’s monthly Harmonized Index of Consumer Prices (HICP) obtained from Statistics Austria with 2015 as its base year. The temporal disaggregation of the HICP, which was necessary for inflation adjustment, was undertaken using the ‘tempdisagg’ package for R [81]. All further calculations were also performed in R [82] and RStudio [83], thereby drawing primarily on the functions implemented in the ‘forecast’ package [84,85].

Due to the daily frequency of the data, the presence of seasonal patterns is likely. Figure 1 (hotel room demand) and 2 (inflation-adjusted ADR) show the original time series as well as its trend, weekly ($m=7$) and annual seasonal patterns ($M=365.25$), and remainder components across all hotel classes as obtained by Seasonal-Trend decomposition using Locally estimated scatterplot smoothing (STL decomposition; [86]), while employing the ‘mstl()’ function of the ‘forecast’ package. Given the weekly and annual seasonality across variables and hotel classes, with distinct troughs in hotel room demand for most of January and February and on Sundays, the applicability of forecast models allowing for seasonal patterns is evident (see Figure 1). As can also be seen from Figure 1, both patterns are comparably less pronounced for the ‘luxury’ hotel class. Since the annual seasonal pattern has a much higher amplitude than the weekly seasonal pattern across hotel classes, the focus of this study is on the former. Moreover, the weekly seasonal pattern also appears to be less regular.

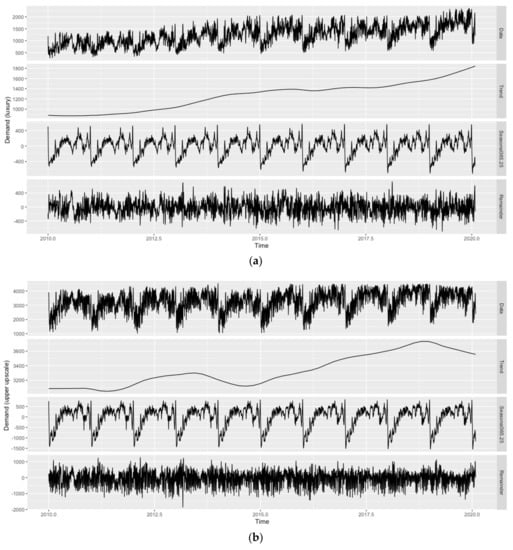
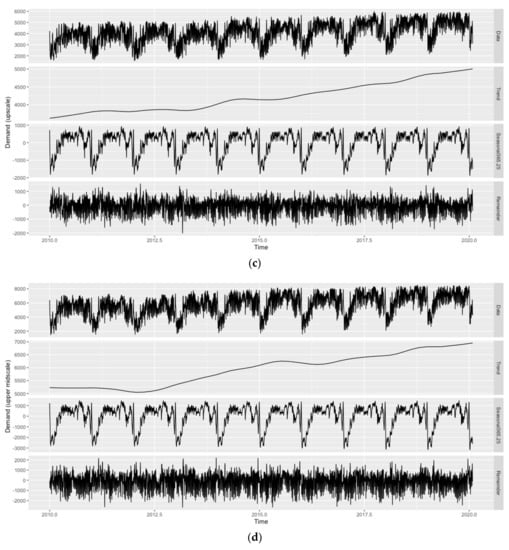
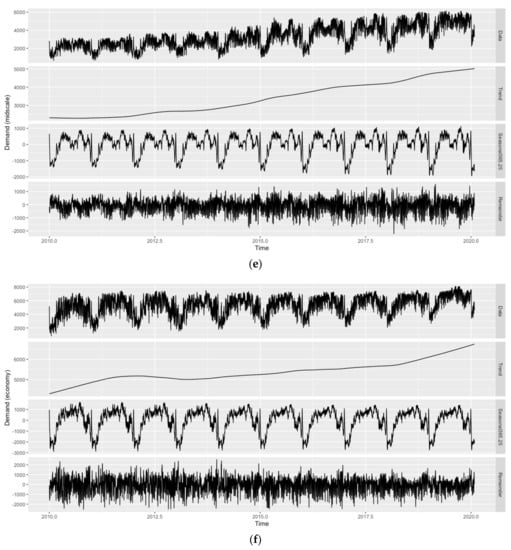
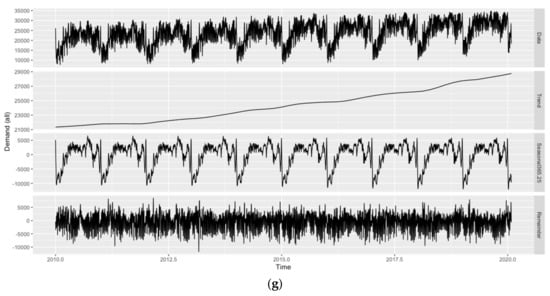
Figure 1. Evolution and STL decomposition of hotel room demand in Vienna. Hotel classes from top to bottom: (a) ‘luxury’, (b) ‘upper upscale’, (c) ‘upscale’, (d) ‘upper midscale’, (e) ‘midscale’, (f) ‘economy’, and (g) ‘all’. Source: STR SHARE Center, own illustration using R.

In line with Pereira [5], quarterly or monthly seasonal patterns are not visible and would not be reasonable either, as, for instance, the first days of January still belong to the Christmas/New Year high season, while the remainder of the month belongs to the aforementioned low season. Similarly, January and February observations belong to the same quarter as March observations, yet March cannot be characterized as part of the annual trough. It should further be noted that STL decomposition has only been applied to showcase the different trends and seasonal components in the data. How to deal with any of these components in the forecast models, e.g., whether to treat trends as stochastic or deterministic if present, is determined during the model selection stage (see Section 3).

Since the sample period runs from 1 January 2010 to 31 January 2020 (i.e., after the Financial Crisis/Great Recession period from 2008 to 2009 and before the COVID-19 pandemic starting in March 2020), no structural breaks are visible for either of the variables across hotel classes. Vienna is a popular destination for Meetings, Incentives, Conventions and Exhibitions (MICE) tourism, which mostly follows a regular schedule and can, therefore, be considered part of the seasonal component. The only major one-eff event during the sample period, the Eurovision Song Contest taking place in Vienna in May 2015, did not seem to have a noticeable impact on hotel room demand across hotel classes (other major one-off events taking place in Vienna but outside the sample period can be found with the 2008 UEFA European Football Championship or the terrorist attacks of November 2020). Concerning trending patterns, a continuing upward trend for hotel room demand is visible across hotel classes, with the exception of the ‘upper upscale’ hotel class toward the end of the sample period (see Figure 1).

Similar to hotel room demand, inflation-adjusted ADR peaks during the Christmas/New Year high season, but also features two smaller peaks: one in the first half of the year and the other in the second half (see Figure 2). The latter pattern is present in all hotel classes, yet comparably less pronounced for the ‘luxury’ and ‘midscale’ hotel classes. As can also be seen from Figure 2, the amplitude of annual seasonality is comparably high for the ‘luxury’ hotel class. All hotel classes, except for ‘luxury’ and ‘economy’, show a moderate upward trend in terms of the inflation-adjusted ADR over the whole sample period. Similar to hotel room demand, the weekly seasonal pattern is much less pronounced than the annual seasonal pattern across hotel classes and less regular. However, in contrast to hotel room demand, the trend in the inflation-adjusted ADR also shows cyclical behavior, with the years from 2013 to 2014 and 2016 to 2017 representing the cycle’s troughs.

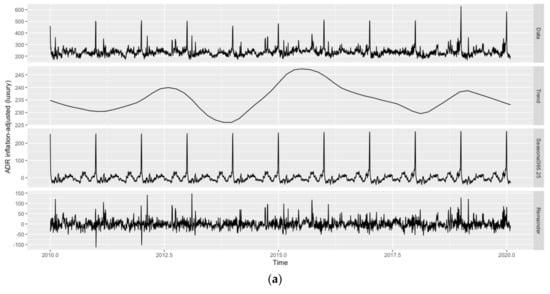
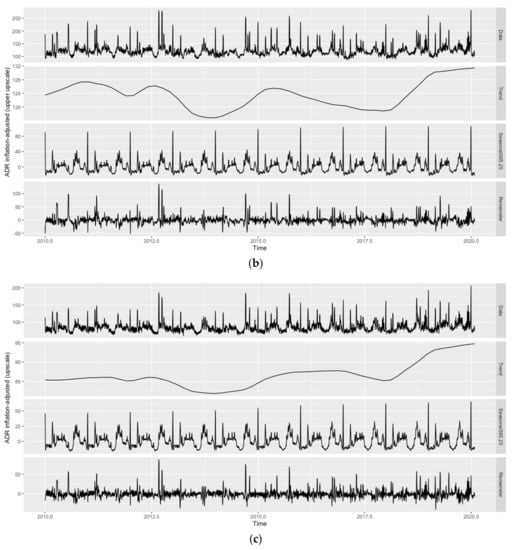
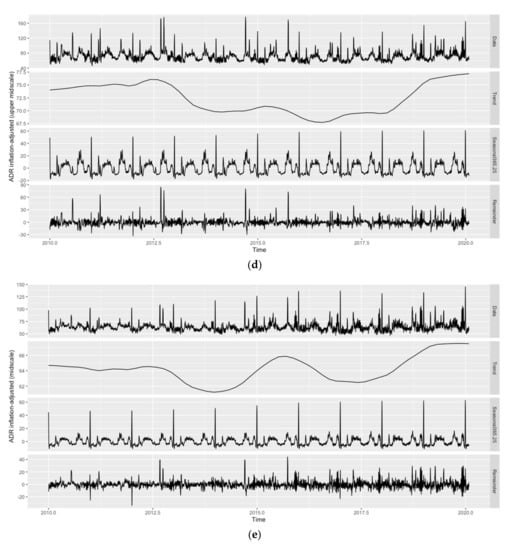
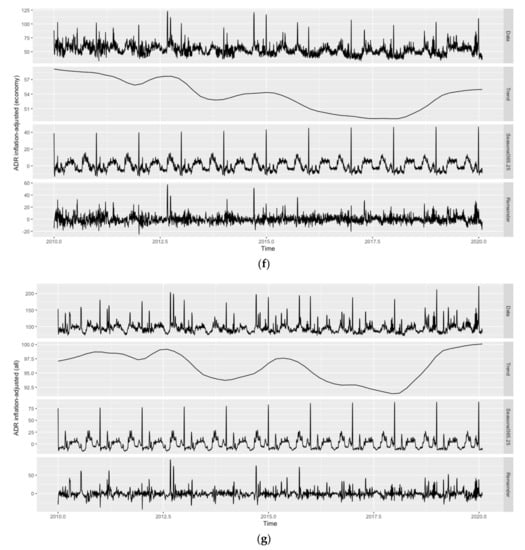
Figure 2. Evolution and STL decomposition of inflation-adjusted ADR in Vienna. Hotel classes from top to bottom: (a) ‘luxury’, (b) ‘upper upscale’, (c) ‘upscale’, (d) ‘upper midscale’, (e) ‘midscale’, (f) ‘economy’, and (g) ‘all’. Source: STR SHARE Center, own illustration using R.

3. Methodology

This study employs six different forecast models suitable for seasonal data, as well as five different forecast combination techniques. Section 3.1 gives a brief overview of the six applied forecast models, whereas Section 3.2 reviews the five applied forecast combination techniques. All forecasts from the single models are obtained using the ‘forecast’ package while combining those forecasts and the forecast evaluation (see Section 4) are carried out in EViews Version 11. In the following, both hotel room demand and the inflation-adjusted ADR are employed in natural logarithms to ensure variance stabilization. Detailed estimation results and in-sample goodness-of-fit measures across forecast models and hotel classes are available from the author upon request.

3.1. Forecast Models

3.1.1. Seasonal Naïve

The first and simplest model forecasting hotel room demand, $HRD$, applied in this study is the Seasonal Naïve forecast, which also serves as a benchmark, which should, ideally, be outperformed by more sophisticated forecast models. In the Seasonal Naïve model, the forecast $\widehat{HR{D}_{T+h|T}}$ of $HRD$ in period $T+h$, with $T$ denoting the forecast origin and $h$ the forecast horizon, corresponds to the realization of $HRD$ on the same day one year previously. Thus:

$$\widehat{HR{D}_{T+h|T}}=HR{D}_{T+h-M},$$

(1)

where $M=365.25$ in Equation (1) denotes the length of the annual seasonal pattern.

3.1.2. Error Trend Seasonal (ETS)

The second forecast model employed is the ETS model developed by Hyndman et al. [18,19]. This is a state-space framework comprising various traditional exponential smoothing methods and consists of one signal equation in the forecast variable $HRD$ and various state equations for the different components of the data. In general, the following ETS $\left(·,·,·\right)$ specifications are possible:

$$E\left(Error\right)\in \left\{A,M\right\}, T\left(Trend\right)\in \left\{N,A,A_d,M,M_d\right\}, S\left(Seasonal\right)\in \left\{N,A,M\right\},$$

(2)

where $A$ in Equation (2) denotes additive, $M$ multiplicative, $N$ none, $A_d$ additive damped, and $M_d$ denotes multiplicatively damped [21]. The optimal model specification of this and the remaining three forecast models is selected by the minimum Akaike Information Criterion (AIC; [87]) for all hotel classes and their total. As the ‘ets()’ function of the ‘forecast’ package cannot deal with seasonal patterns within daily data, the ‘stlm()’ function is employed. This function first deseasonalizes the data with STL decomposition and then parses the deseasonalized data to the ‘ets()’ function, where the search for optimal model specifications is carried out only for non-seasonal ETS models. Finally, the forecast values are reseasonalized by applying the last year of the seasonal component obtained from STL decomposition [84,85].

3.1.3. Seasonal Autoregressive Integrated Moving Average (SARIMA)

The third forecast model used in the present study is the SARIMA model [14]. A SARIMA $\left(p,d,q\right)\times {\left(P,D,Q\right)}_M$ model reads as follows:

$$\mathsf{\Phi }\left(L\right)\varphi \left(L\right){\nabla }_M^D{\nabla }^{d}HR{D}_t=a+\mathsf{\Theta }\left(L\right)\theta \left(L\right)e_t,$$

(3)

where $\mathsf{\Phi }\left(L\right), \varphi \left(L\right),\mathsf{\Theta }\left(L\right), \theta \left(L\right)$ in Equation (3) denote lag polynomials of orders $P, p, Q, q$, respectively. ${\nabla }_M^D$ represents the degree of seasonal integration of the forecast variable, $HRD$, while ${\nabla }^d$ represents the degree of non-seasonal integration. Finally, $a$ denotes a potentially non-zero mean and $e$ the error term.

As mentioned before, the optimal model specification (i.e., the optimal lag orders $P^{*},p^{*},Q^{*},q^{*}$) is selected by minimizing the AIC. The maximum lag order of the non-seasonal AR and MA components is set to $p^{max}=q^{max}=7$ (to indirectly allow for the weekly seasonal pattern), while the maximum lag order of the seasonal AR and MA components is set to $P^{max}=Q^{max}=2$. The maximum degree of non-seasonal integration is set to $d^{max}=2$, whereas the maximum degree of seasonal integration is set to $D^{max}=1$. The degree of seasonal integration is determined by conducting the Augmented Dickey–Fuller (ADF) unit root test. Given the daily frequency of the data, a measure of seasonal strength computed from an STL decomposition is employed to select the number of seasonal differences. In this study, the ‘auto.arima()’ function of the ‘forecast’ package is used to implement the SARIMA model while enabling parallel computing.

3.1.4. Trigonometric Seasonality, Box–Cox Transformation, ARMA Errors, Trend and Seasonal Components (TBATS)

The fourth forecast model under scrutiny is one that can deal with multiple seasonal patterns at a time (in the present case: $m=7$ and $M=365.25$): the TBATS model [20]. A TBATS $\left(\omega ,\phi ,p,q,\left\{m_1,k_1\right\},\dots ,\left\{m_T,k_T\right\}\right)$ model for the forecast variable $HRD$ reads as follows [20]:

$$HR{D}_t^{\omega }=\ln HR{D}_t\left(\omega =0\right),$$

(4)

$$HR{D}_t^{\omega }=l_{t-1}+\phi b_{t-1}+{\sum }_{i=1}^T{s}_{t-1}^i+d_t,$$

(5)

$$l_t=l_{t-1}+\phi b_{t-1}+\alpha d_t,$$

(6)

$$b_t=\left(1-\phi \right)b+\phi b_{t-1}+\beta d_t,$$

(7)

$$\varphi \left(L\right)d_t=\theta \left(L\right)e_t,$$

(8)

$$s_t^i={\sum }_{j=1}^{k_i}{s}_{j,t}^i,$$

(9)

$$s_{j,t}^i=s_{j,t-1}^i\cos {\lambda }_j^i+s_{j,t-1}^{*i}\sin {\lambda }_j^i+{\gamma }_1^i{d}_t,$$

(10)

$$s_{j,t}^{*i}=-s_{j,t-1}\sin {\lambda }_j^i+s_{j,t-1}^{*i}\cos {\lambda }_j^i+{\gamma }_2^i{d}_t.$$

(11)

Equation (4) represents the Box–Cox transformation, where $\omega =0$ as $HRD$ is employed in natural logarithm throughout. Equation (5) is the measurement equation in $HRD$. Equation (6) is the equation for the local level $l_t$ in period $t$. Equation (7) is the equation for the short-run trend $b_t$ in period $t$ with $b$ denoting the long-term trend. Equation (8) gives the ARMA $\left(p,q\right)$ process $d_t$ with $e_t$ assumed to be distributed $~N\left(0,{\sigma }_e^2\right)$ and $\varphi \left(L\right),\theta \left(L\right)$ denoting lag polynomials of orders $p,q$, respectively. $\phi$ indicates the damping parameter of the trend, whereas $\alpha ,\beta$ are smoothing parameters.

Equations (9)–(11) correspond to the trigonometric representation of the $i$-th seasonal component $s_t^i$. Equation (10) is the equation for the stochastic level of the $i$-th seasonal component $s_{j,t}^i$. Equation (11) is the equation for the stochastic growth in the level of the $i$-th seasonal component $s_{j,t}^{*i}$. ${\lambda }_j^i$ is defined as ${\lambda }_j^i=2\pi j/m_i$. $k_i$ represents the number of Fourier terms needed for the $i$-th seasonal component. Finally, ${\gamma }_1^i,{\gamma }_1^i$ denote smoothing parameters [20]. The optimal model specification is again selected by minimizing the AIC ($p^{max}=q^{max}=7$). The ‘tbats()’ function of the ‘forecast‘ package is used to implement the TBATS model in this study while enabling parallel computing.

3.1.5. Seasonal Neural Network Autoregression (Seasonal NNAR)

The fifth employed forecast model is the Seasonal NNAR model [21]. A Seasonal NNAR ${\left(p,P,\kappa \right)}_M$ model for the forecast variable $HRD$ is a multilayer feed-forward neural network comprising (1) one input layer, (2) one hidden layer with several hidden neurons, and (3) one output layer [21]. Each layer consists of several nodes and receives inputs from the previous layer such that the sequence (1) → (2) → (3) holds. Consequently, the outputs of one layer correspond to the inputs of the subsequent layer. The inputs for a single hidden neuron $\kappa$ ($\kappa =1,\dots ,\mathsf{{\rm K}}$) from the hidden layer $z_{\kappa }\left(HR{D}_{t-\tau }\right)$ are a linear combination consisting of a weighted average of the outputs of the input layer $HR{D}_{t-\tau }$, which are transformed by a nonlinear sigmoid function to become the inputs for the output layer $o_{\kappa }(z_{\kappa })$:

$$z_{\kappa }\left(HR{D}_{t-\tau }\right)=b_{\kappa }+{\sum }_{\tau =1}^{p^{*},MP}{w}_{\kappa \tau }HR{D}_{t-\tau },$$

(12)

$$o_{\kappa }(z_{\kappa })=1/\left(1+e^{-z_{\kappa }\left(HR{D}_{t-\tau }\right)}\right),$$

(13)

while the parameters $b_{\kappa }$ and $w_{\kappa \tau }$ in Equation (12) are learned from the data [21]; starting from random starting weights for $b_{\kappa }$ and $w_{\kappa \tau }$ and setting the decay parameter equal to 0.1, the neural network is trained 100 times, while the lag order of the seasonal AR component is set to $P=1$. The optimal lag order of the non-seasonal AR component $p^{*}$ is again selected by minimizing the AIC. The number of hidden neurons $\kappa$, in turn, is determined according to the rule $\kappa =\left(p^{*}+P+1\right)/2$ and rounded to the nearest integer [21]. In this study, the ‘nnetar()’ function of the ‘forecast’ package is used to implement the Seasonal NNAR model while enabling parallel computing.

3.1.6. Seasonal NNAR with an External Regressor

The sixth and final forecast model is the Seasonal NNAR model with an external regressor [21], a variant of the forecast model presented in Section 3.1.5. In this variant, the seasonal naïve forecast of inflation-adjusted ADR is employed across hotel classes as a candidate predictor (see Section 2). Also here, the ‘nnetar()’ function of the ‘forecast’ package is used to implement the Seasonal NNAR model with an external regressor while enabling parallel computing.

As can be seen from Figure 3, hotel room demand and inflation-adjusted ADR feature a positive correlation for hotel class ‘all’, which ostensibly appears to violate the law of demand. However, it should be noted that the ADR is not the price offered to customers before booking a hotel, but the price realized as a result of successful hotel revenue management [22,23]. Thus, Giffen or Veblen effects can be safely ruled out. Calculating correlation coefficients between the remaining components of the two variables after STL decomposition (in order to preclude any potentially confounding influence of the trend or seasonal components) reveals only positive values for all hotel classes: ‘luxury’ (0.25), ‘upper upscale’ (0.44), ‘upscale’ (0.45), ‘upper midscale’ (0.39), ‘midscale’ (0.38), ‘economy’ (0.27), and ‘all’ (0.48). Graphs for the remaining hotel classes are available from the author upon request.

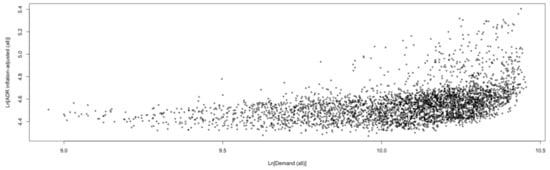
Figure 3. Scatterplot of hotel room demand and inflation-adjusted ADR in Vienna for hotel class ‘all’. Source: STR SHARE Center, own illustration using R.

Apart from these non-negligible positive correlations, the null hypothesis of bivariate Granger causality tests [88]—of inflation-adjusted ADR not Granger-causing hotel room demand (both in natural logarithms)—is rejected at the 0.1% significance level across hotel classes when using the ‘grangertest()’ function. Consequently, it is ex-ante and very likely that the information contained in the inflation-adjusted ADR is relevant to the forecaster at the forecast origin in terms of improving forecast accuracy (yet, these results do not claim or imply any exogeneity of the inflation-adjusted ADR). Detailed test results are available from the author upon request.

3.2. Forecast Combination Techniques

In the following, a combined forecast, $c{f}_t^h$, for different forecast horizons, $h$ ($h=1,\dots H$), is to be understood as a combination of $n$ ($n=1,\dots ,N$), not perfectly collinear single forecasts, $f_{t,n}^h$, observed at the same time point, $t$ ($t=1,\dots ,T$).

3.2.1. Mean Forecast

The first and simplest forecast combination technique applied in this study is the mean forecast, which also serves as a benchmark, which should, ideally, be outperformed by more sophisticated forecast combination techniques [28,33]. It reads as follows:

$$c{f}_t^h={\sum }_{n=1}^N\frac{1}{N}{f}_{t,n}^h.$$

(14)

3.2.2. Median Forecast

A time-varying alternative to the mean forecast that is more robust to outliers is the median forecast, whereby the median forecast at each point in time receives a weight of 1 and all other forecasts a weight of 0 [28,33]:

$$c{f}_t^h=\mathrm{med}\left(f_{t,1}^h,\dots ,f_{t,N}^h\right).$$

(15)

3.2.3. Regression-Based Weights

The combined forecast with regression-based weights $w_n^{h,OLS}$ as obtained from ordinary least squares (OLS) regression [34], where the intercept $\alpha$ is included to correct for forecast bias, reads as follows:

$$c{f}_t^h=\alpha +{\sum }_{n=1}^N{w}_n^{h,OLS}{f}_{t,n}^h.$$

(16)

3.2.4. Bates–Granger Weights

Bates and Granger [35] recommend assigning higher weights to those single forecasts characterized by a lower mean square error (MSE), thus, rewarding those forecast models with a better historical track record:

$$c{f}_t^h={\sum }_{n=1}^N\frac{1/MS{E}_n^h}{{\sum }_{n=1}^N\left(1/MS{E}_n^h\right)}{f}_{t,n}^h.$$

(17)

3.2.5. Bates–Granger Ranks

Finally, Aiolfi and Timmermann [36] suggest using the rank of the MSE of the single forecasts to make Bates–Granger-type weights independent of correlations between forecast errors:

$$c{f}_t^h={\sum }_{n=1}^N\frac{1/MSE-Ran{k}_n^h}{{\sum }_{n=1}^N(1/MSE-Ran{k}_n^h)}{f}_{t,n}^h.$$

(18)

4. Forecasting Procedure and Forecast Evaluation Results

4.1. Forecasting Procedure

Given the relatively long sample period, pseudo-ex-ante out-of-sample point forecasts from the forecast models for the forecast horizons $h=1, 7, 30$, and $90$ days ahead are produced based on rolling windows moving one day ahead at a time. Due to the absence of structural breaks (see Section 2) and the associated computational burden, all optimal model specifications per hotel class are only selected once. For the same reasons, all forecast models are only estimated once per hotel class for the first rolling window, which ranges from 1 January 2010 to 31 January 2019. The evaluation window for $h=1$, thus, ranges from 1 February 2019 to 30 January 2020, resulting in 364 counterfactual observations. For $h=7$, it ranges from 7 February 2019 to 30 January 2020, resulting in 358 observations. For $h=30$, it ranges from 2 March 2019 to 30 January 2020, resulting in 335 observations. Finally, for $h=90$, the evaluation window ranges from 1 May 2019 to 30 January 2010, resulting in 275 counterfactual observations.

Forecast accuracy is measured in terms of the root mean square error (RMSE), the mean absolute error (MAE), the mean absolute percentage error (MAPE), the mean absolute scaled error (MASE), as well as the sum of ranks over these four measures. One forecast combination technique (i.e., regression-based weights) and one forecast accuracy measure (i.e., MASE), require the splitting of the evaluation samples into training and test sets [34,89]. In doing so, the first 90 observations per forecast horizon, forecast model, and hotel class are withheld for the training set. Thus, the different forecast accuracy measures can be calculated based on test sets comprising 274 ($h=1$), 268 ($h=7$), 245 ($h=30$), and 185 ($h=90$) forecast values, respectively. However, a forecast encompassing test with the null hypothesis that a specific forecast model contains all information enclosed in the remaining forecast models [27,28] is carried out as step 1 of the two-step forecast combination procedure suggested by Costantini et al. [26] to investigate if combining the forecasts obtained from (some of) the forecast models is a viable option in the first place. Only those models surviving these forecast encompassing tests are considered for forecast combination in step 2 of the procedure in terms of the different forecast combination techniques.

4.2. Forecast Evaluation Results

Figure 4 shows an exemplary visual comparison of all forecast models for hotel class ‘all’ and $h=1$ for the period from 1 October 2019 to 31 January 2020 (for better visibility). Prior to consulting the forecast accuracy measures, a mere visual inspection of this graph shows that none of the employed forecast models are widely off track and that they are able to pick up the seasonal drop in hotel room demand after New Year. Graphs for the remaining hotel classes and forecast horizons are available from the author upon request (in Figure 4 as well as in Table 1 and Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6, the Seasonal NNAR model (with an external regressor) is abbreviated as ‘NNAR(X)’.).

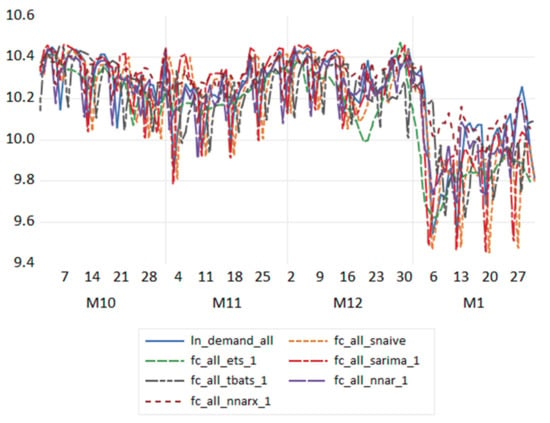
Figure 4. Historical data (solid line) and forecast comparison graph of all forecast models for hotel class ‘all’ and $h=1$ for the period from 1 October 2019 to 31 January 2020. Source: STR SHARE Center, own illustration using EViews Version 11.

Table 1. Forecast evaluation results for the hotel class ‘all’. Source: STR SHARE Center, own calculations using R and EViews.

h = 1	Forecast encompassing tests						h = 7	Forecast encompassing tests
	Forecast	F-stat	F-prob					Forecast	F-stat	F-prob
	FC_ALL_SNAIVE	14.25286	0.0000					FC_ALL_SNAIVE	5.974651	0.0000
	FC_ALL_ETS_1	18.87846	0.0000					FC_ALL_ETS_7	17.68664	0.0000
	FC_ALL_SARIMA_1	10.52937	0.0000					FC_ALL_SARIMA_7	9.682864	0.0000
	FC_ALL_TBATS_1	24.45411	0.0000					FC_ALL_TBATS_7	12.42974	0.0000
	FC_ALL_NNAR_1	30.80203	0.0000					FC_ALL_NNAR_7	44.34023	0.0000
	FC_ALL_NNARX_1	22.58761	0.0000					FC_ALL_NNARX_7	50.42701	0.0000
	Forecast accuracy measures							Forecast accuracy measures
	Forecast	RMSE	MAE	MAPE (%)	MASE	Sum of ranks		Forecast	RMSE	MAE	MAPE (%)	MASE	Sum of ranks
	FC_ALL_SNAIVE	0.146487	0.105342	1.032703	0.679529	40		FC_ALL_SNAIVE	0.145821	0.103941	1.019405
	FC_ALL_ETS_1	0.123992	0.090336	0.884891	0.58273	36		FC_ALL_ETS_7	0.125901	0.0911	0.892613	0.591363	24
	FC_ALL_SARIMA_1	0.112078	0.081361	0.797155	0.524835	28		FC_ALL_SARIMA_7	0.114661	0.083522	0.818122	0.542171	11
	FC_ALL_TBATS_1	0.164269	0.12752	1.248491	0.822593	44		FC_ALL_TBATS_7	0.177067	0.135932	1.330711	0.882383	40
	FC_ALL_NNAR_1	0.098745	0.065549	0.641903	0.422837	14		FC_ALL_NNAR_7	0.137623	0.099317	0.972022	0.644702	28
	FC_ALL_NNARX_1	0.119957	0.082927	0.818325	0.534937	32		FC_ALL_NNARX_7	0.159384	0.122729	1.195656	0.796678	36
	Mean forecast	0.094129	0.069624	0.683052	0.449123	18		Mean forecast	0.110752	0.085315	0.83513	0.55381	14
	Median forecast	0.096246	0.067842	0.666685	0.437628	16		Median forecast	0.107691	0.081208	0.796267	0.52715	4
	Regression-based weights	0.105409	0.072597	0.712363	0.468301	24		Regression-based weights	NA	NA	NA	NA	NA
	Bates–Granger weights	0.091046	0.063548	0.624425	0.409929	5		Bates–Granger weights	0.111568	0.085415	0.835928	0.554459	18
	Bates–Granger ranks	0.089713	0.064701	0.6353	0.417367	7		Bates–Granger ranks	0.111669	0.085069	0.832228	0.552213	13
h = 30	Forecast encompassing tests						h = 90	Forecast encompassing tests
	Forecast	F-stat	F-prob					Forecast	F-stat	F-prob
	FC_ALL_SNAIVE	4.70036	0.0004					FC_ALL_SNAIVE	5.759609	0.0001
	FC_ALL_ETS_30	22.47783	0.0000					FC_ALL_ETS_90	15.75179	0.0000
	FC_ALL_SARIMA_30	8.658692	0.0000					FC_ALL_SARIMA_90	10.83232	0.0000
	FC_ALL_TBATS_30	10.52756	0.0000					FC_ALL_TBATS_90	6.634232	0.0000
	FC_ALL_NNAR_30	53.26993	0.0000					FC_ALL_NNAR_90	15.66648	0.0000
	FC_ALL_NNARX_30	42.31334	0.0000					FC_ALL_NNARX_90	11.3257	0.0000
	Forecast accuracy measures							Forecast accuracy measures
	Forecast	RMSE	MAE	MAPE (%)	MASE	Sum of ranks		Forecast	RMSE	MAE	MAPE (%)	MASE	Sum of ranks
	FC_ALL_SNAIVE	0.142607	0.100674	0.988135	0.688402	29		FC_ALL_SNAIVE	0.151693	0.106548	1.048301	1.012717	31
	FC_ALL_ETS_30	0.133547	0.096637	0.94704	0.660797	24		FC_ALL_ETS_90	0.154056	0.111514	1.094633	1.059918	35
	FC_ALL_SARIMA_30	0.112318	0.080998	0.794006	0.553859	6		FC_ALL_SARIMA_90	0.134052	0.094104	0.926258	0.89444	23
	FC_ALL_TBATS_30	0.180336	0.13818	1.352622	0.944866	44		FC_ALL_TBATS_90	0.192798	0.145528	1.426656	1.383215	44
	FC_ALL_NNAR_30	0.142021	0.103142	1.009649	0.705278	31		FC_ALL_NNAR_90	0.131494	0.09408	0.92644	0.894212	21
	FC_ALL_NNARX_30	0.152278	0.115943	1.131326	0.792811	36		FC_ALL_NNARX_90	0.155056	0.129769	1.26728	1.233428	39
	Mean forecast	0.112132	0.085827	0.840426	0.586879	11		Mean forecast	0.123793	0.092402	0.907239	0.878263	16
	Median forecast	0.112006	0.083631	0.820768	0.571863	7		Median forecast	0.120317	0.088897	0.874222	0.844948	12
	Regression-based weights	0.154694	0.118239	1.154535	0.80851	40		Regression-based weights	0.159707	0.100148	0.991589	0.951887	31
	Bates–Granger weights	0.114843	0.087296	0.854541	0.596924	16		Bates–Granger weights	0.119477	0.087807	0.862761	0.834588	8
	Bates–Granger ranks	0.117663	0.089036	0.871403	0.608822	20		Bates–Granger ranks	0.117543	0.085939	0.844424	0.816833	4

Table 1 and Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 in Appendix A summarize the forecast evaluation results for all forecast models, forecast combination techniques, forecast horizons, and hotel classes: Table 1 for ‘all’, Table A1 for the hotel class ‘luxury’, Table A2 for ‘upper upscale’, Table A3 for ‘upscale’, Table A4 for ‘upper midscale’, Table A5 for ‘midscale’, and Table A6 for ‘economy’. The smallest RMSE, MAE, MAPE, MASE, and sum of rank values for each hotel class and forecast horizons are indicated in boldface. According to the various forecast accuracy measures, the best forecast model or forecast combination technique, respectively, per hotel class and forecast horizon is typically indicated consistently, with only six exceptions for the RMSE (‘upscale’ for $h=1, 7$, ‘upper midscale’ for $h=30$, ‘economy’ for $h=30$, ‘all for $h=1, 30$), which is not too surprising as this is the only employed forecast accuracy measure based on squared forecast errors.

Given that six forecast models and five forecast combination techniques are competing, the lowest possible sum of ranks across the four forecast accuracy measures is equal to 4, whereas the highest possible sum of ranks equals 44. Given the six hotel classes and four forecast horizons, a total of 28 cases in terms of the sum of ranks can be distinguished, which are analyzed in more detail in the following. Except for regression-based weights (most prominently: ‘economy’ for $h=30$), none of the forecast models or forecast combination techniques result in extremely high forecast errors and should, therefore, not be discarded from the beginning. In four cases (‘upper midscale’ for $h=7, 30$, ‘economy’ for $h=90$, ‘all’ for $h=7$), regression-based weights cannot even be calculated, as the $X^{T}X$ matrix of the OLS regression is singular and, therefore, cannot be inverted. As already noted by Nowotarski et al. [90], the high correlation of the predictions stemming from the forecast models can make unconstrained regression-based weights unstable. Therefore, the use of this particular forecast combination technique is not recommended for hotel revenue managers, nor beyond this group.

With respect to the single models, the ETS model is able to achieve the lowest sum of ranks in four cases (‘luxury’ for $h=1, 7, 30$, ‘economy’ for $h=7$), the Seasonal NNAR model in three cases (‘luxury’ for $h=90$, ‘upscale’ for $h=90$, ‘midscale’ for $h=90$), and the SARIMA model in two cases (‘upper upscale’ for $h=1$, ‘all’ for $h=30$). The Seasonal Naïve model, the TBATS model, and the Seasonal NNAR model with an external regressor never achieve the lowest sum of ranks. The fact the that simple Seasonal Naïve benchmark is outperformed by at least one competing forecast model or forecast combination technique on each occasion proves the general viability of using more complex forecasting approaches. One reason why the TBATS model does not perform so well could be the fact that one of two seasonal patterns in the data, the weekly seasonal pattern, is not particularly pronounced (see Section 2). Including the seasonal naïve forecast of the inflation-adjusted ADR as an external regressor in the Seasonal NNAR model does not seem to have a positive effect on forecast accuracy either, at least not directly. However, the information included in these forecast models should not be discarded. As all F-test statistics of the forecast encompassing tests are statistically significantly different from zero—at least at the 10% level and in many cases even at the stricter 0.1% level—all forecast models seem to possess some unique information and, therefore, survive step 1 of the two-step forecast combination procedure suggested by Costantini et al. [26]. Thus, all forecast models should be considered for forecast combination.

Apart from the aforementioned regression-based weights, the relevance of forecast combination materializes in terms of superior forecast accuracy of the remaining forecast combination techniques in 19 of 28 cases. The mean forecast is characterized by the lowest sum of ranks in one case (‘upper upscale’ for $h=30$). The time-varying and comparably more robust median forecast achieves the lowest sum of ranks in five cases (‘upper upscale’ for $h=7$, ‘upscale’ for $h=1, 7, 30$, ‘all’ for $h=7$), as does the Bates–Granger weights approach (‘upper midscale’ for $h=30, 90$, ‘midscale’ for $h=1, 30$, ‘all’ for $h=1$). Finally, Bates–Granger ranks, which make Bates–Granger-type weights independent of correlations between forecast errors and can, therefore, be interpreted as a refinement of traditional Bates–Granger weights, achieve the lowest sum of ranks in eight cases (‘upper upscale’ for $h=90$, ‘upper midscale’ for $h=1, 7$, ‘midscale’ for $h=7$, ‘economy’ for $h=1, 30, 90$, ‘all’ for $h=90$). Together, combined forecasts based on Bates–Granger weights and Bates–Granger ranks provide the highest level of forecast accuracy in the relative majority of cases (i.e., in 13 of 28).

5. Conclusions

The present study employed daily data made available by the STR SHARE Center over the period from 1 January 2010 to 31 January 2020 for six Viennese hotel classes and their total. The forecast variable of interest was hotel room demand. As forecast models, (1) Seasonal Naïve, (2) ETS, (3) SARIMA, (4) TBATS, (5) Seasonal NNAR, and (6) Seasonal NNAR with an external regressor (seasonal naïve forecast of the inflation-adjusted ADR) were employed. Forecast evaluation was carried out for forecast horizons $h$ = 1, 7, 30, and 90 days ahead based on rolling windows. As forecast combination techniques, (a) mean, (b) median, (c) regression-based weights, (d) Bates–Granger weights, and (e) Bates–Granger ranks were calculated.

In the relative majority of cases (i.e., in 13 of 28), combined forecasts based on Bates–Granger weights and Bates–Granger ranks provided the highest level of forecast accuracy in terms of typical forecast accuracy measures (RMSE, MAE, MAPE, and MASE) and their lowest sum of ranks. The mean and the median forecast performed best in another six cases, thus, making forecast combination a worthwhile endeavor in 19 of 28 cases. However, due to its instability, forecast combination with regression-based weights is not recommended. Concerning single models, the ETS model was able to achieve the lowest sum of ranks in four cases, the Seasonal NNAR model in three cases, and the SARIMA model in two cases. Although the Seasonal Naïve model, the TBATS model, and the Seasonal NNAR model with an external regressor never achieved the lowest sum of ranks, considering the information contained in these models proved worthwhile for forecast combination according to forecast encompassing test results.

One limitation of this study is its temporal and geographical focus. Another limitation is that the data used therein are not freely available and need to be purchased. Furthermore, data at the individual hotel level were not available to the author, which, however, would have suffered from a lack of representativity. Nonetheless, the suggested forecast models and two-step forecast combination procedure can be applied to other time periods, (city) destinations, and datasets, thus, making this research fully replicable. Especially practitioners (e.g., revenue managers working in smaller (boutique) hotels without access to a professional revenue management system; [13,38]) benefit from the results of this study as it provides a toolkit in terms of employing the proposed methodology on their own hotel-level dataset to easily generate reliable hotel room demand forecasts. If a single hotel did not possess a long enough sample of time-series data, also expanding windows instead of rolling windows could be easily implemented.

Once the author gets access to data beyond 31 January 2020, an investigation of predictive performance for the forecast models and forecast combination techniques during the COVID-19 pandemic within adequately designed forecasting scenarios along the lines of Zhang et al. [44] would be of particular interest, as would observing which of the employed forecast models would be the fastest to pick up any directional changes. As this would constitute a forecasting exercise not for normal but rather for turbulent times (i.e., during and with a severe structural break), such an exercise would call for a separate investigation. Another idea for future research could be the inclusion of seasonal naïve forecasts of web-based leading indicators as predictors in addition to the seasonal naïve forecast of the inflation-adjusted ADR, for which, of course, daily data would need to be available. Not only would this approach satisfy the need for this type of predictor to be ex-ante [77] but would also take up a recent recommendation by Hu and Song [91] to combine these two types of tourism (and hotel room) demand predictors. Finally, other multi-step forecast combination procedures based on the Model Confidence Set (MCS; [92]) as suggested by Amendola et al. [93] or Aras [94] could be considered.