Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data
Abstract
:1. Introduction
2. Motivational Data on Ground Motion in Landslide
3. The Error-Correction Cointegration (ECC) Approach for VAR Time Series
3.1. ECC–VAR(p) Model
3.2. Making Statistical Inferences from the ECC–VAR Model
3.3. Forecasting Based on the Fitted ECC–VAR Model
4. The EDQ Technique for Vector Time Series Dimension Reduction
5. Applying the ECC–VAR–EDQ Method to Analyze the InSAR Landslide Data
5.1. Unit Root Test and Cointegration Test for the EDQ Series
5.2. Estimating and Fitting the ECC(r)–VAR(p) Model for the EDQ Series
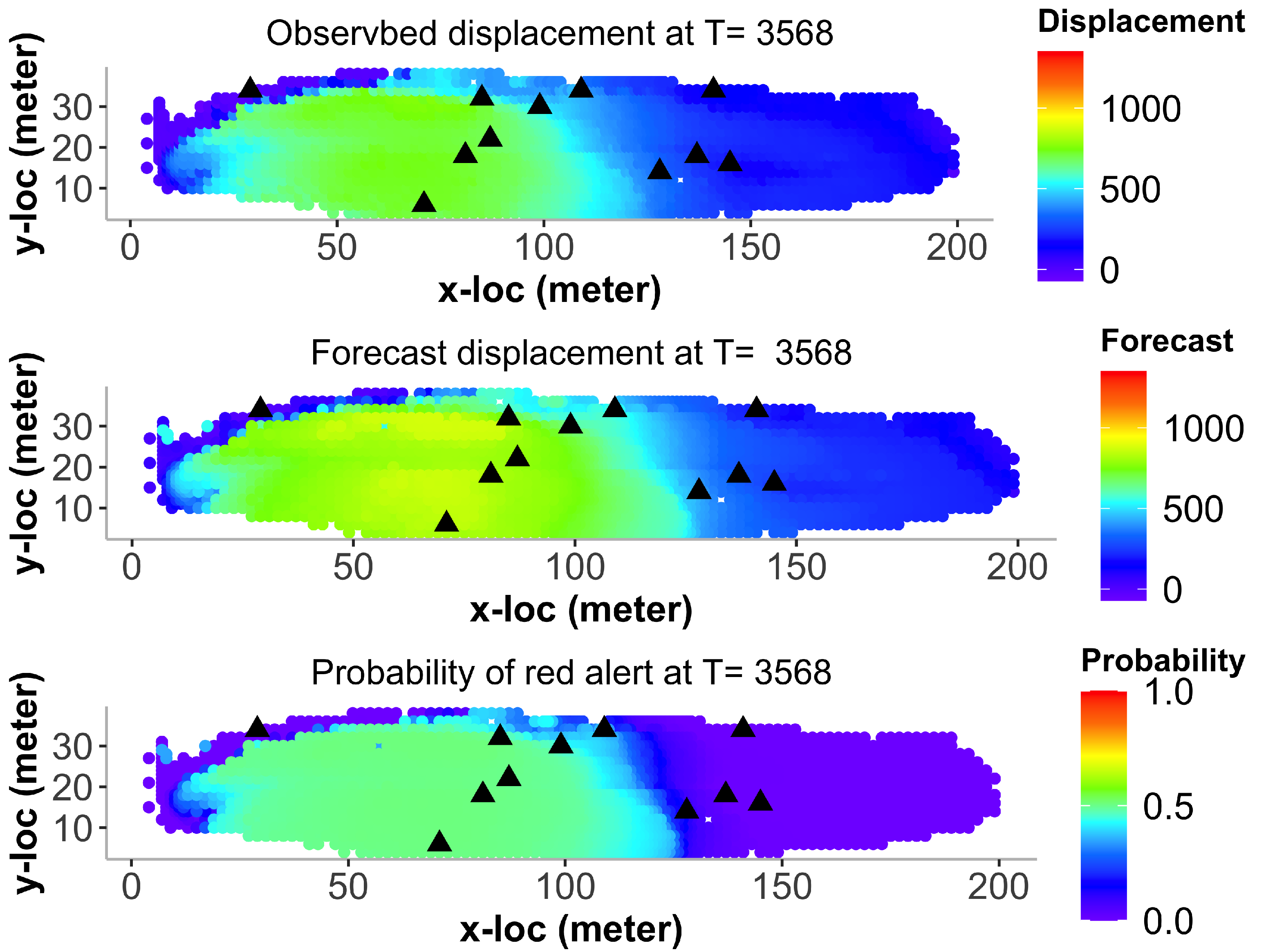
5.3. Landslide Displacement Forecasting
6. Probabilistic Landslide Prediction via the ECC–VAR–EDQ Method
6.1. Forecast Intervals for Displacement and Velocity
6.2. Probability of Future Risk of Landslide
6.3. Landslide Prediction for All Locations
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dick, G.J.; Eberhardt, E.; Cabrejo-Liévano, A.G.; Stead, D.; Rose, N.D. Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can. Geotech. J. 2014, 52, 515–529. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.J. Landslide Hazard and Risk-Concluding Comment and Perspectives. In Landslide Hazard and Risk; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Chapter 26; pp. 765–774. [Google Scholar] [CrossRef]
- Intrieri, E.; Carlá, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth-Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Wang, H.; Qian, G.; Tordesillas, A. Modeling big spatio-temporal geo-hazards data for forecasting by error-correction cointegration and dimension-reduction. Spat. Stat. 2020, 36, 100432. [Google Scholar] [CrossRef]
- Tsay, R.S. Multivariate Time Series Analysis: With R and Financial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Peña, D.; Tsay, R.S.; Zamar, R. Empirical dynamic quantiles for visualization of high-dimensional time series. Technometrics 2019, 61, 429–444. [Google Scholar] [CrossRef]
- Wessels, S.D.N. Monitoring and Management of a Large Open Pit Failure. Ph.D. Thesis, University of the Witwatersrand, Johannesburg, South Africa, 2009. [Google Scholar]
- Harries, N.; Noon, D.; Rowley, K. Case studies of slope stability radar used in open cut mines. In Stability of Rock Slopes in Open Pit Mining and Civil Engineering Situations; SAIMM Johannesburg: South Africa, 2006; pp. 335–342. [Google Scholar]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Stacey, T. Stability of Rock Slopes in Open Pit Mining and Civil Engineering Situations; The South African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2006. [Google Scholar]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Pfaff, B. Analysis of Integrated and Cointegrated Time Series with R; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Johansen, S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxf. B Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Phillips, P.C.; Wu, Y.; Yu, J. Explosive behavior in the 1990s Nasdaq: When did exuberance escalate asset values? Int. Econ. Rev. 2011, 52, 201–226. [Google Scholar] [CrossRef] [Green Version]
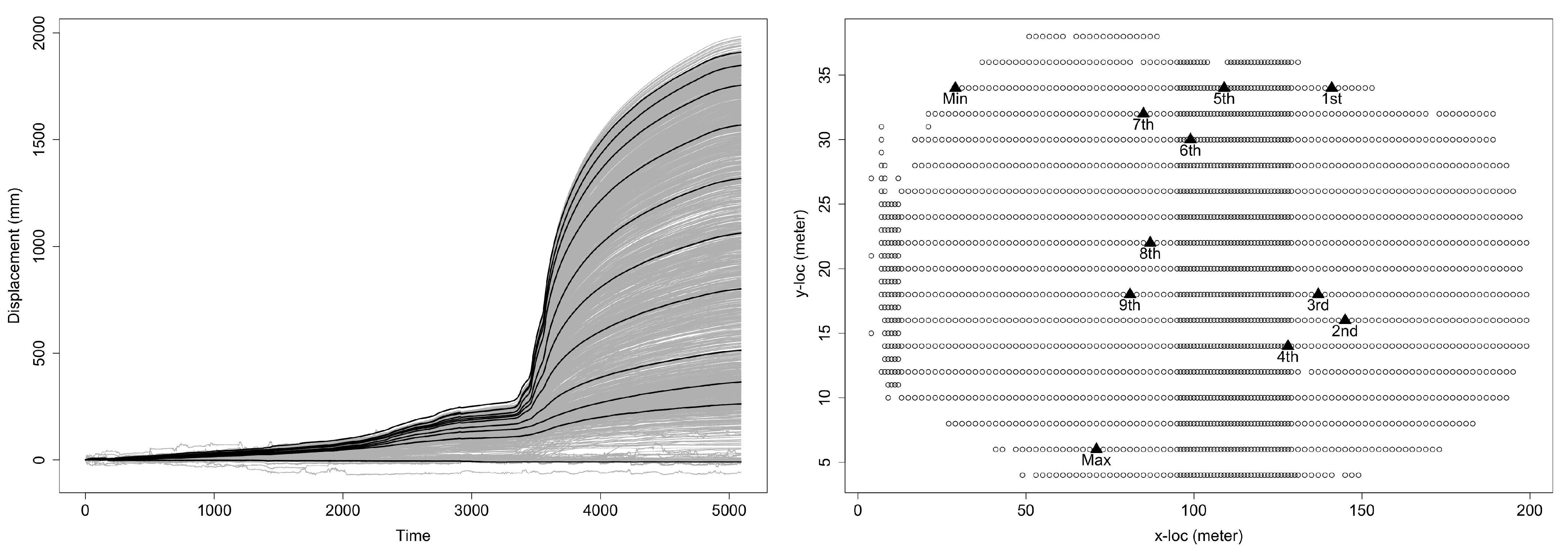






| Quantile Level | Selected Pixel | Quantile Level | Selected Pixel |
|---|---|---|---|
| Min | 202 | 0.6 | 827 |
| 0.1 | 1432 | 0.7 | 672 |
| 0.2 | 1454 | 0.8 | 685 |
| 0.3 | 1392 | 0.9 | 630 |
| 0.4 | 1307 | Max | 534 |
| 0.5 | 995 |
| Quantile Level p | Pixel ID | Augment Dickey−Fuller(ADF) |
|---|---|---|
| Min | 202 | −0.9334/−26.8762 *** |
| 0.1 | 1432 | −2.9837 **/−21.3401 *** |
| 0.2 | 1454 | −4.6048 ***/−21.5254 *** |
| 0.3 | 1392 | −3.1837 **/−17.0134 *** |
| 0.4 | 1307 | −3.3355 **/−17.7037 *** |
| 0.5 | 995 | −2.8695 **/−16.1240 *** |
| 0.6 | 827 | −1.7187/−14.2224 *** |
| 0.7 | 672 | −1.4623/−13.3679 *** |
| 0.8 | 685 | −1.3172/−13.9375 *** |
| 0.9 | 630 | −1.5063/−11.7859 *** |
| Max | 534 | −1.3808/−17.9545 *** |
| Hypothesis | Statistic | 10% | 5% | 1% |
|---|---|---|---|---|
| 0.42 | 6.50 | 8.18 | 11.65 | |
| 5.82 | 15.66 | 17.95 | 23.52 | |
| 16.77 | 28.71 | 31.52 | 37.22 | |
| 35.19 | 45.23 | 48.28 | 55.43 | |
| 57.56 | 66.49 | 70.60 | 78.87 | |
| 120.14 | 85.18 | 90.39 | 104.20 | |
| 253.29 | 118.99 | 124.25 | 136.06 | |
| 404.85 | 151.38 | 157.11 | 168.92 | |
| 628.63 | 186.54 | 192.84 | 204.79 | |
| 998.73 | 226.34 | 232.49 | 246.27 | |
| 1869.85 | 269.53 | 277.39 | 292.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, G.; Tordesillas, A.; Zheng, H. Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data. Forecasting 2021, 3, 850-867. https://doi.org/10.3390/forecast3040051
Qian G, Tordesillas A, Zheng H. Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data. Forecasting. 2021; 3(4):850-867. https://doi.org/10.3390/forecast3040051
Chicago/Turabian StyleQian, Guoqi, Antoinette Tordesillas, and Hangfei Zheng. 2021. "Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data" Forecasting 3, no. 4: 850-867. https://doi.org/10.3390/forecast3040051
APA StyleQian, G., Tordesillas, A., & Zheng, H. (2021). Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data. Forecasting, 3(4), 850-867. https://doi.org/10.3390/forecast3040051






