Different Forecasting Horizons Based Performance Analysis of Electricity Load Forecasting Using Multilayer Perceptron Neural Network

Abstract

With an uninterrupted power supply to the consumer, it is obligatory to balance the electricity generated by the electricity load. The effective planning of economic dispatch, reserve requirements, and quality power provision for accurate consumer information concerning the electricity load is needed. The burden on the power system engineers eased electricity load forecasting is essential to ensure the enhanced power system operation and planning for reliable power provision. Fickle nature, atmospheric parameters influence makes electricity load forecasting a very complex and challenging task. This paper proposed a multilayer perceptron neural network (MLPNN) with an association of recursive fine-tuning strategy-based different forecasting horizons model for electricity load forecasting. We consider the atmospheric parameters as the inputs to the proposed model, overcoming the atmospheric effect on electricity load forecasting. Hidden layers and hidden neurons based on performance investigation performed. Analyzed performance of the proposed model with other existing models; the comparative performance investigation reveals that the proposed forecasting model performs rigorous with a minimal evaluation index (mean square error (MSE) of 1.1506 × 10⁻⁰⁵ for Dataset 1 and MSE of 4.0142 × 10⁻⁰⁷ for Dataset 2 concern to the single hidden layer and MSE of 2.9962 × 10⁻⁰⁷ for Dataset 1, and MSE of 1.0425 × 10⁻⁰⁸ for Dataset 2 concern to two hidden layers based proposed model) and compared to the considered existing models. The proposed neural network possesses a good forecasting ability because we develop based on various atmospheric parameters as the input variables, which overcomes the variance. It has a generic performance capability for electricity load forecasting. The proposed model is robust and more reliable.

1. Introduction

1.1. Background

The growing trends in the industry and day-to-day life need electricity to be an indispensable resource in the universe. However, because of irregular load and uncertainty, it is a burden to the power system engineers. The requirement of the consumer is a reliable and uninterruptible power supply. Concerning the variation in atmospheric weather conditions, the electricity load fluctuates [1]. The improper planning on generating electricity to the electricity demand creates an outage problem, power quality problem, and interruption of power provided to the consumer. Electricity load forecasting is obligatory to overcome the above-said issues.

Estimation of future parameter points concerning the time is known as forecasting. Knowledge about the electricity load requirement is essential in planning the power supply scheduling and economic dispatch. More load forecasting models were developed in the existing literature using different methods, namely, numerical weather prediction, statistical methods (regression and artificial neural network), and hybrid methods [2,3,4,5,6]. Therefore, accurate forecasting of electricity load is obligatory and plays a significant role in the utility system’s planning and development activities.

The electricity load forecasting possesses a fickle nature, which varies concerning factors such as working daytime, holidays, festival days, seasonal effects (summer consumption is high compared to winter), etc. The meteorological variable’s influence on electricity load takes account, which declares the output lead decay of the forecast error. In general, the accurate forecasting of electricity load primaries and the need for grid integration, planning, and control of the grid-connected system ensures the customer’s uninterruptible power provision. This paper explores a simple and high accuracy model, such as a different forecasting horizons model for electricity load forecasting using a multilayer perceptron neural network.

1.2. Literature Studies

The generic model necessitates one in the forecasting field, and a lot of research work is existing, which is implied by many forecasting models in the literature. The previously carried out research reported in the literature is as follows.

Momoh, J.A. et al. 1997 [7] performed short-term load forecasting using a backpropagation training algorithm-based neural network. Erkmen, I. and Topalli, A.K. 2003 [8] carried out short-term load forecasting based on four methods depending on AI (artificial intelligence), backpropagation learning algorithm momentum-based weight updating multilayer perceptron network lead better results with a low error value. López et al. 2018 [9] pointed out autoregressive and neural network-based short-term load forecasting and performed a performance comparison. According to the result analysis, the regressive model leads to better results on special days, and the neural network model achieves better results on cold days. Vasar Cristian et al. 2007 [10] performed feed-forward and Elman recurrent neural network-based short-term load forecasting. According to the two-day ahead prediction results, it is observed that better performance and Elman network is recommended for increased input and neurons for each layer compared to the Elman network feed-forward. Remarks: (1) Elman neural network needs a more extensive training period, (2) feed-forward is application-oriented, (3) no assurance of the guaranteed results. Filipe Rodrigues et al. 2014 [11] presented a Leven-berg-Marquardt algorithm associated feed-forward neural network for load forecasting and hourly energy consumption. Based on the 93 households logged data set experimentation, the proposed artificial neural network leads to better forecasting for both load and energy consumption as MAPE of 12.9% and 4.2%, respectively. Changhao Xia et al. 2010 [12] performed a virtual forecaster employing radial basis function neural network and virtual instrument technology. From the experimentation with short-term forecasting with BPN, GRNN, RBFN, it is noticed, RBFN achieves less MAPE, and the investigation with medium-term forecasting with other models RBFN performs better.

Ayca Kumluc Topalli et al. 2006 [13] carried out Elman recurrent neural network design with a hybrid learning algorithm for short-term forecasting and performed performance comparison with ARMA. The result proves that the proposed Elman neural network achieves better performance in terms of reduced average percentage error than ARMA (ARMA model error: 2.33%, RNN model error: 1.60%). Tomonobu Senjyu et al. 2002 [14] performed a neural network to incorporate the correction of a similar day data-based one-hour ahead load forecasting model. The validation with the Okinawa Electrical Power Company 4 case study performance analysis observed that Case 4 achieves minimal error (i.e., MAPE: 1.18.). Zhang et al. 2018 [15] performed short-term load forecasting employing recurrent neural networks with multiple time series. The sequential information between continuous and discrete-time series is learned with the aid of multiple time series. Hence, the RNN model leads to better short-term forecasting concerning the load.

Jian Luo et al. 2018 [16] suggested very short-time load forecasting using a dynamic regression model incorporating the anomaly threshold. The corrected load data are replaced with forecasted hourly load data development of smart grid technology for highly accurate load forecasting. The performance improvement concern for fine-tuning is required, and multi-time horizon forecasting does not address it. Yiyan Li et al. 2018 [17] performed data-driven linear clustering-based load forecasting for a long-term horizon. The limitation is the occurrence of network issues because of the non-optimal selection of clustering criteria and levels. Jingrui Xie, Tao HONG 2018 [18] pointed out sun position-based 24 solar term calendars for load forecasting. Limitations are entrapped in overfitting issues and complex to design the model. The next hour ahead load forecast (short-term horizon) was performed using ANN by Santos PJ et al. 2005 [19].

In the literature, an artificial neural network (ANN) based load forecasting model proposed by various researchers still forecasting models with highly accurate forecasting with minimal forecasting error is required. Although many researchers have developed a lot of forecasting models, still an accurate load forecasting model is needed because if a small load forecasting error leads to the increased investment cost and causes imbalance. A simple and generic forecasting model is required in load forecasting to handle power system load management. With this motivation, this paper proposed a generic, simple, and easy-to-implement forecasting model based on a multilayer perceptron neural network. The proposed model is simple in the aspects of design complexity, computation burden, and cost. The proposed model consists of a single input layer with six inputs, a single hidden layer, and one output layer. To reduce the computational burden and cost of the network, a single hidden layer is used [20]; the proposed model uses a perceptron learning algorithm. The authors suggested a multilayer perceptron neural network with an association of recursive fine-tuning strategy-based forecasting model for electricity load forecasting applications, which leads to minimal forecasting error with feasible convergence.

1.3. Contributions and Novelty

The contributions of this paper are as follows:

• The atmospheric weather parameters were considered the proposed model’s inputs, leading to overcoming the weather’s impact on the electricity load forecasting.
• Analyze the proposed multilayer perceptron neural network performance in terms of various hidden neurons in the hidden layer and various hidden layers. This analysis explains the neural network stability, the impact of hidden neurons, hidden layers, time-series data impact, and the trial-error method based on optimal hidden neurons to fix the hidden layer of the proposed forecasting model.
• Perform different forecasting horizons based on electricity load forecasting (long-term, medium-term, short-term, and very short-term time horizon). These different forecasting horizons-based electricity forecasting provides the effective planning and control operation of utility systems to improve the economy, overcome grid unbalancing, power quality problems, and reserve resources.
• Substantiate the validity by employing real-time acquired two dataset-based experimental simulations and performed a comparative analysis with existing models. The obtained results are inferences outperforming the forecasting ability of the proposed model with minimal forecasting error.

Novelty: This paper proposed the multilayer perceptron neural network with recursive fine-tuning strategy and performed statistical analysis with various hidden neurons, hidden layers concerned with different forecasting horizon of electricity load forecasting. Hence, even a single hidden layer is adopted, the proposed forecasting model results in better performance than the other existing methods used for the comparative analysis.

2. Proposed Model Implementation

The proposed model implementation comprises two essential stages, 1: data collection, preprocessing, and splitting, 2: model development and evaluation, implementing the structural flow of the proposed model is depicted in Figure 1. The developed model performance is validated on the training data set; if the performance is not acceptable, the fine-tuning process continues to update the weight to achieve a minimal error or stopping criterion (maximum number of iterations). Once the performance is acceptable, the model is evaluated on the testing data set to measure the error evaluation index, check the load forecasting model performance based on the error evaluation index. The detailed description of the proposed model implementation is described as follows:

2.1. Data Collection

Dataset 1: ERCOT (Electric Reliability Council of Texas) electricity market data set for ten years from 2009 to 2019 was used for numerical experimentation to validate the proposed forecasting model. The electricity load (MW), temperature (°C), humidity (%), wind speed (m/s), solar irradiance (W/m), and pressure (bar) are taken as the proposed model inputs, and the forecast electricity load is the proposed model output. The collected data set comprises 5.256 × 10⁶ data points of each taken input variable. Figure 2a shows the collected Dataset 1, with real-time electricity load data concerning time.

Dataset 2: European load dataset (ENTSO-E Data) period of 2006 to 2015, hourly load data of country Austria, coverage ratio approximate 100% (whole country load) collected from the Open Power System Data platform, and atmospheric parameters—temperature (°C), humidity (%), wind speed (m/s), solar irradiance (W/m), and pressure (bar) are acquired from National Oceanic and Atmospheric Administration, United States. The collected data comprises 7.884 × 10⁴ data points of each taken input variable. Figure 2b shows the collected Dataset 1—real-time electricity load data concerning data points. The considered weather data in Dataset 1 and Dataset 2 are the measured data.

2.2. Data Preprocessing (Normalization)

The collected data are processed by employing a min–max data normalization method, which overcomes the variance present in the data set by scale the real-time collected data between zero (0) to one (1). Therefore, the accuracy is improved and makes the computation easy. The real-time collected data have been normalized based on the following equation.

$$V_p^{\prime }=\left(\frac{V_p-V_{\min }}{V_{\max }-V_{\min }}\right)\left(V_{\max }^{\prime }-V_{\min }^{\prime }\right)+V_{\min }^{\prime }$$

(1)

where $V_p$ presents the real-time input data, $V_{\min }$ is the real-time minimum input data, $V_{\max }$ the real-time maximum input data, $V_{\min }^{\prime }$ is the minimum target value, and $V_{\max }^{\prime }$ is the maximum target value.

2.3. Data Splitting

The collected real-time data set is split into training and testing data sets. Dataset 1: The collected data comprises 5.256 × 10⁶ real-time data of each taken input variable, 70 percentage data (3.6792 × 10⁶) split as a training data set. The remaining unseen 30 percentage data (1.5768 × 10⁶) are split as a testing data set. Dataset 2: The collected data comprises 7.884 × 10⁴ real-time data of each taken input variable, 70 percentage data (5.5188 × 10⁴) split as a training data set. The remaining unseen 30 percentage data (2.3652 × 10⁴) are split as a testing data set. The proposed forecasting model is trained by the training data set and the performance validated by the testing data set.

2.4. Development of Proposed Model

The proposed multilayer perceptron network belongs to the feed-forward neural network; the network learns by supervised learning rules to solve the complex problem with higher computational efficiency than a single-layer neural network [20]. The proposed multilayer perceptron neural network architecture is shown in Figure 3, which comprises three layers, namely, the input layer, hidden layer, and output layer. The proposed multilayer perceptron neural network is learned by the backpropagation learning rule; the activation function for the hidden and output layer is a hyperbolic tangent sigmoid and purelin activation function, respectively.

During the training process, a recursive fine-tuning strategy is incorporated to aid better accuracy and convergence. Figure 3 infers the proposed model, each layer performs independent computations on receiving the information results transferred to a successive layer as an input, and finally, the network output is computed.

The proposed neural network model is fully connected, and the hidden layer neurons have nonlinear transfer functions to learn the linear and nonlinear relationship between the input and output vectors.

Table 1. Proposed multilayer perceptron neural network implementation parameters.

MLPNN	Variable
Input neurons	6 inputs
Number of hidden layers	1
Output neuron	1
Number of epochs	100
Threshold	1
Learning rate	0.9

describes the implementation parameters of the proposed multilayer perceptron neural networks. For the neural network design process, there is no standing rule of thumb available.

The authors choose the parameters based on the literature knowledge [21,22,23,24] and trial-and-error methods. Electricity load, temperature, humidity, wind speed, solar irradiance, and pressure are the input neurons of the input layer, single hidden layer, and hidden neuron numbers selected based on the lowest evaluation index. The output layer has the forecast electricity load as an output neuron.

Table 2. Mathematical modeling of the proposed neural network variables.

Variables	Mathematical Model
$V_1,V_2,V_3,V_4,V_5,V_6:U$	Electricity Load, Temperature, Humidity, Wind speed, Solar Irradiance, and Pressure: Forecast Electricity Load
Input vector	$V=\left[EL,T,H,WS,SI,P\right]$
Output vector	$U=\left[E{L}_f\right]$
Weight vector of input to hidden vector	$V{H}_w=\left[\begin{array}{l}V{H}_w{}_{11},V{H}_{w12},\dots ,V{H}_w{}_{1n},V{H}_{w21},V{H}_{w22},\dots ,V{H}_{w2n},V{H}_{w31},V{H}_{w32},\dots ,V{H}_{w3n},\\ V{H}_{w41},V{H}_{w42},\dots ,V{H}_{w4n},V{H}_{w51},V{H}_{w52},\dots ,V{H}_{w5n},V{H}_{w61},V{H}_{w62}\dots ,V{H}_{w6n}\end{array}\right]$
Net input of the hidden layer	$S_{inq}={\displaystyle \sum _{p=1}^6{\displaystyle \sum _{q=1}^n{V}_{p}V{H}_{wpq}}}$
The output of the hidden layer	$S_q=f\left({\displaystyle \sum _{p=1}^6{\displaystyle \sum _{q=1}^n{V}_{p}V{H}_{wpq}}}\right)$
Weight vector of the hidden to output vector	$H{U}_w=\left[H{U}_{w1},H{U}_{w2},\dots \dots ,H{U}_{wn}\right]$
Net input of the output layer	$U_{in}={\displaystyle \sum _{q=1}^n\left(S_{q}H{U}_{wq}\right)}$
Output	$U=f\left({\displaystyle \sum _{q=1}^n\left(S_{q}H{U}_{wq}\right)}\right)\hspace{1em},q=1,2,\dots \dots ,n$

presents the mathematical modeling of the proposed neural network variables.

where $V$ is the input, $V{H}_w$ is the weights between input and hidden layer, n is the number of hidden neurons, $H{U}_w$ is the weight between the hidden and output layer, and f is the activation function.

2.5. Selection of Hidden Neurons

According to the analysis based on hidden neurons in the hidden layer of the proposed neural network for the considered electricity load forecasting, the hidden neuron number in the hidden layer based on the proposed model result, the minimal evaluation index that the hidden neuron number identified as the optimal hidden neuron numbers of the proposed multilayer perceptron neural network-based forecasting model. The neural network’s major problem is a hidden neuron selection in the hidden layer; there is no rule to select the hidden neurons in the neural network’s hidden layer [21,22,23,24,25,26,27]. The proposed model optimal hidden neurons are estimated by examining the hidden neurons from one to thirty hidden neurons in the hidden layer and computing the evaluation indexes for each hidden neuron-based developmental model.

2.6. Validation and Evaluation Index

The proposed model is trained by the training data set, and after a trained model, the performance is validated by the mean computation of the evaluation index based on the testing data set. The prominent errors such as correlation coefficient (R), root mean square error (RMSE), mean square error (MSE), mean absolute percentage error (MAPE), mean absolute error (MAE), and mean relative error (MRE) are considered as the evaluation index. Equations (2)–(7) are formulations of the considered evaluation index.

$$\mathrm{R}=1-{\left(\frac{{\displaystyle \sum _{t=1}^T\left(E{L}_t^{\prime }-E{L}_t^f\right)}}{{\displaystyle \sum _{t=1}^{T}E{L}_t^f}}\right)}^2$$

(2)

$$\mathrm{RMSE}=\sqrt{\left(\frac{1}{T}{\displaystyle \sum _{t=1}^T{(E{L}_t^{\prime }-E{L}_t^f)}^2}\right)}$$

(3)

$$\mathrm{MSE}=\frac{1}{T}{\displaystyle \sum _{t=1}^T(E{L}_t^{\prime }}-E{L}_t^f{)}^2$$

(4)

$$\mathrm{MAPE}=\frac{100}{T}\left({\displaystyle \sum _{t=1}^T\left|(E{L}_t^{\prime }-E{L}_t^f)/\overline{E}{\overline{L}}_t\right|}\right.)$$

(5)

$$\mathrm{MAE}=\frac{1}{T}{\displaystyle \sum _{t=1}^T(E{L}_t^{\prime }}-E{L}_t^f)$$

(6)

$$\mathrm{MRE}=\frac{1}{T}{\displaystyle \sum _{t=1}^T\left|(E{L}_t^{\prime }-E{L}_t^f)/\overline{E}{\overline{L}}_t\right|}$$

(7)

where, T is the total number of data points, $E{L}_t^{\prime }$ presents the real-time target output, $\overline{E}{\overline{L}}_t$ is the average real-time target output, and $E{L}_t^f$ is the forecast output.

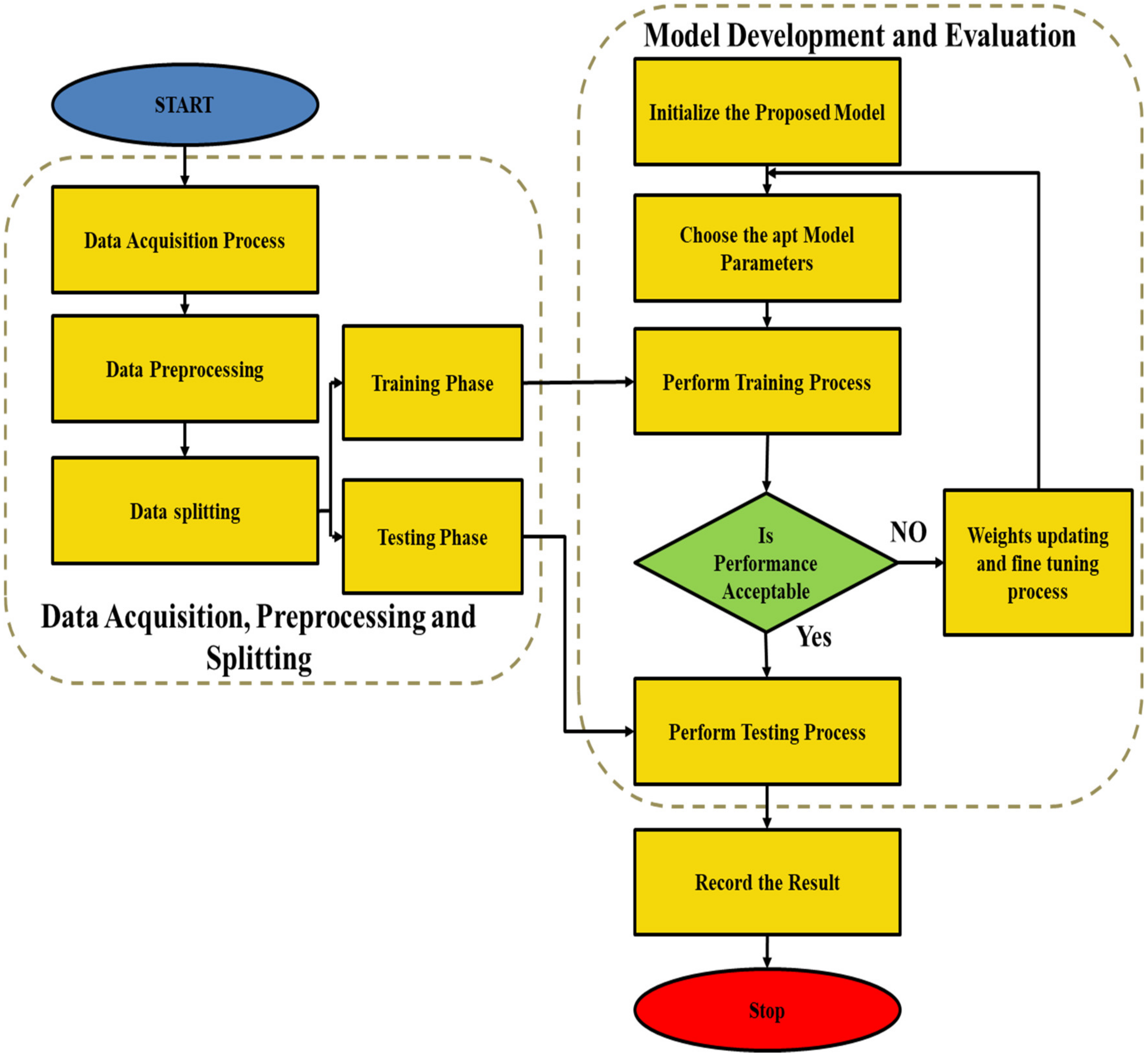
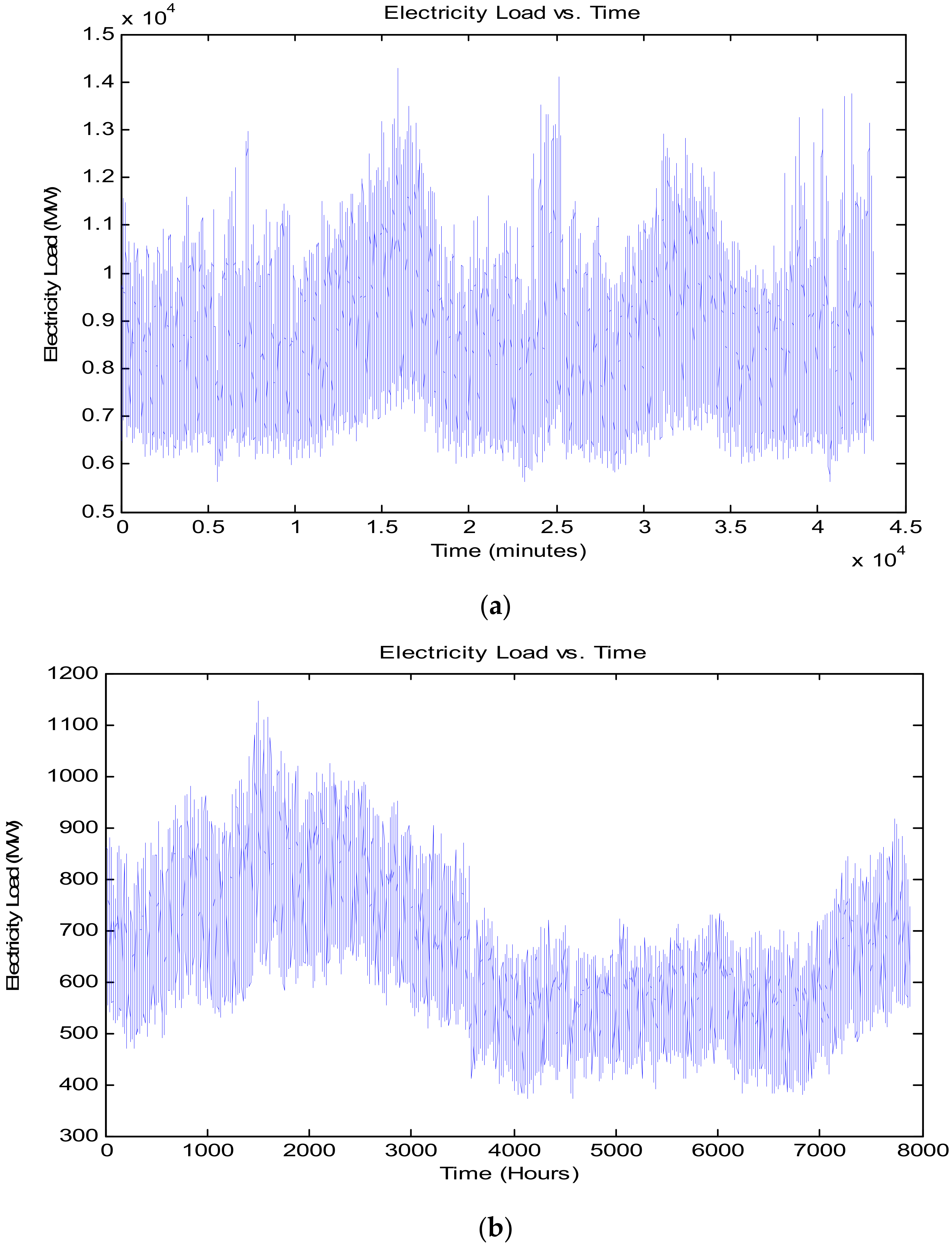
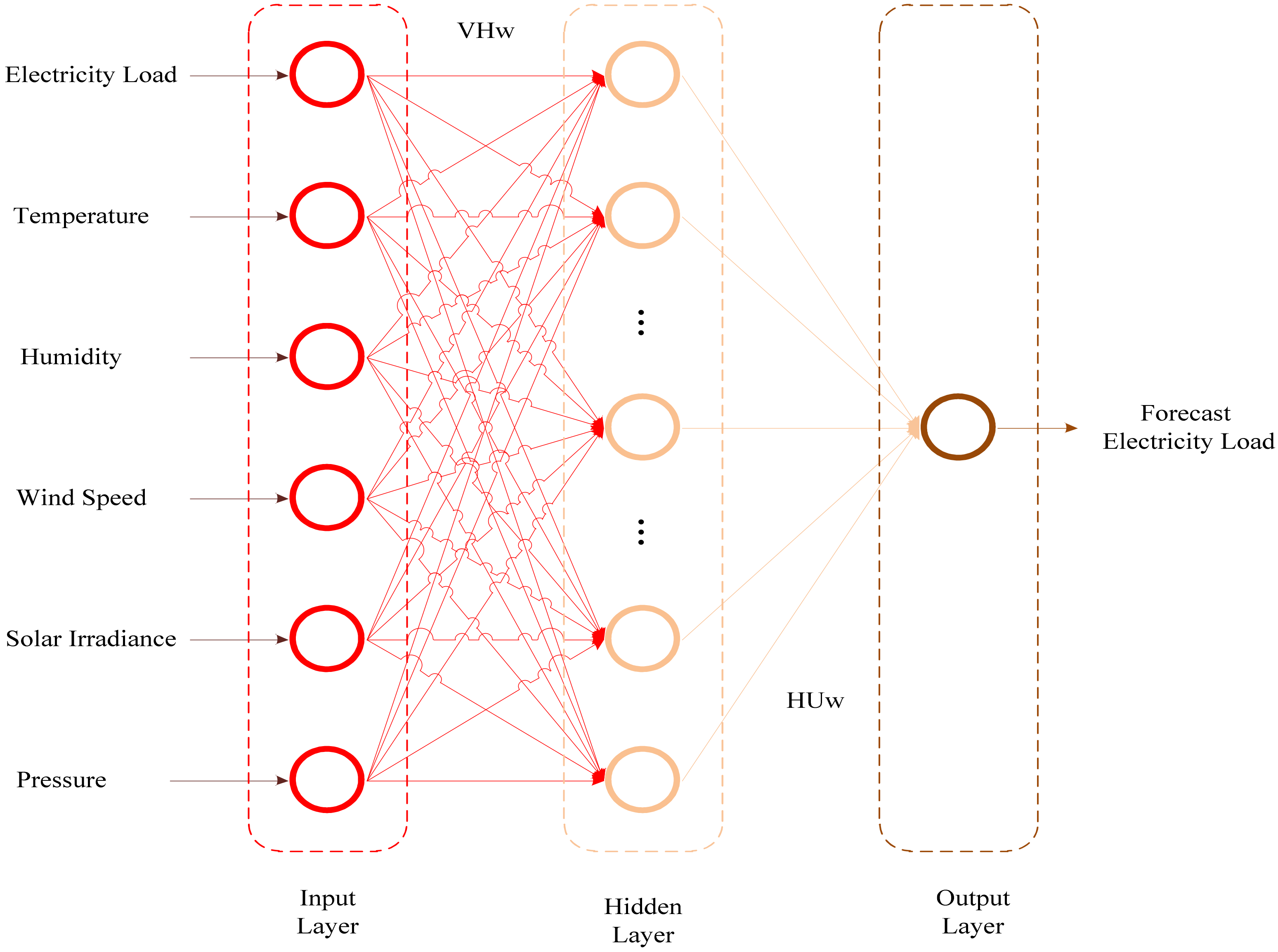
3. Proposed Model Result and Discussion

Electricity load forecast depends on various factors such as geographical location, atmospheric weather conditions, types of days and seasons, subsidies, and energy tariffs. Hence, it possesses irregularities and uncertainty; it creates demanding and challenging tasks for accurate electricity load forecasting. This paper endeavors an electricity load forecasting model using a multilayer perceptron neural network; the proposed model was experimentally conducted on the MATLAB platform. The proposed forecasting model was run on an Acer laptop with a Pentium (R) dual-core processor of 2.30 GHz, RAM: 2 GB. The presented forecasting model’s performance was validated using ERCOT data sets. ERCOT data sets and ENTSO-E data sets with different input parameters are collected and used as training and testing sets.

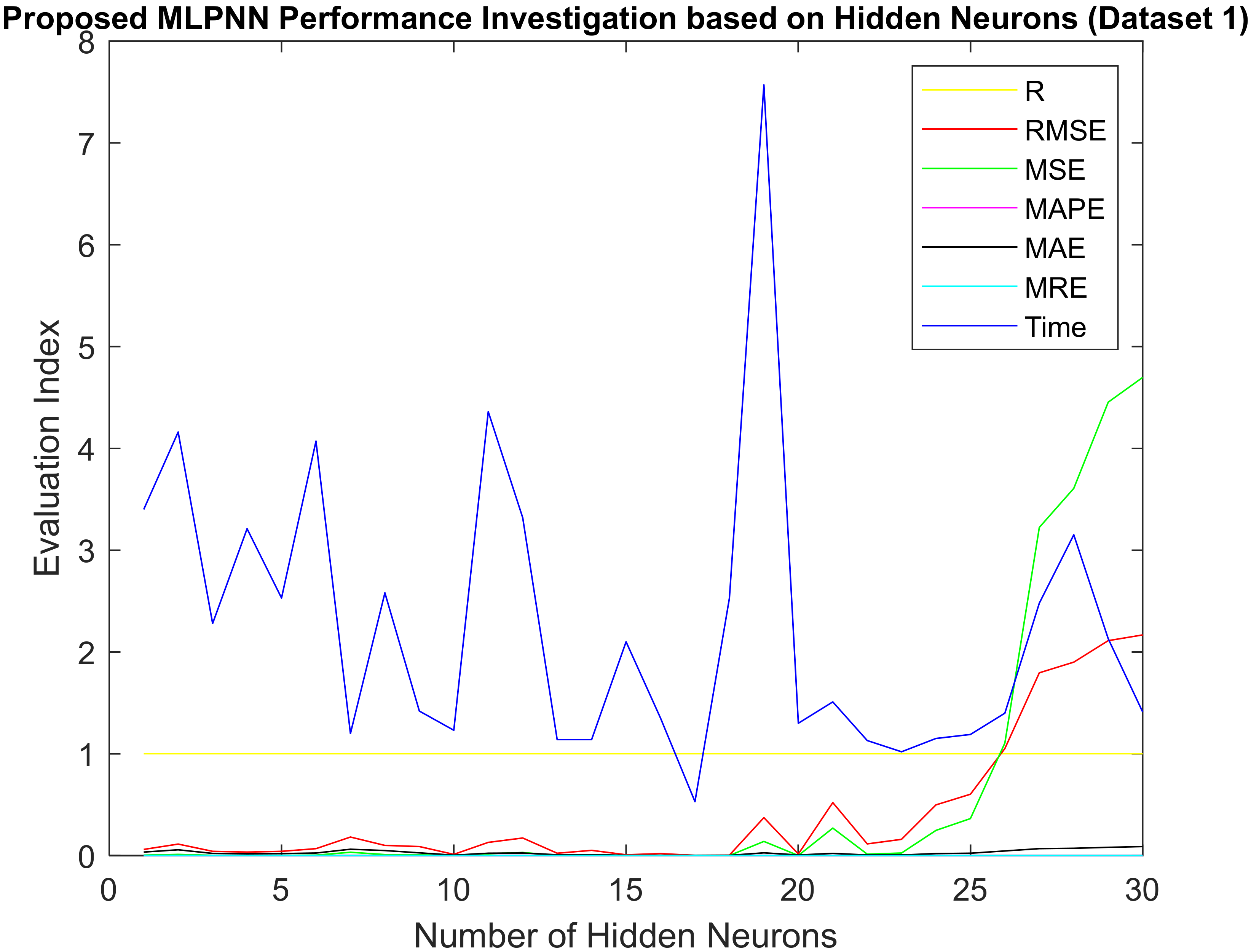
The hidden neurons possess a critical role in the artificial neural network’s stability and accuracy; improper selection of hidden neurons leads to poor performance, underfitting, and overfitting problems. Hence, this paper carried out a performance investigation concerning the various hidden neuron placements in the hidden layer of the proposed multilayer perceptron neural network to resolve the hidden neurons’ issues. The proposed model-based results regarding various hidden neurons concern the electricity load forecasting tabulated in

Table 3. Proposed Multilayer Perceptron Neural Network Performance Investigation based on Hidden Neurons (Dataset 1). The best result highlighted in bold.

Number of Hidden Neurons	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
1	1	0.0611	0.0037	3.9780 × 10−04	0.0345	3.9780 × 10−06	3.40
2	1	0.1123	0.0126	6.5644 × 10−04	0.0569	6.5644 × 10−06	4.16
3	1	0.0415	0.0017	2.4281 × 10−04	0.0210	2.4281 × 10−06	2.28
4	1	0.0350	0.0012	2.0209 × 10−04	0.0175	2.0209 × 10−06	3.21
5	1	0.0415	0.0017	2.2467 × 10−04	0.0195	2.2467 × 10−06	2.53
6	1	0.0683	0.0047	2.8929 × 10−04	0.0251	2.8929 × 10−06	4.07
7	1	0.1814	0.0329	7.2299 × 10−04	0.0627	7.2299 × 10−06	1.20
8	1	0.0993	0.0099	5.7910 × 10−04	0.0502	5.7910 × 10−06	2.58
9	1	0.0877	0.0077	3.0617 × 10−04	0.0265	3.0617 × 10−06	1.42
10	1	0.0110	1.2147 × 10−04	4.6222 × 10−05	0.0040	4.6222 × 10−07	1.23
11	1	0.1299	0.0169	2.6603 × 10−04	0.0231	2.6603 × 10−06	4.36
12	1	0.1727	0.0298	2.8220 × 10−04	0.0245	2.8220 × 10−06	3.32
13	1	0.0223	4.9842 × 10−04	9.4412 × 10−04	0.0082	9.4412 × 10−06	1.14
14	1	0.0506	0.0026	1.2202 × 10−04	0.0106	1.2202 × 10−06	1.14
15	1	0.0082	6.7078 × 10−05	3.1766 × 10−05	0.0028	3.1766 × 10−07	2.10
16	1	0.0186	3.4761 × 10−04	3.6966 × 10−05	0.0032	3.6966 × 10−07	1.35
17	1	0.0034	1.1506 × 10−05	2.3633 × 10−05	0.0021	2.3633 × 10−07	0.53
18	1	0.0041	1.6756 × 10−05	3.1653 × 10−05	0.0027	3.1653 × 10−07	2.53
19	1	0.3729	0.1391	2.3504 × 10−04	0.0264	2.3504 × 10−06	7.57
20	1	0.0154	2.3689 × 10−04	5.0313 × 10−05	0.0058	5.0313 × 10−07	1.30
21	1	0.5202	0.2706	2.5002 × 10−04	0.0217	2.5002 × 10−06	1.51
22	1	0.1139	0.0130	6.9052 × 10−05	0.0060	6.9052 × 10−07	1.13
23	1	0.1600	0.0256	7.1411 × 10−05	0.0062	7.1411 × 10−07	1.02
24	1	0.4983	0.2483	2.2323 × 10−04	0.0193	2.2323 × 10−06	1.15
25	1	0.6028	0.3633	2.6556 × 10−04	0.0230	2.6556 × 10−06	1.19
26	1	1.0518	1.1062	5.1499 × 10−04	0.0446	5.1499 × 10−06	1.40
27	1	1.7956	3.2243	7.9421 × 10−04	0.0688	7.9421 × 10−06	2.48
28	1	1.8995	3.6079	8.2907 × 10−04	0.0719	8.2907 × 10−06	3.15
29	1	2.1105	4.4542	9.3820 × 10−04	0.0813	9.3820 × 10−06	2.13
30	1	2.1674	4.6975	0.0010	0.0887	1.0238 × 10−05	1.41

and

Table 4. Proposed Multilayer Perceptron Neural Network Performance Investigation based on Hidden Neurons (Dataset 2). The best result highlighted in bold.

Number of Hidden Neurons	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
1	1	0.0036	1.2624 × 10−05	3.4874 × 10−04	0.0021	3.4874 × 10−06	3.29
2	1	0.0057	3.2881 × 10−05	6.1681 × 10−04	0.0037	6.1681 × 10−06	2.22
3	1	0.0019	3.7200 × 10−06	2.0454 × 10−04	0.0012	2.0454 × 10−06	1.24
4	1	0.0047	2.1769 × 10−05	2.1105 × 10−04	0.0013	5.1105 × 10−06	1.12
5	1	8.0651 × 10−04	6.5047 × 10−07	7.9919 × 10−05	4.8235 × 10−04	7.9919 × 10−07	0.50
6	1	0.0069	4.7877 × 10−05	6.9094 × 10−04	0.0042	6.9094 × 10−06	0.52
7	1	0.0060	3.6134 × 10−05	6.8661 × 10−04	0.0041	6.8661 × 10−06	1.01
8	1	0.0129	1.6665 × 10−04	8.6983 × 10−04	0.0052	8.6983 × 10−06	1.40
9	1	0.0119	1.4146 × 10−04	7.6589 × 10−04	0.0046	7.6589 × 10−06	1.12
10	1	0.0032	1.0426 × 10−05	1.5744 × 10−04	9.5022 × 10−04	1.5744 × 10−06	1.53
11	1	0.0224	5.0346 × 10−04	2.3288 × 10−04	0.0014	2.3288 × 10−06	0.58
12	1	0.0203	4.1312 × 10−04	4.9893 × 10−04	0.0030	4.9893 × 10−06	2.36
13	1	0.0150	2.2623 × 10−04	2.0179 × 10−04	0.0012	2.0179 × 10−06	3.25
14	1	0.0219	4.8096 × 10−04	3.6904 × 10−04	0.0022	3.3904 × 10−06	5.33
15	1	0.0088	7.7729 × 10−05	1.2778 × 10−04	7.7123 × 10−04	1.2778 × 10−06	3.02
16	1	0.0015	2.3690 × 10−06	9.3744 × 10−05	8.2954 × 10−04	9.3744 × 10−07	1.39
17	1	6.3358 × 10−04	4.0142 × 10−07	7.5578 × 10−05	4.5615 × 10−04	7.5578 × 10−07	0.34
18	1	0.0464	0.0022	5.1669 × 10−04	0.0031	5.1669 × 10−06	3.27
19	1	0.0017	3.0617 × 10−06	9.7188 × 10−05	8.5399 × 10−04	9.7188 × 10−07	2.59
20	1	0.0050	2.4763 × 10−05	3.0130 × 10−04	9.8185 × 10−04	3.0130 × 10−06	0.56
21	1	0.0125	1.5509 × 10−04	3.4901 × 10−04	0.0021	3.4901 × 10−06	1.08
22	1	0.0028	7.5683 × 10−06	1.2190 × 10−04	9.3573 × 10−04	1.2190 × 10−06	1.31
23	1	0.0137	1.8660 × 10−04	1.2801 × 10−04	0.0013	1.2801 × 10−06	1.09
24	1	0.0693	0.0048	3.2042 × 10−04	0.0019	3.2045 × 10−06	3.24
25	1	0.0550	0.0030	2.5498 × 10−04	0.0015	2.5498 × 10−06	3.07
26	1	0.1015	0.0103	5.4809 × 10−04	0.0033	5.4809 × 10−06	4.13
27	1	0.0853	0.0073	3.8967 × 10−04	0.0024	3.8967 × 10−06	3.15
28	1	0.0964	0.0093	7.0402 × 10−04	0.0042	7.0402 × 10−06	2.04
29	1	0.0880	0.0077	4.4857 × 10−04	0.0027	4.4857 × 10−06	1.30
30	1	0.0279	7.7623 × 10−04	5.2729 × 10−04	0.0037	5.2729 × 10−06	1.32

.

The number of hidden neurons that influence the neural network is understood clearly from Table 3 and Table 4, Figure 4 and Figure 5, respectively, for Dataset 1 and Dataset 2, which shows that the hidden neurons are essential in neural network stability, and convergence.

From the careful investigation of Table 3 and Table 4, it is noted that the proposed model with 17 hidden neurons in the hidden layer achieves the minimal evaluation index as RMSE = 0.0034, MSE = 1.1506 × 10⁻⁰⁵, MAPE = 2.3633 × 10⁻⁰⁵, MAE = 0.0021, MRE = 2.3633 × 10⁻⁰⁷ and R = 1, convergence time is 0.53 min for dataset 1, RMSE = 6.3358 × 10⁻⁰⁴, MSE = 4.0142 × 10⁻⁰⁷, MAPE = 7.5578 × 10⁻⁰⁵, MAE = 4.5615 × 10⁻⁰⁴, MRE = 7.5578 × 10⁻⁰⁷ and R = 1, convergence time is 0.34 min for dataset 2. Hence, this hidden neuron (17) was selected as the optimal hidden neuron. Further investigation concerning different forecasting horizons was performed based on the optimal hidden neurons based on the implemented proposed model.

Table 5. Comparison of Real-Time Target and Forecast Electricity Load (Dataset 1).

Real-Time Target Electricity Load (MW)	Forecast Electricity Load (MW)	Time Stamp (Min)	Real-Time Target Electricity Load (MW)	Forecast Electricity Load (MW)	Time Stamp (Min)
7907.3112	7907.31	30	9682.0480	9682.05	450
8334.4280	8334.43	60	9589.1496	9589.15	480
8747.0421	8747.04	90	9362.0017	9362	510
9068.7479	9068.75	120	9084.8079	9084.81	540
9104.6281	9104.63	150	8849.6005	8849.6	570
9169.8488	9169.85	180	8654.6023	8654.6	600
9129.6883	9129.69	210	8576.9714	8576.97	630
8985.0682	8985.07	240	8413.9785	8413.98	660
8878.6100	8878.61	270	8218.8493	8218.85	690
8775.4818	8775.48	300	8289.3583	8289.36	720
8678.0824	8678.08	330	8225.9592	8225.96	750
8540.0108	8540.01	360	8170.3303	8170.33	780
8431.2587	8431.26	390	7973.1823	7973.18	810
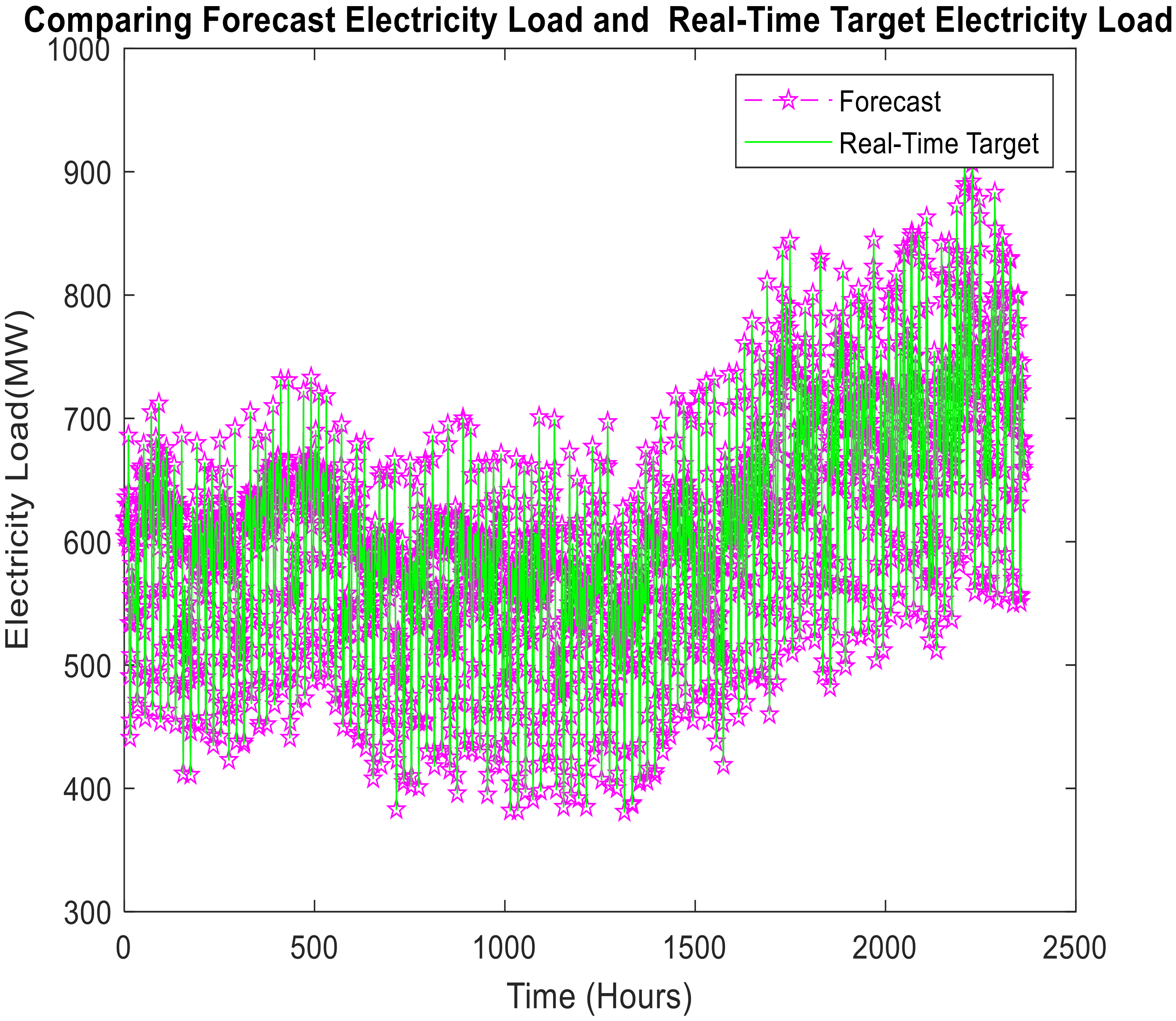
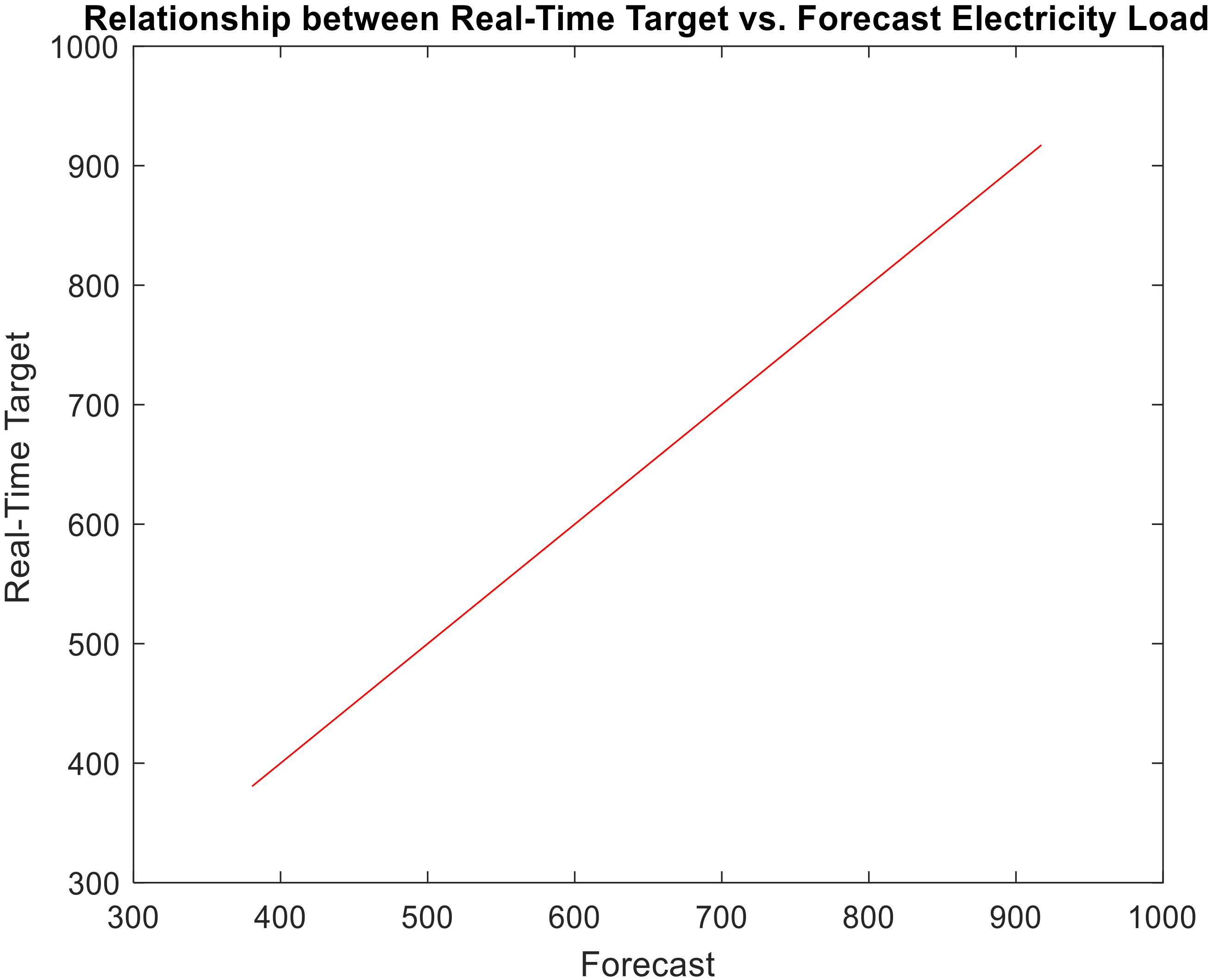
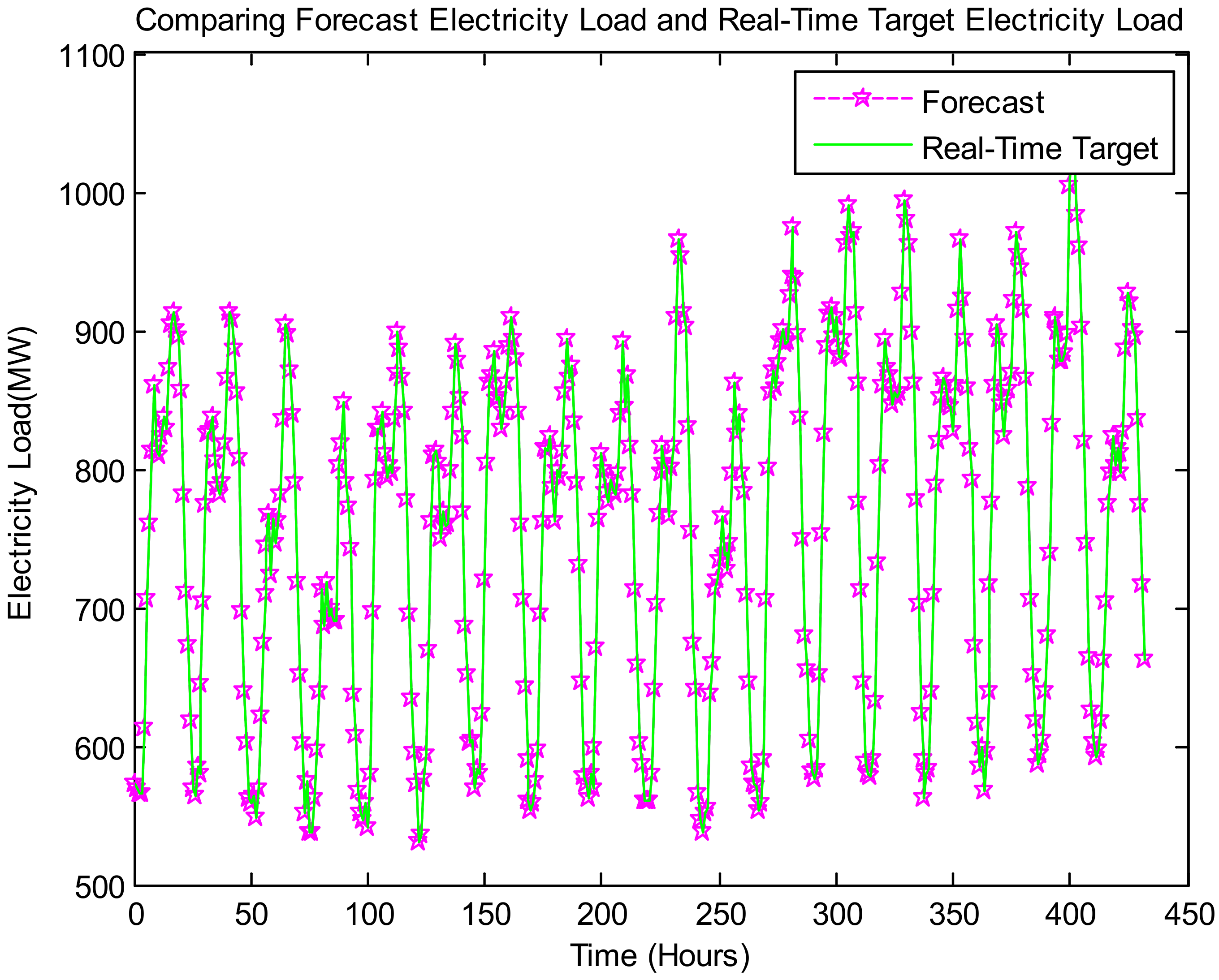
8347.8180	8347.82	420	7738.8076	7738.81	840

and Figure 6 present the comparison of real-time and forecast electricity load (Dataset 1).

Table 6. Comparison of Real-Time Target and Forecast Electricity Load (Dataset 2).

Real-Time Target Electricity Load (MW)	Forecast Electricity Load (MW)	Time Stamp (Min)	Real-Time Target Electricity Load (MW)	Forecast Electricity Load (MW)	Time Stamp (Min)
618	617.9994	30	441	441.0008	450
604	603.9995	60	455	455.0002	480
619	618.9994	90	508	507.9997	510
636	635.9994	120	534	534.0003	540
630	629.9993	150	556	556.0004	570
615	614.9994	180	582	582	600
607	606.9995	210	565	565.0003	630
599	598.9996	240	568	568.0003	660
596	595.9997	270	564	564.0003	690
607	606.9995	300	536	536.0003	720
686	686.0004	330	552	552.0004	750
640	639.9994	360	553	553.0004	780
534	534.0003	390	542	542.0004	810
491	490.9993	420	542	542.0004	840

and Figure 7 depict the comparison of real-time and forecast electricity load (Dataset 2). As observed from the obtained simulation results shown in Table 5 and Table 6 and Figure 6 and Figure 7 is the proposed model to accurately match the forecast electricity load with the target real-time electricity load. It indicates the proposed model’s validity.

Decaying the power shortage issue and meeting the future electric energy requirement, different forecasting horizons based on electricity forecasting are obligatory. Our primary motive is to forecast the highly accurate load forecasting concern for various time horizons. The input electricity load depends on the time horizon forecast range. The output load is the ahead forecasting concern with different forecasting horizons compared with the real-time target load.

Long-term forecasting: The proposed long-term forecasting model can forecast the weekly/monthly/yearly ahead load forecast. Long-term load forecasting plays a significant role in power system planning, expansion, and operation management.

Medium-term load forecasting: The proposed medium-term load forecasting model forecasts 6 h to 24 h (1 day) ahead of the load forecast. Medium-term load forecasting is helpful for power system load scheduling, load balancing, reserve planning, and control.

Short-term load forecasting: The suggested short-term load forecasting model forecasts the load in 30 min to 6 h ahead of the load forecast. Short-term load forecasting is essential for unit commitment, economic dispatch, and the electricity market.

Very short-term load forecasting: The presented very short-term load forecasting covers a period of 1 min to 30 min ahead of the load forecast. Very short-term load forecasting is helpful for the deregulated power industry and energy prizing.

In this paper, the authors propose a different forecasting horizons model mentioned above, range or period ahead load forecasting, which overcomes the issues related to energy and load management and aids power system engineers. Although the authors already specified the proposed model inputs in Table 1 and Table 2 and Figure 1 to make it clearly understood it was mentioned again as the proposed load forecasting model built based on six inputs, namely, electricity load (MW), temperature (°C), humidity (%), wind speed (m/s), solar irradiance (W/m), and pressure (bar). For Dataset 1 comprises 5.256 × 10⁶ data points of each taken input variable, and Dataset 2 shall comprise 7.884 × 10⁴ data points of each taken input variable. Depending on the time horizon, as mentioned above, the input time span varies.

The horizon of long-term load forecasting is years ahead, the horizon of medium-term load forecasting is 24 h ahead, the horizon of short-term load forecasting is 6 h ahead, and the horizon of very short-term load forecasting is 30 min ahead. Therefore, the proposed multilayer perceptron neural network-based forecasting model performance was investigated with concern to the different forecasting horizons, namely long-term, medium-term, short-term, and very short-term electricity load forecasting. The obtained results based on the proposed model concern to different forecasting horizons presented in

Table 7. Multilayer Perceptron Neural Network Performance Analysis based on Different Forecasting Horizons (Dataset 1).

Forecasting Horizons	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
Long-Term Forecasting	1	0.0034	1.1506 × 10−05	2.3633 × 10−05	0.0021	2.3633 × 10−07	0.53
Medium-Term Forecasting	1	0.0055	2.9774 × 10−05	2.2685 × 10−05	0.0019	2.2685 × 10−07	0.32
Short-Term Forecasting	1	0.0317	0.0010	7.8244 × 10−05	0.0070	7.8244 × 10−07	0.14
Very Short-Term Forecasting	1	0.1585	0.0251	0.0015	0.1346	1.5219 × 10−05	0.05

and

Table 8. Multilayer Perceptron Neural Network Performance Analysis based on Different Forecasting Horizons (Dataset 2).

Forecasting Horizons	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
Long-Term Forecasting	1	6.3358 × 10−04	4.0142 × 10−07	7.5578 × 10−05	4.5615 × 10−04	7.5578 × 10−07	0.34
Medium-Term Forecasting	1	0.0058	3.3713 × 10−05	2.5651 × 10−04	0.0019	2.5651 × 10−06	0.20
Short-Term Forecasting	1	0.0154	2.3704 × 10−04	9.1914 × 10−04	0.0060	9.1914 × 10−06	0.07
Very Short-Term Forecasting	1	0.0155	2.4112 × 10−04	0.0020	0.0123	2.0396 × 10−05	0.04

show that the proposed model can forecast the electricity load in all time horizons, namely, long-term, medium-term, short-term, and very short-term, with minimum evaluation index (RMSE, MSE, MAPE, MAE, MRE) and converge faster for both datasets.

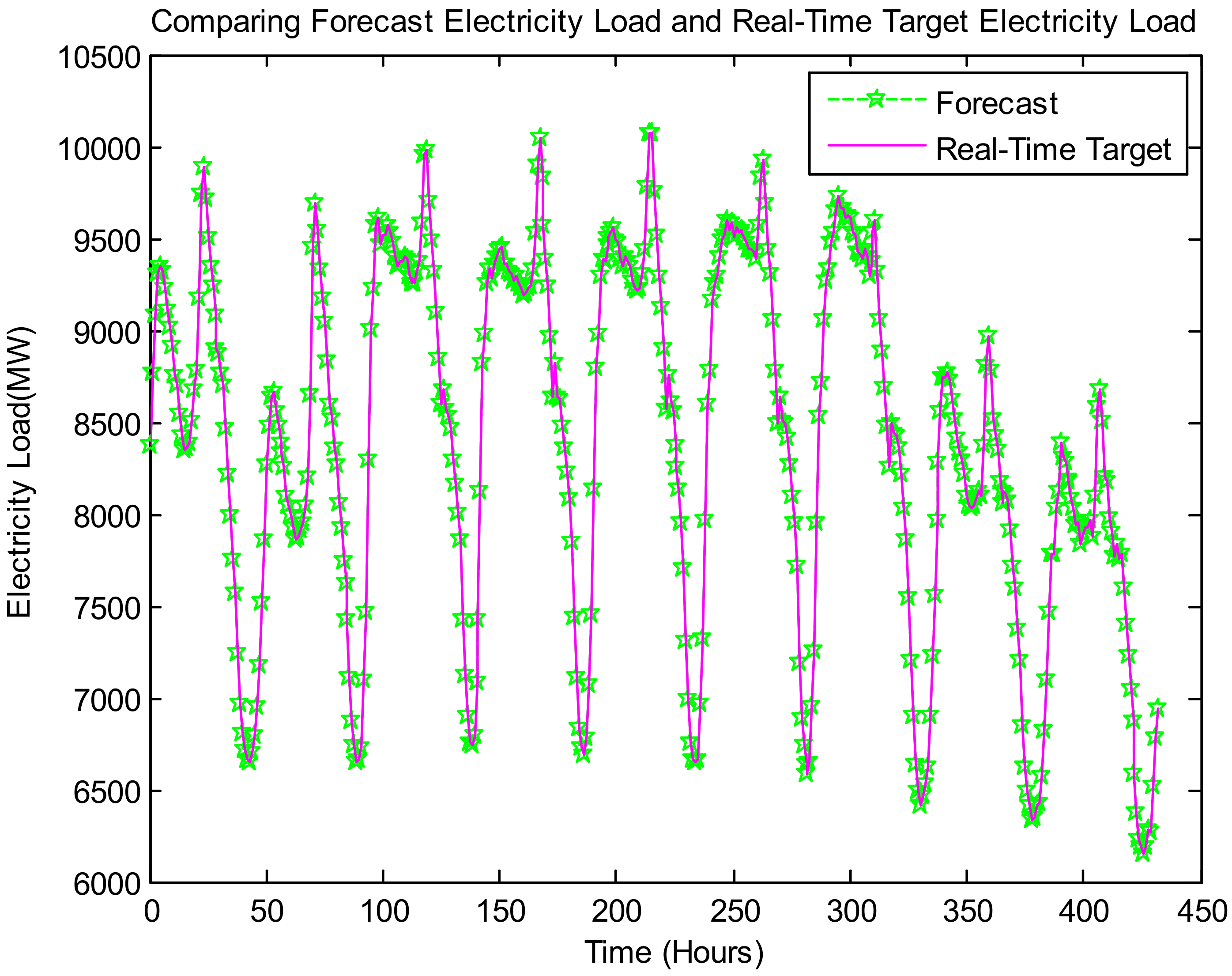
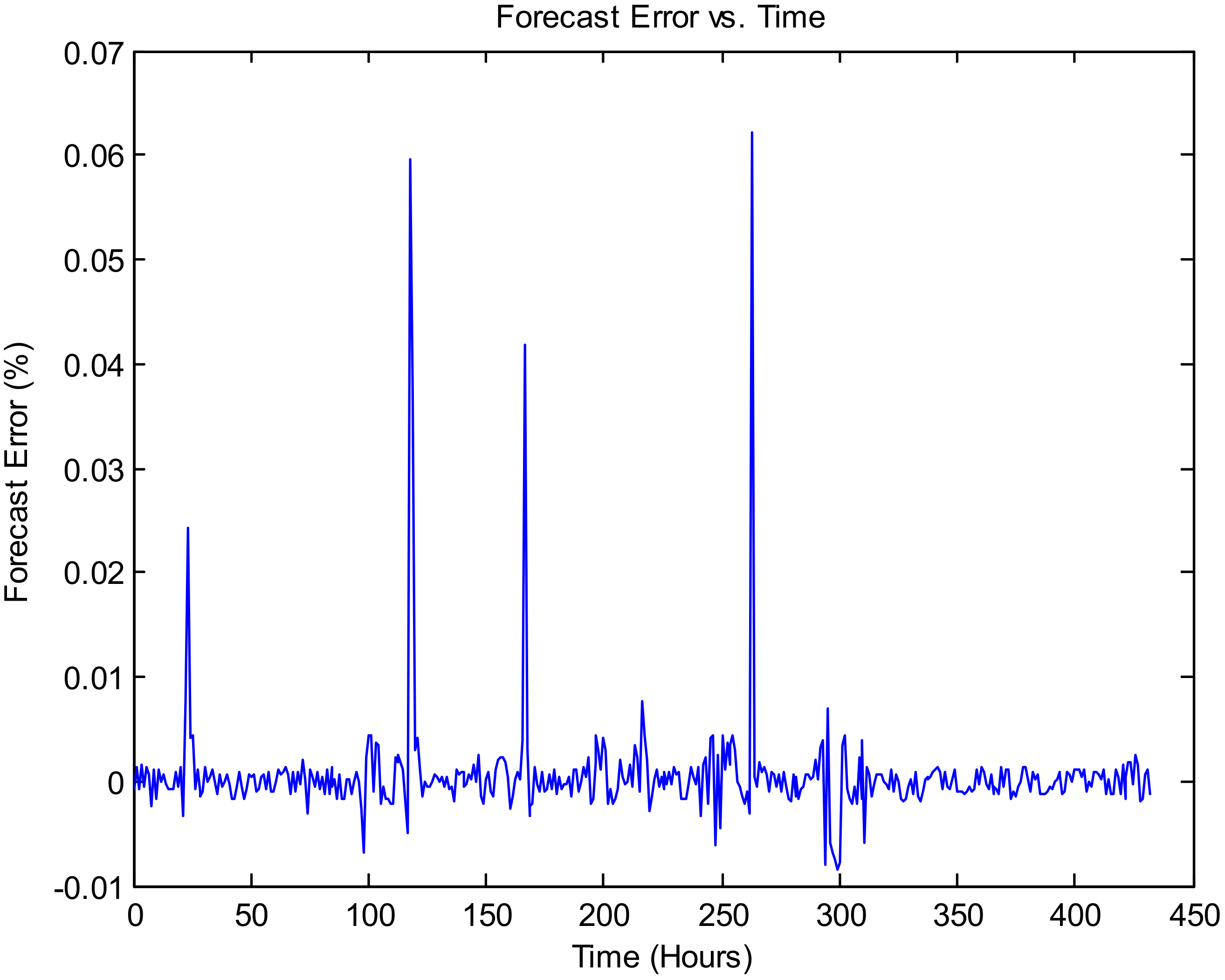
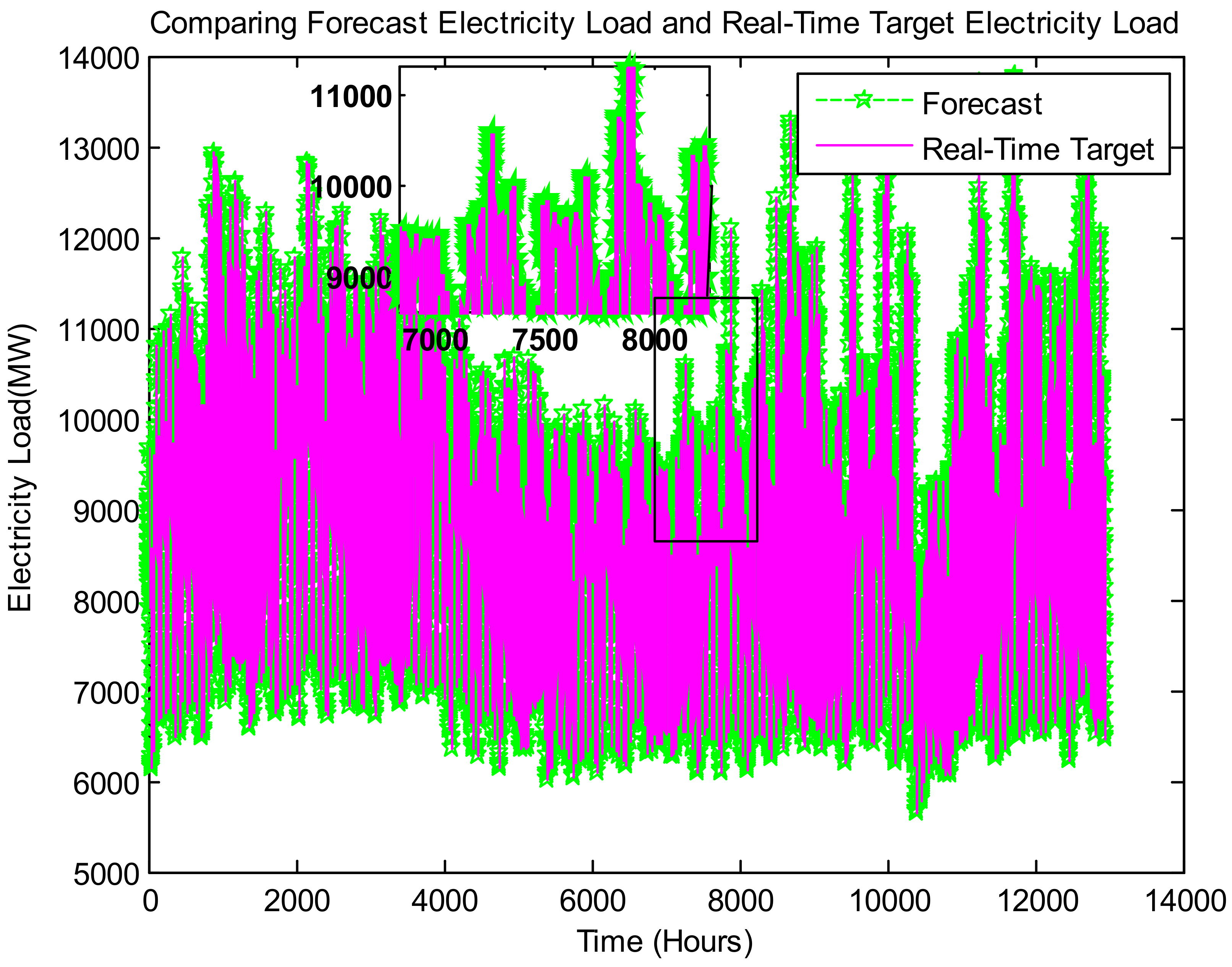
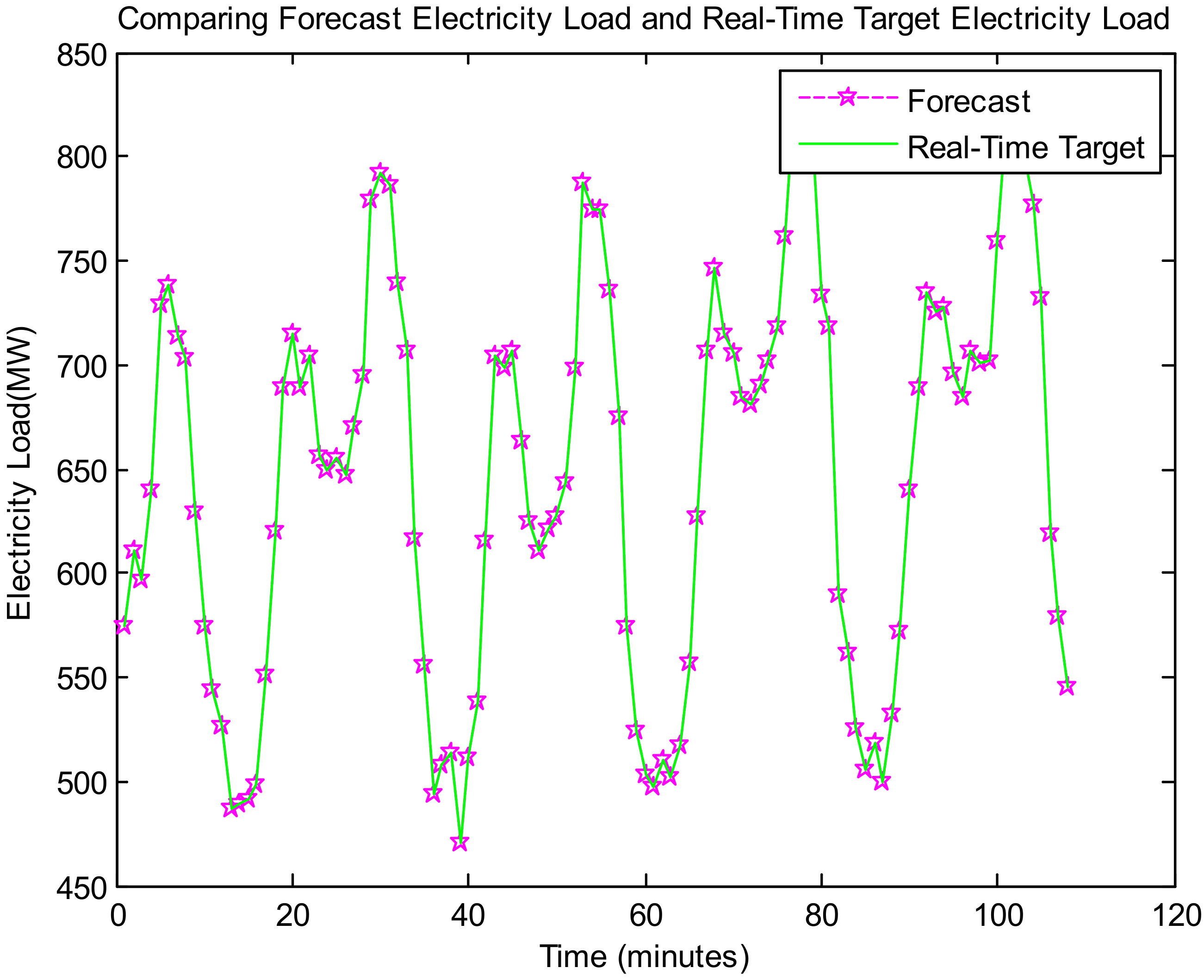
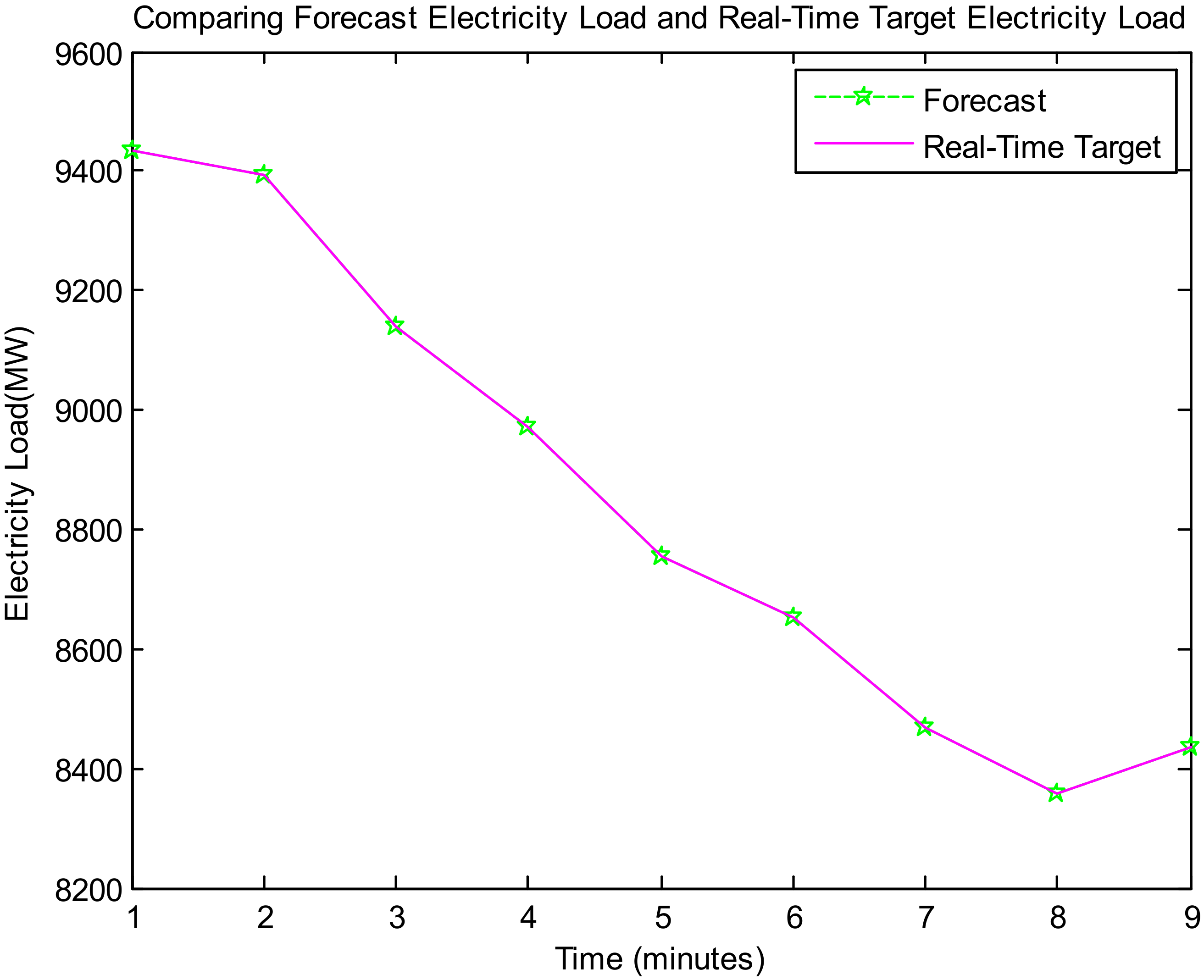
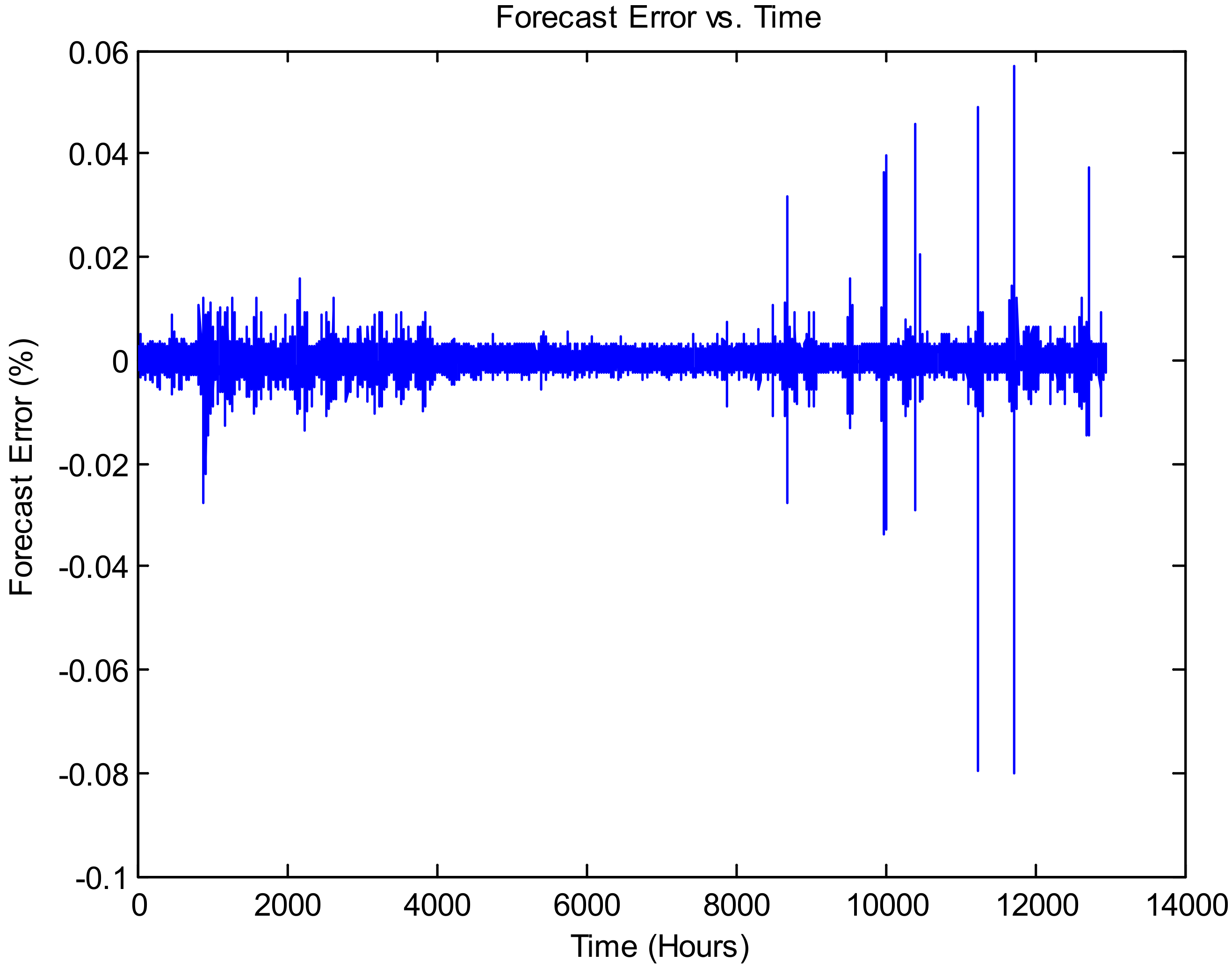
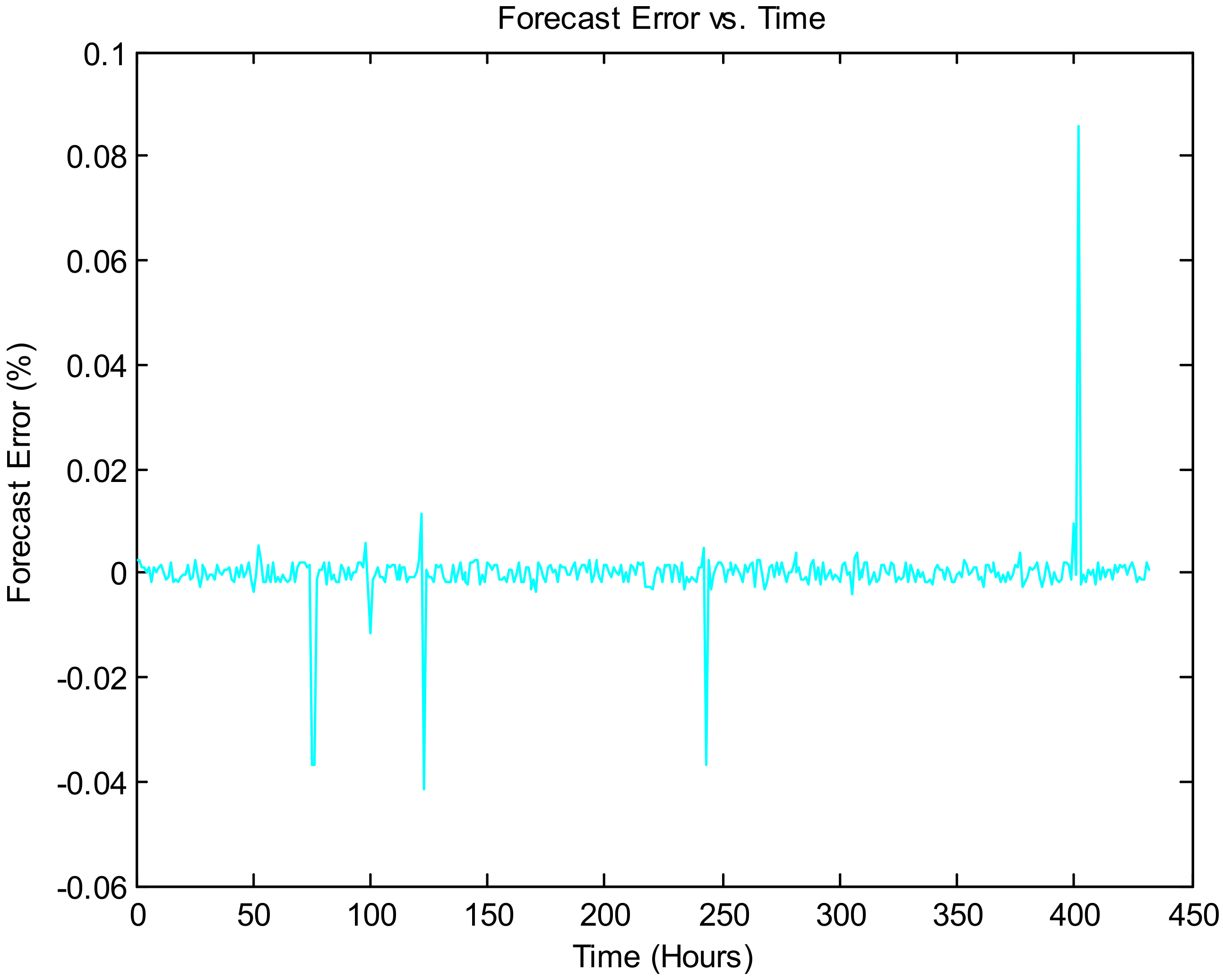
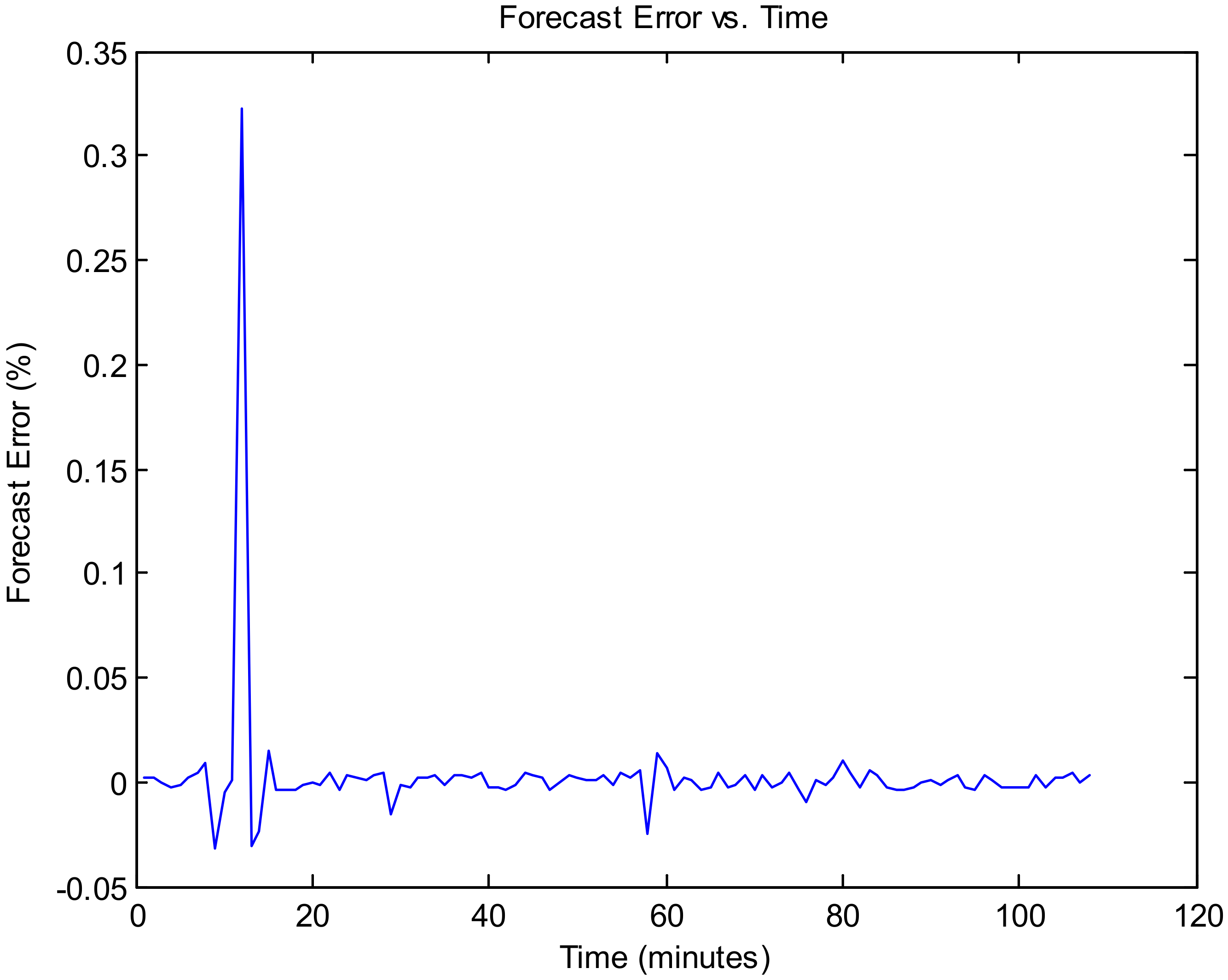
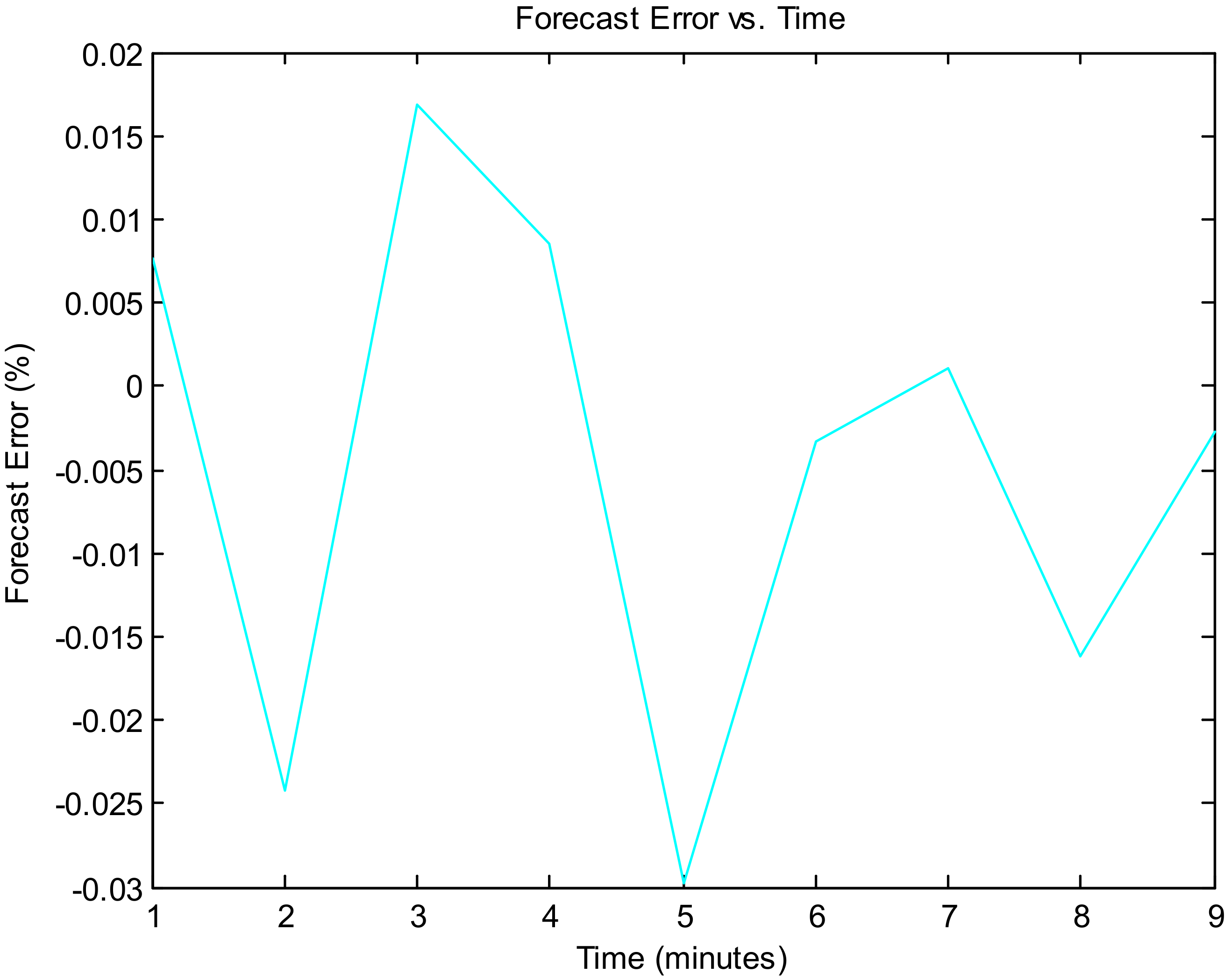
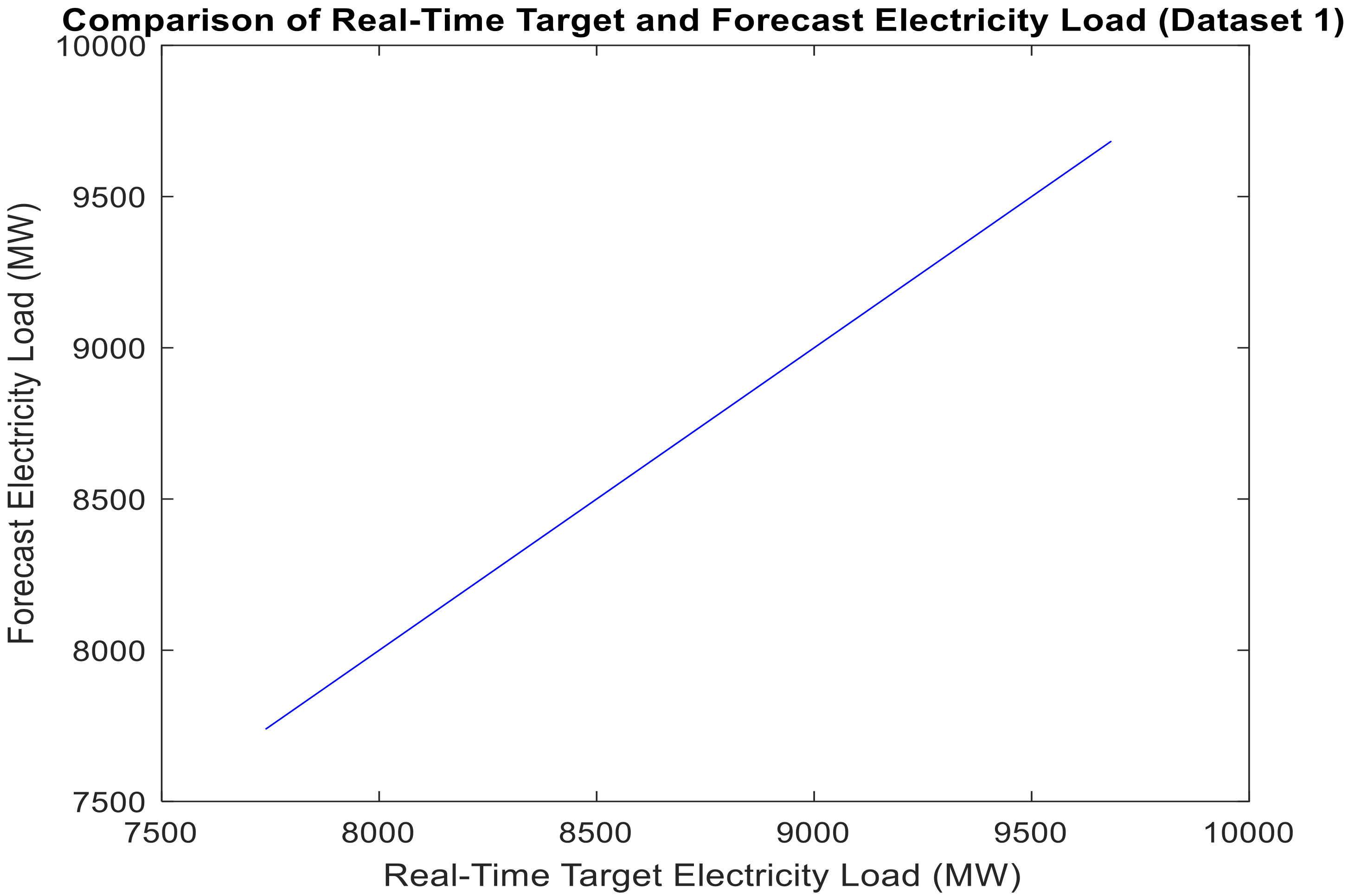
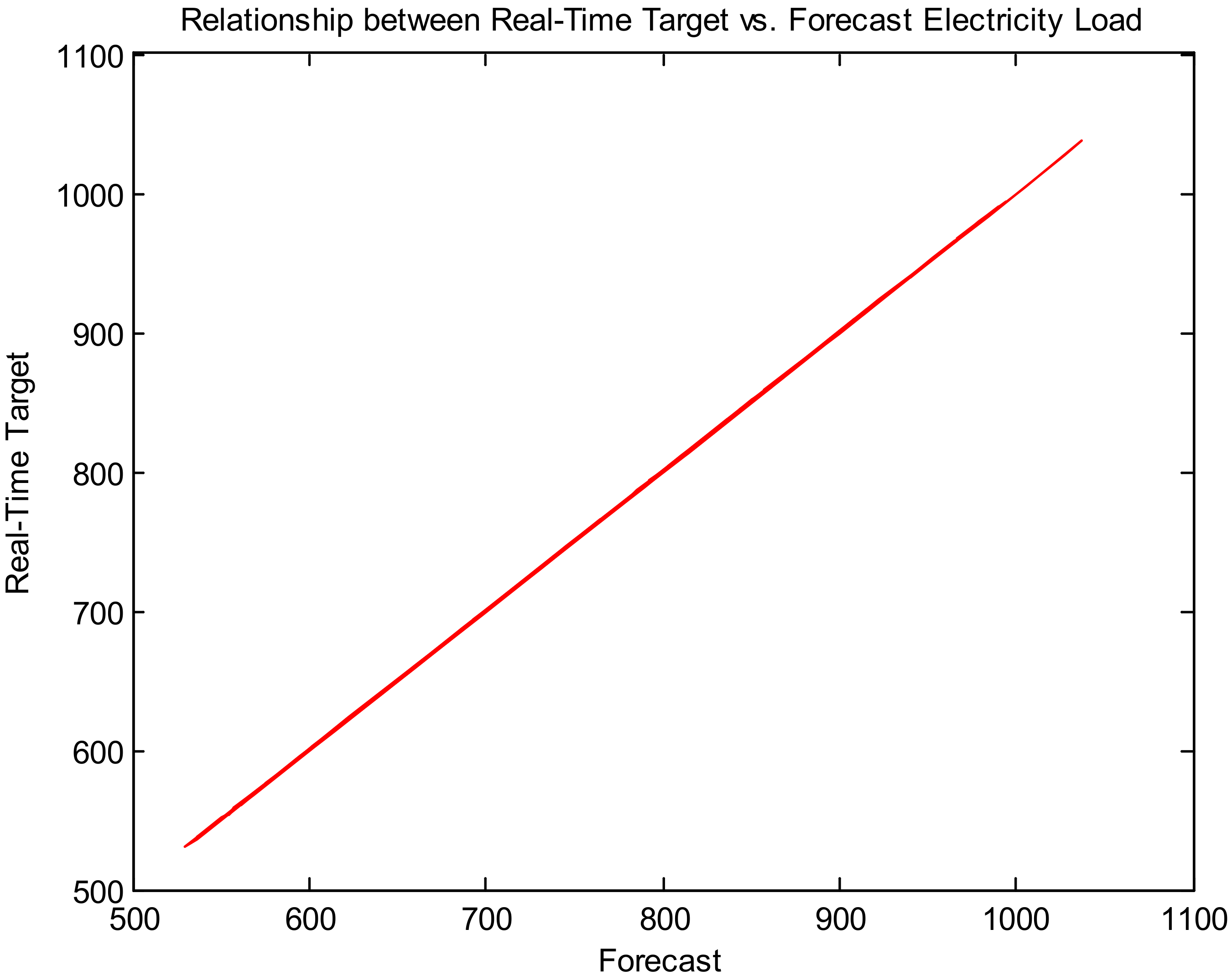
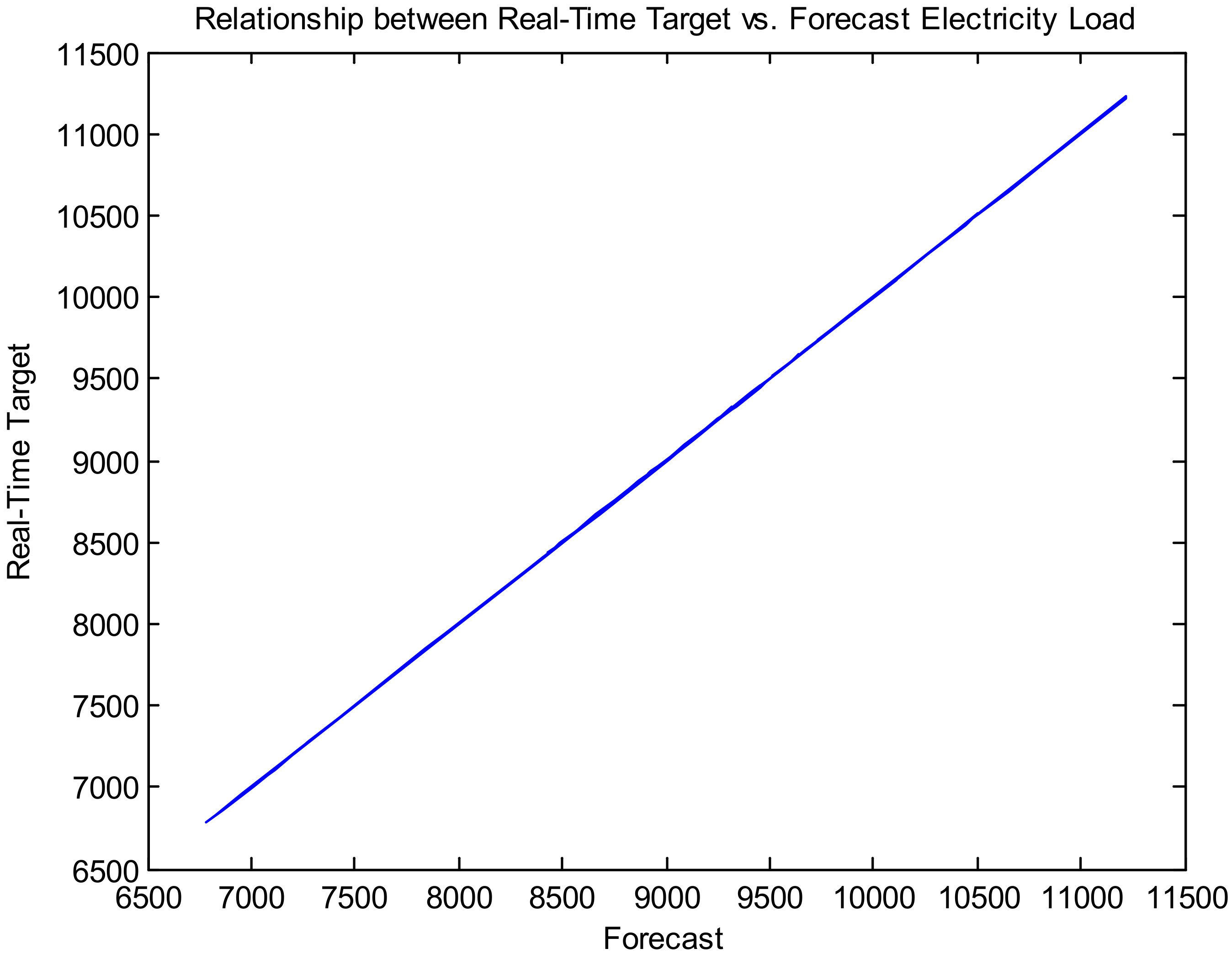
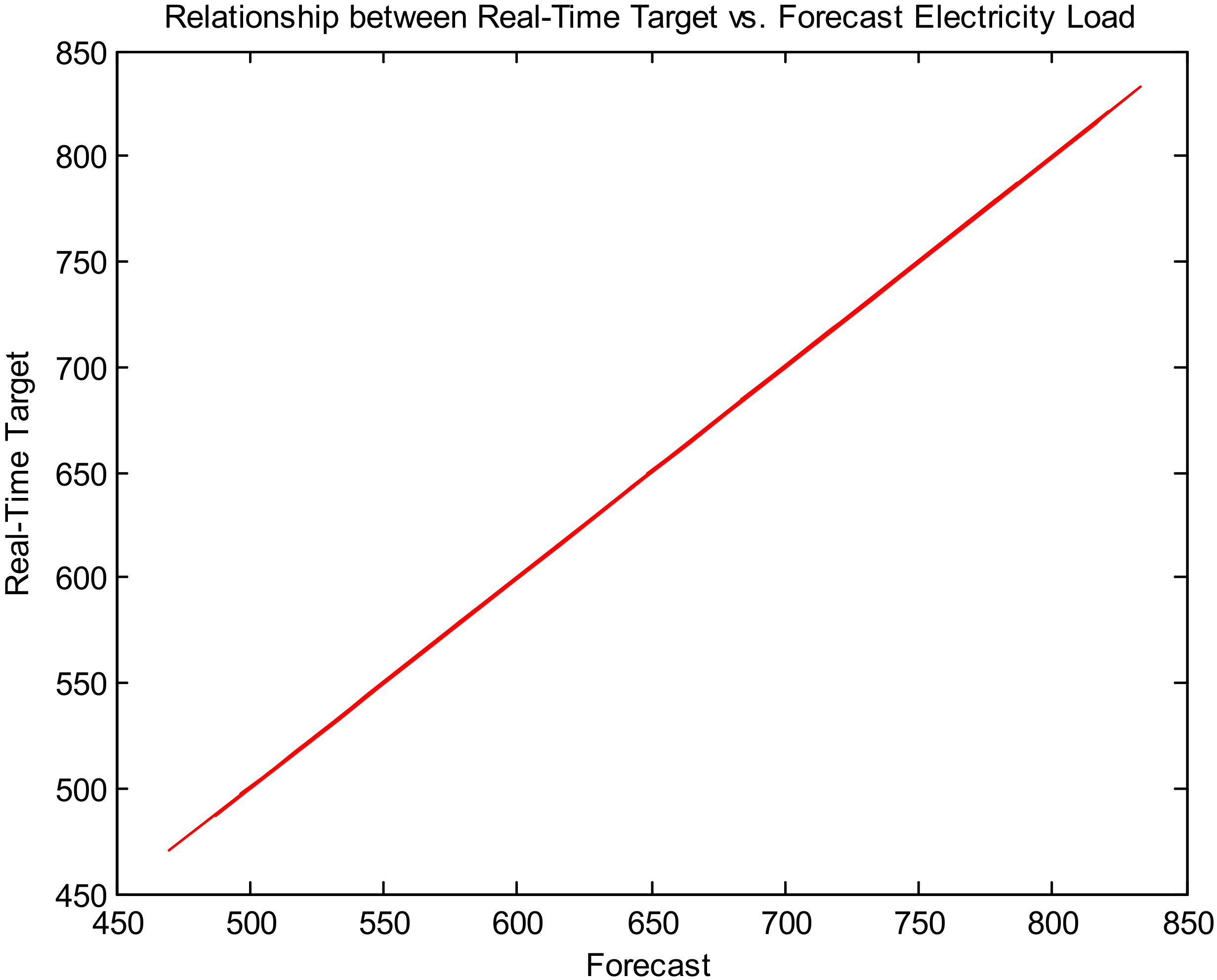
Figure 8, Figure 9 and Figure 10 show the results of long-term load forecasting concern on dataset 1. Figure 8 represents the proposed model-based output, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of years ahead. Figure 9 illustrates the forecasting error vs. time, and Figure 10 presents the relationship between real-time target and forecast electricity load for a long-term time horizon (dataset 1). Figure 11, Figure 12 and Figure 13 show the results of long-term load forecasting concern on Dataset 2. Figure 11 represents the proposed model-based output, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of years ahead. 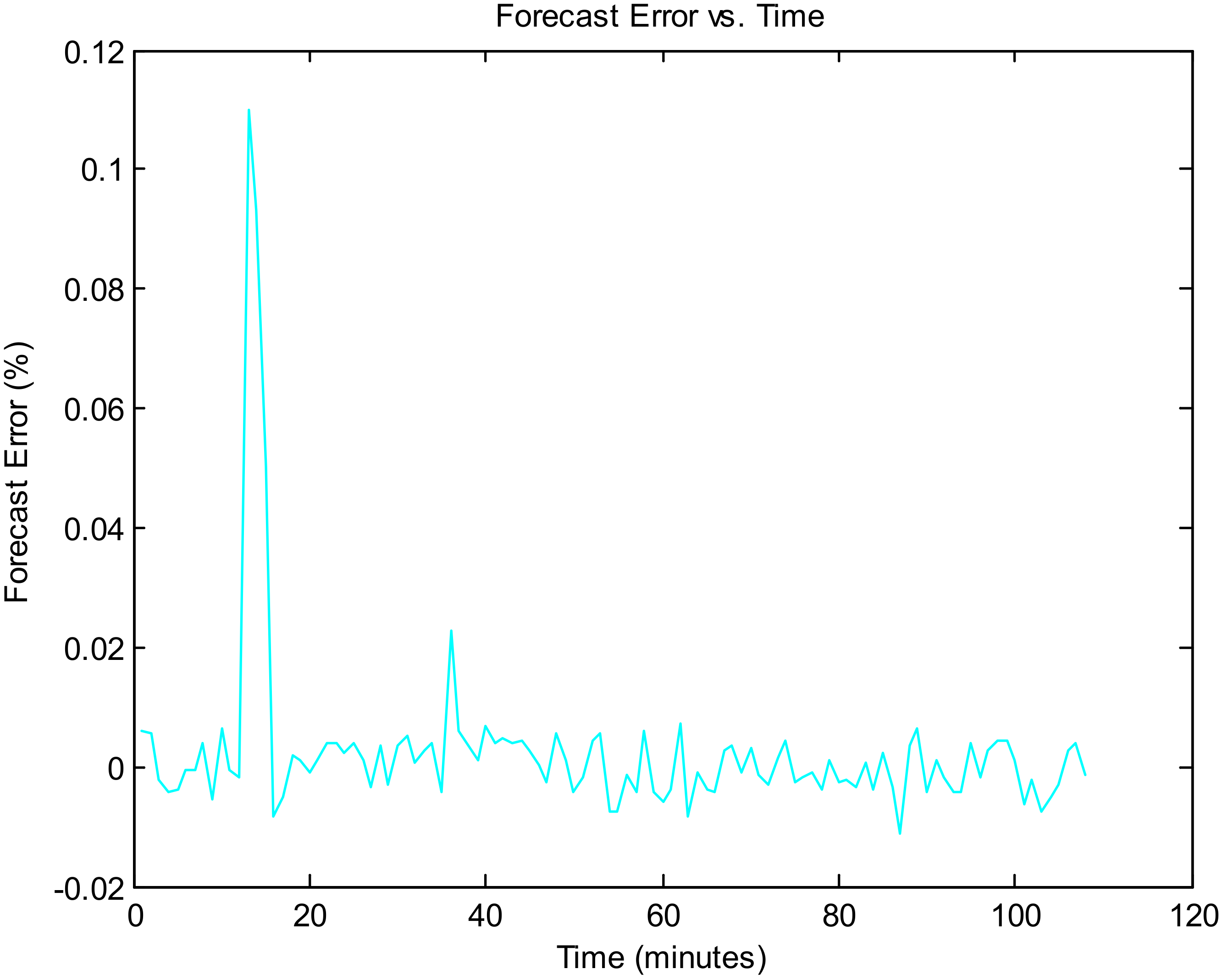Figure 12 shows the forecasting error vs. 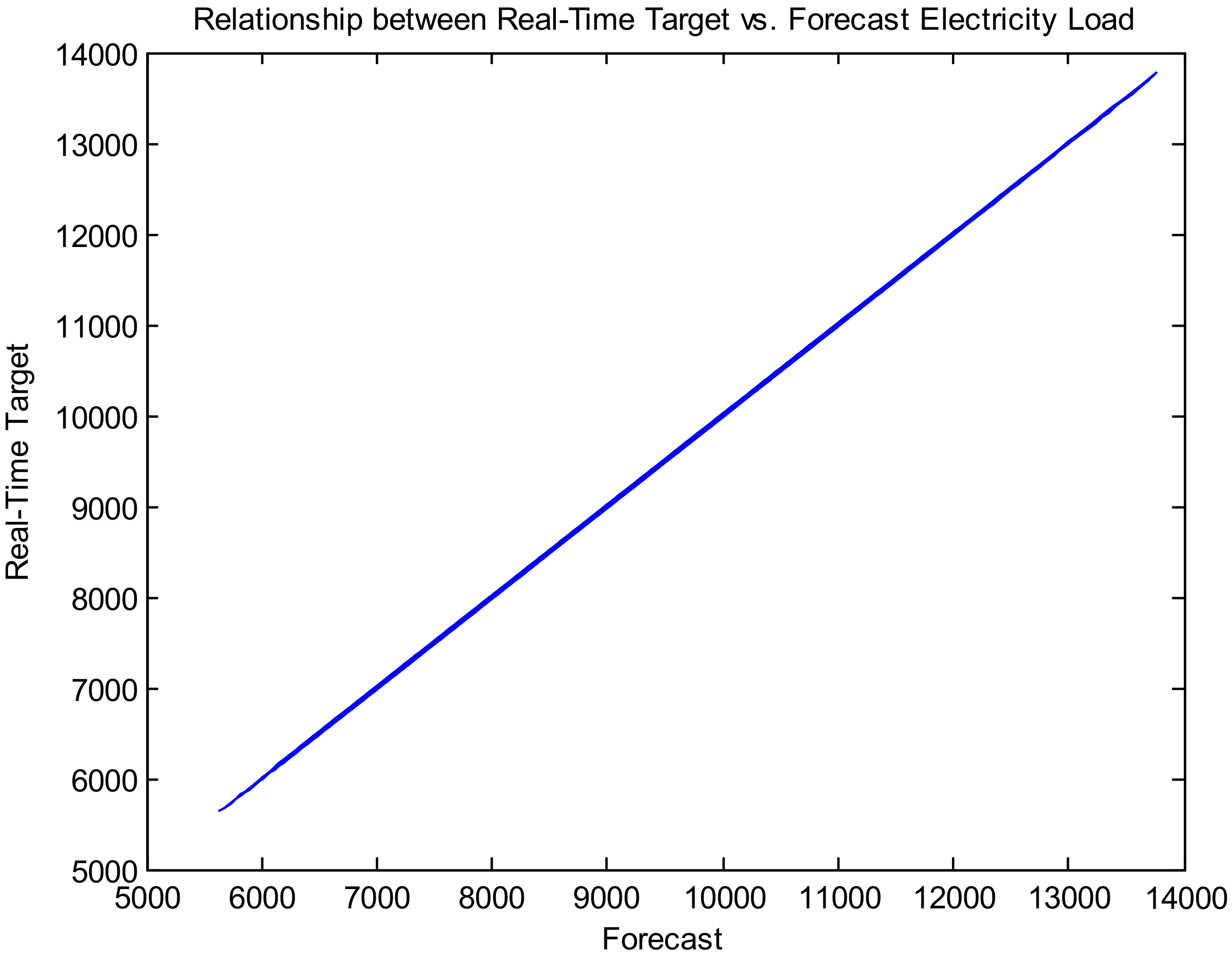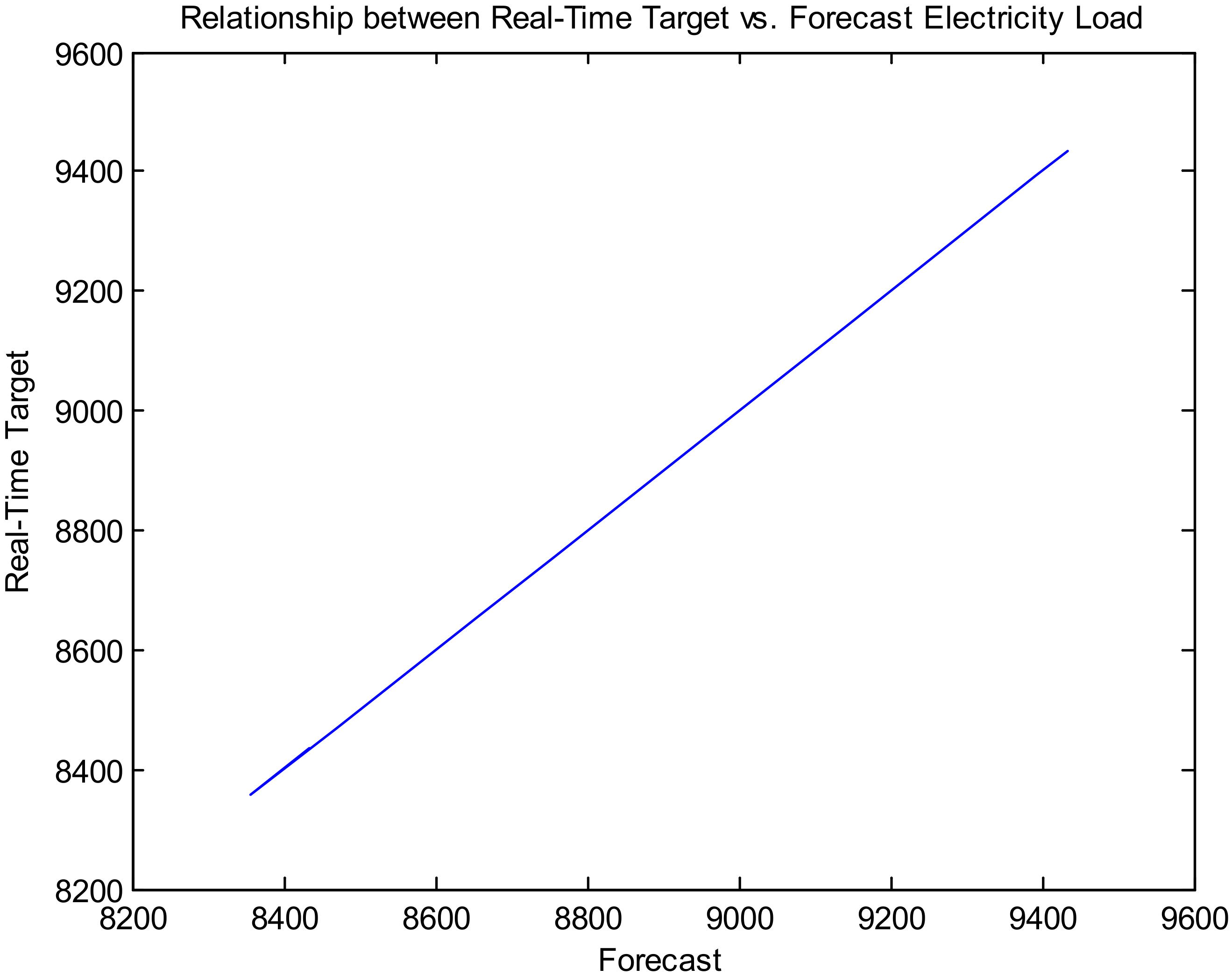time, and Figure 13 depicts the relationship between the real-time target and the forecast electricity load for a long-term time horizon (Dataset 2).

Similarly, Figure 14, Figure 15 and Figure 16 show the results of medium-term load forecasting concern on Dataset 1. Figure 14, Figure 15 and Figure 16 represent the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 24 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a medium-term time horizon, respectively (Dataset 1). Figure 17, Figure 18 and Figure 19 show the results of medium-term load forecasting concern on Dataset 2. Figure 17, Figure 18 and Figure 19 represent the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 24 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a medium-term time horizon, respectively (Dataset 2).

Figure 20, Figure 21 and Figure 22 show the results of short-term load forecasting concern on Dataset 1. Figure 20, Figure 21 and Figure 22 represents the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 6 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a short-term time horizon (Dataset 1). Figure 23, Figure 24 and Figure 25 show the results of short-term load forecasting concern on Dataset 2. Figure 23, Figure 24 and Figure 25 represents the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 6 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a short-term time horizon (Dataset 2).

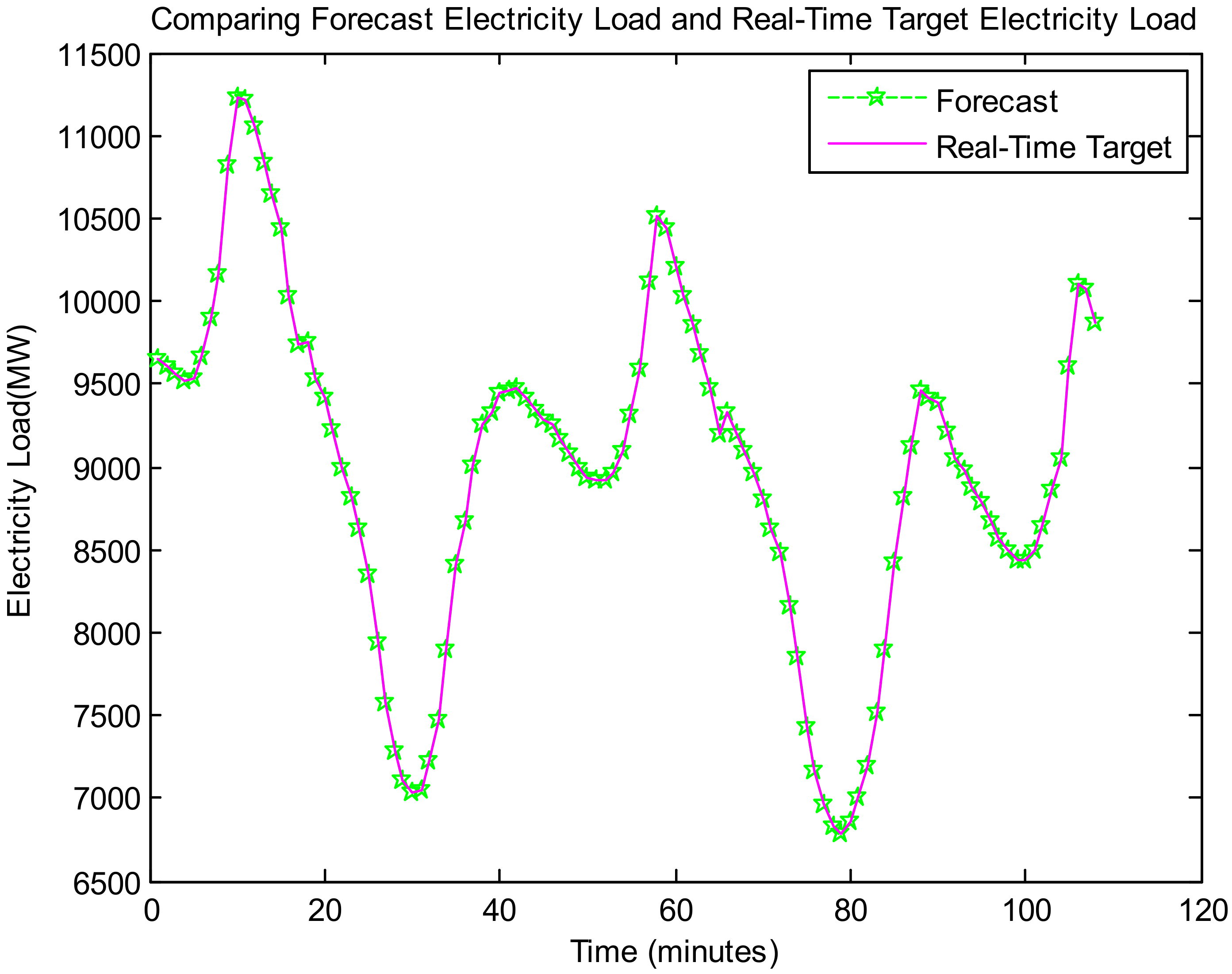
Figure 26, Figure 27 and Figure 28 show the results of very short-term load forecasting concern on dataset 1. Figure 26, Figure 27 and Figure 28 represents the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 30 min ahead, the forecasting error vs. time, and the relationship between real-time target and forecast electricity load for the very short-term time horizons, respectively (Dataset 1). Figure 29, Figure 30 and Figure 31 show the results of very short-term load forecasting concern on Dataset 1. Figure 29, Figure 30 and Figure 31 represent the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time electricity load in the horizon of 30 min ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for the very short-term time horizons, respectively (Dataset 2).

Figure 8, Figure 14, Figure 20, and Figure 26 show that the output results concerned to Dataset 1 (forecast electricity load) exactly match the target real-time electricity load for different forecasting horizons. Therefore, the forecasting errors are minimal, inferred from Figure 9, Figure 15, Figure 21, and Figure 27. The relationship between real-time target and forecast electricity load is linear, understood clearly from Figure 10, Figure 16, Figure 22, and Figure 28. Similarly, Figure 11, Figure 17, Figure 23, and Figure 29 show that the output results concerned to Dataset 2 (forecast electricity load) exactly match the target real-time electricity load for different forecasting horizons. Therefore, the forecasting errors are minimal, inferred from Figure 12, Figure 18, Figure 24, and Figure 30. The relationship between real-time target and forecast electricity load is linear, understood clearly from Figure 13, Figure 19, Figure 25, and Figure 31.

To better understand the proposed model’s effectiveness regarding different forecasting horizons, the graphical representation of the proposed model performance investigation is based on the different forecasting horizons depicted in Figure 32 (Dataset 1) and Figure 33 (Dataset 2).

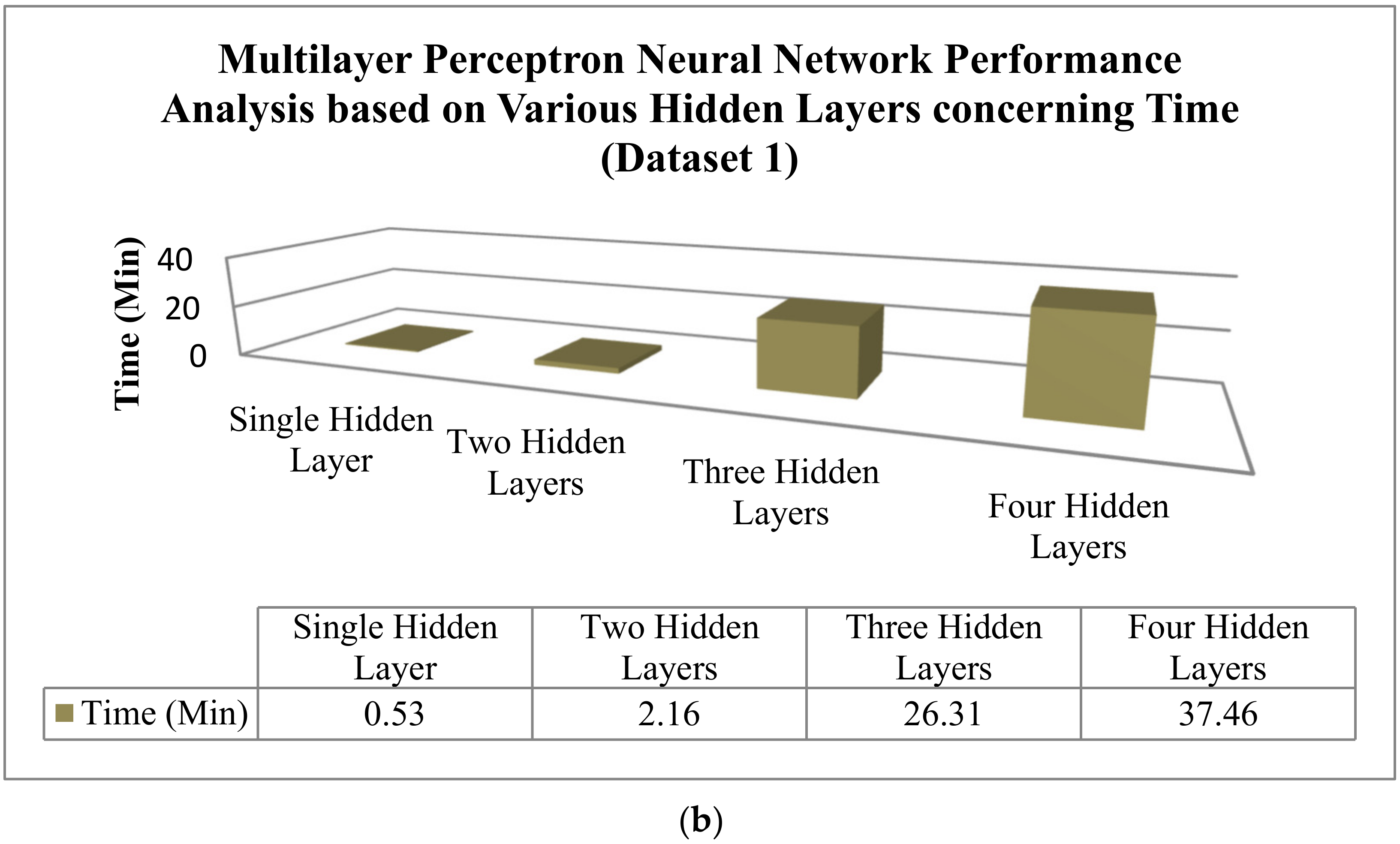
The authors carried out performance analysis with various hidden layers, namely, single hidden layer, two hidden layers, three hidden layers, and four hidden layers based on the obtained results are tabulated in

Table 9. Multilayer Perceptron Neural Network Performance Analysis based on Various Hidden Layers (Dataset 1). The best result highlighted in bold.

MLPN with Various Hidden Layer	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
Single Hidden Layer	1	0.0034	1.1506 × 10−05	2.3633 × 10−05	0.0021	2.3633 × 10−07	0.53
Two Hidden Layers	1	5.4737 × 10−04	2.9962 × 10−07	4.0204 × 10−06	3.6012 × 10−04	4.0204 × 10−08	2.16
Three Hidden Layers	1	0.0063	3.9356 × 10−05	3.7044 × 10−05	0.0033	3.7044 × 10−07	26.31
Four Hidden Layers	1	0.0024	5.9191 × 10−06	1.4484 × 10−05	0.0013	1.4484 × 10−07	37.46

and

Table 10. Multilayer Perceptron Neural Network Performance Analysis based on Various Hidden Layers (Dataset 2). The best result highlighted in bold.

MLPN with Various Hidden Layer	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
Single Hidden Layer	1	6.3358 × 10−04	4.0142e-07	7.5578 × 10−05	4.5615 × 10−04	7.5578 × 10−07	0.34
Two Hidden Layers	1	1.0210 × 10−04	1.0425 × 10−08	1.1327 × 10−05	6.8365 × 10−05	1.1327 × 10−07	1.40
Three Hidden Layers	1	0.0025	6.3659 × 10−06	2.9744 × 10−04	0.0018	2.9744 × 10−06	20.55
Four Hidden Layers	1	0.0018	3.1809 × 10−06	1.8707 × 10−04	0.0011	1.8707 × 10−06	32.08

, respectively, for Dataset 1 and Dataset 2. According to the universal approximation theorem [28,29], the multilayer perceptron neural network with two hidden layers can solve any problem. If the number of hidden layers is increased by more than two, it may cause an issue with respect to convergence and learning. From Figure 34a,b and Figure 35a,b, and Table 9 and Table 10, it is noticed that the results of the two hidden layer-based developed models perform well with improved accuracy.

To further analyze the performance, in addition to the above considered six inputs, the time-series data (holiday) was included as one of the proposed model’s inputs. The obtained results based on structure (1-17-1), one input layer with seven inputs, a single hidden layer with 17 hidden neurons, and one output layer for two datasets are tabulated in

Table 11. Multilayer Perceptron Neural Network Performance Analysis based on Seven Inputs, Including Time-Related Data (Holiday).

MLPN with 7 Inputs (1-17-1)	R	RMSE (MW)	MSE (MW)	MAPE (%)	MAE (MW)	MRE (MW)	Time (Min)
Data set 1	1	3.3494 × 10−04	1.1219 × 10−07	2.4396 × 10−06	2.1852 × 10−04	2.4396 × 10−08	1.28
Dataset 2	1	9.1288 × 10−05	8.3334 × 10−09	1.0124 × 10−05	6.1104 × 10−05	1.0124 × 10−07	0.59

. From Table 11, it is noticed that the load forecasting model performance improved considering the time series as one of the inputs to the forecasting model. It perceives the importance of time series data on load forecasting.

The issues due to uncertainty in electricity load can be resolved by electricity load forecasting. Various electricity load forecasting models have endeavored during the past two decades, but a simple, faster, and highly accurate forecasting model is the thrust field in electricity load forecasting. Therefore, this paper proposed a multilayer perceptron neural network-based exact forecast for electricity forecasting required for the utility system’s effective operation.

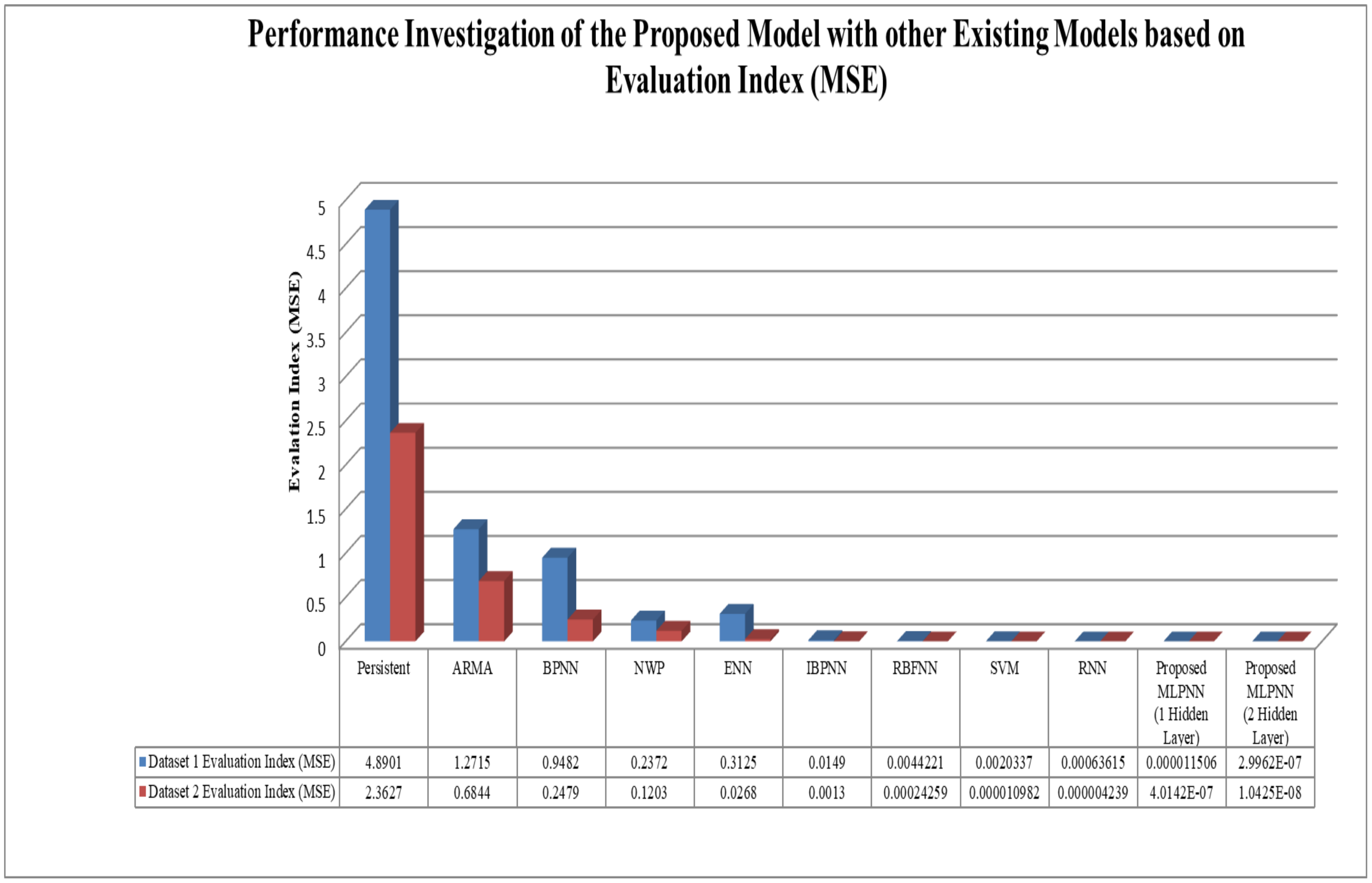
The proposed model’s performance is further investigated against other existing models that concern long-term electricity load forecasting. The corresponding outputs are based on the proposed model and other existing models reported in

Table 12. Performance Investigation of the Proposed Model with other Existing Models. The best result highlighted in bold.

S. No	Models	Authors	Dataset 1	Dataset 2
			Evaluation Index (MSE)	Evaluation Index (MSE)
1	Persistent	Dutta, Shreya et al. 2017 [30]	4.8901	2.3627
2	Auto-Regressive Moving Average	Pappas, S.S. et al. 2008 [31]	1.2715	0.6844
3	Back Propagation Neural Network	Momoh, J.A. et al. 1997 [7]	0.9482	0.2479
4	Numerical Weather Prediction	Qiuyu, Lu et al. 2017 [32]	0.2372	0.1203
5	Elman Neural Network	Vasar Cristian et al. 2007 [10]	0.3125	0.0268
6	Improved Back Propagation Neural Network	Madhiarasan and Deepa S.N. 2016 [23]	0.0149	0.0013
7	Radial Basis Function Neural Network	Xia et al. 2010 [12]	4.4221 × 10−03	2.4259 × 10−04
8	Support Vector Machine	Hong, Wei-Chiang 2009 [33]	2.0337 × 10−03	1.0982 × 10−05
9	Recurrent Neural Network	Zhang et al. 2018 [15]	6.3615 × 10−04	4.2390 × 10−06
10	Proposed Multilayer Perceptron Neural Network (Single Hidden Layer)	Madhiarasan and Louzazni 2021	1.1506 × 10−05	4.0142 × 10−07
11	Proposed Multilayer Perceptron Neural Network (Two Hidden Layer)	Madhiarasan and Louzazni 2021	2.9962 × 10−07	1.0425 × 10−08

. For comparative analysis, we use the existing model’s setting parameters as mentioned by the respective authors, and we performed an evaluation on the considered two datasets. The results were compared with previous models such as persistence, autoregression moving average, backpropagation neural network, numerical weather prediction, Elman neural network, improved back propagation neural network, radial basis function neural network, support vector machine, and recurrent neural network, comparative analysis proves the significance of the proposed model.

Table 12 infers that the proposed model-based results demonstrate superior performance and minimal evaluation index mean square error (MSE) of 1.1506 × 10⁻⁰⁵ for Dataset 1 and MSE of 4.0142 × 10⁻⁰⁷ for Dataset 2 with concern to the single hidden layer and MSE of 2.9962 × 10⁻⁰⁷ for Dataset 1, and MSE of 1.0425 × 10⁻⁰⁸ for Dataset 2 concern the two hidden-layers based proposed model than the considered existing models. For a better understanding, the graphical representation of the proposed model’s performance investigation with other existing models is shown in Figure 36. The presented model-based forecasting simulation results indicate the superiority and outperforming capability that of the existing models.

4. Conclusions

The developing countries’ growth regarding the industrial enhancement of any country’s electricity is a driving force to decide the development and economy. To ensure effective planning and achieve better energy system operation, accurate electricity load forecasting receives a center of attention. Electricity load forecasting with the lowest error value is a requisite to perform a better reliable power system working.

The improper planning of power systems concerning the electricity load causes issues as follows:

• Grid Collapse Issue.
• Power Outage Issue.
• Power Stability Issue.
• Power Quality Issue.
• Security and Safety Issues.
• Power Interruption Issue.

A highly desirable way to reduce the above-said problems is to model a simple, faster, and high accurate electricity load forecasting model. The precise load forecasting model leverages economic loss minimization, reduces the grid operating expenses, and improves power quality and continuous power provision to the consumer. Therefore, this work presents a multilayer perceptron neural network-based different forecasting horizons for electricity load forecasting.

This paper summarizes in key points as follows:

• Perform the proposed model design implementation;
• Analysis of the hidden neurons’ impact on the proposed forecasting model and identified 17 numbers of hidden neurons as the optimal hidden neurons of the proposed model through the lowest error indexes;
• The identified hidden neurons-based proposed forecasting model performance was further analyzed concerning various time horizon-based electricity load forecasting and performance assessed employing the error indexes. In all time horizons, the proposed model-based simulation results in a good forecast with minimal forecasting errors;
• Finally, a performance investigation is performed with respect to various hidden layers and the inclusion of time series data (holiday) as one of the inputs. Perform a comparative analysis with other existing model concerns on electricity load forecasting on two datasets, which substantiates the proposed model’s better performance ability than other existing forecasting model concerns for long-term forecasting. Hence, the proposed multilayer perceptron neural network with recursive fine-tuning strategy-based forecasting model confirms the validity on two datasets with much the lowest forecasting error.