Examining Deep Learning Architectures for Crime Classification and Prediction
Abstract
:1. Introduction
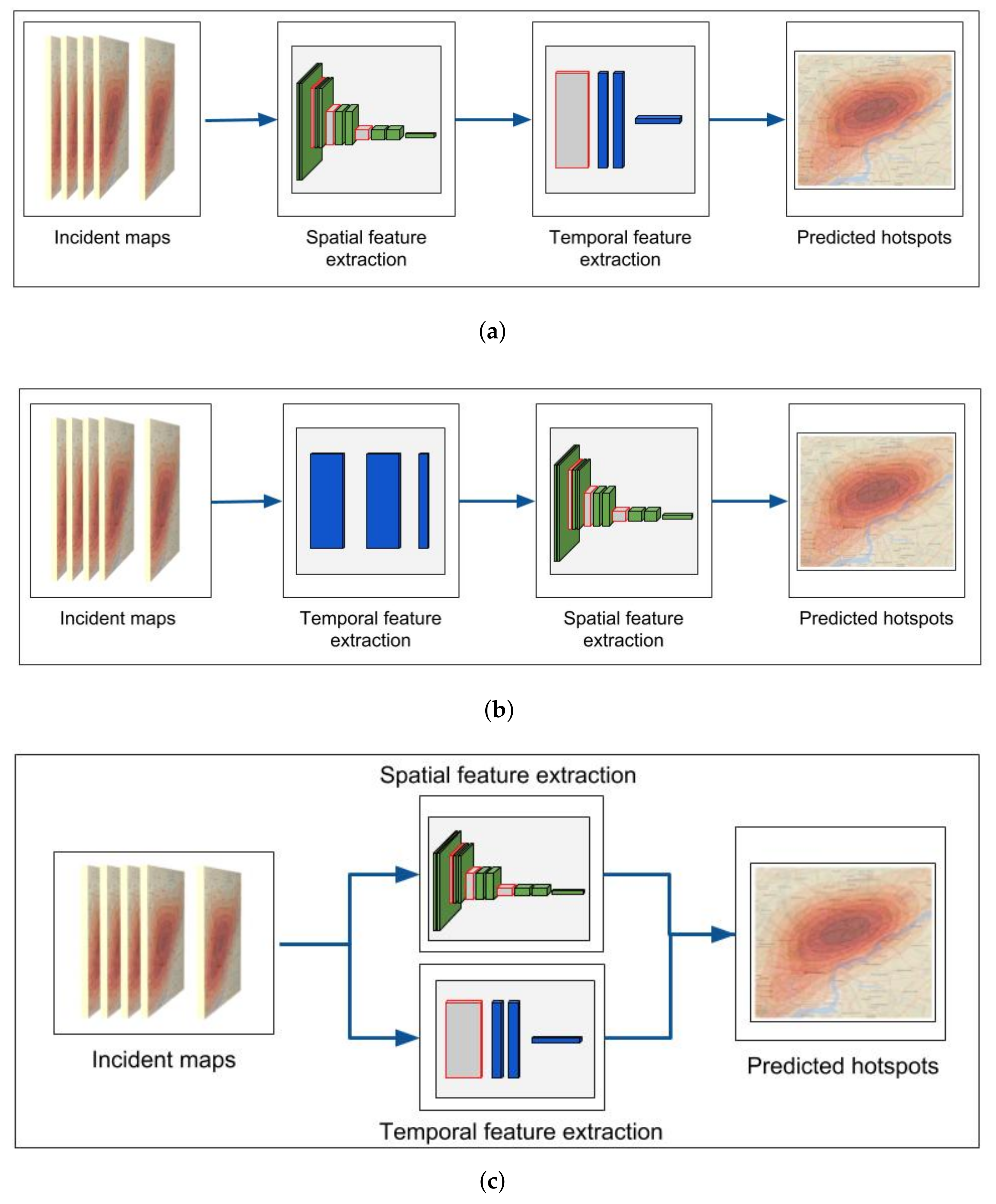
- We present 3 fundamental DL architecture configurations for crime prediction based on encoding: (a) the spatial and then the temporal patterns, (b) the temporal and then the spatial patterns, (c) temporal and spatial patterns in parallel.
- We experimentally evaluate and select the most efficient configuration to deepen our investigation.
- We compare our models with 10 state-of-the-art algorithms on 5 different crime prediction datasets that contain more than 10 years of crime report data.
- Finally, we propose a guide for designing DL models for crime hotspot prediction and classification.
2. Related Work
3. Problem Formulation
4. Proposed Methodology
5. Experimental Setup
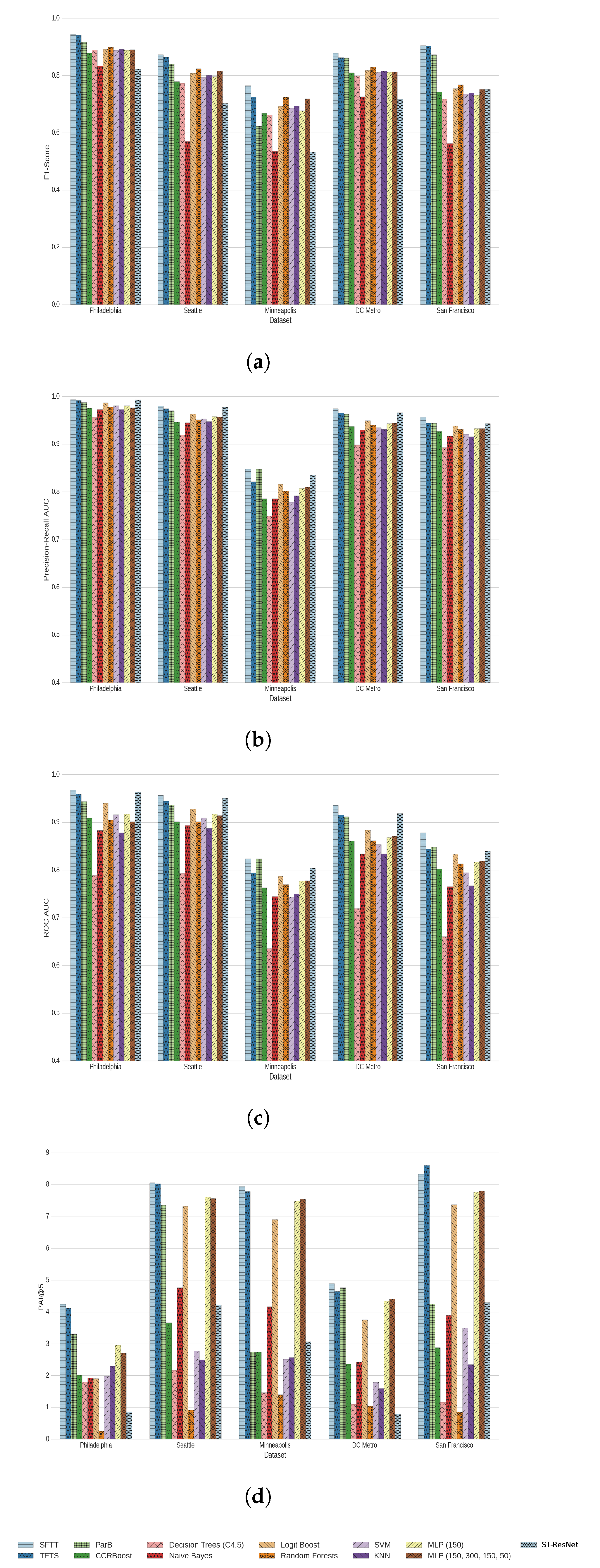
5.1. Algorithms
- CCRBoost [33]. CCRBoost starts with multi-clustering followed by local feature learning processes to discover all possible distributed patterns from distributions of different shapes, sizes, and time periods. The final classification label is produced using groupings of the most suitable distributed patterns.
- ST-ResNet [11]. The original ST-ResNet model uses 3 submodels with residual connections, which each has 4 input channels in parallel, to extract indicators from 3 trends: previous week, time of day and recent events. In our problem, the temporal resolution is not hourly but daily so the 3 periods are replaced by day of month, day of week and recent events equivalently.
- Decision Trees(C4.5) [42] using confidence factor of 0.25; Decision Trees is a non-parametric supervised learning method that predicts the value of a target variable by learning simple decision rules inferred from the data features.
- Naive Bayes [9] classifier with a polynomial kernel; Naive Bayes methods are a set of supervised learning algorithms based on applying Bayes’ theorem with the “naive” assumption of independence between every pair of features.
- LogitBoost [43] using 100 as its weight threshold; The LogitBoost algorithm uses Newton steps for fitting an additive symmetric logistic model by maximum likelihood.
- Random Forests [8] with 10 trees; A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and use averaging to improve the predictive accuracy and control over-fitting.
- Support Vector Machine (SVM) [10] with a linear kernel; SVMs are learning machines implementing the structural risk minimisation inductive principle to obtain good generalisation on a limited number of learning patterns.
- k Nearest Neighbours [44] with 3 neighbours; kNN is a classifier that makes a prediction based on the majority vote of the k nearest samples on the feature vector space.
- MultiLayer Perceptron (MLP(150)) [26] with one hidden layer of 150 neurons;
- MultiLayer Perceptron (MLP(150, 300, 150, 50)) [45] with four hidden layers of 150, 300, 150 and 50 neurons each;
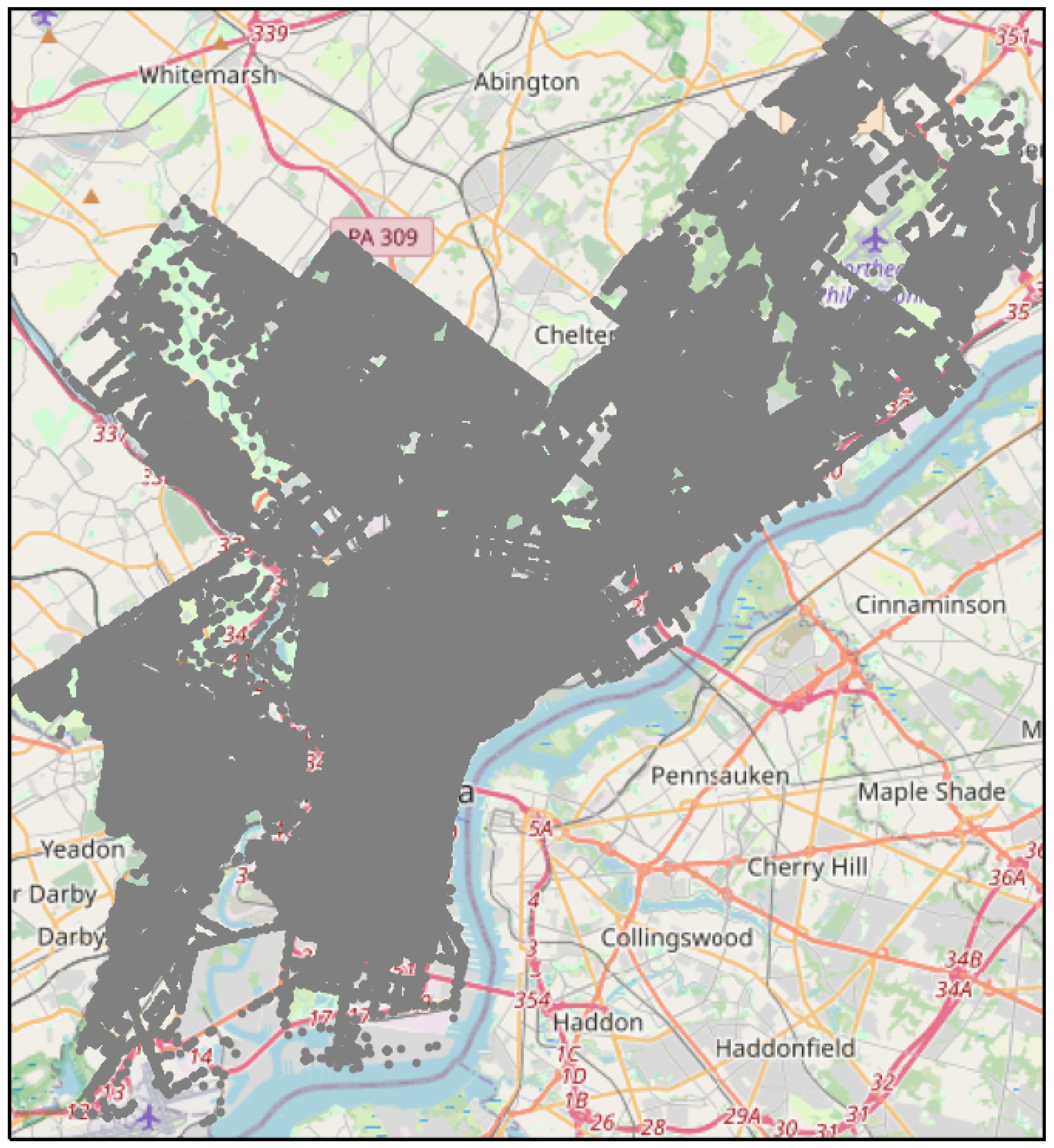
5.2. Datasets
5.3. Metrics
6. Results
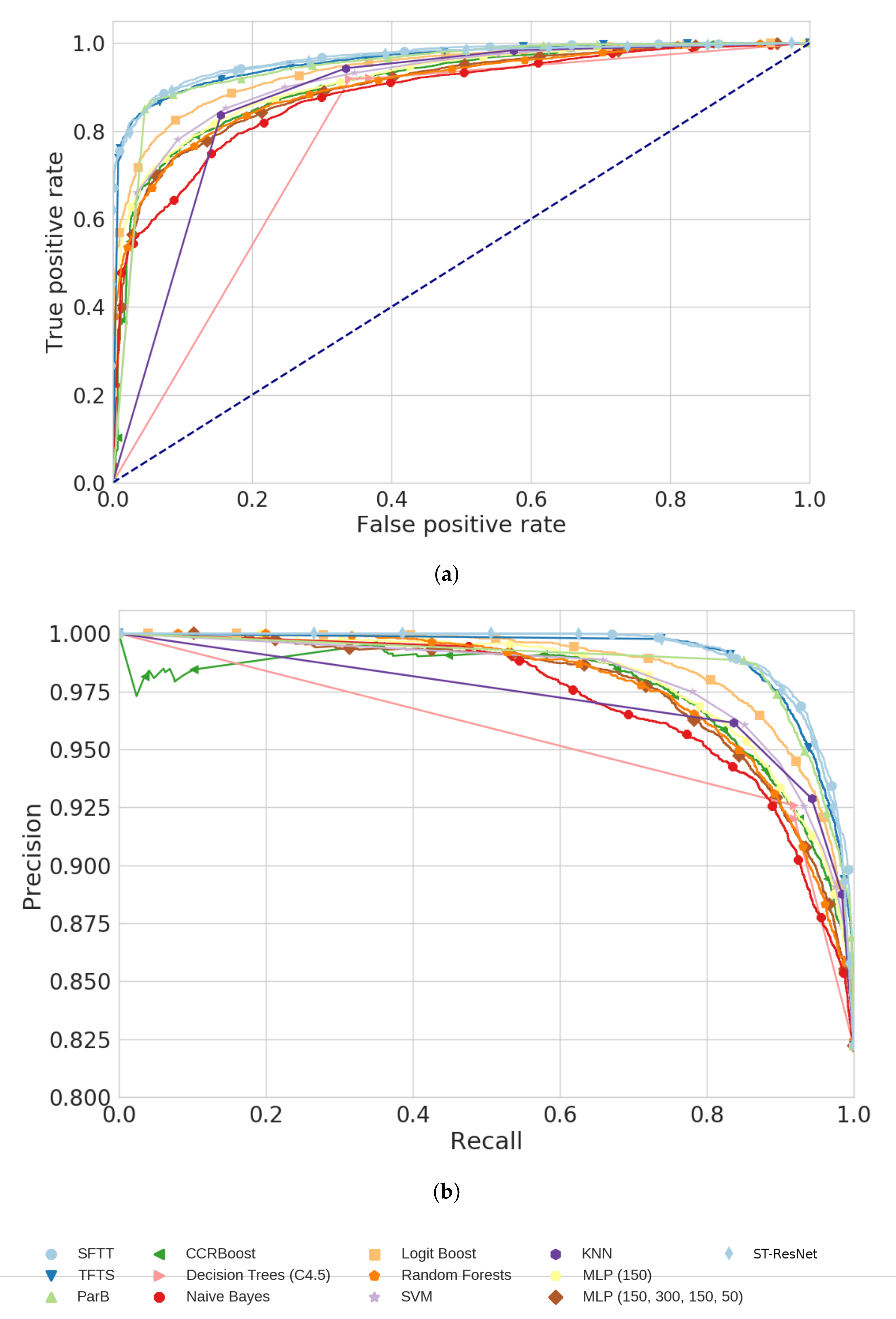
6.1. Evaluation of Models
6.2. Evaluation of Cell Size
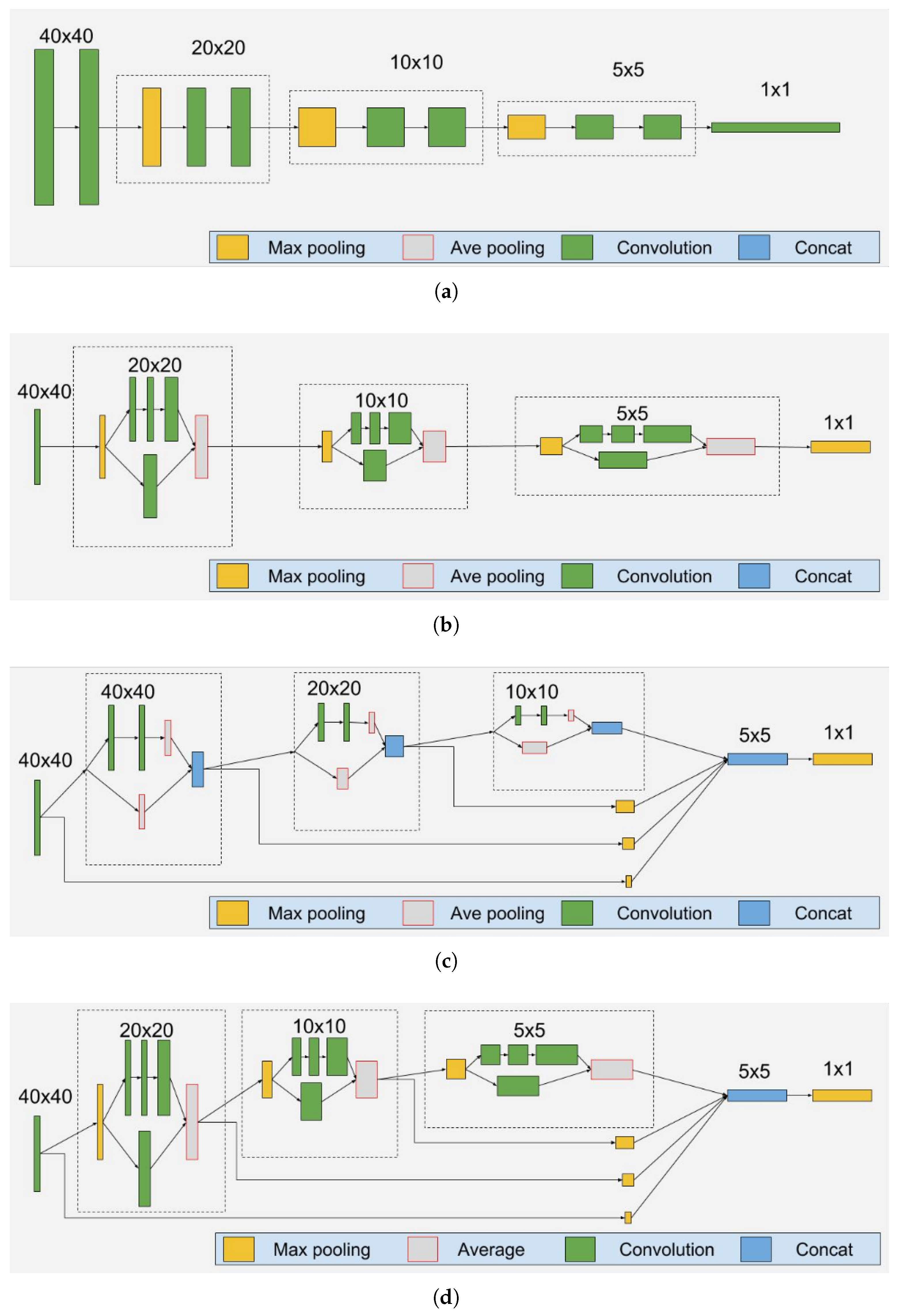
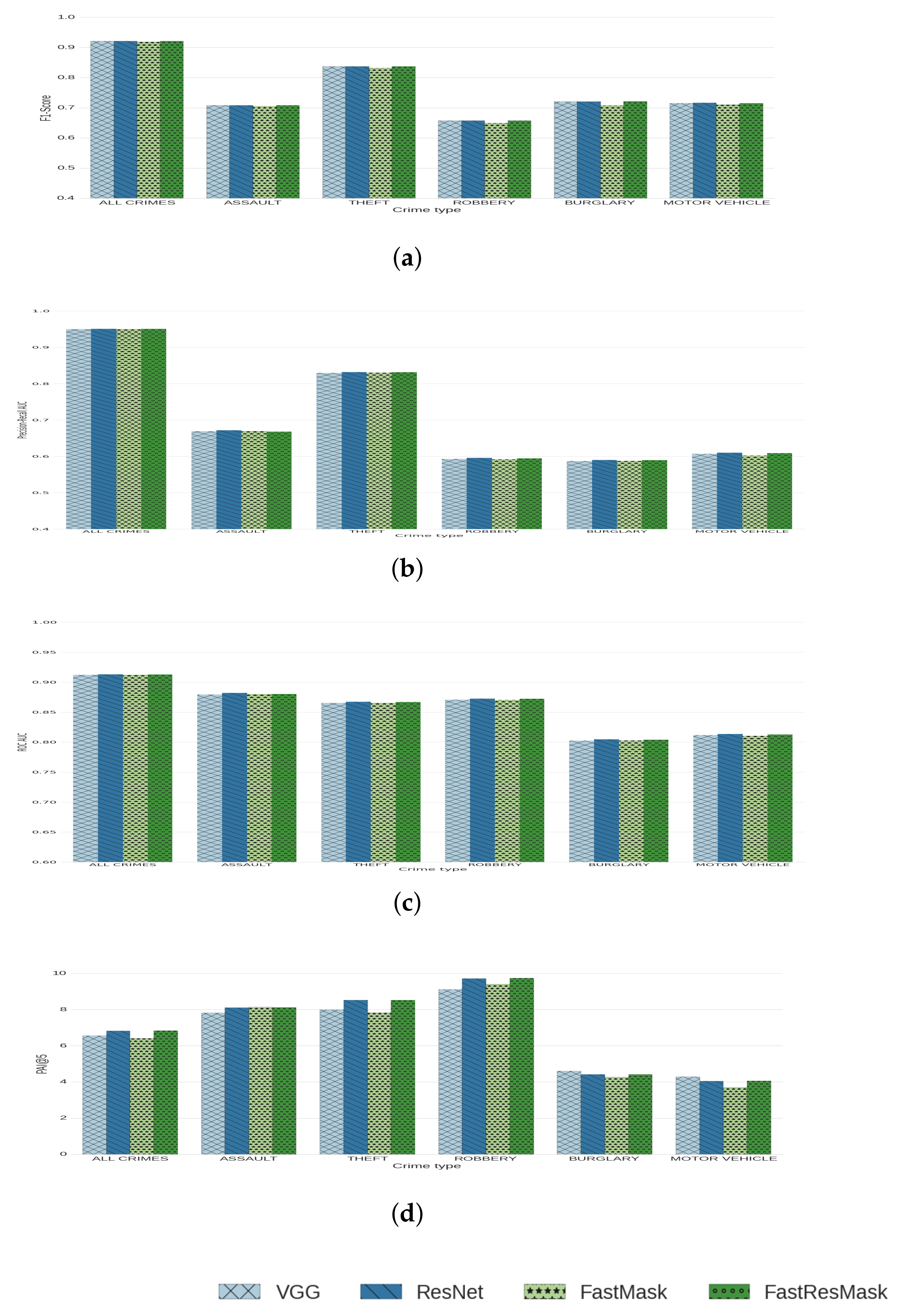
6.3. Evaluation of Spatial Body
6.4. Evaluation of Temporal Body
6.5. Evaluation of Batch Normalisation and Dropout
6.6. Multi-Label Hotspot Classification
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Dataset | Seattle | Philadelphia | Minneapolis | DC Metro | San Fransisco | |
|---|---|---|---|---|---|---|
| Crime Category | ||||||
| Homicide | HOMICIDE | Homicide - Criminal | DASTR | HOMICIDE | ||
| Homicide - Gross Negligence | MURDR | |||||
| Homicide - Justifiable | ADLTTN | |||||
| JHOMIC | ||||||
| Robbery | ROBBERY | Robbery No Firearm | SHOPLF | ROBBERY | ROBBERY | |
| Robbery Firearm | ROBBIZ | |||||
| ROBPER | ||||||
| ROBPAG | ||||||
| Arson | RECKLESS BURNING | Arson | ARSON | ARSON | ARSON | |
| FIREWORK | ||||||
| Vice | CAR PROWL | Rape | CSCR | SEX ABUSE | SEX OFFENSES FORCIBLE | |
| PROSTITUTION | Prostitution and Commercialized Vice | PROSTITUTION | ||||
| PORNOGRAPHY | SEX OFFENSES NON FORCIBLE | |||||
| STAY OUT OF AREA OF PROSTITUTION | PORNOGRAPHY/OBSCENE MAT | |||||
| Motor Vehicle | VEHICLE THEFT | Motor Vehicle Theft | TFMV | MOTOR VEHICLE THEFT | VEHICLE THEFT | |
| Recovered Stolen Motor Vehicle | AUTOTH | RECOVERED VEHICLE | ||||
| TMVP | ||||||
| MVTHFT | ||||||
| Narcotics | NARCOTICS | Narcotic / Drug Law Violations | DRUG/NARCOTIC | |||
| STAY OUT OF AREA OF DRUGS | ||||||
| Assault | ASSAULT | Other Assaults | ASLT4 | ASSAULT W/DANGEROUS WEAPON | ASSAULT | |
| DISTURBANCE | Aggravated Assault Firearm | ASLT2 | WEAPON LAWS | |||
| INJURY | Disorderly Conduct | ASLT1 | DISORDERLY CONDUCT | |||
| DISPUTE | Aggravated Assault No Firearm | ASLT3 | ||||
| DISORDERLY CONDUCT | Offenses Against Family and Children | DASLT2 | ||||
| DASLT3 | ||||||
| DISARM | ||||||
| DASLT1 | ||||||
| Other | OTHER PROPERTY | All Other Offenses | ONLTHT | THEFT F/AUTO | WARRANTS | |
| TRAFFIC | Weapon Violations | NOPAY | OTHER OFFENSES | |||
| FRAUD | Burglary Non-Residential | COINOP | NON-CRIMINAL | |||
| WARRANT ARREST | Fraud | COMPUT | SUSPICIOUS OCC | |||
| THREATS | Vagrancy/Loitering | SCRAP | DRUNKENNESS | |||
| EXTORTION | Embezzlement | FORGERY/COUNTERFEITING | ||||
| COUNTERFEIT | DRIVING UNDER THE INFLUENCE | SECONDARY CODES | ||||
| WEAPON | Forgery and Counterfeiting | MISSING PERSON | ||||
| BURGLARY-SECURE PARKING-RES | Other Sex Offenses (Not Commercialized) | FRAUD | ||||
| LOST PROPERTY | Liquor Law Violations | KIDNAPPING | ||||
| DUI | Gambling Violations | RUNAWAY | ||||
| OBSTRUCT | Public Drunkenness | DRIVING UNDER THE INFLUENCE | ||||
| ELUDING | Receiving Stolen Property | FAMILY OFFENSES | ||||
| MAIL THEFT | nan | LIQUOR LAWS | ||||
| VIOLATION OF COURT ORDER | BRIBERY | |||||
| EMBEZZLE | EMBEZZLEMENT | |||||
| FORGERY | SUICIDE | |||||
| ANIMAL COMPLAINT | LOITERING | |||||
| THEFT OF SERVICES | EXTORTION | |||||
| ILLEGAL DUMPING | GAMBLING | |||||
| RECOVERED PROPERTY | BAD CHECKS | |||||
| LIQUOR VIOLATION | ||||||
| FALSE REPORT | ||||||
| LOITERING | ||||||
| HARBOR CALLs | ||||||
| FRAUD AND FINANCIAL | ||||||
| [INC - CASE DC USE ONLY] | ||||||
| ESCAPE | ||||||
| PUBLIC NUISANCE | ||||||
| BIAS INCIDENT | ||||||
| HARBOR CALLS | ||||||
| GAMBLE | ||||||
| METRO | ||||||
| nan | ||||||
| Theft | STOLEN PROPERTY | Thefts | THEFT | THEFT/OTHER | LARCENY/THEFT | |
| BIKE THEFT | Theft from Vehicle | TBLDG | VANDALISM | |||
| SHOPLIFTING | Vandalism/Criminal Mischief | TFPER | STOLEN PROPERTY | |||
| PROPERTY DAMAGE | THFTSW | |||||
| PURSE SNATCH | ||||||
| PICKPOCKET | BIKETF | |||||
| Burglary | BURGLARY | Burglary Residential | BURGD | BURGLARY | BURGLARY | |
| TRESPASS | BURGB | TRESPASS | ||||
| LOOT | TREA | |||||
References
- Perry, W.L. Predictive Policing: The Role of Crime Forecasting in Law Enforcement Operations; Rand Corporation: Santa Monica, CA, USA, 2013. [Google Scholar]
- Cohen, L.E.; Felson, M. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Cornish, D.B.; Clarke, R.V. The Reasoning Criminal: Rational Choice Perspectives on Offending; Transaction Publishers: Piscataway, NJ, USA, 2014. [Google Scholar]
- Grubesic, T.H.; Mack, E.A. Spatio-temporal interaction of urban crime. J. Quant. Criminol. 2008, 24, 285–306. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bowers, K.; Hirschfield, A. New insights into the spatial and temporal distribution of repeat victimization. Br. J. Criminol. 1997, 37, 224–241. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bernasco, W.; Bowers, K.J.; Elffers, H.; Ratcliffe, J.; Rengert, G.; Townsley, M. Space–time patterns of risk: A cross national assessment of residential burglary victimization. J. Quant. Criminol. 2007, 23, 201–219. [Google Scholar] [CrossRef] [Green Version]
- Bowers, K.J.; Johnson, S.D. Who commits near repeats? A test of the boost explanation. West. Criminol. Rev. 2004, 5, 12–24. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. The optimality of naive Bayes. AA 2004, 1, 3. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, D.; Zhang, D.; Brantingham, P.J.; Bertozzi, A.L. Deep Learning for Real Time Crime Forecasting. arXiv 2017, arXiv:1707.03340. [Google Scholar]
- Levine, N.; CrimeStat, I. A Spatial Statistics Program for the Analysis of Crime Incident Locations; Ned Levine and Associates: Houston, TX, USA; The National Institute of Justice: Washington, DC, USA, 2002.
- Williamson, D.; McLafferty, S.; McGuire, P.; Ross, T.; Mollenkopf, J.; Goldsmith, V.; Quinn, S. Tools in the Spatial Analysis of Crime. Mapping and Analysing Crime Data; Hirschfield, A., Bowers, K., Eds.; Taylor & Francis: London, UK; New York, NY, USA, 2001; Volume 1, p. 187. [Google Scholar]
- Rosenblatt, M.; Lii, K.S.; Politis, D.N. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Chainey, S.; Tompson, L.; Uhlig, S. The utility of hotspot mapping for predicting spatial patterns of crime. Secur. J. 2008, 21, 4–28. [Google Scholar] [CrossRef]
- Eck, J.; Chainey, S.; Cameron, J.; Wilson, R. Mapping Crime: Understanding Hotspots; U.S. Department of Justice Office of Justice Programs: Washington, DC, USA, 2005. Available online: https://discovery.ucl.ac.uk/id/eprint/11291/1/11291.pdf (accessed on 12 June 2019).
- Chainey, S.; Ratcliffe, J. GIS and Crime Mapping; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bishop, C.M. Pattern recognition. Mach. Learn. 2006, 128, 1–58. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- de Queiroz Neto, J.F.; dos Santos, E.M.; Vidal, C.A. MSKDE-Using Marching Squares to Quickly Make High Quality Crime Hotspot Maps. In Proceedings of the 2016 29th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Sao Paulo, Brazil, 4–7 October 2016; pp. 305–312. [Google Scholar]
- Mohler, G.O.; Short, M.B.; Brantingham, P.J.; Schoenberg, F.P.; Tita, G.E. Self-exciting point process modeling of crime. J. Am. Stat. Assoc. 2011, 106, 100–108. [Google Scholar] [CrossRef]
- Ratcliffe, J.H. A temporal constraint theory to explain opportunity-based spatial offending patterns. J. Res. Crime Delinq. 2006, 43, 261–291. [Google Scholar] [CrossRef]
- Ghazvini, A.; Abdullah, S.N.H.S.; Kamrul Hasan, M.; Bin Kasim, D.Z.A. Crime Spatiotemporal Prediction with Fused Objective Function in Time Delay Neural Network. IEEE Access 2020, 8, 115167–115183. [Google Scholar] [CrossRef]
- Nakaya, T.; Yano, K. Visualising Crime Clusters in a Space-time Cube: An Exploratory Data-analysis Approach Using Space-time Kernel Density Estimation and Scan Statistics. Trans. GIS 2010, 14, 223–239. [Google Scholar] [CrossRef]
- Toole, J.L.; Eagle, N.; Plotkin, J.B. Spatiotemporal correlations in criminal offense records. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 38. [Google Scholar] [CrossRef]
- Olligschlaeger, A.M. Artificial neural networks and crime mapping. Crime Mapp. Crime Prev. 1997, 1, 313–348. [Google Scholar]
- Kianmehr, K.; Alhajj, R. Effectiveness of support vector machine for crime hot-spots prediction. Appl. Artif. Intell. 2008, 22, 433–458. [Google Scholar] [CrossRef]
- Yu, C.H.; Ward, M.W.; Morabito, M.; Ding, W. Crime forecasting using data mining techniques. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining Workshops, Vancouver, BC, Canada, 11 December 2011; pp. 779–786. [Google Scholar]
- Gorr, W.; Olligschlaeger, A.; Thompson, Y. Short-term forecasting of crime. Int. J. Forecast. 2003, 19, 579–594. [Google Scholar] [CrossRef]
- Feng, M.; Zheng, J.; Ren, J.; Hussain, A.; Li, X.; Xi, Y.; Liu, Q. Big Data Analytics and Mining for Effective Visualization and Trends Forecasting of Crime Data. IEEE Access 2019, 7, 106111–106123. [Google Scholar] [CrossRef]
- Eftelioglu, E.; Shekhar, S.; Kang, J.M.; Farah, C.C. Ring-Shaped Hotspot Detection. IEEE Trans. Knowl. Data Eng. 2016, 28, 3367–3381. [Google Scholar] [CrossRef]
- Xu, J.; Tan, P.N.; Zhou, J.; Luo, L. Online Multi-Task Learning Framework for Ensemble Forecasting. IEEE Trans. Knowl. Data Eng. 2017, 29, 1268–1280. [Google Scholar] [CrossRef]
- Yu, C.H.; Ding, W.; Morabito, M.; Chen, P. Hierarchical Spatio-Temporal Pattern Discovery and Predictive Modeling. IEEE Trans. Knowl. Data Eng. 2016, 28, 979–993. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Two-stream convolutional networks for action recognition in videos. Adv. Neural Inf. Process. Syst. arXiv 2014, arXiv:1406.2199. [Google Scholar]
- Wu, Z.; Wang, X.; Jiang, Y.G.; Ye, H.; Xue, X. Modeling spatial-temporal clues in a hybrid deep learning framework for video classification. In Proceedings of the 23rd ACM international conference on Multimedia, Brisbane, Australia, 26–30 October 2015; ACM: New York, NY, USA, 2015; pp. 461–470. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ruta, D.; Gabrys, B.; Lemke, C. A generic multilevel architecture for time series prediction. IEEE Trans. Knowl. Data Eng. 2011, 23, 350–359. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hu, H.; Lan, S.; Jiang, Y.; Cao, Z.; Sha, F. FastMask: Segment Multi-scale Object Candidates in One Shot. arXiv 2016, arXiv:1612.08843. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An optimal algorithm for approximate nearest neighbor searching fixed dimensions. J. ACM (JACM) 1998, 45, 891–923. [Google Scholar] [CrossRef] [Green Version]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Oxley, M.E.; Suter, B.W. The multilayer perceptron as an approximation to a Bayes optimal discriminant function. IEEE Trans. Neural Netw. 1990, 1, 296–298. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In Proceedings of the Thirty-first AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://github.com/keras-team/keras (accessed on 20 February 2017).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 20 July 2017).
- NVIDIA CUDA Programming Guide NVIDIA. 2010. Available online: http://developer.download.nvidia.com (accessed on 24 April 2018).
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]

| Algorithm | Training Time | # Parameters |
|---|---|---|
| CCRBoost | 0:00:38 | - |
| Decision Trees (C4.5) | 0:00:02 | - |
| Naive Bayes | 0:00:03 | - |
| Logit Boost | 0:00:05 | - |
| SVM | 0:01:17 | - |
| Random Forests | 0:00:03 | - |
| KNN | 0:00:02 | - |
| MLP (150) | 0:00:13 | - |
| MLP (150, 300, 150, 50) | 0:00:24 | - |
| ST-ResNet | 0:05:59 | 1.343.043 |
| SFTT-VGG19 | 0:48:11 | 30.117.120 |
| TFTS | 0:24:32 | 10.260.016 |
| ParB | 3:15:05 | 31.942.280 |
| SFTT-ResNet | 0:17:53 | 7.348.899 |
| SFTT-FastMask | 0:17:57 | 6.917.264 |
| SFTT-FastResMask | 1:53:09 | 7.610.299 |
| Dataset | Start Year | End Year | Num. of Incidents |
|---|---|---|---|
| Philadelphia | 2006 | 2017 | 2,203,785 |
| Seattle | 1996 | 2016 | 684,472 |
| Minneapolis | 2010 | 2016 | 136,121 |
| DC Metro | 2008 | 2017 | 313,410 |
| San Francisco | 2003 | 2015 | 878,049 |
| Crime Type | Philadelphia | Seattle | Minneapolis | DC Metro | San Francisco |
|---|---|---|---|---|---|
| ASSAULT | 80.28 | 12.84 | 3.08 | 6.32 | 14.96 |
| THEFT | 116.72 | 21.34 | 17.46 | 27.39 | 40.44 |
| ROBBERY | 20.74 | 2.99 | 6.13 | 10.56 | 4.74 |
| BURGLARY | 23.76 | 17.06 | 12.36 | 9.81 | 8.65 |
| MOTOR VEHICLE | 27.94 | 10.01 | 14.44 | 8.43 | 7.77 |
| ARSON | 1.37 | 0.10 | 0.32 | 0.10 | 0.29 |
| HOMICIDE | 0.80 | 0.03 | 0.74 | 0.27 | 0.0 |
| VICE | 4.36 | 22.59 | 0.72 | 0.59 | 1.59 |
| NARCOTICS | 27.90 | 3.21 | 0.0 | 0.0 | 5.54 |
| OTHER | 102.37 | 40.15 | 0.09 | 23.24 | 51.81 |
| # CELLS | 752 | 818 | 1123 | 702 | 1057 |
| Algorithm | F1score | AUCPR | AUROC | PAI@5 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 | 24 | 32 | 40 | 16 | 24 | 32 | 40 | 16 | 24 | 32 | 40 | 16 | 24 | 32 | 40 | |
| CCRBoost | 0.93 | 0.92 | 0.88 | 0.88 | 0.99 | 0.99 | 0.98 | 0.97 | 0.92 | 0.92 | 0.90 | 0.91 | 1.87 | 1.94 | 1.86 | 2.00 |
| Decision Trees (C4.5) | 0.93 | 0.92 | 0.90 | 0.89 | 0.99 | 0.97 | 0.97 | 0.96 | 0.85 | 0.80 | 0.78 | 0.79 | 0.59 | 1.51 | 1.54 | 1.80 |
| Naive Bayes | 0.92 | 0.87 | 0.84 | 0.83 | 0.98 | 0.98 | 0.98 | 0.97 | 0.82 | 0.89 | 0.86 | 0.88 | 1.21 | 2.82 | 2.00 | 1.93 |
| Logit Boost | 0.94 | 0.92 | 0.91 | 0.89 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.96 | 0.94 | 0.94 | 0.81 | 1.73 | 2.52 | 1.91 |
| SVM | 0.94 | 0.93 | 0.91 | 0.90 | 0.99 | 0.99 | 0.98 | 0.98 | 0.91 | 0.93 | 0.90 | 0.90 | 0.06 | 0.12 | 0.19 | 0.25 |
| Random Forests | 0.94 | 0.92 | 0.90 | 0.89 | 1.00 | 0.99 | 0.98 | 0.98 | 0.97 | 0.94 | 0.91 | 0.92 | 1.04 | 2.44 | 1.93 | 1.98 |
| KNN | 0.94 | 0.92 | 0.91 | 0.89 | 0.99 | 0.98 | 0.97 | 0.97 | 0.86 | 0.87 | 0.84 | 0.88 | 0.93 | 1.66 | 1.89 | 2.29 |
| MLP (150) | 0.94 | 0.92 | 0.90 | 0.89 | 0.98 | 0.99 | 0.98 | 0.98 | 0.84 | 0.94 | 0.91 | 0.92 | 2.21 | 2.09 | 2.30 | 2.95 |
| MLP (150, 300, 150, 50) | 0.94 | 0.92 | 0.90 | 0.89 | 0.97 | 0.99 | 0.98 | 0.98 | 0.79 | 0.91 | 0.91 | 0.90 | 1.31 | 2.10 | 2.15 | 2.70 |
| ST-ResNet | 0.91 | 0.88 | 0.86 | 0.82 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.96 | 0.96 | 0.96 | 3.30 | 1.62 | 2.55 | 2.56 |
| SFTT | 0.99 | 0.97 | 0.96 | 0.94 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 0.98 | 0.97 | 0.97 | 4.02 | 4.34 | 4.14 | 4.33 |
| TFTS | 0.99 | 0.97 | 0.95 | 0.94 | 1.00 | 0.98 | 0.99 | 0.99 | 0.95 | 0.81 | 0.93 | 0.96 | 4.30 | 4.40 | 4.10 | 4.12 |
| ParB | 0.99 | 0.96 | 0.94 | 0.92 | 0.99 | 0.99 | 0.99 | 0.99 | 0.88 | 0.91 | 0.94 | 0.94 | 4.32 | 3.41 | 3.29 | 3.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stalidis, P.; Semertzidis, T.; Daras, P. Examining Deep Learning Architectures for Crime Classification and Prediction. Forecasting 2021, 3, 741-762. https://doi.org/10.3390/forecast3040046
Stalidis P, Semertzidis T, Daras P. Examining Deep Learning Architectures for Crime Classification and Prediction. Forecasting. 2021; 3(4):741-762. https://doi.org/10.3390/forecast3040046
Chicago/Turabian StyleStalidis, Panagiotis, Theodoros Semertzidis, and Petros Daras. 2021. "Examining Deep Learning Architectures for Crime Classification and Prediction" Forecasting 3, no. 4: 741-762. https://doi.org/10.3390/forecast3040046
APA StyleStalidis, P., Semertzidis, T., & Daras, P. (2021). Examining Deep Learning Architectures for Crime Classification and Prediction. Forecasting, 3(4), 741-762. https://doi.org/10.3390/forecast3040046







