A Real-Time Data Analysis Platform for Short-Term Water Consumption Forecasting with Machine Learning
Abstract
:1. Introduction
2. Machine-Learning Algorithms for Water Consumption Forecasting
2.1. Forecasting with Machine-Learning Algorithms
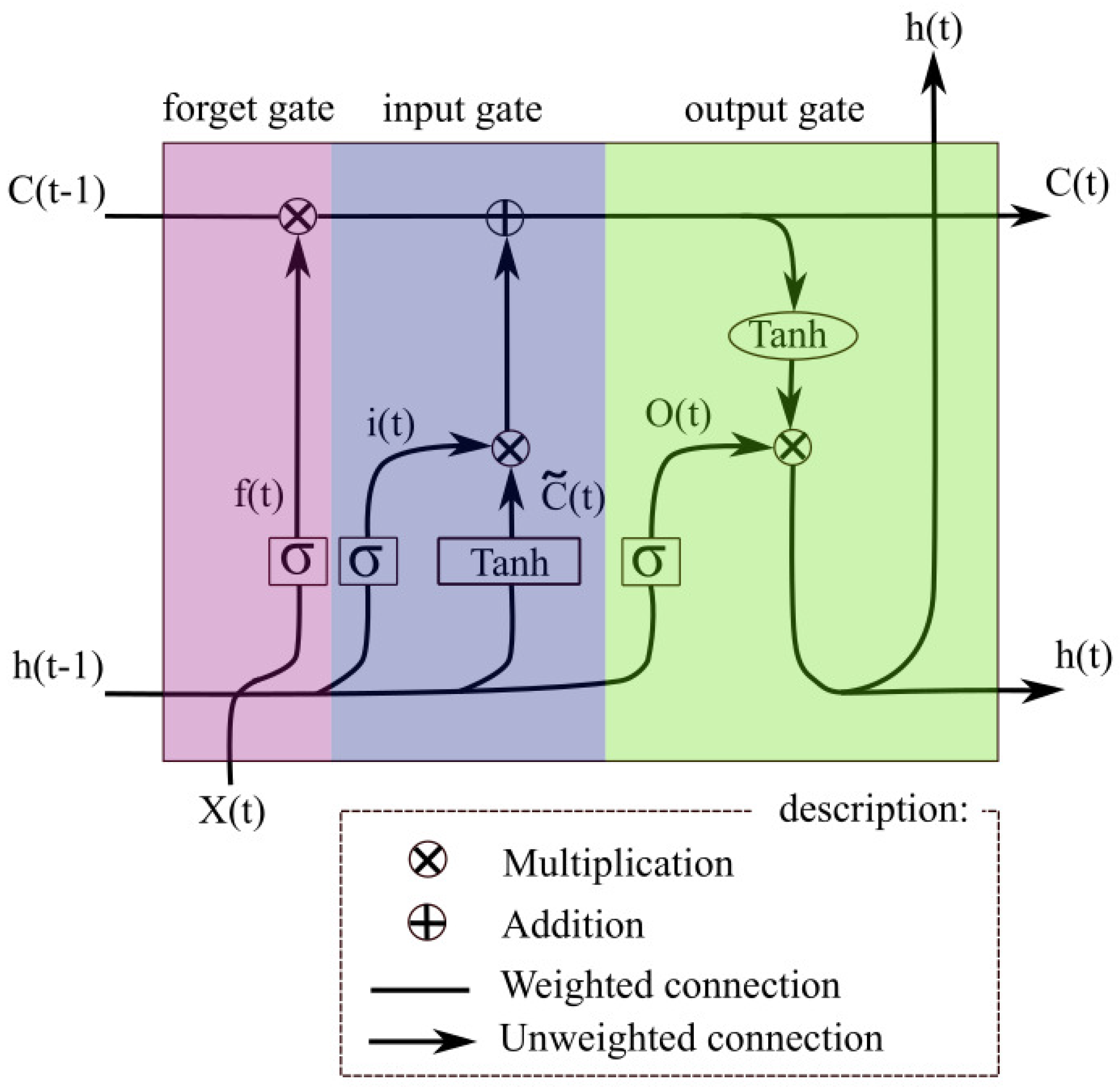
2.2. Forecasting Framework Based on LSTM
3. Proposed Architecture and ML Framework to Collect and Analyze Water Consumption Data
3.1. Data Collecting with Smart Meters
3.2. Data Description
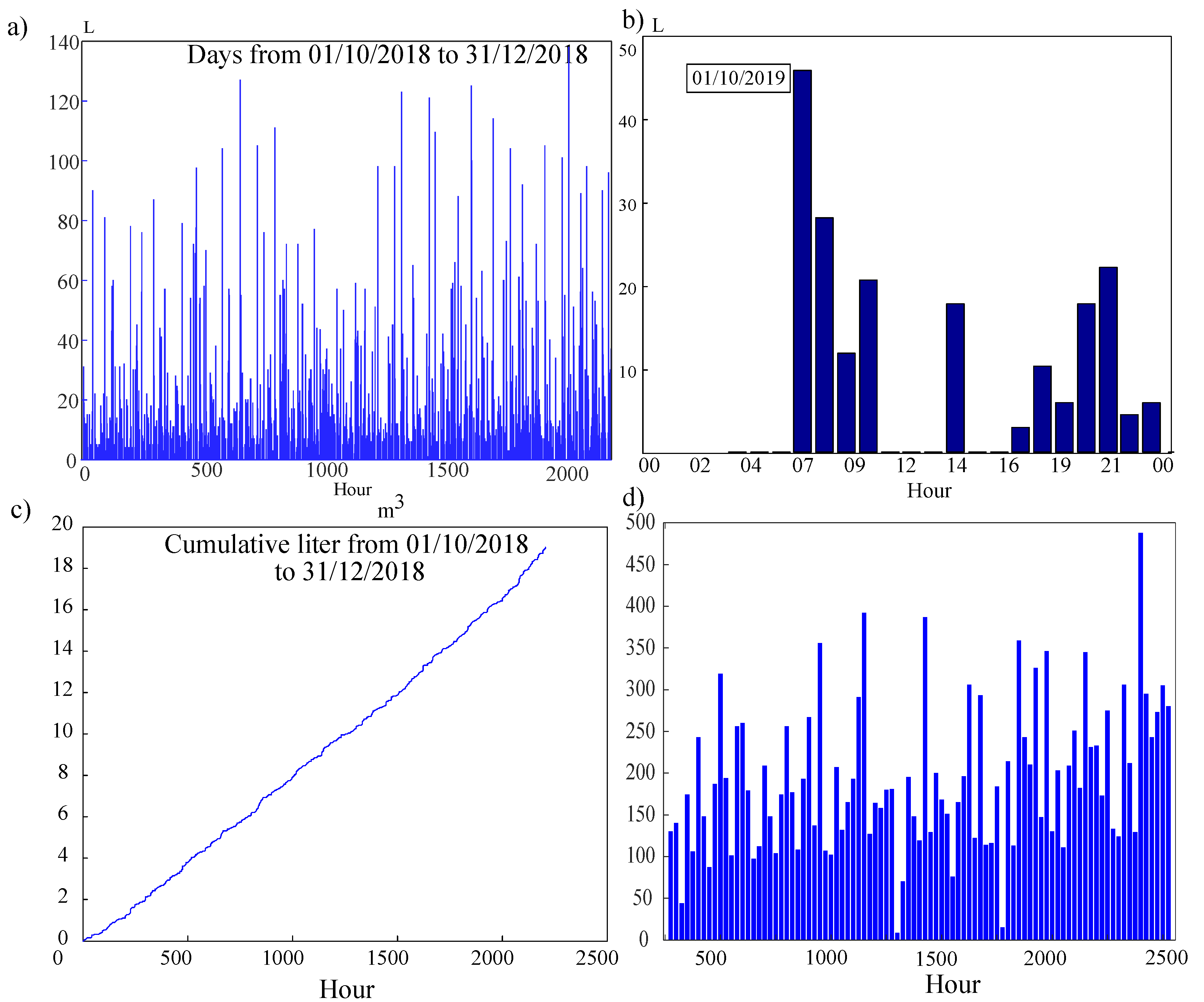
3.2.1. Water Consumption Time Series
3.2.2. Cumulated Water Consumption: The Index and the Load Curve
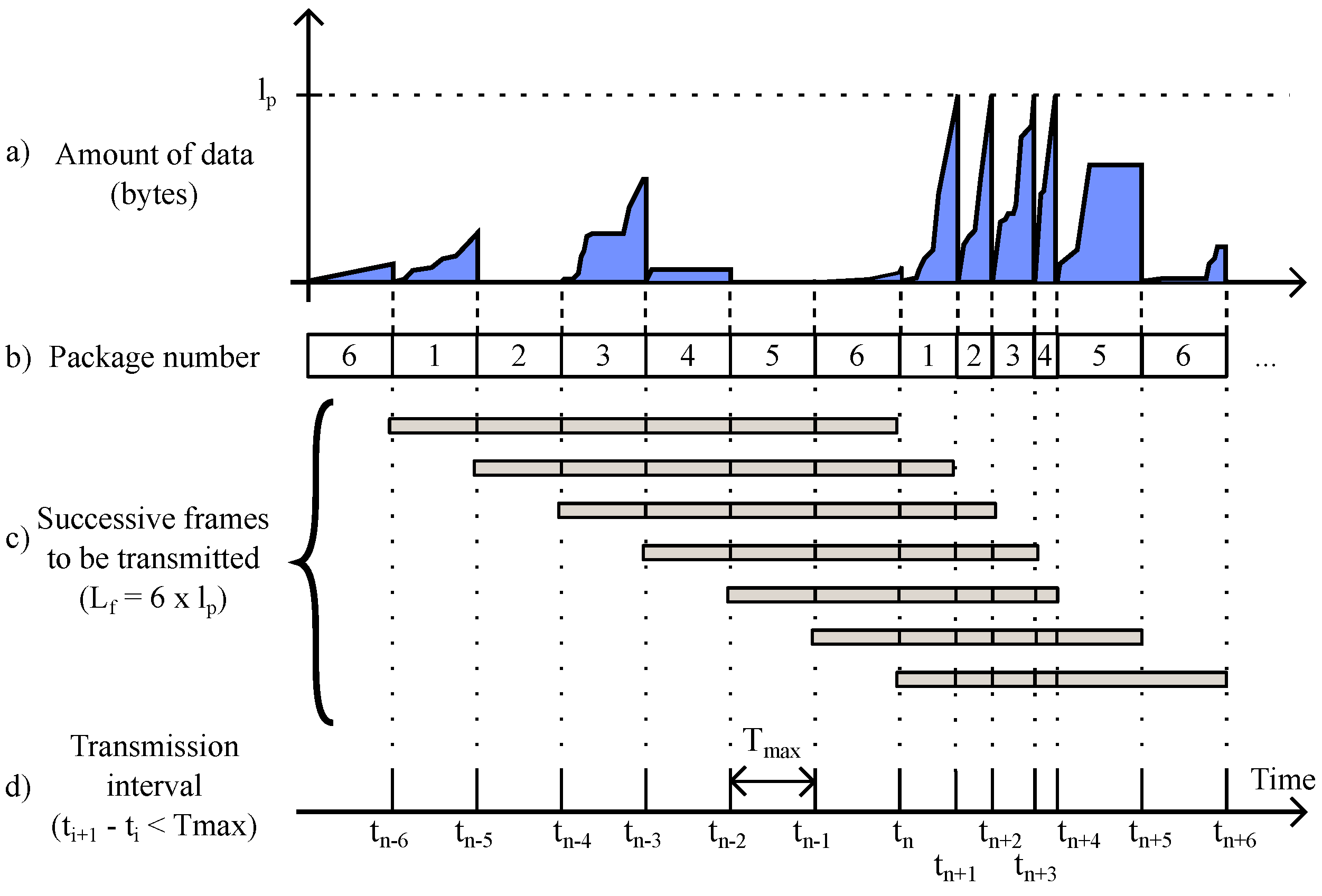
3.2.3. Sampled Water Consumption Data Series
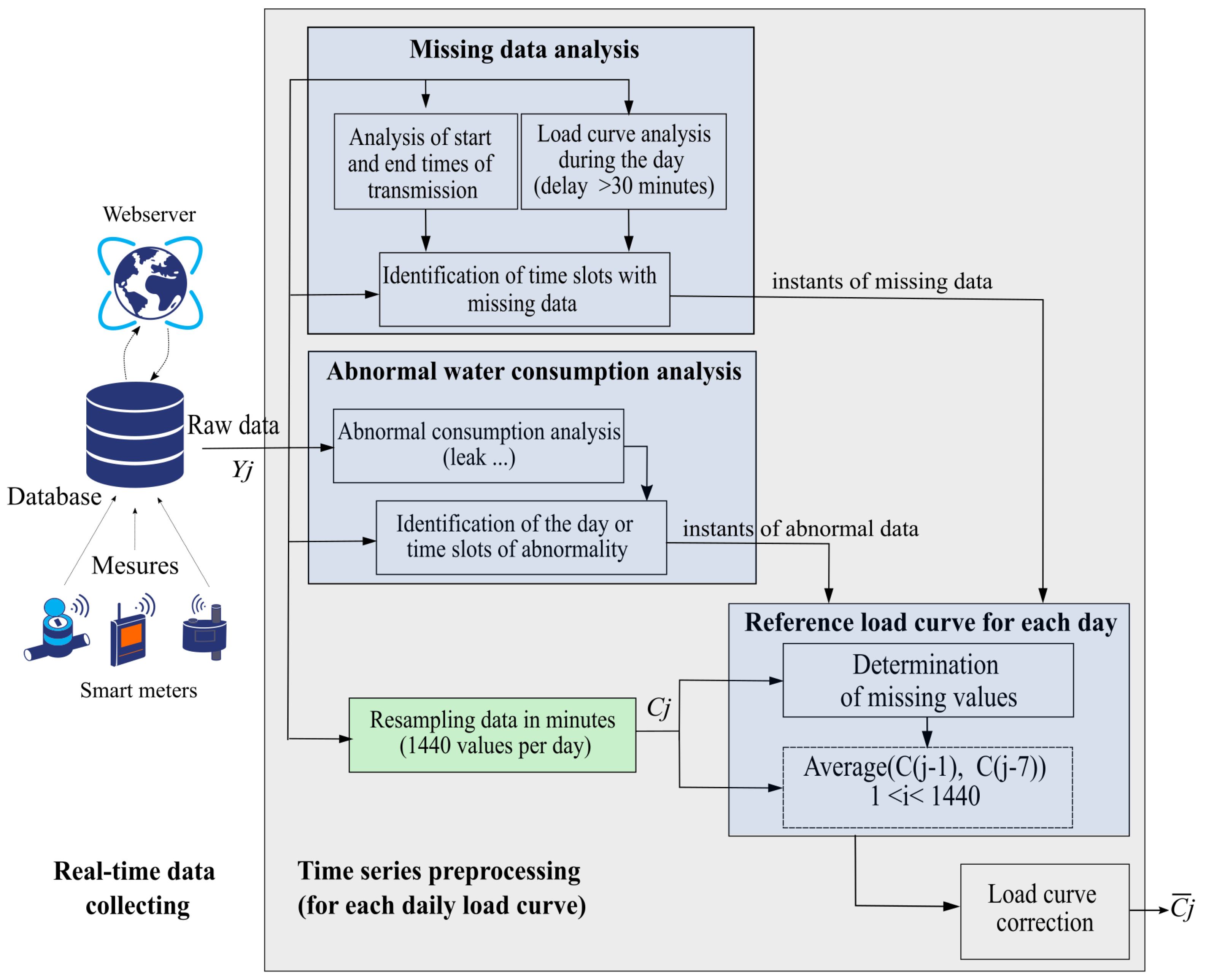
3.3. Data Integrity Checking and Interpolation
4. Water Consumption Forecasting
4.1. Hourly Water Consumption Forecasting
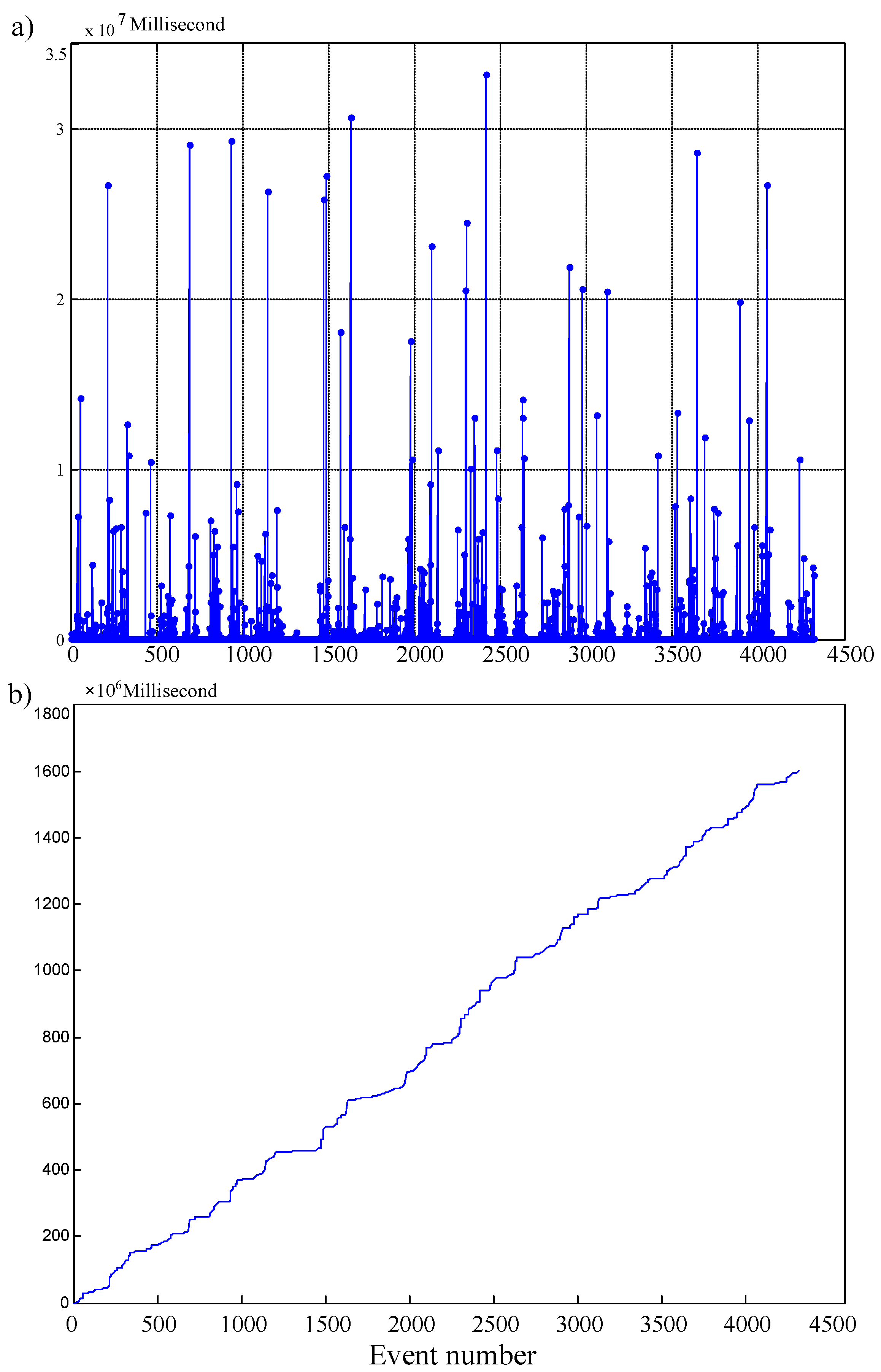
4.2. Forecasting Events of Water Consumption in Milliseconds
4.3. Discussion on the Hourly and Events Water Consumption Forecasting
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMI | Advanced Metering Infrastructure |
| BPNN | Back-Propagation Neural Network |
| BPTT | Back-Propagation Through Time |
| LC | Load Curve |
| LSTM | Long Short-Term Memory |
| ML | Machine Learning |
| RMSE | Root Mean Square Error |
| SQL | Structured Query Language |
References
- Roccetti, M.; Delnevo, G.; Casini, L.; Salomoni, P. A Cautionary Tale for Machine Learning Design: Why we Still Need Human-Assisted Big Data Analysis. Mob. Netw. Appl. 2020, 25, 1075–1083. [Google Scholar] [CrossRef]
- Walker, D.; Creaco, E.; Vamvakeridou-Lyroudia, L.; Farmani, R.; Kapelan, Z.; Savić, D. Forecasting Domestic Water Consumption from Smart Meter Readings Using Statistical Methods and Artificial Neural Networks. Procedia Eng. 2015, 119, 1419–1428. [Google Scholar] [CrossRef] [Green Version]
- Petropoulos, F.; Spiliotis, E. The Wisdom of the Data: Getting the Most Out of Univariate Time Series Forecasting. Forecasting 2021, 3, 478–497. [Google Scholar] [CrossRef]
- de Souza Groppo, G.; Costa, M.A.; Libânio, M. Predicting water demand: A review of the methods employed and future possibilities. Water Supply 2019, 19, 2179–2198. [Google Scholar] [CrossRef]
- Boudhaouia, A.; Wira, P. Power and Water Consumption Monitoring with IoT Devices and Machine Learning Methods in a Smart Building; Presses Universitaires de Strasbourg: Strasbourg, France, 2019; Volume 346. [Google Scholar]
- Yang, L.; Yang, S.H. Domestic water consumption monitoring and behaviour intervention by employing the internet of things technologies. Procedia Comput. Sci. 2017, 111, 367–375. [Google Scholar] [CrossRef]
- Spiegel, J. Nouvelle Stratégie de Collecte de Données Pour les Compteurs d’eau Communicants. Ph.D. Thesis, Université de Haute Alsace, Mulhouse, France, 2019. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Rehfeld, K.; Marwan, N.; Heitzig, J.; Kurths, J. Comparison of correlation analysis techniques for irregularly sampled time series. Nonlinear Process. Geophys. 2011, 8, 389–404. [Google Scholar] [CrossRef] [Green Version]
- Boudhaouia, A.; Wira, P. Water Consumption Analysis for Real-Time Leakage Detection in the Context of a Smart Tertiary Building. In Proceedings of the 2018 International Conference on Applied Smart Systems (ICASS), Medea, Algeria, 24–25 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Boudhaouia, A.; Wira, P. Comparison of machine learning algorithms to predict daily water consumptions. In Proceedings of the 2021 International Conference on Design & Test of integrated micro & nano-Systems (DTS), Sfax, Tunisia, 7–10 June 2021; pp. 1–6. [Google Scholar]
- Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; Hussain, T.; Shad, M.Y.; Mohamd Shoukry, A.; Hussain Gani, S. Forecasting Drought Using Multilayer Perceptron Artificial Neural Network Model. Adv. Meteorol. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Candelieri, A.; Soldi, D.; Archetti, F. Short-term forecasting of hourly water consumption by using automatic metering readers data. Procedia Eng. 2015, 119, 844–853. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Liu, M.; Liu, D.; Sun, G.; Zhao, Y.; Wang, D.; Liu, F.; Fang, X.; He, Q.; Xu, D. Deep Learning Detection of Inaccurate Smart Electricity Meters: A Case Study. IEEE Ind. Electron. Mag. 2020, 14, 79–90. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Abadi, M.L.; Same, A.; Oukhellou, L.; Cheifetz, N.; Mandel, P.; Feliers, C.; Chesneau, O. Predictive Classification of Water Consumption Time Series Using Non-homogeneous Markov Models. In Proceedings of the IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 323–331. [Google Scholar] [CrossRef]
- Huntra, P.; Keener, T.C. Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014. ISPRS Int. J. Geo-Inf. 2017, 6, 249. [Google Scholar] [CrossRef] [Green Version]
- Alvisi, S.; Franchini, M.; Marinelli, A. A short-term, pattern-based model for water-demand forecasting. J. Hydroinformatics 2007, 9, 39–50. [Google Scholar] [CrossRef] [Green Version]
- de Souza Groppo, G.; Costa, M.A.; Libânio, M. Forecasting Water Demand in Residential, Commercial, and Industrial Zones in Bogotá, Colombia, Using Least-Squares Support Vector Machines. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Kenney, D.S.; Goemans, C.; Klein, R.; Lowrey, J.; Reidy, K. Residential Water Demand Management: Lessons from Aurora, Colorado. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 192–207. [Google Scholar] [CrossRef]
- Saigal, S.; Mehrotra, D. Performance comparison of time series data using predictive data mining techniques. Adv. Inf. Min. 2012, 4, 57–66. [Google Scholar]
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A. Benefits and challenges of using smart meters for advancing residential water demand modeling and management: A review. Environ. Model. Softw. 2015, 72, 198–214. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, J.; Hermann, G.; Wira, P. A Comparative Experimental Study of Compression Algorithms for Enhancing Energy Efficiency in Smart Meters. In Proceedings of the IEEE 16TH International Conference of Industrial Informatics (INDIN 2018), Porto, Portugal, 18–20 July 2018. [Google Scholar]
- Benkabou, S.E. Détection d’Anomalies dans les séries Temporelles: Application aux Masses de Données sur les Pneumatiques. Ph.D. Thesis, Université Claude Bernard, Lyon, France, 2018. [Google Scholar]
- Lee, J.; Kim, J.; Ko, W. Day-Ahead Electric Load Forecasting for the Residential Building with a Small-Size Dataset Based on a Self-Organizing Map and a Stacking Ensemble Learning Method. Appl. Sci. 2019, 9, 1231. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]

| LSTM | BPNN | |
|---|---|---|
| Hidden Layer number | 2 | 3 |
| Number of neurons | 100/100 | 200/100/100 |
| Activation function | relu/relu | relu/relu/relu |
| Train RMSE (l) | 0.19 | 3.54 |
| Test RMSE (l) | 6.05 | 20.19 |
| Total execution time (ms) | 19.81 | 24.05 |
| LSTM | BPNN | |
|---|---|---|
| Hidden Layer number | 2 | 1 |
| Number of neurons | 200/120 | 150 |
| Activation function | relu/relu | relu |
| Train RMSE ( ms) | 0.33 | 0.39 |
| Test RMSE ( ms) | 0.13 | 0.48 |
| Total execution time (s) | 37.73 | 24.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudhaouia, A.; Wira, P. A Real-Time Data Analysis Platform for Short-Term Water Consumption Forecasting with Machine Learning. Forecasting 2021, 3, 682-694. https://doi.org/10.3390/forecast3040042
Boudhaouia A, Wira P. A Real-Time Data Analysis Platform for Short-Term Water Consumption Forecasting with Machine Learning. Forecasting. 2021; 3(4):682-694. https://doi.org/10.3390/forecast3040042
Chicago/Turabian StyleBoudhaouia, Aida, and Patrice Wira. 2021. "A Real-Time Data Analysis Platform for Short-Term Water Consumption Forecasting with Machine Learning" Forecasting 3, no. 4: 682-694. https://doi.org/10.3390/forecast3040042
APA StyleBoudhaouia, A., & Wira, P. (2021). A Real-Time Data Analysis Platform for Short-Term Water Consumption Forecasting with Machine Learning. Forecasting, 3(4), 682-694. https://doi.org/10.3390/forecast3040042







