Abstract
In a context of growing uncertainty caused by the COVID-19 pandemic, the opinion of businesses and consumers about the expected development of the main variables that affect their activity becomes essential for economic forecasting. In this paper, we review the research carried out in this field, placing special emphasis on the recent lines of work focused on the exploitation of the predictive content of economic tendency surveys. The study concludes with an evaluation of the forecasting performance of quarterly unemployment expectations for the euro area, which are obtained by means of machine learning methods. The analysis reveals the potential of new analytical techniques for the analysis of business and consumer surveys for economic forecasting.
1. Introduction
The expectations of economic agents about the development of the main variables that affect their activity are key for economic forecasting. In this paper, we review the evolution of the research carried out in this field, focusing on those works centered in exploiting the informational content of economic tendency surveys (ETS) with forecasting purposes. In ETS, respondents are asked whether they expect a certain variable to rise, fall, or remain unchanged. There are many ETS. Some of the most well-known are collected by the University of Michigan, the Federal Reserve Bank of Philadelphia, the Organisation for Economic Co-operation and Development (OECD), and the European Commission (EC). Survey responses from ETS are commonly used to design composite sentiment indicators such as the Michigan Index of Consumer Confidence. In 1961, the EC launched the Joint Harmonised Programme of Business and Consumer Surveys (BCS) with the aim of unifying the survey methodologies in the member states, allowing comparability between countries. The EC constructs economic sentiment indicators as the arithmetic mean of a subset of predetermined survey expectations.
Data obtained from BCS have traditionally been used for forecasting purposes [1,2,3,4,5], mainly due to their forward-looking nature. BCS have also been used in testing different expectations formation schemes and other economic hypotheses, such as the Phillips curve or the rationality of agents’ expectations [6,7]. In recent years, the information coming from BCS has increasingly been used to proxy economic uncertainty [8,9,10]. Since uncertainty is not directly observable, one way to proxy it is through indicators of disagreement among survey respondents [11,12,13,14,15]. The analysis of economic uncertainty has gained renewed interest since the 2008 financial crisis, but the difficulty of measuring it has led researchers to design several strategies to proxy it. One way to estimate uncertainty is by using the realized volatility in equity markets [16,17]. Another alternative is based on the notion of econometric unpredictability, calculating the latter as the conditional volatility of the unpredictable components of a broad set of economic variables [18,19]. The ex-post nature of this approach has given rise to a third way of approximating economic uncertainty based on the generation of survey-derived measures of expectations dispersion, which are subjective in nature.
Disagreement metrics that are based on survey expectations have the advantage of being able to use forward-looking information coming from the questions about the expected future evolution of economic variables. While most studies rely on quantitative macroeconomic expectations made by professional forecasters [20,21,22], in this paper we will review some of the latest approaches devised to compute agents’ disagreement from qualitative survey responses on the expected direction of change.
However, given the qualitative nature of agents’ responses, survey expectations coming from BCS have usually been quantified. In this paper, we review the different quantification approaches proposed in the literature, which have advanced together with the development of new statistical techniques. In this sense, machine learning techniques offer new possibilities of conversion [23,24]. We review the latest applications in this field, and describe a new approach to obtain quantitative measures of agents’ expectations from qualitative survey data based on the application of genetic algorithms (GAs). The proposed approach, which can be regarded as a data-driven method for sentiment indicators construction, presents several advantages over previous methods. On the one hand, no assumptions are made regarding agents’ expectations. On the other hand, it not only provides direct estimates of the target variable but also easy-to-implement indicators that make exclusive use of survey information. This procedure allows capturing the potential non-linear relationships between survey variables and selecting the optimal lag structure for each variable entering the composite indicators. This feature offers an overview of the most relevant interactions between the variables, allowing for the identification of unknown patterns.
To assess the potential of the methodology in the exploitation of the information coming from ETS, we finally evaluate the performance of indicators of employment sentiment generated by means of genetic programming (GP). These evolved expressions combine consumer survey expectations to provide estimates of the unemployment rate. We design a nowcast experiment and compare the proposed sentiment indicators to those obtained by other quantification procedures used as a benchmark.
The remainder of the paper is organized as follows. The next section reviews the literature and describes the methods used in the literature to transform survey responses into quantitative estimates of economic aggregates and uncertainty. Section 3 presents the information contained in BCS and analyses the data used in this research. An application to nowcast unemployment rates in the euro area (EA) is provided in Section 4. Finally, conclusions are given in Section 5.
2. Literature Review
Survey expectations elicited from ETS have advantages over experimental expectations, as they are based on the knowledge of agents who operate in the market and provide detailed information about many economic variables. Additionally, above all, they are available ahead of the publication of official quantitative data. These characteristics make them particularly useful for prediction. Additionally, since BCS questionnaires are harmonized, survey results allow comparisons among different countries’ business cycles and have become an indispensable tool for monitoring the evolution of the economy.
Survey respondents are usually asked about subjective and also about objective variables and are faced with three response options: up, unchanged, and down at a given time period t. denotes the percentage of respondents reporting an increase, the no change %, and the decrease %. The most common way of presenting survey data is the balance statistic, , which is obtained as the subtraction between the two extreme categories:
Thus, the balance statistic can be regarded as a diffusion index. For a detailed analysis of the diffusion indexes, see [25]. In some surveys, such as the EC consumer survey, respondents are faced with three additional response categories; two at each end of the scale: a lot better/much higher/sharp increase, and a lot worse/much lower/sharp decrease. Additionally, they have a “don’t know” option (). As a result, measures the % of consumers reporting a sharp increase, a slight increase, no change, a slight fall, and a sharp fall. In the case of five reply options, the balance statistic is computed as:
As a result, one of the main features of expectations from ETS is that they are measured by means of a qualitative scale. While this makes these surveys easy to answer and to tabulate, over the years there have been numerous methods proposed in the literature to transform this information into quantitative estimates of the target variable [26,27]. This strand of the literature concerning the conversion of qualitative responses has evolved hand in hand with the development of econometric techniques. Next, we revise the evolution of the main quantification procedures proposed in the literature.
2.1. Quantification of Qualitative Survey Expectations
The balance statistic was proposed by [28,29], who defined it as a measure of the average changes expected in the quantitative variable of reference. Let be the actual average percentage change of variable , and the specific change for agent i at time t. By discriminating between agents according to whether they reported an increase or a decrease, and assuming that the expected changes (,) remain constant both over time and across respondents, the author formalized the relationship between actual changes in a variable and respondents’ expectations as , where is a mean zero disturbance. The sub index denotes the period in which the survey was responded, i.e., the period in which the expectation was formed; while the supra index denotes the period to which the expectation refers. Thus, by means of ordinary least squares, estimates of and can be obtained, and then used to generate one-period-ahead forecasts of in:
This framework was augmented by [30,31], allowing for an asymmetrical relationship between individual changes and the evolution of the quantitative variable of reference. By regressing actual values of the variable on respondents’ perceptions of the past (,), non-linear estimates of the parameters can be obtained and used in the following expression to generate forecasts of :
This approach to the quantification of expectations came to be known as the regression method. In the following years, this framework was expanded by [32], who made positive and negative individual changes dependent on past values of the quantitative variable of reference, and proposed a non-linear dynamic regression model to quantify survey responses.
A drawback of the regression approach to quantifying survey responses is that there is no empirical evidence that agents judge past values in the same way as when they formulate expectations about the future [26]. As a result, the regression approach is restricted to expectations of variables over which agents have direct control, be it prices or production. Additionally, the implementation of this method requires the availability of individual data. For an appraisal of individual firm data on expectations, see [33].
Alternatively, in [34], the author developed a theoretical framework to generate quantitative estimates from the balance statistic. Based on the assumption that respondents report a variable to go up (or down) if the mean of their subjective probability distribution lies above (or below) a certain level, the author defined the indifference threshold, also known as the difference limen. Let denote the unobservable expectation that agent i has over the change of variable , the indifference interval can be defined as , where and are the lower and upper limits of the indifference threshold for agent i at time t. Assuming that response bounds are symmetric and fixed both across respondents and over time (, ), and that agents base their responses according to an independent subjective probability distribution that has the same form across respondents, an aggregate density function can be derived. Thus, and could be regarded as consistent estimates of population proportions. This framework is summarized in Figure 1, where the individual density functions are assumed to be normally distributed.
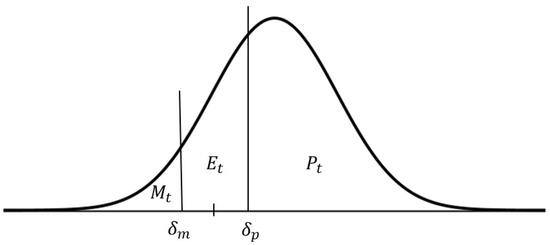
Figure 1.
Density function of agents’ average aggregate expectations.
This theoretical framework was further developed by [35], configuring what came to be known as the probability approach or the Carlson–Parkin method. The main notion behind this quantification procedure lies in the fact that estimates of are conditional on a particular value for the imperceptibility parameter () and a specific form for the aggregate density function. The authors assumed that the individual density functions were normally distributed and estimated by assuming that over the in-sample period, is an unbiased estimate of . Consequently, the role of becomes scaling aggregate expectations , such that the average value of equals . Therefore, qualitative responses can be transformed into quantitative estimates as follows:
where and respectively correspond to the abscissa of and , and the imperceptibility parameter is computed as:
There is no consensus on the type of probability distribution aggregate average expectations come from. Researchers have used alternative distributions [36,37,38,39]. While the normality hypothesis was rejected at first [40,41], later evidence was found that normal distributions provided expectations that were as accurate as those produced by other non-normal distributions [42,43,44,45]. Recently, using data from consumers’ price expectations in the EA [46] proved that the distribution choice provided only minor improvements in forecast accuracy, while other assumptions such as unbiased expectations and the number of survey response categories played a pivotal role.
Another strand of the literature has focused on refining the probability approach by relaxing the assumptions of symmetry and constancy of the indifference bounds, which is . Different alternatives have been proposed in the literature in order to introduce dynamic imperceptibility parameters in the probability framework for quantification. While some authors chose to make the threshold parameters depend on time-varying quantitative variables [47,48,49], others imposed the unbiasedness condition over predefined subperiods [50]. By introducing the assumption that the imperceptibility parameters were subject to both permanent and temporary shocks, and using the Cooley–Prescott model, the probabilistic approach was allowed to include asymmetric and time-varying indifference thresholds [51].
More recently, this framework was further developed by using a state-space representation that allowed for asymmetric and dynamic response thresholds generated by a first-order Markov process [52,53]:
where and are autoregressive parameters; and are two independent and normally distributed disturbances with mean zero and variances and ; and and are respectively derived from the Carlson–Parkin framework depicted in Figure 1 as: and . Assuming null initial conditions, the authors used the Kalman filter for parameter estimation.
Picking up the notion that the indifference parameters may be dependent on past values of an economic variable, in [54] a smooth transition model was used to allow for time variation in the scaling parameter. Similarly, based on the results obtained by [55], where it is shown that inflation expectations depend on agents’ previous experience, in [56], the author expanded the Carlson–Parkin framework by determining an experience horizon and assuming that agents’ expectations are distributed in the same way as the actual variable was distributed over the period defined by the experience horizon.
There is inconclusive evidence regarding the variation of the indifference thresholds across agents. Since this hypothesis can only be tested by means of the analysis of individual expectations or by generating experimental expectations via Monte Carlo simulations, further improvements of quantification procedures have mostly been developed at the micro level, comparing the individual responses with firm-by-firm realizations [57,58,59,60]. A procedure to quantify individual categorical expectations was developed based on the assumption that responses were triggered by a latent continuous random variable [57]; the authors found evidence against constant thresholds in time. Another variant of the Carlson–Parkin method developed at the micro level, with asymmetric and time invariant thresholds, pivoted around the “conditional absolute null” property, which can be regarded as an assumption based on the empirical finding that the median of realized quantitative values corresponding to “no change” is zero [58]. This approach allowed for solving the zero-response problem that occurs when all respondents fall into one of the extreme responses (an increase or a decrease).
Using a matched sample of qualitative and quantitative individual stock market forecasts, in [59], the authors corroborated the importance of introducing asymmetric and dynamic indifference parameters, but found that individual heterogeneity across respondents did not play a major role in forecast accuracy. Based on a matched sample of households, and using a hierarchical ordered probit model, in [60], the authors found strong evidence against the threshold constancy, symmetry, homogeneity, and overall unbiasedness assumptions of the probability method, showing that when the unbiasedness assumption is replaced by a time-varying calibration, the resulting quantified series is found to better track the quantitative benchmark.
In parallel with the analysis at the micro level, the methodology has also been developed by means of experimental expectations. As with quantified survey expectations, simulated expectations have usually been used to test economic hypotheses, such as rational expectations [61], and to assess the performance of the different quantification methods. In this regard, some authors have focused on the estimation of the measurement error introduced by the probabilistic method [62,63]. In [62], the author proposed a refinement of the Carlson–Parkin method. In [64], computer-generated expectations were computed to assess the forecasting performance of different quantification methods; the author also presented a variation of the balance statistic that took into account the proportion of respondents reporting that the variable remains unchanged.
By means of a simulation experiment, in [65], the author additionally showed that the omission of neutral responses resulted in an overestimation of the level of individual heterogeneity across respondents. Dispersion-based metrics of disagreement among respondents have been used in recent years to proxy economic uncertainty. In this sense, in [66], the authors generalized the Carlson–Parkin procedure to generate cross-sectional and time-varying proxies of the variance. Using data from the CESifo Business Climate Survey for Germany and from the Philadelphia Fed’s Business Outlook Survey for the US, in [11], the authors proposed the following measure of disagreement based on the dispersion of respondents’ expectations to proxy economic uncertainty:
This metric is the square root of the balance statistic. Since then, several measures of disagreement among survey expectations have been increasingly used to proxy economic uncertainty [11,12,13,14]. The omission of E in the calculation of the balance statistic, and consequently in (9), implies a loss of the information concerning the degree of uncertainty of the respondents. In order to overcome this limitation, in [65], the authors presented a methodological framework to derive a geometric measure of disagreement that explicitly incorporated the share of neutral responses. This metric can be interpreted as the percentage of discrepancy among responses. The original framework uses a positional approach to determine the likelihood of disagreement among election outcomes [67]. Using agents’ expectations from the CESifo World Economic Survey (WES) about the country’s situation regarding the overall economy, the authors found that the proposed measure (10) coevolved with the standard deviation of the balance (9).
This metric of disagreement for BCS can be derived as follows. Assuming that the number of answering categories is three—rise (P), fall (M), and no change (E)—and given that that the sum of the shares of responses adds to a one, a potential representation of the vector of aggregated shares of responses is as a point on a simplex that encompasses all possible combinations of responses (Figure 2). In the equilateral triangle, the vector of responses, denoted as blue point, corresponds to the unique convex combination of three reply options for each period in time.
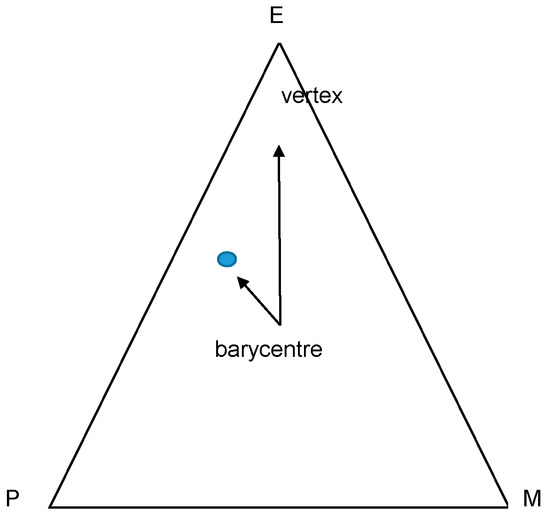
Figure 2.
Simplex for three reply options (P, E, M).
Each vertex in Figure 2 corresponds to a point of maximum consensus; conversely, the center of the simplex corresponds to the point of maximum disagreement, indicating that the answers are distributed equally among all response categories for a given time period. In this framework, in which all vertices are at the same distance to the center, the proportion of consensus is given by the relative weight of the distance of the point to the barycenter, which can be formalized as:
This metric is bounded between zero and one and conveys a geometric interpretation. Therefore, the proportion of (geometric) disagreement can be computed as .
This framework has been expanded for a larger quantity of reply options [68,69]. If the number of answering categories is noted as N, and denotes the aggregate percentage of responses in category i at time t, where , the level of disagreement could be computed as:
As in (10), this metric is bounded between zero and one, and can be regarded as a metric of qualitative variation that gives the proportion of disagreement among respondents. In [68], the author designed a simulation experiment and sampled the distribution of D for and for , finding that for three answering categories, the statistic encompassed a wider range and its distribution of scores was more uniform. In references [46,56], the authors showed that the number of response categories is crucial to the forecast accuracy of quantified expectations.
There seems to be no consensus in the literature regarding the information content of disagreement among agents to refine predictions. On the one hand, in [70], the authors did not find evidence that uncertainty helped in refining forecasts of GDP and inflation in the EA. On the other hand, in references [71,72], the authors found that including uncertainty indicators as predictors improved accuracy of forecasts of economic activity in Croatia, the UK, the US, and the EA. In [73], the authors found that macroeconomic uncertainty contained useful information to predict employment, especially in the construction and manufacturing industries. In [74], the author applied expression (10) in order to compute an indicator of employment, which was included as a predictor in time-series models, obtaining better forecasts of unemployment rates than with ARIMA models.
Similarly, with the aim of assessing the predictive power of disagreement, in [12], a vector autoregressive (VAR) framework was used to generate out-of-sample recursive forecasts for output growth, inflation, and unemployment rates for different forecast horizons. The author obtained more accurate predictions of GDP with disagreement in business expectations (about manufacturing production), and of unemployment with disagreement among consumers’ expectations (about unemployment). It was also found that disagreement in business surveys Granger-caused macroeconomic aggregates in most countries, while the opposite happened for disagreement in consumer surveys.
2.2. Machine Learning Techniques for the Conversion of Survey Data on the Expected Direction of Change
In this subsection, we describe a new approach to obtain quantitative measures of agents’ expectations from qualitative survey data based on the application of GAs. Given the data-driven nature of this methodology, no assumptions are made regarding agents’ expectations.
This empirical modeling approach is based on the GP estimation of a symbolic regression (SR) [75]. GP is a soft-computing search procedure based on evolutionary computation. As such, it is founded on the implementation of algorithms that apply Darwinian principles of the theory of natural selection to automated problem solving. See [76] for a review of the literature on the application of evolutionary computation to economic modeling and forecasting.
This optimization algorithm represents programs in tree structures that learn and adapt by changing their size, shape, and composition of the models. Unlike conventional regression analysis, which is based on a certain ex-ante model specification, SR can be regarded as a free-form regression approach in which the GP algorithm searches for relationships between variables and evolves the functions until it reaches a solution that can be described by the algebraic expression that best fits the data.
This simultaneous procedure offers, on the one hand, an overview of the most relevant interactions between the variables analyzed and the type of relationship between them. On the other, it helps to identify a priori unknown interactions. The implementation of the process starts from the generation of a random population of functions, expressed as programs. From this initial population, the algorithm makes a first selection of the fittest. From this point on, successive simulations are concatenated that generate new, more suitable generations. In order to guarantee diversity in the population, genetic operators are applied in each simulation: reproduction, crossing, and mutation. Reproduction aims to copy the function, while crossover and mutation consist of the exchange or substitution of parts of the function.
By applying these operations recursively, similar to the evolution of species, the fitness of the members increases with each generation. In order to assess the degree of fitness, a loss function is used. The process is programmed to stop, either when an individual program reaches a predefined fitness level, or when a predetermined number of generations is reached. The end result would be the best individual function found throughout the process. See [24] for a detailed description on the implementation of GP, and [77,78] for a detailed review of the main issues of GP.
GP was first proposed by [75] to evaluate the non-linear interactions between price level, GNP, money supply, and the velocity of money. Given the versatility of the procedure, and its suitability to find unknown patterns in large databases, GP attracts more and more researchers from different areas with the aim of carrying out complex modeling tasks. It has only been recently that it has begun to be applied in the quantification of the qualitative information contained in the ETS, with the aim of estimating economic growth [79,80,81,82] and also the evolution of unemployment [83].
In [80,81,82], the authors used GP to derive mathematical functional forms that combined survey indicators from the CESifo WES to approximate year-on-year growth rates of quarterly GDP. In the WES, a panel of experts are asked to assess their country’s general situation at present and expectations regarding the overall economy, foreign trade, etc. The authors use the generated proxies of economic growth as building blocks in a regularized regression to estimate the evolution of GDP. In [79], the authors used survey expectations from the WES to generate two evolved indicators: a perceptions index, using agents’ assessments about the present, and an expectations index with their expectations about the future. Recently, in [24], the authors used the balances of the survey variables contained in Table 1 for thirteen European countries and the EA to generate country-specific business confidence indicators via GP to nowcast and to forecast quarter-on-quarter growth rates of GDP. They also replicated the analysis with the information contained in Table 2 to generate empirical consumer confidence indicators. When assessing the out-of-sample forecasting performance of recursively evolved sentiment indicators, the authors obtained superior results than with time-series models. In Section 4, we assess the performance of quarterly unemployment expectations obtained by applying evolved expressions obtained through GP, analyzing the ability of the generated series of expectations to nowcast unemployment rates in the midst of the pandemic.

Table 1.
Survey indicators—industry survey.

Table 2.
Survey indicators—consumer survey.
3. Data
This section briefly described the data used in the empirical analysis. BCS are addressed to households and representatives of the manufacturing industry, services, retail trade, and construction. Currently, the harmonized questionnaires are conducted in 33 countries. Results of the surveys are published at the end of each month and are freely available at the website of the EC [84]. In the industry survey, manufacturers are asked about firm-specific factors such as expected production and selling prices, while consumers are asked about subjective and also about objective variables such as the country’s general economic situation. In Table 1 and Table 2, we respectively present the questions contained in the questionnaires of the industry and the consumer survey.
The different strata regarding income, education, age, and gender are displayed in Table 3.

Table 3.
Sociodemographic groups—survey subcategories.
In Table 4 and Table 5 we present a descriptive analysis of survey results for the sample period (2005:Q1–2020:Q2). Statistics were computed for each stratum according to income, education, age, and gender. Regarding income, group the 4th quartile (RE4) presents the highest mean values for almost all variables; while RE1, the lowest. Similarly, both for men and for higher educational levels and lower age ranges, we obtained higher average values in most of the variables. We can observe that variables X3, X5, and X7 were the ones that show higher dispersion. These results are indicative of the existence of substantial differences across the different sociodemographic groups. In the next section, we assessed the performance of quarterly unemployment expectations quantified by means of the employment sentiment indicators obtained through GP. We analyzed the ability of the generated series of expectations to nowcast unemployment rates for each of the sociodemographic groups.

Table 4.
Summary statistics—mean survey results for subcategories of consumers (2005:Q1–2020:Q2).

Table 5.
Summary statistics—standard deviation of survey results for subcategories of consumers (2005:Q1–2020:Q2).
4. Empirical Analysis
This section briefly analyzed the forecasting performance of quarterly expectations of unemployment for the EA obtained via GP. On the one hand, we made use of qualitative survey data. Specifically, we employed the seasonally adjusted balances from the consumer survey conducted by the EC [84]. We used all monthly and quarterly questions in Table 2 for all the strata listed in Table 3. Since variables X13, X14, and X15 were published in a quarterly basis, we averaged the balances in each quarter. On the other hand, we also employed quantitative information as a target variable. We used the seasonally adjusted unemployment rates provided by the OECD, which are also freely available [85].
Unemployment expectations are generated by means of a set of employment sentiment indicators, which in turn are derived through a set of GP experiments during the in-sample period (2005.Q1 to 2015.Q2) [86]. See Table A1 in Appendix A for the conversion formulae specific to each stratum. The main aim was to generate expressions that combined the balances of each survey question in order to provide quantitative estimations of expected unemployment rates for different sociodemographic groups. Given the current context, marked by high uncertainty in the labor market due to a crisis caused by the COVID-19 pandemic, we evaluate to what extent the GP-generated indicators are able to capture the evolution of unemployment in the EA during the last four years and a half (2016.Q1 to 2020.Q2), which were used as the out-of-sample period.
The procedure starts with a SR model that links the unemployment rate in the EA to the fifteen survey variables and their corresponding lags:
where are the different balances from the consumer survey and is a scalar referring to the quarterly rate of unemployment in the EA at time t. The experiment was designed so that the algorithm automatically selected the optimal lag structure, limiting the maximum number of lags to four quarters. For the sake of simplicity and replicability, the integration schemes were restricted to the main four mathematical operations.
GP was used to estimate the model, searching the space of mathematical expressions that best track the evolution of the unemployment. Expression (12) was evolved through 100 generations in order to derive a formal expression that combined survey variables to yield an estimation of the expected unemployment rate:
The same procedure was independently repeated for each consumer group during the in-sample period. In Figure 3, we compared the evolution of the unemployment rate in the EA together with that of the unemployment expectations obtained with the evolved expression (13). See Figure A1 in Appendix A for a graphical analysis for each consumer group.
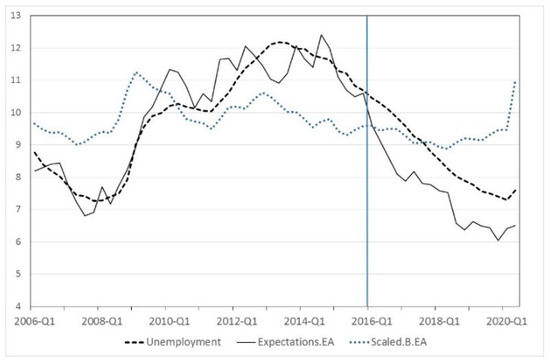
Figure 3.
Evolution of unemployment expectations in the euro area (EA).
Figure 3 also includes the evolution of the scaled balance of question X7 (Scaled.B.EA), which is the survey question regarding consumers’ unemployment expectations. The balance is scaled by regressing unemployment rates on X7 during the in-sample subperiod. This procedure was proposed by [29], and can be regarded as a specific case of the regression method for quantifying aggregate survey responses.
As it can be seen in Figure 3, in spite of the fact that the scaled balance contains useful leading information about the evolution of the unemployment rate, it does not seem a good indicator for point forecasts. The obtained unemployment expectations provide a better fit in terms of capturing the cyclical properties of the actual unemployment rate, and they are much more responsive to recessionary developments in 2008 and 2009. Consequently, we used an additional method as a benchmark. Some authors have used dynamic-factor models [87] and sparse partial least squares [88] with similar purposes. In our case, due to the lack of data availability, and since our main aim is to obtain sentiment indicators that allow transforming qualitative survey data into estimates of the unemployment rate, we used the least absolute shrinkage and selection operator (LASSO). As this procedure simultaneously performs variable selection and regularization, it is a directly comparable technique to the proposed methodology. Its features allow enhancing the prediction accuracy, the interpretability of the results, and obtaining sentiment indicators, which are directly implementable. See [89] for a detailed description of the technique.
In Figure 4, we present a bar chart, which shows the relative frequency with which each survey variable appears in the obtained expressions, both by means of GP and LASSO. We can observe that in both cases, variable X9 (“major purchases over next 12 months”) and variable X10 (“savings at present”) are the most frequent variables selected by the GA and the LASSO. To a lesser extent, quarterly variable X15 (“expected home improvements”) was also frequently selected. This result hints at the predictive potential of these three survey indicators. Notwithstanding, in spite of their leading properties, all three variables have always been omitted by the EC in the construction of the official consumer confidence indicators.
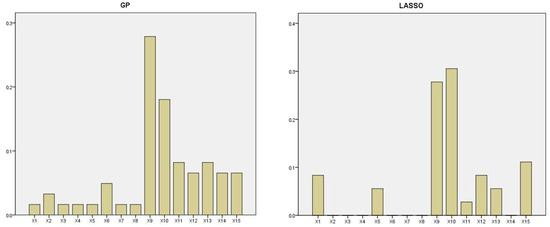
Figure 4.
Bar chart with relative frequency of variable selection—genetic programming (GP) vs. the least absolute shrinkage and selection operator (LASSO).
To evaluate the performance of the evolved expressions, we assess the out-of-sample accuracy in a nowcasting experiment. The estimations of the current unemployment rate are done at the end of each quarter, once all survey information is published. Providing that official unemployment data are not available until some weeks later, this experiment can be regarded as a nowcasting exercise. Making exclusive use of the latest survey data published by the EC, the indicators provide the estimation of unemployment of each consumer group before the official rates are released. For further discussion on nowcasting, see [90,91] and the references cited therein.
We computed the mean absolute forecast error (MAFE) and the root mean squared forecast error (RMSFE) for the out-of-sample period:
where refers to the forecast error at time t. As a rise of unemployment is very different from a reduction of it, we additionally computed a directional accuracy (DA) measure that gives the proportion of out-of-sample periods in which the realized and the predicted direction coincides. See [92] for a detailed evaluation of directional forecasts. The results of Figure 3 are further confirmed in Table 6, where we compare nowcasts of the unemployment rate generated with expression (13) to those obtained with LASSO and with the scaled balance of variable X7 for each group.

Table 6.
Out-of-sample accuracy (2016.Q1–2020.Q2)—unemployment rate nowcasts EA.
Table 6 shows the results of the different accuracy measures for the expectations of unemployment obtained with the different procedures. The results highlight that the unemployment nowcasts obtained with expression (13) outperform the rest of the methods. For each sociodemographic group, the lowest forecast errors are respectively obtained for female respondents (FEM), for consumers between 30 and 49 years (AG2), with secondary education (ED2) and within the first income quartile (RE1). Behavioral economics offers a plausible explanation for this result. In [93], the authors showed that consumer groups with the highest odds for negative outcomes on the job market perceived and processed economic information more intensively than the rest. This phenomenon is known as the “availability heuristic”. In our case, it has resulted in more accurate unemployment estimations for those strata; the only exception to this pattern being income, where the group with higher rents showed more accurate nowcasts of the unemployment rate.
The obtained results reveal the potential of the proposed procedure for the conversion of survey balances into quantitative estimates of the target variable. This methodology also provides researchers with ad-hoc expressions that can be regarded as a data-driven sentiment indicators that can be directly used to nowcast economic variables. Since survey data are published ahead of official quantitative data, especially in the case of GDP, this approach represents a very easy-to-implement forecasting tool.
Our results connect with previous research by [87,94,95,96]. In [94], the authors used GP to derive conversion expressions at a regional level, finding that the forecasting performance of the survey-based indicators improved during periods of higher growth. Similarly, in [95], the authors implemented GP to develop a set of empirical models to forecast GDP, investment, and loan rates in Poland and found that the proposed approach outperformed artificial neural network models. The ability of GAs for economic forecasting was further analyzed in [87], where the authors used it to predict quarterly GDP growth and monthly inflation. In a recent study [96], the authors used GP for constructing country-specific sentiment indicators to quantify reported directional responses and to track the evolution of year-on-year growth rates of GDP in the Baltic republics and the EU.
The evaluation of the predictive capacity of survey expectations carried out in this study also addresses the question about the information content of business and consumer expectations, and whether more sophisticated aggregation schemes based on machine learning can provide more accurate forecasts of economic variables. Our findings are in line with previous research by [1,97,98,99,100,101,102,103,104]. Recently, in [4], the authors used survey data from South Africa to investigate the accuracy of directional and point forecasts of investment and found that for shorter horizons, survey forecasts enhanced by time-series data significantly improved point forecasting accuracy. In [102], it was shown that accounting for consumer and business sentiments led to improved forecast accuracy of consumption in Indonesia. Similarly, in [104], the authors found that household expectations, quantified by means of a hierarchical ordered probit model, proved useful to track the actual inflation rate in India. All this evidence points to the importance of ETS to complement and refine economic forecasts, especially in a context of growing uncertainty such as the one we are in due to the unexpected impact of the pandemic.
5. Discussion and Conclusions
In this study, we reviewed the literature about the exploitation of the informational content of business and consumer surveys for forecasting purposes. We first reviewed the different quantification methods used for converting the qualitative responses on the expected direction of change into quantitative estimates of agents’ expectations. Second, we described the most recent advances in the field, based on the application of machine learning techniques. We also presented some of the latest measures of disagreement that capture cross-sectional heterogeneity of agents’ survey expectations, which are used to proxy economic uncertainty and to refine the predictions of macroeconomic variables.
In the second part, we assessed the performance of unemployment expectations obtained by means of genetic programming. This empirical modeling procedure allows generating sentiment indicators that capture the non-linear relationships between variables. The resulting expressions can be regarded as conversion formulas of survey balances into expectations of unemployment. This approach presents several advantages over previous quantification methods. First, it is not based on any a priori assumption about agents’ expectations. Second, the resulting expressions provide direct quantitative estimates of the target variable, as opposed to most sentiment indicators. Finally, they are easily implementable, as they make exclusive use of the latest published survey data.
As the exercise was replicated for different sociodemographic groups in order to compare the expectations of unemployment between them, we analyzed the relative frequency with which each survey variable appears in the obtained expressions for each stratum. We found that expected major purchases and home improvements, and current savings, were the variables most frequently selected by the algorithm. We compared the results with those obtained by a shrinkage method, obtaining very similar results. This finding shows the leading properties of these three survey variables.
In addition, we performed an out-of-sample nowcasting exercise in which quarterly unemployment expectations obtained from consumer surveys were iteratively generated. The obtained quantified expectations for each sociodemographic group were then used to track the evolution of the unemployment rate. When evaluating the accuracy of consumers’ unemployment expectations obtained with the evolved expressions, we found that they outperformed those obtained with two alternative quantification procedures used as a benchmark. In addition, the presented approach allows capturing the potential non-linear relationships and selecting the optimal lag structure for each survey variable entering the sentiment indicators of unemployment.
We want to note that in spite of the ability of the obtained evolved expectations to capture unemployment dynamics, it has to be taken into account that the applied quantification approach is a strictly data-driven method, and therefore the derived sentiment indicators lack any theoretical background. Another limitation of the proposed quantification procedure is that, as opposed to those based on standard regression, the significance of the obtained parameters cannot be tested. The study has focused on economic tendency surveys, omitting most of the research done with other surveys by professional forecasters, in which quantitative expectations are directly elicited. Other aspects left for further research are the implementation of alternative dimensionality-reduction techniques such as dynamic-factor models and sparse partial least squares, and the extension of the analysis to economic tendency surveys in the United States and other countries outside Europe.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: European Commission. Available online: https://ec.europa.eu/info/business-economy-euro/indicators-statistics/economic-databases/business-and-consumer-surveys_en (accessed on 5 January 2021); Organisation for Economic Co-operation and Development. Available online: https://data.oecd.org/unemp/unemployment-rate.htm (accessed on 5 January 2021).
Acknowledgments
I want to thank the Editors and three anonymous reviewers for their useful comments and suggestions.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
In this Appendix section, we included the evolved expressions obtained for the conversion of the balances corresponding to the different consumer groups into estimates of the unemployment rate. See [86] for a detailed analysis. In Figure A1 we graphically compared the evolution of the unemployment rate in the EA to that expected by each consumer group, which is obtained through the expressions contained in Table A1.

Table A1.
Evolved indicators of unemployment for each sociodemographic group.
Table A1.
Evolved indicators of unemployment for each sociodemographic group.
| Group | Expression |
|---|---|
| RE1 | |
| RE2 | |
| RE3 | |
| RE4 | |
| AG1 | |
| AG2 | |
| AG3 | |
| AG4 | |
| ED1 | |
| ED2 | |
| ED3 | |
| MAL | |
| FEM |
See Table 3 for the codification of the consumer survey subcategories.
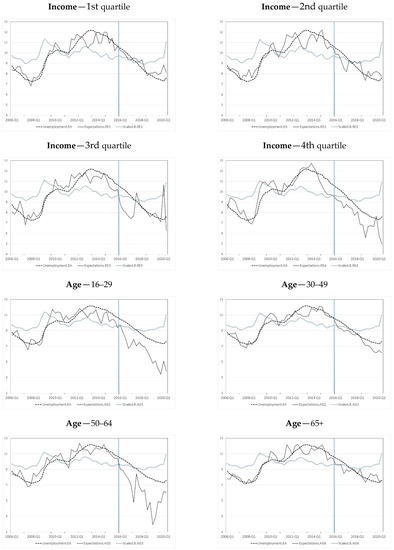

Figure A1.
Evolution of unemployment expectations for each consumer group. Notes: The black line represents the evolution of the unemployment expectations for each sociodemographic group of consumers, the dashed black line the evolution of the unemployment rate, and the grey dotted line the evolution of the scaled balance of survey question X7 for each group. The vertical line in 2016.Q1 marks the beginning of the out-of-sample period.
In Figure A1 we graphically compared the evolution of the expected unemployment rate for each consumer group up until the second quarter of 2020. We can observe that the out-of-sample performance of the evolved indicators, from 2016.Q1 on, substantially varies across the different groups of consumers.
References
- Altug, S.; Çakmaklı, C. Forecasting inflation using survey expectations and target inflation: Evidence for Brazil and Turkey. Int. J. Forecast. 2016, 32, 138–153. [Google Scholar] [CrossRef]
- Bruestle, S.; Crain, W.M. A mean-variance approach to forecasting with the consumer confidence index. Appl. Econ. 2015, 47, 2430–2444. [Google Scholar] [CrossRef]
- Claveria, O.; Pons, E.; Suriñach, J. Las encuestas de opinión empresarial como instrumento de control y predicción de los precios industriales. Cuad. Aragoneses Econ. 2003, 13, 515–530. Available online: https://dialnet.unirioja.es/ejemplar/83835 (accessed on 14 January 2021).
- Driver, C.; Meade, N. Enhancing survey-based investment forecasts. J. Forecast. 2018, 38, 236–255. [Google Scholar] [CrossRef]
- Kaufmann, D.; Scheufele, R. Business tendency surveys and macroeconomic fluctuations. Int. J. Forecast. 2017, 33, 878–893. [Google Scholar] [CrossRef]
- Binder, C.C. Whose expectations augment the Phillips curve? Econ. Lett. 2015, 136, 35–38. [Google Scholar] [CrossRef]
- Bovi, M. Are the representative agent’s beliefs based on efficient econometric models? J. Econ. Dyn. Control. 2013, 37, 633–648. [Google Scholar] [CrossRef]
- Claveria, O. On the aggregation of survey-based economic uncertainty indicators between different agents and across variables. J. Bus. Cycle Res. 2020. [Google Scholar] [CrossRef]
- Henzel, S.R.; Rengel, M. Dimensions of macroeconomic uncertainty: A common factor analysis. Econ. Inq. 2016, 55, 843–877. [Google Scholar] [CrossRef]
- Meinen, P.; Roehe, O. On measuring uncertainty and its impact on investment: Cross-country evidence from the euro area. Eur. Econ. Rev. 2017, 92, 161–179. [Google Scholar] [CrossRef]
- Bachmann, R.; Elstner, S.; Sims, E.R. Uncertainty and economic activity: Evidence from business survey data. Am. Econ. J. Macroecon. 2013, 5, 217–249. [Google Scholar] [CrossRef]
- Claveria, O. Uncertainty indicators based on expectations of business and consumer surveys. Empirica 2020, 1–23. [Google Scholar] [CrossRef]
- Girardi, B.A.; Reuter, A. New uncertainty measures for the euro area using survey data. Oxf. Econ. Pap. 2016, 69, 278–300. [Google Scholar] [CrossRef]
- Mokinski, F.; Sheng, X.S.; Yang, J. Measuring disagreement in qualitative expectations. J. Forecast. 2015, 34, 405–426. [Google Scholar] [CrossRef]
- Lahiri, K.; Sheng, X. Measuring forecast uncertainty by disagreement: The missing link. J. Appl. Econ. 2010, 25, 514–538. [Google Scholar] [CrossRef]
- Binding, G.; DiBiasi, A. Exchange rate uncertainty and firm investment plans evidence from Swiss survey data. J. Macroecon. 2017, 51, 1–27. [Google Scholar] [CrossRef]
- Bekaert, G.; Hoerova, M.; Duca, M.L. Risk, uncertainty and monetary policy. J. Monet. Econ. 2013, 60, 771–788. [Google Scholar] [CrossRef]
- Chuliá, H.; Guillén, M.; Uribe, J. Measuring uncertainty in the stock market. Int. Rev. Econ. Financ. 2017, 48, 18–33. [Google Scholar] [CrossRef]
- Jurado, K.; Ludvigson, S.C.; Ng, S. Measuring uncertainty. Am. Econ. Rev. 2015, 105, 1177–1216. [Google Scholar] [CrossRef]
- Clements, M.P.; Galvão, A.B. Model and survey estimates of the term structure of US macroeconomic uncertainty. Int. J. Forecast. 2017, 33, 591–604. [Google Scholar] [CrossRef]
- Dovern, J. A multivariate analysis of forecast disagreement: Confronting models of disagreement with survey data. Eur. Econ. Rev. 2015, 80, 16–35. [Google Scholar] [CrossRef]
- Krueger, F.; Nolte, I. Disagreement versus uncertainty: Evidence from distribution forecasts. J. Bank. Financ. 2016, 72, S172–S186. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. A new approach for the quantification of qualitative measures of economic expectations. Qual. Quant. 2016, 51, 2685–2706. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Economic forecasting with evolved confidence indicators. Econ. Model. 2020, 93, 576–585. [Google Scholar] [CrossRef]
- Pinto, S.; Sarte, P.D.; Sharp, R. The information content and statistical properties of diffusion indexes. Int. J. Cent. Bank. 2020, 47–99. Available online: https://www.ijcb.org/journal/ijcb20q3a2.htm (accessed on 8 December 2020).
- Nardo, M. The quantification of qualitative survey data: A critical assessment. J. Econ. Surv. 2003, 17, 645–668. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Weale, M. Survey expectations. In Handbook of Economic Forecasting; Elliott, G., Granger, C.W.J., Timmermann, A., Eds.; Elsevier North-Holland: Amsterdam, The Netherlands, 2006; Volume 1, pp. 715–776. ISBN 978-0-444-51395-3. [Google Scholar]
- Anderson, O. Konjunkturtest und statistik. Allg. Stat. Arch. 1951, 35, 209–220. [Google Scholar]
- Anderson, O. The business test of the IFO-institute for economic research, Munich, and its theoretical model. Rev. l’Institut Int. Stat./Rev. Int. Stat. Inst. 1952, 20, 1. [Google Scholar] [CrossRef]
- Pesaran, M.H. Expectation formation and macroeconomic modelling. In Contemporary Macroeconomic Modelling; Malgrange, P., Muet, P.A., Eds.; Basil Blackwell: Oxford, UK, 1984; pp. 27–55. ISBN 978-0-631-13471-8. [Google Scholar]
- Pesaran, M.H. Formation of inflation expectations in British manufacturing industries. Econ. J. 1985, 95, 948. [Google Scholar] [CrossRef]
- Smith, J.; McAleer, M. Alternative procedures for converting qualitative response data to quantitative expectations: An application to Australian manufacturing. J. Appl. Econ. 1995, 10, 165–185. [Google Scholar] [CrossRef]
- Zimmermann, K.F. Analysis of business surveys. In Handbook of Applied Econometrics Volume II: Microeconomics; Wiley: Oxford, UK, 1999; pp. 407–411. [Google Scholar]
- Theil, H. Recent experiences with the Munich business test: An expository article. Monet. Policy 1992, 23, 303–313. [Google Scholar] [CrossRef]
- Carlson, J.A.; Parkin, M. Inflation expectations. Economica 1975, 42, 123. [Google Scholar] [CrossRef]
- Foster, J.; Gregory, M. Inflation expectations: The use of qualitative survey data. Appl. Econ. 1977, 9, 319–330. [Google Scholar] [CrossRef]
- Batchelor, R. Aggregate expectations under the stable laws. J. Econ. 1981, 16, 199–210. [Google Scholar] [CrossRef]
- Fishe, R.P.; Lahiri, K. On the estimation of inflationary expectations from qualitative responses. J. Econ. 1981, 16, 89–102. [Google Scholar] [CrossRef]
- Visco, I. Price Expectations in Rising Inflation; North-Holland: Amsterdam, The Netherlands, 1984; ISBN 978-0-444-86836-7. [Google Scholar]
- Batchelor, R.A.; Dua, P. The accuracy and rationality of UK inflation expectations: Some quantitative evidence. Appl. Econ. 1987, 19, 819–828. [Google Scholar] [CrossRef]
- Lahiri, K.; Teigland, C. On the normality of probability distributions of inflation and GNP forecasts. Int. J. Forecast. 1987, 3, 269–279. [Google Scholar] [CrossRef]
- Balcombe, K. The Carlson-Parkin method applied to NZ price expectations using QSBO survey data. Econ. Lett. 1996, 51, 51–57. [Google Scholar] [CrossRef]
- Berk, J.M. Measuring inflation expectations: A survey data approach. Appl. Econ. 1999, 31, 1467–1480. [Google Scholar] [CrossRef]
- Dasgupta, S.; Lahiri, K. A comparative study of alternative methods of quantifying qualitative survey responses using NAMP data. J. Bus. Econ. Stat. 1992, 10, 391–400. [Google Scholar] [CrossRef]
- Mitchell, J. The use of non-normal distributions in quantifying qualitative survey data on expectations. Econ. Lett. 2002, 76, 101–107. [Google Scholar] [CrossRef]
- Lolić, I.; Sorić, P. A critical re-examination of the Carlson–Parkin method. Appl. Econ. Lett. 2018, 25, 1360–1363. [Google Scholar] [CrossRef]
- Batchelor, R.A. Quantitative v. qualitative measures of inflation expectationsa. Oxf. Bull. Econ. Stat. 2009, 48, 99–120. [Google Scholar] [CrossRef]
- Bennett, A. Output expectations of manufacturing industry. Appl. Econ. 1984, 16, 869–879. [Google Scholar] [CrossRef]
- Kariya, T. A generalization of the Carlson-Parkin method for the estimation of expected inflation rate. Econ. Stud. Q. 1990, 41, 155–165. [Google Scholar] [CrossRef]
- Batchelor, R.A.; Orr, A.B. Inflation expectations revisited. Economica 1988, 55, 317. [Google Scholar] [CrossRef]
- Seitz, H. The estimation of inflation forecasts from business survey data. Appl. Econ. 1988, 20, 427–438. [Google Scholar] [CrossRef]
- Claveria, O.; Pons, E.; Suriñach, J. Quantification of expectations. Are they useful for forecasting inflation? Econ. Issues 2006, 11, 19–38. Available online: http://www.economicissues.org.uk/Vol11.html#a7 (accessed on 24 September 2020).
- Claveria, O.; Pons, E.; Ramos, R.; Ramos-Lobo, R. Business and consumer expectations and macroeconomic forecasts. Int. J. Forecast. 2007, 23, 47–69. [Google Scholar] [CrossRef]
- Rosenblatt-Wisch, R.; Scheufele, R. Quantification and characteristics of household inflation expectations in Switzerland. Appl. Econ. 2015, 47, 2699–2716. [Google Scholar] [CrossRef]
- Malmendier, U.; Nagel, S. Learning from inflation experiences. Q. J. Econ. 2016, 131, 53–87. [Google Scholar] [CrossRef]
- Zuckarelli, J. A new method for quantification of qualitative expectations. Econ. Bus. Lett. 2015, 4, 123. [Google Scholar] [CrossRef]
- Mitchell, J.; Smith, R.J.; Weale, M.R. Quantification of qualitative firm-level survey data. Econ. J. 2002, 112, C117–C135. [Google Scholar] [CrossRef]
- Müller, C. You CAN Carlson–Parkin. Econ. Lett. 2010, 108, 33–35. [Google Scholar] [CrossRef]
- Breitung, J.; Schmeling, M. Quantifying survey expectations: What’s wrong with the probability approach? Int. J. Forecast. 2013, 29, 142–154. [Google Scholar] [CrossRef]
- Lahiri, K.; Zhao, Y. Quantifying survey expectations: A critical review and generalization of the Carlson–Parkin method. Int. J. Forecast. 2015, 31, 51–62. [Google Scholar] [CrossRef]
- Common, M.S. Testing for rational expectaations with qualitative survey data. Manch. Sch. 1985, 53, 138–148. [Google Scholar] [CrossRef]
- Löffler, G. Refining the Carlson–Parkin method. Econ. Lett. 1999, 64, 167–171. [Google Scholar] [CrossRef]
- Terai, A. Measurement error in estimating inflation expectations from survey data. OECD J. J. Bus. Cycle Meas. Anal. 2010, 2009, 133–156. [Google Scholar] [CrossRef]
- Claveria, O. Qualitative Survey Data on Expectations. Is There an Alternative to the Balance Statistic? Economic Forecasting; Molnar, A.T., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2010; pp. 181–190. Available online: https://www.bookdepository.com/es/Economic-Forecasting-Alan-T-Molnar/9781607410683 (accessed on 24 September 2020).
- Claveria, O. A new metric of consensus for Likert-type scale questionnaires: An application to consumer expectations. J. Bank. Financ. Technol. 2021, 1–8. [Google Scholar] [CrossRef]
- Mitchell, J.; Mouratidis, K.; Weale, M.R. Uncertainty in UK manufacturing: Evidence from qualitative survey data. Econ. Lett. 2007, 94, 245–252. [Google Scholar] [CrossRef]
- Saari, D.G. Complexity and the geometry of voting. Math. Comput. Model. 2008, 48, 1335–1356. [Google Scholar] [CrossRef]
- Claveria, O. A new metric of consensus for likert scales. SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Claveria, O. A new consensus-based unemployment indicator. Appl. Econ. Lett. 2018, 26, 812–817. [Google Scholar] [CrossRef]
- Poncela, P.; Senra, E. Measuring uncertainty and assessing its predictive power in the euro area. Empir. Econ. 2016, 53, 165–182. [Google Scholar] [CrossRef]
- Junttila, J.; Vataja, J. Economic policy uncertainty effects for forecasting future real economic activity. Econ. Syst. 2018, 42, 569–583. [Google Scholar] [CrossRef]
- Soric, P.; Lolic, I. Economic uncertainty and its impact on the Croatian economy. Public Sect. Econ. 2017, 41, 443–477. [Google Scholar] [CrossRef]
- Sakutukwa, T.; Yang, H.-S. The role of uncertainty in forecasting employment by skill and industry. Appl. Econ. Lett. 2017, 25, 1288–1291. [Google Scholar] [CrossRef]
- Claveria, O. Forecasting the unemployment rate using the degree of agreement in consumer unemployment expectations. J. Labour Mark. Res. 2019, 53, 3. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Claveria, O.; Monte, E.; Torra, S. Quantification of survey expectations by means of symbolic regression via genetic programming to estimate economic growth in Central and Eastern European economies. East. Eur. Econ. 2016, 54, 171–189. [Google Scholar] [CrossRef]
- Dabhi, V.K.; Chaudhary, S. Empirical modeling using genetic programming: A survey of issues and approaches. Nat. Comput. 2014, 14, 303–330. [Google Scholar] [CrossRef]
- White, D.R.; McDermott, J.; Castelli, M.; Manzoni, L.; Goldman, B.W.; Kronberger, G.; Jaśkowski, W.; O’Reilly, U.-M.; Luke, S. Better GP benchmarks: Community survey results and proposals. Genet. Program. Evolvable Mach. 2012, 14, 3–29. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Using survey data to forecast real activity with evolutionary algorithms. A cross-country analysis. J. Appl. Econ. 2017, 20, 329–349. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Assessment of the effect of the financial crisis on agents’ expectations through symbolic regression. Appl. Econ. Lett. 2017, 24, 648–652. [Google Scholar] [CrossRef][Green Version]
- Claveria, O.; Monte, E.; Torra, S. A data-driven approach to construct survey-based indicators by means of evolutionary algorithms. Soc. Indic. Res. 2016, 135, 1–14. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Evolutionary computation for macroeconomic forecasting. Comput. Econ. 2019, 53, 833–849. [Google Scholar] [CrossRef]
- Sorić, P.; Lolić, I.; Claveria, O.; Monte, E.; Torra, S. Unemployment expectations: A socio-demographic analysis of the effect of news. Labour Econ. 2019, 60, 64–74. [Google Scholar] [CrossRef]
- European Commission. Available online: https://ec.europa.eu/info/business-economy-euro/indicators-statistics/economic-databases/business-and-consumer-surveys_en (accessed on 19 September 2020).
- Organisation for Economic Co-Operation and Development. OECD Regional Typology; OECD Publishing: Paris, France, 2011. [Google Scholar]
- Claveria, O.; Lolic, I.; Monte, E.; Torra, S.; Sorić, P. Economic determinants of employment sentiment: A socio-demographic analysis for the euro area. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Kapetanios, G.; Marcellino, M.; Papailias, F. Forecasting inflation and GDP growth using heuristic optimisation of information criteria and variable reduction methods. Comput. Stat. Data Anal. 2016, 100, 369–382. [Google Scholar] [CrossRef]
- Fuentes, J.; Poncela, P.; Rodríguez, J. Sparse partial least squares in time series for macroeconomic forecasting. J. Appl. Econ. 2014, 30, 576–595. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Giannone, D.; Reichlin, L.; Small, D. Nowcasting: The real-time informational content of macroeconomic data. J. Monet. Econ. 2008, 55, 665–676. [Google Scholar] [CrossRef]
- Caruso, A. Nowcasting with the help of foreign indicators: The case of Mexico. Econ. Model. 2018, 69, 160–168. [Google Scholar] [CrossRef]
- Blaskowitz, O.; Herwartz, H. On economic evaluation of directional forecasts. Int. J. Forecast. 2011, 27, 1058–1065. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Empirical modelling of survey-based expectations for the design of economic indicators in five European regions. Empirica 2018, 46, 205–227. [Google Scholar] [CrossRef]
- Duda, J.; Szydło, S. Collective intelligence of genetic programming for macroeconomic forecasting. In Computer Vision; Springer International Publishing: Berlin/Heidelberg, Germany, 2011; pp. 445–454. [Google Scholar]
- Claveria, O.; Monte, E.; Torra, S. A genetic programming approach for estimating economic sentiment in the Baltic countries and the European Union. Technol. Econ. Dev. Econ. 2021, 27, 262–279. [Google Scholar] [CrossRef]
- Sorić, P. Consumer confidence as a GDP determinant in New EU Member States: A view from a time-varying perspective. Empirica 2018, 45, 261–282. [Google Scholar] [CrossRef]
- Dreger, C.; Kholodilin, K.A. Forecasting private consumption by consumer surveys. J. Forecast. 2011, 32, 10–18. [Google Scholar] [CrossRef]
- Gelper, S.S.; Croux, C. On the construction of the European Economic sentiment indicator. Oxf. Bull. Econ. Stat. 2010, 72, 47–62. [Google Scholar] [CrossRef]
- Girardi, A.; Gayer, C.; Reuter, A. The role of survey data in nowcasting Euro area GDP growth. J. Forecast. 2015, 35, 400–418. [Google Scholar] [CrossRef]
- Klein, L.R.; Özmucur, S. The use of consumer and business surveys in forecasting. Econ. Model. 2010, 27, 1453–1462. [Google Scholar] [CrossRef]
- Juhro, S.M.; Iyke, B.N. Consumer confidence and consumption expenditure in Indonesia. Econ. Model. 2020, 89, 367–377. [Google Scholar] [CrossRef]
- Martinsen, K.; Ravazzolo, F.; Wulfsberg, F. Forecasting macroeconomic variables using disaggregate survey data. Int. J. Forecast. 2014, 30, 65–77. [Google Scholar] [CrossRef]
- Das, A.; Lahiri, K.; Zhao, Y. Inflation expectations in India: Learning from household tendency surveys. Int. J. Forecast. 2019, 35, 980–993. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).