Electrical Load Forecast by Means of LSTM: The Impact of Data Quality

Abstract

Accurate forecast of aggregate end-users electric load profiles is becoming a hot topic in research for those main issues addressed in many fields such as the electricity services market. Hence, load forecast is an extremely important task which should be understood more in depth. In this research paper, the dependency of the day-ahead load forecast accuracy on the basis of the data typology employed in the training of LSTM has been inspected. A real case study of an Italian industrial load with samples recorded every 15 min for the year 2017 and 2018 was studied. The effect in the load forecast accuracy of different dataset cleaning approaches was investigated. In addition, the Generalised Extreme Studentized Deviate hypothesis testing was introduced to identify the outliers present in the dataset. The populations were constructed on the basis of an autocorrelation analysis that allowed for identifying a weekly correlation of the samples. The accuracy of the prediction obtained from different input dataset has been therefore investigated by calculating the most commonly used error metrics, showing the importance of data processing before employing them for load forecast.

1. Introduction

Smart grids are going to substantially change the electricity system in the near future. Due to the wide spread existence of metering and sensoring technologies, the relationship among customers, electricity supplier, and distribution system operator (DSO) will become more and more complex.

In fact, customers are going to play an active role, adapting their needs in accordance with a dynamic electricity market. In this scenario, wide opportunities and challenges may rise for DSO in the management of the electrical system [1]. Furthermore, the new topic of virtual power plant (VPP) is rising. VPP is the sum of several power plants that is aggregating the overall power of mixed distributed energy resources for enhancing power generation, trading or selling electrical energy on the electricity market [2]. This kind of aggregated power plant includes industrial loads which can be combined to power generation and therefore its forecast should be as much accurate as possible in order to guarantee certain hourly load profiles.

In view of the above, the issue of providing accurate electric load forecast, studied since the 1960s, is gaining even more importance. In literature, widely adopted are the auto-regressive models, which are based on the assumption that the load at a given time can be expressed as a linear combination of past observations and a number of exogenous variables, summed with a white noise (zero mean, normal distribution). Based on this idea, many models were developed, such as autoregressive (AR), AR with exogenous inputs (ARX), AR with moving average (ARMA) and Seasonal ARIMAX, which were successfully implemented for the load forecast application in [3,4,5]. Thanks to the availability of computational power, machine learning (ML) techniques have flourished in the last 20 years. These approaches have given the possibility to relax the linear assumption underlying the previous models, opening huge possibilities in terms of increased accuracy in the forecast prediction. These models, in fact, are able to infer trends from historical data, without any prior assumption regarding the underlying model [6]. In the wide range of available ML model, recurrent neural network (RNN) were widely adopted, and, in particular, Long-Short Term Memory were proven to return the best result [7,8]. This particular deep leaning models, in fact, are able to overcome problems such as vanishing gradient [9] experienced in the early days.

Among the others, the main question this paper wants to address is how much the load forecast accuracy is affected by the quality of the samples in the load time series. In order to investigate this issue, the effect of different strategies for dataset cleaning are studied, moving from a simple removal of incorrect measurements to holidays identification to, eventually, the implementation of a complete procedure for outliers detection, namely the Generalized Extreme Studentized Deviate (Generalized ESD) test [10].

In view of the day-ahead forecast, a real example of an industrial load that has been monitored between the years 2017 and 2018 is presented here.

This paper extends the preliminary analysis provided in [11] providing more details on the motivations, deepening the investigation of the implemented techniques that are adopted and testing them against a manual recognition. Above all, however, the most important content of this extension is represented by the provided outliers’ detection study, enforced and supported by the analysis of real industrial loads’ case studies.

2. Methods

In the following sections, the methodologies adopted in this work are thoroughly explained. In Section 2.1, the ML algorithm implemented for the load forecast is described while, in Section 2.2, the outliers’ detection technique is detailed.

2.1. LSTM Forecasting Method

Several existing forecasting methods are nowadays available and, among all, there are many techniques that are commonly adopted in the time series analysis such as auto-regressive moving average (ARIMA) or artificial neural network (ANN) based load forecast methods [12]. However, many features in the data of the load are affecting the choice of the forecasting method mainly according to the end-user time behavior (daily, weekly, or season) and classification (industrial, household, etc...). Many reviews about load forecast observe that, according to the time horizon, the forecasting method accuracy may be affected. Hence, the forecasting processes can be grouped into four main categories based on their horizons [13,14], which are summarized in the following

Table 1. Load forecast time term classification.

Acronym	Load Forecasting Classification	Time Horizon
VSTLF	very short term	1 day
STLF	short term	2 weeks
MTLF	medium term	3 years
LTLF	long term	>3 years

:

However, more often, the conclusion, as it is stated here [15], is that, over the past several decades, the majority of the load forecasting literature has been filled with attempts to determine the best technique for load forecasting. It is very important to understand that a universally best method simply does not exist, and it is the data that determine which technique should be used. Among all the available methodologies, Long-Short Term Memory (LSTM) neural networks are one of the most promising for the time series forecasting. They were first introduced in [16], and, since then, have been refined, and many authors contributed to their development in many different fields [17,18]. They belong to the class of Recurrent Neural Networks (RNN), but, due to their functional unit, the cell, LSTM overcome the problem related RNN learning long term dependencies [19,20].

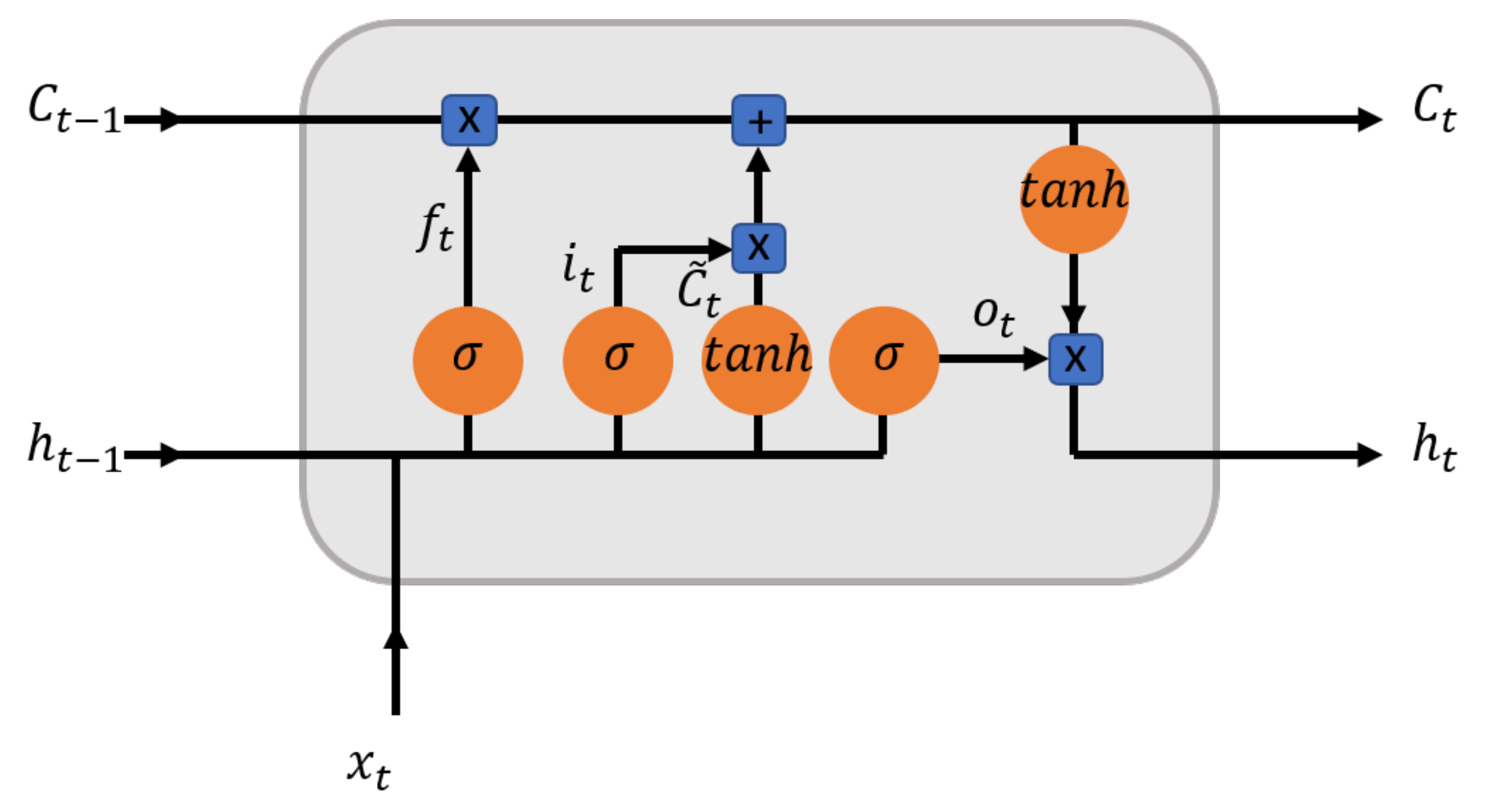
All RNN ultimately present the form of a chain of repeating neural network modules. As for LSTM, each module is called cell (Figure 1). The core concept of the LSTM is the cell state C, which can be associated with the memory of the network. From one cell to the next, new and relevant information can be added or removed from the cell state via the so called “gates”.

The circles in Figure 1 are either sigmoid ($\sigma$) or tansigmoid (tanh) layers. The operation represented in the squares are the pointwise multiplications (x) and pointwise addition (+). The variable h represents the previous hidden state, while, with x, the current input is given.

• Forget gate
  The first gate, also called “forget gate” (Equation (1), where $W_f$ and $b_f$ are the weights and biases associates with the forget gate and $[·,·]$ is a simple vector concatenation) tells which information of the cell state $C_{t-1}$ should be retained or forgotten:

  $$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

  (1)
• Input gate
  The input gate, on the other hand, decides which new information should be stored in the cell state for later use. It provides the following two operations:

  $$i_t=\sigma (W_i·[h_{t-1},x_t]+b_i)$$

  (2)

  $${\tilde{C}}_t=tanh(W_C·[h_{t-1},x_t]+b_C)$$

  (3)
• Cell state
  The new cell state, to be used in the next steps, can hence be computed as:

  $$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

  (4)

  where the operator * is the point-wise multiplication.
• Output gate
  Once the cell state has been updated, an output ($h_t$), dependent on the current input $x_t$ and on previous information, must be produced. In the output gate, the following operations are computed:

  $$o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)$$

  (5)

  $$h_t=o_t\times tanh\left(C_t\right)$$

  (6)

Further details regarding the network structure used in this paper are later described in Section 4.3.

2.2. Outliers Detection

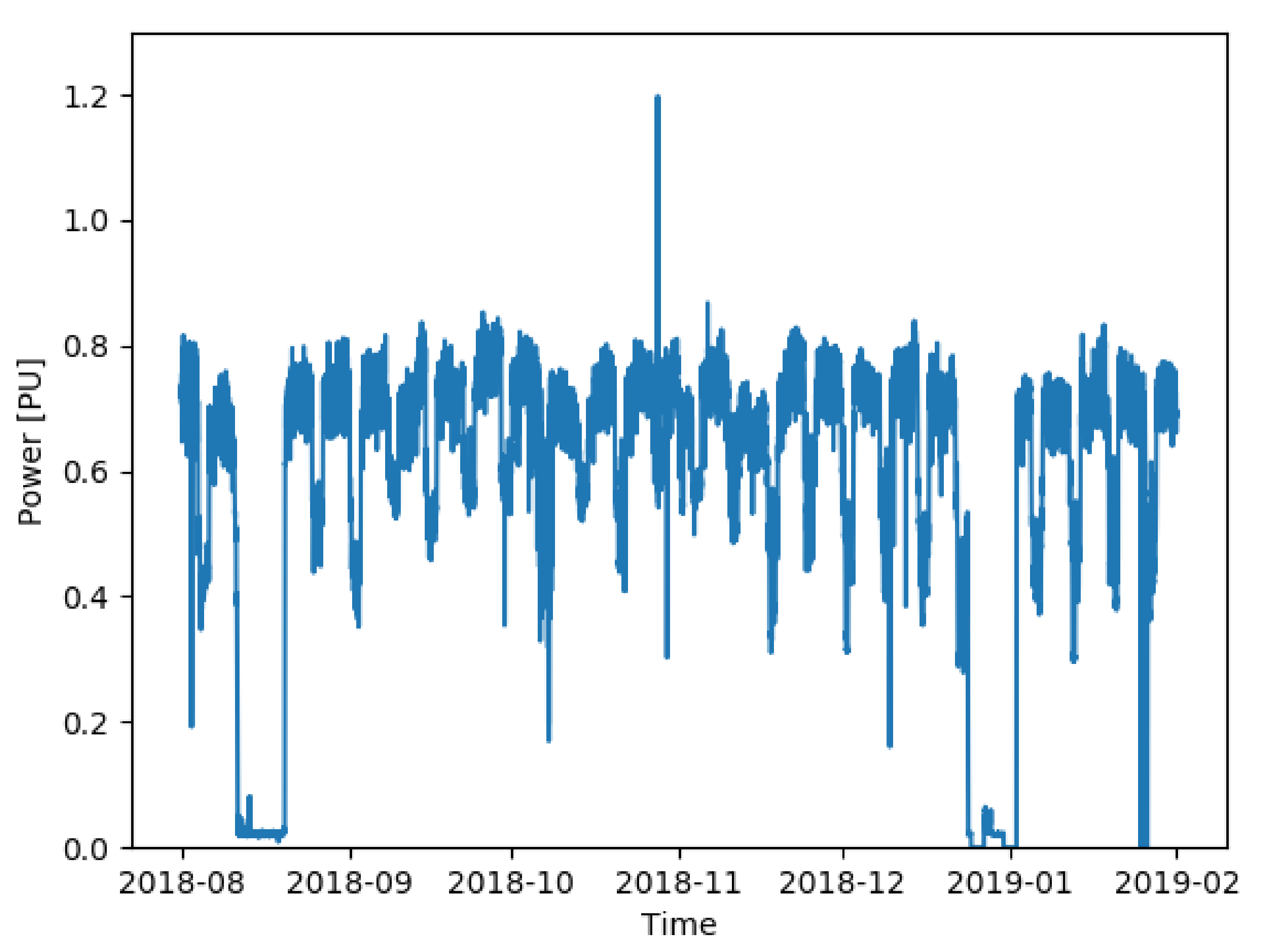
When dealing with time series deriving from real time measurements, the presence of erratic values or extreme events not representative of the problem under study is very likely to occur. In Figure 2, an example is provided. Two periods can be identified here where the power plant was not in operation due to holidays (August 2018 and December 2018/January 2019) or unexpected failures in the measuring system (February 2019). Moreover, in November 2018, a spike can be observed in the measurements that, if not erratic, must be identified anyway since it is not representative of the series. When dealing with a machine learning algorithm, those occurrences must be carefully understood and treated to avoid the so-called “Garbage in Garbage out” (GIGO) or “Rubbish in Rubbish out” (RIRO) behavior.

In order to detect those erratic behaviors, the samples have to undergo a cleaning procedure and a robust and reliable methodology must be defined. In this work, the Generalized ESD test is implemented to detect the outliers. This hypothesis testing was firstly introduced in [10] by Rosner in 1983 and is able to overcome the limits posed by the Grubbs [21,22] test and the Tietjen–Moore test [23,24]. These two types of latter hypothesis testing, in fact, rely on the knowledge of the number of outliers and can return a distorted conclusion. On the other hand, the Generalized ESD only requires the maximum number of outliers that can be found in a population. Given r, the maximum number of outliers in a population, the Generalized ESD detects k outliers, where $k\le r$. The population on which the test is applied requires that the dataset is univariate and follows an approximately normal distribution.

$$\left\{\begin{array}{cc}{H}_0:& \mathrm{There}\mathrm{are}\mathrm{no}\mathrm{outliers}\mathrm{in}\mathrm{the}\mathrm{data}\mathrm{set}\\ H_1:& \mathrm{There}\mathrm{are}\mathrm{up}\mathrm{to}\mathrm{r}\mathrm{outliers}\mathrm{in}\mathrm{the}\mathrm{data}\mathrm{set}\end{array}\right.$$

(7)

The Test Statistic can be computed as follows:

$$R_i=\frac{ma{x}_i|x_i-\overline{x}|}{s}$$

(8)

where $\overline{x}$ and s are the sample mean and sample standard deviation, respectively. The procedure consists of removing the observation maximizing ${\max }_i|x_i-\overline{x}|$ and then recomputing the above statistic with $n-1$ observations. The process is repeated until r observations have been removed. This results in r test statistics ($R_1,R_2,\dots ,R_r$).

From the $R_i$ test statistics, the following critical values can be computed:

$${\lambda }_i=\frac{(n-i)t_{p,n-i-1}}{\sqrt{\left(n-i-1+t_{p,n-i-1}^2\right)(n-i+1)}}i=1,2,\dots ,r$$

(9)

where $t_{p,\nu }$ is the 100p percentage point from the Student’s t-distribution with $\nu$ degrees of freedom and

$$p=1-\frac{\alpha }{2(n-i+1)}$$

(10)

The number of outliers is determined finding the largest i realizing the condition ${\lambda }_i<R_i$.

Once the outliers are identified, a procedure must be implemented to handle them properly. In fact, the mere elimination of those samples may lead to the erosion of the available dataset that would finally determine an overall decrease of the performances due to the reduced number of samples in input to the LSTM. Several studies have been conducted and are available in literature (e.g., in [25]) and, in the current work, every time a sample is detected as outliers, it is substituted with the median value of the population it is extracted from.

3. Error Metrics

Different error metrics are adopted in forecast assessment and, as it has been previously showed in [26], the typology of data could affect the load forecast result. The load forecast error $e_t$ made in the t-th sample of time is the starting point. It is the difference between the values of the actual load power $P_{m,t}$ and the forecast one $P_{f,t}$ [27]:

$$e_t=P_{m,t}-P_{f,t}$$

(11)

Moving from this definition, the most commonly used error definitions can be inferred [28,29], such as:

• the Normalized Mean Absolute Error $NMAE$:

  $$NMAE=\frac{{\sum }_{t=1}^N\left|e_t\right|}{N·P_n}·100,$$

  (12)

  where the percentage of the absolute error is referred to as the rated power $P_n$, and N is the number of samples considered in the time frame;
• the Normalized Root Mean Square Error $nRMSE$ is based on the maximum power output $\left(P_n\right)$:

  $$nRMSE=\frac{1}{P_n}·\sqrt{\frac{{\sum }_{t=1}^N{|e_t|}^2}{N}}·100$$

  (13)
• the Nash–Sutcliffe Efficiency Index $E_f$, was firstly introduced in [30] in a very different context such as hydrology. Its implications were later discussed in many articles such as [31]. Its definition is the following:

  $$E_f=1-\frac{{\sum }_{i=1}^N{(P_{f,i}-P_{m,i})}^2}{{\sum }_{i=1}^N{(P_{m,i}-{\overline{P}}_m)}^2}$$

  (14)

  where ${\overline{P}}_m$ is the mean power measurement of the whole period under study. The range of this index is $(-\infty ,1]$, where 1 is reached only when forecast and measurements overlap corresponding to the perfect forecast. The Nash–Sutcliffe model efficiency coefficient (NSE) is used to assess the predictive power. An efficiency of 1 (NSE = 1) corresponds to a perfect match of modeled discharge to the observed data. An efficiency of 0 (NSE = 0) indicates that the model predictions are as accurate as the mean of the observed data, whereas an efficiency less than zero (NSE < 0) occurs when the observed mean is a better predictor than the model or, in other words, when the residual variance (described by the numerator in the expression above) is larger than the data variance (described by the denominator). Essentially, the closer the model efficiency is to 1, the more accurate the model is. The efficiency coefficient is sensitive to extreme values and might yield sub-optimal results when the dataset contains large outliers in it.

All of these metrics are calculated here in order to compare different scenarios analyzed which are excluding part of the samples in the training of Deep learning LSTM.

4. Case Study

The LSTM forecasting method previously described is applied here to a real case study. An Italian industrial electrical load was monitored for more than two consecutive years (2017, 2018 to the end of January 2019) and quarter-hourly data have been recorded. The dataset structure comprises three columns:

• date time column (yyyy-MM-dd HH:mm), with quarter-hour time step;
• electrical load measurements;
• sensor fault message (not mandatory).

4.1. Dataset Cleaning

In order to inspect the marginal benefit of different cleaning procedure, four methodologies are here presented. It must be highlighted that the cleaning procedure is implemented in the training dataset while the test dataset is not manipulated, for the sake of a fair comparison.

• No cleaning performed: the full dataset is provided in the input to the LSTM model. The obtained results can be considered as a benchmark to evaluate the effectiveness of the following approaches. The forecast was performed on 34,368 samples because the first days of the year 2018 were provided as input as historical measurements;
• Removal of holidays. This case represents a cleaning procedure that can be implemented on the data looking and analyzing them manually. In fact, when dealing with industrial electrical load, no assumption can be made a priori regarding the plant operating status throughout the year. In this particular case, the plant shut down followed the Italian national holidays (e.g., Christmas and Easter) and other periods had to be removed as well showing the same trend (e.g., part of July and August);
• Removal of the outliers through the Generalized ESD. This methodology, whose implementation is further explained in the following section, is able to perform the dataset cleaning without any prior knowledge on the status of the plant and its scheduling activity. Furthermore, no information regarding any error occurred in the system is needed here;
• Error removal (information provided by the plant manager and data communication error): the case is representative of a full knowledge scenario, very unlikely to occur in real cases, where comprehensive information regarding the time series data are given such as unavailability, error caused in the data transmission, etc.

4.2. Generalized ESD Application

In order to clean the available dataset and not provide erratic values to the network in the training phase, the Generalized ESD hypotheses testing is presented through an application. This statistical approach requires that the population are from a normal distribution. The data, in their original form, are not compliant with this requirement, and, for this reason, the following steps are individuated.

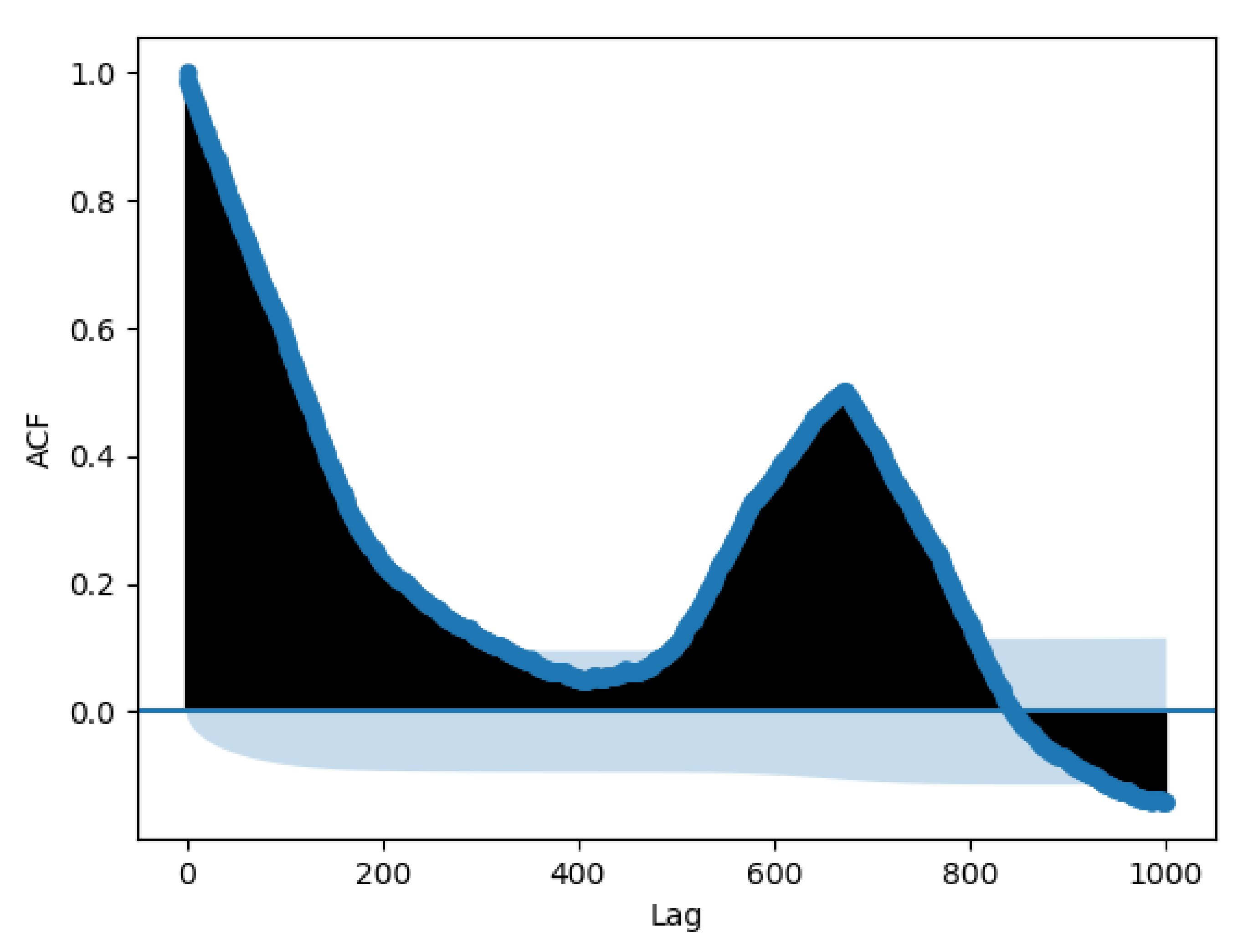
From the autocorrelation plot in Figure 3, a significant spike can be observed at 672 samples a week. For this reason, the data are gathered on a weekly basis, and 672 populations are found (sampling rate every 15 min) of approximately 52 individuals (52 weeks/year).

In Figure 4, a single exemplifying population is highlighted in orange belonging to all the Tuesdays at 1:30 p.m. of the year 2017. As it is possible to see, there are some samples in the lower region, which occurred during holidays, unexpected power plants shut-downs, and faults in the measuring system.

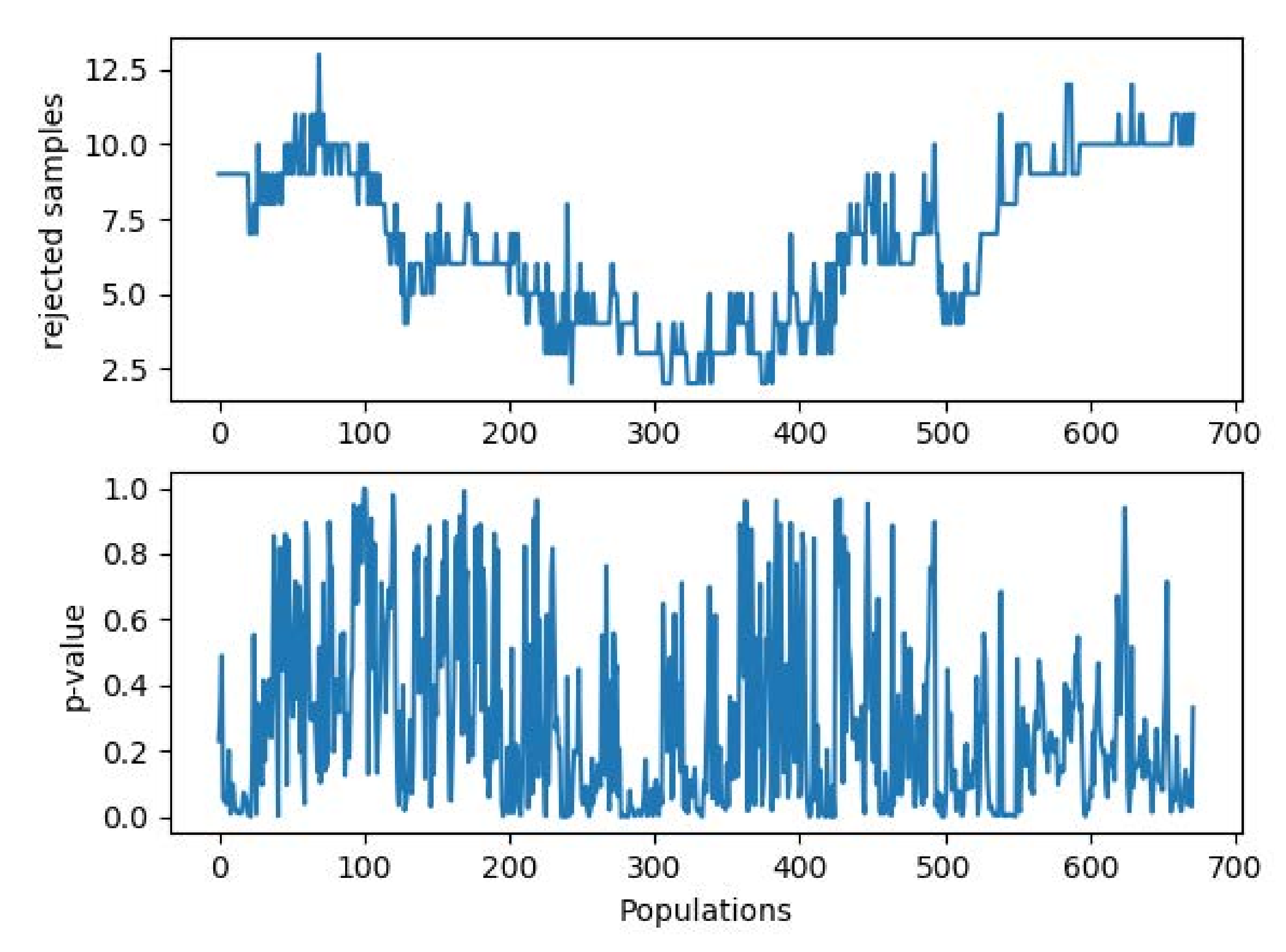
The cleaning process must be performed through the Generalized ESD applied to all the above described populations, and the results are given in Figure 5. In the upper graph, the number of excluded samples per population is given. As it is possible to see, not every population has the same number of rejected observations. The maximum number of outliers that the algorithm was set to find was fixed to 25. This amount is never reached for any population, and the maximum number of excluded samples was 13. On the lower graph, the results of the normality test on the cleaned populations are given in terms of p-values. As can be inferred, most of the populations (≥95%) can be assumed deriving from a Gaussian distribution with significance $\alpha =0.025$.

Once the outliers are identified, they must be properly substituted or erased. It is worth highlighting that, when dealing with time series, the elimination of a single sample can have a broader impact since the sampling sequence and the time dependencies could be lost. For this reason, if the erratic samples are sporadic and not consecutive, in this work, they are replaced with the median value of the population they belong to. If whole days/periods have to be removed, the whole week the erratic days/periods belong to is removed.

4.3. Dataset Aggregation and LSTM Architecture

Once different cleaning procedures on the data are properly implemented, the model architecture can be suitably optimized. The available dataset for the training phase is then divided into sub-portions to address both the training and the validation with a ratio 0.8:0.2. A grid search approach was then implemented in order to optimize the network topology and history size to be given as input to the model. This approach allows for optimizing the available parameters and hyperparameters running multiple independent simulations varying their values in a predefined range [32]. As for the scope, a three layer network having a fully connected layer on top of two layers LSTM was used.

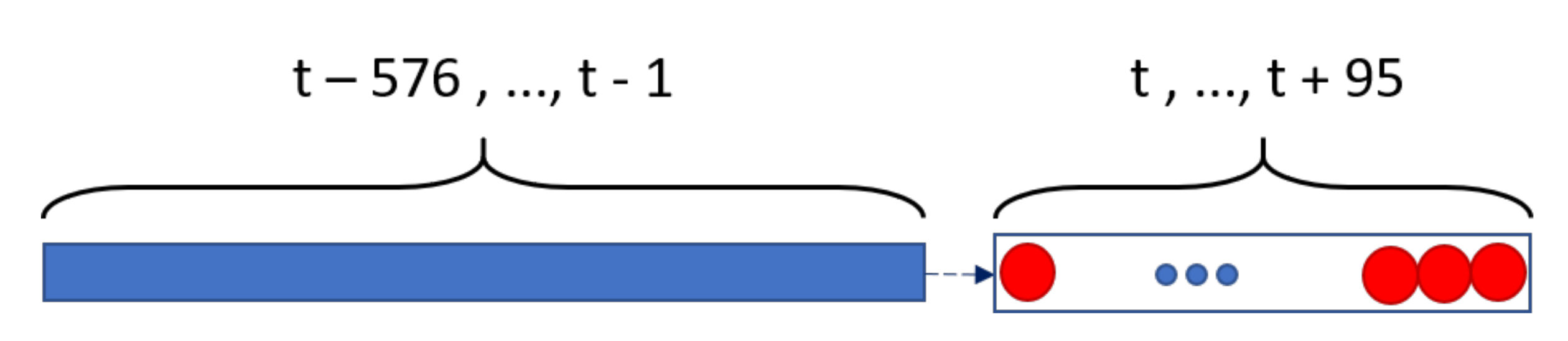
Regarding the inputs, six days were identified as the best solution to be provided to forecast the following one. The database is then assembled in order to provide couples of input and output series from which the algorithm can learn and infer from. In Figure 6, the single input and target given to the LSTM is explained. In blue, the history size of 6 days (576 quarter hourly samples) is provided to forecast the following day (96 quarter hourly samples) represented as red circles.

5. Results and Discussion

In this section, the results of the simulations performed with the four cleaning approaches (three actual cleaning process and the case in which no actions are taken) are presented. For all of the above cases, the 2017 data are used to train the model while the 2018 data to test it. It is worth highlighting that, for the sake of a fair comparison, the test data are the same for the four cases.

The number of samples available to train and test the different network are reported in

Table 2. Training and test feature.

Methodology	Training Size (Days)	Test Size (Days)
No cleaning	358	243
Holidays removal	224	243
GESD	358	243
Error removal	308	243

.

When no action are taken, 358 couples of Input/Output could be assembled. Indeed, this is the maximum number achievable needing a series of six days as input. The same amount of data, thanks to the substitution procedure, is available with the GESD approach. The removal of holidays and of error partially erode the available number of data.

In

Table 3. Load forecast results in terms of accuracy.

Metric	No Removal	Holidays Removal	Outliers Removal	Error Removal
NMAE(%)	4.11	3.70	3.30	3.37
nRMSE (%)	7.80	6.43	4.93	5.30
E${}_f$ (-)	0.54	0.68	0.81	0.79

, the forecast accuracy obtained with the four considered approaches is reported. As it is possible to notice, the worst performance is achieved in case no cleaning process is implemented. On the other hand, the best result, in all the considered metrics, is instead obtained when the cleaning of the outliers through the Generalised ESD is applied. The removal of the samples deviating from the characteristics behavior of the load, therefore, allows the LSTM to infer and learn the load pattern and to accurately predict its future behavior.

It is worth noticing that the outliers removal approach is the most promising and produces the best accuracy. In fact, its adoption allows for automatically detecting non-representative trends of the load such as holidays and erratic values, together with other occurrences. Furthermore, as a very import aspect when dealing with real industrial application, the procedure does not require any additional information regarding the data composing the time series, which are usually uneasy or impossible to retrieve, since any erratic behavior is automatically individuated.

Moving from the benchmark, it is then validated that, as expected, properly cleaning the available data, though requiring huge effort, allows for greatly reducing the number of errors made. In

Table 4. Load forecast increase of accuracy with respect to the benchmark (no cleaning procedure).

Metric	Holidays Removal	Outliers Removal	Error Removal
NMAE	10.0	19.8	18.0
nRMSE	17.5	36.7	32.0
E${}_f$	27.7	52.0	48.3

, the accuracy increase is expressed in percentage points. The best result is obtained through the Generalized ESD, which is able to increase the accuracy of 19.8%, 36%, and 52% in terms of NMAE, nRMSE, and EF, respectively.

6. Conclusions

In the present work, four dataset cleaning processes are presented with the aim of improving the load forecast for the following 24 h computed through a Long-Short Term Memory model. In particular, the effect of different dataset cleaning procedure is inspected. The first approach used as a benchmark does not exclude any available data. The second removes the holidays, which very often show a significant deviation from the normal behavior due to a shutting down of the operations. The third implements the outliers removal through the Generalized Extreme Studentized Deviation hypotheses testing with replacement while the last approach, excluding the erratic values on the basis of the information provided by the plant, hence representing a full knowledge scenario.

The Generalized ESD methodology is demonstrated to be the most promising one, returning the highest performance for all the considered metrics and, moreover, does not require any prior additional information apart from the electrical load measurements.

From the benchmark case, it was finally possible to reduce the error committed for the period under study of 19.8%, 36%, and 52% in terms of NMAE, nRMSE, and EF, respectively.