Benchmarking Real-Time Streamflow Forecast Skill in the Himalayan Region
Abstract
1. Introduction
2. Materials and Methods
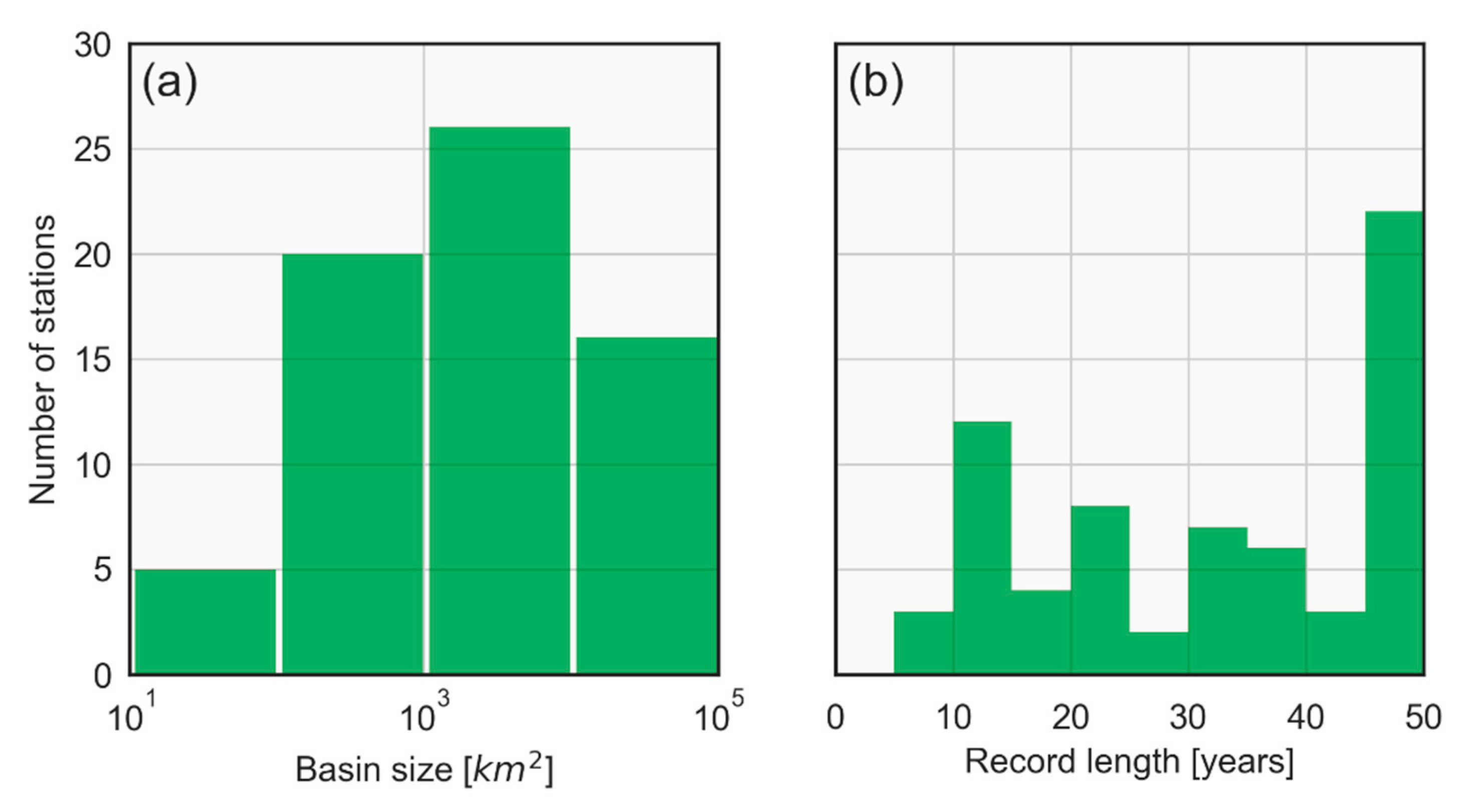
2.1. Study Area and Data
2.2. Experimental Design
2.3. Evaluation Metrics
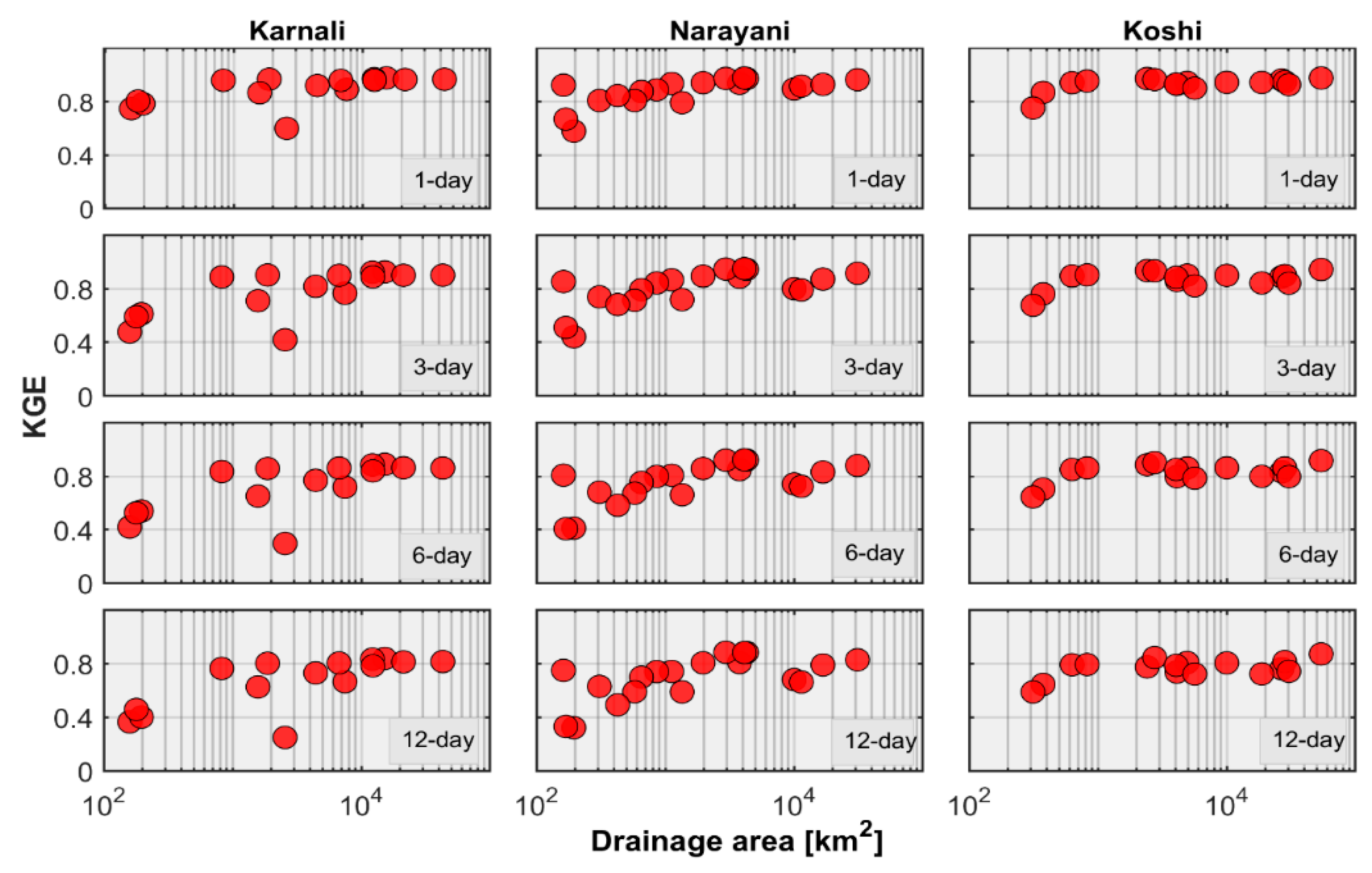
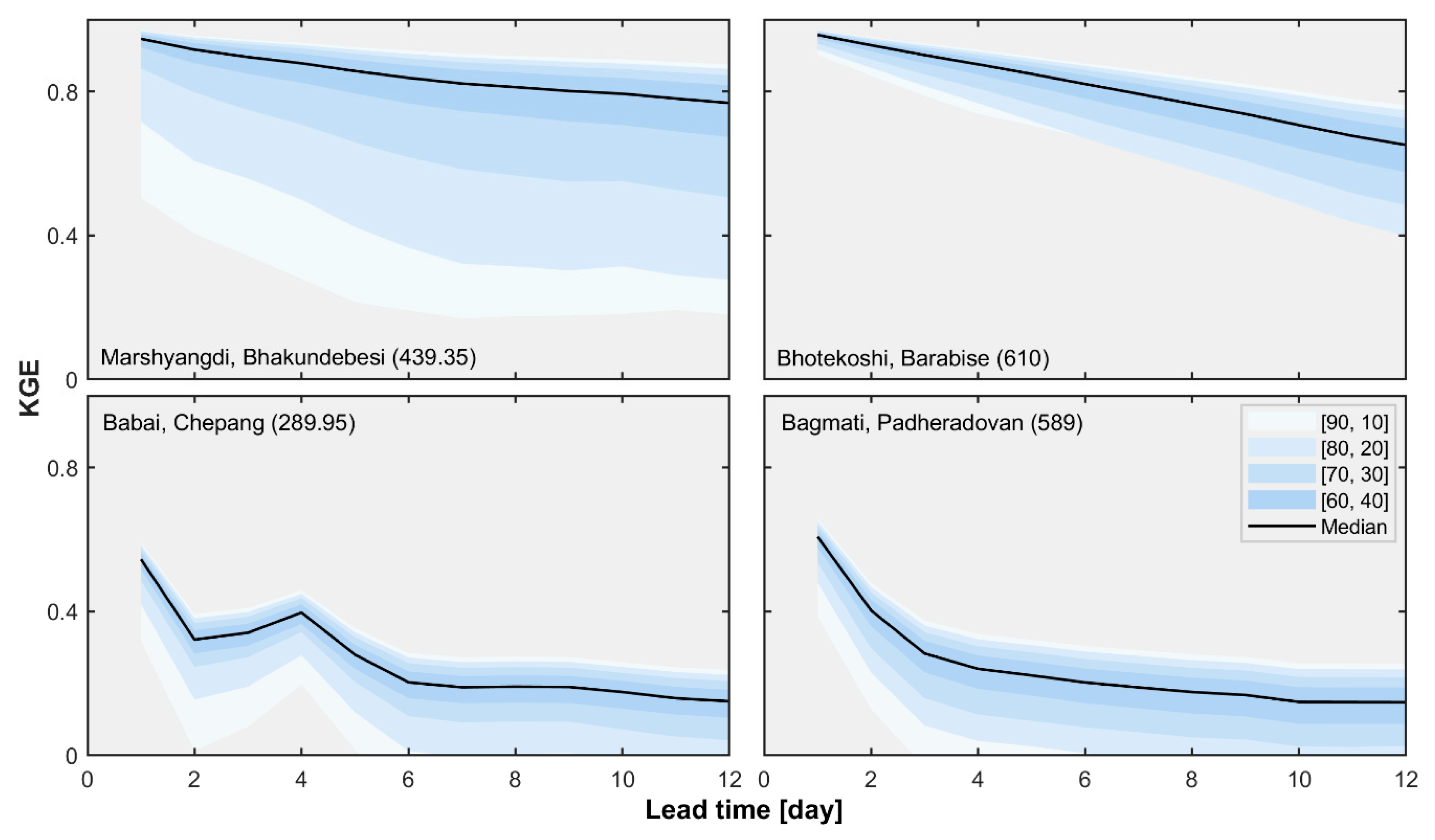
3. Results
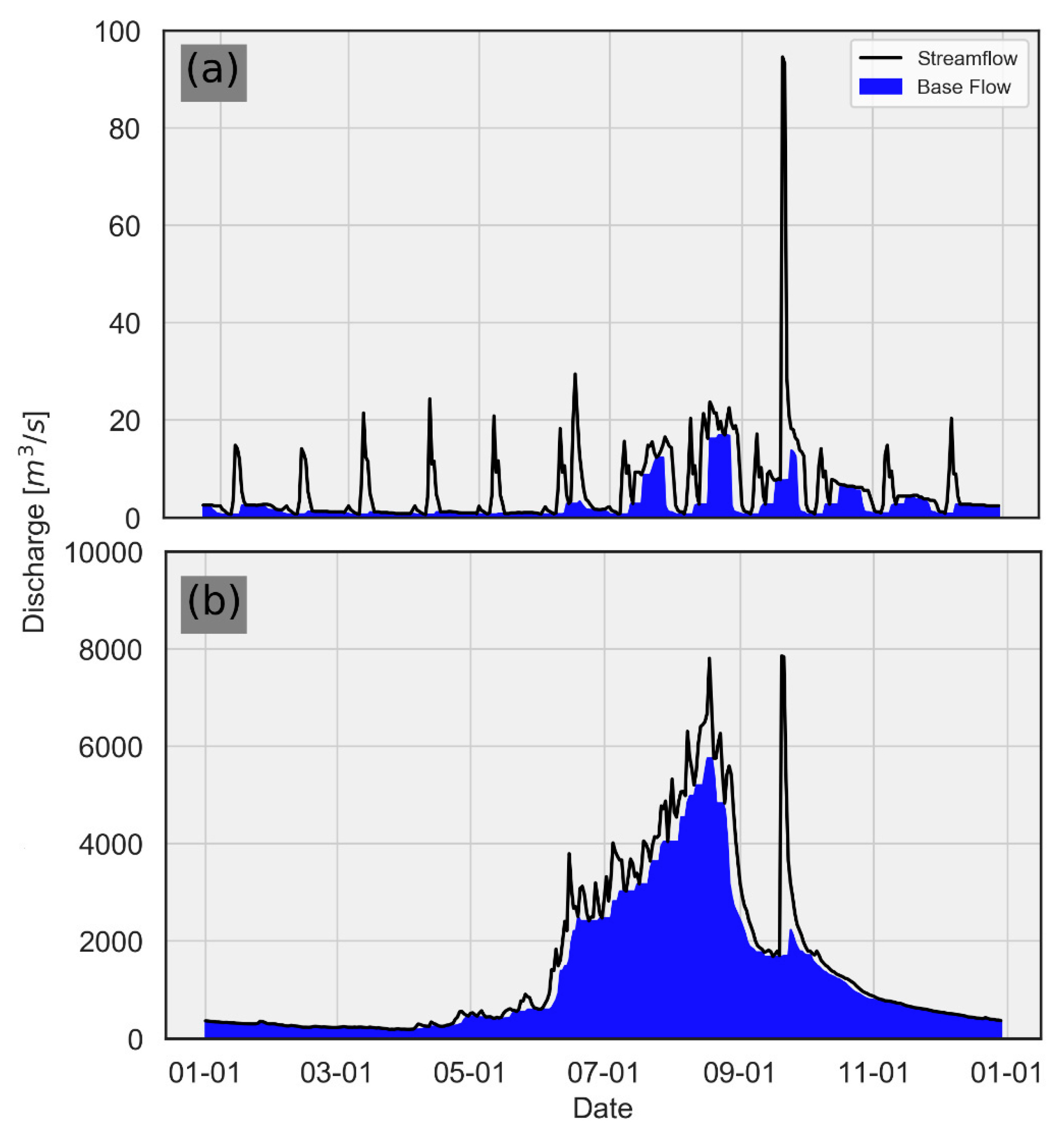
3.1. Basin-Wise Forecasts
3.2. Regional Streamflow Forecasts
4. Discussion
5. Conclusions
- ▪
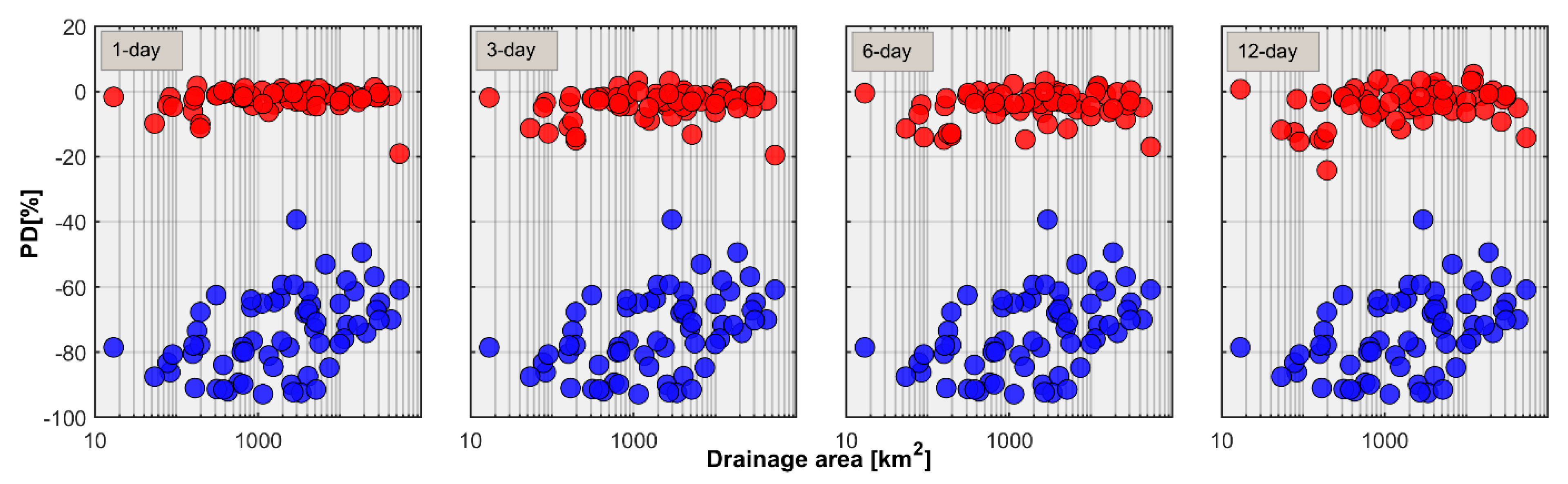
- Persistence-based forecast skill shows strong dependence with the basin scale and forecast lead time. Anomaly persistence forecasts outperform others at small basin scales and longer lead times and hence can be a better selection for benchmarking the real-time streamflow forecasting system in the Himalayan region of Nepal.
- ▪
- The forecast skill shows strong dependence with the flow regime and flow threshold. The verification results show higher forecast skill for perennial rivers over intermittent rivers and moderate flow quantiles over high flow quantiles.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Palash, W.; Jiang, Y.; Akanda, A.S.; Small, D.L.; Nozari, A.; Islam, S. A Streamflow and Water Level Forecasting Model for the Ganges, Brahmaputra, and Meghna Rivers with Requisite Simplicity. J. Hydrometeorol. 2018, 19, 201–225. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and Uncertainties in Hydrological Modeling of Remote Hindu Kush-Karakoram-Himalayan (HKH) Basins: Suggestions for Calibration Strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Sharma, S.; Siddique, R.; Reed, S.; Ahnert, P.; Mendoza, P.; Mejia, A. Relative effects of statistical preprocessing and postprocessing on a regional hydrological ensemble prediction system. Hydrol. Earth Syst. Sci. 2018, 22, 1831–1849. [Google Scholar] [CrossRef]
- Gurung, D.R.; Giriraj, A.; Aung, K.S.; Shrestha, B.; Kulkarni, A.V. Snow-Cover Mapping and Monitoring in the Hindu Kush-Himalayas; The International Centre for Integrated Mountain Development: Lalitpur, Nepal, 2011; pp. 1–44. [Google Scholar]
- Khadka, D.; Babel, M.S.; Shrestha, S.; Tripathi, N.K. Climate change impact on glacier and snow melt and runoff in Tamakoshi basin in the Hindu Kush Himalayan (HKH) region. J. Hydrol. 2014, 511, 49–60. [Google Scholar] [CrossRef]
- Paudel, K.P.; Andersen, P. Monitoring snow cover variability in an agropastoral area in the Trans Himalayan region of Nepal using MODIS data with improved cloud removal methodology. Remote Sens. Environ. 2011, 115, 1234–1246. [Google Scholar] [CrossRef]
- Mukherji, A.; Molden, D.; Nepal, S.; Rasul, G.; Wagnon, P. Himalayan waters at the crossroads: Issues and challenges. Int. J. Water Resour. Dev. 2015, 31, 151–160. [Google Scholar] [CrossRef]
- Bhattarai, B.C.; Regmi, D. Impact of Climate Change on Water Resources in View of Contribution of Runoff Components in Stream Flow: A Case Study from Langtang Basin, Nepal. J. Hydrol. Meteorol. 2016, 9, 74–84. [Google Scholar] [CrossRef]
- Dhami, B.; Himanshu, S.K.; Pandey, A.; Gautam, A.K. Evaluation of the SWAT model for water balance study of a mountainous snowfed river basin of Nepal. Environ. Earth Sci. 2018, 77, 1–20. [Google Scholar] [CrossRef]
- Government of Nepal Ministry of Energy Water Resources and Irrigation; Department of Hydrology and Meteorology. Standard Operating Procedure for Flood Early Warning System in Nepal; Department of Hydrology and Meteorology: Kathmandu, Nepal, 2018.
- Gautam, D.K.; Phaiju, A.G. Community Based Approach to Flood Early Warning in West Rapti River Basin of Nepal. J. Integr. Disaster Risk Manag. 2013, 3, 155–169. [Google Scholar] [CrossRef]
- Smith, P.J.; Brown, S.; Dugar, S. Community-based early warning systems for flood risk mitigation in Nepal. Nat. Hazards Earth Syst. Sci. 2017, 17, 423–437. [Google Scholar] [CrossRef]
- Budimir, M.; Donovan, A.; Brown, S.; Shakya, P.; Gautam, D.; Uprety, M.; Cranston, M.; Sneddon, A.; Smith, P.; Dugar, S. Communicating Complex Forecasts for Enhanced Early Warning in Nepal. Geosci. Commun. Discuss. 2019, 1–32. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 1–18. [Google Scholar] [CrossRef]
- Sharma, S.; Siddique, R.; Balderas, N.; Fuentes, J.D.; Reed, S.; Ahnert, P.; Shedd, R.; Astifan, B.; Cabrera, R.; Laing, A.; et al. Eastern U.S. verification of ensemble precipitation forecasts. Weather Forecast. 2017, 32, 117–139. [Google Scholar] [CrossRef]
- Pappenberger, F.; Scipal, K.; Buizza, R. Hydrological aspects of meteorological verification. Atmos. Sci. Lett. 2008, 9, 43–52. [Google Scholar] [CrossRef]
- Kayastha, R.B.; Steiner, N.; Kayastha, R.; Mishra, S.K.; Forster, R.R. Comparative Study of Hydrology and Icemelt in Three Nepal River Basins Using the Glacio-Hydrological Degree-Day Model ( GDM ) and Observations From the Advanced Scatterometer. Front. Earth Sci. 2020, 7, 1–13. [Google Scholar] [CrossRef]
- WRI Aqueduct Global Flood Risk Country Rankings. 2015. Available online: https://www.wri.org/resources/data-sets/aqueduct-global-flood-risk-country-rankings (accessed on 29 June 2020).
- Ghimire, G.R.; Krajewski, W.F. Exploring Persistence in Streamflow Forecasting. J. Am. Water Resour. Assoc. 2020, 56, 542–550. [Google Scholar] [CrossRef]
- Mittermaier, M.P. The Potential Impact of Using Persistence as a Reference Forecast on Perceived Forecast Skill. Weather Forecast. 2008, 23, 1022–1031. [Google Scholar] [CrossRef]
- Bennett, J.C.; Robertson, D.E.; Shrestha, D.L.; Wang, Q.J. Selecting reference streamflow forecasts to demonstrate the performance of NWP-forced streamflow forecasts. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 2611–2617. [Google Scholar]
- Ghimire, G.R.; Jadidoleslam, N.; Krajewski, W.F.; Tsonis, A.A. Insights On Streamflow Predictability Across Scales Using Horizontal Visibility Graph Based Networks. Front. Water 2020. accepted for publication. [Google Scholar]
- van den Dool, H. Empirical Methods in Short-Term Climate Prediction; Oxford University Press: Oxford, UK, 2007; ISBN 0-19-920278-8/978-0-19-920278-2. [Google Scholar]
- Fraedrich, K.; Ziehmann-Schlumbohm, C. Predictability Experiments with Persistence Forecasts in a Red-noise Atmosphere; Royal Meteorological Society: Reading, UK, 1994; ISBN 0035-9009. [Google Scholar]
- Wu, W.; Dickinson, R.E. Warm-season rainfall variability over the U.S. Great Plains and its correlation with evapotranspiration in a climate simulation. Geophys. Res. Lett. 2005, 32, 215. [Google Scholar] [CrossRef]
- Pagano, T.; Garen, D. A Recent Increase in Western U.S. Streamflow Variability and Persistence. J. Hydrometeorol. 2005, 6, 173–179. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ghimire, G.R.; Quintero, F. Streamflow Forecasting without Models. J. Hydrometeorol. 2020, in press. [Google Scholar]
- Karki, R.; Talchabhadel, R.; Aalto, J.; Baidya, S.K. New climatic classification of Nepal. Theor. Appl. Climatol. 2016, 125, 799–808. [Google Scholar] [CrossRef]
- Uddin, K.; Shrestha, H.L.; Murthy, M.S.R.; Bajracharya, B.; Shrestha, B.; Gilani, H.; Pradhan, S.; Dangol, B. Development of 2010 national land cover database for the Nepal. J. Environ. Manag. 2015, 148, 82–90. [Google Scholar] [CrossRef]
- Shrestha, M.L. Interannual variation of summer monsoon rainfall over Nepal and its relation to Southern Oscillation Index. Meteorol. Atmos. Phys. 2000, 75, 21–28. [Google Scholar] [CrossRef]
- Mool, P.K.; Wangda, D.; Bajracharya, S.R.; Joshi, S.P.; Kunzang, K.; Gurung, D.R. Inventory of Glaciers, Glacial Lakes and Glacial Lake Outburst Floods: Monitoring and Early Warning Systems in the Hindu Kush-Himalayan Region—Bhutan; International Centre for Integrated Mountain Development: Khumaltar, Nepal, 2001. [Google Scholar]
- DHM, N. Climate Normals; The Department of Hydrology and Meteorology: Kathmandu, Nepal, 2010.
- Gautam, M.R.; Acharya, K. Streamflow trends in Nepal. Hydrol. Sci. J. 2012, 57, 344–357. [Google Scholar] [CrossRef]
- Sloto, R.a.; Crouse, M.Y. Hysep: A Computer Program for Streamflow Hydrograph Separation and Analysis; Water-Resources Investigations Report 96-4040; U.S. Geological Survey: Reston, VA, USA, 1996; p. 54.
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: Kolkata, India, 1997; ISBN 0521004055. [Google Scholar]
- Perez, G.; Mantilla, R.; Krajewski, W.F. The influence of spatial variability of width functions on regional peak flow regressions. Water Resour. Res. 2018, 54, 7651–7669. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Connecting the power-law scaling structure of peak-discharges to spatially variable rainfall and catchment physical properties. Adv. Water Resour. 2014, 71, 32–43. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R.; Small, S.J. Exploring the effects of hillslope-channel link dynamics and excess rainfall properties on the scaling structure of peak-discharge. Adv. Water Resour. 2014, 64, 9–20. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Analyzing the effects of excess rainfall properties on the scaling structure of peak discharges: Insights from a mesoscale river basin. Water Resour. Res. 2015, 51, 3900–3921. [Google Scholar] [CrossRef]
- Arnal, L.; Wood, A.W.; Stephens, E.; Cloke, H.L.; Pappenberger, F. An efficient approach for estimating streamflow forecast skill elasticity. J. Hydrometeorol. 2017, 18, 1715–1729. [Google Scholar] [CrossRef]
- Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking ensemble streamflow prediction skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [Google Scholar] [CrossRef]
- Wood, A.W.; Pagano, T.; Roos, M. Tracing The Origins of ESP, HEPEX Blog. 2016. Available online: https://hepex.inrae.fr/tracing-the-origins-of-esp/ (accessed on 29 June 2020).





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, G.R.; Sharma, S.; Panthi, J.; Talchabhadel, R.; Parajuli, B.; Dahal, P.; Baniya, R. Benchmarking Real-Time Streamflow Forecast Skill in the Himalayan Region. Forecasting 2020, 2, 230-247. https://doi.org/10.3390/forecast2030013
Ghimire GR, Sharma S, Panthi J, Talchabhadel R, Parajuli B, Dahal P, Baniya R. Benchmarking Real-Time Streamflow Forecast Skill in the Himalayan Region. Forecasting. 2020; 2(3):230-247. https://doi.org/10.3390/forecast2030013
Chicago/Turabian StyleGhimire, Ganesh R., Sanjib Sharma, Jeeban Panthi, Rocky Talchabhadel, Binod Parajuli, Piyush Dahal, and Rupesh Baniya. 2020. "Benchmarking Real-Time Streamflow Forecast Skill in the Himalayan Region" Forecasting 2, no. 3: 230-247. https://doi.org/10.3390/forecast2030013
APA StyleGhimire, G. R., Sharma, S., Panthi, J., Talchabhadel, R., Parajuli, B., Dahal, P., & Baniya, R. (2020). Benchmarking Real-Time Streamflow Forecast Skill in the Himalayan Region. Forecasting, 2(3), 230-247. https://doi.org/10.3390/forecast2030013








