Benford Behavior in Stick Fragmentation Problems

Abstract

Benford’s law states that in many real-world datasets, the probability that the leading digit is d equals ${log}_{10}((d+1)/d)$ for all $1\le d\le 9$. We call this weak Benford behavior. A dataset is said to follow strong Benford behavior if the probability that its significand (i.e., the significant digits in scientific notation) is at most s equals ${log}_{10}\left(s\right)$ for all $s\in [1,10)$. We investigate Benford behavior in a multi-proportion stick fragmentation model, where a stick is split into m substicks according to fixed proportions at each stage. This generalizes previous work on the single proportion stick fragmentation model, where each stick is split into two substicks using one fixed proportion. We provide a necessary and sufficient condition under which the lengths of the stick fragments converge to strong Benford behavior in the multi-proportion model.

1. Introduction

In the late nineteenth century, astronomer Simon Newcomb observed that in the logarithmithic books at his workplace, certain pages were “more worn than others” [1]. In particular, there was more wear and tear in the earlier pages than the later pages. He deduced that there is a “bias” towards smaller leading digits, with the digit 1 showing up roughly $30\%$ of the time, the digit 2 showing up roughly $18\%$ of the time, and so on. 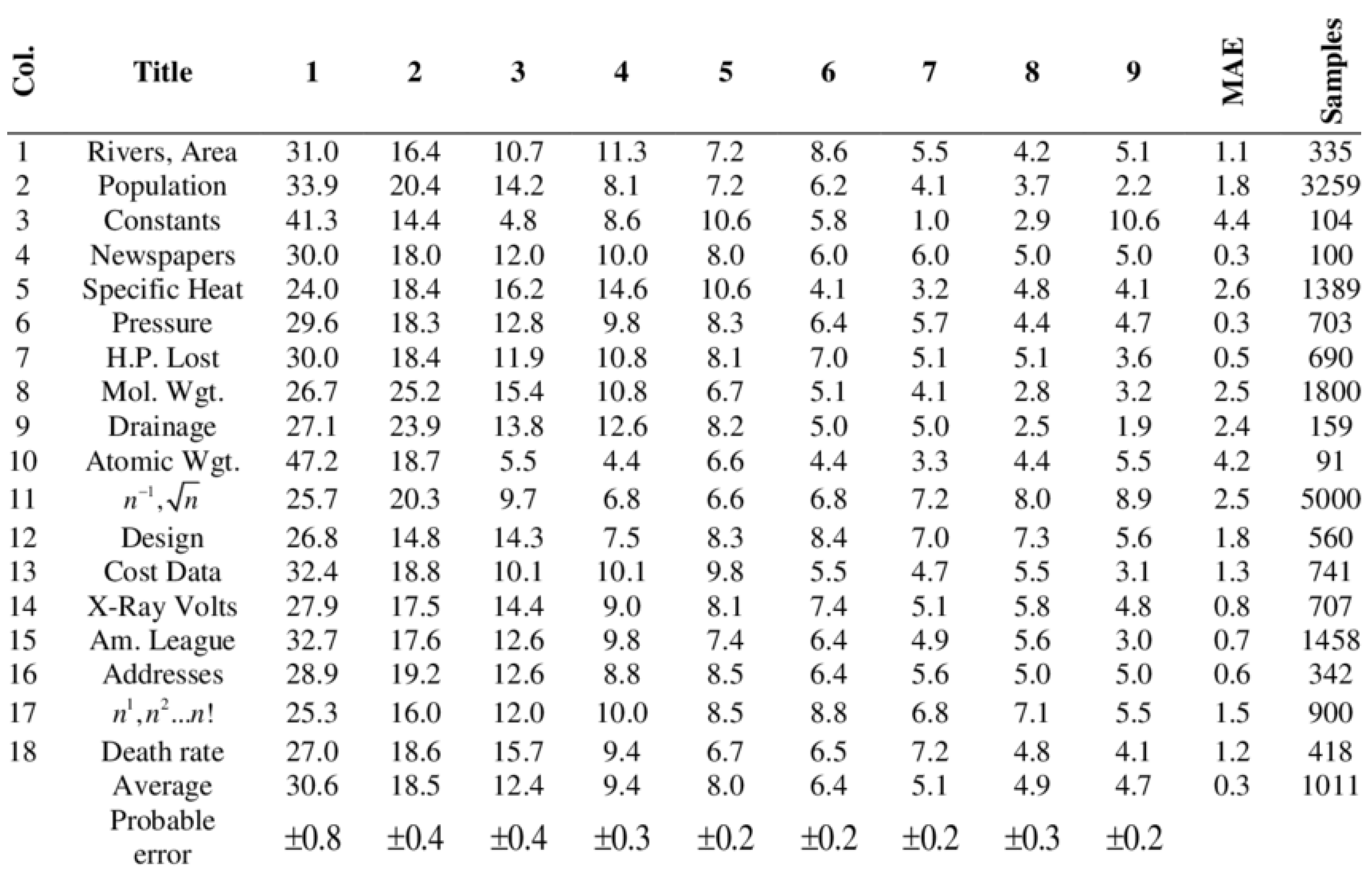Newcomb’s findings were practically ignored until about fifty years later, when physicist Frank Benford published his own research on the distribution of leading digits in Reader’s Digest [2]. Benford displayed a table of roughly 20,000 observations from twenty different sets of data, shown in Figure 1.

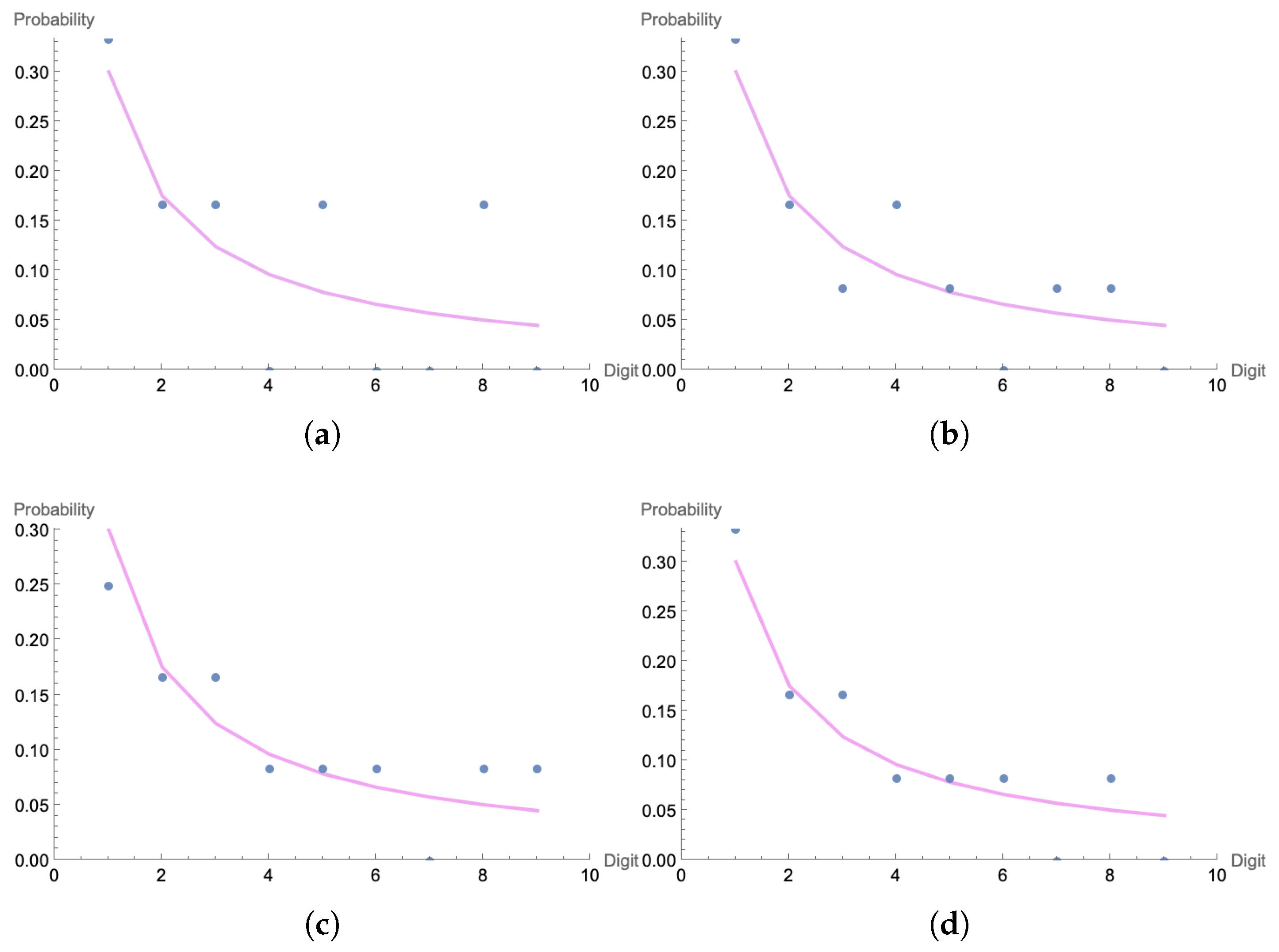
Benford called this distribution the “law of Anomalous Numbers”. However, due to the popularity of his publication, the phenomena eventually became known as “Benford’s law”; see Figure 2 for probabilities. Benford’s law is a powerful phenomena that occurs in a variety of data, including accounting, elections, finance, geosciences, physics, population data, street addresses, and more. The law’s prevalence makes it a valuable tool for ensuring data integrity. For example, it is often used in fraud detection for tax returns, insurance claims, and expense reports [3,4]. For further details on the history of Benford’s law, see [5,6,7,8,9].

There is extensive research on fragmentation problems related to Benford’s law, which is the subject of our paper. In [10], Kakutani considered the following fragmentation problem: Start with the initial set $Q_0=\{0,1\}$ and a fixed constant $\alpha \in (0,1)$. At each stage, from $Q_k=\{x_1,\dots ,x_{k+2}\mid x_1<\cdots <x_{k+2}\}$, construct $Q_{k+1}$ by adding the point $x_i+\alpha (x_{i+1}-x_i)$, where $x_{i+1}-x_i={max}_{1\le j\le k+1}|x_{j+1}-x_j|$. Kakutani was able to show that as $k\to \infty$, the points of $Q_k$ converge to a uniform distribution on $[0,1]$ and are therefore non-Benford. This problem has been generalized to various setting; see [11,12,13,14,15,16] for examples. For other decomposition problems, see [17,18] for fragmentation in two dimensions, [19] for fragmentation in a fractal setting, and [20] for discrete fragmentation.

In this paper, we investigate a fragmentation problem inspired by the work by Becker et al. [21], who studied the stick fragmentation problem. Their model begins with a stick of length L and a density function f on $[0,1]$ from which proportions are sampled. At Stage 1, the stick is split into two substicks at proportion $p_1$. At Stage 2, the left substick is split into two substicks at proportion $p_2$, while the right substick is split into two substicks at proportion $p_3$. Iterating this procedure for N stages can produce up to $2^N$ sticks.

Becker et al. analyzed three versions of this process: (i) the unrestricted case, in which a new proportion is drawn from f at each stage and all sticks split; (ii) the restricted case, in which a new proportion is drawn at each stage but only one of the two substicks splits; and (iii) the fixed-proportion case, in which all sticks split but a single proportion p is fixed in advance and applied throughout. For the restricted and unrestricted cases, they established convergence to strong Benford behavior under mild conditions on the Mellin transform of f and on the mean and variance of ${log}_{10}X$ for $X\sim f$. For the fixed-proportion case, they proved that convergence occurs if and only if ${log}_{10}(p/(1-p))$ is irrational.

We extend the fixed single-proportion stick fragmentation problem to a fixed multi-proportion setting. Specifically, we begin with a stick of length L, an integer $m\ge 2$, and any proportions $p_1,p_2,\dots ,p_m\in (0,1)$ satisfying $p_1+p_2+\cdots +p_m=1$, independent of L. At Stage 1, the stick is split into m substicks of lengths $p_{1}L,p_{2}L,\dots ,p_{m}L$. At Stage 2, each of these substicks is split into m smaller substicks according to the same proportions. In general, at Stage N, every substick from Stage $N-1$ is split into m substicks using $p_1,p_2,\dots ,p_m$. After N stages, the process produces $m^N$ substicks.

Our principal question is whether the stick lengths exhibit Benford behavior. The novelty of this model lies in dividing the subdivision into more than two substicks at each stage, which renders the techniques used in Becker et al. [21] inapplicable. Our main result is a necessary and sufficient condition under which this fixed multi-proportion stick fragmentation model yields stick lengths converging to strong Benford’s behavior.

Theorem 1. 

Let $m>2$ be an integer, and choose $p_1,p_2,\dots ,p_m\in (0,1)$ such that $p_1+p_2+\cdots +p_m=1$. At each stage, a stick is split into m substicks according to the proportions $p_1,p_2,\dots ,p_{m-1}$. After N stages, the process produces $m^N$ sticks, whose lengths are $A_{k_1,k_2,\dots ,k_m}=L{p}_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m}$ for all non-negative integers $k_1,k_2,\dots ,k_m$ with $k_1+k_2+\cdots +k_m=N$. For $1\le i\le m-1$, set $y_i={log}_{10}(p_i/p_{i+1})$. Then the stick lengths converge to strong Benford behavior if and only if $y_i$ is irrational for some $1\le i\le m-1$.

1.1. Definitions and Theory of Benford’s Law

We begin with the definition of Benford’s law (see, for example, [8,22]).

Definition 1 

(Benford’s Law for the Leading Digit). A dataset is said to satisfy Benford’s law for the leading digit if the frequency of having the leading digit d is given by ${log}_{10}((d+1)/d)$ for all $1\le d\le 9$.

There are several approaches to proving that a dataset follows Benford’s law. A standard method is to use the Uniform Characterization Theorem. For this, we first introduce the notion of the significand of a real number.

Definition 2 

(The Significand). For any $x>0$, we can uniquely write

$$x=S_{10}\left(x\right)·{10}^{k_{10}\left(x\right)},$$

(1)

where $S_{10}\left(x\right)\in [1,10)$ and $k_{10}\left(x\right)\in \mathbb{Z}$. Equivalently, $k_{10}\left(x\right)=\lfloor {log}_{10}\left(x\right)\rfloor$ and $S_{10}\left(x\right)=x/{10}^{k_{10}\left(x\right)}$. We call $S_{10}\left(x\right)$ the significand of x.

The following definition generalizes Benford’s law from the leading digit to the entire significand.

Definition 3. 

A sequence of random variables ${\left\{X^{\left(N\right)}\right\}}_{N=1}^{\infty }$ is said to converge to strong Benford’s law if

$$\underset{N\to \infty }{lim}\mathbb{P}(S_{10}\left(X^{\left(N\right)}\right)\le s)={log}_{10}\left(s\right)$$

(2)

for all $s\in [1,10)$. Note that the index N typically represents the size of the dataset, so convergence to strong Benford’s law should be interpreted as an asymptotic property.

Definition 4 

(Uniform Distribution Modulo 1). A sequence of random variables ${\left\{X^{\left(N\right)}\right\}}_{N=1}^{\infty }$ is said to converge to being equidistributed mod 1 if

$$\underset{N\to \infty }{lim}\mathbb{P}(X^{\left(N\right)}\mathrm{mod} 1\le s)=s$$

(3)

for all $s\in [0,1]$.

We are now ready to state the Uniform Characterization Theorem [8].

Theorem 2 

(Uniform Characterization Theorem). A sequence of random variables converges to strong Benford’s law if and only if the sequence of their base-10 logarithms converges to being equidistributed mod 1.

Thus, convergence to strong Benford’s law is equivalent to convergence to equidistribution modulo 1. Consequently, proving or disproving convergence to strong Benford’s law can be reduced to proving or disproving convergence to equidistribution modulo 1. In what follows, we illustrate the above definitions with an example of random variables that converge to strong Benford behavior, as well as an example of random variables that do not.

Example 1. 

Let $X^{\left(N\right)}=e^{Y^{\left(N\right)}}$, where $Y^{\left(N\right)}$ is normally distributed with mean 0 and variance N. No assumptions are made on the dependence structure among the $Y^{\left(N\right)}$. Then the sequence ${\left\{X^{\left(N\right)}\right\}}_{N=1}^{\infty }$ converges to strong Benford’s law. This follows from the fact that ${\left\{Y^{\left(N\right)}\right\}}_{N=1}^{\infty }$ is equidistributed modulo 1. For details, see [8].

Example 2. 

Let $X^{\left(N\right)}$ be uniformly distributed on $[0,1]$ for all $N\ge 1$, with no assumptions on dependence among the $X^{\left(N\right)}$. Then for every N,

$$\begin{array}{c}\hfill \mathbb{P}(S_{10}\left(X^{\left(N\right)}\right)\le s)=s.\end{array}$$

(4)

By comparison with Definition 3, it follows that ${\left\{X^{\left(N\right)}\right\}}_{N=1}^{\infty }$ does not converge to strong Benford’s law.

1.2. Fixed-Proportion Stick Fragmentation Model and the Multinomial Distribution

Now that we have a proper foundation for Benford’s law, it is time to describe in detail the model used in this paper. The model can be viewed as an extension of a model introduced by Becker et al., called the fixed single-proportion stick fragmentation model [21].

Suppose we start with a stick of length L. We split the stick at a fixed proportion of $0<p<1$. After the first break, we obtain two sticks of lengths $Lp$ and $L(1-p)$. We then split each of these two sticks again at the same fixed proportion p, producing four sticks of lengths $L{p}^2$, $Lp(1-p)$, $L(1-p)p$, and $L{(1-p)}^2$. Repeating this process for N stages, we obtain $2^N$ sticks in total, with $N+1$ distinct lengths. These lengths follow a binomial distribution.

Becker et al. were interested in whether the leading digits of the significands of the stick lengths converge to strong Benford’s law. They discovered a necessary and sufficient condition for this convergence and proved it in [21].

Theorem 3 

(Fixed Single-Proportion Stick Fragmentation Theorem [21]). Consider the fixed single-proportion stick fragmentation model. Choose y so that ${10}^y=(1-p)/p$. The fragmentation model produces stick lengths that converge to strong Benford’s law if and only if y is irrational.

In the non-Benford case, Becker et al. observed cyclic behavior in the significands and used the multisection formula [23]. By contrast, establishing the Benford case was more difficult. They adopted methods from [22,24,25], applying truncation to demonstrate roughly equal probability across intervals, and ultimately proved equidistribution modulo 1. In summary, they showed that stick lengths governed by a binomial distribution converge to strong Benford’s law when the ratio equals 10 and is raised to an irrational power and fail to converge when the ratio equals 10 and is raised to a rational power.

We now extend their fixed single-proportion stick fragmentation model to what we call the fixed multi-proportion stick fragmentation model. Becker et al. considered only the case in which the stick L is cut at a single fixed proportion p at each stage. We generalize this by cutting the stick at multiple distinct fixed proportions $p_1,p_2,\dots ,p_{m-1}$ at every stage. Our model is as follows:

Suppose we have a stick of length L. We split the stick simultaneously at fixed proportions $p_1,p_2,\dots ,p_{m-1}\in (0,1)$, with $p_1+\cdots +p_{m-1}<1$. Define $p_m:=1-(p_1+\cdots +p_{m-1})$. Thus, after Stage 1, we obtain sticks of lengths $L{p}_1,L{p}_2,\dots ,L{p}_m$. At Stage 2, we cut each stick obtained from the previous stage at the same fixed proportions $p_1,p_2,\dots ,p_{m-1}$. The resulting stick lengths from Stage 2 are $L{p}_1^2,L{p}_1{p}_2,\dots ,L{p}_1{p}_m$, $L{p}_2{p}_1,L{p}_2^2,\dots ,L{p}_2{p}_m$, and so on. 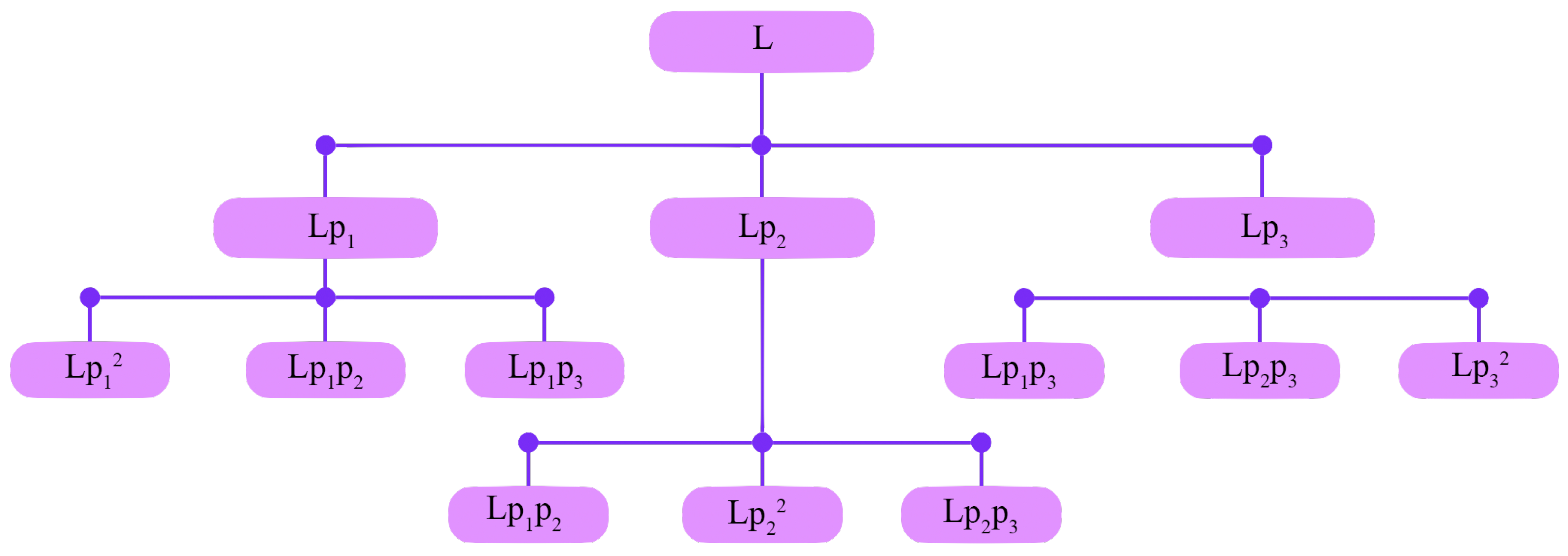After Stage N, we are left with $m^N$ sticks in total, with $\left({\displaystyle \genfrac{}{}{0pt}{}{m+N-1}{N}}\right)$ distinct lengths (see Figure 3 for the case where $m=3$ and $N=2$). The number of distinct lengths arises because the process can be interpreted as unordered sampling with replacement.

Moreover, the stick lengths are distributed according to a generalization of the binomial distribution known as the multinomial distribution, which is defined in terms of the multinomial coefficient, which itself is a generalization of the binomial coefficient. We recall the following definition and result (see [26]).

Definition 5 

(Multinomial Coefficient). For any non-negative integer N and positive integer m, the multinomial coefficient is

$$\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k_1,k_2,\dots ,k_m}}\right)={\displaystyle \frac{N!}{k_1!k_2!\cdots k_m!}}$$

(5)

for $k_1+k_2+\cdots +k_m=N$. A random vector $\left(X\right)=(X_1,X_2,\dots ,X_m)$ follows a multinomial distribution with parameters N and $\left(p\right):=(p_1,p_2,\dots ,p_m)$ if

$$\begin{array}{c}\hfill \mathbb{P}(\left(X\right)=\left(k\right))=\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k_1,k_2,\cdots ,k_m}}\right)p_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m}\end{array}$$

(6)

for all $\left(k\right):=(k_1,k_2,\dots ,k_m)$ with $k_1+k_2+\cdots +k_m=N$.

Remark 1. 

Formula (5) gives the number of ways to choose N objects with exactly $k_j$ objects of type j, which is when order does not matter.

Theorem 4 

(Multinomial Theorem). Let N be any non-negative integer and $p_1,p_2,\dots ,p_m$ be real numbers. Then

$${(p_1+p_2+\cdots +p_m)}^N=\sum _{k_1+k_2+\cdots +k_m\ge 0}\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k_1,k_2,\dots ,k_m}}\right)p_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m},$$

(7)

where the $k_j$s are non-negative integers summing to N.

2. Fixed Multi-Proportion Stick Fragmentation Model

Recall that we are interested in studying whether or not a stick fragmentation process results in stick lengths that converge to strong Benford’s law. For Becker et al., they were able to prove that if the ratio $(1-p)/p$ is equal to 10 and to an irrational power, the stick lengths will follow strong Benford’s law, but if the ratio is equal to 10 and to a rational power, then the distribution of stick lengths will not follow strong Benford’s law.

In what follows, we generalize the results of Becker et al. to the fixed multi-proportion stick fragmentation model we introduced in Section 1.2. In particular, we present Theorem 1 again along with the proof for the necessity of the condition.

Theorem 1. 

Let $m>2$ be an integer, and choose $p_1,p_2,\dots ,p_m\in (0,1)$ such that $p_1+p_2+\cdots +p_m=1$. At each stage, a stick is split into m substicks according to the proportions $p_1,p_2,\dots ,p_{m-1}$. After N stages, the process produces $m^N$ sticks, whose lengths are $A_{k_1,k_2,\dots ,k_m}=L{p}_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m}$ for all non-negative integers $k_1,k_2,\dots ,k_m$ with $k_1+k_2+\cdots +k_m=N$. For $1\le i\le m-1$, set $y_i={log}_{10}(p_i/p_{i+1})$. Then the stick lengths converge to strong Benford behavior if and only if $y_i$ is irrational for some $1\le i\le m-1$.

We prove the necessity of the condition; i.e., if $y_i$ is rational for all $1\le i\le m-1$, then the stick fragmentation model produces lengths that do not converge to strong Benford’s law. The sufficiency of the condition, i.e., if $y_i$ is irrational for some $1\le i\le m-1$, then the model produces lengths that converge to strong Benford’s law, is more technical; see [27] for details. Before presenting the proof, we refer the reader to numerical simulations supporting the theorem. See Figure A1 for rational cases and Figure A2 for irrational cases.

Proof. 

By the Uniform Characterization Theorem 2, it suffices to show that

$$\begin{array}{c}\hfill {log}_{10}\left(A_{k_1,k_2,\dots ,k_m}\right)=L{log}_{10}\left(p_1^{k_1}{p}_2^{k_2}\dots p_m^{k_m}\right)\end{array}$$

(8)

is not equidistributed mod 1. Since Benford’s law is scale-invariant [6], we may assume $L=1$ without the loss of generality. Each stick length $A_{k_1,k_2,\dots ,k_m}$ factors as

$$\begin{array}{c}\hfill A_{k_1,k_2,\dots ,k_m}=p_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m}={\left({\displaystyle \frac{p_1}{p_2}}\right)}^{k_1}{\left({\displaystyle \frac{p_2}{p_3}}\right)}^{k_1+k_2}\cdots {\left({\displaystyle \frac{p_{m-1}}{p_m}}\right)}^{{\sum }_{j=1}^{m-1}{k}_j}{\left(p_m\right)}^N.\end{array}$$

(9)

Since $y_i$ is rational for all $1\le i\le m-1$, write $y_i=a_i/b_i$ with $a_i\in \mathbb{Z}$, $b_i\in {\mathbb{Z}}_{>0}$, and $\gcd (a_i,b_i)=1$. Then

$$\begin{array}{c}\hfill A_{k_1,k_2,\dots ,k_m}={\left({10}^{{\displaystyle \frac{a_1}{b_1}}}\right)}^{k_1}{\left({10}^{{\displaystyle \frac{a_2}{b_2}}}\right)}^{k_1+k_2}\cdots {\left({10}^{{\displaystyle \frac{a_{m-1}}{b_{m-1}}}}\right)}^{{\sum }_{j=1}^{m-1}{k}_j}{\left(p_m\right)}^N.\end{array}$$

(10)

Taking ${log}_{10}$ gives

$$\begin{array}{c}\hfill {log}_{10}\left(A_{k_1,k_2,\dots ,k_m}\right)=k_1\left({\displaystyle \frac{a_1}{b_1}}\right)+(k_1+k_2)\left({\displaystyle \frac{a_2}{b_2}}\right)+\cdots +\left(\sum _{j=1}^{m-1}{k}_j\right)\left({\displaystyle \frac{a_{m-1}}{b_{m-1}}}\right)+N{log}_{10}\left(p_m\right).\end{array}$$

(11)

The term $k_1(a_1/b_1)$ has at most $b_1$ distinct values under mod 1, since it is periodic with a period of at most $b_1$. More generally, $\left({\sum }_{j=1}^i{k}_j\right)(a_i/b_i)$ has at most $b_i$ distinct values under mod 1. The term $N{log}_{10}\left(p_m\right)$ is constant across all $A_{k_1,k_2,\dots ,k_m}$. Hence, ${log}_{10}\left(A_{k_1,k_2,\dots ,k_m}\right)$ has at most ${\prod }_{i=1}^{m-1}{b}_i$ distinct values, independent of N. This number is also finite for fixed m, $b_1,\dots ,b_{m-1}$.

Since a uniform distribution on $[0,1]$ is continuous and thus not discrete, ${log}_{10}\left(A_{k_1,k_2,\dots ,k_m}\right)$ cannot be equidistribted mod 1. Thus, the fragmentation process produces stick lengths that do not converge in distribution to strong Benford’s law. □

3. Conclusions

In this paper, we extended the fixed single-proportion stick fragmentation model of Becker et al. [21] to the fixed multi-proportion setting and determined precisely when Benford behavior arises. We proved the necessity of the condition by showing that in the purely rational case, the logarithms of the stick lengths lie on a finite lattice and convergence fails. This provides a sharp criterion that fully characterizes Benford behavior in the multi-proportion model.

Our results show that the emergence of Benford’s law is governed by the arithmetic properties of the proportions. Numerical simulations confirm these results, illustrating clear non-Benford behavior in rational cases and rapid convergence otherwise. This work thus generalizes earlier results and clarifies the precise mechanism by which Benford behavior arises in a deterministic fragmentation process.

4. Future Work

Our proof of necessity in Theorem 1 shows that ${log}_{10}\left(A_{k_1,k_2,\dots ,k_m}\right)$ takes at most ${\prod }_{i=1}^{m-1}{b}_i$ distinct values and therefore is not equidistributed mod 1. However, it does not explicitly determine the exact distribution. An interesting direction for future work is to ask whether the distribution converges to a discrete uniform distribution and, if not, to characterize it under various assumptions.