Predictions of War Duration

Abstract

The durations of wars fought between 1480 and 1941 A.D. were found to be well represented by random numbers chosen from a single-event Poisson distribution with a half-life of (1.25 ± 0.1) years. This result complements the work of L.F. Richardson who found that the frequency of outbreaks of wars can be described as a Poisson process. This result suggests that a quick return on investment requires a distillation of the many stressors of the day, each one of which has a small probability of being included in a convincing well-orchestrated simple call-to-arms. The half-life is a measure of how this call wanes with time.

1. Introduction

War is what humans do—it is human nature. Other social species might appear to wage war, like ants, but not with the sophistication and forethought that humans bring to war. Humans form into tribes that wage war on other tribes seemingly for the benefit of those at the top of the tribe hierarchy. War is complex, it requires mobilizing men and machines and moving them to the killing grounds. War is complex, it requires making weapons of war, it requires clothing, feeding, and sheltering the fighters, repairing them when they are wounded. War needs to happen during the day and night, and during all seasons. War needs an infrastructure of command-and-control, and logistics. War needs to convince young men and women to fight and kill other young men and women. War needs parents willing to risk the lives of their children. War needs a reason(s) for society to say yes. War is something humans cannot seem to avoid. War may be complex, but we do it regardless.

There are other things found in nature that are very complex, so complex that sometimes, perhaps paradoxically, some of their properties can be described in simple ways. There are 92 elements that make up our universe. These elements exist in different forms, some of which are stable, but many are not. What happens inside the nucleus of an element is very complex. There are neutrons and protons bound together by strong force, but these can interchange because of the weak force. The theories that explain why these elements are stable, or not, are complex constructions of quantum mechanics and Einstein’s theory of relativity. Yet, an unstable element can change by an apparently simple process called radioactive decay. For all the underlying complexities of what happens inside a nucleus, radioactive decay can be described with simple equations. The purpose of this paper is to analyze the duration of war from a physics perspective [1] with simple equations such as those used to describe radioactive decay. Is war so complex that it is simple?

This paper complements the work of L.F. Richardson who found that the frequency of outbreaks of wars can be described as a Poisson process [2]. A tribute to the work of Richardson can be found in the series of papers edited by Gleditsch [3].

In complementary contrast to the work of Richardson on the frequency of outbreaks, this paper shows an analysis of the distribution of the duration of wars and, perhaps not surprisingly, it is found that how long wars last can also be described as a Poisson process.

2. Theory and Results

Radioactive decay has two outcomes: a nucleus has decayed or not. War is similar: you are at war, or not. Bernoulli trials are used to describe situations where there are two possible outcomes such as true or false, and yes or no. As an example, we can calculate the probability of finding one nucleus that has undergone radioactive decay in a group of nuclei. Let p be the average decay probability of a nucleus and let n be the number of nuclei. There are n choices for the nucleus that will decay, each with probability p, so the probability of finding a decayed nuclei will be the product np. If one nucleus decays, then the rest of the nuclei will not decay if we are to have only one decay in the lot. The probability that a nucleus will not decay is equal to ‘one’ minus the probability that it will decay, or (1 − p). (The ‘one’ is because the probabilities for yes and no, or true and false, must add to one because there are only two choices). There are (n − 1) nuclei that will not decay for the current example calculation where one nucleus decays and all the others do not. The probability of finding one decay event, B₁, in n nuclei is the product of the probability of all the possible single successful decays, np, and the probability of the n − 1 failures:

$$B_1=np{(1-p)}^{n-1}$$

(1)

The connection with war is that Equation (1) will be related to the probability of finding a single occurrence of war in the world. Equation (1) is not useful for the current analysis because n and p are not known separately. For many practical applications, n is large, p is small, and np is small compared with n. In these applications Equation (1) takes a different form—the derivation that follows is standard; it is included here to emphasize the importance of small p and large n to the final form. To derive the form where p is small and n is large, we notice that Equation (1) is unchanged if we take the natural logarithm of the righthand side and then use the exponential function, which is the anti-logarithmic function, to reverse the logarithmic transformation, we get:

$$\begin{array}{cc}\hfill B_1& =\exp [\ln np{(1-p)}^{n-1}]\hfill \\ & =\exp [\ln np+(n-1)\ln (1-p)]\hfill \end{array}$$

(2)

The last term in Equation (2), ln(1 − p), can be expanded as a Taylor series:

$$\begin{array}{cc}\hfill \ln (1-p)& =-p-{\displaystyle \frac{1}{2}}{p}^2-{\displaystyle \frac{1}{3}}{p}^3-\mathrm{\dots }\hfill \\ & \approx -p \mathrm{for} \mathrm{small} p\hfill \end{array}$$

(3)

Substituting Equation (3) for small p into Equation (2) yields:

$$B_1\approx \exp [\ln np+(n-1)(-p)] \mathrm{for} \mathrm{small} p$$

(4)

If n is large, then n − 1 ≈ n, and Equation (4) becomes:

$$P_1=np\exp (-np) \mathrm{for} \mathrm{small} p \mathrm{and} \mathrm{large} n$$

(5)

Equation (5) is the Poisson probability of finding a single event, be it a single radioactive decay in the presence of many similar nuclei that could decay but do not, or a single war in the world. For war, n could represent the large number of potential conflicts, each one of which has only a small probability of erupting into war in any one year.

The product np is often replaced by a single parameter, λ. Using arguments like those that led to Equation (5), leads to the Poisson probabilities proposed for the number of wars, k, in the world:

$$\begin{array}{l}{P}_0=\exp (-\lambda )\\ P_1=\lambda \exp (-\lambda )\\ P_2={\displaystyle \frac{{\lambda }^2}{2}}\exp (-\lambda )\\ P_3={\displaystyle \frac{{\lambda }^3}{3!}}\exp (-\lambda )\end{array}$$

(6)

In general,

$$P_k={\displaystyle \frac{{\lambda }^k}{k!}}\exp (-\lambda )$$

(7)

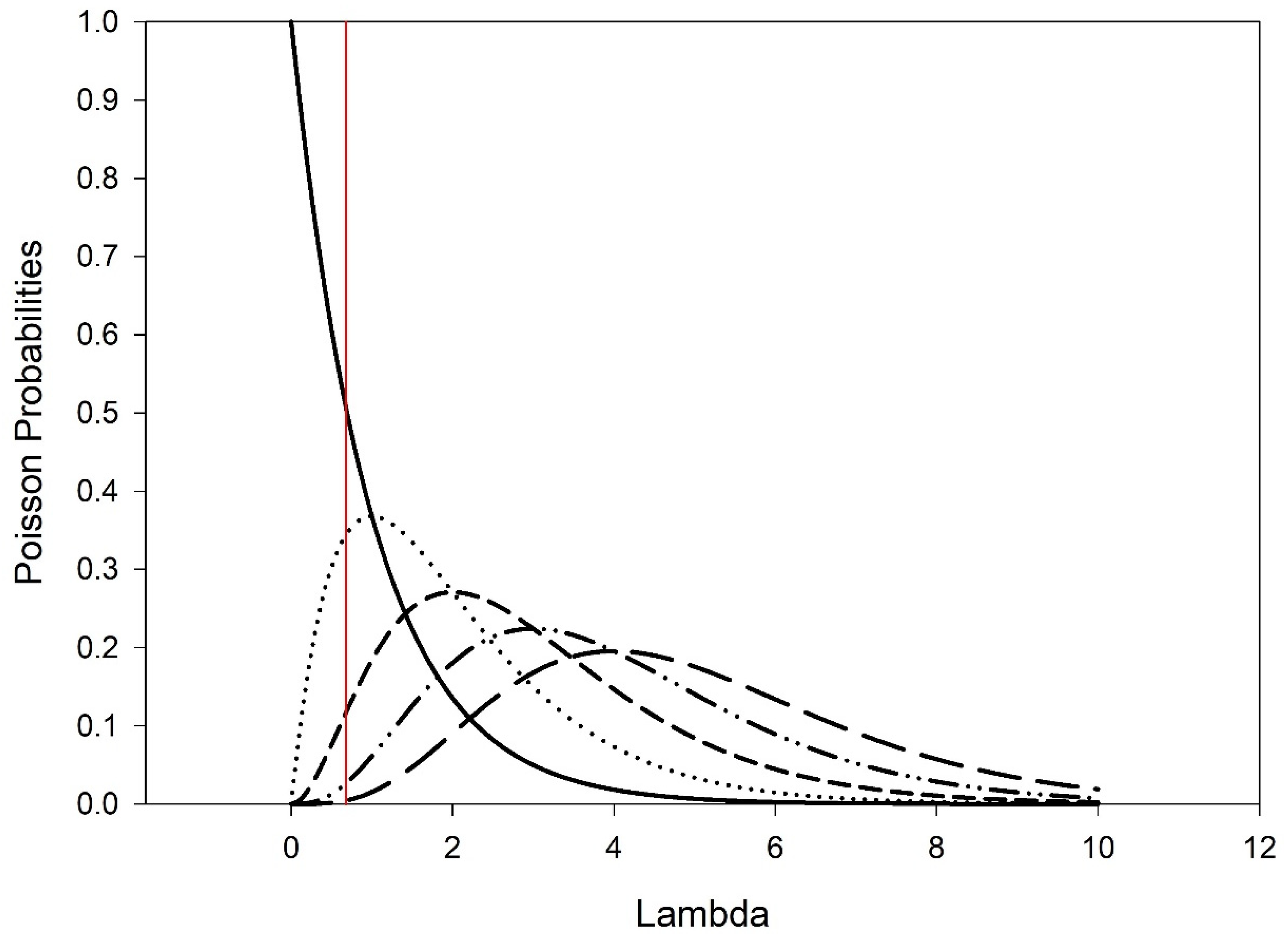
Poisson equations are plotted in Figure 1. The Poisson distribution given by Equation (7) applies to systems with large numbers of possible events each of which has a low probability of occurring. The number of such events happening in a fixed time interval (e.g., one year) is a random number with a Poisson distribution.

In his seminal paper published towards the end of World War II, L.F. Richardson analyzed the number of outbreaks of wars per year using the Poisson equations [2]; see a very slightly updated version of his results in

Table 1. Number of outbreaks of k wars per year from 1500 to 1931 A.D. based on Richardson [2] with λ = 0.68.

k	0	1	2	3	4	≥5	Total
Number of such years	223	142	48	15	4	0	N = 432
Relative probability	0.516	0.329	0.111	0.035	0.009	0.000	1.000
Poisson probability	0.503	0.343	0.117	0.027	0.0045	0.000	1.000

. As examples, between 1500 and 1931 A.D., there were 223 years where no wars started (i.e., k = 0) and 142 years where one war started (i.e., k = 1). The Poisson probabilities in Table 1 are given by the intersections of the vertical line in Figure 1 at λ = 0.68 with the P_k curves determined by weighted least squares regression.

The remarkable agreement of the observed probabilities for the outbreak of war in any year with the Poisson probabilities led Richardson to hypothesize [2]:

‘in any year there were the same large number n of occasions on which a war might have broken out, and the same small probability p of its doing so on each occasion, so that np = λ.’.

Apparently, war is a consequence of our collective frustration.

There is no time dependence in the Poisson Equations (6) and (7), or Figure 1. If the number of events happens over time, t, then the Poisson equations can be modified with λ = t/τ, where τ is a time constant equal to the reciprocal of the average rate for the probability at which events occur. In this instance, the Poisson probability for a single event becomes:

$$P_1={\displaystyle \frac{t}{\tau }}\exp (-t/\tau )$$

(8)

The horizontal axis in Figure 1 will now become time dependent and scaled by the time constant. The peak of the P₁ distribution will be when λ = 1, or t = τ. Equation (8) will be used to describe the distribution of the durations of wars.

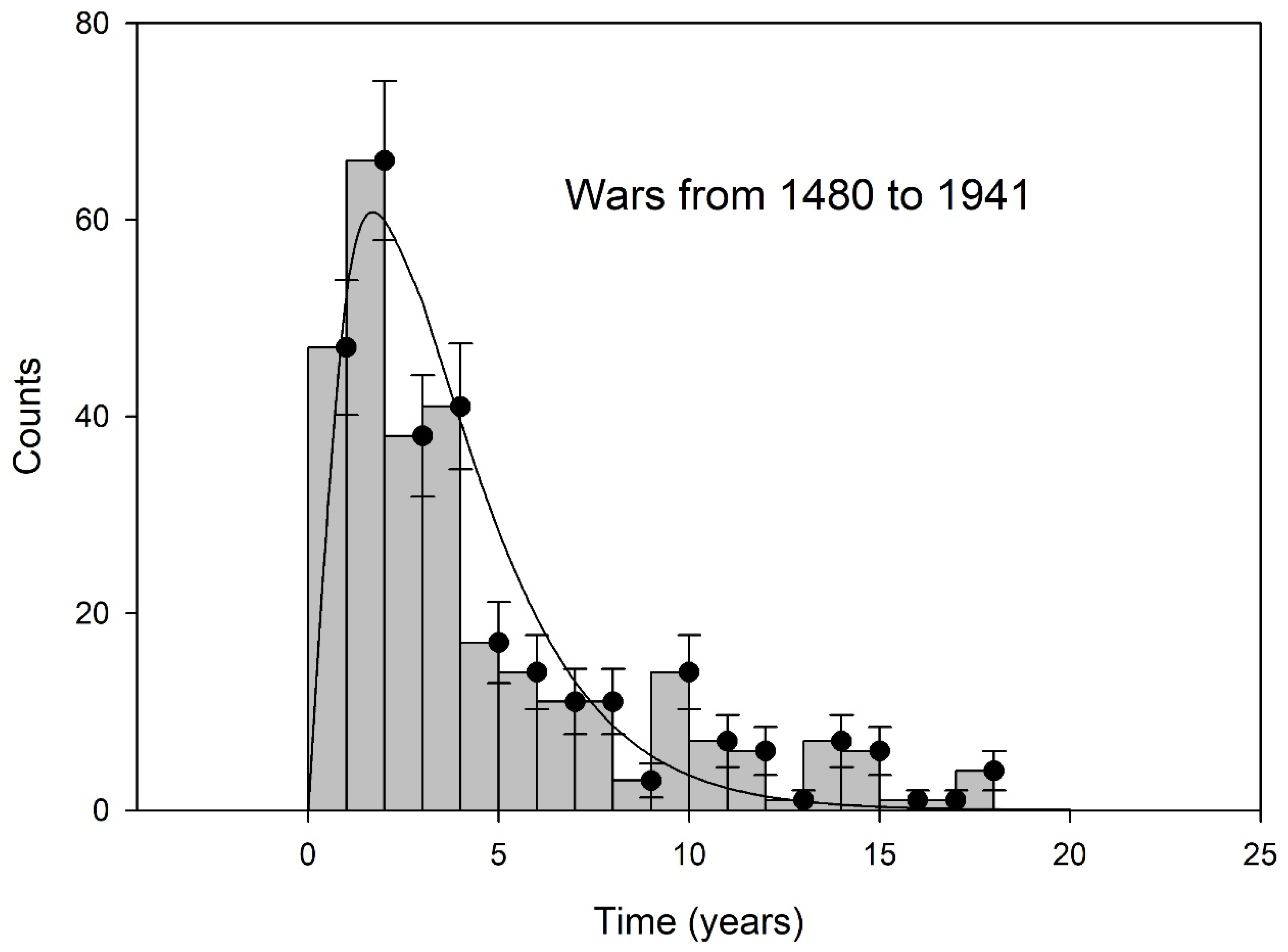
The durations of wars were obtained from the differences between the end date and the starting date of the wars listed in Appendix XX of the book by Quincy Wright [4]—wars in this list have consistently defined end and start dates. These durations were binned in one-year intervals from 0 to 18 years, i.e., 0 to 1, 1 to 2, 2 to 3, etc. The counts in each bin are plotted as a histogram in Figure 2. The error bars in Figure 2 are equal to the square root of the counts in each bin. The counts in each bin are labeled with a common duration d equal to the value at the end of the time interval of each bin. These counts can be calculated with Equation (8):

$$\mathrm{The} \mathrm{predicted} \mathrm{counts} \mathrm{of} \mathrm{wars} \mathrm{of} \mathrm{duration} d: C(d)=C_T\times P_1/\tau$$

(9)

where C_T is the total number of wars in the sample. The results of fitting Equation (9) to categorized (i.e., binned) war durations are shown in Figure 2.

A half-life can be calculated from the value of τ, (1.80 ± 0.14) years, determined from the regression of the war durations to Equation (9). The half-life is most often associated with the simple exponential decay for P₀ given by Equation (6) modified with λ = t/τ:

$$P_0=\exp (-t/\tau )$$

(10)

The half-life is the time when P₀ drops to half of its initial value:

$$\begin{array}{cc}\hfill t_{1/2}& =\tau \ln 2\hfill \\ & =1.25\pm 0.1 \left[\mathrm{yrs}\right].\hfill \end{array}$$

(11)

A half-life can also be estimated from the number of outbreaks of wars in Table 1. The Poisson probability is 0.503 for k = 0 and λ = 0.68. Hence, this value of λ is associated with the half-life: t_1/2 = λ τ = 0.68 × (1.80 ± 0.14) = 1.2 years. The agreement of these two half-lives, one calculated from how long wars last and the other calculated from how many years in which there were no outbreaks of war, is expected, but it is remarkable, nonetheless. For a more detailed study of how the onset of wars might relate to duration see [5].

3. Discussion

The original result reported by Richardson shown in Table 1, that the number of outbreaks of war in a year followed Poisson statistics, was interpreted by some to mean wars just happen randomly like radioactive decay, which also obeys Poisson statistics. Smith commented on Table 1 [6]:

“Considering the small numbers involved, the agreement is remarkably good. To a first approximation, mankind behaves as if there were a large number of potential conflicts, each one of which has only a small probability of erupting in any one year. This is obviously an oversimplification; but it has enough truth to be quite disturbing in its implications.”.

This comment echoes Richardson’s hypothesis quoted earlier and uses words that come from the derivation of the Poisson distribution formulas (i.e., large n and small p).

This random happenstance interpretation was not well received by those who thought humans were more sophisticated than radioactive decay: when humans go to war to kill other humans they do so with a purpose. The durations of wars shown in Figure 2 suggest any new interpretation should include a discussion of time because it seems that how long a war lasts is pre-ordained or at least constrained by the P₁ distribution and a half-life. Any explanation will have to be simple without many details to match the simplicity of the Poisson distribution.

War is a way for the rich and powerful in society to become richer and more powerful, especially if they are on the victorious side. For a war to happen, the rich and powerful must convince the poor and weak of their society to give up their time and risk their lives battling the poor and weak of a rival society. There needs to be a convincing call-to-arms for a war to happen, otherwise the poor and weak will stay home. There are many calls that have worked in the past and will no doubt work again. These calls include for king and country, to defend the faith, to promulgate the faith, to show the mercy of the faith, to kill the unbelievers, to establish order, to protect our kind, to avenge a wrong, and the old lie: dulce et decorum est Pro patria mori; the call does not have to be true, just effective. The rich and powerful employ astute propagandists to probe for the stressors in society that can be manipulated and morphed into a call-to-arms, a rallying cry, that will provide a reason for war to those who will do the fighting. This call-to-arms is then relayed to the combatants through well controlled media and messaging. There are a multitude of stressors in society, but each has only a small probability of being manipulated in a way to incite people to war. But eventually, seemingly randomly, a short list of grievous issues worth dying for is culled from the list of stressors, some issues being more tangible and important than others [7]. From these issues a convincing call-to-arms is found, and this rallying cry is the ‘reason’ to go to war.

In this interpretation the half-life is a consequence of how the ability of the ‘reason’ to rally the poor and weak wanes with time. War is hell. Any reason, all reasons, can sustain risking life and limb for only so long. With time, the horrors of war mitigate the reason for the war amongst those fighting the war. The Poisson analysis of the duration of wars suggests that the compelling nature of the reason to go to war must be consistent with the half-life of 1.25 years. Going to war requires a powerful emotional commitment that is buttressed by the state-sponsored reason for the war. The half-life is proposed to be a measure of how difficult it is to maintain this commitment in light of the realities of war. This interpretation is anthropomorphic but pleasing because it allows for some aspect of the human condition to mitigate the seeming inevitability of the randomness of the Poisson distribution. Half of wars end after a winter campaign suggesting that cold lessens the clarion call: battles are interrupted by night and wars by winter. The mitigating effect of fighting over four seasons, and especially over a winter, is more difficult to realize if the mean duration of wars is the statistic used instead of the half life: the mean duration, equal to 2τ = 3.6 years, includes 3 or 4 winters: mean values are not representative of Poisson distributions because they do not represent the most probable values, i.e., the peak values.

There are billions of humans on the planet each with a small probability of being rich and powerful and in the right place at the right time when there is exploitable unrest to be manipulated for the benefit of the few and the detriment of the many who will kill and be killed for reasons that in hindsight will appear trite and made-up. The half-life would then be a consequence of evolution, it has the value it has because societies suffering wars with longer half-lives did not survive and/or the rich and powerful wanted a timely return on investment—war is a great investment, but eventually those fighting it lose their commitment and, in the worst instances, a revolution ensues that can be bad for the rich and powerful, as seen in the French and Russian revolutions.

Or maybe, humans form complex societies all of which are inherently unstable like some nuclei. If there were an instrument like a Geiger counter for societies, war would be just another click. God might be playing dice.

A consequence of the success of the Poisson distribution demonstrated in this paper is that all attempts to construct predictive models of durations of war will fail. Random events cannot be predicted. Thus, Cioffi-Revilla [8] predicted the duration of an Iraq–UN war could be “anywhere between days and years, fully across two orders of magnitude …”. Bennett and Stam [9] presented detailed hazard-model analyses of 78 wars with up to 17 independent variables. They found values for the mean absolute error in their ability to predict the duration of wars ranged between 330% and 1000% in naïve models. The prediction error (on average) in their complete best model was 3.3 times higher and lower than the actual length of the war. To provide some context, if the true duration of a war were 10 years, the best hazard-model prediction would be anywhere between 3 and 33 years. They conclude “But while individual hypothesis tests indicate that the individual parameters are statistically significant, and likelihood ratio tests indicate that the overall model provides a statistically significant improvement in fit to the data versus the null, much of the variation in war duration clearly remains to be explained in ongoing work.” Statistical significance can be misleading [10]. Models with 17 variables should not only be able to fit an elephant and wiggle his trunk [11] but make him dance. The suggestion that more than 17 parameters are needed to explain ‘much of the variation in war duration’ leads to many parameters (i.e., reasons), each necessarily with a small probability of being a reason for wars to end.

A contemporary example of a failure to predict how long a war will last is Putin’s war on Ukraine. At its onset, the war was predicted to last no more than two weeks, so said the pundits, Putin, and the Generals [12]. The war has been going on for years. Russian generals and military pundits no doubt have many reasons for why the war has lasted longer than the predicted duration at the onset.

Another example is the prediction by US Secretary of Defense Donald Rumsfeld for the length of the war with Iraq: “It is unknowable how long that conflict [the war in Iraq] will last. It could last six days, six weeks. I doubt six months.” [13]. The war lasted 8 years.

The best models for the durations of wars cannot produce predictions within an order of magnitude of observed values; arguably, not being able to predict within an ‘order of magnitude’ is no better than guessing. An alternative interpretation of the results of Bennett and Stam, and Cioffi-Revilla, and Putin’s war, is that the durations of wars cannot be predicted, which leads to the Poisson process proposed in this paper. An interesting conclusion of Bennett and Stam is that war is not duration-dependent. How long a war will eventually last does not depend on how long it has lasted. Thus, predictions of the end of war cannot be made with any reasonable confidence partway through a war. This independence of the future with the past is a characteristic of a random Poisson process.

Prorok and Huth [14] review over 50 papers that offer new insight into how long wars might last. These insights are often contradictory. For instance, “A major innovation in this literature in the past 10 to 15 years has been the extension of the bargaining model of war from its original application in the context of war onset … to its use in the context of war duration, termination, and outcome.” Bargaining models focus on relative military capabilities and battlefield developments. “This focus, however, has spawned a backlash in recent years, as patterns that contradict the implications of bargaining models are detected and theorized.” [14]. Many different conflicting models should be expected for models of random events.

In a survey of closely related domestic political conflict (DPC) models, Lichbach made the provocative conclusion that “Nobody Cites Nobody Else” [15]; the gist of this conclusion might be relevant to the current discussion of international conflict. “The fact that few formal modelers accord other formal modelers the respect of being cited implies that maybe the skeptics are right and the models really do not deserve respect.” Skeptics always raise one question: “what has really been accomplished by these formal models? Are they mere mathematical curiosities, interesting exercises in technical virtuosity, or will we really understand DPC better” because of these models? Few modelers build on the models of previous modelers, “formal modelers of domestic political conflict keep reinventing the wheel.” A more charitable interpretation is that these models are not cited because they do not work. Causal models cannot be found to describe random events, by the definition of the word ‘random’.

The P₁ model accounts for about 80% of the variability shown in the duration histogram (Figure 2), i.e., the Coefficient of Determination is R² = 0.8, suggesting that as much as 20% of the variability might be attributed to additional processes that could be non-random. There are not enough details in the data to distinguish a non-random process. An example of a non-random process might be seen for countries who start wars when they expect them to be short and then seek to end wars quickly when their prewar estimates of short wars turn out to be incorrect. Such a process might skew the histogram to the right and shorter times [5].

Instead of looking for the reasons we go to war, the current results suggest it is better to focus on how to mitigate the consequences of the randomness of war. Wars start and end randomly. People generally believe themselves to be masters of their fates. Challenge people to reconcile attending a randomly orchestrated war, killing and maybe being killed, and then told to stop killing after some random time all for some reasons of the day. Perhaps, someday in the distant future we will realize that war is “instinctive. But the instinct can be fought. We’re human beings with the blood of a million savage years on our hands, but we can stop it. We can admit that we’re killers, but we’re not going to kill today. That’s all it takes. Knowing that we won’t kill today.” [16].

The interpretation of the current results suggests a mitigating solution, at least in theory. Wars will be harder to justify if there is a truly free press that challenges the foundations of the call to arms without fear and intimidation of being labeled traitors by the minions of the rich and powerful elites who orchestrate wars: a truly free press that shows the horrors of war; a truly free press that will remind us that the foes of today will be the friends of tomorrow. Perhaps, if people realize that they are most likely being conned by war hucksters, they will think twice about joining the fray—all for the want of free journalists with clarion counter-calls. Unfortunately, most press and news organizations are owned by the elites—another optimistic (naïve?) theory destroyed by a troublesome fact.

4. Conclusions

A simple Poisson analysis has been presented that describes the duration of wars fought between 1480 and 1941 A.D. These durations are well described by random numbers with a Poisson distribution for a single event happening with a peak probability time constant of (1.80 ± 0.14) years, which corresponds to a half life of (1.25 ± 0.1) years. These results are interpreted, to a ‘first approximation’, with the need to have a few simple issues to incite people to go to war. It is argued that these issues are developed from a large number of possible underlying stressors in society that are manipulated to form a call-to-arms, a rallying cry. Each of these stressors has only a small probability of contributing to the call-to-arms. The half life is proposed to be a measure of how the effectiveness of the call-to-arms wanes with time in the grime light of the realities of war that limits the time for a good return on investment. This interpretation is obviously an oversimplification, but it has enough truth to be quite disturbing in its implications, especially to someone contemplating heeding the call. Parents, teach your children statistics.