Still No Free Lunch: Failure of Stability in Regulated Systems of Interacting Cognitive Modules

Abstract

The asymptotic limit theorems of information and control theories, instantiated as the Rate Distortion Control Theory of bounded rationality, enable examination of stability across models of cognition based on a variety of fundamental, underlying probability distributions likely to characterize different forms of embodied ‘intelligent’ systems. Embodied cognition is inherently unstable, requiring the pairing of cognition with regulation at and across the various and varied scales and levels of organization. Like contemporary Large Language Model ‘hallucination,’ de facto ‘psychopathology’—the failure of regulation in systems of cognitive modules—is not a bug but an inherent feature of embodied cognition. What particularly emerges from this analysis, then, is the ubiquity of failure-under-stress even for ‘intelligent’ embodied cognition, where cognitive and regulatory modules are closely paired. There is still No Free Lunch, much in the classic sense of Wolpert and Macready. With some further effort, the probability models developed here can be transformed into robust statistical tools for the analysis of observational and experimental data regarding regulated and other cognitive phenomena.

1. Introduction

Recent studies by Wang et al. [1], Dulberg et al. [2], and others argue that AI must evolve into a distributed ecosystem in which multiple AI entities interact, specialize, and collectively enhance intelligence. A central assertion is that a modular architecture can learn more efficiently and effectively to manage multiple homeostatic objectives, in nonstationary environments, and as the number of objectives increases.

Much of the origin of this approach lies in the early work of Wolpert and Macready [3,4] —more recently, Shalev-Schwartz and Ben-David [5]—demonstrating that an optimizer tuned to be ‘best’ on one particular kind of problem must inevitably be ‘worst’ at some complementary problem set. Complex problems that divide ‘naturally’ into modular subcomponents can then be—it is hoped—efficiently addressed by an interacting system of cognitive modules, each individually tuned to be ‘best’ on the different problem components most representative of the embedding challenge environment. Success in such a ‘game’ requires matching cognitive system subcomponents to problem subcomponents in real time. This is not easy. As an anonymous commentator put the matter [6],

Apparently a proved theorem cannot be entirely circumvented by a framework consistent in the same formal foundation system, so [Mixture of Experts] just redistributes the challenge across the framework’s underlying components.

In particular, the maintenance of dynamic homeostasis under the Clauswitzian ‘selection pressures’ of fog, friction, and adversarial intent is far from trivial, and, among humans, even after some considerable evolutionary pruning, high-level cognitive process remains liable to debilitating ‘culture-bound syndromes’ often associated with environmental stress and related, inherently toxic, exposures and subsequent developmental trajectories (e.g., [7], Ch. 3).

We are, then, very broadly concerned with the maintenance of cognitive stability in a modular system under the burdens of what, in control theory, is called ‘topological information’ [8] imposed by disruptive circumstances, internally or externally generated.

Maturana and Varela [9] hold that the living state is cognitive at every scale and level of organization. Atlan and Cohen [10] characterize cognition as the ability to choose an action—or a proper subset—from the full set of those available, in response to internal and/or environmental signals. Such a choice reduces uncertainty in a formal manner and implies the existence of an information source dual to the cognitive process studied. The argument is direct and places cognition under the constraints of the asymptotic limit theorems of information theory [11,12,13].

More recently, the Data Rate Theorem [8] establishes conditions under which an inherently unstable dynamical process can be stabilized by the imposition of control information at a rate exceeding the rate at which the process generates its own ‘topological information’. The model depicts a vehicle driven at high speed along a twisting, potholed roadway. The driver must impose steering, braking, and gear-shift information at a rate greater than the road imposes its own topology, given the chosen speed.

Most real-world cognitive phenomena, from the living state to such embodied machine cognition as High Frequency Stock Trading [14,15,16], must act in concert with–be actively paired with–a regulator to successfully meet the demands of real-world, real-time function:

• Blood pressure must respond to changing physiological needs while remaining within tolerable limits.
• The immune system must engage in routine cellular maintenance and pathogen control without causing autoimmune disease by attacking healthy tissue.
• The stream of consciousness in higher animals must be kept within ‘riverbanks’ useful to the animal and its social groupings, particularly among organized hominids, the most deadly predators on Earth for the best part of half a million years.
• Human institutions and organizations, via ‘rule-of-law’ or ‘doctrine’ constraints, are notorious for cognition-regulation pairing.

Here, using the asymptotic limit theorems of information and control theories, we will explore, in a sense, the ‘metabolic’, ‘free energy’ and other such costs of this necessary pairing as the number of basic, interacting submodules rises, uncovering a truly remarkable set of scaling properties across the ‘fundamental underlying probability distributions’ likely to power and constrain a variety of important cognitive phenomena.

The probability models arising ‘naturally’ from this effort can serve as the basis of new statistical tools for the analysis of data related to the stability of cognitive phenomena across a broad range of phenomena. However, like the regression models derived from the Central Limit Theorem and related results, such tools do not, in themselves, ‘do the science’. This work has, consequently, focused on a range of models and modeling strategies. Not everything follows a $y=mx+b$ pattern. Sometimes things go as $y=m{x}^2+b$ or worse, hence our insistence on the analysis of dynamics across different underlying probability distributions.

Some current attempts at comprehensive cognitive models, e.g., ’integrated information theory’, ’the free energy principal’, ‘quantum consciousness’, have made claims of existential universality akin to a general relativity of biology and mind. This work, far more modestly, aims to derive tools that can aid the analysis of observational and experimental data, the only sources of new knowledge rather than new speculation.

That said, we do not at all denigrate the model-based speculations that might arise from our approach, provided they are ultimately constrained by effective feedback from data and experiment.

The development, unfortunately, is far from straightforward, and requires the introduction of some considerable methodological boilerplate, extending relatively simple ‘first order’ approaches abducted from statistical physics and the Onsager model of nonequilibrium thermodynamics, generalizing, in a sense, the results of Khaluf et al. [17], Kringlebach et al. [18], and other recent work.

An often-overlooked but essential matter is that information sources are not, like physical processes are assumed to be, microreversible, i.e., in English ‘the’ has a much higher probability than the sequence ‘eht’, implying a directed homotopy ultimately leading to groupoid symmetry-breaking cognitive phase transitions. Much–but not all–of this will be safely hidden in the relatively simple first-order formalism developed below.

Another common misunderstanding is the interpretation of Shannon uncertainty, as expressed mathematically, as an actual entropy. Following Feynman [19] and Bennett [20], information should be treated as a form of free energy that can be used to construct partition functions leading to higher-order free-energy constructs. This is, as Feynman remarks, a subtle matter.

More generally, as Khinchin [12] indicates, for nonergodic stationary systems, each message stream converges to its own source uncertainty that cannot be expressed in ‘entropy’ format. A standard approach from statistical physics, however, still allows construction of a partition function in such cases, hence an iterated free energy, and, via a Legendre Transform, a compound entropy measure. The gradient of that compound entropy can be taken as a thermodynamic force, thereby defining the rate-of-change of the underlying variates, thereby permitting standard stochastic extensions of the models. Again, however, this provides only an entry-level, first-order attack on a barbed-wire thicket of cognitive phenomena and their inevitable pathologies.

Although modern medicine can often perform seeming miracles against an increasingly wide spectrum of infectious and chronic diseases, the culture-bound syndromes of ‘madness’ remain largely intractable.

The narrowly trained designers and builders of cutting-edge artificial intelligence systems and entities are entering a Brave New World.

2. An Introduction to Method

2.1. Resources

Real-world, real-time systems are necessarily embedded in and of an environment that includes themselves. There must be at least three resource streams necessary for correct function:

• The rate at which elements of the system can communicate with each other, characterized by some channel capacity $\mathcal{C}$.
• The rate at which ‘sensory information’ is available from the embedding circumstance, according to the channel capacity $\mathcal{H}$.
• The rate at which ‘material/materiel’ resources can be provided, a rate $\mathcal{M}$. For an organism, this might be measured by the rate at which metabolic free energy is provided.

These rates cross-correlate and interact, generating a (minimally) 3 × 3 matrix $\mathbf{Z}$. An $n\times n$ matrix will have n scalar measures $r_i$ invariant under similarity transformations that are determined by the standard expression:

$$p\left(\gamma \right)=det[\mathbf{Z}-\gamma \mathbf{I}]=\sum _{k=0}^n{(-1)}^k{r}_k{\gamma }^{n-k}$$

(1)

I is the identity matrix, ‘det’ the determinant, and $\gamma$ a real-valued parameter. The first is the matrix trace, and the last is the determinant. We build a scalar resource rate measure from the $r_k$.

An elementary index might be $Z=\mathcal{C}\times \mathcal{H}\times \mathcal{M}$, but matters are not likely quite that simple.

We do, however, impose a first-order model, assuming that a single scalar index $Z(r_1,\dots ,r_n)$ can be constructed that sufficiently represents information and material resource rates. This argument is analogous to principal component analysis based on a correlation matrix. Wallace [21] outlines difficulties inherent to more than a single such index.

2.2. Rate Distortion Control Theory

An ‘embodied’ formalism emerges via a ‘Rate Distortion Control Theory’ based on the Rate Distortion Theorem (RDT) [11,12]. The RDT addresses transmission under conditions of noise over an information channel. There will be, for that channel and a particular scalar measure of average distortion D between what is sent and what is received, a minimum necessary channel capacity $R\left(D\right)$.

The theorem asks, in effect, what is the ‘best’ channel for transmission of a message with the least possible average distortion. $R\left(D\right)$ can be defined for nonergodic information sources via a limit argument based on the ergodic decomposition of a nonergodic source into a ‘sum’ of ergodic sources. The RDT can be reconfigured in a control theory context if we envision a system’s topological information from the Data Rate Theorem as another form of noise, adding to the average distortion D. See Figure 1.

The punctuation implied by the Data Rate Theorem (DRT) [8] happens if there is a critical maximum average distortion beyond which control fails.

Embodied cognition, characterized by continuous interaction with a real world having its own intents and capabilities—as indexed by the distortion between what is wanted and what is observed—is inherently a phenomenon of ‘bounded rationality’ in the sense of Ortega and Braun [22]. Cognition without such embodied interaction, however, as Dreyfus [14], Fjelland [15], and many others have noted, risks a narrow boundedness without rationality.

2.3. The ‘Tuning Theorem’

Parallel to both Rate Distortion Control Theory and the No Free Lunch Theorem is the ‘tuning theorem’, inverse of the Shannon Coding Theorem (SCT). The SCT holds that an ‘infinite’ message stream encoded so that its probabilities are ‘typical’ with respect to the channel along which it is transmitted can be sent with arbitrarily small error so long as the transmission rate is ≤C, the ‘capacity’ of that channel.

A relatively simple argument ([7], Section 12.2) shows that, conversely, if a message must be sent at a maximum possible rate, there is a channel which is effectively ‘transmitted by the message’ at an effective dual channel capacity $C^{*}$, where the channel probabilities are now made ‘typical’ with respect to that particular message. An inherently unstable system’s optimal ‘control message’ can thus be transmitted at the maximum rate by a ‘tuned channel’ optimized for that message. Different optimal control messages must be transmitted by different optimal channels; hence, the No Free Lunch Theorem: there is no single optimal channel for all possible control messages.

3. A Single Cognition-Regulation Pairing

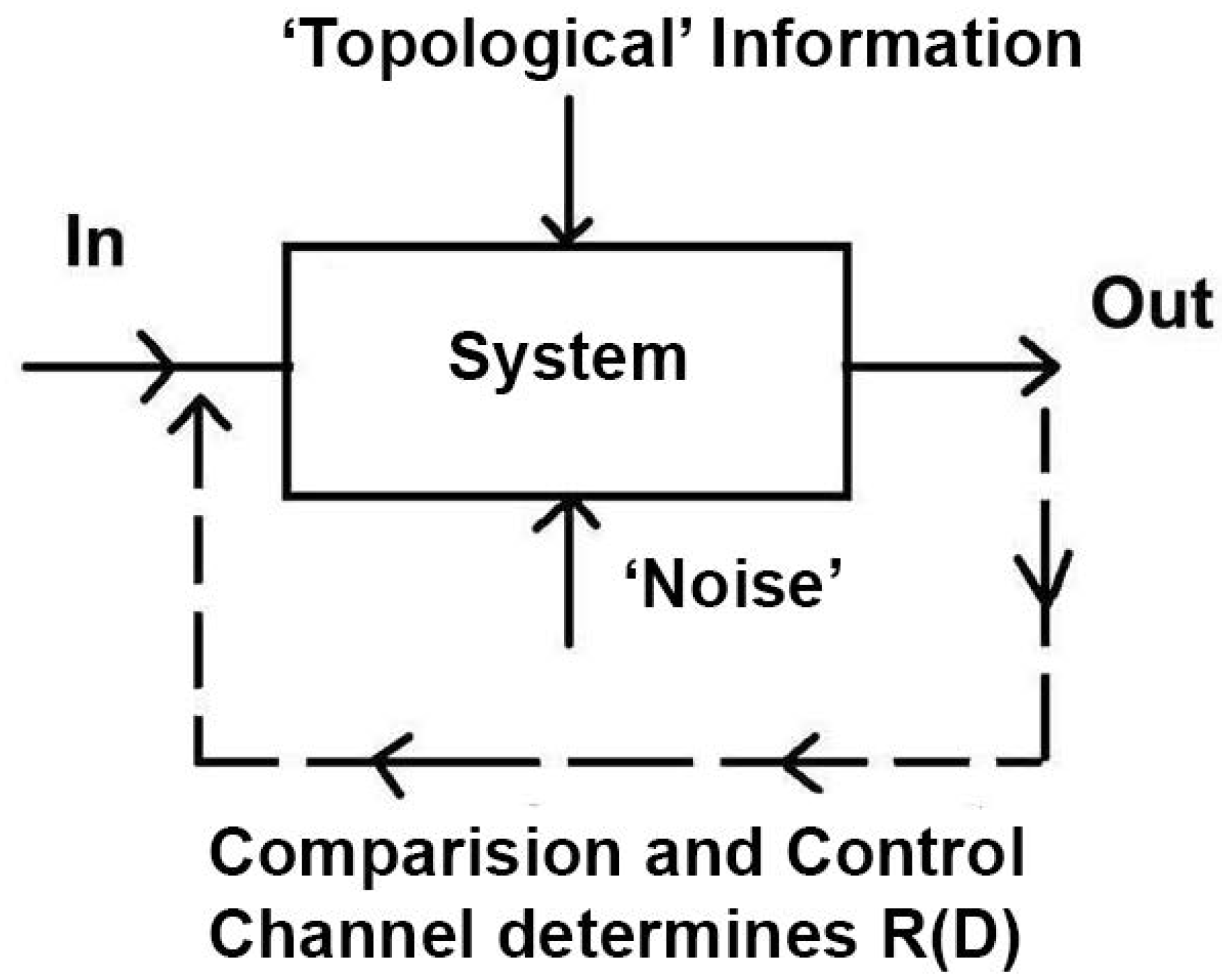
Here, we are interested in the dynamics of interaction between two entities—a ‘system-of-interest’ and its paired regulating apparatus—engaged separately in ‘real-world’ evaluations according to Figure 1, where each entity is concerned with its own channel capacity $R_i\left(D_i\right)$—increasing R to lower the distortion between what it intends and what it observes.

In rough consonance with the approaches of Ortega and Braun [22] and Kringlebach et al. [18], we consider a ‘simple’ probability distribution underlying overall system dynamics, say $\rho \left(x\right)$, and construct an iterated probability for each component of the interaction individually, having the following form:

$$P_j={\displaystyle \frac{\rho (R_j/g_j\left(Z_j\right))}{\rho (R_1/g_1\left(Z_1\right))+\rho (R_2/g_2\left(Z_2\right))}}$$

(2)

where $g\left(Z\right)$ represents a temperature analog that must be further characterized, and each $R_j$, again following Feynman’s ([19], p. 146) adaptation of Bennett’s [20] analysis, is itself to be interpreted as an initial free energy measure. Bennett argued that information itself has a kind of ‘fuel value’ or free energy content. Following Feynman, we take this and run with it. In what follows, ‘channel capacities’ $R_i$ will be used to build higher-order, iterated, free energy measures following from the statistical mechanical partition function.

That is, this formulation leads directly to a partition function definition of an iterated free energy F [23,24,25]:

$$\rho (F/<g>)=\rho (R_1/g_1\left(Z_1\right))+\rho (R_2/g_2\left(Z_2\right))$$

(3)

where $<g>$ is some appropriate ‘average temperature’ that we take here as follows:

$$<g>\equiv \sqrt{g_1\left(Z_1\right)g_2\left(Z_2\right)}$$

(4)

We next impose a first-order model, $g\left(Z\right)=g\times Z$, where the constant g is an affordance index that determines how well the resource rate Z can actually be utilized, and, for convenience, take $\rho \left(x\right)$ as the Boltzmann Distribution, solving for F as follows:

$$F=-\left(\sqrt{g_1{Z}_1{g}_2{Z}_2}\right)ln\left({\mathrm{e}}^{-{\displaystyle \frac{R_1}{g_1{Z}_1}}}+{\mathrm{e}}^{-{\displaystyle \frac{R_2}{g_2{Z}_2}}}\right)$$

(5)

Dynamics are then defined in second order at the nonequilibrium steady state according to an Onsager nonequilibrium thermodynamics model [26]:

$$\begin{array}{c}\hfill S\equiv -F+Z_{1}dF/d{Z}_1+Z_{2}dF/d{Z}_2\\ \hfill d{Z}_j/dt\propto \partial S/\partial Z_j=0,j=1,2\end{array}$$

(6)

where S, as the Legendre Transform of F [24], is an entropy-analog, and we are able to omit the ‘diffusion coefficient’ in the second line of Equation (6).

Solving the two relations $\partial S/\partial Z_j=0$ for the $R_j$ leads to three solution sets for the nonequilibrium steady state (nss)—i.e., homeostatic/allostatic—conditions. The physically nontrivial one is the equipartition

$$\begin{array}{c}\hfill {\displaystyle \frac{R_1}{g_1{Z}_1}}={\displaystyle \frac{R_2}{g_2{Z}_2}}\equiv X\\ \hfill Z_2=\left({\displaystyle \frac{g_1{R}_2}{g_2{R}_1}}\right)Z_1\\ \hfill Z\equiv (Z_1+Z_2)=\left({\displaystyle \frac{1}{X}}\right)\left({\displaystyle \frac{R_1}{g_1}}+{\displaystyle \frac{R_2}{g_2}}\right)\end{array}$$

(7)

1. Note that pathological values of $R_1,g_1$ and $Z_1$ can force $Z_2$—the regulatory system supply demand—to grow so large that it becomes unsustainable. That is, homeostasis/allostasis of a cognitive/control dyad can be driven to failure by sufficient ‘environmental’ stress.

2. The ‘total energy rate’ Z can be lowered by raising the ‘affordance’ measures $g_j$.

This relatively simple example provides a useful starting point for significant generalizations, at the expense of considerable, often nontrivial, conceptual and formal development.

4. Extending the Model I

As Stanley et al. [27] describe, empirical evidence has been mounting that supports the intriguing possibility that a number of systems arising in disciplines as diverse as physics, biology, ecology, and economics may have certain quantitative features that are intriguingly similar. These properties are conventionally grouped under the headings of ‘scale invariance’ and ‘universality’ in the study of phase transitions.

Here, using the equipartition implied by Equation (7), we impose a quasi-scale-invariant model and explore the resulting patterns of phase transition that affect and afflict homeostasis and allostasis under ‘stress’. The ‘quasi’ arises because one cannot simply abduct the dynamics of physical processes to the dynamics of cognition, particularly biocognition. At the very least, information sources ‘dual’ to cognitive phenomena [13] are not micro-reversible, displaying, as mentioned above, directed homotopy.

An inverse argument generalizes the nss equipartition derived above across a full set of probability distributions likely to be characterized by biological, institutional, and machine cognition.

Fix the $R_j/\left(g_j\left(Z_j\right)\right)\equiv X$, and assume there are $n\ge 2$ contending/cooperating agents, taking n as an integer. (In analogy with physical theory, we might actually need to take $n\to V\left(n\right)$ for some monotonic increasing function of n.)

We are, again, envisioning at least an individual enmeshed in a social environment. Then, on this basis, calculate the most general possible form of the corresponding average R.

The relations of interest for possible underlying probability distributions are then taken according to the first-order quasi-scale invariant expressions:

$$\begin{array}{c}\hfill \rho \left({\displaystyle \frac{FX}{R(R_1,\dots ,R_n)}}\right)=n\rho \left(X\right)\\ \hfill F=\left({\displaystyle \frac{{\rho }^{-1}\left(n\rho \left(X\right)\right)}{X}}\right)R\left(R_1,\dots ,R_n\right)\end{array}$$

(8)

where, again, n is an integer, and the appropriate functional form of $R=R(R_1,\dots R_n)$ must now be found.

See Khaluf et al. [17] for a discussion of ‘ordinary’ scale invariance, where $\rho \left(\lambda x\right)=Q\left(\lambda \right)\rho \left(x\right)$ for some monotonic increasing function $Q\left(\lambda \right)$.

In general, it may be necessary to replace n with some appropriate monotonic increasing function $V\left(n\right)$, but for algebraic simplicity, we will continue with the simple, first-order model.

Equation (6) is reexpressed in terms of the $R_j$, imposing the nonequilibrium steady state condition:

$$\partial R_j/\partial t\propto \partial S/\partial R_j\equiv 0$$

(9)

for all possible $R_j$, so that the $R_j/\left(g\left(Z_j\right)\right)$ are indeed fixed at the same value across all possible probability distributions.

What functional forms of R make this true?

The argument is not quite trivial but straightforward. Requiring $\partial S/\partial R_j=0$ in Equation (6), generalizes to a full class of ‘averaging’ functions $R(R_1,\dots ,R_n)$, given proper dimensional extension of S.

For n dimensions, a direct solution by induction is as follows:

$$R=R\left(R_1,R_2,\dots ,R_n\right)=f\left({\displaystyle \frac{R_2}{R_1}},\dots ,{\displaystyle \frac{R_n}{R_1}}\right)R_1$$

(10)

which applies to both arithmetic and geometric averages. This is a simplification from a more elaborate treatment that would add considerable mathematical overhead to an already burdened development.

We will reconsider this problem, and that of Equation (4), from a different and perhaps deeper perspective below.

Here, we carry the argument further, treating Equation (8) as an explicit function of X a nonequilibrium steady state, and extending the Onsager analysis:

$$\begin{array}{c}\hfill \rho \left({\displaystyle \frac{F\left(X\right)X}{R\left(X\right)}}\right)\equiv \rho \left(Q\right)=n\rho \left(X\right)\\ \hfill F\left(X\right)=\left({\displaystyle \frac{{\rho }^{-1}\left(n\rho \left(X\right)\right)}{X}}\right)R\left(X\right)={\displaystyle \frac{Q(n,X)}{X}}R\left(X\right)\\ \hfill S\equiv -F\left(X\right)+X{\displaystyle \frac{d}{dX}}F\left(X\right)\\ \hfill dX/dt\propto \partial S/\partial X=0\\ \hfill R(n,X)={\displaystyle \frac{X(C_{1}X+C_2)}{Q(n,X)}}\end{array}$$

(11)

where in the third line we again invoke the Legendre Transform to define an ‘entropy’ in terms of a ‘free energy’.

Again, it may be necessary to replace the integer n in the first line of Equation (11) by an appropriate monotonic increasing function $V\left(n\right)$. In physical systems, typically $V\left(n\right)\sim n^{\alpha },\alpha >0$.

Higher order ‘Onsager-like’ [26] expressions for the entropy-analog may well be needed, for example,

$$S\equiv -F+\sum _j{ϵ}_j{X}^j{d}^{j}F/d{X}^j$$

(12)

for appropriate ${ϵ}_j$. Such expressions may be system-specific, again leading to the second relation in Equation (11), but producing more involved expressions for $F\left(X\right)$.

Below, we extend the argument to cases where $dX/dt\propto dS/dX=f\left(X\right(t\left)\right)\to 0$ as t increases, introducing ‘frictional’ delays.

Here, the essential point is that calculating $Q(n,X)$ allows finding critical values $X_C\left(n\right)$ under different probability distributions and ‘Onsager-type’–or other–models. Again, scaling with n may not be the simple linear model used here.

Thus, a direct, comprehensive, approach to system stability, via this approach, is to ‘simply’ demand that $Q(n,X)\ne 0$ be real-valued, given that $\rho \left(x\right)$ is a probability distribution on $0\le x\le \infty$.

For, in order, Boltzmann, k-order Lomax, and Cauchy Distributions—instantiating the non-zero requirement—and sequentially, the Rayleigh, k-order Erlang, and k-order chi-square distributions,

$$\begin{array}{c}\hfill X_C=ln\left(n\right)\\ \hfill X_C=n^{1/(k+1)}-1\\ \hfill X_C=\sqrt{n-1}\\ \hfill X_C=\sqrt{-W\left(m,-{\displaystyle \frac{{\mathrm{e}}^{-1}}{n^2}}\right)}\\ \hfill X_C=-\left(k-1\right)W\left(m,-{\mathrm{e}}^{-1}{\left({\displaystyle \frac{1}{n}}\right)}^{{\displaystyle \frac{1}{k-1}}}\right)\\ \hfill X_C=-\left(k-2\right)W\left(m,-{\displaystyle \frac{{\left(k-2\right)}^{\frac{k}{k-2}}{\left({\mathrm{e}}^{\frac{1}{k-2}}\right)}^2}{{\left({\left(k-2\right)}^{\frac{1}{k-2}}\right)}^2{\left(n^{\frac{1}{k-2}}\right)}^2{\mathrm{e}}^{\frac{k}{k-2}}\left(k-2\right)}}\right)\end{array}$$

(13)

where all scale parameters have been set equal to one and, in general, one might expect $n\to V\left(n\right)$ for some appropriate increasing function. Again, detailed development would add more mathematical overhead to an already overburdened argument.

Note the following:

• The second condition is most easily proved by direct substitution.
• $W(m,x)$ is the Lambert W-function of order m that satisfies the following relation:

$$W(m,x)exp\left[W\right(m,x\left)\right]=x$$

W is real-valued only for $m=0,-1$ and $x>-exp[-1]$.

• Equation (13) is strictly equivalent to the condition that there is no solution to $\rho \left(Q\right)=n\rho \left(X\right)$ if $n\rho \left(X\right)>{max}_{x\ge 0}\rho \left(x\right)$. If the distribution is nonmonotonic and a solution exists, there will be more than one solution form. The first three relations of Equation (13) are associated with monotonic distributions having mode zero.

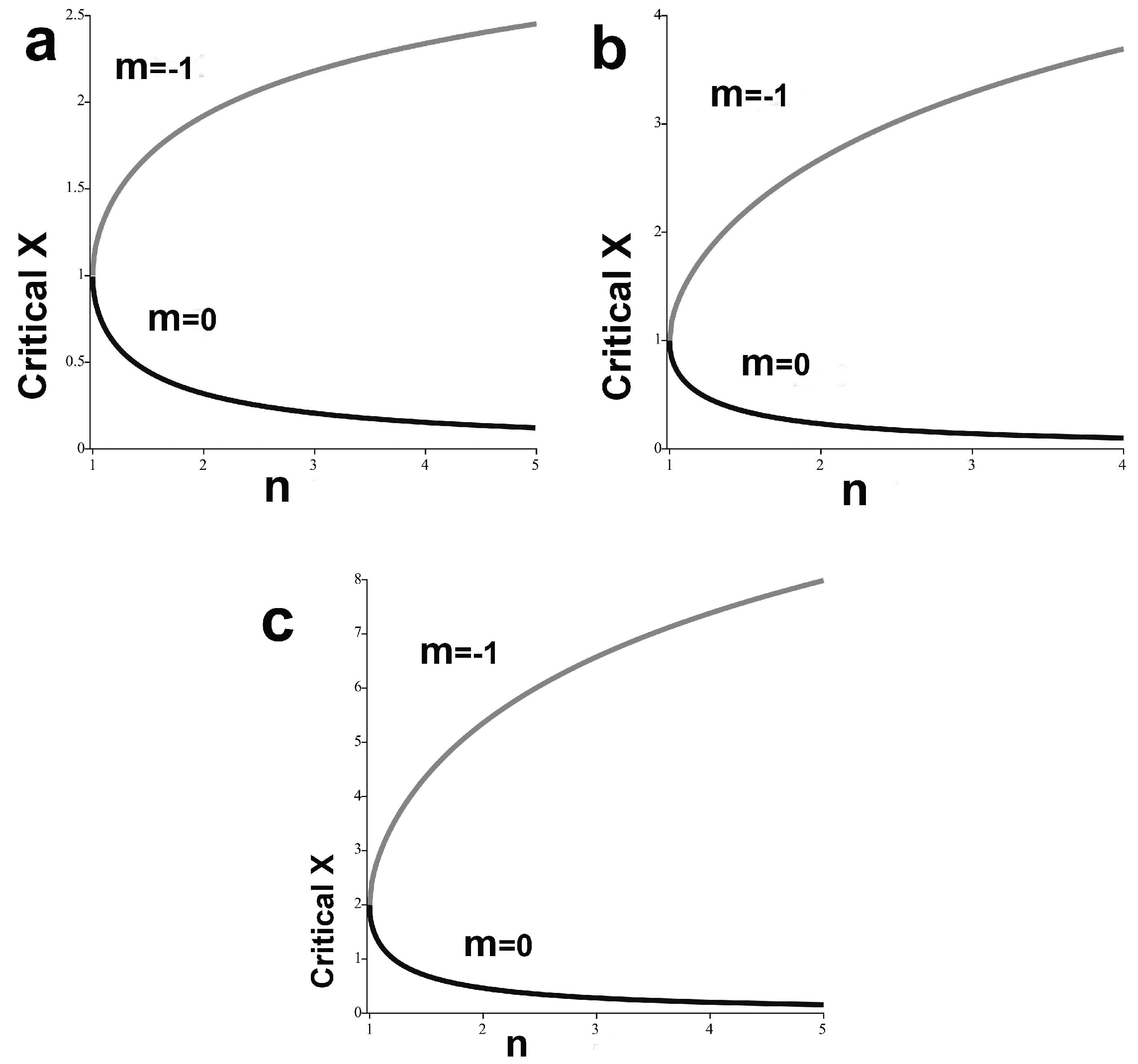
We are concerned with the rising branches representing cooperation between system subcomponents, displaying in Figure 2, patterns of limiting behavior with increasing n for, respectively, the Rayleigh, second-order Erlang, and fourth-order Chi Square Distributions. These are nonmonotonic. The regimes above the top branch of the ‘C’ are stable for cooperating systems.

The essential point for this analysis is that, like $X_C=ln\left(n\right)$ for the Boltzmann Distribution, the ‘cost’ in X for cooperating modes does not increase linearly with rising n. For the Boltzmann Distribution model, doubling n, i.e., pairing each cognitive submodule with a regulator, increases the rate of ‘resource’ demand as $ln\left(n\right)\to ln\left(2n\right)=ln\left(n\right)+ln\left(2\right)$.

For cooperating cognition/regulation dyads, the ‘cost’ in units of X does not increase in proportion to the shift $n\to 2n$. From the perspective of evolution under selection pressure, this seems a small price to pay for a grand increase in stability of function.

Again, here, the $m=-1$ branches can be taken as indexing cooperative coalitions, while the $m=0$ branches represent contending system dynamics under rising n, which is another matter.

After some algebra, results similar to Figure 2 are found for the Levy and Weibull distributions, although the Levy is difficult to parse.

We can now extend the ‘energy’ argument of Equation (7), recalling that, for all j, $R_j/g_j\left(Z_j\right)\equiv X$, the equipartition value. Applying the arguments above, we set $X\equiv X_C\left(n\right)$ from Equation (13) for the appropriate underlying probability distribution.

Then

$$\begin{array}{c}\hfill g_j\left(Z_j\right)={\displaystyle \frac{R_j}{X_C\left(n\right)}}\\ \hfill Z_j=g_j^{-1}\left({\displaystyle \frac{R_j}{X_C\left(n\right)}}\right)\\ \hfill Z_C=\sum _j{Z}_j=\sum _j{g}_j^{-1}\left({\displaystyle \frac{R_j}{X_C\left(n\right)}}\right)\end{array}$$

(14)

For convenience, we assume a set of n identical systems, with fixed forms for the $g_j\left(Z_j\right)=g\left(Z_j\right)$ and fixed values of the $R_j=R$ under some particular probability distribution. Then

$$Z_C=\sum _j{Z}_j=n{g}^{-1}\left({\displaystyle \frac{R}{X_C\left(n\right)}}\right)$$

(15)

Recall that, if g is monotonic increasing, so is $g^{-1}$.

For example, assuming a Boltzmann Distribution,

$$Z_C=n{g}^{-1}\left({\displaystyle \frac{R}{ln\left(n\right)}}\right)$$

(16)

which does not increase linearly with n by virtue of the division by $ln\left(n\right)$ in $g^{-1}$.

Adopting the simple linear model $g\left(Z\right)\equiv g\times Z$,

$$\begin{array}{c}\hfill {\displaystyle \frac{R}{g{Z}_C}}={\displaystyle \frac{X_C\left(n\right)}{n}}\\ \hfill Z_C={\displaystyle \frac{n}{X_C\left(n\right)}}{\displaystyle \frac{R}{g}}\end{array}$$

(17)

which makes intuitive sense.

Further, the first relation of Equation (17) can be solved for n (or $V\left(n\right)$), generating necessary conditions for $Z_C$.

For example, under the Boltzmann Distribution,

$$n={\displaystyle \frac{-W\left(m,-\frac{R}{g{Z}_C}\right)}{\frac{R}{g{Z}_C}}}$$

(18)

for $m=0,-1$ in the Lambert W-function, imposing the necessary condition:

$$\begin{array}{c}\hfill {\displaystyle \frac{R}{g{Z}_C}}\le exp[-1]\\ \hfill Z_C\ge {\displaystyle \frac{R}{g}}exp\left[1\right]\end{array}$$

(19)

From Equations (15)–(17), this is a general result for the linear model: That is, the same expression—with different right-hand terms—is ‘easily’ found for the other probability distributions leading to Equation (13).

5. Extending the Model II

5.1. The Basic Idea

The burdens of fog, friction, and adversarial intent characterize evolutionary selection pressures at every scale and level of organization of cognitive processes, whether biological, social, institutional, machine, or their various composites.

Here, in addressing these matters, we again assume the equipartition implied by Equation (7) as a basic condition, and impose a kind of ‘Born-Oppenheimer Approximation’ [28] in which large-scale changes to the overall system are assumed to occur slowly enough that equipartition is ‘almost always’ sufficiently satisfied.

Under that basic assumption, friction is ‘easily’ introduced by extending the next-to-last relation of Equation (11), so that

$$\begin{array}{c}\hfill S\equiv -F\left(X\right)+X{\displaystyle \frac{d}{dX}}F\left(X\right)\\ \hfill dX/dt\propto dS/dX=X{d}^{2}F/d{X}^2=f\left(X\right)\\ \hfill F\left(X\right)=\int \int {\displaystyle \frac{f\left(X\right)}{X}}dXdX+C_{1}X+C_2\end{array}$$

(20)

Here, we take the following:

$$\begin{array}{c}\hfill f\left(X\right)=\beta -\alpha X\left(t\right)\\ \hfill X\left(t\right)={\displaystyle \frac{\beta }{\alpha }}\left(1-exp[-\alpha t]\right)\to \beta /\alpha \end{array}$$

(21)

so that $\alpha$ becomes the (inverse) index of Clausewitzian friction, i.e., the delay in reaching the maximum possible value of X.

Then

$$F\left(X\right)=\beta \left(Xln\left(X\right)-X\right)-{\displaystyle \frac{\alpha X^2}{2}}+C_{1}X+C_2$$

(22)

where $C_1$ and $C_2$ are important local boundary conditions that emerge ‘naturally’ from solving the differential equations. Solutions are indeed sensitive to these boundary conditions.

From Equation (11), depending on the underlying probability distribution $\rho \left(X\right)$, recall that

$$\begin{array}{c}\hfill R(n,X)={\displaystyle \frac{XF\left(X\right)}{Q(n,X)}}\\ \hfill \rho \left(Q\right(n,X\left)\right)\equiv n\rho \left(X\right)\end{array}$$

(23)

where Q is characteristic of that distribution. Again, in general, $n\to V\left(n\right)$.

Assuming monotononic Boltzmann and nonmonotonic Rayleigh and second-order Erlang Distributions, i.e., $\rho \left(x\right)=exp[-x],xexp[-x^2/2],xexp[-x]$, the $Q(n,X)$ are, respectively,

$$\begin{array}{c}\hfill X-ln\left(n\right)\\ \hfill {\displaystyle \frac{X{\mathrm{e}}^{-\frac{X^2}{2}}}{\sqrt{-\frac{X^2{\mathrm{e}}^{-X^2}}{W\left(m,-X^2{n}^2{\mathrm{e}}^{-X^2}\right)}}}}\\ \hfill -W\left(m,-nX{\mathrm{e}}^{-X}\right)\end{array}$$

(24)

where $W(m,x)$ is the Lambert W-function of order $m=0,-1$.

Recall that F is defined by $dS/dX=X{d}^{2}F/d{X}^2=dX/dt=f\left(X\right)$ so that F is given as the last relation of Equation (20).

Fixing $\alpha =1$ in the expression for F based on the exponential relation $f\left(X\right)=\beta -\alpha X$, with $C_1=1,C_2=2$, then $R(n,\beta )$ is as in Figure 3a–c. Note the two solutions for the Rayleigh and Erlang Distributions, depending on the order of the Lambert W-function as indicated.

Recall that R is an average channel capacity for control across the full system: This is not a trivial matter. Here, relatively narrow troughs are bracketed by high—essentially unattainable—demands for bandwidth under friction measured by $\alpha$.

5.2. Fog and Friction

In addition to the burden of Clausewitzian ‘friction’, inherent to the relation $dX/dt=f\left(X\right(t\left)\right)\to 0$, the effect of ‘fog-of-war’ can be explored by expanding the expression for $dX/dt$ in Equation (20) as a stochastic differential equation:

$$d{X}_t=f\left(X_t\right)dt+\sigma X_{t}d{B}_t$$

(25)

where $d{B}_t$ is taken as Brownian white noise, and the last term represents ‘ordinary’ volatility, here in the context of two models, the ‘exponential’ and the ‘Arrhenius’, given a Boltzmann Distribution and n cognitive modules with the equipartition assumption on X.

The exponential model follows Equations (21) and (22). For the Arrhenius model,

$$\begin{array}{c}\hfill X\left(t\right)=\beta exp[-\alpha /t]\\ \hfill dX/dt=f\left(X\right)={\displaystyle \frac{X}{\alpha }}{\left(ln(X/\beta )\right)}^2\\ \hfill F\left(X\right)={\displaystyle \frac{ln{\left(\frac{X}{\beta }\right)}^2{X}^2}{2\alpha }}-{\displaystyle \frac{3X^{2}ln\left(\frac{X}{\beta }\right)}{2\alpha }}+{\displaystyle \frac{7X^2}{4\alpha }}+C_{1}X+C_2\end{array}$$

(26)

Assuming the Boltzmann Distribution–so that $Q=X-ln\left(n\right)$ in Equation (23), where n is the number of linked modules–we calculate the nonequilibrium steady state conditions $<d{R}_t>=0$ for both examples using the Ito Chain Rule [29]. The resulting expressions are relatively simple, but too lengthy for the author’s LaTeX compiler.

For both forms of F, exponential and Arrhenius, $\alpha =1,\beta =3,C_1=-1,C_2=3$. Figure 4 shows the resulting NSS solution sets, expressed as $X(n,\sigma )$. As n and $\sigma$ increase, the solution sets are destabilized.

It is interesting to repeat this calculation for the second-order Erlang Distribution, which represents a process of two sequential, identical Exponential Distributions (e.g., a two-fold staged decision), using the convolution integral method described in the Mathematical Appendix A. Then

$$\begin{array}{c}\hfill \rho \left(x\right)=xexp[-x]\\ \hfill Q(n,X)=-W\left(m,-{\displaystyle \frac{nX}{{\mathrm{e}}^X}}\right)\end{array}$$

(27)

where, again, $W(m,x)$ is the Lambert W-function of order m.

Taking all other parameter values exactly as in Figure 4, Figure 5 again represents the nonequilibrium steady state solution sets $X(n,\sigma )$ for the Arrhenius and exponential models defining $dX/dt=f\left(X\right)$. The solution sets become counterintuitively convoluted with increasing ‘noise’ $\sigma$.

These examples show how Clausewitzian ‘friction’ defined by $\alpha$ in the expressions for $dX/dt=f\left(X\right)$ becomes idiosyncratically synergistic with ‘fog’ uncertainties characterized by $\sigma$. That is, what appear to be ‘slight’ differences in frictional dynamics—different forms of delay in response to perturbation—can have an amplified impact on the dynamics of uncertainty in response to perturbation. Similar results will afflict all probability models across any modular conformations and forms of the friction relation $f\left(X\right)$.

These results are not encouraging, as any embodied cognitive system, dynamically tuned modular or otherwise, will always encounter rising rates of ‘noise’ in chaotic, unsecured, or adversarial environments, given the necessarily delayed response to such perturbations.

The statistical tools derived from this general approach will likely be as flexible for the study of cognitive phenomena as have been the ‘ordinary’ regression equations used in the analysis of more usual observational and experimental data, in particular, providing benchmarks against which to compare observed patterns.

Cognition, cognitive dynamics—and their inherent failure modes—are hard to understand and remediate, and their effective remediation requires new methods and approaches.

What seems to emerge from the synergism between uncertainty and frictional delay in response to that uncertainty in cognitive dynamics is the dire need for analogs to the long-evolved innate and adaptive immune systems, i.e., a basic, rapid ‘implanted’ response, followed by a more detailed ‘learned’ response.

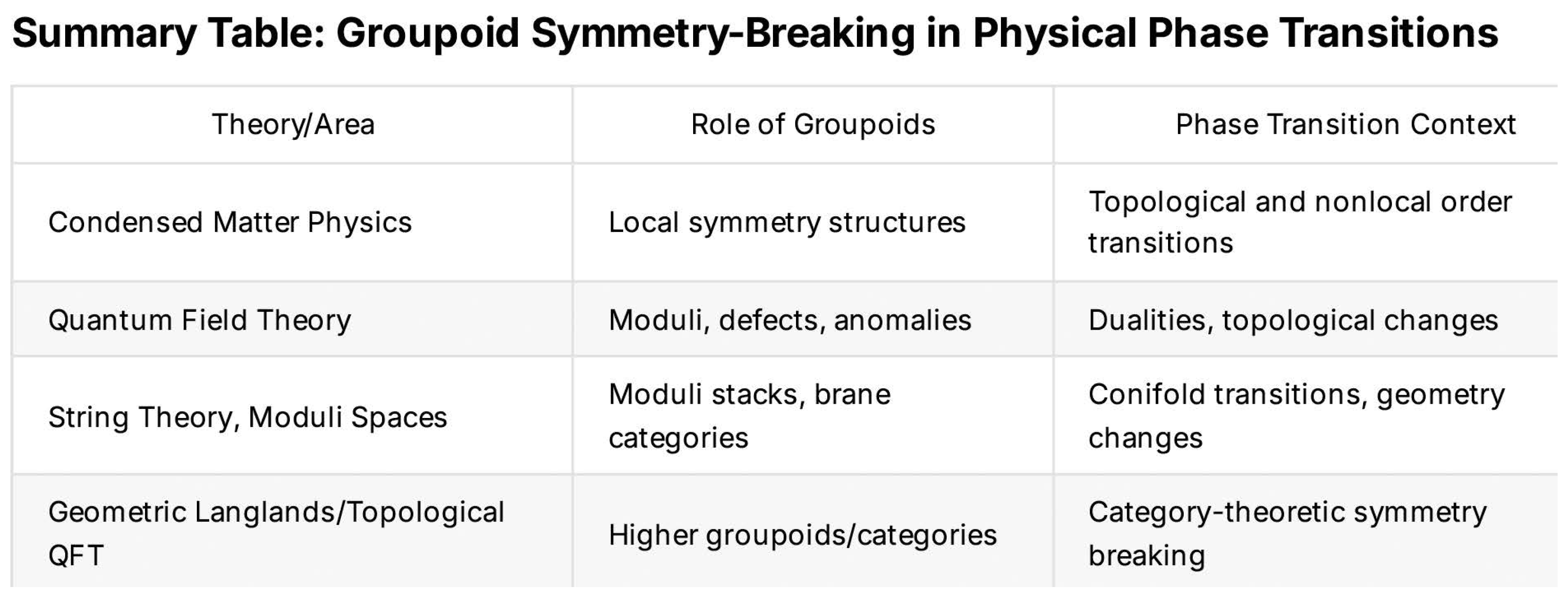
6. Groupoid Symmetry-Breaking Phase Transitions

There is yet more to be teased out from behind the veils of Clausewitzian Fog-and-Friction. So far, we have treated ‘underlying probability distributions’ as the central, fixed star in a kind of planetary dynamic, leading to the methodological harvests of Equation (13) and what follows from the network relation $\rho \left(Q\right)=n\rho \left(X\right)$ (recalling that, in general, $n\to V\left(n\right)\sim n^{\alpha }$).

What happens when $\rho \left(X\right)$ is itself perturbed by fog and friction?

Most simply, this can be found by calculating the nonequilibrium steady state:

$$<d{\rho }_t>=0$$

based on the generalized ‘frictional’ stochastic differential equation

$$d{X}_t=f\left(X_t\right)dt+\sigma h\left(X_t\right)d{B}_t$$

(28)

using the Ito Chain Rule.

The relation defining the NSS is ‘easily’ found as follows:

$$\begin{array}{c}\hfill {\sigma }^2=-{\displaystyle \frac{2f\left(X\right)\left(\frac{d}{dX}\rho \left(X\right)\right)}{h{\left(X\right)}^2\left(\frac{d^2}{d{X}^2}\rho \left(X\right)\right)}}=\\ \hfill -{\displaystyle \frac{2X\frac{d^2}{d{X}^2}F\left(X\right)\left(\frac{d}{dX}\rho \left(X\right)\right)}{h{\left(X\right)}^2\left(\frac{d^2}{d{X}^2}\rho \left(X\right)\right)}}\end{array}$$

(29)

where the second form follows from the second expression in Equation (20), i.e., $dX/dt\propto dS/dX=X{d}^{2}F/d{X}^2=f\left(X\right)$.

Equation (29) generates solution set equivalence classes $\{\sigma ,X\}$ that can be seen as arising from the functions $X\left(\sigma \right)$ or $\sigma \left(X\right)$.

1. For reasons that will become more salient, if not intrusive, we are principally concerned with these equivalence classes rather than with the functions themselves.

2. The term

$$-{\displaystyle \frac{d\rho /dX}{d^2\rho /d{X}^2}}$$

may be interpreted as the scale of change or ‘characteristic length’ relating how sharply the density changes versus its curvature at a point. It is analogous to, but different from, the classic ‘hazard rate’ at which signals are detected. For the Exponential Distribution $mexp[-mX]$, the hazard rate is m and the characteristic length $1/m$.

3. For convenience, we adopt ‘simple volatility’, i.e., $h\left(X\right)=X$, with $f\left(X\right)$ as the exponential and Arrhenius models from above for, respectively, the Boltzmann and Second Order Erlang Distributions, and plot $\sigma \left(X\right)$ to generate Figure 6.

Again, the second-order Erlang represents the convolution of two identical exponential distributions, akin to replacing ‘mission command’ initiative with a two-stage ‘detailed command’ protocol in military or business enterprise [30].

The distributions are, respectively, monotonic and nonmonotonic. The results, in Figure 6, are a Boltzmann-exponential, b Boltzmann–Arrhenius, c Erlang-exponential, and d Erlang–Arrhenius. Again,

$$\begin{array}{c}\hfill \rho \left(X\right)=exp[-X],Xexp[-X]\\ \hfill f\left(X\right)=\beta -\alpha X,\left(X/\alpha \right){\left(ln(X/\beta )\right)}^2\end{array}$$

(30)

Here, $\alpha =1,\beta =3$ in both expressions for $f\left(X\right)$.

These distinct solution sets, representing markedly different fundamental interactions between internal probabilities, ‘friction’ from $\alpha$ and $\beta$, and ‘fog’ from $\sigma$, can be grouped together as equivalence classes even as the internal parameters defining $\rho \left(X\right)$ and $f\left(X\right)$ are varied.

As the Mathematical Appendix A explores in some detail, equivalence classes lead to an important generalization of elementary ideas of group symmetry, i.e., groupoids, for which products are not defined between all possible element pairings [31].

The simplest groupoid is the disjoint union of groups. Imagine two bags containing the same number of identical ball bearings, each of which can be characterized by the three-dimensional rotation group. Remove a ball bearing from one bag, make a deep indentation in it with a hard-metal punch, and return it to the original bag. The disjoint union of three-dimensional rotation groups in one of the bags has now been broken. One bearing is now symmetric only via rotation about an axis defined by the indentation.

The physical act of striking a ball bearing with a hard-metal punch has triggered a groupoid symmetry-breaking phase transition, analogous to, but distinct from, group symmetry-breaking phase transitions such as melting a snow crystal, evaporating a liquid, or burning a diamond.

Each panel of Figure 6 defines a particular set of equivalence classes that, via the somewhat mind-bending arguments of the Appendix A, defines a groupoid. Changes within fog/friction/probability patterns under the perturbations of external circumstances—like the hard-metal punch on the ball bearing—trigger punctuated groupoid symmetry-breaking phase transitions in the kind of systems we have studied. That is, sufficiently challenged cognitive structures will experience sudden shifts among the panels of a vastly enlarged version of Figure 6.

A more extensive discussion of groupoid symmetry-breaking phase transitions by the Perplexity AI system is found in the Appendix A.

Cognition, even with regulation, is a castle made of sand.

7. Iterated System Temperature

Subsystems of living organisms consume metabolic free energy (MFE) at markedly different rates. For example, among humans, Heart/Kidneys, Brain, and Liver typically require, respectively, 440, 240, and 200 KCal/Kg/day of MFE, while resting Skeletal Muscles and Adipose Tissue require only 13 and 4.5 Kcal/Kg/day ([32], Table 4).

These marked differences, however, are encapsulated within a ‘normal body temperature’ of ≈98.6 deg.F.

This is not as simple as it seems, nor as treated in the first iteration of Equations (4) and (10) above.

Here, we have, via an ‘equipartition’ argument, condensed closely interacting nonequilibrium steady state subcomponents of a larger enterprise in terms of the quantity X from Equations (20)–(29). Taking the perspective of the previous section, more can be done, in particular, leading to the definition of an ‘iterated temperature’ construct that seems akin to the normal body temperature.

The essential assumption is, again, that, under the stochastic burden of Equation (28), the basic underlying probability distribution is preserved in a nonequilibrium steady state $<d{\rho }_t>=0$, leading to the second form of Equation (29). Then the ‘free energy’ construct $F\left(X\right)$ is expressed as follows:

$$F\left(X\right)=\int \int -{\displaystyle \frac{{\sigma }^{2}h{\left(X\right)}^2\left(\frac{d^2}{d{X}^2}\rho \left(X\right)\right)}{2X\left(\frac{d}{dX}\rho \left(X\right)\right)}}dXdX+C_{1}X+C_2$$

(31)

Recall now, from above, the embodied Rate Distortion Control Theory partition function argument defining ‘free energy’ F in terms of a temperature analog g:

$$\rho (F/g)={\int }_0^{\infty }\rho (R/g)dR=g$$

(32)

where, g, has become an iterated function of X, the equipartition energy measure. From here on, we will write this as $G^{*}$ to differentiate it from the ‘simple’ temperature analog of previous studies.

That is, here, we are interested in the solution to the following relation:

$$\rho (F/G^{*})=G^{*}\left(X\right)$$

(33)

given the NSS condition $<d{\rho }_t>=0$, i.e., the quasi-preservation of the underlying basic probability distribution of the overall system.

We are, in a sense, reprising the calculations of Equations (4) and (10) from a different perspective.

More specifically, we contrast a simple one-stage ‘mission command’ system based on a Boltzmann Distribution with a two-stage ‘detailed command’ process that passes decisions across two sequential Boltzmann stages, giving a process described overall by a second-order Erlang Distribution. Under the impact of ‘noise’ defined by Equation (28), each ‘cultural’ form attempts homeostasis, the preservation of its inherent nature, i.e., $<d{\rho }_t>=0$.

Thus, we, respectively, set $\rho \left(x\right)=exp[-x],xexp[-x]$ and assume ordinary volatility $h\left(X\right)=X$. Then, again via the Ito Chain Rule calculation [29],

$$\begin{array}{c}\hfill F_B(\sigma ,X)={\displaystyle \frac{1}{12}}{\sigma }^2{X}^3+C_{1}X+C_2,\\ \hfill G_B^{*}={\displaystyle \frac{-F_B}{W(m,-F_B)}}\\ \hfill F_E(\sigma ,X)=\\ \hfill {\displaystyle \frac{{\sigma }^2}{4}}\left({\displaystyle \frac{X^3}{3}}-X^2-2ln\left(X-1\right)\left(X-1\right)-2+2X\right)+C_{1}X+C_2,\\ \hfill G_E^{*}={\displaystyle \frac{-F_E}{2W\left(m,\pm \frac{\sqrt{F_E}}{2}\right)}}\end{array}$$

(34)

where $W(m,x)$ is the Lambert W-function of orders $m=0,-1$. The $G^{*}(X,\sigma )$ expressions are then the iterated temperatures of the entire system under the reduced equipartition defining X across subsystems.

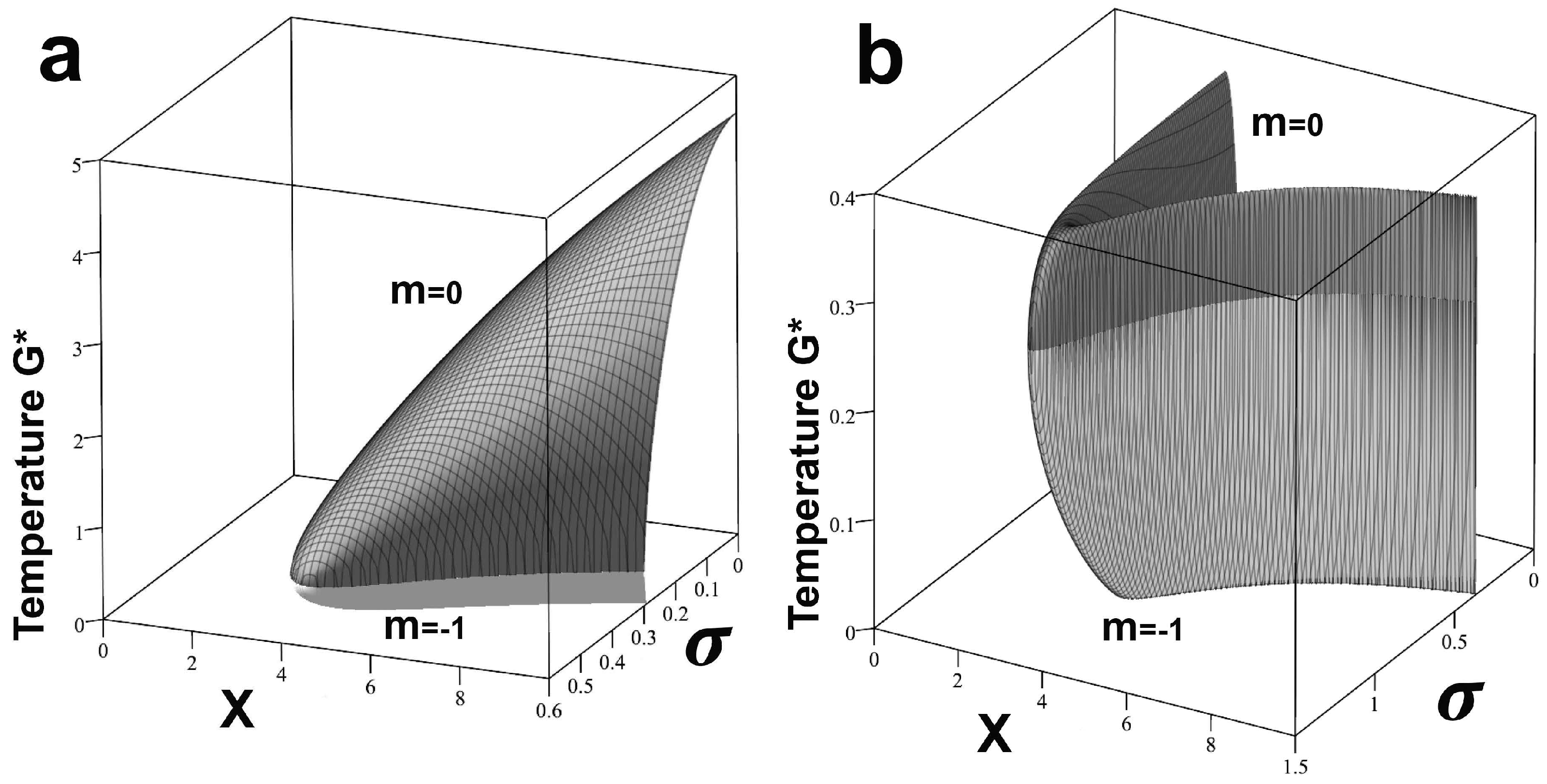
Here, we adopt the negative-$\sqrt{F_E}$ form of the W-function in $G_E^{*}$, as the positive form generates only negative temperatures that, in physical systems, are associated with grossly unstable ‘excited states’.

Figure 7a,b show the two forms of $G^{*}(X,\sigma )$, setting $C_1=-1,C_2=3$, with $m=0,-1$ as indicated.

Sufficient ‘noise’ $\sigma$ drives both systems into zones of instability where the relation $<d{\rho }_t>=0$ fails. This occurs, via the properties of the W-function, for, respectively, $F_B(X,\sigma )>exp[-1]$ and $\sqrt{F_E}/2>exp[-1]$ or $F_E<0$. The contrast between stable zones is noteworthy: the Detailed Command model is at best only slightly stable compared with our version of Mission Command.

Again, each mode of the underlying ‘culture’, when stressed, attempts to maintain homeostasis as the nonequilibrium steady state $<d{\rho }_t>=0$.

It is ‘not difficult’ to extend these results across orders of iteration of the underlying Boltzmann Distribution via a k-stage ‘cancer initiation’ model based on the Gamma Distribution:

$$\rho (m,k,X)={\displaystyle \frac{m^k{X}^{k-1}{\mathrm{e}}^{-\mathit{mX}}}{\Gamma \left(k\right)}}$$

(35)

where $\Gamma \left(x\right)$ is the Gamma Function that generalizes the factorial function for integers.

Then the nss condition $<d{\rho }_t>=0$, under the Ito Chain Rule, gives the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{d^2}{d{X}^2}}F\left(X\right)={\displaystyle \frac{{\sigma }^2\left(m^2{X}^2-2mXk+2mX+k^2-3k+2\right)}{2mX-2k+2}}\\ \hfill G^{*}=-{\displaystyle \frac{mF}{kW\left(n,-\frac{\Gamma {\left(k\right)}^{\frac{1}{k}}{F}^{\frac{1}{k}}}{k}\right)}}\\ \hfill \end{array}$$

(36)

The first relation can easily be solved as $F={\sigma }^{2}H(m,k,X)+C_{1}X+C_2$ in an expression too long to be written on this page.

We can conceptually simplify matters slightly by generating a three-dimensional ‘criticality surface’ $\{k,\sigma ,X\}$ across the decision level index k by (1), using the necessary condition for real-valued Lambert W-functions of orders $n=0,-1$, and (2), setting $m=1$, while varying the boundary conditions $C_1,C_2$. This is done via the second expression of Equation (36):

$$\begin{array}{c}\hfill {\displaystyle \frac{\Gamma {\left(k\right)}^{\frac{1}{k}}{F}^{\frac{1}{k}}}{k}}={\mathrm{e}}^{-1}\\ \hfill F={\displaystyle \frac{k^k{\mathrm{e}}^{-k}}{\Gamma \left(k\right)}}\end{array}$$

(37)

The result is shown in Figure 8a,b for two boundary condition pairs: $\{C_1=-1,C_2=3\}$ and $\{C_1=1,C_2=2\}$.

One possible inference from this development is that the approach we have taken permits the development of a very rich body of statistical tools for data analysis. Like all such matters, however, error estimates and basic validity entail a correspondingly rich range of possible devils-in-the-details.

In the Mathematical Appendix, we explore a ‘higher iteration’ in the detailed command structure, i.e., doubling the two-level dynamic based on the second-order Erlang Distribution. The figure shows an initial two-stage ‘tactical’ decision level, followed by a second two-stage ‘operational’ or ‘strategic’ command level. The results are not reassuring.

It is important to note that other selection pressures may operate. That is, Equation (31) assumes the most essential matter is the preservation of the underlying probability distribution through the nonequilibrium steady state $<d{\rho }_t>=0$. What if environmental selection pressure enforces the preservation of some other quantity, for example, a ‘Weber-Fechner’ sensory signal detection mode $Q\left(X\right)=ln(1+X)$ instead of $\rho \left(X\right)$? Then $<d{Q}_t>=0$, under the Ito Chain Rule, leads to the following:

$$\begin{array}{c}\hfill F_Q(\sigma ,X)={\displaystyle \frac{{\sigma }^2}{2}}\left({\displaystyle \frac{X^2}{2}}-ln\left(1+X\right)\left(1+X\right)+1+X\right)+C_{1}X+C_2\\ \hfill G_B^{*}={\displaystyle \frac{-F_Q}{W(m,-F_Q)}}\\ \hfill G_E^{*}={\displaystyle \frac{-F_Q}{2W\left(m,-\frac{\sqrt{F_Q}}{2}\right)}}\end{array}$$

(38)

Taking $C_1=-1,C_2=3$ again produces something much like Figure 7.

We can take this one step further by defining a ‘collective cognition rate’ based on the underlying probability distribution of the overall multi-modular system, given the Rate Distortion Control Theory model in Figure 1. The essential point is to define ‘system temperature’ as $G^{*}$ from Equations (34) or (38). Then, given the distribution form $\rho$, and a basic Data Rate Theorem stability limit $R_0$, the cognition rate, in analogy with a chemical physics reaction rate approach (e.g., Laidler [33]) becomes the following:

$$L\equiv {\displaystyle \frac{{\int }_{R_0}^{\infty }\rho (R/G^{*})dR}{{\int }_0^{\infty }\rho (R/G^{*})dR}}$$

(39)

For the particular Boltzmann and second-order Erlang Distributions studied here, Figure 7 and friends are transformed as follows:

$$\begin{array}{c}\hfill G^{*}\to exp[-R_0/G^{*}]\\ \hfill G^{*}\to exp[-R_0/G^{*}]\left(1+{\displaystyle \frac{R_0}{G^{*}}}\right)\end{array}$$

(40)

Details are left as an exercise. The general forms of $L(X,\sigma )$ are, however, similar to Figure 7.

Note that the ‘Boltzmann’ part of Equation (40) produces the classic inverted-U ‘Yerkes-Dodson Effect’ pattern of cognition rate vs. ‘arousal’ X across a variety of plausible $<d{Q}_t>=0$ nonequilibrium steady state restrictions [30,34].

8. Discussion

There seem to be ‘universality classes’ for cognitive systems, determined by the nature of the underlying probability distributions, e.g., monotonic or nonmonotonic, and by the nature of their embedding environments. Other examples may become manifest across different cognitive phenomena, scales, and/or levels of organization.

In particular, the transcendental Lambert W-function is used to solve equations in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm [35]. Similarly, problems from thermodynamic equilibrium theory with fixed heat capacities parallel the results shown in Figure 2.

Indeed, Wang and Moniz [36] make explicit use of the Lambert W-function in the study of classical physical system phase transitions, using arguments that are recognizably similar to those developed here for cognitive phase transitions. Likewise, Roberts and Vallur [37] use the W-function in their study of the zeros of the QCD partition function, another phase transition analysis.

The Perplexity AI system [38] contrasts physical and cognitive phase transition models in these terms:

Both physical and ‘cognitive’ theories are based on probability distribution arguments ‘in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm’. Cognitive phenomena, of course, act over much richer and more dynamic probability landscapes. Cognitive system probability models will, consequently, require sophisticated and difficult conversions into statistical tools useful for the analysis of observational and experimental data.

Khinchin [39] explored in great detail the rigorous mathematical foundations of statistical mechanics, based on such asymptotic limit theorems of probability theory as the Central Limit and Ergodic Theorems. Here, we outline the need for the parallel, yet strikingly different, development of a rigorous ‘statistical mechanics of cognition’ based on the asymptotic limit theorems of information and control theories. Such developments must, however, inherently reflect the directed homotopy and groupoid symmetry-breaking mechanisms inherent to cognitive phenomena.

There are important matters buried in this formalism:

• We study systems at various scales and levels of organization that are, by Figure 1, fully embodied in the sense of Dreyfus [14], so that their cognitive dynamics may be, or become, ‘intelligent’ in his sense.
• is basically a ‘rate’ variate, and the existence of a minimum stable $X_C$ for cooperating cognitive/regulation dyads is consistent with John Boyd’s OODA Loop analysis in which a central aim is to force the rate of confrontation to exceed the operating limit of one’s opponent, breaking homeostatic or allostatic ‘stalemate’. Predator/prey cycles of post and riposte come to mind.
• The cost of pairing cognitive with regulatory submodules, which is necessary for even basic stability in dynamic environments, scales sublinearly with the inherent doubling of modular numbers across a considerable range of basic underlying probability distributions likely to characterize embodied cognition. This appears to be a general matter with important evolutionary implications across biological, social, institutional, and machine domains.
• Nonetheless, in spite of ‘best case’ assumptions and deductions, failure of nominally ‘effective’ cognition on dynamic environments is not a ‘bug’, but is an inevitable feature of the cognitive process of any and all configurations, at any and all scales and levels of organization, including systems supposedly stabilized by close coupling between cognitive and regulatory submodules. See the Appendix for a surprisingly broad literature review by the Perplexity AI system.

The last point has particularly significant implications. A recent study of nuclear warfare command, control, and communications (NC3) by Saltini et al. [40] makes the assertion

Because… [strategic warning, decision support and adaptive targeting]… are independent and tightly coupled, the potential role of AI is not limited to a single application; instead, it can simultaneously enhance multiple aspects of the NC3 architecture.

The introduction of AI entities—even when tightly coupled with draconian regulatory modules—cannot be assumed to significantly stabilize or enhance NC3 or any other critical system. Placing NC3 architectures under AI control merely shifts, obscures, and obfuscates failure modes.

This being said, as a reviewer has noted, the approach advocated here has a number of limitations:

• The g and $\rho$ families used here are simplifications. Real systems may deviate. Sensitivity analysis—$\sigma$ and SDE’s—helps but does not establish universality.
• Validation has been minimal by design. Thresholds/phase transitions should be viewed as testable predictions, not established empirical facts.
• Results may not hold in adversarial, highly non-stationary, or strongly path-dependent settings without additional assumptions or new proofs.

Again, this being said, on the basis of our—and much similar—work, the Precautionary Principle should constrain the use of AI in such safety-critical domains as NC3.

Further work will be needed to fully characterize the effects of Clausewitzian fog and friction across the full set of probability distributions likely to underlie a wide spectrum of observed cognitive phenomena, but what emerges from this analysis is the ubiquity of failure-under-stress even for ‘intelligent’ embodied cognition, even when cognitive and regulatory modules are closely paired.

There is still No Free Lunch, much in the classic sense of Wolpert and MacReady [3,4].