Mapping Research on the Birnbaum–Saunders Statistical Distribution: Patterns, Trends, and Scientometric Perspective

Abstract

This article provides a critical assessment of the Birnbaum–Saunders (BS) distribution, a pivotal statistical model for lifetime data analysis and reliability estimation, particularly in fatigue contexts. The model has seen successfully applied across diverse fields, including biological mortality, environmental sciences, medicine, and risk models. Moving beyond a basic scientometric review, this study synthesizes findings from 353 peer-reviewed articles, selected using PRISMA 2020 protocols, to specifically trace the evolution of estimation techniques, regression methods, and model extensions. Key findings reveal robust theoretical advances, such as Bayesian methods and bivariate/spatial adaptations, alongside practical progress in influence diagnostics and software development. The analysis highlights key research gaps, including the critical need for scalable, auditable software and structured reviews, and notes a peak in scholarly activity around 2019, driven importantly by the Brazil-Chile research alliance. This work offers a consolidated view of current BS model implementations and outlines clear future directions for enhancing their theoretical robustness and practical utility.

1. Introduction

The Birnbaum–Saunders (BS) distribution [1,2] has become a central model in reliability [3,4,5,6] and lifetime analysis due to its solid theoretical foundation and flexibility for modeling fatigue life phenomena based on the Miner rule [7]. A large body of work has examined its statistical properties [8,9], estimation and inference methods [10,11,12,13], modeling and diagnostics [14,15,16,17,18,19], as well as practical applications [20,21,22] and its univariate and multivariate extensions [23,24,25,26,27,28,29,30,31,32,33].

Recent contributions further expand the BS framework through methodological advances and new application domains. These include stable-type damage formulations [34], censored-data inference [35], Bayesian methods [36], shrinkage estimation [37], analysis of imprecise data [38], updated fatigue-data modeling [39], neutrosophic models [40], hybrid censored data [41], ranked set sampling [42], frailty models [43], quantile regression [44], estimation equations [45], clustered count data [46], generalized confidence intervals [47], and autoregressive and spatial models [48,49,50,51].

Additional developments involve control charts and monitoring schemes [52,53,54,55], inference for extended BS forms [56], and models addressing contamination, finance, and other emerging contexts [57,58].

Research on cumulative damage and fatigue life processes [59], which underpin the original derivation of the BS model, continues to evolve through bibliometric, methodological, and applied studies [60]. Complementary work on flexible lifetime models and probabilistic structures also enriches the broader reliability literature [61,62,63].

Despite this substantial progress, a synthesis that maps the structure, evolution, and thematic trends of BS-related research remains limited. This motivates a systematic exploration aimed at clarifying research patterns, identifying dominant topics, and highlighting emerging opportunities across the BS modeling landscape.

In this article, first, we provide a structured synthesis of BS models linking theory to practice. Second, we construct a quantitative bibliometric map of the field—covering 366 peer-reviewed studies screened to 19 November 2025 under preferred reporting items for systematic reviews and meta-analyses (PRISMA) 2020 [64] to characterize collaboration patterns, thematic clusters, and structural gaps [60].

What is new relative to prior tutorials and narrative reviews is that we (i) focus explicitly on BS models in a single unified notation; (ii) offer a concise overview of practical considerations relevant to applied BS modeling, including commonly used diagnostics and currently available software implementations; and (iii) provide reproducible materials. These three points highlight both methodological advances and the remaining obstacles to wider adoption—most notably the need for scalable, auditable software and routine diagnostics—while offering concrete guidance for applied teams.

This review addresses the following research questions (RQs), which guide both the bibliometric mapping and the synthesis of methodological developments:

RQ1

Theory and methods—What theoretical advances, estimation techniques, and model extensions have been developed for the BS family?

RQ2

Applications and impact—In which scientific domains has the BS distribution been most influential, and how has its use evolved across disciplines?

RQ3

Research structure—What collaboration networks, thematic clusters, and knowledge gaps characterize BS-related literature?

RQ4

Future directions—What emerging trends and methodological priorities are suggested by bibliometric evidence and text analytics?

To address these RQs, this study has the following objectives:

(i)

To map the methodological and applied evolution of the BS distribution using curated bibliometric data and targeted literature synthesis.

(ii)

To identify dominant themes, research communities, and structural gaps through network visualization and thematic analysis.

(iii)

To highlight emerging trajectories and future research opportunities informed by quantitative evidence from text mining and citation dynamics.

We compiled a curated dataset of 366 Web of Science articles on the BS distribution and analyzed it using bibliometric methods, network mapping, and latent Dirichlet allocation (LDA) topic modeling [65]. This dataset offers an overview of the evolution of BS research and its main theoretical and applied developments.

This study expands upon the analysis presented in [60], which focused on a more limited dataset and a narrower set of scientometric indicators. While some methodological components are related, the present work incorporates an updated and substantially larger body of literature, a broader scientometric framework, and more refined graphical outputs. These enhancements allow for a more comprehensive and current perspective on research developments in the BS distribution.

The remainder of this article is organized as follows. Section 2 presents background on BS models and its characteristics. In Section 3, we detail our analytical strategy and the scientometric methodology. In Section 4, the main findings are reported. Section 5 provides some aspects related to implementation and insights from topic modeling, whereas Section 6 concludes with a final synthesis and outlook for the BS field.

2. Theoretical and Methodological Foundations

This section presents the mathematical toolkit for the BS distribution and related models, covering notation and main characteristics.

2.1. The Birnbaum–Saunders Distribution

The two-parameter BS distribution, denoted as $\mathrm{BS}(\alpha , \beta )$, where $\alpha >0$ and $\beta >0$ represent the shape and scale parameters, respectively, was originally introduced in [1] as a life distribution derived from cumulative damage under cyclic stress. The BS distribution has interesting statistical and mathematical properties, one of them being that it can be expressed as a mixture of inverse Gaussian distributions [66,67].

The BS distributed random variable, T say, is defined by a monotonic transformation of a standard normal distributed random variable $Z\sim \mathrm{N}(0, 1)$ whose relationship is given by

$$Z={\displaystyle \frac{1}{\alpha }}\left(\sqrt{{\displaystyle \frac{T}{\beta }}}-\sqrt{{\displaystyle \frac{\beta }{T}}}\right).$$

The variable T can be generated from Z by the expression established as

$$T=\beta {\left({\displaystyle \frac{\alpha Z}{2}}+\sqrt{{\left({\displaystyle \frac{\alpha Z}{2}}\right)}^2+1}\right)}^2.$$

The square of the random variable Z is related to T by a transformation that follows a chi-squared distribution with one degree of freedom stated as

$$V=Z^2={\displaystyle \frac{1}{{\alpha }^2}}\left({\displaystyle \frac{T}{\beta }}+{\displaystyle \frac{\beta }{T}}-2\right)\sim {\chi }^2\left(1\right).$$

As mentioned, the distribution is defined by two parameters: $\alpha >0$ (the shape parameter) and $\beta >0$ (the scale parameter, which is also the median). For a random variable $T>0$ following a BS distribution with parameters $\alpha$ and $\beta$, the probability density function (PDF) is given by

$$f_T(t;\alpha , \beta )={\displaystyle \frac{1}{2\alpha \beta \sqrt{2\pi }}}\left({\left({\displaystyle \frac{t}{\beta }}\right)}^{-1/2}+{\left({\displaystyle \frac{t}{\beta }}\right)}^{3/2}\right)exp\left(-{\displaystyle \frac{1}{2{\alpha }^2}}\left({\displaystyle \frac{t}{\beta }}+{\displaystyle \frac{\beta }{t}}-2\right)\right), t>0, \alpha >0, \beta >0.$$

The cumulative distribution function (CDF) of $T\sim \mathrm{BS}(\alpha , \beta )$ is defined as

$$F_T(t;\alpha , \beta )=\mathrm{\Phi }\left({\displaystyle \frac{1}{\alpha }}\left({\left({\displaystyle \frac{t}{\beta }}\right)}^{1/2}-{\left({\displaystyle \frac{t}{\beta }}\right)}^{-1/2}\right)\right), t>0, \alpha >0, \beta >0,$$

where $\mathrm{\Phi }$ is the CDF of the standard normal distribution. This connection highlights the relationship between the BS and standard normal distributions.

The above stochastic representation enables random generation from the BS model by simulating random numbers from $Z\sim \mathrm{N}(0, 1)$ and applying the transformation.

Parameter interpretation is direct: $\beta$ acts as a scale parameter and is also the median of T, while $\alpha$ controls skewness and tail-weight so that larger $\alpha$ increases asymmetry and dispersion.

The quantile function of $T\sim \mathrm{BS}(\alpha , \beta )$ is formulated as

$$Q\left(p\right)=\beta {\left({\displaystyle \frac{\alpha z\left(p\right)}{2}}+\sqrt{{\left({\displaystyle \frac{\alpha z\left(p\right)}{2}}\right)}^2+1}\right)}^2, 0<q<1, \alpha >0, \beta >0.$$

where $z\left(p\right)$ is the pth quantile of the standard normal distribution. In particular, at $p=0.5$, we obtain $z\left(0.5\right)=0$, yielding $Q\left(0.5\right)=\beta$. Hence, $\beta$ is both the median and scale parameter.

The mean, variance, as well as coefficients of skewness and kurtosis (which depend only on the shape parameter $\alpha$) of $T\sim \mathrm{BS}(\alpha , \beta )$ are given by

$$\mathbb{E}\left(T\right)=\beta \left(1+{\displaystyle \frac{{\alpha }^2}{2}}\right), Var\left(T\right)={\displaystyle \frac{{\beta }^2{\alpha }^2}{2}}\left(1+{\displaystyle \frac{5{\alpha }^2}{4}}\right).$$

$$\mathrm{Skewness}\left(T\right)={\displaystyle \frac{4\alpha \left(11{\alpha }^2+6\right)}{{\left(5{\alpha }^2+4\right)}^{3/2}}}, \mathrm{Kurtosis}\left(T\right)=3+{\displaystyle \frac{6{\alpha }^2\left(93{\alpha }^2+40\right)}{{\left(5{\alpha }^2+4\right)}^2}}.$$

Consequently, increasing $\alpha$ increases skewness and excess kurtosis. The distribution is unimodal and typically exhibits positive asymmetry (right-skewness). For small $\gamma$, the distribution tends to become symmetrical around $\delta$, and its variability decreases. As $\gamma$ increases, the distribution shows heavier tails, indicating that $\gamma$ modifies the skewness and kurtosis. The hazard function of $T\sim \mathrm{BS}(\alpha , \beta )$ is unimodal [68,69], and the distribution is closed under scaling (for $b>0$, $bT\sim \mathrm{BS}(\alpha , b\beta )$) and inversion ($1/T\sim \mathrm{BS}(\alpha , 1/\beta )$).

2.2. The Log-Birnbaum–Saunders Distribution

Let $T\sim \mathrm{BS}(\alpha , \beta )$. Then, the log-Birnbaum–Saunders (log-BS, also known as sinh-normal) distribution is obtained from $Y=log\left(T\right).$ Equivalently, using a normal variable $Z\sim \mathrm{N}(0, 1)$, we have that

$$Y=\mu +{\displaystyle \frac{1}{2}}arcsinh\left({\displaystyle \frac{\alpha Z}{2}}\right),$$

where $\mu =log\left(\beta \right)$ and $\alpha >0$. Then, Y defines the log-BS distribution, denoted by $Y\sim \text{log-BS}(\alpha , \mu )$.

Using the monotonicity of the logarithm, we reach

$$Q_Y\left(p\right)=log\left(\beta {\left({\displaystyle \frac{\alpha z_p}{2}}+\sqrt{{\left({\displaystyle \frac{\alpha z_p}{2}}\right)}^2+1}\right)}^2\right)=\mu +2log\left({\displaystyle \frac{\alpha z_p}{2}}+\sqrt{{\left({\displaystyle \frac{\alpha z_p}{2}}\right)}^2+1}\right).$$

Thus, $\mu =log\left(\beta \right)$ is a location parameter and the median of Y, while $\alpha$ controls tail-weight and departure from normality.

The moment generating function of Y can be written as

$$m_Y\left(r\right)=exp\left(r\mu \right)\left({\displaystyle \frac{K_{r/2+1/2}(1/{\delta }^2)+K_{r/2-1/2}(1/{\delta }^2)}{2K_{1/2}(1/{\delta }^2)}}\right),$$

where $K_{\lambda }$ is the modified Bessel function of the third kind and $\delta =1/\alpha$. The mean and variance of Y follow by differentiation of $m_Y\left(r\right)$ at $r=0$. Note that $\mathbb{E}\left(Y\right)\ne \mu$ in this parametrization.

Random numbers y of a random variable Y following the log-BS distribution can be obtained by simulating z from $Z\sim \mathrm{N}(0, 1)$, computing

$$y=\mu +{\displaystyle \frac{1}{2}}arcsinh\left({\displaystyle \frac{\alpha z}{2}}\right),$$

and, if desired, transforming back via $t=exp\left(y\right)$ to obtain BS distributed random numbers. Alternatively, one can simulate $V=Z^2\sim {\chi }^2\left(1\right)$, use

$$X={\displaystyle \frac{1}{2\alpha }}\left((2+{\mu }^{2}V)+\sqrt{{(2+{(1/\alpha )}^{2}V)}^2-4}\right),$$

and then set $Y=log\left(X\right)$. The PDF and CDF of $Y\sim \text{log-BS}(\alpha , \mu )$ are given by

$$f_Y(y;\alpha , \mu )=\varphi \left({\displaystyle \frac{2}{\alpha }}sinh\left({\displaystyle \frac{y-\mu }{2}}\right)\right){\displaystyle \frac{1}{\alpha }}cosh\left({\displaystyle \frac{y-\mu }{2}}\right), y\in \mathbb{R},$$

$$F_Y(y;\alpha , \mu )=\mathrm{\Phi }\left({\displaystyle \frac{2}{\alpha }}sinh\left({\displaystyle \frac{y-\mu }{2}}\right)\right), y\in \mathbb{R},$$

where $\varphi$ is the PDF of the standard normal distribution.

The log-BS distribution is symmetrical around $\mu$, which is the location parameter and the median of the distribution. When the shape parameter $\alpha$ is small, the log-BS distribution converges to the normal distribution.

2.3. Computational Implementation of the BS Distribution

This subsection forms part of the methodological background of the review and is not involved in the bibliometric or scientometric analyses presented later. Open-source computational tools play an important role in supporting the application of BS models. The BS and log-BS distributions have dedicated implementations in the R software [70], with the following main packages:

• bs—Estimation, inference, and simulation for BS models [71].
• gbs—Generalized BS models and regression extensions [72].

In practice, these implementations are commonly complemented with standard diagnostic tools available in R—including probability plots, residual analyses, and information criteria—to evaluate goodness-of-fit and to monitor numerical stability across estimation routines.

Both BS packages can be secured (accessed on 10 December 2025) at

• https://cran.r-project.org/src/contrib/Archive/bs
• https://cran.r-project.org/src/contrib/Archive/gbs
• http://www.victorleiva.cl

3. Bibliometric Methodology

This section details the technical procedures used to assemble, pre-process, and analyze the bibliographic corpus (366 documents). We present the search and screening method, construction and normalization of co-occurrence matrices, graph layout and clustering, thematic mapping, and the LDA method with collapsed Gibbs inference. All steps were implemented in the R software; see Section 3.9.

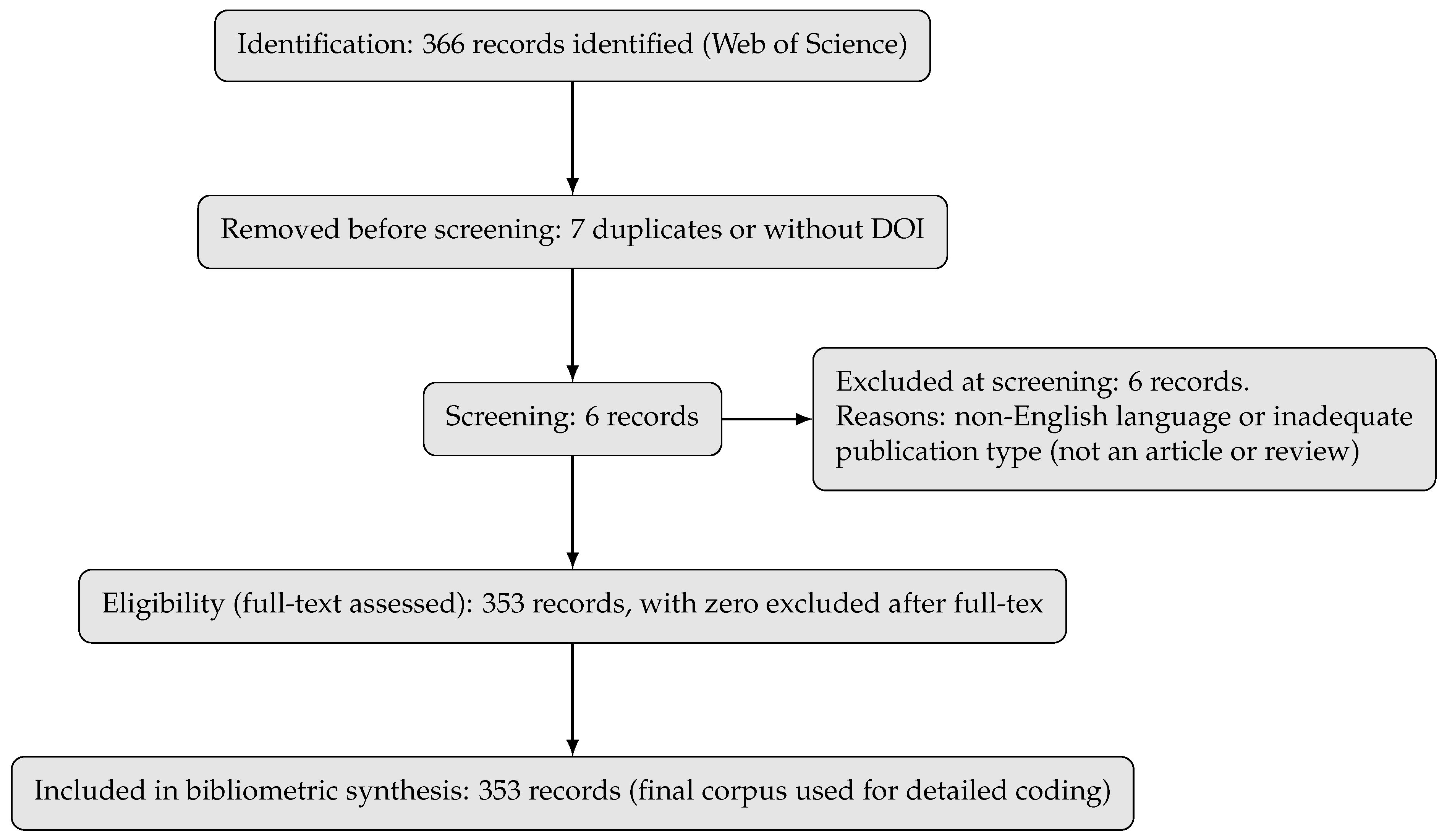
3.1. Search and Screening (PRISMA Method)

We followed PRISMA 2020 [64] procedures to identify and select records. The search was executed on Web of Science (titles, English-language) up to 19 November 2025 using keywords related to the BS family.

To ensure full reproducibility, the exact Web of Science search strings are now provided: (birnbaum AND saunders) and (birnbaum-saunders). Records were deduplicated at the digital object identifier (DOI) level and screened in two stages (title/abstract, then full text). Inclusion criteria and screening decisions were recorded. The final corpus contains 353 documents. Articles dated 2026 correspond to early-access items already indexed in Web of Science at the time of the search (19 November 2025), which justifies their inclusion.

The terms were refined through preliminary searches based on foundational studies, ensuring adequate coverage of relevant approaches. Initial queries retrieved 366 records. To ensure the relevance and quality of included studies, we applied the following filtering criteria:

• Inclusion of peer-reviewed items (journal articles and peer-reviewed conference proceedings).
• Exclusion of records lacking core metadata (title, abstract, or DOI), consistent with the pre-specified English-language scope.
• Removal of any residual duplicates after DOI harmonization across databases.

Then, eligibility was assessed in two stages. First, titles and abstracts were screened independently by two reviewers. Non-peer-reviewed documents (for example, theses, conference abstracts) and purely narrative reviews were excluded. The second stage involved full-text assessment of the remaining articles. No further exclusions occurred at this point. Following this process, as mentioned, 353 articles were retained for inclusion. Figure 1 summarizes the selection workflow using the PRISMA-2020 format [73]. Therefore, we identified 366 records across Web of Science, removed 7 records, and 6 records were excluded with incomplete metadata (missing DOI, title, or abstract). All 353 records retrieved at full text were eligible and entered into the bibliometric synthesis.

With the final corpus established, the next step was to convert its bibliographic metadata into quantitative structures amenable to scientometric and network analyses. In particular, we built co-occurrence matrices for authors, keywords, and country affiliations and then normalized those matrices to obtain weighted graphs. The rationale and formulas behind this transformation are detailed below.

3.2. Construction and Normalization of Co-Occurrence Matrices

Let $\mathcal{V}=\{v_1, \dots , v_N\}$ be the set of entities (authors, keywords, countries). For a corpus of D documents, we build the symmetric co-occurrence matrix $M=\left[m_{ij}\right]$ where

$$m_{ij}=\sum _{d=1}^D{\omega }_{ij}^{\left(d\right)}, i, j=1, \dots , N,$$

and ${\omega }_{ij}^{\left(d\right)}$ is the contribution of document d to pair $(v_i, v_j)$. We adopt a mixed counting scheme as follows:

• Fractional pair counting—If document d contains $p_d$ distinct entities, each unordered pair $(i, j)$, $i\ne j$, receives ${\omega }_{ij}^{\left(d\right)}=1/\left({\displaystyle \genfrac{}{}{0pt}{}{p_d}{2}}\right).$
• Full counting for margins—The diagonal stores the document frequency $f_i={\sum }_d{1}_{\{v_i\in d\}}$ so $m_{ii}=f_i$.

This mixed scheme downweights documents with large entity lists while preserving marginal interpretability. To obtain an association measure robust to node marginal frequencies, we compute the normalized weighted adjacency matrix $W=\left[w_{ij}\right]$, whose array is given by

$$w_{ij}=m_{ij}/f_i{f}_j, i\ne j, w_{ii}=0.$$

(1)

Alternative normalizations (Salton/cosine, Jaccard, Association Strength) were tested for sensitivity. The formulation stated in (1) (association strength) provides stable interpretable maps for sparse bibliometric networks [74].

We prune weak links by thresholding $w_{ij}\leftarrow 0$, if $w_{ij}<\epsilon$, with a light threshold $\epsilon =0.05$ (sensitivity checks used $\epsilon \in [0.03, 0.07]$). Regarding the pruning threshold, $\epsilon =0.05$ was selected after exploratory checks showed that smaller values produced overly dense and non-informative networks, whereas larger values removed relevant connections. Although a full sensitivity analysis was not undertaken, we acknowledge this limitation and clarify the rationale for the chosen threshold. For keyword networks, we retain only the largest connected component for layout stability; for country networks, isolates are preserved to capture emerging collaborations.

3.3. Network Layout and Community Detection

To embed the graph $G=(V, E, W)$ in two dimensions, we use a weighted Kamada–Kawai (KK) energy minimization. Let ${\mathit{x}}_i={(x_i, y_i)}^{\top }$ be coordinates of node $v_i$. The KK objective is given by

$$E\left(\mathit{x}\right)={\displaystyle \frac{1}{2}}\sum _{1\le i<j\le N}{k}_{ij}{\left(\parallel {\mathit{x}}_i-{\mathit{x}}_j\parallel -{\ell }_{ij}\right)}^2,$$

(2)

where we set the preferred distance ${\ell }_{ij}={\ell }_0/w_{ij}$ (stronger ties ⇒ shorter preferred distance) and stiffness $k_{ij}=\kappa /{\ell }_{ij}^2$. We rescale $w_{ij}\in (0, 1]$, use ${\ell }_0=1$ and $\kappa =1$ unless otherwise specified. Pairs with $w_{ij}=0$ are omitted from the sum.

Communities are detected via modularity optimization (Louvain algorithm) with default resolution [75]. As sensitivity checks, we compared partitions obtained with the Walktrap and Leiden algorithms and found qualitatively similar groupings.

Centrality measures are computed as follows:

• Betweenness on the unweighted simple graph (shortest-path counts).
• Closeness using weighted shortest-path distances $d_{ij}=1/w_{ij}$ (reported for nodes in the largest component).
• Pagerank on the row-normalized weighted adjacency with damping factor $0.85$ [76].

3.4. Thematic Mapping (Callon Centrality–Density)

After partitioning keywords into clusters $T_{\alpha }$, for $\alpha =1, \dots , m$, we compute Callon density $D_{\alpha }$ and centrality $C_{\alpha }$ as

$$\begin{array}{cccc}\hfill D_{\alpha }& =100\times {\displaystyle \frac{{\sum }_{\genfrac{}{}{0pt}{}{i<j}{v_i,v_j\in T_{\alpha }}}{w}_{ij}}{\left(\genfrac{}{}{0pt}{}{|T_{\alpha }|}{2}\right)}}, \hfill & \hfill C_{\alpha }& =10\times {\displaystyle \frac{{\sum }_{v_i\in T_{\alpha }}{\sum }_{v_j\notin T_{\alpha }}{w}_{ij}}{|T_{\alpha }|}}.\hfill \end{array}$$

Plotting points $(C_{\alpha }, D_{\alpha })$ yields a diagram with quadrants defined by median values of $\left\{C_{\alpha }\right\}$ and $\left\{D_{\alpha }\right\}$ and interpreted as motor, basic/transversal, niche, or emerging/declining themes [77,78].

3.5. Matrix Construction, Normalization, Graphs, and Clustering

The pseudocodes of matrix construction, normalization, graph layout, and clustering are presented in Algorithms 1 and 2.

Algorithm 1: Construction and normalization of the co-occurrence matrix

Algorithm 2: Layout and community detection

1 Input: Weighted adjacency W, seed for layouts 2 Output: Coordinates $\left\{{\mathit{x}}_i\right\}$, community labels 3 Rescale weights $w_{ij}\in [0, 1]$ 4 Compute preferred distances ${\ell }_{ij}=1/w_{ij}$ for $w_{ij}>0$ 5 Initialize coordinates (such as random or spectral) 6 Minimize energy (2) via iterative optimizer (Newton–Raphson or quasi-Newton) until convergence 7 Run Louvain algorithm on W to obtain communities 8 Compute centralities (betweenness, closeness, PageRank) 9 return coordinates, community labels, centralities

3.6. Latent Dirichlet Allocation for Topic Modeling

We apply LDA to document abstracts (and optionally titles+keywords) to recover latent topics. LDA assumes the following generative process for each document d:

1.

Draw document length $N_d\sim \mathrm{Poisson}\left(\lambda \right)$.

2.

Draw topic mixture ${\theta }_d\sim \mathrm{Dirichlet}\left(\alpha \right)$.

3.

For each word position $n=1, \dots , N_d$:

(a)

Draw topic $z_{d,n}\sim \mathrm{Categorical}\left({\theta }_d\right)$.

(b)

Draw word $w_{d,n}\sim p\left(w\right|z_{d,n}, \beta )$.

Figure 2 displays a flowchart of the generative process of LDA.

We use symmetric Dirichlet priors with $\alpha =1/K$ (document-topic) and $\beta =1/V$ (topic-word) as initializations. Hyperparameter tuning and coherence/perplexity metrics guide final choices. The Dirichlet density for ${\theta }_d$ is stated as

$$p\left({\theta }_d\right|\alpha )={\displaystyle \frac{\mathrm{\Gamma }\left({\sum }_{i=1}^K{\alpha }_i\right)}{{\prod }_{i=1}^K\mathrm{\Gamma }\left({\alpha }_i\right)}}\prod _{i=1}^K{\theta }_{di}^{{\alpha }_i-1}.$$

For topic-word distributions ${\varphi }_k$, we have

$$p\left({\varphi }_k\right|\beta )={\displaystyle \frac{\mathrm{\Gamma }\left({\sum }_{j=1}^V{\beta }_j\right)}{{\prod }_{j=1}^V\mathrm{\Gamma }\left({\beta }_j\right)}}\prod _{j=1}^V{\varphi }_{kj}^{{\beta }_j-1}.$$

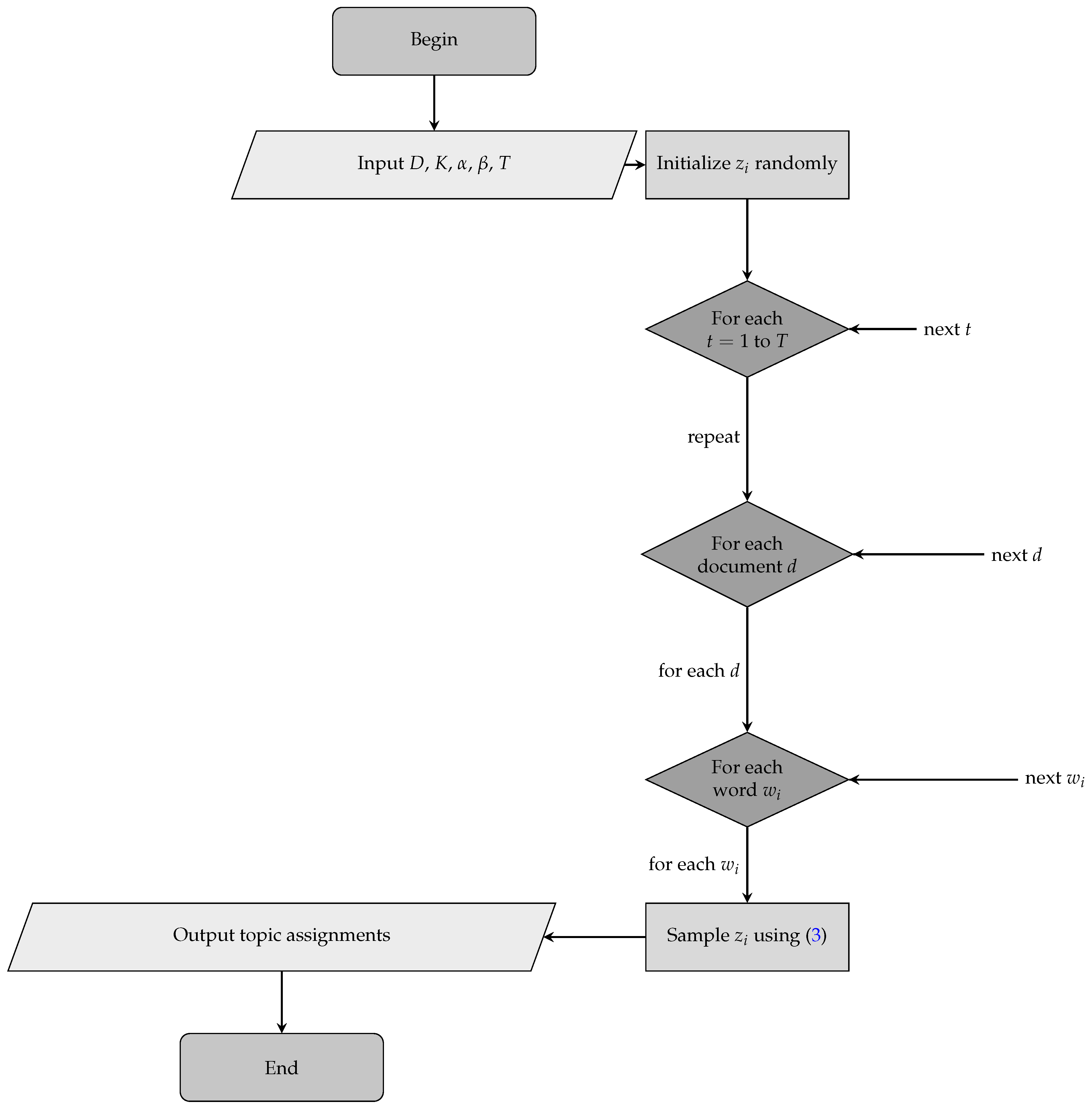
3.7. Collapsed Gibbs Sampling

We perform collapsed Gibbs sampling (integrating out $\theta$ and $\varphi$) to sample topic assignments. The conditional probability for assigning topic k to word token i (word $w_i$ in document $d_i$) is stated as

$$p(z_i=k\mid {\mathit{z}}_{-i}, \mathit{w})\propto \left({\displaystyle \frac{n_{-i,k}^{\left(w_i\right)}+\beta }{n_{-i,k}^{(·)}+V\beta }}\right)\left({\displaystyle \frac{n_{-i,k}^{\left(d_i\right)}+\alpha }{n_{-i}^{\left(d_i\right)}+K\alpha }}\right),$$

(3)

where $n_{-i,k}^{\left(w\right)}$ is the count of word w assigned to topic k excluding token i; $n_{-i,k}^{(·)}$ is the total words assigned to topic k excluding i; $n_{-i,k}^{\left(d\right)}$ is the count of words in document d assigned to k excluding i; and $n_{-i}^{\left(d\right)}$ is the total number of words in document d excluding i. The pseudocode of collapsed Gibbs sampling for LDA is presented in Algorithm 3, whereas a flowchart for the collapsed Gibbs process is shown in Figure 3. Algorithm 3 presents an extended and refined version of Algorithm 1 previously published in [60]. While the core methodology is the same, the current formulation provides additional details, clarifications, and improvements in implementation, allowing for clearer application and better reproducibility. This makes the relationship with the prior publication explicit while highlighting the novel contributions of the present study.

Algorithm 3: Collapsed Gibbs sampling for LDA

3.8. Model Selection: Coherence and Perplexity

We evaluate candidate K using coherence and perplexity. A coherence score (one variant) is given by

$$C_v\approx {\displaystyle \frac{1}{\left|W\right|}}\sum _{i<j}log\left({\displaystyle \frac{p(w_i, w_j)+\epsilon }{p\left(w_i\right)p\left(w_j\right)}}\right),$$

where $p(w_i, w_j)$ is the probability of co-occurrence of words $w_i, w_j$ in the reference corpus, $p\left(w_i\right)$ marginal probabilities, and $\epsilon$ a smoothing constant. Perplexity on held-out set $D_{\mathrm{test}}$ is formulated as

$$\mathrm{perplexity}\left(D_{\mathrm{test}}\right)=exp\left(-{\displaystyle \frac{{\sum }_{d\in D_{\mathrm{test}}}log\left(p\left({\mathit{w}}_d\right)\right)}{{\sum }_{d\in D_{\mathrm{test}}}{N}_d}}\right).$$

We balance coherence (interpretability) and perplexity (predictive fit) to select K.

3.9. Implementation Details in R

All preprocessing (metadata cleaning, DOI harmonization, tokenization, stopword removal, lemmatization) and analyses were conducted using the following R packages:

• bibliometrix for metadata extraction and basic bibliometric summaries;
• igraph for graph objects, metrics, and community detection;
• ggraph + ggplot2 for visualization;
• tidytext/text2vec for text preprocessing and LDA;
• topicmodels/lda for LDA and Gibbs sampling (or custom Gibbs implementation for greater control);
• SnowballC and tm for stemming/token filtering.

The implementation in R-style pseudocode is displayed in Algorithm 4.

Algorithm 4: Implementation method (R pseudocode)

4. Empirical Results

This section contains the practical exploration of the research landscape within the statistical domain, focusing on the BS distribution. We analyze the current research on the mentioned domain, identifying prevailing themes, collaboration networks, and emerging trends.

4.1. Systematic Review

This section summarizes the main descriptive insights derived from the final corpus of 353 articles obtained after the screening process described in Section 3.1. The systematic review provides an overview of publication patterns, thematic focus, and key contributors in the BS literature, serving as the foundation for the subsequent scientometric and topic–modeling analyses.

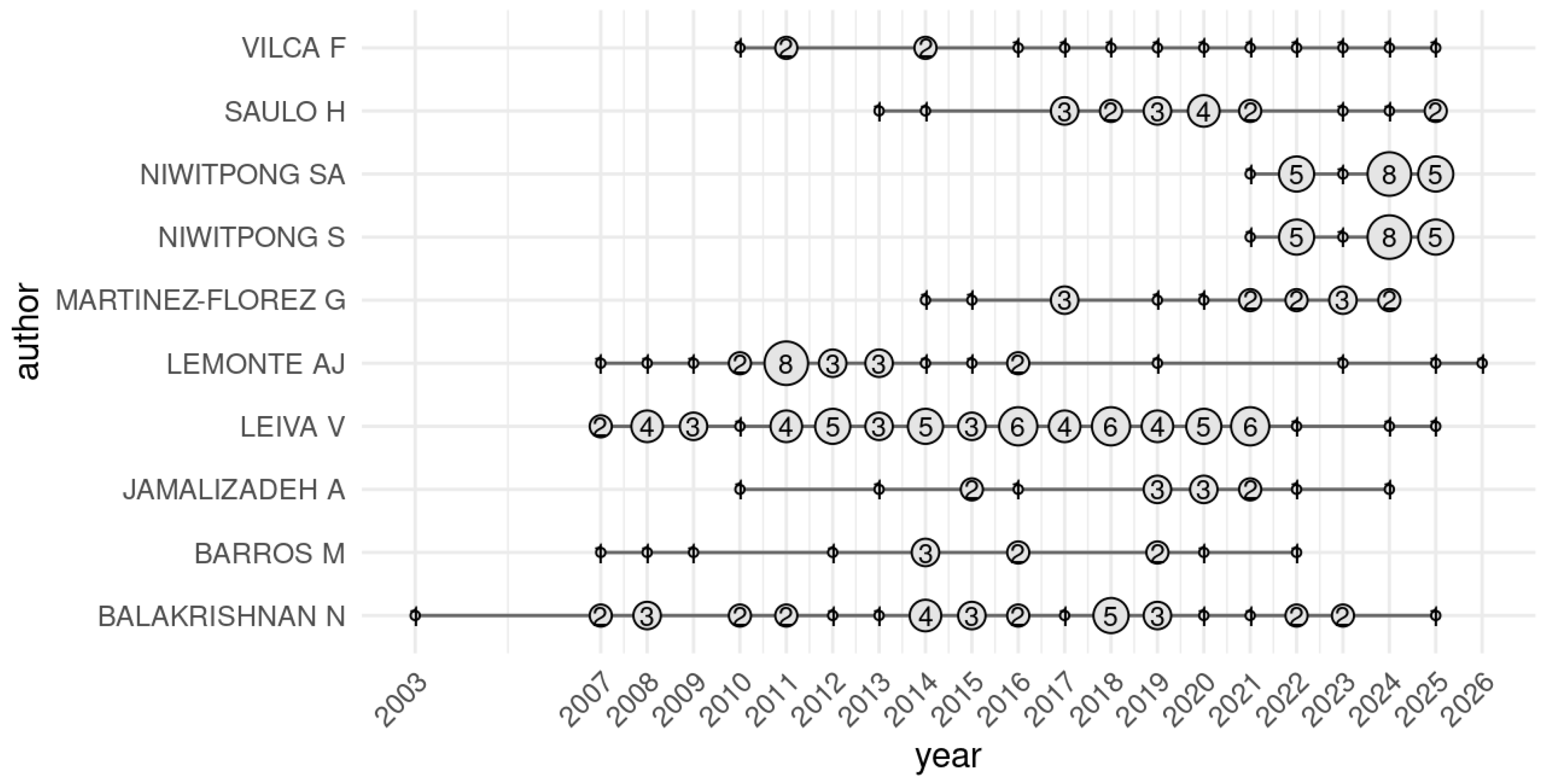
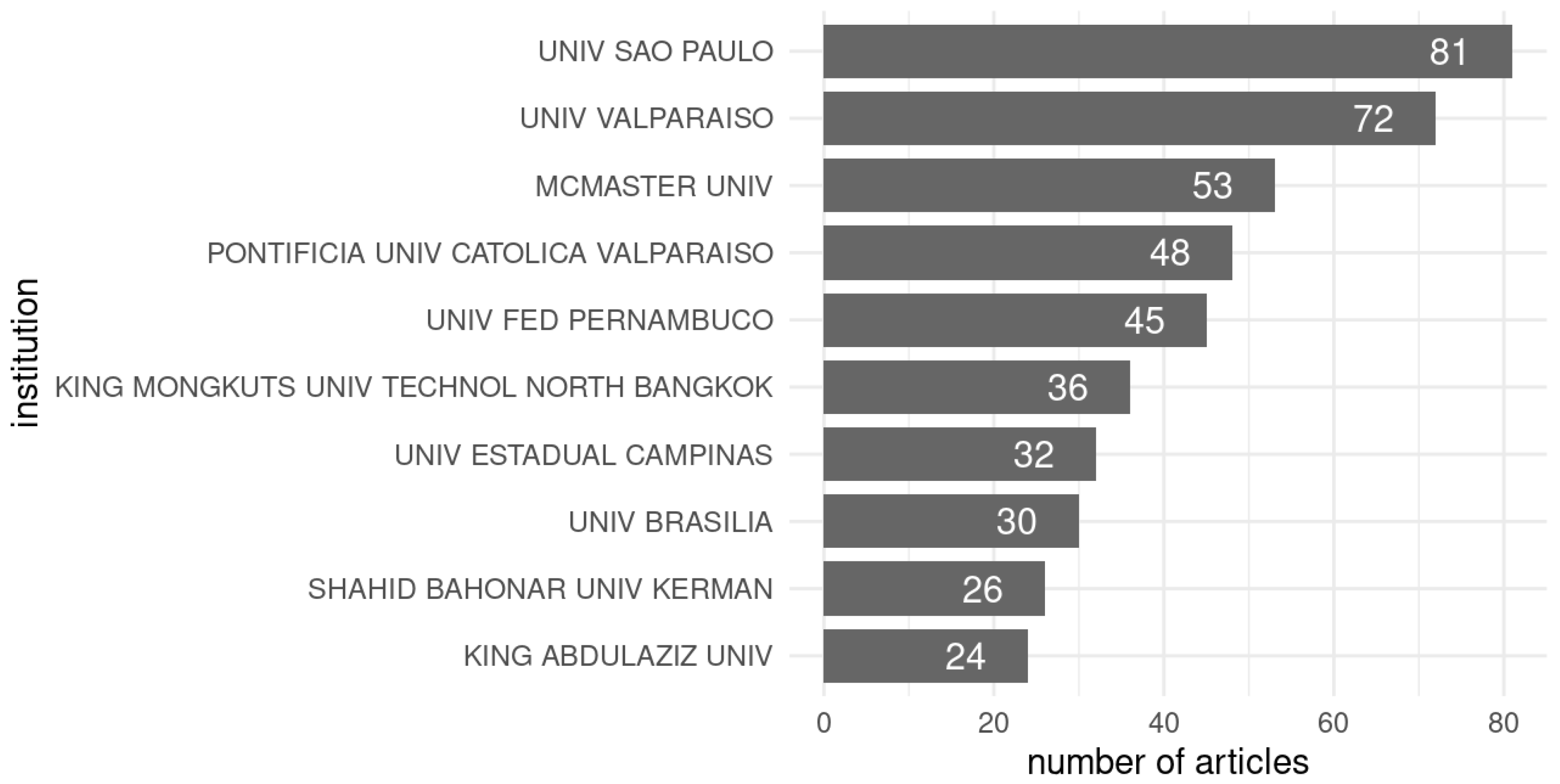
4.2. Descriptive Profile of the Corpus

The bibliometric/scientometric analysis began with an examination of the trends in the volume of articles published over time. Using the 353 most relevant articles, the range of publications spans from January 1980 to November 2025, including two cases with early publications already listed for 2026.

As indicated in

Table 1. Number of articles per year.

Year	Number of Articles	Year	Number of Articles	Year	Number of Articles
1980	1	2001	1	2015	12
1981	2	2003	4	2016	19
1982	2	2004	3	2017	16
1987	1	2006	3	2018	16
1991	1	2007	5	2019	31
1993	2	2008	10	2020	21
1994	3	2009	6	2021	25
1995	2	2010	11	2022	23
1997	1	2011	17	2023	16
1998	1	2012	14	2024	28
1999	2	2013	12	2025	23
2000	1	2014	13	2026	2

, there has been an increase in scholarly activity over the years, indicating a growing interest and engagement with this subject. The data reveal an important upward trend from the years 2011 to 2021, followed by a decline in the number of publications from 2021 onwards. This pattern suggests a peak in research activity around 2021, with subsequent fluctuations in interest or shifts in research focus. Figure 4 and Figure 5 show the number of articles and citations per year, respectively.

In terms of document type, 336 of the included articles are original research articles, 17 are review articles, and 6 are conference proceedings. The predominance of original research reflects an active and ongoing interest in methodological development. Conversely, the small number of reviews suggests that synthesis-oriented contributions remain relatively limited, possibly due to the technical complexity and evolving scope of the field. This shows the potential value of structured overviews, such as the present one, that aim to consolidate dispersed efforts across subdomains.

To identify the primary outlets for research dissemination, we examined the journals with the highest number of publications. Understanding where the majority of research is published helps to highlight key venues that importantly contribute to the field’s development. Identifying these journals provides insights into the main channels through which new findings are disseminated and which journals are central to the academic conversation in this area.

Table 2. Top 10 most productive journals.

Journal	Number of Articles
Computational Statistics and Data Analysis	33
Journal of Statistical Computation and Simulation	26
Applied Stochastic Models in Business and Industry	23
Communications in Statistics - Simulation and Computation	20
Communications in Statistics - Theory and Methods	20
Journal of Applied Statistics	17
IEEE Transactions on Reliability	12
Mathematics	12
Symmetry	11
Brazilian Journal of Probability and Statistics	8

and Figure 6 list the top 10 journals by number of articles published.

To understand the impact and dissemination of research, we organized the selected articles based on the number of citations. This organization highlights the most influential works and provides insights into which studies have had the greatest impact on the research community.

Table 3. Top 20 articles distributed by the number of citations.

Authors	Title	Journal	Year	Citations
Balakrishnan N; Leiva V; Lopez J [79]	Acceptance sampling plans from truncated life tests based on the generalized Birnbaum-Saunders distribution	Communications in Statistics - Simulation and Computation	2007	221
Rieck JR; Nedelman JR [80]	A log linear-model for the Birnbaum-Saunders distribution	Technometrics	1991	192
Ng HKT; Kundu D; Balakrishnan N [81]	Modified moment estimation for the two-parameter Birnbaum-Saunders distribution	Computational Statistics and Data Analysis	2003	163
Engelhardt M; Bain LJ; Wright FT [82]	Inferences on the parameters of the Birnbaum-Saunders fatigue life distribution based on maximum-likelihood estimation	Technometrics	1981	113
Kundu D; Kannan N; Balakrishnan N [68]	On the hazard function of Birnbaum-Saunders distribution and associated inference	Computational Statistics and Data Analysis	2008	109
Cordeiro GM; Lemonte AJ [83]	The $\beta$-Birnbaum-Saunders distribution, an improved distribution for fatigue life modeling	Computational Statistics and Data Analysis	2011	108
Leiva V; Barros M; Paula GA; Galea M [84]	Influence diagnostics in log-Birnbaum-Saunders regression models with censored data	Computational Statistics & Data Analysis	2007	108
Balakrishnan N; Kundu D [21]	Birnbaum-Saunders distribution: A review of models, analysis, and applications	Applied Stochastic Models in Business and Industry	2019	104
Mohammadi K; Alavi O; Mcgowan JG [85]	Use of Birnbaum-Saunders distribution for estimating wind speed and wind power probability distributions: a review	Energy Conversion and Management	2017	100
Leiva V; Barros M; Paula GA; Sanhueza A [72]	Generalized Birnbaum-Saunders distributions applied to air pollutant concentration	Environmetrics	2008	97
Lio Yl; Tsai TR; Wu SJ [86]	Acceptance sampling plans from truncated life tests based on the Birnbaum-Saunders distribution for percentiles	Communications in Statistics - Simulation and Computation	2010	96
Lemonte AJ; Cribari-Neto F; Vasconcellos KL [8]	Improved statistical inference for the two-parameter Birnbaum-Saunders distribution	Computational Statistics and Data Analysis	2007	93
Paula GA; Leiva V; Barros M; Liu S [87]	Robust statistical modeling using the Birnbaum-Saunders-t distribution applied to insurance	Applied Stochastic Models in Business and Industry	2012	90
Gomez HW; Olivares-Pacheco JF; Bolfarine H [88]	An extension of the generalized Birnbaum-Saunders distribution	Statistics and Probability Letters	2009	89
Sanhueza A; Leiva V; Balakrishnan N [89]	The generalized Birnbaum-Saunders distribution and its theory, methodology, and application	Communications in Statistics - Theory and Methods	2008	85
Bhattacharyya GK; Fries A [67]	Fatigue failure models - Birnbaum-Saunders vs inverse Gaussian	IEEE Transactions on Reliability	1982	83
Baklizi A; El Masri AE [90]	Acceptance sampling based on truncated life tests in the Birnbaum Saunders model	Risk Analysis	2004	80
Leiva V; Marchant C; Saulo H; Aslam M; Rojas F [91]	Capability indices for Birnbaum-Saunders processes applied to electronic and food industries	Journal of Applied Statistics	2014	77
Pradhan B; Kundu D [92]	Inference and optimal censoring schemes for progressively censored Birnbaum-Saunders distribution	Journal of Statistical Planning and Inference	2013	77
Galea M; Leiva V; Paula GA [93]	Influence diagnostics in log-Birnbaum-Saunders regression models	Journal of Applied Statistics	2004	77

lists the top 20 articles distributed by the number of citations, showing seminal works that have shaped the field.

Analyzing Table 2 and Table 3 reveals that certain journals consistently publish highly impactful research. Notably, the Computational Statistics and Data Analysis stands out, with multiple entries among the top-cited articles, indicating its relevant role in the dissemination of research related to statistical computation and methods, fatigue life prediction, cumulative damage models, and reliability. This journal appears frequently, highlighting its prominence in the field and its influence on advancing knowledge in these areas.

Other key journals include Journal of Statistical Computation and Simulation, Applied Stochastic Models in Business and Industry, and Communications in Statistics-Simulation and Computation, as well as Communications in Statistics-Theory and Methods, all of which are well-represented in the top-cited articles list of Table 2.

These journals are pivotal in publishing influential research on statistical methods. Additionally, journals such as Journal of Applied Statistics and IEEE Transactions on Reliability also have notable entries in the top-cited articles list. These journals reflect their important roles in publishing high-impact research on statistical applications and modeling, as well as reliability analysis, respectively. The presence of these journals underscores their contribution to the field and their role in shaping ongoing research discussions.

Figure 7, Figure 8, Figure 9 and Figure 10 display information associated with the top 10 most productive authors on the thematic as well as the presence of them and other authors over time. In addition, these figures provide details about the top 10 most productive institutions and the top 5 most productive institutions over time.

Figure 11 shows a comparative analysis of scientific output and international collaboration for selected countries, where the articles are categorized as single country publication (SCP), with all co-authors being affiliated with institutions within the same country, and multiple country publication (MCP), which results from international collaboration with co-authors from more than one country. This figure indicates that China is the most productive country in terms of total articles. However, its output is predominantly domestic (SCP).

In contrast, countries like Chile, Canada, and the USA demonstrate a strong emphasis on international collaboration, with a high proportion of their output being MCP. Notably, Chile’s scientific output in this field appears to be highly globalized, with many more international collaborations (MCP) than domestic ones (SCP). The Brazilian pattern is similar to that from China, being dominated by SCP publications.

The geographical distribution of the studies provides insight into global research efforts within our domain. As reported in

Table 4. Distribution of articles by country, with the case of Chile having the number in parentheses as it corresponds to the value obtained using bibliometrix based on the corresponding author, while the higher number results from our case-by-case analysis.

Country	Number of Articles
Brazil	129
Chile	82 (22)
Canada	42
China	28
Thailand	21
United States	21
Iran	19
India	15
Taiwan	8
Australia	6
Saudi Arabia	6
Colombia	5
Egypt	4
Pakistan	4
Singapore	4
Algeria	3
Italy	3
Japan	3
South Korea	3
Greece	2
Netherlands	2
Turkey	2
Argentina	1
Germany	1
Jordan	1
Poland	1
Portugal	1
South Africa	1
Spain	1

and depicted in Figure 12, the analysis shows a wide range of countries, indicating widespread interest in this topic across different regions. Brazil leads with 129 articles, followed by Chile with 82 (22 according to the corresponding author), Canada with 42, China with 28, and Thailand with 21. The United States contributes 21 articles, Iran 19, and India 15. Other notable contributors include Taiwan with eight articles, Australia and Saudi Arabia with six each, and several countries such as Colombia, Egypt, Pakistan, and Singapore with four–five articles each. This distribution highlights the important research output from these countries, reflecting their active role in exploring statistical and reliability topics related to the BS distribution.

The distribution of articles by continent further emphasizes the global interest in these research topics. As summarized in

Table 5. Distribution of articles by continent.

Continent	Number	Percentage
Africa	8	2.23
Asia	114	31.75
Europe	11	3.06
North America	63	17.55
Oceania	6	1.67
South America	157	43.73

, Asia leads with 114 articles (31.75%), followed by South America with 157 articles (43.73%), and North America with 63 articles (17.55%). Europe contributes 11 articles (3.06%), Africa 8 articles (2.23%), and Oceania 6 articles (1.67%). This distribution shows the diverse geographic engagement and the importance of this research topic across different regions. Figure 13 shows the concentration of research efforts in Asia and South America, indicating strong regional focuses on these topics. The substantial contributions from North America and Europe also reveal the global relevance and collaboration in statistical methods and theory based on BS models.

4.3. Network Analysis

Following the geographic distribution analysis, we further explored the collaborative dynamics within the specified research areas. Understanding the collaborative network is crucial, as it reflects the interdisciplinary and international nature of research efforts in this area.

To identify the collaborations, we extracted all countries mentioned in the affiliations of the authors and analyzed the co-authorships between different countries. This process involved identifying all countries listed in the author affiliations and determining all possible pairs of collaborating countries. Then, we counted the frequency of each country pair to identify the most frequent collaborations.

Table 6. Top collaborations by frequency of co-authorship.

Country Pair	Number of Articles
Brazil–Chile	57
Iran–Mali	17
Brazil–Colombia	14
Brazil–Canada	12
Chile–Colombia	12
Canada–China	8
Canada–India	8
Canada–Saudi Arabia	8
Chile–Portugal	8
Canada–Chile	7
Iran–South Africa	7
Chile–Spain	6
Chile–Italy	5
Brazil–Peru	4
Brazil–Saudi Arabia	4
Canada–Iran	4
Canada–Mali	4
Mali–South Africa	4
Singapore–Taiwan	4
Australia–Brazil	3

summarizes the top collaborations, showing the frequency of co-authorship between country pairs. These findings highlight the active collaboration networks that exist between countries, facilitating the exchange of knowledge and driving forward the research agenda in statistical and reliability studies. These findings underscore the importance of international collaboration in advancing research in these fields. The presence of strong bilateral partnerships highlights how countries with relevant research outputs work together to push the boundaries of knowledge and innovation.

The network visualization shown in Figure 14 reveals a complex web of collaborations spanning multiple countries, showing the global interest and shared efforts towards advancing research in statistical and reliability studies based on the BS distribution.

The most prominent nodes, such as Chile, Brazil, Canada, China, and Saudi Arabia, emerge as the central hubs of collaboration (indicated by their large size and darker shade, representing the highest number of connections). These are followed by other important hubs like France, Portugal, and Spain. Note that the Iran–Mali collaboration has an unusually high frequency (see Table 6), which reflects the affiliation metadata retrieved from Web of Science.

Several articles originate from research groups with co-authors linked to institutions in both countries, which explains the elevated count. This network structure clearly indicates the key role of these countries in fostering international research partnerships. Crucially, these collaborations extend beyond the central high-output countries to include nations with fewer connections (smaller and clearer nodules), suggesting an inclusive research environment that encourages knowledge exchange and mutual growth. The diversity and extensive reach of the network highlight the universality of these research topics and their potential to bring together researchers from varied backgrounds and disciplines.

This analysis of the collaborative landscape enriches our understanding of how the scientific community is converging around these topics. It provides valuable insights into the synergies that drive research progress and innovation. Such collaborations demonstrate the vibrant research community’s commitment to exploring the potential of these topics to revolutionize the domain.

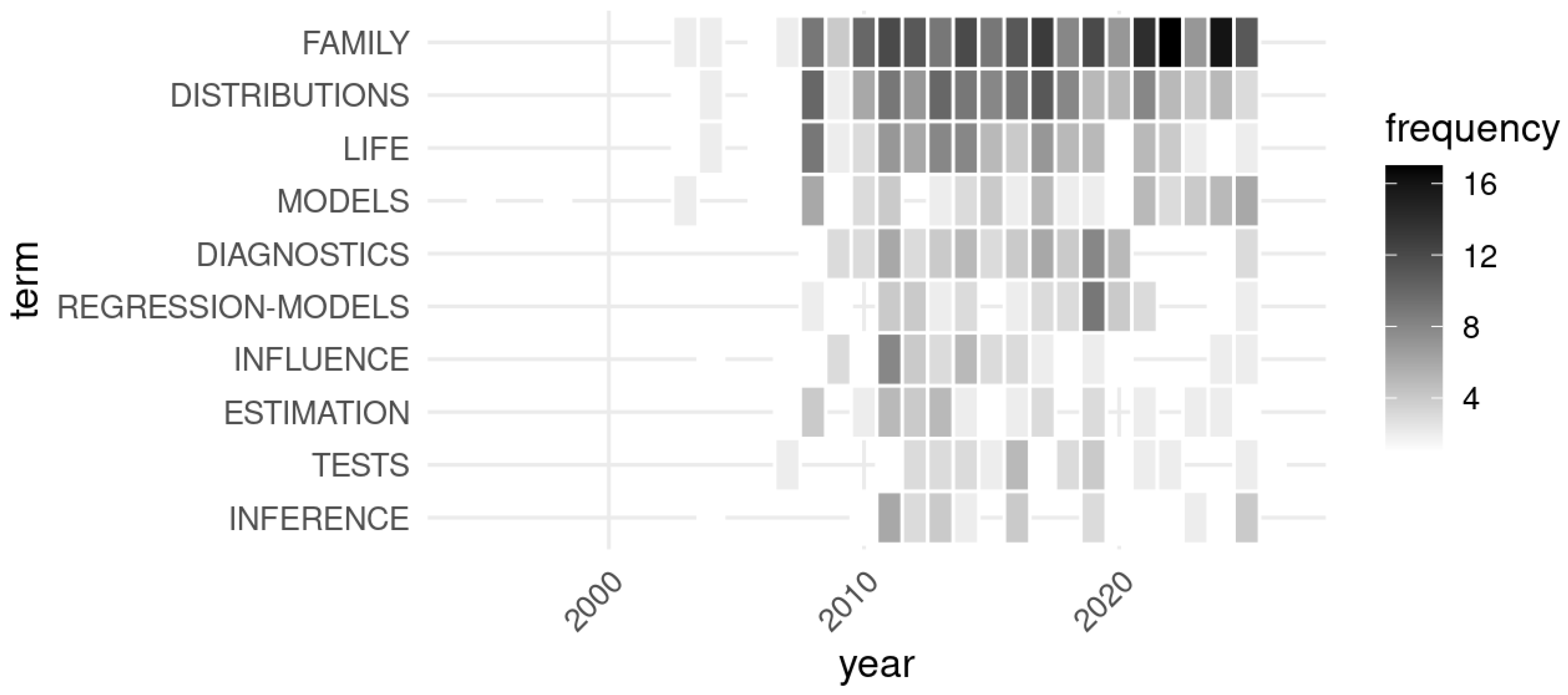
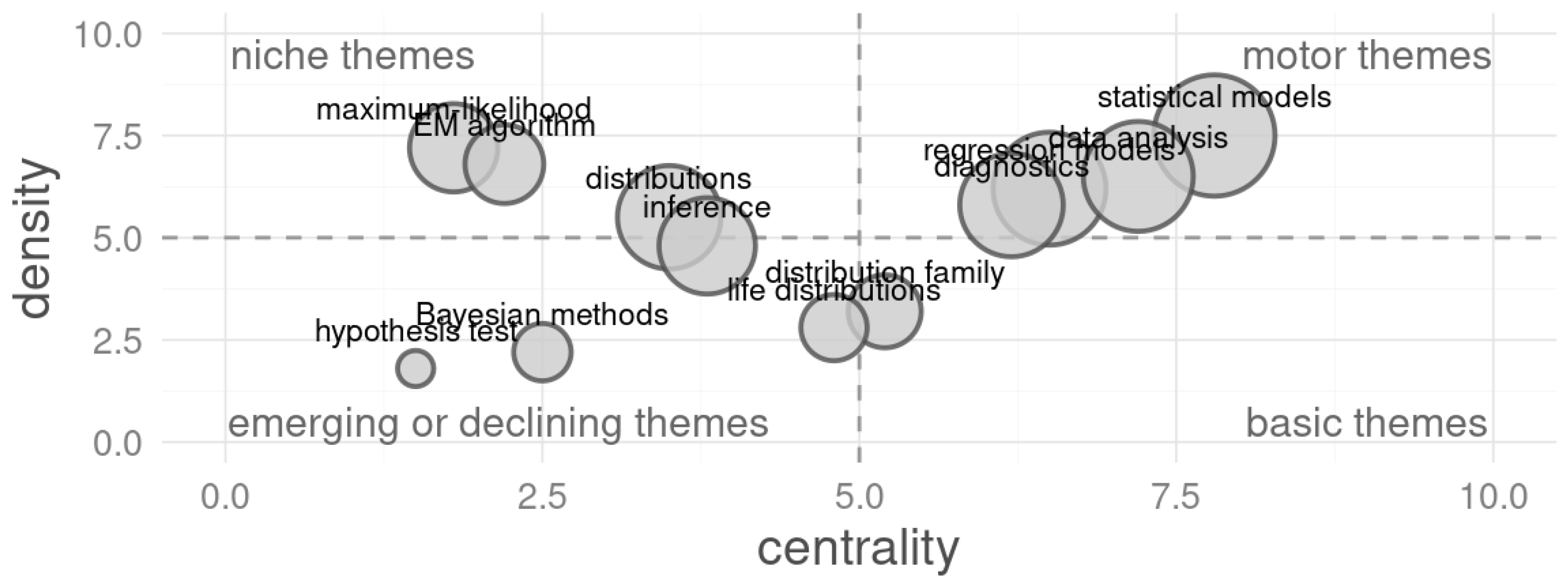
4.4. Thematic Analysis of Keywords

To deepen our understanding of the research area within the specified domains, we conducted a thematic analysis of keywords. This analysis identifies the most prevalent themes and concepts explored by researchers.

Table 7. Keywords and their frequency percentages.

Keyword	Percentage (%)
Birnbaum–Saunders distribution	7.36%
likelihood methods	3.10%
interval estimation	2.64%
lifetime data	2.18%
fatigue life distribution	2.12%
EM algorithm	1.24%
distribution	1.14%
Monte Carlo simulation	1.09%
R software	1.09%
sinh-normal (log-BS) distribution	0.62%
bootstrap	0.62%
estimation	0.62%
simulation	0.57%
kurtosis	0.52%

and Figure 15 present the keywords and their frequency percentages, while Figure 16 states the corresponding word cloud of the most frequent keywords. This information allows themes to be identified, offering insights into the focal points of current studies, showing their influence and coherence within the research network.

The heatmap of Figure 17 displays the annual frequency of appearance (or usage) of ten key statistical/data science terms (term) over the analyzed period (year). The color intensity (white-to-black scale) indicates frequency, where black represents a high frequency (up to 16) and white represents a low or zero frequency. The heatmap reveals interesting trends in the usage or appearance of these terms throughout the period, particularly highlighting a turning point around the year 2010.

During the post-2010 surge, significant frequency growth was detected with most terms showing a sustained increase in their frequency of use (indicated by the dark gray to black bars) starting around 2010. Before this year, activity was very low or non-existent. The dominant terms correspond to distribution family and models, which appear to be the most frequent in the 2010–2023 period, with many cells showing the darkest color (frequency $\ge 16$).

Terms like distributions and models show a consistently high presence from approximately 2010 onwards, with some specific terms and their evolution being statistically focused on terms as influence diagnostics, regression models, local influence, and estimation, showing a pattern of high or medium frequency in the 2010–2023 period. Notably, regression models and influence diagnostics present high peaks in certain years. Basic statistical terms, such as tests and inference, also increase after 2010 but generally at a medium or low frequency compared with the top terms (scale of 4 to 8). Note that tests and inference state more intermittent or less intense usage.

Some isolated terms, such as lifetime, had low to medium frequency in the 2010s but seem to have decreased or stabilized its usage in the 2020s. The term statistical models appears briefly in 2000, suggesting an early but sporadic presence before the major leap.

In summary, the overall pattern suggests that the field to which these terms belong experienced an explosion or increased visibility (an increase in activity or literature) starting in 2010, coinciding with the rise of data science and big data, which led to a much more frequent use of statistical and modeling terminology.

The thematic map presented in Figure 18 visually represents the relationships between various themes. By highlighting both the development (as represented by density) and relevance (evidenced by centrality) of each theme, the map facilitates a comprehensive understanding of the dynamics and potential areas for innovation in this field of study.

The thematic map is divided into four quadrants, each representing clusters of related research topics, with the position of a theme providing insight into its role, and is identified as follows:

• First quadrant (upper right-motor themes)—This quadrant is primarily characterized by themes such as statistical models, data analysis, regression models, and diagnostics. These themes are well-developed (high density) and highly influential (high centrality) within the field. Their pivotal role as core structural themes drives the research progress in this domain.
• Second quadrant (upper left-niche themes)—Featuring terms like maximum likelihood, EM algorithm and distributions inference, this quadrant highlights specialized areas with strong internal connections (high density) but low centrality to the broader network. These themes represent specific computational procedures and methodological backbones that are highly detailed but operate somewhat independently of the field’s most central topics.
• Third quadrant (lower left-emerging or declining themes)—This quadrant includes hypothesis test and Bayesian methods. Situated in the area of low centrality and low density, these themes may represent foundational methodologies that are either losing specific research focus in favor of more complex algorithms, or are niche applications that have not yet gained broad traction in the current bibliometric landscape.
• Fourth quadrant (lower right-basic themes)—This quadrant, which contains topics such as life distributions and distribution family closer to the center, is intended to house themes that are fundamental and essential for the field structure (high centrality) but are less developed (low density). They are the transversal groundwork upon which more specialized and motor themes are built.

Combining quantitative keyword analysis with qualitative visual representation provides a robust understanding of research trends and focal points within the field. These combined insights are essential for guiding future research directions, fostering collaboration, and addressing the evolving challenges and opportunities in statistical and reliability studies.

The findings in this section summarize the main patterns identified through the bibliometric and topic-modeling analyses. These results serve as the basis for the interpretation developed next in Section 5, where their implications for the evolution of BS research and emerging directions in the field are examined.

5. Unveiling Thematic Structures: Topic Modeling Implementation

This section concentrates on applying LDA to extract underlying themes from the entire corpus. This modeling approach serves to expose latent thematic structures and scholarly trends not readily apparent through simple descriptive metrics.

5.1. Model Setup and Text Corpus Processing

The analysis of latent themes utilized a refined dataset consisting of 353 articles, meticulously selected from an initial pool of 366 records. For each document, the title, abstract, and author keywords were aggregated into a singular text field, ensuring maximum thematic coverage for the model training. The procedure was implemented using the topicmodels package of R [94], adhering to established computational linguistics practices. The textual preparation involved four sequential steps before feeding data to the LDA algorithm, stated as follows:

• Uniformity enforcement—Converting all characters to lowercase to ensure textual consistency across the document set.
• Noise elimination—Removing punctuation, numerical data, and standard English stopwords to isolate content-bearing terms.
• Matrix generation—Forming the document-term matrix based on term frequencies, which is the requisite input for LDA.
• Topic count optimization—Evaluating model stability across $K=2$ to $K=15$ topics using $C_v$ coherence scores and perplexity metrics [95,96]. This evaluation confirmed that $K=6$ yielded the most optimal balance between interpretability and thematic granularity.

The final LDA model was configured with $K=6$. The inference process was conducted via Gibbs sampling, executing a total of $\mathrm{10,000}$ iterations, with the initial 200 samples discarded as a burn-in period to ensure reliable convergence [97].

5.2. Synthesis of Latent Topics and Network Modules

A comprehensive thematic landscape was constructed by integrating the six themes identified by LDA with the existing keyword clustering results. This synergy offers a deeper understanding of the disciplinary intersections within the corpus. The resulting topics are delineated as follows, with their primary linkages to the keyword modules (also viewable in Table 8 in detail):

• Topic I (engineering failure)—This theme primarily reflects the concepts within Cluster 1, emphasizing long-term material resilience and damage assessment. Key terms like fatigue and life prediction highlight the primary focus on structural integrity preservation.
• Topic II (lifetime data modeling)—This theme crosses Modules 2 and 4, concentrating on mathematical frameworks for reliability engineering. The integration of statistical distributions and regression analysis underscores the use of analytical tools for modeling observed data across various conditions.
• Topic III (BS distribution inference)—Strongly tied to Module 2, this topic is dedicated to robust parameter estimation. Emphasis on maximum, likelihood, and estimation reflects the sophisticated statistical procedures used for reliability assessment concerning the BS distribution.
• Topic IV (computational methods)—Aligned with Modules 2 and 4, this topic bridges computation and forecasting. It focuses heavily on simulation techniques like Monte Carlo alongside general model estimation, crucial for anticipating component behavior.
• Topic V (advanced models)—Exhibits a robust connection with Modules 2 and 4, highlighting generalized statistical paradigms. The necessity for precise estimation methods and reliable confidence interval determination is a central technical focus here.
• Topic VI (forecasting)—Directly linked to Module 1, this reinforces the engineering basis of the study. Recurring vocabulary like cumulative damage and life prediction indicates a foundational research stream focused on anticipating material failure modes.

Table 8. Dominant terms in each topic identified by LDA.

Topic	Label	Terms
I	Engineering failure	cumulative damage; fatigue; life prediction
II	Lifetime data modeling	lifetime; regression analysis; statistical distributions
III	BS distribution inference	censoring; estimation method;
		maximum likelihood; robustness
IV	Computational methods	model estimation; monte carlo; simulation
V	Advanced models	confidence interval; estimation methods; influence diagnostics;
		multivariate models; regression models;
VI	Forecasting	accelerated life models; cumulative damage; diagnostics
		life prediction; regression

Table 8. Dominant terms in each topic identified by LDA.

Topic	Label	Terms
I	Engineering failure	cumulative damage; fatigue; life prediction
II	Lifetime data modeling	lifetime; regression analysis; statistical distributions
III	BS distribution inference	censoring; estimation method;
		maximum likelihood; robustness
IV	Computational methods	model estimation; monte carlo; simulation
V	Advanced models	confidence interval; estimation methods; influence diagnostics;
		multivariate models; regression models;
VI	Forecasting	accelerated life models; cumulative damage; diagnostics
		life prediction; regression

The combined thematic analysis establishes important currents and reveals a structural asymmetry: Modules 3 and 5 from the keyword clustering do not map directly onto any of the six major LDA topics. This observed discrepancy stems from the fundamental difference in analytical granularity between the two methodologies. Module 3 (estimation methods) contains highly specific technical phrases like Akaike information criterion and bootstrap Bartlett correction, which define dense local areas of research. Similarly, Module 5 (statistical diagnostics) involves niche terminology such as local influence and asymptotic normality. These specialized sub-fields, while critical and internally coherent within the network clustering, are insufficiently pervasive across the entire document set to emerge as distinct, broad themes in the LDA model. This reinforces the complementary nature of network clustering (which reveals specific expertise pockets) and topic modeling (which provides a high-level thematic overview of the research landscape).

6. Final Synthesis and Outlook for the Birnbaum–Saunders Field

This section synthesizes the evidence gathered throughout the investigation, addressing the research questions (RQ1–RQ4) and outlining paths for subsequent scholarship.

6.1. Key Findings Organized by Research Questions

• RQ1 [Advances in BS theory and methods] The core focus of theoretical development centers on generating robust statistical extensions for the BS family. Major methodological leaps encompass the refinement of Bayesian methods, the implementation of shrinkage estimators, and the creation of regression frameworks suitable for grouped or hybrid censored data. Furthermore, specialized contexts involving ordered set sampling, frailty concepts, and spatial/autoregressive structures have seen model adaptation. The necessity for strong inferential capacity is met through sophisticated influence diagnostics and bivariate modeling strategies.
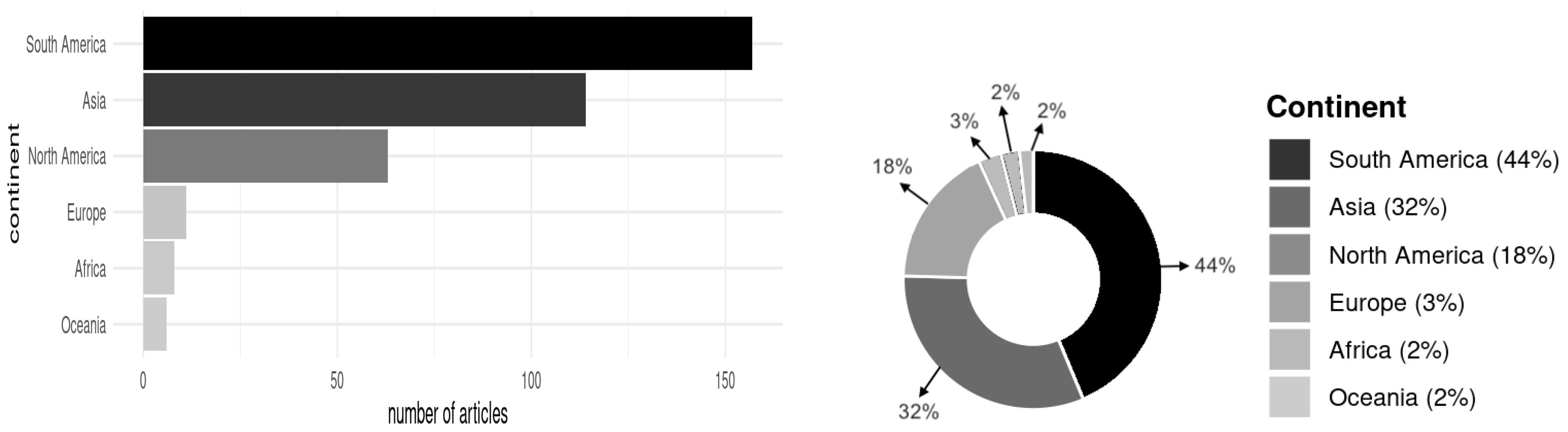
• RQ2 [Practical impact and domain applications] The primary utility of the BS distribution remains in lifetime data evaluation and the forecasting of material failure (such as in fatigue contexts). However, its adoption has diversified significantly, now proving valuable across fields such as biological mortality studies, environmental forecasting, medical statistics, neural signal processing, and complex financial/risk models (including, for instance, insurance risk and power generation estimation).
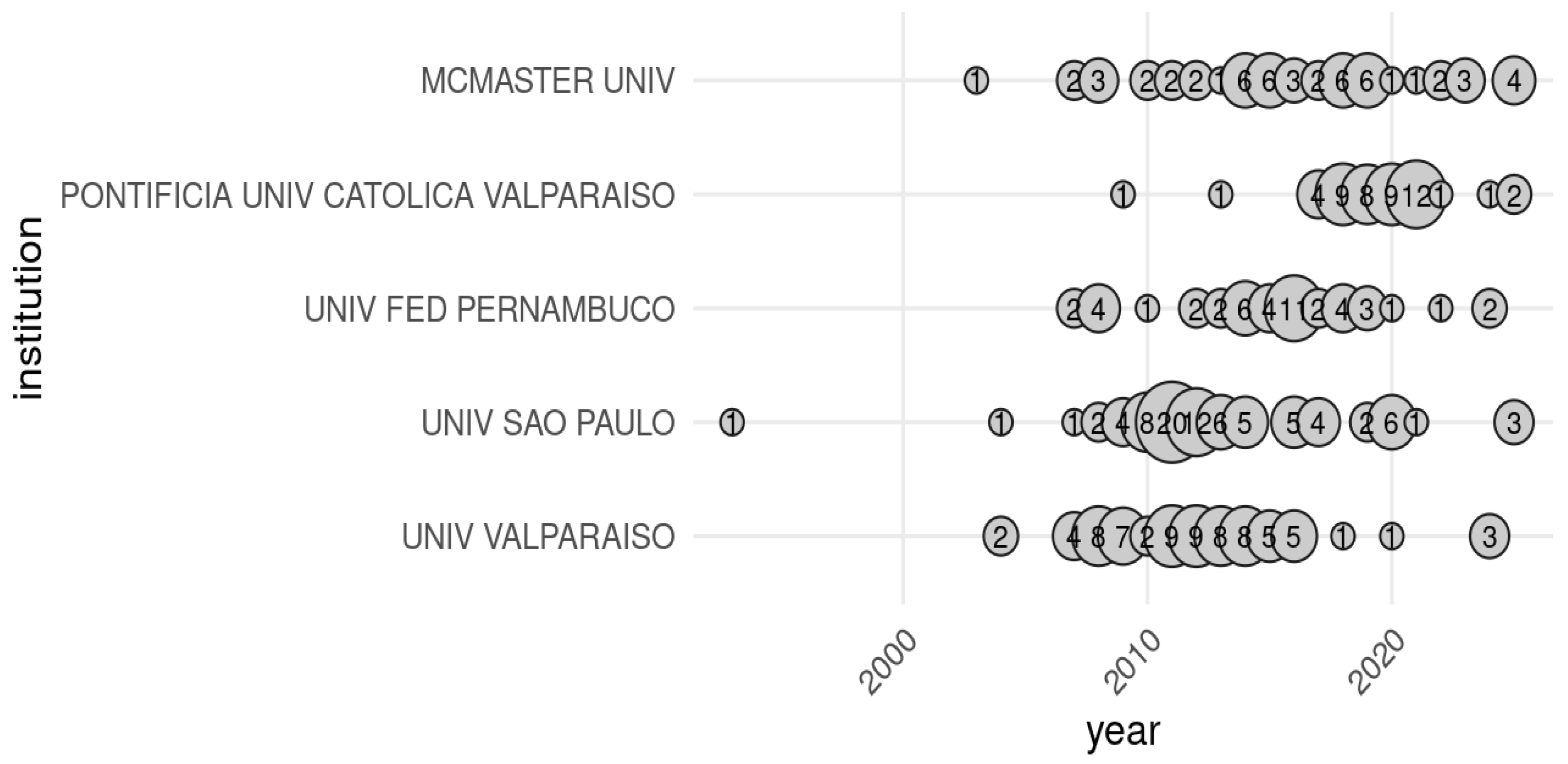
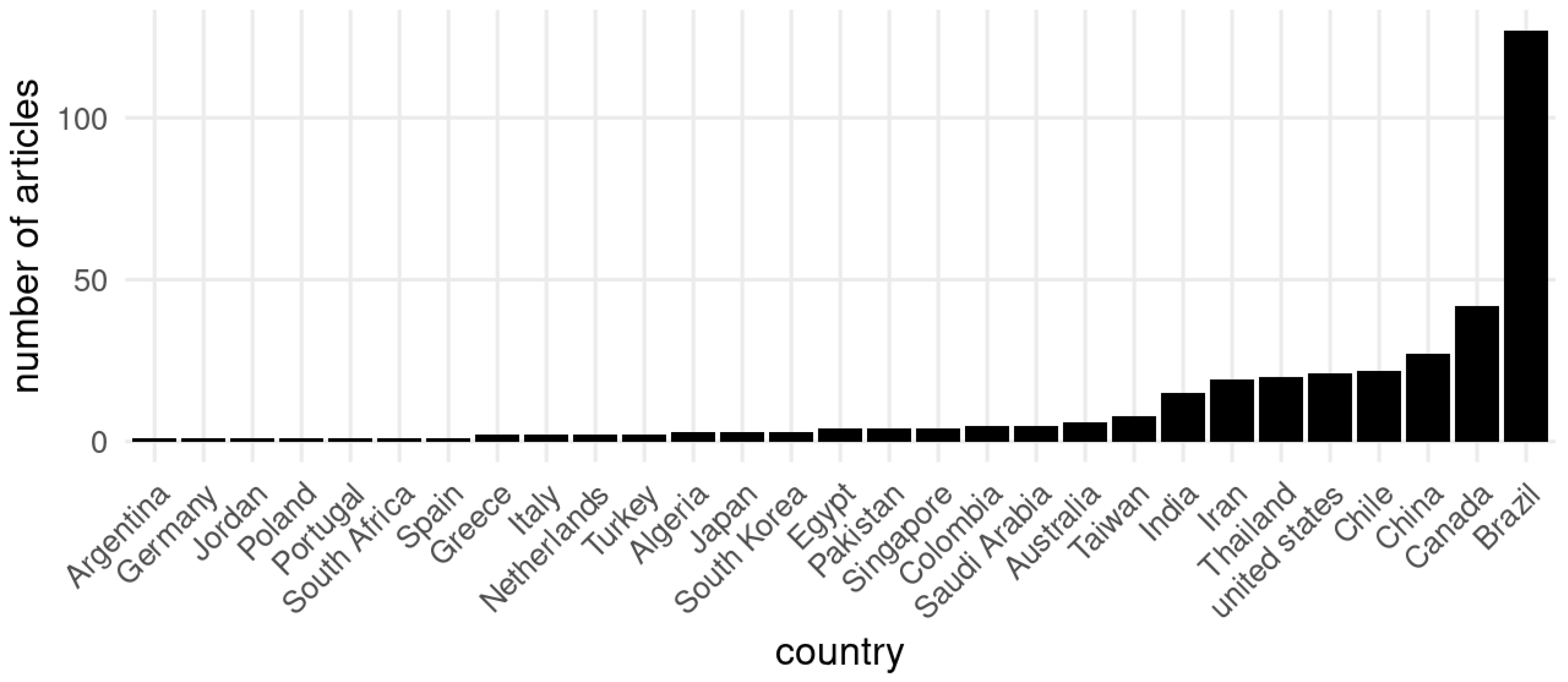
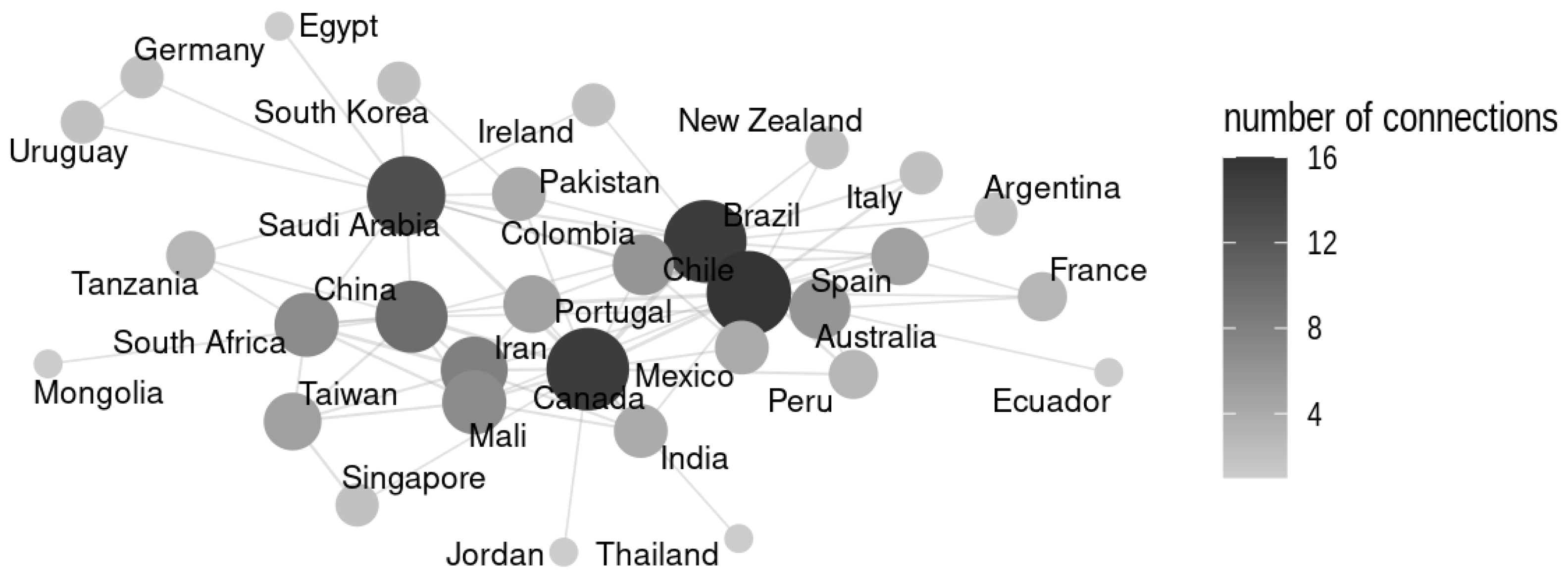
• RQ3 [Structural characteristics and gaps in the literature] The field is characterized by a substantial output of original research articles (over 350 works examined), with the highest frequency of publications recorded near 2019. The collaboration landscape reveals significant international partnerships, most notably the strong axis between Brazil and Chile. Concerning dissemination, the journal Computational Statistics and Data Analysis stands out as an exceptionally influential publication venue. A critical deficiency noted is the scarcity of structured review papers and the need for user-friendly, auditable software tools.
• RQ4 [Trajectories for future research] The analytical results strongly suggest that future efforts should prioritize advanced BS model development, software creation, and comprehensive diagnostic toolkits. It is crucial to translate theoretical findings into established practical decision-making criteria for applied teams. Methodologically, exploring frontiers such as dynamic or neural topic modeling is highly recommended to extract subtler insights from the evolving thematic structure of the literature.

6.2. Summary of Analysis and Research Contributions

This comprehensive study has furnished a detailed mapping of the scholarly terrain encompassing statistical reliability and the BS distribution. Our dual approach, leveraging both bibliometric and thematic data analytics, successfully isolated dominant trends, the most productive contributors, and the focal points of influence, thereby generating substantial value for researchers and practitioners.

The foundational dataset comprised 353 carefully filtered articles (originating from 366 records), all sourced via the Web of Science platform, establishing a reliable basis for observing the field’s trajectory. Bibliometric findings clearly indicated rapid scholarly growth, with sustained interest in statistical methods for reliability peaking around 2019. This affirms the continuing and expanding interest in robust lifetime data analysis.

We have identified the foremost channels for knowledge exchange, which include a wide array of specialized journals such as Computational Statistics and Data Analysis, Journal of Statistical Computation and Simulation, Applied Stochastic Models in Business and Industry, Communications in Statistics - Simulation and Computation, Communications in Statistics-Theory and Methods, Journal of Applied Statistics, and IEEE Transactions on Reliability. These journals collectively drive discourse and promote high-caliber research.

Globally, the research activity is geographically diverse, benefiting from important input from Asia and the South American countries of Brazil, Chile, and China. The wide global participation confirms the universal relevance of these reliability topics. Further scrutiny of co-authorship networks highlighted the vitality of strong bilateral research ties that accelerate the transfer of innovative ideas.

The subsequent thematic investigation, rooted in keyword analysis and cluster detection via the Louvain method, pinpointed ten distinct research modules. These ranged from fundamental areas like material durability and cumulative damage to complex, advanced statistical models. These clusters collectively define the essential investigative domains underpinning the field. To enrich this structural view, the LDA model was employed to discern underlying thematic topics. The chosen optimal model (yielding six topics, confirmed by coherence and perplexity metrics) provided a balanced thematic synthesis. Notably, these six topics largely overlapped with the initial keyword clusters, validating the structural coherence. However, Clusters 3 and 5 (dedicated to specialized estimation methods and statistical diagnostics, respectively) did not align with the broader LDA topics. This distinction highlights that while keyword clusters capture dense, specialized academic niches, LDA is better suited for revealing the pervasive, macro-level themes that span the entire document collection. This integrated methodological framework demonstrates the synergistic power of combining clustering (for granular specialization) and topic modeling (for macroscopic thematic currents), resulting in a profound understanding of the research landscape essential for future strategic planning and interdisciplinary collaboration.

6.3. Caveats and Future Trajectories

While the study offers strong insights, certain inherent limitations must be acknowledged. The output is sensitive to the chosen LDA parameters and the performance metrics utilized. Additionally, focusing exclusively on the 353 most relevant articles, while maximizing analysis quality, inherently limits the scope by omitting potential secondary insights from a larger dataset. Future work should prioritize the following aspects:

• Corpus expansion—Broadening the literature base to include diverse databases for a more exhaustive perspective.
• Temporal dynamics—Executing a longitudinal analysis to track the evolution of thematic interest and methodological shifts over time.
• Interdisciplinary synergy—Encouraging research that bridges statistical methods with specialized engineering or domain-specific fields to unlock novel solutions.
• Methodological sophistication—Deploying next-generation analytical techniques, such as dynamic or neural topic modeling, to gain even richer structural insights.

In conclusion, this investigation provided an evidence-based roadmap of the research landscape related to the BS distribution, stating actionable findings derived from rigorous data analytics. By clearly identifying structural gaps, key influences, and emerging directions, this study was designed to stimulate strategic research efforts and support global collaborations in the field.