Proximal Causal Inference for Censored Data with an Application to Right Heart Catheterization Data
Abstract
1. Introduction
2. Methodology
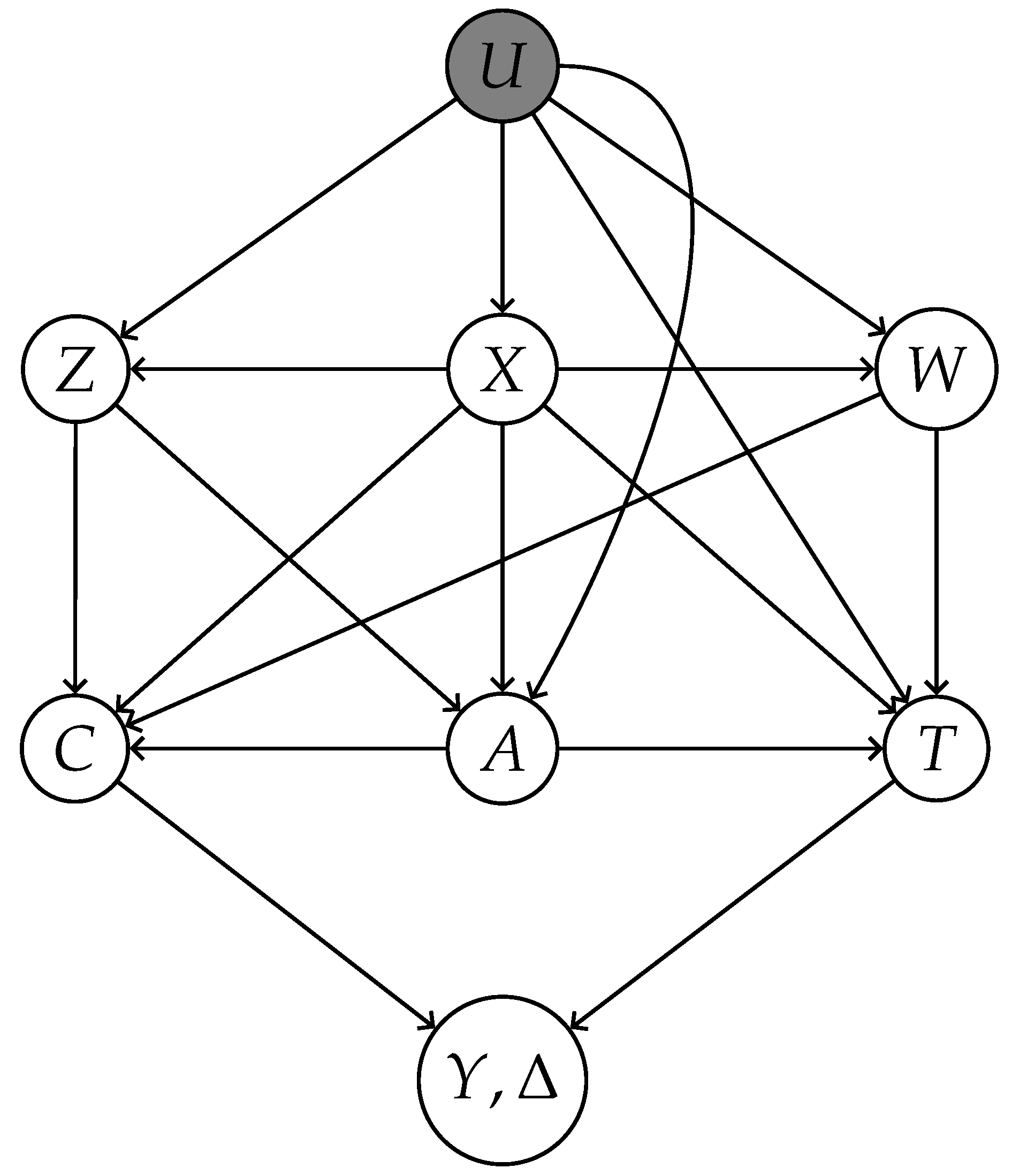
2.1. Preliminaries
- X: Measured common causes of both treatment A and outcome T.
- Z: Treatment-inducing confounding proxies—causes of A confounded with T exclusively through unmeasured confounder U.
- W: Outcome-inducing confounding proxies—causes of T confounded with A exclusively through U.
- 1.
- and are conditionally independent given , that is, .
- 2.
- T and Z are conditionally independent given , that is, .
- 1.
- almost surely.
- 2.
- almost surely.
- 3.
- almost surely.
- 4.
- almost surely.
2.2. Estimation Using Outcome Bridge
2.3. Estimation Using Treatment Bridge
2.4. Estimation Using Both Bridges
3. Theoretical Results
- (i)
- If and , then is a consistent estimator of ψ;
- (ii)
- If and , then is a consistent estimator of ψ;
- (iii)
- If and either or holds, then is a consistent estimator of ψ.
4. Simulations
- Correct specification: Using the original variables X and W for h, and X and Z for q.
- Outcome bridge misspecification: Replacing W with a transformed variable in h.
- Treatment bridge misspecification: Replacing Z with in q.
- Double misspecification: Simultaneously substituting and in h and q.
5. RHC Data Revisited
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
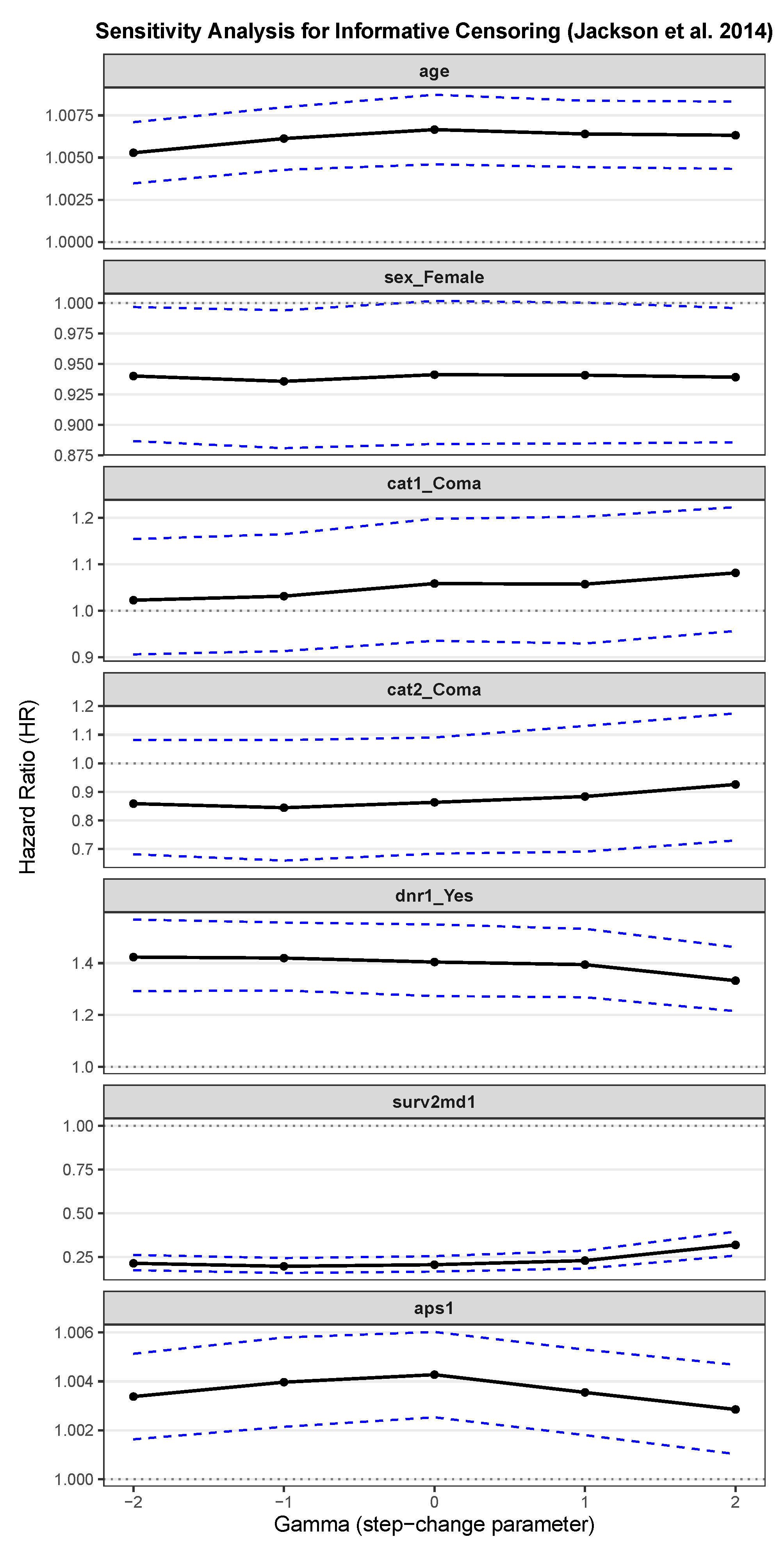
Appendix E. Sensitivity Analysis for Informative Censoring
References
- Cornfield, J.; Haenszel, W.; Hammond, E.C.; Lilienfeld, A.M.; Shimkin, M.B.; Wynder, E.L. Smoking and lung cancer: Recent evidence and a discussion of some questions. J. Natl. Cancer Inst. 1959, 22, 173–203. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Goldberger, A.S. Structural equation methods in the social sciences. Econometrica 1972, 40, 979–1001. [Google Scholar] [CrossRef]
- Baker, S.G.; Lindeman, K.S. The paired availability design: A proposal for evaluating epidural analgesia during labor. Stat. Med. 1994, 13, 2269–2278. [Google Scholar] [CrossRef] [PubMed]
- Robins, J.M.; Rotnitzky, A.; Zhao, L.P. Estimation of regression coefficients when some regressors are not always observed. J. Am. Stat. Assoc. 1994, 89, 846–866. [Google Scholar] [CrossRef]
- Angrist, J.D.; Imbens, G.W.; Rubin, D.B. Identification of causal effects using instrumental variables. J. Am. Stat. Assoc. 1996, 91, 444–455. [Google Scholar] [CrossRef]
- Fan, Q.; Zhong, W. Variable selection for structural equation with endogeneity. J. Syst. Sci. Complex. 2018, 31, 787–803. [Google Scholar] [CrossRef]
- Miao, W.; Geng, Z.; Tchetgen Tchetgen, E.J. Identifying causal effects with proxy variables of an unmeasured confounder. Biometrika 2018, 105, 987–993. [Google Scholar] [CrossRef]
- Tchetgen Tchetgen, E.J.; Ying, A.; Cui, Y.; Shi, X.; Miao, W. An introduction to proximal causal learning. arXiv 2020, arXiv:2009.10982. [Google Scholar]
- Cui, Y.; Pu, H.; Shi, X.; Miao, W.; Tchetgen Tchetgen, E. Semiparametric proximal causal inference. J. Am. Stat. Assoc. 2024, 119, 1348–1359. [Google Scholar] [CrossRef]
- Qi, Z.; Miao, R.; Zhang, X. Proximal learning for individualized treatment regimes under unmeasured confounding. J. Am. Stat. Assoc. 2024, 119, 915–928. [Google Scholar] [CrossRef]
- Shi, X.; Li, K.; Miao, W.; Hu, M.; Tchetgen, E.T. Theory for identification and inference with synthetic controls: A proximal causal inference framework. arXiv 2021, arXiv:2108.13935. [Google Scholar]
- Kallus, N.; Mao, X.; Uehara, M. Causal inference under unmeasured confounding with negative controls: A minimax learning approach. arXiv 2021, arXiv:2103.14029. [Google Scholar]
- Ghassami, A.; Ying, A.; Shpitser, I.; Tchetgen, E.T. Minimax kernel machine learning for a class of doubly robust functionals with application to proximal causal inference. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 28–30 March 2022; pp. 7210–7239. [Google Scholar]
- Sverdrup, E.; Cui, Y. Proximal causal learning of conditional average treatment effects. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 33285–33298. [Google Scholar]
- Ying, A.; Miao, W.; Shi, X.; Tchetgen Tchetgen, E.J. Proximal causal inference for complex longitudinal studies. J. R. Stat. Soc. Ser. Stat. Methodol. 2023, 85, 684–704. [Google Scholar] [CrossRef]
- Dukes, O.; Shpitser, I.; Tchetgen Tchetgen, E.J. Proximal mediation analysis. Biometrika 2023, 110, 973–987. [Google Scholar] [CrossRef]
- Shen, T.; Cui, Y. Optimal treatment regimes for proximal causal learning. Adv. Neural Inf. Process. Syst. 2023, 36, 47735–47748. [Google Scholar]
- Zhang, J.; Li, W.; Miao, W.; Tchetgen, E.T. Proximal causal inference without uniqueness assumptions. Stat. Probab. Lett. 2023, 198, 109836. [Google Scholar] [CrossRef]
- Miao, W.; Shi, X.; Li, Y.; Tchetgen Tchetgen, E.J. A confounding bridge approach for double negative control inference on causal effects. Stat. Theory Relat. Fields 2024, 8, 262–273. [Google Scholar] [CrossRef]
- Liu, J.; Park, C.; Li, K.; Tchetgen Tchetgen, E.J. Regression-based proximal causal inference. Am. J. Epidemiol. 2025, 194, 2030–2036. [Google Scholar] [CrossRef]
- Bennett, A.; Kallus, N. Proximal reinforcement learning: Efficient off-policy evaluation in partially observed markov decision processes. Oper. Res. 2024, 72, 1071–1086. [Google Scholar] [CrossRef]
- Bai, Y.; Cui, Y.; Sun, B. Proximal Inference on Population Intervention Indirect Effect. arXiv 2025, arXiv:2504.11848. [Google Scholar]
- Li, Y.; Han, E.; Hu, Y.; Zhou, W.; Qi, Z.; Cui, Y.; Zhu, R. Reinforcement Learning with Continuous Actions Under Unmeasured Confounding. arXiv 2025, arXiv:2505.00304. [Google Scholar]
- Ying, A.; Cui, Y.; Tchetgen Tchetgen, E.J. Proximal causal inference for marginal counterfactual survival curves. arXiv 2022, arXiv:2204.13144. [Google Scholar]
- Li, K.; Linderman, G.C.; Shi, X.; Tchetgen Tchetgen, E.J. Regression-based proximal causal inference for right-censored time-to-event data. arXiv 2024, arXiv:2409.08924. [Google Scholar] [CrossRef]
- Akosile, M.; Zhu, H.; Zhang, S.; Johnson, N.; Lai, D.; Zhu, H. Reassessing the Effectiveness of Right Heart Catheterization (RHC) in the Initial Care of Critically Ill Patients using Targeted Maximum Likelihood Estimation. Int. J. Clin. Biostat. Biom. 2018, 4, 018. [Google Scholar] [CrossRef] [PubMed]
- Connors, A.F.; Speroff, T.; Dawson, N.V.; Thomas, C.; Harrell, F.E.; Wagner, D.; Desbiens, N.; Goldman, L.; Wu, A.W.; Califf, R.M.; et al. The effectiveness of right heart catheterization in the initial care of critically III patients. JAMA 1996, 276, 889–897. [Google Scholar] [CrossRef]
- Hirano, K.; Imbens, G.W. Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Serv. Outcomes Res. Methodol. 2001, 2, 259–278. [Google Scholar] [CrossRef]
- Diggle, P.; Kenward, M.G. Informative drop-out in longitudinal data analysis. J. R. Stat. Soc. Ser. Appl. Stat. 1994, 43, 49–73. [Google Scholar] [CrossRef]
- Scharfstein, D.O.; Robins, J.M. Estimation of the failure time distribution in the presence of informative censoring. Biometrika 2002, 89, 617–634. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random Survival Forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Kuroki, M.; Pearl, J. Measurement bias and effect restoration in causal inference. Biometrika 2014, 101, 423–437. [Google Scholar] [CrossRef]
- Kompa, B.; Bellamy, D.; Kolokotrones, T.; Beam, A. Deep learning methods for proximal inference via maximum moment restriction. Adv. Neural Inf. Process. Syst. 2022, 35, 11189–11201. [Google Scholar]
- Dikkala, N.; Lewis, G.; Mackey, L.; Syrgkanis, V. Minimax estimation of conditional moment models. Adv. Neural Inf. Process. Syst. 2020, 33, 12248–12262. [Google Scholar]
- Mastouri, A.; Zhu, Y.; Gultchin, L.; Korba, A.; Silva, R.; Kusner, M.; Gretton, A.; Muandet, K. Proximal causal learning with kernels: Two-stage estimation and moment restriction. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 7512–7523. [Google Scholar]
- Künzel, S.R.; Sekhon, J.S.; Bickel, P.J.; Yu, B. Metalearners for estimating heterogeneous treatment effects using machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 4156–4165. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B. Random survival forests for R. R News 2007, 7, 25–31. [Google Scholar]
- Jackson, D.; White, I.R.; Seaman, S.; Evans, H.; Baisley, K.; Carpenter, J. Relaxing the independent censoring assumption in the Cox proportional hazards model using multiple imputation. Stat. Med. 2014, 33, 4681–4694. [Google Scholar] [CrossRef]
- Bang, H.; Robins, J.M. Doubly robust estimation in missing data and causal inference models. Biometrics 2005, 61, 962–973. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC Press: Philadelphia, PA, USA, 1994. [Google Scholar]
- Huang, A.A.; Huang, S.Y. Increasing transparency in machine learning through bootstrap simulation and shapely additive explanations. PLoS ONE 2023, 18, e0281922. [Google Scholar] [CrossRef]
- Brooks, B.R.; Berry, J.D.; Ciepielewska, M.; Liu, Y.; Zambrano, G.S.; Zhang, J.; Hagan, M. Intravenous edaravone treatment in ALS and survival: An exploratory, retrospective, administrative claims analysis. eClinicalMedicine 2022, 52, 101590. [Google Scholar] [CrossRef]
| Scenario 1 | bias | 89.50 | 54.21 | 1.17 | 4.65 | 2.19 |
| MSE | 82.05 | 33.66 | 4.86 | 19.16 | 5.77 | |
| Scenario 2 | bias | 107.72 | 36.20 | 61.29 | 4.65 | 3.54 |
| MSE | 127.03 | 19.62 | 70.74 | 19.16 | 20.09 | |
| Scenario 3 | bias | 99.71 | 45.37 | 1.17 | 18.10 | 0.23 |
| MSE | 101.68 | 24.10 | 4.86 | 16.08 | 4.32 | |
| Scenario 4 | bias | 134.56 | 25.67 | 37.12 | 44.62 | 46.31 |
| MSE | 193.55 | 12.41 | 20.88 | 36.12 | 28.55 |
| Scenario 1 | bias | 88.24 | 54.87 | 1.14 | 4.24 | 1.77 |
| MSE | 79.76 | 34.41 | 4.41 | 17.17 | 4.75 | |
| Scenario 2 | bias | 107.09 | 37.14 | 59.07 | 4.24 | 3.47 |
| MSE | 124.34 | 20.21 | 64.18 | 17.17 | 16.71 | |
| Scenario 3 | bias | 98.26 | 45.33 | 1.14 | 15.72 | 0.26 |
| MSE | 98.72 | 23.96 | 4.41 | 14.29 | 4.01 | |
| Scenario 4 | bias | 133.50 | 25.64 | 37.17 | 44.83 | 46.26 |
| MSE | 189.09 | 12.30 | 20.55 | 34.51 | 27.97 |
| Scenario 1 | bias | 42.27 | 33.06 | 0.45 | 2.85 | 0.78 |
| MSE | 18.41 | 13.88 | 1.15 | 9.88 | 1.23 | |
| Scenario 2 | bias | 59.18 | 28.27 | 41.69 | 2.85 | 3.50 |
| MSE | 42.04 | 11.12 | 36.77 | 9.88 | 11.33 | |
| Scenario 3 | bias | 47.21 | 21.53 | 0.45 | 10.73 | 0.03 |
| MSE | 22.89 | 7.35 | 1.15 | 8.72 | 1.04 | |
| Scenario 4 | bias | 78.46 | 17.26 | 27.72 | 33.43 | 34.37 |
| MSE | 69.17 | 5.99 | 12.47 | 21.44 | 16.50 |
| Variable | Min | Max | Median | Mean |
|---|---|---|---|---|
| Outcome / Treatment | ||||
| A | 0.000 | 1.000 | 0.000 | 0.381 |
| Y | 0.000 | 1943.000 | 166.000 | 186.400 |
| 0.000 | 1.000 | 1.000 | 0.649 | |
| Treatment proxies (Z) | ||||
| pafi1 | 11.600 | 937.500 | 202.500 | 222.300 |
| paco21 | 1.000 | 156.000 | 37.000 | 38.750 |
| Outcome proxies (W) | ||||
| ph1 | 6.579 | 7.770 | 7.400 | 7.388 |
| hema1 | 2.000 | 66.190 | 30.000 | 31.870 |
| Control Covariates (X) | ||||
| age | 18.040 | 101.850 | 64.050 | 61.380 |
| sex_Female | 0.000 | 1.000 | 0.000 | 0.443 |
| cat1_Coma | 0.000 | 1.000 | 0.000 | 0.076 |
| cat2_Coma | 0.000 | 1.000 | 0.000 | 0.016 |
| dnr1_Yes | 0.000 | 1.000 | 0.000 | 0.114 |
| surv2md1 | 0.000 | 0.962 | 0.628 | 0.593 |
| aps1 | 3.000 | 147.000 | 54.000 | 54.670 |
| Method | 95% CI | |
|---|---|---|
| UDR | −10.169 | (−22.892, 2.897) |
| UPCI | −7.770 | (−21.037, 6.388) |
| DR | −20.999 | (−52.652, 10.698) |
| PIPW | 1.389 | (−58.438, 48.830) |
| POR | −23.447 | (−54.099, 6.483) |
| PR | −14.781 | (−41.204, 11.162) |
| Method | 95% CI | |
|---|---|---|
| Scenario 1: Z =pafi1, W =hema1 | ||
| UDR | −10.482 | (−21.813, 2.783) |
| UPCI | −8.124 | (−23.159, 9.206) |
| DR | −21.442 | (−52.444, 14.228) |
| PIPW | −7.022 | (−63.541, 55.390) |
| POR | −24.124 | (−54.040, 11.595) |
| PR | −18.816 | (−46.669, 8.624) |
| Scenario 2: Z =paco21, W =hema1 | ||
| UDR | −10.401 | (−21.990, 2.051) |
| UPCI | −1.845 | (−22.985, 21.379) |
| DR | −25.039 | (−54.214, 6.172) |
| PIPW | −6.482 | (−95.827, 63.307) |
| POR | −22.117 | (−52.369, 4.567) |
| PR | −15.049 | (−48.228, 9.625) |
| Scenario 3: Z =paco21, W =ph1 | ||
| UDR | −11.337 | (−23.347, 1.107) |
| UPCI | −21.170 | (−51.597, 15.252) |
| DR | −27.807 | (−57.290, 2.800) |
| PIPW | 20.098 | (−54.771, 105.359) |
| POR | −39.741 | (−65.748, −10.356) |
| PR | −26.708 | (−65.234, 13.710) |
| Scenario 4: Z =pafi1, W =ph1 | ||
| UDR | −10.362 | (−21.593, 1.958) |
| UPCI | −15.077 | (−29.430, −4.247) |
| DR | −19.277 | (−48.289, 13.538) |
| PIPW | −6.715 | (−162.882, 49.252) |
| POR | −28.134 | (−54.053, 3.064) |
| PR | −19.556 | (−47.399, 4.201) |
| Scenario 5: Cox hazard estimation | ||
| UDR | −10.169 | (−22.892, 2.897) |
| UPCI | −7.770 | (−21.037, 6.388) |
| DR | −23.925 | (−75.414, 23.950) |
| PIPW | 2.995 | (−87.198, 83.571) |
| POR | −23.157 | (−61.011, 22.261) |
| PR | −15.871 | (−55.629, 25.948) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Gao, Y.; Qi, M. Proximal Causal Inference for Censored Data with an Application to Right Heart Catheterization Data. Stats 2025, 8, 66. https://doi.org/10.3390/stats8030066
Hu Y, Gao Y, Qi M. Proximal Causal Inference for Censored Data with an Application to Right Heart Catheterization Data. Stats. 2025; 8(3):66. https://doi.org/10.3390/stats8030066
Chicago/Turabian StyleHu, Yue, Yuanshan Gao, and Minhao Qi. 2025. "Proximal Causal Inference for Censored Data with an Application to Right Heart Catheterization Data" Stats 8, no. 3: 66. https://doi.org/10.3390/stats8030066
APA StyleHu, Y., Gao, Y., & Qi, M. (2025). Proximal Causal Inference for Censored Data with an Application to Right Heart Catheterization Data. Stats, 8(3), 66. https://doi.org/10.3390/stats8030066





