Quantile Estimation Based on the Log-Skew-t Linear Regression Model: Statistical Aspects, Simulations, and Applications
Abstract
1. Introduction
2. Quantiles of the LST Distribution
3. Quantile Estimation Using the LSTLRM
- 1.
- Generate a random sample, , of .
- 2.
- Calculate , .
- 3.
- Perform steps 1 and 2 m times to yield , , .
- 4.
- Calculate and , for .
- 5.
- The lower and upper bounds of are and , respectively.
4. Simulation Studies
5. Data Analyses
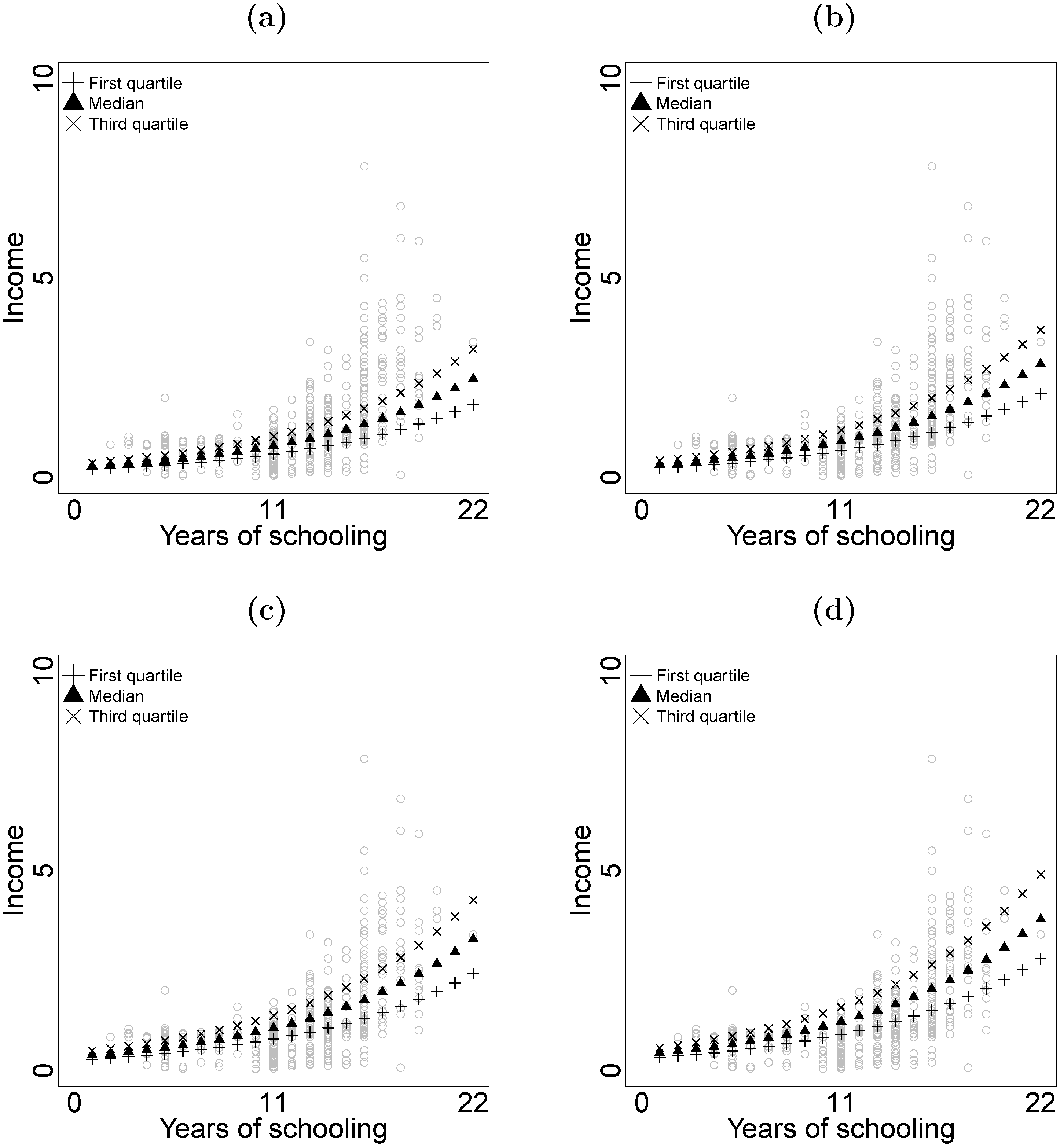
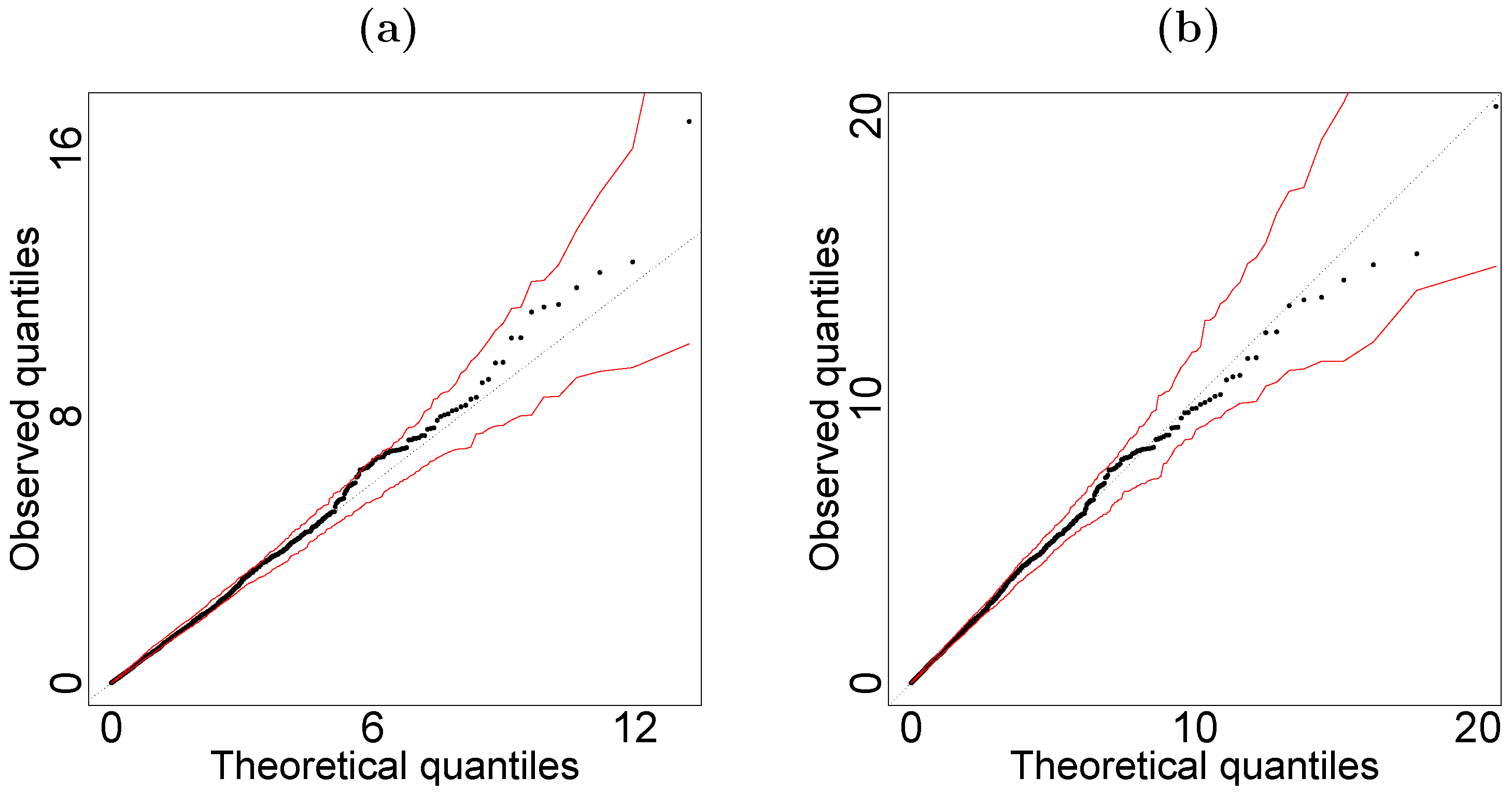
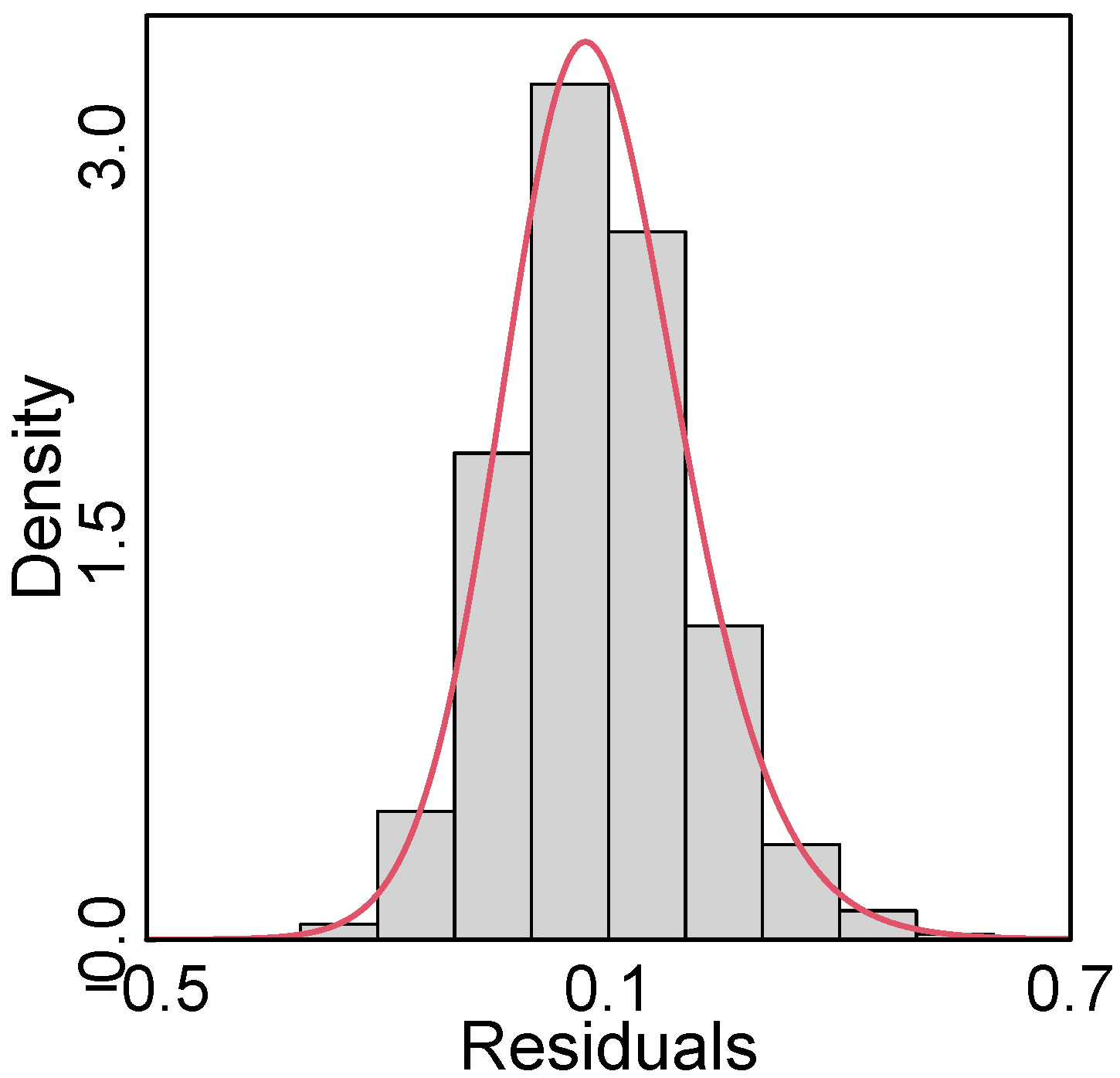
5.1. Women’s Income Data
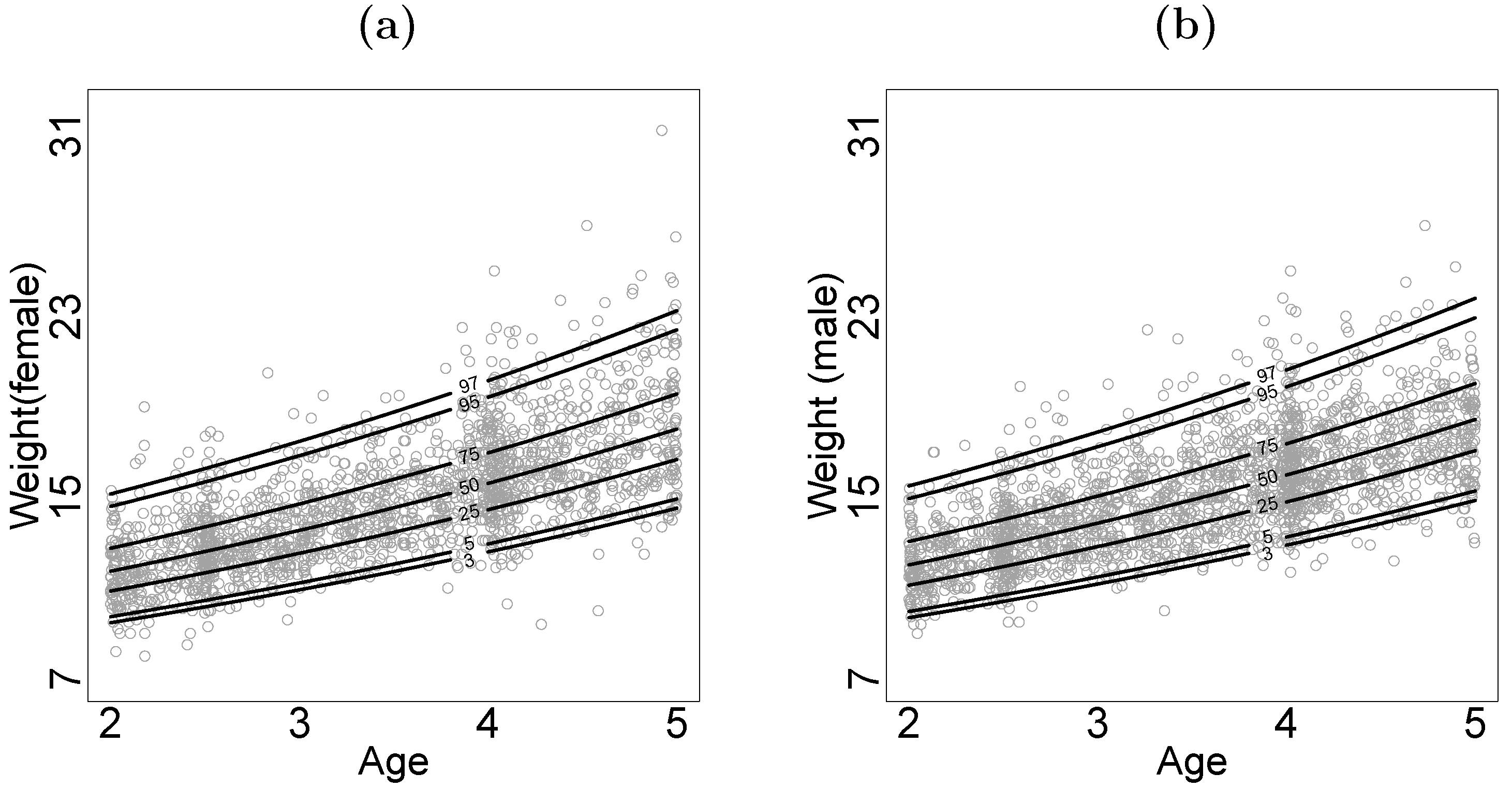
5.2. Children’s Weight Data
6. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- World Health Organization. WHO Child Growth Standards: Length/Height-for-Age, Weight-for-Age, Weight-for-Length, Weight-for-Height and Body Mass Index-for-Age: Methods and Development; World Health Organization: Geneva, Switzerland, 2006; Available online: https://apps.who.int/iris/handle/10665/43413 (accessed on 23 June 2025).
- World Health Organization. WHO Child Growth Standards: Head Circumference-for-Age, Arm Circumference-for-Age, Triceps Skinfold-for-Age and Subscapular Skinfold-for-Age: Methods and Development; World Health Organization: Geneva, Switzerland, 2007; Available online: https://apps.who.int/iris/handle/10665/43706 (accessed on 23 June 2025).
- Zhou, C. A Quantile Regression Analysis on the Relations between Foreign Direct Investment and Technological Innovation in China. In Proceedings of the 2011 International Conference of Information Technology, Computer Engineering and Management Sciences, Nanjing, China, 24–25 September 2011; pp. 38–41. [Google Scholar]
- Machado, J.A.F.; Mata, J. Counterfactual decomposition of changes in wage distributions using quantile regression. J. Appl. Econom. 2005, 20, 445–465. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar] [CrossRef]
- Mazucheli, J.; Alves, B.; Menezes, A.F.B.; Leiva, V. An overview on parametric quantile regression models and their computational implementation with applications to biomedical problems including COVID-19 data. Comput. Methods Programs Biomed. 2022, 221, 106816. [Google Scholar] [CrossRef]
- Morán-Vásquez, R.A.; Mazo-Lopera, M.A.; Ferrari, S.L.P. Quantile modeling through multivariate log-normal/independent linear regression models with application to newborn data. Biom. J. 2021, 63, 1290–1308. [Google Scholar] [CrossRef]
- Morán-Vásquez, R.A.; Giraldo-Melo, A.D.; Mazo-Lopera, M.A. Quantile estimation using the log-skew-normal linear regression model with application to children’s weight data. Mathematics 2023, 11, 3736. [Google Scholar] [CrossRef]
- Marchenko, Y.V.; Genton, M.G. Multivariate log-skew-elliptical distributions with applications to precipitation data. Environmetr. Off. J. Int. Environmetr. Soc. 2010, 21, 318–340. [Google Scholar] [CrossRef]
- Azzalini, A. The Skew-Normal and Related Families; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Azzalini, A.; Del Cappello, T.; Kotz, S. Log-skew-normal and log-skew-t distributions as models for family income data. J. Income Distrib. 2002, 11, 2. [Google Scholar] [CrossRef]
- Morán-Vásquez, R.A.; Ferrari, S.L.P. Box–Cox elliptical distributions with application. Metrika 2019, 82, 547–571. [Google Scholar] [CrossRef]
- Vanegas, L.H.; Paula, G.A. An extension of log-symmetric regression models: R codes and applications. J. Stat. Comput. Simul. 2016, 86, 1709–1735. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Using the Box-Cox t distribution in GAMLSS to model skewness and kurtosis. Stat. Model. 2006, 6, 209–229. [Google Scholar] [CrossRef]
- Azzalini, A. The R Package sn: The Skew-Normal and Related Distributions Such as the Skew-t and the SUN, Version 2.1.0. 2022. Available online: https://cran.r-project.org/package=sn (accessed on 23 June 2025).
- Atkinson, A.C. Two graphical displays for outlying and influential observations in regression. Biometrika 1981, 68, 13–20. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Riani, M.; Atkinson, A.C.; Morelli, G.; Corbellini, A. The Use of Modern Robust Regression Analysis with Graphics: An Example from Marketing. Stats 2025, 8, 6. [Google Scholar] [CrossRef]
- Azzalini, A.; Salehi, M. Some Computational Aspects of Maximum Likelihood Estimation of the Skew-t Distribution. In Computational and Methodological Statistics and Biostatistics. Emerging Topics in Statistics and Biostatistics; Bekker, A., Chen, D.-G., Ferreira, J.T., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 23 June 2025).
- de Castro Romero, L.; Barroso, V.M.; Santero-Sánchez, R. Does Gender Equality in Managerial Positions Improve the Gender Wage Gap? Comparative Evidence from Europe. Economies 2023, 11, 301. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Castro, L.M.; González-Farías, G.; Muñoz-Gajardo, K.A. Student-t censored regression model: Properties and inference. Stat. Methods Appl. 2012, 21, 453–473. [Google Scholar] [CrossRef]
- Cowell, F.A.; Victoria-Feser, M.P. Robustness properties of inequality measures. Econom. J. Econom. Soc. 1996, 64, 77–101. [Google Scholar] [CrossRef]
- Saulo, H.; Vila, R.; Borges, G.V.; Bourguignon, M.; Leiva, V.; Marchant, C. Modeling income data via new parametric quantile regressions: Formulation, computational statistics, and application. Mathematics 2023, 11, 448. [Google Scholar] [CrossRef]
- Altonji, J. Race and Gender in the Labor Market. In Handbook of Labor Economics/North Holland; Elsevier: Amsterdam, The Netherlands, 1999; Volume 3, pp. 3143–3259. [Google Scholar]
- Card, D.; Lemieux, T. Wage dispersion, returns to skill, and black-white wage differentials. J. Econom. 1996, 74, 319–361. [Google Scholar] [CrossRef][Green Version]
- Departamento Administrativo Nacional de Estadística (DANE). Gran Encuesta Integrada de Hogares (GEIH). 2021. Available online: https://microdatos.dane.gov.co/index.php/catalog/750/get-microdata (accessed on 23 June 2025).
- MEDATA: Estrategia de Datos de Medellín. Estado Nutricional de Menores de 6 Años Programa de Crecimiento y Desarrollo 2022. Available online: https://medata.gov.co/dataset/estado-nutricional-de-menores-de-6-anos-programa-de-crecimiento-y-desarrollo (accessed on 23 June 2025).
- Gidi, N.W.; Berhane, M.; Girma, T.; Abdissa, A.; Lim, R.; Lee, K.; Nguyen, C.; Russell, F. Anthropometric measures that identify premature and low birth weight newborns in Ethiopia: A cross-sectional study with community follow-up. Arch. Dis. Child. 2020, 105, 326–331. [Google Scholar] [CrossRef]
- Paulsen, C.B.; Nielsen, B.B.; Msemo, O.A.; Møller, S.L.; Ekmann, J.R.; Theander, T.G.; Bygbjerg, I.C.; Lusingu, J.P.A.; Minja, D.T.R.; Schmiegelow, C. Anthropometric measurements can identify small for gestational age newborns: A cohort study in rural Tanzania. BMC Pediatr. 2019, 19, 120. [Google Scholar] [CrossRef]
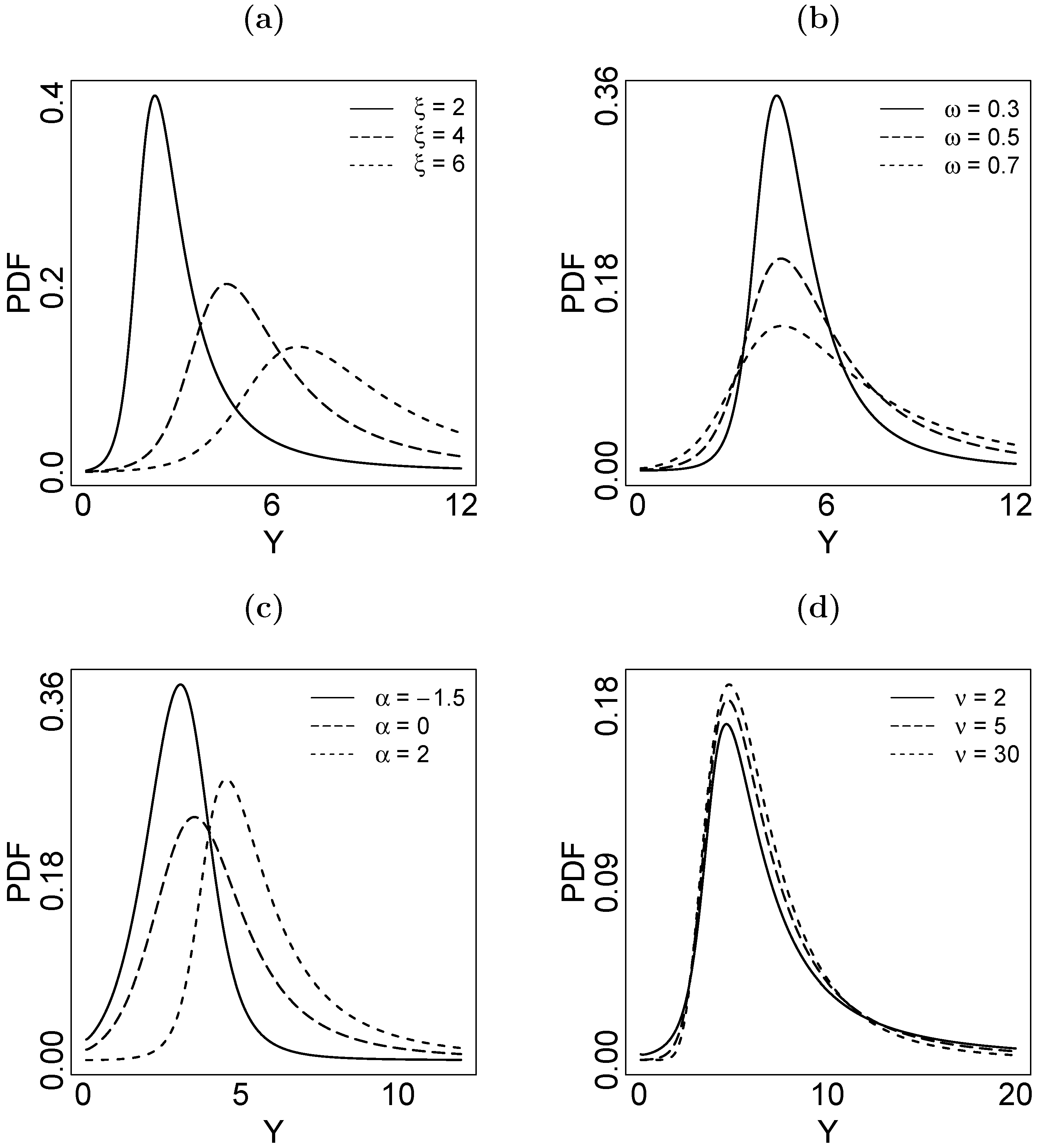
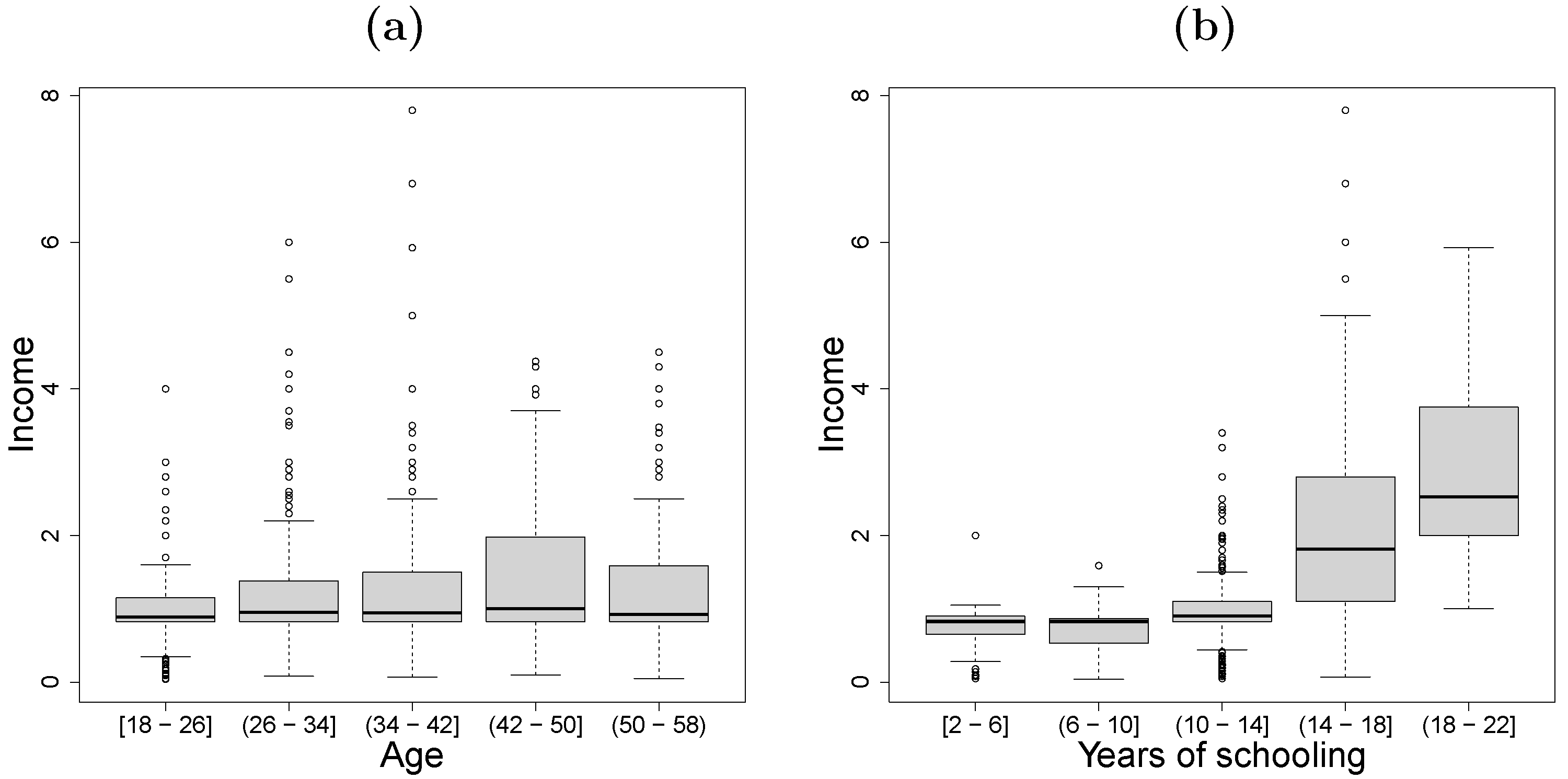
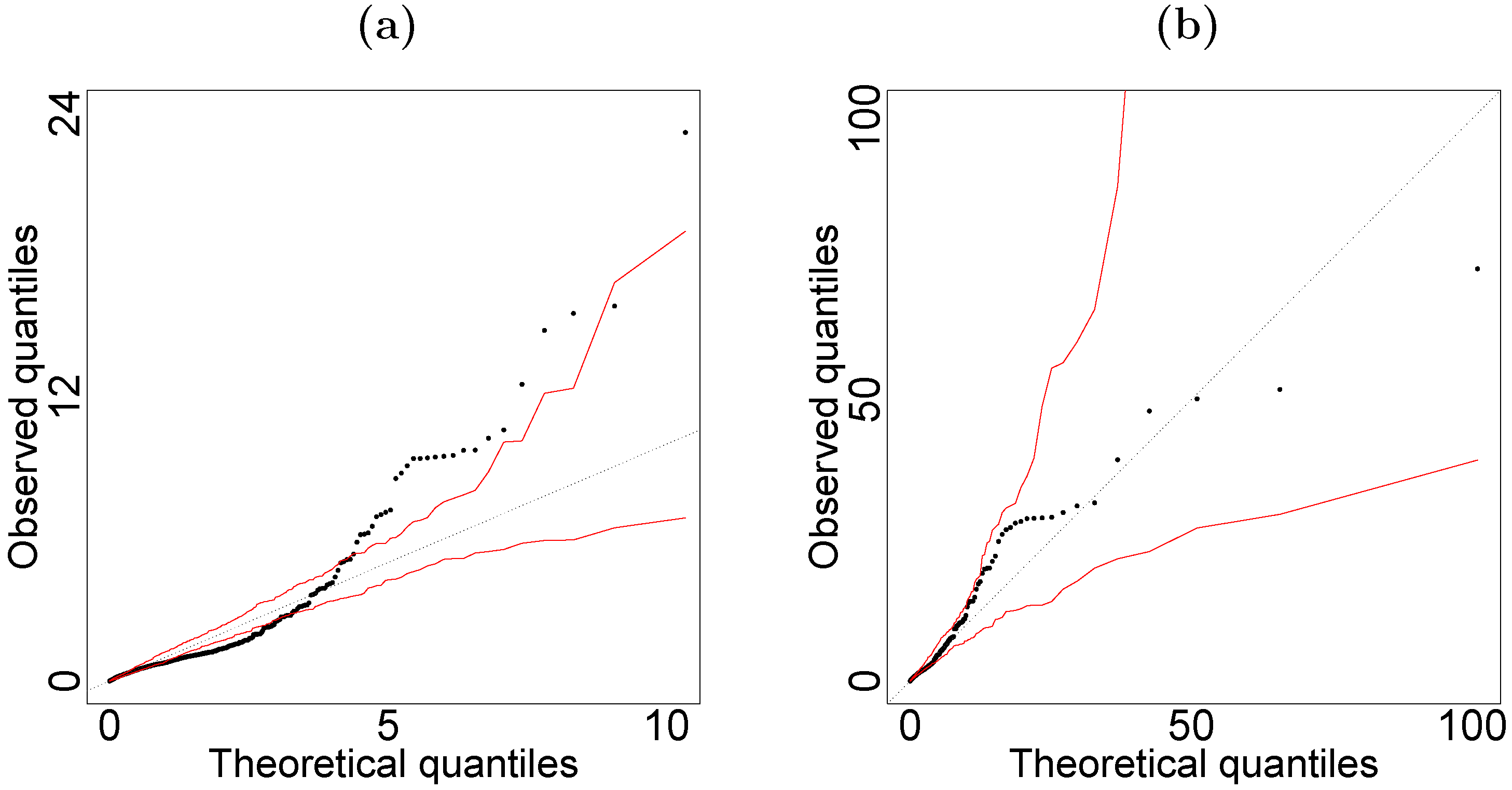
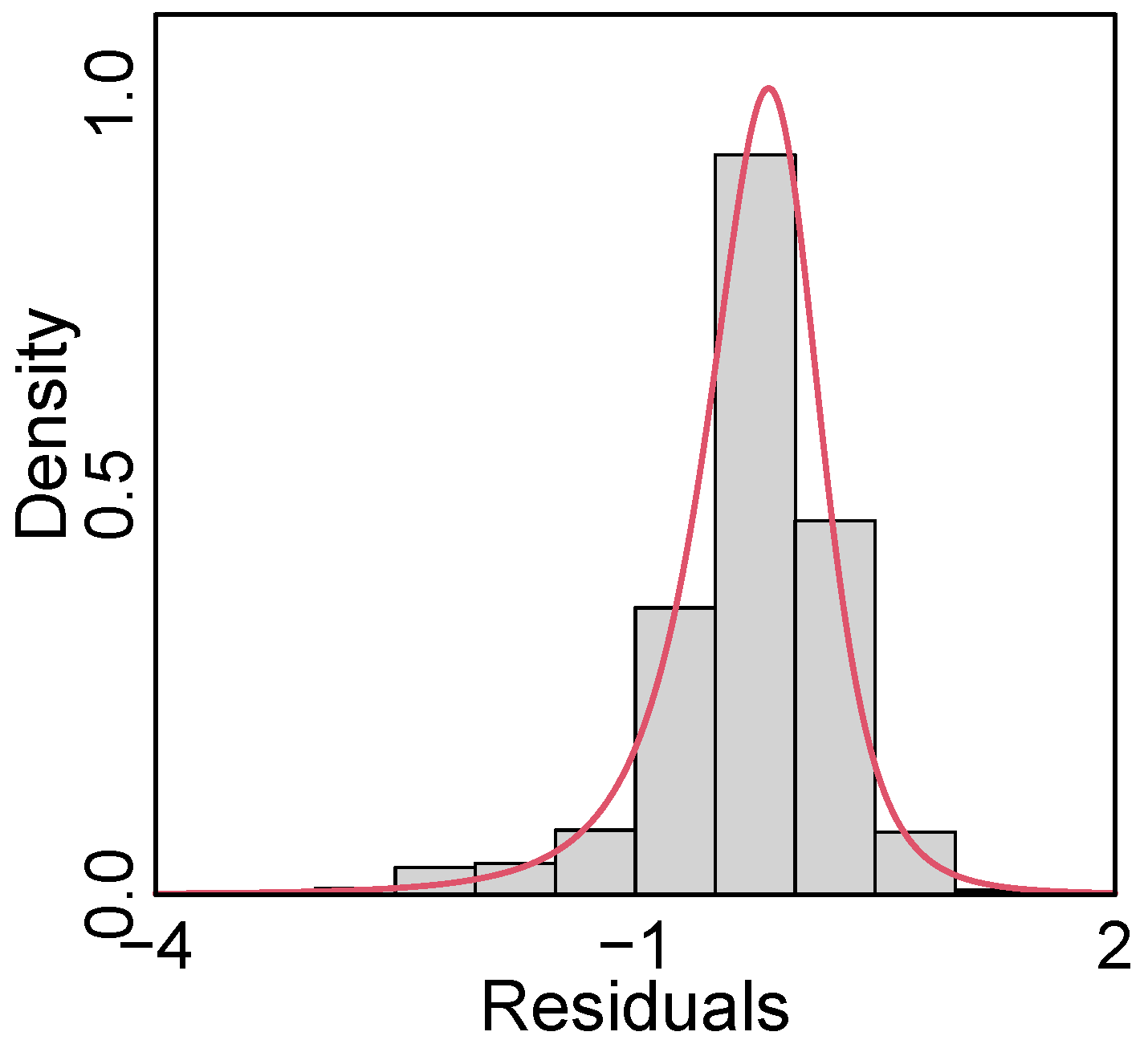
| True Parameter | Median | MAD | Median | MAD | Median | MAD | Median | MAD | |
|---|---|---|---|---|---|---|---|---|---|
| −1.4863 | −1.5029 | 0.2625 | −1.4881 | 0.1714 | −1.4861 | 0.0797 | −1.4847 | 0.0549 | |
| 0.0141 | 0.0140 | 0.0034 | 0.0141 | 0.0028 | 0.0141 | 0.0012 | 0.0141 | 0.0009 | |
| 0.1032 | 0.1029 | 0.0147 | 0.1035 | 0.0086 | 0.1033 | 0.0040 | 0.1032 | 0.0029 | |
| 0.4230 | 0.4144 | 0.0812 | 0.4253 | 0.0624 | 0.4239 | 0.0266 | 0.4231 | 0.0191 | |
| −0.8377 | −0.8706 | 0.6470 | −0.9111 | 0.4463 | −0.8544 | 0.1768 | −0.8458 | 0.1254 | |
| 3.3462 | 3.3163 | 1.1832 | 3.5137 | 0.9473 | 3.3943 | 0.3800 | 3.3613 | 0.2684 | |
| LSTLRM | QR | LSTLRM | QR | LSTLRM | QR | LSTLRM | QR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True Quantile | Median | MAD | Median | MAD | Median | MAD | Median | MAD | Median | MAD | Median | MAD | Median | MAD | Median | MAD | |
| 0.3135 | 0.3346 | 0.0786 | 0.3727 | 0.0890 | 0.3037 | 0.0491 | 0.3306 | 0.0629 | 0.3268 | 0.0242 | 0.3477 | 0.0330 | 0.2935 | 0.0157 | 0.3124 | 0.0205 | |
| 0.4074 | 0.4315 | 0.0723 | 0.4602 | 0.0877 | 0.3895 | 0.0448 | 0.4167 | 0.0587 | 0.4233 | 0.0221 | 0.4481 | 0.0290 | 0.3806 | 0.0144 | 0.4039 | 0.0185 | |
| 0.8139 | 0.8404 | 0.0505 | 0.8837 | 0.0607 | 0.7608 | 0.0329 | 0.8086 | 0.0400 | 0.8409 | 0.0158 | 0.8894 | 0.0194 | 0.7592 | 0.0103 | 0.8053 | 0.0123 | |
| 1.1030 | 1.1272 | 0.0496 | 1.1906 | 0.0603 | 1.0282 | 0.0314 | 1.0976 | 0.0398 | 1.1386 | 0.0156 | 1.2094 | 0.0197 | 1.0286 | 0.0104 | 1.0960 | 0.0123 | |
| 1.4318 | 1.4476 | 0.0676 | 1.5550 | 0.0843 | 1.3308 | 0.0426 | 1.4362 | 0.0546 | 1.4769 | 0.0209 | 1.5827 | 0.0274 | 1.3347 | 0.0141 | 1.4358 | 0.0169 | |
| 2.2065 | 2.1891 | 0.2087 | 2.4660 | 0.3065 | 2.0197 | 0.1348 | 2.2466 | 0.1910 | 2.2674 | 0.0681 | 2.4698 | 0.0933 | 2.0534 | 0.0449 | 2.2528 | 0.0594 | |
| 2.5431 | 2.5097 | 0.3168 | 2.8332 | 0.4771 | 2.3094 | 0.2052 | 2.5879 | 0.3067 | 2.6075 | 0.1063 | 2.8533 | 0.1500 | 2.3639 | 0.0701 | 2.6083 | 0.0947 | |
| Covariate | Estimate | SE | Lower | Upper | p-Value |
|---|---|---|---|---|---|
| Intercept | −1.4863 | 0.0927 | −1.6679 | −1.3047 | <0.0001 |
| Age | 0.0141 | 0.0016 | 0.0110 | 0.0171 | <0.0001 |
| Years of schooling | 0.1032 | 0.0052 | 0.0930 | 0.1134 | <0.0001 |
| Explanatory Variable | Estimate | SE | Lower | Upper | p-Value |
|---|---|---|---|---|---|
| Intercept | 2.0984 | 0.0114 | 2.0761 | 2.1207 | <0.0001 |
| Gender | 0.0233 | 0.0040 | 0.0154 | 0.0312 | <0.0001 |
| Age | 0.1425 | 0.0023 | 0.1380 | 0.1470 | <0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morán-Vásquez, R.A.; Giraldo-Melo, A.D.; Mazo-Lopera, M.A. Quantile Estimation Based on the Log-Skew-t Linear Regression Model: Statistical Aspects, Simulations, and Applications. Stats 2025, 8, 58. https://doi.org/10.3390/stats8030058
Morán-Vásquez RA, Giraldo-Melo AD, Mazo-Lopera MA. Quantile Estimation Based on the Log-Skew-t Linear Regression Model: Statistical Aspects, Simulations, and Applications. Stats. 2025; 8(3):58. https://doi.org/10.3390/stats8030058
Chicago/Turabian StyleMorán-Vásquez, Raúl Alejandro, Anlly Daniela Giraldo-Melo, and Mauricio A. Mazo-Lopera. 2025. "Quantile Estimation Based on the Log-Skew-t Linear Regression Model: Statistical Aspects, Simulations, and Applications" Stats 8, no. 3: 58. https://doi.org/10.3390/stats8030058
APA StyleMorán-Vásquez, R. A., Giraldo-Melo, A. D., & Mazo-Lopera, M. A. (2025). Quantile Estimation Based on the Log-Skew-t Linear Regression Model: Statistical Aspects, Simulations, and Applications. Stats, 8(3), 58. https://doi.org/10.3390/stats8030058






