Abstract
The objective of this research is to evaluate four distinct models for multi-population mortality projection in order to ascertain the most effective approach for forecasting the impact of the COVID-19 pandemic on mortality. Utilizing data from the Human Mortality Database for five countries—Finland, Germany, Italy, the Netherlands, and the United States—the study identifies the generalized additive model (GAM) within the age–period–cohort (APC) analytical framework as the most promising for precise mortality forecasts. Consequently, this model serves as the basis for projecting the impact of the COVID-19 pandemic on future mortality rates. By examining various pandemic scenarios, ranging from mild to severe, the study concludes that projections assuming a diminishing impact of the pandemic over time are most consistent, especially for middle-aged and elderly populations. Projections derived from the superior GAM-APC model offer guidance for strategic planning and decision-making within sectors facing the challenges posed by extreme historical mortality events and uncertain future mortality trajectories.
1. Introduction
In recent decades, life expectancy in the developed world has shown a substantial increase, exemplified by a notable 56.7% reduction in the mortality rate of 80-year-old men in the USA from 1933 to 2019. This trend, reflecting societal advancements and improved healthcare systems, underscores the importance of accurately predicting mortality trends for informed decision-making by policymakers, pension schemes, insurers, and social security systems. The emergence of the COVID-19 pandemic has further underscored the need to understand its impact on mortality trends over the short- to mid-term. Our study focuses on assessing the impact of COVID-19 on mortality trends, aiming to enhance existing mortality models while maintaining explainability.
The literature presents a diverse range of approaches to mortality modeling, from traditional stochastic models like those discussed by [1] to modern methods such as the use of machine learning (ML) techniques. Recent studies have shown that methods like pure Gradient Boosting or Random Forest perform exceptionally well [2], while others have explored hierarchical approaches with ML building upon simpler LC models [3]. Furthermore, recent advancements include the application of neural networks to enhance mortality models, such as the Common-Age-Effect Model proposed by [4] and the extension of LC models for multiple populations demonstrated by [5]. Generalized Additive Models (GAMs), a well-established model class, was first introduced by [6] and has been applied in the mortality context; [7] describes a Bayesian APC model with an autoregressive prior on the age, period, and cohort terms; and [8] proposed the use of a bivariate spline function within a GAM to effectively capture two-dimensional cohort information. A similar model was applied by [9] for projecting cancer incidence and mortality in Finland, by [10] for mortality in the UK, and by [11] for projecting breast cancer mortality in Spain. However, none of them model and extrapolate GAM in the APC framework with a tensor product in a multi-populational fashion. The literature on accounting for COVID in mortality projections is also growing, e.g., [12], which uses the stochastic Li and Lee model; [13], which proposes parsimonious decomposition of the mortality surface on a polynomial basis with regularization and cross-validation; and [4], which quantifies the impact of the 2020 mortality shock by calibrating the Lee–Carter model. However, none of the aforementioned studies employ GAM in APC and evaluate scenarios post-pandemic.
To compare with the traditional stochastic mortality models, LC [1] and age–period–cohort (APC) [14], alongside contemporary ML methodology proposed by [3], this study introduces a cross-country GAM within an APC framework, utilizing a smoothed second-order spline with penalty points. To our knowledge, this research is the first to integrate the GAM method into the APC framework in a multi-population context and employ it to extrapolate the impact of COVID-19 on future mortality trends. We examine Germany, Finland, the Netherlands, Italy (representing Europe), and the United States (representing North America) using data from the Human Mortality Database [15]. We employ a cross-country approach, enabling the model to learn from multiple countries concurrently, thereby capturing both universal trends and country-specific variations in mortality patterns.
Our research makes three key contributions, which are visually summarized in Figure 1. First, we compare the predictive performance of four models, including traditional single-population and contemporary multi-populational models, for modeling and projecting future mortality rates for five countries. We find that the most promising approach is based on a GAM, where cohorts are represented as an interaction between age and period. This framework, adaptable for both aggregated and individual survival data, introduces a state-of-the-art method for the field of multi-populational cross-country mortality research. Secondly, we introduce partial APC plots as a novel graphical tool in mortality research, enabling the analysis of specific APC structures. This tool aids in communicating complex temporal patterns and highlights gender-specific and cross-country differences. Finally, we provide fresh insights into the factors driving the impact of the COVID-19 pandemic on mortality for the five countries. Through analyzing age, period, and cohort associations in a multi-population context using a GAM within an APC framework, we extrapolate mortality rates into the future. Four scenarios, representing varying degrees of pandemic impact, are evaluated against observed mortality data post-pandemic to identify the most accurate scenario.
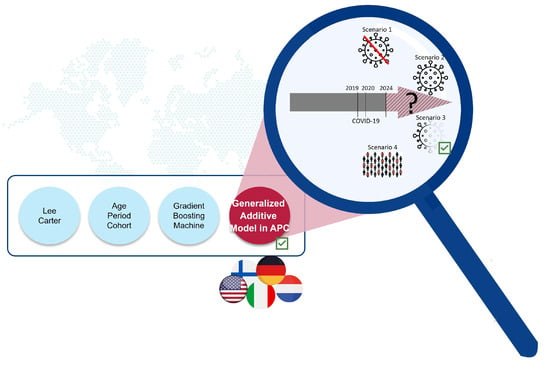
Figure 1.
Schematic illustration of the key findings: (1) GAM-APC is the most effective approach for mortality forecasting. (2) The model provides multi-populational and cross-country insights. (3) Among the four pandemic impact scenarios, Scenario 3, which assumes a diminishing impact of COVID-19, is the most consistent, particularly for middle-aged and elderly populations.
The practical implications of our findings are considerable. Our research demonstrates the efficacy of the GAM within the APC framework and its capacity to extrapolate mortality forecasts, accounting for the impact of the COVID-19 pandemic. This offers invaluable insights for policymakers and stakeholders, providing guidance in navigating the uncertainties brought about by the pandemic, with a particular emphasis on matters pertaining to life insurance and pension funds.
Our study follows a structured approach, beginning with an overview of the database and methodology. We then compare the predictive performance of benchmark methods across countries, offering insights into optimal trend forecasting techniques. Additionally, we conduct scenario analyses to evaluate the impact of COVID-19 on mortality trends. Finally, we conclude by summarizing our key findings and implications.
2. Data and Methods
2.1. Data
The study relies on the Human Mortality Database (HMD) [15], which provides mortality rates , death counts , and population sizes categorized by age a, year t, gender g, and country c. The selection of countries is based on their geographic context and the contrasting impact of the COVID-19 pandemic. Specifically, Finland (until 2019), Germany (until 2017), Italy (until 2018), and the Netherlands (until 2019) represent Europe, while the United States (until 2019) represents North America.
For the most recent years up until 2023, the Short-Term Mortality Fluctuations (STMF) [16] series offers partial information on mortality rates and population, grouped by week and age categories. However, the study requires data on a yearly basis and in a metric age scale. To address this, we employ a methodology to construct mortality data on a yearly basis and in a metric age scale, which are then combined with the original HMD data. This process is based partly on the proposal by [12] and further detailed in Appendix A.
Figure 2’s heatmaps visualize mortality rate changes in the United States, showing a decreasing trend over the years. Darker red colors indicate higher mortality rates, with females generally exhibiting lower rates than males, especially in older age categories. Infant mortality rates have strongly improved, transitioning from red to white. The diagonal lines symbolize distinct birth cohorts, highlighting the three primary effects examined in this study: age, period, and cohort.
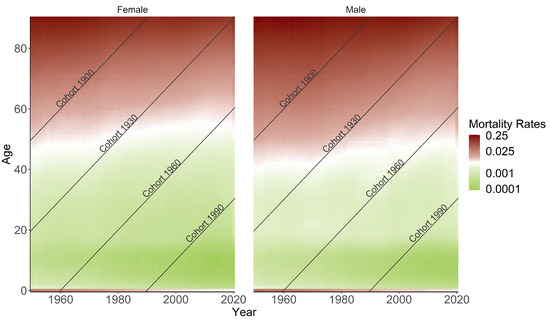
Figure 2.
Heatmaps of mortality rates for the US population are shown, with age groups and periods represented horizontally and vertically, respectively. The diagonal lines display unique cohorts.
2.2. Methods
The aim of the developed and applied methodology is to enhance mortality modeling by prioritizing predictive performance and future trend forecasting. To achieve this goal, four different methods have been benchmarked and outlined below: traditional ones such as Lee–Carter (LC) and age–period–cohort (APC); a more modern two-step approach using Gradient Boosting Machine (GBM); and finally, Generalized Additive Model (GAM) within the APC framework.
2.2.1. Lee–Carter (LC)
The classical LC model, initially proposed by Lee and Carter (1992) [1], estimates and forecasts mortality rates at age a in year t. This model is applicable on single-populational data, considering one gender category for each country:
Here, represents the age-specific average over time, describes the rate of mortality improvement at age a, and denotes the general trend of mortality at time t. The error terms reflect the residual age- and year-specific historical influence on mortality rates that the model cannot capture. The authors suggest using the singular value decomposition (SVD) method to find the least squares solution to minimize the residual sum of squares. The original method is embedded in a single-populational Poisson regression model by [17]:
The expected number of deaths according to the LC fit can be calculated as using linear predictor with constraints like [18].
2.2.2. Age–Period–Cohort (APC)
The APC model extends the LC model by including a cohort effect and omitting the age-specific improvement rates, yielding in the following linear predictor: . The cohort is generally computed by . This model is applicable on single-populational data and has its origins in the fields of medicine and demography, going back a long way ([14,19]). However, [20] was the first who considered this type of model in the actuarial field. With the Poisson distribution assumption and the log link function remaining the same, it can be traced back to the general shape of Generalized APC models [18]. The identifiability is ensured with the following constraints: , , and , indicating that the cohort effect oscillates around zero with no apparent linear trend.
2.2.3. Two-Step Approach with Gradient Boosting Machine (GBM)
In this study, we adopt the two-step approach proposed by [3] to refine mortality rate estimations derived from the LC model using Gradient Boosting Machine (GBM).
Firstly, we employ the LC model to estimate mortality rates separately for each country c and gender g. Secondly, we leverage GBM to adjust these estimations by estimating the improvement factor , which corrects for underestimations (values greater than 1) or overestimations (values smaller than 1). This step involves training GBM with hyperparameter optimization on a multi-populational level using age, year, cohort, gender, and country as features, with death counts as the target variable:
The adapted exposure is calculated as . Although the software does not permit the direct inclusion of as an offset, we circumvent this limitation by scaling the death counts by exposure and using as weights, a method shown to be mathematically equivalent to using death counts as target and exposure as offset in the Poisson case by [21]. Details on the GBM methodology are given in Appendix B. Finally, the refined mortality rates are obtained as .
2.2.4. Generalized Additive Model (GAM) in APC Framework
We integrate the APC framework into GAM in a multi-populational setting, allowing for the modeling of nonlinear, smooth effect structures and facilitating the capture of complex relationships.
In the traditional regression framework, collinearity arises among the three temporal components (age, period, and cohort) leading to identification problems. To mitigate this, we employ a bivariate tensor product with penalized B-splines between age and period, establishing a two-dimensional interaction surface. This surface inherently incorporates cohort information along its diagonals, as illustrated in Figure 2. By doing so, we address the identification problem without imposing restrictive assumptions or constraints [8,14].
By employing multi-populational modeling, within the same GAM framework, we estimate a separate bivariate function for each country and gender interaction. This enables the capture of specific mortality patterns within each subpopulation while allowing countries to learn from each other’s experiences through the intercept term.
Finally, we fit a semiparametric additive Poisson regression with a log link, using death counts as the target and offsetting for population size . The model structure is formulated as follows:
Here, represents the bivariate function for the interaction of age a and period t, specific to each gender g and country c combination.
To visualize the marginal effects of each component effectively, temporal developments are condensed in one specific dimension (either age, period, or cohort) and averaged over the respective other component. This approach allows for examining the effects of age or period by country and gender while considering the cohort values as post-stratification [22,23,24]:
For forecasting purposes, the impact of COVID-19 on mortality rates is incorporated into the mortality model using an additional variable called . This variable is specific to each country c and takes the value of 0 for years until 2019 and 1 for the years 2020 and 2021, representing the period during which the COVID-19 pandemic has proven to have a strong impact. The values taken for future predictions are subject to the scenario assumptions elaborated in Section 3.
The interaction allows the model to capture the country-specific impact of the pandemic on mortality rates during the years 2020 and 2021 and, thus, project into the future.
To forecast the mortality rates into the future, we follow a differentiated approach, as outlined in Figure 3. For the time-dependent components (period and cohort) of the LC, APC as well as the final rates of the two-step approach with GBM ARIMA model as random walk with linear drift and automated parameter estimation are selected [25,26,27]. The forecast of mortality rates for GAM is based on extrapolation of the spline fit, assuming a globally quadratic structure and a persistent curvature outside the observed data. The choice of degrees of freedom for the covariates can be either predetermined or estimated automatically. We caution against extrapolating too far into the future [24].
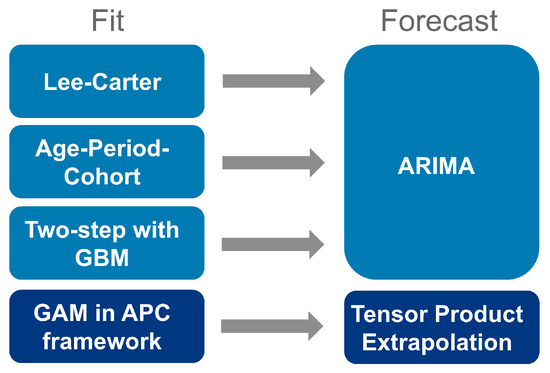
Figure 3.
Illustration of the models used for fit and forecast.
We employed R for the technical implementation of the LC and APC models [28], and their forecasting [25], as well as for GAM [29]. Additionally, for the two-step approach, we utilized Python 3.11.10 to implement a Light GBM algorithm [30] and Hyperopt [31] for hyperparameter optimization.
To evaluate the accuracy of the models, the root-mean-square error (RMSE) is calculated, which measures the average difference between the mortality rates and the observed mortality rates across all ages a, years t, genders g, and countries c. The RMSE is computed as follows:
where n represents the total number of observations.
3. Results
This section begins with an evaluation of predictive performance, both in-sample and out-of-sample, for all four models. Table 1 gives an overview of the different training and test sets used in the analysis. It should be noted that for the purposes of benchmarking, years up to and including 2019 are used on the assumption that they are not affected by the impact of the COVID-19 pandemic. This approach eliminates any year-specific artifacts that might otherwise affect the assessment of the predictive performance of the models themselves. The single-populational models LC, APC, and GBM (based on LC in the first step) are limited to using data from Germany from 1990 onwards due to data inconsistencies before reunification. In order to maintain comparability across the tensor–product spanned by years and ages, it is necessary to ensure that the multi-population GAM is coherent. This is because GAM requires a joint coverage of years—a prerequisite for coherent modeling. As a result, available years for all countries will be restricted to 1990–2015 to ensure sufficient training for capturing current effects on mortality rates and projecting them into the future for 2016–2019. Conversely, to ensure comparability among the LC, APC, and GBM models, we permit a shorter training period for Germany (until 2010), resulting in a longer testing period. This approach is especially appropriate for LC, which, due to its linear nature, does not require extensive historical data to accurately forecast future trends.

Table 1.
Model training and test periods for benchmarking.
Focusing on in-sample RMSE for single-populational LC, APC, multi-populational GBM, and GAM models, we fit the training periods range from 1950 to 2010 for Finland, Italy, the Netherlands, and the US, and from 1990 to 2010 for Germany. GAM models are fitted from 1990 to 2015 for all countries. In-sample error is calculated within the same range as the model training period and reveals that the two-step approach with GBM and GAM in the APC framework exhibits superior performance over traditional stochastic mortality models LC and APC. There is no clear preference between GBM and GAM, with both achieving strong reductions in RMSE compared to LC and APC for in-sample predictions. Table A1 in Appendix D provides an overview of the goodness-of-fit for information reasons.
GBM demonstrates proficiency in adaptive learning, which enables it to discern intricate, non-linear relationships that markedly enhance model fit. However, this also gives rise to the possibility of overfitting, whereby the learning process is influenced by noise rather than the underlying trends, thereby enhancing training performance but not ensuring better long-term generalization. Table 2 highlights the differences in computational efficiency. The APC model, being slightly larger and taking longer to run than the LC model, reflects its added complexity due to the cohort dimension. As expected, LightGBM (GBM) takes significantly longer to train and uses substantially more memory than GAM. This is because gradient boosting involves iterative training and optimization across many decision trees, which requires more computational resources than fitting a GAM model in Appendix C. The model size of GBM is also larger than that of GAM, reflecting its complexity and the higher number of parameters.

Table 2.
Computational efficiency for training, summarized for all 10 single populations for LC and APC.
Table 3 presents the out-of-sample results for different models, indicating the forecasting quality across countries and genders. Out-of-sample RMSE is calculated based on forecast periods ranging from 2011 to 2019 for LC, APC, and GBM models, while GAM forecasts span from 2016 to 2019 for all countries.

Table 3.
Out-of-sample RMSE comparison for LC, APC, GBM, and GAM models. Forecast for LC, APC, and GBM based on ARIMA (2011–2019), while GAM extrapolates tensor product (2016–2019).
The differing training periods for the multi-populational GAM model and single-populational models were necessary to ensure coherent modeling based on historical data availability. We used RMSE as a consistent metric to measure mean forecast error across models, and despite concerns regarding GAM’s shorter training period, outlier analysis confirmed the reliability of its RMSE mean.
While GBM shows improved fit and forecast performance, GAM exhibits stronger improvement in forecast accuracy, especially for short-term forecasts within a few years. The GAM-based APC model achieves notable reductions not only in fit but also in forecast errors compared to the classical APC model, implying improved accuracy of mortality rate predictions. The choice of GAM for further analysis is justified based on its superior forecast performance.
One key highlight of the GAM in APC framework is its multi-populational nature, enabling the interpretation of exponential marginal effects, with age, period, and cohort being the components analyzed further. Figure 4 displays the effects of the model based on these components: Both age and cohort effects conform to expectations; thus, higher ages correspond to higher mortality rates while cohort effects reflect variations stemming from individuals’ unique experiences based on their birth year [32,33,34]. Conversely, similar reverse effects are observable for age and cohort.
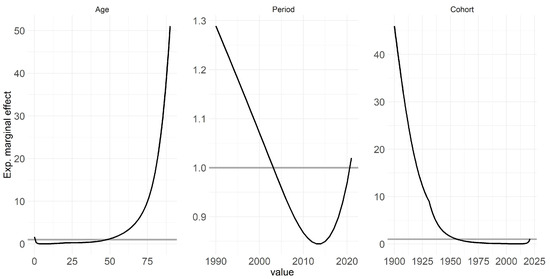
Figure 4.
The figure illustrates the estimated marginal effects of age, period, and cohort on mortality rates across multiple countries and genders based on GAM fitted for years 1990–2020.
The period effect, which indicates the improvement of mortality over time and is influenced by external factors affecting all age groups equally at a given point in time, exhibits a notable increase leading up to 2020 [35,36]. However, the period effect notably spikes, particularly approaching 2020, signifying a strong influence of this year on mortality rates. Specifically, the strides made in improving mortality rates over preceding years or even decades appear to have been offset by the effect of COVID-19, resulting in a regression to levels observed around 2003. Appendix D contains this figure stratified by countries and genders for more detailed interpretation.
Following the benchmarking of the four models, we delve into an analysis of the effects of each temporal component on mortality rates throughout the considered time period. Finally, based on GAM in APC framework, we assess the trend forecast into the future considering the impact of COVID-19.
Even though the impact of COVID-19 is, fortunately, diminishing in the present time, its impact on historical (and future) data and the persisting uncertainties in the future cannot be overlooked. These factors necessitate continued attention for many years to come. It is important to note that the idea and methodology employed in this study extend beyond COVID-19 and encompass other events, especially those occurring at the edge of time series, which can present challenges for standard breakpoint analyses.
The scenarios depicted herein must be viewed in light of a meticulous plausibility assessment and the underlying assumptions. To validate the scenario-based findings, we engaged with epidemiological experts. This collaboration is paramount for ensuring the reliability and robustness of the analysis, especially given the complexities inherent in such events. Comparing our framework with expert opinions in the literature, as conducted by citetelenti2021after, reveals a high level of agreement.
Scenario 1: In this scenario, the assumption is made that COVID-19 will disappear in the future. The model is trained using data up to 2019 only, excluding the years 2020 and 2021. The predictions are then made for the years 2020–2025, assuming no long-term effects of COVID-19 on mortality. This approach treats COVID-19 as a special event that does not have any influence on mortality in the upcoming years. The model focuses on the underlying mortality trend without considering the impact of COVID-19 and, thus, without the COVID-indicator.
Scenario 2: In Scenario 2, the expectation is that the full effect of COVID will persist in the future. The model is trained on mortality data up to and including 2021, encompassing years impacted by COVID-19. The indicator variable is incorporated, set to 0 for years before 2019 and 1 for 2020 and 2021. Predictions are then made for subsequent years, assuming that remains set to 1 to indicate the ongoing presence of COVID-19. This scenario assumes that the COVID-related situation will continue similarly as it did until 2021 and that it will have a consistent effect on mortality over the coming years.
Scenario 3: In this scenario, the assumption is made that the COVID effect will flatten over time. Similar to Scenario 2, the model is trained using mortality data up to and including 2021. However, in this case, the COVID-19 effect is assumed to decrease exponentially over time. The predictions take into account the diminishing impact of COVID-19 in the future, reflecting the belief that the effect of COVID-19 on health and mortality will slowly flatten out and eventually disappear after a few years. Therefore, the indicator takes exponentially decreasing values between 1 and 0 for each year.
Scenario 4: In Scenario 4, the focus is on adjusting for excess mortality associated with COVID-19. The years 2020 and 2021 are treated as outliers, but the excess mortality is explicitly considered. The model calculates the difference between the expected death counts and the actual mortality counts for these two years to account for the excess mortality. It is assumed that the excess mortality will not average out over the coming years and must be explicitly accounted for. The baseline mortality, representing the mortality trend without the influence of COVID-19, remains unchanged. This scenario allows for separate consideration of the excess mortality caused by COVID-19 while keeping the baseline mortality unchanged.
The formulation of potential future scenarios related to the pandemic is a complex undertaking, shaped by a multitude of factors, including political decisions and societal acceptance. Despite the inherent challenges, these presented scenarios offer a valuable foundation for mortality forecasts, taking into account the evolving attitudes of life insurers and contributing to the ongoing discourse surrounding the impact of the pandemic. A summary of the key assumptions underlying each scenario is provided in Table 4.

Table 4.
Discussion of assumptions underlying COVID-19 mortality impact scenarios.
Table 5 presents the different training and test periods used in the scenario analysis, now also considering years after 2019.

Table 5.
Overview of different scenario periods.
Figure 5 presents outcomes for four scenarios across various countries and genders, focusing on 80-year-olds. We chose age 80 for illustration, but the overall structure is similar for other ages, albeit with less intense COVID-19 effects for younger age groups. Notable high-value outliers for Italy, the US, and the Netherlands in 2020 and 2021 indicate a pronounced impact of COVID-19. Different trend forecasts capture varying effects of COVID-19 on mortality rates. Scenario 1 represents a milder assumption, while Scenario 2 depicts a more severe projection. Future forecasts vary by country and age group, influenced by past behaviors and responses to the pandemic. Trend forecasts in different scenarios generally align with plausibility. Excluding 2020 and 2021 in Scenario 1 results in lower mortality rates, while adjusting for excess mortality in Scenario 4 leads to even lower rates, considering the population shift due to previous deaths. Scenario 2 with full COVID effect shows the highest mortality trend, which is particularly evident for older age groups. However, younger populations appear less affected. Scenario 3 starts similar to Scenario 2 but gradually decreases over time. Different countries show distinct trends, likely influenced by COVID’s demographic and political impact. The Netherlands’ observed rates in years 2022 and 2023 align with Scenario 2, whereas Italy and the US show patterns more consistent with the flattening effect. German scenarios show less differentiation, aligning closely with observations, while Finland’s forecast suggests lower mortality rates than observed.
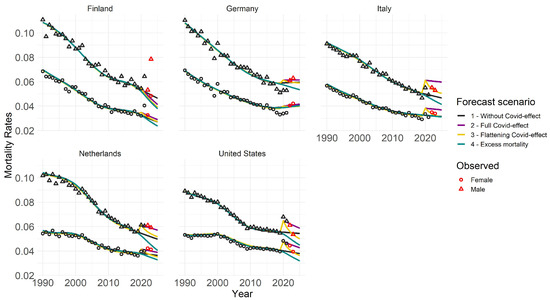
Figure 5.
Trend forecasts for 80-year-olds across four distinct scenarios. Training data span from 1990 to a maximum of 2021, depending on the scenario, with forecasts projected up to 2025. Circles and triangles represent observed rates, with red markers indicating those used for validation purposes.
The heatmap (Figure 6) illustrates both a cross-country and country-specific perspective on the y-axis, while age groups are delineated on the x-axis. Colors within the heatmap indicate the normalized RMSE (NRMSE) values for the years 2022 and 2023 when compared with the observed mortality rates from STMF and processed in accordance with Appendix A.
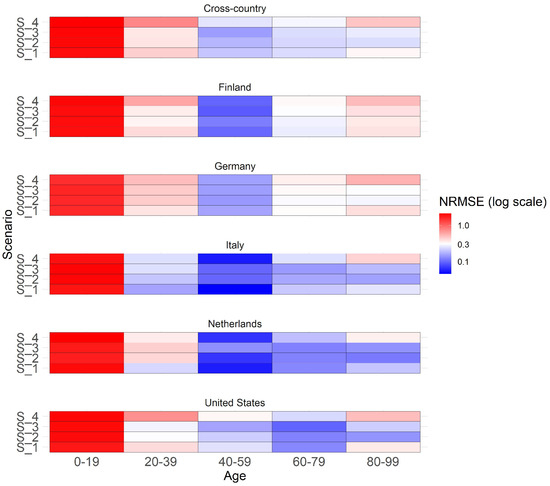
Figure 6.
Heatmap showing the normalized RMSE of scenarios for extrapolated years 2022 and 2023 for males across different countries and age groups. The cross-country section presents a summary of the NRMSE across all countries.
NRMSE is calculated by dividing RMSE by the mean of observed mortality rates in a specific category with values ranging usually from 0 to 1. A value of 0 means perfect predictions, while 1 suggests predictions are as accurate as predicting the mean. Values above 1 often suggest that the model’s performance may not be optimal. We prioritize the analysis on males since previous findings suggest a more pronounced emphasis on the COVID effect for this gender, although the overall patterns for females exhibit similarity. For males in the 20-year age brackets, the graph shows a generally good overall forecast accuracy, especially for ages over 20, as colors tend towards blue for middle and older ages, indicating smaller NRMSE values closer to 0 and suggesting better forecast accuracy. No clear scenario preference is evident in the cross-country view across all age groups. In general, Scenario 3 (flattening COVID effect) tends to perform well for middle-aged individuals and, in addition, also Scenario 4 (COVID full effect) for older ages. Substantial variations in scenario performance are observed across different countries and age groups. For younger age groups, Scenario 1 (no COVID effect) performs best in Italy and the Netherlands, where substantial COVID impact was observed. Middle-aged groups demonstrate similarly high performance across all scenarios. Older age groups show stronger scenario differences with a clear preference for Scenarios 2 and 3, indicating better fit. Scenarios do not perform well for those under 19, possibly due to the unique characteristics and weak impact of COVID in this age group. Appendix D contains the same graph with individual ages instead of grouped age buckets for a more detailed overview.
4. Conclusions
To summarize, this research work focused on addressing the challenge of capturing the mortality-related extreme event at the edge of a time series—in particular, COVID-19’s effect on future mortality forecasting.
The key findings of our research include identifying the GAM within APC framework as the most effective method for forecasting future mortality rates across multiple countries. This innovative approach, utilizing a smoothed second-order spline, surpasses traditional stochastic models (e.g., LC) and machine learning techniques (e.g., GBM) in predictive accuracy. By applying the GAM-APC model to data from Germany, Finland, Italy, the Netherlands, and the United States, the study provides valuable cross-country and multi-populational insights into mortality trends. This enables the capture of both universal mortality patterns and country-specific variations, offering a comprehensive understanding of global and localized mortality dynamics. The research develops and evaluates four pandemic impact scenarios (ranging from mild to severe) to forecast the impact of COVID-19 on future mortality rates. It concludes that scenarios assuming a diminishing impact of the pandemic over time are the most consistent, especially for middle-aged and elderly populations.
To ensure a rigorous assessment, these scenarios and their underlying assumptions were thoroughly evaluated and discussed in collaboration with epidemiological experts. This approach including the content of scenarios aligns with existing literature and enhances the credibility of the forecast analysis [42].
Overall, this work contributes to the existing literature by introducing traditional, enhanced, and novel models, comparing different approaches and providing insights into future trends in mortality rates while considering the impact of COVID-19 in a cross-country context. The specific contribution of the GAM approach with the APC framework in this research lies in its novel application for mortality trend forecasting, particularly incorporating the impact of COVID-19 in a multi-populational cross-country fashion.
Despite the current waning impact of COVID-19, it is crucial to acknowledge the lasting importance of historical data and the persisting uncertainties that lie ahead. These factors emphasize the need for ongoing attention in the years to come. It is important to acknowledge that the concept and methodology utilized in this study extend beyond COVID-19, encompassing other events that occur at the edges of time series data. Looking ahead to future research directions, the GAM with APC framework has a promising potential for expanding the feature set by the inclusion of socioeconomic status, income, and education as additional factors, allowing for a more complete understanding of mortality trends.
Author Contributions
Conceptualization, A.N., C.H. and S.P.; methodology, A.N., C.H. and S.P.; formal analysis, A.N.; writing—original draft preparation, A.N.; writing— review and editing, A.N., C.H. and S.P.; visualization, A.N.; supervision, C.H.; funding acquisition, A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data and the code are available at https://doi.org/10.5281/zenodo.13905807.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Data Preparation
This section discusses the methodology employed to enrich existing mortality data obtained from [16], focusing on the number of deaths and population size for recent years absent in the [15] dataset. The primary challenge addressed is the aggregation of data into rough age categories, while the study requires a metric age scale.
The methodology involves several steps. Firstly, weekly population sizes are derived from the mortality dataset followed by extrapolation to annual levels. Using mortality rates and death counts, the weekly population size can be calculated. These weekly data are then aggregated to annual figures. Similarly, weekly death counts are summed to obtain annual totals. To construct annual death counts and populations for individual ages for the aforementioned years, specific procedures were applied, as described below. The methodology ensures that the derived data align with observed mortality patterns within each age group.
Once the weekly population is extrapolated to the annual level by multiplying by a factor of 52, the approach leverages cohort-wise population patterns from previous years (2015–2019) and assumes a similar age distribution for 2020–2023. The initial population course, i.e., for 2020, is created by shifting the population size pattern of 2019 one year forward. This shift leads to an initial gap at age 0 in 2020, which is linearly extrapolated based on data from 2018 and 2019. The resulting population values are adjusted to match observed data within age groups.
A three-stage approach is employed to distribute death counts from grouped to metric age scale on an annual basis. Firstly, averaged weights for each age in each age bucket are computed based on data from the previous five years (2015–2019): . Secondly, these weights are applied to the averaged death counts in each age group to correct for deviations from the mean: . Finally, the corrected death counts are adjusted to ensure equal counts in both grouped and metric versions within each age group: .
The resulting mortality rates are computed by dividing death counts by population size for each individual age and subpopulation. These enriched mortality data are used to impute the [15] dataset for the years 2020–2023. The same procedure is applied across all subpopulations and missing years.
Appendix B. Details on Gradient Boosting Machine
Gradient Boosting is another form of an ensemble learner that is based on the weighted combination of weak predictive learners such as Decision Trees, usually outperforming Random Forest. The model is built stepwise and optimized by a differentiable loss function, minimizing the in-sample loss [43]. It builds the model stepwise, like other boosting methods, and generalizes by allowing optimization of any differentiable loss function. Whereas multiple samples of the original training dataset are used to fit a separate decision tree to each one independent of the others and to combine all trees into a single predictive model in bagging, boosting grows the trees sequentially, meaning the information gained from the previous trees is used to grow the current one. This helps to overcome the major issue of training a single large Decision Tree by possibly resulting in an overfitting problem. The gradient boosting algorithm instead learns by constructing a new model based on the previous one and adding the ith base learner :
The model is improved in such a way that the current residual will be used as an outcome to fit a new Decision Tree and to add this into the originally fitted function with the notion to update the residuals. So, the gradient boosting algorithm fits the new predictor to the residual errors made by the previous predictor. The shrinkage parameter helps to run the process even slower, allowing for more trees and more detailed enhancement of the residuals. All parameters of the Decision Trees undergo optimization through the training of Poisson boosted trees, with the objective of minimizing the negative log-likelihood associated with the Poisson distribution, serving as the designated loss function. Overall, in contrary to the bagging methodology, each tree depends on the previous ones [44]. Even though the gradient boosting keeps on minimizing the errors, this can cause overfitting in cases where there is a lot of noise in the data and is computationally time and memory expensive, especially because trees are built sequentially (not in parallel as Random Forest does). Due to the high flexibility, the gradient boosting algorithm also tends to be harder to tune than Random Forest [43]. In this study, we specifically utilized LightGBM [45], employing Microsoft’s library for implementing these models, which have demonstrated high accuracy in various scenarios [30].
Appendix C. Details on Hyperparameter Optimization
For hyperparameter optimization of the GBM, we used Hyperopt, a Python library that employs the Tree Parzen Estimator (TPE) algorithm. TPE is an efficient method that utilizes a probabilistic model to guide the search for optimal hyperparameters. The TPE workflow can be summarized as follows: First, TPE begins by randomly sampling a few hyperparameter combinations to create an initial set of observations, serving as the starting point for optimization. Next, TPE models the relationship between hyperparameter values and the performance metric (e.g., loss or accuracy), estimating the probability that a configuration will yield better results.
TPE then balances exploration, trying new configurations, and exploitation, focusing on promising configurations based on probabilistic models. It emphasizes configurations likely to lead to better results, similar to how gradient descent focuses on the gradient of the loss function. As TPE evaluates more configurations, it iteratively refines its probabilistic models, making more informed decisions.
By continually balancing exploration and exploitation, TPE efficiently navigates the hyperparameter space, eventually converging on an optimal set of hyperparameters for a given machine learning model. For a deeper understanding of the TPE algorithm and its practical application, refer to [46,47].
As for GAMs, each smooth term has associated smoothing parameters that control the trade-off between fit and smoothness. The mgcv package’s gam() function automates the process of smoothing parameter optimization when the method is set to Restricted Maximum Likelihood (REML). After specifying the model, the mgcv package automatically selects the optimal smoothing parameters by maximizing the restricted likelihood, using an internal Newton–Raphson numerical optimization algorithm. The result is a model with optimally chosen smoothing parameters that balance fit and smoothness according to the restricted likelihood criterion [24].
Appendix D. Additional Results
The analysis in Table A1 highlights the superior in-sample predictive performance of the two-step GBM and GAM models within the APC framework over traditional LC and APC models, with no clear preference between GBM and GAM, across various training periods for different countries.

Table A1.
In-sample RMSE comparison for LC, APC, GBM, and GAM models. LC, APC, and GBM are fitted from 1950 to 2010 (Finland, Italy, Netherlands, US) and 1990 to 2010 (Germany). GAM is fitted from 1990 to 2015 for all countries.
Table A1.
In-sample RMSE comparison for LC, APC, GBM, and GAM models. LC, APC, and GBM are fitted from 1950 to 2010 (Finland, Italy, Netherlands, US) and 1990 to 2010 (Germany). GAM is fitted from 1990 to 2015 for all countries.
| Country | Female | Male | ||||||
|---|---|---|---|---|---|---|---|---|
| LC | APC | GBM | GAM | LC | APC | GBM | GAM | |
| FIN | 0.0045 | 0.0015 | 0.0035 | 0.0011 | 0.0072 | 0.0027 | 0.0066 | 0.0013 |
| DE | 0.0015 | 0.0022 | 0.0004 | 0.001 | 0.0021 | 0.0021 | 0.0007 | 0.001 |
| ITA | 0.0025 | 0.0021 | 0.001 | 0.001 | 0.0012 | 0.0025 | 0.0008 | 0.001 |
| NLD | 0.0019 | 0.0032 | 0.0014 | 0.001 | 0.0017 | 0.0015 | 0.0014 | 0.001 |
| US | 0.0014 | 0.0033 | 0.0005 | 0.0013 | 0.0017 | 0.0028 | 0.0004 | 0.0011 |
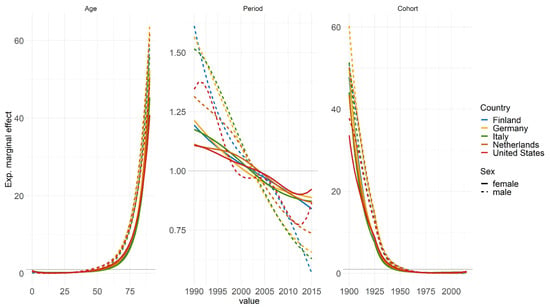
Figure A1.
Estimated marginal effects of age, period, and cohort on mortality rates, differentiated by countries and genders. The horizontal lines represent the level of no effect. The GAM model was fitted for the years 1990–2015 and ages 0–90.
GAM enables the interpretation of exponential marginal effects, with age, period, and cohort being the components analyzed and differentiated by countries and gender. Notably, while the descending trend in period effect for women is relatively consistent and shallow across all countries, men exhibit a much steeper decline, indicating a stronger improvement in mortality rates over the years. There are noticeable increases in mortality rates for Italy and the US in recent years, particularly for US males, which may be associated with factors such as the opioid crisis.
The heatmap depicted in Figure A2 offers a detailed examination on an individual age basis for assessing the scenario analysis across the years 2022 and 2023.
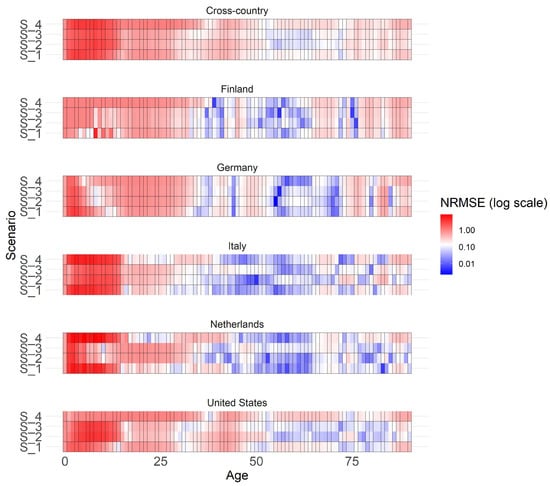
Figure A2.
Heatmap showing the normalized RMSE of scenarios for extrapolated years 2022 and 2023 for males across different countries and individual ages.
References
- Lee, R.D.; Carter, L.R. Modeling and forecasting US mortality. J. Am. Stat. Assoc. 1992, 87, 659–671. [Google Scholar]
- Bjerre, D.S. Tree-based machine learning methods for modeling and forecasting mortality. ASTIN Bull. J. IAA 2022, 52, 765–787. [Google Scholar] [CrossRef]
- Levantesi, S.; Pizzorusso, V. Application of machine learning to mortality modeling and forecasting. Risks 2019, 7, 26. [Google Scholar] [CrossRef]
- Schnürch, S.; Kleinow, T.; Korn, R.; Wagner, A. The impact of mortality shocks on modelling and insurance valuation as exemplified by COVID-19. Ann. Actuar. Sci. 2022, 16, 498–526. [Google Scholar] [CrossRef]
- Richman, R.; Wüthrich, M.V. A neural network extension of the Lee–Carter model to multiple populations. Ann. Actuar. Sci. 2021, 15, 346–366. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized additive models: Some applications. J. Am. Stat. Assoc. 1987, 82, 371–386. [Google Scholar] [CrossRef]
- Bray, I. Application of Markov chain Monte Carlo methods to projecting cancer incidence and mortality. J. R. Stat. Soc. Ser. C Appl. Stat. 2002, 51, 151–164. [Google Scholar] [CrossRef]
- Clements, M.S.; Armstrong, B.K.; Moolgavkar, S.H. Lung cancer rate predictions using generalized additive models. Biostatistics 2005, 6, 576–589. [Google Scholar] [CrossRef]
- Bashir, S.A.; Estève, J. Projecting cancer incidence and mortality using Bayesian age-period-cohort models. J. Epidemiol. Biostat. 2001, 6, 287–296. [Google Scholar]
- Dodds, S.; Williams, L.J.; Roguski, A.; Vennelle, M.; Douglas, N.J.; Kotoulas, S.-C.; Riha, R.L. Mortality and morbidity in obstructive sleep apnoea–hypopnoea syndrome: Results from a 30-year prospective cohort study. ERJ Open Res. 2020, 6, 00057–2020. [Google Scholar] [CrossRef]
- Clèries, R.; Ribes, J.; Esteban, L.; Martinez, J.M.; Borras, J.M. Time trends of breast cancer mortality in Spain during the period 1977–2001 and Bayesian approach for projections during 2002–2016. Ann. Oncol. 2006, 17, 1783–1791. [Google Scholar] [CrossRef] [PubMed]
- Robben, J.; Antonio, K.; Devriendt, S. Assessing the impact of the COVID-19 shock on a stochastic multi-population mortality model. Risks 2022, 10, 26. [Google Scholar] [CrossRef]
- Barigou, K.; Loisel, S.; Salhi, Y. Parsimonious predictive mortality modeling by regularization and cross-validation with and without Covid-type effect. Risks 2020, 9, 5. [Google Scholar] [CrossRef]
- Clayton, D.; Schifflers, E. Models for temporal variation in cancer rates. II: Age–period–cohort models. Stat. Med. 1987, 6, 469–481. [Google Scholar] [CrossRef] [PubMed]
- Human Mortality Database; University of California, Berkeley, CA, USA; Max Planck Institute for Demographic Research, Max Planck Society for the Advancement of Science e.V., Munich, Germany. 2024. Available online: https://www.mortality.org/ (accessed on 1 March 2024).
- Short-term Mortality Fluctuations (STMF); University of California, Berkeley, CA, USA; Max Planck Institute for Demographic Research, Max Planck Society for the Advancement of Science e.V., Munich, Germany. 2024. Available online: https://www.mortality.org/ (accessed on 1 March 2024).
- Brouhns, N.; Denuit, M.; Vermunt, J.K. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insur. Math. Econ. 2002, 31, 373–393. [Google Scholar] [CrossRef]
- Villegas Ramirez, A. Mortality: Modelling, Socio-Economic Differences and Basis Risk. Ph.D. Dissertation, City University London, London, UK, 2015. [Google Scholar]
- Hobcraft, J.; Menken, J.; Preston, S. Age, Period, and Cohort Effects in Demography: A Review; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Currie, I.D.; Durban, M.; Eilers, P.H. Smoothing and forecasting mortality rates. Stat. Model. 2004, 4, 279–298. [Google Scholar] [CrossRef]
- Yan, J.; Guszcza, J.; Flynn, M.; Wu, C.S.P. Applications of the offset in property-casualty predictive modeling. Casualty Actuar. Soc.-Forum 2009, 1, 366–385. [Google Scholar]
- Weigert, M.; Bauer, A.; Gernert, J.; Karl, M.; Nalmpatian, A.; Küchenhoff, H.; Schmude, J. Semiparametric APC analysis of destination choice patterns: Using generalized additive models to quantify the impact of age, period, and cohort on travel distances. Tour. Econ. 2022, 28, 1377–1400. [Google Scholar] [CrossRef]
- Bauer, A.; Weigert, M.; Jalal, H. APCtools: Descriptive and Model-based Age-Period-Cohort Analysis. J. Open Source Softw. 2022, 7, 4056. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and testing linear models with multiple structural changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Zeileis, A.; Kleiber, C.; Kramer, W.; Hornik, K. Testing and Dating of Structural Changes in Practice, Computational Statistics and Data Analysis. Comput. Stat. Data Anal. 2003, 44, 109–123. [Google Scholar] [CrossRef]
- Ramirez Villegas, M.A.; Millossovich, P.; Kaishev, V. StMoMo: An R Package for Stochastic Mortality Modelling. 2016. Available online: Https://cran.r-project.org/web/packages/StMoMo/StMoMo.pdf (accessed on 25 July 2024).
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; R package version 1.8-23, 2015; Available online: https://cran.r-project.org/web/packages/mgcv/index.html (accessed on 1 October 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bergstra, J.; Komer, B.; Eliasmith, C.; Yamins, D.; Cox, D.D. Hyperopt: A python library for model selection and hyperparameter optimization. Comput. Sci. Discov. 2015, 8, 014008. [Google Scholar] [CrossRef]
- Hamilton, A.D.; Jang, J.B.; Patrick, M.E.; Schulenberg, J.E.; Keyes, K.M. Age, period and cohort effects in frequent cannabis use among US students: 1991–2018. Addiction 2019, 114, 1763–1772. [Google Scholar] [CrossRef]
- Crimmins, E.M.; Shim, H.; Zhang, Y.S.; Kim, J.K. Differences between men and women in mortality and the health dimensions of the morbidity process. Clin. Chem. 2019, 65, 135–145. [Google Scholar] [CrossRef]
- Trovato, F.; Lalu, N.M. Narrowing sex differentials in life expectancy in the industrialized world: Early 1970’s to early 1990’s. Soc. Biol. 1996, 43, 20–37. [Google Scholar] [CrossRef]
- Rosella, L.C.; Calzavara, A.; Frank, J.W.; Fitzpatrick, T.; Donnelly, P.D.; Henry, D. Narrowing mortality gap between men and women over two decades: A registry-based study in Ontario, Canada. BMJ Open 2016, 6, e012564. [Google Scholar] [CrossRef]
- Perls, T.T.; Fretts, R.C. Why Women Live Longer than Men-What gives women the extra years? Sci. Am. 1998, 2, 100–103. [Google Scholar]
- Sudre, C.H.; Murray, B.; Varsavsky, T.; Graham, M.S.; Penfold, R.S.; Bowyer, R.C.E.; Pujol, J.C.; Klaser, K.; Antonelli, M.; Canas, L.S.; et al. Attributes and predictors of Long-COVID. Nat. Med. 2021, 27, 626–631. [Google Scholar] [CrossRef]
- Kunzler, A.M.; Röthke, N.; Günthner, L.; Stoffers-Winterling, J.; Tüscher, O.; Coenen, M.; Rehfuess, E.; Schwarzer, G.; Binder, H.; Schmucker, C.; et al. Mental burden and its risk and protective factors during the early phase of the SARS-CoV-2 pandemic: Systematic review and meta-analyses. Glob. Health 2021, 17, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef] [PubMed]
- Johns Hopkins University. COVID-19 Dashboard. 2021. Available online: https://coronavirus.jhu.edu/map.html (accessed on 1 October 2024).
- Boudourakis, L.; Uppal, N. Decreased COVID-19 mortality—A cause for optimism. JAMA Intern. Med. 2021, 181, 478–479. [Google Scholar] [CrossRef] [PubMed]
- Telenti, A.; Arvin, A.; Corey, L.; Corti, D.; Diamond, M.S.; Garcìa-Sastre, A.; Garry, R.F.; Holmes, E.C.; Pang, P.S.; Virgin, H.W. After the pandemic: Perspectives on the future trajectory of COVID-19. Nature 2021, 596, 495–504. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Deprez, P.; Shevchenko, P.V.; Wüthrich, M.V. Machine learning techniques for mortality modeling. Eur. Actuar. J. 2017, 7, 337–352. [Google Scholar] [CrossRef]
- Oram, E.; Dash, P.B.; Naik, B.; Nayak, J.; Vimal, S.; Nataraj, S.K. Light gradient boosting machine-based phishing webpage detection model using phisher website features of mimic URLs. Pattern Recognit. Lett. 2021, 152, 100–106. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems 2011, Granada, Spain, 12–14 December 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).