Scoring Individual Moral Inclination for the CNI Test
Abstract
1. Introduction
1.1. Item Response Theory
1.2. Moral Dilemmas and CNI Model
2. Methods
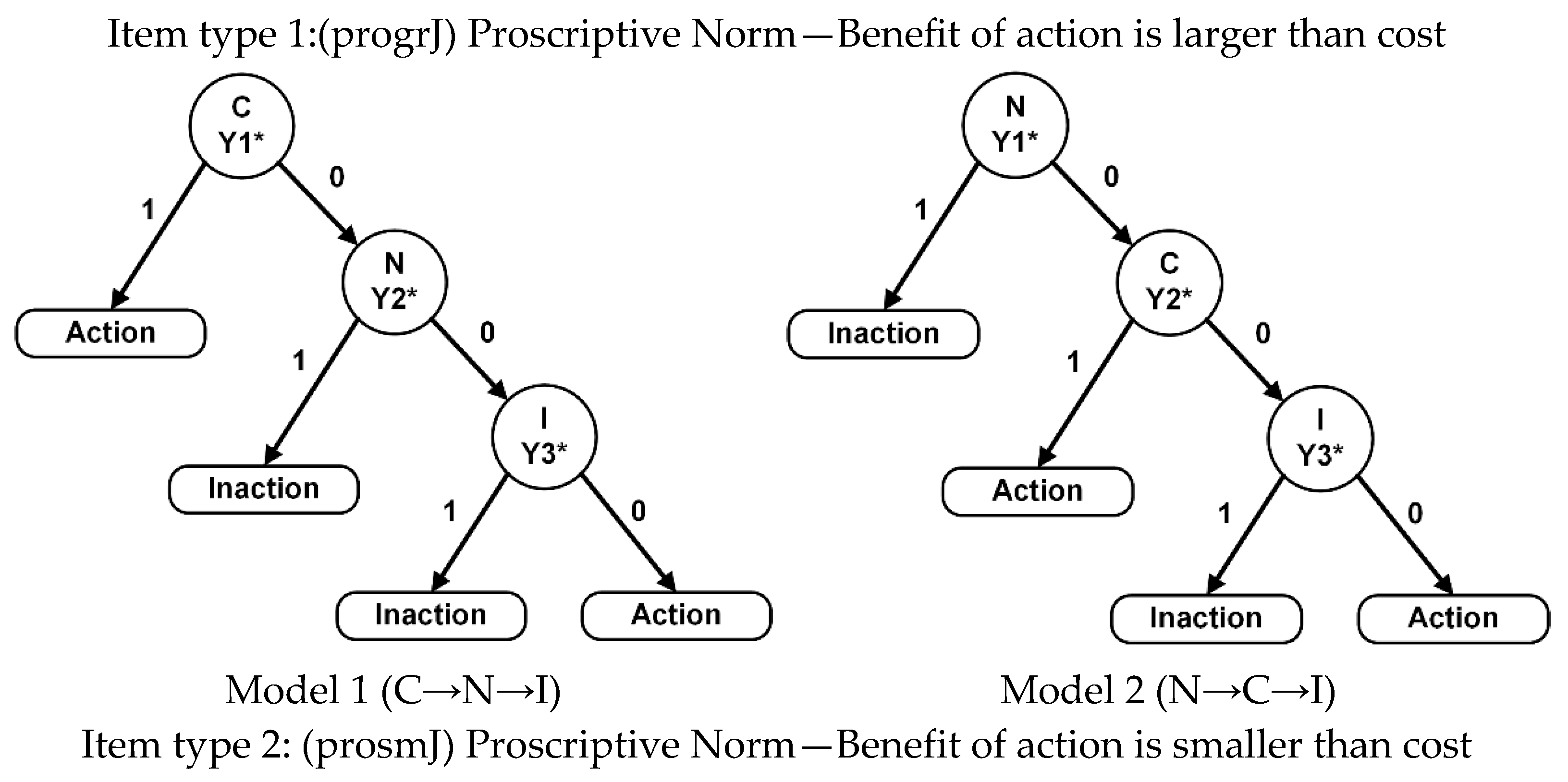
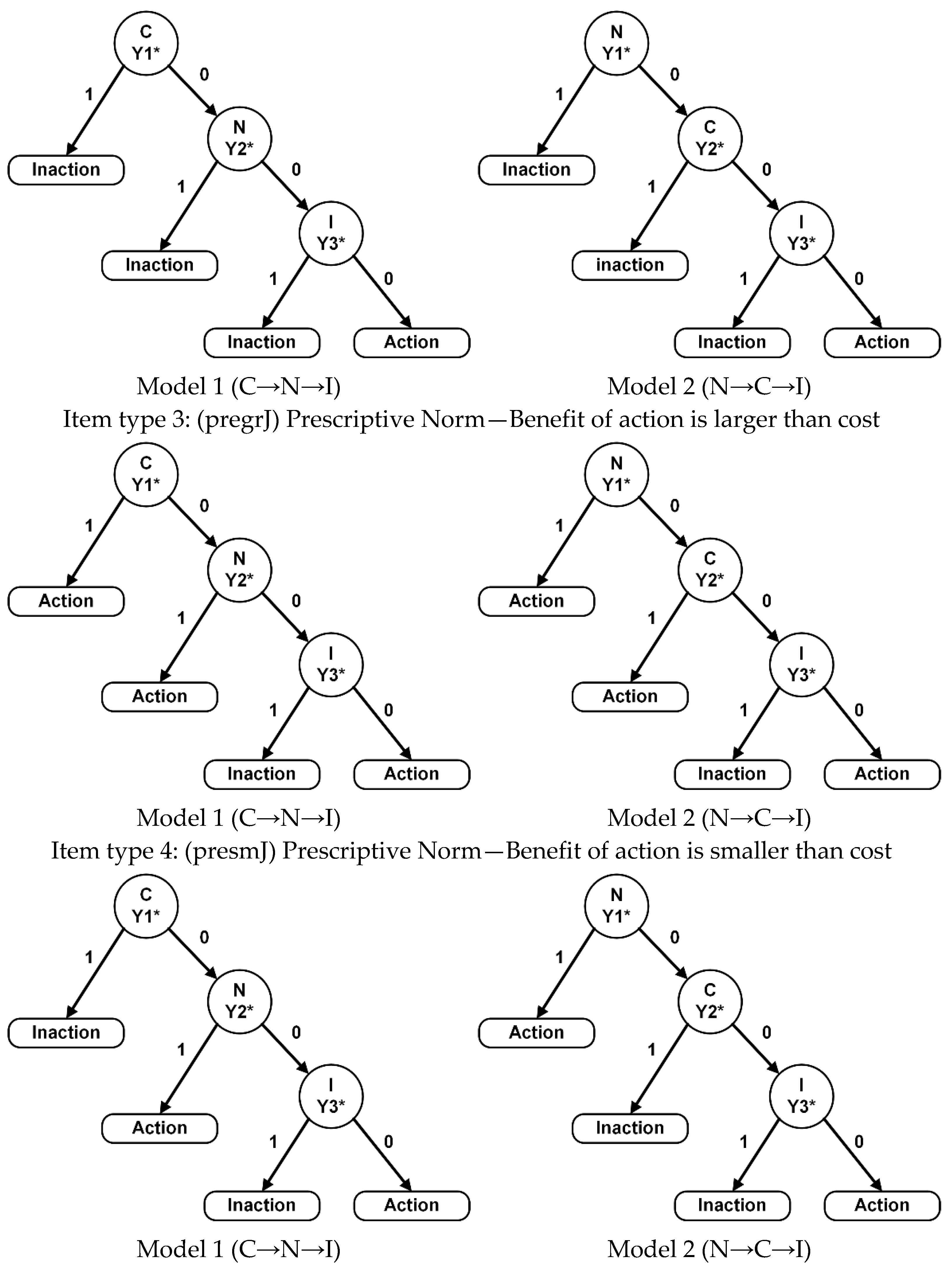
2.1. The CNI Model
2.2. The Proposed Approach
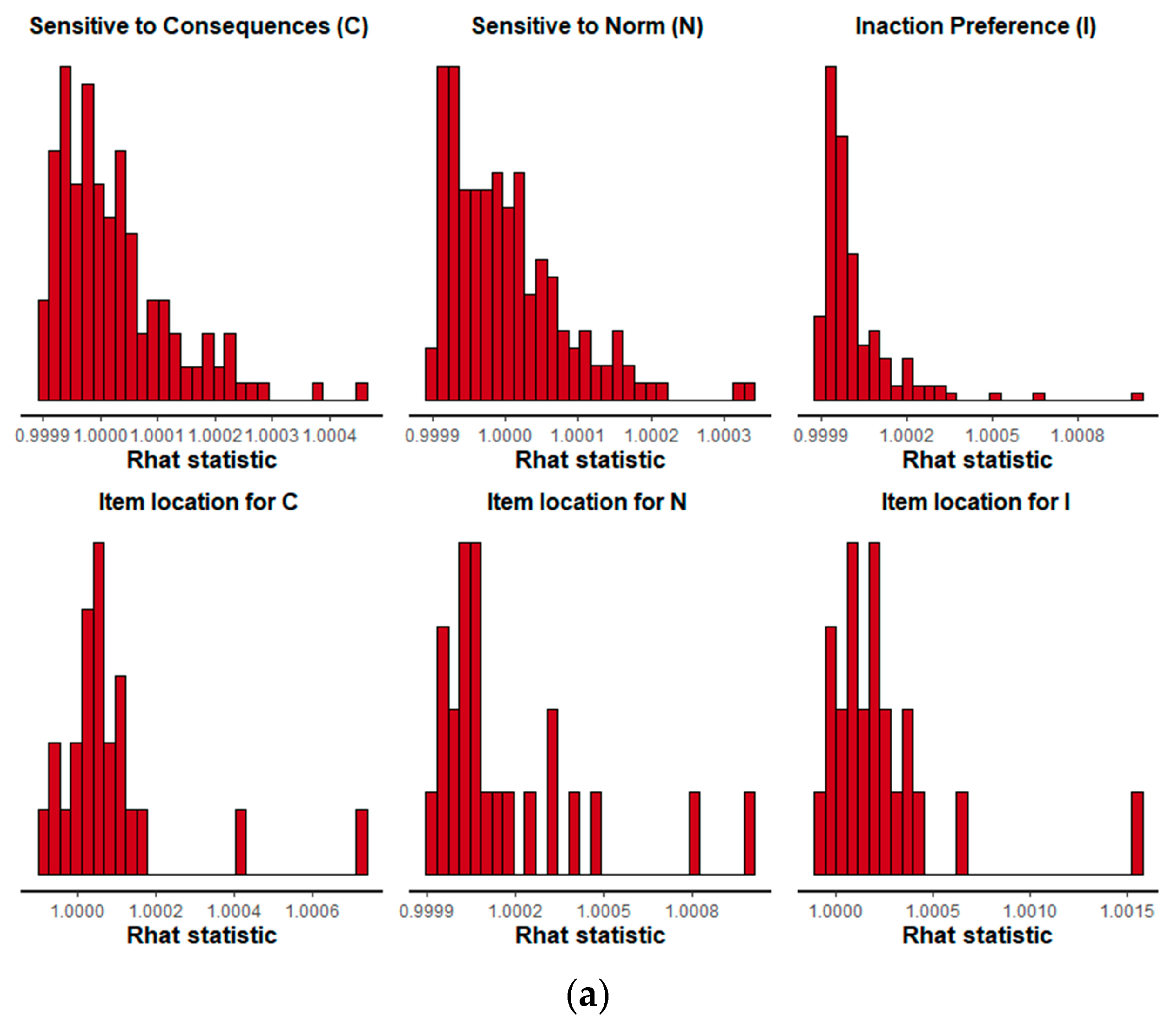
2.3. Data Analysis
3. Results
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Embretson, S.E.; Reise, S.P. Item Response Theory for Psychologists; L. Erlbaum Associates: Mahwah, NJ, USA, 2000. [Google Scholar]
- Thissen, D. Marginal maximum likelihood estimation for the one-parameter logistic model. Psychometrika 1982, 47, 175–186. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- De Boeck, P.; Partchev, I. IRTrees: Tree-Based Item Response Models of the GLMM Family. J. Stat. Softw. Code Snippets 2012, 48, 1–28. [Google Scholar] [CrossRef]
- Böckenholt, U.; Meiser, T. Response style analysis with threshold and multi-process IRT models: A review and tutorial. Br. J. Math. Stat. Psychol. 2017, 70, 159–181. [Google Scholar] [CrossRef] [PubMed]
- Jeon, M.; De Boeck, P.; van der Linden, W. Modeling answer change behavior: An application of a generalized item response tree model. J. Educ. Behav. Stat. 2017, 42, 467–490. [Google Scholar] [CrossRef]
- Ma, W. A diagnostic tree model for polytomous responses with multiple strategies. Br. J. Math. Stat. Psychol. 2019, 72, 61–82. [Google Scholar] [CrossRef]
- Ma, W.; Guo, W. Cognitive diagnosis models for multiple strategies. Br. J. Math. Stat. Psychol. 2019, 72, 370–392. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, D. Would You Kill the Fat Man? The Trolley Problem and What Your Answer Tells Us about Right and Wrong; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Körner, A.; Deutsch, R.; Gawronski, B. Using the CNI model to investigate individual differences in moral dilemma judgments. Personal. Soc. Psychol. Bull. 2020, 46, 1392–1407. [Google Scholar] [CrossRef]
- McHugh, C.; McGann, M.; Igou, E.R.; Kinsella, E.L. Searching for moral dumbfounding: Identifying measurable indicators of moral dumbfounding. Collabra Psychol. 2017, 3, 23. [Google Scholar] [CrossRef]
- Haidt, J.; Bjorklund, F.; Murphy, S. Moral Dumbfounding: When Intuition Finds No Reason; University of Virginia: Charlottesville, VA, USA, 2000; pp. 191–221, Unpublished manuscript. [Google Scholar]
- Bentham, J. A Utilitarian View, Animal Rights and Human Obligations; Athlone: London, UK, 1789; pp. 25–26. [Google Scholar]
- Kant, I. Foundations of the Metaphysics of Morals; Beck, L.W., Translator. Original work published 1785; Bobbs-Merrill: Indianapolis, IN, USA, 1959. [Google Scholar]
- Greene, J.D.; Sommerville, R.B.; Nystrom, L.E.; Darley, J.M.; Cohen, J.D. An fMRI investigation of emotional engagement in moral judgment. Science 2001, 293, 2105–2108. [Google Scholar] [CrossRef]
- Gawronski, B.; Armstrong, J.; Conway, P.; Friesdorf, R.; Hütter, M. Consequences, norms, and generalized inaction in moral dilemmas: The CNI model of moral decision-making. J. Personal. Soc. Psychol. 2017, 113, 343–376. [Google Scholar] [CrossRef]
- Conway, P.; Goldstein-Greenwood, J.; Polacek, D.; Greene, J.D. Sacrificial utilitarian judgments do reflect concern for the greater good: Clarification via process dissociation and the judgments of philosophers. Cognition 2018, 179, 241–265. [Google Scholar] [CrossRef]
- Conway, P.; Gawronski, B. Deontological and utilitarian inclinations in moral decision making: A process dissociation approach. J. Personal. Soc. Psychol. 2013, 104, 216. [Google Scholar] [CrossRef] [PubMed]
- van den Bos, K.; Müller, P.A.; Damen, T. A Behavioral Disinhibition Hypothesis of Interventions in Moral Dilemmas. Emot. Rev. 2011, 3, 281–283. [Google Scholar] [CrossRef]
- Spranca, M.; Minsk, E.; Baron, J. Omission and commission in judgment and choice. J. Exp. Soc. Psychol. 1991, 27, 76–105. [Google Scholar] [CrossRef]
- Kahane, G.; Everett, J.A.; Earp, B.D.; Farias, M.; Savulescu, J. ‘Utilitarian’judgments in sacrificial moral dilemmas do not reflect impartial concern for the greater good. Cognition 2015, 134, 193–209. [Google Scholar] [CrossRef] [PubMed]
- Marshall, J.; Watts, A.L.; Lilienfeld, S.O. Do psychopathic individuals possess a misaligned moral compass? A meta-analytic examination of psychopathy’s relations with moral judgment. Personal. Disord. Theory Res. Treat. 2018, 9, 40–50. [Google Scholar] [CrossRef]
- Patil, I. Trait psychopathy and utilitarian moral judgement: The mediating role of action aversion. J. Cogn. Psychol. 2015, 27, 349–366. [Google Scholar] [CrossRef]
- Pletti, C.; Lotto, L.; Buodo, G.; Sarlo, M. It’s immoral, but I’d do it! Psychopathy traits affect decision-making in sacrificial dilemmas and in everyday moral situations. Br. J. Psychol. 2017, 108, 351–368. [Google Scholar] [CrossRef]
- Luke, D.M.; Gawronski, B. Psychopathy and moral dilemma judgments: A CNI model analysis of personal and perceived societal standards. Soc. Cogn. 2021, 39, 41–58. [Google Scholar] [CrossRef]
- Gawronski, B.; Conway, P.; Armstrong, J.; Friesdorf, R.; Hütter, M. Effects of incidental emotions on moral dilemma judgments: An analysis using the CNI model. Emotion 2018, 18, 989–1008. [Google Scholar] [CrossRef]
- Białek, M.; Paruzel-Czachura, M.; Gawronski, B. Foreign language effects on moral dilemma judgments: An analysis using the CNI model. J. Exp. Soc. Psychol. 2019, 85, 103855. [Google Scholar] [CrossRef]
- Białek, M.; Muda, R.; Stewart, K.; Niszczota, P.; Pieńkosz, D. Thinking in a foreign language distorts allocation of cognitive effort: Evidence from reasoning. Cognition 2020, 205, 104420. [Google Scholar] [CrossRef]
- Zhang, L.; Kong, M.; Li, Z.; Zhao, X.; Gao, L. Chronic stress and moral decision-making: An exploration with the CNI model. Front. Psychol. 2018, 9, 1702. [Google Scholar] [CrossRef] [PubMed]
- Luke, D.M.; Gawronski, B. Political ideology and moral dilemma judgments: An analysis using the CNI model. Personal. Soc. Psychol. Bull. 2021, 47, 1520–1531. [Google Scholar] [CrossRef]
- Kroneisen, M.; Heck, D.W. Interindividual differences in the sensitivity for consequences, moral norms, and preferences for inaction: Relating basic personality traits to the CNI model. Personal. Soc. Psychol. Bull. 2020, 46, 1013–1026. [Google Scholar] [CrossRef]
- Erdfelder, E.; Auer, T.S.; Hilbig, B.E.; Aßfalg, A.; Moshagen, M.; Nadarevic, L. Multinomial processing tree models: A review of the literature. Z. Psychol./J. Psychol. 2009, 217, 108–124. [Google Scholar] [CrossRef]
- Galesic, M.; Bosnjak, M. Effects of questionnaire length on participation and indicators of response quality in a web survey. Public Opin. Q. 2009, 73, 349–360. [Google Scholar] [CrossRef]
- Liu, C.; Liao, J. CAN algorithm: An individual level approach to identify consequence and norm sensitivities and overall action/inaction preferences in moral decision-making. Front. Psychol. 2021, 11, 547916. [Google Scholar] [CrossRef] [PubMed]
- Böckenholt, U. Modeling motivated misreports to sensitive survey questions. Psychometrika 2014, 79, 515–537. [Google Scholar] [CrossRef]
- Betancourt, M. Identifying the Optimal Integration Time in Hamiltonian Monte Carlo. arXiv 2016, arXiv:1601.00225. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 1, 1539–1623. [Google Scholar]
- Stan Development Team. RStan: The R interface to Stan. 2020. Available online: http://mc-stan.org/ (accessed on 3 July 2023).
- Béguin, A.A.; Glas, C.A.W. MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika 2001, 66, 541–561. [Google Scholar] [CrossRef]
- Luo, Y.; Jiao, H. Using the Stan program for Bayesian item response theory. Educ. Psychol. Meas. 2018, 78, 384–408. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Gabry, J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2015, 27, 1413–1432. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Haidt, J. The emotional dog and its rational tail: A social intuitionist approach to moral judgment. Psychol. Rev. 2001, 108, 814. [Google Scholar] [CrossRef]
- Kohlberg, L. Stages of Moral Development as a Basis for Moral Education; Center for Moral Education, Harvard University: Cambridge, UK, 1971; pp. 24–84. [Google Scholar]

| ELPD LOO | ELPD WAIC | |||
|---|---|---|---|---|
| Estimate | SE | Estimate | SE | |
| Model 1 (CNI) | −1651.6 | 34.2 | −1642.3 | 33.9 |
| Model 2 (NCI) | −3894.1 | 81.0 | −3585.5 | 75.6 |
| CNI Model Parameters | NCI Model Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Item Type | Item No. | ||||||
| progrJ: Proscriptive Norm— Benefit of action is larger than cost | 1 | 0.37 | −0.94 | 0.71 | −0.65 | 1.63 | −1.06 |
| 2 | 2.37 | −1.71 | 0.60 | −0.04 | −0.64 | −0.71 | |
| 3 | 1.25 | −1.14 | 1.54 | −0.99 | 0.44 | −0.67 | |
| 4 | 4.82 | −1.19 | 1.83 | 0.54 | −1.33 | 1.43 | |
| 5 | 1.76 | 0.45 | −0.36 | 1.55 | 1.90 | −0.91 | |
| 6 | 5.68 | −0.71 | −0.82 | 2.68 | −1.45 | −0.25 | |
| prosmJ: Proscriptive Norm— Benefit of action is smaller than cost | 7 | 0.03 | −0.16 | 2.57 | −0.62 | 0.75 | 2.28 |
| 8 | 2.77 | −1.93 | 1.08 | 1.78 | −1.64 | 0.92 | |
| 9 | 3.14 | −0.86 | 1.54 | 2.07 | −0.50 | 1.40 | |
| 10 | 1.42 | −1.26 | 0.93 | 0.75 | −0.85 | 0.70 | |
| 11 | −0.36 | −1.30 | 1.03 | −0.73 | −0.77 | 0.67 | |
| 12 | 0.90 | −1.09 | 0.18 | 0.24 | −0.75 | 0.24 | |
| pregrJ: Prescriptive Norm— Benefit of action is larger than cost | 13 | −0.70 | 0.25 | −1.84 | −1.25 | 1.24 | −1.92 |
| 14 | 3.73 | −0.99 | −1.34 | 2.69 | −0.92 | −1.47 | |
| 15 | 3.36 | −0.24 | −0.63 | 1.96 | −0.02 | −0.87 | |
| 16 | −0.14 | −0.84 | −1.40 | −0.77 | −0.29 | −1.47 | |
| 17 | 0.39 | −1.22 | −1.48 | −0.47 | −0.71 | −1.70 | |
| 18 | −1.34 | −0.07 | −2.35 | −1.64 | 0.48 | −2.35 | |
| presmJ: Prescriptive Norm— Benefit of action is smaller than cost | 19 | 0.37 | 1.89 | 1.04 | 0.31 | 2.93 | 0.91 |
| 20 | 1.56 | −1.60 | −0.96 | −0.55 | 0.04 | 1.05 | |
| 21 | 0.80 | −1.34 | −1.55 | −1.06 | 0.76 | 1.10 | |
| 22 | 5.02 | −1.98 | −1.84 | 0.12 | −2.11 | −1.54 | |
| 23 | 0.97 | 0.15 | 1.80 | 0.67 | 3.19 | 3.52 | |
| 24 | 4.52 | −1.87 | −2.13 | −0.31 | −1.82 | −1.02 | |
| CNI Model | NCI Model | |||||
|---|---|---|---|---|---|---|
| Mean | −0.26 | 0.12 | 0.01 | −0.04 | 0.00 | 0.01 |
| Standard deviation | 1.58 | 1.84 | 1.10 | 1.55 | 1.85 | 1.09 |
| Minimum | −2.84 | −3.74 | −4.04 | −3.34 | −3.79 | −3.87 |
| Maximum | 4.56 | 2.75 | 2.48 | 3.47 | 3.49 | 2.32 |
| C-Original | N-Original | I-Original | Psychopathy | |
|---|---|---|---|---|
| C1 | 0.848 *** | 0.144 | 0.146 | −0.288 *** |
| N1 | 0.163 * | 0.826 *** | 0.237 ** | −0.563 *** |
| I1 | 0.147 | 0.233 ** | 0.499 *** | −0.258 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lugu, B.; Ma, W.; Han, H. Scoring Individual Moral Inclination for the CNI Test. Stats 2024, 7, 894-905. https://doi.org/10.3390/stats7030054
Chen Y, Lugu B, Ma W, Han H. Scoring Individual Moral Inclination for the CNI Test. Stats. 2024; 7(3):894-905. https://doi.org/10.3390/stats7030054
Chicago/Turabian StyleChen, Yi, Benjamin Lugu, Wenchao Ma, and Hyemin Han. 2024. "Scoring Individual Moral Inclination for the CNI Test" Stats 7, no. 3: 894-905. https://doi.org/10.3390/stats7030054
APA StyleChen, Y., Lugu, B., Ma, W., & Han, H. (2024). Scoring Individual Moral Inclination for the CNI Test. Stats, 7(3), 894-905. https://doi.org/10.3390/stats7030054








