Redefining Significance: Robustness and Percent Fragility Indices in Biomedical Research

Abstract

The p-value has long been the standard for statistical significance in scientific research, but this binary approach often fails to consider the nuances of statistical power and the potential for large sample sizes to show statistical significance despite trivial treatment effects. Including a statistical fragility assessment can help overcome these limitations. One common fragility metric is the fragility index, which assesses statistical fragility by incrementally altering the outcome data in the intervention group until the statistical significance flips. The robustness index takes a different approach by maintaining the integrity of the underlying data distribution while examining changes in the p-value as the sample size changes. The percent fragility index is another useful alternative that is more precise than the fragility index and is more uniformly applied to both the intervention and control groups. Incorporating these fragility metrics into routine statistical procedures could address the reproducibility crisis and increase research efficacy. Using these fragility indices can be seen as a step toward a more mature phase of statistical reasoning, where significance is a multi-faceted and contextually informed judgment.

1. Introduction

In scientific research, the p-value has long been the gatekeeper of statistical significance, distinguishing the signal from the noise. Traditionally, a p-value less than 0.05 has been the threshold for deeming results significant. Yet, this binary approach often fails to consider the nuances of statistical power and the potential for large sample sizes to show statistical significance despite trivial treatment effects [1]. Assigning an arbitrary, fixed p-value threshold of 0.05 has been thought to be a significant reason for the reproducibility crisis in medicine [2].

To address these reproducibility concerns, researchers have developed various measures of statistical fragility for 2 × 2 contingency tables, such as the unit fragility index (UFI) [3], fragility index (FI) [4], fragility quotient (FQ) [5], and percent fragility index (pFI) [6]. These measures aim to quantify the robustness of research findings by assessing the impact of small changes in data on statistical significance. However, all of these measures require the modification of the underlying distribution of the raw data. They measure how stable a p-value threshold of 0.05 is to alterations in the underlying distribution of the research data. While the UFI and FI both increase with an increasing sample size, the pFI and FQ quantify the statistical fragility while considering changes in the sample size.

The robustness index (RI) takes a different approach to statistical fragility [7]. It also looks at the stability of a p-value threshold of 0.05. However, unlike the UFI, FI, FQ, and pFI, it maintains the integrity of the distribution of the underlying data. The RI does not require any manipulation of data distribution but instead looks at changes in the p-value as the sample size increases or decreases. The distribution of the study outcomes remains fixed; only the sample size changes. The RI thus allows for a more standardized way to compare research studies with different sample sizes. By maintaining the integrity of raw data distributions and not artificially manipulating data, the RI can fill a critical gap in the current knowledge of statistical fragility and improve the reproducibility of medical research.

This perspective article demonstrates how each primary statistical fragility metric is calculated. Two case examples show how these various fragility metrics are applied. Finally, the clinical application and importance of the fragility metrics are discussed.

2. Calculation of the Fragility Indices

The fragility indices are all similar in that they look at the standard 2 × 2 contingency table, which compares a binary intervention with a binary outcome. A single sample of the population of interest is evaluated. This sample is divided into two groups based on whether or not they receive the investigational treatment or serve as a control group. The outcome is typically divided into variants of a good outcome versus a neutral or bad outcome.

2.1. Case Study #1: Small Sample Size

A research study was conducted on 30 cancer patients to evaluate the effectiveness of allopurinol in preventing mucositis. This sample was evenly divided into two groups: those who received the intervention (allopurinol mouthwashes) and those who received a placebo. The good outcome was defined as no mucositis, and the bad outcome was the development of mucositis (either mild or moderate grade). In the allopurinol group, 11 patients did not develop mucositis, and 4 did. In the placebo group, eight patients did not develop mucositis, and seven did [8].

2.1.1. Calculation of the Unit Fragility Index

First, the 2 × 2 contingency table is set according to the study’s outcomes (

Table 1. Baseline outcomes for the case study.

Treatment Groups	No Mucositis	Mucositis	Total
Allopurinol	11	4	15
Placebo	8	7	15
Total	19	11	30

p = 0.4497.

).

The p-value of the original outcomes is calculated using the Fisher exact test (p = 0.4497). Then, the data are incrementally manipulated until the statistical significance flips from nonsignificant to significant. In this case, cell a (the top left cell) is increased by one. The other cells are adjusted to maintain the marginal totals: cell b (top right) is decreased by one, cell c (bottom left) is decreased by one, and cell d (bottom right) is increased by one. In standard notation, this is written as a, b, c, d = (12, 3, 7, 8). The Fisher exact test is then performed on the manipulated data (p = 0.1281). Since the results remain statistically nonsignificant, the incremental manipulation of the data is repeated. Each cell in the table is now altered by 2, resulting in a table of (13, 2, 6, 9). The p-value is now 0.0209, flipping the results to statistical significance. Because it took two unit changes to flip the significance, the UFI = 2, as shown in

Table 2. Calculation of the Unit Fragility Index.

Treatment Groups	No Mucositis	Mucositis	Total
Allopurinol	13 (11 + 2)	2 (4 − 2)	15
Placebo	6 (8 − 2)	9 (7 + 2)	15
Total	19	11	30

p = 0.0209 and UFI = 2.

.

Note that for the UFI, the marginal totals for both the rows and columns remain unchanged.

2.1.2. Calculation of the Fragility Index

As originally defined, the FI is only applied to research outcomes with a statistically significant p-value. However, it has since been applied to both statistically significant and statistically nonsignificant research findings. When applied to statistically nonsignificant research findings, the term “reverse fragility index” is sometimes utilized [9]. Regardless, the principle remains the same: the FI (or reverse FI) represents the integer value required to flip the study’s significance.

Using the same case study as before, the 2 × 2 contingency table is set according to the study’s outcomes, and the p-value is calculated using the Fisher exact test. Working incrementally, the outcomes of only the interventional group (in this case, those receiving allopurinol) are altered until the significance flips. When the contingency table is organized with the outcomes in the columns and the treatment groups in the rows, the marginal totals for the rows remain fixed, but the marginal totals for the columns change. For our example, the results remain nonsignificant after one increment (12, 3, 8, 7) (p = 0.2451). After two increments (13, 2, 8, 7), the results are still nonsignificant (p = 0.1086). The results are statistically significant after three increments (14, 1, 8, 7) (p = 0.0352), as shown in

Table 3. Calculation of the fragility index.

Treatment Groups	No Mucositis	Mucositis	Total
Allopurinol	14 (11 + 3)	1 (4 − 3)	15
Placebo	8	7	15
Total	22	8	30

p = 0.0352 and FI = 3.

. In this case, the FI = 3.

Note that the FI is applied only to one row, keeping the marginal total for that row fixed but changing the marginal totals for the columns. This is in contrast to the UFI, where changes are applied to all four cells, keeping all the marginal totals fixed.

2.1.3. Calculation of the Percent Fragility Index

The pFI represents the average percent change in each cell required to flip the significance. Similar to the UFI, the marginal totals remain fixed. However, the pFI increments each cell on a continuous scale rather than by integer values. This increment, a decimal value rather than an integer, is a variation in the UFI. The original description of the pFI called for dividing this value by the maximum value of all four cells; in this scenario, the value was divided by 11. However, a more cautious approach would be multiplying the exact FI by 4 and dividing by the total sample size to give the average percentage that each cell must change to flip the significance, as shown in Equation (1).

pFI = (exact FI × 4)/n

(1)

where n = sample size.

The 2 × 2 contingency table is set according to the study’s outcomes using the same data. The chi-square test is utilized for the pFI calculation because it does not require integer values, unlike the Fisher exact test. This allows for the incremental adjustment of the cell values by decimal amounts, which is necessary for precisely calculating the pFI. For this specific calculation, Yates’ continuity correction appears overly conservative and thus is not recommended [10,11,12]. Therefore, to standardize the pFI calculation, Yates’s continuity correction is not utilized. For Table 1, using the chi-square test, the p-value is 0.2557.

Working incrementally, the cells are adjusted until the statistical significance flips. Note that the increment is always first applied to the cell with the largest value, and the other cells are then modified to keep the marginal totals fixed. The pFI in this case study is 1.09, as shown in

Table 4. Calculation of the percent fragility index.

Treatment Groups	No Mucositis	Mucositis	Total
Allopurinol	12.09 (11 + 1.09)	2.91 (4 − 1.09)	15
Placebo	6.91 (8 − 1.09)	8.09 (7 + 1.09)	15
Total	19	11	30

p = 0.0500 and the pFI = 14.53%.

.

2.1.4. Calculation of the Fragility Quotients

Fragility Quotients are designed to normalize the fragility indices UFI and FI for the sample size. The FQ is the quotient for the FI, while the Unit Fragility Quotient (UFQ) is the quotient for the UFI. The pFI is inherently a quotient equal to the exact UFI multiplied by 4 and divided by the sample size.

The definition of the FQ is shown in Equation (2) and for the UFQ is in Equation (3):

FQ = FI/n

(2)

UFQ = UFI/n

(3)

However, a more consistent approach to adjust for the sample size is to divide the total change in the contingency table by the sample size. Because the FI alters two cells and the UFI alters four cells, the adjusted Fragility Quotient (aFQ), the adjusted Unit Fragility Quotient (aUFQ), and for comparison, the pFI are defined as follows in Equations (4)–(6):

aFQ = (FI × 2)/n = (3 × 2)/30 = 20%

(4)

aUFQ = (UFI × 4)/n = (2 × 4)/30 = 27%

(5)

pFI = (exact UFI × 4)/n = (1.09 × 4)/30 = 14.5%

(6)

2.1.5. Calculation of the Robustness Index

The RI assesses the statistical fragility by considering that large sample sizes are much more likely to find a statistically significant difference [13]. Instead of altering the data distribution within a 2 × 2 contingency table, the RI looks at the effect of changing the sample size. The RI is the smallest multiplicand (for nonsignificant findings) or divisor (for significant findings) that will flip the significance of the contingency table. Smaller RI values represent more fragile findings, and larger RI values indicate more robust findings. The RI calculation involves multiplying or dividing the cells by a decimal value (the multiplicand or divisor) to determine the point at which the statistical significance flips. As the resulting cell values are non-integers, the chi-square test is employed for significance testing, as it can handle decimal values, unlike the Fisher exact test, which requires integer values. To standardize the calculation of the RI to be in line with the pFI, Yates’s continuity correction is not routinely applied.

For our base scenario shown in Table 1, the RI is calculated by multiplying the sample size until the p-value flips significance from its initial value of 0.2557 to 0.05 or less. The RI for this scenario is 2.98, with the results shown in

Table 5. Calculation of the robustness index.

Treatment Groups	No Mucositis	Mucositis	Total
Allopurinol	32.8 (11 × 2.98)	11.9 (4 × 2.98)	44.7 (15 × 2.98)
Placebo	23.8 (8 × 2.98)	20.9 (7 × 2.98)	44.7 (15 × 2.98)
Total	56.6 (19 × 2.98)	32.8 (11 × 2.98)	89.4 (30 × 2.98)

p = 0.0498 and the RI = 2.98.

.

The inverse relationship between the p-value and RI is shown in Figure 1. The RI shows that if the distribution of the outcomes is unchanged but the sample size increases by a factor of 2.98, then the significance will flip from nonsignificant to significant.

2.1.6. Comparison of the Fragility Indices, Quotients, and Robustness Index

Note that for this case study, the FI is the largest at 3, the UFI is the next largest at 2, and the smallest increment is the pFI at 1.09. Overall, the UFI makes the greatest change to the contingency table (a change of 2 applied to all four cells = 8), the FI makes next largest change (a change of 3 applied to two cells = 6), and the pFI makes the smallest change (a change of 1.09 applied to all four cells = 4.36). Overall, the aUFQ suggests that the table must be changed by 27% to flip the significance; the aFQ states that a 20% change in the table is required to flip the significance; the pFI states that a minimum 14.5% change in the outcomes is required to flip the significance. Since a smaller change in the outcomes is associated with greater statistical fragility, the pFI represents the most conservative of these metrics.

It is important to note that the FI keeps the marginal totals for the rows fixed but alters the marginal totals for the columns. The UFI and pFI both keep all the marginal totals fixed. The FI and UFI use the Fisher exact test for significance testing, whereas the pFI utilizes the chi-square test. These distinctions should be considered when interpreting and comparing these fragility measures.

The RI is not directly comparable to the UFI, FI, pFI, or Fragility Quotients. It simply represents how much the sample size must change to flip the statistical significance of the contingency table. In this scenario, when the sample size is increased by a factor of 2.98, the findings become statistically significant, meaning that if the researchers had evaluated about 90 patients instead of 30, they would have found a statistically significant difference.

Overall, these fragility metrics indicated moderately robust findings in spite of the small sample size. The cells must be modified by an average of over 10% in all cases to change the statistical significance, and an RI of greater than 2 also suggests moderate robustness.

2.2. Case Study #2: Large Sample Size

A retrospective observational study was conducted looking at 776,927 hospitalized patients to compare the influence of patient and physician sex on 30-day mortality rates [14]. The sample was divided into two groups: those treated by a female physician and those treated by a male physician. The primary outcome was the mortality rate at 30 days after hospital admission. Multiple analyses were performed, but for this case study, we will focus on the 30-day mortality for all the patients after adjustment for the patient characteristics, physician characteristics, and hospital-level averages of exposures, as shown in

Table 6. The 30-day mortality for all patients by treating physician sex after adjustment for patient characteristics, physician characteristics, and hospital-level averages of exposures.

Treating Physician Sex	Alive	Deceased	Total
Female	218,458	21,507	239,965
Male	487,870	49,092	536,962
Total	706,328	70,599	776,927

p = 0.011.

. Given the large sample size, we will exclusively utilize the chi-square test for the calculation of the p-values.

2.2.1. Calculation of the Unit Fragility Index and Quotient

Since the baseline data show a statistically significant finding, the UFI is determined by calculating the change required to flip the p-value to being nonsignificant. In this case, the original 2 × 2 contingency table (218,458, 21,507, 487,870, 49,092) is modified by 70 to result in a table (218,389, 21,576, 487,939, 49,023) which is not statistically significant (p > 0.05). In this case, the UFI = 70. Again, it is important to note that the marginal totals remain fixed, and the data in each cell are slightly modified.

The UFQ is the UFI/n = 0.000090 and the aUFQ = 0.00036. The aUFQ is the preferred quotient for comparison with the other fragility indices. In this example, it indicates that the statistical significance could be flipped with a change in the table of just 0.036%.

2.2.2. Calculation of the Fragility Index and Quotient

Again, since the baseline data show a statistically significant finding, the FI is determined by calculating the change required to flip the p-value to being nonsignificant. Again, note that this is sometimes referred to as the “reverse” fragility index. Also, it is important to keep in mind that the FI was designed to only modify the outcomes of the intervention group. Since there is no intervention group in this case study, the female physician group will be arbitrarily set as the intervention group.

In this case study, the first row of the original 2 × 2 contingency table is modified by 108 to result in a table (218,350, 21,615, 487,870, 49,092) which is not statistically significant (p > 0.05). So in this case, the (reverse) FI = 108, as shown in

Table 7. When the female physician sample is set as the intervention group, the FI is 108.

Treating Physician Sex	Alive	Deceased	Total
Female	218,350	21,615	239,965
Male	487,870	49,092	536,962
Total	706,220	70,707	776,927

p > 0.05.

.

However, when there is no clear intervention group, as in this case study, calculating the FI can become problematic, and in some situations like this case study, the FI cannot be calculated at all. Specifically, if we change the contingency table such that male physicians represent the intervention group and female physicians represent the control group, the FI is not calculable. Specifically, when we modify each cell in the top row of the contingency table by 299, a maximum p-value of 0.034 is reached, as shown in

Table 8. When the rows are switched, the FI is no longer able to be calculated.

Treating Physician Sex	Alive	Deceased	Total
Male	488,169	48,793	536,962
Female	218,458	21,507	239,965
Total	706,328	70,599	776,927

Maximum p = 0.034. In this scenario, increasing or decreasing the FI above or below 299 will result in a smaller p-value; the p-value cannot be flipped to being nonsignificant by only modifying the outcomes of the male physicians.

. Modifying the row by more than or less than 299 will decrease the p-value. In this case, there is no value that will flip the table from significant to nonsignificant if only the top row is modified.

If we consider the female physician group as the intervention group, the FI = 108, the FQ is the FI/n = 0.000139, and the aFQ = 0.000278. In this scenario, the aFQ indicates that the findings could change from significant to nonsignificant with a change in the table of just 0.028%. This only applies when the female physician group is considered the intervention group. None of these values can be calculated if the male physician group is considered as the intervention group.

2.2.3. Calculation of the Percent Fragility Index

The exact UFI is 69.1 so the pFI = 0.000356, indicating that the significance could be flipped with a change in the table of only 0.036%.

2.2.4. Calculation of the Robustness Index

The RI is calculated by increasing or decreasing the sample size until the significance flips. The distribution of the outcomes is unchanged. In this case study, the RI is 1.694, which represents the original sample size of 776,927 divided by 458,635, as shown in

Table 9. When the sample size is divided by 1.694, the findings are no longer significant.

Treating Physician Sex	Alive	Deceased	Total
Female	128,960	12,696	141,656
Male	287,999	28,980	316,979
Total	416,959	41,676	458,635

p > 0.05.

.

Figure 2 shows the relationship between the p-value and RI. If the distribution of the outcomes is unchanged but the sample size decreases by a factor of 1.694, then the findings would flip from significant to nonsignificant.

2.2.5. Comparison of the Fragility Indices and Quotients

In this case study, we see that the calculation of the FI is highly dependent upon which group is considered the intervention group. The FI was designed to test the fragility of research comparing an intervention to a placebo or routine care. For studies with no clear intervention group, such as this case study comparing outcomes by female versus male physicians, the FI and the FQ are not appropriate metrics for statistical fragility and at times cannot even be calculated. Note, however, that the UFI, UFQ, and pFI remain the same regardless of which group is considered the intervention group because they affect all four cells, not just two, of the 2 × 2 contingency table.

In this case study, which examines large sample sizes, the RI may potentially be the most appropriate metric for statistical fragility because it can be applied in all situations and does not alter the outcome data.

In spite of the large sample size of this study, these findings are highly fragile. In this research study, a 20% random sample of a Medicare database was evaluated. If a random sample of 12% had been evaluated, then the findings would not have been statistically significant even if the outcome distribution was the same. In addition, the adjustments made by the researchers to attempt to account for specific physician and patient characteristics easily could have changed the significance of the findings, since less than a 0.05% change in the outcome distribution could flip the significance. An error of just 0.05% could change the statistical significance and change the researchers’ conclusion that the patients treated by female physicians had better outcomes. It could be argued that this conclusion, based on a statistically significant p-value, is misleading and erroneous because of the high fragility of the findings.

3. Clinical Interpretation of Fragility Metrics

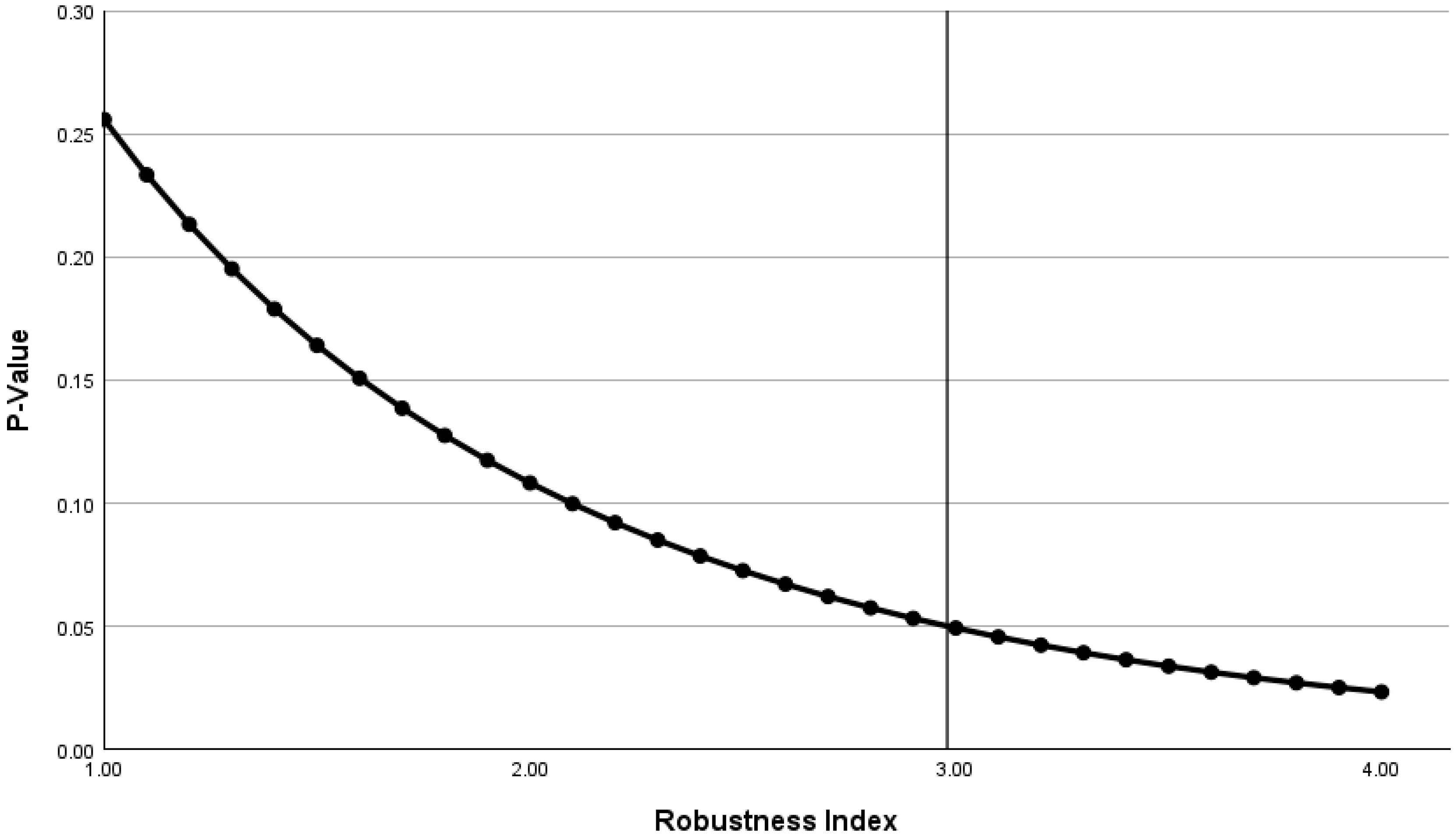
There are currently no widely agreed-upon cutoff values for any of these fragility metrics to categorize statistical findings as fragile or robust. Given the high correlation of the fragility indices with the p-value [15], there is an ongoing debate about whether utilizing these metrics of fragility is valuable [16]. Nevertheless, from an intuitive standpoint, the fragility metrics can help us understand the data better. For example, an RI of 3 indicates that if the sample size was increased by a factor of 3, a nonsignificant finding would become significant. Similarly, the pFI is readily understandable; for instance, a pFI of 4% indicates that a 4% change in the outcomes in any direction (e.g., due to random events, miscategorization, or loss to follow-up) could potentially flip the statistical significance.

3.1. Interpretation of the Fragility Indices

Although no specific cutoff values have been established, it is generally considered that when the FI or UFI is less than the number of research subjects lost to follow-up, the findings are fragile and should be interpreted cautiously [17].

3.2. Interpretation of the Fragility Quotients

Again, no established cutoff values exist for any of the various fragility quotients. However, using a similar logic to that utilized for the p-value, a quotient of less than 5% could perhaps suggest statistical fragility. However, because the data manipulation involved in calculating these indices is unidirectional, it is suggested that a quotient of 3% or less may be more appropriate to indicate fragility. Given the non-uniform data manipulation of the FQ (only the outcomes of the intervention group are altered) and the coarse incrementation of both the FQ and UFQ, it is suggested that the pFI is the most reproducible and most conservative quotient in assessing the statistical fragility across a broad range of biomedical research applications.

3.3. Interpretation of the Robustness Index

While no established cutoff values exist regarding the RI, it is suggested that an RI of 2 or less indicates statistical fragility, a value of 2 to 5 indicates intermediate fragility, and a value of 5 or greater is consistent with statistical robustness. Regardless of whether the original findings are significant or nonsignificant, as the RI increases, the robustness of the findings increases. In all cases, a small RI suggests fragility and a large RI suggests robustness.

4. Discussion

There is a reproducibility crisis in biomedical research, with seemingly important research findings discovered to be either false or questionable when verification studies are performed [18]. Multiple factors contribute to the irreproducibility of research. One factor is publication bias, where researchers face pressure to publish positive and novel findings, leading to the selective reporting of results. Another issue is a lack of transparency in reporting study methods, data, and analyses and the unavailability of raw data [19]. However, even if these issues were fully addressed, there would still be ongoing reproducibility problems due to inappropriate statistical analyses [20].

The American Statistical Association (ASA) released a statement in 2016 addressing the misuse and misinterpretation of p-values in scientific research [21]. The statement emphasizes that p-values alone do not provide a good measure of evidence regarding a model or hypothesis and that scientific conclusions should not be based solely on whether a p-value passes a specific threshold. The ASA also highlights the importance of proper inference, full reporting, and transparency in research. The concerns raised in the ASA statement align with the issues discussed in this manuscript, particularly the need for more comprehensive statistical tools to assess the robustness of research findings.

Including a fragility analysis as a routine statistical procedure could potentially address the reproducibility crisis and increase research efficacy. Small sample sizes do not always indicate poor research or low reproducibility. Research on large sample sizes often spuriously finds minute population differences with no clinical value. The RI and Fragility Quotients (in particular, the pFI) could help address these concerns with both small and large sample sizes.

Currently, the FI and FQ are the primary metrics being utilized to evaluate the fragility or robustness of biomedical research. While the concept of the FI is intuitively easy to grasp, it has significant limitations. First of all, it depends upon a strict definition of an intervention and a control group, so it cannot be consistently applied to comparison studies with no distinct intervention group. In comparison studies, if the two groups are switched, the FI can change and it will not be consistent in its results. Furthermore, in some situations, the FI simply will not result in flipping the statistical significance of a study, such as demonstrated in the second case study above. Although the FI and FQ have become widely utilized, these insurmountable numerical challenges suggest that better fragility metrics are necessary. On the other hand, the RI, pFI, and/or the UFI/UFQ appear more stable and widely applicable. More investigation into these metrics of fragility should be explored, as well as the development of additional tools to assess the fragility of statistical tests beyond the 2 × 2 contingency table.

The ASA’s 2016 statement on p-values underscores the need for alternative approaches to assess the strength of scientific evidence. The statement encourages the use of other methods, such as confidence intervals, Bayesian methods, and false discovery rates, which can provide more direct information about the size of an effect or the correctness of a hypothesis. The RI and pFI, as discussed in this manuscript, offer additional tools to evaluate the fragility of research findings and complement the recommendations made in the ASA statement.

The RI provides a distinctly unique approach to statistical fragility compared to the fragility indices. First of all, it does not alter the distribution of the data but assumes that the data presented are as accurate as possible. It assumes that the data distribution found by the researchers is the best possible estimate. All the other metrics of fragility engage in data manipulation in one direction only. This assumes that any missing data have a unidirectional rather than random bias. The RI, however, does not make any such assumptions. It is a purely numerical process that utilizes the well-recognized fact that large sample sizes are much more likely to contain statistically significant findings, even when the differences are small and clinically meaningless. Nevertheless, a more rigorous and thorough evaluation of the RI along with other metrics of statistical fragility is necessary.

It is unlikely that the p-value will be abandoned, in spite of numerous concerns regarding its arbitrary approach to defining significance. A p-value of 0.05 or less has become deeply embedded in the biomedical literature, including in the approval process for new pharmaceuticals [22]. Thus, it is recommended that at a minimum, the statistical analyses in research studies include a fragility analysis using a standardized fragility metric that can be widely applied and compared across different types of studies, outcomes, and sample sizes.

While the ASA’s 2016 statement does not call for the complete abandonment of p-values, it does emphasize the need for researchers to recognize their limitations and to use them in conjunction with other statistical tools. The inclusion of fragility metrics in the statistical analysis of research studies aligns with the ASA’s recommendations for a more comprehensive and nuanced approach to statistical inference.

One alternative to the p-value is the relative risk index, which represents the residual of a contingency table divided by the sample size [15]. While this may ultimately be more applicable to clinicians deciding upon the management of individual patients, its novelty and lack of standardization currently make it unsuitable to replace the p-value.

In fields where the stakes of research outcomes are high, such as medicine or public policy, fragility metrics may become an invaluable component of the analytical arsenal. They allow decision-makers to discern between results genuinely indicative of an underlying phenomenon and those that may be statistical mirages. In doing so, fragility metrics underpin a more responsible form of data-driven decision-making that recognizes the complexity and conditional nature of statistical evidence. Fragility metrics invite scientists and practitioners to evaluate statistical findings more critically and to view research results with an appropriate but not excessive degree of skepticism.

5. Conclusions

Metrics of fragility, particularly the RI and pFI, are objective tools to assess the statistical fragility of biomedical research. The pFI has the advantage over older fragility metrics because it is more precise and widely applicable than the UFI and FI. Additionally, it is less biased than the FI because it is uniformly applied to all outcomes, not selectively. In cases with no clear intervention group, the FI can lead to inconsistent results, suggesting an underlying instability of this metric. While the FI, UFI, and pFI all perform a unidirectional shift in the outcomes data, the RI does not alter the raw data but analyzes it in a way that simply considers the influence of sample sizes. Overall, current metrics of statistical fragility would benefit from further evaluation regarding how they perform and compare across a wide variety of research studies.

Incorporating fragility indices into research practices can be seen as a step toward a more mature phase of statistical reasoning, where significance is not just a matter of crossing a threshold but a multi-faceted and contextually informed judgment.