Contrastive Learning Framework for Bitcoin Crash Prediction
Abstract
1. Introduction
- We propose a deep learning framework based on contrastive learning for extracting latent representations for time series data and tackle downstream time series classification task.
- We apply the proposed framework to predict crashes of Bitcoin. To the best of our knowledge, we are the first to employ contrastive learning in analyzing cryptocurrencies.
- We investigate the performance of multiple time series augmentation methods in contrastive learning based model, and the effect of some augmentation parameters.
- We compare our proposed framework against six state-of-the-art classification models, which include both ML and DL models.
- We explore the efficacy of ensemble techniques in an effort to improve the overall classification performance.
- We compare and combine the CL framework with the Log Periodic Power Law Singularity (LPPLS) model, which is also unprecedented, to the best of our knowledge.
2. Related Work and Background
2.1. Financial Crashes
2.2. Contrastive Learning
2.3. Contrastive Learning for Time Series
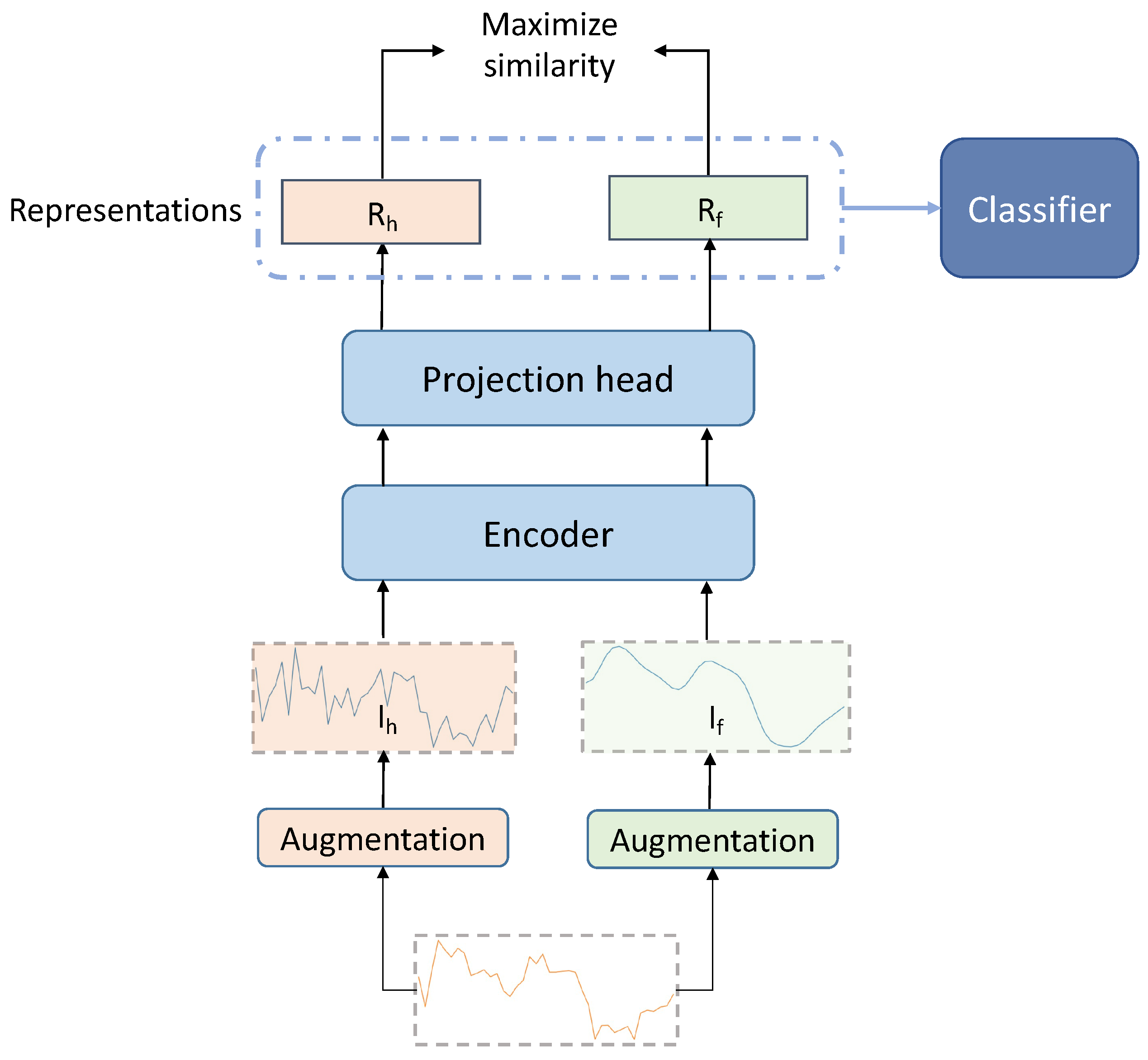
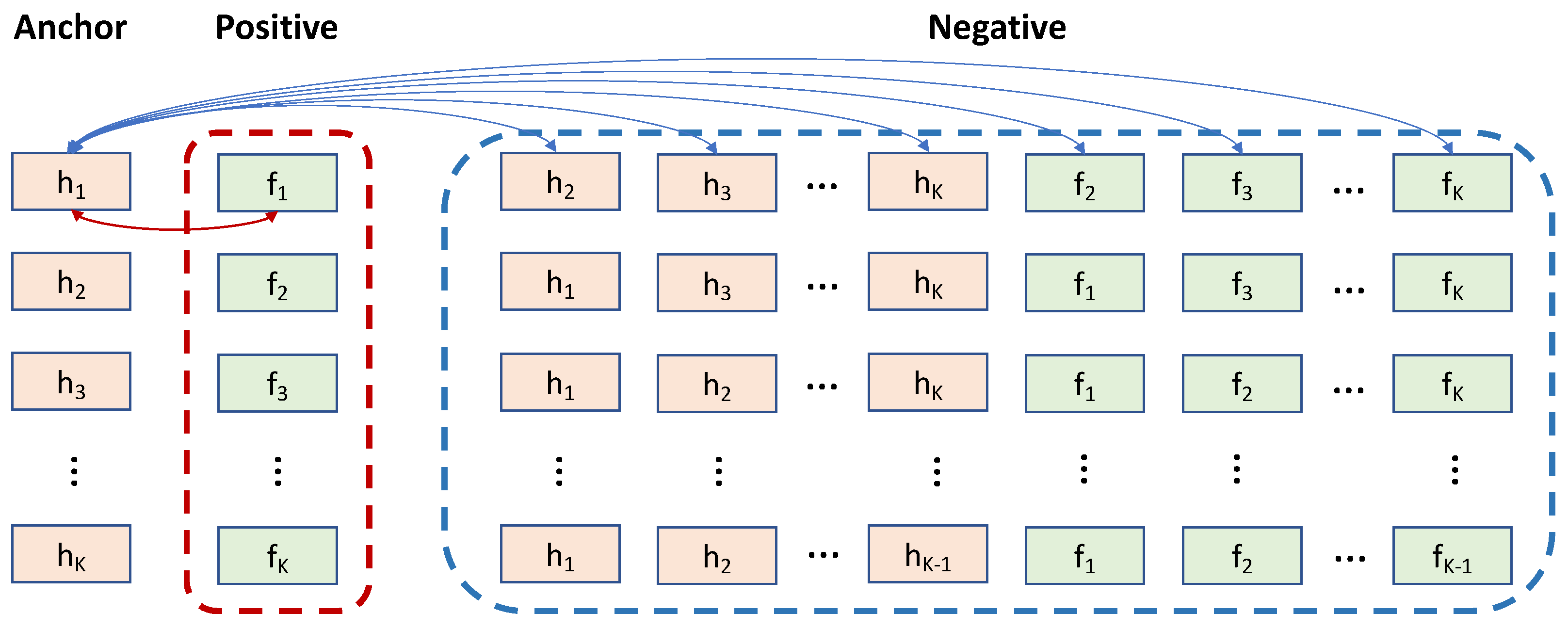
3. Methods
3.1. Problem Definition
3.2. The Epsilon Drawdown Method
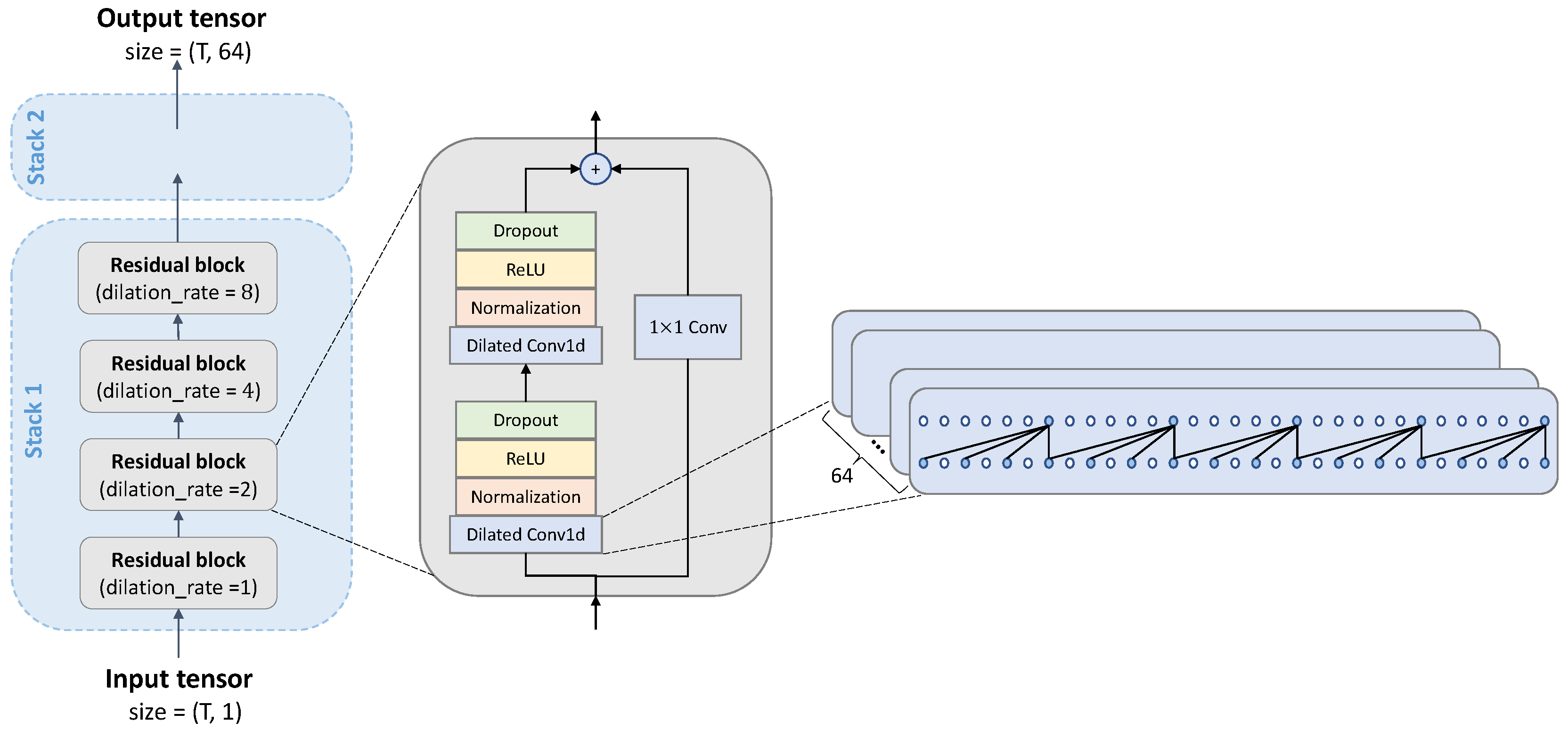
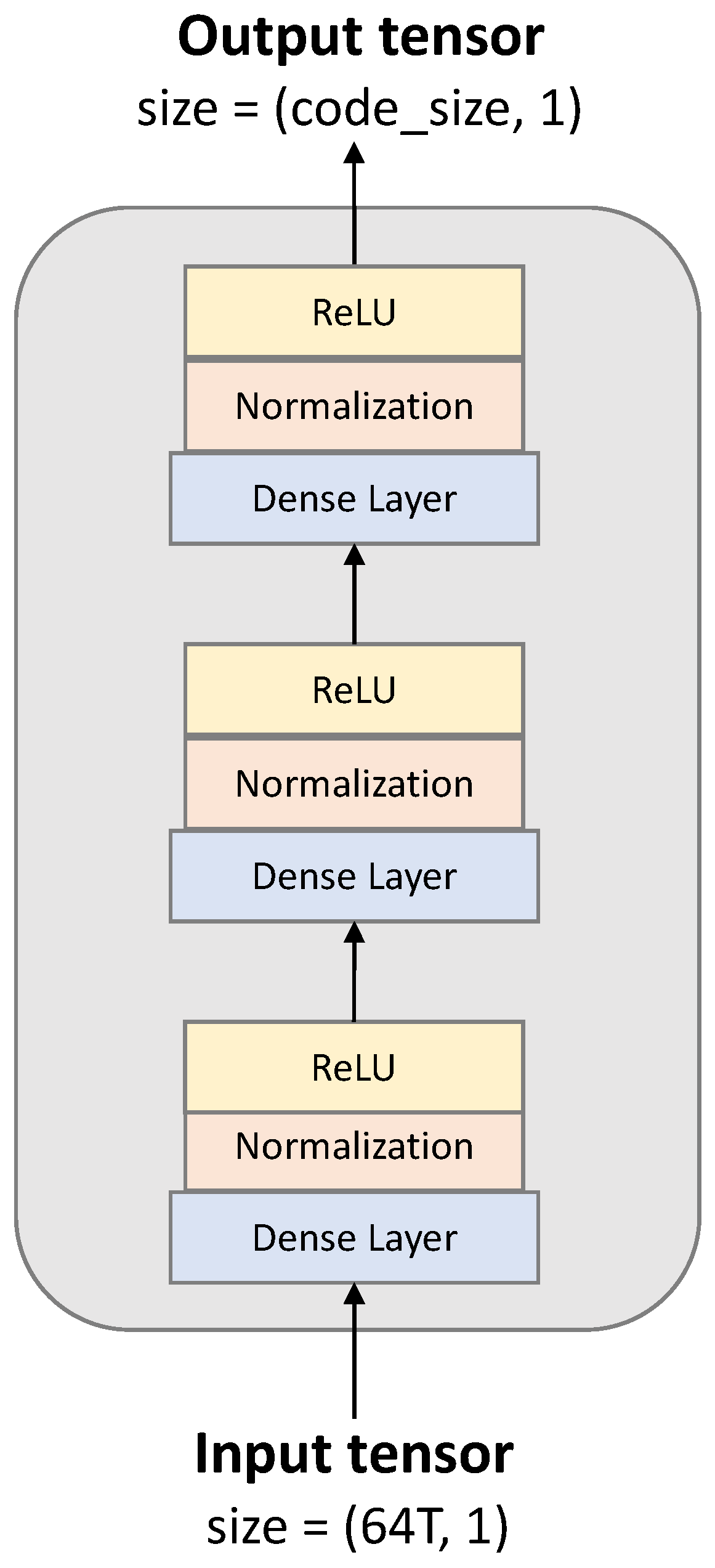
3.3. Model Architecture
- for sampling, we apply the augmentations that are not only commonly used for images but also reasonable for time series sequences, maintaining the overall trend of the sequence so as not to change the original input too much;
- we remain the projection head for the downstream task
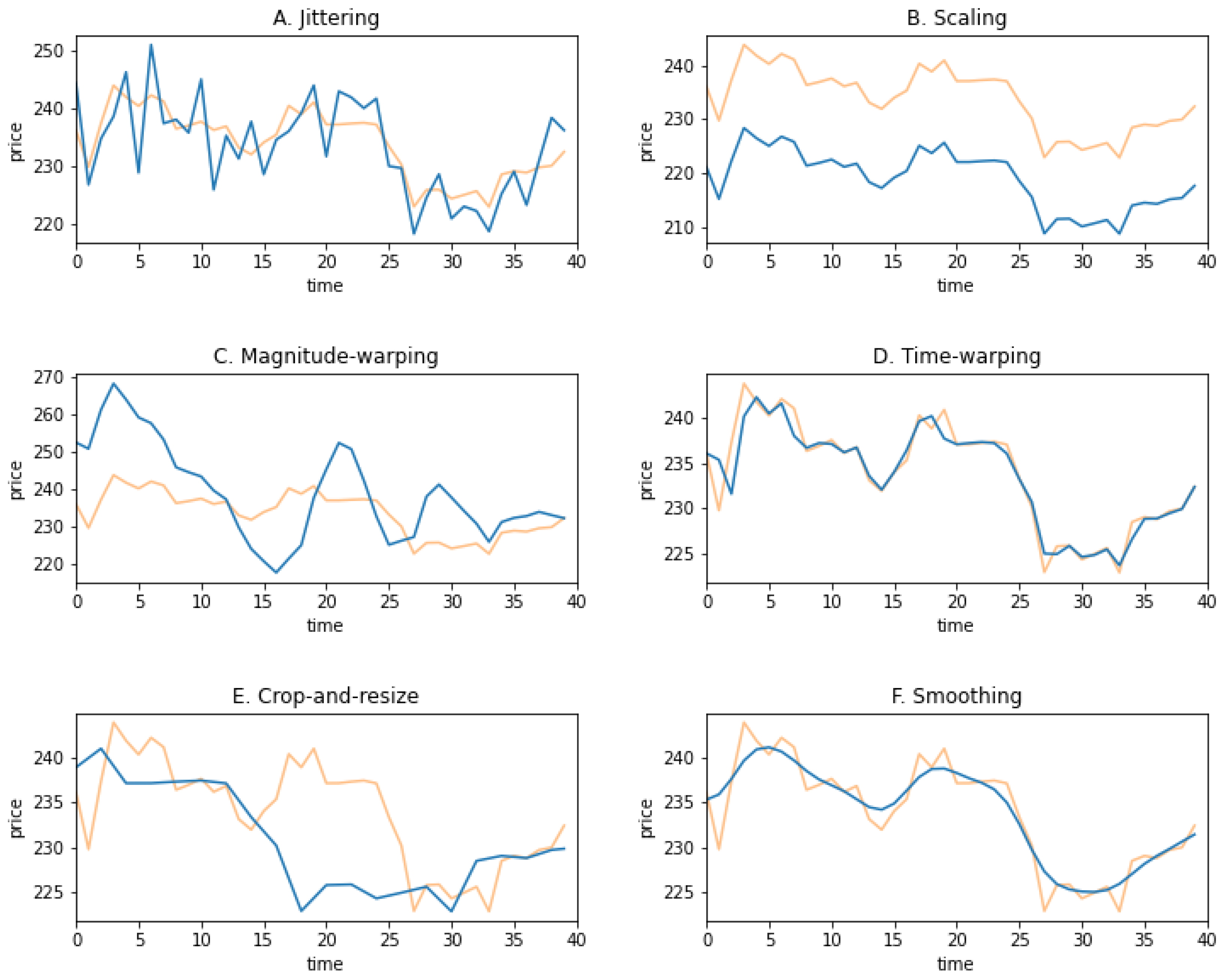
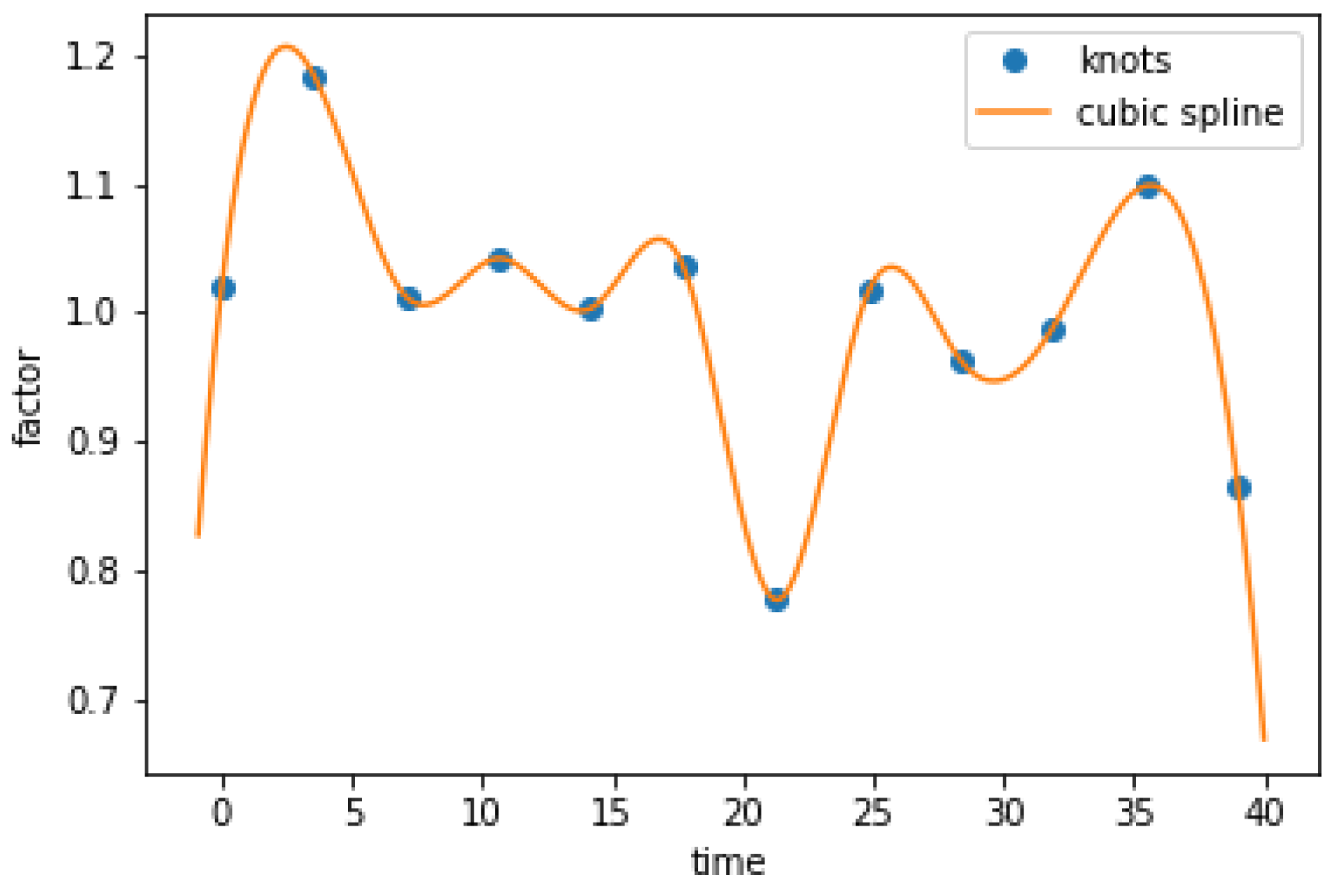
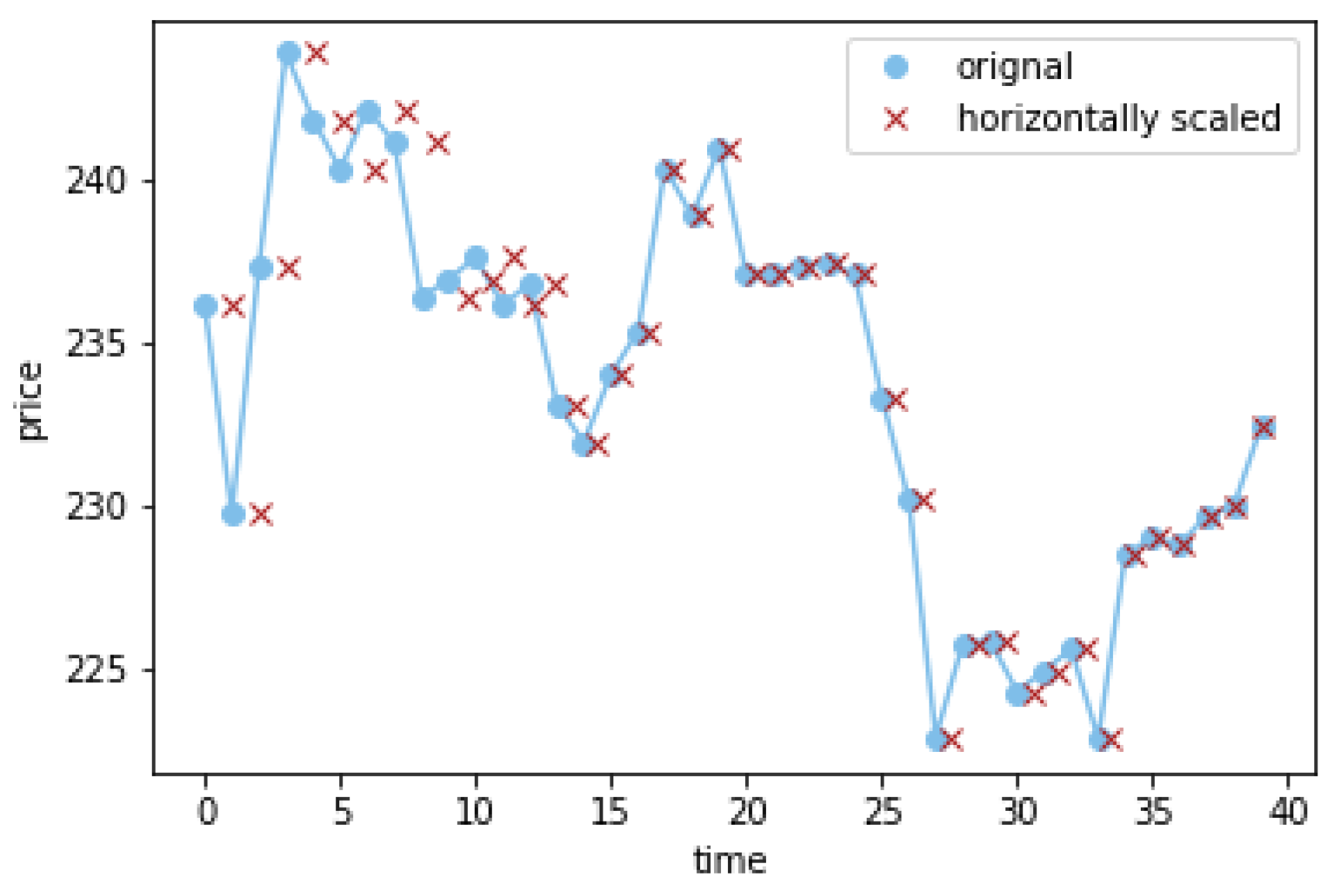
3.4. Data Augmentation
4. Experiments
4.1. Data
4.2. Contrastive Model Setup
4.3. Baseline Models
- Machine learning models include Random Forests (RF) [47], Support Vector Machine (SVM) [48], Gradient Boosting Machine [49] and XGBoost [50]. We used scikit-learn and XGBoost Python libraries to implement these models. Models are trained by using the extracted features from each window, instead of raw time series sequence data. Specifically, for each window, the average/standard deviation (std) of daily price ()/return ()/volatility () of the last 5 days, 10 days, 15 days,…, 30 days are calculated. In addition, tsfeatures Python library is applied to extract more advanced time series properties (see Table 4).In the training process, grid-search and 5-fold time-split cross-validation are employed. The configuration parameters of grid-search for each classification model are shown in Table 5.
- Deep learning models contain LSTM [51] and the same TCN architecture used for contrastive learning but trained in a fully supervised manner. We used Both baseline models take the same input as the downstream classifier of the proposed contrastive learning framework. The LSTM model have two layers of a LSTM-ReLU-BatchNorm combination, followed by the projection head as CL and a dense layer with sigmoid activation function. For the TCN baseline model, two stacks of TCN followed by the projection head and a dense layer classifier are trained to directly predict the two desired classes for windows. We use batch of 32,200 epochs and class weights of {0:0.2, 1:0.8} to train the two DL models. Python library Tensorflow is also employed to implement the models.
- Contrastive learning model uses the same architecture of the proposed framework but replacing the TCN encoder to an LSTM, which is consist of two layers of a LSTM-ReLU-BatchNorm combination. We denote this competitor as CL-LSTM. Similarly, the encoder is trained in self-supervised manner, using the same input and same experimental setup with CL-TCN.
- LPPLS Confidence Indicator is constructed by using the shrinking windows whose length is decreased from 360 days to 30 days. For each fixed end point , we shift start point in steps of 30 days, hence totally 12 of fittings are generated. To estimate parameters and filter fittings, we apply the following search space and filtering condition in Table 6.
4.4. Augmentation Comparison and Analysis
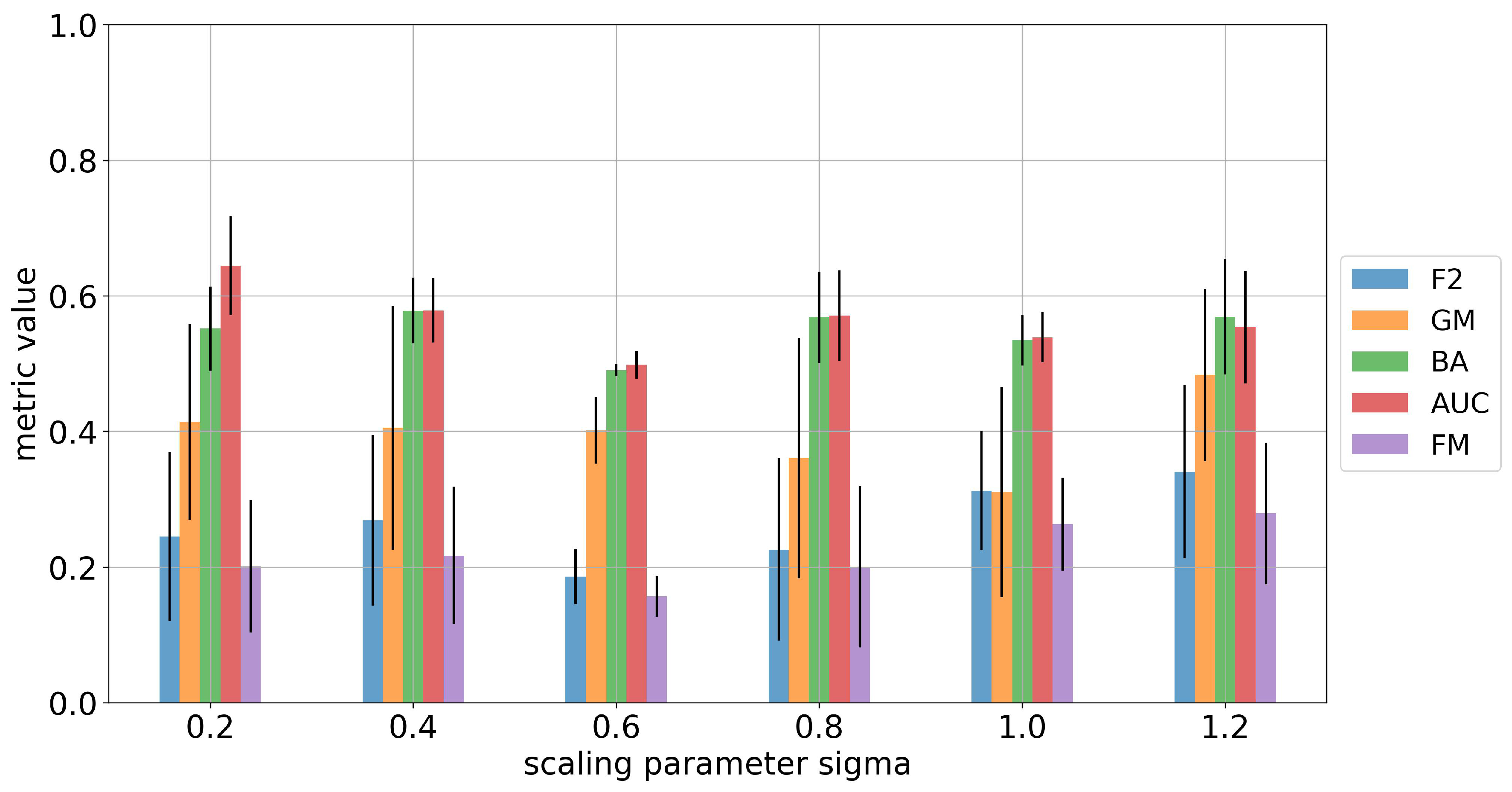
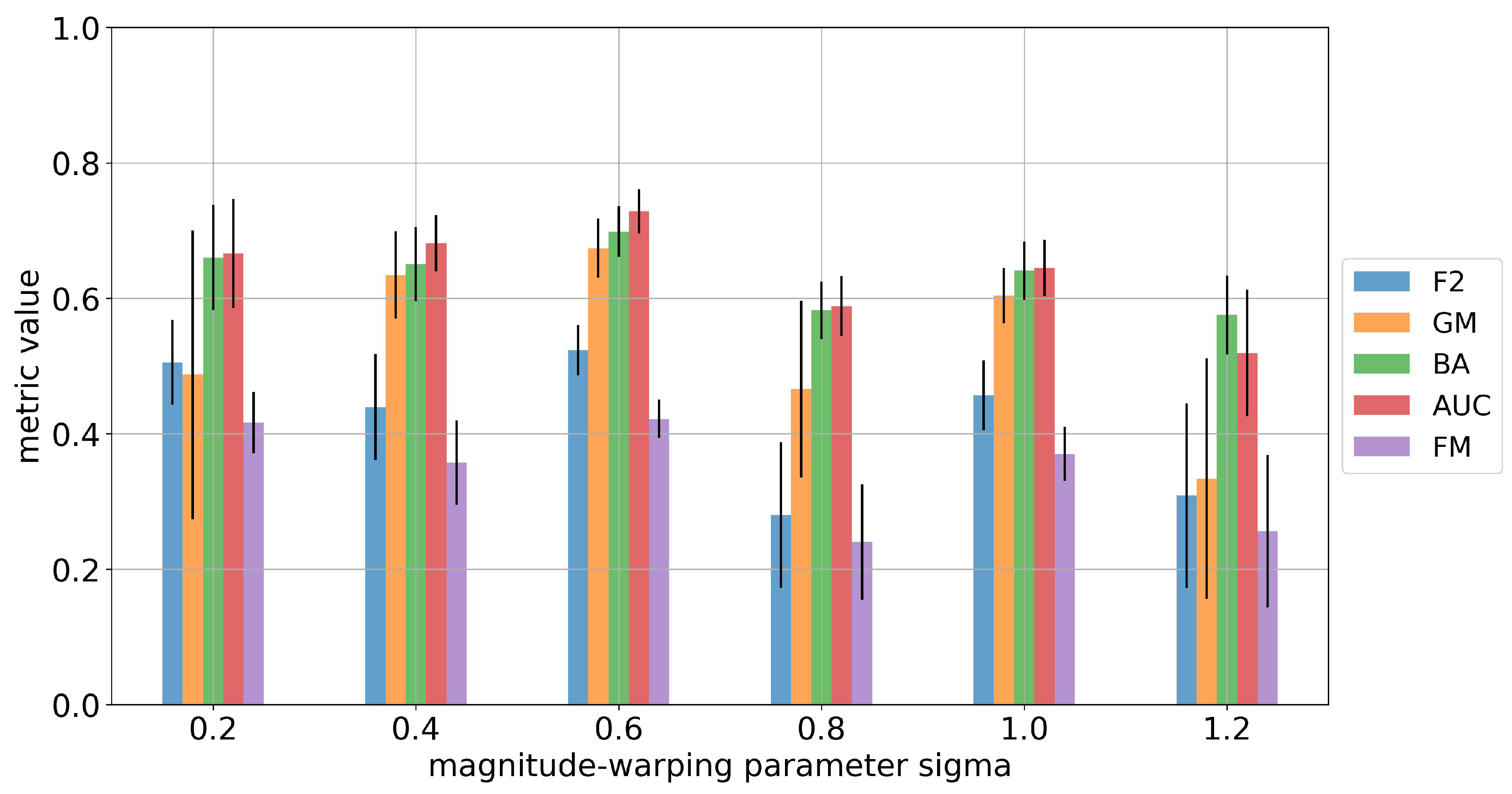
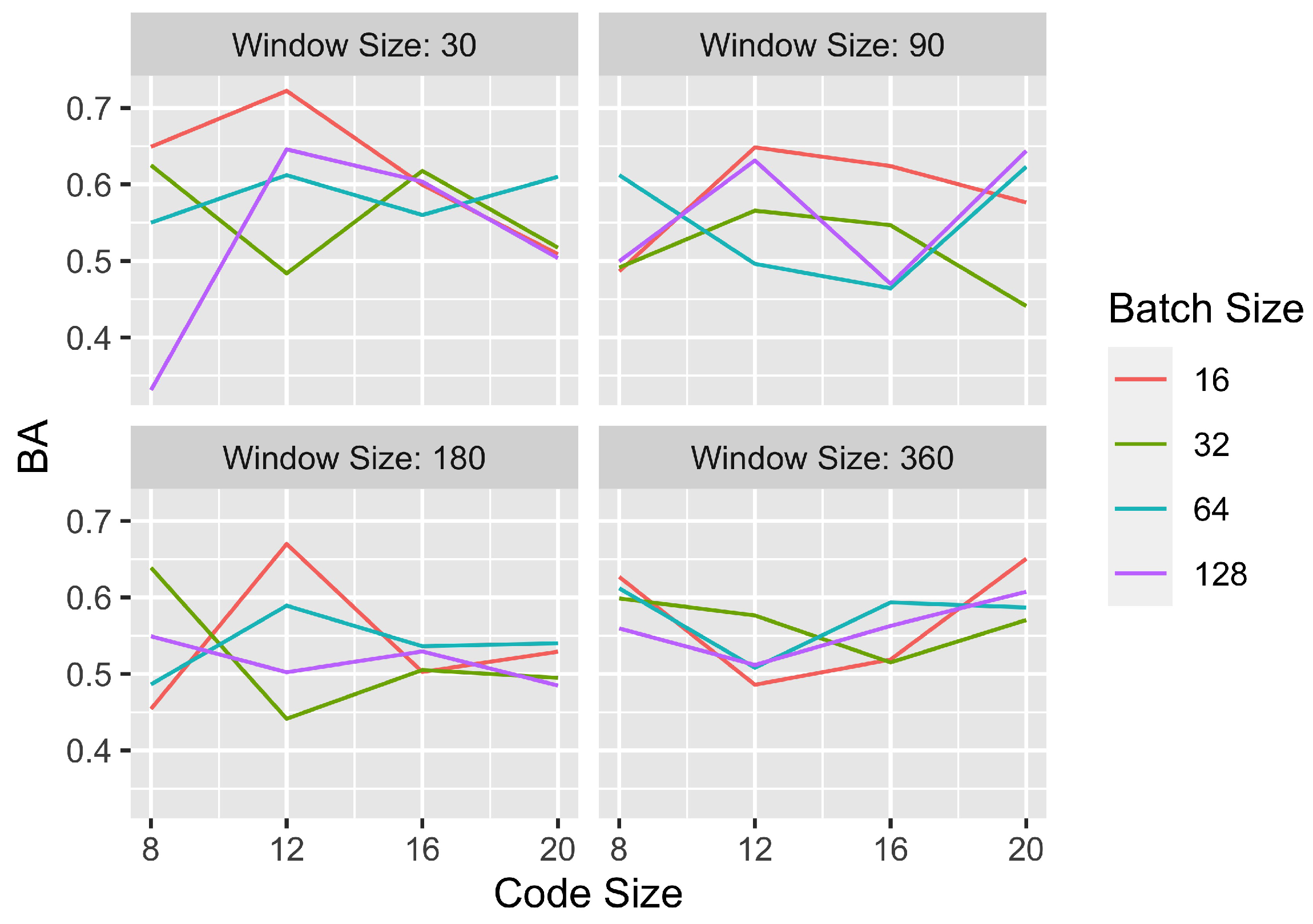
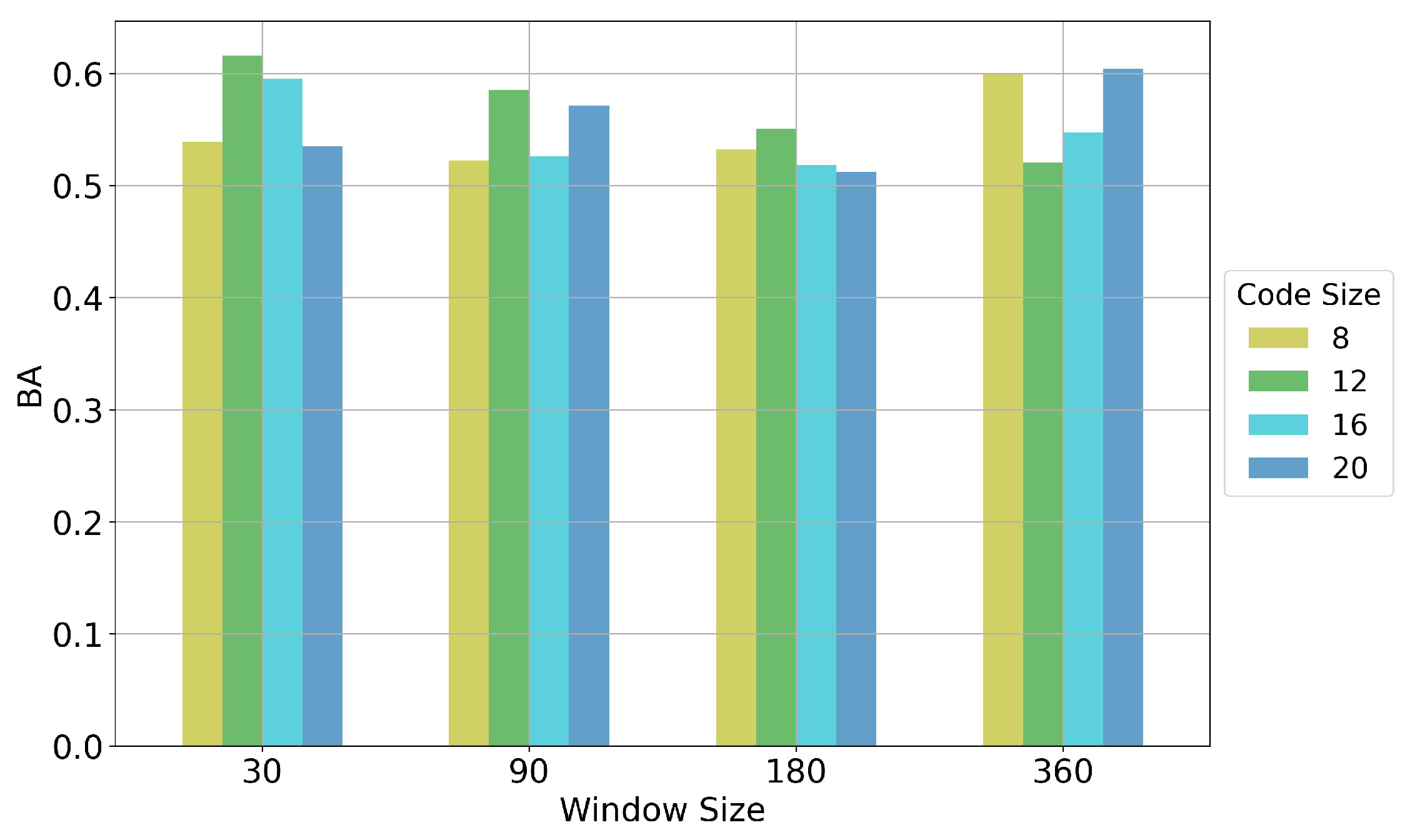
4.5. Fine-Tuning and Sensitivity Analysis
- Window size is the length of original time series sequence input. We think that different window sizes contain different information, so it should be large enough to contain the most useful information for prediction but not too long to make the model hard to catch the key properties of the sequence. We select window sizes of 30, 90, 180 and 360 days for the experiment.
- Batch size specifies the number of positive pairs (K) of augmented windows that are processed before the model is updated, so in our case there are training samples in each batch. In the experiment, the batch size is chosen to be 16, 32, 64 and 128.
- Code size indicates the length of the embedding vector (representations) that is extracted from the encoder network. The code size is tested to range between 8 and 24.
4.6. Baseline Comparison
4.7. Ensemble Model
- Hard VoteIn hard voting (also known as majority voting), every individual classifier votes for a class, and the majority wins. The ensemble’s anticipated target label is, statistically speaking, the mode of the distribution of the labels’ individual predictions. In this case, the selected three base models generate binary predictions separately. If more than 2 models infer positive output then the ensemble model output is marked as positive, otherwise marked as negative.
- Soft Vote (Simple Average and Weighted Average)In soft voting, every individual classifier provides a probability value that a specific data point belongs to a particular target class. A simple average strategy is firstly applied and converted to binary predictions for evaluation. For weighted average, the evaluation metric value of each base classifier is used to weight and then average the predictions. As multiple metrics are adopted in evaluation above (F2, GM, BA, FM), the weight can be calculated by looping through them. Different weighted average output can be generated, and consequently the final binary label by metric is gathered.
- Logistic RegressionLogistic regression is conducted by using the predicted probabilities of the 3 selected and the LPPLS indicator as 4 features to fit on the train set, then predict on the test set.
- CL IndicatorSame as constructing LPPLS indicator, we recursively train CL-TCN with shrinking window of 360 days to 30 days with a step size of 30 days, hence the 12 CL models are obtained. For each time point, we use 12 models to make prediction and then calculate the fraction of models that classify it as class 1.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Features from Tsfeatures
Appendix A.2. Figures
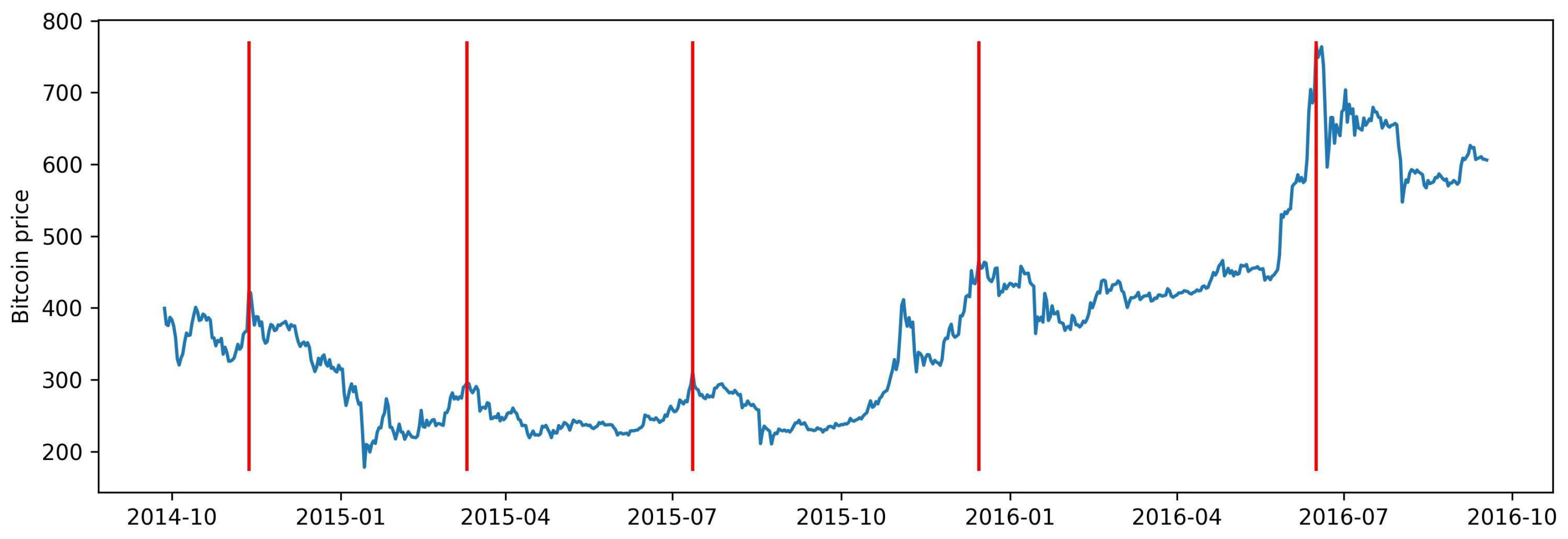
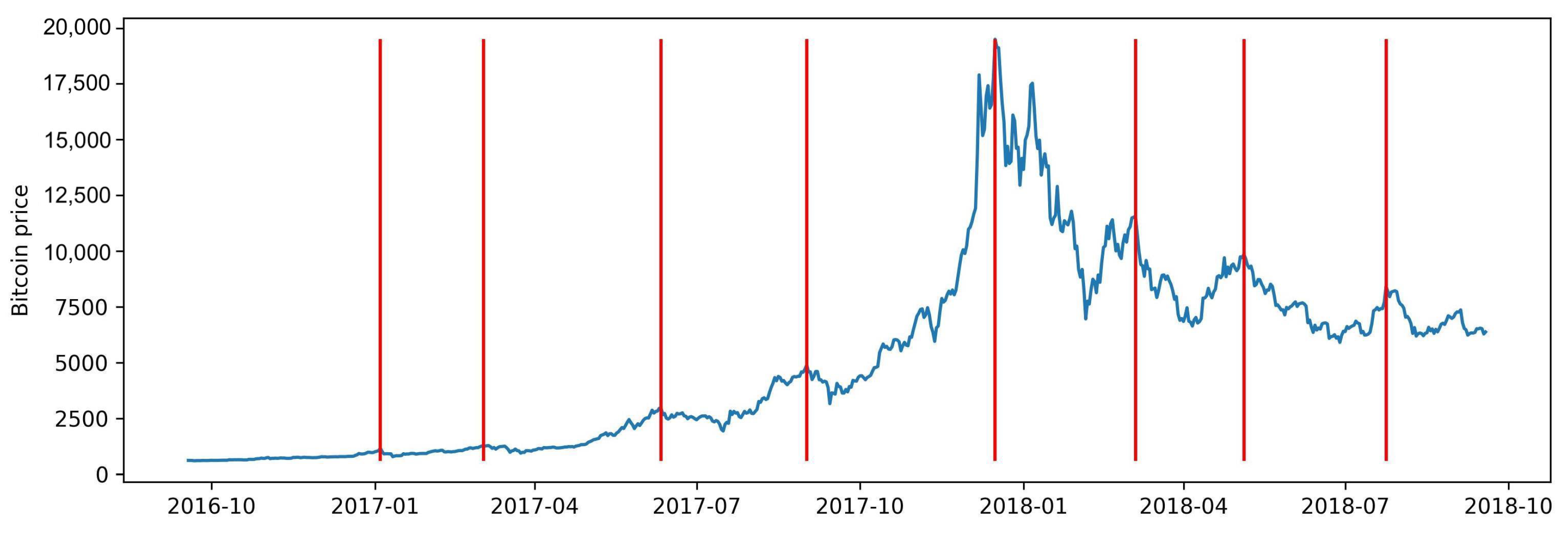





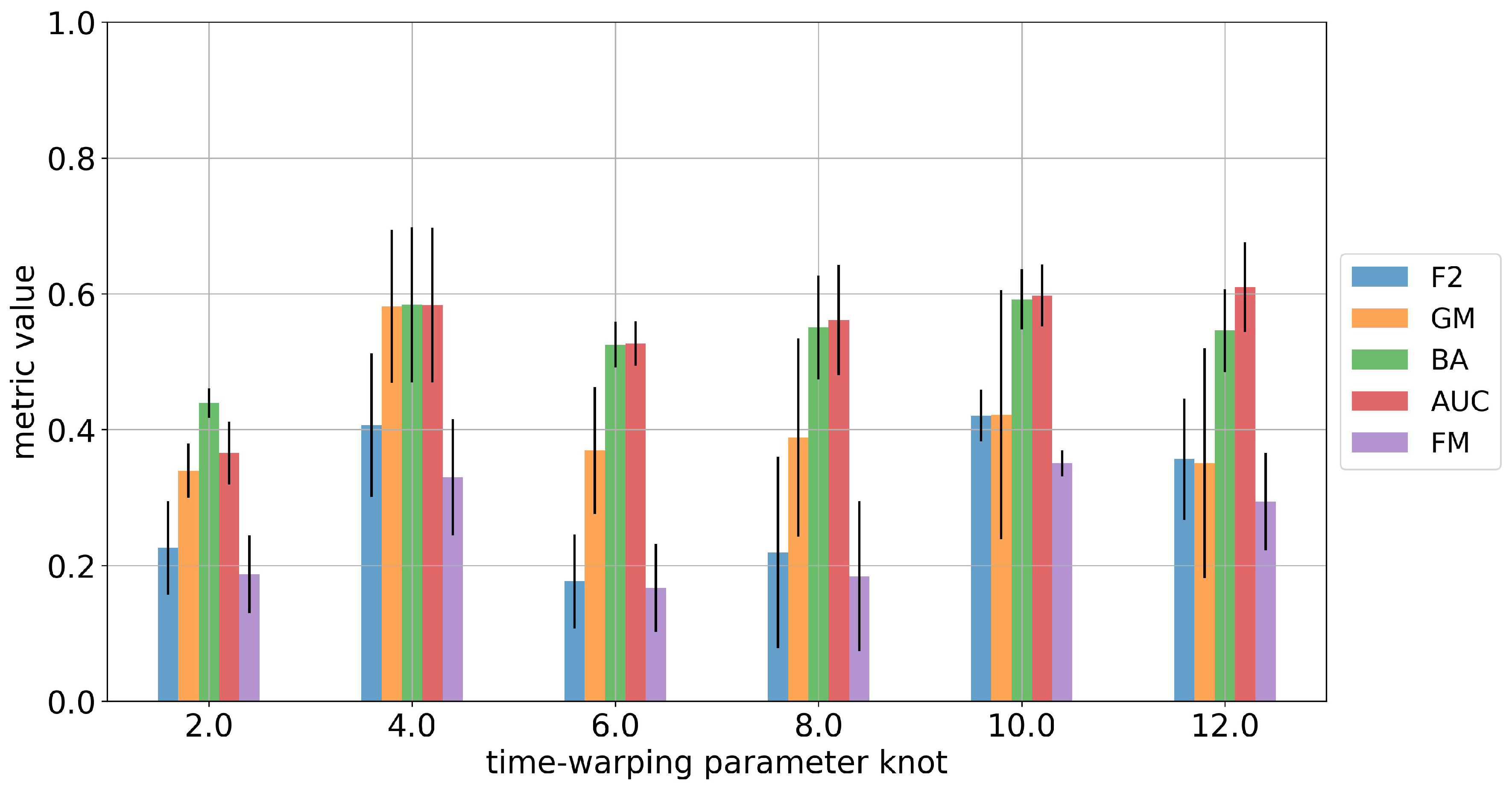
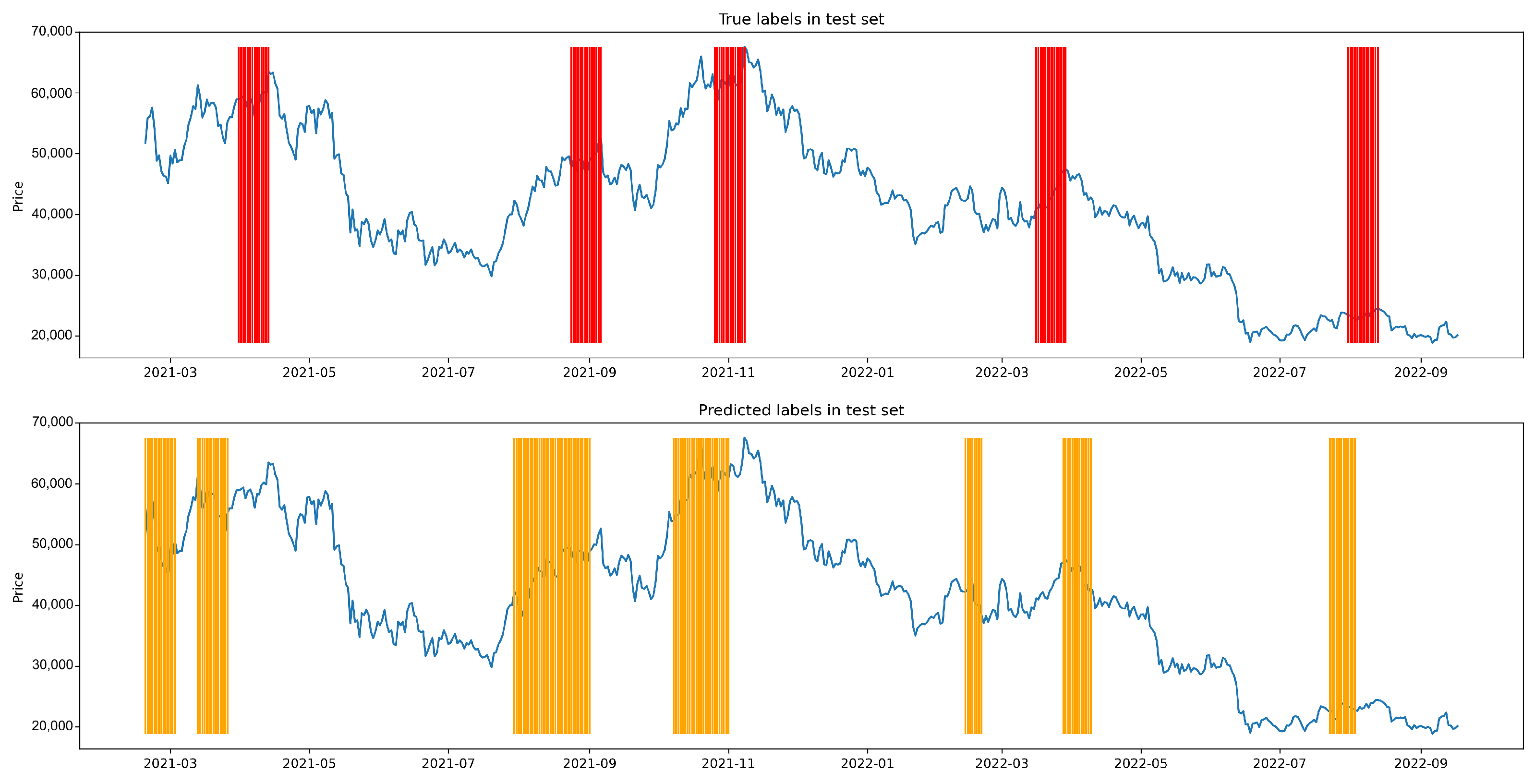
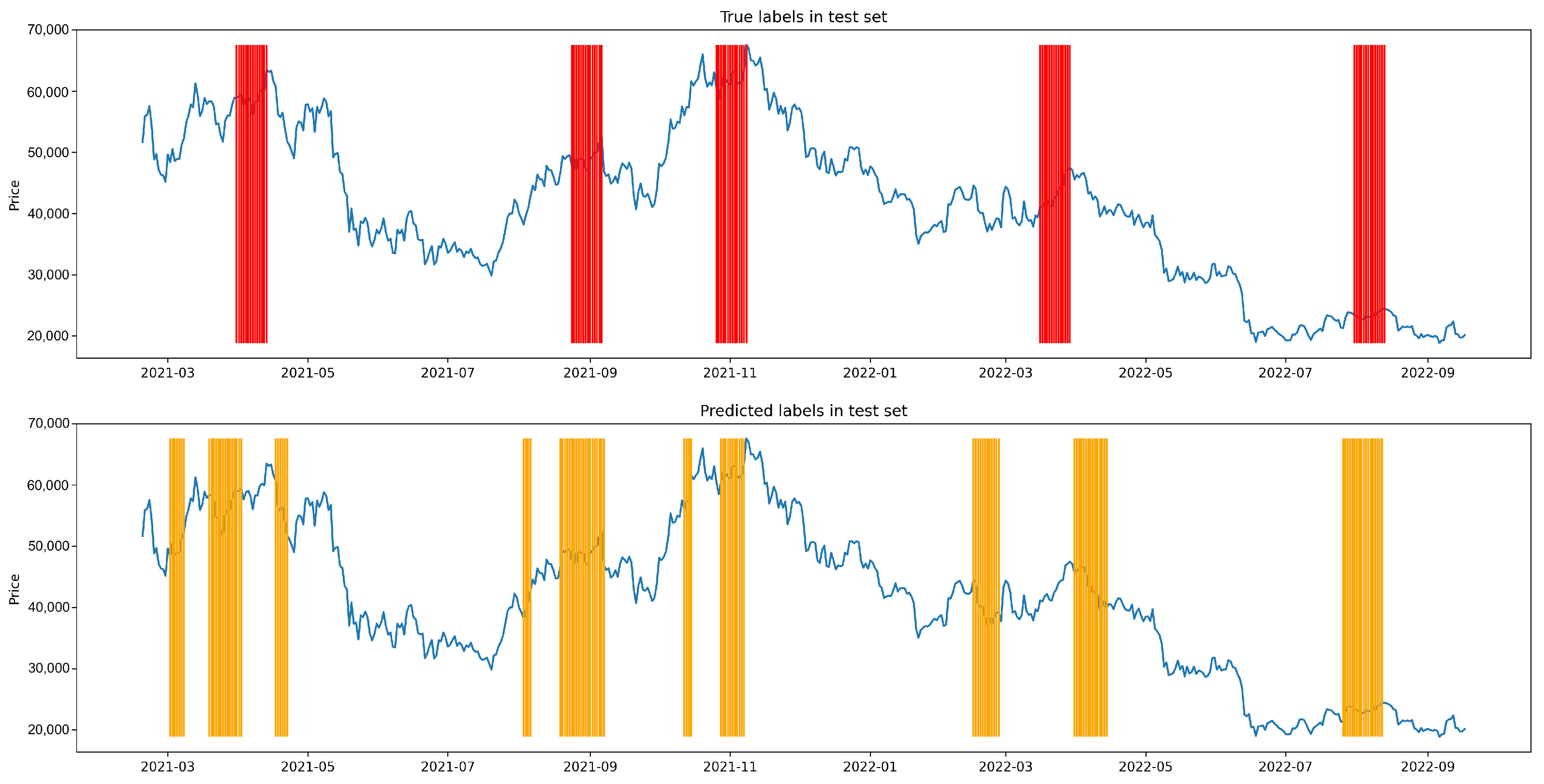
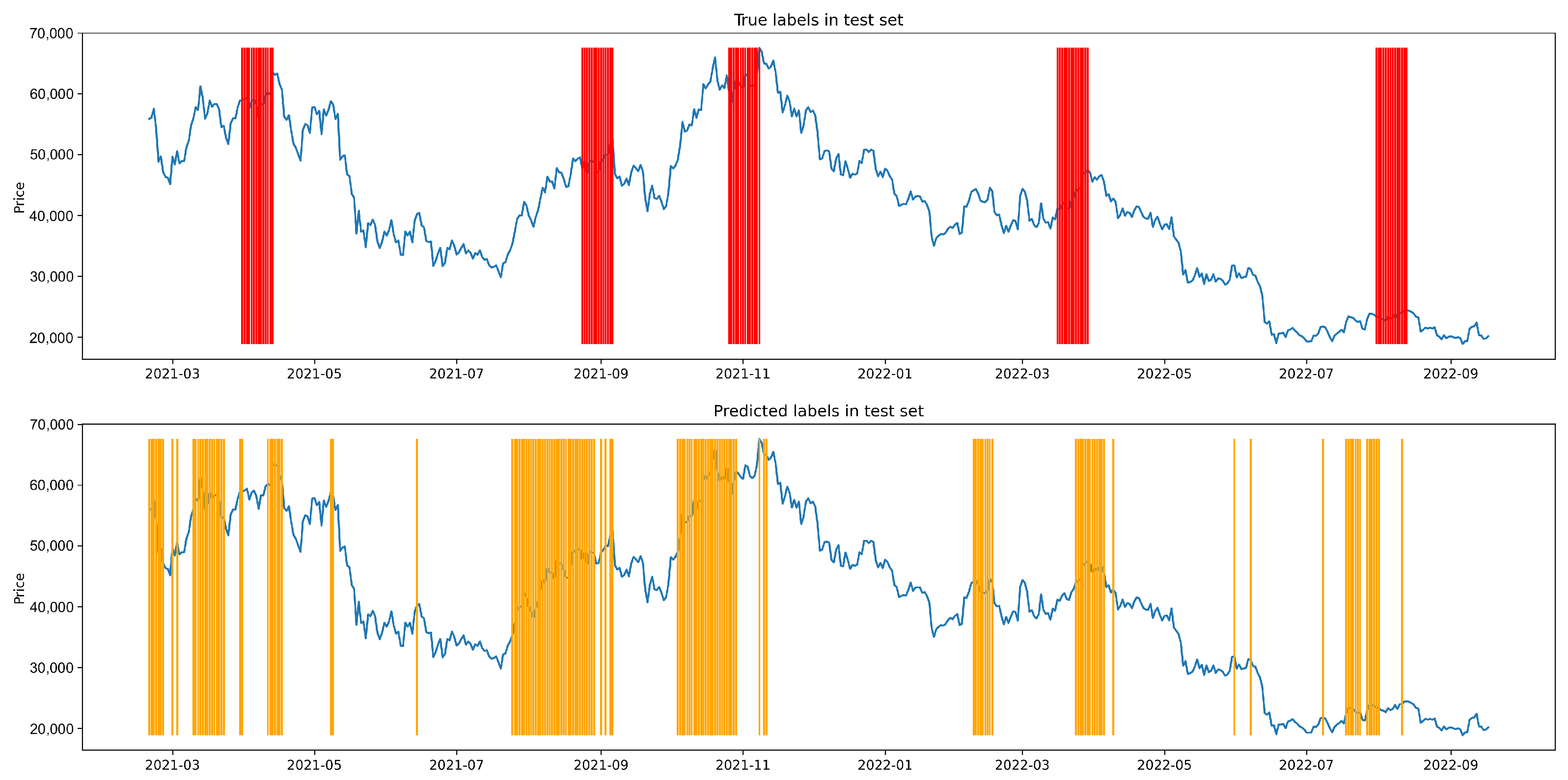

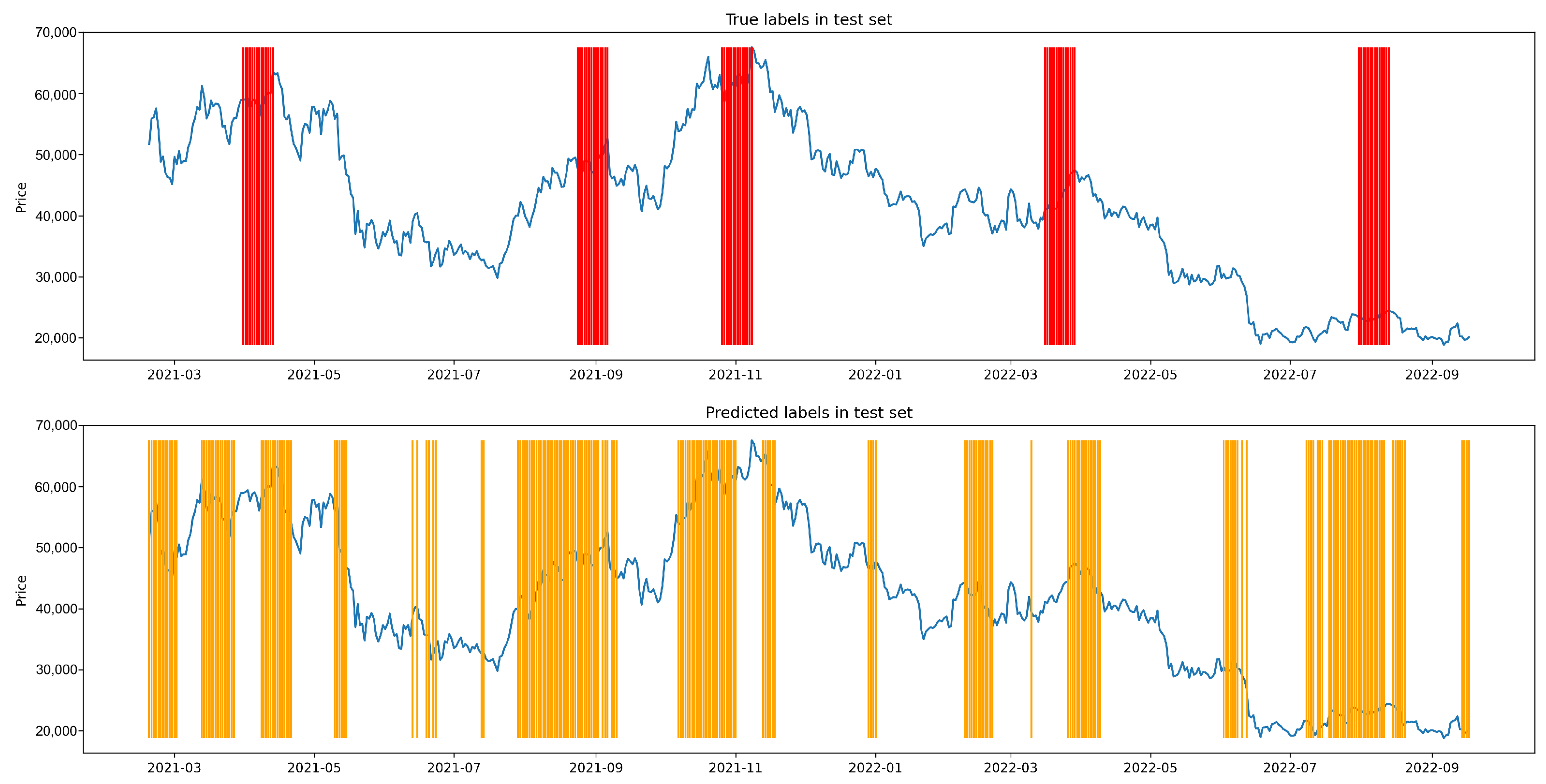
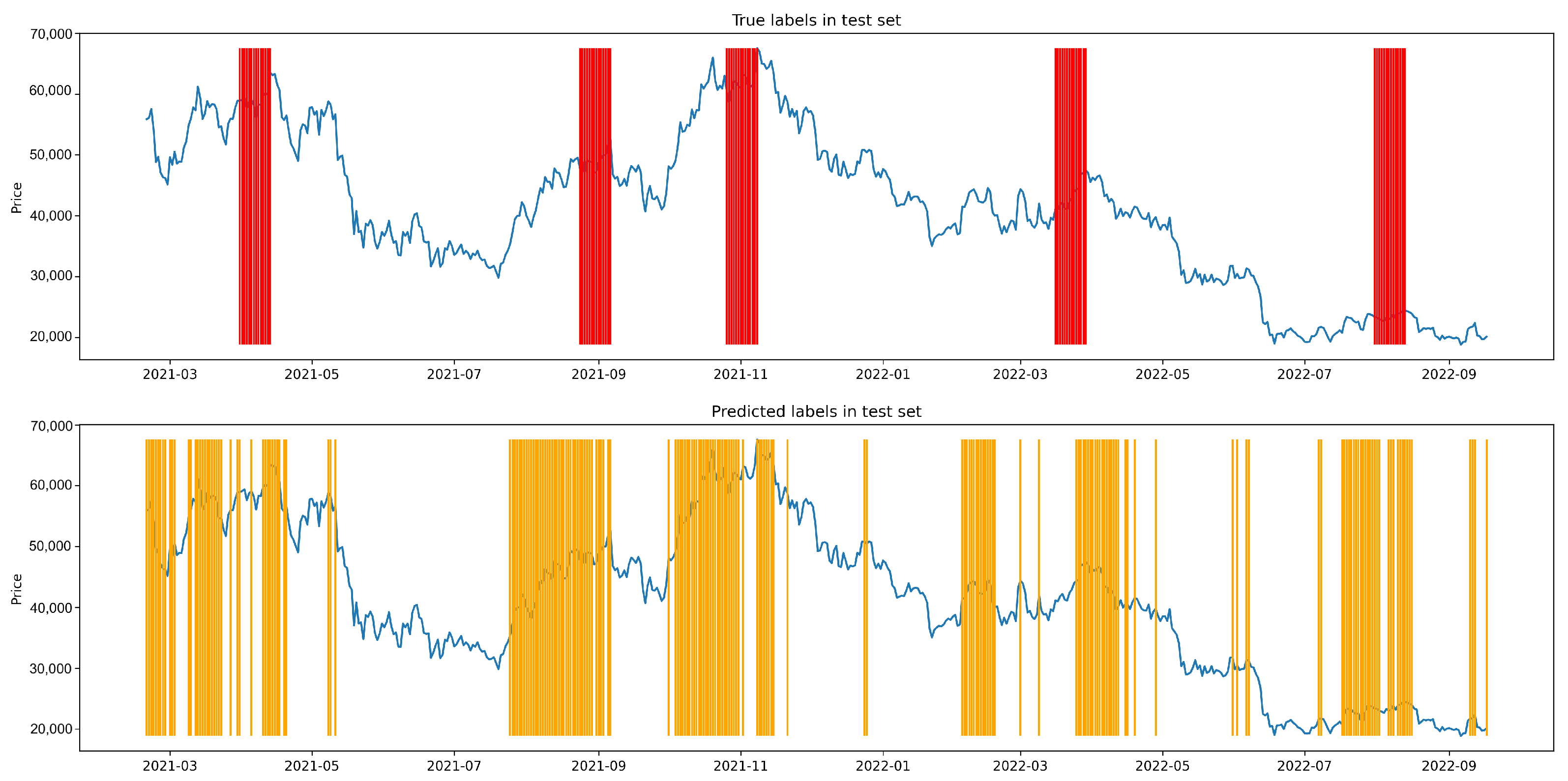
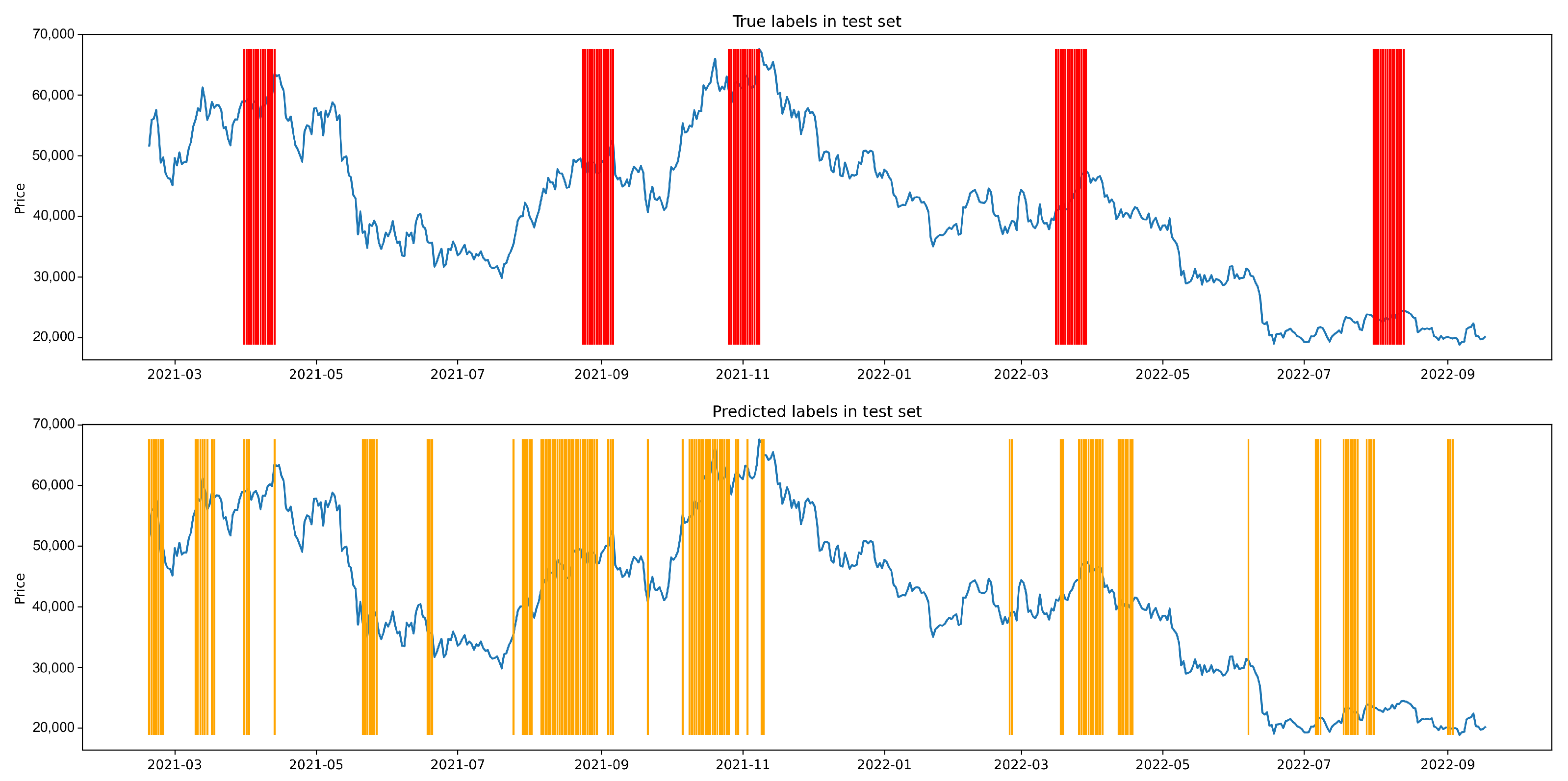

Appendix A.3. Shuffle Experiment
| F2 | GM | BA | FM | |
|---|---|---|---|---|
| original | 0.54 ± 0.06 | 0.71 ± 0.04 | 0.72 ± 0.04 | 0.44 ± 0.04 |
| shuffle | 0.31 ± 0.18 | 0.40 ± 0.18 | 0.47 ± 0.16 | 0.26 ± 0.14 |
Appendix A.4. Drawdowns in Bitcoin Hourly Price Data
| Peak Time | Peak Price | End Time | End Price | Drop | Duration |
|---|---|---|---|---|---|
| 4/21/22 12:00 | 42,709.7 | 4/26/22 20:00 | 38,084.5 | 10.8% | 128 |
| 4/28/22 17:00 | 40,187.5 | 5/5/22 15:00 | 36,914.7 | 8.1% | 166 |
| 5/5/22 16:00 | 37,056.9 | 5/12/22 6:00 | 26,759.8 | 27.8% | 158 |
| 5/12/22 16:00 | 29,695.5 | 5/12/22 18:00 | 28,267.1 | 4.8% | 2 |
| 5/13/22 14:00 | 30,759.5 | 5/14/22 15:00 | 28,796.2 | 6.4% | 25 |
| 5/15/22 23:00 | 31,308.2 | 5/18/22 23:00 | 28,734.2 | 8.2% | 72 |
| 5/20/22 11:00 | 30,453.1 | 5/20/22 16:00 | 28,884.4 | 5.2% | 5 |
| 5/23/22 6:00 | 30,483.2 | 5/27/22 17:00 | 28,380.7 | 6.9% | 107 |
| 5/31/22 16:00 | 32,194.6 | 6/7/22 2:00 | 29,395.2 | 8.7% | 154 |
| 6/7/22 21:00 | 31,424.5 | 6/14/22 1:00 | 21,049.5 | 33.0% | 148 |
| 6/14/22 7:00 | 22,881.0 | 6/18/22 20:00 | 17,744.9 | 22.4% | 109 |
| 6/18/22 22:00 | 19,072.5 | 6/19/22 5:00 | 18,128.8 | 4.9% | 7 |
| 6/19/22 22:00 | 20,638.7 | 6/20/22 1:00 | 19,730.8 | 4.4% | 3 |
| 6/20/22 10:00 | 20,843.5 | 6/20/22 18:00 | 20,018.0 | 4.0% | 8 |
| 6/21/22 14:00 | 21,569.9 | 6/22/22 20:00 | 19,985.2 | 7.3% | 30 |
| 6/26/22 11:00 | 21,700.1 | 6/30/22 20:00 | 18,741.2 | 13.6% | 105 |
| 7/1/22 1:00 | 20,385.3 | 7/3/22 13:00 | 18,986.6 | 6.9% | 60 |
| 7/5/22 0:00 | 20,398.1 | 7/5/22 13:00 | 19,401.6 | 4.9% | 13 |
| 7/8/22 3:00 | 22,097.0 | 7/13/22 12:00 | 19,134.0 | 13.4% | 129 |
| 7/17/22 6:00 | 21,543.6 | 7/17/22 23:00 | 20,788.4 | 3.5% | 17 |
| 7/18/22 15:00 | 22,533.7 | 7/18/22 20:00 | 21,542.2 | 4.4% | 5 |
| 7/18/22 23:00 | 22,441.3 | 7/19/22 6:00 | 21,723.6 | 3.2% | 7 |
| 7/20/22 15:00 | 24,169.7 | 7/26/22 15:00 | 20,787.2 | 14.0% | 144 |
| 7/30/22 15:00 | 24,562.4 | 8/4/22 19:00 | 22,499.1 | 8.4% | 124 |
| 8/8/22 13:00 | 24,174.5 | 8/10/22 0:00 | 22,798.8 | 5.7% | 35 |
| 8/11/22 12:00 | 24,768.6 | 8/12/22 11:00 | 23,695.4 | 4.3% | 23 |
| 8/15/22 2:00 | 24,887.2 | 8/19/22 23:00 | 20,875.0 | 16.1% | 117 |
| 8/26/22 13:00 | 21,730.7 | 8/28/22 23:00 | 19,628.0 | 9.7% | 58 |
| 8/30/22 4:00 | 20,463.3 | 8/30/22 16:00 | 19,649.4 | 4.0% | 12 |
| 8/31/22 3:00 | 20,390.8 | 9/7/22 2:00 | 18,661.6 | 8.5% | 167 |
| 9/13/22 11:00 | 22,539.4 | 9/19/22 8:00 | 18,454.6 | 18.1% | 141 |
| 9/19/22 22:00 | 19,633.8 | 9/20/22 17:00 | 18,852.4 | 4.0% | 19 |
| 9/21/22 18:00 | 19,644.2 | 9/22/22 0:00 | 18,418.0 | 6.2% | 6 |
| 9/23/22 4:00 | 19,456.3 | 9/23/22 18:00 | 18,672.0 | 4.0% | 14 |
| 9/27/22 12:00 | 20,296.4 | 9/28/22 2:00 | 18,626.5 | 8.2% | 14 |
| 9/30/22 14:00 | 19,956.7 | 10/2/22 23:00 | 19,042.9 | 4.6% | 57 |
| 10/6/22 4:00 | 20,376.8 | 10/11/22 18:00 | 18,976.9 | 6.9% | 134 |
| 10/12/22 21:00 | 19,178.1 | 10/13/22 12:00 | 18,403.6 | 4.0% | 15 |
| 10/14/22 1:00 | 19,885.4 | 10/20/22 0:00 | 18,993.0 | 4.5% | 143 |
| 10/26/22 15:00 | 20,840.7 | 10/28/22 7:00 | 20,099.4 | 3.6% | 40 |
| 10/29/22 9:00 | 20,934.5 | 11/2/22 22:00 | 20,102.9 | 4.0% | 109 |
| 11/5/22 3:00 | 21,427.9 | 11/9/22 21:00 | 15,841.8 | 26.1% | 114 |
| 11/10/22 16:00 | 17,797.3 | 11/10/22 17:00 | 17,202.9 | 3.3% | 1 |
| 11/10/22 20:00 | 17,990.0 | 11/14/22 5:00 | 15,876.6 | 11.7% | 81 |
| 11/14/22 12:00 | 16,791.8 | 11/14/22 20:00 | 16,270.6 | 3.1% | 8 |
| 11/15/22 17:00 | 16,996.9 | 11/21/22 21:00 | 15,652.8 | 7.9% | 148 |
| 11/24/22 1:00 | 16,748.6 | 11/28/22 2:00 | 16,133.0 | 3.7% | 97 |
| 12/5/22 8:00 | 17,361.8 | 12/7/22 7:00 | 16,774.4 | 3.4% | 47 |
| 12/14/22 18:00 | 18,314.6 | 12/19/22 22:00 | 16,403.1 | 10.4% | 124 |
| 1/18/23 14:00 | 21,422.4 | 1/18/23 16:00 | 20,619.5 | 3.7% | 2 |
| 1/21/23 19:00 | 23,268.6 | 1/22/23 20:00 | 22,459.9 | 3.5% | 25 |
| 1/25/23 21:00 | 23,569.8 | 1/27/23 1:00 | 22,672.6 | 3.8% | 28 |
| 1/29/23 19:00 | 23,900.7 | 1/30/23 20:00 | 22,723.1 | 4.9% | 25 |
| 2/2/23 0:00 | 24,158.6 | 2/6/23 23:00 | 22,759.4 | 5.8% | 119 |
| 2/8/23 0:00 | 23,320.0 | 2/13/23 17:00 | 21,471.7 | 7.9% | 137 |
| 2/16/23 16:00 | 24,967.3 | 2/16/23 23:00 | 23,611.8 | 5.4% | 7 |
| 2/21/23 6:00 | 25,014.8 | 2/25/23 21:00 | 22,916.1 | 8.4% | 111 |
| 3/1/23 8:00 | 23,875.8 | 3/8/23 5:00 | 21,988.6 | 7.9% | 165 |
| 3/8/23 15:00 | 22,157.6 | 3/10/23 10:00 | 19,673.7 | 11.2% | 43 |
| 3/11/23 5:00 | 20,792.5 | 3/11/23 12:00 | 20,069.2 | 3.5% | 7 |
| 3/14/23 16:00 | 25,954.7 | 3/15/23 16:00 | 24,157.1 | 6.9% | 24 |
| 3/19/23 18:00 | 28,338.2 | 3/20/23 3:00 | 27,350.7 | 3.5% | 9 |
| 3/22/23 16:00 | 28,680.7 | 3/28/23 10:00 | 26,735.9 | 6.8% | 138 |
| 3/30/23 2:00 | 28,989.1 | 4/3/23 20:00 | 27,610.0 | 4.8% | 114 |
| 4/14/23 6:00 | 30,962.3 | 4/20/23 19:00 | 28,124.3 | 9.2% | 157 |
| 4/21/23 3:00 | 28,331.1 | 4/24/23 16:00 | 27,156.0 | 4.1% | 85 |
| 4/26/23 12:00 | 29,995.8 | 5/1/23 20:00 | 27,680.8 | 7.7% | 128 |
| 5/6/23 0:00 | 29,695.9 | 5/12/23 6:00 | 26,294.3 | 11.5% | 150 |
| 5/15/23 17:00 | 27,512.6 | 5/18/23 17:00 | 26,469.6 | 3.8% | 72 |
| 5/23/23 5:00 | 27,407.9 | 5/25/23 1:00 | 26,096.4 | 4.8% | 44 |
| 5/29/23 0:00 | 28,232.0 | 6/1/23 2:00 | 26,721.2 | 5.4% | 74 |
| 6/3/23 15:00 | 27,309.6 | 6/6/23 12:00 | 25,513.6 | 6.6% | 69 |
| 6/6/23 23:00 | 27,241.0 | 6/10/23 5:00 | 25,520.5 | 6.3% | 78 |
| 6/13/23 11:00 | 26,186.1 | 6/15/23 8:00 | 24,865.1 | 5.0% | 45 |
| 6/23/23 17:00 | 31,256.1 | 6/30/23 13:00 | 30,002.4 | 4.0% | 164 |
| 7/6/23 8:00 | 31,303.9 | 7/6/23 23:00 | 29,931.9 | 4.4% | 15 |
| 7/13/23 19:00 | 31,663.5 | 7/20/23 18:00 | 29,687.3 | 6.2% | 167 |
| 7/23/23 18:00 | 30,259.9 | 7/24/23 17:00 | 29,033.6 | 4.1% | 23 |
| 8/2/23 1:00 | 29,855.1 | 8/7/23 15:00 | 28,820.4 | 3.5% | 134 |
| 8/9/23 12:00 | 30,043.5 | 8/16/23 5:00 | 29,110.5 | 3.1% | 161 |
| 8/16/23 7:00 | 29,167.8 | 8/22/23 21:00 | 25,620.4 | 12.2% | 158 |
| 8/23/23 19:00 | 26,639.8 | 8/25/23 14:00 | 25,831.1 | 3.0% | 43 |
| 8/29/23 18:00 | 27,975.1 | 9/1/23 17:00 | 25,452.6 | 9.0% | 71 |
| 9/8/23 0:00 | 26,392.0 | 9/11/23 19:00 | 25,001.4 | 5.3% | 91 |
| Training | Test | |
|---|---|---|
| Period | 2022-04-27 9:00:00 ∼ 2023-06-10 00:00:00 | 2023-06-10 1:00:00 ∼ 2023-09-19 23:00:00 |
| # Windows | 9787 | 2447 |
| # Label = 1 | 1677 | 264 |
| F2 | GM | BA | FM | |
|---|---|---|---|---|
| RF | ||||
| SVM | ||||
| GBM | ||||
| XGB | ||||
| LSTM | ||||
| TCN | ||||
| CL-LSTM | ||||
| CL-TCN |
References
- Bouri, E.; Gil-Alana, L.A.; Gupta, R.; Roubaud, D. Modelling long memory volatility in the Bitcoin market: Evidence of persistence and structural breaks. Int. J. Financ. Econ. 2019, 24, 412–426. [Google Scholar] [CrossRef]
- Gradojevic, N.; Kukolj, D.; Adcock, R.; Djakovic, V. Forecasting Bitcoin with technical analysis: A not-so-random forest? Int. J. Forecast. 2021, 39, 1–17. [Google Scholar] [CrossRef]
- Wheatley, S.; Sornette, D.; Huber, T.; Reppen, M.; Gantner, R.N. Are Bitcoin bubbles predictable? Combining a generalized Metcalfe’s Law and the Log-Periodic Power Law Singularity model. R. Soc. Open Sci. 2019, 6, 180538. [Google Scholar] [CrossRef]
- Geuder, J.; Kinateder, H.; Wagner, N.F. Cryptocurrencies as financial bubbles: The case of Bitcoin. Financ. Res. Lett. 2019, 31, S1544612318306846. [Google Scholar] [CrossRef]
- Shu, M.; Zhu, W. Real-time prediction of Bitcoin bubble crashes. Phys. A Stat. Mech. Its Appl. 2020, 548, 124477. [Google Scholar] [CrossRef]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. arXiv 2020, arXiv:2002.05709. [Google Scholar]
- Jing, L.; Tian, Y. Self-Supervised Visual Feature Learning With Deep Neural Networks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4037–4058. [Google Scholar] [CrossRef] [PubMed]
- Laptev, N.; Yosinski, J.; Li, L.E.; Smyl, S. Time-series Extreme Event Forecasting with Neural Networks at Uber. In Proceedings of the ICML 2017 TimeSeries Workshop, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar] [CrossRef]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.H.; Buchatskaya, E.; Doersch, C.; Pires, B.A.; Guo, Z.D.; Azar, M.G.; et al. Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning. NeurIPS 2020, 33, 21271–21284. [Google Scholar]
- Johansen, A.; Sornette, D. Stock market crashes are outliers. Eur. Phys. J. B 1998, 1, 141–143. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Large Stock Market Price Drawdowns Are Outliers. J. Risk 2001, 4, 69–110. [Google Scholar] [CrossRef]
- Stiglitz, J.E. The Lessons of the North Atlantic Crisis for Economic Theory and Policy; MIT Press: 2014; pp. 335–347. [CrossRef]
- Focardi, S.M.; Fabozzi, F.J. Can We Predict Stock Market Crashes. J. Portf. Manag. 2014, 40, 183–195. [Google Scholar] [CrossRef]
- Sornette, D. Why Stock Markets Crash: Critical Events in Complex Financial Systems. J. Risk Insur. 2002, 72, 190. [Google Scholar]
- Galbraith, J.K. The Great Crash 1929; Harper Business: New York, NY, USA, 2009. [Google Scholar]
- Becker, S.; Hinton, G.E. Self-organizing neural network that discovers surfaces in random-dot stereograms. Nature 1992, 355, 161–163. [Google Scholar] [CrossRef] [PubMed]
- Bromley, J.; Bentz, J.W.; Bottou, L.; Guyon, I.; LeCun, Y.; Moore, C.; Sackinger, E.; Shah, R. Signature verification using a “Siamese” time delay neural network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 669–688. [Google Scholar] [CrossRef]
- Le-Khac, P.H.; Healy, G.; Smeaton, A.F. Contrastive Representation Learning: A Framework and Review. IEEE Access 2020, 8, 193907–193934. [Google Scholar] [CrossRef]
- Chen, X.; He, K. Exploring Simple Siamese Representation Learning. arXiv 2020. [Google Scholar] [CrossRef]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation Learning with Contrastive Predictive Coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Mohsenvand, M.; Izadi, M.; Maes, P. Contrastive Representation Learning for Electroencephalogram Classification. In Proceedings of the Machine Learning for Health NeurIPS Workshop, Virtual, 11 December 2020; pp. 238–253. Available online: https://proceedings.mlr.press/v136/mohsenvand20a.html (accessed on 13 January 2024).
- Franceschi, J.Y.; Dieuleveut, A.; Jaggi, M.; Jaggi, M. Unsupervised Scalable Representation Learning for Multivariate Time Series. arXiv 2019, arXiv:1901.10738. [Google Scholar]
- Eldele, E.; Ragab, M.; Chen, Z.; Wu, M.; Kwoh, C.K.; Li, X.; Guan, C. Time-Series Representation Learning via Temporal and Contextual Contrasting. arXiv 2022, arXiv:2208.06616. [Google Scholar] [CrossRef] [PubMed]
- Yue, Z.; Wang, Y.; Duan, J.; Yang, T.; Huang, C.; Tong, Y.; Xu, B. TS2Vec: Towards Universal Representation of Time Series. arXiv 2022, arXiv:2106.10466. [Google Scholar] [CrossRef]
- Pöppelbaum, J.; Chadha, G.S.; Schwung, A. Contrastive learning based self-supervised time-series analysis. Appl. Soft Comput. 2022, 117, 108397. [Google Scholar] [CrossRef]
- Deldari, S.; Smith, D.V.; Xue, H.; Salim, F.D. Time Series Change Point Detection with Self-Supervised Contrastive Predictive Coding. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 3124–3135. [Google Scholar] [CrossRef]
- Hou, M.; Xu, C.; Liu, Y.; Liu, W.; Bian, J.; Wu, L.; Li, Z.; Chen, E.; Liu, T.Y. Stock Trend Prediction with Multi-granularity Data: A Contrastive Learning Approach with Adaptive Fusion. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, QLD, Australia, 1–5 November 2021; pp. 700–709. [Google Scholar] [CrossRef]
- Wang, G. Coupling Macro-Sector-Micro Financial Indicators for Learning Stock Representations with Less Uncertainty. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4418–4426. [Google Scholar]
- Feng, W.; Ma, X.; Li, X.; Zhang, C. A Representation Learning Framework for Stock Movement Prediction. SSRN Electron. J. 2022, 144, 110409. [Google Scholar] [CrossRef]
- Zhan, D.; Dai, Y.; Dong, Y.; He, J.; Wang, Z.; Anderson, J. Meta-Adaptive Stock Movement Prediction with Two-Stage Representation Learning. In Proceedings of the NeurIPS 2022 Workshop on Distribution Shifts: Connecting Methods and Applications, New Orleans, LA, USA, 3 December 2022. [Google Scholar]
- Zhang, X.; Zhao, Z.; Tsiligkaridis, T.; Zitnik, M. Self-Supervised Contrastive Pre-Training For Time Series via Time-Frequency Consistency. arXiv 2022, arXiv:2206.08496. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Shocks, Crashes and Bubbles in Financial Markets. Bruss. Econ. Rev. 2010, 53, 201–253. [Google Scholar]
- Filimonov, V.; Sornette, D. Power Law Scaling and ’Dragon-Kings’ in Distributions of Intraday Financial Drawdowns. Chaos Solitons Fractals 2015, 74, 27–45. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Oord, A.v.d.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef] [PubMed]
- Nan, M.; Trascau, M.; Florea, A.M.; Iacob, C.C. Comparison between Recurrent Networks and Temporal Convolutional Networks Approaches for Skeleton-Based Action Recognition. Sensors 2021, 21, 2051. [Google Scholar] [CrossRef] [PubMed]
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal Convolutional Networks Applied to Energy-Related Time Series Forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Hewage, P.R.P.G.; Behera, A.; Trovati, M.; Pereira, E.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. Fusion Found. Methodol. Appl. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Gopali, S.; Abri, F.; Siami-Namini, S. A Comparison of TCN and LSTM Models in Detecting Anomalies in Time Series Data. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 2415–2420. [Google Scholar] [CrossRef]
- Sohn, K. Improved Deep Metric Learning with Multi-Class N-Pair Loss Objective; Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 1857–1865. [Google Scholar]
- Rashid, K.M.; Louis, J. Times-series data augmentation and deep learning for construction equipment activity recognition. Adv. Eng. Inform. 2019, 42, 100944. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Teräsvirta, T.; Lin, C.F.; Granger, C.W.J. Power of the neural network linearity test. J. Time Ser. Anal. 1993, 14, 209–220. [Google Scholar] [CrossRef]

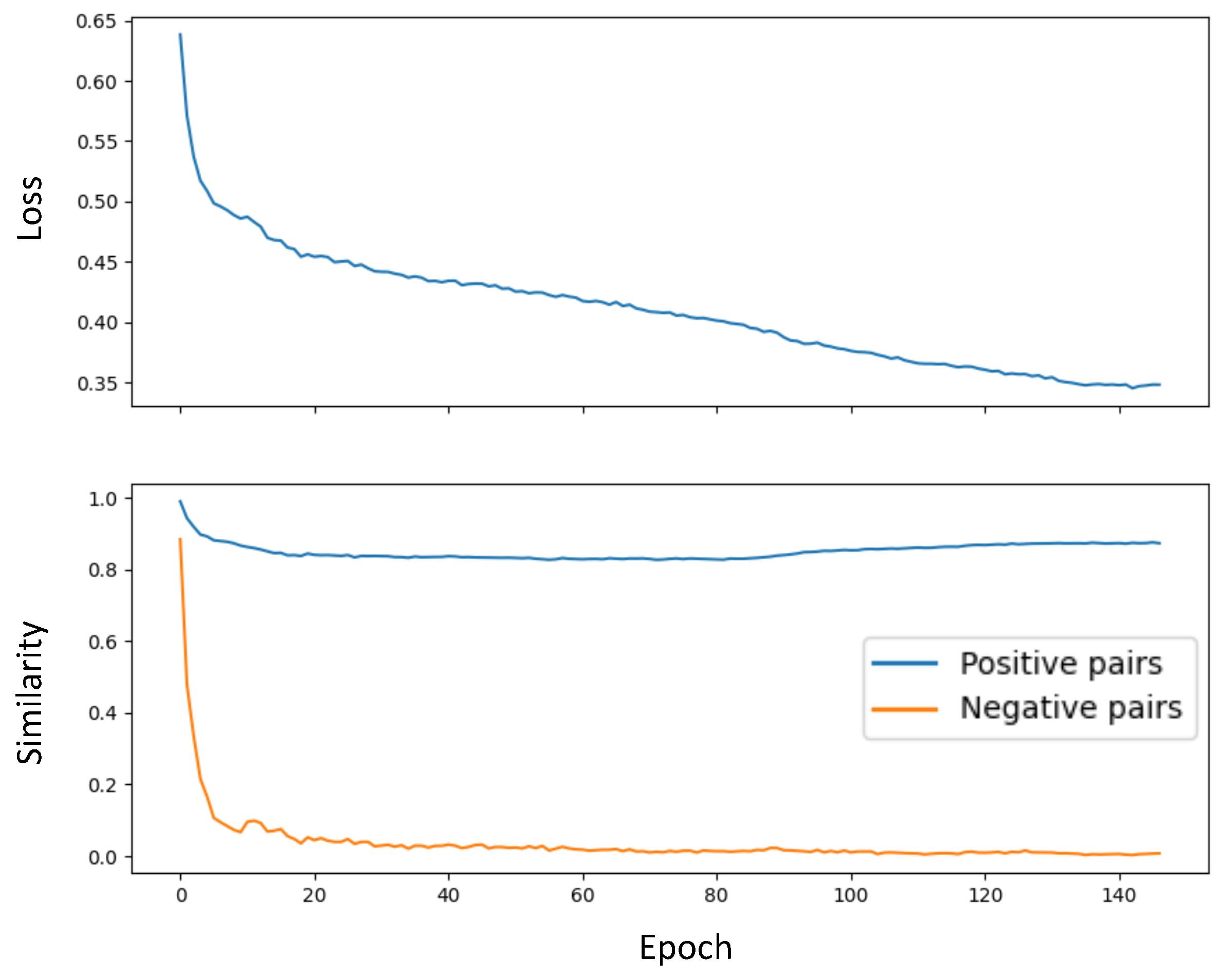
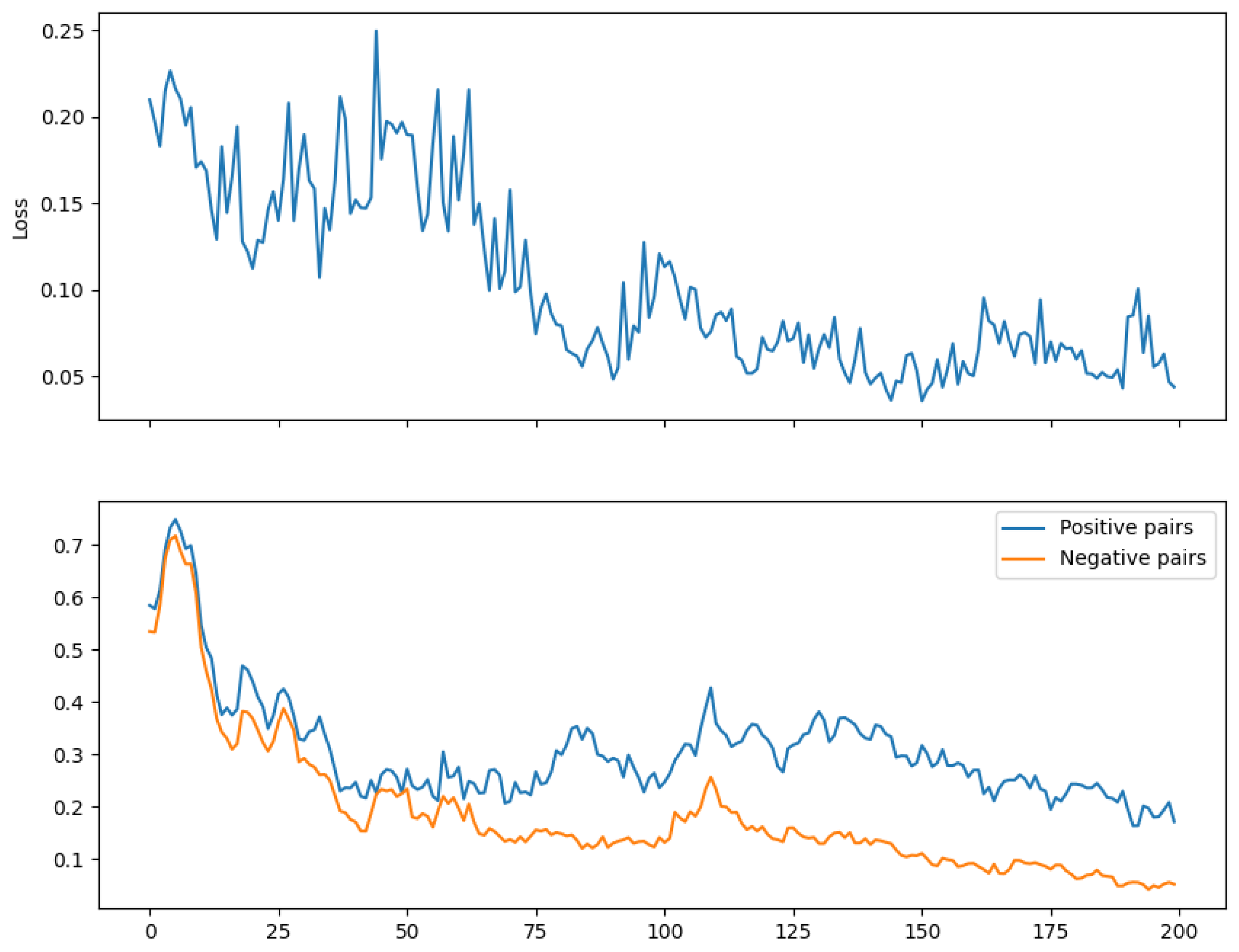
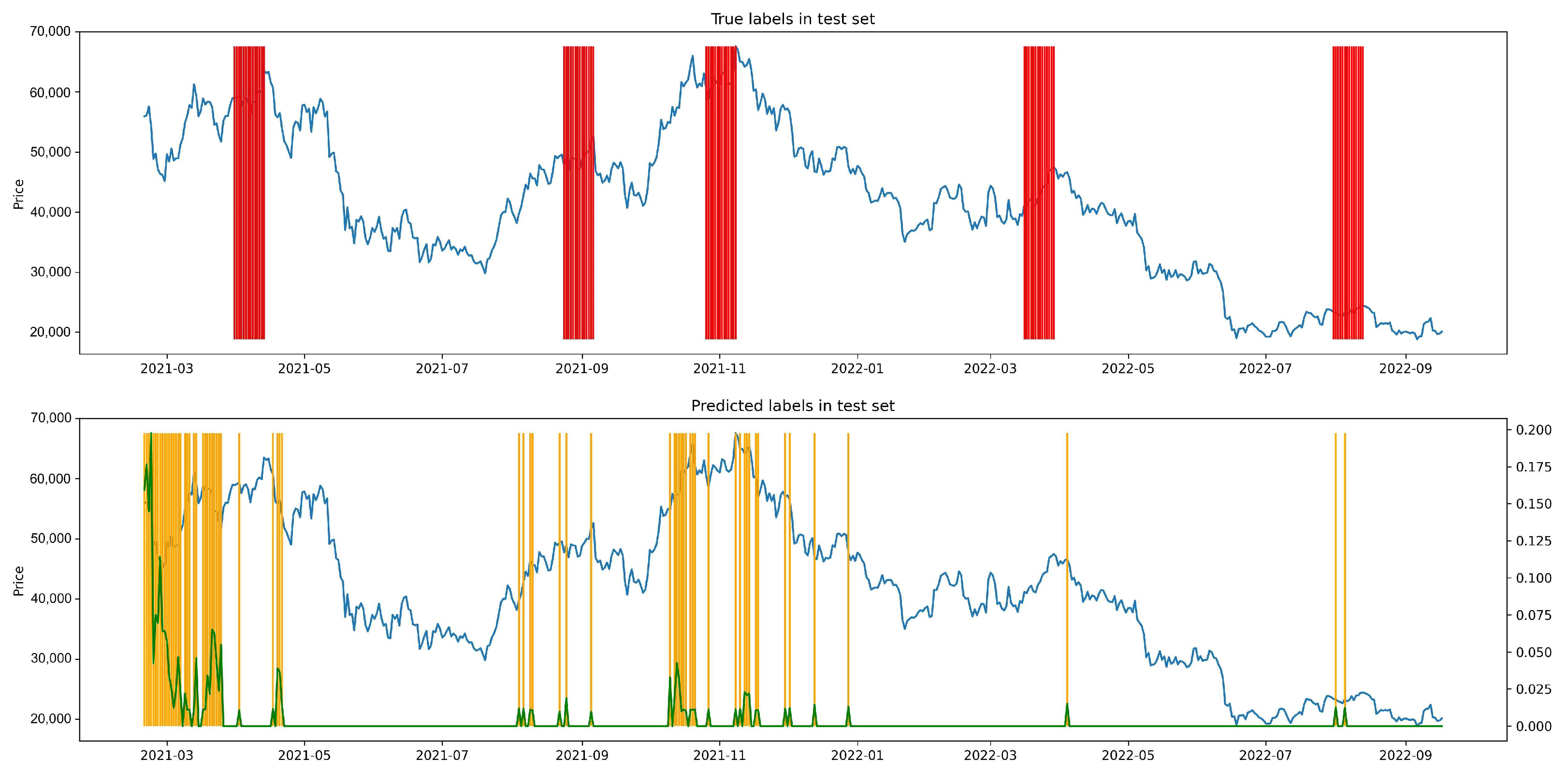
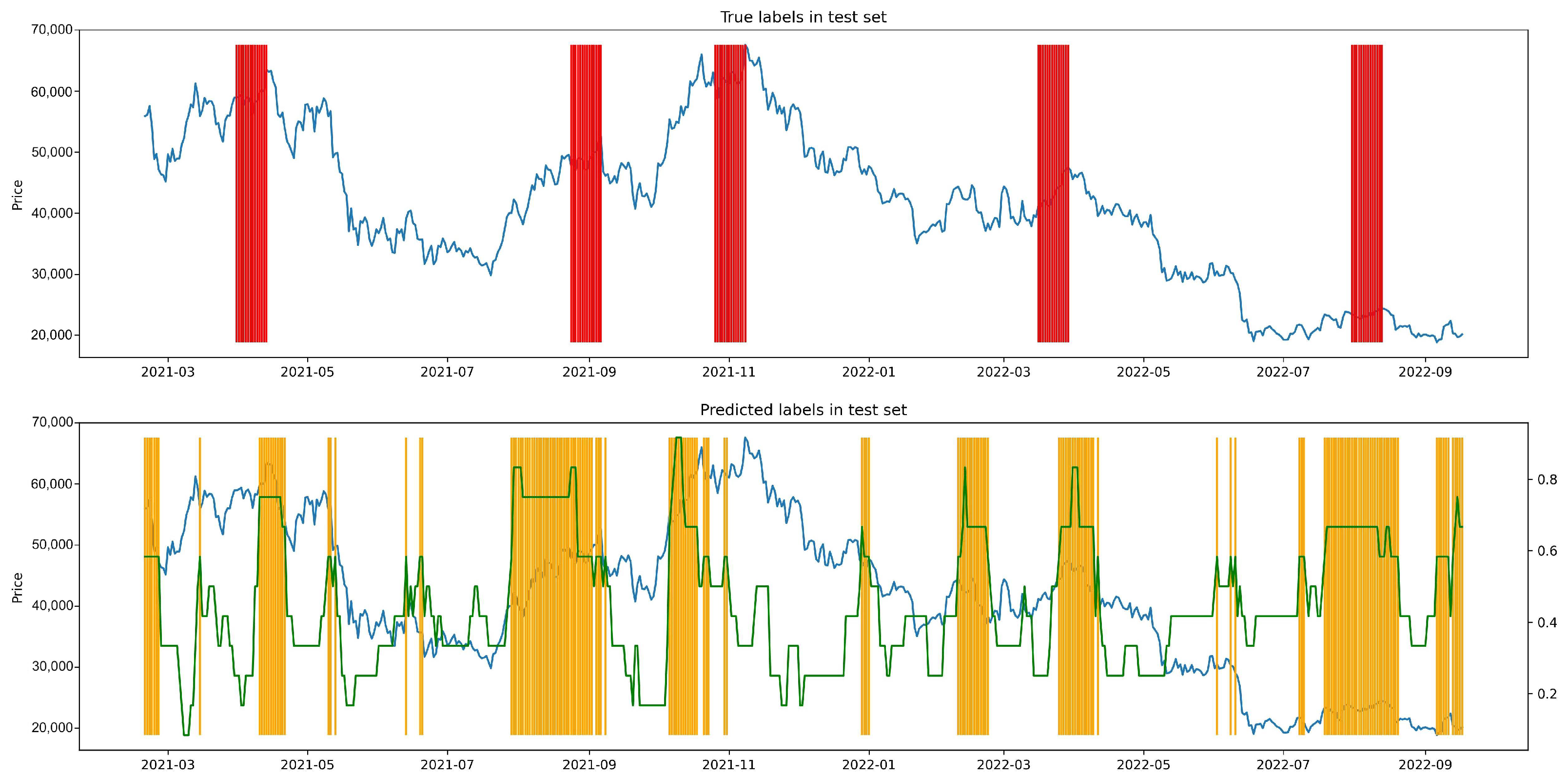
| Paper | Framework | Data | Task |
|---|---|---|---|
| Mohsenvand et al., 2020 [23] | SimCLR | non-financial | Classification |
| Deldari et al., 2021 [28] | CPC | non-financial | Change point detection |
| Hou et al., 2021 [29] | CPC | CSI-300, CSI-800, NASDAQ100 | Stock Trend Prediction |
| Wang et al., 2021 [30] | CPC | ACL18, KDD17 | Stock Trend Prediction |
| Eldele et al., 2022 [25] | non-financial | Classification | |
| Poppelbaum et al., 2022 [27] | SimCLR | non-finanical | Classification |
| Feng et al., 2022 [31] | SimCLR | CSI-500 | Stock Trend Prediction |
| Yue et al., 2022 [26] | non-financial | Classification | |
| Zhan et al., 2022 [32] | SimCLR | ACL18, KDD17 | Stock Trend Prediction |
| Zhang et al., 2022 [33] | non-financial | Classification |
| Peak Day | Peak Price | End Day | End Price | Drop | Duration |
|---|---|---|---|---|---|
| 2014-11-12 | 423.6 | 2015-01-14 | 178.1 | 58.0% | 63 |
| 2015-03-11 | 296.4 | 2015-04-14 | 219.2 | 26.1% | 34 |
| 2015-07-12 | 310.9 | 2015-08-24 | 210.5 | 32.3% | 43 |
| 2015-12-15 | 465.3 | 2016-01-15 | 364.3 | 21.7% | 31 |
| 2016-06-16 | 766.3 | 2016-08-02 | 547.5 | 28.6% | 47 |
| 2017-01-04 | 1154.7 | 2017-01-11 | 777.8 | 32.6% | 7 |
| 2017-03-03 | 1275.0 | 2017-03-24 | 937.5 | 26.5% | 21 |
| 2017-06-11 | 2958.1 | 2017-07-16 | 1929.8 | 34.8% | 35 |
| 2017-09-01 | 4892.0 | 2017-09-14 | 3154.9 | 35.5% | 13 |
| 2017-12-16 | 19,497.4 | 2018-02-05 | 6955.3 | 64.3% | 51 |
| 2018-03-05 | 11,573.3 | 2018-04-06 | 6636.3 | 42.7% | 32 |
| 2018-05-05 | 9858.2 | 2018-06-28 | 5903.4 | 40.1% | 54 |
| 2018-07-24 | 8424.3 | 2018-08-10 | 6184.7 | 26.6% | 17 |
| 2019-06-26 | 13,016.2 | 2019-07-16 | 9477.6 | 27.2% | 20 |
| 2019-10-27 | 9551.7 | 2019-12-17 | 6640.5 | 30.5% | 51 |
| 2020-02-12 | 10,326.1 | 2020-03-12 | 4970.8 | 51.9% | 29 |
| 2021-04-13 | 63,503.5 | 2021-04-25 | 49,004.3 | 22.8% | 12 |
| 2021-09-06 | 52,633.5 | 2021-09-21 | 40,693.7 | 22.7% | 15 |
| 2021-11-08 | 67,566.8 | 2022-01-22 | 35,030.3 | 48.2% | 75 |
| 2022-03-29 | 47,465.7 | 2022-06-18 | 19,017.6 | 59.9% | 81 |
| 2022-08-13 | 24,424.1 | 2022-09-06 | 18,837.7 | 22.9% | 24 |
| Training | Test | |
|---|---|---|
| period | 2014-10-30∼2021-02-18 | 2021-02-19∼2022-09-17 |
| # windows | 2304 | 576 |
| # label = 1 | 224 | 70 |
| Category | #Features | Features |
|---|---|---|
| General | 5 | median, min, max, skewness, kurtosis |
| ACF | 6 | acf1, acf10, dacf1, dacf10, d2acf1, d2acf10 |
| PACF | 3 | pacf5, dpacf5, d2pacf5 |
| STL | 6 | trend, spike, linearity, curvature, stl1, stl10 |
| Other | 7 | nonlinearity, entropy, lumpiness, stability, max_level_shift, max_var_shift, max_kl_shift |
| Model | Parameters | Values |
|---|---|---|
| RF | n_estimators | 100, 150, 200, 250 |
| max_depth | 5, 6, 7, 8 | |
| SVM | C | 0.1, 1, 10, 100 |
| gamma | 0.001, 0.01, 0.1, 1 | |
| kernel | sigmiod, rbf, poly | |
| GBM | learning_rate | 0.01, 0.03, 0.1, 0.3 |
| n_estimators | 100, 150, 200, 250 | |
| subsample | 0.6, 0.8, 1 | |
| max_depth | 5, 6, 7, 8 | |
| XGB | learning_rate | 0.01, 0.03, 0.1, 0.3 |
| n_estimators | 100, 150, 200, 250 | |
| subsample | 0.6, 0.8, 1 | |
| max_depth | 5, 6, 7, 8 |
| Item | Notation | Search Space | Filtering Condition |
|---|---|---|---|
| 3 nonlinear parameters | m | ||
| Number of oscillations | — | ||
| Damping | — | ||
| Relative error | — |
| Augmentation | F2 | GM | BA | FM |
|---|---|---|---|---|
| None | ||||
| Jittering | ||||
| Scaling | ||||
| Magnitude-warping | ||||
| Time-warping | ||||
| Crop-and-resize | ||||
| Smoothing |
| Augmentation | F2 | GM | BA | FM |
|---|---|---|---|---|
| None, None | ||||
| Jittering, Time-warping | ||||
| Jittering, Magnitude-warping | ||||
| Time-warping, Magnitude-warping |
| Augmentation | F2 | GM | BA | FM |
|---|---|---|---|---|
| None, None | ||||
| Jittering, Time-warping | ||||
| Jittering, Magnitude-warping | ||||
| Time-warping, Magnitude-warping |
| F2 | GM | BA | FM | |
|---|---|---|---|---|
| RF | ||||
| SVM | ||||
| GBM | ||||
| XGB | 0.46 ± 0.004 | 0.66 ± 0.003 | 0.66 ± 0.003 | 0.37 ± 0.003 |
| LSTM | ||||
| TCN | 0.50 ± 0.07 | 0.68 ± 0.04 | 0.69 ± 0.05 | 0.40 ± 0.06 |
| CL-LSTM | ||||
| CL-TCN | 0.54 ± 0.06 | 0.71 ± 0.04 | 0.72 ± 0.04 | 0.44 ± 0.04 |
| Simple Average | Weighted Average | Hard Vote | Logistic | CL-TCN | |
|---|---|---|---|---|---|
| F2 | 0.534 | 0.495 | 0.516 | 0.311 | 0.535 |
| GM | 0.710 | 0.687 | 0.700 | 0.538 | 0.711 |
| BA | 0.715 | 0.687 | 0.700 | 0.575 | 0.722 |
| FM | 0.430 | 0.400 | 0.416 | 0.265 | 0.436 |
| LPPLS-Indicator | CL-Indicator | |
|---|---|---|
| F2 | 0.075 | 0.423 |
| GM | 0.254 | 0.634 |
| BA | 0.487 | 0.642 |
| FM | 0.081 | 0.349 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Shu, M.; Zhu, W. Contrastive Learning Framework for Bitcoin Crash Prediction. Stats 2024, 7, 402-433. https://doi.org/10.3390/stats7020025
Liu Z, Shu M, Zhu W. Contrastive Learning Framework for Bitcoin Crash Prediction. Stats. 2024; 7(2):402-433. https://doi.org/10.3390/stats7020025
Chicago/Turabian StyleLiu, Zhaoyan, Min Shu, and Wei Zhu. 2024. "Contrastive Learning Framework for Bitcoin Crash Prediction" Stats 7, no. 2: 402-433. https://doi.org/10.3390/stats7020025
APA StyleLiu, Z., Shu, M., & Zhu, W. (2024). Contrastive Learning Framework for Bitcoin Crash Prediction. Stats, 7(2), 402-433. https://doi.org/10.3390/stats7020025







