A Note on Simultaneous Confidence Intervals for Direct, Indirect and Synthetic Estimators
Abstract
1. Introduction
2. Simultaneous Confidence Intervals for Domains
3. Considered Direct and Indirect Estimators
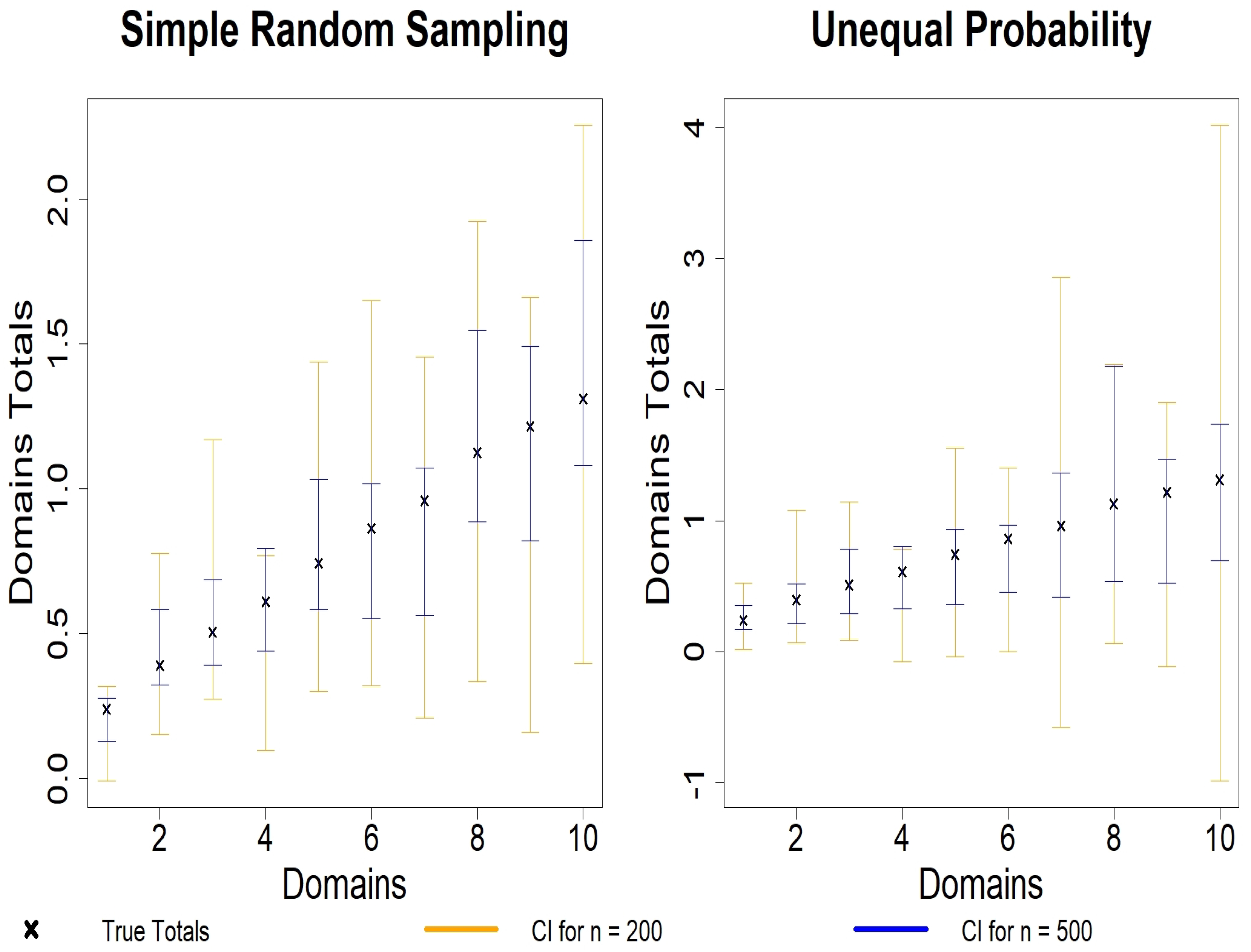
4. Simulation Studies
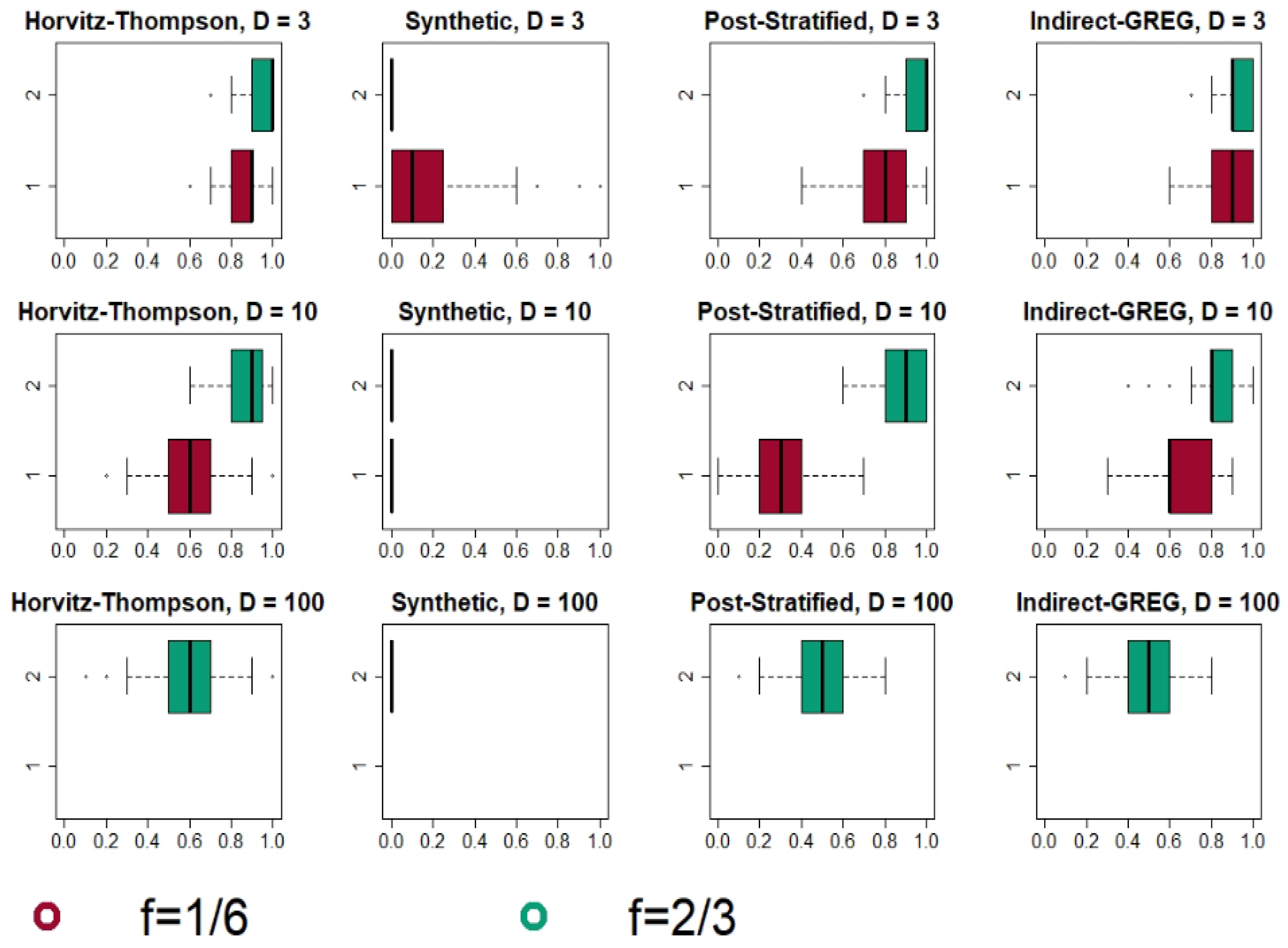
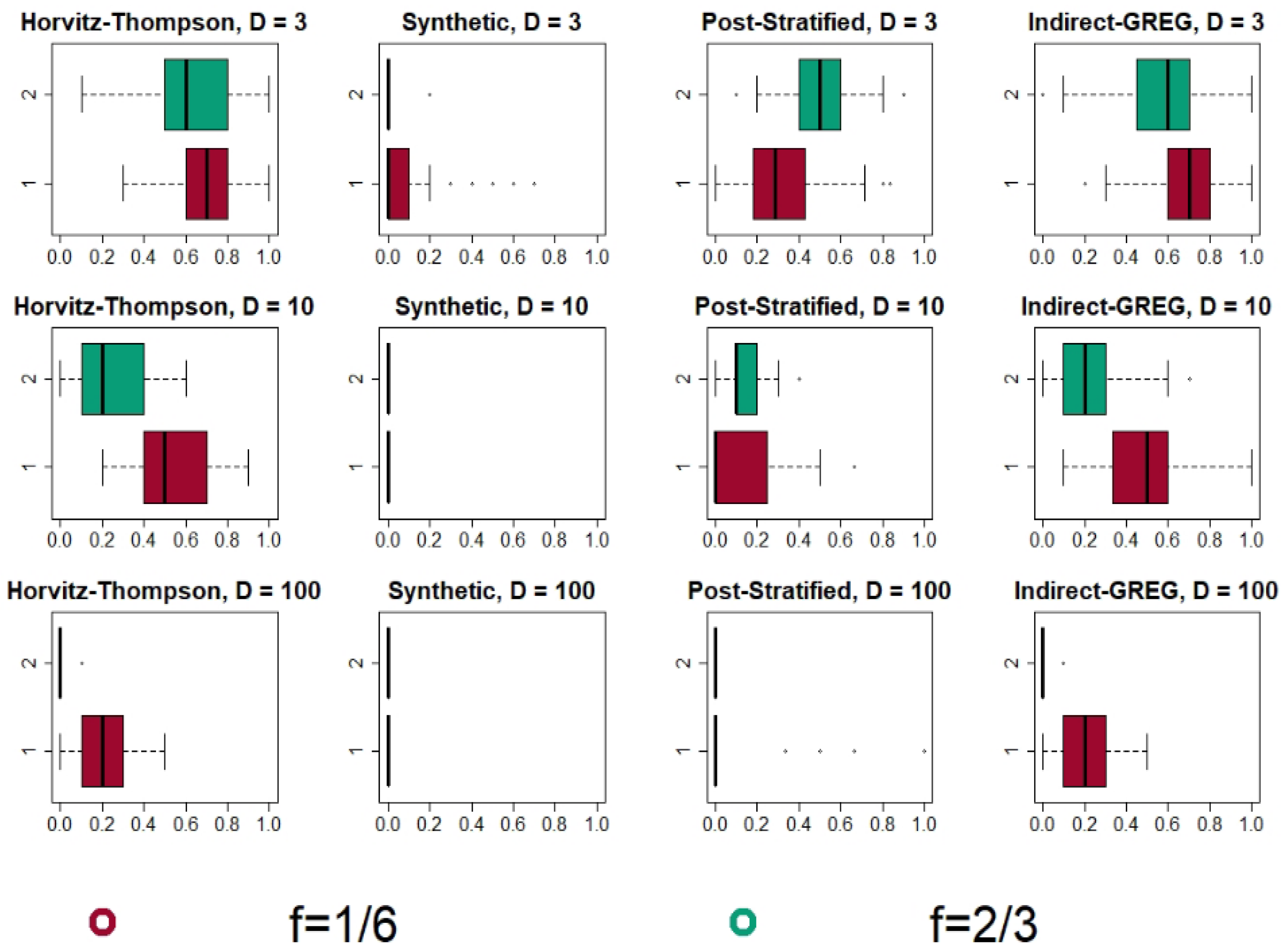
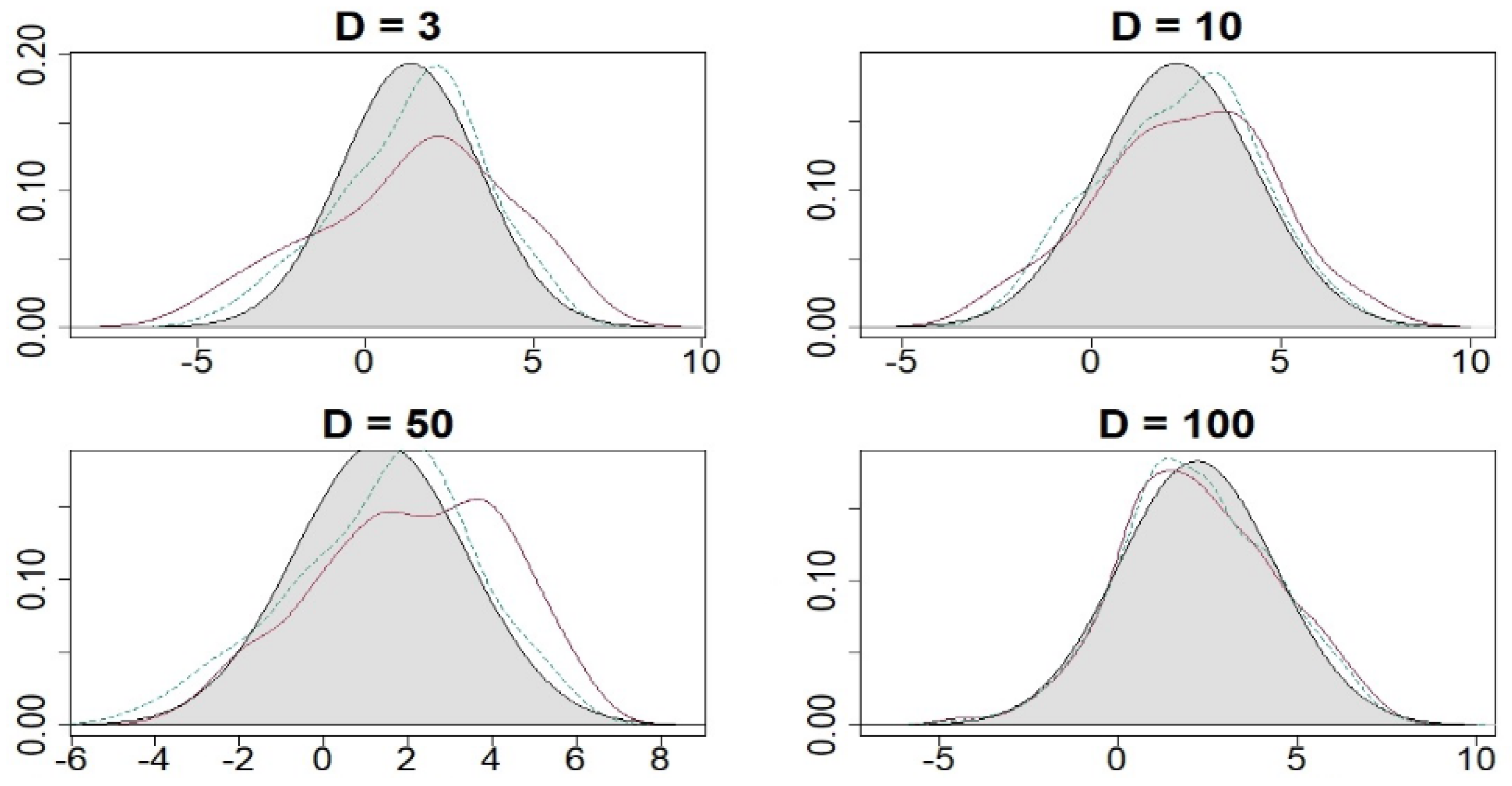
4.1. Simulation Designs
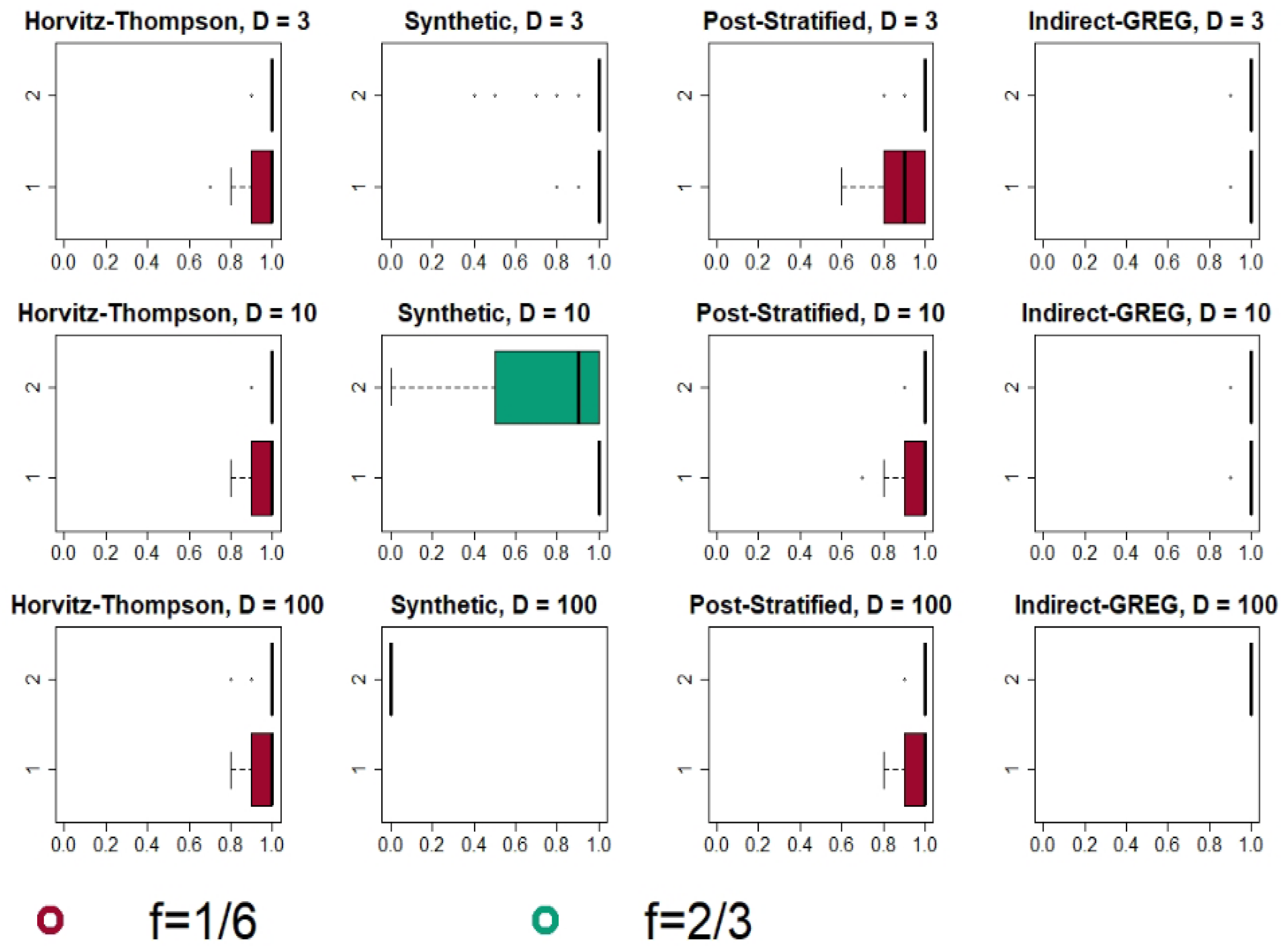
4.2. Simulation Results
4.2.1. Bonferroni and Šidák Method: Results and Analysis
4.2.2. Max-Type Statistic with Bootstrap and an Overall Comparison
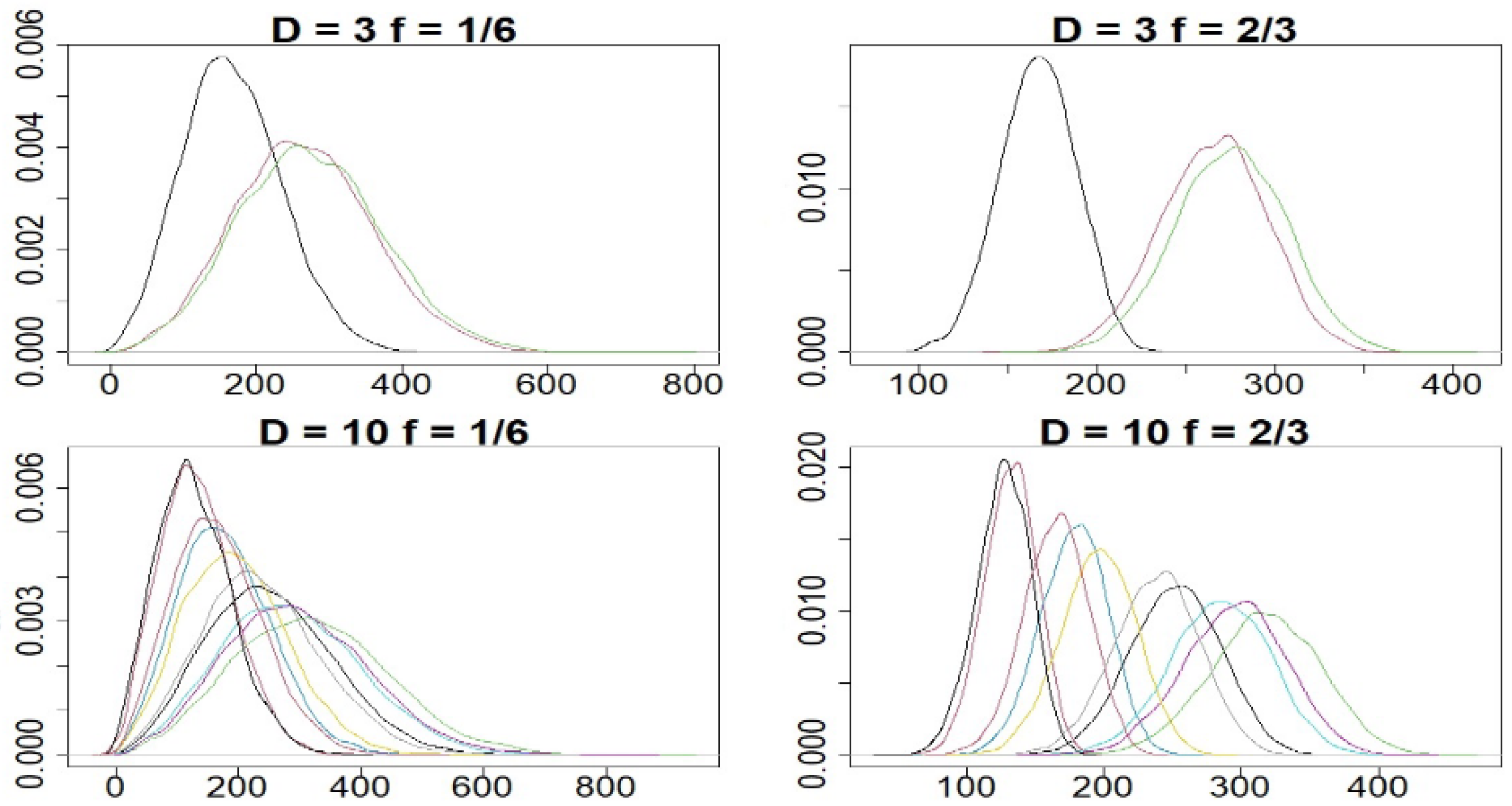
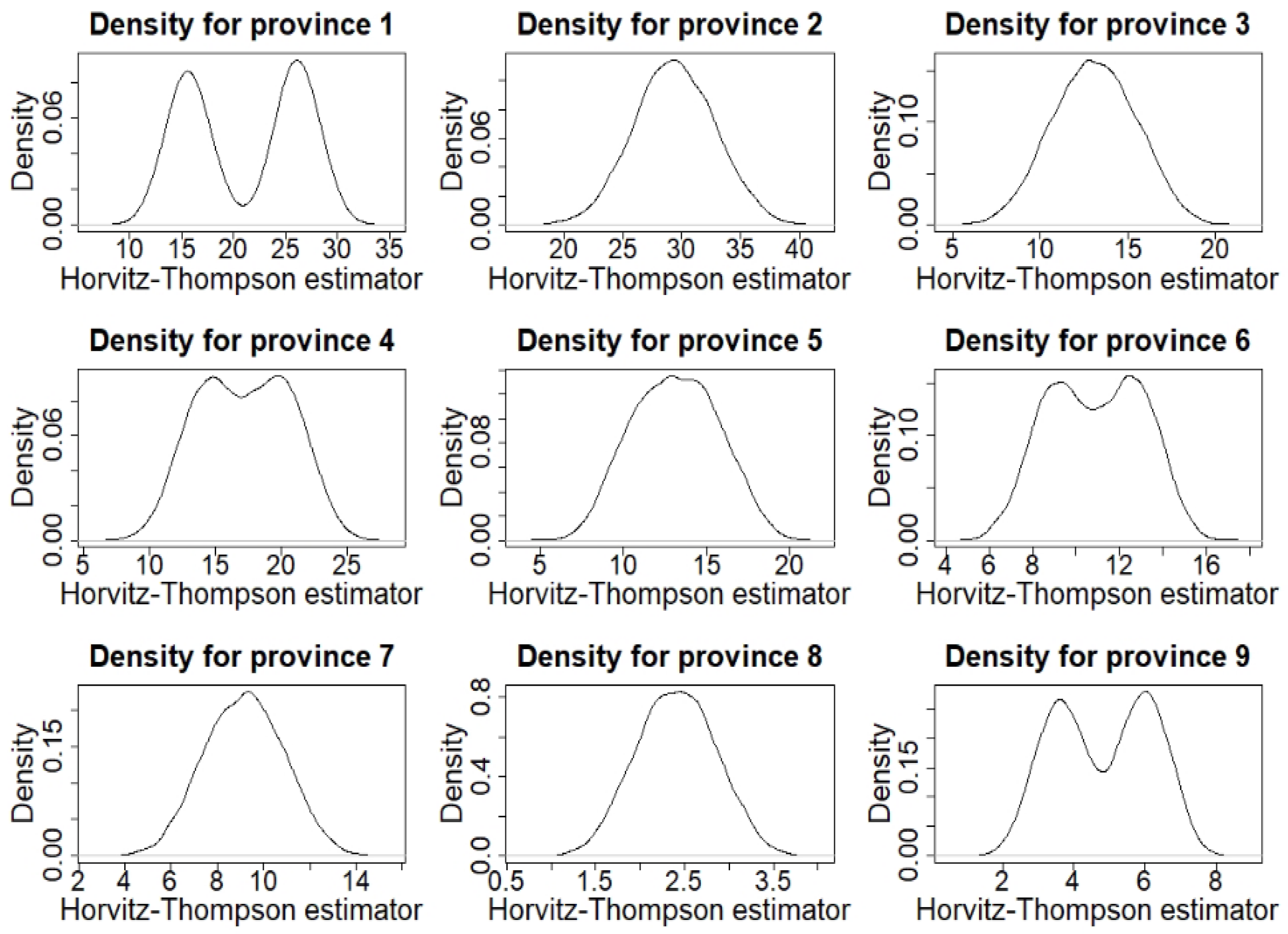
5. Estimating Total Tax Incomes: A Simulation Study with Belgian Data
6. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pfeffermann, D. New Important Developments in Small Area Estimation. Stat. Sci. 2013, 28, 40–68. [Google Scholar] [CrossRef]
- Tillé, Y. Sampling and Estimation from Finite Populations; Wiley Series in Survey Methodology; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Morales, D.; Lefler, M.D.E.; Pérez, A.; Hobza, T. A Course on Small Area Estimation and Mixed Models; Statistics for Social and Behavioral Sciences; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Little, R. To model or not to model? Competing modes of inference for finite population sampling. J. Am. Stat. Assoc. 2004, 99, 546–556. [Google Scholar] [CrossRef]
- Stanke, H.; Finley, A.; Domke, G. Simplifying Small Area Estimation With rFIA: A Demonstration of Tools and Techniques. Front. For. Glob. Chang. 2022, 5. [Google Scholar] [CrossRef]
- Lohr, S. Sampling: Design and Analysis; Chapman and Hall, CRC Press: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Eurostat. Guidelines on Small Area Estimation for City Statistics and Other Functional Geographies; European Union: Maastricht, The Netherlands, 2019. [Google Scholar]
- Tzavidis, N.; Zhang, L.C.; Luna, A.; Schmid, T.; Rojas-Perilla, N. From start to finish: A framework for the production of small area official statistics. J. R. Statist. Soc. A 2018, 181, 927–979. [Google Scholar] [CrossRef]
- Hochberg, Y.; Tamhane, A. Multiple Comparison Procedures; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Romano, J.; Wolf, M. Exact and approximate stepdown methods for multiple hypothesis testing. J. Am. Stat. Assoc. 2005, 100, 94–108. [Google Scholar] [CrossRef]
- Reluga, K.; Lombardía, K.; Sperlich, S. Simultaneous Inference for Empirical Best Predictors with a Poverty Study in Small Areas. J. Am. Stat. Assoc. 2023, 118, 583–595. [Google Scholar] [CrossRef]
- Reluga, K.; Lombardía, K.; Sperlich, S. Simultaneous Inference for linear mixed model parameters with an application to small area estimation. Int. Stat. Rev. 2023, 91, 193–217. [Google Scholar] [CrossRef]
- Burris, K.; Hoff, P. Exact Adaptive Confidence Intervals for Small Areas. J. Surv. Stat. Methodol. 2020, 8, 206–230. [Google Scholar] [CrossRef]
- Kramlinger, P.; Krivobokova, T.; Sperlich, S. Marginal and Conditional Multiple Inference for Linear Mixed Model Predictors. J. Am. Stat. Assoc. 2023, 118, 2344–2355. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple Comparisons Among Means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Šidák, Z. Rectangular confidence regions for the means of multivariate normal distributions. J. Am. Stat. Assoc. 1967, 62, 626–633. [Google Scholar]
- Chauvet, G. Méthodes de Bootstrap en Population Finie. Ph.D. Thesis, Université de Rennes 2, Incheon, Republic of Korea, 2007. [Google Scholar]
- Estevao, V.M.; Särndal, C.E. Borrowing Strength Is Not the Best Technique Within a Wide Class of Design-Consistent Domain Estimators. J. Off. Stat. 2004, 20, 645–669. [Google Scholar]
- Horvitz, D.G.; Thompson, D.J. A generalization of sampling without remplacement from a finite universe. J. Am. Stat. Assoc. 1952, 47, 663–685. [Google Scholar] [CrossRef]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling, 1st ed.; Springer Series in Statistics; Springer Inc.: New York, NY, USA, 1992. [Google Scholar]
- Ghosh, M.; Rao, J. Small Area Estimation: An Appraisal. Stat. Sci. 1994, 9, 55–93. [Google Scholar] [CrossRef]
- Hájek, J. Discussion of an essay on the logical foundations of survey sampling, part ones by D. Basu. In Foundations of Statistical Inference; Godambe, V.P., Sprott, D.A., Eds.; Toronto, Holt, Rinehart and Winston of Canada: Toronto, ON, Canada, 1971. [Google Scholar]
- Lehtonen, R.; Veijanen, A. Design-Based Methods of Estimation for Domains and Small Areas; Handbook of Statistics; Elsevier B.V.: Amsterdam, The Netherlands, 2009; Volume 29B, Chapter 31; pp. 219–249. [Google Scholar]
- Tillé, Y.; Matei, A. Sampling: Survey Sampling; R Package Version 2.9. 2021. Available online: https://cran.r-project.org/web/packages/sampling/index.html (accessed on 8 February 2024).


| f | Bonferroni | Šidák | Max-Type | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H-T | D-G | Syn | P-S | I-G | H-T | D-G | Syn | P-S | I-G | H-T | D-G | Syn | P-S | I-G | |
| = 2 | D = 3 | ||||||||||||||
| 1/6 | 0.874 | 0.355 | 0.187 | 0.773 | 0.887 | 0.874 | 0.355 | 0.205 | 0.773 | 0.887 | 0.946 | 0.946 | 0.991 | 0.895 | 0.999 |
| 2/3 | 0.953 | 0.87 | 0 | 0.953 | 0.918 | 0.953 | 0.87 | 0 | 0.953 | 0.917 | 0.987 | 0.998 | 0.951 | 0.983 | 0.998 |
| 1/6 | 0.865 | 0.355 | 0.546 | 0.677 | 0.869 | 0.864 | 0.355 | 0.565 | 0.676 | 0.869 | 0.948 | 0.969 | 0.986 | 0.914 | 1 |
| 2/3 | 0.946 | 0.87 | 0.015 | 0.926 | 0.943 | 0.945 | 0.87 | 0.014 | 0.926 | 0.942 | 0.992 | 1 | 0.687 | 0.987 | 1 |
| = 0.02 | |||||||||||||||
| 1/6 | 0.873 | 0.355 | 0.971 | 0.773 | 0.902 | 0.873 | 0.355 | 0.978 | 0.773 | 0.902 | 0.952 | 0.954 | 0.995 | 0.895 | 1 |
| 2/3 | 0.948 | 0.87 | 0.572 | 0.953 | 0.932 | 0.948 | 0.87 | 0.57 | 0.953 | 0.929 | 0.978 | 1 | 0.956 | 0.983 | 1 |
| 1/6 | 0.869 | 0.355 | 0.912 | 0.677 | 0.872 | 0.867 | 0.355 | 0.919 | 0.676 | 0.871 | 0.943 | 0.971 | 0.993 | 0.914 | 1 |
| 2/3 | 0.946 | 0.87 | 0.015 | 0.926 | 0.943 | 0.945 | 0.87 | 0.014 | 0.926 | 0.942 | 0.992 | 1 | 0.687 | 0.987 | 1 |
| = 2 | D = 10 | ||||||||||||||
| 1/6 | 0.63 | 0.017 | 0 | 0.274 | 0.654 | 0.629 | 0.017 | 0 | 0.274 | 0.654 | 0.949 | 0.87 | 1 | 0.947 | 0.993 |
| 2/3 | 0.88 | 0.73 | 0 | 0.873 | 0.825 | 0.88 | 0.729 | 0 | 0.872 | 0.824 | 0.991 | 1 | 0.731 | 0.992 | 0.999 |
| = 0.02 | |||||||||||||||
| 1/6 | 0.618 | 0.017 | 0.708 | 0.274 | 0.701 | 0.616 | 0.017 | 0.724 | 0.274 | 0.7 | 0.951 | 0.879 | 1 | 0.947 | 0.999 |
| 2/3 | 0.868 | 0.73 | 0.005 | 0.873 | 0.855 | 0.867 | 0.729 | 0.005 | 0.872 | 0.855 | 0.99 | 1 | 0.61 | 0.992 | 1 |
| = 2 | D = 50 | ||||||||||||||
| 1/6 | 0.142 | 0 | 0 | 0 | 0.171 | 0.141 | 0 | 0 | 0 | 0.171 | 0.977 | 1 | 1 | 0.964 | 0.998 |
| 2/3 | 0.724 | 0.448 | 0 | 0.661 | 0.637 | 0.724 | 0.446 | 0 | 0.66 | 0.636 | 0.984 | 1 | 0.007 | 0.999 | 1 |
| = 0.02 | |||||||||||||||
| 1/6 | 0.105 | 0 | 0 | 0 | 0.224 | 0.105 | 0 | 0 | 0 | 0.223 | 0.962 | 1 | 1 | 0.964 | 1 |
| 2/3 | 0.703 | 0.448 | 0 | 0.661 | 0.647 | 0.701 | 0.446 | 0 | 0.66 | 0.645 | 0.987 | 1 | 0.006 | 0.999 | 1 |
| = 2 | D = 100 | ||||||||||||||
| 1/6 | 0.019 | 0 | 0 | 0 | 0.039 | 0.019 | 0 | 0 | 0 | 0.039 | 0.973 | 1 | 1 | 0.962 | 0.988 |
| 2/3 | 0.582 | 0.257 | 0 | 0.511 | 0.508 | 0.578 | 0.253 | 0 | 0.51 | 0.506 | 0.988 | 1 | 0 | 0.993 | 1 |
| = 0.02 | |||||||||||||||
| 1/6 | 0.008 | 0 | 0 | 0 | 0.052 | 0.008 | 0 | 0 | 0 | 0.051 | 0.96 | 1 | 1 | 0.962 | 0.998 |
| 2/3 | 0.577 | 0.257 | 0 | 0.511 | 0.549 | 0.575 | 0.253 | 0 | 0.51 | 0.547 | 0.995 | 1 | 0 | 0.993 | 1 |
| D = 5 | D = 10 | D = 50 | |
|---|---|---|---|
| N | 1000 | 2000 | 10,000 |
| n | 750 | 1500 | 8500 |
| f | 0.75 | 0.75 | 0.85 |
| Coverage | 0.93 | 0.92 | 0.9 |
| D = 3 | D = 10 | D = 50 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | 0.25 | 0.5 | 0.75 | 0.8 | 0.9 | 0.25 | 0.5 | 0.75 | 0.8 | 0.9 | 0.25 | 0.5 | 0.75 | 0.8 | 0.9 |
| Max-Type | 2.56 | 2.63 | 2.88 | 3.03 | 3.65 | 3.35 | 3.2 | 3.43 | 3.36 | 3.75 | 4.32 | 3.86 | 4.16 | 4.91 | 4.57 |
| Bonferroni | 2.42 | 2.41 | 2.4 | 2.4 | 2.4 | 2.82 | 2.81 | 2.81 | 2.81 | 2.81 | 3.29 | 3.29 | 3.29 | 3.29 | 3.29 |
| f | Bonferroni | Šidák | Max-Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H-T | Syn | P-S | I-G | H-T | Syn | P-S | I-G | H-T | Syn | P-S | I-G | |
| = 2 | D = 3 | |||||||||||
| 1/6 | 0.713 | 0.08 | 0.3183 | 0.7065 | 0.713 | 0.08 | 0.3183 | 0.70355 | 0.883 | 0.297 | 0.8404 | 0.99 |
| 2/3 | 0.625 | 0.002 | 0.492 | 0.569 | 0.624 | 0.002 | 0.489 | 0.568 | 0.843 | 0.067 | 0.804 | 0.923 |
| = 0.02 | ||||||||||||
| 1/6 | 0.727 | 0.773 | 0.291 | 0.671 | 0.726 | 0.773 | 0.291 | 0.667 | 0.894 | 0.793 | 0.836 | 1 |
| 2/3 | 0.628 | 0.428 | 0.492 | 0.497 | 0.625 | 0.426 | 0.489 | 0.497 | 0.851 | 0.538 | 0.804 | 0.962 |
| = 2 | D = 10 | |||||||||||
| 1/6 | 0.532 | 0 | Na | 0.469 | 0.531 | 0 | Na | 0.464 | 0.884 | 0.009 | Na | 1 |
| 2/3 | 0.253 | 0 | 0.151 | 0.229 | 0.25 | 0 | 0.151 | 0.229 | 0.905 | 0.002 | 0.863 | 0.961 |
| = 0.02 | ||||||||||||
| 1/6 | 0.507 | 0.51 | 0.078 | 0.476 | 0.505 | 0.508 | 0.0779 | 0.473 | 0.889 | 0.526 | 0.739 | 1 |
| 2/3 | 0.269 | 0.058 | 0.151 | 0.126 | 0.268 | 0.058 | 0.151 | 0.123 | 0.905 | 0.179 | 0.863 | 0.987 |
| = 2 | D = 50 | |||||||||||
| 1/6 | 0.287 | 0 | Na | 0.316 | 0.286 | 0,00 | Na | 0.315 | 0.8 | 0.003 | Na | 1 |
| 2/3 | 0.004 | 0.001 | 0 | 0.004 | 0.004 | 0 | 0 | 0.004 | 0.946 | 0.001 | 0.926 | 0.946 |
| = 0.02 | ||||||||||||
| 1/6 | 0.367 | 0.021 | Na | 0.367 | 0.367 | 0.02 | Na | 0.367 | 0.794 | 0.2882 | Na | 0.794 |
| 2/3 | 0.005 | 0.001 | 0 | 0 | 0.005 | 0.001 | 0 | 0 | 0.934 | 0.019 | 0.926 | 0.995 |
| = 2 | D = 100 | |||||||||||
| 1/6 | 0.197 | 0 | Na | 0.289 | 0.197 | 0,00 | Na | 0.286 | 0.651 | 0.009 | Na | 1 |
| 2/3 | 0.001 | 0 | 0 | 0 | 0.001 | 0 | 0 | 0 | 0.964 | 0 | 0.93 | 0.991 |
| = 0.02 | ||||||||||||
| 1/6 | 0.286 | 0.004 | Na | 0.361 | 0.282 | 0.0043 | Na | 0.358 | 0.65 | 0.4243 | Na | 1 |
| 2/3 | 0 | 0.001 | 0 | 0 | 0 | 0.001 | 0 | 0 | 0.957 | 0.007 | 0.93 | 0.994 |
| Provinces | Arrondissements | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bonferroni | Šidák | Max-Type | Bonferroni | Šidák | Max-Type | |||||||
| H-T | I-GREG | H-T | I-GREG | H-T | I-GREG | H-T | I-GREG | H-T | I-GREG | H-T | I-GREG | |
| 0.3647 | 0.4138 | 0.3637 | 0.4124 | 0.9618 | 1 | 0.0917 | 0.0196 | 0.091 | 0.0196 | 0.9019 | 0.9679 | |
| 0.4824 | 0.606 | 0.4813 | 0.6054 | 0.9753 | 1 | 0.0206 | 0.0292 | 0.0204 | 0.0291 | 0.9677 | 0.9998 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valvason, C.Q.; Sperlich, S. A Note on Simultaneous Confidence Intervals for Direct, Indirect and Synthetic Estimators. Stats 2024, 7, 333-349. https://doi.org/10.3390/stats7010020
Valvason CQ, Sperlich S. A Note on Simultaneous Confidence Intervals for Direct, Indirect and Synthetic Estimators. Stats. 2024; 7(1):333-349. https://doi.org/10.3390/stats7010020
Chicago/Turabian StyleValvason, Christophe Quentin, and Stefan Sperlich. 2024. "A Note on Simultaneous Confidence Intervals for Direct, Indirect and Synthetic Estimators" Stats 7, no. 1: 333-349. https://doi.org/10.3390/stats7010020
APA StyleValvason, C. Q., & Sperlich, S. (2024). A Note on Simultaneous Confidence Intervals for Direct, Indirect and Synthetic Estimators. Stats, 7(1), 333-349. https://doi.org/10.3390/stats7010020






