The Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-G Family of Distributions with Applications

Abstract

The new Ristić and Balakhrisnan or Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-G (RB-TL-TII-EHL-G) family of distributions is introduced and investigated in this paper. This work derives and studies some of the main statistical characteristics of this new family of distributions. The maximum likelihood estimation technique is used to estimate the model parameters, and a simulation study is used to assess the consistency of the estimators. Applications to three real-life datasets from various fields show the value and adaptability of the new RB-TL-TII-EHL-G family of distributions. From our results, it is evident that the new proposed distribution is flexible enough to characterize datasets from different fields compared to several other existing distributions in the literature.

1. Introduction

Probability distributions play an important role in statistical modeling and analysis in different fields including engineering, medicine, and life sciences. However, classical lifetime distributions such as the exponential distribution, Rayleigh distribution, Pareto distribution, and Weibull distribution have a limited range of behavior when it comes to modeling new varieties of real datasets. Hence, researchers have been increasingly interested in generating new families with high flexibility to act as alternatives to available distributions. Some of the newly generated distributions in the literature include the following: the extended exponential-Weibull distribution by [1], the beta Burr-type X distribution by [2], theheavy-tailed log-logistic distribution by [3], the half-Cauchy generalized exponential distribution by [4], the novel alpha power Gumbel distribution by [5], the Weibull-G family of probability distributions by [6], the type II quasi-Lambert-G family of probability distributions by [7], the novel-G family of distributions by [8], thePoisson reciprocal Rayleigh family of distributions by [9], a quasi-Poisson Topp-Leone generated-G family of distributions by [10], the Poisson generated family of distributions by [11], the Gompertz-G family of distributions by [12], the exponentiated Weibull-H family of distributions by [13], the power Lindley-G family of distributions by [14], the Marshall-Olkin odd power generalized Weibull-G family of distributions by [15], the exponential T-X family of distributions by [16], the type II exponentiated half logistic Topp-Leone-Marshall-Olkin-G family of distributions by [17], the type II exponentiated half logistic generated family of distributions by [18], type II exponentiated half logistic-Topp-Leone-G power series class of distributions by [17], the type II half logistic exponential distribution by [19], and the type II exponentiated half logistic-Gompertz Topp-Leone-G family of distributions by [20], to mention a few.

The gamma transformation has been used to extend various distributions available in the literature. The following are some generated distributions via the gamma transformation: the unit gamma-G class of distributions by [21], the Zografos-Balakrishnan-G family of distributions by [22], the gamma odd power generalized Weibull-G family of distributions by [23], the gamma-generalized inverse Weibull distribution by [24], the Ristić and Balakrishnan Lindley-Poisson distribution by [25], the gamma odd Burr III-G family of distributions by [26], the Zografos-Balakrishnan Burr XII distribution by [27], the Zografos-Balakrishnan Lindley distribution by [28], the gamma odd Burr X-G family of distributions by [29], the gamma Lindley distribution by [30], the gamma Weibull-G family of distributions by [31], the gamma Kumaraswamy-G family of distributions by [32], the gamma extended Weibull family of distributions by [33], and the gamma-Rayleigh distribution by [34], to mention a few.

Our basic motivations lie in the flexibility of the new family of distributions to model both monotonic and non-monotonic hazard rate functions by capturing different shapes; the ability of the new model to provide better fits than the baseline and several extended distributions available in the literature; and the applicability of the special cases of the new family of distributions in real-life scenarios. Another interesting part is the role played by the extra shape parameter(s) by introducing skewness and modulating the weight of the tails of any baseline distribution.

Throughout this paper, we will set

$$K_G\left(x;a,\underline{\psi }\right)={\left(\frac{1-G(x;\underline{\psi })}{1+G(x;\underline{\psi })}\right)}^{2a}.$$

The cumulative distribution function (cdf) and probability density function (pdf) of the new Topp-Leone-type II exponentiated half logistic-G family of distributions are given by

$$\begin{array}{ccc}\hfill F(x;b,a,\underline{\psi })& =& {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f(x;b,a,\underline{\psi })& =& 4ab{\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\hfill \\ & \times & \frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}},\hfill \end{array}$$

for $b,a>0$ and baseline parameter vector $\underline{\psi }$ (see [35] for additional details).

The gamma generator proposed by [36] has the cdf and pdf given by

$$F_{RB}(x;\delta )=1-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\delta \right)}}{\int }_0^{-log\left(G\left(x\right)\right)}{t}^{\delta -1-t}dt,\delta >0$$

and

$$f_{RB}(x;\delta )={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\delta \right)}}{\left[-log\left(G\left(x\right)\right)\right]}^{\delta -1}g\left(x\right),x\in \mathbb{R},$$

where $G\left(x\right)$ is the baseline cdf and $\delta >0$ is a shape parameter.

This article is structured as follows: Section 2 presents the proposed family and its sub-families. Section 3 contains the linear representation of the pdf of the RB-TL-TII-EHL-G family of distributions, the reliability function and the quantile function. We derive some of the statistical and mathematical properties under Section 4. Monte Carlo simulation results are given in Section 5. Some of the special cases are presented under Section 6. In Section 7, we present results on applications using real-life data to demonstrate the applicability and flexibility of the fitted model, and finally, we give concluding remarks under Section 8.

2. Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-G (RB-TL-TII-EHL-G) Distribution

In this section, we introduce the new family of distributions with the cdf and pdf given by

$$\begin{array}{cc}\hfill F_{{}_{RB-TL-TII-EHL-G}}(x;\delta ,a,b,\underline{\psi })& =1-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\delta \right)}}{\int }_0^{-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)}{t}^{\delta -1-t}dt\hfill \\ \hfill & =1-\frac{\gamma \left(\delta ,-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

(1)

and

$$\begin{array}{ccc}\hfill f_{{}_{RB-TL-TII-EHL-G}}(x;\delta ,a,b,\underline{\psi })& =& \frac{4ab}{\mathsf{\Gamma }\left(\delta \right)}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\hfill \\ & \times & \frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}},\hfill \end{array}$$

(2)

for $\delta ,a,b>0$ and parameter vector $\underline{\psi }.$ The parameters $\delta ,a$ and b are shape parameters. The pdf helps us visualize shape and characteristics of the distribution, while the cdf provides a more inclusive view of probabilities and allows for various calculations and comparisons. We set $F_{{}_{RB-TL-TII-EHL-G}}(x;\delta ,a,b,\underline{\psi })=F(x;\delta ,a,b,\underline{\psi })$ and $f_{{}_{RB-TL-TII-EHL-G}}(x;\delta ,a,b,\underline{\psi })=f(x;\delta ,a,b,\underline{\psi }),$ respectively.

Sub-Families

• When $\delta =1,$ we obtain the Topp-Leone-Type II-Exponentiated Half Logistic-G (TL-TII-EHL-G) family of distributions with the cdf

  $$\begin{array}{ccc}\hfill F(x;b,a,\underline{\psi })& =& {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b,\hfill \end{array}$$

  for $a,b>0$, and parameter vector $\underline{\psi }$ (see [35]).
• When $a=1,$ we obtain the Gamma-Topp-Leone-Type II-Half Logistic-G (RB-TL-TII-HL-G) family of distributions with the cdf

  $$\begin{array}{cc}\hfill F(x;\delta ,b,\underline{\psi })& =1-\frac{\gamma \left(\delta ,-log\left({\left[1-{\left(\frac{1-G(x;\underline{\psi })}{1+G(x;\underline{\psi })}\right)}^2\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

  for $\delta ,b>0$, and parameter vector $\underline{\psi }.$ This is a new family of distributions.
• When $b=1,$ we obtain the Gamma-Type II-Exponentiated Half Logistic-G (RB-TII-EHL-G) family of distributions with the cdf

  $$\begin{array}{cc}\hfill F(x;\delta ,a,\underline{\psi })& =1-\frac{\gamma \left(\delta ,-log\left(\left[1-K_G\left(x;a,\underline{\psi }\right)\right]\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

  for $\delta ,a>0$, and parameter vector $\underline{\psi }.$ This is a new family of distributions.
• When $a=b=1,$ we obtain the Gamma-Type II-Half Logistic-G (RB-TII-HL-G) family of distributions with the cdf

  $$\begin{array}{cc}\hfill F(x;\delta ,\underline{\psi })& =1-\frac{\gamma \left(\delta ,-log\left(\left[1-{\left(\frac{1-G(x;\underline{\psi })}{1+G(x;\underline{\psi })}\right)}^2\right]\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

  for $\delta$ and parameter vector $\underline{\psi }.$ This is a new family of distributions.
• When $\delta =a=1,$ we obtain the Topp-Leone-Type II-Half Logistic-G (TL-TII-HL-G) family of distributions with the cdf

  $$\begin{array}{ccc}\hfill F(x;b,\underline{\psi })& =& {\left[1-{\left(\frac{1-G(x;\underline{\psi })}{1+G(x;\underline{\psi })}\right)}^2\right]}^b,\hfill \end{array}$$

  for $b>0$ and parameter vector $\underline{\psi }.$ This is a new family of distributions.
• When $\delta =b=1,$ we obtain the Type II-Exponentiated Half Logistic-G (TII-EHL-G) family of distributions with the cdf

  $$\begin{array}{ccc}\hfill F(x;a,\underline{\psi })& =& 1-K_G\left(x;a,\underline{\psi }\right),\hfill \end{array}$$

  for $a>0$ and parameter vector $\underline{\psi }$ (see [18]).
• When $\delta =a=b=1,$ we obtain the new family of distributions with the cdf

  $$\begin{array}{ccc}\hfill F(x;\underline{\psi })& =& 1-{\left(\frac{1-G(x;\underline{\psi })}{1+G(x;\underline{\psi })}\right)}^2,\hfill \end{array}$$

  for parameter vector $\underline{\psi }.$

3. Expansion of Density Function

In this section, we will derive the series expansion of the density function. Let $y=K_G\left(x;a,\underline{\psi }\right)$, and consider the series expansion $\left(-log(1-y)\right)={\sum }_{i=0}^{\infty }{\displaystyle \frac{y^{i+1}}{i+1}}$ and the following generalized binomial series expansion

$$\begin{array}{c}\hfill {(1+z)}^{-t}=\sum _{k=0}^{\infty }{(-1)}^k\left(\genfrac{}{}{0pt}{}{t+k-1}{k}\right)z^k\mathrm{for}\left|z\right|<1,andt>0,\end{array}$$

and using the results on power series raised to a positive integer, by setting $a_s=\frac{1}{s+2}$, that is ${\left({\sum }_{s=0}^{\infty }{a}_s{y}^s\right)}^m={\sum }_{s=0}^{\infty }{b}_{s,m}{y}^s,$ we obtain

$$\begin{array}{ccc}\hfill {\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{\delta -1}& =& b^{\delta -1}{y}^{\delta -1}\left[\sum _{m=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\delta -1}{m}\right)y^m{\left(\sum _{s=0}^{\infty }{\displaystyle \frac{y^s}{s+2}}\right)}^m\right]\hfill \\ & =& b^{\delta -1}{y}^{\delta -1}\left[\sum _{m=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\delta -1}{m}\right)y^m\sum _{s=0}^{\infty }{b}_{s,m}{y}^s\right]\hfill \\ & =& b^{\delta -1}\left[\sum _{m,s=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\delta -1}{m}\right)b_{s,m}{y}^{m+s+\delta -1}\right],\hfill \end{array}$$

(see [37] for details), where $b_{s,m}={\left(s{a}_0\right)}^{-1}{\sum }_{l=1}^s[m(l+1)-s]a_l{b}_{s-l,m}$, $b_{0,m}=a_0^m$. The pdf of RB-TL-TII-EHL-G distribution can now be written as

$$\begin{array}{ccc}\hfill f(x;\delta ,a,b,\underline{\psi })& =& \sum _{v=0}^{\infty }{\omega }_{v+1}{g}_{{}_{v+1}}(x;\underline{\psi }),\hfill \end{array}$$

(3)

(see Appendix A section for details of the derivation), where

$$\begin{array}{ccc}\hfill {\omega }_{v+1}& =& \frac{4ab}{\mathsf{\Gamma }\left(\delta \right)}{b}^{\delta -1}\sum _{m,s,i,j,k,h=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\delta -1}{m}\right)\left(\genfrac{}{}{0pt}{}{b-1}{i}\right)b_{s,m}{(-1)}^{i+j+p+v}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]-1}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]+k}{k}\right)\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right)\frac{1}{v+1},\hfill \end{array}$$

(4)

and $g_{{}_{v+1}}(x;\underline{\psi })=(v+1)G^v(x;\underline{\psi })g(x;\underline{\psi })$ is the exponentiated-G (Exp-G) pdf with power parameter $(v+1)$. Consequently, the mathematical and statistical properties of the RB-TL-TII-EHL-G family of distributions follow directly from those of the Exp-G family of distributions.

Reliability, Hazard Rate and Quantile Functions

The survival function gives us the overall survival probabilities over time, while the hazard rate function (hrf) provides information about the changing risk of the event occurrence. The survival function and hrf of the RB-TL-TII-EHL-G family of distributions are given, respectively, by

$$\begin{array}{c}\hfill S(x;\delta ,a,b,\underline{\psi })=\frac{\gamma \left(\delta ,-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\end{array}$$

(5)

and

$$\begin{array}{ccc}\hfill h(x;\delta ,a,b,\underline{\psi })& =& 4ab{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\hfill \\ & \times & \frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}\hfill \\ & \times & {\left[\gamma \left(\delta ,-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right)\right]}^{-1},\hfill \end{array}$$

(6)

for $\delta ,a,b>0,$ and parameter vector $\underline{\psi }.$ The quantile function is a very useful statistical tool when it comes to generating random numbers. It is also important when obtaining other statistical measures such as median, skewness and kurtosis. It is obtained by inverting the cdf, that is,

$$\begin{array}{cc}\hfill 1-\frac{\gamma \left(\delta ,-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)}& =u,\hfill \end{array}$$

(7)

for $0\le u\le 1.$ Note that Equation (7) can be written as

$$\begin{array}{c}\hfill G(x;\underline{\psi })=\frac{1-{\left(1-{\left[exp\left(-{\gamma }^{-1}\left[\delta ,\mathsf{\Gamma }\left(\delta \right)(1-u)\right]\right)\right]}^{\frac{1}{b}}\right)}^{\frac{1}{2a}}}{\left[1+{\left(1-{\left[exp\left(-{\gamma }^{-1}\left[\delta ,\mathsf{\Gamma }\left(\delta \right)(1-u)\right]\right)\right]}^{\frac{1}{b}}\right)}^{\frac{1}{2a}}\right]}.\end{array}$$

Therefore, the quantile function of the RB-TL-TII-EHL-G family of distributions is given by

$$Q_{{}_X}\left(u\right)=G^{-1}\left[\frac{1-{\left(1-{\left[exp\left(-{\gamma }^{-1}\left[\delta ,\mathsf{\Gamma }\left(\delta \right)(1-u)\right]\right)\right]}^{\frac{1}{b}}\right)}^{\frac{1}{2a}}}{\left[1+{\left(1-{\left[exp\left(-{\gamma }^{-1}\left[\delta ,\mathsf{\Gamma }\left(\delta \right)(1-u)\right]\right)\right]}^{\frac{1}{b}}\right)}^{\frac{1}{2a}}\right]}\right].$$

(8)

4. Mathematical Properties

In this section, we obtain several mathematical and statistical properties of the RB-TL-TII-EHL-G family of distributions. The properties presented include moments, moment-generating function, moments of residual and reversed residual life, Rényi Entropy, distribution of $r^{th}$-order statistics and stochastic ordering. Let the pdf $f(x;\delta ,a,b,\underline{\psi })$ be written as $f\left(x\right)$ throughout this section.

4.1. Moments and Generating Function

Let $Y_{v+1}\sim Exponentiated-G(v+1,\underline{\psi });$ then, the $n^{th}$ raw moment ${\mu }_n^{\prime }$ of the RB-TL-TII-EHL-G family of distributions is given by

$${\mu }_n^{\prime }=E\left(X^n\right)={\int }_{-\infty }^{\infty }{x}^{n}f\left(x\right)dx=\sum _{v=0}^{\infty }{\omega }_{{}_{v+1}}E\left(Y_{v+1}^n\right),$$

where $E\left(Y_{v+1}^n\right)$ is the $n^{th}$ moment of $Y_{v+1}$ and ${\omega }_{{}_{v+1}}$ is given by Equation (4). The moment-generating function (MGF), for $\left|t\right|<1$, is given by:

$$M_X\left(t\right)=\sum _{v=0}^{\infty }{\omega }_{{}_{v+1}}{M}_{v+1}\left(t\right),$$

where $M_{v+1}\left(t\right)$ is the mgf of $Y_{v+1}$ and ${\omega }_{{}_{v+1}}$ is given by Equation (4).

4.2. Moment of Residual and Reversed Residual Life

Moments of the residual life distribution are used to obtain the mean, variance and coefficient of variation of residual life which are extensively used in reliability analysis. The $s^{th}$ moment of the residual life, say ${\varphi }_s\left(t\right)$ of a random variable X, is

$$\begin{array}{c}\hfill {\varphi }_s\left(t\right)=E\left[{\left(X-t\right)}^s\mid X>t\right]=\frac{1}{\overline{F}\left(t\right)}{\int }_t^{\infty }{\left(x-t\right)}^{s}f\left(x\right)dx.\end{array}$$

Consequently, ${\varphi }_s\left(t\right)$ for the RB-TL-TII-EHL-G distribution is given as follows:

$$\begin{array}{c}\hfill {\varphi }_s\left(t\right)=\frac{1}{\overline{F}\left(t\right)}\sum _{v,p=0}^{\infty }\left(\genfrac{}{}{0pt}{}{s}{p}\right){(-t)}^{s-p}{\omega }_{{}_{v+1}}{\int }_t^{\infty }{x}^p{g}_{v+1}(x;\underline{\psi })dx,\end{array}$$

(9)

where ${\omega }_{{}_{v+1}}$ is as defined in Equation (4) and $g_{v+1}(x;\underline{\psi })$ denotes the Exp-G distribution with power parameter $(v+1)$. The mean remaining life (life expectancy at age t) of the RB-TL-TII-EHL-G family of distributions follows from the above formula with $s=1$.

The $s^{th}$ moment of the reversed residual life, say $U_s\left(t\right)$ of a random variable X, is

$$\begin{array}{c}\hfill U_s\left(t\right)=E\left[{\left(t-X\right)}^s\mid X\le t\right]=\frac{1}{F\left(t\right)}{\int }_0^t{\left(t-x\right)}^{s}f\left(x\right)dx.\end{array}$$

Subsequently, $U_s\left(t\right)$ for the RB-TL-TII-EHL-G distribution is given as follows:

$$\begin{array}{c}\hfill U_s\left(t\right)=\frac{1}{F\left(t\right)}\sum _{v,p=0}^{\infty }\left(\genfrac{}{}{0pt}{}{s}{p}\right){(-t)}^{s-p}{\omega }_{{}_{v+1}}{\int }_0^t{x}^p{g}_{v+1}(x;\underline{\psi })dx,\end{array}$$

where ${\omega }_{{}_{v+1}}$ is as defined in Equation (4) and $g_{v+1}(x;\underline{\psi })$ denotes the Exp-G distribution with power parameter $(v+1)$.

4.3. Rényi Entropy

In information theory, Rényi entropy is a measue of randomness or uncertainty in the system. The Rényi entropy of the RB-TL-EHL-G family of distributions is given by

$$I_R\left(q\right)=\frac{1}{1-q}\log \left({\int }_0^{\infty }{f}^q\left(x\right)dx\right),q>0\mathrm{and}q\ne 1,$$

where

$$\begin{array}{ccc}\hfill f^q\left(x\right)& =& \frac{{\left(4ab\right)}^q}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^q}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{q\delta -q}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{qb-q}{\left(1-G(x;\underline{\psi })\right)}^{2aq-q}\hfill \\ & \times & \frac{g^q(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi })\right]}^{2q(a+1)-q}}.\hfill \end{array}$$

Let $y=K_G\left(x;a,\underline{\psi }\right)$, and with the series expansion $\left(-log(1-y)\right)={\sum }_{i=0}^{\infty }{\displaystyle \frac{y^{i+1}}{i+1}}$, as well as the results on power series raised to a positive integer given by ${\left({\sum }_{s=0}^{\infty }{a}_s{y}^s\right)}^m={\sum }_{s=0}^{\infty }{b}_{s,m}{y}^s$ (see [37] for details), we obtain

$$\begin{array}{ccc}\hfill {\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{q\delta -q}& =& b^{q\delta -q}{y}^{q\delta -q}\left[\sum _{m=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)y^m{\left(\sum _{s=0}^{\infty }{\displaystyle \frac{y^s}{s+2}}\right)}^m\right]\hfill \\ & =& b^{q\delta -q}{y}^{q\delta -q}\left[\sum _{m=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)y^m\sum _{s=0}^{\infty }{b}_{s,m}{y}^s\right]\hfill \\ & =& b^{q\delta -q}\left[\sum _{m,s=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)b_{s,m}{y}^{m+s+q\delta -q}\right],\hfill \end{array}$$

where $b_{s,m}={\left(s{a}_0\right)}^{-1}{\sum }_{l=1}^s[m(l+1)-s]a_l{b}_{s-l,m}$, $b_{0,m}=a_0^m$, so that $f^q\left(x\right)$ can be written as:

$$\begin{array}{ccc}\hfill f^q\left(x\right)& =& \frac{{\left(4ab\right)}^q}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^q}{b}^{q\delta -q}\sum _{m,s,i,j,k,h,v=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)b_{s,m}{(-1)}^{i+j+h+v}\left(\genfrac{}{}{0pt}{}{qb-q}{i}\right)\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]-q}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]+q+k-1}{k}\right)\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right)g^q(x;\underline{\psi }){\left(G(x;\underline{\psi })\right)}^v.\hfill \end{array}$$

(see Appendix A section for details of the derivation). Consequently, the Rényi entropy for the RB-TL-TII-EHL-G family of distributions is given by

$$\begin{array}{ccc}\hfill I_R\left(q\right)& =& \frac{1}{1-q}log[\frac{{\left(4ab\right)}^q}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^q}{b}^{q\delta -q}\sum _{m,s,i,j,k,h,v=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)b_{s,m}{(-1)}^{i+j+h+v}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{qb-q}{i}\right)\left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]-q}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]+q+k-1}{k}\right)\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right){\int }_0^{\infty }{\left(\left[1+\frac{v}{q}\right]{\left(G(x;\underline{\psi })\right)}^{\frac{v}{q}}\left(g(x;\underline{\psi })\right)\right)}^{q}dx]\hfill \\ & =& \frac{1}{1-q}log\left[\sum _{v=0}^{\infty }{\tau }_{{}_v}exp\left((1-q)I_{{}_{REG}}\right)\right],\hfill \end{array}$$

(10)

for $q>0,$ $q\ne 1,$ where $I_{{}_{REG}}=\frac{1}{1-q}log\left[{\int }_0^{\infty }{\left(\left[1+\frac{v}{q}\right]{\left(G(x;\underline{\psi })\right)}^{\frac{v}{q}}\left(g(x;\underline{\psi })\right)\right)}^{q}dx\right]$ is the Rényi entropy of Exp-G distribution with power parameter $(\frac{v}{q}+1)$, and

$$\begin{array}{ccc}\hfill {\tau }_{{}_v}& =& \frac{{\left(4ab\right)}^q}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^q}{b}^{q\delta -q}\sum _{m,s,i,j,k,h=0}^{\infty }\left(\genfrac{}{}{0pt}{}{q\delta -q}{m}\right)b_{s,m}{(-1)}^{i+j+h+v}\frac{1}{{\left[1+\frac{v}{q}\right]}^q}\left(\genfrac{}{}{0pt}{}{qb-q}{i}\right)\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]-q}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[m+s+q\delta +i\right]+q+k-1}{k}\right)\left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right).\hfill \end{array}$$

Therefore, the Rényi entropy of the RB-TL-TII-EHL-G family of distributions can be obtained from those of the Exp-G family of distributions.

4.4. Order Statistics

Order statistics are a very useful statistical concept in probability and statistics. We see its applications in several fields including modeling insurance policies, auctions, optimizing production processes, car races, estimating parameters of distributions, and many more. Suppose $X_1,X_2,\dots ,X_n$ are independent and identically distributed random variables from the RB-TL-TII-EHL-G family of distributions. Then, the expression for the pdf of the $r^{th}$-order statistic from the RB-TL-TII-EHL-G distribution can be written as

$$\begin{array}{ccc}\hfill f_{r:n}\left(x\right)& =& \frac{n!f\left(x\right)}{(r-1)!(n-r)!}\sum _{p=0}^{n-r}{(-1)}^p\left(\genfrac{}{}{0pt}{}{n-r}{p}\right){\left[F\left(x\right)\right]}^{p+r-1}.\hfill \end{array}$$

(11)

Note that

$$\begin{array}{ccc}\hfill f\left(x\right){\left[F\left(x\right)\right]}^{p+r-1}& =& \sum _{z=0}^{\infty }\left(\genfrac{}{}{0pt}{}{p+r-1}{z}\right){(-1)}^z\frac{4ab}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^{z+1}}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\hfill \\ & \times & \frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}{\left[\gamma \left(\delta ,-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right)\right]}^z,\hfill \end{array}$$

and using the results on the expansion of the density and the following power series for the incomplete gamma function (see [37]),

$$\gamma (y,\delta )=\sum _{q=0}^{\infty }\frac{{(-1)}^q{y}^{q+\delta }}{(q+\delta )q!},$$

we obtain

$$\begin{array}{ccc}\hfill f\left(x\right){\left[F\left(x\right)\right]}^{p+r-1}& =& \sum _{z=0}^{\infty }\left(\genfrac{}{}{0pt}{}{p+r-1}{z}\right){\left[\sum _{q=0}^{\infty }\frac{{(-1)}^q}{(q+\delta )q!}\right]}^z{(-1)}^z\frac{4ab}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^{z+1}}\hfill \\ & \times & {\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{z(q+\delta )+\delta -1}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}.\hfill \end{array}$$

Now, following the same steps leading to Equation (3), we obtain

$$\begin{array}{c}\hfill f\left(x\right){\left[F\left(x\right)\right]}^{p+r-1}=\sum _{v=0}^{\infty }{a}_{{}_{v+1}}{g}_{v+1}(x;\underline{\psi }),\end{array}$$

(12)

where $g_{{}_{v+1}}(x;\underline{\psi })=(v+1){\left[G(x;\underline{\psi })\right]}^{v}g(x;\underline{\psi })$ is the Exp-G pdf with the power parameter $(v+1)$ and parameter vector $\underline{\psi },$ and

$$\begin{array}{ccc}\hfill a_{v+1}& =& \sum _{z,m,s,i,j,k,h=0}^{\infty }\left(\genfrac{}{}{0pt}{}{p+r-1}{z}\right){\left[\sum _{q=0}^{\infty }\frac{{(-1)}^q}{(q+\delta )q!}\right]}^z\frac{4ab{(-1)}^{z+i+j+p+v}}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^{z+1}}{b}^{z(q+\delta )+\delta -1}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{z(q+\delta )+\delta -1}{m}\right)\left(\genfrac{}{}{0pt}{}{b-1}{i}\right)b_{s,m}\left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right)\frac{1}{v+1}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]-1}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]+k}{k}\right).\hfill \end{array}$$

Thus, by substituting (12) into (11), the pdf of the $r^{th}$-order statistic for the RB-TL-TII-EHL-G family of distributions can be written as

$$\begin{array}{ccc}\hfill f_{r:n}\left(x\right)& =& \frac{n!}{(r-1)!(n-r)!}\sum _{p=0}^{n-r}{(-1)}^p\left(\genfrac{}{}{0pt}{}{n-r}{p}\right)\sum _{v=0}^{\infty }{a}_{{}_{v+1}}{g}_{v+1}(x;\underline{\psi }).\hfill \end{array}$$

(13)

4.5. Probability Weighted Moments (PWMs)

The PWMs of a random variable X are defined by

$$\begin{array}{c}\hfill {\varphi }_{{}_{w,p}}=E\left(X^w{\left(F\left(X\right)\right)}^p\right)={\int }_{-\infty }^{\infty }{x}^{w}F{\left(x\right)}^{p}f\left(x\right)dx.\end{array}$$

Using the results from the derivation of the distribution of the order statistics above, we note that

$$\begin{array}{ccc}\hfill f\left(x\right){\left[F\left(x\right)\right]}^p& =& \sum _{z=0}^{\infty }\left(\genfrac{}{}{0pt}{}{p}{z}\right){\left[\sum _{q=0}^{\infty }\frac{{(-1)}^q}{(q+\delta )q!}\right]}^z{(-1)}^z\frac{4ab}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^{z+1}}\hfill \\ & \times & {\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{z(q+\delta )+\delta -1}\hfill \\ & \times & {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}.\hfill \end{array}$$

Now, following the same steps leading to Equation (3), we obtain

$$\begin{array}{c}\hfill f\left(x\right){\left[F\left(x\right)\right]}^p=\sum _{v=0}^{\infty }{C}_{{}_{v+1}}{g}_{v+1}(x;\underline{\psi }),\end{array}$$

(14)

where $g_{{}_{v+1}}(x;\underline{\psi })=(v+1){\left[G(x;\underline{\psi })\right]}^{v}g(x;\underline{\psi })$ is the Exp-G pdf with the power parameter $(v+1)$ and parameter vector $\underline{\psi },$ and

$$\begin{array}{ccc}\hfill C_{v+1}& =& \sum _{z,m,s,i,j,k,h=0}^{\infty }\left(\genfrac{}{}{0pt}{}{p}{z}\right){\left[\sum _{q=0}^{\infty }\frac{{(-1)}^q}{(q+\delta )q!}\right]}^z\frac{4ab{(-1)}^{z+i+j+p+v}}{{\left(\mathsf{\Gamma }\left(\delta \right)\right)}^{z+1}}{b}^{z(q+\delta )+\delta -1}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{z(q+\delta )+\delta -1}{m}\right)\left(\genfrac{}{}{0pt}{}{b-1}{i}\right)b_{s,m}\left(\genfrac{}{}{0pt}{}{j+k}{h}\right)\left(\genfrac{}{}{0pt}{}{h}{v}\right)\frac{1}{v+1}\hfill \\ & \times & \left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]-1}{j}\right)\left(\genfrac{}{}{0pt}{}{2a\left[\right(m+s+\delta )+i]+k}{k}\right).\hfill \end{array}$$

Thus, the probability weighted moment of the RB-TL-TII-EHL-G family of distributions is given by

$$\begin{array}{c}\hfill {\varphi }_{{}_{w,p}}=E\left(X^w{\left(F\left(X\right)\right)}^p\right)=\sum _{v=0}^{\infty }{C}_{{}_{v+1}}{\int }_{-\infty }^{\infty }{x}^w{g}_{v+1}(x;\underline{\psi }).\end{array}$$

(15)

4.6. Stochastic Orderings

In probability and statistics, the notion of stochastic ordering for random variables is a useful concept. It quantifies the concept of one random variable being bigger than another [38]. The usual stochastic order, the hazard rate order, and likelihood ratio order are perhaps the best-known orders of distribution functions. In this subsection, we present likelihood ratio ordering.

Suppose X and Y are two random variables with the cdfs $F_X\left(t\right)$ and $F_Y\left(t\right)$, respectively, and ${\overline{F}}_X\left(t\right)=1-F_X\left(t\right)$ is the survival function. The random variable X is said to be stochastically smaller than the random variable Y if ${\overline{F}}_X\left(t\right)\le {\overline{F}}_Y\left(t\right)$ or $F_X\left(t\right)\ge F_Y\left(t\right),$$\forall t$. This is denoted by $X{<}_{st}Y$. The hazard rate order and likelihood ratio order are given by $X{<}_{hr}Y$ if $h_X\left(t\right)\ge h_Y\left(t\right)$$\forall t$, and $X{<}_{lr}Y$ if $\frac{f_X\left(t\right)}{f_Y\left(t\right)}$ is decreasing in t, $\forall t$. It is well established that $X{<}_{lr}Y⟹X{<}_{hr}Y⟹X{<}_{st}Y$ [38].

Now consider two independent random variables $X_1$ and $X_2$ following the RB-TL-TII-EHL-G family of distributions with $X_1\sim f_1(x;{\delta }_1,a,b,\underline{\psi })$ and $X_2\sim f_2(x;{\delta }_2,a,b,\underline{\psi }),$ and their pdfs are given by

$$\begin{array}{ccc}\hfill f_1\left(x\right)& =& \frac{4ab}{\mathsf{\Gamma }\left({\delta }_1\right)}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{{\delta }_1-1}{\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}\hfill \\ & \times & {\left(1-G(x;\underline{\psi })\right)}^{2a-1}\frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}\hfill \end{array}$$

(16)

and

$$\begin{array}{ccc}\hfill f_2\left(x\right)& =& \frac{4ab}{\mathsf{\Gamma }\left({\delta }_2\right)}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{{\delta }_2-1}{\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}\hfill \\ & \times & {\left(1-G(x;\underline{\psi })\right)}^{2a-1}\frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}},\hfill \end{array}$$

(17)

respectively. Then

$${\displaystyle \frac{f_1\left(x\right)}{f_2\left(x\right)}}=\frac{\mathsf{\Gamma }\left({\delta }_2\right)}{\mathsf{\Gamma }\left({\delta }_1\right)}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{{\delta }_1-{\delta }_2}.$$

(18)

Differentiating Equation (18) with respect to x yields

$$\begin{array}{cc}\hfill \frac{d}{dx}\left({\displaystyle \frac{f_1\left(x\right)}{f_2\left(x\right)}}\right)& =\frac{4ab\left({\delta }_2-{\delta }_1\right)\mathsf{\Gamma }\left({\delta }_2\right)}{\mathsf{\Gamma }\left({\delta }_1\right)}{\left[-log\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)\right]}^{{\delta }_1-{\delta }_2-1}\hfill \\ \hfill & \times {\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^{b-1}{\left(1-G(x;\underline{\psi })\right)}^{2a-1}\hfill \\ \hfill & \times \frac{g(x;\underline{\psi })}{{\left[1+G(x;\underline{\psi }))\right]}^{2(a+1)-1}}{\left({\left[1-K_G\left(x;a,\underline{\psi }\right)\right]}^b\right)}^{-1}.\hfill \end{array}$$

(19)

Consequently, $\frac{d}{dx}\left[\frac{f_{{}_1}\left(x\right)}{f_{{}_2}\left(x\right)}\right]<0$ if ${\delta }_2<{\delta }_1.$ Thus, the likelihood ratio $X{<}_{lr}Y$ exists. Subsequently, since $X{<}_{lr}Y⟹X{<}_{hr}Y⟹X{<}_{st}Y,$ the hazard rate order and stochastic order also hold.

4.7. Maximum Likelihood Estimation

There are several methods available in the literature for estimating unknown parameters of a probability distribution. Among them, the maximum likelihood method is the most commonly used. The maximum likelihood estimation (MLE) is a technique used in statistics to estimate the unknown parameters of an assumed probability distribution based on some experimental data. In this subsection, we use the maximum likelihood estimation method to obtain estimates of the parameters of the RB-TL-TII-EHL-G family of distributions. Suppose $x_1,x_2,\dots \dots ,x_n$ is the random sample observed from the RB-TL-TII-EHL-G family of distributions with the vector of model parameters $\mathbf{\Delta }={(\delta ,a,b,\underline{\psi })}^T$. Then, the log-likelihood function ${\ell }_n={\ell }_n(\mathbf{\Delta })$ for the parameters from the observed values has the form

$$\begin{array}{ccc}\hfill {\ell }_n(\mathbf{\Delta })& =& nln\left(4ab\right)-nln\left(\mathsf{\Gamma }\left(\delta \right)\right)+(\delta -1)\sum _{i=1}^{n}ln\left[-log\left({\left[1-{\left(\frac{1-G(x_i;\underline{\psi })}{1+G(x_i;\underline{\psi })}\right)}^{2a}\right]}^b\right)\right]\hfill \\ & +& \left(b-1\right)\sum _{i=1}^n\left[1-{\left(\frac{1-G(x_i;\underline{\psi })}{1+G(x_i;\underline{\psi })}\right)}^{2a}\right]+(2a-1)\sum _{i=1}^{n}ln\left(1-G(x_i;\underline{\psi })\right)\hfill \\ & -& \left(2(a+1)-1\right)\sum _{i=1}^{n}ln\left[1+G(x_i;\underline{\psi }))\right]+\sum _{i=1}^{n}ln\left(g(x_i;\underline{\psi })\right).\hfill \end{array}$$

(20)

The elements of the score vector $U=\left(\frac{\partial \ell }{\partial \delta },\frac{\partial \ell }{\partial a},\frac{\partial \ell }{\partial b},\frac{\partial \ell }{\partial {\underline{\psi }}_k}\right)$ are given in Appendix A.

The maximum likelihood estimates of the parameters, denoted by $\widehat{\mathbf{\Delta }}$, are obtained by solving the nonlinear equation ${\left(\frac{\partial \ell }{\partial \delta },\frac{\partial \ell }{\partial a},\frac{\partial \ell }{\partial b},\frac{\partial \ell }{\partial {\underline{\psi }}_k}\right)}^T=\mathbf{0}.$ However, these equations are not in closed form; hence, they are solved by a numerical method such as the Newton–Raphson procedure.

5. Monte Carlo Simulation Results

In this section, a simulation study is used to assess the estimators of the parameters of the Gamma-Topp-Leone-type II-Exponentiated Half Logistic-Weibull (RB-TL-TII-EHL-W) distribution. Here, $N=3000$ samples of size n = 25, 50, 100, 200, 400, 800, 1600 are generated from the RB-TL-TII-EHL-W distribution for different parameter values. For example, in Table 1, the true parameter values are chosen arbitrary to be (0.4, 2.0, 1.0, 0.6) and (1.0, 1.0, 2.0, 0.6). The average bias (ABIAS) and root mean square errors (RMSE) for the estimated parameter, say, $\widehat{\theta },$ for the MLE are calculated as follows:

$$ABias\left(\widehat{\theta }\right)=\frac{{\sum }_{i=1}^N{\widehat{\theta }}_i}{N}-\theta ,\mathrm{and}RMSE\left(\widehat{\theta }\right)=\sqrt{\frac{{\sum }_{i=1}^N{({\widehat{\theta }}_i-\theta )}^2}{N}},$$

respectively. The simulation results are presented in Table 1 and Table 2.

Table 1. Monte Carlo Simulation Results.

(0.4, 2.0, 1.0, 0.6)					(1.0, 1.0, 2.0, 0.6)
Parameter	Sample Size	Mean	RMSE	ABIAS	Mean	RMSE	ABIAS
$\delta$	25	0.6877	3.1506	0.2877	1.3229	0.8782	0.3229
	50	0.3709	0.1177	0.0290	1.2402	0.6605	0.2402
	100	0.3787	0.0802	0.0212	1.1232	0.3570	0.1232
	200	0.3822	0.0603	0.0177	1.1006	0.2738	0.1006
	400	0.3922	0.0433	0.0077	1.0952	0.2100	0.0952
	800	0.3951	0.0365	0.0048	1.0925	0.2000	0.0925
	1600	0.3981	0.0274	0.0018	1.0491	0.1333	0.0491
a	25	2.5400	1.3914	0.5400	1.1886	0.6130	0.1886
	50	2.3977	0.9355	0.3977	1.1187	0.4540	0.1187
	100	2.2693	0.7333	0.2693	1.0664	0.2516	0.0664
	200	2.2078	0.5503	0.2078	1.0298	0.1603	0.0298
	400	2.1536	0.4217	0.1536	1.0125	0.0996	0.0125
	800	2.1325	0.3502	0.1325	1.0010	0.0549	0.0010
	1600	2.0891	0.2558	0.0891	0.9990	0.0295	-0.0009
b	25	1.3057	0.8845	0.3057	2.7881	2.8433	0.7881
	50	1.2950	0.6806	0.2950	2.6862	1.5921	0.6862
	100	1.2521	0.4924	0.2521	2.6663	1.5291	0.6663
	200	1.2051	0.3896	0.2051	2.5486	1.2348	0.5486
	400	1.1270	0.2615	0.1270	2.3736	0.9899	0.3736
	800	1.0838	0.1916	0.0838	2.3047	0.8254	0.3047
	1600	1.0497	0.1160	0.0497	2.1826	0.5966	0.1826
$\lambda$	25	1.6935	2.4098	1.0935	1.1408	1.4770	0.5408
	50	1.5659	2.1364	0.9659	1.0127	1.2357	0.4127
	100	1.4300	1.8248	0.8300	0.9742	1.1543	0.3742
	200	0.9253	1.0925	0.3253	0.7660	0.9116	0.1660
	400	0.8234	0.8786	0.2234	0.7619	0.8445	0.1619
	800	0.6774	0.5516	0.0774	0.6842	0.6534	0.0842
	1600	0.5944	0.3520	0.0055	0.6821	0.5891	0.0821

Table 2. Monte Carlo Simulation Results.

(1.3, 2.5, 1.3, 0.2)					(0.4, 2.0, 0.4, 0.6)
Parameter	Sample Size	Mean	RMSE	ABIAS	Mean	RMSE	ABIAS
$\delta$	25	1.8712	1.0697	0.5712	0.5461	0.5260	0.1461
	50	1.5872	0.8045	0.2872	0.4494	0.2333	0.0494
	100	1.5855	0.7239	0.2855	0.4226	0.1363	0.0226
	200	1.4840	0.5620	0.1840	0.4178	0.0899	0.0178
	400	1.4472	0.4748	0.1472	0.4112	0.0667	0.0112
	800	1.3721	0.3075	0.0721	0.4102	0.0397	0.0102
	1600	1.3202	0.1560	0.0202	0.4070	0.0292	0.0070
a	25	1.8861	1.2069	0.6138	2.5733	1.1101	0.5733
	50	1.9280	1.2898	0.5719	2.4370	0.8351	0.4370
	100	2.0105	1.2688	0.4894	2.3850	0.6897	0.3850
	200	2.1445	1.2661	0.3554	2.2559	0.5008	0.2559
	400	2.2502	1.1785	0.2497	2.1381	0.2995	0.1381
	800	2.4325	1.0837	0.0674	2.0626	0.1716	0.0626
	1600	2.5389	0.7505	0.0389	2.0387	0.1308	0.0387
b	25	1.6020	2.0325	0.3020	1.1007	1.2914	0.7007
	50	1.5671	1.0407	0.2671	0.8581	0.8695	0.4581
	100	1.5539	0.7707	0.2539	0.7758	0.6698	0.3758
	200	1.5071	0.5967	0.2071	0.6940	0.5466	0.2940
	400	1.4872	0.5199	0.1872	0.5694	0.3332	0.1694
	800	1.4103	0.3495	0.1103	0.4961	0.2103	0.0961
	1600	1.3553	0.2097	0.0553	0.4691	0.1741	0.0691
$\lambda$	25	1.9015	1.8505	1.7015	3.1446	3.9098	2.5446
	50	0.5098	1.6226	0.3098	2.0028	2.9795	1.4028
	100	0.2969	0.3970	0.0969	1.2378	1.6666	0.6378
	200	0.2472	0.1398	0.0472	0.8019	0.6485	0.2019
	400	0.2255	0.0846	0.0255	0.6875	0.2265	0.0875
	800	0.2169	0.0568	0.0169	0.6418	0.1240	0.0418
	1600	0.2132	0.0374	0.0132	0.6250	0.0722	0.0250

It can be observed in Table 1 and Table 2 that the mean MLEs are close to the true values of the parameters, and the RMSEs decay toward zero as the sample size increases. This indicates that the maximum likelihood method works well for obtaining estimate of the model parameters of the RB-TL-TII-EHL-W distribution.

6. Special Cases

In this section, we specify the baseline distribution and define some special cases of the RB-TL-TII-EHL-G family of distributions.

6.1. Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-Weibull (RB-TL-TII-EHL-W) Distribution

Consider the Weibull distribution with cdf and pdf given by $G(x;\lambda )=1-exp(-x^{\lambda })$ and $g(x;\lambda )=\lambda x^{\lambda -1}exp(-x^{\lambda })$, respectively, for $\lambda >0$ and $x>0$, as the baseline distribution; then, we obtain the RB-TL-TII-EHL-W distribution with cdf and pdf given by

$$\begin{array}{cc}\hfill F_{{}_{RB-TL-TII-EHL-W}}(x;\delta ,a,b,\lambda )& =1-\frac{\gamma \left(\delta ,-log\left({\left[1-{\left(\frac{exp(-x^{\lambda })}{1+\left(1-exp(-x^{\lambda })\right)}\right)}^{2a}\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f_{{}_{RB-TL-TII-EHL-W}}(x;\delta ,a,b,\lambda )& =& \frac{4ab}{\mathsf{\Gamma }\left(\delta \right)}{\left[-log\left({\left[1-{\left(\frac{exp(-x^{\lambda })}{1+\left(1-exp(-x^{\lambda })\right)}\right)}^{2a}\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-{\left(\frac{exp(-x^{\lambda })}{1+\left(1-exp(-x^{\lambda })\right)}\right)}^{2a}\right]}^{b-1}{\left(exp(-x^{\lambda })\right)}^{2a-1}\hfill \\ & \times & \frac{\lambda x^{\lambda -1}exp(-x^{\lambda })}{{\left[1+\left(1-exp(-x^{\lambda })\right)\right]}^{2(a+1)-1}},\hfill \end{array}$$

for $\delta ,a,b,\lambda >0$.

Figure 1 shows the plots of the pdf and the hrf of the RB-TL-TII-EHL-W distribution for different parameter values. The pdf can take several shapes including right-skewed, left-skewed, unimodal, J and reverse-J shapes. The RB-TL-TII-EHL-W hazard displays increasing, decreasing, bathtub, and upside-down bathtub shapes.

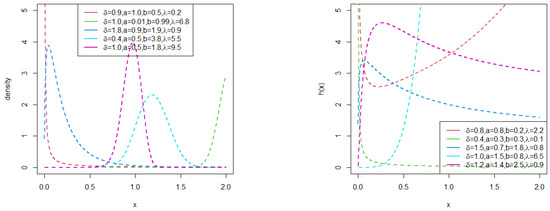
Figure 1. Plots of the pdf and hrf of the RB-TL-TII-EHL-W distribution.

Figure 2 shows the plots of skewness and kurtosis for the TL-TII-EHL-W distribution. We can see that the skewness become right-skewed and kurtosis is leptokurtic with increasing values of a and b and also with increasing values of a and $\lambda .$

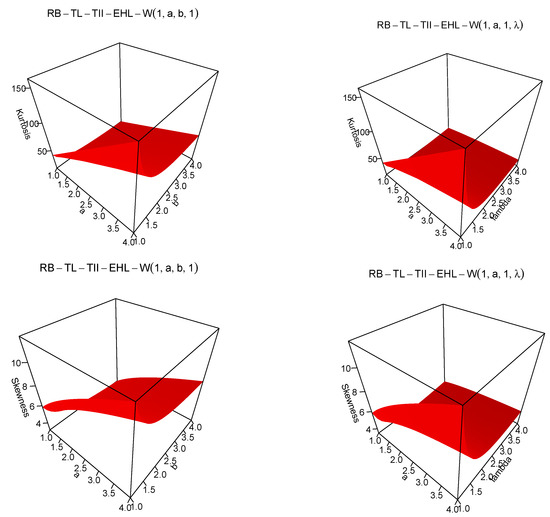
Figure 2. Three-dimensional (3D) plots of skewness and kurtosis for RB-TL-TII-EHL-W distribution.

6.2. Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-Log Logistic (RB-TL-TII-EHL-LLoG) Distribution

Suppose the cdf and pdf of the baseline distribution are given by $G(x;c)=1-{(1+x^c)}^{-1}$ and $g(x;\lambda ,c)=c{x}^{c-1}{(1+x^c)}^{-2}$ for $c>0$ and $x>0;$ then, the new RB-TL-TII-EHL-LLoG distribution has cdf and pdf given by

$$\begin{array}{cc}\hfill F_{{}_{RB-TL-TII-EHL-LLoG}}(x;\delta ,a,b,c)& =1-\frac{\gamma \left(\delta ,-log\left({\left[1-{\left(\frac{{(1+x^c)}^{-1}}{1+\left(1-{(1+x^c)}^{-1}\right)}\right)}^{2a}\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f_{{}_{RB-TL-TII-EHL-LLoG}}(x;\delta ,a,b,c)& =& \frac{4ab}{\mathsf{\Gamma }\left(\delta \right)}{\left[-log\left({\left[1-{\left(\frac{{(1+x^c)}^{-1}}{1+\left(1-{(1+x^c)}^{-1}\right)}\right)}^{2a}\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-{\left(\frac{{(1+x^c)}^{-1}}{1+\left(1-{(1+x^c)}^{-1}\right)}\right)}^{2a}\right]}^{b-1}{\left({(1+x^c)}^{-1}\right)}^{2a-1}\hfill \\ & \times & \frac{c{x}^{c-1}{(1+x^c)}^{-2}}{{\left[1+\left(1-{(1+x^c)}^{-1}\right)\right]}^{2(a+1)-1}},\hfill \end{array}$$

respectively, for $\delta ,a,b,c>0$.

Figure 3 shows the plots of pdf and hrf of RB-TL-TII-EHL-LLoG distribution, respectively. The pdf can take several shapes including right-skewed, left-skewed, unimodal and reverse-J shapes. The RB-TL-TII-EHL-LLoG hazard displays increasing, decreasing, upside-down bathtub, and bathtub followed by upside-down bathtub shapes.

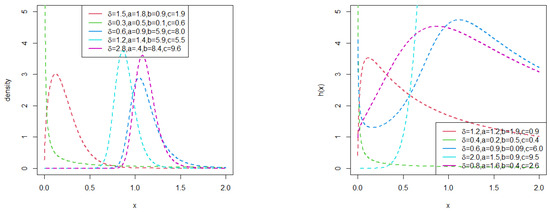
Figure 3. Plots of the pdf and hrf of the RB-TL-TII-EHL-LLoG distribution.

Figure 4 shows the plots of skewness and kurtosis for the RB-TL-TII-EHL-LLoG distribution. We can see that the skewness become right-skewed and kurtosis is leptokurtic with increasing values of a and b and also with increasing values of a and $c.$

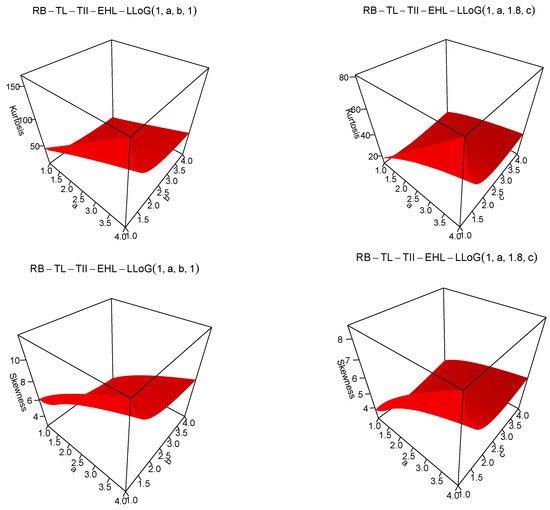
Figure 4. Three-dimensional (3D) plots of skewness and kurtosis for RB-TL-TII-EHL-LLoG distribution.

6.3. Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-Kumaraswamy (RB-TL-TII-EHL-Kum) Distribution

If we consider the Kumaraswamy distribution with cdf and pdf given by $G(x;\lambda ,\gamma )=1-{\left(1-x^{\lambda }\right)}^{\gamma }$ and $g(x;\lambda ,\gamma )=\lambda \gamma x^{\lambda -1}{\left(1-x^{\lambda }\right)}^{\gamma -1}$, respectively, for $\lambda ,\gamma >0$ and $x>0$, as the baseline distribution, then we obtain the RB-TL-TII-EHL-Kum distribution with cdf and pdf given by

$$\begin{array}{cc}\hfill F_{{}_{RB-TL-TII-EHL-Kum}}(x;\delta ,a,b,\lambda ,\gamma )& =1-\frac{\gamma \left(\delta ,-log\left({\left[1-{\left(\frac{{\left(1-x^{\lambda }\right)}^{\gamma }}{1+\left(1-{\left(1-x^{\lambda }\right)}^{\gamma }\right)}\right)}^{2a}\right]}^b\right)\right)}{\mathsf{\Gamma }\left(\delta \right)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f_{{}_{RB-TL-TII-EHL-Kum}}(x;\delta ,a,b,\lambda ,\gamma )& =& \frac{4ab}{\mathsf{\Gamma }\left(\delta \right)}{\left[-log\left({\left[1-{\left(\frac{{\left(1-x^{\lambda }\right)}^{\gamma }}{1+\left(1-{\left(1-x^{\lambda }\right)}^{\gamma }\right)}\right)}^{2a}\right]}^b\right)\right]}^{\delta -1}\hfill \\ & \times & {\left[1-{\left(\frac{{\left(1-x^{\lambda }\right)}^{\gamma }}{1+\left(1-{\left(1-x^{\lambda }\right)}^{\gamma }\right)}\right)}^{2a}\right]}^{b-1}{\left({\left(1-x^{\lambda }\right)}^{\gamma }\right)}^{2a-1}\hfill \\ & \times & \frac{\lambda \gamma x^{\lambda -1}{\left(1-x^{\lambda }\right)}^{\gamma -1}}{{\left[1+\left(1-{\left(1-x^{\lambda }\right)}^{\gamma }\right)\right]}^{2(a+1)-1}},\hfill \end{array}$$

for $\delta ,a,b,\lambda ,\gamma >0$.

Figure 5 shows the plots of the pdf and the hrf of the RB-TL-TII-EHL-Kum distribution for different parameter values. The pdf can take several shapes including right-skewed, left-skewed, U-shape and reverse-J shape. The hrf of the RB-TL-TII-EHL-Kum distribution displays increasing, decreasing, bathtub, and upside-down bathtub followed by bathtub shapes.

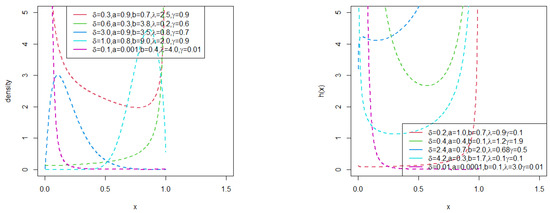
Figure 5. Plots of the pdf and hrf of the RB-TL-TII-EHL-Kum distribution.

7. Applications

In this section, three real datasets are analyzed to illustrate the flexibility, importance and modeling ability of the RB-TL-TII-EHL-G family of distibutions by using its special case, namely RB-TL-TII-EHL-W distribution. We also compare the RB-TL-TII-EHL-W distribution with the well-known models generated via the gamma transformation and modified forms of Weibull models in the literature including the gamma odd power generalized Weibull-Lomax (RB-OPGW-Lx) distribution by [23], the gamma-generalized inverse Weibull (GGIW) distribution by [24], the gamma odd Burr III-log-logistic (RB-BII-LLoG) distribution by [26], the Topp-Leone-Marshall–Olkin Weibull (TLMOW) distribution by [39], the alpha power Topp-Leone-Weibull (APTLW) distribution by [40], the type II exponentiated half logistic Weibull (TIIEHLW) distribution by [18], the odd generalized half logistic Weibull–Weibull (OGHLW-W) distribution by [41], the Marshall–Olkin exponential Weibull (MOEW) distribution by [42], and the odd Lomax generalized exponential (OLGE) distribution by [43].

To compare the fitted models, we used well-known goodness-of-fit statistics such as -2log-likelihood statistic ($-2ln\left(L\right)$), Akaike Information Criterion ($AIC=2p-2ln\left(L\right)$), Consistent Akaike Information Criterion ($CAIC=AIC+2\frac{p(p+1)}{n-p-1}$), Bayesian Information Criterion ($BIC=pln\left(n\right)-2ln\left(L\right)$) (n is the number of observations, and p is the number of estimated parameters), Cramér-von Mises statistic ($W^{*}$), Anderson–Darling statistics ($A^{*}$), Kolmogorov–Smirnov (K-S) statistic, and its p-value. Generally, a fitted distribution can be considered as the proper fitting model for a certain dataset if it is asscociated with smaller values of all the goodness-of-fit statistics except for the p-value of the K-S statistic.

7.1. COVID-19 Data

These data are about COVID-19 collected from Holland. The data were analyzed by [44,45]. This dataset consists of 30 observations and is recorded between 31 March 2020 and 30 April 2020. (See the data in the Appendix A).

Figure 6 shows the profile likelihood plots for parameters of the RB-TL-TII-EHL-W distribution on the COVID-19 data. It can be seen that the MLEs obtained for the RB-TL-TII-EHL-W distribution are unique. This shows that the parameters of the RB-TL-TII-EHL-W distribution are identifiable.

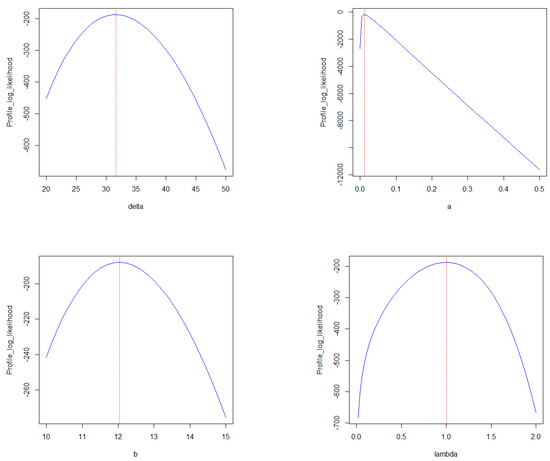
Figure 6. Profile likelihood function plots for parameters of RB-TL-TII-EHL-W distribution on the COVID-19 data.

The data analysis results for the COVID-19 data are given in Table 3. Table 3 indicates that the RB-TL-TII-EHL-W distribution has the lowest values of the $-2ln\left(L\right), AIC, CAIC,$ $BIC, W^{*},A^{*},K-S$ and largest p-value of the $K-S$ statistic among other fitted models. This implies that the RB-TL-TII-EHL-W can be chosen as the best model for modeling the COVID-19 data. The fitted density plots and the probability plots (Figure 7) show that the RB-TL-TII-EHL-W distribution adequately fits the COVID-19 data.

Table 3. MLEs and Goodness-of-Fit Statistics of COVID-19 Data.

	Estimates				Statistics
Model	$\mathit{\delta }$	a	$\mathit{b}$	$\mathit{\lambda }$	$-\mathbf{2}log\mathit{L}$	$\mathit{AIC}$	$\mathit{AICC}$	$\mathit{BIC}$	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	K-S	p-Value
RB-TL-TII-EHL-W	31.5910	0.0119	12.0320	1.0019	375.7258	383.7257	384.1218	394.3795	0.0460	0.2574	0.0646	0.7669
	(7.4281 $\times {10}^{-04}$)	(8.8791 $\times {10}^{-04}$)	(4.3483 $\times {10}^{-03}$)	(6.3719 $\times {10}^{-02}$)
	$\alpha$	$\beta$	$\delta$	k
RB-OPGW-Lx	2.3656	53.9060	1.0790	0.0999	383.0791	391.0791	391.4751	401.7328	0.1156	0.7575	0.0733	0.6187
	(1.6820 $\times {10}^{-01}$)	(1.3300 $\times {10}^{-04}$)	($\times {10}^{-15}$)	(1.0572 $\times {10}^{-02}$)
	k	$\beta$	$\lambda$	$\delta$
GGIW	7.3731	0.2671	0.0026	1.5621	376.2939	384.2939	384.6900	394.9477	0.0515	0.2869	0.0670	0.7269
	(0.0012)	(0.0259)	(0.00048)	(0.0035)
	$\alpha$	$\beta$	$\delta$	$\lambda$
RB-BIII-LLoG	0.0146	36.9600	18.3780	34.8890	378.785	386.7852	387.1812	397.439	0.0759	0.4398	0.0706	0.6656
	(1.0707 $\times {10}^{-03}$)	(2.8804 $\times {10}^{-01}$)	(4.9356 $\times {10}^{-01}$)	(6.2419 $\times {10}^{-04}$)
	b	$\delta$	$\lambda$	$\gamma$
TLMOW	2.5861	0.5294	0.1205	1.3825	376.4293	384.4293	384.8254	395.0831	0.0535	0.2981	0.0678	0.7133
	(2.3351)	(0.6827)	(0.2658)	(0.7581)
	$\theta$	$\alpha$	$\beta$	$\lambda$
APTLW	5.8553	2.7609 $\times {10}^{-05}$	0.5942	0.2816	377.9029	385.903	386.299	396.5567	0.0637	0.3624	0.0673	0.7215
	(4.5983 $\times {10}^{-03}$)	(2.2908 $\times {10}^{-04}$)	(0.0985)	(0.0475)
	a	$\lambda$	$\delta$	$\gamma$
TIIEHLW	21.7121	197.2789	3.4401	0.1250	376.5885	384.5885	384.9845	395.2423	0.0540	0.3030	0.0693	0.6885
	(37.3034)	(1.0424)	(0.2509)	(0.0413)
	$\alpha$	$\beta$	$\lambda$	$\gamma$
OGHLW	2.4469 $\times {10}^{-05}$	1.0482	8.8095	0.1456	390.3392	398.3391	398.7351	408.9928	0.1887	1.2185	0.0801	0.5044
	(4.6219 $\times {10}^{-06}$)	(1.0925 $\times {10}^{-03}$)	(1.2995 $\times {10}^{-04}$)	(9.3622 $\times {10}^{-03}$)
	$\alpha$	$\lambda$	$\beta$	k
MOEW	2.8837 $\times {10}^{07}$	1.7441 $\times {10}^{-01}$	1.4516 $\times {10}^{01}$	1.4997 $\times {10}^{-01}$)	380.8861	388.8859	389.2819	399.5396	0.0912	0.528	0.0722	0.6367
	(9.7681 $\times {10}^{-09}$)	(2.4798 $\times {10}^{-01}$)	(2.8610 $\times {10}^{-01}$)	(3.6792 $\times {10}^{-02}$)
	$\delta$	$\alpha$	b	$\theta$
OGLE	106.3274	0.3341	2.7092	0.2189	380.4094	388.4094	388.8054	399.0631	0.0869	0.4843	0.0738	0.6097
	(158.6800)	(0.4618)	(0.8918)	(0.0922)

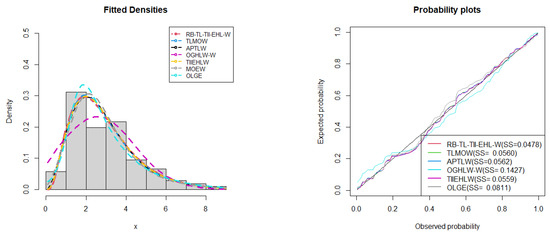
Figure 7. Fitted density superimposed on the histogram and observed probability vs. expected probability plots for the COVID-19 data.

Figure 8 shows the observed and the fitted Kaplan–Meier (K-M) survival curves, theoretical and empirical cumulative distribution (ECDF), total test on time (TTT) scaled plots, and hazard rate function (hrf) plots. We can see that the RB-TL-TII-EHL-W distribution follows the empirical cdf and Kaplan–Meier survival curves very closely. The TTT scaled plot shows an increasing hrf. Furthermore, the estimated hrf in is agreement with the TTT scaled plot, as it also displays an increasing shape for the COVID-19 dataset.

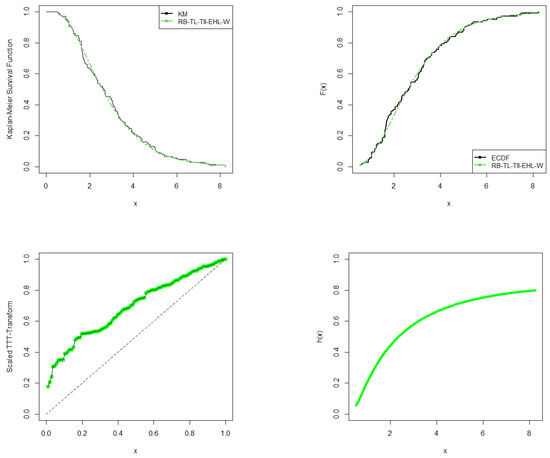
Figure 8. Fitted Kaplan–Meier survival curve, empirical cumulative distribution functions, the total time on the test scaled plot, and the fitted hazard rate function for the COVID-19 data.

7.2. Vehicle Fatalities Data

The data consist of the number of vehicle fatalities for 39 cities in South Carolina for 2012 collected by the National Highway Traffic Safety Administration (www-fars.nhtsa.dot.gov/States, accessed on 11 May 2023). The data were analyzed by [46] (see the data in Appendix A).

Figure 9 shows the profile likelihood plots for parameters of the RB-TL-TII-EHL-W distribution on the vehicle fatalities data. From the plots, we can see that the MLEs for the parameters of the RB-TL-TII-EHL-W distribution are achieved at single and different points.

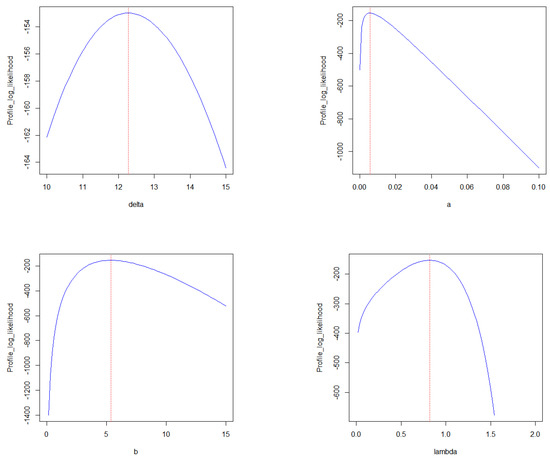
Figure 9. Profile likelihood function plots for parameters of RB-TL-TII-EHL-W distribution on the vehicle fatalities data.

Table 4 gives the MLEs of the fitted distributions together with the standard errors (in parenthesis) and all the values of the considered goodness-of-fit statistics. It is evident that the RB-TL-TII-EHL-W distribution provides the best fit among the competitors, since it has the lowest value of $-2ln\left(L\right)$, $AIC$, $CAIC$, $BIC$, $W^{*}$, $A^{*}$ and K-S statistic. Furthermore, the p-value of the $K-S$ statistic is the largest for the new model, suggesting that the proposed RB-TL-TII-EHL-W model provides the best fit for the vehicle fatalities data. The fitted density plots and the probability plots (Figure 10) show that the RB-TL-TII-EHL-W distribution adequately fits the vehicle fatalities data.

Table 4. MLEs and Goodness-of-Fit Statistics of Vehicle Fatalities Data.

	Estimates				Statistics
Model	$\mathit{\delta }$	a	$\mathit{b}$	$\mathit{\lambda }$	$-\mathbf{2}log\mathit{L}$	$\mathit{AIC}$	$\mathit{AICC}$	$\mathit{BIC}$	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	K-S	p-Value
RB-TL-TII-EHL-W	12.2752	0.0057	5.3660	0.8217	305.9453	313.9453	315.1218	320.5995	0.0368	0.2677	0.0886	0.9192
	(0.0018)	(0.0014)	(0.0095)	(0.0826)
	$\alpha$	$\beta$	$\delta$	k
RB-OPGW-Lx	3.9177	5.1996 $\times {10}^{-02}$	2.6947 $\times {10}^{01}$	1.0968 $\times {10}^{-03}$	380.0707	388.0708	389.2473	394.7251	0.1403	0.8925	0.3341	0.0003
	(4.3035 $\times {10}^{-01}$)	(2.8295 $\times {10}^{-02}$)	( 2.5178 $\times {10}^{-01}$)	(4.6193 $\times {10}^{-04}$)
	k	$\beta$	$\lambda$	$\delta$
GGIW	1.6099 $\times {10}^{-04}$	1.0006	8.0186 $\times {10}^{-02}$	1.4139 $\times {10}^{02}$	309.3782	317.378	318.5545	324.0322	0.0606	0.42001	0.1132	0.6993
	(1.7939 $\times {10}^{-04}$)	(5.3681 $\times {10}^{-04}$)	(7.9390 $\times {10}^{-03}$)	(2.6831 $\times {10}^{-06}$)
	$\alpha$	$\beta$	$\delta$	$\lambda$
RB-BIII-LLoG	8.1979 $\times {10}^{01}$	9.4819 $\times {10}^{-02}$	4.0700 $\times {10}^{-02}$	8.6497 $\times {10}^{-02}$	709.0801	717.0806	718.257	723.7348	0.2085	1.3047	0.3004	0.0017
	(8.0682 $\times {10}^{-05}$)	( 7.7779 $\times {10}^{-02}$)	(8.4369 $\times {10}^{-03}$)	(1.4133 $\times {10}^{-02}$)
	b	$\delta$	$\lambda$	$\gamma$
TLMOW	35.1447	0.2747	0.3352	0.4224	310.2705	318.2705	319.447	324.9248	0.0716	0.4849	0.1230	0.5966
	(0.0010)	(0.2166)	(0.2353)	(0.0900)
	$\theta$	$\alpha$	$\beta$	$\lambda$
APTLW	5.8809 $\times {10}^{01}$	4.7573 $\times {10}^{-04}$	1.5583 $\times {10}^{-01}$	1.0793	308.4781	316.4766	317.653	323.1308	0.0402	0.3019	0.1178	0.6514
	(5.2275 $\times {10}^{-04}$)	(2.4522 $\times {10}^{-03}$)	(3.4123 $\times {10}^{-02}$)	(6.4652 $\times {10}^{-02}$)
	a	$\lambda$	$\delta$	$\gamma$
TIIEHLW	0.0597	0.0789	3.0136	0.5026	360.9537	368.9538	370.1302	375.608	0.0371	0.2727	0.3485	0.0002
	(0.0157)	(0.0452)	(0.7527)	(0.0691)
	$\alpha$	$\beta$	$\lambda$	$\gamma$
OGHLW	2.3879 $\times {10}^{-05}$	0.6967	11.8160	0.0952	309.7039	317.7039	318.8804	324.3582	0.1143	0.7240	0.1221	0.6053
	(9.7110 $\times {10}^{-06}$)	(1.0280 $\times {10}^{-03}$)	(6.0584 $\times {10}^{-05}$)	(9.2143 $\times {10}^{-03}$)
	$\alpha$	$\lambda$	$\beta$	k
MOEW	54.1287	0.0192	1.3654	0.3773	309.2931	317.2931	318.4696	323.9473	0.0670	0.4676	0.0973	0.8539
	(49.8948)	(0.0476)	(0.7965)	(0.1854)
	$\delta$	$\alpha$	b	$\theta$
OGLE	0.1170	10.025	0.4439	0.1237	315.6349	323.6372	324.8136	330.2914	0.1351	0.8479	0.1408	0.4217
	(0.3395)	(18.7865)	(0.3848)	(0.1274)

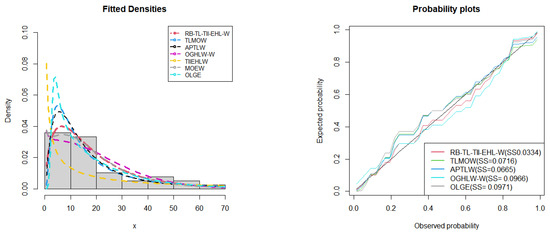
Figure 10. Fitted density superimposed on the histogram and observed probability vs. expected probability plots for the vehicle fatalities data.

Figure 11 shows the observed and the fitted Kaplan–Meier survival curves, ECDF plots, TTT scaled plot and hrf plot. We can see that the RB-TL-TII-EHL-W distribution follows the empirical cdf and Kaplan–Meier survival curves very closely. The TTT scaled plot and hrf plot show that the hrf for the vehicle fatalities data is non-monotonic.

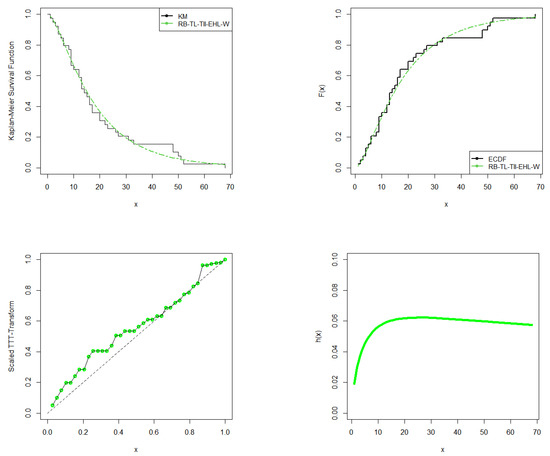
Figure 11. Fitted Kaplan–Meier survival curve, empirical cumulative distribution functions, the total time on the test scaled plot, and the fitted hazard rate function for the vehicle fatalities data.

7.3. Remission Times Data

The dataset is on remission times (months) of 128 bladder cancer patients by [47] (see the data in Appendix A).

The profile likelihood plots for parameters of the RB-TL-TII-EHL-W distribution can be used to check for the identifiability of parameters. From the plots in Figure 12, we can see that the MLEs for the RB-TL-TII-EHL-W distribution are unique; hence, we conclude that the parameters are identifiable.

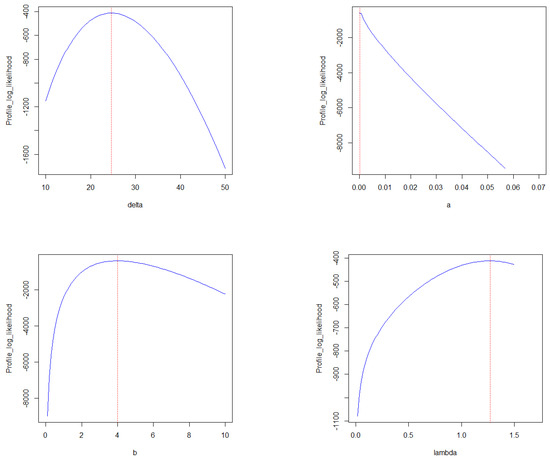
Figure 12. Profile likelihood function plots for parameters of RB-TL-TII-EHL-W distribution on the remission times dataset.

The results are presented in Table 5. From Table 5, it is quite visible that the values of $-2ln\left(L\right)$, $AIC$, $CAIC$, $BIC$, $W^{*}$, $A^{*},K-S$ are smaller and the p-value of the K-S statistic is largest under the RB-TL-TII-EHL-W distribution, indicating that the RB-TL-TII-EHL-W distribution fits the remission times data better than other fitted distributions. The fitted density plots and the probability plots (Figure 13) show that the RB-TL-TII-EHL-W distribution adequately fits the remission times.

Table 5. MLEs and Goodness-of-Fit Statistics of Remission Times Data.

	Estimates				Statistics
Model	$\mathit{\delta }$	a	$\mathit{b}$	$\mathit{\lambda }$	$-\mathbf{2}log\mathit{L}$	$\mathit{AIC}$	$\mathit{AICC}$	$\mathit{BIC}$	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	K-S	p-Value
RB-TL-TII-EHL-W	24.6260	0.00010	4.0077	1.2704	822.8816	830.8816	831.2068	842.2897	0.0579	0.3833	0.0522	0.8752
	(0.0015)	(1.5862 $\times {10}^{-05}$)	(0.0189)	(0.0665)
	$\alpha$	$\beta$	$\delta$	k
RB-OPGW-Lx	1.8034	592.3000	1.0001	0.0100	825.8694	833.8694	834.1946	845.2776	0.0916	0.5778	0.0690	0.5744
	(1.2081 $\times {10}^{-01}$)	(2.1182 $\times {10}^{-06}$)	(1.8869 $\times {10}^{-15}$)	(2.2921 $\times {10}^{-03}$)
	k	$\beta$	$\lambda$	$\delta$
GGIW	12.7271	0.1990	0.0016	0.2197	877.5066	836.542	836.8672	847.9502	0.1316	0.8126	0.0702	0.552
	(1.0673)	(0.0206)	(0.0012)	(0.0241)
	$\alpha$	$\beta$	$\delta$	$\lambda$
RB-BIII-LLoG	0.2066	35.6475	17.4118	1.3549	832.1743	840.1743	840.4995	851.5824	0.1428	0.9589	0.0676	0.6004
	(0.2573)	(23.6792)	(13.7133)	(1.6875)
	b	$\delta$	$\lambda$	$\gamma$
TLMOW	16.1350	0.2540	0.3205	0.4398	837.4597	845.4595	845.7847	856.8676	0.1979	1.2993	0.0811	0.3679
	(32.4118)	(0.1033)	(0.4540)	(0.2468)
	$\theta$	$\alpha$	$\beta$	$\lambda$
APTLW	0.3632	2.6272 $\times {10}^{02}$	0.8610	0.1120	827.4507	835.4507	835.7759	846.8588	0.1275	0.7620	0.0727	0.5065
	(0.1239)	(4.8767 $\times {10}^{-05}$)	(0.1241)	(0.0540)
	a	$\lambda$	$\delta$	$\gamma$
TIIEHLW	1.0297 $\times {10}^{03}$	1.0759 $\times {10}^{02}$	2.4004	0.0500	823.0934	831.0934	831.4186	842.5015	0.0710	0.4392	0.0549	0.8351
	(1.8761 $\times {10}^{-06}$)	(1.9066 $\times {10}^{-04}$)	(2.1528 $\times {10}^{-02}$)	(3.2111 $\times {10}^{-03}$)
	$\alpha$	$\beta$	$\lambda$	$\gamma$
OGHLWW	2.1269 $\times {10}^{-05}$	0.6471	14.4550	0.0774	838.0349	846.0347	846.3599	857.4428	0.2477	1.4603	0.0952	0.1962
	(3.4793 $\times {10}^{-06}$)	(4.2738 $\times {10}^{-04}$)	(1.9132 $\times {10}^{-05}$)	(4.3136 $\times {10}^{-03}$)
	$\alpha$	$\lambda$	$\beta$	k
MOEW	2.3544	0.0714	1.0415	0.2405	948.2204	956.2204	956.5456	967.6285	0.2321	1.3721	0.4481	0.0000
	(1.2446)	(0.0372)	(1.0080)	(0.2691)
	$\delta$	$\alpha$	b	$\theta$
OGLE	8.8103	0.2220	0.3397	0.3668	836.6097	844.6097	844.9349	856.0178	0.2298	1.3899	0.0880	0.2745
	(8.3076)	(0.1826)	(0.0966)	(0.1147)

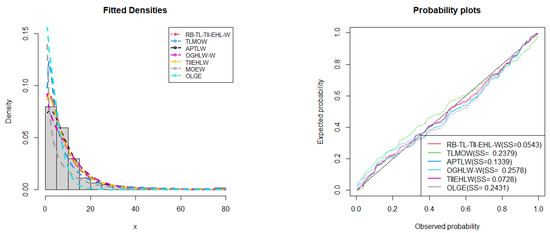
Figure 13. Fitted density superimposed on the histogram and observed probability vs. expected probability plots for the remission times data.

The observed and the fitted Kaplan–Meier survival curves, observed and fitted ECDF, TTT scaled plots and hrf plots of the RB-TL-TII-EHL-W distribution are shown in Figure 14. From the Kaplan–Meier and ECDF plots, it is clear that the RB-TL-TII-EHL-W distribution is a good candidate for modeling the remission times data. The TTT scaled and hrf plots indicate that indeed, the RB-TL-TII-EHL-W distribution is suitable for modeling the remission times data, as they both estimate the hazard rate of the data to be upside-down bathtub.

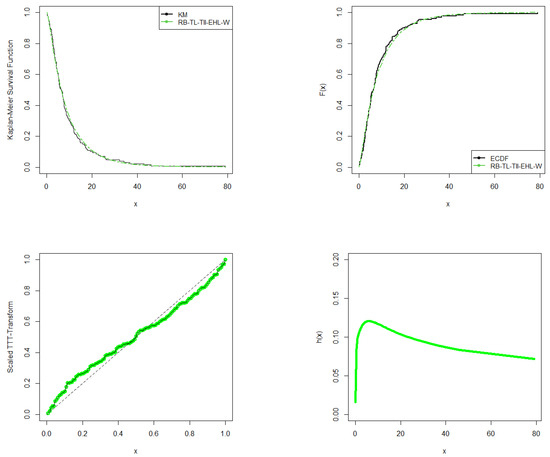
Figure 14. Fitted Kaplan–Meier survival curve, empirical cumulative distribution functions, the total time on the test scaled plot, and the fitted hazard rate function for the remission times data.

8. Conclusions

We have proposed and developed a new generalized family of distributions called the Gamma-Topp-Leone-Type II-Exponentiated Half Logistic-G (RB-TL-TII-EHL-G) distribution. It has been shown that this new family of distributions can be expressed as an infinite linear combination of the exponentiated-G distributions. The maximum likelihood estimation technique was used to estimate the model parameters. Some of the mathematical and statistical properties have been derived and established. The RB-TL-TII-EHL-W model as a special case to this new family of distributions was applied to three datasets, and from the results, it is evident that the new proposed model performs better than several equal-parameter models. In the future, we will seek to use different estimation methods to estimate the unknown parameters and also also apply the new distribution to censored data.