Climate Change: Linear and Nonlinear Causality Analysis

Abstract

The goal of this study is to detect linear and nonlinear causal pathways toward climate change as measured by changes in global mean surface temperature and global mean sea level over time using a data-based approach in contrast to the traditional physics-based models. Monthly data on potential climate change causal factors, including greenhouse gas concentrations, sunspot numbers, humidity, ice sheets mass, and sea ice coverage, from January 2003 to December 2021, have been utilized in the analysis. We first applied the vector autoregressive model (VAR) and Granger causality test to gauge the linear Granger causal relationships among climate factors. We then adopted the vector error correction model (VECM) as well as the autoregressive distributed lag model (ARDL) to quantify the linear long-run equilibrium and the linear short-term dynamics. Cointegration analysis has also been adopted to examine the dual directional Granger causalities. Furthermore, in this work, we have presented a novel pipeline based on the artificial neural network (ANN) and the VAR and ARDL models to detect nonlinear causal relationships embedded in the data. The results in this study indicate that the global sea level rise is affected by changes in ice sheet mass (both linearly and nonlinearly), global mean temperature (nonlinearly), and the extent of sea ice coverage (nonlinearly and weakly); whereas the global mean temperature is affected by the global surface mean specific humidity (both linearly and nonlinearly), greenhouse gas concentration as measured by the global warming potential (both linearly and nonlinearly) and the sunspot number (only nonlinearly and weakly). Furthermore, the nonlinear neural network models tend to fit the data closer than the linear models as expected due to the increased parameter dimension of the neural network models. Given that the information criteria are not generally applicable to the comparison of neural network models and statistical time series models, our next step is to examine the robustness and compare the forecast accuracy of these two models using the soon-available 2022 monthly data.

1. Introduction

In recent years, climate change, especially global warming and sea level rise, has caused increasing alarms among global communities. Mainstream research works based on physics models have identified the potential causal factors in global temperature rise, including, notably, the increased greenhouse gas emission due to human activities [1,2,3,4] and the increased humidity [5,6]. Meanwhile, the physical models have attributed the global sea level rise to glacier and ice sheet mass loss [7,8,9], reduced sea ice coverage [10], and ocean thermal expansion [11,12]. Besides the main stream research works based on physics models, there are also a few works utilizing statistical models, including: linear regression model [13]; structural equation modeling, which is indeed a system of intercorrelated linear regression equations [14,15]; and Granger causality and cointegration analysis, which are traditional time series methods for detecting linear causal relationships [16,17,18,19,20]. There is also a rising trend of utilizing machine learning methods for climate and weather studies in recent years [21,22,23,24,25]; however, none features an explicit causal inference for the pathways leading to global warming and sea level rise as we have presented here. While we have a substantial amount of faith in the existing physics models and the related conclusions, it would be doubly reassuring if we could reach the same conclusions using data-based analytical methods only including both statistical time series models and machine learning methods. This is exactly what we have performed in this work, using these purely data-based methods to identify potential climate change causal factors and to examine whether these causal relationships are linear or nonlinear.

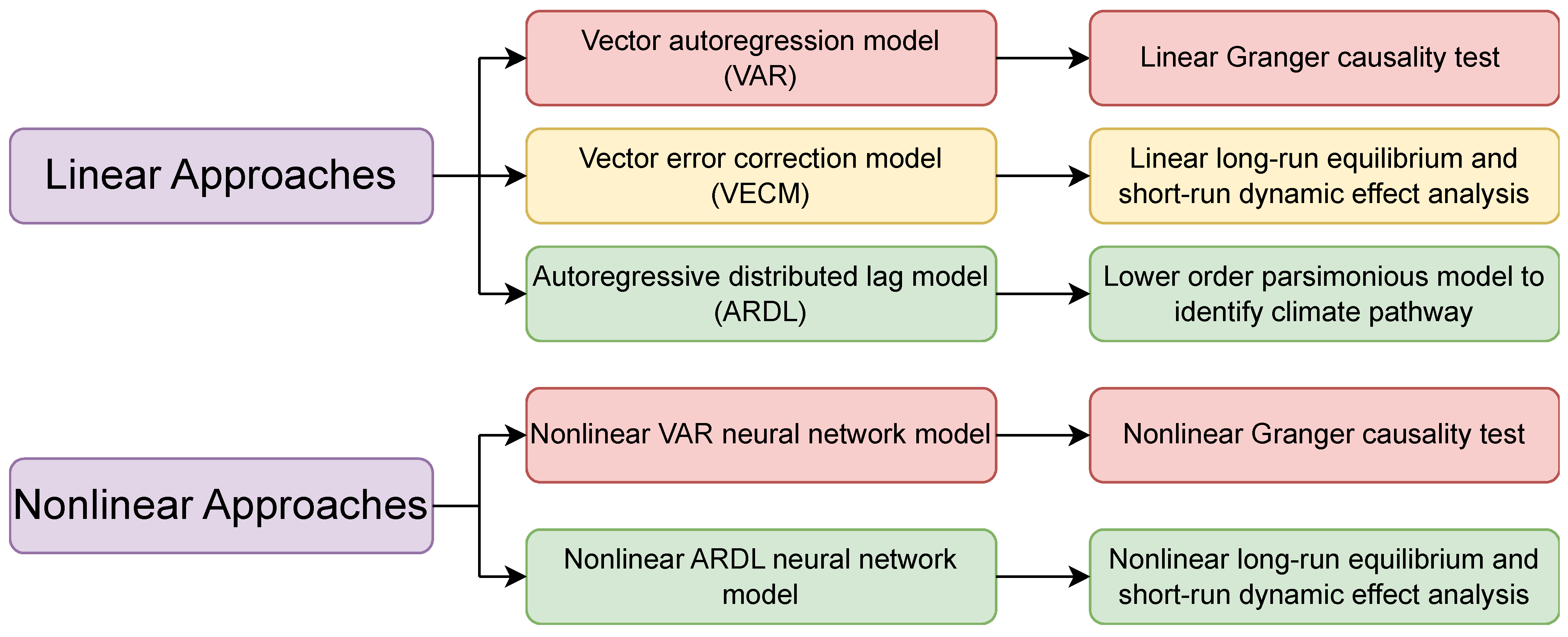
Our main contributions to this study are as follows. Firstly, we have conducted a thorough analysis of linear causal relationships and quantified the long-run cointegration relationships and the short-run dynamics related to global temperature change and sea level change. Secondly, we have developed a novel pipeline to combine time series models such as VAR and ARDL with neural network structures to detect nonlinear causality relationships among the time series data of climate factors. Thirdly, we have applied this pipeline to detect nonlinear causal pathways toward climate change in terms of rising global temperature and sea level and compared the model goodness-of-fit between the nonlinear machine learning models and the linear time series models. (Figure 1).

2. Data and Methodology

2.1. Data Overview and Processing

In this study, seven relevant monthly frequency climate factors from January, 2003 to December, 2021 have been adopted toward the data-driven pathway analysis (the data were retrieved on 7 March 2023):

a.

Global mean sea level (GMSL) in mm, gathered from climate.nasa.gov, which was computed by the NASA Goddard Space Flight Center [26];

b.

Antarctic and Greenland ice sheet mass (IceSheet) in Gt, gathered from climate.nasa.gov, which was computed by the NASA MEaSUREs program [27];

c.

Northern and Southern hemisphere sea ice extent (SeaIce) in Mkm2, gathered from the National Snow and Ice Data Center [28];

d.

Global mean surface temperature (TEMP) (with sea ice area measured by the air above sea ice) in °C, gathered from Berkeley Earth [29];

e.

Global mean specific humidity (Humidity) in kg kg⁻¹ (mass of water vapor per kilogram of moist air), gathered from Copernicus [30];

f.

Greenhouse gases atmosphere concentration, CO₂ in ppm, gathered from Scripps CO₂ program [31]; CH4 in ppb, gathered from NOAA Global Monitoring Laboratory [32]; N₂O in ppb, gathered from NOAA Global Monitoring Laboratory [33];

g.

Sunspot number (SSN), gathered from SILSO [34].

The trend and seasonality decomposition of each variable is shown in Figure 2.

Since there exists strong seasonality in the dataset and the difference in scales is significant between climate factors, all the variables are de-seasoned and normalized (first minus the de-seasoned series mean and then divide it by the de-seasoned series standard deviation) while missing values are imputed via Kalman smoothing before the analysis. We combined the Greenland ice sheet and the Antarctic ice sheet data as one new feature: IceSheet. We also combined the Northern and Southern hemisphere sea ice as another new feature: SeaIce. Furthermore, the three major greenhouse gases, CO₂, CH₄, and N₂O, are found to be highly correlated with each other; to avoid the multicollinearity issue, the global warming potential (GWP), which represents the heat absorbing capacities of greenhouse gases gauged in terms of the heat absorbed by the same amount of CO₂, has been adopted for analyzing the greenhouse gas effect. The GWP is calculated in the CO₂ variable unit and the coefficients are gathered from the global warming potential in 100 years’ time length as calculated by IPCC [35]. These coefficients indicate how much energy the emissions of 1 ton of a gas will absorb over 100 years relative to the emissions of 1 ton of CO₂. Among the three major greenhouse gases (CO₂, CH₄, and N₂O), CH₄ is 28 times more potent, while N₂O is 265 times more potent than CO₂ in warming up the globe. Therefore, we multiply the concentration of each of these gases in the atmosphere with these coefficients to arrive at the following GWP calculation formula:

$$\mathit{GWP}=C{O}_2+28 C{H}_4+265 N_{2}O$$

(1)

2.2. Unit Root Test

A time series is (weakly) stationary if its first two moments are time-invariant and the unit root tests are the statistical procedures used to determine the stationarity [36]. In this study, we have used the augmented Dicky–Fuller (ADF) test and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test to examine the stationarity and to determine the integration order of each time series.

Decomposing each time series $x_t$ as follows:

$$\Delta x_t=\mu +\alpha x_{t-1}+{\displaystyle \sum }_{i=1}^m{\mathsf{\beta }}_i\Delta x_{t-i}+{ϵ}_t,$$

where $\Delta x_t$ is the first difference of $x_t$. For the ADF test, the null hypothesis is $\alpha =0$ while the alternative hypothesis is $\alpha <0$. Rejecting the null hypothesis indicates the time series is stationary.

For the KPSS test, the hypotheses are reversed, with the null hypothesis indicating that the time series is stationary, while the alternative hypothesis is not stationary [36]. By utilizing both unit root tests, we can further ensure the robustness of the test results to minimize the Type 1 and the Type 2 errors.

2.3. Vector Autoregressive Model (VAR) and Granger Causality Test

The vector autoregressive model is a multivariate statistical analysis framework to capture relationships between multiple time series. A VAR model with lag p (VAR(p)) can be expressed as:

$$y_t=c+{\displaystyle \sum }_{\gamma =1}^p{A}_{\gamma }{y}_{t-\gamma }+{ϵ}_t$$

To determine the lag of a VAR model, several criteria such as the Akaike information criterion (AIC), the Bayesian information criterion (BIC), and the Hannan–Quinn criterion (HQC) can be used, with the BIC criterion being the most common choice as it imposes a higher penalty on a larger model (with more parameters).

In this study, we apply the VAR model to formulate and detect the linear causality pathways toward global mean temperature and global mean sea level (TEMP and GMSL) changes. Two VAR pathway models are formulated with one model containing variables potentially related to temperature rise, including TEMP, Humidity, GWP, and SSN; while the other model encompasses potential causal factors for sea level rise, including GMSL, IceSheet, SeaIce, and TEMP. The order of integration for both VAR models are found to be one, as selected by the Bayesian information criterion (BIC).

The Granger causality test is used to determine if one time series is critical in forecasting another one. For multiple time series, the Granger causality test is conducted through a VAR model with stationary time series data. It says that $y_i$ Granger causes another time series $y_j$ if at least one element of $A_{\gamma }\left(j,i\right)$ is significantly not 0 for any $\gamma \in \left[1,p\right]$. The Granger causality tests are usually conducted through an F-test or a Wald chi-squared test.

2.4. Vector Error Correction Model (VECM)

Two or more time series are cointegrated if they can form one or more long-run equilibrium relationship(s). To determine the cointegration relationship between TEMP-related variables and GMSL-related variables, we have adopted the Johansen cointegration test [37].

If the time series variables are all integrated of order 1, namely I(1), and there exists a cointegration relationship among the time series, a vector error correction model (VECM) can be used to detect the long-run equilibrium and the short-run dynamic effect. In VECM, there is an error correction term (ECT) which is determined by the cointegration relationship:

$$EC{T}_t={\beta }_0+\beta \cdot y_t$$

Subsequently, the VECM is written as:

$$\Delta y_t=\mu +\gamma EC{T}_{t-1}+{\displaystyle \sum }_{i=1}^p{A}_i\Delta y_{t-i}+{ϵ}_t$$

Here, the ${{\displaystyle \sum }}_{i=1}^p{A}_i\Delta y_{t-i}$ term represents the short-term dynamics.

2.5. Autoregressive Distributed Lag Model (ARDL)

The Johansen cointegration test and the VECM are strict on the integration order assumption, which is that all the time series must be of the same integration order. Conversely, the assumptions for the autoregressive distributed lag model (ARDL) are much more relaxed and so it can be applied to mixed integration order data. The ARDL can be formulated as follows:

$$\Delta y_t=\mu +{\displaystyle \sum }_{i=1}^p{\mathsf{\alpha }}_{\mathrm{i}}\Delta y_{t-i}+{\displaystyle \sum }_{i=0,}^p{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{k}}{\mathsf{\beta }}_{\mathrm{ij}}\Delta x_{j,t-i}+{\lambda }_0{y}_{t-1}+{\displaystyle \sum }_{j=1}^k{\lambda }_j{x}_{t-1}+{ϵ}_t$$

Here, the long-run equilibrium is represented as $EC{T}_{t-1}={\lambda }_0{y}_{t-1}+{{\displaystyle \sum }}_{j=1}^k{\lambda }_j{x}_{t-1}$. The ARDL bound test is often used to detect the long-run cointegration relationship with the null hypothesis being ${\lambda }_i=0$ for all $i\in \left[0,k\right]$, which means that there is no cointegration relationship.

Notably, co-integrated time series must have Granger causality in either one way or both directions, while the presence of Granger causality in either one way or both directions does not necessarily imply that the time series are cointegrated. Therefore, co-integration should be a stronger indication of Granger causality, in both directions. In summary, besides being able to differentiate the long-run and short-run relationships, the VECM and ARDL models can also help identify dual-directional Granger causality, and thereby serve as an alternative to the paradigm of VAR model with Granger causality test.

2.6. Nonlinear VAR Neural Network Model

Based on the VAR model structure and the Granger causality test, and inspired from the work of Rosoł et al. [38], we propose a statistical procedure to detect nonlinear Granger causality among multiple time series data. The basic idea and procedures are trivial and shown as the following:

• Fit an artificial neural network with all the predictors of the VAR model (full model):

$$y_t=f\left(y_{t-1},\dots ,y_{t-p},x_{1,t-1},\dots ,x_{m,t-1},x_{1,t-2},\dots ,x_{m,t-p}\right)+{ϵ}_t$$

2.

Fit the same artificial neural network structure without a predictor ($x_i$) to test for its causal relationship with the response variable (partial model):

$$y_t=f\left(y_{t-1},\dots ,y_{t-p},x_{1,t-1},\dots x_{i-1,t-1},x_{i+1,t-1},x_{m,t-1},\dots \right)+{ϵ}_t$$

3.

Examine if the residuals as measured by the sum squares of error (SSE) or mean absolute error (MAE) have increased significantly in the partial model compared to the full model;

4.

Repeat steps 2 and 3 above until all the predictors are tested.

If the residuals of the partial model are significantly larger than the full model, the tested predictor is critical in forecasting the response variable, which also indicates the tested predictor nonlinear Granger cause for the response variable if the SSE of the neural network model is smaller than that of the corresponding linear model.

Due to the limitation of data size (not large enough for training) and stochastic properties of the numerical solutions (for example, the stochastic gradient descent), the neural network results are not as stable as the linear model and are dependent upon the random seeds as well as the initial coefficients. To avoid these issues, instead of comparing the median absolute mean of residuals via the Wilcoxon test [38], we chose to repeat the full model and each partial models N times with different random seeds, and then comparing the medians of the sum squares of error (SSE) and mean absolute error (MAE) of the full model and the partial models. The detailed procedure is as follows.

1.

Fit N artificial neural network with all the predictors of the VAR model (full model) with different random seeds and record the SSE of each model: $SS{E}_f=\left\{SS{E}_{f1},SS{E}_{f2},\dots ,SS{E}_{fN}\right\}$;

2.

Fit N artificial neural network of the same structure without a given predictor to test its causal relationship with the response variable (partial model), with different random seeds and record the SSE of each model: $SS{E}_p=\left\{SS{E}_{p1},SS{E}_{p2},\dots ,SS{E}_{pN}\right\}$;

3.

Conduct a Wilcoxon rank sum test on $SS{E}_f$ and $SS{E}_p$ to test if the median of $SS{E}_f$ is significantly smaller than $SS{E}_p$;

4.

Repeat steps 2 and 3 until all the predictors are tested.

The procedure of comparing Mean absolute error (MAE) is similar, just replace SSE with MAE.

2.7. Nonlinear ARDL Neural Network Model

Similarly, we have also developed a nonlinear ARDL neural network based on the combined ARDL model and the artificial neural network (ANN) to detect the nonlinear long-run equilibrium relationship and the nonlinear relationship. The detailed procedure is as follows:

• Fit N artificial neural network with all the predictors of the ARDL model (full model) with different random seeds and record the SSE of each model:

$$SS{E}_f=\left\{SS{E}_{f1},SS{E}_{f2},\dots ,SS{E}_{fN}\right\}$$

$$\Delta y_t=f\left(y_{t-1},x_{1,t-1},\dots ,x_{m,t-1}, \Delta y_{t-1},\dots ,\Delta y_{t-p},\Delta x_{1,t},\dots ,\Delta x_{m,t},\Delta x_{1,t-1},\dots ,\Delta x_{m,t-p}\right)+{ϵ}_t$$

2.

Fit N artificial neural network of the same structure without the cointegration part (partial cointegration model), with different random seed and record the SSE of each model:

$$SS{E}_{pc}=\left\{SS{E}_{pc1},SS{E}_{pc2},\dots ,SS{E}_{pcN}\right\}$$

$$\Delta y_t=f\left(\Delta y_{t-1},\dots ,\Delta y_{t-p},\Delta x_{1,t},\dots ,\Delta x_{m,t},\Delta x_{1,t-1},\dots ,\Delta x_{m,t-p}\right)+{ϵ}_t$$

3.

Conduct a Wilcoxon rank sum test on $SS{E}_f$ and $SS{E}_{pc}$ to test if the median of $SS{E}_f$ is significantly smaller than that of $SS{E}_{pc}$, which in turn would indicate if there exists a long-run equilibrium among the multiple time series;

4.

Fit N artificial neural network of the same structure without the predictor to test its nonlinear relationship with the response variable (partial model), with different random seeds and record the SSE of each model:

$$SS{E}_p=\left\{SS{E}_{p1},SS{E}_{p2},\dots ,SS{E}_{pN}\right\}$$

$$\Delta y_t=f\left(y_{t-1},x_{1,t-1},\dots ,x_{i-1,t-1},x_{i+1,t-1}\dots ,x_{m,t-1}, \Delta x_{1,t},\dots ,\Delta x_{i-1,t},\Delta x_{i+1,t},\dots \right)+{ϵ}_t$$

5.

Conduct a Wilcoxon rank sum test on $SS{E}_f$ and $SS{E}_p$ to test if the median of $SS{E}_f$ is significantly smaller than that of $SS{E}_p$ to test if there exists a nonlinear relationship between the tested predictor and the response variable;

6.

Repeat steps 4 and 5 until all the predicting variables are tested.

The procedure of comparing MAE is similar; simply replace SSE with MAE.

It should be mentioned that the nonlinear autoregressive distributed lag (NARDL) model proposed by Shin and colleagues [39] also provides an asymmetric dynamic multipliers method to analyze the nonlinear long-run equilibrium and short-term dynamic relationships. The NARDL model formulates the problems as:

$$y_t={\displaystyle \sum }_{j=1}^p{y}_{t-j}+{\displaystyle \sum }_{j=0}^q\left({\theta }_j^{+}{x}_{t-j}^{+}+{\theta }_j^{-}{x}_{t-j}^{-}\right)+ϵ\_t$$

in which, $x_{t-j}^{+}=\max \left(x_{t-j}, 0\right)$ and $x_{t-j}^{-}=\min \left(x_{t-j}, 0\right)$.

NARDL is widely applied in different research areas, such as business [40], economics [41], and finance [42,43]. When comparing with the machine learning methods such as the neural network in this article, NARDL has more of an advantage in its clear statistical properties, but neural network is more similar to a blackbox, with a structure that provides a more flexible way of complexity and nonlinear function selection. We aim to compare the NARDL model to the neural network structure in the future for climate studies.

3. Results

3.1. Unit Root Tests and Integration Order

To determine the integration order of each time series, the augmented Dicky–Fuller (ADF) test with lag 12 and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test were performed, and the stationarities of level (original time series data) and difference (differenced time series data) were tested. The p-values are listed in

Table 1. Augmented Dicky–Fuller (ADF) test and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test results: p-value for the de-seasoned original time series (Level), and its first-order difference (Difference).

	ADF Test		KPSS Test
Variable	Level	Difference	Level	Difference
GMSL	0.20	$\le 0.01$	$\le 0.01$	$\ge 0.1$
IceSheet	0.24	0.02	$\le 0.01$	$\ge 0.1$
SeaIce	0.51	$\le 0.01$	$\le 0.01$	$\ge 0.1$
TEMP	0.20	$\le 0.01$	0.02	$\ge 0.1$
Humidity	0.30	$\le 0.01$	$\le 0.01$	$\ge 0.1$
GWP	0.81	$\le 0.01$	$\le 0.01$	$\ge 0.1$
SSN	0.65	$\le 0.01$	$\le 0.01$	$\ge 0.1$

.

Both the ADF test and KPSS showed that the levels are not stationary while the first-order differences are stationary, which indicates that the data integration orders are all I(1). That is, the de-seasoned original time series data are all integrated of order one.

3.2. Linear Granger Causality

To demonstrate the linear Granger causality among these climate variables, we fit two separate VAR(1) models and Engle–Granger tests, one for each response variable, global mean sea level (GMSL), and global mean surface temperature (TEMP), respectively. The confirmed VAR models and the Engle–Granger test results are shown in

Table 2. Granger causality results based on the VAR(1) models with GMSL-related variables and TEMP-related variables, with the p-values of the F-test and the Wald chi-squared test shown.

GMSL-Related Model			TEMP-Related Model
	F-Test	Chisq-Test		F-Test	Chisq-Test
GMSL ≤ IceSheet	<0.001	<0.001	TEMP ≤ Humidity	<0.001	<0.001
GMSL ≤ SeaIce	0.929	0.928	TEMP ≤ GWP	<0.001	<0.001
GMSL ≤ TEMP	0.124	0.123	TEMP ≤ SSN	0.136	0.135
------------------------			------------------------
IceSheet ≤ GMSL	0.679	0.679	Humidity ≤ TEMP	0.003	0.002
IceSheet ≤ SeaIce	0.986	0.986	Humidity ≤ GWP	0.303	0.301
IceSheet ≤ TEMP	0.856	0.856	Humidity ≤ SSN	0.051	0.050
------------------------			------------------------
SeaIce ≤ GMSL	0.335	0.334	GWP ≤ TEMP	0.423	0.422
SeaIce ≤ IceSheet	0.360	0.359	GWP ≤ Humidity	0.978	0.978
SeaIce ≤ TEMP	0.055	0.054	GWP ≤ SSN	0.949	0.949
------------------------			------------------------
TEMP ≤ GMSL	<0.001	<0.001	SSN ≤ TEMP	0.318	0.317
TEMP ≤ IceSheet	0.023	0.022	SSN ≤ Humidity	0.109	0.108
TEMP ≤ SeaIce	0.341	0.340	SSN ≤ GWP	0.797	0.797

.

GMSL-related VAR model:

$$GMS{L}_t=0.014+0.856 GMS{L}_{t-1}-0.132 IceShee{t}_{t-1}-0.001 SeaIc{e}_{t-1}+0.016 TEM{P}_{t-1}$$

(2)

$$IceShee{t}_t=-0.014-0.005 GMS{L}_{t-1}+0.995 IceShee{t}_{t-1}+0.001 TEM{P}_{t-1}$$

(3)

$$SeaIc{e}_t=-0.012-0.165 GMS{L}_{t-1}-0.144 IceShee{t}_{t-1}+0.813 SeaIc{e}_{t-1}-0.094 TEM{P}_{t-1}$$

(4)

$$TEM{P}_t=0.004+0.711 GMS{L}_{t-1}+0.404 IceShee{t}_{t-1}-0.040 SeaIc{e}_{t-1}+0.559 TEM{P}_{t-1}$$

(5)

TEMP-related VAR model:

$$TEM{P}_t=0.003+0.421 TEM{P}_{t-1}+0.269 Humidit{y}_{t-1}+0.247 GW{P}_{t-1}+0.053 SS{N}_{t-1}$$

(6)

$$Humidit{y}_t=0.003+0.163 TEM{P}_{t-1}+0.740 Humidit{y}_{t-1}+0.040 GW{P}_{t-1}+0.054 SS{N}_{t-1}$$

(7)

$$GW{P}_t=0.015+0.003 TEM{P}_{t-1}+1.000 GW{P}_{t-1}$$

(8)

$$SS{N}_t=-0.003-0.080 TEM{P}_{t-1}+0.116 Humidit{y}_{t-1}-0.015 GW{P}_{t-1}+0.798 SS{N}_{t-1}$$

(9)

The VAR models and Granger causality test results are consistent with the current physics-models-based results. The positive parameters from each feature at time t−1 to time t shows the consistent developing trend of each feature. IceSheet mass significantly causes GMSL changing by new water input, which is represented by the negative coefficient form IceSheet to GMSL. The positive coefficients from Humidity to TEMP and from TEMP to Humidity imply that they significantly affect each other with water vapor heat trap effect and water cycle theory. Furthermore, GWP leads the TEMP changing by the greenhouse effect. The thermal expansion effect of TEMP to GMSL, however, is less significant; the reason could be that the effect is not linear and needs to be formulated by a nonlinear model, which we will examine next using the neural network models.

3.3. Long-Run Equilibrium and Short-Run Dynamic Effect

3.3.1. Johansen Test

We first adopted the Johansen procedure to detect potential cointegration relationships in GMSL-related variables and in TEMP-related variables. Results of the Johansen procedure (

Table 3. Johansen procedure results for cointegration relationship detection, test statistics, and p-value range are shown.

GMSL-Related Model			TEMP-Related Model
	Statistic	p-Value		Statistic	p-Value
At least 1 cointegration	44.43	<0.01	At least 1 cointegration	72.78	<0.01
At least 2 cointegration	28.59	<0.01	At least 2 cointegration	24.35	0.01–0.05
At least 3 cointegration	10.00	>0.1	At least 3 cointegration	9.20	>0.1
At least 4 cointegration	0.04	>0.1	At least 4 cointegration	1.24	>0.1

) indicate that there could be one to two cointegration relationship(s) in each model.

3.3.2. Vector Error Correction Model (VECM)

To further identify the co-integration relationship, we resorted to two VECM models to detect the long-run equilibrium and short-run effect among related climate variables. VECM can be applied only if all the time series variables are integrated of the same order, such as order one, namely, I(1). VECM with order one (also referred to as lag one) is an equivalent transformation of a VAR(2) model, but, importantly, with the added benefit of focusing on the analysis of a long-run equilibrium (error correction terms; cointegration relationships) and short-run dynamic effect (differential terms). For each model, we have confirmed one strong cointegration relationship based on the VECM model. The VECM equations are shown below, with the corresponding significance levels provided in

Table 4. Significance levels (p-values) of the coefficients in GMSL-related VECM model.

	ECT	$\Delta \mathit{G}\mathit{M}\mathit{S}{\mathit{L}}_{\mathit{t}-1}$	$\Delta \mathit{I}\mathit{c}\mathit{e}\mathit{S}\mathit{h}\mathit{e}\mathit{e}{\mathit{t}}_{\mathit{t}-1}$	$\Delta \mathit{S}\mathit{e}\mathit{a}\mathit{I}\mathit{c}{\mathit{e}}_{\mathit{t}-1}$	$\Delta \mathit{T}\mathit{E}\mathit{M}{\mathit{P}}_{\mathit{t}-1}$
GMSL equation	0.004	<0.001	0.197	0.242	0.918
IceSheet equation	0.871	0.481	0.045	0.691	0.269
SeaIce equation	0.371	0.967	0.934	0.113	0.779
TEMP equation	0.005	0.160	0.347	0.588	<0.001

and

Table 5. Significance levels (p-values) of the coefficients in GMSL-related VECM model.

	ECT	$\Delta \mathbf{T}\mathbf{E}\mathbf{M}{\mathit{P}}_{\mathit{t}-1}$	$\Delta \mathbf{H}\mathbf{u}\mathbf{m}\mathbf{i}\mathbf{d}\mathbf{i}\mathbf{t}{\mathit{y}}_{\mathit{t}-1}$	$\Delta \mathbf{G}\mathbf{W}{\mathit{P}}_{\mathit{t}-1}$	$\Delta \mathbf{S}\mathbf{S}{\mathit{N}}_{\mathit{t}-1}$
TEMP equation	<0.001	0.400	0.030	0.307	0.710
Humidity equation	<0.001	0.221	0.030	0.818	0.327
GWP equation	0.036	0.011	0.017	<0.001	0.413
SSN equation	0.562	0.894	0.184	0.329	<0.001

.

GMSL-related VECM model:

$$\left\{\begin{array}{l}\Delta GMS{L}_t=0.021-0.107 EC{T}_{t-1}-0.266 \Delta GMS{L}_{t-1}+0.246 \Delta IceShee{t}_{t-1}-0.015 \Delta SeaIc{e}_{t-1}+0.001 \Delta TEM{P}_{t-1} \\ \\ \Delta IceShee{t}_t=-0.016-0.002 EC{T}_{t-1}+0.017 \Delta GMS{L}_{t-1}-0.137 \Delta IceShee{t}_{t-1}-0.002 \Delta SeaIc{e}_{t-1}+0.004 \Delta TEM{P}_{t-1}\\ \\ \Delta \mathrm{S}eaIc{e}_t=-0.010-0.172 EC{T}_{t-1}+0.014 \Delta GMS{L}_{t-1}-0.083 \Delta IceShee{t}_{t-1}+0.107 \Delta SeaIc{e}_{t-1}+0.016 \Delta TEM{P}_{t-1}\\ \\ \Delta TEM{P}_t=0.031+0.605 EC{T}_{t-1}-0.537 \Delta GMS{L}_{t-1}+1.046 \Delta IceShee{t}_{t-1}-0.041 \Delta SeaIc{e}_{t-1}-0.314 \Delta TEM{P}_{t-1}\end{array}\right.$$

(10)

where $EC{T}_{t-1}=GMS{L}_{t-1}+0.880 IceShee{t}_{t-1}+0.046 SeaIc{e}_{t-1}-0.112 TEM{P}_{t-1}$.

TEMP-related VECM model:

$$\left\{\begin{array}{l}\Delta TEM{P}_t=-0.017-0.529 EC{T}_{t-1}-0.063 \Delta TEM{P}_{t-1}-0.190 \Delta Humidit{y}_{t-1}+1.492 \Delta GW{P}_{t-1}-0.021 \Delta SS{N}_{t-1} \\ \\ \Delta Humidit{y}_t=0.005+0.203 EC{T}_{t-1}-0.073 \Delta TEM{P}_{t-1}-0.152 \Delta Humidit{y}_{t-1}-0.268 \Delta GW{P}_{t-1}+0.043 \Delta SS{N}_{t-1}\\ \\ \Delta GW{P}_t=0.019+0.008 EC{T}_{t-1}-0.008 \Delta TEM{P}_{t-1}+0.009 \Delta Humidit{y}_{t-1}-0.274 \Delta GW{P}_{t-1}-0.002 \Delta SS{N}_{t-1}\\ \\ \Delta SS{N}_t=0.030-0.057 EC{T}_{t-1}+0.011 \Delta TEM{P}_{t-1}-0.132 \Delta Humidit{y}_{t-1}-1.625 \Delta GW{P}_{t-1}-0.259 \Delta SS{N}_{t-1}\end{array}\right.$$

(11)

where $EC{T}_{t-1}=TEM{P}_{t-1}-0.628 Humidit{y}_{t-1}-0.321 GW{P}_{t-1}-0.047 SS{N}_{t-1}$.

3.3.3. Autoregressive Distributed Lag Model (ARDL)

When the integration orders of time series variables are not all equal, the ARDL models are applied with a more relaxed integration order assumption. The ARDL bound test is performed to test the cointegration relationship in each ARDL model. In this work, the related climate factors are found to be integrated of the same order of one; however, ARDL is still employed to show the key relationship for each individual response variable of interest, namely global mean sea level or global mean temperature, respectively, in a univariate linear modeling approach in contrast to the multivariate modeling approach of VECM. The ARDL equations are shown below, with the corresponding significance levels provided in

Table 6. The significance (p-value) of ARDL model equations.

	ECT	$\Delta IceShee{t}_t$	$\Delta SeaIc{e}_t$	$\Delta TEM{P}_t$
GMSL equation	<0.01	0.146	0.379	0.498
	ECT	$\Delta Humidit{\mathit{y}}_{\mathit{t}}$	$\Delta GW{\mathit{P}}_{\mathit{t}-1}$	$\Delta SS{\mathit{N}}_{\mathit{t}-1}$
TEMP equation	<0.01	<0.01	0.753	0.413

and

Table 7. ARDL bound test result.

	F-Statistics	p-Value
GMSL model	4.52	0.01–0.05
TEMP model	25.69	<0.01
Critical value bounds	Lower Bound	Upper Bound
10% critical value	2.72	3.77
5% critical value	3.23	4.35
1% critical value	4.29	5.61

. Compared to VECM, each individual ARDL is more flexible to formulate the problem with a lower order parsimonious model. We can see that these univariate ARDL models (Equation System 12 below) involve only time t and (t−1), whereas the multivariate VECM model (Equation System 11 above) includes time t, (t−1) and (t−2). By showing both VECM and ARDL models, we can demonstrate the climate pathways from both the system and the component perspectives:

$$\left\{\begin{array}{cc}\hfill \Delta GMS{L}_t& =0.009-0.154 GMS{L}_{t-1}-0.140 IceShee{t}_{t-1}-0.003 SeaIc{e}_{t-1}+0.017 TEM{P}_{t-1}\hfill \\ & -0.282 \Delta IceShee{t}_t-0.012 \Delta SeaIc{e}_t+0.008 \Delta TEM{P}_t\hfill \\ \\ \hfill \Delta TEM{P}_t& =0.011-0.655 TEM{P}_{t-1}+0.404 Humidit{y}_{t-1}+0.215 GW{P}_{t-1}+0.033 SS{N}_{t-1}\hfill \\ & +0.554 \Delta Humidit{y}_t-0.417 \Delta GW{P}_t+0.042 \Delta SS{N}_t\hfill \end{array}\right.$$

(12)

Based on the significance levels and coefficients of the Johansen procedure, the VECM results, and the ARDL results, we found that IceSheet and TEMP both affect GMSL through a long-run equilibrium. The negative coefficient of IceSheet implies that a lower IceSheet mass will cause GMSL to increase via new water input, while the positive coefficient of TEMP implies that a TEMP increase will cause GMSL to increase directly by a water thermal expansion and indirectly by a melting IceSheet. Moreover, the effect of SeaIce to GMSL is not significant and there is no short-run dynamic effect. Meanwhile, TEMP is mainly modulated by both the long-term and the short-term effects of the greenhouse gases (GWP) and Humidity—the latter caused by the water vapor heat trap effect and the effect of SSN on TEMP is not as significant as the former two (GWP and Humidity).

3.4. Nonlinear Causality Detection

To detect the nonlinear causality of GMSL rise and TEMP change, a combined procedure based on artificial neural network (ANN) with one hidden layer of two nodes, and VAR model is formulated. Each neural network is repeated 100 times with different random seeds, the mean and standard deviation of the sum squares of error (SSE) and mean absolute error (MAE) are listed below. We use the Wilcoxon test to determine if the SSE increases significantly without each given predicting variable (

Table 8. Sum squares of error (SSE) and mean absolute error (MAE) of the nonlinear VAR neural network model and Wilcoxon test results for GMSL-related model (each model was repeated 100 times with different initial random seeds).

Models	$\mathbf{SSE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value	$\mathbf{MAE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value
Full model	$1.916\pm 0.026$	-	$0.074\pm 0.001$	-
Without IceSheet	$2.161\pm 0.020$	<2.2 × 10−16	$0.077\pm 0.001$	<2.2 × 10−16
Without SeaIce	$1.921\pm 0.025$	0.008	$0.074\pm 0.001$	0.192
Without TEMP	$1.955\pm 0.027$	<2.2 × 10−16	$0.074\pm 0.001$	1.0 × 10−9
Linear model	$2.077$	<2.2 × 10−16	0.076	<2.2 × 10−16

and

Table 9. Sum squares of error (SSE) and mean absolute error (MAE) of the nonlinear VAR neural network model and Wilcoxon test results for TEMP-related model (each model was repeated 100 times with different initial random seeds).

Models	$\mathbf{SSE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value	$\mathbf{MAE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value
Full model	$55.987\pm 0.584$	-	$0.397\pm 0.002$	-
Without Humidity	$60.721\pm 0.629$	<2.2 × 10−16	$0.415\pm 0.003$	<2.2 × 10−16
Without GWP	$62.468\pm 0.991$	<2.2 × 10−16	$0.431\pm 0.004$	<2.2 × 10−16
Without SSN	$57.065\pm 0.429$	<2.2 × 10−16	$0.402\pm 0.003$	<2.2 × 10−16
Linear model	$58.400$	<2.2 × 10−16	0.407	<2.2 × 10−16

). Boxplots of the SSE comparisons are shown in Figure 3 and Figure 4 for GMSL and TEMP respectively.

The nonlinear VAR neural network model for GMSL implies that there exists nonlinear Granger causality in the GMSL model based on the significant decrease in SSE and MAE of the neural network model in comparison to the linear VAR model. Increases in SSEs and MAEs of the partial models show that IceSheet and TEMP all impact GMSL change significantly. SeaIce’s effect is only significant in terms of the SSE metric, but not in the MAE metric. The impact of IceSheet is the strongest corresponding to the model with the highest SSE and MAE, while the impact of SeaIce is the weakest corresponding to the model with the lowest SSE and MAE.

The SSE and MAE of the neural network model decreases significantly compared to that of the linear VAR model, which indicates that nonlinear causality does exist in the TEMP model. The increased SSE and the Wilcoxon test demonstrates that Humidity, GWP, and SSN all impact TEMP change significantly with the impact of Humidity and GWP being stronger, while the impact of SSN being the weakest.

3.5. Nonlinear ARDL Model

Similarly, to detect the nonlinear long-run equilibrium and short-run dynamic effect of GMSL rise and TEMP rise, we have developed a novel pipeline based on an artificial neural network (ANN) with one hidden layer of two nodes and ARDL model. Each neural network is repeated 100 times with different random seeds, the mean and standard deviation of SSE and MAE are listed below, and we used the Wilcoxon test to determine if the SSE or MAE increases significantly without a specific predictor variable (

Table 10. Sum squares of error (SSE) and mean absolute error (MAE) of the nonlinear ARDL neural network model and Wilcoxon test results for GMSL-related model (each model was repeated 100 times with different initial random seeds).

Models	$\mathbf{SSE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value	$\mathbf{MAE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value
Full model	$1.635\pm 0.096$	-	$0.067\pm 0.002$	-
Without long-run equilibrium	$2.020\pm 0.066$	<2.2 × 10−16	$0.075\pm 0.001$	<2.2 × 10−16
Without IceSheet	$1.915\pm 0.087$	<2.2 × 10−16	$0.072\pm 0.002$	<2.2 × 10−16
Without SeaIce	$1.721\pm 0.087$	9.3 × 10−10	$0.069\pm 0.002$	2.6 × 10−10
Without TEMP	$1.730\pm 0.078$	5.5 × 10−12	$0.069\pm 0.002$	4.9 × 10−13
Linear model	$2.03$2	<2.2 × 10−16	0.076	<2.2 × 10−16

and

Table 11. Sum squares of error (SSE) of the nonlinear ARDL neural network model and Wilcoxon test results for GMSL-related model.

Models	$\mathbf{SSE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value	$\mathbf{MAE} (\mathit{m}\mathit{e}\mathit{a}\mathit{n} \pm \mathit{S}\mathit{D})$	Wilcoxon Test p-Value
Full model	$35.249\pm 2.481$	-	$0.305\pm 0.012$	-
Without long-run equilibrium	$61.977\pm 2.259$	<2.2 × 10−16	$0.424\pm 0.008$	<2.2 × 10−16
Without Humidity	$49.763\pm 1.839$	<2.2 × 10−16	$0.369\pm 0.011$	<2.2 × 10−16
Without GWP	$43.690\pm 1.948$	<2.2 × 10−16	$0.347\pm 0.010$	<2.2 × 10−16
Without SSN	$38.432\pm 1.890$	<2.2 × 10−16	$0.321\pm 0.010$	<2.2 × 10−16
Linear model	$47.519$	<2.2 × 10−16	0.360	<2.2 × 10−16

). Boxplots of the SSE and MAE comparisons are shown in Figure 5 and Figure 6 for GMSL and TEMP respectively.

The nonlinear ARDL neural network and Wilcoxon test of the GMSL model indicate that the effect of IceSheet, SeaIce, and TEMP to GMSL is nonlinear, with the neural network model decreasing the SSE and MAE significantly. Furthermore, these three variables impact GMSL significantly as models without any one of these three variables would increase the prediction SSE significantly. Detailed SSE and MAE increases and the corresponding p-values show that the effect of IceSheet is much stronger than those of TEMP and SeaIce.

The nonlinear ARDL neural network and Wilcoxon test results of the TEMP model demonstrate the nonlinear effect on TEMP caused by Humidity, GWP, and SSN, as the SSE and MAE decreases dramatically in the neural network model compared to the linear ARDL model. Moreover, the SSE and MAE of the neural network morel increased significantly upon removing any one of these variables, indicating that all three variables affect TEMP changing. From the SSE increase amount and p-values, we found that Humidity has the strongest effect on TEMP, followed by GWP and then SSN.

4. Conclusions and Future Work

In this work, we have performed a thorough data-based analysis of causal factors toward global mean temperature (TEMP) increase and global mean sea level (GMSL) rise, both linearly, using statistical time series models, and nonlinearly, using artificial neural network models. For TEMP change, the impact of global mean specific humidity (Humidity) and global warming potential (GWP) of the greenhouse gases are both significant, linearly and nonlinearly. At the same time, the effect of the sunspot number (SSN) is relatively small and only significant in the nonlinear neural network model. For GMSL change, the most significant factor, both linearly and nonlinearly, is the Antarctic and Greenland ice sheet mass (IceSheet), while the ocean thermal expansion as measured by TEMP came second, and would only impact the GMSL change nonlinearly, and the Northern and Southern Hemisphere sea ice extent (SeaIce) came third with only a weak nonlinear effect.

The unique contribution of our work is that we have delineated whether the causal relationships between each of the key climate variables to global warming or sea level rise is linear or nonlinear or both. Traditional physics-models-based analyses do not differentiate between these relationships and thus we compared our work to those models using the combined linear and nonlinear causal factors and found very good agreement. We also found excellent agreement between our linear causal factors with the classical linear statistical models. For example, GWP is found to be a significant causal factor for global warming by both physics-based and statistical models, and we found GWP to be significant both linearly and nonlinearly. The sunspot number was found to be insignificant for global warming by structural equation modeling, a multivariate linear statistical model [14,15], while the physics-based models, targeting both linear and nonlinear causal factors indiscriminately, have found it to be weakly related to global warming [44]. This is also in perfect agreement with our data-based models as we found the effect of the sunspot number to be relatively small and only significant in the nonlinear neural network model.

Given that the usual information criteria (AIC and BIC, etc.) toward gauging model goodness-of-fit are not generally applicable to the comparison of neural network models and statistical time series models, in order to better examine the robustness and compare the forecast accuracy of these two types of models, we shall perform a follow-up predictive study using models derived from this work and the soon available 2022 monthly climate data.

We also point out a limitation of our study due to the limited sample size (namely, number of years) available for the analysis. For non-stationary time series data, the Toda–Yamamoto procedure [45] is the proposed method for causality analysis. However, due to our modest sample size, the asymptotic distribution of the test statistic would not hold true, and thus we found the Toda–Yamamoto causality analysis not significant. This conflicts with the fact that co-integrated time series must have Granger causality in one way or both directions, while the presence of Granger causality in either one way or both directions does not necessarily imply that the series are cointegrated. Therefore, co-integration should be a stronger indication of Granger causality in both directions. We have therefore used the co-integration as an indication of Granger causality instead of the Toda–Yamamoto procedure.

On another note, the neural net VAR and ARDL models proposed in this paper can be seen as an alternative of other nonlinear time series analysis methods, including the nonlinear autoregressive distributed lag (NARDL) models [39,40,42], and those based on state-space reconstruction [46,47,48]. Furthermore, other approaches such as power transformations can also be considered to accommodate potential nonlinear relationships. For example, linear VAR and ARDL in logarithms are widely employed in economic and financial applications [49]. Noteworthy is that we can combine the transformations of data and the linear models to see if the resulting performance is comparable to that of the neural network models. If so, the transformation plus linear model would be preferred as it is an open-box in contrast to the machine learning model, which is a blackbox.

Finally, we point out that the physics-based and the data-driven models are not mutually exclusive. In fact, they can be integrated to complement each other for better forecasting in a more timely and computationally efficient manner. A plethora of white papers on how to integrate AI/machine learning methods to the physical earth systems models, for example, has been provided in the following website by the US Department of Energy (https://www.ai4esp.org/white-papers/, accessed on 4 May 2023). It is our sincere hope that our work will help to elicit more interest in this important area at this critical moment in history.