Abstract
A phylogenetic regression model that incorporates the network structure allowing the reticulation event to study trait evolution is proposed. The parameter estimation is achieved through the maximum likelihood approach, where an algorithm is developed by taking a phylogenetic network in eNewick format as the input to build up the variance–covariance matrix. The model is applied to study the common sunflower, Helianthus annuus, by investigating its traits used to respond to drought conditions. Results show that our model provides acceptable estimates of the parameters, where most of the traits analyzed were found to have a significant correlation with drought tolerance.
1. Introduction
Hybridizations among closely related species have frequently occurred in nature. Under Mayr’s biological species concept, hybrid species can be defined as organisms formed by cross-fertilization between individuals of different species [1,2]. Hybrid speciation occurs in at least two ways: allopolyploid speciation and diploid (homoploid) hybrid speciation. While allopolyploidy is hybrid speciation between two species resulting in a new species that has the complete diploid chromosome complement of both its parents, diploid hybrid speciation results from a normal sexual event in which each gamete has a haploid complement of the nuclear chromosomes from its parent, but gametes that form the zygote come from different species [3]. This means that, in hybrid speciation, the new species may have the same number of chromosomes as its parent (diploid hybridization) or the sum of the number of chromosomes of its parents (polyploid hybridization).
Phylogenetic comparative methods (PCMs) are commonly applied to study correlated trait evolution; most methods were developed by incorporating a phylogenetic tree to represent the affinity among a group of related species [4,5,6]. However, if evolution involved ancient hybridizations, then we cannot simply use the phylogeny to represent the affinity among species, but instead should use the phylogenetic network (which is a directed acyclic graph, coupled with time constraints). Currently, in the literature, we can observe the development of statistical methods using phylogenetic networks to investigate trait evolution including the hybridization process [7,8,9,10]. Note that approaches to phylogenetic analysis typically involve constructing networks using molecular data [11,12], while our approach employs the given phylogenetic network with known topology and branch lengths to study the evolution of traits.
The objective of our research is to examine the evolution of traits in both hybrid and non-hybrid species, specifically through the lens of reticulation evolution. This phenomenon involves the merging of genetic material from different species, resulting in the creation of hybrid offspring that exhibit a unique combination of traits inherited from their parents. Our study aims to investigate the implications of reticulation evolution for correlated trait evolution in a linear regression framework.
The paper is organized as follows. In Section 2, we model the hybrid on the given phylogenetic network and create a phylogenetic regression model to analyze trait data that account for the hybrid information. In Section 3, a heuristic algorithm is proposed to build the variance–covariance matrix given a phylogenetic network and we propose a maximum likelihood framework for parameter estimation. In Section 4, the novel regression model is applied to study the drought tolerance of sunflowers. The discussion for this work is provided in Section 5, and the conclusions are given in Section 6.
2. Model
2.1. Relation between the Hybrid and Its Parents
Figure 1 displays a phylogenetic network that illustrates the connection between three species—X, R, and Y. Species R is a hybrid of species X and Y, and it came into existence at a specific time, . The root node O served as the ancestor for the three species. The purpose of the network is to show the relationships between the species.
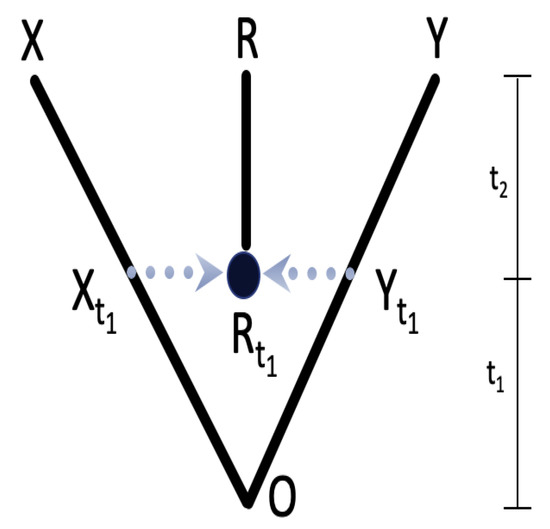
Figure 1.
A three-taxa phylogenetic network. The hybrid species R of X and Y on the tips of the network was formed at .
To model trait evolution with hybridization, we treat the hybrid node on the phylogenetic network by allowing a burst of new variation at the hybridization event. We achieve this by incorporating a hybridization parameter . Consider that the trait of the hybrid species is defined in the log scale [7,8] via , where is the proportion of the hybrid trait inherited from parent X (i.e., is the proportion of the hybrid trait inherited from parent Y), and is denoted as the hybridization parameter that is designed to model an increase in the variance of the hybrid species.
In raw scale modeling, the relation can be expressed by exponentiation to obtain . For a setting, we use , where the hybrid was assumed to be inherited equally from both parents. The arithmetic–geometric inequality establishes that . As typically ranges between , it follows that shares this range with . Because the quantitative phenotypic traits are inherently non-negative, the inequality of arithmetic and geometric means condition is met. By incorporating a model that permits variation in the hybrid’s variance to be computed from an additive operation on X, Y through , we establish the relationship between the hybrid species R and its parent organisms X and Y in Equation (1):
By incorporating this additive structure, below, we provide an approach to modeling hybrid trait evolution. In Equation (1), the affinity among species at time t in the phylogenetic network can be derived as follows. For any other species Z, the affinity between Z and R is
In particular, when , we have
Given a phylogenetic network of n taxa, one can use Equations (2) and (3) to derive the corresponding similarity matrix , where describe the affinities between taxa i and j, possibly with hybrid species.
Below, we use the Brownian motion (BM) in modeling trait evolution [5,13,14] with the definition in Equation (1) to construct the model and variance–covariance matrix for a group of related species in Section 2.2.
2.2. Covariance Matrix under the Brownian Motion Model
Under the assumption of the BM process for trait evolution [15], we can define as stochastic variables with , where is the ancestral value at the root of the tree, and are parameters of the rate of evolution, and and are the Brownian motion variables with and for trait X and Y, respectively.
Given the network with a known topology and branch length (times) as shown in Figure 1, we have , , and as X and Y are independent. Since the hybrid R is produced at time , the variation in the hybrid R is decomposed into two parts: one comes from its parent at and the other comes from its evolution from to . Hence, we have
Since evolution on different branches occurs independently, the covariation between the hybrid and its parents is . Therefore, with Equations (1)–(3), the corresponding similarity matrix is obtained as in Figure 1.
Previous work has explained trait evolution in a logarithmic scale, using different parameter notations for the hybrid vigor [7,8,9], while we use . However, it is worth noting that both of these prior methods do account for the hybrid effect. Our proposed approach offers an alternative method of constructing the variance–covariance matrix, which differs from the methods used in the literature. We must acknowledge that our method has a limitation in its ability to handle gene flow, as it can only account for reticulation events. This limitation has been discussed in the literature [8].
2.3. Stepwise Procedure for Constructing the Variance–Covariance Matrix
In this study, we present a novel method for constructing the variance–covariance matrix using a matrix multiplication technique. The proposed approach involves a three-step process, as illustrated in Figure 2.
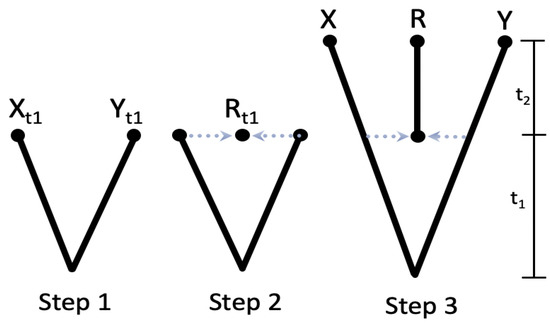
Figure 2.
Evolution scenario for 3-taxa phylogenetic network containing a reticular hybridization event.
Figure 2 describes an evolutionary scenario for a phylogenetic network with three taxa, which involves a reticular hybridization event. The scenario consists of three main steps:
- 1.
- Step 1: the root O speciates into two distinct taxa denoted as and .
- 2.
- Step 2: a hybrid species, denoted as R, is produced as a result of hybridization between X and Y at a specific time point, denoted as .
- 3.
- Step 3: after , the three species X, R, and Y continue to evolve without undergoing any further speciation or hybridization, ultimately reaching the current time point of .
Note that this calculation of the covariance matrix is a three-step process [16], with both steps able to be described using matrix operations.
First, in step 1 in Figure 2, a speciation at the root yields two species at with the covariance in Equation (5):
Next, in step 2, there is the instantaneous hybridization event at time . This can be accomplished mathematically by multiplying the previous 2-by-2 matrix describing the variance in Equation (5) in X and Y by a path matrix on the left and on the right:
where is shown in Equation (7)
Finally, the last step is elongation by adding , where is the 3-by-3 identity matrix. The corresponding covariance structure is shown in Equation (8):
Alternatively, standard speciation events, as depicted in Figure 3, can be analyzed using analogous matrix operations.
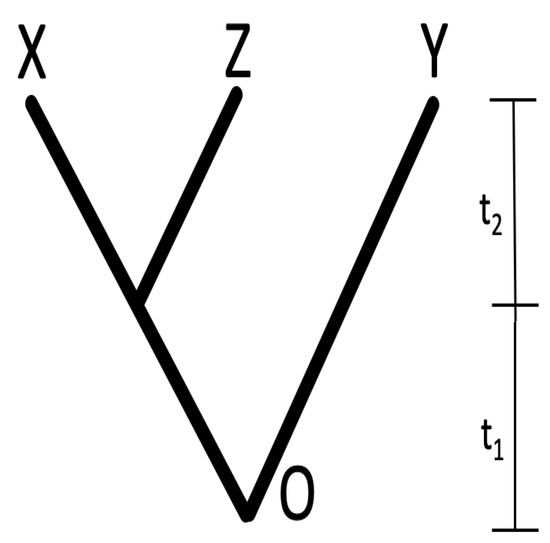
Figure 3.
A phylogenetic tree of 3 taxa. are taxa; O is the root. X and Z share the same branch length on . Y is independent with both X and Z.
The instantaneous speciation event shown in Figure 3 at time is accomplished by multiplying on the left and on the right by the transpose of the matrix:
For the tree case with only speciation, as shown in Figure 3, one can construct the similarity matrix in Equation (10):
These operations can be generalized to the k existing species case whenever the taxon arises by hybridization or speciation. Since the form of changes depending on whether the hybridization of speciation is involved, we adopt the following notation: let denote the by j matrix obtained from the j by j identity matrix by inserting a row with a one in column j and zeros elsewhere, where column j denotes the taxon involved in the speciation event. Let denote the by j matrix obtained from the j by j identity matrix by inserting a row with in columns i and j and zeros elsewhere, where columns i and j denote the taxa involved in the hybridization event. Then, the adjustment from time to time is as given in Equation (11):
where, for hybridization, , and for speciation, , which sets , as is evident from Equation (9) when we compare it with Equation (7).
Our proposed methodology can indeed handle a general ultrametric phylogenetic network with an arbitrary number of hybrid nodes, as later demonstrated in the case study with 13 species and 3 hybrid species in Section 4, as well as the six-taxa network with two hybrids presented in Appendix A.2.
2.4. The Statistical Model and Likelihood Function
Under the regression model framework, let be the trait values for n species, some of which are possibly old hybrids. Let be the design matrix from the covariate trait, where is the vector of 1s, and we have
Let , and the negative log-likelihood function given the traits and network is
The least-square estimate is shown in Equation (14):
As the model assumes a Gaussian process distribution, the estimation of model parameters can be conducted through maximum likelihood inference, utilizing the Nelder–Mead optimization method in the R software [17]. One of the Nelder–Mead optimization’s primary benefits is that it can be utilized in a variety of problem settings, without requiring knowledge of the objective function’s derivatives. In our specific likelihood function, the covariance matrix contains embedded parameters denoted by .
We use maximum likelihood analysis to estimate the hybridized parameter by optimizing the negative log-likelihood function, where is the determinant of . We set the bound for as for the purpose of optimization. We use the golden section method to search for the maximum likelihood estimator (MLE) of the negative log-likelihood function for the Brownian motion model.
Let . By taking the partial differentiation of with respect to and , the Hessian matrix can be obtained:
which is useful to compute the variance of parameters for further inference.
For the Gaussian random variable (here, the Brownian motion), the second derivatives of the objective function are constant for because the objective function is a quadratic function . Therefore, the Hessian matrix can be computed without obtaining the mean vector . We apply the R function hessian [18] to compute the Hessian matrix.
It is known that under regularity conditions (smoothness of the likelihood function) [19], the estimator (by iterating a finite number of times) is asymptotically distributed as where n is the taxa size and converge to in probability. It is assumed that the response variable Y is continuous and that the error terms are normally distributed with a mean of 0 and a covariance matrix of , which means that the Brownian motion assumption is applied to each tip variable in the response trait vectors Y. The predictor variables are non-stochastic and fixed. Based on these assumptions, the likelihood of the linear regression model is given by an equation, Equation (13), and in order to show that this equation meets the regularity conditions, several properties must be satisfied. The likelihood function must be well-defined, non-negative, continuous in and , and differentiable with respect to , , and separately. These properties are satisfied because the likelihood function is a product of non-negative terms, the exponential function is always positive, and the sum of continuous functions is continuous. Additionally, the derivatives of the likelihood function with respect to and are continuous. However, we note to the reader that the regularity condition’s likelihood function in Equation (13) depends on a certain range of the parameters for the network models proposed here and in the literature [7,8]. The derivative of the likelihood function with respect to involves the inverse of the covariance matrix , which depends on the network structure. First, is symmetric as a covariance matrix. If is a positive definite matrix, the derivative of the likelihood with respect to will be continuous. The inference can be used to infer the regression effect pending the condition of the . In the empirical analysis, we verify the positive definite property of the .
According to Varga and Nabben [20] and Nabben and Varga [21], if the covariance matrix is an ultrametric matrix, meaning that it satisfies certain mathematical inequalities (i.e., for all , for all i, j, and k), then the derivative of the likelihood function with respect to will be continuous. This is because ultrametricity implies the stronger condition of the triangle inequality, which ensures that the matrix is always positive definite and has no negative eigenvalues. To ensure that all regularity conditions are met, it would be ideal to determine the parameter space for that would make ultrametric before analysis. However, this strict condition depends on the given network and cannot be solved analytically in general. For example, in the case of a three-taxon network, as shown in Equation (6), the parameter space for would need to be constrained to to meet the ultrametric condition.
3. Algorithm and Inference
An extended Newick format (eNewick) uses unique syntax to represent a given phylogenetic network in linear form [22]. A phylogenetic network can be transformed into a phylogenetic tree with some replicated nodes, adequately tagged according to the hybrid nodes, and then traversing the resulting phylogenetic network in postorder to obtain the eNewick description of the phylogenetic network. We modified their representation in the function newick2phylog in the ade4 package [23] in the R software to obtain the eNewick format. The function Newick2phylog [23] in the ade4 package of the R software program was designed to read in phylogenies in Newick format and return an array with three columns, where the first column contains the ancestral nodes and the second and third columns have the two descendants of the corresponding ancestor. Note that the number of rows (ancestors) in this array is as a hybrid node requires two incoming ancestors while a species node only has one ancestor. The root is also included in the count. To provide an example, in a taxa network with one hybrid (), as in Figure 1, we have the number of rows equal to 4, which is calculated as . This is also shown in the following Table 1.

Table 1.
Ancestral–descendant relationship corresponding to Figure 1.
The algorithm can generate the covariance matrix by starting from the root, adding a new node in each step, and terminating until the desired matrix of n species is built. For the tree case, each descendant has a unique ancestor. For the node with the reticulated event, the function reads a descendant such as a hybrid species with two ancestors; in one of the ancestral rows, the descendant will be listed by name, and in the other row, the descendant will have a attached to the end of the name. After determining the ancestral–descendant relationships, we find the times from the root at which speciation events or hybridization events occur: , , , ⋯, etc. Note that there are branches, and we build the phylogenetic similarity matrix up from the root. For times , there are two species present whose evolution is independent given the root. The relationship matrix up until is thus a diagonal matrix with t on the diagonal. For each event, we adjust the similarity matrix according to Equation (11) for the Brownian motion model as follows to generate the variance–covariance matrix for n tips by starting with the root, adding a new node at each speciation or hybridization event, and terminating when the process reaches the tips. A concrete example with detailed illustration is provided in Appendix A.2.
Our proposed methodology uses a feasible generalized least-squares approach to estimate the model parameters and , as well as the regression parameter , through a joint estimation approach. An alternating search procedure is utilized to simultaneously obtain the estimate for and the covariance by maximizing the likelihood of the model parameters and minimizing the squared residuals of the regression parameters, as illustrated in Algorithm 1.
| Algorithm 1: Procedure for Parameter Estimation. |
| Require:
Predictive traits , and Y, network .
Ensure: Regression estimator , hybrid vigor estimator , and rate estimator .
|
4. Empirical Analysis
Hybridization is common in nature, with at least 25% of plant species showing hybridization. Sunflowers are an example of a species that has adapted to a wide range of environmental conditions, including soil types, temperature, and salinity. Studies show that hybridization frequently occurs among sunflowers, resulting in genetically hybrid species. Sunflowers have various uses, including traditional Chinese medicine, edible oil, and soil phytoremediation [24]. The family of Helianthus is the subject of ongoing research on the adaptation of hybrid species to their environment. Sunflowers, in particular, have adapted to tolerate drought and salty conditions in their habitats with lower precipitation levels. Selective sweeps in sunflowers have revealed candidate genes for adaptation to drought and salt tolerance [25]. Studies have also shown that sunflowers vary in their tolerance to drought [26].
The study focused on exploring the correlation between traits and drought tolerance, with soil moisture, precipitation, and rainfall in the area considered as possible factors that affect the response variable, Y. The precipitation data used as the covariates were collected from the WorldClim database [27,28]. The geographical data of the longitude and latitude of sunflowers were collected from the Global Biodiversity Information Facility (GBIF) database [29], and the R package raster [30,31] was used to download the corresponding data for analysis. To further investigate sunflowers’ adaptation to drought tolerance conditions, a phylogenetic regression method was proposed, which can analyze trait data from both hybrid and typical species in the evolutionary mechanism. This method was applied to study a group of common sunflowers, Helianthus annuus, using data from the efloras database [32]. The collected traits include the plant height, petiole, pedicel, hemispherical bract, bract, stalk, leaf, ray flower, disk, corolla, and calyx achene of sunflowers. The predictor variable used in the study was the annual precipitation amount measured in various locations, which was obtained using the raster package from the WorldClim database. For example, the precipitation data for uncommon species located at latitude degrees and longitude degrees were obtained with a setting resolution of minutes.
The presented data in Table 2 showcase the response traits of sunflowers, including various characteristics such as annuals, petioles, peduncles, involucres, phyllaries, paleae laminae, ray florets, disc florets, corollas, cypselae, and pappi. The covariate trait in question is the annual precipitation (AnnPrec), which represents the yearly precipitation levels at the location of the observed sunflowers.

Table 2.
Sunflowers and their traits. Each column represents a sunflower species, while each row records the trait collected from the database.
This dataset offers valuable insights into the relationship between the response traits of sunflowers and the annual precipitation levels in their growing location. Such findings could have significant implications for plant breeding and cultivation in regions with varying levels of precipitation. As such, a thorough analysis of the presented data can provide critical information that can contribute to the development of more robust and resilient plant species in the future. In light of this, further investigation and exploration of the data presented in Table 2 are warranted, as they may reveal essential correlations and trends that can deepen our understanding of sunflowers and their responses to varying levels of precipitation.
The network in Figure 4 is a modification from [33], where 11 sunflowers species are given at the genus level.
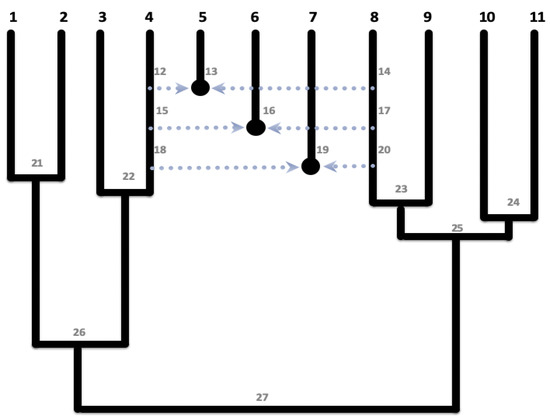
Figure 4.
Sunflower network regraphed from [33]. Species on the tip from the leftmost (labeled with the number 1) to the rightmost (labeled with the number 1) are 1. praecox, 2. debilis, 3. neglectus, 4. petiolaris, 5. anomalus, 6. deserticola, 7. paradoxus, 8. annuus, 9. argophyllus, 10. bolanderi, and 11. exilis, where deserticola, anomalus, and paradoxus are hybrids from petiolaris and annuus. The eNewick format is .
To investigate whether precipitation has a significant impact on traits, it is necessary to check whether the regression slope is zero, represented by the null hypothesis . The results of the analysis using the phylogenetic regression model are presented in Table 3. The table reports GLS estimates for , along with its 95% confidence interval, as well as estimates for the rate parameter and the hybrid parameter .

Table 3.
The table provides estimates and corresponding standard errors for the hybrid effect (), the rate of evolution (), and the slope () for each of the 12 response traits of sunflowers under a network relationship. The slope estimate represents the effect of precipitation on the particular trait, with a positive value indicating a positive relationship and a negative value indicating a negative relationship. The 95% confidence interval (CI) for the slope estimate provides a range of plausible values for the true effect of precipitation on the trait.
Table 3 provides the estimates of hybrid effect , rate of evolution , and slope , along with their corresponding standard errors for different response traits in a study. The table also provides information about whether the slope estimate is statistically significant or not (significant set to Yes or No) at the 5% significance level.
For example, for the response trait “Annuals”, the hybrid effect estimate is with a standard error of 0.07, indicating that the response of annuals has moderate hybrid weakness among sunflower species. The rate of evolution estimate is with a standard error of 0.087, indicating that the evolutionary rate of annuals is relatively slow. The slope estimate is with a 95% CI of , suggesting that precipitation has a significant positive effect on the trait. The significance of the effect is indicated by the “Significant?” column, which shows “Yes” for a significant effect based on the 95% confidence interval of the slope estimate.
Similarly, the second-to-last row for the response trait Cypselae indicates that the hybrid effect estimate is (hybrid vigor) with standard error , the rate of evolution estimate is with standard error , and the slope estimate is with a 95% confidence interval . Additionally, the slope estimate is statistically significant (significance set to Yes) for this trait.
In summary, the table provides estimates and corresponding standard errors for the hybrid effect, rate of evolution, and slope, along with their significance levels for different response traits in a study. These estimates can be used to make inferences about the relationship between the variables being studied and the response traits under consideration.
We further evaluate the correlations among the parameter estimates , and using the 12 sunflower trait datasets; there is a moderate positive correlation () between the rate of evolution () and the regression slope (), suggesting that an increase in the rate of evolution is associated with an increase in the magnitude of the regression slope. There is a moderate negative correlation () between the rate of evolution () and the hybrid effect parameter (), suggesting that an increase in the rate of evolution is associated with a decrease in the magnitude of the hybrid effect parameter. There is a weak negative correlation () between the regression slope () and the hybrid effect parameter (), suggesting that there is a weak relationship between these variables, and as the hybrid effect parameter increases, the regression slope tends to decrease, but the relationship is not particularly strong.
We performed a benchmark analysis to evaluate the proposed methodology. The baseline model used for comparison is a simple linear regression model. Another model used for comparison is the tree model, which assumes a Brownian motion model [34]. These models were used for the benchmark analysis of our network model. While the existing methodology may not be directly comparable, the analysis still provides insights into baseline estimation and allows us to compare the performance of the proposed methodology with existing baselines. The result is shown in Table 4. The first row of the table compares the performance of the tree model and linear regression model using the “Annuals” trait. The tree model has a benchmark ratio of 1.006, indicating that its RMSE is 0.6% higher than that of the linear regression model. Similarly, the network model has a benchmark ratio of 1.077, which means that its RMSE is 7.7% higher than that of the linear regression model. The results indicate that the tree model has slightly poorer performance compared to the linear regression model, while the network model performs even worse than the linear regression model. This is expected because the network model is more complex. However, despite the larger RMSE values obtained from the network model, the values are still reasonable when compared to the baseline model.

Table 4.
The benchmark analysis involves the use of 12 traits, with RMSE1 computed via a simple linear regression baseline model, RMSE2 computed via the tree model [34], and RMSE3 computed via the proposed network model. The fourth and fifth columns of the table present the benchmark ratio for each model.
5. Discussion
The model utilized to examine trait values in phylogenetic networks through hybridization modeling is of fundamental importance and represents an essential tool in the analysis of this type of data. There is room for improvement by using more appropriate representations for the hybrid R based on its parents X and Y to find suitable functions , which would allow us to model events such as horizontal gene transfers or recombination that are biologically different from hybridization and can affect trait values.
We acknowledge that the covariance structure is complex, which creates difficulties in demonstrating the positive definiteness of the Hessian matrix of the likelihood function. This makes it challenging to ensure that the likelihood is jointly convex in all parameters. However, our regression model meets certain conditions, including having a well-defined likelihood function and satisfying the assumption of non-singularity. Our empirical analysis confirms that our method achieves the global maximum within its domain. This is supported by the fact that is positive definite for each dataset, as detailed in Appendix A.1.3.
In order to enhance the current model’s capability to analyze phylogenetic network data, several future research avenues could be pursued. Firstly, the model could be extended to include more complex evolutionary processes, such as the Ornstein–Uhlenbeck (OU) model [35] or the early burst model [36]. The OU model could be implemented by introducing a force parameter to the covariance matrix construction, and the optimization process would require a multidimensional search. For instance, if implementing the OU process [35], one would need to take the non-independent increment condition into account to construct the covariance matrix. One can also consider implementing non-Gaussian processes [37] in the network for trait evolution. Secondly, the algorithm could be generalized to handle the hard polytomy by analyzing multifurcating phylogenetic networks for regression analysis [38].
It is also worthwhile to take into account situations in which characteristics may conform to probability distributions beyond the normal distribution and to evaluate the resilience of our proposed methodology when the assumption of normality is not met. In particular, researchers should examine model misspecification problems [39] and study the consequences of non-normal distributions on the efficacy of the model, as has been done in previous studies [40].
Incorporating more parameters into the model would enable a more functional role of interaction with the hybrid parameters, particularly in the context of richer models such as the OU and early burst models. Furthermore, future work could explore the integration of discrete character evolution or the joint analysis of both discrete and continuous characters [41,42], as well as extend the proposed approach to accommodate diverse types of trait distributions. The development of such extensions would contribute to a better understanding of the evolution of biological traits, and may have practical applications in fields such as conservation biology and agriculture [43].
6. Conclusions
A phylogenetic regression model that incorporates a network structure to examine trait evolution in the context of reticulation events is proposed. Maximum likelihood estimation is utilized to estimate parameters, and an algorithm is developed to build the variance–covariance matrix using a phylogenetic network in eNewick format as input. This model is applied to investigate the response of common sunflower, Helianthus annuus, traits to drought conditions.
Parameter estimation is conducted through maximum likelihood, a widely used method in evolutionary biology, which allows for the estimation of model parameters that maximize the probability of the observed data. Additionally, an algorithm is developed to build the variance–covariance matrix, a crucial component of the model, using a phylogenetic network in eNewick format as input.
Overall, the proposed model and associated methods offer a novel approach to studying trait evolution in the context of reticulation events. By applying the model to the common sunflower and investigating its response to drought conditions, new insights can be gained into the evolutionary patterns of this important species.
Funding
This research and APC were funded by the National Science and Technology Council, Taiwan. MOST 111-2118-M-035-004-.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
I would like to express my sincere gratitude to the reviewers for their valuable feedback, which significantly enhanced the quality and rigor of the analysis. Additionally, I am grateful to Elizabeth Houseworth and Yo-Lun Tsai for their inspiration and support in the early stages of this work.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Appendix A.1. Script and Data files
All files in the manuscript can be accessed at http://tonyjhwueng.info/phyreghyb (accessed on 10 March 2023).
Appendix A.1.1. Model
- 1.
- BM: http://tonyjhwueng.info/phyreghyb/bmhydRegV3.r (accessed on 10 March 2023).
Appendix A.1.2. Sunflower Precipitation Dataset
The data for each sunflower can be accessed by executing the R script at the following link:
- 1.
- Precipitation data script: http://tonyjhwueng.info/phyreghyb/worldclim (accessed on 10 March 2023).
Appendix A.1.3. Figures and Tables
- 1
- Figure 1: http://tonyjhwueng.info/phyreghyb/3taxanetwork.pptx (accessed on 10 March 2023).
- 2
- Figure 2: http://tonyjhwueng.info/phyreghyb/3taxanetworkstep.pptx (accessed on 10 March 2023).
- 3
- Figure 3: http://tonyjhwueng.info/phyreghyb/3taxatree.pptx (accessed on 10 March 2023).
- 4
- Figure 4: http://tonyjhwueng.info/phyreghyb/sfnet.pptx (accessed on 10 March 2023).
- 5
- Figure A1: http://tonyjhwueng.info/phyreghyb/sixtaxanetwork.pptx (accessed on 10 March 2023).
- 6
- Table 2: http://tonyjhwueng.info/phyreghyb/precdatatolatex.html (accessed on 10 March 2023).
- 7
- Table 3: http://tonyjhwueng.info/phyreghyb/RegSunflower.html (accessed on 10 March 2023).
- 8
- Positive definite of : https://tonyjhwueng.info/phyreghyb/pdultracheck.html (accessed on 10 March 2023).
- 9
- Table 4: https://tonyjhwueng.info/phyreghyb/AnnPrecAllResponseTrait.html (accessed on 10 March 2023).
Appendix A.2. Demonstration of Algorithm under Brownian Motion Model
Consider the phylogenetic network given in Figure A1. There are 6 extant taxa, 2 hybridization events, and 9 ancestral nodes in the network.
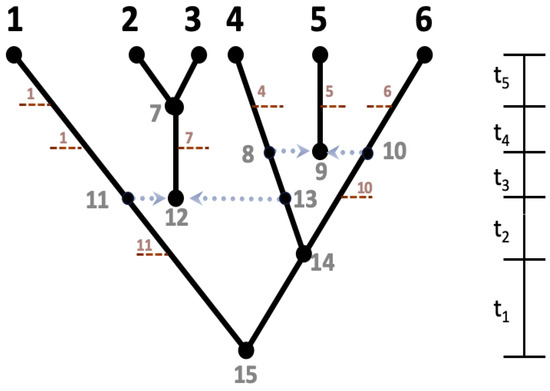
Figure A1.
A six-taxa phylogenetic network where 2, 3, and 5 are the hybrid descendants. The eNewick format for the network topology is .
The ancestral–descendant data gathered from the eNewick2phylog function and modified are shown as follows:
| Ancestor | [15] | [14] | [12] | [11] | [13] | [9] | [8] | [10] | [7] |
| Descendants | [11,14] | [13,10] | [7] | [1],[12] | [12,8] | [5] | [4,9] | [9,6] | [2,3] |
From this, we can determine the event times and which times lead to which descendants as follows:
| Node | [1] | [2] | [3] | [4] | [5] | [6] | [7] | [8] |
| Length |
| Node | [9] | [10] | [11] | [12] | [13] | [14] | [15] |
| Length | 0 | 0 | 0 |
We also identify the sequence of temporary similarity matrices built up from the root to the tips in terms of the nodes at each event (speciation or hybridization):
This sequence contains information for speciation and hybridization events where the speciation replaces the ancestor node with the corresponding two descendants (e.g., for speciation, is replaced by ). For hybridization, the hybrid node is inserted between its parents (e.g., indicates that [12] is hybrid and is inserted between [11] and [13]).
For the first similarity matrix, we obviously have
Going from [11,14] → [11,13,10] involves a straightforward speciation event and the new similarity matrix becomes
Going from [11,13,10] → [11,12,13,10] involves a hybridization. The variance for the hybrid [12] can be calculated from with the following formula: .
Moreover, the covariance between the hybrid species [12] and other species can be obtained by following the formula: All other elements in can be tracked from because they are identical. Therefore, the covariance for species , and at is
We elongate from [11,12,13,10]→[1,7,8,10] to obtain
The next event from [1,7,8,10] → [1,7,8,9,10] is another hybridization. The matrix for species is constructed by inserting the hybrid between its parents and .
We elongate from [1,7,8,9,10] to [1,7,4,5,6] to obtain
where
The final step from [1,7,4,5,6]→ [1,2,3,4,5,6] involves a speciation event. The final similarity matrix is given as
If we assign branch lengths by setting , the eNewick format with branch lengths input into the R program will be as follows. Input: network .
Output: The similarity matrix for the species on the tips of the tree is
It can be seen that the covariance matrix is a 6 by 6 matrix where the upper diagonal is shown due to its symmetry.
References
- Rieseberg, L.H.; Carney, S.E. Plant hybridization. New Phytol. 1998, 140, 599–624. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, N.; Owens, G.L.; Hovick, S.M.; Rieseberg, L.H.; Whitney, K.D. Hybridization speeds adaptive evolution in an eight-year field experiment. Sci. Rep. 2019, 9, 6746. [Google Scholar] [CrossRef] [PubMed]
- Bock, D.G.; Kantar, M.B.; Rieseberg, L.H. Population Genomics of Speciation and Adaptation in Sunflowers; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Harmon, L.J.; Weir, J.T.; Schulte, L.A. Phylogenies and Comparative Methods in Ecology and Evolution; University of California Press: Berkeley, CA, USA, 2005. [Google Scholar]
- Harvey, P.H.; Pagel, M.D. Comparative methods for explaining adaptations. Nature 1991, 351, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Clutton-Brock, T.H. Phylogenetic Perspectives on the Evolution of Mammalian Social Behavior; University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Bastide, P.; Solis-Lemus, C.; Kriebel, R.; Sparks, K.W.; Ané, C. Phylogenetic comparative methods on phylogenetic networks with reticulations. Syst. Biol. 2018, 67, 800–820. [Google Scholar] [CrossRef]
- Jhwueng, D.C.; O’Meara, B. Trait evolution on phylogenetic networks. bioRxiv 2015, 023986. [Google Scholar] [CrossRef]
- Teo, B.; Rose, J.P.; Bastide, P.; Ané, C. Accounting for within-species variation in continuous trait evolution on a phylogenetic network. bioRxiv 2022, 490814. [Google Scholar] [CrossRef]
- Jacquemyn, H.; Merckx, V.; Brys, R.; Tyteca, D.; Cammue, B.P.; Honnay, O.; Lievens, B. Analysis of network architecture reveals phylogenetic constraints on mycorrhizal specificity in the genus Orchis (Orchidaceae). New Phytol. 2011, 192, 518–528. [Google Scholar] [CrossRef]
- Solís-Lemus, C.; Bastide, P.; Ané, C. PhyloNetworks: A package for phylogenetic networks. Mol. Biol. Evol. 2017, 34, 3292–3298. [Google Scholar] [CrossRef]
- Solís-Lemus, C.; Ané, C. Inferring phylogenetic networks with maximum pseudolikelihood under incomplete lineage sorting. PLoS Genet. 2016, 12, e1005896. [Google Scholar] [CrossRef]
- Felsenstein, J. Phylogenies and the comparative method. Am. Nat. 1985, 125, 1–15. [Google Scholar] [CrossRef]
- Revell, L.J. Phylogenetic signal and linear regression on species data. Methods Ecol. Evol. 2010, 1, 319–329. [Google Scholar] [CrossRef]
- Ané, C. Analysis of comparative data with hierarchical autocorrelation. Ann. Appl. Stat. 2008, 2, 1078–1102. [Google Scholar] [CrossRef]
- Jhwueng, D.C. Some Problems in Phylogenetic Comparative Methods. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 2010. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Gilbert, P.; Varadhan, R. numDeriv: Accurate Numerical Derivatives; R Package Version 2016.8-1.1, CRAN Repository. 2019. Available online: https://cran.r-project.org/web/packages/numDeriv/index.html (accessed on 21 February 2023).
- Wald, A. Note on the consistency of the maximum likelihood estimate. Ann. Math. Stat. 1949, 20, 595–601. [Google Scholar] [CrossRef]
- Varga, R.S.; Nabben, R. On symmetric ultrametric matrices. In Numerical Linear Algebra; De Gruyter: Berlin, Germany, 1993; pp. 193–199. [Google Scholar]
- Nabben, R.; Varga, R.S. A linear algebra proof that the inverse of a strictly ultrametric matrix is a strictly diagonally dominant Stieltjes matrix. SIAM J. Matrix Anal. Appl. 1994, 15, 107–113. [Google Scholar] [CrossRef]
- Cardona, G.; Rosselló, F.; Valiente, G. Extended Newick: It is time for a standard representation of phylogenetic networks. BMC Bioinform. 2008, 9, 532. [Google Scholar] [CrossRef]
- Dray, S.; Dufour, A.B. The ade4 package: Implementing the duality diagram for ecologists. J. Stat. Softw. 2007, 22, 1–20. [Google Scholar] [CrossRef]
- Tsai, Y.L. Regression Analysis of Hybrid Species’s Trait Data. Master’s Thesis, Feng-Chia University, Taichung, Taiwan, 2016. [Google Scholar]
- Kane, N.C.; Rieseberg, L.H. Selective sweeps reveal candidate genes for adaptation to drought and salt tolerance in common sunflower, Helianthus annuus. Genetics 2007, 175, 1823–1834. [Google Scholar] [CrossRef]
- Koziol, L.; Rieseberg, L.H.; Kane, N.; Bever, J.D. Reduced drought tolerance during domestication and the evolution of weediness results from tolerance—Growth trade-offs. Evol. Int. J. Org. Evol. 2012, 66, 3803–3814. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Cerasoli, F.; D’Alessandro, P.; Biondi, M. Worldclim 2.1 versus Worldclim 1.4: Climatic niche and grid resolution affect between-version mismatches in Habitat Suitability Models predictions across Europe. Ecol. Evol. 2022, 12, e8430. [Google Scholar] [CrossRef]
- GBIF. Global Biodiversity Information Facility Database. Rumex acetosella L. 2010. Available online: https://www.gbif.org/ (accessed on 31 January 2023).
- Hijmans, R.J.; Van Etten, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.; Lamigueiro, O.; Bevan, A.; Racine, E.; Shortridge, A. Raster Package in R Version. 2023. Available online: https://cran.r-project.org/web/packages/raster/raster.pdf (accessed on 10 March 2023).
- van Etten, R.J.H.J. Raster: Geographic Analysis and Modeling with Raster Data; R Package Version 2.0-12, CRAN Repository. 2012. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 21 February 2023).
- Brach, A.R.; Song, H. eFloras: New directions for online floras exemplified by the Flora of China Project. Taxon 2006, 55, 188–192. [Google Scholar] [CrossRef]
- Gross, B.; Rieseberg, L. The ecological genetics of homoploid hybrid speciation. J. Hered. 2004, 96, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Ho, L.S.T.; Ane, C. A linear-time algorithm for Gaussian and non-Gaussian trait evolution models. Syst. Biol. 2014, 63, 397–408. [Google Scholar] [PubMed]
- Hansen, T.F. Stabilizing selection and the comparative analysis of adaptation. Evolution 1997, 51, 1341–1351. [Google Scholar] [CrossRef]
- Harmon, L.J.; Losos, J.B.; Jonathan Davies, T.; Gillespie, R.G.; Gittleman, J.L.; Bryan Jennings, W.; Kozak, K.H.; McPeek, M.A.; Moreno-Roark, F.; Near, T.J.; et al. Early bursts of body size and shape evolution are rare in comparative data. Evol. Int. J. Org. Evol. 2010, 64, 2385–2396. [Google Scholar] [CrossRef] [PubMed]
- Blomberg, S.P.; Rathnayake, S.I.; Moreau, C.M. Beyond Brownian motion and the Ornstein-Uhlenbeck process: Stochastic diffusion models for the evolution of quantitative characters. Am. Nat. 2020, 195, 145–165. [Google Scholar] [CrossRef]
- Jhwueng, D.C.; Liu, F.C. Effect of Polytomy on the Parameter Estimation and Goodness of Fit of Phylogenetic Linear Regression Models for Trait Evolution. Diversity 2022, 14, 942. [Google Scholar] [CrossRef]
- McCulloch, C.E.; Neuhaus, J.M. Prediction of random effects in linear and generalized linear models under model misspecification. Biometrics 2011, 67, 270–279. [Google Scholar] [CrossRef]
- Sheng, Y.; Yang, C.; Curhan, S.; Curhan, G.; Wang, M. Analytical methods for correlated data arising from multicenter hearing studies. Stat. Med. 2022, 41, 5335–5348. [Google Scholar] [CrossRef]
- Caetano, D.S.; O’Meara, B.C.; Beaulieu, J.M. Hidden state models improve state-dependent diversification approaches, including biogeographical models. Evolution 2018, 72, 2308–2324. [Google Scholar] [CrossRef]
- Grundler, M.C.; Rabosky, D.L. Complex ecological phenotypes on phylogenetic trees: A hidden Markov model for comparative analysis of multivariate count data. Syst. Biol. 2019, 69, 1200–1211. [Google Scholar] [CrossRef] [PubMed]
- Boyko, J.D.; O’Meara, B.C.; Beaulieu, J.M. A Novel Method for Jointly Modeling the Evolution of Discrete and Continuous Traits. Evolution 2023, 77, 836–851. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).