1. Introduction
The study of special functions and their applications has increasingly grown in the last 50 years. This comes together with the advent of powerful computation techniques and devices which have allowed applied scientists to envision real-world applications to this class of functions.
Even though great work has been carried out in applying the existing theory of special functions to physical and engineering problems, theoretical studies have also been taken into account.
About 25 years ago, the interest in the so-called Lambert W-function tremendously increased as important physical applications and the basic theory of this function were discussed in the seminal work of [
1]. The fact that Lambert W-function is linked to exponential-like equations provides a great number of applications in almost every branch of science, as this type of equation is common.
Apparently unrelated to Lambert W-function, the so-called generalized hypergeometric functions have been considered as solutions to ordinary and partial differential equations [
2]. This generalized class of functions has as special cases a great number of elementary and special functions, leading researchers to recognize such functions as higher-order special functions.
So far, no relation between Lambert W-function and hypergeometric-type functions has been established. In the theory of special functions, finding such correlations is of great interest, leading to more compact and rigorous representations. This approach is frequent in the literature as seen, for example, in [
3,
4,
5]. In addition, by connecting functions which apparently have no relation, important analytical continuation strategies can be envisioned.
In the present paper, the relation between Lambert W-function and generalized hypergeometric functions is discussed. It will be shown that this link can be accomplished in two different ways, namely, by solving the trinomial equation originally studied by Euler in [
6] and by Lambert; and by means of the direct and inverse Mellin transform of Lambert W-function.
The paper is organized as follows:
Section 2 presents some general concepts about generalized hypergeometric functions, while
Section 3 introduces the Lambert-W function and its application to solve Lambert’s trinomial equation.
Section 4 presents the solution of Lambert’s trinomial equation both in terms of hypergeometric functions and in terms of the Lambert-W function. Then,
Section 5 indicates how general hypergeometric functions and the Lambert-W function can be related while represented as contour integrals. Finally,
Section 6 presents the conclusions of the present work.
2. Generalized Hypergeometric Functions
In the present paper, the H-function is the first class of generalized hypergeometric functions which will be explored. This function is defined as a contour complex integral by [
2]:
where:
and
are integers such that
and
,
and
are positive real quantities, and all the
and
are complex numbers. The contour
L runs from
to
such that the poles of
,
lie to the left of
L and the poles of
,
lie to the right of
L.
By performing the variable change
and adjusting the contour
L to
, where the integral runs from
to
, the H-function can be alternatively defined as:
for which the same parameter domains’ restrictions apply.
By considering the definition in (
3), the H-function can be expressed in computable form as [
2]:
When the poles of
are simple, we have:
for
if
and for
if
, where
and
.
When the poles of
are simple, we have
for
if
and for
if
.
Both representations above apply when the poles of the gamma function in the numerator of the quotients are simple. When this simplification does not hold, residue theorem has to be applied. For details about this theorem, one may refer to [
7].
Another well-known example of generalized hypergeometric function, which is a special case of the H-function, is the Meijer G-function [
2]. More recently, the R-function has also shown its applicability to a number of statistical problems [
8].
The R-function (see [
8]) is defined as a contour complex integral which contains powers of Gamma functions in their integrands by:
in which
is defined in Equation (
2) and
,
,
, and
are chosen such that the integral on the right-hand side of Equation (
6) exists.
Several functions are special cases of both the H-function and the R-function, for example, generalized hypergeometric series
, MacRobert’s E-function, generalized Bessel–Maitland function, Kratzel function, Wright generalized hypergeometric function, Bessel functions, Whittaker function, Mittag–Leffler function, trigonometric functions, exponentials, and so on [
2]. In actuality, several authors have studied the properties and generalizations of such hypergeometric functions, such as [
9,
10,
11,
12,
13,
14].
3. Lambert W-Function and Lambert’s Trinomial Equation
Formally, Lambert W-function of a real variable
x can be defined as [
1]:
It is worth noticing that for
, there are two possible branches of
, namely,
stands for the branch in which
, while
stands for the branch in which
.
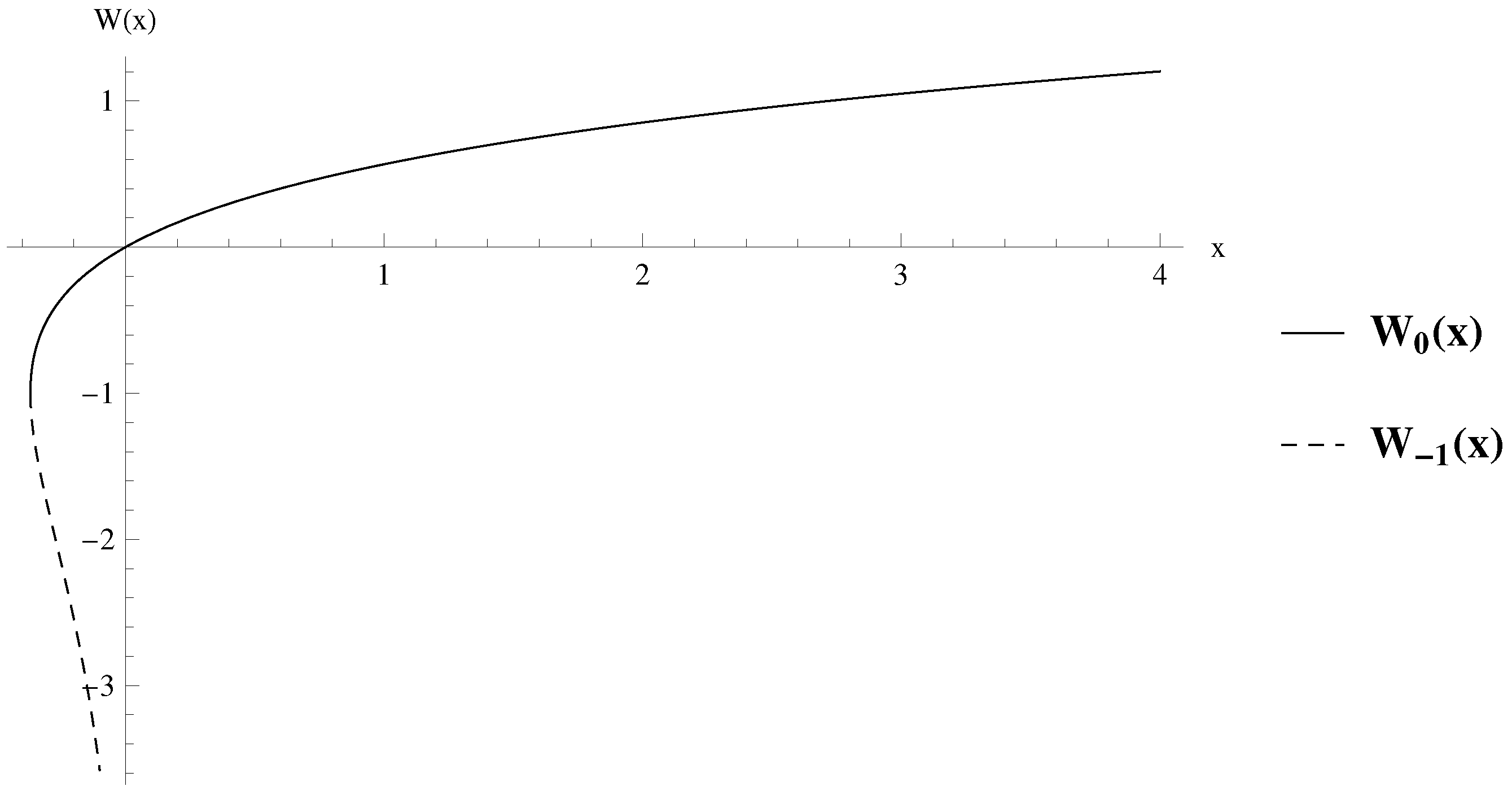
Figure 1 shows the behavior of the function as well as its real branches. The latter are represented by a full line (
) and a dashed line (
).
When the Lambert W-function of a complex variable is considered, there are infinitely many branches. This comes from multi-branches of the logarithm function involved in the inversion of Equation (
7).
While studying previous works by Lambert, Euler [
6] considered the solution of the following trinomial equation, where
and
:
By means of taking the limit
in Equation (
8), the following is obtained [
1]:
The solution to Equation (
9) is easily obtained in terms of Lambert W-function as
[
1].
In the present paper, in order to show the relation between Lambert W-function and the H-function, Equation (
8) will be solved and the limit will be applied later on.
4. Solution to Lambert’s Trinomial Equation
As pointed out in [
1], Equation (
8) can be brought back to Lambert’s original trinomial equation by setting
,
and
. This way, as in the case of Equation (
8),
and
and we can rearrange (
8) using these variable changes to obtain
In order to solve equations similar to (
8) and (
10), Rathie and Ozelim [
15] applied Lagrange’s inversion theorem [
16]. After a series solution was obtained, those authors compared such series to computable representations of the H-function. This way, following the same rationale, we will use the results from [
15] to find the solution of Lambert’s transcendental equation in terms of the H-function.
Theorem 1. The transformed version of Lambert’s trinomial equation, as presented in (10), can be solved analytically in terms of the H-function as: In the expressions above, stands for the H-function (see [2]). Proof. Rathie and Ozelim [
15] obtained general solutions, in terms of the H-function, to trinomial equations. In their work, they considered that
and solved the following equation:
Thus, by comparing (
10) and (
15), it is possible to see that when
,
,
and
, the solutions to the trinomial equation can be given as pointed out in [
15]. □
4.1. Particular Case When
We are interested in the particular case where , in order to match our H-function solutions to the Lambert W-function solution.
Corollary 1. The branch of the W-function can be related to the H-function solutions in equations from (11) to (14) as:iforotherwise. Here,denotes the complex conjugate of. Additionally,iforotherwise. Proof. When
, as pointed out by [
1], the trinomial Equation (
8) reduces to Equation (
9), whose solution can be given in terms of Lambert W-function as
. We can see that the branches satisfying the solutions are
when
and
when
. Finally, numerical checks reveal that the correct branch which matches the equations is
. □
4.2. New Series Expansion Formulas for
So far, the relation between Lambert W-function and the H-function has been presented in terms of closed-form representations. On the other hand, it is possible to explore numerical alternatives to such representation, as subsequently shown.
Corollary 2. By considering the alternative representation of in terms of the H-function, the following new series representations for arise: Proof. Both the H-functions in Equations (
16) and (
18) can be converted to a series by directly using the results in (
4) and (
5). The same is also possible for the H-functions in Equations (
17) and (
19), which ends the proof. □
The Gamma functions in both Equations (
20) and (
21) show up after applying Lagrange’s inversion theorem, as indicated in [
15]. Such ratios may present numerical challenges to some software, especially when the values of the Gamma functions increase.
Corollary 3. In order to avoid calculating the ratios of Gamma functions in (20) and (21), such equations can be rewritten as:and Proof. Each ratio of Gamma functions can be further simplified by noticing that [
15]:
By combining (
24) with (
20) and (
21), (
22) and (
23) follow. □
It can be seen that, not only it was possible to show that Lambert W-function is a limiting case of the H-function, but also that a new series could be obtained for . In addition, when , , since we are dealing with the real values of the branch.
5. Relation to Generalized Hypergeometric Functions of Higher Rank
We can establish another relation between the Lambert W-function and generalized hypergeometric functions by looking at its Mellin transform. As pointed out in [
17], the Mellin transform of the W-function can be given as:
for
.
It is possible to invert the Mellin transform of the W-function to obtain its contour integral representation. This leads to:
By applying the residue Theorem [
2] to calculate the contour integral in Equation (
26), the series for
is obtained.
Linking the Lambert-W function to such high class hypergeometric function as the R-function can shed light onto problems which could not be addressed in terms of the H-function. These problems can be found in many areas, such as complex multivariate distributions in the area of the inference on multiple time series [
18,
19,
20], multivariate statistical analysis [
21], and distribution of the likelihood ratio criterion for testing specific conditions for the covariance matrix and mean vector of multivariate normal distributions [
22,
23,
24,
25].
In addition, in physics, this type of special function can be applied to problems involving the energy loss of fast particles by ionization [
26,
27]. Therefore, there are plenty of future works which may benefit from this relation, both in terms of new analytical results and representations, as well as in new computational calculations made easier by the Lambert-W function.
6. Conclusions
In the present paper we could establish relations between H-functions and R-function and the branches and of the W-function, respectively. These results were obtained for the first time, establishing a connection between the two classes of functions. Further studies may lead to other relations, allowing interesting new analytic continuation strategies for both classes of functions. The new series are also able to compute for arbitrary precision, even when .
While the new relations directly follow from previous results presented in the literature, they have not been made available to date. The limiting procedure carried out is novel for these classes of functions, which may shed light on the relation between apparently unrelated functions.
Author Contributions
Conceptualization, L.C.d.S.M.O.; methodology, P.N.R. and L.C.d.S.M.O.; software, L.C.d.S.M.O.; validation, P.N.R. and L.C.d.S.M.O.; formal analysis, P.N.R. and L.C.d.S.M.O.; investigation, L.C.d.S.M.O.; writing—original draft preparation, L.C.d.S.M.O.; writing—review and editing, P.N.R.; supervision, P.N.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding and the APC was gently waived by the Editorial Office of Stats.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used are available upon request to the corresponding author.
Acknowledgments
The authors acknowledge the support provided by the University of Brasilia (UnB).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the LambertWfunction. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Pathan, M.A.; Shahwan, M.J.S. New representations of the voigt functions. Demonstr. Math. 2006, 39, 75–80. [Google Scholar] [CrossRef]
- Alzer, H.; Richards, K.C. Series representations for special functions and mathematical constants. Ramanujan J. 2016, 40, 291–310. [Google Scholar] [CrossRef]
- Rathie, A.K.; Rathie, P.N.; Ozelim, L.C.S.M. On a new identity for the H-function with applications to the summation of hypergeometric series. Turk. J. Math. 2018, 42, 924–935. [Google Scholar] [CrossRef]
- Euler, L. De serie Lambertina plurimisque eius insignibus proprietatibus. Acta Acad. Sci. Imp. Petropolitanae 1783, 1779, 29–51. [Google Scholar]
- Springer, M.D. The Algebra of Random Variables; John Wiley: New York NY, USA, 1979. [Google Scholar]
- Rathie, P.N. Generalized Hypergeometric Functions and Exact Distributions of Test Statistics. Am. J. Math. Manage. Sci. 1988, 9, 155–172. [Google Scholar] [CrossRef]
- Dziok, J.; Srivastava, H. Classes of analytic functions associated with the generalized hypergeometric function. Appl. Math. Comput. 1999, 103, 1–13. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Agarwal, P.; Jain, S. Generating functions for the generalized Gauss hypergeometric functions. Appl. Math. Comput. 2014, 247, 348–352. [Google Scholar] [CrossRef]
- Srivastava, H. Generalized hypergeometric functions with integral parameter differences. Indag. Math. (Proc.) 1973, 76, 38–40. [Google Scholar] [CrossRef]
- Saxena, R.K.; Kumar, R. A basic analogue of the generalized H-function. Le Mat. 1995, 50, 263–271. [Google Scholar]
- Nisar, K.S.; Rahman, G.; Choi, J.; Mubeen, S.; Muhammad, A. Generalized hypergeometric k-functions via (k, s)-fractional calculus. J. Nonlinear Sci. Appl. 2017, 10, 1791–1800. [Google Scholar] [CrossRef][Green Version]
- Nisar, K.S. On the generalized modified k-bessel functions of the first kind. Commun. Korean Math. Soc. 2017, 32, 909–914. [Google Scholar] [CrossRef]
- Rathie, P.N.; Ozelim, L.C.S.M. General Solutions to Certain Real Degree Equations and their Applications. Adv. Stud. Contemp. Math. 2012, 22, 325–341. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Corless, R.M.; Jeffrey, D.J.; Knuth, D.E. A sequence of series for the Lambert W function. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation-ISSAC ’97, Maui, HI, USA, 21–23 July 1997; ACM Press: New York, NY, USA, 1997; pp. 197–204. [Google Scholar] [CrossRef]
- Krishnaiah, P. Some recent developments on complex multivariate distributions. J. Multivar. Anal. 1976, 6, 1–30. [Google Scholar] [CrossRef]
- Arora, K. A Study of G, H and R-Functions and Their Applications to Statistics. Ph.D. Thesis, Maharshi Dayanand Saraswathi University, Ajmer, Rajasthan, India, 1993. [Google Scholar]
- Rathie, P.N. On the R-function and the distribution of a LRC in multinormal complex case. Int. J. Math. Stat. Sci. 1994, 3, 133–146. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis; John Wiley: New York, NY, USA, 1984. [Google Scholar]
- Nagarsenker, B.N.; Pillai, K.C.S. Distribution of the likelihood ratio criterion for testing a hypothesis specifying a covariance matrix. Biometrika 1973, 60, 359–364. Available online: https://academic.oup.com/biomet/article-pdf/60/2/359/619118/60-2-359.pdf (accessed on 1 November 2022). [CrossRef]
- Nagarsenker, B.N.; Pillai, K.C.S. Distribution of the likelihood ratio criterion for testing Σ=Σ0, μ=μ0. J. Multivar. Anal. 1974, 4, 114–122. [Google Scholar] [CrossRef][Green Version]
- Korin, B.P. On the distribution of a statistic used for testing a covariance matrix. Biometrika 1968, 55, 171–178. [Google Scholar] [CrossRef]
- Rathie, A.k. A generalization of generalized hypergeometric functions. Int. J. Math. Stat. Sci. 1996, 5, 119–133. [Google Scholar]
- Landau, L.D. On the energy loss of fast particles by ionization. J. Phys. (USSR) 1944, 8, 201–205. [Google Scholar]
- Borsch-Supan, W. On the evaluation of the function for real values of λ. J. Res. Natl. Bur. Stand. Sect. B Math. Math. Phys. 1961, 65, 245–250. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).