Abstract
The USDA National Agricultural Statistics Service (NASS) and other federal statistical agencies have used probability-based surveys as the foundation for official statistics for over half a century. Non-survey data that can be used to improve the accuracy and precision of estimates such as administrative, remotely sensed, and retail data have become increasingly available. Both frequentist and Bayesian models are used to combine survey and non-survey data in a principled manner. NASS has recently adopted Bayesian subarea models for three of its national programs: farm labor, crop county estimates, and cash rent county estimates. Each program provides valuable estimates at multiple scales of geography. For each program, technical challenges had to be met and a strenuous review completed before models could be adopted as the foundation for official statistics. Moving models out of the research phase into production required major changes in the production process and a cultural shift. With the implemented models, NASS now has measures of uncertainty, transparency, and reproducibility of its official statistics.
1. Introduction
The United States Department of Agriculture (USDA) National Agricultural Statistics Service (NASS), one of thirteen U.S. federal statistical agencies, provides official statistics on all facets of U.S. agriculture including crop and livestock production, acreages planted to various crops, and prices paid and received. For more than fifty years, NASS has conducted probability-based surveys. Over time, reliable administrative, remotely sensed, and other non-survey data that can be used to supplement the survey data have become increasingly available. Traditionally, the NASS Agricultural Statistics Board has relied on expert opinion to produce official statistics using the survey estimates as a foundation informed by these disparate non-survey data. Although external reviews have consistently found that NASS estimates are the gold standard for the agricultural industry, the process lacked transparency and reproducibility and did not lead to valid measures of uncertainty.
In the early 2000s, NASS, through collaborations with the National Institute of Statistical Sciences, the University of Florida, and the University of Maryland, began exploring the use of small area estimation as an approach to combine information from survey and non-survey data to produce estimates with valid measures of uncertainty. In 2014, NASS entered into a cooperative agreement with the Committee on National Statistics (CNSTAT) to review the NASS county estimate programs, crop county estimates, and cash rent county estimates. In its consensus report [1], the CNSTAT panel recommended that NASS transition to model-based estimates.
Small area models have gained increased attention by federal statistical agencies. They can “borrow strength” from related areas across space and/or time or through auxiliary information to provide “indirect” but reliable estimates for small areas with small or even zero sample sizes while also increasing the precision. Two major types of small area models, area-level and unit-level models, have been developed based on both frequentist and Bayesian methods. Pfeffermann [2] and Rao and Molina [3] provided a comprehensive overview of the development, methods, and applications of small area estimation including various types of area-level and unit-level models. For continuous responses, the first and most common model in small area estimation is the Fay–Herriot (FH) model [4]. The FH model is an area-level model based on a “normal-normal-linear” assumption; that is, the direct estimates and area-level random effects are each assumed to follow a normal distribution, and a linear regression function relates the true estimates of interest to the covariates. Battese et al. [5] proposed the popular unit-level model, nested-error regression (NER) model, when data are available on the individual sampled units. In practice, because unit-level models generally require substantially more computational time, area-level models are more applicable for the production of official statistics that are published with tight timelines.
In recent years, subarea-level models, which are extensions of area-level models, have been used to estimate small area means, not only by borrowing strength from related areas, but also by borrowing strength from subareas, to obtain more efficient subarea estimators, provided that observations are available at both the area and subarea levels. The studies in Torabi and Rao [6] and Fuller and Goyeneche [7] illustrated frequentist approaches to model fitting and estimation for the subarea-level model with known sampling variances. Erciulescu et al. [8] proposed and discussed the subarea-level model using a Bayesian approach. Because the interest for NASS programs is in constructing summaries for different levels of geography (county, state, regional, and U.S. levels), the Bayesian approach to model fitting and estimation is preferable. Bayesian inference potentially improves the efficiency of estimates because prior information can be incorporated into models based on model requirements such as known bounds, and coherency can be enforced across surveys. Furthermore, Bayesian inference is straightforward and exact for obtaining estimates for any known functions of the model parameters.
Based on a rigorous review process of the proposed new methodology, NASS has been moving to adopt models for several of its programs. Small area estimation has become the basis for official statistics in three major programs: farm labor, crop county estimates, and cash rent county estimates. For farm labor, estimates are produced for regions comprised of adjoining states and the nation. For crop county estimates and cash rent county estimates, estimates are published for counties, states, and the nation. In Section 2, each program’s purpose, survey, and available non-survey data are described. An overview of the small area models that have been adopted is provided in Section 3. The process of moving the models into production is described in Section 4. The final section focuses on the lessons learned and opportunities for future developments.
2. Survey Programs with Small Area Estimates
The NASS has adopted small area estimation as the basis for publishing estimates for three programs: farm labor, crop county estimates, and cash rent county estimates. Each program provides valuable official statistics that are used by stakeholders to administer programs, provide services, or set policy. A probability-based survey serves as the foundation for each program, and non-survey data that can inform the estimates are available. An overview of each program is provided in this section.
2.1. Farm Labor Program
The NASS has published wage rates for farm labor since 1866, and U.S. farm employment estimates have been published since 1910. The Department of Labor needs reliable agricultural labor data for setting the adverse effect wage rates (AEWR), which is the minimum wage that employers of non-immigrant H-2A visa agricultural workers must offer and pay U.S. and alien workers. Currently, the AEWR is set to the annual weighted average hourly wage rate for field and livestock workers combined. The Department of Labor also uses the NASS estimates of farm labor wage rates in the administration of the H-2A program for non-immigrants who enter the U.S. for temporary or seasonal agricultural work and to inform setting child labor regulations.
The Farm Labor Survey is conducted semi-annually in April and October in cooperation with the U.S. Department of Labor. The target population includes all agricultural operations with $1000 or more in annual sales (or potential sales). Data are collected for reference weeks in January and April during the April survey and for reference weeks in July and October during the October survey. The reference week is the Sunday to Saturday period that includes the 12th day of the month. The NASS uses a dual frame approach consisting of list frame and area frame components to provide complete coverage of this target population. The farm labor list frame and area frame samples are each selected using a hierarchical stratified sampling design with strata defined by state and, within the state, by the peak number of farm workers or calculated farm value of sales.
The survey provides the basis for the employment and wage estimates for all workers directly hired by U.S. agricultural operations (excluding Alaska) for each of the four quarterly reference weeks at the regional and national levels (see Figure 1 [9]). The quarterly estimates, in turn, provide the basis for the annual average estimates.
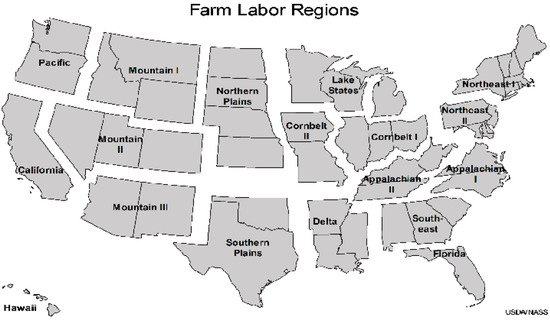
Figure 1.
The regions for which farm labor estimates are developed.
The data collected during the Farm Labor Survey are used to develop estimates of the number of hired workers and average hours worked per worker during each reference week. In addition, the estimates of the average hourly wage rates for field workers, livestock workers, field and livestock workers combined, and all hired workers (including supervisors/managers and other workers) are derived at the regional and U.S. levels. Traditionally, the direct survey estimates were reviewed and could be adjusted by NASS staff and the Agricultural Statistics Board. Adjustments were considered primarily when the difference between either the estimated previous year’s and current year’s wage rates or the estimated previous quarter’s and current quarter’s wage rates (after allowing for seasonal fluctuations) was large. The adjusted estimate was restricted to being between the two rates being compared so that the difference was reduced, but the direction of change was not. If the number of responses within a state was substantial, then the survey estimate received the greatest weight. If only a small number of responses were received, then the previous year’s or quarter’s published value and the estimates from the surrounding states or region were given more weight. Any model to replace the expert opinion used to integrate the survey and non-survey data needs to respect the guidelines used in the review process.
The NASS publishes the estimates in May and November for the U.S. as a whole, each of the 15 multi-state labor regions, and the single-state regions of California, Florida, and Hawaii. In both May and November, the report includes quarterly estimates of the number of hired workers and average hours worked per worker during each reference week. It also includes the quarterly estimates of the average hourly wage rates for field workers, livestock workers, field and livestock workers combined, and all hired workers (including supervisors/managers and other workers). The November report additionally provides the following annual data based on the quarterly estimates: the average number of workers; the weighted average hours worked per worker; and weighted average hourly wage rates for field workers, field and livestock workers combined, and all hired workers.
2.2. Crop County Estimates Program
The NASS began publishing estimates of the final acreages, yield, and production for principal crops in 1866 [10]. The quarterly agricultural surveys are conducted to capture activities throughout the life cycle of the crop including planting intentions (March), early estimates of planted acreage (June), and estimates of the harvest and output activities for small grains crops (September) and major row crops (December). The annual June area survey sample, which is drawn from an area frame, provides an undercoverage adjustment for the list-based samples obtained during the September and December agricultural surveys. The NASS Agricultural Statistics Board releases the state and national estimates of the planted and harvested acreages, yield, and production for small grains in late September and for row crops in January of the following year. These estimates are based on the coverage-adjusted national and state survey estimates informed by non-survey data such as administrative and remotely sensed data.
County-level crop estimates have been produced since 1917 [11]. Although initially federally funded, the program evolved into partnerships with the states via cooperative agreements. The crop surveys were usually funded by the states, with NASS staff in state offices defining the samples, identifying the processes, and developing the estimates. As the USDA’s support of the farm sector has evolved so that aid is increasingly conditioned on each producer’s own revenue experience, the NASS initiated the probability-based county agricultural production survey (CAPS) in a few states in 2011, and the remaining eligible states in 2012, to augment the agricultural survey for county-level estimates. The CAPS list frame sample is stratified by state and drawn using maximal Brewer selection with Poisson permanent-random-number (PRN) sampling, which is sometimes referred to as multivariate probability proportional to size (MPPS) sampling [12]. The MPPS design allows for target sample sizes for all commodities of interest to be set at the county level. The agricultural survey and CAPS samples are pooled and reweighted, and the combined sample is referred to as the CAPS sample. Sampling variances for crop acreage and production are estimated using a delete-a-group Jackknife and sampling variances for yield are estimated using a second order Taylor series approximation for the ratio [12,13]. The CAPS sample provides survey data with which to estimate the acreages and production of selected crops at the county level for use in state and federal programs in 44 states. County-level estimates of crop acreage, yield, and production inform many agricultural support and crop insurance programs administered by other USDA agencies including the Farm Service Agency and the Risk Management Agency, which manages the Federal Crop Insurance Corporation.
The NASS conducts the row crop CAPSs in 43 states and the small grains CAPSs in 37 states (Figure 2). The commodity crops targeted may differ from state to state and from year to year, depending on the required coverage for nationally reported crops and the needs of other stakeholders such as specific state program commodities. The official county estimates for small grains (e.g., barley, oats and wheat) are published in December. The first row crop county estimates for corn, soybeans, sunflower, and sorghum are published in February of the following calendar year. Row crop county estimates for additional commodities are subsequently released at intervals, concluding with the release of the county estimates of potatoes in October. Because the CAPS data collection extends beyond the release of the national and state-level official statistics, the county estimates are benchmarked to previously published state acreages, production, and yield to ensure the consistency of estimates at all sub-state levels. Traditionally, the Agricultural Statistics Board has used expert opinion to combine the survey estimates of the planted and harvested acres, yield, and production derived from the CAPS with administrative and remotely sensed data to produce the official estimates. Strong administrative data are obtained from the Farm Services Agency (FSA) and the Risk Management Agency (RMA).
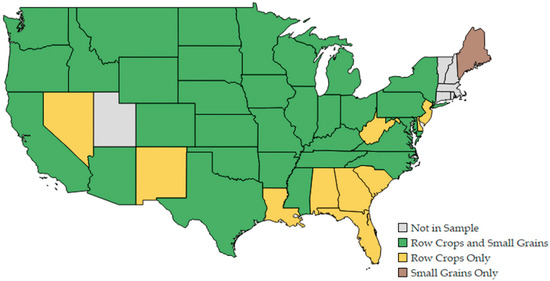
Figure 2.
The states for which no (grey) estimate, at least one row crop (yellow) estimate, at least one small grain (brown) estimate, or at least one row crop estimate and one small grain crop estimate (green) are published.
A producer who participates in any USDA program during a calendar year completes the FSA-578 form. On the form, the producer identifies each specific field and for that field, provides the acreage planted, the crop and date of planting, and some information on farm practices such as whether irrigation is used. Coverage varies with the crop and state. As an example, the FSA coverage for Illinois is over 99% of all land planted to corn. In the process of managing the USDA crop insurance program, RMA collects information on the specific field being insured, the acreage and crop planted to that field, and whether the field is harvested. The NASS estimates honor the lower bounds of planted acreage from the FSA and RMA planted acreage data and harvested acreage from the RMA data. Because survey estimates are sometimes below and at other times above these bounds, NASS staff have historically manually adjusted the survey estimates to reflect these lower bounds and to benchmark the adjusted estimates. Rounding rules such as the number of acres planted to corn in the county is published to the nearest 100 acres were also manually enforced.
2.3. Cash Rent Program
The Cash Rents Survey provides the basis for the county estimates of the cash rent paid for three land-use categories: irrigated cropland, non-irrigated cropland, and pasture. From 1950 to 1974, a list survey of real estate appraisers was used to estimate the state-level cash rents. Beginning in 1974, producers provided information about their rental agreements by responding to questions on the June area survey. In the 2008 farm bill, the NASS was mandated to provide the mean rental rates for all counties (not just states) with at least 20,000 acres of crop land.
To produce quality estimates at the county level, the NASS initiated the Cash Rents Survey, which is conducted annually in all states but Alaska. The target population is the set of all agricultural operations that have or will rent land in any of the three land-use categories on a cash basis during the current crop year, which in some cases crosses two calendar years. Land that has a non-cash component to the rental agreement such as rentals for a share of the crop or for livestock, on a fee per head or per pound of gain, or by animal unit month, is excluded. Land that is rented free of charge or includes buildings is also excluded. The Cash Rent Survey sample of about 225,000 agricultural operations is drawn from the NASS list frame, which is a list of all known U.S. farms. The sample is stratified by state and county within the state to produce state and county-level estimates. Data collection occurs from late February until the end of June. Variances for cash rental rate estimates are constructed using a second-order Taylor series expansion for the ratio.
From the Cash Rents Survey, the county, state, and national rental rates ($/acre) for each land-use category (irrigated, non-irrigated, and pasture) are published (see Figure 3 [14] for the 2021 state-level published cash rental rate estimates for non-irrigated land).
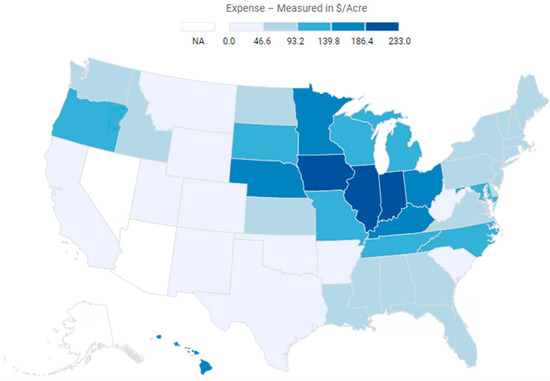
Figure 3.
The state-level published estimates of the cash rental rate for non-irrigated cropland measured in $/acre in 2021.
Although the total value of cash rents and acres rented on a cash basis are computed, these values have not been published. Historically, the direct survey estimates were reviewed and, if deemed appropriate, adjusted by the NASS staff or the Agricultural Statistics Board. The primary reason for adjustment was a large difference between the previous year’s published cash rental rate and the current year’s survey estimate. The adjusted estimate was restricted to being between, or on, the current survey estimate and the previous year’s published estimate so that the direction of change was honored. If the number of responses within a county was substantial, then the survey estimate received the greatest weight. If only a small number of responses was received, then the previous year’s published value and the estimates from surrounding counties or the agricultural statistics district were given more weight. Any model to replace the expert opinion needs to follow the guidelines used in the review process.
The NASS releases estimates for counties in August. Of the 3112 counties in the U.S. excluding Alaska, 2758 (88.6%) had 20,000 or more acres of combined cropland and pasture at the time of the 2017 Census of Agriculture. Each year, the NASS has published at least one county estimate of the cash rental rate in 93 to 95% of the target counties, but some land-use practices may be underserved.
3. Small Area Models
When integrating survey and non-survey data, two basic approaches are used. One aggregates information from each source at a specified geographic level such as a county, and then combines the information through modeling. The other links data from diverse sources at the record level and then develops the model of interest. As discussed in Section 5, the NASS has not been able to link the survey and non-survey data at the farm level. Thus, the models that have been implemented in production integrate information from diverse sources based on data aggregated at a specified geospatial level.
Small area models are now being used to produce estimates for farm labor, crop county estimates, and cash rent county estimates. For each of the subarea models, the area and the subarea are defined. For farm labor, the region (see Figure 1) is the area, and the state within region is the subarea. For both crop county estimates and cash rent county estimates, the agricultural statistics district is the area, and the county within the agricultural statistics district is the subarea. An agricultural statistics district is a predefined group of neighboring counties within a state that have similar agriculture. The number of agricultural statistics districts within a state varies from one for small states to 15 for Texas, with a median number of nine.
The small area models that the NASS has implemented can all be viewed as extensions to the two-stage FH model [4]. In the first stage, the subarea-level means from the survey are assumed to follow a distribution with mean and sampling variance , which is estimated using the survey design and weights. The second stage relates the s to the covariates through a regression , where represents the prediction error associated with the regression model and is assumed to have mean 0. Thus, the corresponding probability-based surveys discussed in the last section serve as the foundation for the models, and the information from the non-survey data are incorporated as covariates in the regression. The NASS publishes the coefficient of variation (CV) with its point estimates. For the models developed here, the CV is based on the point estimate and its standard error from the posterior distribution.
3.1. Small Area Models for Farm Labor Estimates
The NASS Farm Labor Report is published semiannually and provides estimates of the number of workers, average hours worked per week, and average wage rates by worker type at the regional, and national levels. For each worker type, three subarea models, one for each variable of interest, are fit. The farm labor region is the area, and the state within region is the subarea. The distribution of the number of workers is highly right-skewed so a normal subarea-level model is based on the log transformation. The distributions of hours worked per week and wage rates, which are also non-negative, are symmetric; thus, normal subarea-level models are fit to these variables.
Each model is outlined below, and the modeling details are in Chen et al. [15]. To estimate the number of workers, let i =1, 2, …, 18 be an index for the 18 labor regions and let j = 1, 2, …, ni be the jth state in the ith region. Furthermore, define k = 1, 2, 3, 4 as an index for the four worker types: (1) field workers, (2) livestock workers, (3) supervisors, and (4) other workers. Let denote the true number of workers of type k in state j and region i;; and and be, respectively, the direct survey estimate and the associated survey variance of . The covariates including an intercept are (see Table A1 in Appendix A for a list of the covariates).
The model for the number of workers is then
where is, by the delta method, the estimate for the sampling variances after log transformation; is the area-level random effect representing the region-level variability; and are, respectively, the least squares estimates of and the estimated covariance matrix of ; and represents the positive real numbers. The uniform priors for scale parameters and are motived by Gelman [16] and Browne and Draper [17]. The uniform prior on the real line is functionally equivalent to a proper U(0,1/ε) prior for very small ε.
After obtaining the posterior distribution of , the estimators , where wk represents the number of workers, follow from back transformation and are used to obtain the posterior means and measures of uncertainty for the number of workers by each worker type. The aggregated regional level posterior summaries for the number of workers by different worker types are obtained based on state-level MCMC samples (see Chen et al. [15] for details).
Because the distributions of the average hours worked per week and the average wage rate per hour are symmetric, a normal subarea model is applied to each of these response variables.
As in the lognormal subarea model, is the area-level random effect representing the region-level variability; the coefficients of have an empirical diffuse prior; and the prior distributions for and are noninformative uniform priors (see Table A1, Appendix A for a list of the model covariates).
After obtaining the posterior distribution of , for , where hr and wg represent average hours worked per week and average wage per hour, respectively, the estimators follow from the identity transformation and are used to obtain the posterior means and measures of uncertainty for hr and wg by each worker type. The aggregated regional level posterior summaries for hours and wage rate by different worker types are obtained conditional on the state-level MCMC samples of the number of workers (see Chen et al. [15]).
The detailed model evaluations including model effectiveness, model efficiency, and a comparison between survey estimates and subarea model estimates can be found in Chen et al. [15]. Furthermore, a 2020 case study illustrates the improvement in the direct estimates for areas with small sample sizes by using auxiliary information and borrowing information across areas and subareas.
3.2. Small Area Models for Crop County Estimates
In the Crop County Estimates program, estimates of the planted and harvested acres, yield and production for each county in the target population of a specified crop are produced. Production (or yield) can be derived from the yield (or production) and harvested acres as the product of yield and harvested acres (or the ratio of production to harvested acres). Thus, only three models are needed: (1) planted acres, (2) harvested acres, and (3) yield or production. Reflecting the agricultural process, the model for planted acres is modeled first. The harvested acres model is modeled next and must reflect two constraints: (1) If the acres planted to the specified crop is zero, then the number of harvested acres is zero; and (2) the number of acres harvested can be no more than the number of planted acres. Because the number of planted acres can vary widely from farm to farm with a few farms planting many more acres than the majority of the others, production tends to be highly skewed whereas yield tends to be more normally distributed. Therefore, a yield model was developed, and production was derived from the estimates of the yield and harvested acres. Of course, yield and production must be zero if no acres are planted or harvested.
All crop county estimates must honor two constraints that follow from the available information. First, the state and U.S. estimates of the planted and harvested acres, yield, and production are published before the county estimates of those same quantities, and the state estimates are coherent with the national estimates; that is, the estimated state-level numbers of the planted and harvested acres and production sum to the published U.S. estimates. To maintain coherence in the estimates, the estimates of the planted and harvested acres and production for counties within a state must total the state-level estimates. Ratio benchmarking similar to that of Nandram and Sayit [18] enforces this coherence. Second, the yield, as the ratio of production to harvested acres, needs to aggregate to the corresponding state-level estimates. The study by Erciulescu et al. [19] explored the preservation of triplet relationships among the numerator totals, denominator totals, and their ratios for two nested, smaller-than-state geographies.
Erciulescu et al. [8] suggested a subarea model for planted acres and applied ratio benchmarking. The area is an agricultural statistics district, and a county within a district is the subarea.
Let be the number of planted acres in county j = 1, 2, …, , within agricultural statistics district i = 1, 2, …, m. Furthermore, let the county sample size be and be the direct survey estimate with the estimated sampling variance . The total number of counties in a state is , and the state sample size is . The county-level auxiliary information is (see Table A2, Appendix A for a list of the model covariates). Further assume that the county-level random effects have independent, normal distributions with mean 0 and variance and the district-level random effects are independent, normally distributed with mean 0 and variance . Then,
The prior distribution for the model parameter is a normal distribution with mean and variance being the least squares estimates of . With known and with no district-level effects , Model (1) reduces to the FH area-level model [4].
The number of acres planted to a specified crop within a county is at least as large as the number of acres that the producers reported to either the FSA or RMA as having been planted in that county. Often, the direct survey estimate of planted acres for a county is above this lower bound, but due to sampling variation, this is not always the case (see Figure 4). The NASS has long used expert opinion to ensure that this lower bound was honored. Developing the methodology to enforce this lower bound within (1) was technically challenging. Nandram et al. [20] and Chen et al. [21] proposed and implemented the constrained model (4) for planted acres.
where is the vector of the maximum of the acres planted to the specified crop reported to the FSA and RMA for each county i in an agricultural statistics district j, and is the prepublished state-level estimate of the planted acres. Ratio benchmarking was applied so that the total of the estimated planted acres within each county totaled the state-level estimate of acres planted to the crop. Adding the constraint to the model and applying ratio benchmarking led to estimates that were consistent with the expert opinion used by the members of the Agricultural Statistics Board, which enabled the model to be considered for production.
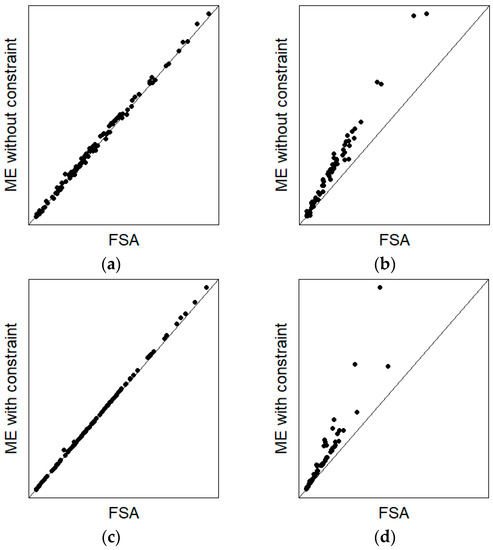
Figure 4.
A plot of the modeled county estimates of acres planted to corn versus the acres planted to corn reported to the FSA for (a) Illinois and (b) Pennsylvania when the constraint that the estimate must be at least as large as the FSA reported value is not included in the model and for (c) Illinois and (d) Pennsylvania when the constraint is included in the model.
Erciulescu et al. [8] proposed and implemented a subarea model for harvested acre estimates analogous to the one for planted acres in (1). In contrast, a subarea model for failed acre estimates was developed where the number of failed acres was equal to the number of planted acres less the number of acres harvested. Through its insurance program, the RMA collects information on failed acres due to drought, storms, or other events. The number of acres reported as having failed within a county provides a lower bound for that county’s number of failed acres, which is the difference in the number of acres planted and those harvested. Thus, conditioned on the model-based planted acre estimates, the model incorporated a constraint to honor the lower bound of failed acres obtained from the RMA administrative data, and the model-based harvested acre estimates can be derived from the planted acre and failed acre estimates. In such a model setting, the two relationships, (i) between planted acres and harvested acres and (ii) between the model-based failed acres and RMA administrative failed acres can be satisfied. In the end, ratio benchmarking was applied so that the total of the estimated harvested acres within each county totaled the state-level estimate of acres harvested to the crop.
The subarea models for yield are of the same form as model (1) with representing the direct survey estimates of yield and its associated sampling variance, respectively, for county i within agricultural statistics district j. The National Commodity Crop Productivity Indices (NCCPIs), which measure the quality of the soil for growing non-irrigated crops in climate conditions best suited for corn (NCCPI-corn), wheat (NCCPI-wheat), and cotton (NCCPI-cotton), are incorporated as covariates in . The mean and variance of the posterior distribution of the yield are, respectively, the modeled estimate of the yield of county i in agricultural statistics district j and its estimated variability.
It is worth noting that some sampling variances are not stable or are unavailable due to zero or small sample sizes for certain counties, which differ with commodity. Erciulescu et al. [22] discussed the challenges of missing data when fitting the subarea level model to obtain the crop total estimates for the whole nation. A nearest neighbor imputation method was proposed to impute missing data including the missing sampling variances. In addition, an approach based on Taylor’s approximation and Bayesian modeling was applied to smooth unstable, modeled sampling variances (see [23]).
Detailed model evaluations in terms of effectiveness and model efficiency have been conducted. For instance, Nandram et al. [20] showed how to incorporate the area-specific inequality constraints and benchmarking into the Fay–Herriot model using simulated datasets with properties resembling an Illinois corn crop. Chen et al. [21] examined the performance of the model with inequality constraints and, through a case study, illustrated the improvement in the county-level estimates in terms of accuracy and precision while preserving the required relationships. Erciulescu et al. [19] discussed the yield model and different methods of applying benchmarking constraints to a triplet (numerator, denominator, ratio) and illustrated results for 2014 for corn and soybeans in Indiana, Iowa, and Illinois. Based on these results, small area models implemented in crop county estimates for total acre and yield estimates provide accurate indirect estimates while improving the precision.
3.3. Small Area Models for Cash Rent County Estimates
The Agricultural Statistics Board began using a univariate area-level model for cash rental rates in 2013 [24]. The model was based on the average and change in the current and previous years’ cash rental rates for county i, which are orthogonal under the normality assumption. Information on the total value of agricultural production, the published county-level crop yield estimates, and the NCCPIs were incorporated into the model. Two-stage benchmarking [25] was used to ensure coherence in the estimates at the county, agricultural statistics district, state, and national levels. However, the two-stage benchmarking led to a few negative estimates. The model did not provide estimates of the total value from the cash rentals or the total land rented, both of which are important for assessing coverage, which is a published metric of quality. Furthermore, the modeling assumption of equality of variances in the two years is not always appropriate, and the survey outliers impact the estimates in two years, not just one. Thus, although the modeled estimates were reviewed by the Agricultural Statistics Board, they were not used as the foundation for publication.
In its review, the CNSTAT panel recommended that the NASS develops a bivariate, unit-level hierarchical Bayesian model to estimate the county-level cash rents that do not depend on the assumption of equal variances in two survey years [1]. Erciulescu et al. [26] partitioned the respondents into three sets: those reporting only in the previous year, those reporting only in the current year, and those reporting in both years. They then developed a unit-level bivariate, hierarchical Bayesian model that incorporated covariates of other available information that differed by state. The two-stage benchmarking was conditioned on the direct survey estimates for rented acres, which could be adjusted in the review process. Accounting for the correlations (counties and operations) from one year to the next in the resulting model led to a level of computational intensity that made it difficult to complete and review results in the available production window. Therefore, this model was not considered further for production.
In 2021, the NASS implemented county-level models for the acres rented and rental rates and derived the total dollars from the cash rents as the product of the two modeled estimates for non-irrigated cropland, irrigated cropland, and permanent pasture. The adopted two-component mixture model of the county-level cash rents has the advantage that the two years of data are together, but the two correlations are avoided by using a power prior that partly discounts past data (see [27,28]). In addition, the structure of the model can adjust the outliers among the county estimates. Chakraborty et al. [29] and Goyal et al. [30] provided a full Bayesian approach to adjusting outliers from this type of model. The basic assumption of the county-level model is that the two years are similar. A discounting factor “” (see [27,28]) associated with the previous year data was introduced in the model to adjust for differences from the current year data. The discounting factor was the same for all counties within the same region. Furthermore, it was assumed that outliers were present but less prevalent than the remaining reported data. Because the variance with outliers should be greater than that without the outliers, a mixture model was used to adjust for outliers and robustness.
Let be the index of counties with responses in year 1 (previous year) and let be the index of counties with responses in year 2 (current year). That is, there are counties sampled only in year 1, sampled on both years, and sampled only in year 2. Let be the survey indications and survey sampling variances from year 1 and be the survey indications and survey sampling variances from year 2. Let be the known auxilliary information: the corresponding previous year county-level official estimates, the number of positive responses, and NCCPIs (see Table A3, Appendix A).
The two-component mixture model was used to estimate the cash rental rates at the county level. The model for year 1 is
and, for year 2, the model is
It was assumed that (1) a proportion of the p counties had estimates that were outliers, (2) the prior was informative with discounting factor , and (3) the variance in the normal data (not outliers) was smaller than the variance with outliers. Here, it is convenient that . Note that the parameters were the same over the counties and years. The prior for was . The county estimates were benchmarked to the state and national estimates using the ratio benchmarking method at the end.
3.4. Computations
Markov chain Monte Carlo (MCMC) methods have been used to approximate the posterior marginals in the hierarchical Bayesian small area models described in this section. MCMC can be computationally intensive if the models are complicated and intractable. The computation time is one key factor when the candidate models are evaluated for production, especially for the crop county estimates project, which involves multiple commodities for all targeted counties in the U.S.
The models were fit by MCMC simulation using RJAGS [31]. Convergence diagnostics were conducted. The convergence was monitored using trace plots, the multiple potential scale reduction factors ( close to 1), and the Geweke test of stationarity for each chain (see [32,33]). More details can be found in [15,19,20,21].
4. Moving the Models into Production
Because all models presented here rely on regressions at the subarea level (state for farm labor and county for crops county estimates and cash rents county estimates), the subarea direct survey estimates were used as covariates in each model. Consequently, no changes were made in the survey process from the sample design to data collection to production of the direct survey estimates. The integration of the survey and non-survey data through the modeling process led to changes in the review processes by the NASS field office staff and the Agricultural Statistics Board. Transitioning to these models being the foundation for major survey programs including those associated with the principal federal economic indicators has required substantial changes in the final stages of the NASS processes and a major cultural shift.
In 2020, the farm labor program was the first of the small area models to move into production. The leaders of the Agricultural Statistics Board clearly communicated the decision to move to model-based estimates. A team was formed that assumed the responsibility for revising the NASS processes and the production schedule to incorporate the time needed to run the models after the direct survey estimates were produced. Staff members outside of research were trained in how to run the models. Initially, the research staff assumed responsibilities for producing the modeled estimates in production. In 2021, the modeling transitioned to production staff with the support of the research staff. Although some outliers were identified when generating the direct survey estimates, other outliers were found during modeling. The schedule had to include the time to investigate each of the outliers to ensure that they properly represented the reported data (had no errors) and to then use the integer calibration algorithm [34] to distribute the outliers’ weights within the state. For the reviews within the state field offices and by the Agricultural Statistics Board, tools are available to facilitate the review process, but were not designed for the inclusion of modeled estimates or their measures of uncertainty. These tools had to be revised to integrate the modeled estimates into the review process.
Following the 2020 growing season, small area models became the foundation for crop county estimates for the 13 nationally reported crops. Whereas the staff involved with producing the farm labor estimates after data collection were primarily housed in headquarters, the NASS staff in the 44 field offices were heavily involved with the county estimates program. Prior to implementation of the modeled estimates, they had the responsibility of reviewing the estimates, adjusting the estimates to reflect the constraints from administrative data, rounding them according to prespecified rules, and ensuring their coherence from the county to state to national levels. Similar concerns of moving from a survey-based approach that used expert opinion to incorporate information to a fully model-based approach with review to verify the adequacy of the model results were expressed. Again, the NASS leadership, especially the leaders of the Agricultural Statistics Board, provided clear direction and encouragement for the adoption of the new models. The modeled estimates were coherent, and an automated rounding process that maintained that coherence was implemented. Upon completion of the first year’s model-based publication, staff expressed an appreciation for the quality of the estimates and the reduction in staff time devoted to review, rounding, and ensuring the coherence of the estimates.
The two successes in the farm labor and the crop county estimates programs resulted in staff being more receptive to producing model-based county cash rental rates. However, strong leadership continues to be important in the implementation process. In 2021, the first year that small area models were employed to produce county estimates, the state cash rental rates were set using the traditional survey-based methods. The NASS staff responsible for the program requested modeled state estimates for 2022, a signal that they are increasingly comfortable with publishing modeled estimates. The research team had begun working on the state estimates prior to the 2021 publication; however, the work was not complete enough for them to be confident of using them in production. After the 2021 estimates were produced, the team began working to finalize the county and state estimate models that were coherent with the survey-based national estimates. These revised models were used to produce the 2022 county and state-level cash rental rates.
5. Discussion
In 2014, the NASS entered into a cooperative agreement with CNSTAT to review the NASS county estimate programs, crop county estimates, and cash rent county estimates. The consensus report [1], released in 2017, recommended, among other things, that the NASS should evolve its Agricultural Statistics Board process so that (1) county-level estimates would be based on models incorporating multiple data sources with uncertainty measures and (2) the Agricultural Statistics Board would review the predictions, macro-edit, and ensure that models are continually reviewed. Although farm labor was not included in the CNSTAT review, the panel would have also likely extended the recommendations to include that program.
An important decision in the development of modeled estimates is the unit of analysis. All models discussed here combined direct survey estimates at a specified geospatial scale (state for farm labor and county for crop county estimates and cash rent county estimates) with non-survey information at that same scale. This requires that survey samples are designed to produce estimates at that geospatial scale. For most of its programs, the NASS currently designs samples to provide estimates with a specified level of precision at the state level. When developing in-season predictions of yield, the variability within a state can be substantial, and modeling at the state level is not always able to provide predictions of the desired quality. Perhaps samples that provide valid estimates at a lower geospatial scale should be considered; this would require major revisions in the current sample designs. Alternatively, if the survey and non-survey data are linked at the farm level, then modeling could be conducted at that level.
The NASS list frame, which is a list of all known U.S. farms, is not georeferenced; all relevant non-survey data are georeferenced. Linking the survey and non-survey data has been challenging. The FSA-578 form is the primary source of non-survey, administrative data. The NASS and FSA have different definitions of a farm, so linking the data from the two is complicated, especially for large producers who are responsible for a large portion of the total agricultural production. Survey data are collected at the farm level. Because most, even small, farms have multiple agricultural fields, it is generally not possible to associate survey responses with fields. For example, suppose a producer has four sections (1 section = 1 square mile = 640 acres) of cropland. If they report that three sections are planted with corn and the others with soybeans, it is still unknown which of the fields have corn and which have soybeans. To ask the producer to report the crop planted to each field is too burdensome. If the survey asks the producer to respond for only one field, massive amounts of information will be lost from not collecting information from the other fields they cultivate. Determining how best to integrate the survey and non-survey data at the field or farm level is an area of current research.
The NASS has transitioned to model-based estimates as the CNSTAT panel has recommended for the crop county estimates, the cash rent county estimates, and farm labor estimates. All models combine data at a specified level of geography above the farm level (state or county), and this subarea level becomes the unit of analysis. These models cannot capture the variability within the subareas. However, with this approach, the survey process is not impacted. Once the direct estimates are produced at the desired level of analysis, the non-survey data aggregated to the same subarea level can inform the estimates through regressions.
The NASS conducts more than a hundred national surveys and produces more than 400 reports each year. An annual publication calendar details the day and time each report is to be released, and the NASS has consistently released its reports according to schedule more than 99% of the time. With tight production timelines and a staff level that has decreased from over 1200 in 2010 to less than 850 today, any major change in methodology requires not only a careful evaluation of the proposed methodology, but also revisions in the production processes that bring additional risk to the quality of the report and the ability to release it on time. This naturally leads to a hesitancy among many staff to adopt revisions that would lead to substantial changes in production, which presents cultural issues in addition to technological ones. Strong, supportive leadership is a key to overcoming these cultural barriers, especially when initially moving to new processes.
The value of the modeled estimates has become increasingly evident. For farm labor, the automated approach to addressing outliers has improved the quality and reduced the staff time required to produce the estimates. In the case of the crop county estimates, the modeled estimates reflect the expert opinion that was used to adjust the survey estimates, and the automation of modeling, rounding, and enforcing coherence across geospatial scales has led to substantial savings in staff time. For cash rents, an innovative approach to addressing outliers has improved the quality and reduced the staff time required to produce the estimates. Based on these successes, the NASS is exploring other opportunities to use models to integrate survey and non-survey data.
Author Contributions
Conceptualization, L.J.Y.; Methodology, L.C.; Writing—Original Draft Preparation, L.J.Y.; Writing—Review and Editing, L.J.Y. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Agricultural Statistics Service.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The findings and conclusions in this paper are those of the authors and should not be construed to represent any official USDA or U.S. Government determination or policy. This research was supported by the U.S. Department of Agriculture, National Agricultural Statistics Service.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. List of the Covariates

Table A1.
The covariate definitions for the farm labor models.
Table A1.
The covariate definitions for the farm labor models.
| Model | Name | Description |
|---|---|---|
| LNN model | Log (previous year official estimated number of workers) | Log state-level official estimates of number of workers by types |
| Type | The categorical data of the work types | |
| State | The categorical data of state | |
| Usable number of reports | The survey usable reports in each domain | |
| NN model | Previous year official estimated average wage rates or average hours per week | State-level official estimates of average wage rates or average hours per week by worker types |
| Type | the categorical data of the work types | |
| State | The categorical data of state | |
| Usable number of reports | The survey usable reports in each domain |

Table A2.
The covariate definitions for the crop county estimate models.
Table A2.
The covariate definitions for the crop county estimate models.
| Model | Name | Description |
|---|---|---|
| Total acreage model | Max (FSA, RMA) | The maximum value between county-level FSA planted acres and RMA planted acres for the corresponding crop commodity |
| Max (FSA failed acres, RMA failed acres) | The maximum value between county-level FSA failed acres and RMA failed acres for the corresponding crop commodity | |
| Yield model | NCCPI | The county-level National Commodity Crop Productivity Index (NCCPI) |

Table A3.
The covariate definitions for the cash rental rate models.
Table A3.
The covariate definitions for the cash rental rate models.
| Model | Name | Description |
|---|---|---|
| Cash Rental Rate Model | Previous year’s survey estimates and sampling variances | County-level survey’s direct estimates and sampling variances from previous year by land types |
| Previous year’s official estimated | County-level previous year’s official estimates by land types | |
| NCCPI | The county-level National Commodity Crop Productivity Index (NCCPI) | |
| Usable number of reports | The county-level survey usable reports in each domain |
References
- National Academies of Sciences, Engineering, and Medicine. In Improving Crop Estimates by Integrating Multiple Data Sources; The National Academies Press: Washington, DC, USA, 2017. [CrossRef]
- Pfeffermann, D. New Important Developments in Small Area Estimation. Stat. Sci. 2013, 28, 40–68. [Google Scholar] [CrossRef]
- Rao, J.N.K.; Molina, I. Small Area Estimation; John Wiley & Sons, Inc.: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Fay, R.E.; Herriot, R.A. Estimates of income for small places: An application of James-Stein procedures to census data. JASA 1979, 74, 269–277. [Google Scholar] [CrossRef]
- Battese, G.E.; Harter, R.M.; Fuller, W.A. An error-components model for prediction of county crop areas using survey and satellite data. JASA 1988, 83, 28–36. [Google Scholar]
- Torabi, M.; Rao, J.N.K. On small area estimation under a subarea level model. J. Multivar. Anal. 2014, 127, 36–55. [Google Scholar] [CrossRef]
- Fuller, W.A.; Goyeneche, J.J. Estimation of The State Variance Component. 1998; unpublished manuscript. [Google Scholar]
- Erciulescu, A.L.; Cruze, N.B.; Nandram, B. Model-based county-level crop estimates incorporating auxiliary sources of information. J. R. Stat. Soc. Ser. A 2019, 182, 283–303. [Google Scholar] [CrossRef]
- USDA National Agricultural Statistics Service. Farm Labor; Farm Labor 25 May 2022. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/x920fw89s/mp48tj815/0c484p887/fmla0522.pdf (accessed on 2 September 2022).
- USDA National Agricultural Statistics Service. Crop Production Historical Track Records. 2019. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/c534fn92g/x059ch00p/f4752r51h/croptr19.pdf (accessed on 2 September 2022).
- Iwig, W.C. The National Agricultural Statistics Service County Estimates Program. In Indirect Estimators in U.S. Federal Programs; Schaible, W., Ed.; Springer: New York, NY, USA, 1996; (accessed on 2 September 2022). [Google Scholar] [CrossRef]
- Kott, P.S.; Bailey, J.T. The theory and practice of Maximal Brewer Selection with Poisson PRN sampling. In Proceedings of the 2000 International Conference on Establishment Surveys in Buffalo, New York, NY, USA, 17–21 June 2000; Available online: https://ww2.amstat.org/meetings/ices/2000/proceedings/S04.pdf (accessed on 2 September 2022).
- Kott, P.S. Assessing linearization variance estimators. In Proceedings of the American Statistical Association, Survey Research Methods Section; American Statistical Association: Alexandria, VA, USA, 1989; Available online: https://www.asasrms.org/Proceedings/papers/1989_030.pdf (accessed on 2 September 2022).
- USDA NASS. 2021—Rent, Cash, Cropland, Non-Irrigated—Expense—Measured in $/Acre. Available online: https://www.nass.usda.gov/Data_Visualization/Commodity/index.php (accessed on 2 September 2022).
- Chen, L.; Cruze, N.B.; Young, L.J. Model-Based Estimates for Farm Labor Quantities. Stats 2022, 5, 738–754. [Google Scholar] [CrossRef]
- Gelman, A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Browne, W.J.; Draper, D. A comparison of Bayesian and likelihood-based methods for fitting multilevel models. Bayesian Anal. 2016, 1, 473–514. [Google Scholar] [CrossRef]
- Nandram, B.; Sayit, H. A Bayesian analysis of small area probabilities under a constraint. Surv. Methodol. 2011, 37, 137–152. [Google Scholar]
- Erciulescu, A.L.; Cruze, N.B.; Nandram, B. Benchmarking A Triplet of Official Estimates. Environ. Ecol. Stat. 2018, 25, 523–547. [Google Scholar] [CrossRef]
- Nandram, B.; Cruze, N.B.; Erciulescu, A.L.; Chen, L. Bayesian Small Area Models under Inequality Constraints with Benchmarking and Double Shrinkage; Research Report RDD-22-02; National Agricultural Statistics Service, USDA: Washington, DC, USA, 2022. Available online: https://www.nass.usda.gov/Education_and_Outreach/Reports,_Presentations_and_Conferences/reports/ResearchReport_constraintmodel.pdf (accessed on 2 September 2022).
- Chen, L.; Nandram, B.; Cruze, N.B. Hierarchical Bayesian Model with Inequality Constraints for US County Estimates. J. Off. Stat. 2022, accepted. [Google Scholar]
- Erciulescu, A.L.; Cruze, N.B.; Nandram, B. Statistical challenges in combining survey and auxiliary data to produce official statistics. J. Off. Stat. 2020, 36, 63–88. [Google Scholar] [CrossRef]
- Bejleri, V.; Cruze, N.; Erciulescu, A.L.; Benecha, H.; Nandram, B. Mitigating Standard Errors of County-Level Survey Estimates When Data are Sparse. In JSM Proceedings, Survey Research Methods Section; American Statistical Association: Vancouver, CA, USA, 2018. [Google Scholar]
- Berg, E.; Cecere, W.; Ghosh, M. Small area estimation for county-level farmland cash rental rates. J. Surv. Stat. Methodol. 2014, 2, 1–37. [Google Scholar] [CrossRef]
- Ghosh, M.; Steorts, R.C. Two-stage benchmarking as applied to small area estimation. Test 2013, 22, 670–687. [Google Scholar] [CrossRef]
- Erciulescu, E.; Berg, E.; Cecere, W.; Ghosh, M. Bivariate hierarchical Bayesian model for estimating cropland cash rental rates at the county level. Surv. Methodol. 2019, 45, 199–216. [Google Scholar]
- Ibrahim, J.G.; Chen, M.-H.; Gwon, Y.; Chen, F. The Power Prior: Theory and Applications. Stat. Med. 2015, 34, 3724–3749. [Google Scholar] [CrossRef]
- Ibrahim, J.G.; Chen, M.-H. Power prior distributions for regression models. Stat. Sci. 2000, 15, 46–60. Available online: https://www.jstor.org/stable/2676676 (accessed on 19 July 2022).
- Chakraborty, A.; Datta, G.S.; Mandal, A. Robust hierarchical bayes small area estimation for the nested error linear regression model. Int. Stat. Rev. 2019, 87, S158–S176. [Google Scholar] [CrossRef]
- Goyal, S.; Datta, G.S.; Mandal, A. A hierarchical Bayes unit-level small area estimation model for normal mixture populations. Sankhya B 2021, 83, 215–241. [Google Scholar] [CrossRef]
- Plummer, M. JAGS: A Program for Analysis of Bayesian Graphical Models Using Gibbs Sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), Vienna, Austria, 20–22 March 2003; Available online: https://www.r-project.org/conferences/DSC-2003/Proceedings/Plummer.pdf (accessed on 19 July 2022).
- Geweke, J. Evaluating the Accuracy of Sampling-Based Approaches to the Calculation of Posterior Moments. Bayesian Stat. 1992, 4, 169–193. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Sartore, L.; Toppin, K.; Spiegelman, C. Introducing a New Integer Calibration Procedure. USDA NASS Research Report RDD-a6-STS. 2016. Washington DC. Available online: https://www.nass.usda.gov/Education_and_Outreach/Reports,_Presentations_and_Conferences/reports/New_Integer_Calibration_%20Procedure_2016.pdf (accessed on 6 September 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).