Evaluation of the Gauss Integral

Abstract

The normal or Gaussian distribution plays a prominent role in almost all fields of science. However, it is well known that the Gauss (or Euler–Poisson) integral over a finite boundary, as is necessary, for instance, for the error function or the cumulative distribution of the normal distribution, cannot be expressed by analytic functions. This is proven by the Risch algorithm. Regardless, there are proposals for approximate solutions. In this paper, we give a new solution in terms of normal distributions by applying a geometric procedure iteratively to the problem.

1. Introduction

The normal or Gaussian distribution plays a prominent role in almost all fields of science, as the sum of random variables tends to the normal distribution if the quite general conditions of the central limit theorem [1] are satisfied. Besides the unbounded normal integral, the bounded integral or error function is crucial for the determination of probabilities. However, there is no analytic expression found for this function, a fact that can be tested by using the Risch algorithm [2,3]. Powerful modern computer facilities but also simple personal computers allow for a numerical calculation of the error function with any needed precision. However, if a multitude of such calculations has to be performed in a limited time, for instance, in Monte Carlo simulations, the processing time becomes essential. In order to speed up these calculations, simple and more educated approximations have been proposed in the literature. The spectrum of approximations contains, for instance, the Gaussian exponential function, including either numerical constants [4] or powers and square roots [5], approximations using ordinary and hyperbolic tangent functions [6], a rational function of an exponential function with the exponent given by a power series [7], or an approximation by Jacobi theta functions [8]. Without knowing the error function explicitly, expectation values can be calculated by an approximation of the normal distribution by a series in ordinary exponential functions [9].

The present paper contains a continuation of this topic. Employing a geometric approach, we provide an approximation of the squared error function by a finite sum of N Gaussian exponential functions with different widths, where the values of which are constrained to fixed intervals. We show that, by fine-tuning these width parameters, one can optimise the precision, which, even for the leading order $N=1$, is better than the error estimates given by the constraints in Ref. [5]. In addition, by choosing N as appropriately large, one can afford an arbitrary precision. On the other hand, even on a personal computer, the calculation with our leading order approximation is obtained 34 times faster than an exact numerical calculation, the processing time for higher orders being multiplied by N.

Our paper is organised as follows. In Section 2, we introduce the basic concepts for the calculation of the Gaussian integral that are necessary for the understanding of our geometric approach. The precisions of the leading order approximation obtained here and simple, straightforward extensions of this approximation are discussed in Section 3. In Section 4, we explain the geometric background for our approximation and provide a systematic way to create higher order approximations. The iterative construction of higher order approximations is explained in general in Section 5 in terms of partitions before we turn to the partition into $N=2^p$ intervals for increasing values of p. In Section 6, we explain a similar ternary construction. In Section 7, we provide our conclusions and an outlook on possible extensions. The convergence of our iterative procedure is discussed in more detail in Appendix A. In addition, we discuss the continuum limit, which, of course, cannot be part of the algorithm but allows, as a bonus, for a different representation of the error function.

2. Basic Concepts

The error function is based on the standard normal density distribution

$$\rho \left(x\right)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2}$$

(1)

which does not have a direct practical meaning, while it is desirable to evaluate the integral of this function over a bounded interval $[-t,t]$, leading to the probability $P\left(t\right)$ to find the result within this interval,

$$P\left(t\right)={\int }_{-t}^t\rho \left(x\right)dx={\int }_{-t}^t\rho \left(y\right)dy.$$

(2)

From Equations (1) and (2), the square of probability is given by

$$P^2\left(t\right)=\frac{1}{2\pi }{\int }_{-t}^t\rho \left(x\right)dx{\int }_{-t}^t\rho \left(y\right)dy=\frac{1}{2\pi }{\int }_{-t}^t{\int }_{-t}^t{e}^{-(x^2+y^2)/2}dxdy,$$

(3)

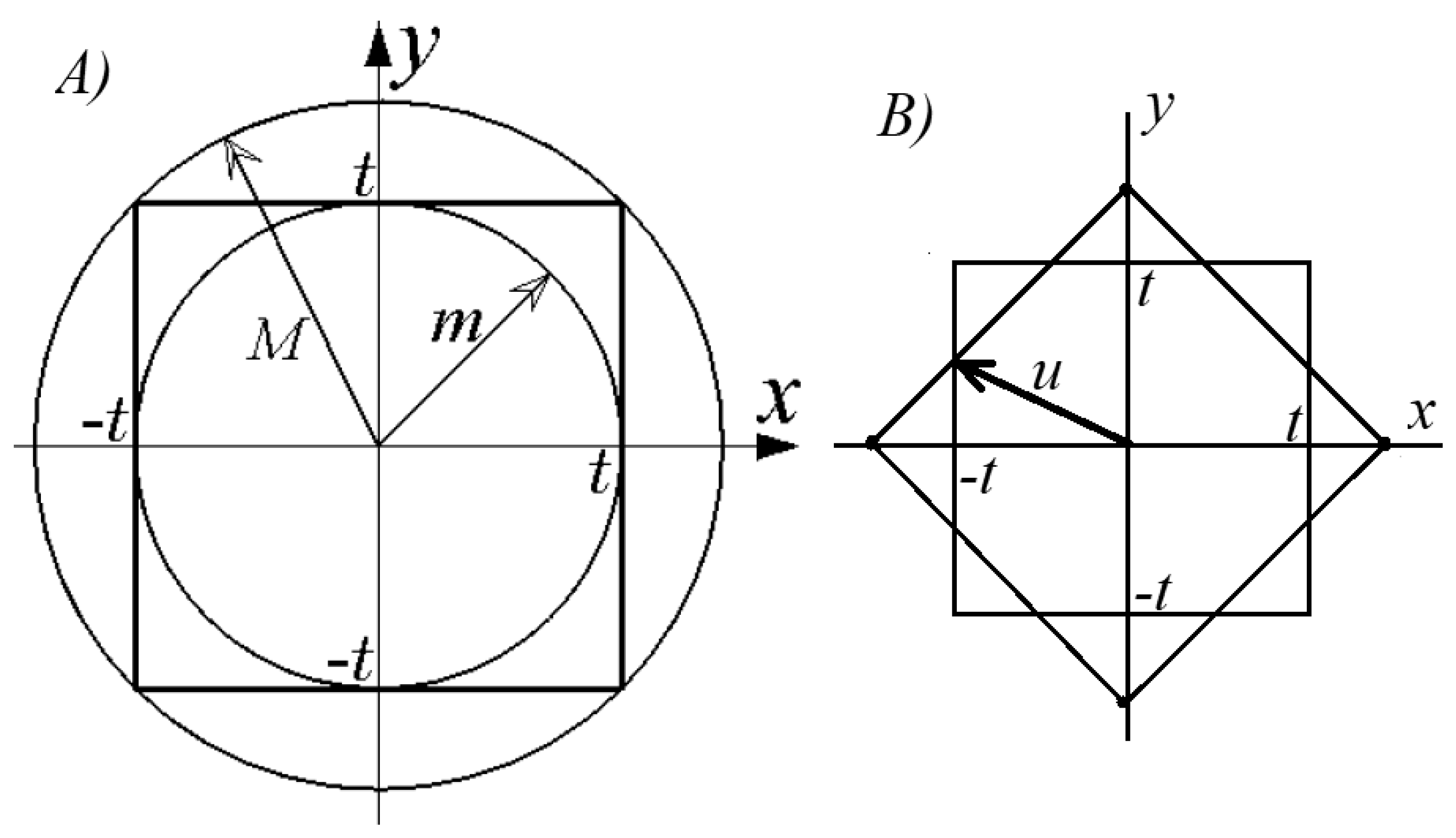
where the integration area is a square in Figure 1A. Introducing polar coordinates $x=rcos\phi$ and $y=rsin\phi$, one obtains

$$P^2=\frac{1}{2\pi }\int \int e^{-r^2/2}rdrd\phi .$$

(4)

The integral in Equation (4) is analytically calculable if the integration is performed over the interior of some circle with radius R. Indeed,

$$I^2\left(R\right)=\frac{1}{2\pi }{\int }_0^{2\pi }d\phi {\int }_0^R{e}^{-r^2/2}rdr=1-e^{-R^2/2}.$$

(5)

Here, the function $I\left(R\right)$ increases monotonically with R as the integral in Equation (4) is taken over a positive function. This is why $I(R=m)<P<I(R=M)$, with $m=t$ and $M=t\sqrt{2}$; see Figure 1A. Therefore,

$$P\left(t\right)=\sqrt{1-e^{-k^2\left(t\right)t^2/2}},$$

(6)

where $1<k\left(t\right)<\sqrt{2}$. Using a PC for analyzing the set of Equations (1), (2), and (6), one concludes that $k\left(t\right)$ is even more constrained by $1<k\left(t\right)<\sqrt{4/\pi }$. Hence,

$$P_m\left(t\right)<P\left(t\right)<P_M\left(t\right),$$

(7)

and $P_M\left(t\right)-P_m\left(t\right)$ has a maximum of $0.0592$ at $t=t_0=1.0668$. The Inequality (7) proves to be incomparably elegant, easy to remember, and much more accurate than the best result of Ref. [5], which, if transformed into the present formalism, will be

$$P_m\left(t\right)=1-4\sqrt{\frac{2}{\pi }}\frac{\exp (-t^2/2)}{3t+\sqrt{t^2+8}},$$

(8)

$$P_M\left(t\right)=1-\frac{1}{\sqrt{2\pi }}(\sqrt{t^2+4}-t)\exp (-t^2/2).$$

(9)

The largest range $P_M\left(t\right)-P_m\left(t\right)\approx 0.330$ for these constraints occurs for $t=0$. Compared to this, even at the leading order observed so far, our value for $P_M\left(t\right)-P_m\left(t\right)<0.0592\ll 0.330$ is more restrictive. In more detail, if, in Equation (6), we choose $k=\sqrt{4/\pi }$, the error will be below $0.006$, but if we take $k=1.116$, the maximal error is only $0.0033$. Even modern reviews on this subject do not have better results [10].

3. Simple Extensions

By adding additional terms to the leading order approximation, one can increase the precision further. For the normal integral

$$P\left(t\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-t}^t{e}^{-x^2/2}dx$$

(10)

and the leading order approximation, for $k_1=1.116$, one has

$$|P\left(t\right)-\sqrt{1-e^{-k_1^2{t}^2/2}}|<0.0033.$$

(11)

However, the precision increases by a factor of $14\approx 0.0033/0.00024$ by using

$$|P\left(t\right)-\sqrt{1-\frac{1}{2}(e^{-k_1^2{t}^2/2}+e^{-k_2^2{t}^2/2})}|<0.00024,$$

(12)

where $k_1=1.01$, $k_2=1.23345$. The next order of precision has

$$|P\left(t\right)-\sqrt{1-\frac{1}{3}(e^{-k_1^2{t}^2/2}+e^{-k_2^2{t}^2/2}+e^{-k_3^2{t}^2/2})}|<0.00003,$$

(13)

where $k_1=1.02335$, $k_2=1.05674$, and $k_3=1.28633$. Therefore, this formula with three exponentials is at least 8 times more precise than the one with two exponentials, and it is at least 110 times more precise than Equation (11) with one exponential only. Finally, it is $11,000\approx 0.33/0.00003$ times more precise than the approximation in Ref. [5]. As it turns out, the values for the parameters $k_i$ for i running from 1 to N take values between 1 and $\sqrt{2}$, while the sum of the exponential factors is divided by N. Still, there is a degree of arbitrariness in the determination of these parameters. In order to remove this arbitrariness, in the following, we develop an iterative method based on geometry.

4. Geometric Background of Our Procedure

In order to understand our method, we refer to Figure 1B for the first step. Starting with the square with side length $2t$ representing the square $P^2\left(t\right)$ of the probability, we turn this square by an angle of $\pi /4$ to obtain $P^2\left(t\right)$ again. In union and intersection, these two overlayed squares construct two eight-angle figures. In order to obtain the area of the larger figure, one has to subtract the area of the smaller figure from the twofold square area, as this smaller figure is covered twice by the two squares. Accordingly, for the integrals over the probability density, one obtains the relation

$$\mathsf{\Omega }\left(t\right)=2P^2\left(t\right)-\omega \left(t\right)$$

(14)

between the probabilities. Now,

$$\omega \left(t\right)=1-e^{-k_1^2{t}^2/2},\mathsf{\Omega }\left(t\right)=1-e^{-k_2^2{t}^2/2},$$

(15)

where

$$1<k_1<1/cos\theta ,1/cos\theta <k_2<\sqrt{2},$$

(16)

and the angle $\theta =\pi /8$ is enclosed between the x axis and the vector u shown in Figure 1B. We study $\Delta (k_1,k_2,t)=P(k_1,k_2,t)-P\left(t\right)$ with

$$P(k_1,k_2,t)=\sqrt{1-\frac{1}{2}\left(e^{-k_1^2{t}^2/2}+e^{-k_2^2{t}^2/2}\right)}.$$

(17)

Drawing three-dimensional graphics and looking for a minimum of $|\Delta (k_1,k_2,t\left)\right|$, one obtains

$$|\Delta (k_1,k_2,t\left)\right|<0.00024,$$

(18)

where $k_1=1.01$ and $k_2=1.23345$. This is the starting point.

5. Basic Construction of the Procedure

In order to construct the iteration, one performs a partition of the figure describing $\omega \left(t\right)$, $\mathsf{\Omega }\left(t\right)$, or both of these, by repeating the geometric construction shown before. For instance, taking only the larger eight-angle figure describing $\mathsf{\Omega }\left(t\right)$, one can turn this figure by an angle $\theta =\pi /16$ and overlay the new figure with the old one. In doing so, one can separate a new larger and smaller 16-angle figure in the same way as was carried out before for the 8-angle figures. Accordingly, by geometric means, one obtains new constraints. In order to describe the procedure in a unique way, in each iterative step, we rename $k_n$ by $k_{2n}$, and, if this new $k_{2n}$ is subject to a partition, the smaller and larger figure of this partition are related to the values $k_{2n-1}$ and $k_{2n}$, respectively.

Using the case in the previous section as an illustrative example for the procedure, we might keep the smaller eight-angle figure related to $\omega \left(t\right)$ but apply a partition to the larger eight-angle figure related to $\mathsf{\Omega }\left(t\right)$. Accordingly, $k_1$ is replaced by $k_2$ and $k_2$ is replaced by $k_4$, but this new $k_4$ is again split up into $k_3$ and $k_4$. The constraint for the lowest parameter $k_2$ (the former $k_1$) remains the same,

$$1\le k_2\le 1/cos(\pi /8)$$

(19)

whereas, for the two new higher parameters, we obtain

$$1/cos(2\pi /16)\le k_3\le 1/cos(3\pi /16)$$

(20)

and

$$1/cos(3\pi /16)\le k_4\le 1/cos(4\pi /16)=\sqrt{2}.$$

(21)

The intervals are consecutive, but $\pi /8$ is replaced by $2\pi /16$ in order to indicate the new partition. Finally, the upper limit stays at $1/cos(4\pi /16)=1/cos(\pi /4)=\sqrt{2}$. For these values $k_2$, $k_3$, and $k_4$, one obtains the approximation

$$P\left(t\right)\approx P(k_2,k_3,k_4,t)$$

(22)

with

$$P(k_2,k_3,k_4,t)=\sqrt{1-\frac{1}{2}{e}^{-k_2^2{t}^2/2}-\frac{1}{4}{e}^{-k_3^2{t}^2/2}-\frac{1}{4}{e}^{-k_4^2{t}^2/2}}$$

(23)

because of the geometric transformations of Figure 1 and the corresponding double use of Equation (14). Note that the set of parameters $k_2$, $k_3$, $k_4$ is different from the set $k_1$, $k_2$, and $k_3$ in Equation (13). Indeed, if, for Equation (23), one uses $k_2=1.025187$, $k_3=1.1249$, and $k_4=1.31336$, the precision improves to $0.000015$. Still, it is obvious that this example is only half of an iteration step, and one could definitely achieve a greater result by also performing the partition for the smaller eight-angle figure, leading to four parameters separated uniformly,

$$1\le k_1\le \frac{1}{cos(\pi /16)}\le k_2\le \frac{1}{cos(\pi /8)}\le k_3\le \frac{1}{cos(3\pi /16)}\le k_4\le \sqrt{2}.$$

(24)

Therefore, a full iteration step is increasing the number of parameters $k_n$ by a factor of two, and, after p full iteration steps, one has $N=2^p$ parameters. Each iteration step is finalized by optimizing the N (or less) parameters $k_n$. For any finite (or even very large) N, the constraints

$$k_n^{\min }\left(N\right)\le k_n\le k_n^{\max }\left(N\right)$$

(25)

with $k_n^{\min }\left(N\right)=k_{n-1}^{\max }\left(N\right)$ can be calculated from geometry observations in a similar fashion. In practice, for a small set of parameters, we use a graphical method. For instance, the method applied to obtain the three values $k_2$, $k_3$, and $k_4$ in Equation (23) was to look for the solution of the system of three equations

$$Q(t=1)=0,Q(t=\sqrt{2})=0,Q(t=2)=0,$$

(26)

where

$$Q\left(t\right)=P^2(k_2,k_3,k_4,t)-P^2\left(t\right).$$

(27)

The values $t=1$, $\sqrt{2}$, and 2 are used as nodes for this approximation. Their choice depends on the application of the approximation and has to be adjusted to the number of width parameters to be determined. Each equation in (26) can be treated individually. Therefore, the solution is very easy to find. From $Q(t=1)=0$, one extracts the function $k_2=k_2(k_3,k_4)$. Inserting these solutions into $Q(t=\sqrt{2})=0$, one extracts the two positive functions $k_3=k_3\left(k_4\right)$ and $k_3={\tilde{k}}_3\left(k_4\right)$. Inserting these solutions into $Q(t=2)=0$ and plotting the function $Q(t=2,k_4)$, one finds the position of the zero, which proves to be $k_4=1.31336$. Using this knowledge, one obtains $k_3=k_3\left(k_4\right)$ and $k_2=k_2(k_3,k_4)$ as well. However, as $k_3={\tilde{k}}_3\left(k_4\right)$ is given for $k_4<1$ only, this is not a valid solution, as $k_n\ge 1$ for all n. Note that the graphical method cannot be applied any more for $N\ge 4$. Instead, we used a random number generator to create values for the parameters $k_n$ in the respective intervals in Equation (24). Proceeding in this way, for $N=4$ ($p=2$), we obtain the values $k_1=1.00725$, $k_2=1.04665$, $k_3=1.12192$, and $k_4=1.3129$, and a precision of $0.00001$, which is, again, the lowest precision for a given N. As becomes obvious, the lowest precisions are obtained for uniform partitions. This is not only the case for N being a power of 2 but also for N being a power of 3, as discussed in the next section.

6. A Similar Ternary Procedure

As the approximation (13) gained high precision, we tried and succeeded in finding a geometric interpretation for this, as is shown in Figure 2. In this ternary approach, the initial step is to rotate the square not by an angle of $\pi /4$ as in the previous approach but by an angle of $\pi /6$. The overlapping squares in Figure 2 can be split up into three 12-angle figures that, at the same time, determine the constraints for the parameters $k_i$,

$$1\le k_1\le 1/cos(\pi /12)\le k_2\le 1/cos(\pi /6)\le k_3\le 1/cos(\pi /4).$$

(28)

Note that the values $k_1=1.02335$, $k_2=1.05674$ and $k_3=1.28633$ chosen in Equation (13) fit into these intervals. This procedure can be continued iteratively in a ternary way, i.e., turning the 12-angle figures by an angle of $\pi /18$, and generally by the angle $\alpha =\pi /(2·3^p)$. In the next section, we deal with the convergence of this and the previous procedure for increasing values of p.

7. Conclusions and Outlook

In this paper, we have given an approximation for the Gauss integral with a finite boundary in terms of the square root of a normalized sum of normal distributions plus one, each of those distributions depending on the (symmetric) boundary $[-t,t]$ of the integral and a set of maximally N parameters $k_n$. By simple geometrical means, it is shown that these parameters are constrained to intervals given by the inverse cosine with equally distributed angles. We performed this approximation procedure in both a binary ($N=2^p$) and a ternary way ($N=3^p$) and showed that the procedure converges for an increasing degree p. The continuum limit leads to a further approximation.