Has the Market Started to Collapse or Will It Resist?

Abstract

Many people are concerned about the stock market in 2022 as it faces several threats, from rising inflation rates to geopolitical events. The S&P 500 Index has already dropped about 10% from the peak in early January 2022 until the end of February 2022. This paper aims at updating the crisis indicator to predict when the market may experience a significant drawdown, which we developed in Crisis Risk Prediction with Concavity from Polymodel (2022). This indicator uses regime switching and Polymodel theory to calculate the market concavity. We found that concavity had not increased in the past 6 months. We conclude that at present, the market does not bear inherent dynamic instability. This does not exclude a possible collapse which would be due to external events unrelated to financial markets.

1. Introduction

Many financial analysts hold the idea that the market may collapse in the next few months [1,2].

Firstly, the expected rising interest rates puts a downside pressure on the stock market. Federal Reserve (Fed) officials are coalescing around a plan to raise interest rates steadily starting in March. Stock valuation is based on discounted future revenue, and the higher interest rates reduce the current value. Moreover, rising interest rates may lead people to rebalance investments from the stock market into the bond market. The fear of surging interest rates may lead the stock market to collapse before the policy is executed [3].

Secondly, the Fed announced they would smoothly shrink the central bank’s bond holdings, which would decrease the money supply, with the hope to cool down inflation.

In addition, following quantitative easing in 2020 and 2021, the price-to-earnings ratios (P/E ratios) of many companies soared to higher levels than their historical average, incurring a downward pressure on prices [1].

Last but not the least, the current Russia–Ukraine crisis increases uncertainty. So far, the reaction of the S&P 500 Index has been moderate. During the week of 18–25 February 2022, the index lost 5% and made it back.

Such volatility happened several times during the COVID-19 pandemic crisis, and is not necessarily a sign that the market is prone to a major collapse.

Following the methodology developed in Kuang and Douady [4], using market data till January 2022 (updated till the end of March 2022), we updated the crisis indicator, which is a statistical test to predict market drawdowns larger than 18%. Our finding is that a major drawdown of the market is unlikely given current economic conditions in the near future. Of course, this prediction would not hold in case of a sudden deterioration of the geopolitical situation.

2. Methodology

We follow the methodology in Kuang and Douady [4], which we briefly describe here.

2.1. Identification of a Crisis

We define a financial crisis as a large drawdown from peak to trough. A drawdown of a financial asset refers to the decline of that asset from its past peak price, and is quoted as a percentage. In this paper, we assume that a crisis happens when the drawdown reaches 18%. The start time and end time of a crisis are the previous peak price date and the bottom price date.

While the usual crisis threshold is a 20% market decline [5], we chose 18% to include famous drawdowns such as the 1998 and 2018 crises listed in

Table 1. Crises List.

Price Peak Date	Price Bottom Date	MDD
17 July 1998	31 August 1998	19.34%
24 March 2000	9 October 2002	49.15%
9 October 2007	9 March 2009	56.78%
20 September 2018	24 December 2018	19.78%
19 February 2020	23 March 2020	33.92%

.

2.2. Concavity Increases as Crisis Risk Arises

We built a model assuming that the distribution of returns in the market is a normal mixture. There are several assumptions in the model.

We made several assumptions in our toy model. Suppose there are two regimes $R_1$ and $R_2$. $R_1$ is the state of a normal market and $R_2$ corresponds to the market during a crisis. X and Y are the returns of two financial assets. Based on the arguments of Longin and Solnik [6], Ang and Chen [7], and other researchers, the correlation of market returns increases during financial crises.

• $R_1$ is the market state of a normal market. Under $R_1$, $X\sim \mathcal{N}(0,{\sigma }_X^2)$, $Y\sim \mathcal{N}(0,{\sigma }_Y^2)$. $Corr(X,Y)=\rho$.
• $R_2$ is the market state of a crisis. Under $R_2$, $X\sim \mathcal{N}(0,{\sigma }_X^{{}^{\prime }2})$, $Y\sim \mathcal{N}(0,{\sigma }_Y^{{}^{\prime }2})$. $Corr(X,Y)={\rho }^{\prime }$.
• Since the volatility of returns and the correlation between returns usually rise during crises, we assume that ${\sigma }_X^{\prime }>{\sigma }_X$, ${\sigma }_Y^{\prime }>{\sigma }_Y$, and ${\rho }^{\prime }>\rho$. We further assume that the “beta” between the two stocks increases as well, i.e., $\frac{{\sigma }_Y^{\prime }}{{\sigma }_X^{\prime }}{\rho }^{\prime }>\frac{{\sigma }_Y}{{\sigma }_X}\rho$.
• The true probabilities of the market being in each state are $P\left(R_1\right)=p_1$ and $P\left(R_2\right)=p_2$. These probabilities may change over time. If the market is not in a crisis, $p_1>p_2$.

In Kuang and Douady [4], we derived the relationship between Y and X analytically and approximated it into a polynomial equation with the Chebyshev approximation. Next, we integrated the negative part of the second derivative of the polynomial to measure the concavity between Y and X. We found out that the concavity between Y and X increased before a crisis as $p_2$ rose.

2.3. Polymodel

To measure the crisis risk of the U.S. market, we calculate the concavity between the S&P 500 Index and other indices. We use the nonlinear Polymodel methodology as explained in Kuang and Douady [4]. The S&P 500 Index Y is separately represented with respect to several other indices $X_1$, …, $X_n$.

$$\left\{\begin{array}{c}\hfill Y=f_1\left(X_1\right)+{ϵ}_1\\ \hfill Y=f_2\left(X_2\right)+{ϵ}_2\\ \hfill ⋮\\ \hfill Y=f_n\left(X_n\right)+{ϵ}_n\end{array}\right.$$

(1)

For each $X_i$, we compute the concavity between Y and $X_i$, we then weigh the information by attributing a relevance score to each $X_i$ and summarize the information across all the $X_i$’s with a weighted average. $f_i\left(X_i\right)$ is a nonlinear function of $X_i$. It is a general linear combination of nonlinear base functions:

$$f_i\left(X_i\right)=\sum _{k=0}^K{\beta }_{ik}{U}_k\left(X_i\right)$$

(2)

In our experiments, functions $U_k\left(X_i\right)$ are Chebyshev polynomials of $X_i$, of degree k [8]. They are orthogonal with respect to weighting function $\sqrt{1-x^2}$ on $[-1,1]$. To apply the second kind of Chebyshev polynomials, we normalize $X_i$ to $X_i^{*}$. Suppose the sample mean of $X_i$ is $m_i$, and sample standard deviation is $st{d}_i$, let $X_i^{*}=\frac{X_i-m_i}{{std}_i}$.

We compute the regression coefficients ${\beta }_{ik}$ for each $f_i\left(X_i\right)=E\left[Y\right|X_i]$, stabilized by ridge regression in model fitting. The objective function of a ridge regression is:

$$arg\underset{\beta }{min}\sum _{j=1}^m{(y_j-Z_j^T\beta )}^2+\lambda {\beta }^{T}W\beta$$

(3)

$\beta =\left({\beta }_0,{\beta }_1,\dots ,{\beta }_K\right),Z_j=\left(U_0\left(x_{ij}\right),U_1\left(x_{ij}\right),\dots ,U_K\left(x_{ij}\right)\right)$. m is the number of training data points. W is the penalty weight matrix in order to put more constraints on coefficients of higher degrees, and set $W=diag\left([0,1,4,...,K^2]\right)$.

We derive the formula of ${\widehat{\beta }}_{ridge,\lambda }$:

$${\widehat{\beta }}_{ridge,\lambda }={(Z^{T}Z+\lambda W)}^{-1}{Z}^{T}y$$

(4)

$\lambda$ controls the amount of regularization. To make the Polymodel stable, we simply set $\lambda =0.1$ in our experiments. After fitting parameters in Polymodel, we evaluate the relevance of each factor $X_i$ by a factor score. We apply a nontypical p-value to measure the fitting of regression that is robust to all kinds of sample distributions of X and Y. In practice, we shuffle samples of Y in order to keep its distribution but destroy its potential relationship with X. At the kth shuffling, we fit the regression model with shuffled Y samples and calculate $R_{\mathrm{shuffle}\left(k\right)}^2$. We repeat that process 1000 times. Next, we calculate the percentage of all $R_{\mathrm{shuffle}\left(k\right)}^2$ that are larger than the actual $R^2$, which is our p-value. We evaluate the relevance of a factor $X_i$ with score $M_i=-ln(p-\mathrm{value})$ of $Y=f_i\left(X_i\right)+{ϵ}_i$. The higher the factor score, the more relevant the factor.

2.4. Measure the Concavity from the Polymodel

Suppose the concavity between Y and every $X_i$ is $Con{c}_i$; the concavity of Y is the weighted sum of them.

$$\begin{array}{cc}\hfill & Con{c}_i=Conc\left(f_i\left(X_i\right)\right)={\int }_{-\infty }^{+\infty }-min(f_i^{{}^{″}}\left(x_i\right),0)d{x}_i\hfill \\ \hfill & Conc\left(Y\right)=\frac{{\sum }_{i=1}^n{M}_{i}Con{c}_i}{{\sum }_{i=1}^n{M}_i}\hfill \end{array}$$

(5)

The concavity is the integral of the negative part of the second derivative of the polynomial between Y and X. After fitting the polynomials, we calculate the analytical function of their second derivative. We then calculate the integral numerically. In the financial market, most return values fall in a range covering the sample mean. If we assume the relationship between Y and $X_i$ outside of $[m_i-st{d}_i,m_i+st{d}_i]$ is linear, we just need to calculate the integral in that range to measure the amount of nonlinearity of the model. $m_i$ is the sample mean of $X_i$, and $st{d}_i$ is the sample standard deviation of $X_i$. Detailed derivations are in Kuang and Douady [4].

To avoid the potentially spurious influence of extreme values in Equation (5), we exclude factors which generate extreme concavity values in the top or bottom two percentiles of all factors.

3. Empirical Results

3.1. Data

The monthly return of S&P 500 Index is Y in the Polymodel. The factor pool contains 181 factors, including 78 global equity indices, 25 currency indices, 48 bond and yield indices, 26 commodity indices, and 4 volatility indices. Different types of factors capture the changes of market behaviors caused by different sources. The factors we use are from Ye and Douady [9]. We downloaded the data from Bloomberg. Our data is from January 1990 to January 2022. Considering some indices only exist in part of this whole period, while fitting the Polymodel at the end of every month, we only include indices that have been in existence for at least 36 months before that month in the model. Each month, the Polymodel is fitted on return data from the past 36 months. The results after 2018 are totally out-of-sample.

We use the daily price of the S&P 500 Index from Yahoo Finance to identify crises. Coding is in Python 3.

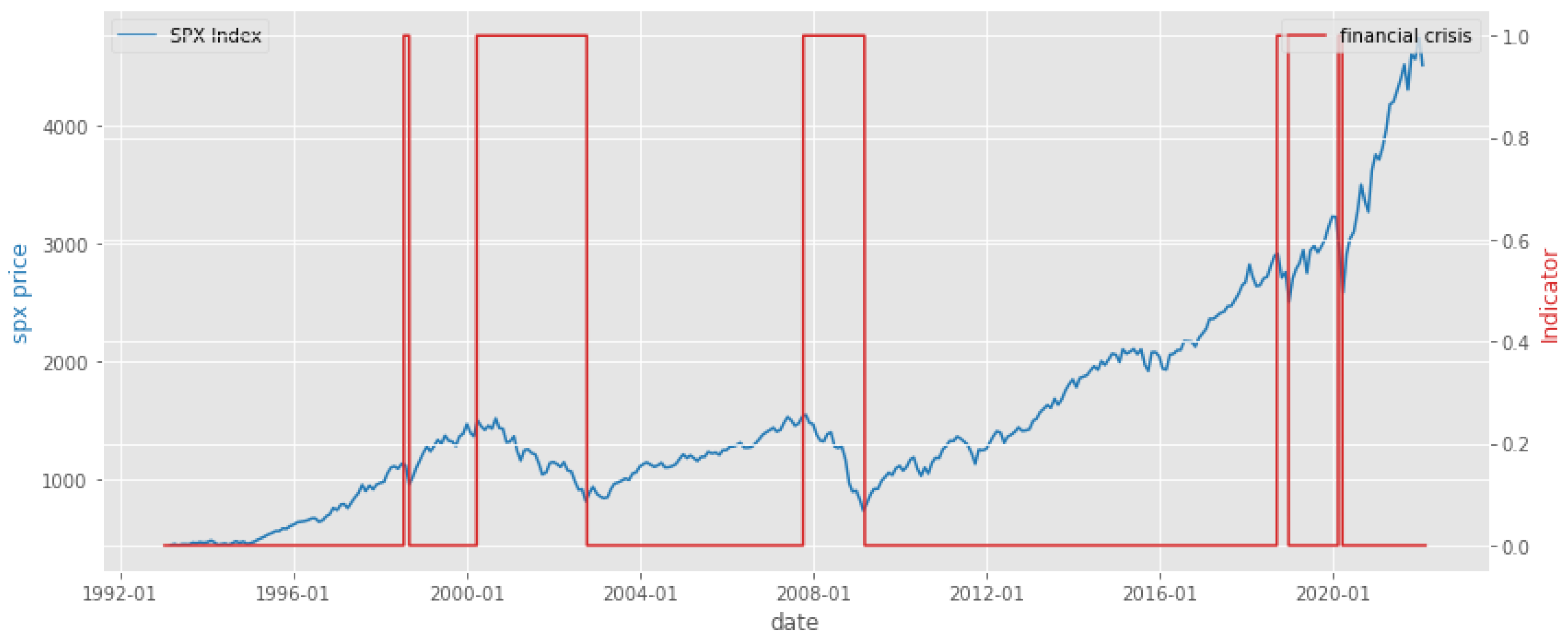
3.2. Historical Crises

According to the method of identifying a crisis in Section 2.1, Figure 1 presents the historical “crises” under this definition from 1993. The price peak date and bottom date of each crisis are listed in Table 1.

From Table 1, the maximum drawdown (MDD) in a crisis may be from close to 20% to more then 50%. The drawdown may last for several months or a couple of years before it recovers.

At the date of this draft, the market drop from the previous peak on 3 January 2022 reached 11.9% until 23 February 2022. The question is to find out if the market is prone to collapse with a cumulated drawdown exceeding 18% or if it will resist in the forthcoming months.

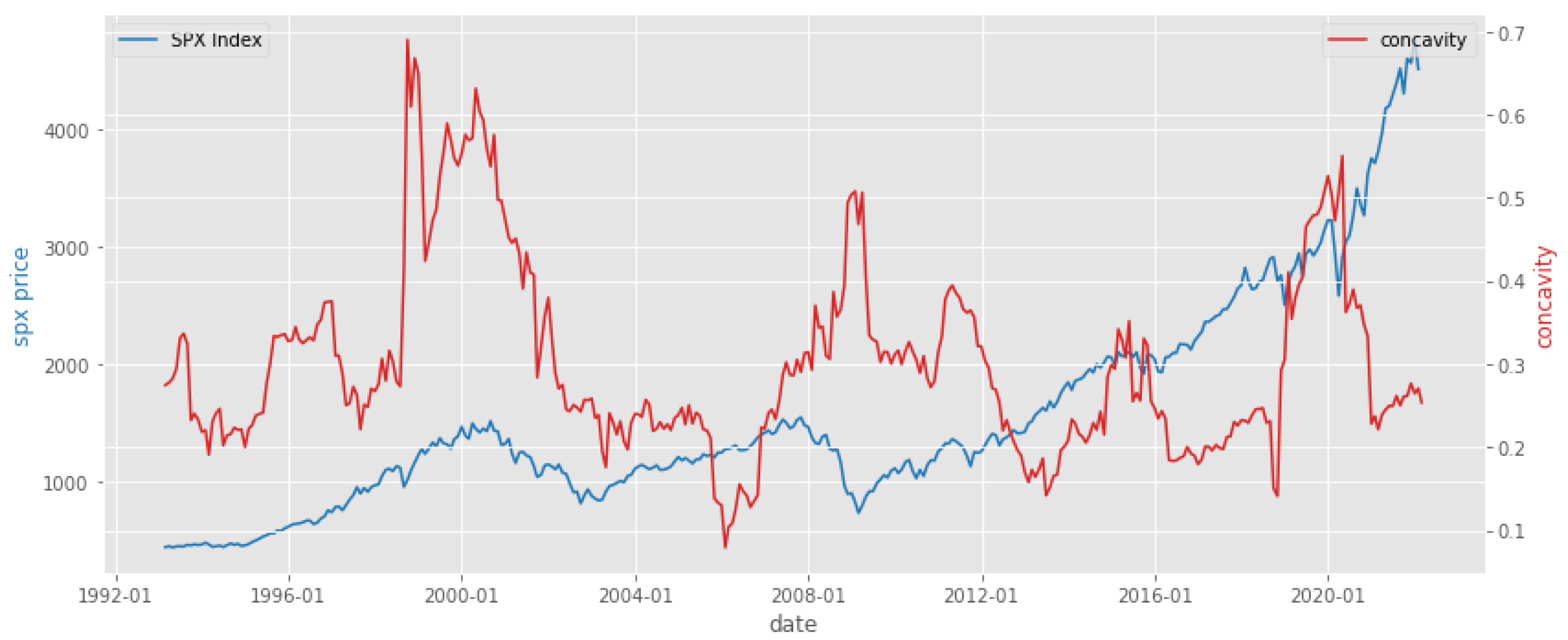
3.3. Concavity Results

The concavity of S&P 500 is displayed in Figure 2. That figure reveals that, for all the previous crises except December 2018, the concavity upsurges before the crisis. In addition, the concavity level is higher before the crises beginning in 2000, 2007, and 2020 than crises beginning in 1998 and 2018, which matches the MDD levels of those crises in Table 1.

Meanwhile, the recent concavity rises slowly, which is different from the previous crisis, as displayed in Figure 3. To make the results more readable, we set up a criterion to evaluate if the concavity rises at every month. We compare the current concavity with its 90th percentile during the past 3 years. Figure 4 indicates that the concavity increases before previous crises. In 2015, after the concavity increased, there was no crisis according to the crisis definition, however, the market still dropped with an MDD of 14.16%. To avoid confusion between the yellow line and red line, we let the yellow line equal 0.5 if there is a concavity rise signal. Concavity-relevant results in all figures are acquired before the corresponding monthon the x-axis.

As can be observed on the graphs above, the concavity is in mild increase at levels far below the peak of March 2020, yet at a level comparable to the pre-December 2018 correction.

4. Conclusions

The U.S. market has been volatile since 2022. The market already dropped about 10% from the peak. Many financial analysts are concerned about a potential crisis.

In this paper, we updated the crisis indicator developed in Kuang and Douady [4] to address the question of whether the market is prone to collapse or not in the coming months. Our finding is that the indicator is in a very mild increase showing no sign of dynamic instability. Of course, a major collapse could be a result of geopolitical events currently ongoing in Europe, although this would be independent of internal instability of the market.

Latest Update

As of the end of March 2022, the market had a maximum drawdown of 13% since its peak on 3 January 2022, still below our 18% threshold. This is consistent with the crisis indicator not surging. As of today, the crisis indicator remains at moderate levels, as shown in Figure 5.