Abstract
In finite populations, pseudo-population bootstrap is the sole method preserving the spirit of the original bootstrap performed from iid observations. In spatial sampling, theoretical results about the convergence of bootstrap distributions to the actual distributions of estimators are lacking, owing to the failure of spatially balanced sampling designs to converge to the maximum entropy design. In addition, the issue of creating pseudo-populations able to mimic the characteristics of real populations is challenging in spatial frameworks where spatial trends, relationships, and similarities among neighbouring locations are invariably present. In this paper, we propose the use of the nearest-neighbour interpolation of spatial populations for constructing pseudo-populations that converge to real populations under mild conditions. The effectiveness of these proposals with respect to traditional pseudo-populations is empirically checked by a simulation study.
1. Introduction
The original bootstrap method [1] is not directly applicable without replacement sampling from finite populations because the values of the survey variable Y in the samples are not iid. Ref. [2] provides an extended survey of the bootstrap methods for finite populations, classifying them into three main groups: (i) the pseudo-population bootstrap (PPB) methods, where a pseudo-population (PP) that mimics the true one is first created from the sample and bootstrap samples are then selected from the resulting PP by a resampling design; (ii) direct bootstrap methods, where bootstrap samples are selected from the original sample or a rescaled version of it using a replacement sampling different from the original sampling design; (iii) bootstrap weights methods, where instead of creating bootstrap samples, the sample remains fixed and bootstrap weights are generated instead. In our opinion, the PPB techniques that adopt as resampling scheme the same scheme used to select the original sample are the most convincing (see also [3]). Even if PBB techniques may be computationally intensive with large samples, so that official statistical offices usually adopt weighted bootstraps [2], PBB techniques preserve the original spirit of the classical bootstrap [1] where samples are iid data from an unknown distribution and bootstrap samples, like the original ones, are iid data from the empirical distribution.
At least to our knowledge (but see also [2]), for many years the literature on PPB only dealt with the properties of bootstrap variance estimators, neglecting asymptotic considerations involving the whole bootstrap distribution. This is in contrast to the original spirit by [4] that point out the asymptotic coincidence of the distribution of the bootstrapped estimator with the actual one is an essential requirement (see also [5], chapter 3). To meet this requirement, Ref. [3] assume a superpopulation model generating an infinite sequence of Y values with a vector of design variables associated to each of them. Conditional to the realised sequence, a sequence of finite populations of increasing size is constructed and sampled by a sequence of designs with inclusion probabilities proportional to a function of the design variables. As the population size increases, the sequence of designs is requested to converge to the rejective sampling design of maximum entropy (e.g., [6]), usually referred to as conditional Poisson sampling (CPS). In this scenario, the authors consider population parameters that are Hadamard differentiable functionals of the population distribution function and plug-in estimators of these parameters achieved by substituting the Hajék estimator of the distribution function into the functional, then proving a functional central limit theorem for these estimators. As discussed in the next section, various forms of central limit theorem have a long-standing in finite population sampling. What is really novel in [3] is that the authors give conditions on PPs, ensuring that the bootstrap distributions of the plug-in estimators resampled from these PPs by means of suitable resampling schemes (including that adopted to select the original sample) asymptotically coincide with the actual distributions of these estimators. At least to our knowledge, the paper by [3] is the sole one providing a unified framework that theoretically justifies the use of PPB in a wide range of situations, including the most common sampling schemes and a large collection of parameters (e.g., totals, averages, quantiles, Lorenz curves, inequality indexes, etc.).
Unfortunately, results by [3] cannot be exploited in spatial surveys, where populations to be sampled are collections of units located onto a study region with a Y value attached to each location. The crucial issue is that the most effective designs usually adopted in spatial sampling are aimed at achieving spatial balance, i.e., samples of units evenly spread over the study region (e.g., [7]). To this purpose, locations play the role of design variables, and spatial balance is usually obtained by schemes that avoid the selection of contiguous units. As a consequence, spatial designs give rise to a large portion of samples (those including neighbourhoods) that cannot be selected. Therefore, spatial designs do not generally converge to CPS as requested by [3]. That is exemplified in the Appendix A, where it is proven that two sampling schemes that in different ways exclude the selection of contiguous or neighbouring units, fail to converge to CPS. In addition, the issue of creating PPs able to mimic the characteristics of the real populations is challenging in spatial framework where spatial trends, relationships, and similarities among neighbouring locations are invariably present.
Based on these considerations, in this paper we propose the use of PPs suitable to work in spatial surveys. For some aspects, the proposed PPs are similar to the hot-deck PPs by [3] in which, given the set of sampled units, the Y value assigned at any other location is the value of the sample unit that is nearest in the space of the values of a size variable X. In an analogous way, but involving locations, we here propose to assign at any unsampled unit the value observed at the sampled unit that is nearest in the geographical space.
Owing to its simplicity, the principle here proposed for constructing spatial PPs constitutes a widely extended practice for mapping spatial populations, and it is commonly referred to as the nearest-neighbour interpolator (NNI). In the past, NNI has been invariably adopted as a descriptive technique. In a model-dependent perspective, Ref. [8] (Section 5.9) classified NNI among “non stochastic methods of spatial prediction”, i.e., descriptive mapping techniques for which no stochastic model is assumed and no inference is attempted. Recently, Ref. [9] approached NNI from a design-based point of view, proving its design-based consistency under mild assumptions about Y values. Under these conditions, for populations and sample sizes sufficiently large, the resulting PPs are likely to be good pictures of the true spatial populations.
The main purposes of this paper are essentially two: (i) to propose the use of PPs based on NNI that are able to converge to the true populations under mild conditions required for the Y values and for the spatial sampling schemes, so that one can expect intuitively that the bootstrap distribution of an estimator should converge to the actual distribution; (ii) to empirically evidence by means of a simulation study the superiority of the PPs based on the NNI in fitting the true populations with respect to PPs commonly used in the literature and the subsequent superiority in the convergence of the bootstrap distributions toward the actual distributions of the involved estimators. The paper is organised as follows: Section 2 is devoted to the problem of estimating totals and averages in spatial surveys pointing out the reasons and the opportunity of adopting PPB for performing a reliable design-based inference on the distributions of the Horvitz–Thompson (HT) estimators. In Section 3, some criteria to construct PPs suitable to work with spatial populations are considered, including the NNI criterion. In Section 4, the PPs considered in Section 3 are compared by a simulation study in terms of the performance of the bootstrap distributions to fit the actual distribution of the HT estimators of totals under two schemes usually adopted in spatial sampling, as well as in terms of the coverage of bootstrap confidence intervals. Concluding remarks are provided in Section 5.
2. Statement of the Problem
Design-based inference has been widely adopted for estimating totals and averages of finite spatial populations, especially in agricultural, forest, and environmental studies. Examples include estimation of totals of agricultural productions for an area frame of agricultural holdings [10], estimation of total or average of volumes for a population of trees settled in a forest stand [11], estimation of the total timber volume for a population of forest compartments in an administrative district [12], and estimation of the average of eutrophication indexes in the population of small lakes of United States [13]. In these cases, estimation is customarily performed via the HT criterion or suitable model-assisted modifications able to exploit auxiliary information, such as generalised regression estimators or ratio estimators that are, however, functions of HT estimators (e.g., [14], chapter 6).
With this goal in mind, consider a study region which is supposed to be a connected and compact set of . As it is customary in the finite population asymptotic framework (e.g., [15]), in spatial surveys we suppose to be an infinite sequence of locations onto and to be the corresponding sequence of Y values, where for brevity . Moreover, let be the corresponding sequence of a strictly positive size variable X, where for brevity .
By a little abuse of notation, we denote locations by their labels. A sequence of spatial populations is considered, where consists of the first locations from , consists of the first locations from , and so on, in such a way that turns out to be a sequence of nested populations of increasing sizes within . Finally, suppose a sequence of spatial designs to select spatially balanced samples from of fixed and increasing size for a fixed sampling fraction . For each k and for each location , denote by the first-order inclusion probability induced by the kth design that is taken proportional to the size variable X. The key motivation for this choice is the efficiency of the HT estimator of population totals and averages when there is a strong direct relationship between X and Y. For simplicity we assume
Note, however, that equal probability designs are included in (1) when the size variable X is invariably equal to one. For each k and for each pair of locations , denote by the second-order inclusion probability induced by the kth design. As pointed out in the introduction, for most spatial schemes these probabilities vanish for pairs of neighbouring locations for the purpose of achieving spatially balanced samples.
Spatially balanced schemes have a long standing in spatial sampling. Examples are the generalised random-tessellation stratified sampling (GRTSS) by [13], the spatially correlated Poisson sampling (SCPS) by [16], the local pivotal method (LPM) by [11], and the doubly balanced spatial sampling (DBSS) by [17] that not only ensures spatial balance but also ensures balance with respect to a set of auxiliary variables besides those adopted to determine the inclusion probabilities. More recently, additional schemes were proposed such as the spatial determinantal sampling designs by [18] (see also [19]), the weakly associated vector sampling by [20], and the tessellation pivotal method by [21].
By using spatial schemes that spread samples, the selection of neighbouring units is avoided, which means that a large portion of second-order inclusion probabilities is null. As these sampling designs are nonmeasurable, it is impossible to estimate the variance of the HT estimator of total without bias. As stated by [16], variance estimation is “a bit tricky” in spatial sampling.
In addition, once a variance estimate is achieved, the traditional construction of confidence intervals using the standard normal quantiles would require the existence of a finite-population central limit theorem. Convergence to normality has been usually derived for large entropy designs (e.g., [22] and references therein) and more recently extended to Adamard differentiable functionals of the distribution function, in turn estimated by HT and/or Hajék criteria, by [23] and by [3], but once again under designs approaching CPS. More general results are obtained by [24] for a quite large class of designs including high-entropy designs as special case, but at the cost of working in a superpopulation setup. A central limit theorem for negatively associated designs is given by [25], but at the cost of requiring that the variance of the HT estimator converges to the variance of Poisson sampling such that, as evidenced by [21], it is a quite difficult requirement for fixed-size designs. The problem has been even solved by the two authors that provide a suitable variance estimator and prove convergence to normality of the HT estimator, but only for the case of tessellation pivotal sampling as well as by [18] that prove a central limit theorem for determinantal sampling.
However, from a wide point of view, as stated in the introduction and argued in the Appendix A, the exclusion of neighbouring units in the samples decreases the entropy of spatial designs that do not generally converge to large entropy designs as the population and sample sizes increase, thus generally precluding the use of finite-population central limit theorems available in the literature. Therefore, in spatial surveys, the use of PPB may be a suitable solution for making inferences on the distribution of the HT estimator and for constructing confidence intervals.
3. Spatial Pseudo-populations
The effectiveness of any PPB rests on the capacity of constructing PPs able to well depict the real population from which the sample has been selected. However, as stated in the introduction, some PPs commonly adopted in PPB are not suitable to mimic spatial populations. First of all, PPs such as the Holmberg PP [26] or the double-calibrated PP [3] that provide random population sizes must be avoided. Indeed, if the resulting PP size is smaller than the size of the real population, we have to arbitrarily discard a set of locations without any insight about how to choose them; on the other hand, if the resulting size is greater, we have to arbitrarily add locations, also in this case without any insight on the way in which the new units should be located on . Moreover, PPs in which the Y values of the sampled units are assigned to an established number of units in the populations, such as the conditional Poisson PP [3], should be avoided because we have to arbitrarily assign such values to units without any insight about the locations at which these values should be assigned.
The multinomial PP (MPP) by [27] is one among the “traditional” PPs that can also be applied in spatial sampling. For each location , MPP independently assigns to j the values and with probability
The resulting PP has obviously the same size of the real population. Even if virtually applicable in spatial surveys, MPP takes into consideration only the information provided by the size variable X, completely neglecting the spatial locations, while in most cases the Y values strictly depend on locations. As such, MPP is likely to provide poor representations of real populations.
The hot-deck PP (HDPP) is another PP that can be applied in spatial surveys. HDPP has been proposed by [3] based on the idea that the values of the size variable are good proxies for the Y values. Then, for each location , HDPP assigns to j the values and
where is the sample indicator variable that is equal to 1 if , and it is equal to 0 otherwise and , i.e., HDPP predicts the Y value at any unsampled location j by the Y value of the sampled location that is nearest to j in the space of the X values. Practically speaking, prediction (2) constitutes a NNI in the X space. Even if HDPPs do not directly consider the information provided by locations, locations enter in the predictions by the fact that any is actually a function of its location.
Alternatively, we here propose the use of NNI in which predictions are completely based on the spatial coordinates. NNI exploits the well-known Tobler’s first law of geography, for which the Y values at locations that are close in space tend to be more similar than those at locations that are far apart [28]. Therefore, for each location , this criterion, henceforth referred to as NNPP, assigns to j the values and
where in this case , i.e., we predict the Y value at any unsampled location j by the Y value of the sampled location that is nearest to j in the geographical space. Practically speaking, NNPP assigns the value of a sampled unit to each unsampled unit inside the Voronoi cell constructed around the sampled unit.
Ref. [9] approach the NNI (3) from a design-based perspective. Based on the sole assumption that the function y, defined on is measurable and bounded by L, they derive the following inequality for any location and any (see Theorem 1 in [9])
where is the set of locations in within the -ball around , is the largest difference from within the -ball around , the intersection event in the second term of (4) is the event that no sample location is within the -ball around , and denotes expectation with respect to the k-th design . Inequality (4) establishes that the design-based expectations of the absolute NNI errors are bounded by the sum of two terms: the first depending on the roughness of Y values around and the second depending on the sampling design. Therefore, consistency of NNI holds if both terms approach 0 as . If y is continuous at then the first terms approach 0 as in such a way that consistency depends on the ability of the sampling schemes to select locations around . Practically speaking, the sampling scheme adopted should be able to asymptotically provide spatial balance, i.e., to evenly spread sampled locations in such a way that, as k increases, each location of is likely to have neighbouring locations sampled. It is worth noting that this consistency condition is satisfied by elementary schemes such as simple random sampling without replacement (SRSWOR) and stratified spatial sampling with proportional allocation. Unfortunately, owing to their complexity, we cannot prove that the common spatial schemes mentioned in Section 2 satisfy this requirement. However, stated the effectiveness of these schemes in providing spatial balance and their empirical performance invariably superior to that of SRSWOR (e.g., [29]), consistency of NNI should also hold with these schemes. Owing to consistency, for population and sample sizes sufficiently large, NNPPs are likely to provide a precise representation of the real spatial population. It is also worth noting that as any model, Tobler’s law may be wrong. That is not frequent, but may appear in nature when competitions for resources occurs (e.g., light/water availability for trees). However, the great appeal of design-based NNI is that, even when Tobler’s law is not suitable, consistency of NNI is ensured by the continuity of y joined with the use of sampling schemes able to provide an asymptotic spatial balance.
On the other hand, it should be pointed out that consistency cannot be proven for the HDPPs in which the nearest locations are identified in the X space. Indeed, it is very natural to think the Y values linked with the X values by a deterministic function t plus a term e that depends on and quantifies the error achieved by deterministically predicting by .In practice, a very general scenario for the Y values is
It is worth noting that (5) is not an assumption but just a reckoning relationship that invariably holds once we choose a deterministic function t suitable to link Y with X. Owing to (5), it is apparent that the first term of (4) cannot approach 0 even if approaches 0. In practice, even if the distances in the X space become smaller and smaller, i.e., if approaches , then may approach t(, nothing ensures that approaches , owing to the presence of the spatial component that is not accounted for. These considerations evidence the theoretical appeal of NNPPs over HDPPs.
Finally, a relevant difference between the MPPs with respect to HDPPs and NNPPs is that the last two only depend on the selected sample , in such a way that once the sample is selected there is only one PP from which bootstrap samples are selected (conditional approach). On the other hand, MPPs depend on the sample as well as on the random assignment of the sample values to the population. In this case, we can construct a PP at any resampling occasion from which a bootstrap sample is selected (unconditional approach). Obviously, the unconditional approach is more computationally intensive and time consuming [3]. For this reason, as well as for performing a fair comparison of the PP criteria, only the conditional approach is considered.
4. Simulation Study
The purpose of this study is to empirically evaluate the performance of the different criteria for constructing PPs from which resampling is performed to approximate the distribution of the HT estimators of totals in spatial sampling. Comparison is performed with respect to several spatial populations showing different spatial patterns, several spatially balanced sampling schemes, and several population sizes whose increase mimics the sequence of nested populations theoretically supposed throughout the paper.
4.1. Artificial Populations
To generate finite and nested spatial populations, an artificial surface on the unit square was considered, where for any point the surface was defined by
where the constant ensured a maximum Y value of 10 (see Figure 1). The surface (6) was chosen to represent the major characteristics of spatial populations. It was continuous, in such a way that the Y values in neighbouring locations tended to be similar, thus entailing a positive spatial autocorrelation in the resulting populations. Moreover, it varied relevantly throughout the unit square showing an increasing trend toward the centre of the square, thus entailing a spatial stratification with different values of the survey variable in different parts of the square.
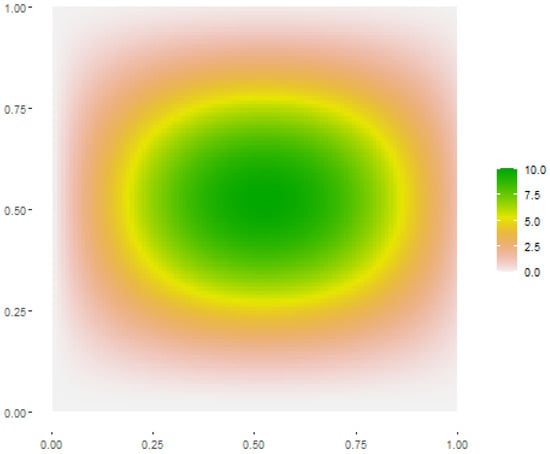
Figure 1.
Map of the artificial surface adopted to generate the finite spatial populations of points.
From (6), three nested populations of and points were located in the unit square in accordance with four spatial patterns referred to as regular (RE), random (RA), trended (TR), and clustered (CL) patterns.
For RE pattern, the nested populations were constructed generating the first 250 points completely at random on the unit square but discarding those having distances smaller than to those previously generated, then adding a further 250 points completely at random on the unit square but discarding those having distances smaller than to those previously generated, and finally adding a further 500 points completely at random, discarding those having distances smaller than . For the RA pattern, the nested populations were constructed by simply generating 1000 points completely at random in the unit square and then assigning the first 250 to the first population, the first 500 to the second population, and all of them to the third.
For the TR pattern, the nested populations were constructed generating 1000 points of coordinates ) where were independent random numbers uniformly distributed on . Then, the first 250 points were assigned to the first population, the first 500 to the second population, and all of them to the third. Finally, for the CL pattern, the nested populations were constructed generating 10 cluster centres completely at random on the unit square and then assigning 25 points to each cluster generated from a spherical normal distribution centred on the cluster centre with variances , then adding a further 25 points to each cluster from the same normal distribution and finally adding a further 50 points to each cluster from the same distribution. Points falling outside the unit square were discarded and newly generated. For each spatial pattern, Figure 2 shows the resulting populations of maximum size 1000.
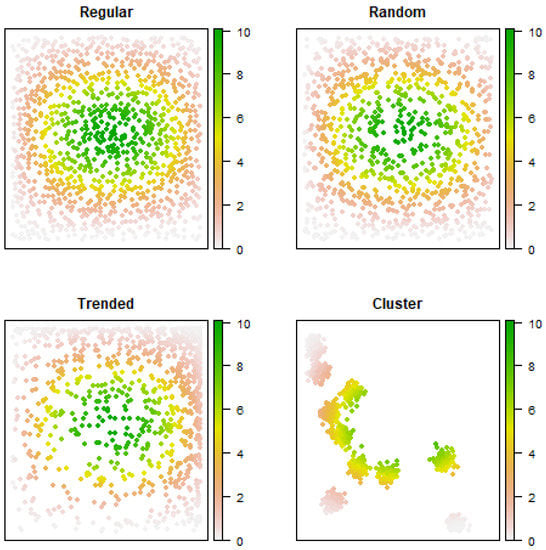
Figure 2.
Maps of the largest spatial populations of 1000 points adopted in the simulation.
For each pattern, the Y values were given by (6) at the generated points, while the X values where generated from the Y values by
where the s were independent random variables uniformly distributed on and k is a multiplicative constant that ensured a correlation of 0.7 between the 1000 values of X and Y. Population totals obviously changed with spatial patterns and population sizes.
4.2. Sampling, Estimation, and Resampling
For any spatial population arising from the combination of spatial patterns and population sizes, samples of fixed size n = 0.1 N were independently selected by means of LPM and DBSS with first order inclusion probabilities given by (1). Moreover, the DBSS is balanced also with respect to the horizontal coordinates (), the vertical coordinates (), and their squared values (), in such a way that the resulting samples were not only spread on the unit square, but they had approximately the same barycentre and the same dispersion of the whole population [17]. LPM and DBSS were performed using the R functions lpm1 and lcube, respectively, from the BalancedSampling library.
Then, for each sample selected at the i-th simulation run (), the HT estimate of the population total was computed by means of
where was the total of the size variable in the population. Moreover, from the sample , a PP ( was created in accordance with each of the three criteria considered in Section 3, i.e., MPP, HDPP, and NNPP. Because NN techniques require efficient algorithms to perform the many controls necessary for identifying closest units in both geographical or X spaces, we used the NND.hotdeck function in the R StatMatch library for constructing HDPPs and NNPPs. For constructing MPP, we used the basic R function sample.
Then, the ability of the resulting PP in fitting the real population was determined by means of the root of the average squared error
From each PP, bootstrap samples
were selected adopting the same sampling scheme adopted to select the original sample , and for each bootstrap sample the HT estimate of the population total was computed by means of
where was the total of the size variable in the i-th PP.
Finally, the bootstrap estimate of the relative standard error of the HT estimator of total was achieved by means of
where
was the bootstrap estimate of variance and
was the bootstrap mean. The bootstrap distribution of the HT estimator of total was approximated by
and the 95% bootstrap confidence interval for was given by − , where is the m-th order statistic from . The interval length was also considered.
4.3. Performance Indicators
For each combination of spatial patterns, population sizes, and PP criteria, the Monte Carlo distributions of the root of average squared error were adopted to empirically determine the fitting performance of the criteria
For each combination of spatial patterns and population sizes, the Monte Carlo distributions of the HT estimators of total were adopted to empirically determine the actual distribution of the estimator
and the relative standard error
where
was the Monte Carlo variance. Once the distribution and the precision of the HT estimator were empirically determined, the ability of PPB to mimic the actual distribution of the HT estimator was determined for each of the four PP criteria by means of their worst-fitting performance
where, for each simulation run i and each PP criteria, the fitting performance of the bootstrap distribution was quantified by the two-sample Kolmogorov–Simrnov (KS) statistic
Moreover, the mimic ability of PPs was quantified by the capacity of the 95% bootstrap confidence intervals to approach the nominal level of 95% that was determined by means of their empirical coverage
associated with their average length
Finally, the capacity of the bootstrap distributions to reproduce the actual precision of the HT estimators was determined comparing the empirical expectations of the bootstrap relative standard error estimators with the actual relative standard errors. Because the actual relative standard error and their bootstrap estimates were likely to approach 0 as population and sample sizes increased, the ratio
was adopted, where
4.4. Results
Table 1 and Table 2 report the simulation results for the two spatial schemes (LPM and DBSS) adopted in the simulation. The results empirically confirmed the theoretical and practical considerations argued in the paper.

Table 1.
Values of relative standard errors (RSE) of the Horvitz–Thompson estimator of totals, pseudo-population fitting indexes (FIT), ratios of expectations of bootstrap RSE estimators to the actual values (RAT), coverages of the 0.95 bootstrap confidence intervals (C) and expectations (in parentheses) of their lengths (L), and the worst of the two-sample Kolmogorov–Smirnov statistics (WF). The values are computed from samples and bootstrap samples independently selected by means of the local pivotal method (LPM) for each spatial pattern (SP), each pseudo-population (PP) and each populations size and with a sampling fraction of 0.1.

Table 2.
Values of relative standard errors (RSE) of the Horvitz–Thompson estimator of totals, pseudo-population fitting indexes (FIT), ratios of expectations of bootstrap RSE estimators to the actual values (RAT), coverages of the 0.95 bootstrap confidence intervals (C) and expectations (in parentheses) of their lengths (L), and the worst of the two-sample Kolmogorov–Smirnov statistics (WF). The values are computed from samples and bootstrap samples independently selected by means of the doubly balanced spatial sampling (DBSS) for each spatial pattern (SP), each pseudo-population (PP) and each populations size and with a sampling fraction of 0.1.
For both schemes and for all the spatial patterns, the RSEs quickly decreased as the population sizes increased, showing the presumable consistency of the HT estimator of population totals under these schemes. These findings agreed with [30], which theoretically proved the consistency of the HT estimation in spatial populations under very simple schemes such as SRSWOR but without proving the consistency under more complex spatially balanced schemes such as LPM and DBSS, owing to the lack of analytical expressions of the second-order inclusion probabilities. However, stated the superiority of these schemes in providing spatial balance with respect to SRSWOR, they concluded that “consistency presumably holds also for these schemes”.
For both schemes and for all spatial patterns, the fitting performance (FIT) of the NNPPs quickly improved as the population sizes increased, showing, also in this case, the presumable consistency of the NNI under these spatial schemes, as argued in Section 3 but not theoretically proven, once again owing to the complexity of the schemes and the lack of analytical expressions of second-order inclusion probabilities. As also theoretically argued in Section 3, consistency did not hold for the HDPPs. Indeed, as the population sizes increased, FIT indexes remain quite the same, or even increased or weakly decreased. The fitting performance was even worse for MPPs with FIT values that were about two times those achieved by HDPPs.
The fitting performance of PPs heavily impacted the ability of PPB distributions to fit the actual distributions of HT estimators. RAT values achieved under NNPPs are always greater than 1 but invariably smaller than those achieved under HDPPs and MPPs and quickly approach 1 as population sizes decrease, showing a tendency to be moderately conservative. On the other hand, RAT values achieved by HDPPs and MPPs showed a tendency to a large overestimation that unsuitability masked the actual precision of the two spatial strategies and that did not decrease, but sometimes even increased, as the population sizes increased.
The superiority of NNPPs was also demonstrated by the performance of bootstrap confidence intervals that for all the PP criteria showed coverages similar to or greater than the nominal level but with average lengths that in the case of NNPPs are much smaller, in some cases even two–three times smaller than those achieved by HDPPs and MPPs.
The same conclusion held for maximum values of the two-sample Kolmogorov–Smirnov statistic, as the WF values achieved under NNPPs were invariably smaller than those achieved under HDPPs and MPPs, and they quickly decreased as the population sizes increased while those achieved under HDPPs and MPPs remained quite stable.
Finally, in comparative terms, DBSS invariably outperformed LPM for all the performance criteria adopted in the study. That was a quite obvious result, as DBSS exploited the information provided by the spatial coordinates in addition to information provided by the size variable that was the sole exploited by LPM.
5. Final Remarks
Spatial surveys, and especially agricultural, forest, and environmental surveys, are usually aimed at estimating aggregate resources of ecological importance (e.g., crop, biomass, abundance, extent, and species richness) with quantifiable precision, in accordance with the purposes of the so-called descriptive inference without accomplishing the purpose of the so-called analytic inference, i.e., reconstructing—and hence explaining—the spatial process generating these aggregates [31]. Probably for this reason, spatial surveys have been traditionally approached from a design-based perspective, bypassing the complex task of modelling spatial phenomena, viewing these phenomena as fixed, and attributing uncertainty only to sampling (e.g., [32,33]). In this scenario, national forest inventories constitute the most prominent examples, as design-based inference has been adopted in Scandinavian countries from the beginning of the past century to estimate forest attributes at the country level (e.g., [34]). In the last years, even the mapping of ecological resources, traditionally approached in the realm of the model-based geostatistical procedures (e.g., [8]), has been approached in a design-based perspective by [9] that derives the design-based properties of the NNI.
Because in a design-based framework properties of any estimator are completely determined by the sampling design, the design choice is then crucial in this context. Regarding the sampling schemes usually adopted in spatial surveys, in this paper we have emphasised the importance of spatial balance, i.e., the capacity of the sampling schemes to evenly spread locations over the study region in such a way that no portion of the region is over- or under-represented. At the same time, we have also outlined the drawbacks involved by the use of spatially balanced schemes, i.e., (a) the lack of convergence of these schemes to CPS that precludes the exploitation of finite population central limit theorems, and (b) the presence of some second-order inclusion probabilities equal to 0 that preclude the unbiased estimation of variance.
Because the use of PPB seems to be a viable solution to overcome both the issues, the focus of the paper has switched to the choice of PPs capable of providing good representations of the spatial populations from which balanced samples are selected. At this step, the results by [9] have been crucial. The authors proved the design-based consistency of the NNI under mild conditions regarding the spatial populations and the sampling schemes. Conditions about populations simply require the smoothness of the Y values in neighbouring locations that well approach the theoretical condition of local continuity, while conditions on the sampling scheme simply require an asymptotical spatial balance that is satisfied even by SRSWOR. Therefore, when using spatial schemes explicitly tailored for achieving spatial balance, the consistency of NNI should hold a fortiori. For these reasons, the NNI of real populations has been proposed as a criterion for constructing PPs in spatial surveys, referred to as NNPPs. The obvious intuition behind this proposal is that if the NNPPs converge to the true populations, bootstrap distributions arising from these maps should converge to the actual distributions of the estimators. In practice, the consistency of NNPP causes one to think that, as the population and sample size increase, a convergence similar to that proven by [3] should occur, i.e., the PPB distributions should converge to the actual distribution at the cost of requiring an asymptotical spatial balance of the design adopted to select the original and bootstrap samples, instead of requiring the convergence to CPS. The theoretical proof of this conjecture, which has been empirically confirmed by the simulation study of Section 4, is one target of our future work.
On the other hand, the achievement of a central limit theorem universally valid for low-entropy spatially balanced schemes seems to be too wide an objective. Probably, the solution would be to prove central limit theorems for single designs as recently done by [18] for the determinantal sampling designs and by [21] for the tessellation pivotal method.
Author Contributions
Conceptualisation, L.F.; methodology, L.F.; software, R.M.D.B. and A.M.; validation, R.M.D.B., A.M. and S.F.; formal analysis, L.F.; investigation, L.F., S.F., R.M.D.B. and A.M.; data curation, R.M.D.B. and A.M.; writing—original draft preparation, L.F.; writing—review and editing, R.M.D.B., A.M. and S.F.; visualisation, A.M.; supervision, S.F.; project administration, L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Let be a spatial population of units and be the family of the possible samples of size n that can be selected from . Denote by the probability measure induced by SRSWOR onto , in such a way that for each .
Now, consider a successive scheme that performs n sequential drawings by excluding at each drawing the nearest neighbour of the previously selected units [35]. Obviously, in this case, the family of possible samples reduces to . If , from straightforward combinatorial considerations it follows that
in such a way that for each sample , where denotes the probability measure induced by the rejective scheme onto .
Accordingly, the Hellinger distance between the two designs is given by
Because
it follows that
where denotes the sampling fraction.
Therefore,
i.e., as the population size increases, the sequence of designs selecting a constant fraction p of units cannot converge to SRSWOR for any . Therefore, because SRSWOR converges to CPS, for the triangular property of distances it follows that does not converge to a CPS with equal first-order inclusion probability.
Similarly, consider the one-per-stratum sampling (OPSS) scheme in which, supposing N be a multiple of n, the population is stratified into n clusters of neighbouring locations and a location is randomly selected within each cluster [36]. In this case, the family of possible samples reduces to the samples of size n with a unique location per cluster. Therefore and for each sample , where denotes the probability measure induced by OPSS onto . Accordingly, the Hellinger distance between the two designs is given by
For N and n sufficiently large, owing to the Stirling formula
from which it follows that
in such a way that
i.e., as the population size increases, the sequence of OPSS designs selecting a constant fraction p of units cannot converge to SRSWOR for any . Therefore, because SRSWOR converges to CPS, for the triangular property of distances it follows that does not converge to CPS with equal first-order inclusion probability.
References
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Mashreghi, Z.; Haziza, D.; Léger, C. A survey of bootstrap methods in finite population sampling. Stat. Surv. 2016, 10, 1–52. [Google Scholar] [CrossRef]
- Conti, P.; Marella, D.; Mecatti, F.; Andreis, F. A unified principled framework for resampling based on pseudo-populations: Asymptotic theory. Bernoulli 2020, 26, 1044–1069. [Google Scholar] [CrossRef] [Green Version]
- Bickel, P.J.; Freedman, D.A. Some asymptotic theory for the bootstrap. Ann. Stat. 1981, 9, 1196–1217. [Google Scholar] [CrossRef]
- Shao, J.; Tu, D. The Jackknife and Bootstrap; Springer: New York, NY, USA, 1995. [Google Scholar]
- Hajék, J. Asymptotic theory of rejective sampling with varying probabilities from a finite population. Ann. Math. Stat. 1964, 35, 1491–1523. [Google Scholar] [CrossRef]
- Brown, J.A.; Robertson, B.L.; McDonald, T. Spatially balanced sampling: Applications to environmental surveys. Procedia Environ. Sci. 2015, 27, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Cressie, N.A.C. Statistics for Spatial Data; Revised ed.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Fattorini, L.; Marcheselli, M.; Pisani, C.; Pratelli, L. Design-based properties of the nearest neighbour spatial interpolator and its bootstrap mean squared error estimator. Biometrics 2021. Online ahead of print. [Google Scholar] [CrossRef]
- Nusser, S.M.; House, C.C. Sampling, data collection, and estimation in agricultural surveys. In Handbook of Statistics 29A. Sample Surveys: Designs, Methods and Applications; Pfefferman, D., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 471–486. [Google Scholar]
- Grafström, A.; Lundström, N.L.P.; Schelin, L. Spatially balanced sampling through the pivotal method. Biometrics 2012, 68, 514–520. [Google Scholar] [CrossRef]
- Baffetta, F.; Fattorini, L.; Franceschi, S.; Corona, P. Design-based approach to k-nearest neighbours technique for coupling field and remotely sensed data in forest surveys. Remote Sens. Environ. 2009, 113, 463–475. [Google Scholar] [CrossRef] [Green Version]
- Stevens, D.J.; Olsen, A.R. Spatially balanced sampling of natural resources. J. Am. Stat. Assoc. 2004, 99, 262–278. [Google Scholar] [CrossRef]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: New York, NY, USA, 1992. [Google Scholar]
- Isaki, C.T.; Fuller, W.A. Survey design under the regression superpopulation model. J. Am. Stat. Assoc. 1982, 77, 89–96. [Google Scholar] [CrossRef]
- Grafström, A. Spatial correlated Poisson samplings. J. Stat. Plan. Inference 2012, 14, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Grafström, A.; Tillé, Y. Doubly balanced spatial sampling with spreading and restitution of auxiliary totals. Environmetrics 2013, 24, 120–131. [Google Scholar] [CrossRef] [Green Version]
- Loonis, V.; Mary, X. Determinantal sampling designs. J. Stat. Plan. Inference 2019, 199, 60–88. [Google Scholar] [CrossRef] [Green Version]
- INSEE. Handbook of Spatial Analysis; Institut National de la Statistique et des Études Économiques: Montrouge, France, 2018.
- Jauslin, R.; Tillé, Y. Spatial spread sampling using weakly associated vectors. J. Agric. Biol. Environ. Stat. 2020, 25, 431–451. [Google Scholar] [CrossRef]
- Chauvet, G.; Le Gleut, R. Inference under pivotal sampling: Properties, variance estimation and application to tessellation for spatial sampling. Scand. J. Stat. 2021, 48, 108–131. [Google Scholar] [CrossRef]
- Berger, Y. Rate of convergence to normal distribution for the Horvitz–Thompson estimator. J. Stat. Plan. Inference 1998, 67, 209–226. [Google Scholar] [CrossRef]
- Bertail, P.; Chautru, E.; Clémençon, S. Empirical processes in survey sampling with (conditional) Poisson designs. Scand. J. Stat. 2017, 44, 97–111. [Google Scholar] [CrossRef]
- Boistard, H.; Lopuhaä, H.P.; Ruiz-Gazen, A. Functional central limit theorems for single-stage sampling designs. Ann. Stat. 2017, 45, 1728–1758. [Google Scholar] [CrossRef] [Green Version]
- Brändén, P.; Jonasson, J. Negative dependence in sampling. Scand. J. Stat. 2012, 39, 830–838. [Google Scholar] [CrossRef] [Green Version]
- Holmberg, A. A bootstrap approach to probability proportional to size sampling. In Proceedings of the Section on Survey Research Methods, Dallas, VA, USA, 9–13 August 1998; pp. 378–383. [Google Scholar]
- Sverchkov, M.; Pfefferman, D. Prediction of finite population totals based on the sample distribution. Surv. Methodol. 2004, 30, 79–92. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. J. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Fattorini, L.; Corona, P.; Chirici, G.; Pagliarella, M.C. Design-based strategies for sampling spatial units from regular grids with applications to forest surveys, land use and land cover estimation. Environmetrics 2015, 26, 216–228. [Google Scholar] [CrossRef] [Green Version]
- Fattorini, L.; Marcheselli, M.; Pisani, C.; Pratelli, L. Design-based consistency of the Horvitz–Thompson estimator under spatial sampling with applications to environmental surveys. Spat. Stat. 2020, 35, 100404. [Google Scholar] [CrossRef]
- Smith, T.M.F. Biometrika Centenary: Sample surveys. Biometrika 2001, 88, 67–134. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Gregoire, T.G.; Valentine, H.T. Sampling Strategies for Natural Resources and the Environment; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Tomppo, L.M.; Gschwantner, R.E.; McRoberts, R.E. National Forest Inventories: Pathways for Common Reporting; Springer: Heidelberg, Gremany, 2010. [Google Scholar]
- Fattorini, L. Applying the Horvitz–Thompson criterion in complex designs: A computer intensive perspective for estimating inclusion probabilities. Biometrika 2006, 93, 269–278. [Google Scholar] [CrossRef]
- Breidt, F.J. Markov chain designs for one-per-stratum sampling. Surv. Methodol. 1995, 21, 63–70. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).