Importance of Weather Conditions in a Flight Corridor
Abstract
:1. Introduction
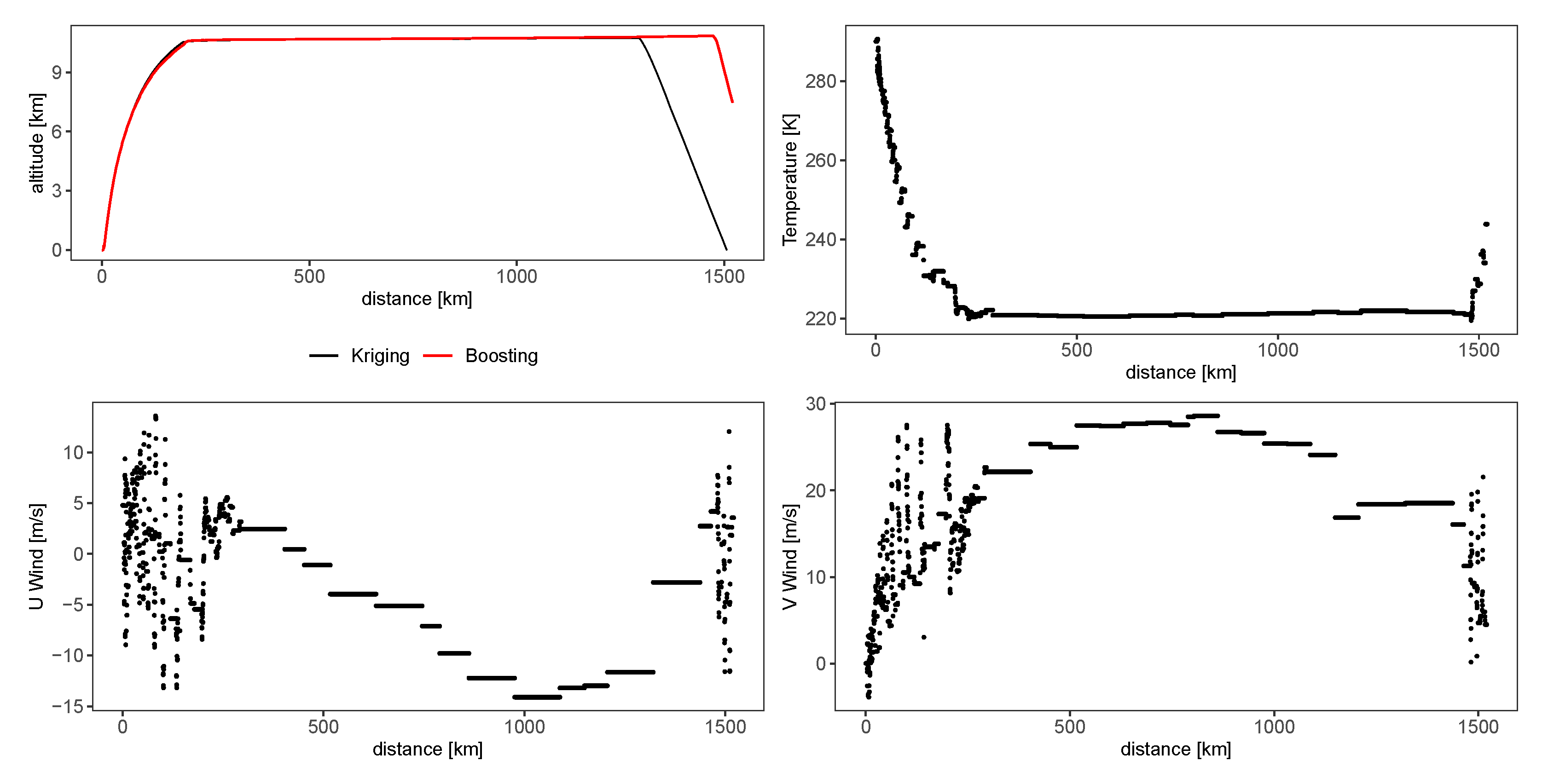
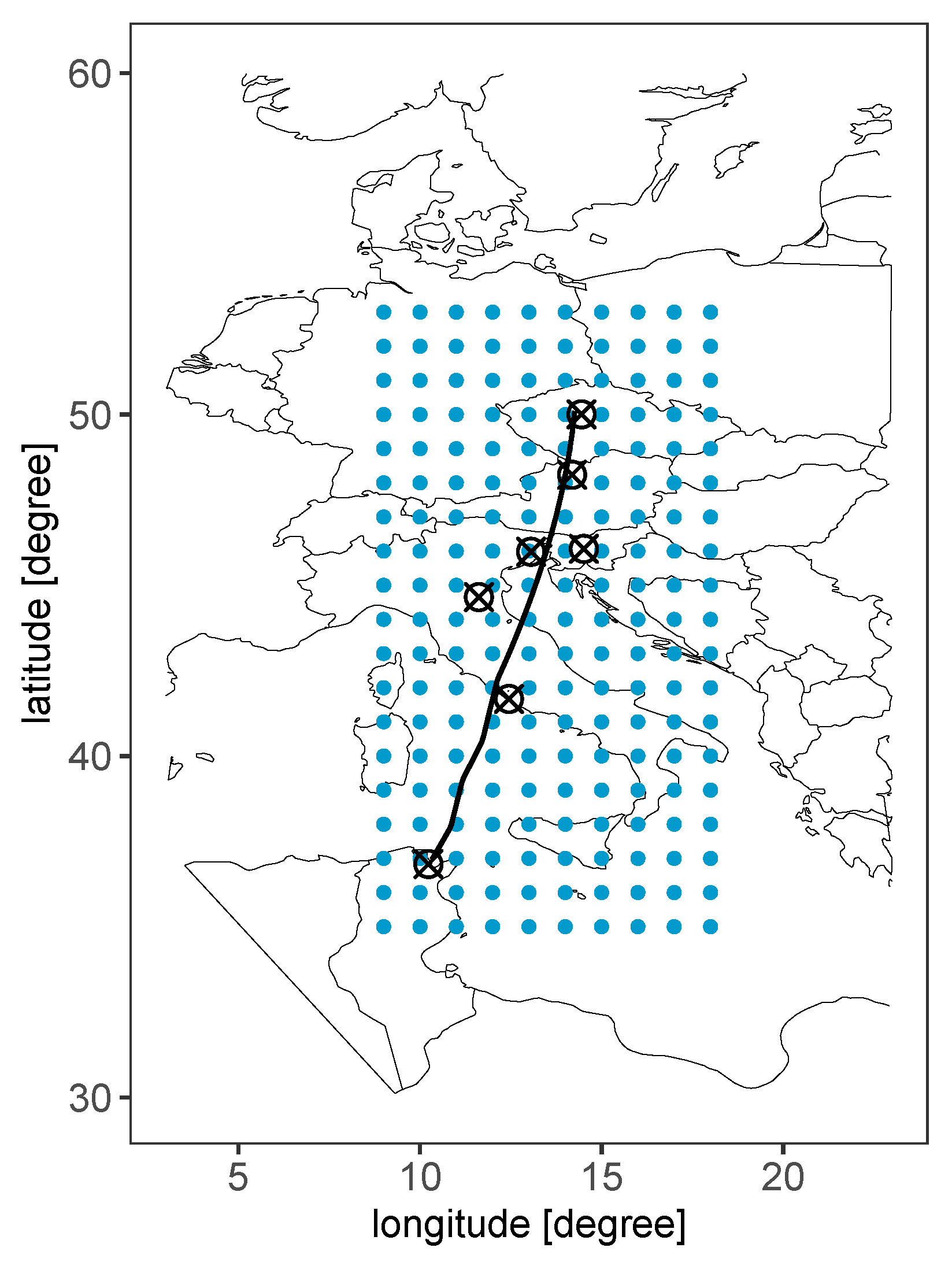
2. Data
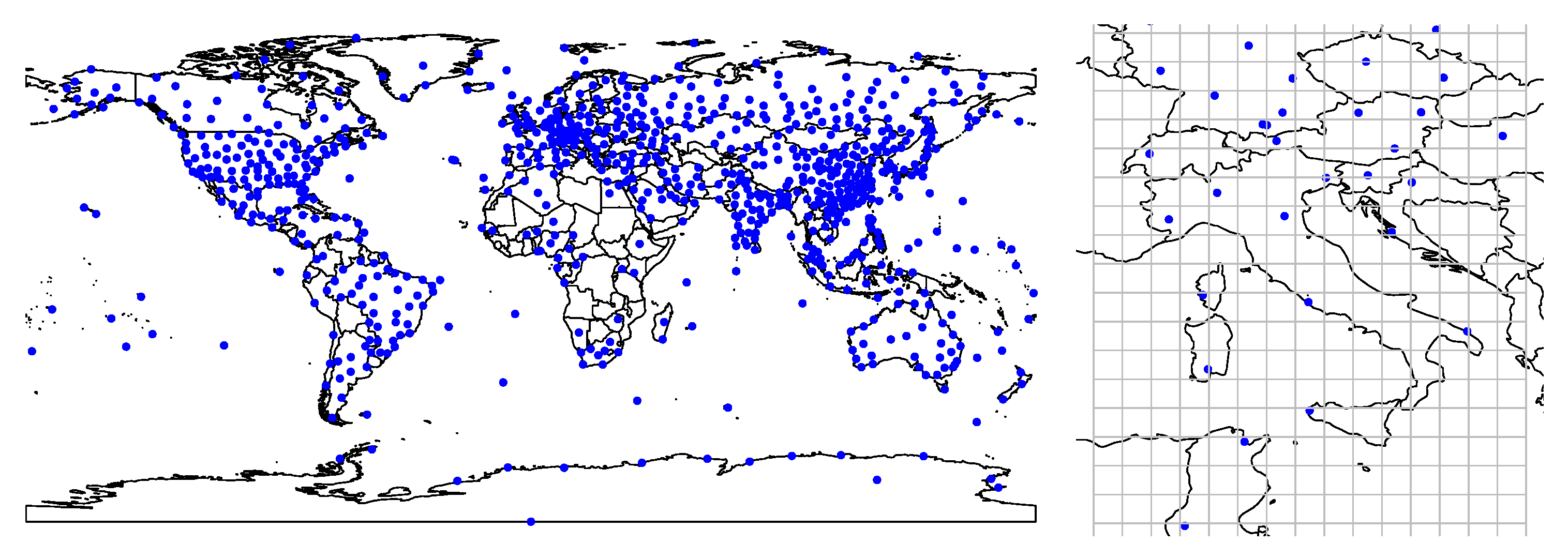
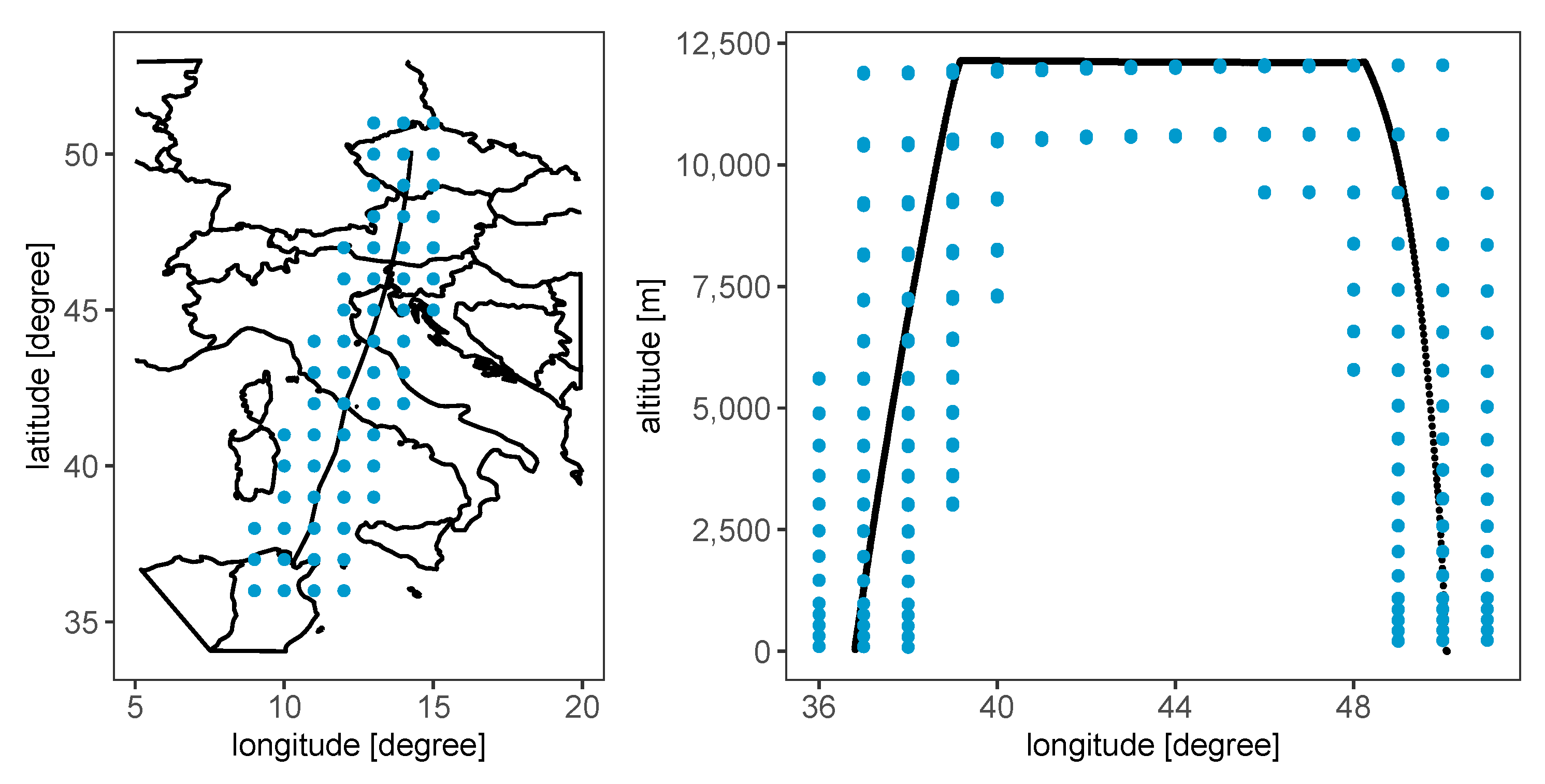
2.1. Data Sources
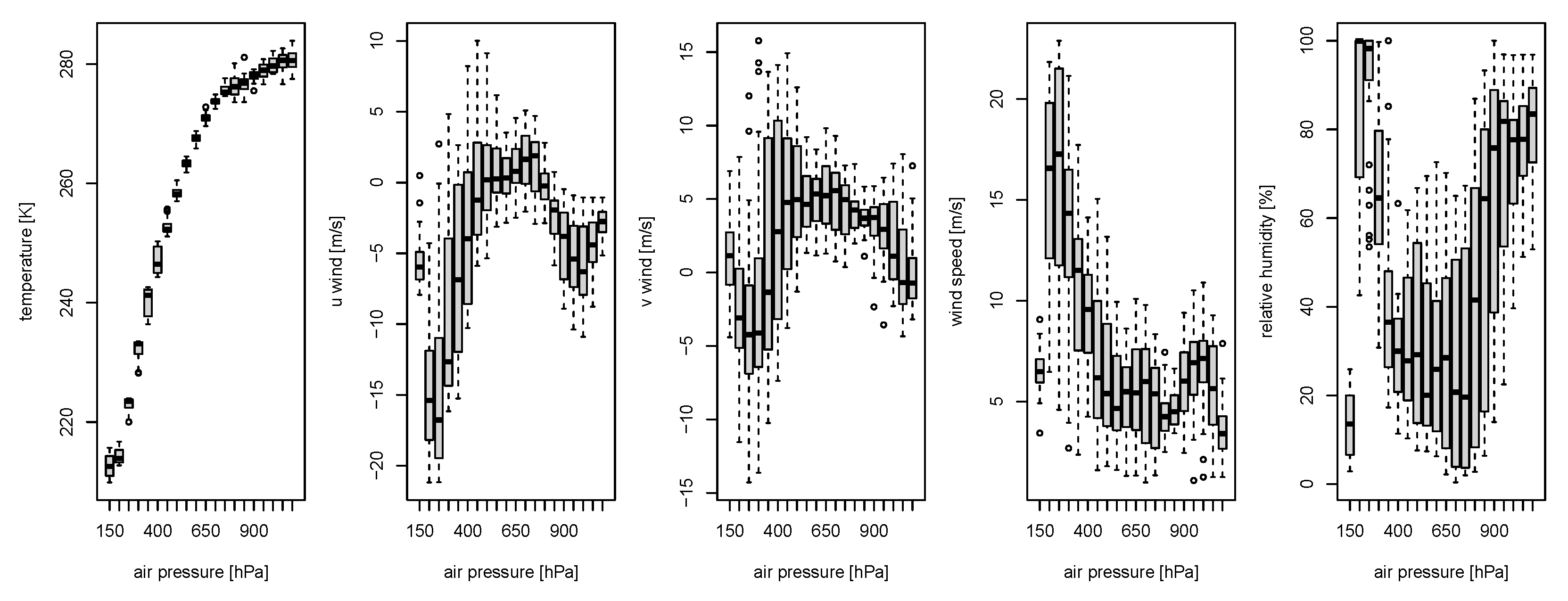
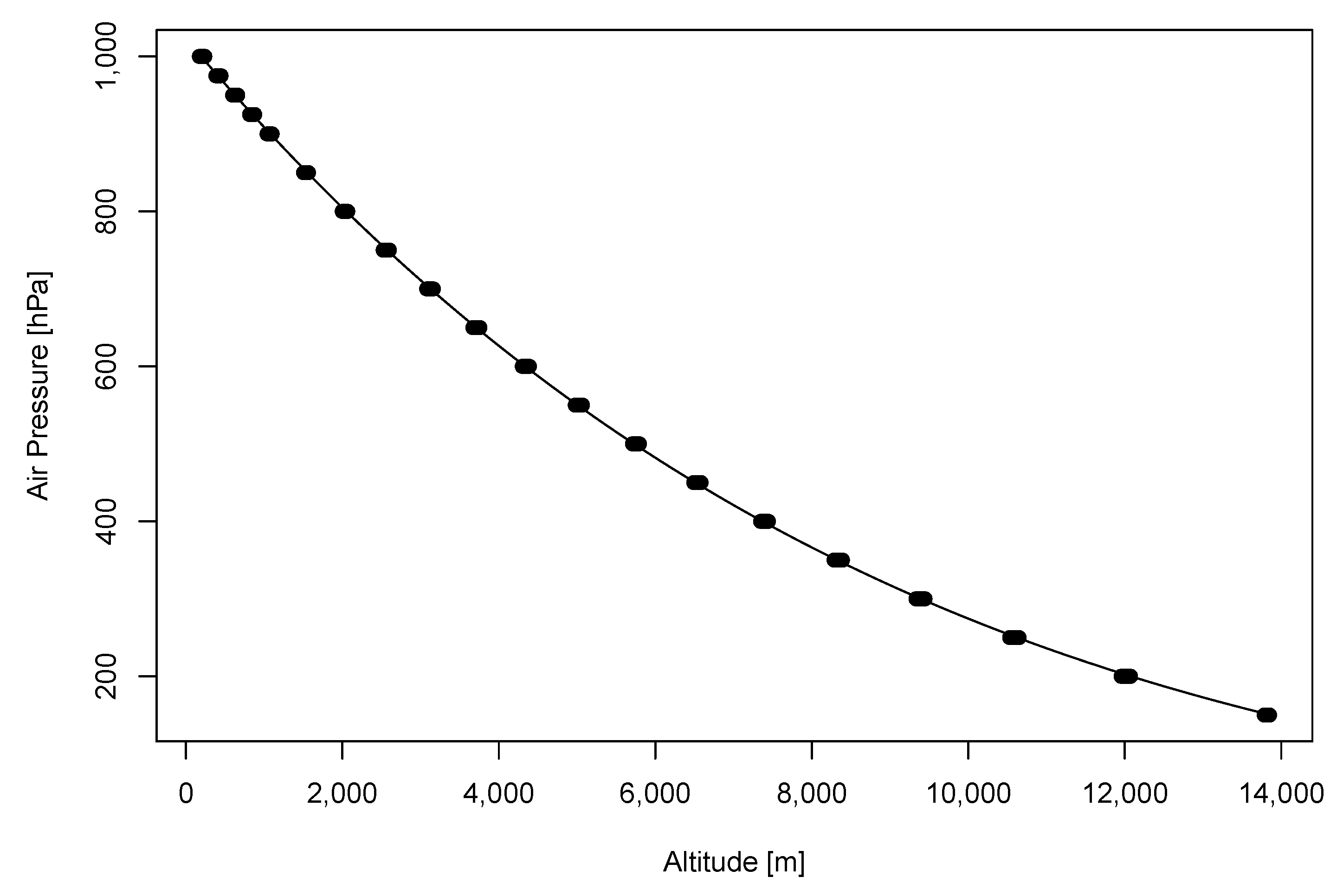
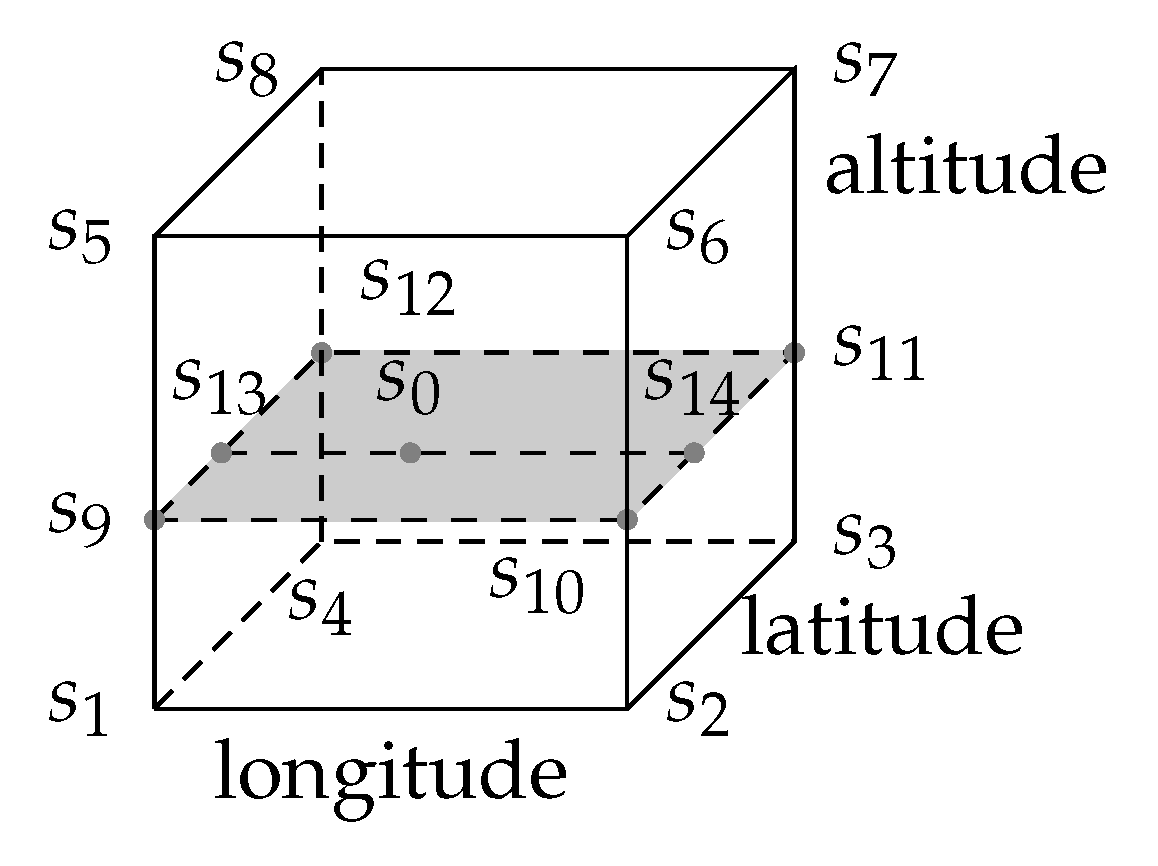
2.2. Data Description
3. Interpolation Methods
3.1. Linear Interpolation
3.2. Kriging
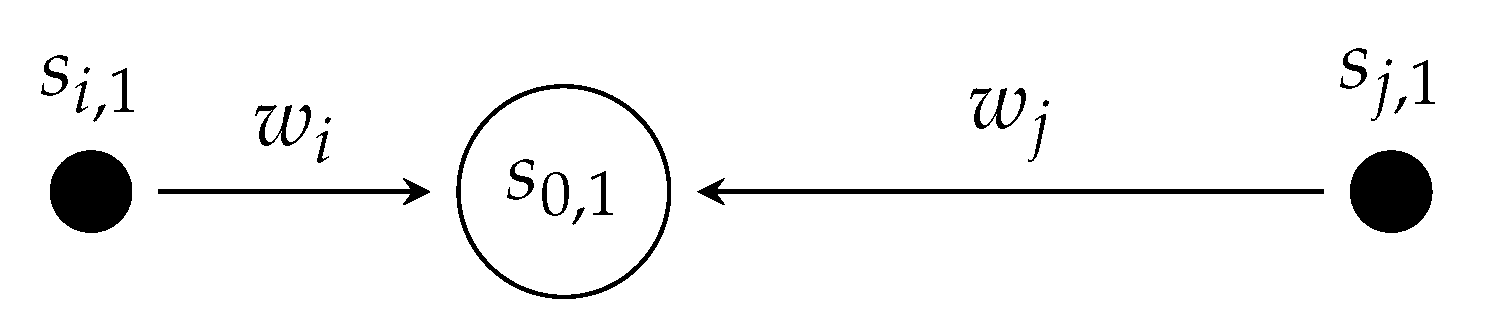
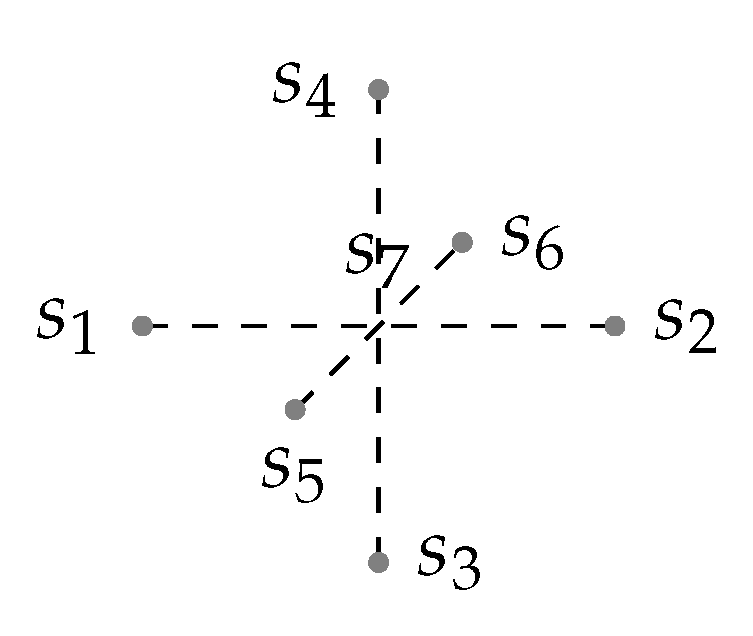
3.2.1. Estimation of Kriging Weights
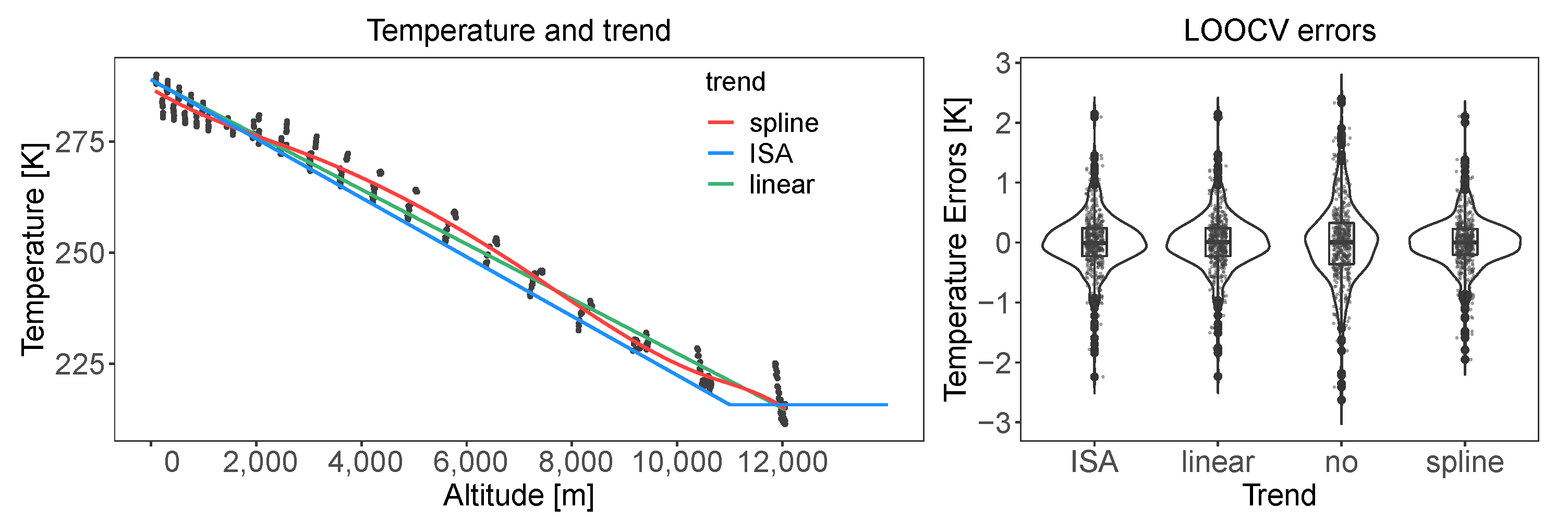
3.2.2. Trend
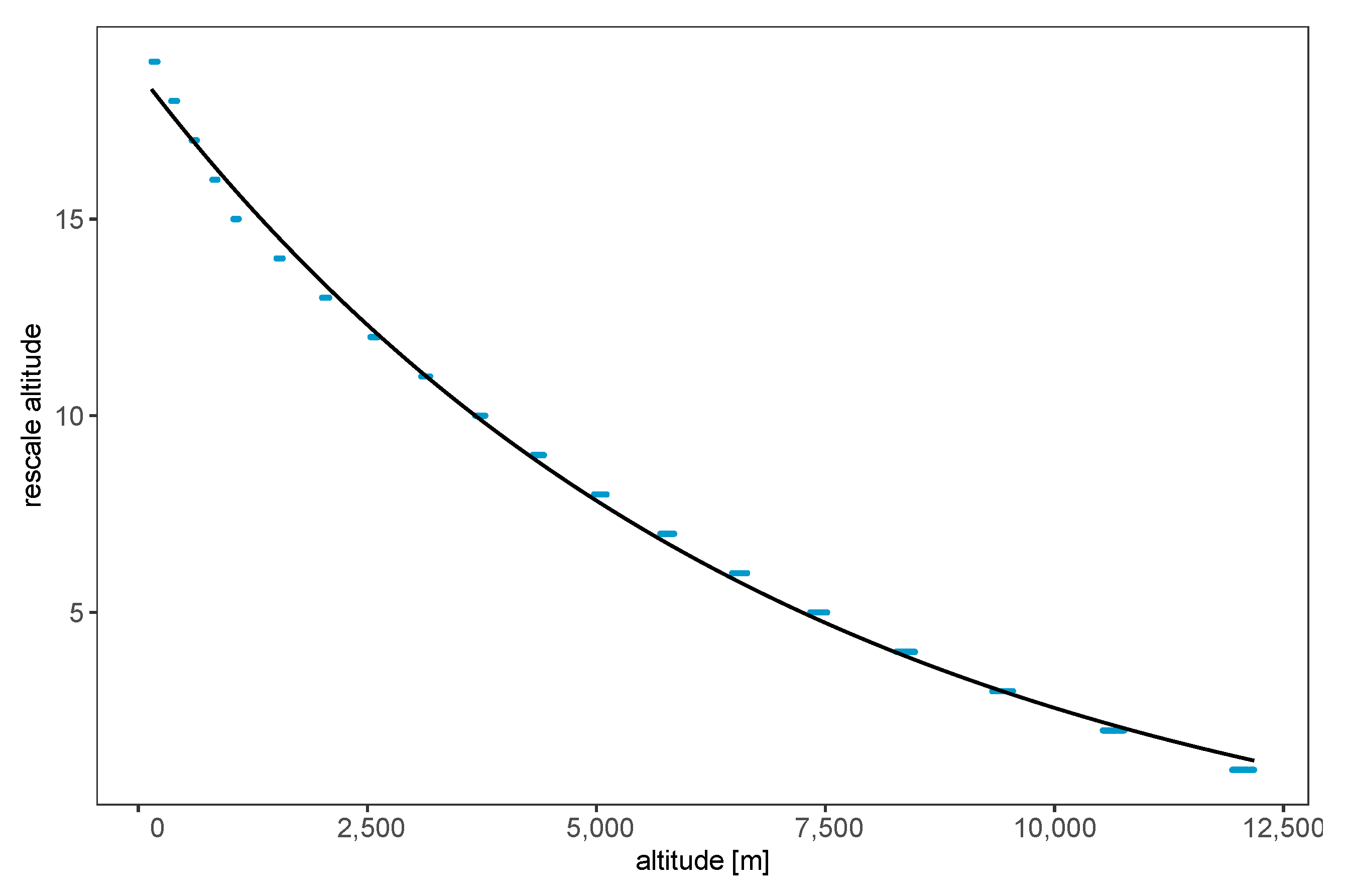
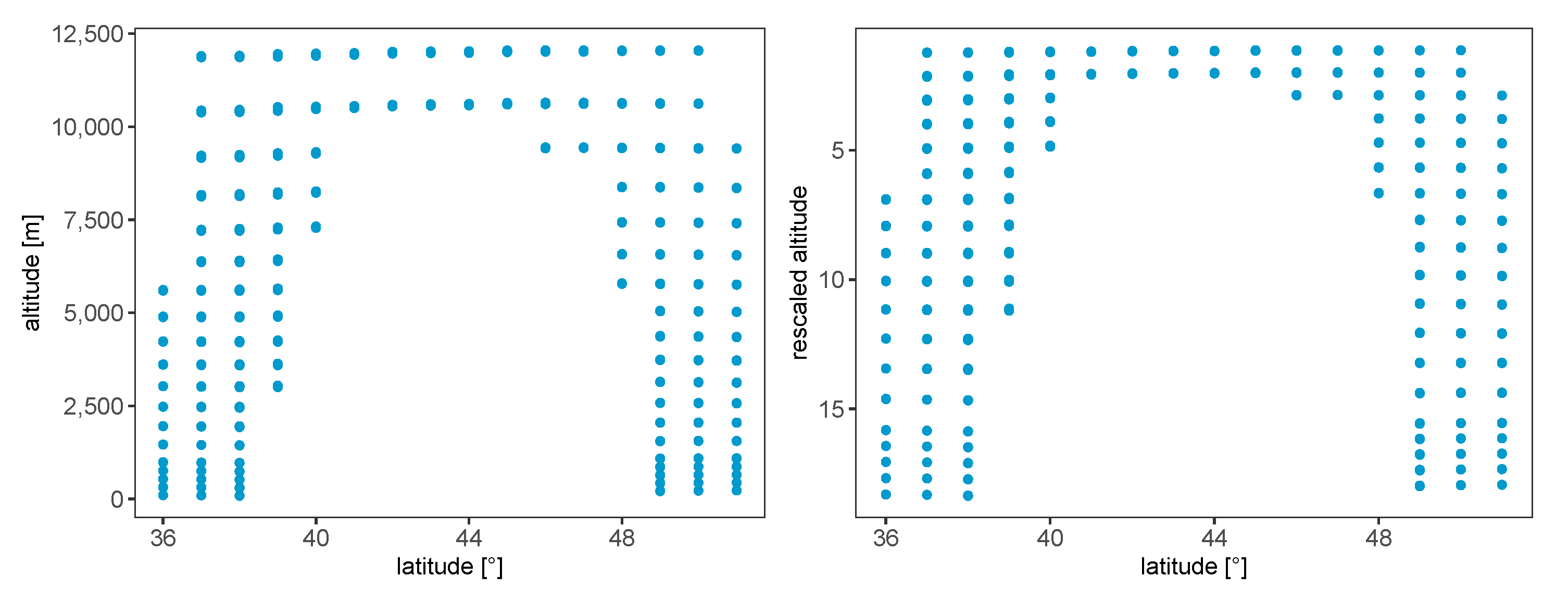
3.2.3. Scaling Factor and Function
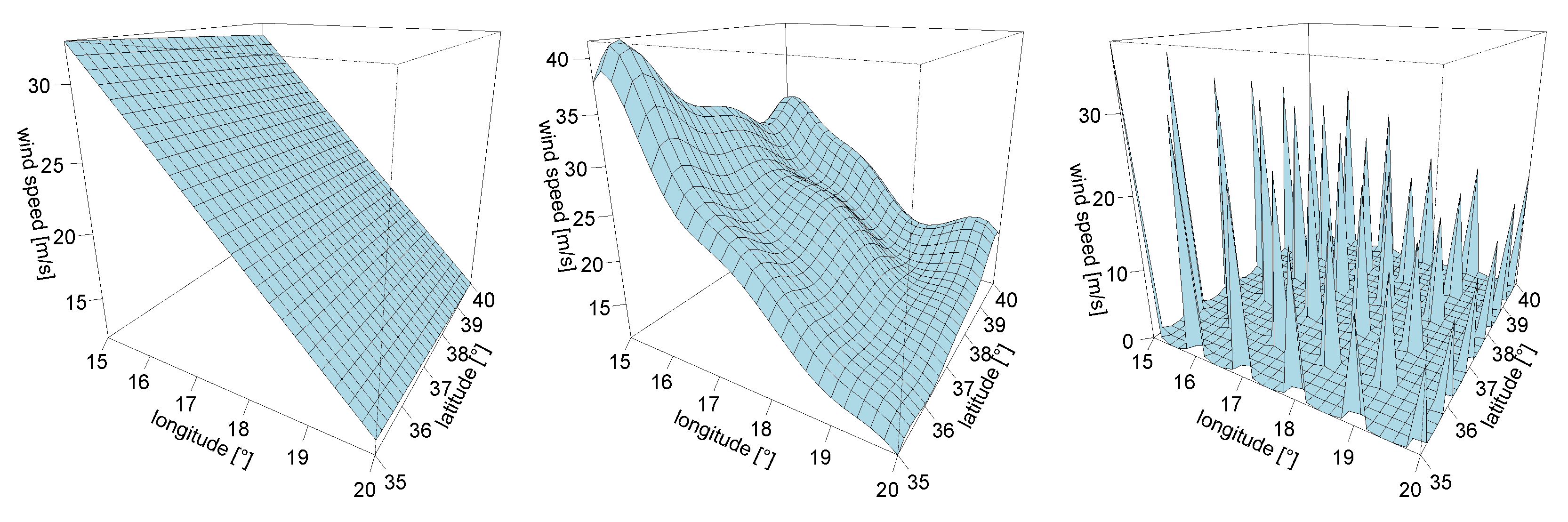
3.3. Feedforward Neural Networks
3.4. Decision Tree
3.5. Comparison of Methods
4. Monte Carlo Simulation
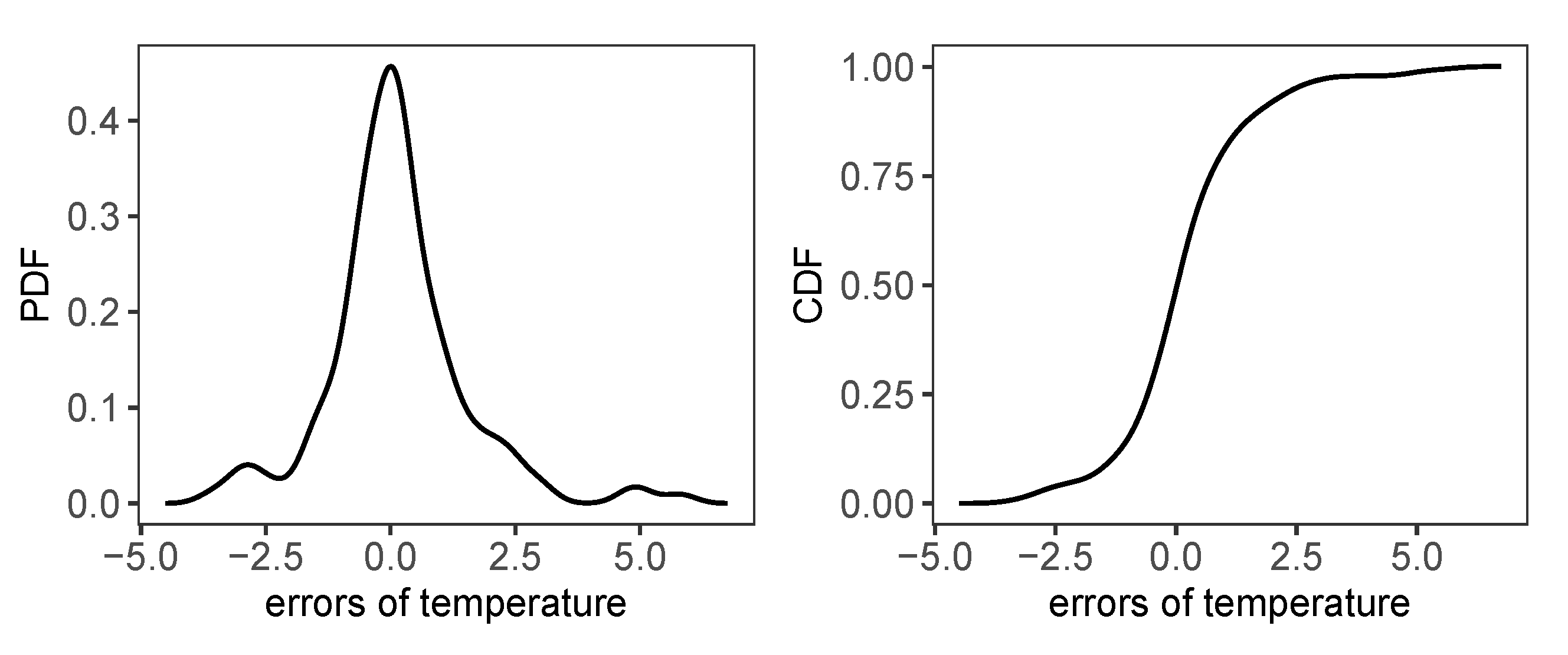
- We regard the data collected by the releasing balloons as the accurate weather data and compare the interpolation results by the Ordinary Kriging with GFS data as input. The errors are defined as the difference between the balloon data and the interpolated values by Ordinary Kriging with the GFS inputs . For ,
- Quantify and investigate the dependency among the errors , , and ;
- Select bivariate copulas such thatwhere the empirical margins with and ;
- Generate uniform pseudo-noise based on the selected copula model;
- Generate random errors with . In this step, instead of using empirical distribution function, the kernel smoothed one is used in order to avoid purely bootstrapped observations;
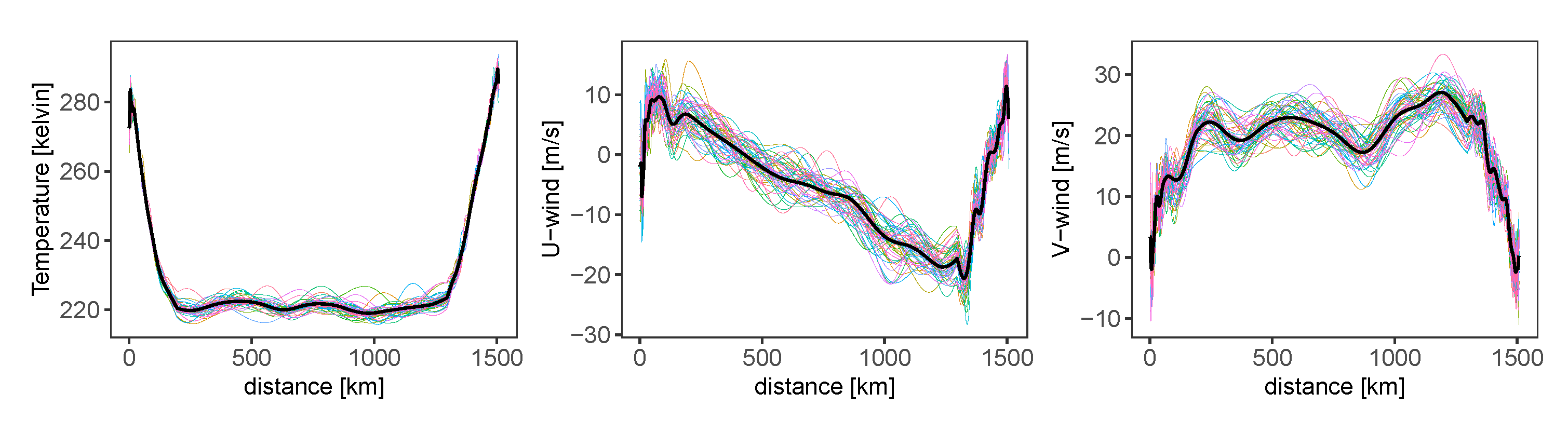
- Generate weather scenarios with GFS data and errors where weather data at each location of GFS grid has the simulated error added,
- Calculate the trajectories with Ordinary Kriging interpolations and simulated weather scenarios,
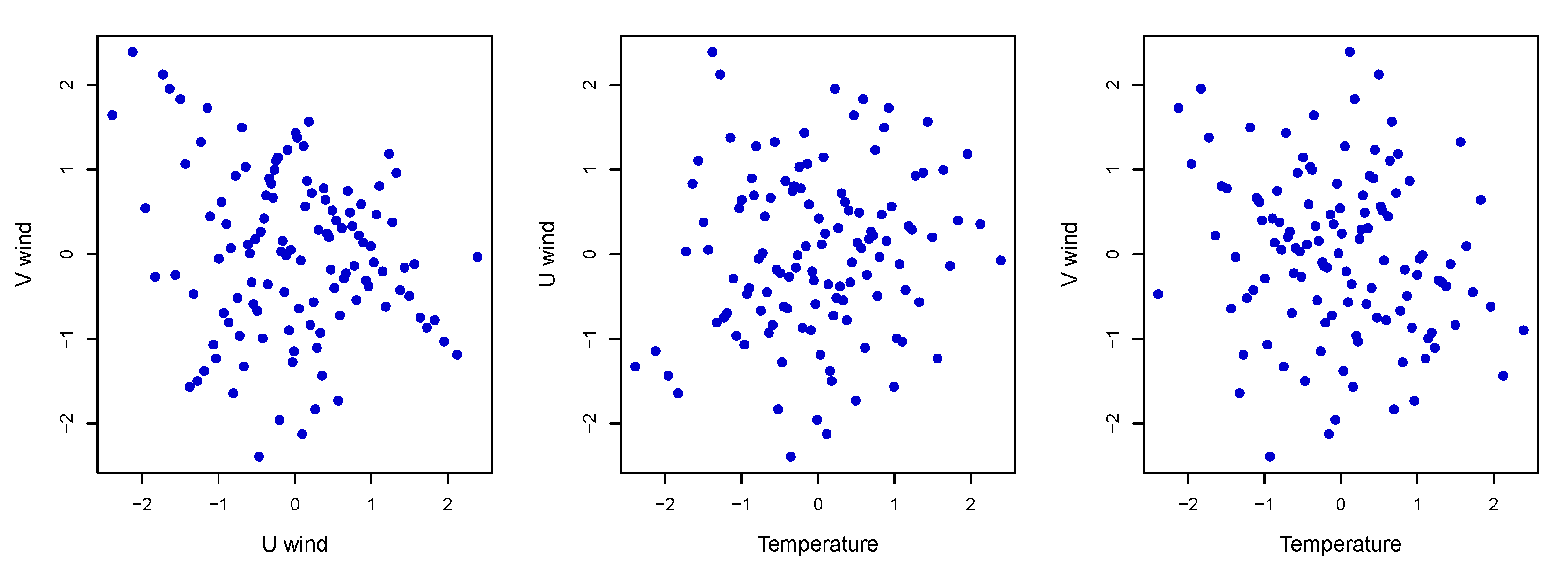
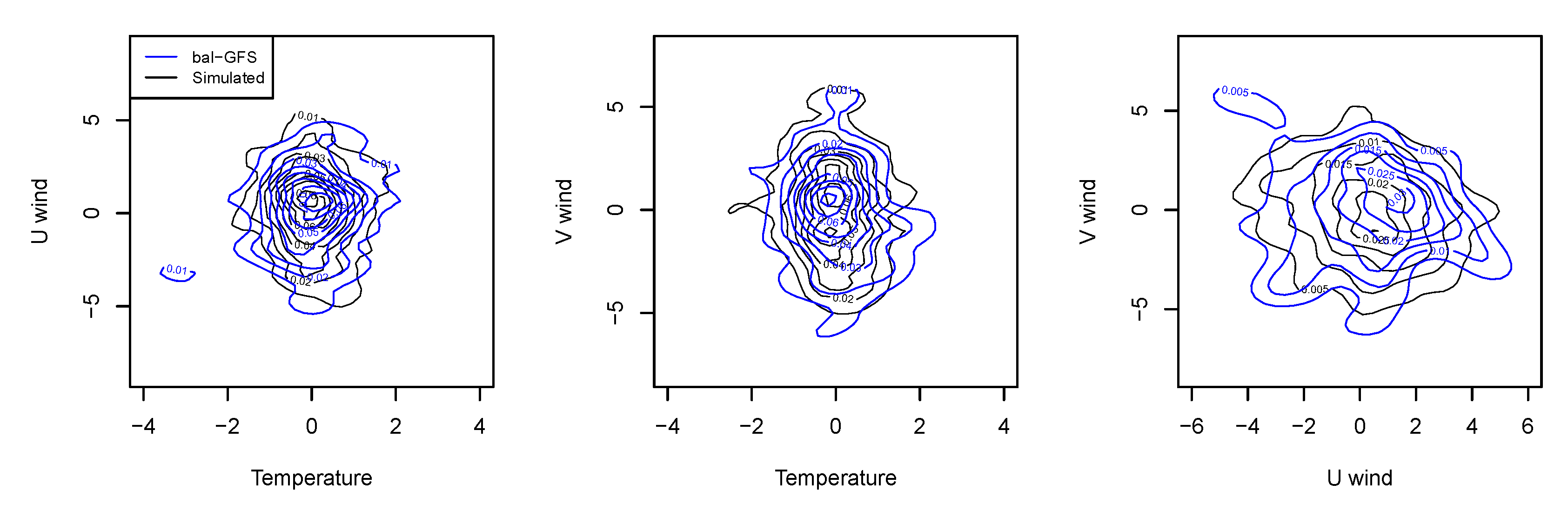
4.1. Dependency
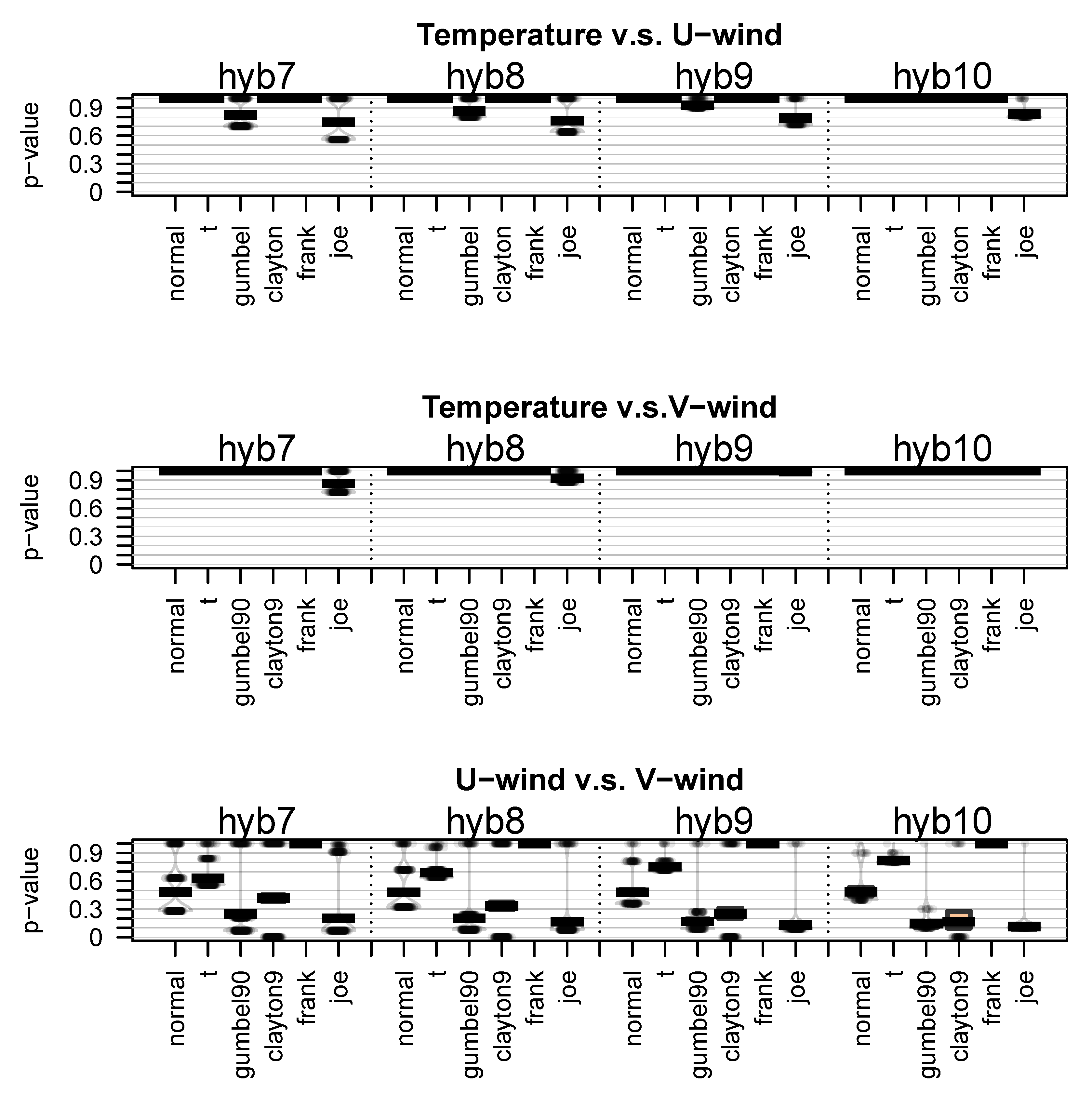
4.2. Modelling the Dependency
4.3. Empirical Margins and Random Number Generator
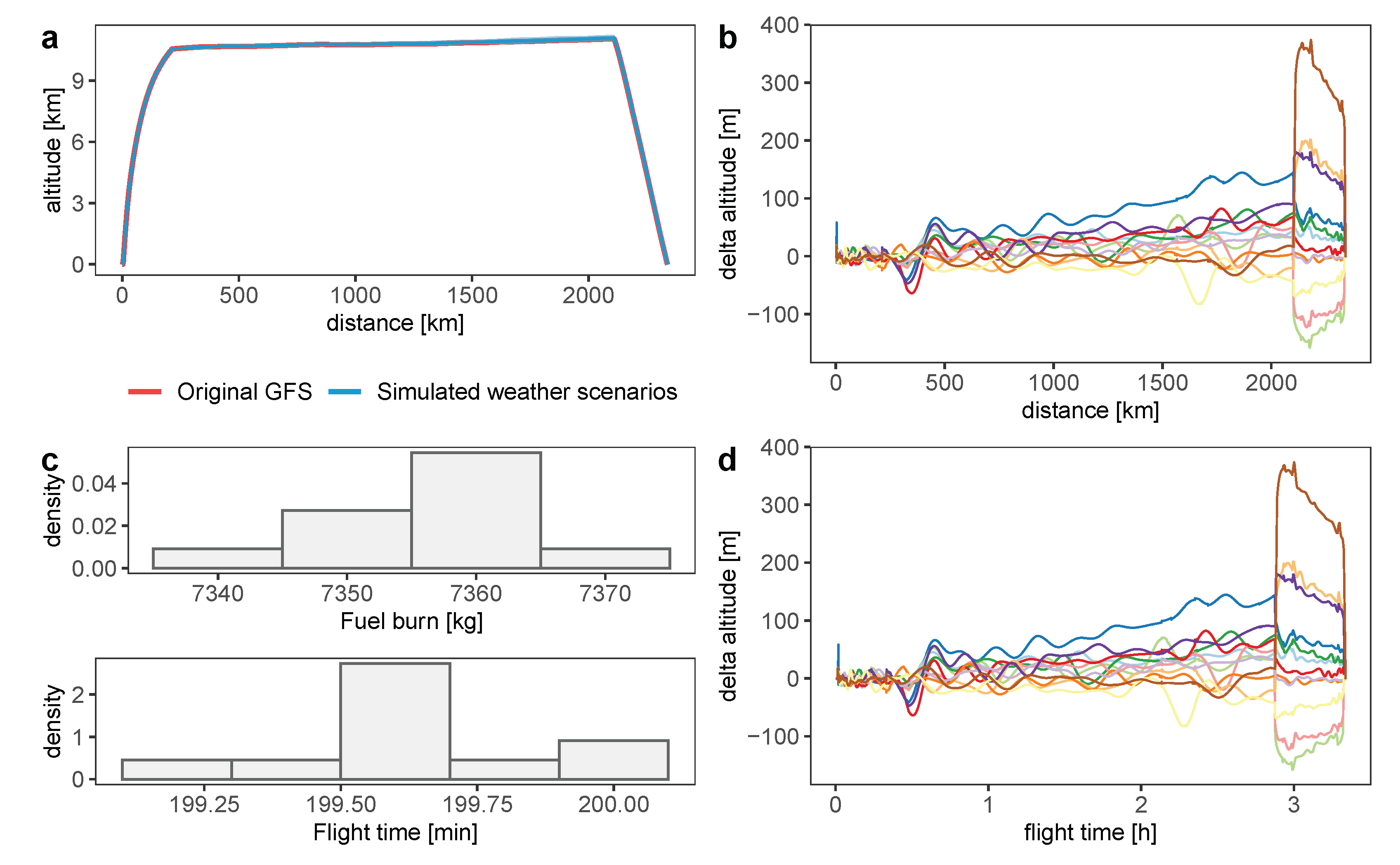
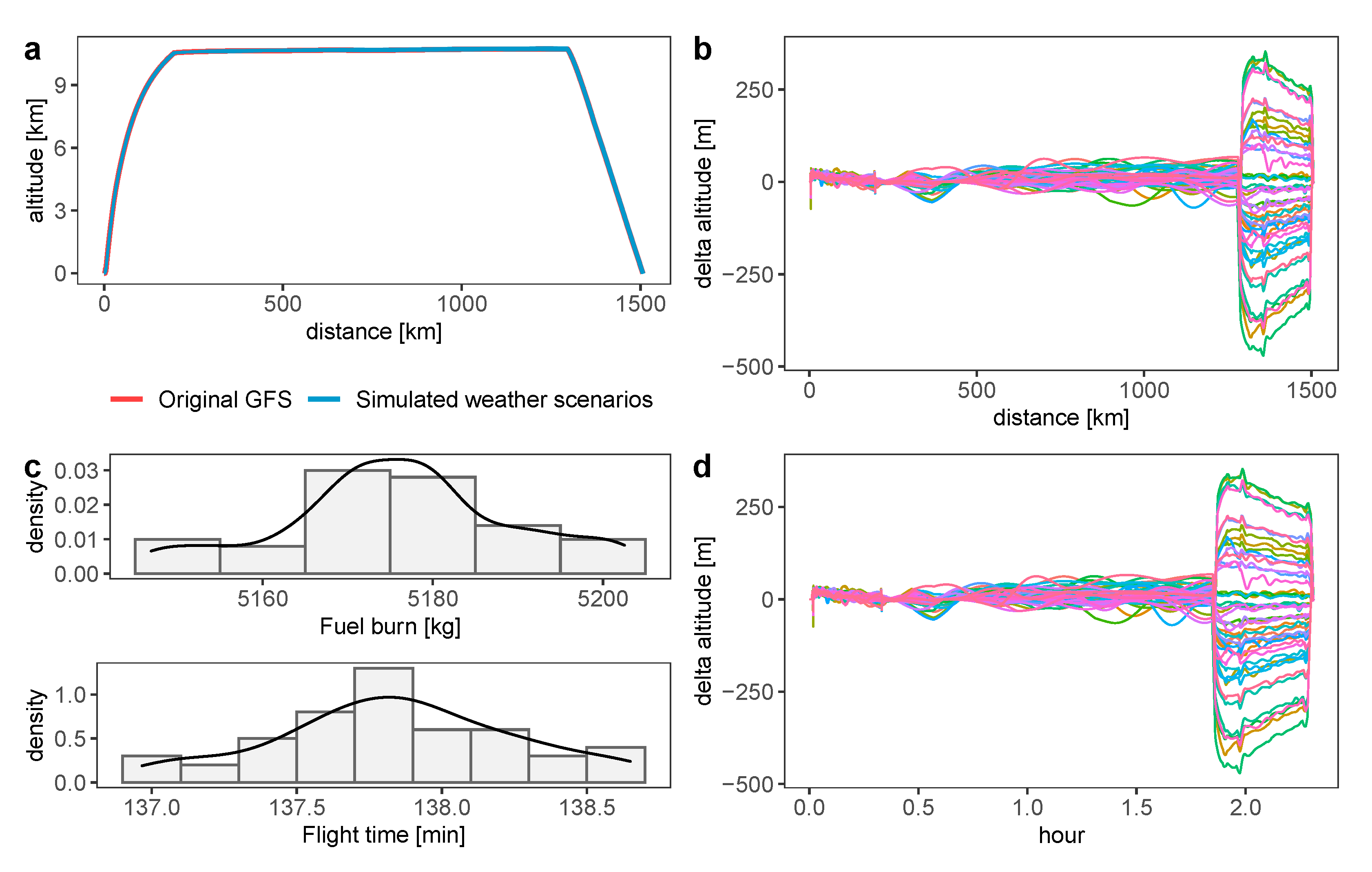
4.4. Trajectory Simulation Results
5. Conclusions
- the kernel method works better than machine learning methods for the meteorological data interpolation for a flight trajectory;
- even though errors in GFS data and Ordinary Kriging are inevitable, the inaccuracy of the data has a very minor impact on the trajectory, total fuel burn, and flight time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. A Trajectory from Nantes to Athens

References
- Rosenow, J.; Fricke, H. Flight performance modeling to optimize trajectories. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2016, Braunschweig, Germany, 13–15 September 2016. [Google Scholar]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Johnson, J.E.; Laparra, V.; Pérez-Suay, A.; Mahecha, M.D.; Camps-Valls, G. Kernel methods and their derivatives: Concept and perspectives for the earth system sciences. PLoS ONE 2020, 15, e0235885. [Google Scholar] [CrossRef] [PubMed]
- Heryudono, A.R.H.; Driscoll, T.A. Radial Basis Function Interpolation on Irregular Domain through Conformal Transplantation. J. Sci. Comput. 2010, 44, 286–300. [Google Scholar] [CrossRef] [Green Version]
- Rosenow, J.; Lindner, M.; Scheiderer, J. Advanced Flight Planning and the Benefit of In-Flight Aircraft Trajectory Optimization. Sustainability 2021, 13, 1383. [Google Scholar] [CrossRef]
- Wynnyk, C.M. Wind analysis in aviation applications. In Proceedings of the 2012 IEEE/AIAA 31st Digital Avionics Systems Conference (DASC), Williamsburg, VA, USA, 14–18 October 2012; IEEE: Williamsburg, VA, USA, 2012; p. 5C2-1. [Google Scholar]
- Förster, S.; Rosenow, J.; Lindner, M.; Fricke, H. A Toolchain for Optimizing Trajectories under Real Weather Conditions and Realistic Flight Performance; Greener Aviation: Brussels, Belgium, 2016. [Google Scholar]
- Zhang, Y.; McGovern, S. Application of the Rapid Update Cycle (RUC) to Aircraft Flight Simulation. In Volume 14: New Developments in Simulation Methods and Software for Engineering Applications, ASME International Mechanical Engineering Congress and Exposition; ASME: New York, NY, USA, 2008; pp. 45–53. [Google Scholar] [CrossRef] [Green Version]
- Félix Patrón, R.S.; Botez, R.M. Flight Trajectory Optimization Through Genetic Algorithms Coupling Vertical and Lateral Profiles. In Volume 1: Advances in Aerospace Technology, ASME International Mechanical Engineering Congress and Exposition; ASME: New York, NY, USA, 2014; p. V001T01A048. [Google Scholar] [CrossRef]
- Olivares, A.; Soler, M.; Staffetti, E. Multiphase mixed-integer optimal control applied to 4D trajectory planning in air traffic management. In Proceedings of the 3rd International Conference on Application and Theory of Automation in Command and Control Systems, Napoli, Italy, 28–30 May 2013; pp. 85–94. [Google Scholar]
- Friedland, C.J.; Joyner, T.A.; Massarra, C.; Rohli, R.V.; Treviño, A.M.; Ghosh, S.; Huyck, C.; Weatherhead, M. Isotropic and anisotropic kriging approaches for interpolating surface-level wind speeds across large, geographically diverse regions. Geomat. Nat. Hazards Risk 2017, 8, 207–224. [Google Scholar] [CrossRef]
- Zhu, A.X.; Lu, G.; Liu, J.; Qin, C.Z.; Zhou, C. Spatial prediction based on Third Law of Geography. Ann. GIS 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Wong, D.W.; Yuan, L.; Perlin, S.A. Comparison of spatial interpolation methods for the estimation of air quality data. J. Expos. Sci. Environ. Epidemiol. 2004, 14, 404–415. [Google Scholar] [CrossRef] [Green Version]
- Heddam, S.; Keshtegar, B.; Kisi, O. Predicting total dissolved gas concentration on a daily scale using kriging interpolation, response surface method and artificial neural network: Case study of Columbia river Basin Dams, USA. Nat. Resour. Res. 2020, 29, 1801–1818. [Google Scholar] [CrossRef]
- Rigol, J.P.; Jarvis, C.H.; Stuart, N. Artificial neural networks as a tool for spatial interpolation. Int. J. Geogr. Inf. Sci. 2001, 15, 323–343. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Li, J.; Siwabessy, J.; Huang, Z.; Nichol, S. Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods. Geosciences 2019, 9, 180. [Google Scholar] [CrossRef] [Green Version]
- Trüb, R.; Moser, D.; Schäfer, M.; Pinheiro, R.; Lenders, V. Monitoring meteorological parameters with crowdsourced air traffic control data. In Proceedings of the 2018 17th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Porto, Portugal, 11–13 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 25–36. [Google Scholar]
- Stone, E.K.; Kitchen, M. Introducing an approach for extracting temperature from aircraft GNSS and pressure altitude reports in ADS-B messages. J. Atmos. Ocean. Technol. 2015, 32, 736–743. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Romain, C.; Botez, R.M. 3D Cruise trajectory optimization inspired by a shortest path algorithm. Aerospace 2020, 7, 99. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Gratton, G. Initial Airworthiness; Springer: Berlin, Germany, 2016. [Google Scholar]
- Dalmau, R.; Pérez-Batlle, M.; Prats, X. Estimation and prediction of weather variables from surveillance data using spatio-temporal Kriging. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Esmaeilbeigi, M.; Chatrabgoun, O. An efficient method based on RBFs for multilayer data interpolation with application in air pollution data analysis. Comput. Appl. Math. 2019, 38, 1–20. [Google Scholar] [CrossRef]
- Fasshauer, G.; McCourt, M. Kernel-Based Approximation Methods Using MATLAB; World Scientific Publishing Company: London, UK, 2015; Volume 19. [Google Scholar]
- Nash, J.C.; Varadhan, R. Unifying Optimization Algorithms to Aid Software System Users: Optimx for R. J. Stat. Softw. 2011, 43, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Montero, J.M.; Fernández-Avilés, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; John Wiley & Sons: New York, NY, USA, 2015; Volume 998. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Perperoglou, A.; Sauerbrei, W.; Abrahamowicz, M.; Schmid, M. A review of spline function procedures in R. BMC Med. Res. Methodol. 2019, 19, 46. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: Cambridge, UK, 2016; Volume 5. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software. Available online: https://tensorflow.org (accessed on 3 March 2020).
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 3 March 2020).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin, Germany, 2009. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B.M. Hands-on Machine Learning with R; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16, 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: New York, NY, USA, 2013; Volume 751. [Google Scholar]
- Möller, A.; Lenkoski, A.; Thorarinsdottir, T.L. Multivariate probabilistic forecasting using ensemble Bayesian model averaging and copulas. Q. J. R. Meteorol. Soc. 2013, 139, 982–991. [Google Scholar] [CrossRef] [Green Version]
- Lazoglou, G.; Anagnostopoulou, C. Joint distribution of temperature and precipitation in the Mediterranean, using the Copula method. Theor. Appl. Climatol. 2019, 135, 1399–1411. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Größer, J.; Okhrin, O. Copulae: An overview and recent developments. In Wiley Interdisciplinary Reviews: Computational Statistics; Wiley Online Library: New York, NY, USA, 2021; p. e1557. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: Berlin, Germany, 2007. [Google Scholar]
- Hofert, M.; Kojadinovic, I.; Mächler, M.; Yan, J. Elements of Copula Modeling with R; Springer: Berlin, Germany, 2019. [Google Scholar]
- Zhang, S.; Okhrin, O.; Zhou, Q.M.; Song, P.X.K. Goodness-of-fit test for specification of semiparametric copula dependence models. J. Econ. 2016, 193, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Okhrin, O.; Trimborn, S.; Waltz, M. gofCopula: Goodness-of-Fit tests for copulae. R J. 2021, 13, 467–498. [Google Scholar] [CrossRef]
- Huang, W.; Prokhorov, A. A goodness-of-fit test for copulas. Econ. Rev. 2014, 33, 751–771. [Google Scholar] [CrossRef] [Green Version]
- Genest, C.; Quessy, J.F.; Rémillard, B. Goodness-of-fit procedures for copula models based on the probability integral transformation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Breymann, W.; Dias, A.; Embrechts, P. Dependence structures for multivariate high-frequency data in finance. Quant. Financ. 2003, 3, 1–14. [Google Scholar] [CrossRef]
- Scaillet, O. Kernel-based goodness-of-fit tests for copulas with fixed smoothing parameters. J. Multivar. Anal. 2007, 98, 533–543. [Google Scholar] [CrossRef]
- Phillips, N. Yarrr: A Companion to the E-Book “Yarrr!: The Pirate’s Guide to R”. Computer Software Manual]. R Package Version 0.1. 5. 2017. Available online: https:/CRAN.R-project.org/package=yarrr (accessed on 7 January 2019).
- Demarta, S.; McNeil, A.J. The t copula and related copulas. Int. Stat. Rev. 2005, 73, 111–129. [Google Scholar] [CrossRef]

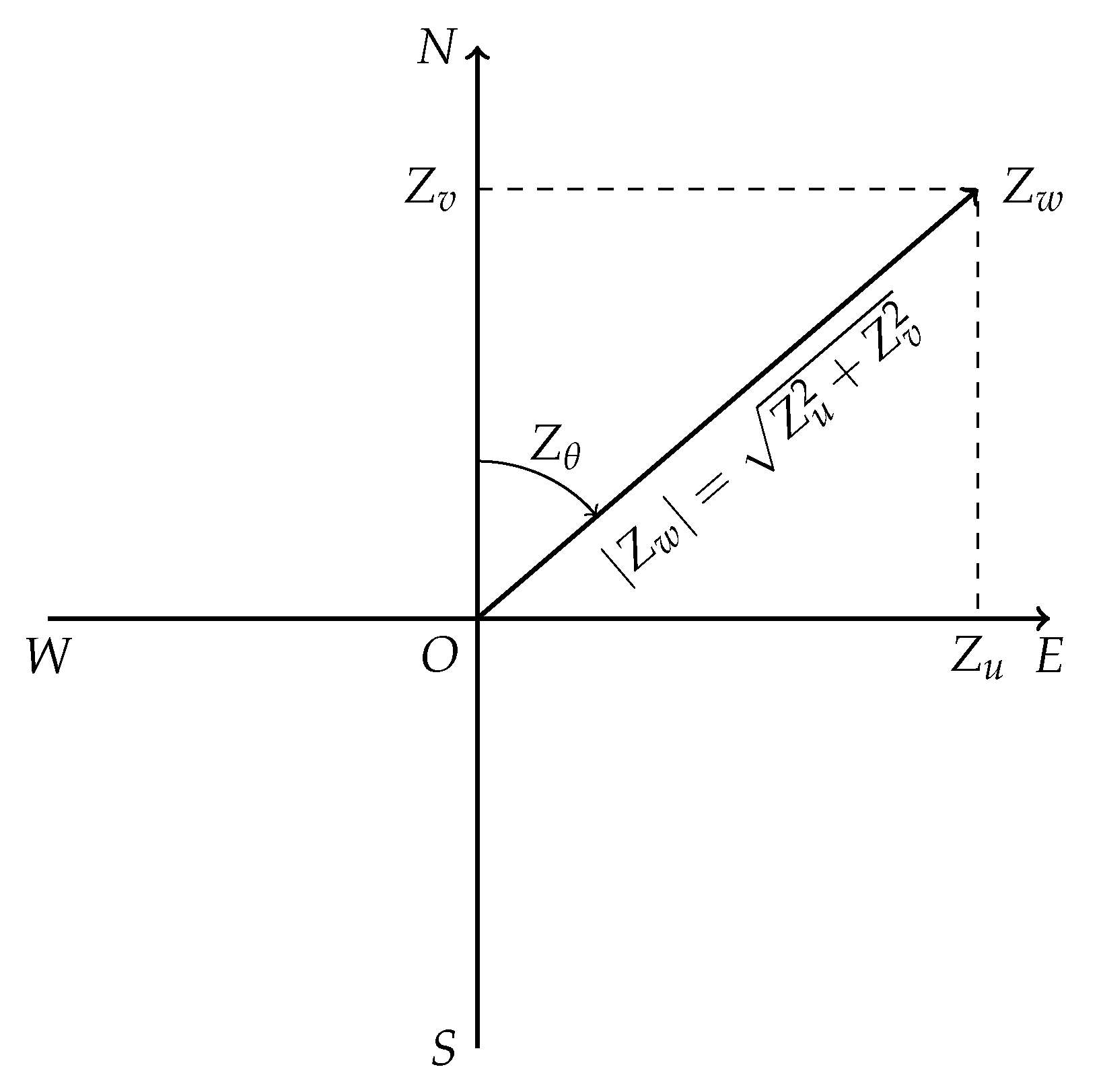
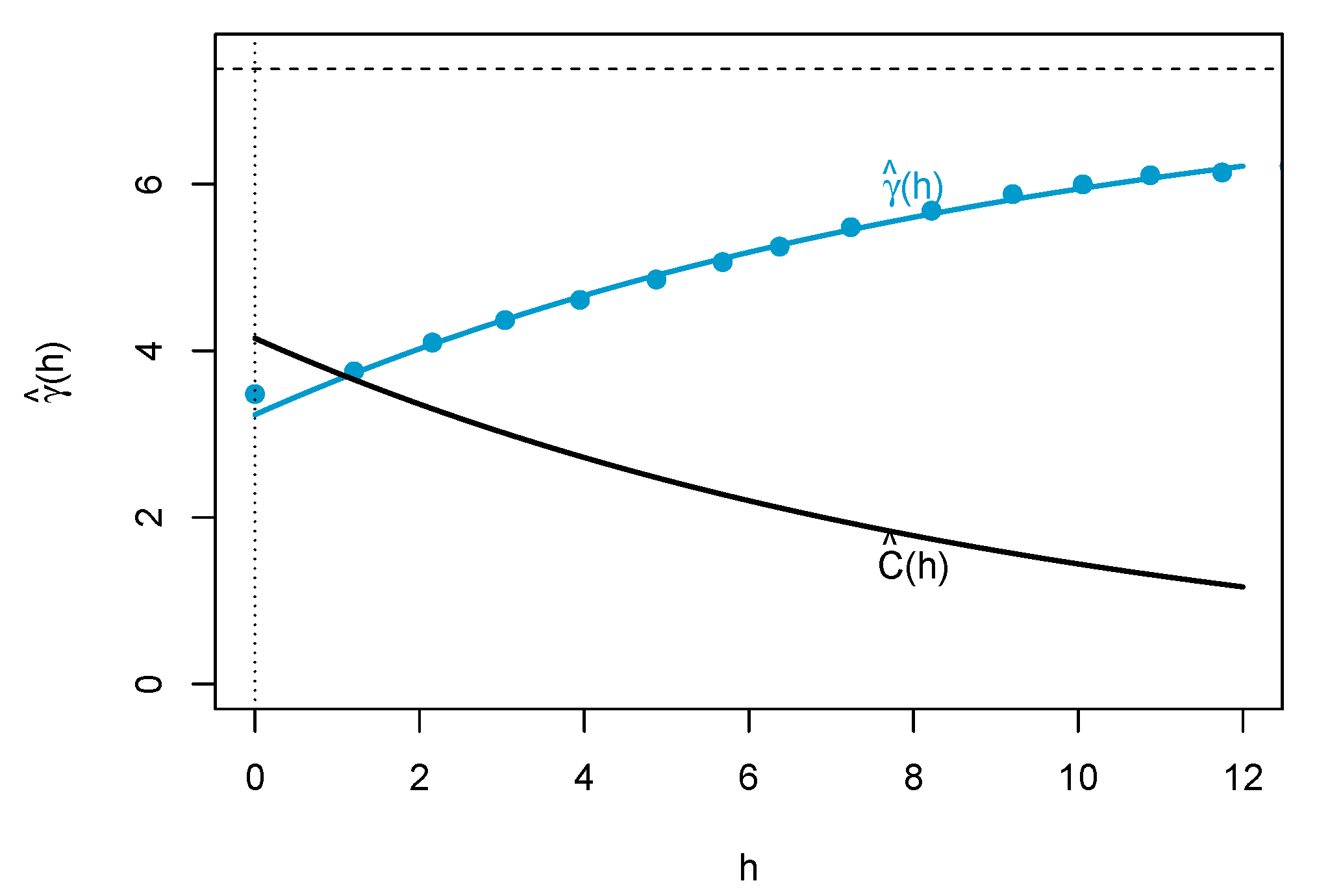


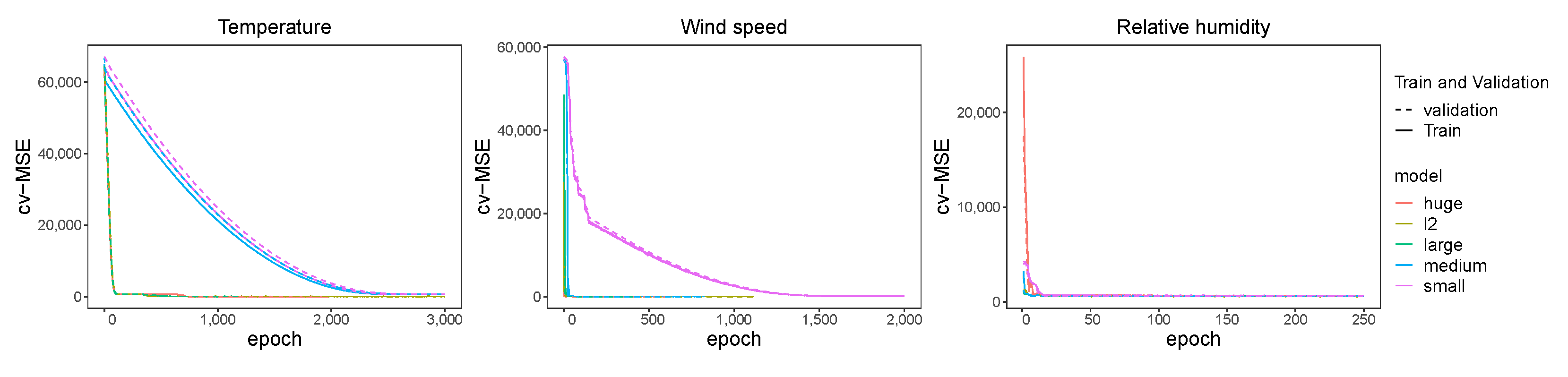
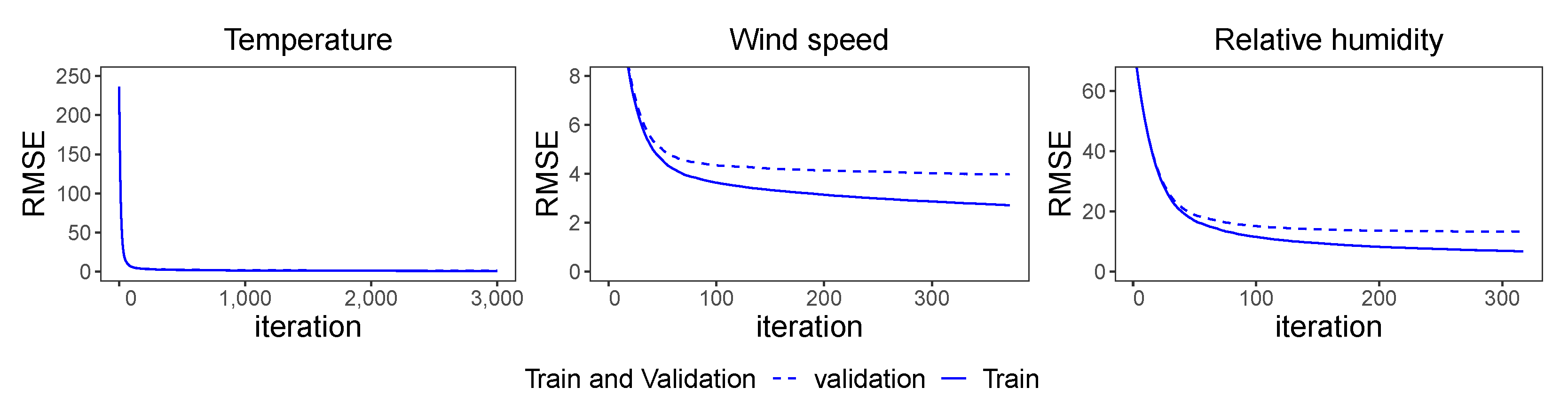

| Model Size | Units | Activation | cv-MSE 1 | |||
|---|---|---|---|---|---|---|
| Temperature (K2) | Wind Speed () | Relative Humidity (%2) | ||||
| Hidden layers | Small | 50 | tanh | 652.70 | 78.07 | 599.68 |
| Medium | 300 | tanh | 652.80 | 33.54 | 582.77 | |
| 50 | tanh | |||||
| Large | 400 | tanh | 17.05 | 34.83 | 581.41 | |
| 100 | tanh | |||||
| 50 | linear | |||||
| Huge | 500 | tanh | 7.16 | 33.16 | 424.28 | |
| 300 | tanh | |||||
| 100 | tanh | |||||
| 50 | linear | |||||
| α | 0 | 0.001 | 0.01 | 0.1 | 1 | 10 | 100 | 1000 |
|---|---|---|---|---|---|---|---|---|
| Temperature (K) | 9.84 | 6.03 | 7.28 | 11.07 | 18.59 | 9.50 | 29.46 | 536.56 |
| Wind speed () | 38.84 | 39.36 | 39.58 | 40.50 | 39.06 | 41.16 | 77.55 | 77.69 |
| Relative humidity (%) | 593.05 | 585.94 | 559.01 | 536.48 | 481.06 | 600.70 | 654.94 | 652.03 |
| Methods | loo-MSE | ||
|---|---|---|---|
| Temperature (K2) | Wind Speed () | Relative Humidity (%2) | |
| Ordinary Kriging | 11.79 | 3.53 | 69.10 |
| the RBF method | 0.42 | 1.93 | 85.73 |
| Neural Network | 13.05 | 47.33 | 678.50 |
| Bagging | 15.04 | 16.15 | 153.29 |
| GBM | 2.39 | 13.34 | 179.21 |
| Linear Interpolation | 9.31 | 13.01 | 178.11 |
| Temperature (K) | U-wind (m/s) | 0.12 | 0.19 | 0.08 | 0.08 (positive) |
| Temperature (K) | V-wind (m/s) | −0.19 | 0.04 | −0.12 | 0.02 (negative) |
| U-wind (m/s) | V-wind (m/s) | −0.13 | 0.16 | −0.10 | 0.06 (negative) |
| Family | |||
|---|---|---|---|
| Gumbel | |||
| Clayton | |||
| Frank | |||
| Joe |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Fricke, H.; Okhrin, O.; Rosenow, J. Importance of Weather Conditions in a Flight Corridor. Stats 2022, 5, 312-338. https://doi.org/10.3390/stats5010018
Chen G, Fricke H, Okhrin O, Rosenow J. Importance of Weather Conditions in a Flight Corridor. Stats. 2022; 5(1):312-338. https://doi.org/10.3390/stats5010018
Chicago/Turabian StyleChen, Gong, Hartmut Fricke, Ostap Okhrin, and Judith Rosenow. 2022. "Importance of Weather Conditions in a Flight Corridor" Stats 5, no. 1: 312-338. https://doi.org/10.3390/stats5010018
APA StyleChen, G., Fricke, H., Okhrin, O., & Rosenow, J. (2022). Importance of Weather Conditions in a Flight Corridor. Stats, 5(1), 312-338. https://doi.org/10.3390/stats5010018








