All-NBA Teams’ Selection Based on Unsupervised Learning

Abstract

All-NBA Teams’ selections have great implications for the players’ and teams’ futures. Since contract extensions are highly related to awards, which can be seen as indexes that measure a players’ production in a year, team selection is of mutual interest for athletes and franchises. In this paper, we are interested in studying the current selection format. In particular, this study aims to: (i) identify the factors that are taken into consideration by voters when choosing the three All-NBA Teams; and (ii) suggest a new selection format to evaluate players’ performances. Average game-related statistics of all active NBA players in regular seasons from 2013-14 to 2018-19, were analyzed using LASSO (Logistic) Regression and Principal Component Analysis (PCA). It was possible: (i) to determine an All-NBA player profile; (ii) to determine that this profile can cause a misrepresentation of players’ modern and versatile gameplay styles; and (iii) to suggest a new way to evaluate and select players, through PCA. As the results of this paper a model is presented that may help not only the NBA to better evaluate players, but any basketball league; it also may be a source to researchers that aim to investigate player performance, development, and their impact over many seasons.

1. Introduction

The evolution of a sport can occur in a variety of ways, e.g., that gameplay style may change over the years. Basketball, a sport invented in 1981 by Canadian James Naismith, is obviously susceptible to these changes. Throughout the years of its existence, multiple rules were developed or added to improve and change the game, as studied by Štrumbelj et al. [1], and Nourayi [2].

The most impacting changes in basketball’s gameplay has been, arguably, the creation of the three-point line, which in the National Basketball Association (NBA) League was introduced in the 1979–80 season. Thus, since the moment of its creation, in every league, but mainly in the NBA, recognized as one of the biggest and more competitive basketball leagues in the world, the sport has changed gradually over the years [3].

As a result of these changes, it is possible to notice that concepts, styles, and strategies that were commonly used in the past may not correspond to what is seen in the contemporary sport [4]. This affects the roles and functions performed by players on court [5], their classifications, and ways to evaluate/compare them.

Since its early years, the interest in analyzing, awarding and selecting the best players in the NBA has been very important. In the big-data Era, this relevance evolves constantly, and sports analytics has a growing impact [6].

Concerning the NBA awards, together with the Most Valuable Player (MVP), Defensive Player of The Year (DPOY), Sixth Man of The Year (SMOY), and other awards, the NBA annually selects the All-NBA Teams. These are teams that are formed, in theory, of the fifteen best players in the league, in that season, divided into first, second and third teams selected by one-hundred media figures nominated by the NBA itself.

The All-NBA Teams’ selection has many implications for players and teams. Since contract extensions are highly related to awards, which can be seen as indexes that measure a players’ production year by year, this is something of mutual interest to athletes and franchises [7].

To players, bigger contracts usually mean financial security. On the other hand, to franchises, especially small-market teams, they lead to the contractual security of having a long-term contract with one of the top talents of the NBA in their team, not only for competing purposes, but also for revenue [8].

As Yang and Lin [9] found evidence that the size of the local market is positively correlated with player salaries, small-market teams need the assurance that a valuable player cannot leave the franchise without any trade value.

Therefore, it is of importance to better study how the All-NBA Teams’ selection is done. Berri et al. [10] studied the All-Rookie Teams’ selection, which is voted by NBA coaches (as opposed to the media in the All-NBA case) and found that points scored had the greatest impact on voting, showing that even coaches might rely upon personal preferences, visual observations and lack of quantitative analysis. As the current All-NBA selection format is through media voting, unfortunately the same might happen, where biases created by subjective opinions can create inconsistencies in the process.

Another important question is that the All-NBA Teams’ structure has been the same since 1956, in which the voters select two guards, two forwards and one center for each ideal team. In modern basketball, this is an extremely relevant question, due to the fact that it is not possible anymore to label players’ functions in court only by their position names.

Traditional positions define roles that are limited when translated to what modern NBA players do on court. Centers are not limited to play in the painted area gathering rebounds and blocking shots anymore; guards are not only responsible for creating offensive opportunities to teammates and acting mainly in the three-point line; and forwards are now recognized as being more versatile players, as studied by Sampaio et al. [11].

Examples of players that cannot be defined anymore by classical positions grow more and more common in the NBA, and perhaps one of the most representative players of these changes is Draymond Green of the Golden State Warriors. During a five-year period (2013-2018), in which the Warriors dominated the NBA and Western Conference, Green developed an essential role, which consisted in being a hybrid between center and forward.

Due to his versatility, Draymond can defend almost any position in court, and especially against centers more focused on the classical role, and offensively had a three-point percentage, good enough to draw attention from the opposition, thus the Golden State Warriors popularized the style widely known and discussed today as Small-Ball.

In these situations, Green was neither a classical forward or a classical center. However, to the league he is classified as a forward, which raises the question of how to evaluate fairly the performance of a player that, on court, plays such a different role than that he is labeled as.

Like Draymond Green, players such as LeBron James, Giannis Antetokounmpo, Nikola Jokić and many others can impact the game in so many ways that they cannot be labeled by their original/classical positions. In these cases, alare players that are classified as small forward, power forward, and center, responsible for coordinating the offensive actions of their teams, a function previously exclusively assigned to (point) guards.

Page et al. [12] showed the NBA evolution in the increasing desire for players that are able to play more than one position on court and perform multiple tasks. Bianchi et al. [13] studied these changes, confirming that classical positions no longer represent the modern players’ style of play, and created five new positions to better classify these players.

Therefore, identifying the factors that are taken into consideration by the voters nominated by the NBA while choosing the three All-NBA Teams is of extreme relevance to determine if the classical positions and labels are still useful parameters to evaluate athletes’ performances nowadays, or cause misrepresentation of the actual modern style of play and of the choice of best players in a season.

The current format’s restriction to a limited number of players in a certain position also can bring inconsistencies, by limiting All-NBA Teams to having two guards, two forwards and one center, affecting not only the total misrepresentation of what an ideal team should look like, but leafing many players, such as centers, left out of teams and judged by the number of All-NBA Teams spots available, and not by their season overall performance, as should be the case.

However, to the best of our knowledge, none of the previous studies have examined All-NBA Teams’ selection, nor proposed a new selection format. Thus, the present study aims to identify the factors that are taken into consideration by voters when choosing the three All-NBA Teams via LASSO (Logistic) Regression, and suggests a new way to evaluate players’ performances and select teams via Principal Component Analysis (PCA) and its first principal component (PC1).

Through the LASSO Regression, which performs regularization, variable selection, and solves any multicollinearity issues between variables, a more interpretable resulting model helps in investigating which variables are statistically significant to the dependent binary variable created (named All-NBA), which takes values of 0 or 1, indicating the selection or not of a player to any of the All-NBA Teams in the studied years for each position analyzed.

Furthermore, the PCA, an unsupervised machine learning algorithm that performs dimensionality reduction in the initial dataset, helps us to better visualize, understand and describe our data. Through biplots, it is possible to study differences between players’ gameplay styles, without a significant loss in information.

In addition, as the principal components are formed by linear combinations of the original variables, and the PC1 can be defined as the component that explains most of the variance of the original data, it improves the performance evaluation format by providing an alternative that takes into consideration all variables, without losing considerable information in the process.

Since theses selections are not only part of a season’s individual work recognition, but directly influence the players’ contract negotiations, it is extremely important that they are carried out in the best way possible.

The rest of this paper is organized as follows. Section 2 gives a detailed description of the data and of the methods used. Section 3 presents the results and discussion, including analysis of the All-NBA team selection through the LASSO regression model, and suggests an alternative method to evaluate and select All-NBA team players via principal component analysis. The paper ends with a conclusion in Section 4.

2. Materials and Methods

2.1. Data Description

Complete data from all active players between the 2013–2014 to 2018–2019 seasons were obtained from the open-access website “basketball-reference.com”, accessed on 15 December 2021.

The following variables were studied: Player position (POS), Games played (G), Minutes per game (MP), Three-point shots converted per game(3P), Three-point shots attempted per game (3PA), Two-point shots converted per game (2P), Two-point shots attempted per game (2PA), Free-throws converted per game(FT), Free-throws attempted per game (FTA), Offensive rebounds per game (ORB), Defensive rebounds per game (DRB), Assists per game (AST), Blocks per game (BLK), Turnovers per game (TOV), Personal Fouls per game (PF) and Points per game (PTS).

The final dataset, containing 15 per-game average variables of the 3006 observations, i.e., of each active player from each season (between 2013–14 to 2018–19), used in this paper is available upon request.

2.2. LASSO Regression

To study the voters’ All-NBA Teams’ selections, a logistic regression was considered. However, high levels of multicollinearity between covariables were found, and to solve this problem the Least Absolute Shrinkage and Selection Operator (LASSO) Regression was performed, as the LASSO Regression performs L1 regularization, penalizing equally the absolute value of the magnitude of the coefficients aiming to minimize

$${\displaystyle \sum }_{i=1}^n{\left(y_i-{\displaystyle \sum }_j{x}_{ij}{\beta }_j\right)}^2+\lambda {\displaystyle \sum }_{j=1}^P\left|{\beta }_j\right|.$$

(1)

Some of the estimated beta coefficients are shrunk to zero, which results in a more interpretable regression model [14].

In Stage 1, this allowed us to explore the effects of each variable in the selection of a player to an All-NBA Team, determining if a given variable is significant, positively, or negatively, to a players’ All-NBA Team selection. This was done by considering the effects of the fifteen variables defined above in a binary response variable, All-NBA, which takes values of 0 and 1, indicating if a player had been selected to an All-NBA Team in the seasons studied.

All analyses were made using the statistical software R [15].

2.3. Principal Component Analysis (PCA)

In this study, we analyze multivariate data making use of one of the most widely known statistical methods or unsupervised machine learning algorithms, Principal Component Analysis (PCA).

Universally recognized as a technique to perform dimensionality reduction and better visualization [16], Principal Component Analysis has its central idea as describing the variability of the original data as a collection of non-correlated orthogonal variables formed by the linear combination of the original variables in the dataset.

These non-correlated variables, obtained in a decreasing order of importance, are called principal components. Thus, the first principal component (in this paper, referred as PC1) explains most of the original data, followed by the second principal component (PC2) that is orthogonal to PC1 and explains most of the original data that is not explained by the first principal component, followed by the other principal components that adhere to the same principle.

Lastly, when most of the variability of the original data has been explained by a set of principal components, the original variables can be replaced by these, without a significative loss in information, consequently resulting in a dimensionality reduction of the original dataset.

To help visualization of the latent variables and better interpretate the results, we used biplots [17,18]. More information on about Principal Component Analysis can be found in, e.g., Jolliffe [16] and Johnson & Wichern [19].

In Stage 2, after studying the effects of all variables in the selection of a player to the All-NBA Teams, PCA was performed with the game-related dataset, aiming to find similarities and differences between players in different and same positions, and a better method of evaluating and selecting players for the teams through the first principal component (PC1).

3. Results and Discussion

Aiming to study which factors are determinant, based on voters’ choices, in selecting players to one of the All-NBA Teams, LASSO Regression models were adjusted to all data from players available from the 2014-15 to 2018-19 NBA regular seasons.

Average game-data from all active players were standardized and studied. The first six rows from the original dataset can be seen in

Table 1. First six rows of the dataset of all active players in the NBA seasons from 2014 to 2019.

Year	Player	Pos	G	MP	3P	3PA	2P	2PA	FT	FTA	ORB	DRB	AST	STL	BLK	TOV	PF	PTS	All-NBA
2014	Quincy Acy	F	7	8.7	0.3	0.7	0.6	1.3	0.7	1.1	0.7	1.4	0.6	0.6	0.4	0.3	1.1	2.7	0
2014	Quincy Acy	F	56	14.0	0.0	0.2	1.0	2.1	0.5	0.8	1.2	2.4	0.4	0.3	0.4	0.5	2.0	2.7	0
2014	Steven Adams	C	81	14.8	0.0	0.0	1.1	2.3	1.0	1.7	1.8	2.3	0.5	0.5	0.7	0.9	2.5	3.3	0
2014	Jeff Adrien	F	25	10.2	0.0	0.0	0.9	1.6	0.5	1.0	1.3	2.2	0.3	0.3	0.6	0.3	1.4	2.3	0
2014	Jeff Adrien	F	28	25.2	0.0	0.0	4.3	8.4	2.3	3.4	2.5	5.3	1.1	0.6	0.8	1.1	2.6	10.9	0
2014	Arron Afflalo	G	73	35.0	1.8	4.1	4.6	9.7	3.8	4.6	0.4	3.2	3.4	0.5	0.0	2.0	1.9	18.2	0

* G = Games Played, MP = Minutes played, 3P = Three-point shots converted, 3PA = Three-point shots attempted, 2P = Two-point shots converted, 2PA = Two-point shots attempted, FT = Free throws converted, FTA = Free throws attempted, ORB = Offensive rebounds, DRB = Defensive rebounds, AST = Assists, STL = Steals, BLK = Blocks, TOV = Turnovers, PF = Personal Fouls, PTS = Points scored.

. In addition, the All-NBA indicator variable was created to indicate which players have been selected to any of the All-NBA Teams in a season, so a logistic regression model (LASSO) could be adjusted to the data.

Players that eventually changed teams in the middle of the season had their data grouped in the study. As seen in Table 1, players such as Quincy Acy and Jeff Adrien changed teams in the 2014 NBA season, therefore their data is grouped by season.

However, a model that studied the significant variables of players in a general way would not be representative of the voters’ choices. Thus, the original dataset was divided by the players’ classical position, i.e., positions that the voters must select: Guards (Point Guards and Shooting Guards), Forwards (Small Forwards and Power Forwards) and Centers.

3.1. Revisiting the Classical Definition of Basketball Positions

Since this part of the study will be based on players’ classical positions, it is important to revisit the definitions of each. Historically, the main positions in the basketball courts are the same used to select the All-NBA Players, i.e., Guards, Forwards and Centers.

Throughout the years, as the sport evolved, some positions became more specialized than others and the five positions known today have been adopted: Point Guard, Shooting Guard, Small Forward, Power Forward and Center.

Table 2. Classical positions’ brief description.

Position	Role
Point Guard	Is often considered the brain of the team, or the general in court, and usually has the primary function of creating offensive opportunities to his teammates, organizing the offense and coordinating the play calls. Usually is the shortest player on court, the fastest and the best ball handler.
Shooting Guard	Usually is the player that has the most scoring abilities, scoring from the three-point line, mid-range area and slashing, acting both with and without the ball. Can also be the defender responsible for guarding the opposition’s best player.
Small Forward	Often considered the most versatile and athletic player on court, they can score in diverse ways, and help on the defensive end and with rebounding.
Power Forward	Strong and tall players, who have their functions directed more to the post or low block, able to score in physical battles and help the team with rebounding numbers.
Center	Traditionally the tallest player on court, responsible for rebounding the ball both in offense and defense, as he tends to play near the basket. Generally, his main role is paint protection, and offensively is capable of creating opportunities for his teammates through screens, and for himself via size advantage and offensive rebounds.

presents a brief description of what each position’s role is on court.

It is evident that these definitions often do not correspond to the roles of some players in modern day basketball. As an example, LeBron James and Nikola Jokic, are respectively a Small Forward and a Center in their teams, but their key role on court that one of a point guard, without abandoning their traditional roles.

3.2. Stage 1–Studying the Voters’ Picks through LASSO Regression

As mentioned above, the objective of this Stage was to study the All-NBA Teams’ selections through logistic regression, identifying the most crucial factors (variables) for a player to be selected to an All-NBA Team in his respective position. However, since the model’s covariables show high levels of multicollinearity, we opted to adjust a LASSO (Least Absolute and Selection Operator) regression instead of the logistic regression, which performs both variable selection and model regularization to enhance its interpretability [14].

The optimal lambda value was obtained using the “glmnet” package [20] in the R Software [15].

Table 3. Estimated beta coefficients of the statistically significant variables of the LASSO Models, divided by position of active players in the 2018-19 season.

	Guards	Forwards	Centers
Variables	Coefficients	Coefficients	Coefficients
G	0.0496	0.0718	0.0977
MP	-	-	0.1447
3P	2.1453	-	−1.0320
3PA	−0.8843	-	-
2P	0.0053	0.4433	0.1473
2PA	-	-	-
FT	-	0.1391	-
FTA	-	-	0.9852
ORB	-	-	-
DRB	0.1174	0.8524	0.3360
AST	0.4382	0.8473	0.9097
STL	1.8126	1.8672	−1.4266
BLK	−0.5027	0.5603	0.2695
TOV	−0.7137	-	−1.0662
PF	−0.5210	−1.1162	-
PTS	0.5516	0.2252	-

* G = Games Played, MP = Minutes played, 3P = Three-point shots converted, 3PA = Three-point shots attempted, 2P = Two-point shots converted, 2PA = Two-point shots attempted, FT = Free throws converted, FTA = Free throws attempted, ORB = Offensive rebounds, DRB = Defensive rebounds, AST = Assists, STL = Steals, BLK = Blocks, TOV = Turnovers, PF = Personal Fouls, PTS = Points scored.

shows the estimated beta coefficients for the statistically significant variables for each model adjusted. The non-significant variables are assigned with a “-”, signaling that they were not selected to that model by the LASSO regression selection process.

It should be clear that we are using LASSO regression as a predictive model for the All-NBA selections because of its interpretability, and not to make an inference about individual model parameters. This means that when a model parameter is mentioned in this analysis, we are focusing on the overall model itself and its predictability. The subject of selective inference for model parameters in regressions such as LASSO is another wide field of research, with relevant results provided by [21,22].

Table 3 presents which variables have a positive or negative impact in selection of players to the All-NBA Teams in each position, according to the voters’ picks.

Starting on the offensive side of the game, it is possible to see that the number of points produced by a player (PTS) is significative for all positions but Centers, which can indicate that voters still search for classic centers that have roles related more to paint and rim protection (BLK) and defensive rebounding (DRB).

Another point that indicates a search for a more classical Center is the number of three-point shots converted (3P), which among centers has a negative impact, with a high estimated beta coefficient. This can be seen as in contradiction to the modern basketball playstyle, where many centers have been adding the three-point shot to their offensive arsenal.

Furthermore, as shown in other studies [4], the importance of the three-point shot has been growing as a crucial factor in winning games in the regular season, and teams are investing more and more in players in any position that can shoot behind the arc and help to space the floor better. However, in the models adjusted, it is possible to see that only guards reflect this change.

Other offensive variables, such as number of assists (AST), show a positive impact for all positions, which is expected, as the importance of creating offensive opportunities to teammates has been widely highlighted by previous studies. As also expected, the number of turnovers (TOV) must be controlled by players, especially guards, yet what caught more attention in the models is that, for forwards, the variable is not significant, which can reflect the outdated idea that the position does not have a role centered in handling the ball, as guards have. Considering center and turnovers (TOV), usually the idea that centers do not handle the ball as much comes to mind, so the high estimated beta coefficient in the model negatively impacts the selection of a player and may jeopardize centers that, like Jokic, handle the ball more.

The importance of free throws (FT) has been strongly highlighted throughout the years, especially for being the easiest way to score in the game, in theory, given that there is no defense, and it is it important for players to look for these kinds of opportunities. This is displayed by the centers, who by playing a very physical game near the rim can get a lot of opportunities to shoot free throws (FTA), and by the forwards that can generate easy points by drawing contact from the defense and converting free throws (FT).

Moving to the defensive side of the game, what can be seen is, as expected, players in general should not make mistakes defensively that result in a foul (PF), but only centers do not have this variable as being significant in their model.

Steals (STL) and blocks (BLK) show very well the contrast between roles in the classical positions, as it is possible to see that both variables are significant in all models. Centers concede a penalty for stealing the ball (STL), as opposed to guards who are rewarded for this, and when blocking the ball (BLK), centers are rewarded, as opposed to guards who are penalized. Once more, this can reflect the classical defensive functions of these players, where guards are responsible for perimeter defense, centers responsible for rim protection, and forwards also play a more versatile defensive role.

However, defensive schemes, as the offensive side of the game evolved largely around the three-point shot, also evolved. The number of players that can guard more than one position in court, and are not limited to only one defensive role, is constantly increasing. This is even more important and valued nowadays, as switches are extremely common in any defensive scheme.

By analyzing Table 3, an All-NBA Player profile can be constructed for each position from the voter’s picks. As previously presented, these profiles directly reflect the classical positions of basketball, but in a manner even more generalized, given that five positions are used to analyze the game, its lineups and statistics, and to compare players. Yet All-NBA selections still only use three positions, which does not fully represent the complexity and modernity of today’s basketball.

Another interesting point presented in Table 3 is the number of games played (G) and minutes per game (MP). There is no written rule for a specific number of games played for award selections. Still, it is a sensitive point of discussion in the basketball world, and according to the model the number of games played in a season is something taken into consideration by voters. However, curiously, the number of minutes played is only significative for centers.

From this, we can argue that the All-NBA Teams’ selections may not correctly evaluate the performance of the players that impacted their franchises and the league in general in a regular season, given that the model indicates that voters still judge players and their positions by standards that are not aligned with the modernity and complexity of roles and functions in today’s basketball. Accordingly, players who do not fit in a classical profile can be evaluated wrongly and be left out of selections.

3.3. Stage 2–A New Way to Evaluate Players and Select All-NBA Teams

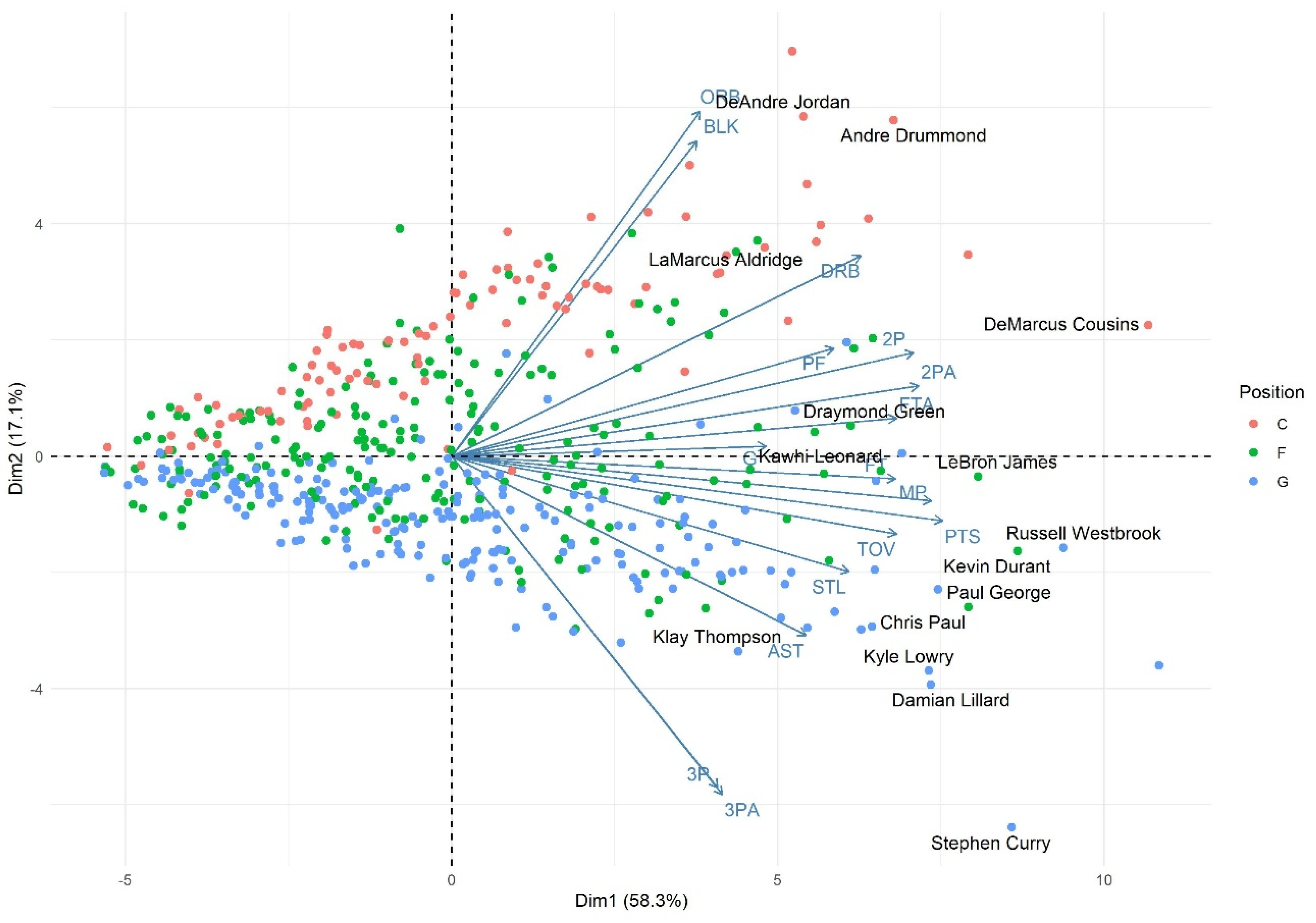
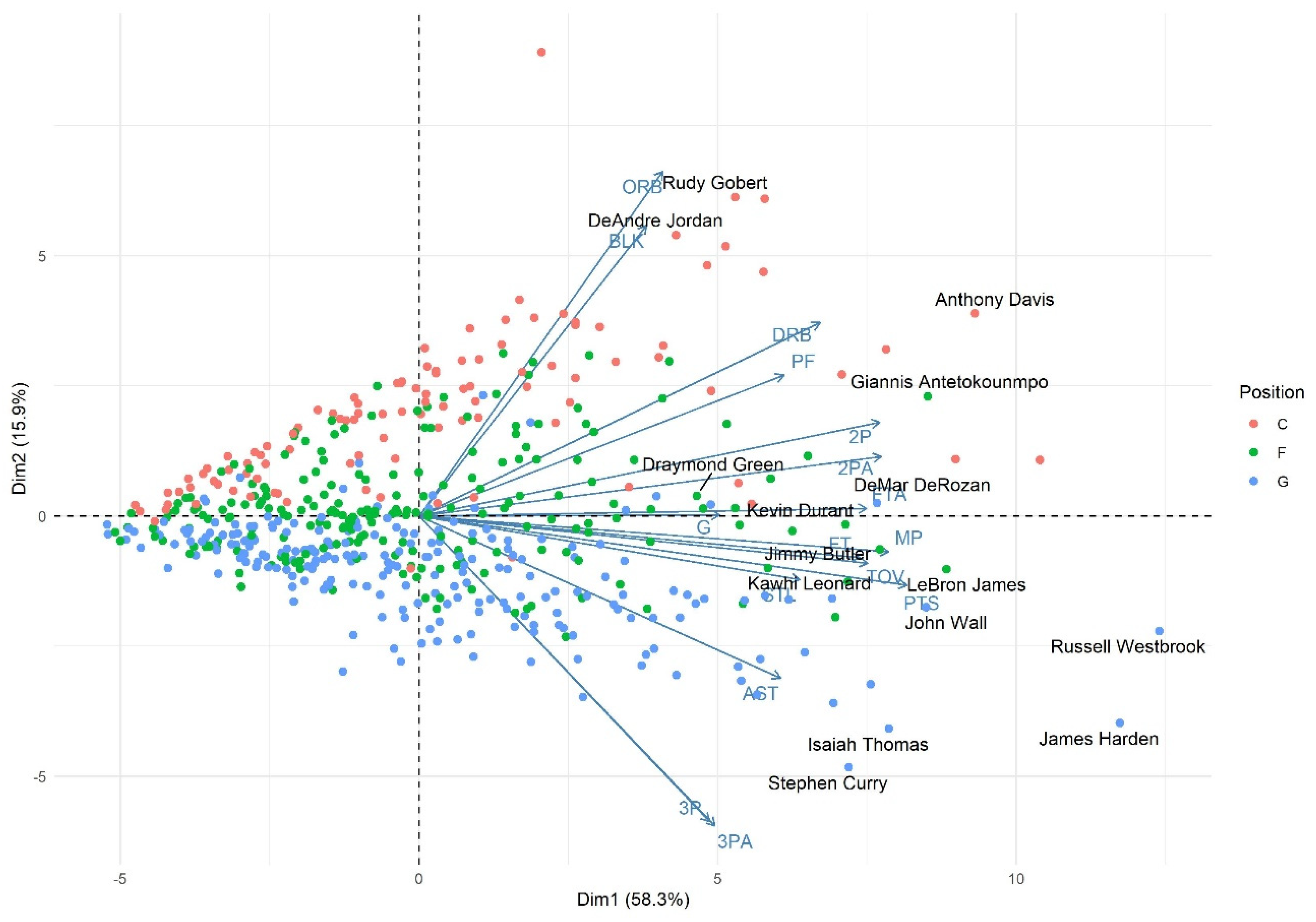
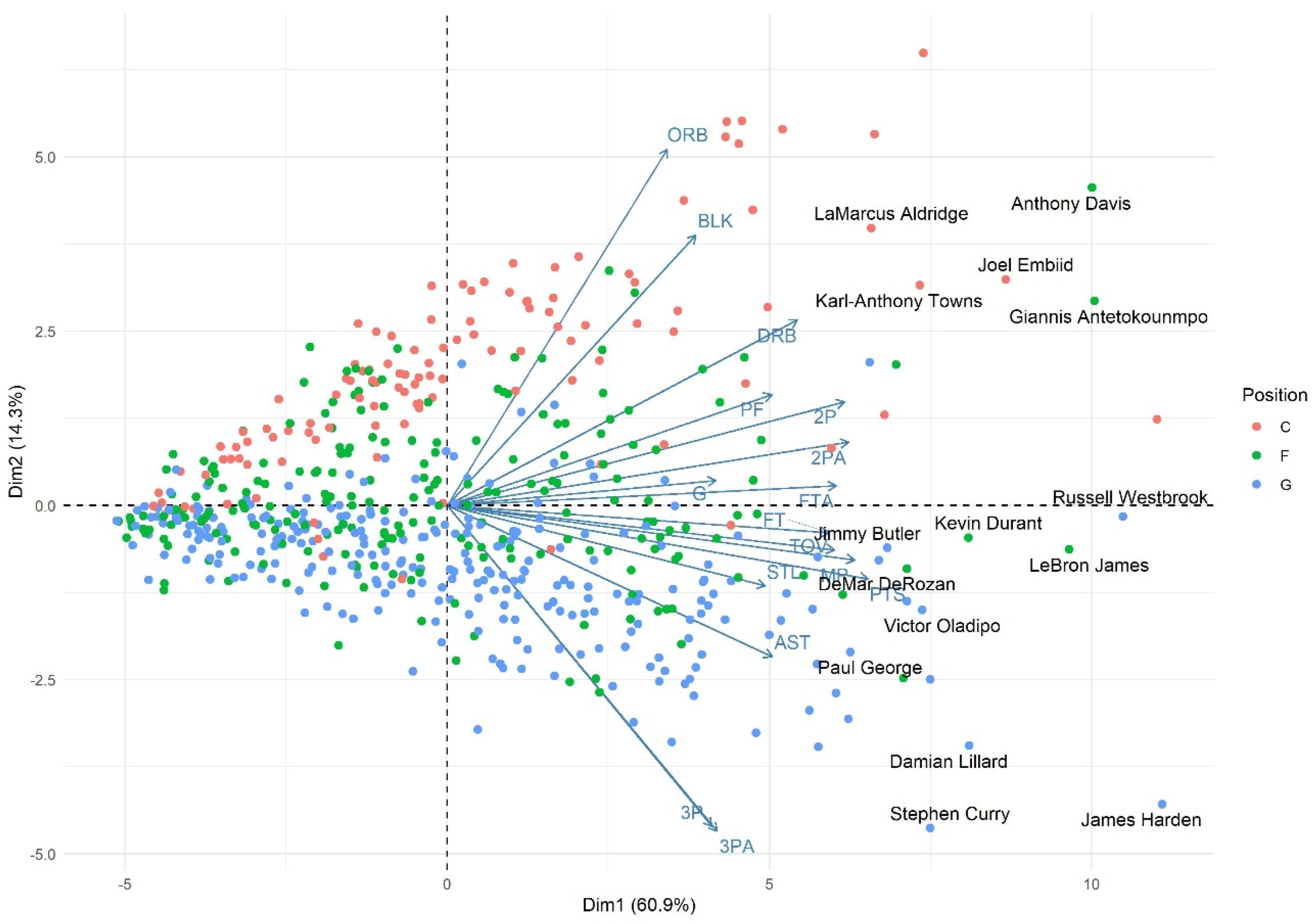
Given the results of this study, a new way of evaluating and comparing players’ regular season performance and All-NBA Teams’ selections, through unsupervised learning, is suggested in Stage 2. For this, Principal Component Analysis (PCA) is performed in all studied seasons, i.e., from 2014-15 to 2018-19. In Stage 2, only the results for the 2018-19 season will be presented; other results can be found in Appendix A.

As shown earlier in Table 1, there is a vast number of variables related to all active layers and, as shown in Stage 1 in all three positions many of the variables are not taken into consideration when analyzing players’ performances and selecting All-NBA Teams. In this way, PCA is an interesting alternative to try to take all variables available into consideration by taking a linear combination that better represents players’ performances without labeling them in positions that no longer represent their roles and functions on court.

Once more, the variables considered in this Stage can be found in Table 1.

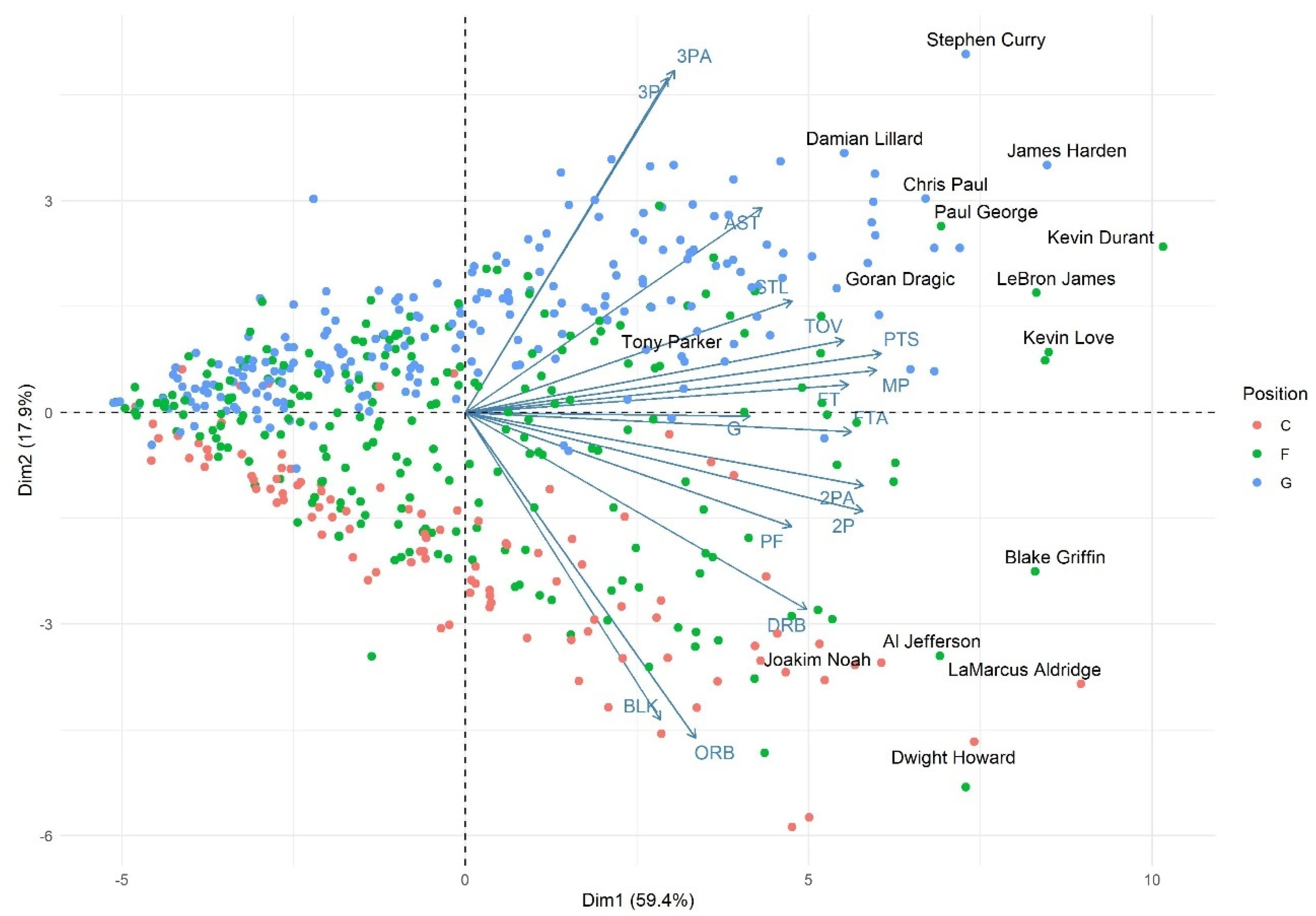
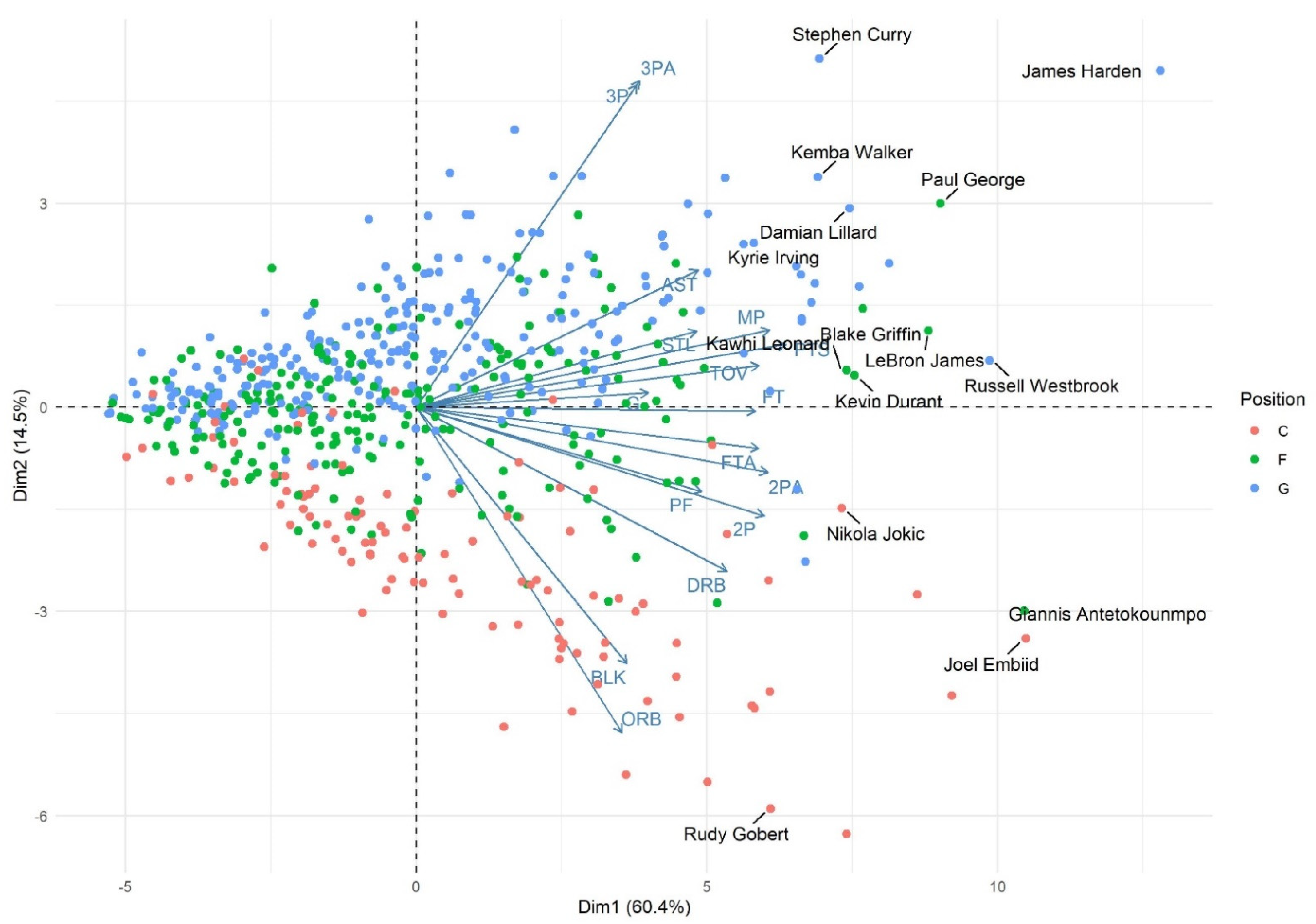
Figure 1 presents the PCA’s first two components (PC1 and PC2), that explain a total of 74.9% of the original data’s variance (60.4% explained by PC1 and 14.5% explained by PC2). The biplot also presents the original variables as arrows and each point in the plot is an active player of the 2018-19 season; furthermore, players nominated to the All-NBA Teams in this year are highlighted.

Analyzing Figure 1, the second principal component (PC2), presented in the vertical axis, seems to be strongly related to the players’ positions.

As the plot’s legend indicates, each of the colors represents one of the positions that are traditionally used to allocate players in the All-NBA Teams. Therefore, the bottom of the biplot has strong influences from variables such as blocks (BLK), offensive rebounds (ORB) and defensive rebounds (DRB), and for that reason players labeled as centers tend to be more present in this area.

In contrast, the upper part of the biplot shows players whose roles are more concentrated far from the basket and closer to the three-point line with the strong influence of three-point shots (3PA/3P), characteristics of players often labeled as guards, especially if we also take into consideration the influence of assists (AST), justifying their presence in this era of the plot.

The biplot’s center is the area where most forwards are, as they tend to be labeled as the most versatile players on court.

The first principal component (PC1) seems to be strongly related to players’ performance in the season, as it is possible to notice from the original data’s arrows a disposition towards PC1. Further evidence of this is that players highlighted in the plot tend to be some of the most talented players in the league, regardless of their overall performance in a given season, and distance themselves from other players, moving to the right side of the biplot.

As mentioned earlier, highlighted players in Figure 1 were selected to one of the All-NBA Teams; therefore, for a better visualization and interpretation of Figure 1,

Table 4. Players selected to the All-NBA Teams in the 2018-19 NBA season.

Player	Position	All-NBA Team
Stephen Curry	Guard	First Team
James Harden	Guard	First Team
Paul George	Forward	First Team
Giannis Antetokounmpo	Forward	First Team
Nikola Jokic	Center	First Team
Kyrie Irving	Guard	Second Team
Damian Lillard	Guard	Second Team
Kawhi Leonard	Forward	Second Team
Kevin Durant	Forward	Second Team
Joel Embiid	Center	Second Team
Russell Westbrook	Guard	Third Team
Kemba Walker	Guard	Third Team
Blake Griffin	Forward	Third Team
LeBron James	Forward	Third Team
Rudy Gobert	Center	Third team

lists all selected players, their positions, and respective All-NBA Teams.

Another interesting point is that it is possible to notice that the two players that competed directly for the Most Valuable Player (MPV) award in 2019, Giannis Antetokounmpo and James Harden, are the players with the highest values in the PC1, which reflects directly the possible relationship between PC1, and player performance given, that they had two, if not the most, of the best player performances in the regular season.

It is also possible to see how Joel Embiid is located very near Antetokounmpo, but was not taken into account for the MVP award, which can be explained by the center’s number of played games in 2019, 64, which eventually turns out to be a significant factor in awarding a player in the NBA, as widely discussed in the media and statistically proven by the LASSO model adjusted in the previous stage of this study.

This kind of analysis allows to better visualize the three classical positions by their respective colors, and through the arrows for variables it is possible to see the differences between styles, both between players labeled in the same position and in distinct positions.

A good example is the difference between Russell Westbrook and James Harden, who play in the same position, but cannot be defined by their classical role on court as presented in Table 1. Westbrook’s gameplay style is more focused on two-point shots, assists and rebounds; on the other hand Harden is a guard focused on scoring via three-point shots.

Yet the biggest difference in gameplay styles might be seen in the forward position, which as often mentioned before is considered to be the most versatile position on court. Two of the most talented players in the league, Lebron James and Giannis Antetokounmpo, show completely unique styles according to the Principal Component Analysis.

Antetokounmpo is placed near Embiid, a center among the tallest players in the league who has a great part of his role focused near the rim. On the other hand, James is placed more closely to the guards, an aspect highlighted during his entire career, and has always been an excellent player in creating opportunities for his teammates.

The contrast between Rudy Gobert and Nikola Jokić also draws attention, as it is possible to see that they perform two extremely distinct roles on court. Gobert shows a classical center’s role, primarily focused on defense, and Jokić plays, arguably, in a way that we have never seen a center play before, as he primarily acts like the primary ball handler and playmaker in court.

These style differences exactly show the problem in evaluating players taking into consideration classical positions in a league that clearly has evolved so much. As pointed out earlier, highlighted points in Figure 1 are players selected to the All-NBA Teams, but it is possible to observe non-highlighted points that had a better performance that season (i.e., higher values in PC1) and were not selected to the teams.

This can be caused by the fifteen-player limitation on All-NBA Teams, especially centers who represent only three of the fifteen selected, together with factors exploited in Stage 1, which can result in an unfair and non-representative player selection, limited to labels that do not reflect the actual talent in the league.

Classifying Players through the First Principal Component (PC1)

Thus, this subsection aims to better select the All-NBA Teams based on the PC1’s results, which is highly associated with players’ performances in a season.

This can be an interesting alternative in taking into consideration all variables available in a traditional box-score related to players, and evaluate them only by their performances, not their positions.

Figure 1 has many non-highlighted points (i.e., players that were not selected to All-NBA Teams) who have higher PC1 values than players selected. Rudy Gobert is a good example, as it is possible to observe at least three players who had higher PC1 values, i.e., had a better performance in the 2018–19 season, yet were not chosen, possibly for the variety of reasons mentioned in this study.

Therefore, is expected that the All-NBA selection through PC1 will see a notable change in the teams.

First, it is important to remember in an unsupervised learning algorithm such as the PCA that the data is standardized. As the objective of this study is to analyze the performance of players of many assorted styles, it is natural that we have better or worse players in certain variables. Thus, it is increasingly important to make sure that the data used are consistent with each other, so that players can be compared as fairly as possible.

After standardization, the linear combination of variables resulting in the first principal component can be seen in the following equation:

$$\begin{gathered} PCA1=Gx0.1940534+MPx0.2954364+3Px0.1842554+3PAx0.1866115+2Px0.2908161 \\ +2PAx0.2940325+FTx0.2834652+FTAx0.2862369+ORBx0.1718160 \\ +DRBx0.2597810+ASTx0.2357161+STLx0.2344572+BLKx0.1757749 \\ +TOVx0.2865330+PFx0.2384333+PTSx0.3091697 \end{gathered}$$

(2)

As mentioned earlier, higher values of PC1 represent better performances in a season, thus the best fifteen players in PC1 should be selected to the All-NBA Teams, accordingly with the Principal Component Analysis, as shown in

Table 5. Players selected to the All-NBA Teams through PC1 in the 2018-10 NBA Season.

Player	Coordinate	Position	Classification
James Harden	12.791784904	Guard	First Team
Joel Embiid	10.482212371	Center	First Team
Giannis Antetokounmpo	10.455564071	Forward	First Team
Russell Westbrook	9.853143545	Guard	First Team
Anthony Davis	9.210075790	Center	First Team
Paul George	9.007734878	Forward	Second Team
LeBron James	8.802954826	Forward	Second Team
Karl Anthony-Towns	8.610240248	Center	Second Team
Devin Booker	8.133390011	Guard	Second Team
Blake Griffin	7.676332697	Forward	Second Team
Bradley Beal	7.614305881	Guard	Third Team
Kevin Durant	7.534005333	Forward	Third Team
Damian Lillard	7.452481664	Guard	Third Team
Andre Drummond	7.399020679	Center	Third Team
Kawhi Leonard	7.396279476	Forward	Third team

.

Comparing Table 5 and Table 4, an interesting point that draws attention is that in the actual selection format there are no criteria based on performance to allocate a player into the first, second or third team. Player allocation is based on votes casted by accumulating one, three or five points depending on which team they were voted in; in this way, players with more points fill the teams from first to third.

Therefore, subjectivity might be a factor that influences player classification where it is not possible to directly determine the difference in performance between players, and this would not be able to justify, differentiate, nor understand properly a player’ allocation into the first, second or third team, which makes unsupervised learning even more appealing when evaluating players.

Allied to a better way of selecting players, the suggested PC1 classification brings the possibility of comparing players in a more consistent way of seeing the difference between players that were selected to the first team or to any other.

The difference in PC1 values observed in Table 5 allied with Figure 1 creates a complete visualization in which it is possible to see the difference between the players mentioned before, such as James Harden, Joel Embiid, Giannis Antetokounmpo and Russell Westbrook, compared to the other players in that season.

The fifth and last player to be selected= through PCA to the All-NBA First Team would be Anthony Davis. In Figure 1, his name is not highlighted because voters did not select him. Yet Davis is the exact pink point directly above Embiid, once more showing that voters did not recognize his high-performance season.

One reason for the Davis non-selection might be the number of games played in the 2018-19 season, in which he played 56 out of the 82 games. As shown in the previous Stage, voters take into consideration the number of games played when selecting a player to an All-NBA Team.

However, this argument is contradictory as LeBron James was selected to the third All-NBA Team, playing one game less than Davis, totaling 55 in the 2018-19 season.

These kinds of inconsistency unfortunately occur in the current selection format adopted by the league, where media narratives and player popularity (LeBron James being, arguably, the greatest player in history and one of the most famous athletes on the planet) might interfere with voters’ opinions and evaluation of players, causing a less objective selection format.

From this, comparing Table 4 and Table 5, differences between teams’ structures are observed. Now that they are not structured in classical positions (two guards, two forwards and one center) and not allocated by voters, we can see that the teams are formed by players sorted in a performance descending order.

An argument that may be presented for the classical position structure is that the All-NBA Teams should ideally be able to play a regular season as a normal team, i.e., having two guards, two forwards and one center that play by Table 1’s definitions. However, that does not represent the modern NBA, as mentioned earlier, and it is more common than ever to see players that are capable of impacting the game in more than one position, role, and manner, on both sides.

There is no point in evaluating and selecting players to All-NBA Teams in a format that create inconsistencies and contradictions, since an ideal team formed only by versatile players is a direct reflection of what is really happening in the league.

To better illustrate this point, it is extremely hard to imagine that the first All-NBA Team formed in Table 5 by James Harden, Joel Embiid, Giannis Antetokounmpo, Russell Westbrook, and Anthony Davis, could not compete at an extremely high level in the NBA. A team formed by three former MVP and two former Defensive Player of the Year (DPOY) has great versatility, as it is possible to see in Figure 1, which shows each gameplay style of these players.

4. Conclusions

In this study, we were interested in studying the All-NBA Teams via voters’ choices. After the identification of patterns, ideal player profiles and key factors for the voters, a new model of player evaluation, based on unsupervised learning, was suggested that takes into consideration the versatility of modern players, analyzes objectively all variables (traditional box-score) related to these players and classifies them as All-NBA players considering only their performances. For this, we considered statistical methods such as LASSO (Logistic) Regression and Principal Component Analysis.

In Stage 1, it was possible to create an All-NBA player profile according to what voters search for in a player, and see that this profile is quite similar to the classical definitions of basketball positions, which can be seen in Table 2. This can create multiple inconsistences in player selection to All-NBA Teams, and a lack of representation of these players’ modern and versatile gameplay style.

In Stage 2, a new way of evaluation and selection is suggested through Principal Component Analysis. It was possible to notice the advantages of having a selection format that can capture the differences between players, without necessarily labeling them into positions which no longer represent their functions on court. Furthermore, through the first principal component (PC1), highly related to players’ performance in a season, these players can be selected as All-NBA in an objective way.

As a result of Stages 1 and 2 of the present study, it was possible to notice that there are strong indications that the current way of evaluating NBA players’ regular seasons, via All-NBA Teams, shows inconsistencies. In addition, it may not reward players that actually had the best performances in the season.

Analyzing player performance over a season can help the league, teams, and the players themselves to identify and discuss the various aspects of the game where performance was satisfactory or where it could be improved, and provides a good opportunity to compare, explain or justify the season’s results with the expectations that were established pre-season. The results presented in this study display a model that achieves all these goals.

Therefore, the present study has the intention of creating greater importance and bringing attention to the All-NBA Teams through better player selection and classification, which can help in comprehension of gameplay style changes, strategies, patterns, and performances of the best players of the league in the present day, past, and future.

The model presented can help not only the NBA but basketball leagues at any level of competition. In addition, it might also be a source for other researchers who aim to investigate player performance, development, and impact in various seasons over the years.