Resampling Plans and the Estimation of Prediction Error

Abstract

This article was prepared for the Special Issue on Resampling methods for statistical inference of the 2020s. Modern algorithms such as random forests and deep learning are automatic machines for producing prediction rules from training data. Resampling plans have been the key technology for evaluating a rule’s prediction accuracy. After a careful description of the measurement of prediction error the article discusses the advantages and disadvantages of the principal methods: cross-validation, the nonparametric bootstrap, covariance penalties (Mallows’ $C_p$ and the Akaike Information Criterion), and conformal inference. The emphasis is on a broad overview of a large subject, featuring examples, simulations, and a minimum of technical detail.

1. Introduction

Modern prediction algorithms such as random forests and deep learning use training sets, often very large ones, to produce rules for predicting new responses from a set of available predictors. A second question—right after “How should the prediction rule be constructed?”—is “How accurate are the rule’s predictions?” Resampling methods have played a central role in the answer. This paper is intended to provide an overview of what are actually several different answers, while trying to keep technical complications to a minimum.

This is a Special Issue of STATS devoted to resampling, and before beginning on prediction rules it seems worthwhile to say something about the general effect of resampling methods on statistics and statisticians. Table 1 shows the law school data [1], a small data set but one not completely atypical of its time. The table reports average scores of the 1973 entering class at 15 law schools on two criteria: undergraduate grade point average (GPA) and result on the “LSAT”, a national achievement test. The observed Pearson correlation coefficient between GPA and LSAT score is

$$\widehat{\rho }=0.776.$$

(1)

How accurate is $\widehat{\rho }$?

Suppose that Dr. Jones, a 1940s statistician, was given the data in Table 1 and asked to attach a standard error to $\widehat{\rho }=0.776$; let’s say a nonparametric standard error since a plot of (LSAT,GPA) looks definitely non-normal. At his disposal is the nonparametric delta method, which gives a first-order Taylor series approximation formula for $\mathrm{se}\left(\widehat{\rho }\right)$. For the Pearson correlation coefficient this turns out to be

$$\widehat{\mathrm{se}}\left(\widehat{\rho }\right)={\left\{\frac{{\widehat{\rho }}^2}{4n}\left[\frac{{\widehat{\mu }}_{40}}{{\widehat{\mu }}_{20}^2}+\frac{{\widehat{\mu }}_{04}}{{\widehat{\mu }}_{02}^2}+\frac{2{\widehat{\mu }}_{22}}{{\widehat{\mu }}_{20}{\widehat{\mu }}_{02}}+\frac{4{\widehat{\mu }}_{22}}{{\widehat{\mu }}_{11}^2}-\frac{4{\widehat{\mu }}_{31}}{{\widehat{\mu }}_{11}{\widehat{\mu }}_{20}}-\frac{4{\widehat{\mu }}_{13}}{{\widehat{\mu }}_{11}{\widehat{\mu }}_{02}}\right]\right\}}^{1/2},$$

(2)

where $n=15$ and ${\widehat{\mu }}_{ij}$ is the mean of ${(\mathrm{GPA}-\overline{\mathrm{GPA}})}^i{(\mathrm{LSAT}-\overline{\mathrm{LSAT}})}^j$, the bars indicating averages.

Table 1. Average scores for admitees to 15 American law schools, 1973. GPA is undergraduate grade point average, LSAT “law boards” score. Pearson correlation coefficient between GPA and LSAT is 0.776.

GPA	LSAT
3.39	576
3.30	635
2.81	558
3.03	578
3.44	666
3.07	580
3.00	555
3.43	661
3.36	651
3.13	605
3.12	653
2.74	575
2.76	545
2.88	572
2.96	594

Table 1. Average scores for admitees to 15 American law schools, 1973. GPA is undergraduate grade point average, LSAT “law boards” score. Pearson correlation coefficient between GPA and LSAT is 0.776.

GPA	LSAT
3.39	576
3.30	635
2.81	558
3.03	578
3.44	666
3.07	580
3.00	555
3.43	661
3.36	651
3.13	605
3.12	653
2.74	575
2.76	545
2.88	572
2.96	594

Jones either looks up or derives (2), evaluates the six terms on his mechanical calculator, and reports

$$\widehat{\mathrm{se}}\left(\widehat{\rho }\right)=0.124,$$

(3)

after which he goes home with the feeling of a day well spent.

Jones’ daughter, a 1960s statistician, has a much easier go of it. Now she does not have to look up or derive Formula (2). A more general resampling algorithm, the Tukey–Quenouille jackknife is available, and can be almost instantly evaluated on her university’s mainframe computer. It gives her the answer

$$\widehat{\mathrm{se}}\left(\widehat{\rho }\right)=0.143.$$

(4)

Dr. Jones is envious of his daughter:

1.

She does not need to spend her time deriving arduous formulas such as (2).

2.

She is not restricted to traditional estimates such as $\widehat{\rho }$ that have closed-form Taylor series expansions.

3.

Her university’s mainframe computer is a million times faster than his old Marchant calculator (though it is across the campus rather than on her desk).

If now, 60 years later, the Jones family is still in the statistics business they’ll have even more reason to be grateful for resampling methods. Faster, cheaper, and more convenient computation combined with more aggressive methodology have pushed the purview of resampling applications beyond the assignment of standard errors.

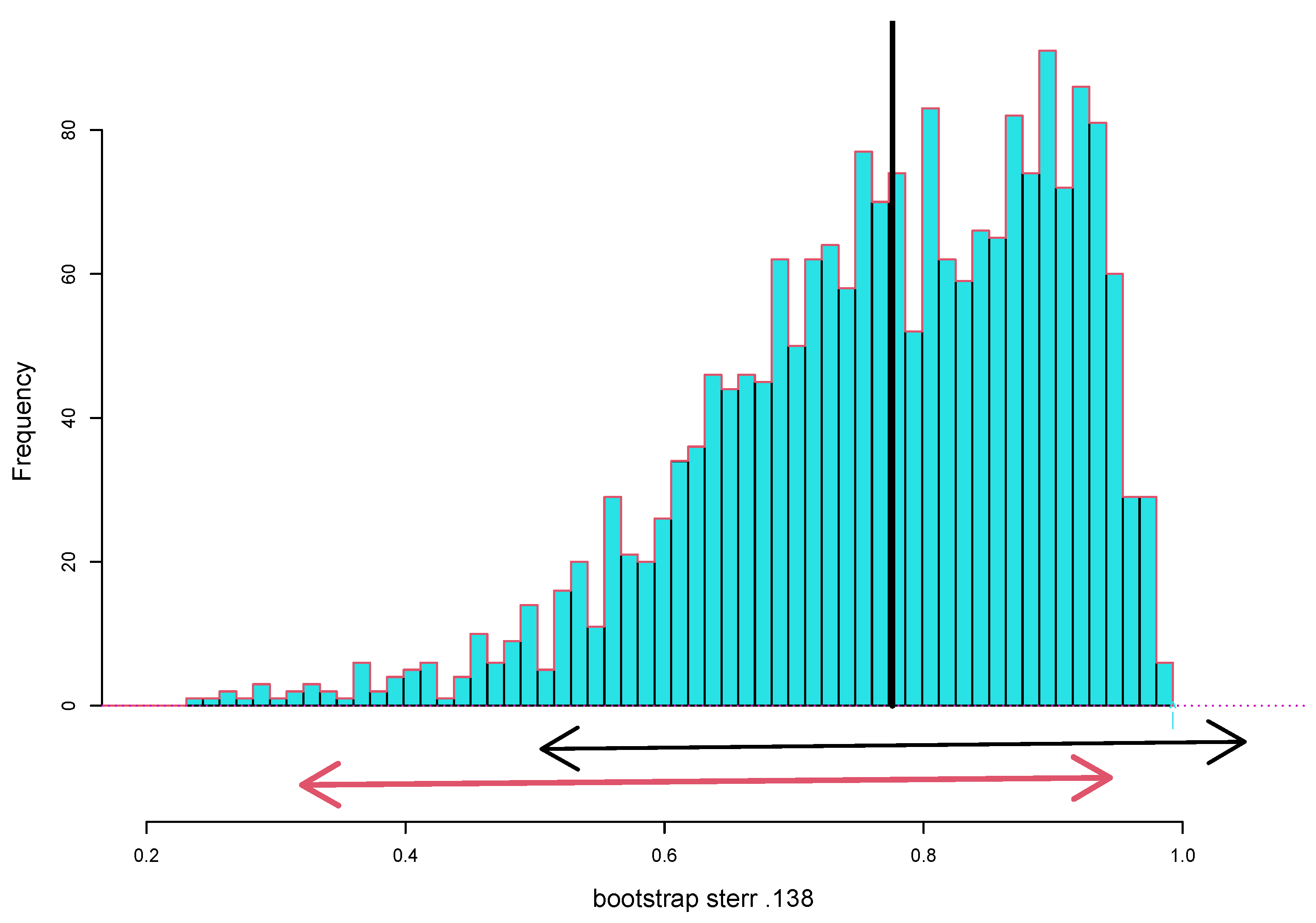
Figure 1 shows 2000 nonparametric bootstrap replications ${\widehat{\rho }}^{*}$ from the law school data (Each ${\widehat{\rho }}^{*}$ is the correlation from a bootstrapped data matrix obtained by resampling the 15 rows of the $15\times 2$ matrix in Table 1 15 times with replacement. See Chapter 11 of [2]). Their empirical standard deviation is the nonparametric bootstrap estimate of standard error for $\widehat{\rho }$,

$$\widehat{\mathrm{se}}\left(\widehat{\rho }\right)=0.138.$$

(5)

Two thousand is 10 times too many replications needed for a standard error, but it is not too many for a bootstrap confidence interval. The arrowed segments in Figure 1 compare the standard approximate 95% confidence limit

$$\rho \in \widehat{\rho }\pm 1.96\widehat{\mathrm{se}}=[0.505,1.048],$$

(6)

$\widehat{\mathrm{se}}=0.138$, with the nonparametric bootstrap interval. (This is the bca interval, constructed using program bcajack from the CRAN package bcaboot [3]. Chapter 11 of [2] shows why bca’s “second-order corrections”, here very large, improve on the standard method.)

$$\rho \in [0.320,0.944].$$

(7)

The standard method does better if we first make Fisher’s z transformation

$$\widehat{\xi }=\frac{1}{2}\log \frac{1+\widehat{\rho }}{1-\widehat{\rho }},$$

(8)

compute the standard interval on the $\xi$ scale, and transform the endpoints back to the $\rho$ scale. This gives 0.95 interval

$$\rho \in [0.275,0.946],$$

(9)

not so different from the bootstrap interval (7), and at least not having its upper limit above 1.00!

This is the kind of trick Dr. Jones would have known. Resampling, here in the form of the bca algorithm, automates devices such as (8) without requiring Fisher-level insight for each new application.

If there was a statistics’ “word of the year” it would be two words: deep learning. This is one of a suite of prediction algorithms that input data sets, often quite massive ones, and output prediction rules. Others in the suite include random forests, support vector machines, and gradient boosting.

Having produced a prediction rule, it is natural to wonder how accurately it will predict future cases, our subject in what follows:

• Section 2 gives a careful definition of the prediction problem, and describes a class of loss functions (the “Q class”) that apply to discrete as well as continuous response variables.
• Section 3 concerns nonparametric estimates of prediction loss (cross-validation and the bootstrap “632 rule”) as well as Breiman’s out-of-bag error estimates for random forests.
• Covariance penalties, including Mallows’ $C_p$ and the Akaike Information Criterion, are parametric methods discussed in Section 4 along with the related concept of degrees of freedom.
• Section 5 briefly discusses conformal inference, the most recent addition to the resampling catalog of prediction error assessments.

2. The Prediction Problem

Statements of the prediction problem are often framed as follows:

• A data set $\mathit{d}$ of n pairs is observed,

  $$\mathit{d}=\left\{(x_i,y_i),i=1,2,\dots ,n\right\},$$

  (10)

  where the $x_i$ are p-dimensional predictor vectors and the $y_i$ are one-dimensional responses.
• The $(x,y)$ pairs are assumed to be independent and identically distributed draws from an unknown $(p+1)$-dimensional distribution F,

  $$(x_i,y_i)\stackrel{\mathrm{iid}}{\sim }F,i=1,2,\dots ,n.$$

  (11)
• Using some algorithm $\mathcal{A}$, the statistician constructs a prediction rule $f(x,\mathit{d})$ that provides a prediction $\widehat{\mu }\left(x\right)$,

  $$\widehat{\mu }\left(x\right)=f(x,\mathit{d})$$

  (12)

  for any vector x in the space of possible predictors.
• A new pair $(x,y)$ is independently drawn from F,

  $$(x,y)\sim F\mathrm{independent}\mathrm{of}\mathit{d},$$

  (13)

  but with only x observable.
• The statistician predicts the unseen y by $\widehat{\mu }\left(x\right)=f(x,\mathit{d})$ and wishes to assess prediction error. Later the prediction error will turn out to directly relate to the estimation error of $\widehat{\mu }\left(x\right)$ for the true conditional expectation of y given x,

  $$\mu \left(x\right)=E_F\{y\mid x\}.$$

  (14)
• Prediction error is assessed as the expectation of loss under distribution F,

  $${\mathrm{Err}}^{\left(u\right)}=E_F\left\{Q\left(y,\widehat{\mu }\left(x\right)\right)\right\},$$

  (15)

  for a given loss function such as squared error: $Q(y,\widehat{\mu })={(y-\widehat{\mu })}^2$.

Here, $E_F$ indicates expectation over the random choice of all $p+1$ pairs $(x_i,y_i)$ and $(x,y)$ in (11) and (13). The u in ${\mathrm{Err}}^{\left(u\right)}$ reflects the unconditional definition of error in (15). The resampling algorithms we will describe calculate an estimate of ${\mathrm{Err}}^{\left(u\right)}$ from the observed data. (One might hope for a more conditional error estimate, say one applying to the observed set of predictors $\mathit{x}$, a point discussed in what follows.)

Naturally, the primary concern within the prediction community has been with the choice of the algorithm $\mathcal{A}$ that produces the rule $\widehat{\mu }\left(x\right)=f(x,\mathit{d})$. Elaborate computer-intensive algorithms such as random forests and deep learning have achieved star status, even in the popular press. Here, however, the “prediction problem” will focus on the estimation of prediction error. To a large extent the prediction problem has been a contest of competing resampling methods, as discussed in the next three sections.

Figure 2 illustrates a simple example: $n=20$ pairs $(x_i,y_i)$ have been observed, in this case with x real. A fourth-degree polynomial $f(x,\mathit{d})$ has been fit by ordinary least squares applied to $\mathit{d}=\{(x_i,y_i),i=1,2,\dots ,20\}$ with the heavy curve tracing out $\widehat{\mu }\left(x\right)=f(x,\mathit{d})$.

In the usual OLS notation, we’ve observed $\mathit{y}={(y_1,y_2,\dots ,y_n)}^{\top }$ from the notional model

$$\mathit{y}=\mathit{X}\beta +\mathit{ϵ},$$

(16)

where $\mathit{X}$ is the $20\times 5$ matrix with ith row $(1,x_i,x_i^2,x_i^3,x_i^4)$, $\beta$ the unknown 5-dimensional vector of regression coefficients, and $\mathit{ϵ}$ a vector of 20 uncorrelated errors having mean 0 and variance ${\sigma }^2$,

$${ϵ}_i\sim (0,{\sigma }^2)\mathrm{for}i=1,2,\dots ,n.$$

(17)

The fitted curve $\widehat{\mu }\left(x\right)=f(x,\mathit{d})$ is given by

$$\widehat{\mu }\left(x\right)=X{\left(x\right)}^{\top }\widehat{\beta },$$

(18)

for $X{\left(x\right)}^{\top }=(1,x_i,x_i^2,x_i^3,x_i^4)$ and $\widehat{\beta }={\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}{\mathit{X}}^{\top }\mathit{y}$ (the OLS estimate), this being algorithm $\mathcal{A}$.

The apparent error, what will be called $\mathrm{err}$ in what follows, is

$$\mathrm{err}=\sum _{i=1}^n\frac{Q(y_i,{\widehat{\mu }}_i)}{n}\left({\widehat{\mu }}_i=f(x_i,\mathit{d})\right)$$

(19)

which equals 1.99 for $Q(y,\widehat{\mu })={(y-\widehat{\mu })}^2$. The usual unbiased estimate for the noise parameter ${\sigma }^2$, not needed here, modifies the denominator in (19) to take account of fitting a 5-vector $\widehat{\beta }$ to $\mathit{d}$,

$${\widehat{\sigma }}^2=\sum _{i=1}^n\frac{Q(y_i,{\widehat{\mu }}_i)}{(n-5)}=2.65.$$

(20)

Dividing the sum of squared errors by $n-p$ rather than n can be thought of as a classical prediction error adjustment; err usually underestimates future prediction error since the ${\widehat{\mu }}_i$ have been chosen to fit the observations $y_i$.

Because this is a simulation, we know the true function $\mu \left(x\right)$ (14), the light dotted curve in Figure 2:

$$\mu \left(x\right)=2+0.2x+\cos \left(\frac{x-5}{2}\right);$$

(21)

the points $y_i$ were generated with normal errors, variance 2,

$$y_i\stackrel{\mathrm{ind}}{\sim }\mathcal{N}\left(\mu \left(x_i\right),2\right),i=1,2,\dots ,n.$$

(22)

Given model (22), we can calculate the true prediction error for estimate $\widehat{\mu }\left(x\right)$ (18). If $y^{*}\sim \mathcal{N}(\mu \left(x\right),2)$ is a new observation, independent of the original data $\mathit{d}$ which gave $\widehat{\mu }\left(x\right)$, then the true prediction error ${\mathrm{Err}}_x$ is

$${\mathrm{Err}}_x=E_{*}{\left(y^{*}-\mu \left(x\right)\right)}^2=2+{\left(\widehat{\mu }\left(x\right)-\mu \left(x\right)\right)}^2,$$

(23)

the notation $E_{*}$ indicating expectation over $y^{*}$. Let $\mathrm{Err}$ denote the average true error over the $n=20$ observed values $x_i$,

$$\mathrm{Err}=\frac{1}{n}\sum _{i=1}^n{\mathrm{Err}}_{x_i}=2+\frac{1}{n}\sum _{i=1}^n{\left(\widehat{\mu }\left(x_i\right)-\mu \left(x_i\right)\right)}^2,$$

(24)

equaling 2.40 in this case. $\mathrm{Err}$ figures prominently in the succeeding sections. Here, it exceeds the apparent error $\mathrm{err}=1.99$ (19) by 21%. ($\mathrm{Err}$ is not the same as ${\mathrm{Err}}^{\left(u\right)}$ (15).)

Prediction algorithms are often, perhaps most often, applied to situations where the responses are dichotomous, $y_i=1$ or 0; that is, they are Bernoulli random variables, binomials of sample size 1 each,

$$y_i\stackrel{\mathrm{ind}}{\sim }\mathrm{Bi}\left(1,\mu \left(x_i\right)\right)\mathrm{for}i=1,2,\dots ,n.$$

(25)

Here $\mu \left(x\right)$ is the probability that $y=1$ given prediction vector x,

$$\mu \left(x\right)=\mathrm{Pr}\{y=1\mid x\}.$$

(26)

The probability model F in (11) can be thought of in two steps: as first selecting x according to some p-dimensional distribution G and then “flipping a biased coin” to generate $y\sim \mathrm{Bi}(1,\mu (x\left)\right)$.

Squared error is not appropriate for dichotomous data. Two loss (or “error”) functions $Q(\mu ,\widehat{\mu })$ are in common use for measuring the discrepancy between $\mu$ and $\widehat{\mu }$, the true and estimated probability that $y=1$ in (25). The first is counting error,

$$Q(\mu ,\widehat{\mu })=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\mu \mathrm{and}\widehat{\mu }\mathrm{are}\mathrm{on}\mathrm{same}\mathrm{side}\mathrm{of}1/2\hfill \\ 2·\left|\mu -\frac{1}{2}\right|\hfill & \mathrm{if}\mathrm{not}.\hfill \end{array}\right.$$

(27)

For $y=0$ or 1, $Q(y,\widehat{\mu })$ equals 0 or 1 if y and $\widehat{\mu }$ are on the same or different sides of $1/2$.

The second error function is binomial deviance (or twice the Kullback–Leibler divergence),

$$Q(\mu ,\widehat{\mu })=2\left\{\mu \log \left(\frac{\mu }{\widehat{\mu }}\right)+(1-\mu )\log \left(\frac{1-\mu }{1-\widehat{\mu }}\right)\right\}.$$

(28)

Binomial deviance plays a preferred role in maximum likelihood estimation. Suppose that $\mathit{\mu }\left(\beta \right)$ is a p-parameter family for the true vector of means in model (25),

$$\mathit{\mu }\left(\beta \right)={\left(\mu (x_1,\beta ),\mu (x_2,\beta ),\dots ,\mu (x_n,\beta )\right)}^{\top }(\beta \in \mathrm{\Omega }\subset {\mathcal{R}}^p).$$

(29)

Then, the maximum likelihood estimate (MLE) $\widehat{\beta }$ is the minimizer of the average binomial deviance (28) between $\mathit{y}={(y_1,y_2,\dots ,y_n)}^{\top }$ and $\mathit{\mu }\left(\beta \right)$,

$$\widehat{\beta }=\underset{\beta }{\mathrm{argmin}}\left\{\frac{1}{n}\sum _{i=1}^{n}Q\left(y_i,\mu (x_i,\beta )\right)\right\};$$

(30)

see Chapter 8 of [2]. Most of the numerical examples in the following sections are based on binomial deviance (30). (If $\widehat{\mu }$ equals 0 or 1 then (30) is infinite. To avoid infinities, our numerical examples truncate $\widehat{\mu }$ to $[0.005,0.995]$.)

Squared error, counting error, and binomial deviance are all members of the Q-class, a general construction illustrated in Figure 3 ([4] Section 3). The construction begins with some concave function $q\left(\mu \right)$; for the dichotomous cases considered here, $\mu \in [0,1]$ with $q\left(0\right)=q\left(1\right)=0$. The error $Q(\mu ,\widehat{\mu })$ between a true value $\mu$ and an estimate $\widehat{\mu }$ is defined by the illustrated tangency calculation:

$$Q(\mu ,\widehat{\mu })=q\left(\widehat{\mu }\right)+\dot{q}\left(\widehat{\mu }\right)(\mu -\widehat{\mu })-q\left(\mu \right),$$

(31)

$\dot{q}\left(\mu \right)=dq\left(\mu \right)/d\mu$ (equivalent to the “Bregman divergence” [5]).

The entropy function

$$q\left(\mu \right)=-2\left\{\mu \log \mu +(1-\mu )\log (1-\mu )\right\}$$

(32)

makes $Q(\mu ,\widehat{\mu })$ equal binomial deviance. Two other common choices are $q\left(\mu \right)=\min \{\mu ,1$$-\mu \}$ for counting error and $q\left(\mu \right)=\mu (1-\mu )$ for squared error.

Working within the Q-class (31), it is easy to express the true error of prediction $\widehat{\mu }\left(x\right)$ at predictor value x where the true mean is $\mu \left(x\right)=E_F\{y\mid x\}$. Letting $y^{*}$ be an independent realization from the distribution of y given x, the true error at x is, by definition,

$$\mathrm{Err}\left(\mu \left(x\right),\widehat{\mu }\left(x\right)\right)=E_{*}\left\{Q\left(y^{*},\widehat{\mu }\left(x\right)\right)\right\},$$

(33)

only $y^{*}$ being random in the expectation.

Lemma 1.

The true error at x (33) is

$$\mathrm{Err}\left(\mu \left(x\right),\widehat{\mu }\left(x\right)\right)=Q\left(\mu \left(x\right),\widehat{\mu }\left(x\right)\right)+q\left(\mu \left(x\right)\right)-c\left(x\right),$$

(34)

with $c\left(x\right)=0$ in the dichotomous case.

Proof. 

From definition (31) of the Q-class,

$$\begin{array}{cc}\hfill E_{*}\left\{Q\left(y^{*},\widehat{\mu }\left(x\right)\right)\right\}& =E_{*}\left\{q\left(\widehat{\mu }\left(x\right)\right)+\dot{q}\left(\widehat{\mu }\left(x\right)\right)\left(y^{*}-\widehat{\mu }\left(x\right)\right)-q\left(y^{*}\right)\right\}\hfill \\ \hfill & =q\left(\widehat{\mu }\left(x\right)\right)+\dot{q}\left(\widehat{\mu }\left(x\right)\right)\left(\mu \left(x\right)-\widehat{\mu }\left(x\right)\right)-E_{*}q\left(y^{*}\right)\hfill \\ \hfill & =Q\left(\mu \left(x\right),\widehat{\mu }\left(x\right)\right)+q\left(\mu \left(x\right)\right)-E_{*}q\left(y^{*}\right),\hfill \end{array}$$

(35)

giving (34) with $c\left(x\right)=E_{*}q\left(y^{*}\right)$. In the dichotomous case $q\left(y^{*}\right)=0$ for $y^{*}$ equal 0 or 1, so $c\left(x\right)=0$.  ☐

To simplify notation, let ${\mu }_i=\mu \left(x_i\right)$ and ${\widehat{\mu }}_i=\widehat{\mu }\left(x_i\right)$, with $\mathit{\mu }={({\mu }_1,{\mu }_2,\dots ,{\mu }_n)}^{\top }$ and $\widehat{\mathit{\mu }}={({\widehat{\mu }}_1,{\widehat{\mu }}_2,\dots ,{\widehat{\mu }}_n)}^{\top }$. The average true error $\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})$ is defined to be

$$\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})=\frac{1}{n}\sum _{i=1}^n\mathrm{Err}({\mu }_i,{\widehat{\mu }}_i)=\frac{1}{n}\sum _{i=1}^n\left[Q({\mu }_i,{\widehat{\mu }}_i)+q\left({\mu }_i\right)-c\left(x_i\right)\right].$$

(36)

It is “true” in the desirable sense of applying to the given prediction rule $\widehat{\mathit{\mu }}$. If we average $\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})$ over the random choice of $\mathit{d}$ in (11), we get the less desirable unconditional error ${\mathrm{Err}}^{\left(u\right)}$ (15).

$\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})$ is minimized by $\widehat{\mathit{\mu }}=\mathit{\mu }$,

$$\mathrm{Err}(\mathit{\mu },\mathit{\mu })=\frac{1}{n}\sum _{i=1}^n\left(q\left({\mu }_i\right)-c\left(x_i\right)\right).$$

(37)

Subtraction from (36) gives

$$\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})-\mathrm{Err}(\mathit{\mu },\mathit{\mu })=\frac{1}{n}\sum _{i=1}^{n}Q({\mu }_i,{\widehat{\mu }}_i).$$

(38)

This is an exact analogue of the familiar squared error relationship. Suppose $\mathit{y}$ and ${\mathit{y}}^{*}$ are independently $\mathcal{N}(\mu ,{\sigma }^{2}I)$ vectors, and that $\mathit{y}$ produces an estimate $\widehat{\mathit{\mu }}$. Then

$$\frac{1}{n}{E}_{*}\parallel {\mathit{y}}^{*}-\widehat{\mathit{\mu }}{\parallel }^2-\frac{1}{n}{E}_{*}{\parallel {\mathit{y}}^{*}-\mathit{\mu }\parallel }^2=\frac{1}{n}\sum _{i=1}^n{({\mu }_i-{\widehat{\mu }}_i)}^2,$$

(39)

which is (38) if $Q(\mu ,\widehat{\mu })={(\mu -\widehat{\mu })}^2$.

At a given value of x, say $x_0$, a prediction $\widehat{\mu }\left(x_0\right)$ can also be thought of as an estimate of $\mu \left(x_0\right)=E_F\{y_0\mid x_0\}$. Lemma 1 shows that the optimum choice of a prediction rule $\widehat{\mu }\left(x_0\right)=f(x_0,\mathit{d})$ is also the optimum choice of an estimation rule: for any rule $f(x,\mathit{d})$,

$$E_F\left\{\mathrm{Err}\left(\mu \left(x_0\right),\widehat{\mu }\left(x_0\right)\right)\right\}=E_F\left\{Q\left(\mu \left(x_0\right),\widehat{\mu }\left(x_0\right)\right)\right\}+q\left(\mu \left(x_0\right)-c\left(x_0\right)\right)$$

(40)

($E_F$ as in (11)), so that the rule that minimizes the expected prediction error also minimizes the expected estimation error $E_F\left\{Q(\mu \left(x_0\right),\widehat{\mu }\left(x_0\right))\right\}$. Predicting y and estimating its mean μ are equivalent tasks within the Q-class.

3. Cross-Validation and Its Bootstrap Competitors

Resampling methods base their inferences on recomputations of the statistic of interest derived from systematic modifications of the original sample. This is not a very precise definition, but it cannot be if we want to cover the range of methods used in estimating prediction error. There are intriguing differences among the methods concerning just what the modifications are and how the inferences are made, as discussed in this and the next two sections.

Cross-validation has a good claim to being the first resampling method. The original idea was to randomly split the sample $\mathit{d}$ into two halves, the training and test sets, ${\mathit{d}}_{\mathrm{train}}$ and ${\mathit{d}}_{\mathrm{test}}$. A prediction model is developed using only ${\mathit{d}}_{\mathrm{train}}$, and then validated by its performance on ${\mathit{d}}_{\mathrm{test}}$. Even if we cheated in the training phase, say by throwing out “bad” points, etc., the validation phase guarantees an honest estimate of prediction error.

One drawback is that inferences based on $n/2$ data points are likely to be less accurate than those based on all n, a concern if we are trying to accurately assess prediction error. “One-at-a-time“ cross-validation almost eliminates this defect: let ${\mathit{d}}_{\left(i\right)}$ be data set (10) with point $(x_i,y_i)$ removed, and define

$${\widehat{\mu }}_{\left(i\right)}=f(x_i,{\mathit{d}}_{\left(i\right)}),$$

(41)

the prediction for case i based on $x_i$ using the rule $f(x_i,{\mathit{d}}_{\left(i\right)})$, constructed using only the data in ${\mathit{d}}_{\left(i\right)}$. The cross-validation estimate of prediction error is then

$${\widehat{\mathrm{Err}}}_{\mathrm{cv}}=\frac{1}{n}\sum _{i=1}^{n}Q(y_i,{\widehat{\mu }}_{\left(i\right)}).$$

(42)

(This assumes that we know how to apply the construction rule $\mathcal{A}$ to subsets of size $n-1$). Because $y_i$ is not involved in ${\widehat{\mu }}_{\left(i\right)}$, overfitting is no longer a concern. Under the independent-draws model (11), ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ is a nearly unbiased estimate of ${\mathrm{Err}}^{\left(u\right)}$ (15) (“nearly” because it applies to samples of size $n-1$ rather than n).

The little example in Figure 2 has $n=20$ points $(x_i,y_i)$. Applying (42) with $Q(y,\widehat{\mu })={(y-\widehat{\mu })}^2$ gave ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}=3.59$, compared with apparent error $\mathrm{err}=1.99$ (19) and true error $\mathrm{Err}=2.40$ (24). This not-very-impressive result has much to do with the small sample size resulting in large differences between the original estimates ${\widehat{\mu }}_i$ and their cross-validated counterparts ${\widehat{\mu }}_{\left(i\right)}$. The single data point at $x_i=6.0$ accounted for 40% of ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$.

Figure 4 concerns a larger data set that will serve as a basis for simulations comparing cross-validation with its competitors: 200 transplant recipients were followed to investigate the subsequent occurrence of anemia; 138 did develop anemia (coded as $y_i=1$) while 62 did not ($y_i=0$). The goal of the study was to predict y from x, a vector of $p=17$ baseline variables including the intercept term (The predictor variables were body mass index, sex, race, patient and donor age, four measures of matching between patient and donor, three baseline medicine indicators, and four baseline general health measures).

A standard logistic regression analysis gave estimated values of the anemia probability $\mathrm{Pr}\{y_i=1\mid x_i\}$ for $i=1,2,\dots ,n=200$ that we will denote as

$${\mathit{\mu }}^{†}=({\mu }_1^{†},{\mu }_2^{†},\dots ,{\mu }_{200}^{†}).$$

(43)

Figure 4 shows a histogram of the 200 ${\mu }_i^{†}$ values. Here we will use ${\mathit{\mu }}^{†}$ as the “ground truth” for a simulation study (rather than analyzing the transplant study itself). The ${\mu }_i^{†}$ will play the role of the true mean $\mu \left(x_i\right)$ in Lemma 1 (34), enabling us to calculate true errors for the various prediction error estimates.

A $200\times 100$ matrix $\mathit{Y}$ of dichotomous responses $y_{ij}$ was generated as independent Bernoulli variables (that is, binomials of sample size 1),

$$y_{ij}\stackrel{\mathrm{ind}}{\sim }\mathrm{Bi}(1,{\mu }_i^{†})$$

(44)

for $i=1,2,\dots ,200$ and $j=1,2,\dots ,100$. The jth column of $\mathit{Y}$,

$${\mathit{y}}_j={(y_{1j},y_{2j},\dots ,y_{200j})}^{\top }$$

(45)

is a simulated binomial response vector (25) having true mean vector ${\mathit{\mu }}^{†}$. $\mathit{Y}$ provides 100 such response vectors.

Figure 4. Logistic regression estimated anemia probabilities for the 200 transplant patients.

Figure 4. Logistic regression estimated anemia probabilities for the 200 transplant patients.

For each one, a logistic regression was run,

$$\mathtt{glm}({\mathit{y}}_j\sim \mathit{X},\mathtt{binomial}),$$

(46)

in the language R, with $\mathit{X}$ the $200\times 17$ matrix of predictors from the transplant study. Cross-validation (“10-at-a-time” cross-validation rather than one-at-a-time: the 200 (x,y) pairs were randomly split into 20 groups of 10 each; each group was removed from the prediction set in turn and its 10 estimates obtained by logistic regression based on the other 190) gave an estimate of prediction error for the jth simulation,

$${\widehat{\mathrm{Err}}}_{\mathrm{cv}}\left(j\right)=\frac{1}{n}\sum _{i=1}^{200}Q(y_{ij},{\widehat{\mu }}_{\left(i\right)j}),$$

(47)

while (36) gave true error

$$\mathrm{Err}\left(j\right)=\frac{1}{n}\sum _{i=1}^{200}\left[Q({\mu }_i^{†},{\widehat{\mu }}_{ij})+q\left({\mu }_i^{†}\right)\right],$$

(48)

where ${\widehat{\mu }}_{ij}$ was the estimated mean from (46).

In terms of mean ± standard deviation the 100 simulations gave

$${\mathrm{Err}}_{\mathrm{cv}}\sim 1.16\pm 0.14\mathrm{and}\mathrm{Err}\sim 1.07\pm 0.12.$$

(49)

${\mathrm{Err}}_{\mathrm{cv}}$ averaged 8% more than $\mathrm{Err}$ (a couple percent of which came from having sample size 190 rather than 200). The standard deviation of ${\mathrm{Err}}_{\mathrm{cv}}$ is not much bigger than the standard deviation of $\mathrm{Err}$, which might suggest that ${\mathrm{Err}}_{\mathrm{cv}}$ was tracking $\mathrm{Err}$ as it varied across the simulations.

Sorry to say, that was not at all the case. The pairs $(\mathrm{Err}\left(j\right),{\mathrm{Err}}_{\mathrm{cv}}\left(j\right))$, $j=1,2,\dots ,100$, are plotted in Figure 5. It shows ${\mathrm{Err}}_{\mathrm{cv}}$ actually decreasing as the true error $\mathrm{Err}$ increases. The unfortunate implication is that ${\mathrm{Err}}_{\mathrm{cv}}$ is not estimating the true error, but only its expectation ${\mathrm{Err}}^{\left(u\right)}$ (15). This is not a particular failing of cross-validation. It is habitually observed for all prediction error estimates—see for instance Figure 9 of [4]—though the phenomenon seems unexplained in the literature.

Cross-validation tends to pay for its low bias with high variability. Efron [1] proposed bootstrap estimates of prediction error intended to decrease variability without adding much bias. Among the several proposals the most promising was the 632 rule. (An improved version 632+ was introduced in Efron and Tibshirani [6], designed for reduced bias in overfit situations where $\mathrm{err}$ (19) equals zero. The calculations here use only 632.) The 632 rule is described as follows:

• Nonparametric bootstrap samples ${\mathit{d}}^{*}$ are formed by drawing n pairs $(x_i,y_i)$ with replacement from the original data set $\mathit{d}$ (10).
• Applying the original algorithm $\mathcal{A}$ to ${\mathit{d}}^{*}$ gives prediction rule $f(x,{\mathit{d}}^{*})$ and predictions

  $$\widehat{\mu }{\left(x\right)}^{*}=f(x,{\mathit{d}}^{*}),$$

  (50)

  as in (12).
• B bootstrap data sets

  $${\mathit{d}}^{*}\left(1\right),{\mathit{d}}^{*}\left(2\right),\dots ,{\mathit{d}}^{*}\left(B\right)$$

  (51)

  are independently drawn, giving predictions

  $${\widehat{\mu }}_{ij}^{*}=f(x_i,{\mathit{d}}^{*}\left(j\right)),$$

  (52)

  for $i=1,2,\dots ,n$ and $j=1,2,\dots ,B$.
• Two numbers are recorded for each choice of i and j, the error of ${\widehat{\mu }}_{ij}^{*}$ as a prediction of $y_i$,

  $$Q_{ij}^{*}=Q(y_i,{\widehat{\mu }}_{ij}^{*})$$

  (53)

  and

  $$N_{ij}^{*}=\#\left\{(x_i,y_i)\in {\mathit{d}}^{*}\left(j\right)\right\},$$

  (54)

  the number of times $(x_i,y_i)$ occurs in ${\mathit{d}}^{*}\left(j\right)$.
• The zero bootstrap ${\widehat{\mathrm{Err}}}_0$ is calculated as the average value of $Q_{ij}^{*}$ for those cases having $N_{ij}=0$,

  $${\widehat{\mathrm{Err}}}_0=\frac{{\sum }_{(i,j):N_{ij}=0}{Q}_{ij}^{*}}{{\sum }_{(i,j):N_{ij}=0}1}$$

  (55)
• Finally, the 632 estimate of prediction error is defined to be

  $${\widehat{\mathrm{Err}}}_{632}=0.632·{\widehat{\mathrm{Err}}}_0+0.368·\mathrm{err},$$

  (56)
  $\mathrm{err}$ being the apparent error rate (19).

${\widehat{\mathrm{Err}}}_{632}$ was calculated for the same 100 simulated response vectors ${\mathit{y}}_j$ (45) used for ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ (each using $B=400$ replications), the 100 simulations giving

$${\widehat{\mathrm{Err}}}_{632}\sim 1.15\pm 0.10,$$

(57)

an improvement on ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}\sim 1.16\pm 0.14$ at (49). This is in line with the 24 sampling experiments reported in [6]. (There, rule $632+$ was used, with loss function counting error (27) rather than binomial deviance. $Q(y,\widehat{\mu })$ is discontinuous for counting error, which works to the advantage of 632 rules.)

Table 2. Mean of $Q(y,\widehat{\mu })$ given the number of times a case $(x_i,y_i)$ occurred in bootstrap sample; first simulation. True Error 0.97, apparent err 0.90.

# Times:	0	1	2	3	4	5
mean Q:	1.44	0.96	0.81	0.69	0.64	0.57

concerns the rationale for the 632 rule. The $n\times B=$ 80,000 values $Q_{ij}^{*}$ for the first of the 100 simulated $\mathit{y}$ vectors were averaged according to how many times $(x_i,y_i)$ appeared in ${\mathit{d}}^{*}\left(j\right)$,

$${\widehat{\mathrm{Err}}}_k=\frac{{\sum }_{(i,j):N_{ij}=k}{Q}_{ij}^{*}}{{\sum }_{(i,j):N_{ij}=k}1},$$

(58)

for $k=0,1,2,3,4,5$. Not surprisingly, ${\widehat{\mathrm{Err}}}_k$ decreases with increasing k. ${\widehat{\mathrm{Err}}}_0$ (55), which would seem to be the bootstrap analogue of ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$, is seen to exceed the true error $\mathrm{Err}$, while $\mathrm{err}$ is below $\mathrm{Err}$. The intermediate linear combination $0.632{\widehat{\mathrm{Err}}}_0+0.368\mathrm{err}$ is motivated in Section 6 of [1], though in fact the argument is more heuristic than compelling. The 632 rules do usually reduce variability of the error estimates compared to cross-validation, but bias can be a problem.

The 632 rule recomputes a prediction algorithm by nonparametric bootstrap resampling of the original data. Random forests [7], a widely popular prediction algorithm, carries this further: the algorithm itself as well as estimates of its accuracy depend on bootstrap resampling calculations.

Regression trees are the essential component of random forests. Figure 6 shows one such tree (constructed using rpart, the R version of CART [8]; Chapters 9 and 15 of [9] describe CART and random forests) as applied to ${\mathit{y}}_1$, the first of the 100 response vectors for the transplant data simulation (44); ${\mathit{y}}_1$ consists of 57 0 s and 143 1 s, average value $\overline{y}=0.72$. The tree-making algorithm performs successive splits of the data, hoping to partition it into bins that are mostly 0 s or 1 s. The bin at the far right—comprising $n=29$ cases having low body mass index, low age, and female gender—has just one 0 and 28 1 s, for an average of 0.97. For a new transplant case $(x,y)$, with only x observable, we could follow the splits down the tree and use the terminal bin average as a quantitative prediction of y.

Random forests improves the predictive accuracy of any one tree by bagging (“bootstrap aggregation”), sometimes also called bootstrap smoothing: B bootstrap data sets ${\mathit{d}}^{*}\left(1\right),{\mathit{d}}^{*}\left(2\right),\dots ,{\mathit{d}}^{*}\left(B\right)$ are drawn at random (51), each one generating a tree such as that in Figure 6. (Some additional variability is added to the tree-building process: only a random subset of the p predictors is deemed eligible at each splitting point.) A new x is followed down each of the B trees, with the random forest prediction being the average of x’s B terminal values. Letting ${\widehat{\mu }}_{ij}=f(x_i,{\mathit{d}}^{*}\left(j\right))$, the prediction at $x_i$ for the tree based on ${\mathit{d}}^{*}\left(j\right)$, the random forest prediction at $x_i$ is

$${\widehat{\mu }}_i=\sum _{j=1}^B{\widehat{\mu }}_{ij}/B.$$

(59)

Figure 6. Regression tree for transplant data, simulation 1.

Figure 6. Regression tree for transplant data, simulation 1.

The predictive accuracy for ${\widehat{\mu }}_i$ uses a device such as that for ${\widehat{\mathrm{Err}}}_0$ (55): Let ${\widehat{\mu }}_{\left(i\right)}$ be the average value of ${\widehat{\mu }}_{ij}$ for bootstrap samples ${\mathit{d}}_j$ not containing $(x_i,y_i)$,

$${\widehat{\mu }}_{\left(i\right)}=\frac{{\sum }_{j:N_{ij}=0}{\widehat{\mu }}_{ij}}{{\sum }_{j:N_{ij}=0}1},$$

(60)

called the “out-of-bag” (oob) estimate of ${\mu }_i$. The oob error estimate is then

$${\widehat{\mathrm{Err}}}_{\mathrm{oob}}\left(x_i\right)=Q(y_i,{\widehat{\mu }}_{\left(i\right)}).$$

(61)

The overall oob estimate of prediction error is

$${\widehat{\mathrm{Err}}}_{\mathrm{oob}}=\frac{1}{n}\sum _{i=1}^n{\widehat{\mathrm{Err}}}_{\mathrm{oob}}\left(x_i\right).$$

(62)

(Notice that the leave-out calculations here are for the estimates ${\widehat{\mu }}_i$, while those for ${\widehat{\mathrm{Err}}}_{632}$ (56) are for the errors $Q_{ij}^{*}$.) Calculated for the 100 simulated response vectors ${\mathit{y}}_j$ (45), this gave

$${\widehat{\mathrm{Err}}}_{\mathrm{oob}}\sim 1.12\pm 0.07,$$

(63)

a better match to the true error $\mathrm{Err}$ than either ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ (49) or ${\widehat{\mathrm{Err}}}_{632}$ (57). In fact the actual match was even better than (63) suggests, as shown in Table 3 of Section 4. This is all the more surprising given that, unlike ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ and ${\widehat{\mathrm{Err}}}_{632}$, ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ is fully nonparametric: it makes no use of the logistic regression model $\mathtt{glm}(y\sim \mathit{X},\mathtt{binomial})$ (46), which was involved in generating the simulated response vectors ${\mathit{y}}_j$ (44) (It has to be added that ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ is not an estimate for the prediction error of the logistic regression model ${\widehat{\mu }}_{\mathtt{glm}}\left(x\right)$ (46), but rather for the random forest estimates ${\widehat{\mu }}_{\mathrm{rf}}\left(x\right)$).

4. Covariance Penalties and Degrees of Freedom

A quite different approach to the prediction problem was initiated by Mallows’ $C_p$ formula [10]. An observed n-dimensional vector $\mathit{y}$ is assumed to follow the homoskedastic model

$$\mathit{y}=\mathit{\mu }+\mathit{ϵ}\mathrm{with}\mathit{ϵ}\sim (\mathbf{0},{\sigma }^2,\mathit{I}),$$

(64)

the notation indicating uncorrelated errors of mean 0 and variance ${\sigma }^2$ as in (17); ${\sigma }^2$ is known. A linear rule

$$\widehat{\mathit{\mu }}=\mathit{M}\mathit{y}$$

(65)

is used to estimate $\mathit{\mu }$ with $\mathit{M}$ a fixed and known matrix. How accurate is $\widehat{\mathit{\mu }}$ as a predictor of future observations?

The apparent error

$$\mathrm{err}=\frac{1}{n}\sum _{i=1}^n{(y_i-{\widehat{\mu }}_i)}^2$$

(66)

is likely to underestimate the true error of $\widehat{\mathit{\mu }}$ given a hypothetical new observation vector ${\mathit{y}}^{*}=\mathit{\mu }+{\mathit{ϵ}}^{*}$ independent of $\mathit{y}$,

$$\mathrm{Err}=\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})=\frac{1}{n}{E}_{*}\sum _{i=1}^n{(y_i^{*}-{\widehat{\mu }}_i)}^2,$$

(67)

the $E_{*}$ notation indicating that $\widehat{\mathit{\mu }}=({\widehat{\mu }}_1,{\widehat{\mu }}_2,\dots ,{\widehat{\mu }}_n)$ is fixed in (67). Mallows’ $C_p$ formula says that

$${\widehat{\mathrm{Err}}}_{\mathrm{cp}}=\mathrm{err}+\frac{2{\sigma }^2}{n}\mathrm{trace}\left(M\right)$$

(68)

is an unbiased estimator of $\mathrm{Err}$,

$$E\left\{{\widehat{\mathrm{Err}}}_{\mathrm{cp}}\right\}=E\left\{\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})\right\};$$

(69)

that is, ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ is not unbiased for $\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})$ but is unbiased for $E\left\{\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})\right\}$ ($\mathit{\mu }$ fixed in the expectation) under model (64)–(65).

One might wonder what has happened to the covariates $x_i$ in $\mathit{d}$ (10)? The answer is that they are still there but no longer considered random–rather as fixed ancillary quantities such as the sample size n. In the OLS model $\mathit{y}=\mathit{X}\beta +\mathit{ϵ}$ for Figure 3 (16)–(18) the covariates $\mathit{x}=(x_1,x_2,\dots ,x_n)$ determine $\mathit{X}$, $\widehat{\beta }={\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}{\mathit{X}}^{\top }\mathit{y}$ and

$$\widehat{\mathit{\mu }}=\mathit{M}\mathit{y}\left(\mathit{M}=\mathit{X}{\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}{\mathit{X}}^{\top }\right),$$

(70)

Formula (65). We could, but do not, write $\mathit{M}$ as ${\mathit{M}}_{\mathit{X}}$.

Mallows’ $C_p$ Formula (68) can be extended to the Q class of error measures, Figure 4. An unknown probability model $\mathit{f}$ —notice that $\mathit{f}$ is not the same as f in (12)— is assumed to have produced $\mathit{y}$ and its true mean vector $\mathit{\mu }$,

$$\mathit{\mu }=E_{\mathit{f}}\left\{\mathit{y}\right\};$$

(71)

an estimate $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$ has been calculated using some algorithm $m(·)$,

$$\mathit{f}⟶\mathit{y}⟶\widehat{\mathit{\mu }}=m\left(\mathit{y}\right);$$

(72)

the apparent error $\mathrm{err}$ (19) and true error $\mathrm{Err}(\mathit{\mu },\widehat{\mathit{\mu }})$ (33) are defined as before,

$$\mathrm{err}=\frac{1}{n}\sum _{i=1}^{n}Q(y_i,{\widehat{\mu }}_i)\mathrm{and}\mathrm{Err}=\frac{1}{n}{E}_{*}\left\{\sum _{i=1}^{n}Q(y_i^{*},{\widehat{\mu }}_i)\right\},$$

(73)

with the ${\widehat{\mu }}_i$ fixed and $\mathit{f}\to {\mathit{y}}^{*}=(y_1^{*},y_2^{*},\dots ,y_n^{*})$ independently of $\mathit{y}$. Lemma 1 for the true error (36) still applies,

$$\mathrm{Err}=\frac{1}{n}\sum _{i=1}^n\left[Q({\mu }_i,{\widehat{\mu }}_i)+q\left({\mu }_i\right)-c\left(x_i\right)\right].$$

(74)

The Q-class version of Mallows’ Formula (68) is derived as Optimism Theorem 1 in Section 3 of [4]:

Theorem 1.

Define

$$a{m}_i=-\dot{q}\left({\widehat{\mu }}_i\right)/2\left(\dot{q}\left(\mu \right)=\frac{d}{d\mu }q\left(\mu \right)\right).$$

(75)

Then

$$\widehat{\mathit{Err}}=\mathit{err}+\frac{2}{n}\sum _{i=1}^n{\mathrm{cov}}_{\mathit{f}}\left(a{m}_i,y_i\right)$$

(76)

where ${\mathrm{cov}}_{\mathit{f}}$ indicates covariance under model (72), is an unbiased estimate of $\mathit{Err}$ in the same sense as (69),

$$E_{\mathit{f}}\left\{\widehat{\mathit{Err}}\right\}=E_{\mathit{f}}\left\{\mathit{Err}\right\}.$$

(77)

The covariance terms in (76) measure how much each $y_i$ affects its own estimate. They sum to a covariance penalty that must be added to the apparent error to account for the fitting process. If $Q(\mu ,\widehat{\mu })$ is binomial deviance then

$$a{m}_i=\log \left[{\widehat{\mu }}_i/(1-{\widehat{\mu }}_i)\right],$$

(78)

the logistic parameter; the theorem still applies as stated whether or not $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$ is logistic regression.

$\widehat{\mathrm{Err}}$ as stated in (76) is not directly usable since the covariance terms ${\mathrm{cov}}_{\mathit{f}}(a{m}_i,y_i)$ are not observable statistics. This is where resampling comes in.

Suppose that the observed data $\mathit{y}$ provides an estimate $\widehat{\mathit{f}}$ of $\mathit{f}$. For instance in a normal regression model $\mathit{y}\sim \mathcal{N}(\mathit{\mu },{\sigma }^2,\mathit{I})$ we could take $\widehat{\mathit{f}}$ to be ${\mathit{y}}^{*}\sim \mathcal{N}(\widehat{\mathit{\mu }},{\sigma }^2\mathit{I})$ for some estimate $\widehat{\mathit{\mu }}$. We replace (72) with the parametric bootstrap model

$$\widehat{\mathit{f}}⟶{\mathit{y}}^{*}⟶{\widehat{\mathit{\mu }}}^{*}=m\left({\mathit{y}}^{*}\right)$$

(79)

and generate B independent replications ${\mathit{y}}^{*}\left(1\right),{\mathit{y}}^{*}\left(2\right),\dots ,{\mathit{y}}^{*}\left(B\right)$, from which are calculated B pairs,

$$\left(y_i^{*}\left(j\right),a{m}_i^{*}\left(j\right)\right),j=1,2,\dots ,B,$$

(80)

for $i=1,2,\dots ,n$ as in (75). The covariances in (76) can then be estimated as

$$\widehat{\mathrm{cov}}\left(a{m}_i,y_i\right)=\frac{1}{B}\sum _{j=1}^B\left(a{m}_i^{*}\left(j\right)-a{m}_i^{*}(·)\right)\left(y_i^{*}\left(j\right)-y_i^{*}(·)\right),$$

(81)

$a{m}_i^{*}(·)={\sum }_{j}a{m}_i^{*}\left(j\right)/B$ and $y_i^{*}(·)={\sum }_j{y}_i^{*}\left(j\right)/B$, yielding a useable version of (76),

$${\widehat{\mathrm{Err}}}_{\mathrm{cp}}=\mathrm{err}+\frac{2}{n}\sum _{i=1}^n\widehat{\mathrm{cov}}\left(a{m}_i,y_i\right),$$

(82)

“cp” standing for “covariance penalty”.

Table 3 compares the performances of cross-validation, covariance penalties, the 632 rule, and the random forest out-of-bag estimates on the 100 transplant data simulations. The results are given in terms of total prediction error, rather than average error as in (47). The bottom line shows their root-mean-square differences from true error $\mathrm{Err}$,

$$\mathrm{rms}={\left[\sum _{i=1}^{100}{\left({\widehat{\mathrm{Err}}}_i-{\mathrm{Err}}_i\right)}^2/100\right]}^{1/2}.$$

(83)

${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ is highest, with ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$, ${\widehat{\mathrm{Err}}}_{632}$, and ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ respectively 71%, 83%, and 65% as large.

Table 3. Transplant data simulation experiment. Top: First 5 of 100 estimates of total prediction error using cross-validation, covariance penalties (cp), the 632 rule, the out-of-bag random forest results, and the apparent error; degrees of freedom (df) estimate from cp. Bottom: Mean of the 100 simulations, their standard deviations, correlations with Errtrue, and root mean square differences from Errtrue. Cp and 632 rules used $B=400$ bootstrap replications per simulation.

	Errtrue	ErrCv	ErrCp	Err632	Erroob	err	df
	194	216.5	232.9	260.6	240.3	180.4	26.2
	199	245.8	220.9	241.0	230.9	173.8	23.5
	192	221.2	225.9	247.6	232.7	180.6	22.7
	234	197.4	200.9	215.2	219.7	162.2	19.4
	302	175.7	178.3	187.1	211.2	144.6	16.9
	Errtrue	ErrCv	ErrCp	Err632	Erroob	err	df
mean	214.0	231.1	216.1	229.4	223.8	169.9	23.1
stdev	23.0	28.7	15.8	19.0	14.6	13.5	4.0
cor.true		−0.58	$-0.61$	$-0.64$	$-0.26$	$-0.41$	$-0.52$
rms		48.8	34.8	40.7	31.6	54.2

Table 3. Transplant data simulation experiment. Top: First 5 of 100 estimates of total prediction error using cross-validation, covariance penalties (cp), the 632 rule, the out-of-bag random forest results, and the apparent error; degrees of freedom (df) estimate from cp. Bottom: Mean of the 100 simulations, their standard deviations, correlations with Errtrue, and root mean square differences from Errtrue. Cp and 632 rules used $B=400$ bootstrap replications per simulation.

	Errtrue	ErrCv	ErrCp	Err632	Erroob	err	df
	194	216.5	232.9	260.6	240.3	180.4	26.2
	199	245.8	220.9	241.0	230.9	173.8	23.5
	192	221.2	225.9	247.6	232.7	180.6	22.7
	234	197.4	200.9	215.2	219.7	162.2	19.4
	302	175.7	178.3	187.1	211.2	144.6	16.9
	Errtrue	ErrCv	ErrCp	Err632	Erroob	err	df
mean	214.0	231.1	216.1	229.4	223.8	169.9	23.1
stdev	23.0	28.7	15.8	19.0	14.6	13.5	4.0
cor.true		−0.58	$-0.61$	$-0.64$	$-0.26$	$-0.41$	$-0.52$
rms		48.8	34.8	40.7	31.6	54.2

For the jth simulation vector ${\mathit{y}}_j$ (45) the parametric bootstrap replications (79) were generated as follows: the logistic regression estimate ${\widehat{\mathit{\mu }}}_j$ was calculated from (46), ${\widehat{\mathit{\mu }}}_j=\mathtt{glm}({\mathit{y}}_j\sim \mathit{X},\mathtt{binomial})\$,\mathtt{fit}$; the bootstrap replications ${\mathit{y}}_j^{*}$ had independent Bernoulli components

$$y_{ij}^{*}\stackrel{\mathrm{ind}}{\sim }\mathrm{Bi}(1,{\widehat{\mu }}_{ij})\mathrm{for}i=1,2,\dots ,200.$$

(84)

$B=400$ independent replications ${\mathit{y}}_j^{*}$ were generated for each $j=1,2,\dots ,100$, giving ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ according to (81)–(82).

Because the resamples were generated by a model of the same form as that which originally gave the ${\mathit{y}}_j$’s (43)–(44), ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ is unbiased for $\mathrm{Err}$. In practice our resampling model $\widehat{\mathit{f}}$ in (79) might not match $\mathit{f}$ in (72), causing ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ to be downwardly biased (and raising its rms). ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$’s nonparametric resamples make it nearly unbiased for the unconditional error rate ${\mathrm{Err}}^{\left(u\right)}$ (15) irrespective of the true model, accounting for the overwhelming popularity of cross-validation in applications.

4.1. A Few Comments

• In computing ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ it is not necessary for $\widehat{\mathit{f}}$ in (79) to be constructed from the original estimate $\widehat{\mathit{\mu }}$. We might base $\widehat{\mathit{f}}$ on a bigger model than that which led to the choice of $m\left(\mathit{y}\right)$ for $\widehat{\mathit{\mu }}$; in the little example of Figure 3, for instance, we could take $\widehat{\mathit{f}}$ to be $\mathcal{N}(\widehat{\mathit{\mu }}\left(6\right),{\sigma }^2\mathit{I})$ where $\widehat{\mathit{\mu }}\left(6\right)$ is the OLS sixth degree polynomial fit, while still taking $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$ to be fourth degree as in (18). This reduces possible model-fitting bias in ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$, while increasing its variability.
• A major conceptual difference between ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ and ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ concerns the role of the covariates $\mathit{x}=(x_1,x_2,\dots ,x_n)$, considered as random in model (10) but fixed in (72). Classical regression problems have usually been analyzed in a fixed-$\mathit{x}$ framework for three reasons:

  1.

  mathematical tractability;

  2.

  not having to specify $\mathit{x}$’s distribution;

  3.

  inferential relevance.

  The reasons come together in the classic covariance formula for the linear model $\mathit{y}=\mathit{X}\beta +\mathit{ϵ}$,

  $$\mathrm{cov}\left(\widehat{\beta }\right)={\sigma }^2{\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}.$$

  (85)

  A wider dispersion of the $x_i$’s in Figure 3 would make $\widehat{\beta }$ more accurate, and conversely.
• It can be argued that because ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ is estimating the conditional error given $\mathit{x}$ it is more relevant to what is being estimated. See [11,12] for a lot more on this question.
• On the other hand, “fixed-$\mathit{x}$” methods such as Mallows’ $C_p$ can be faulted for missing some of the variability contributing to the unconditional prediction error ${\mathrm{Err}}^{\left(u\right)}$ (15). Let $\mathrm{Err}(x,\mathit{d})$ be the conditional error given $\mathit{d}$ for predicting y given x,

  $$\mathrm{Err}(x,\mathit{d})=Q\left(\mu \left(x\right),f(x,\mathit{d})\right)+q\left(\mu \left(x\right)\right)-c\left(x\right)$$

  (86)

  according to Lemma 1 (34). Then

  $${\mathrm{Err}}^{\left(u\right)}=E\left\{{\int }_{\mathcal{X}}g\left(x\right)\mathrm{Err}(x,\mathit{d})dx\right\},$$

  (87)

  where $g\left(x\right)$ is the marginal density of x and E indicates expectation over the choice of the training data $\mathit{d}$.
• In the fixed-$\mathit{x}$ framework of (36), $\mathrm{Err}$ replaces the integrand in (87) with its $\mathit{x}$ average ${\sum }_1^n\mathrm{Err}(x_i,\mathit{d})/n$. We expect

  $${\mathrm{Err}}^{\left(u\right)}>E_{\mathit{f}}\left\{\mathrm{Err}\right\}$$

  (88)

  since $\mathrm{Err}(x,\mathit{d})$ typically increases for values of x farther away from $\mathit{x}$. Rosset and Tibshirani [12] give an explicit formula for the difference in the case of normal-theory ordinary least squares when they show that the factor 2 for the penalty term in Mallows’ $C_p$ formula should be increased to $2+(p+1)/(n-p-1)$. Cross-validation effectively estimates ${\mathrm{Err}}^{\left(u\right)}$ while $C_p$ estimates the fixed-$\mathit{x}$ version of $E\left\{\mathrm{Err}\right\}$.
• With (88) in mind, ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ and ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ are often contrasted as

  $$\mathit{insample}\mathrm{versus}\mathit{outsample}.$$

  (89)

  This is dangerous terminology if it’s taken to mean that ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ applies to prediction errors $\mathrm{Err}(x,\mathit{d})$ at specific points x outside of $\mathit{x}$. In Figure 3 for instance it seems likely that $\mathrm{Err}(11,\mathit{d})$ exceeds ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$, but this is a fixed-$\mathit{x}$ question and beyond the reach of the random-$\mathit{x}$ assumptions underlying (88). See the discussion of Figure 8 in Section 5.

• The sad story told in Figure 5 shows ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ negatively correlated with the true $\mathrm{Err}$. The same is the case for ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ and ${\widehat{\mathrm{Err}}}_{632}$, as can be seen from the negative correlations in the cor.true row of Table 3. ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ is also negatively correlated with $\mathrm{Err}$, but less so. In terms of rms, the bottom row shows that the fully nonparametric ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ estimates beat even the parametric ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$ ones.
• Figure 7 compares the 200 ${\widehat{\mu }}_i$ estimates from the logistic regression estimates (46) with those from random forests, for y the first of the 100 transplant simulations. Random forests is seen to better separate the $y_i=0$ from the $y_i=1$ cases. ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ relates to error prediction for random forest estimates, not for logistic regression, but this does not explain how ${\widehat{\mathrm{Err}}}_{\mathrm{oob}}$ could provide excellent estimates of the true error $\mathrm{Err}$–which in fact were based on the logistic regression model (43)–(44). If this is a fluke it’s an intriguing one.
• There is one special case where the covariance penalty formula (76) can be unbiasedly estimated without recourse to resampling: if $\mathit{f}$ is the normal model $\mathit{y}\sim \mathcal{N}(\mathit{\mu },{\sigma }^{2}I)$, and $Q(y_i,{\mu }_i)={(y_i-{\mu }_i)}^2$—so $a{m}_i={\widehat{\mu }}_i$—then Stein’s unbiased risk estimate (SURE) is defined to be

  $${\widehat{\mathrm{Err}}}_{\mathrm{SURE}}=\mathrm{err}+\frac{2{\sigma }^2}{n}\sum _{i=1}^n\frac{\partial {\widehat{\mu }}_i}{\partial y_i},$$

  (90)

  where the partial derivatives are calculated directly from the functional form of $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$. Section 2 of [4] gives an example comparing ${\widehat{\mathrm{Err}}}_{\mathrm{SURE}}$ with ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}$. Each term $\partial {\widehat{\mu }}_i/\partial y_i$ measures the influence of $y_i$ on its own estimate.

4.2. Degrees of Freedom

The OLS model $\mathit{y}=\mathit{X}\beta +\mathit{ϵ}$ yields the familiar estimate $\widehat{\mathit{\mu }}=\mathit{M}\mathit{y}$ of $\mathit{\mu }=E\left\{\mathit{y}\right\}$, where $\mathit{M}$ is the projection matrix $\mathit{X}{\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}{\mathit{X}}^{\top }$ as in (70); $\mathit{M}$ has

$$\mathrm{trace}\left(\mathit{M}\right)=\mathrm{trace}\left[{\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}{\mathit{X}}^{\top }\mathit{X}\right]=p,$$

(91)

where $p=\mathrm{rank}\left(\mathit{X}\right)$. Mallows’ $C_p$ formula ${\widehat{\mathrm{Err}}}_{\mathrm{cp}}=\mathrm{err}+(2{\sigma }^2/n)\mathrm{trace}\left(\mathit{M}\right)$ becomes

$${\widehat{\mathrm{Err}}}_{\mathrm{cp}}=\mathrm{err}+\frac{2{\sigma }^2}{n}p$$

(92)

in this case. In other words, the covariance penalty that must be added to the apparent error $\mathrm{err}$ is directly proportional to p, the degrees of freedom of the OLS model.

Suppose that $\widehat{\mathit{\mu }}=\mathit{M}\mathit{y}$ with matrix $\mathit{M}$ not necessarily a projection. It has become common to define $\widehat{\mathit{\mu }}$’s degrees of freedom as

$$\mathrm{df}=\mathrm{degrees}\mathrm{of}\mathrm{freedom}=\mathrm{trace}\left(M\right),$$

(93)

$\mathrm{trace}\left(M\right)$ playing the role of p in the $C_p$ Formula (92). In this way, $\mathrm{trace}\left(M\right)$ becomes a lingua franca for comparing linear estimators $\widehat{\mathit{\mu }}=\mathit{M}\mathit{y}$ of different forms. (The referee points out that formulas such as (92) are more often used for model selection rather than error rate prediction. Zhang and Yang [13] consider model selection applications, as does Remark B of [4].)

A nice example is the ridge regression estimator

$${\widehat{\mathit{\mu }}}_{\gamma }=\mathit{X}{\left({\mathit{X}}^{\top }\mathit{X}+\gamma \mathit{I}\right)}^{-1}{\mathit{X}}^{\top }y,$$

(94)

$\gamma$ a fixed non-negative constant; ${\widehat{\mathit{\mu }}}_0$ is the usual OLS estimator while ${\widehat{\mathit{\mu }}}_{\gamma }$ “shrinks” $\widehat{\mathit{\mu }}$ toward $\mathbf{0}$, more so as $\gamma$ increases. Some linear algebra gives the degrees of freedom for (94) as

$${\mathrm{df}}_{\gamma }=\sum _{i=1}^p\frac{e_i}{e_i+\gamma },$$

(95)

where the $e_i$ are the eigenvalues of ${\mathit{X}}^{\top }\mathit{X}$.

The generalization of Mallows’ Formula (68) in Theorem 1 (76) has penalty term

$$\frac{2}{n}\sum _{i=1}^n{\mathrm{cov}}_{\mathit{f}}\left(a{m}_i,y_i\right),$$

(96)

which again measures the self-influence of each $y_i$ on its own estimate ${\widehat{\mu }}_i$. The choice of

$$q\left(\mu \right)=\mu (1-\mu )$$

(97)

in Figure 3 results in $Q(\mu ,\widehat{\mu })={(\widehat{\mu }-\mu )}^2$, squared error, and $a{m}_i={\widehat{\mu }}_i-1/2$, in which case ${\mathrm{cov}}_{\mathit{f}}(a{m}_i,y_i)$ equals ${\sigma }^2{m}_{ii}$, and (96) becomes $(2{\sigma }^2/n)\mathrm{trace}\left(\mathit{M}\right)$, as in Mallows’ Formula (68). This suggests using

$$\mathbf{Cov}=\sum _{i=1}^n{\mathrm{cov}}_{\mathit{f}}\left(a{m}_i,y_i\right)$$

(98)

as a measure of degrees of freedom (or its estimate $\widehat{\mathbf{Cov}}$ from (81)) for a general estimator $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$.

Some support comes from the following special situation: suppose $\mathit{y}$ is obtained from a p-parameter generalized linear model, with prediction error measured by the appropriate deviance function. (Binomial deviance for logistic regression as in the transplant example.) Theorem 2 of [14], Section 6, then gives the asymptotic approximation

$$\mathbf{Cov}\doteq p,$$

(99)

as in (91)–(92), the intuitively correct answer.

Approximation (99) leads directly to Akaike’s information criterion (AIC). In a generalized linear model, the total deviance from the MLE $\widehat{\mathit{\mu }}$ is

$$n·\mathrm{err}=\sum _{i=1}^{n}Q(y_i,{\widehat{\mu }}_i)=2\left[\sum _{i=1}^n\log \left(g_{y_i}\left(y_i\right)/g_{{\widehat{\mu }}_i}\left(y_i\right)\right)\right],$$

(100)

$g_{{\widehat{\mu }}_i}\left(y_i\right)$ denoting the density function ([2], Hoeffding’s Lemma). Suppose we have glm’s of different sizes p we wish to compare. Minimizing $\mathrm{err}+(2/n)\mathbf{Cov}$ over the choice of model is then equivalent to maximizing the total log likelihood $\log g_{\widehat{\mathit{\mu }}}\left(\mathit{y}\right)$ minus a dimensionality penalty,

$$\log \left(g_{\widehat{\mathit{\mu }}}\left(\mathit{y}\right)\right)-\mathrm{Cov}\doteq \log \left(g_{\widehat{\mathit{\mu }}}\left(\mathit{y}\right)\right)-p,$$

(101)

which is the AIC.

Approximation (99) is not razor-sharp: $p=17$ is the transplant simulation logistic regression but the 100 estimates $\widehat{\mathbf{Cov}}$ averaged 23.08 with standard error 0.40. Degrees of freedom play a crucial role in model selection algorithms. Resampling methods allow us to assess $\mathbf{Cov}$ (98) even for very complicated fitting algorithms $\widehat{\mathit{\mu }}=m\left(\mathit{y}\right)$.

5. Conformal Inference

If there is a challenger to cross-validation for “oldest resampling method” it is permutation testing, going back to Fisher in the 1930s. The newest prediction error technique, conformal inference, turns out to have permutation roots, as briefly reviewed next.

A clinical trial of an experimental drug has yielded independent real-valued responses for control and treatment groups:

$$\mathrm{Control}:\mathit{u}=(u_1,\dots ,u_n)\mathrm{and}\mathrm{Treatment}:\mathit{v}=(v_1,\dots ,v_m).$$

(102)

Student’s t-test could be used to see if the new drug was giving genuinely larger responses but Fisher, reacting to criticism of normality assumptions, proposed what we would now call a nonparametric two-sample test.

Let $\mathit{z}$ be the combined data set,

$$\mathit{z}=(\mathit{u},\mathit{v})=(z_1,\dots ,z_{n+m}),$$

(103)

and choose some score function $S\left(\mathit{z}\right)$ that contrasts the last m z-values with the first n, for example the difference of means,

$$S\left(\mathit{z}\right)=\sum _{i=n+1}^{n+m}\frac{z_i}{m}-\sum _{i=1}^n\frac{z_i}{n}.$$

(104)

Define $\mathcal{S}$ as the set of scores for all permutations of $\mathit{z}$,

$$\mathcal{S}=\left\{S\left({\mathit{z}}^{*}\right)\right\},$$

(105)

${\mathit{z}}^{*}$ ranging over the $(m+n)!$ permutations.

The permutation p-value for the treatment’s efficacy in producing larger responses is defined to be

$$p=\#\left\{S\left({\mathit{z}}^{*}\right)\ge S\left(\mathit{z}\right)\right\}/(m+n)!,$$

(106)

the proportion of $\mathcal{S}$ having scores $S\left({\mathit{z}}^{*}\right)$ exceeding the observed score $S\left(\mathit{z}\right)$. Fisher’s key idea was that if in fact all the observations came from the same distribution F,

$$z_i\stackrel{\mathrm{ind}}{\sim }F(i=1,2,\dots ,m+n)$$

(107)

(implying that Treatment is the same as Control), then all $(m+n)!$ permutations would be equally likely. Rejecting the null hypothesis of No Treatment Effect if $p\le \alpha$ has null probability (nearly) $\alpha$.

Usually $(m+n)!$ is too many for practical use. This is where the sampling part of resampling comes in. Instead of all possible permutations, a randomly drawn subset of B of them, perhaps $B=1000$, is selected for scoring, giving an estimated permutation p-value

$$\widehat{p}=\#\left\{S\left({\mathit{z}}^{*}\right)\ge S\left(\mathit{z}\right)\right\}/B.$$

(108)

In 1963, Hodges and Lehmann considered an extension of the null hypothesis (107) to cover location shifts; in terms of cumulative distribution functions (cdfs), they assumed

$$u_i\stackrel{\mathrm{iid}}{\sim }F\left(u\right)\mathrm{and}{v}_i\stackrel{\mathrm{iid}}{\sim }F(v-\Delta ),$$

(109)

where $\Delta$ is a fixed but unknown constant that translates the v’s distribution by $\Delta$ units to the right of the u’s.

For a given trial value of $\Delta$ let

$$\mathit{z}(\Delta )=(u_1,\dots ,u_n,v_1-\Delta ,\dots ,v_m-\Delta )$$

(110)

and compute its permutation p-value

$$\widehat{p}(\Delta )=\#\left\{S\left({\mathit{z}}^{*}(\Delta )\right)\ge S\left(\mathit{z}(\Delta )\right)\right\}.$$

(111)

A 0.95 two-sided nonparametric confidence interval for $\Delta$ is then

$$\Delta :0.025\le \widehat{p}(\Delta )\le 0.975.$$

(112)

The only assumption is that, for the true value of $\Delta$, the $m+n$ components of $\mathit{z}(\Delta )$ are i.i.d., or more generally exchangeable, from some distribution F.

Vovk has proposed an ingenious extension of this argument applying to prediction error estimation, a much cited reference being [15]; see also [16]. Returning to the statement of the prediction problem at the beginning of Section 2, $\mathit{d}=\{(x_i,y_i),i=1,2,\dots ,n\}$ is the observed data and $(x_0,y_0)$ a new (predictor, response) pair, all $n+1$ pairs assumed to be random draws from the same distribution F,

$$(x_i,y_i)\stackrel{\mathrm{iid}}{\sim }F\mathrm{for}i=0,1,\dots ,n;$$

(113)

$x_0$ is observed but not $y_0$, and it is desired to predict $y_0$. Vovk’s proposal, conformal inference, produces an exact nonparametric distribution of the unseen $y_0$.

Let $Y_0$ be a proposed trial value for $y_0$, and define $\mathit{D}$ as the data set $\mathit{d}$ augmented with $(x_0,Y_0)$,

$$\mathit{D}=\left\{\mathit{d},(x_0,Y_0)\right\}.$$

(114)

A prediction rule $f(x,\mathit{D})$ gives estimates

$${\widehat{\mu }}_i=f(x_i,\mathit{D})\mathrm{for}i=0,1,\dots ,n.$$

(115)

(It is required that $f(x,\mathit{D})$ be invariant under reordering of $\mathit{D}$’s elements.)

For some score function $s(y,\widehat{\mu })$ let

$$s_i=s(y_i,{\widehat{\mu }}_i)\mathrm{for}i=1,2,\dots ,n,$$

(116)

where $s(y,\widehat{\mu })$ measures disagreement between y and $\widehat{\mu }\left(x\right)$, larger values of $\left|s\right|$ indicating less conformity between observation and prediction. (More generally $s_i$ can be any function $s(y_i,\mathit{D})$.)

If the proposed trial value $Y_0$ were in fact the unobserved $y_0$ then $s_1,s_2,\dots ,s_n$ and $s_0=s(Y_0,{\widehat{\mu }}_0)$ would be exchangeable random variables, because of the i.i.d. assumption (113). Let $s_{\left(1\right)},s_{\left(2\right)},\dots ,s_{\left(n\right)}$ be the ordered values of $s_1,s_2,\dots ,s_n$. Assuming no ties, the n values

$$s_{\left(1\right)}<s_{\left(2\right)}<\cdots <s_{\left(n\right)}$$

(117)

partition the line into $(n+1)$ intervals, the first and last of which are semi-infinite. Exchangeability implies that $s_0$ has probability $1/(n+1)$ of falling into any one of the intervals.

A conformal interval for the unseen $y_0$ consists of those values of $Y_0$ for which $s_0=s(Y_0,{\widehat{\mu }}_0)$ “conforms” to the distribution (117). To be specific, for a chosen miscoverage level $\alpha$, say 0.05, let $I_0$ and $I_1$ be integers approximately proportion $\alpha /2$ from the endpoints of $1,2,\dots ,n$,

$$I_0=[n\alpha /2]\mathrm{and}{I}_1=\left[n(1-\alpha /2)\right]+1.$$

(118)

The conservative two-sided level $1-\alpha$ conformal prediction interval $\mathcal{C}$ for $y_0$ is

$$\mathcal{C}=\left\{Y_0:s(Y_0,\mathit{D})\in [s_{\left(I_0\right)},s_{\left(I_1\right)}]\right\}.$$

(119)

The argument is the same as for the Hodges–Lehmann interval (112), now with $m=1$ and $\Delta =Y_0$.

Interval (119) is computationally expensive since all of the $s_i$, not just $s_0$, change with each choice of trial value $Y_0$. The jackknife conformal interval begins with the jackknife estimates

$${\widehat{\mu }}_{\left(i\right)}=f\left(x_i,{\mathit{d}}_{\left(i\right)}\right),i=1,2,\dots ,n,$$

(120)

where ${\mathit{d}}_{\left(i\right)}=\{(x_j,y_j),j\ne i\}$, that is $\mathit{d}$ (10) with $(x_i,y_i)$ deleted. The scores $s_i$ (116) are taken to be

$$s_i=s\left(y_i,{\widehat{\mu }}_{\left(i\right)}\right),i=1,2,\dots ,n,$$

(121)

for some function s, for example $s_i=y_i-{\widehat{\mu }}_{\left(i\right)}$. These are compared with

$$s_0=s(Y_0,{\widehat{\mu }}_0),$$

(122)

${\widehat{\mu }}_0=f(x_0,\mathit{d})$, and $\mathcal{C}$ is computed as at (119). Now the score distribution (117) does not depend on $Y_0$ (nor does ${\widehat{\mu }}_0$), greatly reducing the computational burden.

The jackknife conformal interval at $x_0=11$ was calculated for the small example of Figure 2 using

$$s_i=y_i-{\widehat{\mu }}_{\left(i\right)}$$

(123)

for $i=1,2,\dots ,n=20$. For this choice of scoring function, interval (119) is

$$\mathcal{C}={\displaystyle [}{\widehat{\mu }}_0+s_{\left(I_0\right)},{\widehat{\mu }}_0+s_{\left(I_1\right)}{\displaystyle ]};$$

(124)

$y_0\in \mathcal{C}$ with conformal probability $(I_{\left(1\right)}-I_{\left(0\right)})/(n+1)$. The square dots in Figure 8 are the values ${\widehat{\mu }}_0+s_{\left(i\right)}$ for $i=1,2,\dots ,20$, with $y_0$ having probability $1/21$ of falling into each of the 21 intervals. Conformal probability for the full range

$$\left[{\widehat{\mu }}_0+s_{\left(1\right)},{\widehat{\mu }}_0+s_{\left(20\right)}\right]=[3.27,10.99]$$

(125)

is $19/21=0.905$.

Some Comments

• Even when $Y_0$ equals $y_0$, $s_0=s(Y_0,{\widehat{\mu }}_0)$ is not perfectly exchangeable with the $s_i=s(y_i,{\widehat{\mu }}_{\left(i\right)})$ (121): each ${\widehat{\mu }}_{\left(i\right)}$ is based on $n-1$ other cases, while ${\widehat{\mu }}_0$ is based on n. Other stand-ins for the full conformal intervals (119) are favored in the literature but these have their own disadvantages. Barber et al. [17] offer a version of the jackknife intervals, “jackknife +“, with more dependable inferential performance.
• The jackknife scores $s_i$ (121) are also the one-at-a-time cross-validation scores if s is taken to be the prediction loss Q in (42). In this sense, conformal inference can be thought of as a more ambitious version of prediction error estimation, where we try to estimate the entire error distribution rather than just its expectation. The conformal point estimate $\overline{s}=\sum _1^n{s}_i/n$ is the same as ${\widehat{\mathrm{Err}}}_{\mathrm{cv}}$ (42) if s equals Q (which is why “conformal” was not included in Table 3).
• Figure 8 is misleading in an important sense: the 95% coverage claimed in (125) is a marginal inference following from the i.i.d. assumption $(x_i,y_i)\stackrel{\mathrm{iid}}{\sim }F$ for $i=0,1,\dots ,n$ (113), and does not apply conditionally to the particular configuration of x’s and y’s seen in the figure. (See Remark 3 and Section 3 of [16].) The same complaint was leveled against cross-validation in Section 3—for estimating the unconditional error ${\mathrm{Err}}^{\left(u\right)}$ rather than prediction error for the rule at hand—but conformal inference leans even harder on the i.i.d. assumption.
• Classic parametric prediction intervals do apply conditionally. The normal-theory version of model (16) and (17) gives 95% interval

  $${\widehat{\mu }}_0\pm 1.96\sigma \sqrt{1+{\gamma }_0}$$

  (126)

  for response $y_0$ at $x_0=11$, where

  $${\gamma }_0=X{\left(x_0\right)}^{\top }{\left({\mathit{X}}^{\top }\mathit{X}\right)}^{-1}X\left(x_0\right)$$

  (127)

  in notation (18). (At $x_0=11$, (126) gives 95% prediction interval $[-15.6,32.9]$, reflecting the hopelessly large extrapolation variability of the fourth-degree polynomial model; the standard deviation of ${\widehat{\mu }}_0$ at $x_0=11$ is 12.22.) The nonparametric random sampling assumption (113) destroys the geometry seen in Figure 8.
• Rather than $s_i=y_i-{\widehat{\mu }}_{\left(i\right)}$ at (123), we might use scores

  $$s_i=\frac{y_i-{\widehat{\mu }}_{\left(i\right)}}{{\gamma }_i},$$

  (128)

  where ${\gamma }_i=\gamma \left(x_i\right)$ is some measure of prediction difficulty at $x_i$. Conformal inference continues to apply here since the $s_i$ are still exchangeable. Boström et al. [18] give several random forest examples, using out-of-bag estimates for the ${\gamma }_i$.
• Covariate shift estimation offers a more ambitious approach to broadening the reach of conformal prediction; see [19,20]. The underlying probability distribution F in (113) can be thought of in two stages, first choosing x according to say $g\left(x\right)$ and then y given x according to $p(y\mid x)$,

  $$F:x\sim g\left(x\right)\mathrm{and}y\mid x\sim p(y\mid x).$$

  (129)

  It is assumed that (129) holds in a training set, but in the test set where predictions are to be made $g\left(x\right)$ is shifted to $g_{\mathrm{test}}\left(x\right)$,

  $$F_{\mathrm{test}}:x\sim g_{\mathrm{test}}\left(x\right)\mathrm{and}y\mid x\sim p(y\mid x).$$

  (130)

  With sufficiently large training and test sets available, the ratio $g_{\mathrm{test}}\left(x\right)/g\left(x\right)$ can be estimated, allowing a suitably weighted version of conformal interval (124) to be constructed.

• Conformal prediction is less appealing for dichotomous response data but can still be informative. Figure 9 shows its application to the transplant data of Section 3 and Section 4. The score function s is taken to be the deviance residual

  $$s_i=\mathrm{sign}\left(y_i-{\widehat{\mu }}_{\left(i\right)}\right)Q{\left(y_i,{\widehat{\mu }}_{\left(i\right)}\right)}^{1/2},$$

  (131)

  ${\widehat{\mu }}_{\left(i\right)}$ the jackknife logistic regression estimate (120) and $Q(y,\mu )$ binomial deviance (28). The left side of Figure 9 shows the histogram of the 200 $s_i$ values. Any given value of ${\widehat{\mu }}_0$ corresponds to two possible values of $s_0=\mathrm{sign}(y_0-{\widehat{\mu }}_0)Q{(y_0,{\widehat{\mu }}_0)}^{1/2}$, for $y_0$ equal 0 or 1, and two values of the conformal p-value,

  $$p\left({\widehat{\mu }}_0\right)=\#\{s_i\ge s_0\}/201.$$

  (132)

  The right side of Figure 9 graphs $p\left({\widehat{\mu }}_0\right)$ as a function of ${\widehat{\mu }}_0$ for the two cases:

  $$\begin{array}{cc}\hfill {\widehat{\mu }}_0& <0.315\mathrm{gives}\widehat{p}\ge 0.975\mathrm{for}{y}_0=1,\hfill \\ \hfill {\widehat{\mu }}_0& >0.918\mathrm{gives}\widehat{p}\ge 0.025\mathrm{for}{y}_0=0.\hfill \end{array}$$

  (133)

  For ${\widehat{\mu }}_0$ in $[0.315,0.918]$, neither $y_0=0$ or $y_0=1$ can be rejected at the 0.025 level.

Figure 9. (Left) Signed deviance residuals for transplant data. (Right) Attained conformal p-value given $\mu$; solid $y=1$, dashed $y=0$.

Figure 9. (Left) Signed deviance residuals for transplant data. (Right) Attained conformal p-value given $\mu$; solid $y=1$, dashed $y=0$.

As far as prediction error is concerned, cross-validation and covariance penalties are established subjects backed up by a substantial theoretical and applied literature. Conformal prediction, as the new kid on the block, is still in its formative stage, with at least a promising hint of moving beyond complete reliance on the random sampling model (15). All three approaches rely on resampling methodology, very much in the spirit of statistical inference in the 2020s.