Bland–Altman Limits of Agreement from a Bayesian and Frequentist Perspective
Abstract
:1. Introduction
2. Materials and Methods
2.1. Classical Frequentist Bland–Altman Analysis
2.2. Bayesian Bland–Altman Analysis
- What is the probability that a future difference between the two measurements will be between (−δ, δ)?
- Focusing on the LoA, i.e., θ1 = µ − 1.96σ (lower limit) and θ2 = µ + 1.96σ (upper limit), what is the posterior probability of H1: θ1 > −δ and θ2 < δ?
2.3. Worked Example
3. Results
3.1. Frequentist Bland–Altman Analysis
3.1.1. Prediction Interval for a Future Difference
3.1.2. Outer 95% Confidence Limits for the LoA (i.e., θ1 and θ2)
3.2. Bayesian Bland–Altman Analysis
3.2.1. Posterior Probability of a Future Difference Being in (−δ, δ)
3.2.2. Posterior Probability of H1: θ1 > −δ and θ2 < δ
4. Discussion
4.1. Predicting One Future Difference versus Targeting the LoA
4.2. Confidence versus Credibility
- Credibility intervals have a direct probabilistic interpretation in terms of the credibility of possible parameter values which confidence intervals do not have;
- Credibility intervals have no dependence on the sampling and testing intentions of the experimenter. Frequentist confidence intervals tell us about probabilities of data relative to imaginary possibilities generated from the experimenter’s intentions (namely the range of nonrejectable parameter values in null hypothesis significance testing, which focuses on the probability of observing the data as seen or data favoring the alternative hypothesis H1, given H0 were true);
- Credibility intervals are responsive to the experimenter’s prior belief based, for instance, on previous literature findings. Bayesian analysis indicates how much newly gathered data should alter our beliefs. Frequentist confidence intervals do not incorporate prior knowledge.
4.3. Group-Sequential Testing
4.4. Nonparametric Alternatives
4.5. Simplicity versus Interpretability
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tukey, J.W. Exploratory Data Analysis; Pearson: Cambridge, MA, USA, 1977. [Google Scholar]
- Altman, D.G.; Bland, J.M. Measurement in medicine: The analysis of method comparison studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Agreed statistics: Measurement method comparison. Anesthesiology 2012, 116, 182–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carkeet, A. Exact parametric confidence intervals for Bland-Altman limits of agreement. Optom. Vis. Sci. 2015, 92, e71–e80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olofsen, E.; Dahan, A.; Borsboom, G.; Drummond, G. Improvements in the application and reporting of advanced Bland-Altman methods of comparison. J. Clin. Monit. Comput. 2015, 29, 127–139. [Google Scholar] [CrossRef]
- Webpage for Bland-Altman Analysis. Available online: https://sec.lumc.nl/method_agreement_analysis (accessed on 17 December 2021).
- Jones, M.; Dobson, A.; O’Brian, S. A graphical method for assessing agreement with the mean between multiple observers using continuous measures. Int. J. Epidemiol. 2011, 40, 1308–1313. [Google Scholar] [CrossRef] [Green Version]
- Christensen, H.S.; Borgbjerg, J.; Børty, L.; Bøgsted, M. On Jones et al.’s method for extending Bland-Altman plots to limits of agreement with the mean for multiple observers. BMC Med. Res. Methodol. 2020, 20, 304. [Google Scholar] [CrossRef]
- Möller, S.; Debrabant, B.; Halekoh, U.; Petersen, A.K.; Gerke, O. An extension of the Bland-Altman plot for analyzing the agreement of more than two raters. Diagnostics 2021, 11, 54. [Google Scholar] [CrossRef] [PubMed]
- Abu-Arafeh, A.; Jordan, H.; Drummond, G. Reporting of method comparison studies: A review of advice, an assessment of current practice, and specific suggestions for future reports. Br. J. Anaesth. 2016, 117, 569–575. [Google Scholar] [CrossRef] [Green Version]
- Gerke, O. Reporting standards for a Bland-Altman agreement analysis: A review of methodological reviews. Diagnostics 2020, 10, 334. [Google Scholar] [CrossRef] [PubMed]
- Taffé, P. When can the Bland & Altman limits of agreement method be used and when it should not be used. J. Clin. Epidemiol. 2021, 137, 176–181. [Google Scholar] [CrossRef]
- Taffé, P. Assessing bias, precision, and agreement in method comparison studies. Stat. Methods Med. Res. 2020, 29, 778–796. [Google Scholar] [CrossRef] [PubMed]
- Taffé, P.; Peng, M.; Stagg, V.; Williamson, T. MethodCompare: An R package to assess bias and precision in method comparison studies. Stat. Methods Med. Res. 2019, 28, 2557–2565. [Google Scholar] [CrossRef]
- Taffé, P. Effective plots to assess bias and precision in method comparison studies. Stat. Methods Med. Res. 2018, 27, 1650–1660. [Google Scholar] [CrossRef] [PubMed]
- Taffé, P.; Peng, M.; Stagg, V.; Williamson, T. biasplot: A package to effective plots to assess bias and precision in method comparison studies. Stata J. 2017, 17, 208–221. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, P.K.; Nagaraja, H.N. Measuring Agreement: Models, Methods, and Applications; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Carstensen, B. Comparing Clinical Measurement Methods: A Practical Guide; Wiley: Chichester, UK, 2010. [Google Scholar]
- Shoukri, M.M. Measures of Interobserver Agreement and Reliability, 2nd ed.; Chapman & Hall: Boca Raton, FL, USA, 2010. [Google Scholar]
- Dunn, G. Statistical Evaluation of Measurement Errors: Design and Analysis of Reliability Studies, 2nd ed.; Wiley: Chichester, UK, 2004. [Google Scholar]
- Broemeling, L.D. Bayesian Biostatistics and Diagnostic Medicine; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Broemeling, L.D. Bayesian Methods for Measures of Agreement; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Alari, K.M.; Kim, S.B.; Wand, J.O. A tutorial of Bland Altman analysis in a Bayesian framework. Meas. Phys. Educ. Exerc. Sci. 2021, 25, 137–148. [Google Scholar] [CrossRef]
- Vock, M. Intervals for the assessment of measurement agreement: Similarities, differences, and consequences of incorrect interpretations. Biom. J. 2016, 58, 489–501. [Google Scholar] [CrossRef]
- Kruschke, J.K. Doing Bayesian Data Analysis, 2nd ed.; Academic Press/Elsevier: San Diego, CA, USA, 2015. [Google Scholar]
- Bayesian Bland Altman Analysis. Available online: https://kalari.shinyapps.io/BBAA/ (accessed on 17 December 2021).
- Wiinholt, A.; Gerke, O.; Dalaei, F.; Bučan, A.; Madsen, C.B.; Sørensen, J.A. Quantification of tissue volume in the hindlimb of mice using microcomputed tomography images and analysing software. Sci. Rep. 2020, 10, 8297. [Google Scholar] [CrossRef]
- Bučan, A.; Wiinholt, A.; Dalaei, F.; Gerke, O.; Hansen, C.R.; Dhumale, P.; Sørensen, J.A. Validating lymphedema measurements in mice: Micro-CT scans, plethysmometer and caliper. 2021; in preparation. [Google Scholar]
- Pezzullo, J.C. Biostatistics FD (For Dummies); Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bland, J.M.; Altman, D.G. Bayesians and frequentists. BMJ 1998, 317, 1151–1160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitehead, J. The Design and Analysis of Sequential Clinical Trials, 2nd ed.; Wiley: Chichester, UK, 1997. [Google Scholar]
- Jennison, C.; Turnbull, B.W. Group Sequential Methods with Applications to Clinical Trials; Chapman & Hall/CRC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Jennison, C.; Turnbull, B.W. Adaptive and nonadaptive group sequential tests. Biometrika 2006, 93, 1–21. [Google Scholar] [CrossRef]
- Todd, S. A 25-year review of sequential methodology in clinical studies. Stat. Med. 2007, 26, 237–252. [Google Scholar] [CrossRef] [PubMed]
- Wassmer, G.; Brannath, W. Group Sequential and Confirmatory Adaptive Designs in Clinical Trials; Springer: New York, NY, USA, 2016. [Google Scholar]
- Bauer, P.; Bretz, F.; Dragalin, V.; König, F.; Wassmer, G. Twenty-five years of confirmatory adaptive designs: Opportunities and pitfalls. Stat. Med. 2016, 35, 325–347. [Google Scholar] [CrossRef] [PubMed]
- Zapf, A.; Stark, M.; Gerke, O.; Ehret, C.; Benda, N.; Bossuyt, P.; Deeks, J.; Reitsma, J.; Alonzo, T.; Friede, T. Adaptive trial designs in diagnostic accuracy research. Stat. Med. 2020, 39, 591–601. [Google Scholar] [CrossRef]
- Vach, W.; Bibiza, E.; Gerke, O.; Bossuyt, P.M.; Friede, T.; Zapf, A. A potential for seamless designs in diagnostic research could be identified. J. Clin. Epidemiol. 2021, 129, 51–59. [Google Scholar] [CrossRef]
- Hot, A.; Bossuyt, P.M.; Gerke, O.; Wahl, S.; Vach, W.; Zapf, A. Randomized test-treatment studies with an outlook on adaptive designs. BMC Med. Res. Methodol. 2021, 21, 110. [Google Scholar] [CrossRef] [PubMed]
- Zou, K.H.; Liu, A.; Bandos, A.I.; Ohno-Machado, L.; Rockette, H.E. Statistical Evaluation of Diagnostic Performance: Topics in ROC Analysis; Chapman & Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Pocock, S.J. Group sequential methods in the design and analysis of clinical trials. Biometrika 1977, 64, 191–199. [Google Scholar] [CrossRef]
- O’Brien, P.C.; Fleming, T.R. A multiple testing procedure for clinical trials. Biometrics 1979, 35, 549–556. [Google Scholar] [CrossRef]
- Kim, K.; DeMets, D.L. Design and analysis of group sequential tests based on the type I error spending function. Biometrika 1987, 74, 149–154. [Google Scholar] [CrossRef]
- Gerke, O.; Vilstrup, M.H.; Halekoh, U.; Hildebrandt, M.G.; Høilund-Carlsen, P.F. Group-sequential analysis may allow for early trial termination: Illustration by an intra-observer repeatability study. EJNMMI Res. 2017, 7, 79. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Yu, Q. A Bayesian sequential design using alpha spending function to control type I error. Stat. Methods Med. Res. 2017, 26, 2184–2196. [Google Scholar] [CrossRef] [PubMed]
- Stallard, N.; Todd, S.; Ryan, E.G.; Gates, S. Comparison of Bayesian and frequentist group-sequential clinical trial designs. BMC Med. Res. Methodol. 2020, 20, 4. [Google Scholar] [CrossRef] [PubMed]
- Frey, M.E.; Petersen, H.C.; Gerke, O. Nonparametric limits of agreement for small to moderate sample sizes: A simulation study. Stats 2020, 3, 22. [Google Scholar] [CrossRef]
- Gerke, O. Nonparametric limits of agreement in method comparison studies: A simulation study on extreme quantile estimation. Int. J. Environ. Res. Public Health 2020, 17, 8330. [Google Scholar] [CrossRef]
- Hjort, N.L.; Holmes, C.; Müller, P.; Walker, S.G. Bayesian Nonparametrics; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Müller, P.; Quintana, F.A.; Jara, A.; Hanson, T. Bayesian Nonparametric Data Analysis; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Ghosal, S.; van der Vaart, A. Fundamentals of Nonparametric Bayesian Inference; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Dykun, I.; Mahabadi, A.A.; Lehmann, N.; Bauer, M.; Moebus, S.; Jöckel, K.H.; Möhlenkamp, S.; Erbel, R.; Kälsch, H. Left ventricle size quantification using non-contrast-enhanced cardiac computed tomography—association with cardiovascular risk factors and coronary artery calcium score in the general population: The Heinz Nixdorf Recall Study. Acta Radiol. 2015, 56, 933–942. [Google Scholar] [CrossRef]
- Fredgart, M.H.; Lindholt, J.S.; Brandes, A.; Steffensen, F.H.; Frost, L.; Lambrechtsen, J.; Karon, M.; Busk, M.; Urbonavičiene, G.; Egstrup, K.; et al. Association of Left Atrial Size Measured by non-contrast Computed Tomography with Cardiovascular Risk Factors—The Danish Cardiovascular Screening Trial (DANCAVAS). Diagnostics 2018, submitted. [Google Scholar]
- Schluter, P.J. A multivariate hierarchical Bayesian approach to measuring agreement in repeated measurement method comparison studies. BMC Med. Res. Methodol. 2009, 9, 6. [Google Scholar] [CrossRef] [Green Version]
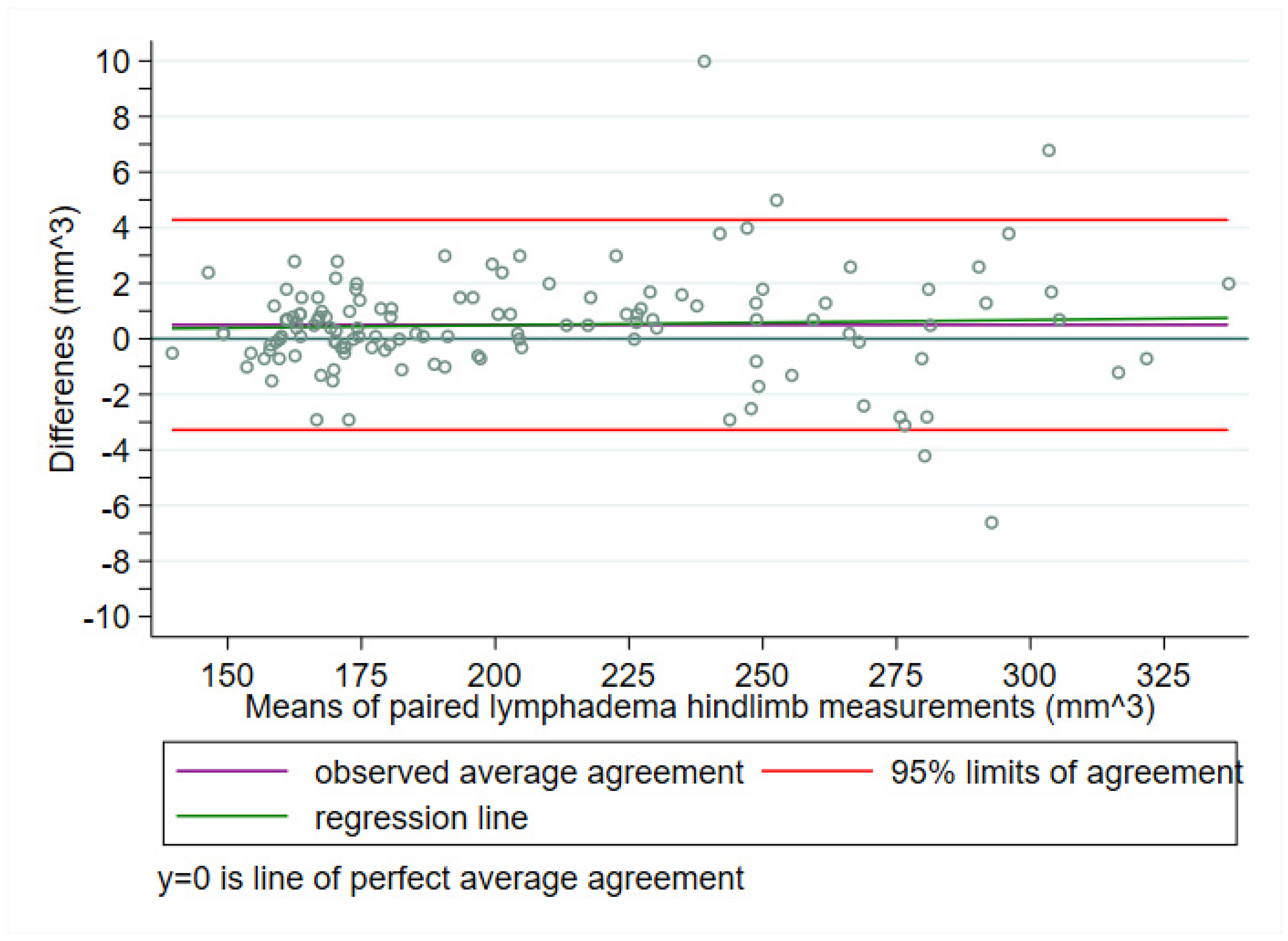

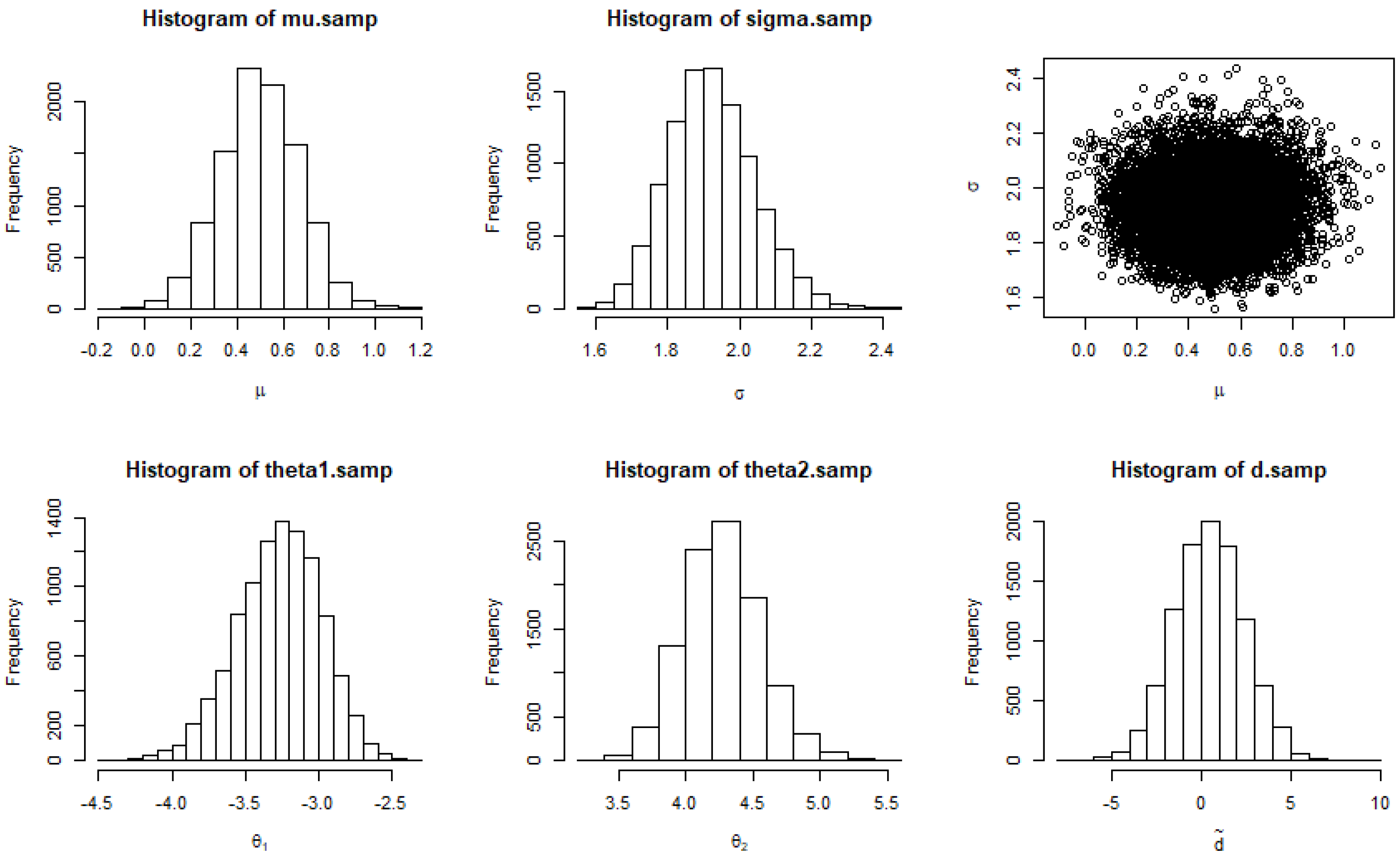
| Study | N | Mean | SD | Min | Q1 | Median | Q3 | Max |
|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 0.12 | 1.13 | −4.2 | −0.5 | 0.1 | 0.8 | 2.4 |
| 2 | 81 | 0.73 | 2.26 | −6.6 | −0.3 | 0.7 | 1.8 | 10 |
| Total | 131 | 0.50 | 1.93 | −6.6 | −0.4 | 0.5 | 1.4 | 10 |
| Variable | Mean | 2.5% | 5% | Q1 | Median | Q3 | 95% | 97.5% |
|---|---|---|---|---|---|---|---|---|
| µ | 0.50 | 0.17 | 0.23 | 0.39 | 0.50 | 0.61 | 0.77 | 0.83 |
| σ | 1.92 | 1.71 | 1.74 | 1.84 | 1.92 | 2.00 | 2.13 | 2.18 |
| θ1 | −3.26 | −3.87 | −3.76 | −3.45 | −3.25 | −3.07 | −2.82 | −2.74 |
| θ2 | 4.27 | 3.74 | 3.82 | 4.07 | 4.26 | 4.46 | 4.77 | 4.87 |
| 0.49 | −3.30 | −2.69 | −0.76 | 0.48 | 1.80 | 3.68 | 4.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerke, O.; Möller, S. Bland–Altman Limits of Agreement from a Bayesian and Frequentist Perspective. Stats 2021, 4, 1080-1090. https://doi.org/10.3390/stats4040062
Gerke O, Möller S. Bland–Altman Limits of Agreement from a Bayesian and Frequentist Perspective. Stats. 2021; 4(4):1080-1090. https://doi.org/10.3390/stats4040062
Chicago/Turabian StyleGerke, Oke, and Sören Möller. 2021. "Bland–Altman Limits of Agreement from a Bayesian and Frequentist Perspective" Stats 4, no. 4: 1080-1090. https://doi.org/10.3390/stats4040062
APA StyleGerke, O., & Möller, S. (2021). Bland–Altman Limits of Agreement from a Bayesian and Frequentist Perspective. Stats, 4(4), 1080-1090. https://doi.org/10.3390/stats4040062







