Parameter Choice, Stability and Validity for Robust Cluster Weighted Modeling
Abstract
:1. Introduction
2. The Cluster Weighted Robust Model
2.1. Penalized Likelihood in Constrained Estimation
3. Exploring the Space of Solutions for CWRM
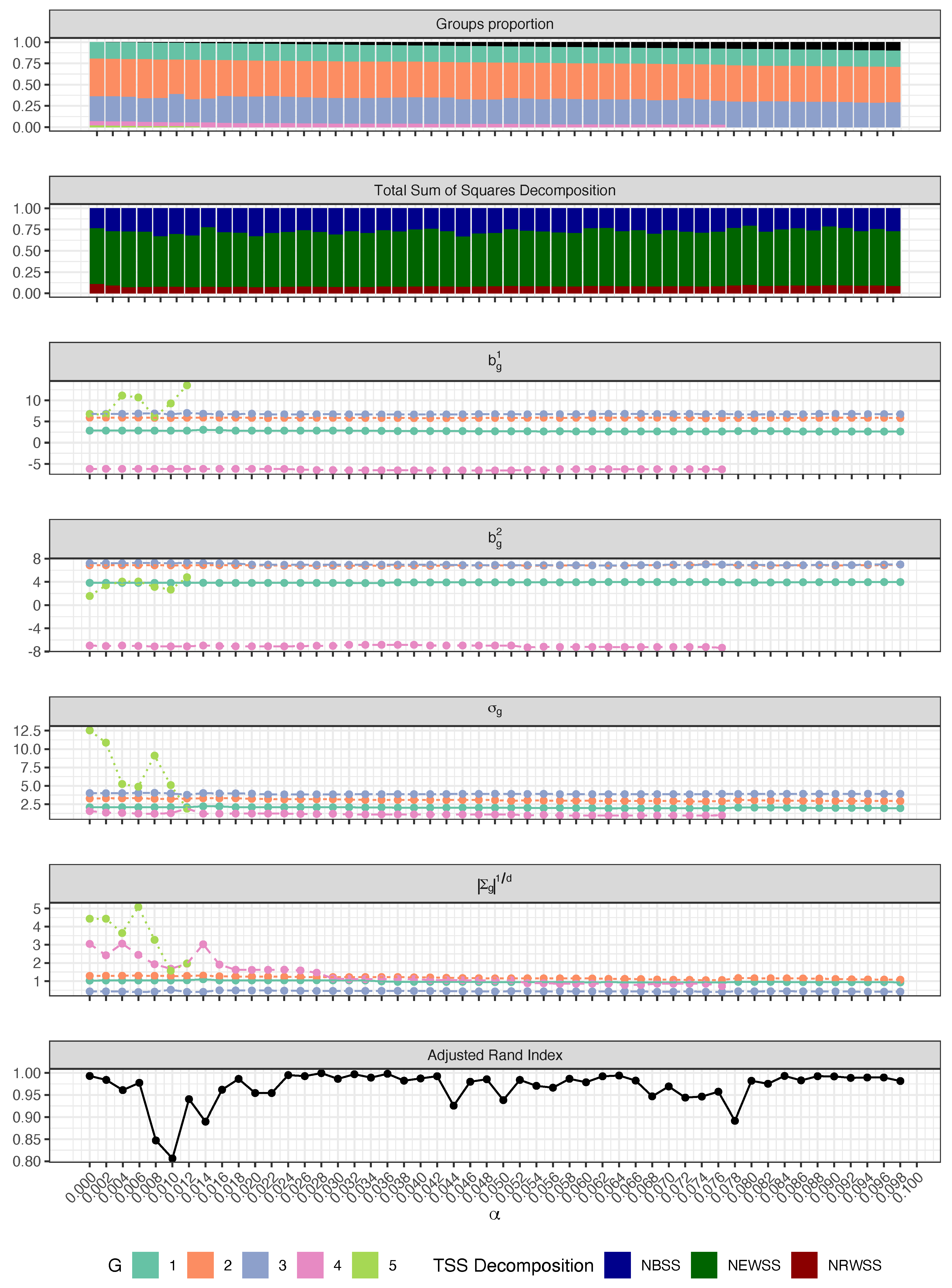
3.1. Step 1: Monitoring the Choice of a Plausible Trimming Level
- Groups proportion via a stacked barplot, profiling sample sizes and appearance of new clusters,
- CWM decomposition of the total sum of squares via a stacked barplot, according to the cluster validation measure introduced in [21],
- Regression coefficients via a G-lines plot, profiling the increase and/or decrease in parameters magnitude,
- Regression standard deviations via a G-lines plot, profiling the increase and/or decrease in variability around the regression hyper-planes,
- Cluster volumes via a G-lines plot, profiling the increase and/or decrease in , ,
- ARI between consecutive cluster allocations via a line plot, following [20].
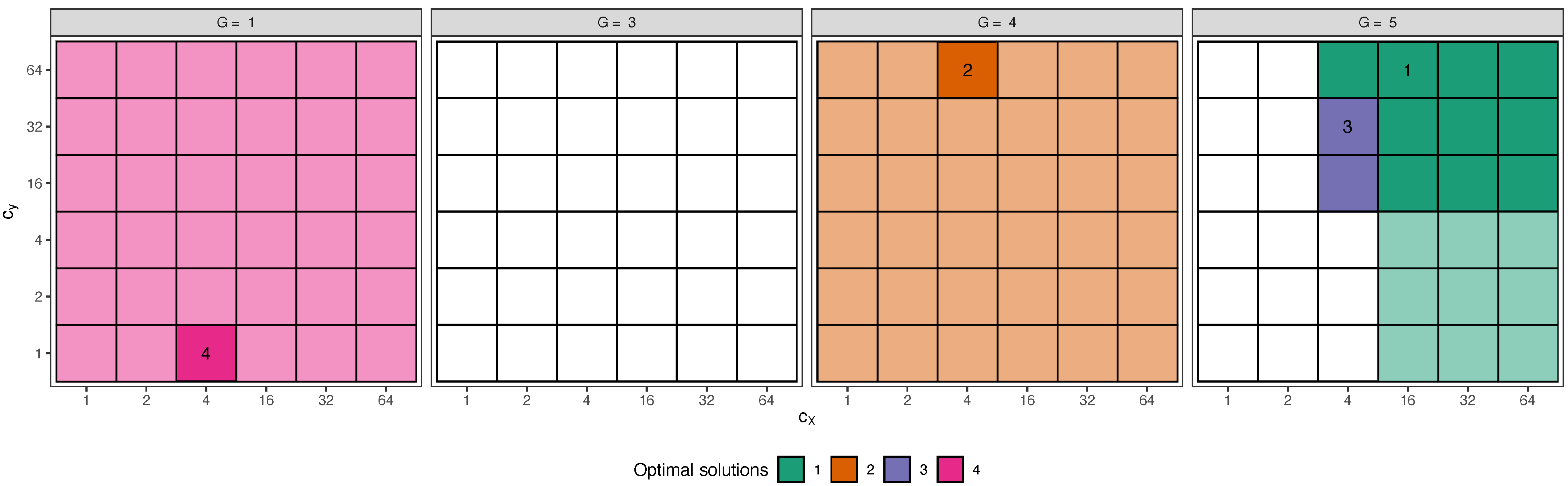
3.2. Step 2: Monitoring Optimal Solutions, in Terms of Validity and Stability
| Algorithm 1 Optimal solution finder |
|
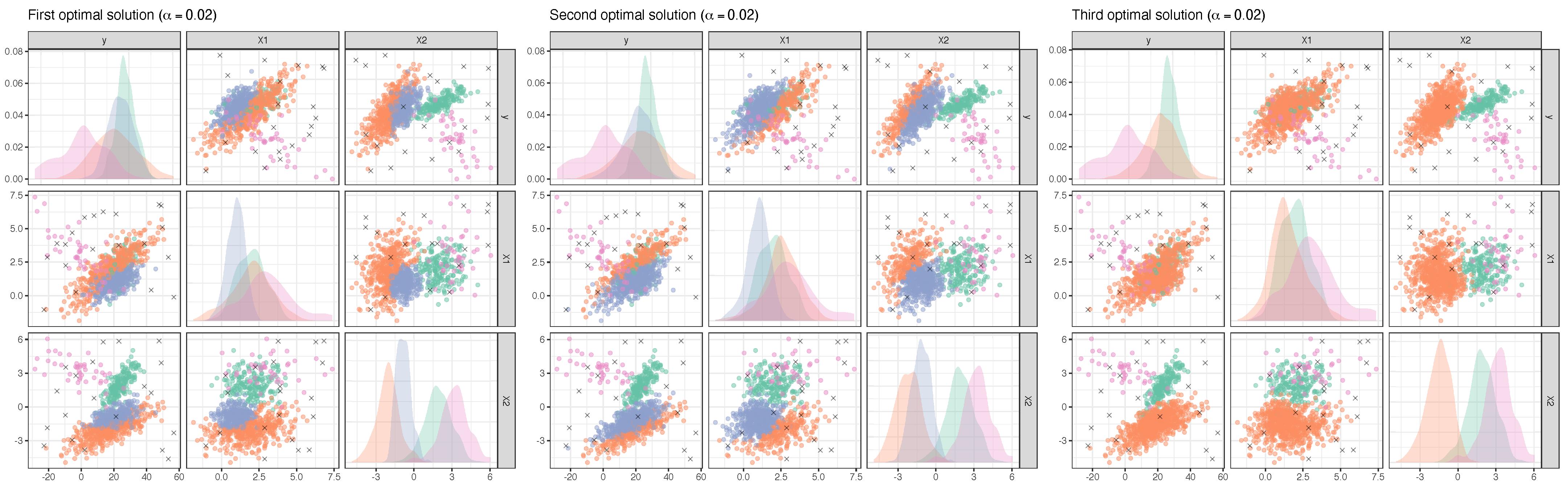
4. Synthetic Experiment with Multiple Plausible Solutions
4.1. Step 1: Choosing the Trimming Level
4.2. Step 2 with : Monitoring Plausible Solutions
4.3. Step 2 with : Monitoring Plausible Solutions
4.4. Step 2 with : Monitoring Plausible Solutions
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis; Wiley Series in Probability and Statistics; John Wiley & Sons, Ltd.: Chichester, UK, 2011; Volume 100, pp. 603–616. [Google Scholar] [CrossRef]
- McLachlan, J.; Peel, D. Finite Mixture Models; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Bouveyron, C.; Celeux, G.; Murphy, T.B.; Raftery, A.E. Model-Based Clustering and Classification for Data Science; Cambridge University Press: Cambridge, UK, 2019; Volume 50. [Google Scholar] [CrossRef]
- Hennig, C. What are the true clusters? Pattern Recognit. Lett. 2015, 64, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Von Luxburg, U.; Ben-David, S.; Luxburg, U.V. Towards a statistical theory of clustering. In Proceedings of the Pascal Workshop on Statistics and Optimization of Clustering, London, UK, 4–5 July 2005; pp. 20–26. [Google Scholar]
- Ackerman, M.; Ben-David, S. Measures of clustering quality: Aworking set of axioms for clustering. In Proceedings of the 21st International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; pp. 121–128. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Cerioli, A.; Riani, M.; Atkinson, A.C.; Corbellini, A. The power of monitoring: How to make the most of a contaminated multivariate sample. Stat. Methods Appl. 2018, 27, 661–666. [Google Scholar] [CrossRef]
- Cerioli, A.; García-Escudero, L.A.; Mayo-Iscar, A.; Riani, M. Finding the number of normal groups in model-based clustering via constrained likelihoods. J. Comput. Graph. Stat. 2018, 27, 404–416. [Google Scholar] [CrossRef] [Green Version]
- Gershenfeld, N. Nonlinear Inference and Cluster-Weighted Modeling. Ann. N. Y. Acad. Sci. 1997, 808, 18–24. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- García-Escudero, L.A.; Gordaliza, A.; Greselin, F.; Ingrassia, S.; Mayo-Iscar, A. Robust estimation of mixtures of regressions with random covariates, via trimming and constraints. Stat. Comput. 2017, 27, 377–402. [Google Scholar] [CrossRef] [Green Version]
- Neykov, N.; Filzmoser, P.; Dimova, R.; Neytchev, P. Robust fitting of mixtures using the trimmed likelihood estimator. Comput. Stat. Data Anal. 2007, 52, 299–308. [Google Scholar] [CrossRef]
- Hathaway, R.J. A Constrained Formulation of Maximum-Likelihood Estimation for Normal Mixture Distributions. Ann. Stat. 1985, 13, 795–800. [Google Scholar] [CrossRef]
- Torti, F.; Perrotta, D.; Riani, M.; Cerioli, A. Assessing trimming methodologies for clustering linear regression data. Adv. Data Anal. Classif. 2019, 13, 227–257. [Google Scholar] [CrossRef] [Green Version]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Riani, M.; Atkinson, A.C.; Cerioli, A.; Corbellini, A. Efficient robust methods via monitoring for clustering and multivariate data analysis. Pattern Recognit. 2019, 88, 246–260. [Google Scholar] [CrossRef] [Green Version]
- Ingrassia, S.; Punzo, A. Cluster Validation for Mixtures of Regressions via the Total Sum of Squares Decomposition. J. Classif. 2020, 37, 526–547. [Google Scholar] [CrossRef]
- Torti, F.; Riani, M.; Morelli, G. Semiautomatic robust regression clustering of international trade data. Stat. Methods Appl. 2021. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappozzo, A.; García Escudero, L.A.; Greselin, F.; Mayo-Iscar, A. Parameter Choice, Stability and Validity for Robust Cluster Weighted Modeling. Stats 2021, 4, 602-615. https://doi.org/10.3390/stats4030036
Cappozzo A, García Escudero LA, Greselin F, Mayo-Iscar A. Parameter Choice, Stability and Validity for Robust Cluster Weighted Modeling. Stats. 2021; 4(3):602-615. https://doi.org/10.3390/stats4030036
Chicago/Turabian StyleCappozzo, Andrea, Luis Angel García Escudero, Francesca Greselin, and Agustín Mayo-Iscar. 2021. "Parameter Choice, Stability and Validity for Robust Cluster Weighted Modeling" Stats 4, no. 3: 602-615. https://doi.org/10.3390/stats4030036
APA StyleCappozzo, A., García Escudero, L. A., Greselin, F., & Mayo-Iscar, A. (2021). Parameter Choice, Stability and Validity for Robust Cluster Weighted Modeling. Stats, 4(3), 602-615. https://doi.org/10.3390/stats4030036





