Fusing Nature with Computational Science for Optimal Signal Extraction
Abstract
1. Introduction
2. Basic SSA and SSA-CT
3. SSA-GA
- Run a basic SSA on training data and find the optimum r.
- Use the training data to build the trajectory matrix where .
- Apply the SVD for and calculate eigenvalues and corresponding eigenvectors . Obtain and .
- Define a chromosome as a vector of length L with binary values:where if jth components is considered for signal reconstruction and , otherwise.
- Build a population containing M chromosomes, i.e., chromosomes . Generate of the chromosomes in the population randomly (from uniform distribution). This will produce chromosomes to . Add and to the population (as extreme solutions). The rest of the population will be the same chromosomes as the basic SSA solution:where r is the grouping parameter from basic SSA (step 1).
- Use a binary crossover function to produce offspring chromosomes. A simple crossover function produce offspring chromosomes as follows:
- (a)
- Pair chromosomes in the population randomly.
- (b)
- For a given pair of chromosomes and generate random number d from uniform distribution ().
- (c)
- Produce offspring chromosomes for and with switching their first d genes:
- Produce weight matrix for each of chromosomes:
- Reconstruct the signal for each weight matrix :
- For each chromosomes generate in-sample h step ahead forecasting and calculate the in-sample RMSE for all chromosomes. Select the M chromosomes with smallest RMSE as the new population.
- Repeat steps 6 to 9 until minimum RMSE in the population does not improve for several iterations.
- Begin with and repeat steps 1 to 10 for , to find the L and grouping parameter which minimizes in-sample RMSE.
4. Empirical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Code | Name of Time Series |
|---|---|
| A001 | US Economic Statistics: Capacity Utilization. |
| A002 | Births by months 1853–2012. |
| A003 | Electricity: electricity net generation: total (all sectors). |
| A004 | Energy prices: average retail prices of electricity. |
| A005 | Coloured fox fur returns, Hopedale, Labrador, 1834–1925. |
| A006 | Alcohol demand (log spirits consumption per head), UK, 1870–1938. |
| A007 | Monthly Sutter county workforce, January 1946–December 1966 priesema (1979). |
| A008 | Exchange rates—monthly data: Japanese yen. |
| A009 | Exchange rates—monthly data: Pound sterling. |
| A010 | Exchange rates—monthly data: Romanian leu. |
| A011 | HICP (2005 = 100)—monthly data (annual rate of change): European Union (27 countries). |
| A012 | HICP (2005 = 100)—monthly data (annual rate of change): UK. |
| A013 | HICP (2005 = 100)—monthly data (annual rate of change): US. |
| A014 | New Homes Sold in the United States. |
| A015 | Goods, Value of Exports for United States. |
| A016 | Goods, Value of Imports for United States. |
| A017 | Market capitalisation—monthly data: UK. |
| A018 | Market capitalisation—monthly data: US. |
| A019 | Average monthly temperatures across the world (1701–2011): Bournemouth. |
| A020 | Average monthly temperatures across the world (1701–2011): Eskdalemuir. |
| A021 | Average monthly temperatures across the world (1701–2011): Lerwick. |
| A022 | Average monthly temperatures across the world (1701–2011): Valley. |
| A023 | Average monthly temperatures across the world (1701–2011): Death Valley. |
| A024 | US Economic Statistics: Personal Savings Rate. |
| A025 | Economic Policy Uncertainty Index for United States (Monthly Data). |
| A026 | Coal Production, Total for Germany. |
| A027 | Coke, Beehive Production (by Statistical Area). |
| A028 | Monthly champagne sales (in 1000’s) (p. 273: Montgomery: Fore. and T.S.). |
| A029 | Domestic Auto Production. |
| A030 | Index of Cotton Textile Production for France. |
| A031 | Index of Production of Chemical Products (by Statistical Area). |
| A032 | Index of Production of Leather Products (by Statistical Area). |
| A033 | Index of Production of Metal Products (by Statistical Area). |
| A034 | Index of Production of Mineral Fuels (by Statistical Area). |
| A035 | Industrial Production Index. |
| A036 | Knit Underwear Production (by Statistical Area). |
| A037 | Lubricants Production for United States. |
| A038 | Silver Production for United States. |
| A039 | Slab Zinc Production (by Statistical Area). |
| A040 | Annual domestic sales and advertising of Lydia E, Pinkham Medicine, 1907 to 1960. |
| A041 | Chemical concentration readings. |
| A042 | Monthly Boston armed robberies January 1966–October 1975 Deutsch and Alt (1977). |
| A043 | Monthly Minneapolis public drunkenness intakes January’66–July’78. |
| A044 | Motor vehicles engines and parts/CPI, Canada, 1976–1991. |
| A045 | Methane input into gas furnace: cu. ft/min. Sampling interval 9 s. |
| A046 | Monthly civilian population of Australia: thousand persons. February 1978–April 1991. |
| A047 | Daily total female births in California, 1959. |
| A048 | Annual immigration into the United States: thousands. 1820–1962. |
| A049 | Monthly New York City births: unknown scale. January 1946–December 1959. |
| A050 | Estimated quarterly resident population of Australia: thousand persons. |
| A051 | Annual Swedish population rates (1000’s) 1750–1849 Thomas (1940). |
| A052 | Industry sales for printing and writing paper (in Thousands of French francs). |
| A053 | Coloured fox fur production, Hebron, Labrador, 1834–1925. |
| A054 | Coloured fox fur production, Nain, Labrador, 1834–1925. |
| A055 | Coloured fox fur production, oak, Labrador, 1834–1925. |
| A056 | Monthly average daily calls to directory assistance January’62–December’76. |
| A057 | Monthly Av. residential electricity usage Iowa city 1971–1979. |
| A058 | Montly av. residential gas usage Iowa (cubic feet)*100 ’71–’79. |
| A059 | Monthly precipitation (in mm), January 1983–April 1994. London, United Kingdom. |
| A060 | Monthly water usage (mL/day), London Ontario, 1966–1988. |
| A061 | Quarterly production of Gas in Australia: million megajoules. Includes natural gas from July 1989. March 1956–September 1994. |
| A062 | Residential water consumption, January 1983–April 1994. London, United Kingdom. |
| A063 | The total generation of electricity by the U.S. electric industry (monthly data for the period January 1985–October 1996). |
| A064 | Total number of water consumers, January 1983–April 1994. London, United Kingdom. |
| A065 | Monthly milk production: pounds per cow. January 62–December 75. |
| A066 | Monthly milk production: pounds per cow. January 62–December 75, adjusted for month length. |
| A067 | Monthly total number of pigs slaughtered in Victoria. January 1980–August 1995. |
| A068 | Monthly demand repair parts large/heavy equip. Iowa 1972–1979. |
| A069 | Number of deaths and serious injuries in UK road accidents each month. January 1969–December 1984. |
| A070 | Passenger miles (Mil) flown domestic U.K. July’62–May’72. |
| A071 | Monthly hotel occupied room av. ’63–’76 B.L.Bowerman et al. |
| A072 | Weekday bus ridership, Iowa city, Iowa (monthly averages). |
| A073 | Portland Oregon average monthly bus ridership (/100). |
| A074 | U.S. airlines: monthly aircraft miles flown (Millions) 1963–1970. |
| A075 | International airline passengers: monthly totals in thousands. January 49–December 60. |
| A076 | Sales: souvenir shop at a beach resort town in Queensland, Australia. January 1987–December 1993. |
| A077 | Der Stern: Weekly sales of wholesalers A, ’71–’72. |
| A078 | Der Stern: Weekly sales of wholesalers B, ’71–’72’ |
| A079 | Der Stern: Weekly sales of wholesalers ’71–’72. |
| A080 | Monthly sales of U.S. houses (thousands) 1965–1975. |
| A081 | CFE specialty writing papers monthly sales. |
| A082 | Monthly sales of new one-family houses sold in USA since 1973. |
| A083 | Wisconsin employment time series, food and kindred products, January 1961–October 1975. |
| A084 | Monthly gasoline demand Ontario gallon millions 1960–1975. |
| A085 | Wisconsin employment time series, fabricated metals, January 1961–October 1975. |
| A086 | Monthly empolyees wholes./retail Wisconsin ’61–’75 R.B.Miller. |
| A087 | US monthly sales of chemical related products. January 1971–December 1991. |
| A088 | US monthly sales of coal related products. January 1971–December 1991. |
| A089 | US monthly sales of petrol related products. January 1971–December 1991. |
| A090 | US monthly sales of vehicle related products. January 1971–December 1991. |
| A091 | Civilian labour force in Australia each month: thousands of persons. February 1978–August 1995. |
| A092 | Numbers on Unemployment Benefits in Australia: monthly January 1956–July 1992. |
| A093 | Monthly Canadian total unemployment figures (thousands) 1956–1975. |
| A094 | Monthly number of unemployed persons in Australia: thousands. February 1978–April 1991. |
| A095 | Monthly U.S. female (20 years and over) unemployment figures 1948–1981. |
| A096 | Monthly U.S. female (16–19 years) unemployment figures (thousands) 1948–1981. |
| A097 | Monthly unemployment figures in West Germany 1948–1980. |
| A098 | Monthly U.S. male (20 years and over) unemployment figures 1948–1981. |
| A099 | Wisconsin employment time series, transportation equipment, January 1961–October 1975. |
| A100 | Monthly U.S. male (16–19 years) unemployment figures (thousands) 1948–1981. |
| Code | F | N | Mean | Med. | SD | CV | Skew. | SW(p) | ADF | Code | F | N | Mean | Med. | SD | CV | Skew. | SW(p) | ADF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A001 | M | 539 | 80 | 80 | 5 | 6 | −0.55 | <0.01 | −0.60 | A002 | M | 1920 | 271 | 249 | 88 | 33 | 0.16 | <0.01 | −1.82 |
| A003 | M | 484 | 2.59 × 10 | 2.61 × 10 | 6.88 × 10 | 27 | 0.15 | <0.01 | −0.90 | A004 | M | 310 | 7 | 7 | 2 | 28 | −0.24 | <0.01 | 0.56 |
| A005 | D | 92 | 47.63 | 31.00 | 47.33 | 99.36 | 2.27 | <0.01 | −3.16 | A006 | Q | 207 | 1.95 | 1.98 | 0.25 | 12.78 | −0.58 | <0.01 | 0.46 |
| A007 | M | 252 | 2978 | 2741 | 1111 | 37.32 | 0.79 | <0.01 | −0.80 | A008 | M | 160 | 128 | 128 | 19 | 15 | 0.34 | <0.01 | −0.59 |
| A009 | M | 160 | 0.72 | 0.69 | 0.10 | 13 | 0.66 | <0.01 | 0.53 | A010 | M | 160 | 3.41 | 3.61 | 0.83 | 24 | −0.92 | <0.01 | 1.58 |
| A011 | M | 201 | 4.7 | 2.6 | 5.0 | 106 | 2.24 | <0.01 | −2.66 | A012 | M | 199 | 2.1 | 1.9 | 1.0 | 49 | 0.92 | <0.01 | −0.79 |
| A013 | M | 176 | 2.5 | 2.4 | 1.6 | 66 | −0.52 | <0.01 | −2.27 | A014 | M | 606 | 55 | 53 | 20 | 35 | 0.79 | <0.01 | −1.41 |
| A015 | M | 672 | 3.39 | 1.89 | 3.48 | 103 | 1.09 | <0.01 | 2.46 | A016 | M | 672 | 5.18 | 2.89 | 5.78 | 111 | 1.13 | <0.01 | 1.91 |
| A017 | M | 249 | 130 | 130 | 24 | 19 | 0.35 | <0.01 | 0.24 | A018 | M | 249 | 112 | 114 | 25 | 22 | −0.01 | 0.01 * | 0.06 |
| A019 | M | 605 | 10.1 | 9.6 | 4.5 | 44 | 0.05 | <0.01 | −4.77 | A020 | M | 605 | 7.3 | 6.9 | 4.3 | 59 | 0.04 | <0.01 | −6.07 |
| A021 | M | 605 | 7.2 | 6.8 | 3.3 | 46 | 0.13 | <0.01 | −4.93 | A022 | M | 605 | 10.3 | 9.9 | 3.8 | 37 | 0.04 | <0.01 | −4.19 |
| A023 | M | 605 | 24 | 24 | 10 | 40 | −0.02 | <0.01 | −7.15 | A024 | M | 636 | 6.9 | 7.4 | 2.6 | 38 | −0.29 | <0.01 | −1.18 |
| A025 | M | 343 | 108 | 100 | 33 | 30 | 0.99 | <0.01 | −1.23 | A026 | M | 277 | 11.7 | 11.9 | 2.3 | 20 | −0.16 | 0.06 * | −0.40 |
| A027 | M | 171 | 0.21 | 0.13 | 0.19 | 88 | 1.26 | <0.01 | −1.81 | A028 | M | 96 | 4801 | 4084 | 2640 | 54.99 | 1.55 | <0.01 | −1.66 |
| A029 | M | 248 | 391 | 385 | 116 | 30 | −0.03 | 0.08 * | −1.22 | A030 | M | 139 | 89 | 92 | 12 | 13 | −0.82 | <0.01 | −0.28 |
| A031 | M | 121 | 134 | 138 | 27 | 20 | 0.05 | <0.01 | 1.51 | A032 | M | 153 | 113 | 114 | 10 | 9 | −0.29 | 0.45 * | −0.52 |
| A033 | M | 115 | 117 | 118 | 17 | 15 | −0.29 | 0.03 * | −0.46 | A034 | M | 115 | 110 | 111 | 11 | 10 | −0.53 | 0.02 * | 0.30 |
| A035 | M | 1137 | 40 | 34 | 31 | 78 | 0.56 | <0.01 | 5.14 | A036 | M | 165 | 1.08 | 1.10 | 0.20 | 18.37 | −1.15 | <0.01 | −0.59 |
| A037 | M | 479 | 3.04 | 2.83 | 1.02 | 33.60 | 0.46 | <0.01 | 0.61 | A038 | M | 283 | 9.39 | 10.02 | 2.27 | 24.15 | −0.80 | <0.01 | −1.01 |
| A039 | M | 452 | 54 | 52 | 19 | 36 | −0.15 | <0.01 | 0.08 | A040 | Q | 108 | 1382 | 1206 | 684 | 49.55 | 0.83 | <0.01 | −0.80 |
| A041 | H | 197 | 17.06 | 17.00 | 0.39 | 2.34 | 0.15 | 0.21 * | 0.09 | A042 | M | 118 | 196.3 | 166.0 | 128.0 | 65.2 | 0.45 | <0.01 | 0.41 |
| A043 | M | 151 | 391.1 | 267.0 | 237.49 | 60.72 | 0.43 | <0.01 | −1.17 | A044 | M | 188 | 1344 | 1425 | 479.1 | 35.6 | −0.41 | <0.01 | −1.28 |
| A045 | H | 296 | −0.05 | 0.00 | 1.07 | −1887 | −0.05 | 0.55 * | −7.66 | A046 | M | 159 | 11,890 | 11,830 | 882.93 | 7.42 | 0.12 | <0.01 | 5.71 |
| A047 | D | 365 | 41.98 | 42.00 | 7.34 | 17.50 | 0.44 | <0.01 | −1.07 | A048 | A | 143 | 2.5 × 10 | 2.2 × 10 | 2.1 × 10 | 83.19 | 1.06 | <0.01 | −2.63 |
| A049 | M | 168 | 25.05 | 24.95 | 2.31 | 9.25 | −0.02 | 0.02 * | 0.07 | A050 | Q | 89 | 15,274 | 15,184 | 1358 | 8.89 | 0.19 | <0.01 | 9.72 |
| A051 | A | 100 | 6.69 | 7.50 | 5.88 | 87.87 | −2.45 | <0.01 | −3.06 | A052 | M | 120 | 713 | 733 | 174 | 24.39 | −1.09 | <0.01 | −0.78 |
| A053 | A | 91 | 81.58 | 46.00 | 102.07 | 125.11 | 2.80 | <0.01 | −3.44 | A054 | A | 91 | 101.80 | 77.00 | 92.14 | 90.51 | 1.43 | <0.01 | −3.38 |
| A055 | A | 91 | 59.45 | 39.00 | 60.42 | 101.63 | 1.56 | <0.01 | −3.99 | A056 | M | 180 | 492.50 | 521.50 | 189.54 | 38.48 | −0.17 | <0.01 | −0.65 |
| A057 | M | 106 | 489.73 | 465.00 | 93.34 | 19.06 | 0.92 | <0.01 | −1.21 | A058 | M | 106 | 124.71 | 94.50 | 84.15 | 67.48 | 0.52 | <0.01 | −3.88 |
| A059 | M | 136 | 85.66 | 80.25 | 37.54 | 43.83 | 0.91 | <0.01 | −1.88 | A060 | M | 276 | 118.61 | 115.63 | 26.39 | 22.24 | 0.86 | <0.01 | −0.47 |
| A061 | Q | 155 | 61,728 | 47,976 | 53,907 | 87.33 | 0.44 | <0.01 | 0.06 | A062 | M | 136 | 5.72 × 10 | 5.53 × 10 | 1.2 × 10 | 21.51 | 1.13 | <0.01 | −0.84 |
| A063 | M | 142 | 231.09 | 226.73 | 24.37 | 10.55 | 0.52 | 0.01 | −0.39 | A064 | M | 136 | 31,388 | 31,251 | 3232 | 10.30 | 0.25 | 0.22 * | −0.16 |
| A065 | M | 156 | 754.71 | 761.00 | 102.20 | 13.54 | 0.01 | 0.04 * | 0.04 | A066 | M | 156 | 746.49 | 749.15 | 98.59 | 13.21 | 0.08 | 0.04 * | −0.38 |
| A067 | M | 188 | 90,640 | 91,661 | 13,926 | 15.36 | −0.38 | 0.01 * | −0.38 | A068 | M | 94 | 1540 | 1532 | 474.35 | 30.79 | 0.38 | 0.05 * | 0.54 |
| A069 | M | 192 | 1670 | 1631 | 289.61 | 17.34 | 0.53 | <0.01 | −0.74 | A070 | M | 119 | 91.09 | 86.20 | 32.80 | 36.01 | 0.34 | <0.01 | −1.93 |
| A071 | M | 168 | 722.30 | 709.50 | 142.66 | 19.75 | 0.72 | <0.01 | −0.52 | A072 | W | 136 | 5913 | 5500 | 1784 | 30.17 | 0.67 | <0.01 | −0.68 |
| A073 | M | 114 | 1120 | 1158 | 270.89 | 24.17 | −0.37 | <0.01 | 0.76 | A074 | M | 96 | 10,385 | 10,401 | 2202 | 21.21 | 0.33 | 0.18 * | −0.13 |
| A075 | M | 144 | 280.30 | 265.50 | 119.97 | 42.80 | 0.57 | <0.01 | −0.35 | A076 | M | 84 | 14,315 | 8771 | 15,748 | 110 | 3.37 | <0.01 | −0.29 |
| A077 | W | 104 | 11,909 | 11,640 | 1231 | 10.34 | 0.60 | <0.01 | −0.16 | A078 | W | 104 | 74,636 | 73,600 | 4737 | 6.35 | 0.64 | <0.01 | −0.59 |
| A079 | W | 104 | 1020 | 1012 | 71.78 | 7.03 | 0.60 | 0.01 * | −0.41 | A080 | M | 132 | 45.36 | 44.00 | 10.38 | 22.88 | 0.17 | 0.15 * | −0.81 |
| A081 | M | 147 | 1745 | 1730 | 479.52 | 27.47 | −0.39 | <0.01 | −1.15 | A082 | M | 275 | 52.29 | 53.00 | 11.94 | 22.83 | 0.18 | 0.13 * | −1.30 |
| A083 | M | 178 | 58.79 | 55.80 | 6.68 | 11.36 | 0.93 | <0.01 | −0.92 | A084 | M | 192 | 1.62 × 10 | 1.57 × 10 | 41,661 | 25.71 | 0.32 | <0.01 | 0.25 |
| A085 | M | 178 | 40.97 | 41.50 | 5.11 | 12.47 | −0.07 | <0.01 | 1.45 | A086 | M | 178 | 307.56 | 308.35 | 46.76 | 15.20 | 0.17 | <0.01 | 1.51 |
| A087 | M | 252 | 13.70 | 14.08 | 6.13 | 44.73 | 0.16 | <0.01 | 1.13 | A088 | M | 252 | 65.67 | 68.20 | 14.25 | 21.70 | −0.53 | <0.01 | −0.53 |
| A089 | M | 252 | 10.76 | 10.92 | 5.11 | 47.50 | −0.19 | <0.01 | −0.05 | A090 | M | 252 | 11.74 | 11.05 | 5.11 | 43.54 | 0.38 | <0.01 | −0.88 |
| A091 | M | 211 | 7661 | 7621 | 819 | 10.70 | 0.03 | <0.01 | 3.27 | A092 | M | 439 | 2.21 × 10 | 5.67 × 10 | 2.35 × 10 | 106.32 | 0.77 | <0.01 | 1.61 |
| A093 | M | 240 | 413.28 | 396.50 | 152.84 | 36.98 | 0.36 | <0.01 | −1.60 | A094 | M | 211 | 6787 | 6528 | 604.62 | 8.91 | 0.56 | <0.01 | 2.69 |
| A095 | M | 408 | 1373 | 1132 | 686.05 | 49.96 | 0.91 | <0.01 | 0.60 | A096 | M | 408 | 422.38 | 342.00 | 252.86 | 59.87 | 0.65 | <0.01 | −1.95 |
| A097 | M | 396 | 7.14 × 10 | 5.57 × 10 | 5.64 × 10 | 78.97 | 0.79 | <0.01 | −2.51 | A098 | M | 408 | 1937 | 1825 | 794 | 41.04 | 0.64 | <0.01 | −1.15 |
| A099 | M | 178 | 40.60 | 40.50 | 4.95 | 12.19 | −0.65 | <0.01 | −0.10 | A100 | M | 408 | 520.28 | 425.50 | 261.22 | 50.21 | 0.64 | <0.01 | −1.65 |
| Forecasting Horizon | ||||||||
|---|---|---|---|---|---|---|---|---|
| Series’ | h = 1 | h = 3 | h = 6 | h = 12 | ||||
| Code | RRMSE | KSPA p-Value | RRMSE | KSPA p-Value | RRMSE | KSPA p-Value | RRMSE | KSPA p-Value |
| A001 | 0.567 | 0.001 | 0.425 | 0.000 | 0.396 | 0.000 | 0.374 | 0.000 |
| A002 | 1.297 | 0.001 | 1.347 | 0.000 | 1.358 | 0.000 | 1.359 | 0.000 |
| A003 | 1.263 | 0.141 | 1.090 | 0.454 | 1.034 | 0.385 | 1.032 | 0.408 |
| A004 | 1.632 | 0.017 | 0.543 | 0.012 | 0.547 | 0.105 | 0.572 | 0.391 |
| A005 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A006 | 1.088 | 0.797 | 1.075 | 0.928 | 1.113 | 0.694 | 1.067 | 0.604 |
| A007 | 2.015 | 0.092 | 2.452 | 0.026 | 3.339 | 0.162 | 667.713 | 0.042 |
| A008 | 1.716 | 0.306 | 1.885 | 0.948 | 2.483 | 0.161 | 6.844 | 0.445 |
| A009 | 0.976 | 1.000 | 0.969 | 0.948 | 0.966 | 0.997 | 0.973 | 1.000 |
| A010 | 1.245 | 0.306 | 0.952 | 0.480 | 0.968 | 0.522 | 0.989 | 0.315 |
| A011 | 0.669 | 0.231 | 0.371 | 0.068 | 0.427 | 0.050 | 0.616 | 0.043 |
| A012 | 1.021 | 0.981 | 1.014 | 0.999 | 1.008 | 1.000 | 1.007 | 0.993 |
| A013 | 1.027 | 1.000 | 1.010 | 1.000 | 1.008 | 1.000 | 1.010 | 0.999 |
| A014 | 1.298 | 0.125 | 1.069 | 0.371 | 1.161 | 0.169 | 1.243 | 0.182 |
| A015 | 2.259 | 0.000 | 1.663 | 0.000 | 1.121 | 0.114 | 0.901 | 0.000 |
| A016 | 1.214 | 0.888 | 1.151 | 1.000 | 1.126 | 0.896 | 1.161 | 0.774 |
| A017 | 0.614 | 0.132 | 0.587 | 0.063 | 0.672 | 0.414 | 0.700 | 0.717 |
| A018 | 1.172 | 0.631 | 0.878 | 0.512 | 1.032 | 0.804 | 1.032 | 0.717 |
| A019 | 1.021 | 0.518 | 1.012 | 0.254 | 1.030 | 0.534 | 1.025 | 0.870 |
| A020 | 1.049 | 0.957 | 1.064 | 0.693 | 1.082 | 0.456 | 1.100 | 0.720 |
| A021 | 1.117 | 0.984 | 1.154 | 0.524 | 1.148 | 0.383 | 1.141 | 0.720 |
| A022 | 1.125 | 0.439 | 1.080 | 0.852 | 1.067 | 0.961 | 1.060 | 0.870 |
| A023 | 1.135 | 0.518 | 1.150 | 0.374 | 1.158 | 0.319 | 1.128 | 0.720 |
| A024 | 1.520 | 0.001 | 1.544 | 0.001 | 1.576 | 0.000 | 1.607 | 0.000 |
| A025 | 1.796 | 0.003 | 1.729 | 0.002 | 1.661 | 0.006 | 1.796 | 0.000 |
| A026 | 2.339 | 0.015 | 1.571 | 0.935 | 1.121 | 0.616 | 1.071 | 0.658 |
| A027 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A028 | 1.081 | 0.987 | 1.054 | 0.422 | 1.062 | 0.501 | 1.072 | 0.160 |
| A029 | 1.059 | 0.777 | 1.059 | 0.791 | 1.059 | 0.915 | 1.051 | 0.844 |
| A030 | 1.627 | 0.707 | 6.047 | 0.545 | 49.035 | 0.420 | 3160.646 | 0.008 |
| A031 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A032 | 1.172 | 0.919 | 1.103 | 0.791 | 1.208 | 0.653 | 1.453 | 0.562 |
| A033 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A034 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A035 | 3.019 | 0.000 | 1.910 | 0.007 | 1.503 | 0.075 | 1.228 | 0.186 |
| A036 | 1.079 | 0.994 | 1.083 | 0.996 | 1.062 | 0.964 | 1.061 | 0.979 |
| A037 | 1.563 | 0.043 | 1.709 | 0.062 | 1.829 | 0.151 | 1.809 | 0.003 |
| A038 | 0.820 | 0.724 | 0.757 | 0.940 | 0.936 | 0.631 | 0.953 | 0.892 |
| A039 | 2.145 | 0.000 | 1.559 | 0.012 | 1.372 | 0.053 | 1.343 | 0.017 |
| A040 | 1.104 | 0.996 | 1.073 | 0.997 | 1.038 | 0.999 | 1.035 | 1.000 |
| A041 | 1.349 | 0.779 | 1.584 | 0.357 | 1.851 | 0.276 | 3.610 | 0.026 |
| A042 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A043 | 1.068 | 0.919 | 1.036 | 0.932 | 1.011 | 0.995 | 0.969 | 0.877 |
| A044 | 1.161 | 0.750 | 1.244 | 0.223 | 1.863 | 0.357 | 3.430 | 0.001 |
| A045 | 1.745 | 0.000 | 1.476 | 0.000 | 1.474 | 0.000 | 1.521 | 0.016 |
| A046 | 0.249 | 0.000 | 0.358 | 0.000 | 0.498 | 0.001 | 0.588 | 0.000 |
| A047 | 0.923 | 0.438 | 0.877 | 0.663 | 0.823 | 0.224 | 0.786 | 0.403 |
| A048 | 0.657 | 0.903 | 0.577 | 0.919 | 1.317 | 0.938 | 4.049 | 0.861 |
| A049 | 1.042 | 0.653 | 1.099 | 0.680 | 1.109 | 0.967 | 1.273 | 0.622 |
| A050 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A051 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A052 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A053 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A054 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A055 | 1.064 | 0.983 | 1.036 | 0.990 | 1.017 | 0.710 | 1.008 | 0.615 |
| A056 | 1.346 | 0.536 | 1.166 | 0.728 | 1.116 | 0.897 | 1.089 | 0.928 |
| A057 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A058 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A059 | 1.059 | 0.874 | 1.044 | 1.000 | 1.056 | 0.990 | 1.044 | 0.996 |
| A060 | 1.460 | 0.124 | 1.439 | 0.133 | 1.353 | 0.374 | 1.317 | 0.174 |
| A061 | 5.321 | 0.000 | 3.518 | 0.012 | 2.806 | 0.004 | 1.565 | 0.000 |
| A062 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A063 | 1.061 | 0.528 | 0.816 | 0.562 | 0.765 | 0.610 | 0.892 | 0.100 |
| A064 | 0.815 | 0.690 | 0.788 | 1.000 | 0.850 | 0.579 | 0.423 | 0.834 |
| A065 | 0.931 | 0.926 | 0.888 | 0.994 | 0.887 | 0.996 | 0.892 | 0.739 |
| A066 | 2.509 | 0.008 | 2.219 | 0.039 | 1.736 | 0.229 | 1.189 | 0.739 |
| A067 | 1.085 | 0.750 | 0.876 | 0.610 | 0.733 | 0.249 | 0.490 | 0.036 |
| A068 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A069 | 1.063 | 0.975 | 1.038 | 0.999 | 1.037 | 0.644 | 1.028 | 0.704 |
| A070 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A071 | 0.874 | 0.653 | 0.858 | 0.680 | 0.845 | 0.396 | 0.883 | 0.999 |
| A072 | 0.910 | 0.979 | 0.869 | 0.723 | 0.903 | 0.766 | 0.946 | 0.952 |
| A073 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A074 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A075 | 1.389 | 0.135 | 1.523 | 0.389 | 1.463 | 0.791 | 1.352 | 0.693 |
| A076 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A077 | 1.089 | 0.915 | 1.084 | 0.997 | 1.172 | 0.808 | 1.373 | 0.707 |
| A078 | 1.105 | 0.996 | 1.084 | 0.997 | 1.095 | 0.958 | 1.083 | 0.707 |
| A079 | 0.970 | 0.915 | 1.018 | 0.754 | 1.105 | 0.958 | 1.235 | 0.707 |
| A080 | 1.081 | 0.999 | 1.055 | 0.979 | 1.032 | 1.000 | 1.032 | 1.000 |
| A081 | 1.084 | 0.987 | 1.068 | 0.990 | 1.092 | 0.938 | 1.086 | 0.861 |
| A082 | 0.977 | 0.998 | 1.040 | 0.844 | 1.059 | 0.744 | 1.049 | 0.991 |
| A083 | 0.781 | 0.383 | 0.847 | 0.562 | 0.900 | 0.977 | 0.592 | 0.665 |
| A084 | 0.634 | 0.004 | 0.544 | 0.033 | 0.396 | 0.041 | 0.054 | 0.002 |
| A085 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A086 | 2.643 | 0.000 | 2.357 | 0.013 | 2.123 | 0.214 | 1.715 | 0.182 |
| A087 | 2.030 | 0.023 | 1.758 | 0.147 | 1.552 | 0.162 | 1.293 | 0.268 |
| A088 | 0.907 | 0.996 | 0.982 | 0.791 | 1.031 | 0.915 | 1.129 | 0.268 |
| A089 | 1.868 | 0.198 | 1.255 | 0.791 | 1.006 | 0.546 | 0.924 | 0.194 |
| A090 | 1.132 | 0.968 | 1.099 | 0.997 | 1.120 | 0.810 | 1.118 | 0.594 |
| A091 | 0.507 | 0.513 | 0.132 | 0.131 | 0.009 | 0.098 | 0.000 | 0.084 |
| A092 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A093 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| A094 | 3.369 | 0.000 | 2.508 | 0.019 | 2.094 | 0.098 | 1.827 | 0.020 |
| A095 | 3.167 | 0.000 | 2.090 | 0.004 | 1.724 | 0.016 | 1.541 | 0.004 |
| A096 | 1.692 | 0.020 | 1.696 | 0.086 | 1.798 | 0.024 | 1.867 | 0.006 |
| A097 | 1.188 | 0.591 | 1.077 | 0.957 | 1.039 | 0.723 | 1.049 | 0.287 |
| A098 | 0.587 | 0.059 | 0.649 | 0.015 | 0.765 | 0.352 | 0.902 | 0.563 |
| A099 | 0.780 | 0.261 | 0.838 | 0.877 | 0.897 | 0.598 | 0.953 | 0.987 |
| A100 | 0.947 | 0.612 | 0.736 | 0.086 | 0.729 | 0.278 | 0.720 | 0.078 |
References
- Yang, X.S. Nature-inspired optimization algorithms: Challenges and open problems. J. Comput. Sci. 2020, 46, 101104. [Google Scholar] [CrossRef]
- Markou, M.; Singh, S. Novelty detection: A review—Part 2: Neural network based approaches. Signal Process. 2003, 83, 2499–2521. [Google Scholar] [CrossRef]
- Shen, W.; Guo, X.; Wu, C.; Wu, D. Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm. Knowl. Based Syst. 2011, 24, 378–385. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A comprehensive review of swarm optimization algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Leardi, R. Genetic algorithms in chemometrics and chemistry: A review. J. Chemom. J. Chemom. Soc. 2001, 15, 559–569. [Google Scholar] [CrossRef]
- Weile, D.S.; Michielssen, E. Genetic algorithm optimization applied to electromagnetics: A review. IEEE Trans. Antennas Propag. 1997, 45, 343–353. [Google Scholar] [CrossRef]
- Bhoskar, M.T.; Kulkarni, M.O.K.; Kulkarni, M.N.K.; Patekar, M.S.L.; Kakandikar, G.M.; Nandedkar, V.M. Genetic algorithm and its applications to mechanical engineering: A review. Mater. Today Proc. 2015, 2, 2624–2630. [Google Scholar] [CrossRef]
- Mirjalili, S.; Dong, J.S.; Sadiq, A.S.; Faris, H. Genetic algorithm: Theory, literature review, and application in image reconstruction. In Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 69–85. [Google Scholar]
- Chaudhry, S.S.; Luo, W. Application of genetic algorithms in production and operations management: A review. Int. J. Prod. Res. 2005, 43, 4083–4101. [Google Scholar] [CrossRef]
- Jauhar, S.K.; Pant, M. Genetic algorithms, a nature-inspired tool: Review of applications in supply chain management. In Proceedings of the Fourth International Conference on Soft Computing for Problem Solving; Springer: New Delhi, India, 2015; pp. 71–86. [Google Scholar]
- Drake, A.E.; Marks, R.E. Genetic algorithms in economics and finance: Forecasting stock market prices and foreign exchange—A review. In Genetic Algorithms and Genetic Programming in Computational Finance; Springer: Boston, MA, USA, 2002; pp. 29–54. [Google Scholar]
- Shin, K.S.; Lee, Y.J. A genetic algorithm application in bankruptcy prediction modeling. Expert Syst. Appl. 2002, 23, 321–328. [Google Scholar] [CrossRef]
- Chou, C.H.; Hsieh, S.C.; Qiu, C.J. Hybrid genetic algorithm and fuzzy clustering for bankruptcy prediction. Appl. Soft Comput. 2017, 56, 298–316. [Google Scholar] [CrossRef]
- Zelenkov, Y.; Fedorova, E.; Chekrizov, D. Two-step classification method based on genetic algorithm for bankruptcy forecasting. Expert Syst. Appl. 2017, 88, 393–401. [Google Scholar] [CrossRef]
- Oreski, S.; Oreski, D.; Oreski, G. Hybrid system with genetic algorithm and artificial neural networks and its application to retail credit risk assessment. Expert Syst. Appl. 2012, 39, 12605–12617. [Google Scholar] [CrossRef]
- Zhang, W.; He, H.; Zhang, S. A novel multi-stage hybrid model with enhanced multi-population niche genetic algorithm: An application in credit scoring. Expert Syst. Appl. 2019, 121, 221–232. [Google Scholar] [CrossRef]
- Mirmirani, S.; Li, H.C. A comparison of VAR and neural networks with genetic algorithm in forecasting price of oil. Adv. Econom. 2004, 19, 203–223. [Google Scholar]
- Chiroma, H.; Abdulkareem, S.; Herawan, T. Evolutionary Neural Network model for West Texas Intermediate crude oil price prediction. Appl. Energy 2015, 142, 266–273. [Google Scholar] [CrossRef]
- Deng, S.; Xiang, Y.; Fu, Z.; Wang, M.; Wang, Y. A hybrid method for crude oil price direction forecasting using multiple timeframes dynamic time wrapping and genetic algorithm. Appl. Soft Comput. 2019, 82, 105566. [Google Scholar] [CrossRef]
- Chen, K.Y.; Wang, C.H. Support vector regression with genetic algorithms in forecasting tourism demand. Tour. Manag. 2007, 28, 215–226. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Chen, L.Y.; Wei, S.Y. SVR with hybrid chaotic genetic algorithms for tourism demand forecasting. Appl. Soft Comput. 2011, 11, 1881–1890. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.Y.; Hong, W.C.; Gu, D.X. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm. Appl. Soft Comput. 2015, 26, 435–443. [Google Scholar] [CrossRef]
- Yuan, F.C.; Lee, C.H. Using least square support vector regression with genetic algorithm to forecast beta systematic risk. J. Comput. Sci. 2015, 11, 26–33. [Google Scholar] [CrossRef]
- Cai, Q.; Zhang, D.; Wu, B.; Leung, S.C. A novel stock forecasting model based on fuzzy time series and genetic algorithm. Procedia Comput. Sci. 2013, 18, 1155–1162. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, Y.; Gan, Y.; Ye, M. A new financial data forecasting model using genetic algorithm and long short-term memory network. Neurocomputing 2020, in press. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Ozturk, H.K.; Ceylan, H. Forecasting total and industrial sector electricity demand based on genetic algorithm approach: Turkey case study. Int. J. Energy Res. 2005, 29, 829–840. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal deep learning lstm model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Liu, D.; Niu, D.; Wang, H.; Fan, L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Nasseri, M.; Asghari, K.; Abedini, M.J. Optimized scenario for rainfall forecasting using genetic algorithm coupled with artificial neural network. Expert Syst. Appl. 2008, 35, 1415–1421. [Google Scholar] [CrossRef]
- Hassani, H. Singular Spectrum Analysis: Methodology and Comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar]
- Hassani, H.; Heravi, S.; Zhigljavsky, A. Forecasting European industrial production with singular spectrum analysis. Int. J. Forecast. 2009, 25, 103–118. [Google Scholar] [CrossRef]
- Hassani, H.; Rua, A.; Silva, E.S.; Thomakos, D. Monthly forecasting of GDP with mixed-frequency multivariate singular spectrum analysis. Int. J. Forecast. 2019, 35, 1263–1272. [Google Scholar] [CrossRef]
- Hassani, H.; Ghodsi, Z.; Silva, E.S.; Heravid, S. From nature to maths: Improving forecasting performance in subspace-based methods using genetics Colonial Theory. Digit. Signal Process. 2016, 21, 101–109. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M.R.; Khan, A.; Silva, E.S. The effect of data transformation on Singular Spectrum Analysis for forecasting. Signals 2020, 1, 4–25. [Google Scholar] [CrossRef]
- Kalantari, M.; Yarmohammadi, M.; Hassani, H. Singular spectrum analysis based on L 1-norm. Fluct. Noise Lett. 2016, 15, 1650009. [Google Scholar] [CrossRef]
- Silva, E.S.; Hassani, H.; Ghodsi, M.; Ghodsi, Z. Forecasting with auxiliary information in forecasts using multivariate singular spectrum analysis. Inf. Sci. 2019, 479, 214–230. [Google Scholar] [CrossRef]
- Kalantari, M.; Hassani, H.; Silva, E.S. Weighted Linear Recurrent Forecasting in Singular Spectrum Analysis. Fluct. Noise Lett. 2020, 19, 2050010. [Google Scholar] [CrossRef]
- Silva, E.S.; Hassani, H.; Heravi, S.; Huang, X. Forecasting tourism demand with denoised neural networks. Ann. Tour. Res. 2019, 74, 134–154. [Google Scholar] [CrossRef]
- Ma, X.; Jin, Y.; Dong, Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Appl. Soft Comput. 2017, 54, 296–312. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Zhang, M. Comparative study on three new hybrid models using Elman Neural Network and Empirical Mode Decomposition based technologies improved by Singular Spectrum Analysis for hour-ahead wind speed forecasting. Energy Convers. Manag. 2017, 147, 75–85. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Ma, P. Wind power forecasting based on singular spectrum analysis and a new hybrid Laguerre neural network. Appl. Energy 2020, 259, 114139. [Google Scholar] [CrossRef]
- Kolidakis, S.; Botzoris, G.; Profillidis, V.; Lemonakis, P. Road traffic forecasting—A hybrid approach combining Artificial Neural Network with Singular Spectrum Analysis. Econ. Anal. Policy 2019, 64, 159–171. [Google Scholar] [CrossRef]
- Sulandari, W.; Lee, M.H.; Rodrigues, P.C. Indonesian electricity load forecasting using singular spectrum analysis, fuzzy systems and neural networks. Energy 2020, 190, 116408. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- Ghodsi, M.; Hassani, H.; Rahmani, D.; Silva, E.S. Vector and recurrent singular spectrum analysis: Which is better at forecasting? J. Appl. Stat. 2018, 45, 1872–1899. [Google Scholar] [CrossRef]
- Hassani, H.; Silva, E.S. A Kolmogorov-Smirnov based test for comparing the predictive accuracy of two sets of forecasts. Econometrics 2015, 3, 590–609. [Google Scholar] [CrossRef]
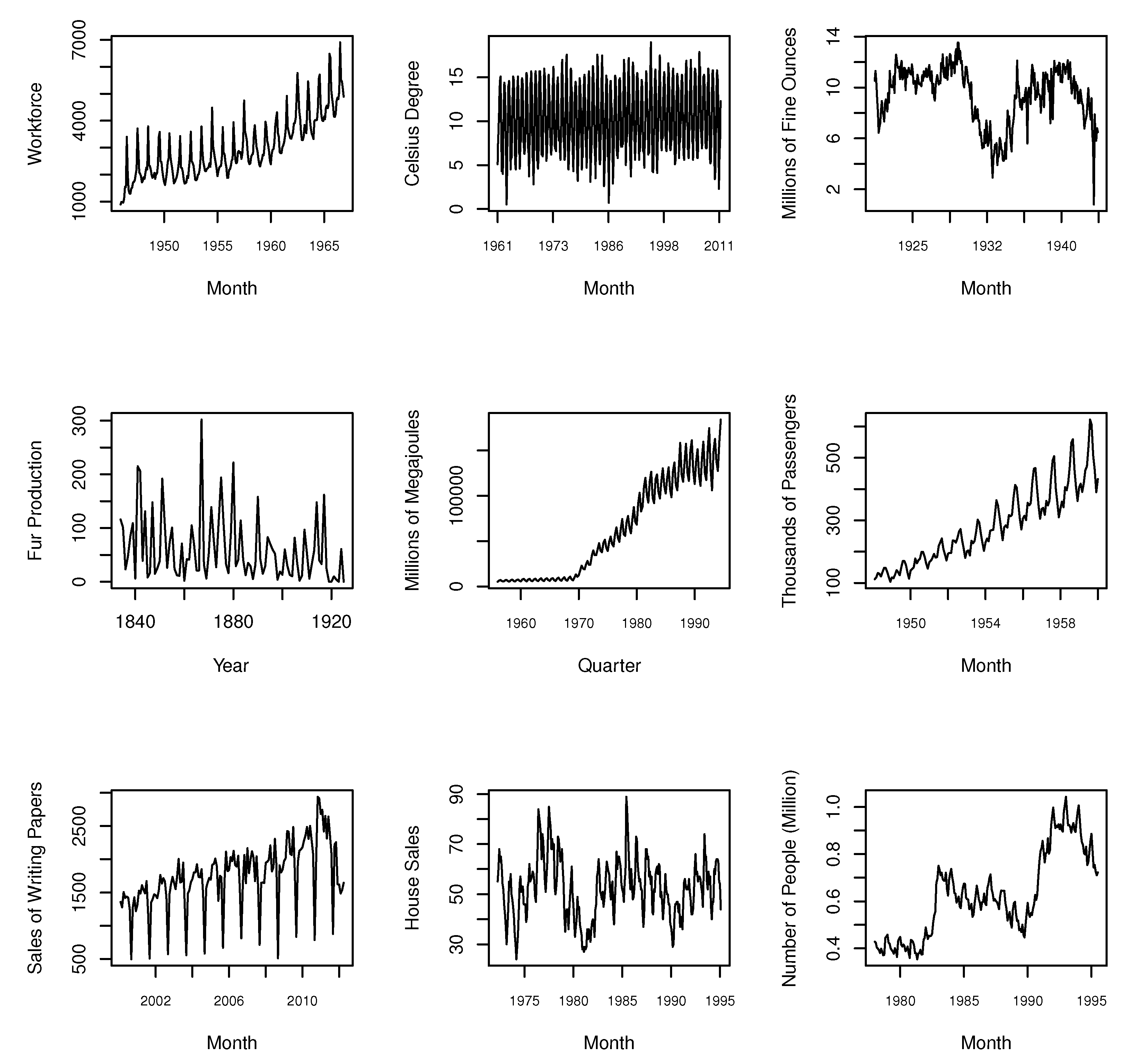
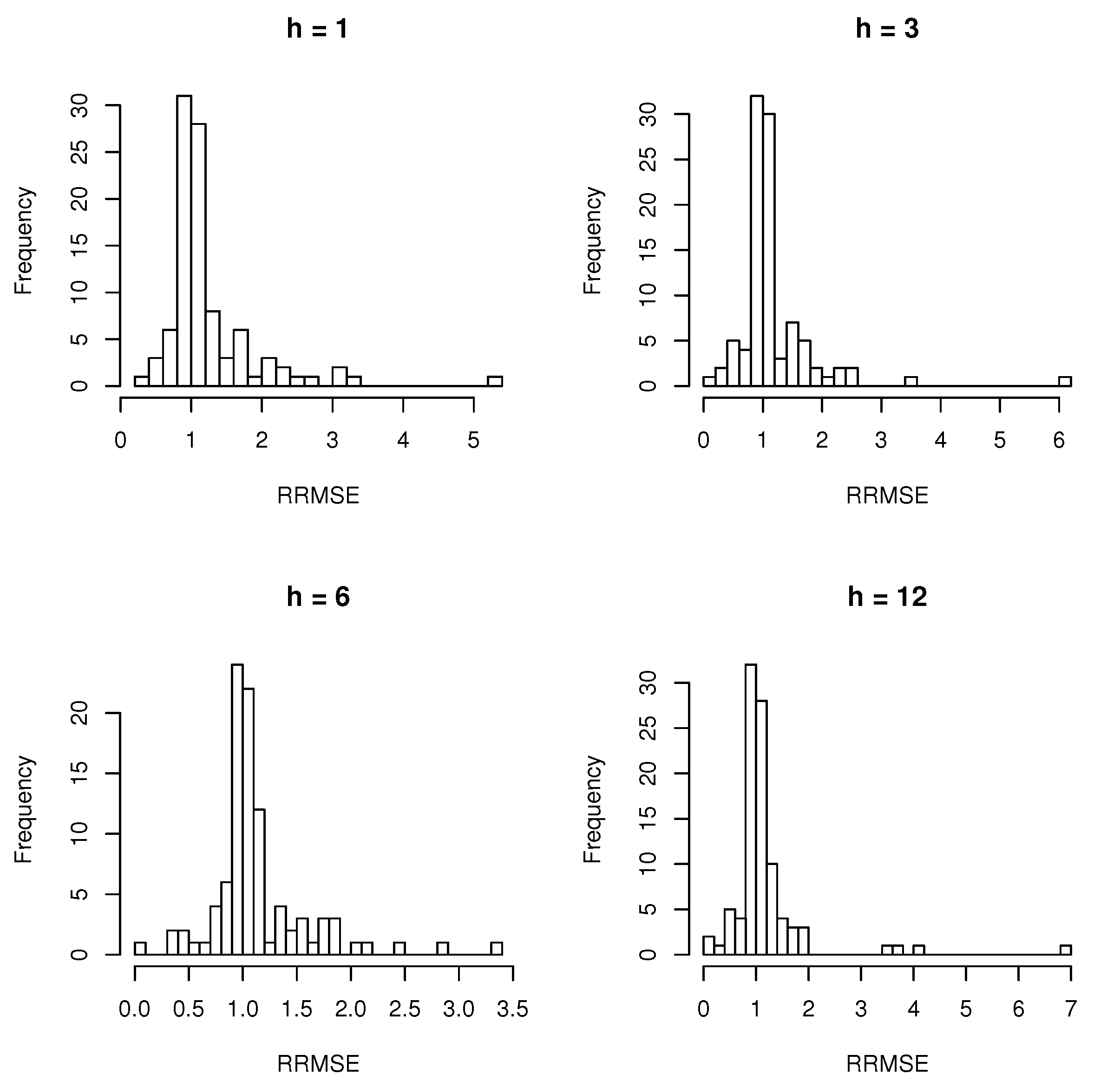
| Factor | Levels | |||||
|---|---|---|---|---|---|---|
| Annual | Monthly | Quarterly | Weekly | Daily | Hourly | |
| Sampling Frequency | 5 | 83 | 4 | 4 | 2 | 2 |
| Positive Skew | Negative Skew | Symmetric | ||||
| Skewness | 61 | 21 | 18 | |||
| Normal | Non-normal | |||||
| Normality | 18 | 82 | ||||
| Stationary | Non-Stationary | |||||
| Stationarity | 14 | 86 | ||||
| Forecasting Horizon | |||||
|---|---|---|---|---|---|
| h = 1 | h = 3 | h = 6 | h = 12 | ||
| RRMSE’s Median | 1.0618 | 1.0362 | 1.0319 | 1.0302 | |
| N. RRMSE < 1 | 21 | 24 | 21 | 24 | |
| N. RRMSE > 1 | 57 | 54 | 57 | 54 | |
| N. RRMSE < 1 (Significantly) | 3 | 5 | 4 | 6 | |
| N. RRMSE > 1 (Significantly) | 17 | 13 | 7 | 14 | |
| RRMSE ∼ Frequency | 0.1975 | 0.1975 | 0.1975 | 0.1975 | |
| Kruskal-Wallis | RRMSE ∼ Normality | 0.9047 | 0.9047 | 0.9047 | 0.9047 |
| p-value’s | RRMSE ∼ Stationarity | 0.1625 | 0.1625 | 0.1625 | 0.1625 |
| RRMSE ∼ Skewness | 0.9618 | 0.9618 | 0.9618 | 0.9618 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassani, H.; Yeganegi, M.R.; Huang, X. Fusing Nature with Computational Science for Optimal Signal Extraction. Stats 2021, 4, 71-85. https://doi.org/10.3390/stats4010006
Hassani H, Yeganegi MR, Huang X. Fusing Nature with Computational Science for Optimal Signal Extraction. Stats. 2021; 4(1):71-85. https://doi.org/10.3390/stats4010006
Chicago/Turabian StyleHassani, Hossein, Mohammad Reza Yeganegi, and Xu Huang. 2021. "Fusing Nature with Computational Science for Optimal Signal Extraction" Stats 4, no. 1: 71-85. https://doi.org/10.3390/stats4010006
APA StyleHassani, H., Yeganegi, M. R., & Huang, X. (2021). Fusing Nature with Computational Science for Optimal Signal Extraction. Stats, 4(1), 71-85. https://doi.org/10.3390/stats4010006






