Kumaraswamy Generalized Power Lomax Distributionand Its Applications
Abstract
1. Introduction
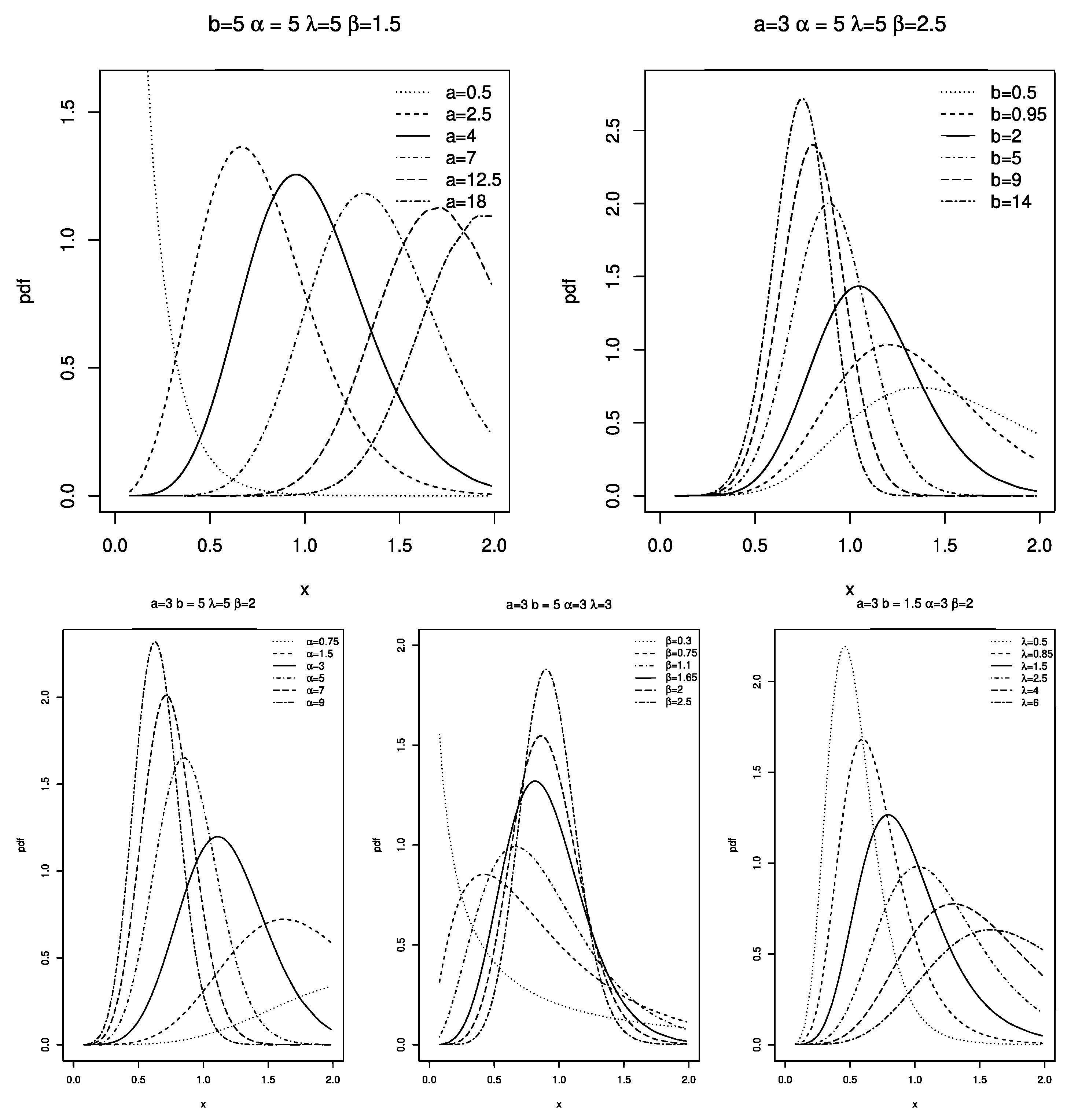
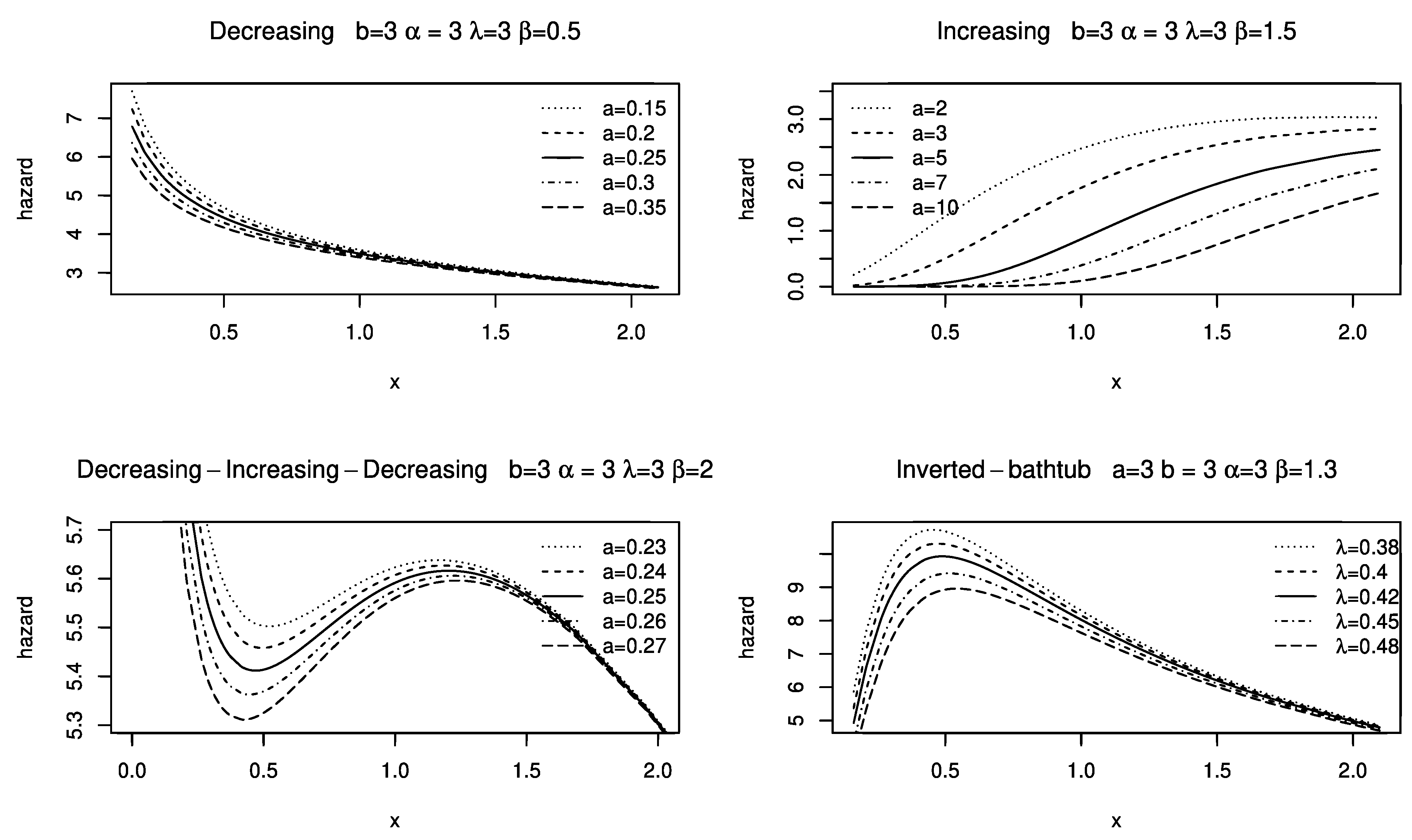
2. The Kumaraswamy Generalized Power Lomax Distribution
3. Moments of the KPL Distribution
4. Information Measures
4.1. Rényi Entropy
4.2. Tsallis Entropy
5. Order Statistics
6. Maximum Likelihood Estimates of the Parameters
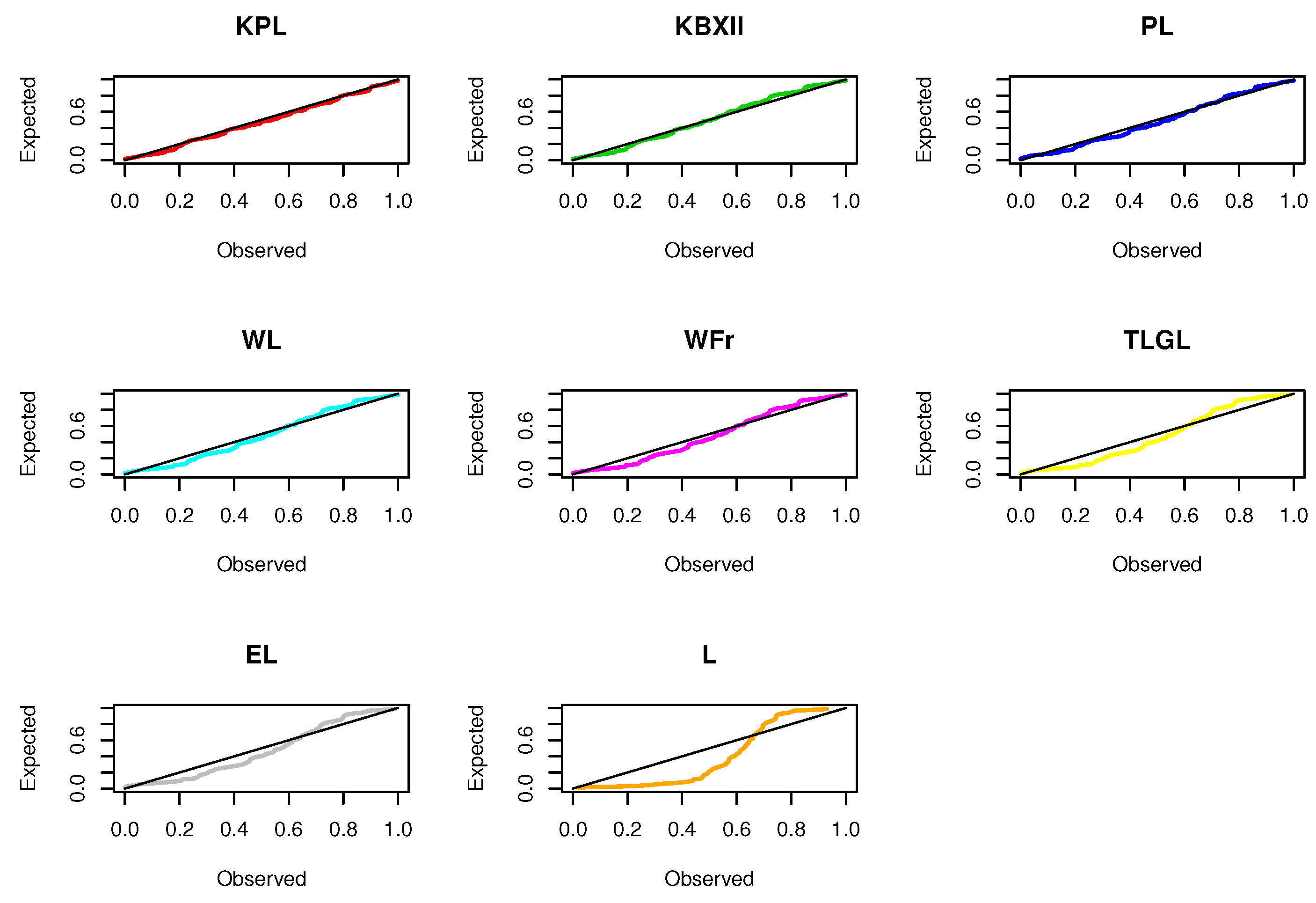
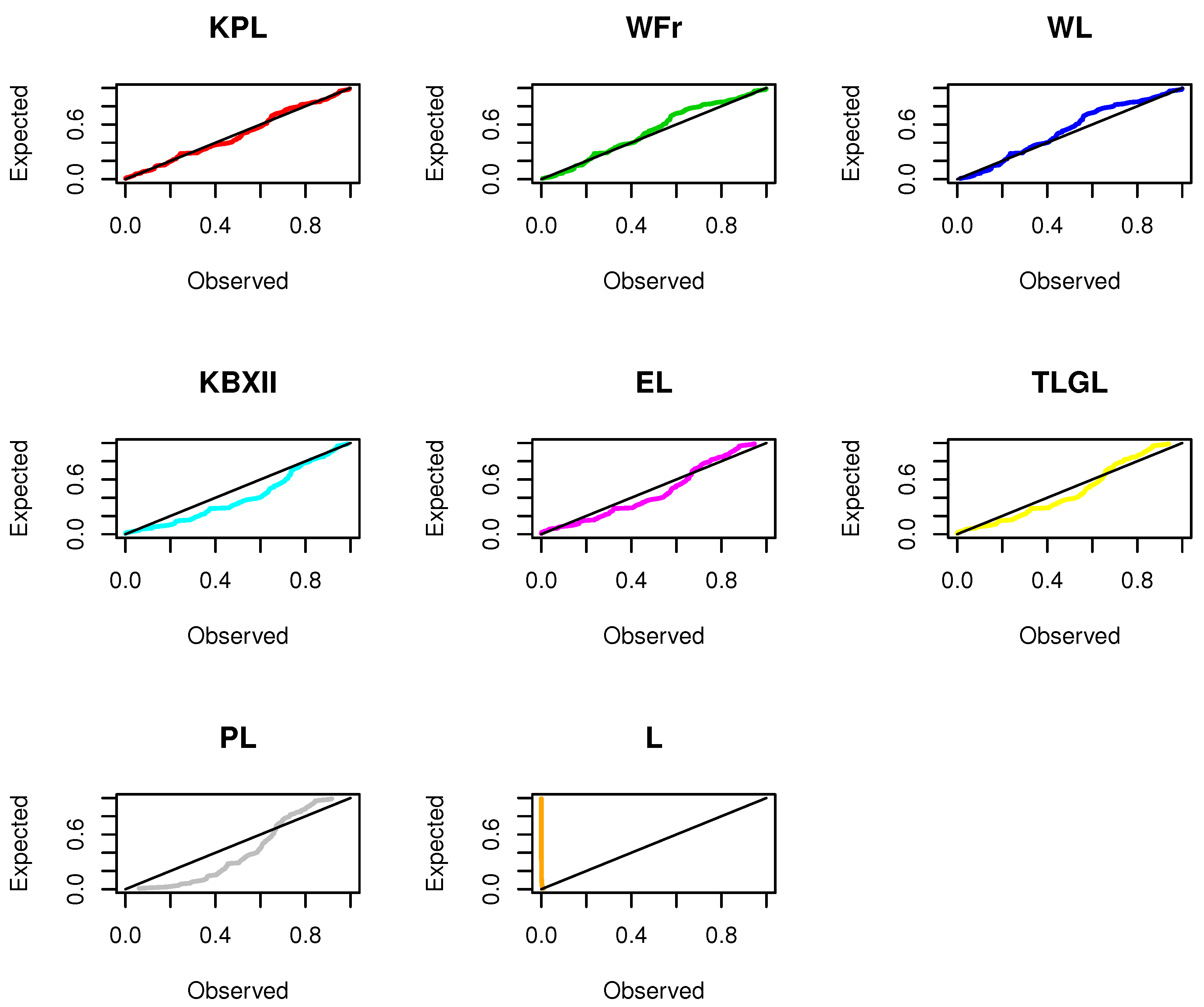
7. Applications of the KPL Model
8. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Kumaraswamy, P. Sinepower probability density function. J. Hydrol. 1976, 31, 181–184. [Google Scholar] [CrossRef]
- Kumaraswamy, P. Extended sinepower probability density function. J. Hydrol. 1978, 37, 81–89. [Google Scholar] [CrossRef]
- Nadarajah, S. On the distribution of Kumaraswamy. J. Hydrol. 2008, 348, 568–569. [Google Scholar] [CrossRef]
- Jones, M.C. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages. Stat. Methodol. 2009, 6, 70–81. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Nadarajah, S.; Ortega, E.M. The Kumaraswamy Gumbel distribution. Stat. Methods Appl. 2012, 21, 139–168. [Google Scholar] [CrossRef]
- De Pascoa, M.A.; Ortega, E.M.; Cordeiro, G.M. The Kumaraswamy generalized gamma distribution with application in survival analysis. Stat. Methodol. 2011, 8, 411–433. [Google Scholar] [CrossRef]
- Paranaíba, P.F.; Ortega, E.M.; Cordeiro, G.M.; Pascoa, M.A.d. The Kumaraswamy Burr XII distribution: Theory and practice. J. Stat. Comput. Simul. 2013, 83, 2117–2143. [Google Scholar] [CrossRef]
- Malinova, A.; Golev, A.; Rahneva, O.; Kyurkchiev, V. Some notes on the Kumaraswamy-Weibull-Exponential cumulative sigmoid. Int. J. Pure Appl. Math. 2018, 120, 521–529. [Google Scholar]
- Malinova, A.; Kyurkchiev, V.; Iliev, A.; Kyurkchiev, N. A note on the transmuted Kumaraswamy quasi Lindley cumulative distribution function. Int. J. Sci. Res. Dev. 2018, 6, 561–564. [Google Scholar]
- Angelova, E.; Arnaudova, V.; Terzieva, T.; Malinova, A. A note on the new Kumaraswamy alpha power inverted exponential family of C.D.F. Neural Parallel Sci. Comput. 2020, 28, 59–67. [Google Scholar]
- Abdul-Moniem, I.B. Recurrence relations for moments of lower generalized order statistics from exponentiated Lomax distribution and its characterization. J. Math. Comput. Sci. 2012, 2, 999–1011. [Google Scholar]
- Lemonte, A.J.; Cordeiro, G.M. An extended Lomax distribution. Statistics 2013, 47, 800–816. [Google Scholar] [CrossRef]
- Shams, T.M. The Kumaraswamy-Generalized Lomax Distribution. Middle-East J. Sci. Res. 2013, 17, 641–646. [Google Scholar] [CrossRef]
- El-Bassiouny, A.H.; Abdo, N.F.; Shahen, H.S. Exponential Lomax Distribution. Int. J. Comput. Appl. 2015, 121, 24–29. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Mansoor, M.; Zubair, M. The Weibull-Lomax distribution: Properties and applications. Hacet. J. Math. Stat. 2015, 44, 461–480. [Google Scholar] [CrossRef]
- Afify, A.Z.; Yousof, H.M.; Cordeiro, G.M.; Ortega, E.M.; Nofal, Z.M. The Weibull Fréchet distribution and its applications. J. Appl. Stat. 2016, 43, 2608–2626. [Google Scholar] [CrossRef]
- Rady, E.H.A.; Hassanein, W.A.; Elhaddad, T.A. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1–22. [Google Scholar] [CrossRef]
- Anwar, M.; Zahoor, J. The Half-Logistic Lomax Distribution for Lifetime Modeling. J. Probab. Stat. 2018, 3152807. [Google Scholar] [CrossRef]
- Hassan, A.S.; Abd-Allah, M. On the Inverse Power Lomax Distribution. Ann. Data Sci. 2019, 6, 259–278. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Khaleel, M.A.; Okagbue, H.I.; Odetunmibi, O.A. The Topp–Leone Lomax (TLLo) Distribution with Applications to Airbone Communication Transceiver Dataset. Wirel. Pers. Commun. 2019, 109, 349–360. [Google Scholar] [CrossRef]
- Al-Marzouki, S.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Topp Leone Power Lomax Distribution with Applications. Mathematics 2020, 8, 4. [Google Scholar] [CrossRef]
- Nagarjuna, V.B.V.; Vardhan, V. Marshall-Olkin Exponential Lomax Distribution: Properties and its Application. Stoch. Model. Appl. 2020, 24, 161–177. [Google Scholar]
- Mathew, J.; Chesneau, C. Some New Contributions on the Marshall–Olkin Length Biased Lomax Distribution: Theory, Modelling and Data Analysis. Math. Comput. Appl. 2020, 25, 79. [Google Scholar] [CrossRef]
- Nair, N.U.; Sankaran, P.; Balakrishnan, N. Quantile-Based Reliability Analysis; Birkhäuser: Basel, Switzerland, 2013. [Google Scholar]
- Rényi, A. On Measures of Entropy and Information; Technical Report; Hungarian Academy of Sciences: Budapest, Hungary, 1961. [Google Scholar]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural a-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Bader, M.; Priest, A. Statistical aspects of fibre and bundle strength in hybrid composites. In Progress in Science and Engineering Composites; Hayashi, T., Kawata, K., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Louzada-Neto, F.; Mazucheli, J.; Achcar, J.A. Uma Introdução à análise de Sobrevivência e Confiabilidade; Sociedad Chilena de Estadística: Valparaíso, Chili, 2001. [Google Scholar]

| Parameters | a | |||||
|---|---|---|---|---|---|---|
| 1 | 1.096343 | 1.360350 | 1.898922 | 3.000000 | 0.1583815 | |
| 2 | 1.313328 | 1.870481 | 2.907724 | 5.000000 | 0.1456513 | |
| 3 | 1.434132 | 2.199940 | 3.641145 | 6.600000 | 0.1432048 | |
| 4 | 1.518195 | 2.448363 | 4.233660 | 7.971429 | 0.1434478 | |
| 5 | 1.582860 | 2.650083 | 4.738448 | 9.190476 | 0.1446359 | |
| 1 | 0.9167115 | 0.8606779 | 0.8251498 | 0.8059774 | 0.020317974 | |
| 2 | 1.0286584 | 1.0695094 | 1.1233040 | 1.1912426 | 0.011371281 | |
| 3 | 1.0808945 | 1.1768814 | 1.2905014 | 1.4248888 | 0.008548480 | |
| 4 | 1.1137116 | 1.2475227 | 1.4053524 | 1.5920104 | 0.007169093 | |
| 5 | 1.1372247 | 1.2996238 | 1.4924269 | 1.7220834 | 0.006343810 | |
| 1 | 0.9515346 | 0.9771163 | 1.075939 | 1.267621 | 0.07169832 | |
| 2 | 1.1398721 | 1.3609060 | 1.703722 | 2.242301 | 0.06159767 | |
| 3 | 1.2428513 | 1.6039652 | 2.154467 | 3.022583 | 0.05928593 | |
| 4 | 1.3141795 | 1.7859622 | 2.516701 | 3.691375 | 0.05889455 | |
| 5 | 1.3690008 | 1.9333437 | 2.824648 | 4.286271 | 0.05918053 | |
| > > > | 3 | 0.9246664 | 1.113072 | 1.936337 | 7.651063 | 0.2580643 |
| 7 | 1.3393890 | 2.214626 | 5.046252 | 24.903052 | 0.4206629 | |
| 10 | 1.5452139 | 2.909026 | 7.447825 | 40.692316 | 0.5213404 | |
| 14 | 1.7598484 | 3.737898 | 10.690728 | 64.504585 | 0.6408318 | |
| 17 | 1.8937766 | 4.309344 | 13.141668 | 84.065516 | 0.7229542 | |
| 3 | 2.381898 | 7.098448 | 27.62178 | 156.1513 | 1.425008 | |
| 7 | 4.209734 | 21.533759 | 141.10721 | 1329.5962 | 3.811897 | |
| 10 | 5.291480 | 33.862448 | 276.77366 | 3248.8381 | 5.862686 | |
| 14 | 6.547543 | 51.716382 | 520.95011 | 7533.2474 | 8.846066 | |
| 17 | 7.398181 | 65.967625 | 749.80026 | 12233.8552 | 11.234540 | |
| 4 | 1.420161 | 2.542323 | 6.287137 | 28.97299 | 0.5254662 | |
| 11 | 2.573373 | 8.204595 | 35.761130 | 289.64094 | 1.5823481 | |
| 17 | 3.301047 | 13.473254 | 75.107768 | 778.33805 | 2.5763424 | |
| 22 | 3.822930 | 18.059557 | 116.502575 | 1397.61270 | 3.4447658 | |
| 36 | 5.056489 | 31.580735 | 269.364002 | 4275.42575 | 6.0126525 |
| (8.651935) | (6.67144) | (4.366995) | (−6.868542) | (1.093022) | |
| 74.85599 | 44.50811 | 19.07065 | 47.17687 | 1.194697 | |
| (8.002526) | (4.365969) | (−2.73485) | (0.207459) | (−0.3513344) | |
| 64.04406 | 19.08434 | 7.479976 | 0.08666441 | 0.1234489 | |
| (6.22343) | (−0.751908) | (−1.357911) | (2.745664) | (−0.3055339) | |
| 38.73797 | 0.5679816 | 1.845981 | 7.551292 | 0.09335099 | |
| (−3.279042) | (−1.111076) | (−4.199035) | (3.525116) | (−0.4977061) | |
| 10.75212 | 1.23449 | 17.6319 | 12.42645 | 0.2477113 | |
| (−3.003313) | (−0.9706962) | (−4.235572) | (0.7994587) | (−0.4568123) | |
| 9.124203 | 1.134068 | 17.94019 | 0.641023 | 0.2086831 | |
| (−0.2668285) | (−1.074196) | (−2.093235) | (0.7068528) | (−0.4322879) | |
| 0.07645446 | 1.187502 | 4.3866 | 0.4997061 | 0.1868756 | |
| Distribution Data Set 1 | |||||
| KPL | 21.1082 | 6.5418 | 5.1957 | 0.4485 | 2.2026 |
| KBXII | 0.4342 | 0.2639 | 7.5759 | 1.9639 | 4.4371 |
| PL | - | 3.4574 | 13.5759 | 3.1625 | |
| WL | 4.0405 | 2.711 | 0.7077 | - | 1.7575 |
| WFr | 6.4647 | 6.8652 | 0.7611 | - | 0.2297 |
| TLGL | 4.8177 | - | 12.3340 | - | 16.0790 |
| EL | 5.4551 | - | 21.9720 | - | 13.2469 |
| Lomax | - | - | 12.3594 | - | 17.9267 |
| Distribution Data Set 2 | |||||
| KPL | 8.9953 | 7.4396 | 2.0506 | 5.5581 | 0.2604 |
| WFr | 0.0823 | 3.8303 | 5.0670 | - | 0.1522 |
| WL | 0.0056 | 0.1645 | 4.3790 | - | 1.2422 |
| KBXII | 8.3595 | 6.4601 | 0.0580 | 4.1935 | 1.5752 |
| EL | 6.1659 | - | 0.6294 | - | 17.4538 |
| TLGL | 9.5741 | - | 0.3008 | - | 7.2733 |
| PL | - | - | 0.9186 | 26.5070 | 0.5654 |
| Lomax | - | - | 0.2847 | - | 24.8517 |
| Distribution | ||||||||
| Data Set 1 | W* | A* | p-Value | AIC | CAIC | BIC | HQIC | |
| KPL | 0.0232 | 0.2272 | 0.0604 | 0.9605 | 125.6272 | 126.5647 | 136.8697 | 130.0929 |
| KBXII | 0.0645 | 0.5108 | 0.0747 | 0.8287 | 129.838 | 130.7755 | 141.0804 | 134.3036 |
| PL | 0.1345 | 0.9450 | 0.0778 | 0.7909 | 131.9917 | 132.3553 | 138.7372 | 134.6711 |
| WL | 0.1860 | 1.2995 | 0.1030 | 0.4476 | 138.8186 | 139.4340 | 147.8126 | 142.3911 |
| WFr | 0.2186 | 1.4956 | 0.1205 | 0.2610 | 141.3542 | 141.9696 | 150.3482 | 144.9267 |
| TLGL | 0.4060 | 2.5291 | 0.1443 | 0.1085 | 152.7280 | 153.0916 | 159.4734 | 155.4073 |
| EL | 0.4265 | 2.6440 | 0.1440 | 0.1098 | 153.4122 | 153.7758 | 160.1577 | 156.0916 |
| Lomax | 0.3213 | 2.0540 | 0.3554 | 4.18 | 204.3163 | 204.4954 | 208.8133 | 206.1026 |
| Data Set 2 | W* | A* | p-Value | AIC | CAIC | BIC | HQIC | |
| KPL | 0.0936 | 0.4740 | 0.0726 | 0.5530 | 2035.768 | 2036.294 | 2049.705 | 2041.428 |
| WFr | 0.1523 | 0.8761 | 0.0957 | 0.2221 | 2039.442 | 2039.790 | 2050.592 | 2043.970 |
| WL | 0.1907 | 1.1122 | 0.1175 | 0.0730 | 2043.763 | 2044.111 | 2054.913 | 2048.292 |
| KBXII | 0.3134 | 1.7692 | 0.1558 | 0.0059 | 2060.251 | 2060.778 | 2074.189 | 2065.912 |
| EL | 0.5717 | 3.2453 | 0.1399 | 0.0182 | 2072.046 | 2072.252 | 2080.408 | 2075.442 |
| TLGL | 0.6155 | 3.5241 | 0.1372 | 0.0218 | 2077.853 | 2078.060 | 2086.215 | 2081.249 |
| PL | 0.1488 | 0.7585 | 0.2486 | 7.22 | 2117.392 | 2117.599 | 2125.755 | 2120.788 |
| Lomax | 0.4167 | 2.3268 | 0.3110 | 1.65 | 2157.868 | 2157.971 | 2163.443 | 2160.132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagarjuna, V.B.V.; Vardhan, R.V.; Chesneau, C. Kumaraswamy Generalized Power Lomax Distributionand Its Applications. Stats 2021, 4, 28-45. https://doi.org/10.3390/stats4010003
Nagarjuna VBV, Vardhan RV, Chesneau C. Kumaraswamy Generalized Power Lomax Distributionand Its Applications. Stats. 2021; 4(1):28-45. https://doi.org/10.3390/stats4010003
Chicago/Turabian StyleNagarjuna, Vasili B.V., R. Vishnu Vardhan, and Christophe Chesneau. 2021. "Kumaraswamy Generalized Power Lomax Distributionand Its Applications" Stats 4, no. 1: 28-45. https://doi.org/10.3390/stats4010003
APA StyleNagarjuna, V. B. V., Vardhan, R. V., & Chesneau, C. (2021). Kumaraswamy Generalized Power Lomax Distributionand Its Applications. Stats, 4(1), 28-45. https://doi.org/10.3390/stats4010003







