1. Introduction
Joint modeling of the conditional second moments, volatilities and correlations, of a vector of asset returns is considerably more complicated (and with far fewer references) than individual volatility modeling. With the exception of realized correlation measures, based on high-frequency data, the literature on conditional correlation modeling is plagued with the “curse of dimensionality”: parametric or semi-parametric correlation models are usually dependent on a large number of parameters (always greater than the number of assets being modeled). Besides the always lurking misspecification problems, one is faced with the difficult task of multi-parameter numerical optimization under various constraints. Some recent advances, see for example Ledoit et al. [
1] and Palandri [
2], propose simplifications by breaking the modeling and optimization problem into smaller, more manageable, sub-problems but one still has to make ad-hoc assumptions about the way volatilities and correlations are parametrized.
In this paper we present a novel approach for modeling conditional correlations building on the NoVaS (NOrmalizing and VAriance Stabilizing) transformation approach introduced by Politis [
3,
4,
5,
6] and significantly extended by Politis and Thomakos [
7,
8]. Our work has both similarities and differences with the related literature. The main similarity is that we also begin by modeling the volatilities of the individual series and estimate correlations using the standardized return series. The main differences are that (a) we do not make distributional assumptions for the distribution of the standardized returns, (b) we assume no “model” for the volatilities and the correlations and (c) calibration-estimation of parameters requires only one-dimensional optimizations in the unit interval and simple numerical integration.
The main advantages of using NoVaS transformations for volatility modeling and forecasting, see Politis and Thomakos [
8], are that the method is data-adaptable without making any a prior assumptions about the distribution of returns (e.g., their degree of kurtosis) and it can work in a multitude of environments (e.g., global and local stationary models, models with structural breaks etc.) These advantages carry-over to the case of correlation modeling. In addition to our main results on correlations we also present some auxiliary results on the use of different criteria for distributional matching thus allowing for a more “automated” application of the NoVaS methodology. Furthermore, we apply NoVaS to portfolio analysis. A referee has suggested that we consider non-linear types of correlations, asymmetric distributions for the returns and other types of portfolios. These are well suited for future research, especially the extensions for non-linear types of association, but this particular extension is beyond the scope of the current paper. The assumption of asymmetric distributions for the returns is innocuous in the current context: the main idea here is a transformation to normality no matter what the original return distribution might be.
The related literature on conditional correlation modeling is focused on finding parsimonious, easy to optimize, parametric and semi-parametric representations of volatilities and correlations, and on approaches that can handle the presence of excess kurtosis in asset returns. Early references for parametric multivariate models of volatility and correlation include Bollerslev, Engle and Woolridge [
9], (the VEC model), Bollerslev [
10] (the constant conditional correlation, CCC model), Bollerslev et al. and Engle et al. [
11] (the BEKK) model), Pelletier and Silvennoinen et al. [
12,
13,
14,
15] (extensions of the CCC-GARCH). For an alternative Bayesian treatment of GARCH models see Vrontos et al. [
16]
Engle [
17] introduced the popular dynamic conditional correlation (DCC) model, which was extended and generalized by various authors: see, among others, Sheppard [
18] and Hafner and Frances [
19]. Independently Tse and Tsui [
20] developed the VC-GARCH. For a review of the class of multivariate GARCH-type models see Bauwens et al. [
21] and Silvennoinen and Teräsvirta [
14] and for a review of volatility and correlation forecast evaluation see Patton and Sheppard [
22]. A recent paper linking BEKK and DCC models is Caporin and McAleer [
23].
Part of the literature treats the problem in a semi-parametric or non-parametric manner, such as in Long and Ullah [
24] and Hafner et al. [
25] Ledoit et al. [
1] and Palandri [
2] propose simplifications to the modeling process, both on a parametrization and optimization level.
The NoVaS approach we present in this paper also has some similarities with copula-based modeling where the marginal distributions of standardized returns are specified and then joined to form a multivariate distribution; for applications in the current context, see Jondeau and Rockinger [
26] and Patton [
27], and see Andersen et al. [
28] for the realized correlation measures.
Finally, although time-series correlation modeling originated in the econometrics literature for financial applications, it caught on recently on the neuroscience literature after Lindquist et al. [
29] presented DCC to the neuroimaging community. Some very recent and related papers on this strand of the literature, some of which propose robust methods, are those of Warnick et al. [
30], John et al. [
31], Lee and Kim [
32,
33], Behboundi and Farnoosh [
34] and Faghiri et al. [
35]
The rest of the paper is organized as follows: in
Section 2, we briefly review the general development of the NoVaS approach; in
Section 3, we present the new results on NoVaS-based modeling and forecasting of correlations; in
Section 4, we present a proposal for “model” selection in the context of NoVaS; in
Section 5, we present some limited simulation results and a possible application of the methodology in portfolio analysis, while in
Section 6, we present an illustrative empirical application;
Section 7 offers some concluding remarks.
3. Multivariate NoVaS & Correlations
We now turn to multivariate NoVaS modeling. Our starting point is similar to that of many other correlation modeling approaches in the literature. In a parametric context one first builds univariate models for the volatilities and then uses the fitted volatility values to standardize the returns and use those for building a model for the correlations. Our approach is similar. The first step is to use the univariate NoVaS transformation to obtain the (properly aligned) studentized series and , for a pair of returns . There are two main advantages with the use of NoVaS in the present context: (a) the individual volatility series are potentially more accurate since there is no problem of parametric misspecification and (b) there is only one univariate optimization per pair of returns analyzed. To fix ideas first remember that the studentized return series use information up to and including time t. Note that this is different from the standardization used in the rest of the literature where the standardization is made from the model not from the data, i.e., from in the present notation. This allows us to use the time t information when computing the correlation measure.
We start by giving a definition concerning the product of two series.
Definition 1. Consider a pair of studentized returns and , which have been scaled to zero mean and unit variance, and let denote their product.
The unconditional correlation can be estimated by the sample mean of the
. The remaining task is therefore to propose a suitable form for the conditional correlation and to estimate its parameters. To stay in line with the “model-free” spirit of this paper, when choosing a method to estimate the conditional correlation, we opt for parsimony, computational simplicity and compatibility with other models in the related literature. The easiest scheme is exponential smoothing as in Equation (
14) which can compactly represented as the following autoregressive model:
and can therefore be estimated by:
for
,
the smoothing parameter and
L a (sufficiently high) truncation parameter. This is of the form of a local average so different weights can be applied. An alternative general formulation could, for example, be as follows:
with
B the backshift operator. Choosing exponential weights, as in univariate NoVaS, we have
For any specification similar to the above, we can impose an “unbiasedness” condition (similar to other models in the literature) where the mean of the conditional correlation matches the unconditional correlation as follows:
Note what exactly is implied by the use of
in the context of Equation (
13): the correlation is still conditional but now using data up to and including time
t. Both
and
options can be used in applications with little difference in their in-sample performance; their out-of-sample performance needs to be further investigated.
Other specifications are, of course, possible but they would entail additional parameters and move us away from the NoVaS smoothing approach. For example, at the expense of one additional parameter we could account for asymmetries in the correlation in a standard fashion such as:
with
the indicator function for negative returns.
Finally, to ensure that the estimated correlations lie within
it is convenient to work with an (optional) scaling condition, such as the Fisher transformation and its inverse. For example, we can model the series:
and then transform and recover the correlations from the inverse transformation:
What is left to do is to estimate . In the following, we propose two approaches. One involves maximum likelihood estimation and is based on the distribution of the product of the two studentized series. The other is more in line with the “model-free” spirit of the NoVaS approach and uses cross-validation.
3.1. Maximum Likelihood Estimation
We first summarize some interesting properties concerning the product of two studentized series in the following proposition.
Proposition 1. With Definition 1, and under the assumptions of strict stationarity and distributional matching the following holds.
Assuming that both studentized series were obtained using the same target distribution then the (conditional or unconditional) density function ofcan be obtained from the result of Rohatgi (1976) and has the generic form of: whereis the joint density of the studentized series. In particular:
- (a)
If the target distribution is normal, and using the unconditional correlation ρ, the density function of is given by Craig (1936) and has the following formwhere: andis the integral of the same function in the interval. Note that the result in Graig (1936) is for the normal not truncated normal distribution; however, the truncation involved in NoVaS has a negligible effect in the validity of the result.
- (b)
If the target distribution is uniform, and again using the unconditional correlation ρ, the density function ofcan be derived using the Karhunen–Loeve transform and is given (apart from a constant) as: where. In this case, and in contrast to the previous case with a truncated normal target distribution, the result obtained is exact.
A similar result as in 1 above holds when we use the conditional correlation, for.
Remark 4. Proposition 1 allows for a straightforward interpretation of unconditional and conditional correlation using NoVaS transformations on individual series. Moreover, note how we can make use of the distributional matching, based on the marginal distributions, to form an explicit likelihood for the product of the studentized series; this is different from the copula-based approach to correlation modeling where from marginal distributions we go to a joint distribution—the joint distribution is just not needed in the NoVaS context. We can now use the likelihood function of the product to obtain an estimate of λ, as in Equation (13). Given the form of the conditional correlation function, the truncation parameter
L and the above transformation we have that the smoothing parameter
is estimated by maximum likelihood as:
Remark 5. Even though we do not need the explicit joint distribution of the studentized series, we still need to know the distribution of the product. Furthermore, using an MLE approach makes the multivariate NoVaS “semi-parametric”. We therefore introduce a second method based on cross validation which does not require knowledge of the distribution, and hence keeps NoVaS model-free.
3.2. Cross Validation (CV)
Our aim in this subsection is to find an estimate for
as in Equation (
13), without using a maximum likelihood method, and without using the density of
. We instead use an error minimization procedure. We start by suggesting different objective functions which we then compare for suitability.
We still use Equation (
13) but without knowing the density of
. We only rely on the data. In the following, we define an objective function
, which describes how well the
is globally suited to describe the conditional correlation.
is then minimized with respect to
, in order to find the optimal
in Equation (
13) to capture the conditional correlation.
CV 1 Since
, a first intuitive approach is to define the objective function by:
CV 2 Assume we observe the series:
and transform them individually with univariate NoVaS to get:
Assuming we used NoVaS with a normal target distribution, due to the properties of the multivariate normal distribution, the best estimator for
given
, is:
Assuming now that we furthermore observe
and therefore the entire series:
we can use the estimates
with
as in Equation (
22) to get to the objective function:
In this context,
T should be chosen large enough, in order to guarantee that the estimate of the conditional correlation in Equation (
13) has enough data to work with. For practical implementation, we use
.
CV 3 To account for the symmetry of the correlation, one can add to the term in Equation (
23) the symmetric term:
with
to get to the objective function:
CV 4 Remaining in the same state of mind as for Method 2 and 3, one might think that
should rather describe the dependency between
and
then between
and
. One could therefore argue, that it would be more sensible to use
as an error. Still, to get to
, one has to go through
, which we get by applying Equation (
22). One can then use the inverse transformation discussed in Equation (
7), namely:
Now, one can once again define the objective error function:
CV 5 With the same motivation as in Method 3, thus to account for the symmetry of the correlation, one could think about using:
CV 6 With the motivation of capturing the correct sign of the correlation, one can define an objective function that gets larger if the sign of the correlation at time point
t is not predicted correctly. More formally, we define the loss function
L:
for
, and with
defined as in Equation (
22). Our objective error function is then:
No matter which of the six methods is used, the goal will in every case be to choose
as in:
Using this estimate in Equation (
13) than yields the captured correlation:
Remark 6. Note however that the captured correlation is first of all the correlation between the series and . We are now interested in the correlation between and . To be more precise, we have an estimate for: What we would like to get is an estimate for With Equation (7), this is in the case of : Since analytic computation of the above term is difficult, it is more sensible to use the iid structure of the
. Assuming a normal target distribution of the NoVaS transformation, we can sample from the multivariate normal distribution of the
with covariance matrix:
We then transform the sampled iid
back to
using the backwards transformation Equation (
25). Doing that, we can for every
t construct an empirical distribution of the
which we then use to compute
using again Equation (
14).
Interestingly, practical application show that the captured correlation barely differs from . This might be due to the fact that at least in the case of a normal target, the distribution of is actually bell shaped albeit with heavy tails. We are still investigating why this empirical finding also holds for a uniform target.
3.3. Going from the Bivariate Paradigm to a Fully Multivariate Setting
All the discussion in
Section 3 has focused on estimating the conditional correlation coefficient of a pair
of studentized returns
and
; the notation
and
was used for the estimator and estimand respectively.
Of course, the realistic challenge is to construct an estimate of the conditional correlation coefficient matrix—denoted —that is associated with a d–dimensional multivariate series, i.e., a vector series that at time t equals .
Our proposal is to construct a matrix estimator whose -th element is given by the aforementioned conditional correlation coefficient of returns and . Hence, for each pair , an optimal estimator of the entry of that involves its own optimal smoothing parameter. For example, suppose that estimating the correlation between series 1 and 2 requires a small whereas for the correlation between series 3 and 4 it would be better to use a large . Using the same smoothing parameter for all the entries of the matrix could be grossly suboptimal.
Our procedure constructs a matrix estimator that is optimized entry-by-entry; the disadvantage is that the estimator will not necessarily be a nonnegative definite matrix. Here, we will adopt the philosophy of Politis [2011], i.e., start with a matrix estimator that is optimized entry-by-entry, and adjust its eigenvalues to make it nonnegative definite.
Although the eigenvalue correction can be performed on the correlation matrix estimator , it is not guaranteed that the result will be a correlation matrix despite being nonnegative definite. Hence, it is more expedient to do the eigenvalue correction on an estimate of the covariance matrix instead, and then turn the corrected covariance matrix estimator into a new correlation matrix estimator.
The complete algorithm is outlined in what follows.
Construct
which is the estimator of the
correlation matrix
. The construction is carried out using entry-by-entry optimized estimators each of which is constructed according to one of the methods described in the previous subsections of
Section 3.
Turn the correlation matrix estimator into a covariance matrix estimator (denoted ) by multiplying each correlation entry by the two respective volatilities, i.e., the square root of local variance estimates. In other words, the entry of consists of the entry of multiplied by the product of the volatility estimate of series i and the volatility estimate of series j.
Calculate the spectral decomposition where T is orthogonal and D diagonal containing the eigenvalues of .
Let denote a version of D where all negative diagonal elements are replaced by zeros (or by a very small positive number—Politis [2011]—if the goal is strict positive definiteness).
Define the new covariance matrix estimator which is by construction nonnegative definite (or even strictly positive definite as mentioned above).
Turn into a new correlation matrix estimator by dividing each entry by the appropriate volatilities. In other words, the entry of consists of the entry of divided by the square root of the product of the and the entry of .
Note that Step 6 of the above algorithm implies that the square root of the entry of is to be treated as a new volatility estimate of series i for the purposes of multivariate modeling. However, this volatility estimate differs little from the standard one obtained from univariate modeling, e.g., the one used in Step 6 of the above algorithm. The reason is that the eigenvalue adjustment towards nonnegative definiteness is just a small-sample correction. The estimators and perform identically in large samples; see Politis [2011] for a discussion in a related context.
4. Using NoVaS in Applications
4.1. Model Selection
The NoVaS methodology offers many different combinations for constructing the volatility measures and performing distributional matching. One can mix squared and absolute returns, uniform and normal marginal target distributions, different matching functions (kurtosis, QQ-correlation and KS-statistic) and different cross validation methods to capture the conditional correlation. In applications one can either proceed by careful examination of the properties of individual series and then use a particular NoVaS combination or we can think of performing some kind of “model selection” by searching across the different combinations and selecting the one that gives us the best results. In the univariate case, the best “results” were defined by the closest distributional match. Details and empirical analysis is given in Politis and Thomakos (2008a,b). In our multivariate setting we are much rather interested in the NoVaS combination that is most suited to capture the correlation.
The choice as to which matching function should be used depends on the target distribution. Even though the kurtosis for instance does make sense when opting for a normal target distribution, it is not the most intuitive choice for a uniform target. Practical experimentation suggests that using the kurtosis as a matching measure works well for the normal target, whereas the QQ-correlation coefficient is more suitable when trying to match a uniform distribution. Another important point that should be made is that we are choosing the same target distribution for both univariate series, as, since we are trying to capture correlation, differently distributed series are undesirable.
The choice as to which combination should be chosen can be made as follows. Consider fixing the type of normalization used (squared or absolute returns) and the target distribution (normal or uniform) and then calculating the correlation between the transformed series with all seven of the described methods in
Section 3.1 and
Section 3.2. Calculate the mean squared error between this captured correlation and the realized correlation. Record the results in a
vector, say
, where
,
returns and
target distribution. Then, repeat the optimizations with respect to all seven methods for all combinations of
. The “optimal” combination is then defined across all possible combinations
as follows:
Since the realized correlation is in general not known in practice, one can alternatively evaluate the quality of the captured correlation between say and by using it to forecast given by . Then the optimal NoVaS transformation is the one that minimizes .
The choice of the truncation parameter
L in Equation (
13) can be based on the chosen length on the individual NoVaS transformations (i.e., on
p from Equation (
2)) or to a multiple of it or it can be selected via the AIC or similar criterion (since there is a likelihood function available).
4.2. Application to Portfolio Analysis
In what follows, we apply the NoVaS transformation to return series for portfolio analysis. We consider the case of a portfolio consisting of two assets, with prices at time t and and continuously compounded returns and . Denote by and the assumed non time varying mean returns. The variances are and and the covariance between the two assets is .
Let us further assume, that the portfolio consists of
units of asset 1 and
units of asset 2. The portfolio return is therefore given by
where we use the linear approximation of the logarithm, because we can expect that returns are going to be small, a setting in which this approximation works well.
is indexed by
, because the choice of the composition of the portfolio has to made before the return in
t is known. We assume that no short sales are allowed, and therefore impose that
for all
t. The portfolio variance is given by
The goal of portfolio analysis in this context is to choose , such that the utility of the investor is maximized.
The utility of the investor is a function of the portfolio return and the portfolio variance. Assuming that the investor is risk-averse with risk aversion parameter
, a general form of the utility function is:
where the last equality is exact if we assume efficient markets.
A rational investor will try to maximize his utility with respect to
:
which simplifies to the minimum variance weight when we assume zero means:
Recall that we need to impose that under the assumption of no short sales. As expected, the optimal hedge ratio depends on the correlation and can therefore be time varying.
5. Simulation Study
In this section we report results from a simulation study. We use two types of simulated data. First, we use a simple bivariate model as a data generating process (DGP), as in [
22], which we call DGP-PS, that allows for consistent realized covariances and correlations to be computed. Next, we assume two univariate GARCH models and specify a deterministic time varying correlation between them.
We start by illustrating the approach discussed in
Section 4.1 and continue with comparing the performance of NoVaS with other standard methods from literature. Finally we conclude by applying NoVaS to portfolio analysis.
5.1. DGP-PS Simulation
Letting
denote the
vector of returns, the DGP-PS is given as follows:
where
is a
matrix with unit diagonals and off-diagonals entries of
. We let
. This is a scalar BEKK-GARCH model of order 1.
We use the model selection approach of the previous section. We compute
of Equation (
30) for all
m and
and repeat the calculations 1000 times. We summarize the mean squared error between the realized correlation
and our estimated conditional correlation
in all 28 combinations in
Table 1.
We use the specified NoVaS transformation, where the kurtosis as in Equation (
9) was used when fitting to a normal target, and the QQ-correlation as in Equation (
11) was used when fitting to a uniform target. Furthermore we set
and used exponential weights.
The NoVaS transformation with normal target and absolute returns, combined with the MLE method to estimate the correlation yields the best result. Using a normal target with squared returns combined with methods CV 2 and CV 4 perform competitively. One can expect that the good performance of the MLE compared to the other methods is due to the Gaussian structure of the data. In this context, and given the nature of the DGP, it would be hard for a non-parametric and “model-free” method to beat a parametric one, especially when using a normal distribution for constructing the model’s innovations. In practice, when the DGP is unknown and the data have much more kurtosis, the results of the NoVaS approach might be different. We explore this in the
Section 6.
We now focus on a different type of simulated data with deterministic and time-varying correlation.
5.2. Multivariate Normal Returns
We now assume that our bivariate return series follows a multivariate normal distribution, where the variances are determined by two volatility processes that follows GARCH dynamics. At the same time we specify a deterministic correlation process between the two return series. More precisely:
where
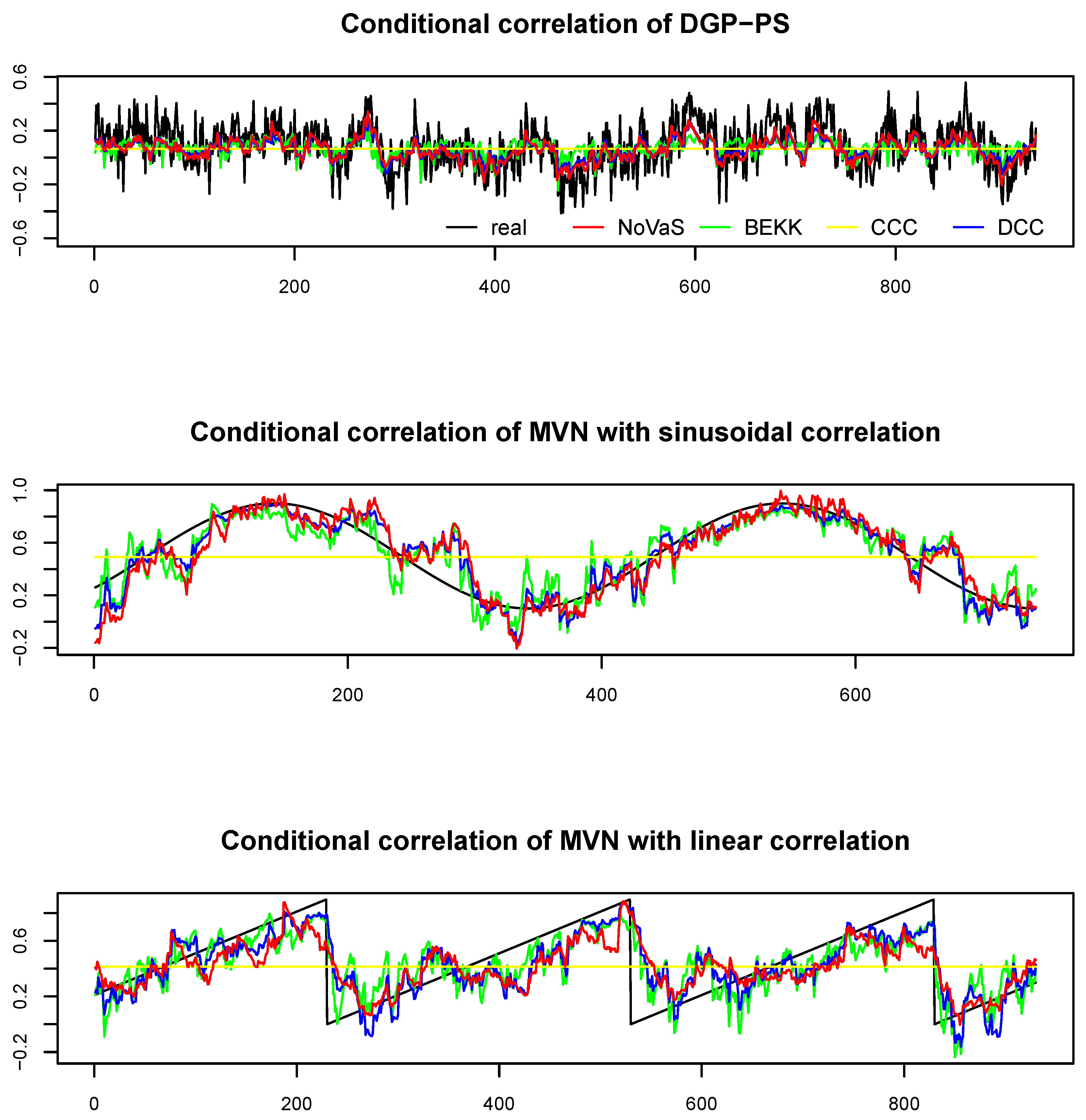
Both examples of , the first implying a sinusoidal correlation, the second a linearly increasing correlation, will be examined.
For both multivariate processes, we again compute the
(as in Equation (
30)). We repeat the computations 1000 times in order to get a robust idea of which method works best.
Table 2 shows the mean squared error between the real deterministic correlation and the estimates using the 28 different NoVaS methods.
As we can see in
Table 2, in the case of a sinusoidal correlation structure, using NoVaS with a uniform target distribution and absolute returns seems to be working best when using the MLE method to capture the correlation, but CV 2 and CV 4 and absolute returns perform competitively. In the case of the linearly increasing correlation, one should again use uniform target either with squared returns and CV 4 or absolute returns and CV2. Interestingly, in this case, using a uniform target distribution clearly outperforms the normal target. We show plots of the resulting estimated correlation in
Figure 1.
5.3. Comparison of NoVaS to Standard Methods and Portfolio Analysis
We now evaluate the performance of NoVaS. To do that we compare the error between the correlation captured by NoVaS to the realized correlation to the error made when capturing the correlation with standard methods from literature. We use baseline methods like a naive approach, where the hedge ratio is defined to be constantly , and a linear model, where the hedge ratio is defined through linear regression. We furthermore compare NoVaS to GARCH based methods like DCC, BEKK and CCC.
In
Table 3, we calculate the mean-squared error between captured correlation and realized correlation of the simulation examples as before. We average over 1000 repetitions of the simulations. NoVaS in
Table 3 corresponds to the method that performed best in capturing the correlation according to
Table 1 and
Table 2 (hence normal target and absolute returns, combined with the MLE method for the DGP-PS data; uniform target with squared returns and the MLE method for sinusoidal correlation; and uniform target with absolute returns and CV 4 for linearly increasing correlation).
Table 3 shows that NoVaS gets outperformed by the classic DCC and BEKK approaches with all three types of simulated data, when considering the MSE between realized and estimated correlation. However, considering the structure of the simulated datasets, NoVaS performs better than expected, especially when considering the correlation between realized and estimated correlation. We expect that NoVaS will perform even better on datasets with heavier tails and less structure.
We now apply NoVaS to portfolio analysis. We use the correlation captured by the different methods above, in order to calculate the optimal hedge ratio defined in Equation (
34). More precisely, the following algorithm is applied:
| Algorithm 1: Computation of portfolio weights and associated returns. |
Assume we observe and for . Fix an window size , for instance . For every , estimate the correlation based on and , , using the methods introduced above. Use Equation ( 34) to derive the optimal portfolio weights, and the portfolio returns.
|
We compute mean, standard deviation and Sharpe ratio of the portfolio returns. The results are shown in
Table 4. The simulations are repeated 100 times, and we show average results.
Table 4 confirms previous results. NoVaS is on structured simulated data not able to outperform known methods based on multivariate GARCH. However, especially when looking at the standard deviation of the returns, NoVaS seems to be on par. In
Figure 1 we show plots of the captured correlation by the different methods of exemplary simulated data.
However, once again, one should not forget that we are dealing with very structured datasets with normal innovation processes. This is something that should be beneficial to parametric GARCH type methods. In the next section, we will observe how NoVaS performs under conditions where the data has heavier tails and the dynamics of the dataset are unknown.
6. Empirical Illustration
In this section we offer a brief empirical illustration of the NoVaS-based correlation estimation using two data sets. First we consider data from the following three series: the S&P500, the 10-year bond (10-year Treasury constant maturity rate series) and the USD/Japanese Yen exchange rate. Then, to assess the performance on smaller samples, we focus on returns of the SPY and the TLT Exchange Traded Funds (ETFs). Daily data are obtained from the beginning of the series and then trimmed and aligned. Daily log-returns are computed and from them we compute monthly returns, realized volatilities and realized correlations. The final data sample is from 01/1971 to 02/2010 for a total of available observations for the first three series, and from 08/2002 to 02/2016 for the second sample for total of .
Figure 2 plots the monthly realized and fitted correlations and
Table 5 and
Table 6 summarizes some descriptive statistics. From
Table 5 and
Table 6 we can see that all the series have excess kurtosis and appear to be non-normally distributed (bootstrapped p-values from the Shapiro–Wilk normality test—not reported—reject the hypothesis of normality). In addition, there is negative skewness for the S&P500, the USD/JPY and the SPY series.
6.1. Capturing the Correlation
After performing univariate NoVaS transformation of the return series individually, we move on to compute the NoVaS-based correlations. We use exponential weights as in Equations (
15) and (
16) with
and
L set to a multiple of the lags used in the individual NoVaS transformations (results are similar when we use
). Applying the model selection approach of
Section 4, we look for the optimal combination of target distribution, squared or absolute returns and the method to capture the correlation. The results are summarized in
Table 7.
When working with the S&P500 and Bonds dataset, the MSE between realized and estimated correlation is minimized when using the MLE Method, together with uniform target and absolute returns. In the other two cases, normal target and squared returns yield better results. The dataset with S&P500 and USD/YEN works best with CV 4, whereas the Bonds and USD/YEN dataset works better with CV 2. In the case of the shorter SPY and TLT index return series, using a normal target distribution and absolute returns, together with the MLE method provides the best result.
We now assess the performance of NoVaS using the same measures as in the simulation study and compare the results with the same methods as before.
Table 8 summarizes the results and
Figure 2 plots the realized correlations along with the fitted values from different benchmark methods.
The table entries show that the NoVaS approach provides better estimates of the conditional correlation than the other models. For all four datasets the mean-squared error when using NoVaS is either better or on par with the other methods, and the correlation between realized and estimated correlation is larger.
Our results are, of course, conditional on the data at hand and the benchmark models. However, we should note that one of the advantages of NoVaS is data-adaptability and parameter parsimony. There are different, more complicated, types of correlation models that include asymmetries, regime switching, factors etc. All these models operate on distributional assumptions, parametric assumptions and are far less parsimonious that the NoVaS approach suggested in this paper. In addition, they are computationally very hard to handle even when the number of series used is small (this is true even for the sequential DCC model of Palandri [2009]). NoVaS-based correlations do not suffer from these potential problems and they can be very competitive in applications.
6.2. Application to Portfolio Analysis
We finally want to give the results of the proposed application in portfolio analysis. As in the previous section with simulated data, we use the captured correlation in order calculate the optimal hedge ratio, as in Equation (
34). We then compare mean, standard deviation and Sharpe ratio of the portfolio returns. We use Algorithm 1, and set
and
.
Table 9 summarizes the results.
The results of
Table 9 show that NoVaS again performs best or on par when comparing to the other methods. In three out of four of our examples, the NoVaS portfolio achieves the highest Sharpe ratio. Only when constructing a portfolio out of Bonds and USD/YEN does the CCC method give a higher Sharpe Ratio, but NoVaS achieves the smallest standard deviation of the returns. In further analysis, not reported here, we compared results based on different choices of the risk aversion coefficient
in Equation (
34), and of
. The performance of NoVaS somehow did not vary.
6.3. Do NoVaS Work Well in Larger Dimensions?
There is but one remaining question that we need to address: is NoVaS the way to go when we increase the dimensionality of a problem? The answer to this question can be a paper of its own so here we provide a short-cut illustrating both the efficacy of the purely multivariate algorithm presented in
Section 3 but also the efficacy in a practical application. To this end we expand our universe of assets to include more than a pair in two sets of experiments: in the first experiment we add just one more asset, to have a representation of equities, fixed income/bonds and cash; in the second experiment we take several assets that comprise the industry components of S&P500. For the first experiment we add SHY as our cash-proxy ETF and for the second experiment we take the 9 ETFs that make industry-groups for the S&P500: XLB, XLE, XLF, XLI, XLK, XLP, XLU, XLV, XLY.
We thus have a 3-dimensional, a 4-dimensional, and a 9-dimensional example of application of the purely multivariate approach. To better understand the way NoVaS operates on these examples we consider two different sample splits for our estimation, one-third and two-thirds of our total available observations. Furthermore, to examine whether the frequency of portfolio rebalancing matters we consider a weekly and a monthly rebalancing. All our results are collected in
Table 10,
Table 11,
Table 12 and
Table 13 that follow.
For the weekly rebalancing we find that across the two sample splits NoVaS has the highest or second highest portfolio return in 7 out of 12 cases examined (63%), but only 4 out of 12 (33%) of the highest or second highest Sharpe ratios. For the monthly rebalancing we find that across the two sample splits NoVaS has the highest or second highest portfolio return in 10 out of 12 cases examined (83%), while it has only 3 out of 12 highest or second highest Sharpe ratios (25%). Although the results presented here are only illustrative, they are suggestive of a further avenue of future research for the application of NoVaS in a purely multivariate setting: (a) clearly the application of NoVaS is a return-generator insofar as portfolio performance is concerned, at the (expected) expense of higher portfolio risk; (b) lower frequency rebalancing improves performance dramatically for returns but leaves Sharpe ratios relatively unchanged; (c) NoVaS is highly competitive in larger dimensions because it involves simpler/less optimization and is robust across sample sizes—a relatively large sample is not a theoretical prerequisite for achieving good estimation performance.
Of course this summary of our multivariate results does not exhaust the problem of NoVaS multivariate applications. It rather leaves open the question as to how further improvements can be made, but as our results show these improvements are necessarily specific to what we are trying to achieve. Further research can show us where multivariate NoVaS fares better, in estimation of correlations or in problems like portfolio allocation.
7. Concluding Remarks
In this paper we extend the univariate NoVaS methodology for volatility modeling and forecasting, put forth by Politis (2003a,b, 2007, 2015) and Politis and Thomakos (2008a, b), to a multivariate context. Using a simple, parsimonious parametrization and smoothing arguments similar to the univariate case, we show how the conditional correlation can be estimated and predicted. A limited simulation study and an empirical application using real data show that the NoVaS approach to correlation modeling can be very competitive, possibly outperform, a popular benchmark as the DCC model. We furthermore evaluate the NoVaS based correlations in the context of portfolio management. An important advantage of the whole NoVaS approach is data-adaptability and lack of distributional or parametric assumptions. This is particularly important in a multivariate context where most of the competitive models are parametric and much more difficult to handle in applications, especially when the number of assets is large.
There are, of course, open issues that we do not address in this paper but are important both in terms of further assessing the NoVaS approach to correlation modeling and in terms of practical usefulness. Some of them are: (a) evaluation of the forecasting performance of NoVaS-based correlations; (b) additional comparisons of NoVaS-based correlations with other benchmark models; (c) a further and more elaborate exploration of how NoVaS can be applied in high-dimension problems, and what the relevant implications may be.