Lp Loss Functions in Invariance Alignment and Haberman Linking with Few or Many Groups
Abstract
:1. Introduction
2. Unidimensional Factor Model with Partial Invariance
2.1. Unidimensional Factor Model
2.1.1. Continuous Items
2.1.2. Dichotomous Items
2.2. Full Invariance, Partial Invariance, and Linking Methods
3. Linking Methods
3.1. Invariance Alignment
3.1.1. A Reformulation as a Two-Step Minimization Problem
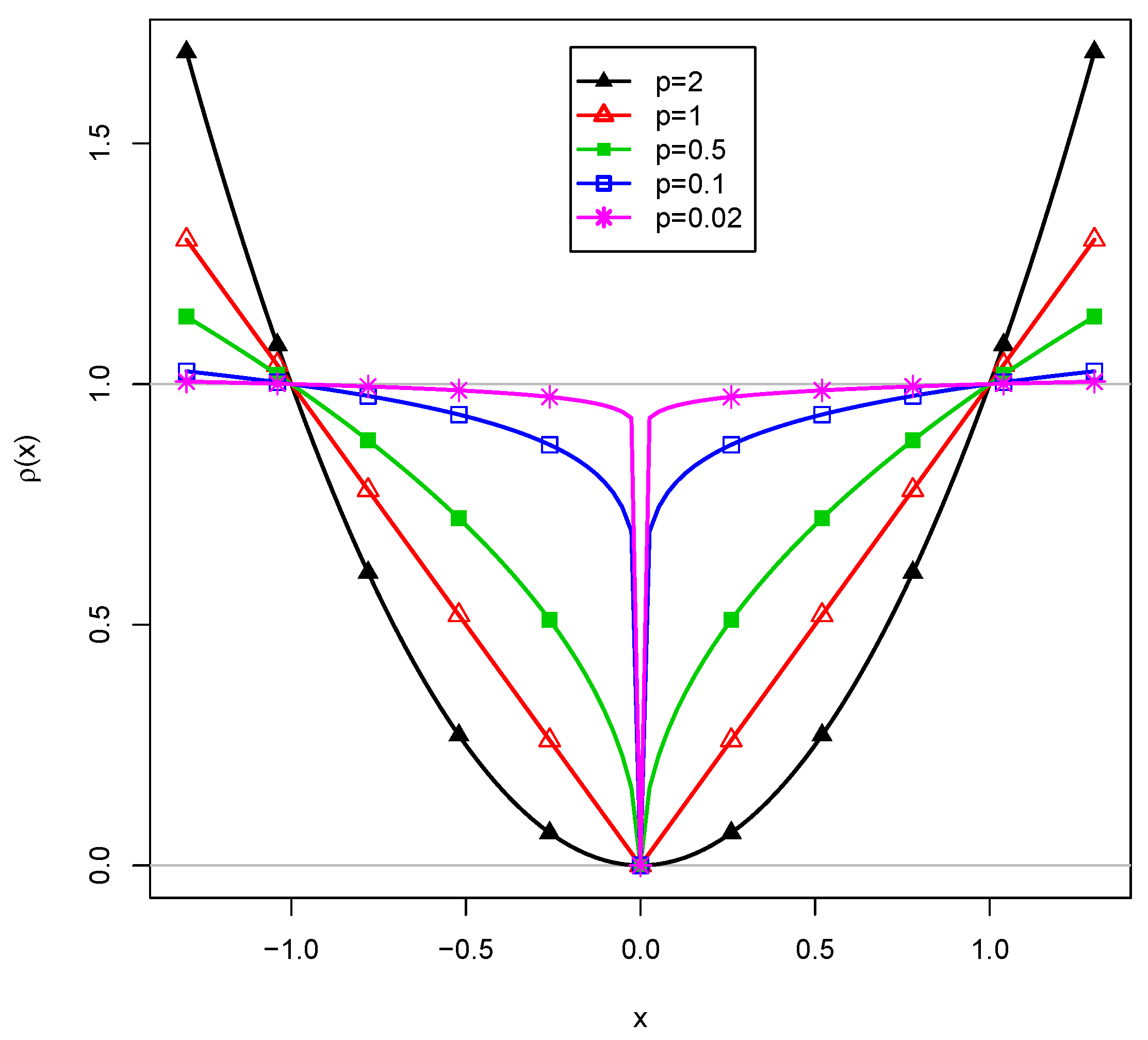
3.1.2. Choice of the Loss Function
3.1.3. Estimation
3.1.4. Previous Simulation Studies and Applications
3.2. Haberman Linking
Estimation and Applications
4. Statistical Properties
4.1. Asymptotic Normality: Standard Errors
4.2. Asymptotic Normality: Linking Errors
4.3. A Simultaneous Assessment of Standard Errors and Linking Errors
4.4. Summary
5. Simulation Studies
5.1. Simulation Study 1: Continuous Items
5.1.1. Simulation Design
5.1.2. Analysis Methods
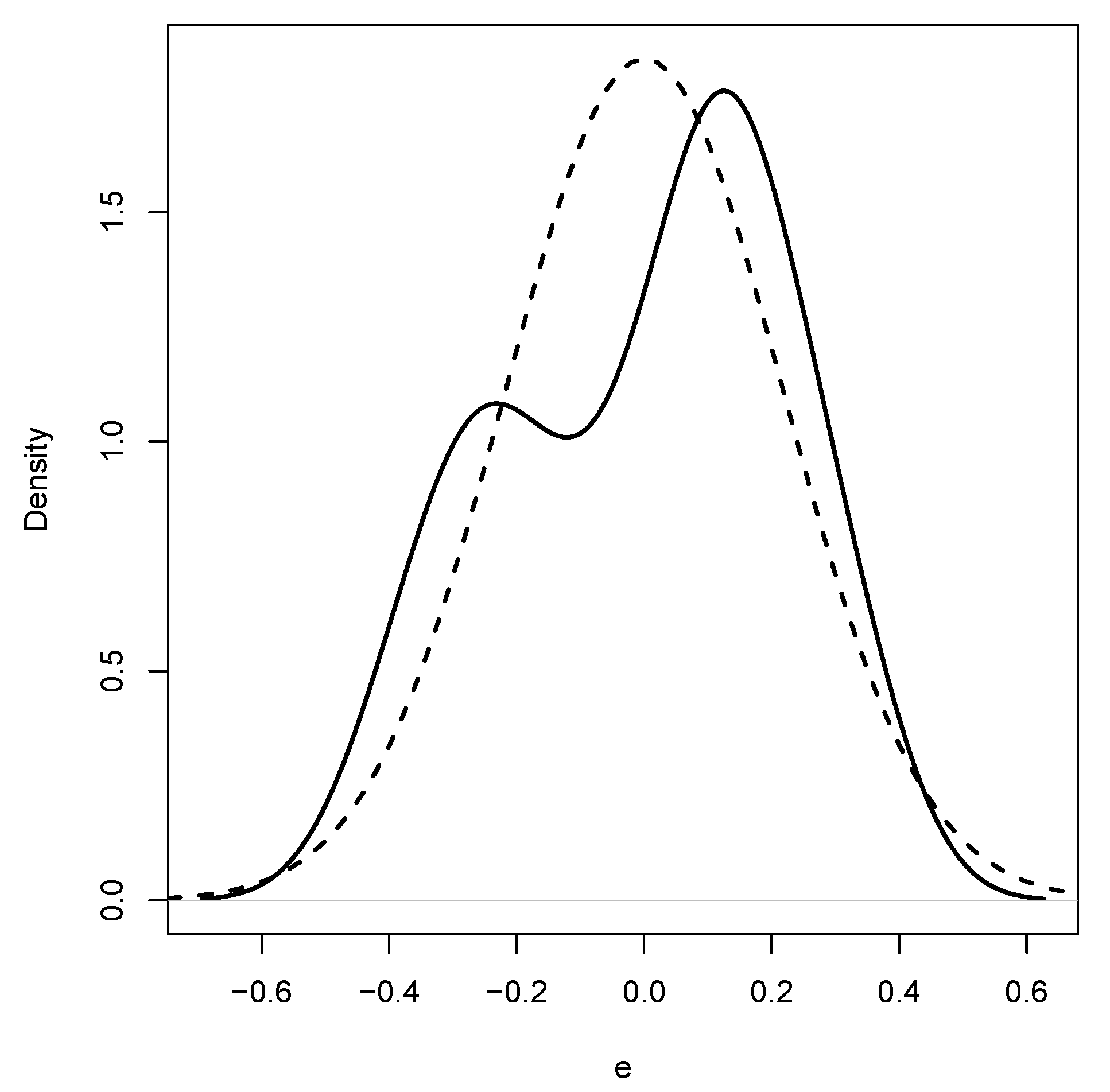
5.1.3. Results
5.1.4. Summary
5.2. Simulation Study 2: Dichotomous Items
5.2.1. Simulation Design
5.2.2. Analysis Methods
5.2.3. Results
5.2.4. Summary
6. Empirical Examples
6.1. 2PL Linking Study: Meyer and Zhou Example
6.1.1. Method
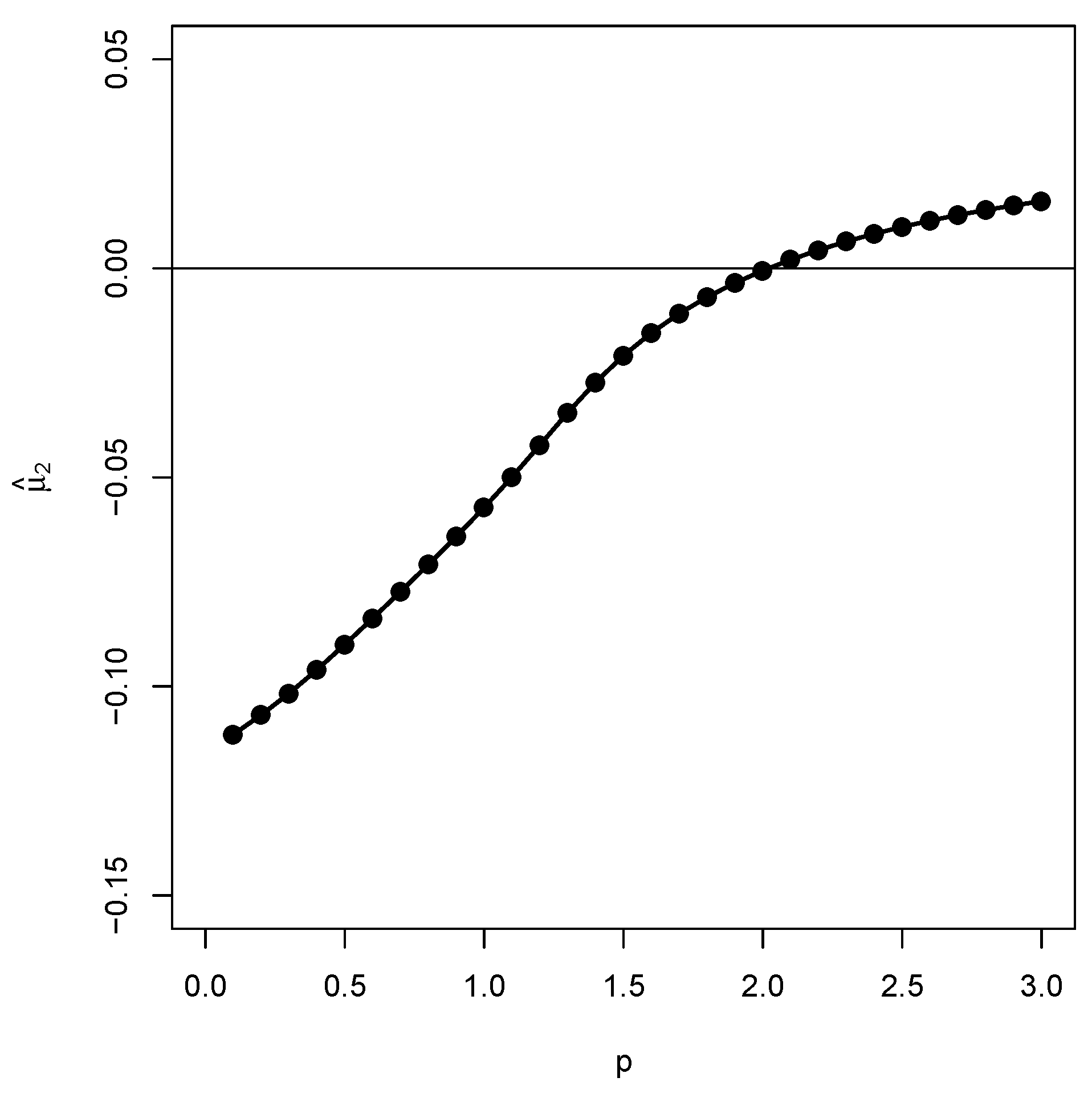
6.1.2. Results
6.2. 1PL Linking Study: Monseur and Berezner Example
6.2.1. Method
6.2.2. Results
6.3. PISA 2006 Reading Study: Country Comparisons
6.3.1. Method
6.3.2. Results
7. Discussion
7.1. Summary and Limitations
7.2. Choice of the Loss Function
7.3. Alternative Approaches to Measurement Noninvariance
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 1PL | one-parameter logistic model |
| 2PL | two-parameter logistic model |
| ABIAS | average absolute bias |
| AN | asymptotic normal distribution |
| ARMSE | average root mean square error |
| DIF | differential item functioning |
| FI | full invariance |
| HL | Haberman linking |
| i.i.d. | independent and identically distributed |
| IA | invariance alignment |
| PISA | programme for international student assessment |
| RMSE | root mean square error |
Appendix A. Additional Results for Simulation Study 1
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
Appendix B. Data Generating Parameters for Simulation Study 2
Appendix C. Additional Results for Simulation Study 2
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
Appendix D. Item Parameters for the 1PL Linking Study
| Item | Testlet | |||
|---|---|---|---|---|
| R055Q01 | R055 | −1.28 | −1.347 | −0.072 |
| R055Q02 | R055 | 0.63 | 0.526 | −0.101 |
| R055Q03 | R055 | 0.27 | 0.097 | −0.175 |
| R055Q05 | R055 | −0.69 | −0.847 | −0.154 |
| R067Q01 | R067 | −2.08 | −1.696 | 0.388 |
| R067Q04 | R067 | 0.25 | 0.546 | 0.292 |
| R067Q05 | R067 | −0.18 | 0.212 | 0.394 |
| R102Q04A | R102 | 1.53 | 1.236 | −0.290 |
| R102Q05 | R102 | 0.87 | 0.935 | 0.067 |
| R102Q07 | R102 | −1.42 | −1.536 | −0.116 |
| R104Q01 | R104 | −1.47 | −1.205 | 0.268 |
| R104Q02 | R104 | 1.44 | 1.135 | −0.306 |
| R104Q05 | R104 | 2.17 | 1.905 | −0.267 |
| R111Q01 | R111 | −0.19 | −0.023 | 0.164 |
| R111Q02B | R111 | 1.54 | 1.395 | −0.147 |
| R111Q06B | R111 | 0.89 | 0.838 | −0.051 |
| R219Q01T | R219 | −0.59 | −0.520 | 0.069 |
| R219Q01E | R219 | 0.10 | 0.308 | 0.210 |
| R219Q02 | R219 | −1.13 | −0.887 | 0.243 |
| R220Q01 | R220 | 0.86 | 0.815 | −0.041 |
| R220Q02B | R220 | −0.14 | −0.114 | 0.027 |
| R220Q04 | R220 | −0.10 | 0.193 | 0.297 |
| R220Q05 | R220 | −1.39 | −1.569 | −0.184 |
| R220Q06 | R220 | −0.34 | −0.142 | 0.196 |
| R227Q01 | R227 | 0.40 | 0.226 | −0.170 |
| R227Q02T | R227 | 0.16 | 0.075 | −0.086 |
| R227Q03 | R227 | 0.46 | 0.325 | −0.132 |
| R227Q06 | R227 | −0.56 | −0.886 | −0.327 |
References
- Mellenbergh, G.J. Item bias and item response theory. Int. J. Educ. Res. 1989, 13, 127–143. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2012. [Google Scholar]
- van de Vijver, F.J.R. (Ed.) Invariance Analyses in Large-Scale Studies; OECD: Paris, France, 2019. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Multiple-group factor analysis alignment. Struct. Equ. Model. 2014, 21, 495–508. [Google Scholar] [CrossRef]
- Haberman, S.J. Linking Parameter Estimates Derived from an Item Response Model through Separate Calibrations; Research Report No. RR-09-40; Educational Testing Service: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- McDonald, R.P. Test Theory: A Unified Treatment; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 1999. [Google Scholar]
- Steyer, R. Models of classical psychometric test theory as stochastic measurement models: Representation, uniqueness, meaningfulness, identifiability, and testability. Methodika 1989, 3, 25–60. [Google Scholar]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- van der Linden, W.J.; Hambleton, R.K. (Eds.) Handbook of Modern Item Response Theory; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Rabe-Hesketh, S.; Skrondal, A.; Pickles, A. Generalized multilevel structural equation modeling. Psychometrika 2004, 69, 167–190. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, The Netherlands, 1960. [Google Scholar]
- Meredith, W. Measurement invariance, factor analysis and factorial invariance. Psychometrika 1993, 58, 525–543. [Google Scholar] [CrossRef]
- Shealy, R.; Stout, W.A. A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 1993, 58, 159–194. [Google Scholar] [CrossRef]
- Byrne, B.M. Adaptation of assessment scales in cross-national research: Issues, guidelines, and caveats. Int. Perspect. Psychol. 2016, 5, 51–65. [Google Scholar] [CrossRef]
- Byrne, B.M.; Shavelson, R.J.; Muthén, B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychol. Bull. 1989, 105, 456–466. [Google Scholar] [CrossRef]
- von Davier, M.; Yamamoto, K.; Shin, H.J.; Chen, H.; Khorramdel, L.; Weeks, J.; Davis, S.; Kong, N.; Kandathil, M. Evaluating item response theory linking and model fit for data from PISA 2000–2012. Assess. Educ. 2019, 26, 466–488. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Dong, Y.; Dumas, D. Are personality measures valid for different populations? A systematic review of measurement invariance across cultures, gender, and age. Pers. Individ. Differ. 2020, 160, 109956. [Google Scholar] [CrossRef]
- Fischer, R.; Karl, J.A. A primer to (cross-cultural) multi-group invariance testing possibilities in R. Front. Psychol. 2019, 10, 1507. [Google Scholar] [CrossRef] [Green Version]
- Han, K.; Colarelli, S.M.; Weed, N.C. Methodological and statistical advances in the consideration of cultural diversity in assessment: A critical review of group classification and measurement invariance testing. Psychol. Assess. 2019, 31, 1481–1496. [Google Scholar] [CrossRef] [PubMed]
- Svetina, D.; Rutkowski, L.; Rutkowski, D. Multiple-group invariance with categorical outcomes using updated guidelines: An illustration using Mplus and the lavaan/semtools packages. Struct. Equ. Model. 2020, 27, 111–130. [Google Scholar] [CrossRef]
- van de Schoot, R.; Schmidt, P.; De Beuckelaer, A.; Lek, K.; Zondervan-Zwijnenburg, M. Editorial: Measurement invariance. Front. Psychol. 2015, 6, 1064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muthén, B.; Asparouhov, T. IRT studies of many groups: The alignment method. Front. Psychol. 2014, 5, 978. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zieger, L.; Sims, S.; Jerrim, J. Comparing teachers’ job satisfaction across countries: A multiple-pairwise measurement invariance approach. Educ. Meas. 2019, 38, 75–85. [Google Scholar] [CrossRef]
- von Davier, M.; von Davier, A.A. A unified approach to IRT scale linking and scale transformations. Methodology 2007, 3, 115–124. [Google Scholar] [CrossRef]
- González, J.; Wiberg, M. Applying Test Equating Methods: Using R; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lee, W.C.; Lee, G. IRT linking and equating. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 639–673. [Google Scholar] [CrossRef]
- Sansivieri, V.; Wiberg, M.; Matteucci, M. A review of test equating methods with a special focus on IRT-based approaches. Statistica 2017, 77, 329–352. [Google Scholar] [CrossRef]
- von Davier, A.A.; Carstensen, C.H.; von Davier, M. Linking competencies in horizontal, vertical, and longitudinal settings and measuring growth. In Assessment of Competencies in Educational Contexts; Hartig, J., Klieme, E., Leutner, D., Eds.; Hogrefe: Göttingen, Germany, 2008; pp. 121–149. [Google Scholar]
- Braeken, J.; Blömeke, S. Comparing future teachers’ beliefs across countries: Approximate measurement invariance with Bayesian elastic constraints for local item dependence and differential item functioning. Assess. Eval. High. Educ. 2016, 41, 733–749. [Google Scholar] [CrossRef]
- Fox, J.P.; Verhagen, A.J. Random item effects modeling for cross-national survey data. In Cross-Cultural Analysis: Methods and Applications; Davidov, E., Schmidt, P., Billiet, J., Eds.; Routledge: London, UK, 2010; pp. 461–482. [Google Scholar] [CrossRef]
- Martin, S.R.; Williams, D.R.; Rast, P. Measurement invariance assessment with Bayesian hierarchical inclusion modeling. PsyArXiv 2019. [Google Scholar] [CrossRef] [Green Version]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Recent methods for the study of measurement invariance with many groups: Alignment and random effects. Sociol. Methods Res. 2018, 47, 637–664. [Google Scholar] [CrossRef]
- van de Schoot, R.; Kluytmans, A.; Tummers, L.; Lugtig, P.; Hox, J.; Muthén, B. Facing off with scylla and charybdis: A comparison of scalar, partial, and the novel possibility of approximate measurement invariance. Front. Psychol. 2013, 4, 770. [Google Scholar] [CrossRef] [Green Version]
- Sideridis, G.D.; Tsaousis, I.; Alamri, A.A. Accounting for differential item functioning using Bayesian approximate measurement invariance. Educ. Psychol. Meas. 2020, 80, 638–664. [Google Scholar] [CrossRef]
- Boer, D.; Hanke, K.; He, J. On detecting systematic measurement error in cross-cultural research: A review and critical reflection on equivalence and invariance tests. J. Cross-Cult. Psychol. 2018, 49, 713–734. [Google Scholar] [CrossRef]
- Davidov, E.; Meuleman, B. Measurement invariance analysis using multiple group confirmatory factor analysis and alignment optimisation. In Invariance Analyses in Large-Scale Studies; van de Vijver, F.J.R., Ed.; OECD: Paris, France, 2019; pp. 13–20. [Google Scholar] [CrossRef]
- Winter, S.D.; Depaoli, S. An illustration of Bayesian approximate measurement invariance with longitudinal data and a small sample size. Int. J. Behav. Dev. 2020, 49, 371–382. [Google Scholar] [CrossRef]
- Avvisati, F.; Le Donné, N.; Paccagnella, M. A meeting report: Cross-cultural comparability of questionnaire measures in large-scale international surveys. Meas. Instrum. Soc. Sci. 2019, 1, 8. [Google Scholar] [CrossRef]
- Cieciuch, J.; Davidov, E.; Schmidt, P. Alignment optimization. Estimation of the most trustworthy means in cross-cultural studies even in the presence of noninvariance. In Cross-Cultural Analysis: Methods and Applications; Davidov, E., Schmidt, P., Billiet, J., Eds.; Routledge: Abingdon, UK, 2018; pp. 571–592. [Google Scholar] [CrossRef]
- Pokropek, A.; Davidov, E.; Schmidt, P. A Monte Carlo simulation study to assess the appropriateness of traditional and newer approaches to test for measurement invariance. Struct. Equ. Model. 2019, 26, 724–744. [Google Scholar] [CrossRef] [Green Version]
- Fox, J. Applied Regression Analysis and Generalized Linear Models; Sage: Thousand Oaks, CA, USA, 2016. [Google Scholar]
- Harvey, A.C. On the unbiasedness of robust regression estimators. Commun. Stat. Theory Methods 1978, 7, 779–783. [Google Scholar] [CrossRef]
- Lipovetsky, S. Optimal Lp-metric for minimizing powered deviations in regression. J. Mod. Appl. Stat. Methods 2007, 6, 20. [Google Scholar] [CrossRef]
- Livadiotis, G. General fitting methods based on Lq norms and their optimization. Stats 2020, 3, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Ramsay, J.O. A comparative study of several robust estimates of slope, intercept, and scale in linear regression. J. Am. Stat. Assoc. 1977, 72, 608–615. [Google Scholar] [CrossRef]
- Sposito, V.A. On unbiased Lp regression estimators. J. Am. Stat. Assoc. 1982, 77, 652–653. [Google Scholar]
- De Boeck, P. Random item IRT models. Psychometrika 2008, 73, 533–559. [Google Scholar] [CrossRef]
- Frederickx, S.; Tuerlinckx, F.; De Boeck, P.; Magis, D. RIM: A random item mixture model to detect differential item functioning. J. Educ. Meas. 2010, 47, 432–457. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z. Evaluating robust scale transformation methods with multiple outlying common items under IRT true score equating. Appl. Psychol. Meas. 2020, 44, 296–310. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z.; Fang, Y.; Chen, H. Using a linear regression method to detect outliers in IRT common item equating. Appl. Psychol. Meas. 2013, 37, 522–540. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z.; Osterlind, S.J. New robust scale transformation methods in the presence of outlying common items. Appl. Psychol. Meas. 2015, 39, 613–626. [Google Scholar] [CrossRef] [PubMed]
- Huynh, H.; Meyer, P. Use of robust z in detecting unstable items in item response theory models. Pract. Assess. Res. Eval. 2010, 15, 2. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. Identification of differential item functioning in multiple-group settings: A multivariate outlier detection approach. Multivar. Behav. Res. 2011, 46, 733–755. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. A robust outlier approach to prevent type I error inflation in differential item functioning. Educ. Psychol. Meas. 2012, 72, 291–311. [Google Scholar] [CrossRef]
- Soares, T.M.; Gonçalves, F.B.; Gamerman, D. An integrated Bayesian model for DIF analysis. J. Educ. Behav. Stat. 2009, 34, 348–377. [Google Scholar] [CrossRef]
- Muthén, L.; Muthén, B. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 1998–2020. [Google Scholar]
- Robitzsch, A. sirt: Supplementary Item Response Theory Models. R Package Version 3.9-4. 2020. Available online: https://CRAN.R-project.org/package=sirt (accessed on 17 February 2020).
- Pennecchi, F.; Callegaro, L. Between the mean and the median: The Lp estimator. Metrologia 2006, 43, 213–219. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria. 2020. Available online: https://www.R-project.org/ (accessed on 1 February 2020).
- Pokropek, A.; Lüdtke, O.; Robitzsch, A. An extension of the invariance alignment method for scale linking. Psych. Test Assess. Model. 2020, 62, 303–334. [Google Scholar]
- Battauz, M. Regularized estimation of the nominal response model. Multivar. Behav. Res. 2019. [Google Scholar] [CrossRef]
- Eddelbuettel, D. Seamless R and C++ Integration with Rcpp; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Eddelbuettel, D.; Balamuta, J.J. Extending R with C++: A brief introduction to Rcpp. Am. Stat. 2018, 72, 28–36. [Google Scholar] [CrossRef]
- Eddelbuettel, D.; François, R. Rcpp: Seamless R and C++ integration. J. Stat. Softw. 2011, 40, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Mansolf, M.; Vreeker, A.; Reise, S.P.; Freimer, N.B.; Glahn, D.C.; Gur, R.E.; Moore, T.M.; Pato, C.N.; Pato, M.T.; Palotie, A.; et al. Extensions of multiple-group item response theory alignment: Application to psychiatric phenotypes in an international genomics consortium. Educ. Psychol. Meas. 2020. [Google Scholar] [CrossRef]
- Kim, E.S.; Cao, C.; Wang, Y.; Nguyen, D.T. Measurement invariance testing with many groups: A comparison of five approaches. Struct. Equ. Model. 2017, 24, 524–544. [Google Scholar] [CrossRef]
- DeMars, C.E. Alignment as an alternative to anchor purification in DIF analyses. Struct. Equ. Model. 2020, 27, 56–72. [Google Scholar] [CrossRef]
- Finch, W.H. Detection of differential item functioning for more than two groups: A Monte Carlo comparison of methods. Appl. Meas. Educ. 2016, 29, 30–45. [Google Scholar] [CrossRef]
- Flake, J.K.; McCoach, D.B. An investigation of the alignment method with polytomous indicators under conditions of partial measurement invariance. Struct. Equ. Model. 2018, 25, 56–70. [Google Scholar] [CrossRef]
- Byrne, B.M.; van de Vijver, F.J.R. The maximum likelihood alignment approach to testing for approximate measurement invariance: A paradigmatic cross-cultural application. Psicothema 2017, 29, 539–551. [Google Scholar] [CrossRef] [PubMed]
- Marsh, H.W.; Guo, J.; Parker, P.D.; Nagengast, B.; Asparouhov, T.; Muthén, B.; Dicke, T. What to do when scalar invariance fails: The extended alignment method for multi-group factor analysis comparison of latent means across many groups. Psychol. Methods 2018, 23, 524–545. [Google Scholar] [CrossRef] [PubMed]
- Muthén, B.; Asparouhov, T. New Methods for the Study of Measurement Invariance with Many Groups. Technical Report. 2013. Available online: https://www.statmodel.com/Alignment.shtml (accessed on 19 May 2020).
- Borgonovi, F.; Pokropek, A. Can we rely on trust in science to beat the COVID-19 pandemic? PsyArXiv 2020. [Google Scholar] [CrossRef]
- Brook, C.A.; Schmidt, L.A. Lifespan trends in sociability: Measurement invariance and mean-level differences in ages 3 to 86 years. Pers. Individ. Differ. 2020, 152, 109579. [Google Scholar] [CrossRef]
- Coromina, L.; Bartolomé Peral, E. Comparing alignment and multiple group CFA for analysing political trust in Europe during the crisis. Methodology 2020, 16, 21–40. [Google Scholar] [CrossRef] [Green Version]
- Davidov, E.; Cieciuch, J.; Meuleman, B.; Schmidt, P.; Algesheimer, R.; Hausherr, M. The comparability of measurements of attitudes toward immigration in the European Social Survey: Exact versus approximate measurement equivalence. Public Opin. Q. 2015, 79, 244–266. [Google Scholar] [CrossRef]
- De Bondt, N.; Van Petegem, P. Psychometric evaluation of the overexcitability questionnaire-two: Applying Bayesian structural equation modeling (BSEM) and multiple-group BSEM-based alignment with approximate measurement invariance. Front. Psychol. 2015, 6, 1963. [Google Scholar] [CrossRef] [Green Version]
- Fischer, J.; Praetorius, A.K.; Klieme, E. The impact of linguistic similarity on cross-cultural comparability of students’ perceptions of teaching quality. Educ. Assess. Eval. Account. 2019, 31, 201–220. [Google Scholar] [CrossRef]
- Goel, A.; Gross, A. Differential item functioning in the cognitive screener used in the longitudinal aging study in India. Int. Psychogeriatr. 2019, 31, 1331–1341. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.; Kim, E.S.; Cao, C.; Allen, T.D.; Cooper, C.L.; Lapierre, L.M.; O’Driscoll, M.P.; Sanchez, J.I.; Spector, P.E.; Poelmans, S.A.Y.; et al. Measurement invariance of the satisfaction with life scale across 26 countries. J. Cross-Cult. Psychol. 2017, 48, 560–576. [Google Scholar] [CrossRef]
- Lek, K.; van de Schoot, R. Bayesian approximate measurement invariance. In Invariance Analyses in Large-Scale Studies; van de Vijver, F.J.R., Ed.; OECD: Paris, France, 2019; pp. 21–35. [Google Scholar] [CrossRef]
- Lomazzi, V. Using alignment optimization to test the measurement invariance of gender role attitudes in 59 countries. Methods Data Anal. 2018, 12, 77–103. [Google Scholar] [CrossRef]
- McLarnon, M.J.W.; Romero, E.F. Cross-cultural equivalence of shortened versions of the Eysenck personality questionnaire: An application of the alignment method. Pers. Individ. Differ. 2020, 163, 110074. [Google Scholar] [CrossRef]
- Milfont, T.L.; Bain, P.G.; Kashima, Y.; Corral-Verdugo, V.; Pasquali, C.; Johansson, L.O.; Guan, Y.; Gouveia, V.V.; Garðarsdóttir, R.B.; Doron, G.; et al. On the relation between social dominance orientation and environmentalism: A 25-nation study. Soc. Psychol. Pers. Sci. 2018, 9, 802–814. [Google Scholar] [CrossRef] [Green Version]
- Munck, I.; Barber, C.; Torney-Purta, J. Measurement invariance in comparing attitudes toward immigrants among youth across Europe in 1999 and 2009: The alignment method applied to IEA CIVED and ICCS. Sociol. Methods Res. 2018, 47, 687–728. [Google Scholar] [CrossRef]
- Rescorla, L.A.; Adams, A.; Ivanova, M.Y. The CBCL/11/2–5’s DSM-ASD scale: Confirmatory factor analyses across 24 societies. J. Autism Dev. Disord. 2019. [Google Scholar] [CrossRef]
- Rice, K.G.; Park, H.J.; Hong, J.; Lee, D.G. Measurement and implications of perfectionism in South Korea and the United States. Couns. Psychol. 2019, 47, 384–416. [Google Scholar] [CrossRef]
- Roberson, N.D.; Zumbo, B.D. Migration background in PISA’s measure of social belonging: Using a diffractive lens to interpret multi-method DIF studies. Int. J. Test. 2019, 19, 363–389. [Google Scholar] [CrossRef]
- Seddig, D.; Leitgöb, H. Approximate measurement invariance and longitudinal confirmatory factor analysis: Concept and application with panel data. Surv. Res. Methods 2018, 12, 29–41. [Google Scholar] [CrossRef]
- Tay, A.K.; Jayasuriya, R.; Jayasuriya, D.; Silove, D. Measurement invariance of the Hopkins symptoms checklist: A novel multigroup alignment analytic approach to a large epidemiological sample across eight conflict-affected districts from a nation-wide survey in Sri Lanka. Confl. Health 2017, 11, 8. [Google Scholar] [CrossRef] [PubMed]
- Wickham, R.E.; Gutierrez, R.; Giordano, B.L.; Rostosky, S.S.; Riggle, E.D.B. Gender and generational differences in the internalized homophobia questionnaire: An alignment IRT analysis. Assessment 2019. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.L. Data Analysis and Approximate Models; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. A review of different scaling approaches under full invariance, partial invariance, and noninvariance for cross-sectional country comparisons in large-scale assessments. Psych. Test Assess. Model. 2020, 62, 233–279. [Google Scholar]
- van der Linden, W.J. Fundamental measurement. In Objective Measurement: Theory into Practice; Wilson, M., Ed.; Ablex Publishing Corporation: Hillsdale, NJ, USA, 1994; Volume 2, pp. 3–24. [Google Scholar]
- Griffin, M.; Hoff, P.D. Lasso ANOVA decompositions for matrix and tensor data. Comp. Stat. Data An. 2019, 137, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Battauz, M. equateMultiple: Equating of Multiple Forms. R Package Version 0.0.0. 2017. Available online: https://CRAN.R-project.org/package=equateMultiple (accessed on 2 November 2017).
- Yao, L.; Haberman, S.J.; Xu, J. Using SAS to Implement Simultaneous Linking in Item Response Theory. SAS Global Forum 2016, Proceedings 2015. Available online: http://support.sas.com/resources/papers/proceedings16/statistician-papers.html (accessed on 19 May 2020).
- Battauz, M. Multiple equating of separate IRT calibrations. Psychometrika 2017, 82, 610–636. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. Mean comparisons of many groups in the presence of DIF: An evaluation of linking and concurrent scaling approaches. OSF Prepr. 2020. [Google Scholar] [CrossRef]
- Becker, B.; Weirich, S.; Mahler, N.; Sachse, K.A. Testdesign und Auswertung des IQB-Bildungstrends 2018: Technische Grundlagen [Test design and analysis of the IQB education trend 2018: Technical foundations]. In IQB-Bildungstrend 2018. Mathematische und Naturwissenschaftliche Kompetenzen am Ende der Sekundarstufe I im Zweiten Ländervergleich; Stanat, P., Schipolowski, S., Mahler, N., Weirich, S., Henschel, S., Eds.; Waxmann: Münster, Germany, 2019; pp. 411–425. [Google Scholar]
- Höft, L.; Bernholt, S. Longitudinal couplings between interest and conceptual understanding in secondary school chemistry: An activity-based perspective. Int. J. Sci. Educ. 2019, 41, 607–627. [Google Scholar] [CrossRef]
- Moehring, A.; Schroeders, U.; Wilhelm, O. Knowledge is power for medical assistants: Crystallized and fluid intelligence as predictors of vocational knowledge. Front. Psychol. 2018, 9, 28. [Google Scholar] [CrossRef]
- Petrakova, A.; Sommer, W.; Junge, M.; Hildebrandt, A. Configural face perception in childhood and adolescence: An individual differences approach. Acta Psychol. 2018, 188, 148–176. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O.; Goldhammer, F.; Kroehne, U.; Köller, O. Reanalysis of the German PISA data: A comparison of different approaches for trend estimation with a particular emphasis on mode effects. Front. Psychol. 2020, 11, 884. [Google Scholar] [CrossRef]
- Rösselet, S.; Neuenschwander, M.P. Akzeptanz und Ablehnung beim Übertritt in die Sekundarstufe I [Acceptance and rejection on tracking to lower secondary education]. In Bildungsverläufe von der Einschulung bis in den Ersten Arbeitsmarkt; Neuenschwander, M.P., Nägele, C., Eds.; Springer: Wiesbaden, Germany, 2017; pp. 103–121. [Google Scholar] [CrossRef] [Green Version]
- Sewasew, D.; Schroeders, U.; Schiefer, I.M.; Weirich, S.; Artelt, C. Development of sex differences in math achievement, self-concept, and interest from grade 5 to 7. Contemp. Educ. Psychol. 2018, 54, 55–65. [Google Scholar] [CrossRef]
- Trendtel, M.; Pham, H.G.; Yanagida, T. Skalierung und Linking [Scaling and linking]. In Large-Scale Assessment mit R: Methodische Grundlagen der österreichischen Bildungsstandards-Überprüfung; Breit, S., Schreiner, C., Eds.; Facultas: Wien, Austria, 2016; pp. 185–224. [Google Scholar]
- Arai, S.; Mayekawa, S.i. A comparison of equating methods and linking designs for developing an item pool under item response theory. Behaviormetrika 2011, 38, 1–16. [Google Scholar] [CrossRef]
- Kang, H.A.; Lu, Y.; Chang, H.H. IRT item parameter scaling for developing new item pools. Appl. Meas. Educ. 2017, 30, 1–15. [Google Scholar] [CrossRef]
- Weeks, J.P. Plink: An R package for linking mixed-format tests using IRT-based methods. J. Stat. Softw. 2010, 35, 1–33. [Google Scholar] [CrossRef]
- Haebara, T. Equating logistic ability scales by a weighted least squares method. Jpn. Psychol. Res. 1980, 22, 144–149. [Google Scholar] [CrossRef] [Green Version]
- Robitzsch, A. Robust Haebara linking for many groups in the case of partial invariance. Preprints 2020, 2020060035. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Stefanski, L.A.; Boos, D.D. The calculus of M-estimation. Am. Stat. 2002, 56, 29–38. [Google Scholar] [CrossRef]
- Benichou, J.; Gail, M.H. A delta method for implicitly defined random variables. Am. Stat. 1989, 43, 41–44. [Google Scholar]
- Andersson, B. Asymptotic variance of linking coefficient estimators for polytomous IRT models. Appl. Psychol. Meas. 2018, 42, 192–205. [Google Scholar] [CrossRef]
- Battauz, M. Factors affecting the variability of IRT equating coefficients. Stat. Neerl. 2015, 69, 85–101. [Google Scholar] [CrossRef]
- Ogasawara, H. Standard errors of item response theory equating/linking by response function methods. Appl. Psychol. Meas. 2001, 25, 53–67. [Google Scholar] [CrossRef]
- Gebhardt, E.; Adams, R.J. The influence of equating methodology on reported trends in PISA. J. Appl. Meas. 2007, 8, 305–322. [Google Scholar]
- Michaelides, M.P. A review of the effects on IRT item parameter estimates with a focus on misbehaving common items in test equating. Front. Psychol. 2010, 1, 167. [Google Scholar] [CrossRef] [Green Version]
- Monseur, C.; Berezner, A. The computation of equating errors in international surveys in education. J. Appl. Meas. 2007, 8, 323–335. [Google Scholar]
- Monseur, C.; Sibberns, H.; Hastedt, D. Linking errors in trend estimation for international surveys in education. IERI Monogr. Ser. 2008, 1, 113–122. [Google Scholar]
- Robitzsch, A.; Lüdtke, O. Linking errors in international large-scale assessments: Calculation of standard errors for trend estimation. Assess. Educ. 2019, 26, 444–465. [Google Scholar] [CrossRef]
- Sachse, K.A.; Roppelt, A.; Haag, N. A comparison of linking methods for estimating national trends in international comparative large-scale assessments in the presence of cross-national DIF. J. Educ. Meas. 2016, 53, 152–171. [Google Scholar] [CrossRef]
- Wu, M. Measurement, sampling, and equating errors in large-scale assessments. Educ. Meas. 2010, 29, 15–27. [Google Scholar] [CrossRef]
- Xu, X.; von Davier, M. Linking Errors in Trend Estimation in Large-Scale Surveys: A Case Study; Research Report No. RR-10-10; Educational Testing Service: Princeton, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Brennan, R.L. Generalizability theory. Educ. Meas. 1992, 11, 27–34. [Google Scholar] [CrossRef]
- Brennan, R.L. Generalizabilty Theory; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Rajaratnam, N.; Gleser, G.C. Theory of generalizability: A liberalization of reliability theory. Brit. J. Stat. Psychol. 1963, 16, 137–163. [Google Scholar] [CrossRef]
- Lancaster, T. The incidental parameter problem since 1948. J. Econom. 2000, 95, 391–413. [Google Scholar] [CrossRef]
- Richardson, A.M.; Welsh, A.H. Robust restricted maximum likelihood in mixed linear models. Biometrics 1995, 51, 1429–1439. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, W. Robust estimation in generalised linear mixed models. Biometrika 2001, 88, 753–765. [Google Scholar] [CrossRef]
- Koller, M. robustlmm: An R package for robust estimation of linear mixed-effects models. J. Stat. Softw. 2016, 75, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Yau, K.K.W.; Kuk, A.Y.C. Robust estimation in generalized linear mixed models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 101–117. [Google Scholar] [CrossRef]
- Hunter, J.E. Probabilistic foundations for coefficients of generalizability. Psychometrika 1968, 33, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Haberman, S.J.; Lee, Y.H.; Qian, J. Jackknifing Techniques for Evaluation of Equating Accuracy; Research Report No. RR-09-02; Educational Testing Service: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Lu, R.; Haberman, S.; Guo, H.; Liu, J. Use of Jackknifing to Evaluate Effects of Anchor Item Selection on Equating with the Nonequivalent Groups with Anchor Test (NEAT) Design; Research Report No. RR-15-10; Educational Testing Service: Princeton, NJ, USA, 2015. [Google Scholar] [CrossRef] [Green Version]
- Michaelides, M.P.; Haertel, E.H. Selection of common items as an unrecognized source of variability in test equating: A bootstrap approximation assuming random sampling of common items. Appl. Meas. Educ. 2014, 27, 46–57. [Google Scholar] [CrossRef]
- Robitzsch, A.; Kiefer, T.; Wu, M. TAM: Test Analysis Modules. R Package Version 3.4-26. 2020. Available online: https://CRAN.R-project.org/package=TAM (accessed on 10 March 2020).
- Meyer, J.P.; Zhu, S. Fair and equitable measurement of student learning in MOOCs: An introduction to item response theory, scale linking, and score equating. Res. Pract. Assess. 2013, 8, 26–39. [Google Scholar]
- OECD. PISA 2006. Technical Report; OECD: Paris, France, 2009. [Google Scholar]
- Oliveri, M.E.; von Davier, M. Analyzing invariance of item parameters used to estimate trends in international large-scale assessments. In Test Fairness in the New Generation of Large-Scale Assessment; Jiao, H., Lissitz, R.W., Eds.; Information Age Publishing: New York, NY, USA, 2017; pp. 121–146. [Google Scholar]
- Glas, C.A.W.; Jehangir, M. Modeling country-specific differential functioning. In A Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; Chapman Hall/CRC Press: London, UK, 2014; pp. 97–115. [Google Scholar] [CrossRef]
- Hennig, C.; Kutlukaya, M. Some thoughts about the design of loss functions. Revstat Stat. J. 2007, 5, 19–39. [Google Scholar]
- Mineo, A.M. On the estimation of the structure parameter of a normal distribution of order p. Statistica 2003, 63, 109–122. [Google Scholar] [CrossRef]
- Mineo, A.M.; Ruggieri, M. A software tool for the exponential power distribution: The normalp package. J. Stat. Softw. 2005, 12, 1–24. [Google Scholar] [CrossRef]
- Giacalone, M.; Panarello, D.; Mattera, R. Multicollinearity in regression: An efficiency comparison between Lp-norm and least squares estimators. Qual. Quant. 2018, 52, 1831–1859. [Google Scholar] [CrossRef] [Green Version]
- Griffin, M.; Hoff, P.D. Testing sparsity-inducing penalties. J. Comput. Graph. Stat. 2020, 29, 128–139. [Google Scholar] [CrossRef] [Green Version]
- van de Vijver, F.J.R. Capturing bias in structural equation modeling. In Cross-Cultural Analysis: Methods and Applications; Davidov, E., Schmidt, P., Billiet, J., Eds.; Routledge: London, UK, 2018; pp. 3–43. [Google Scholar] [CrossRef] [Green Version]
- Kankaraš, M.; Moors, G. Analysis of cross-cultural comparability of PISA 2009 scores. J. Cross-Cult. Psychol. 2014, 45, 381–399. [Google Scholar] [CrossRef] [Green Version]
- Oberski, D.L. Evaluating sensitivity of parameters of interest to measurement invariance in latent variable models. Polit. Anal. 2014, 22, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Oberski, D.J. Sensitivity analysis. In Cross-Cultural Analysis: Methods and Applications; Davidov, E., Schmidt, P., Billiet, J., Eds.; Routledge: Abingdon, UK, 2018; pp. 593–614. [Google Scholar] [CrossRef]
- Buchholz, J.; Hartig, J. Comparing attitudes across groups: An IRT-based item-fit statistic for the analysis of measurement invariance. Appl. Psychol. Meas. 2019, 43, 241–250. [Google Scholar] [CrossRef]
- Tijmstra, J.; Bolsinova, M.; Liaw, Y.L.; Rutkowski, L.; Rutkowski, D. Sensitivity of the RMSD for detecting item-level misfit in low-performing countries. J. Educ. Meas. 2019. [Google Scholar] [CrossRef]
- Buchholz, J.; Hartig, J. Measurement invariance testing in questionnaires: A comparison of three Multigroup-CFA and IRT-based approaches. Psych. Test Assess. Model. 2020, 62, 29–53. [Google Scholar]
- Nye, C.D.; Drasgow, F. Effect size indices for analyses of measurement equivalence: Understanding the practical importance of differences between groups. J. Appl. Psychol. 2011, 96, 966–980. [Google Scholar] [CrossRef]
- Gunn, H.J.; Grimm, K.J.; Edwards, M.C. Evaluation of six effect size measures of measurement non-invariance for continuous outcomes. Struct. Equ. Model. 2020, 27, 503–514. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Belzak, W.; Bauer, D.J. Improving the assessment of measurement invariance: Using regularization to select anchor items and identify differential item functioning. Psychol. Methods 2020. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.H. A penalized likelihood method for multi-group structural equation modelling. Br. J. Math. Stat. Psychol. 2018, 71, 499–522. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Jacobucci, R. Regularized structural equation modeling to detect measurement bias: Evaluation of lasso, adaptive lasso, and elastic net. Struct. Equ. Model. 2019. [Google Scholar] [CrossRef]
- Schauberger, G.; Mair, P. A regularization approach for the detection of differential item functioning in generalized partial credit models. Behav. Res. Methods 2020, 52, 279–294. [Google Scholar] [CrossRef]
- Tutz, G.; Schauberger, G. A penalty approach to differential item functioning in Rasch models. Psychometrika 2015, 80, 21–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.; Chang, X.; Xu, F.; Zhang, H. L1/2 regularization: A thresholding representation theory and a fast solver. IEEE T. Neur. Net. Lear. 2012, 23, 1013–1027. [Google Scholar] [CrossRef]
- Hu, Y.; Li, C.; Meng, K.; Qin, J.; Yang, X. Group sparse optimization via lp,q regularization. J. Mach. Learn. Res. 2017, 18, 960–1011. [Google Scholar]
- Wang, B.; Wan, W.; Wang, Y.; Ma, W.; Zhang, L.; Li, J.; Zhou, Z.; Zhao, H.; Gao, F. An Lp(0≤p≤1)-norm regularized image reconstruction scheme for breast DOT with non-negative-constraint. Biomed. Eng. Online 2017, 16, 32. [Google Scholar] [CrossRef] [Green Version]
- Bechger, T.M.; Maris, G. A statistical test for differential item pair functioning. Psychometrika 2015, 80, 317–340. [Google Scholar] [CrossRef]
- Doebler, A. Looking at DIF from a new perspective: A structure-based approach acknowledging inherent indefinability. Appl. Psychol. Meas. 2019, 43, 303–321. [Google Scholar] [CrossRef]
- Pohl, S.; Schulze, D. Assessing group comparisons or change over time under measurement non-invariance: The cluster approach for nonuniform DIF. Psych. Test Assess. Model. 2020, 62, 281–303. [Google Scholar]
- Schulze, D.; Pohl, S. Finding clusters of measurement invariant items for continuous covariates. Struct. Equ. Model. 2020. [Google Scholar] [CrossRef]
- He, J.; Barrera-Pedemonte, F.; Buchholz, J. Cross-cultural comparability of noncognitive constructs in TIMSS and PISA. Assess. Educ. 2019, 26, 369–385. [Google Scholar] [CrossRef] [Green Version]
- Khorramdel, L.; Pokropek, A.; Joo, S.H.; Kirsch, I.; Halderman, L. Examining gender DIF and gender differences in the PISA 2018 reading literacy scale: A partial invariance approach. Psych. Test Assess. Model. 2020, 62, 179–231. [Google Scholar]
- Lee, S.S.; von Davier, M. Improving measurement properties of the PISA home possessions scale through partial invariance modeling. Psych. Test Assess. Model. 2020, 62, 55–83. [Google Scholar]
- Oliveri, M.E.; von Davier, M. Investigation of model fit and score scale comparability in international assessments. Psych. Test Assess. Model. 2011, 53, 315–333. [Google Scholar]
- Goldstein, H. PISA and the globalisation of education: A critical commentary on papers published in AIE special issue 4/2019. Assess. Educ. 2019, 26, 665–674. [Google Scholar] [CrossRef]
- MacCallum, R.C.; Browne, M.W.; Cai, L. Factor analysis models as approximations. In Factor Analysis at 100; Cudeck, R., MacCallum, R.C., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA; pp. 153–175.
- Camilli, G. The case against item bias detection techniques based on internal criteria: Do item bias procedures obscure test fairness issues. In Differential Item Functioning: Theory and Practice; Holland, P.W., Wainer, H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993; pp. 397–417. [Google Scholar]
- El Masri, Y.H.; Andrich, D. The trade-off between model fit, invariance, and validity: The case of PISA science assessments. Appl. Meas. Educ. 2020, 33, 174–188. [Google Scholar] [CrossRef]
- Huang, X.; Wilson, M.; Wang, L. Exploring plausible causes of differential item functioning in the PISA science assessment: Language, curriculum or culture. Educ. Psychol. 2016, 36, 378–390. [Google Scholar] [CrossRef]
- Kuha, J.; Moustaki, I. Nonequivalence of measurement in latent variable modeling of multigroup data: A sensitivity analysis. Psychol. Methods 2015, 20, 523–536. [Google Scholar] [CrossRef] [Green Version]
- Taherbhai, H.; Seo, D. The philosophical aspects of IRT equating: Modeling drift to evaluate cohort growth in large-scale assessments. Educ. Meas. 2013, 32, 2–14. [Google Scholar] [CrossRef]
- Zwitser, R.J.; Glaser, S.S.F.; Maris, G. Monitoring countries in a changing world: A new look at DIF in international surveys. Psychometrika 2017, 82, 210–232. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A. Lp loss functions in invariance alignment and Haberman linking. Preprints 2020, 2020060034. [Google Scholar] [CrossRef]
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| Item | FormX | Form Y | ||
|---|---|---|---|---|
| 1 | ||||
| 5 | ||||
| 9 | ||||
| 13 | ||||
| 17 | ||||
| 21 | ||||
| 25 | ||||
| 29 | ||||
| p | IA1 | IA2 | IA3 | IA4 | HL1 | HL2 | HL3 | HL4 |
|---|---|---|---|---|---|---|---|---|
| 0.02 | ||||||||
| 0.1 | ||||||||
| 0.25 | ||||||||
| 0.5 | ||||||||
| 1 | ||||||||
| 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1: FI | — | 1.6 | 3.0 | 3.9 | 5.5 | 1.5 | 4.1 | 6.6 | 7.5 |
| 2: IA | 1.6 | — | 2.1 | 2.9 | 4.6 | 0.1 | 3.4 | 6.2 | 7.0 |
| 3: IA | 3.0 | 2.1 | — | 1.0 | 2.8 | 2.0 | 2.1 | 4.6 | 5.4 |
| 4: IA | 3.9 | 2.9 | 1.0 | — | 2.0 | 2.9 | 2.2 | 3.9 | 4.7 |
| 5: IA | 5.5 | 4.6 | 2.8 | 2.0 | — | 4.6 | 3.1 | 4.3 | 4.9 |
| 6: HL | 1.5 | 0.1 | 2.0 | 2.9 | 4.6 | — | 3.4 | 6.2 | 7.0 |
| 7: HL | 4.1 | 3.4 | 2.1 | 2.2 | 3.1 | 3.4 | — | 3.9 | 5.0 |
| 8: HL | 6.6 | 6.2 | 4.6 | 3.9 | 4.3 | 6.2 | 3.9 | — | 1.5 |
| 9: HL | 7.5 | 7.0 | 5.4 | 4.7 | 4.9 | 7.0 | 5.0 | 1.5 | — |
| Country | rg | FI | IA with Power p | HL with Power p | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.5 | 0.02 | 2 | 1 | 0.5 | 0.02 | ||||
| AUS | 7562 | ||||||||||
| AUT | 2646 | ||||||||||
| BEL | 4840 | ||||||||||
| CAN | |||||||||||
| CHE | 6578 | ||||||||||
| CZE | 3246 | ||||||||||
| DEU | 2701 | ||||||||||
| DNK | 2431 | ||||||||||
| ESP | |||||||||||
| EST | 2630 | ||||||||||
| FIN | 2536 | ||||||||||
| FRA | 2524 | ||||||||||
| GBR | 7061 | ||||||||||
| GRC | 2606 | ||||||||||
| HUN | 2399 | ||||||||||
| IRL | 2468 | ||||||||||
| ISL | 2010 | ||||||||||
| ITA | |||||||||||
| JPN | 3203 | ||||||||||
| KOR | 2790 | ||||||||||
| LUX | 2443 | ||||||||||
| NLD | 2666 | ||||||||||
| NOR | 2504 | ||||||||||
| POL | 2968 | ||||||||||
| PRT | 2773 | ||||||||||
| SWE | 2374 | ||||||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. Lp Loss Functions in Invariance Alignment and Haberman Linking with Few or Many Groups. Stats 2020, 3, 246-283. https://doi.org/10.3390/stats3030019
Robitzsch A. Lp Loss Functions in Invariance Alignment and Haberman Linking with Few or Many Groups. Stats. 2020; 3(3):246-283. https://doi.org/10.3390/stats3030019
Chicago/Turabian StyleRobitzsch, Alexander. 2020. "Lp Loss Functions in Invariance Alignment and Haberman Linking with Few or Many Groups" Stats 3, no. 3: 246-283. https://doi.org/10.3390/stats3030019
APA StyleRobitzsch, A. (2020). Lp Loss Functions in Invariance Alignment and Haberman Linking with Few or Many Groups. Stats, 3(3), 246-283. https://doi.org/10.3390/stats3030019





