Figure 1.
This graph plots first log seasonal differences of Industrial Production Index of Intermediate Goods, Capital Goods and Destatis Truck Toll Mileage Index from 2006:01 to 2018:12.
Figure 1.
This graph plots first log seasonal differences of Industrial Production Index of Intermediate Goods, Capital Goods and Destatis Truck Toll Mileage Index from 2006:01 to 2018:12.
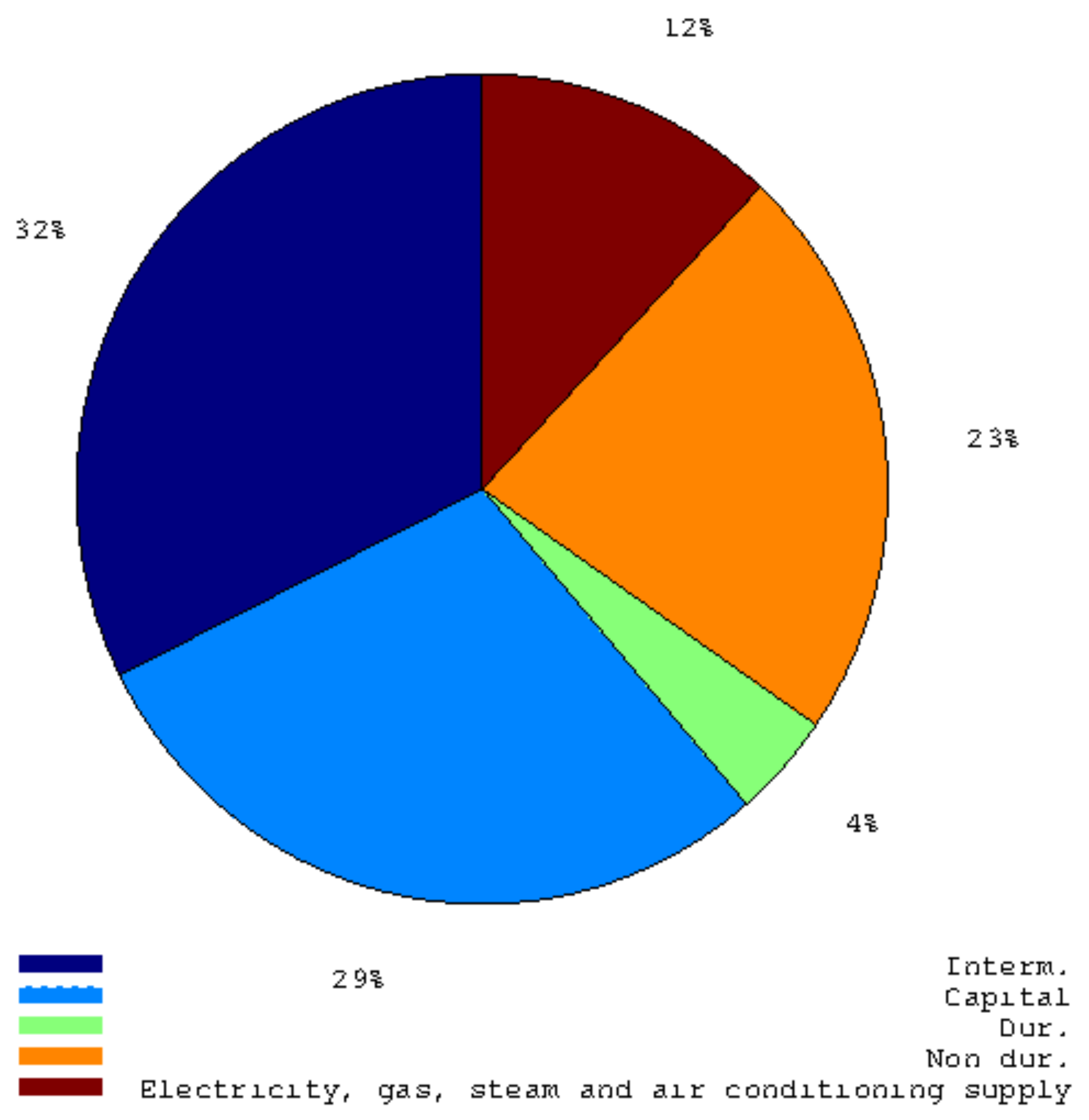
Figure 2.
This pie graph shows the weights of main industry groupings in the Italian Industrial Production Index.
Figure 2.
This pie graph shows the weights of main industry groupings in the Italian Industrial Production Index.
Figure 3.
This pie graph shows the weights of every sub-component concerning the Italian Industrial Production Index of Electricity, gas, steam and air conditioning supply.
Figure 3.
This pie graph shows the weights of every sub-component concerning the Italian Industrial Production Index of Electricity, gas, steam and air conditioning supply.
Figure 5.
Concatenate Seemingly Unrelated Time Series Equations with star system.
Figure 5.
Concatenate Seemingly Unrelated Time Series Equations with star system.
Figure 6.
Graph showing the p-values of the Durbin–Watson test for the VARMA model using the hard data only. The null hypothesis states that residuals are not autocorrelated.
Figure 6.
Graph showing the p-values of the Durbin–Watson test for the VARMA model using the hard data only. The null hypothesis states that residuals are not autocorrelated.
Figure 7.
Graph showing the p-values of the Harvey heteroskedasticity test for the VARMA model using the hard data only. The null hypothesis states that the residuals are not heteroskedastic.
Figure 7.
Graph showing the p-values of the Harvey heteroskedasticity test for the VARMA model using the hard data only. The null hypothesis states that the residuals are not heteroskedastic.
Figure 8.
Graph showing the p-values of the Bowman–Shenton test for the VARMA model using the hard data only. The null hypothesis states that errors are normally distributed.
Figure 8.
Graph showing the p-values of the Bowman–Shenton test for the VARMA model using the hard data only. The null hypothesis states that errors are normally distributed.
Figure 9.
Graph showing the p-values of the Durbin–Watson test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 9.
Graph showing the p-values of the Durbin–Watson test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 10.
Graph showing the p-values of the Bowman–Shenton test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that errors are normally distributed.
Figure 10.
Graph showing the p-values of the Bowman–Shenton test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that errors are normally distributed.
Figure 11.
Graph showing the p-values of the Harvey heteroskedasticity test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 11.
Graph showing the p-values of the Harvey heteroskedasticity test for the VARMA model using both hard and soft data for non-durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 12.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for intermediate goods. A negative value means that BB model prevails.
Figure 12.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for intermediate goods. A negative value means that BB model prevails.
Figure 13.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for intermediate goods. The null hypothesis states that errors are normally distributed.
Figure 13.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for intermediate goods. The null hypothesis states that errors are normally distributed.
Figure 14.
Graph showing the p-values of the Durbin–Watson test for the enhanced model for intermediate goods. The null hypothesis states that residuals are not autocorrelated.
Figure 14.
Graph showing the p-values of the Durbin–Watson test for the enhanced model for intermediate goods. The null hypothesis states that residuals are not autocorrelated.
Figure 15.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for intermediate goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 15.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for intermediate goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 16.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for capital goods.
Figure 16.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for capital goods.
Figure 17.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for capital goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 17.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for capital goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 18.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for capital goods. The null hypothesis states that errors are normally distributed.
Figure 18.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for capital goods. The null hypothesis states that errors are normally distributed.
Figure 19.
Graph showing the p-values of the Durbin–Watson test for the enhanced model for capital goods. The null hypothesis states that residuals are not autocorrelated.
Figure 19.
Graph showing the p-values of the Durbin–Watson test for the enhanced model for capital goods. The null hypothesis states that residuals are not autocorrelated.
Figure 20.
Graph showing the p-values of the Durbin–Watson test for the barebone model for durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 20.
Graph showing the p-values of the Durbin–Watson test for the barebone model for durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 21.
Graph showing the p-values of the Bowman–Shenton test for the barebone model for durable goods. The null hypothesis states that errors are normally distributed.
Figure 21.
Graph showing the p-values of the Bowman–Shenton test for the barebone model for durable goods. The null hypothesis states that errors are normally distributed.
Figure 22.
Graph shows the p-values of the Harvey heteroskedasticity test for the barebone model for durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 22.
Graph shows the p-values of the Harvey heteroskedasticity test for the barebone model for durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 23.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for non-durable goods.
Figure 23.
Graph showing the difference between the Bayesian information criterion of the barebone model and the enhanced model for non-durable goods.
Figure 24.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for non-durable goods. The null hypothesis states that errors are normally distributed.
Figure 24.
Graph showing the p-values of the Bowman–Shenton test for the enhanced model for non-durable goods. The null hypothesis states that errors are normally distributed.
Figure 25.
Graph shows the p-values of the Durbin–Watson test for the enhanced model for non-durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 25.
Graph shows the p-values of the Durbin–Watson test for the enhanced model for non-durable goods. The null hypothesis states that residuals are not autocorrelated.
Figure 26.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for non-durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Figure 26.
Graph showing the p-values of the Harvey heteroskedasticity test for the enhanced model for non-durable goods. The null hypothesis states that the residuals are not heteroskedastic.
Table 1.
Information sources of data.
Table 1.
Information sources of data.
| Name | Series | Sources | Freq. | Time a |
|---|
| IPI | 5 | ISTAT | Monthly | - |
| IPI of Electricity, gas, steam and air conditioning supply | 4 | ISTAT | Monthly | - |
| GigaWatt Electricity net production | 1 | TERNA | Monthly | +20+25 days |
| GigaWatt Electricity Consumption | 1 | TERNA | Monthly | +35+40 days |
| GigaWatt Electricity Consumption | 1 | TERNA | Daily | Every Day |
| Total m3 of Compressed Natural Gas transported | 1 | SNAM | Daily | Every Day |
| Production of m3 of Compressed Natural Gas | 1 | SNAM | Daily | Every Day |
| M3 of Compressed Natural Gas for Thermoelectric use | 1 | SNAM | Daily | Every Day |
| M3 of Compressed Natural Gas for Industrial use | 1 | SNAM | Daily | Every Day |
| Registration of Light Commercial Vehicles in Italy | 1 | ACI | Monthly | +35+40 days |
| Registration of Light Commercial Vehicles in Spain | 1 | ANFAC | Monthly | +35+40 days |
| Registration of Light Commercial Vehicles in France | 1 | CCFA | Monthly | +35+40 days |
| Registration of Light Commercial Vehicles in Germany | 1 | KBA | Monthly | +35+40 days |
| Truck Toll Mileage Index in Germany | 1 | DESTATIS | Monthly | +35+40 days |
| IPI of Manufacture of motor vehicles, trailers and semi-trailers | 1 | ISTAT | Monthly | - |
| Production of passengers cars in Germany | 1 | VDA | Monthly | +35+40 days |
Table 2.
Information sources of data for VARMA using survey data.
Table 2.
Information sources of data for VARMA using survey data.
| Name | Series | Sources | Freq. | Time a |
|---|
| IPI | 1 | ISTAT | Monthly | - |
| GigaWatt Electricity Consumption | 1 | TERNA | Monthly | +35+40 days |
| Truck Toll Mileage Index in Germany | 1 | DESTATIS | Monthly | +35+40 days |
| Climate Index (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| General economy expectations (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Assessment of orders (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Assessment of domestic orders (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Assessment of export orders (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Production growth (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Assessment of stocks of finished products (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Orders expectations (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Production expectations (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
| Price expectations (non-durable goods) | 1 | ISTAT | Monthly | +35+40 days |
Table 3.
Comparison of mean absolute error and root mean squared error with expanding window applied to the VARMA using only hard data and both hard data and soft data, respectively (i.e., ISTAT survey), about the non-durable goods. The forecast windows expands itself from 2008:01 to 2018:12. The ratio between MAEs and RMSEs with respect to the benchmark are shown. A value less than one indicates an improvement over the benchmark.
Table 3.
Comparison of mean absolute error and root mean squared error with expanding window applied to the VARMA using only hard data and both hard data and soft data, respectively (i.e., ISTAT survey), about the non-durable goods. The forecast windows expands itself from 2008:01 to 2018:12. The ratio between MAEs and RMSEs with respect to the benchmark are shown. A value less than one indicates an improvement over the benchmark.
| | Step 1 | Step 2 | Step 3 |
|---|
| TYPE OF RATIO | VARMA | VARMAPLUSND | VARMA | VARMAPLUSND | VARMA | VARMAPLUSND |
| IMAE | 0.2749 | 0.6361 | 0.3142 | 0.9186 | 0.3089 | 0.8245 |
| IMAE-2015 | 0.5316 | 1.0636 | 0.5356 | 1.5651 | 0.6034 | 1.4227 |
| IRMSE | 0.2370 | 0.6228 | 0.2765 | 0.9792 | 0.2670 | 0.7521 |
| IRMSE-2015 | 0.4268 | 1.0627 | 0.5110 | 1.6598 | 0.5447 | 1.4713 |
Table 4.
Tests of equal predictive accuracy and test of forecast encompassing of VARMA using only hard data and both hard data and soft data, respectively (i.e., ISTAT survey), for non-durable goods. The forecast window expands itself from 2008:01 to 2018:12. The three tests are considered at the end of the sample and at the maximum value of forecast benchmark, i.e., August 2009. The p-values near to one show that the null hypothesis of equal predictive accuracy have been accepted with respect to the benchmark of Bulligan et al. For encompass test, the null hypothesis is that the forecast of the benchmark encompasses the forecast of the VARMA.
Table 4.
Tests of equal predictive accuracy and test of forecast encompassing of VARMA using only hard data and both hard data and soft data, respectively (i.e., ISTAT survey), for non-durable goods. The forecast window expands itself from 2008:01 to 2018:12. The three tests are considered at the end of the sample and at the maximum value of forecast benchmark, i.e., August 2009. The p-values near to one show that the null hypothesis of equal predictive accuracy have been accepted with respect to the benchmark of Bulligan et al. For encompass test, the null hypothesis is that the forecast of the benchmark encompasses the forecast of the VARMA.
| | Step 1 | Step 2 | Step 3 |
|---|
| MMDTEST-SUBSAMPLE-LOSS-FUNCTION | VARMA | VARMAPLUSND | VARMA | VARMAPLUSND | VARMA | VARMAPLUSND |
| MMD-0801-1812-ABSERR | 0.9250 | 0.0037 | 0.7183 | 0.1788 | 0.5040 | 0.0621 |
| MMD-0801-1812-ERR2 | 0.5850 | 0.0000 | 0.4887 | 0.2381 | 0.7913 | 0.0205 |
| MMD-0801-0908-ABSERR | 0.7730 | 0.0149 | 0.3122 | 0.2703 | 0.6828 | 0.0795 |
| MMD-0801-0908-ERR2 | 0.6770 | 0.0301 | 0.1723 | 0.7801 | 0.5070 | 0.0368 |
| MMD-0801-0908-ENC | 0.4300 | 0.0017 | 0.4224 | 0.0258 | 0.0258 | 0.0082 |
| MMD-0801-1812-ENC | 0.0000 | 0.0000 | 0.8011 | 0.3929 | 0.0021 | 0.0000 |
Table 5.
Tests of equal predictive accuracy and test of forecast encompassing of VARMA using only hard data and both hard data and soft data, respectively, (i.e., ISTAT survey) for non-durable goods. The forecast windows expands itself from 2008:01 to 2018:12. The three tests are considered at the end of the sample and at the maximum value of forecast benchmark, i.e., August 2009. The p-values near one show that null hypothesis of equal predictive accuracy between the VARMA that uses only hard data and the VARMA that uses hard data plus soft data for non-durable goods has been accepted. For encompass test, the null hypothesis is that the forecast of the VARMA using only hard data encompasses the forecast of the VARMA using only hard data and soft data for non-durable goods.
Table 5.
Tests of equal predictive accuracy and test of forecast encompassing of VARMA using only hard data and both hard data and soft data, respectively, (i.e., ISTAT survey) for non-durable goods. The forecast windows expands itself from 2008:01 to 2018:12. The three tests are considered at the end of the sample and at the maximum value of forecast benchmark, i.e., August 2009. The p-values near one show that null hypothesis of equal predictive accuracy between the VARMA that uses only hard data and the VARMA that uses hard data plus soft data for non-durable goods has been accepted. For encompass test, the null hypothesis is that the forecast of the VARMA using only hard data encompasses the forecast of the VARMA using only hard data and soft data for non-durable goods.
| | Step 1 | Step 2 | Step 3 |
|---|
| MMDTEST-SUBSAMPLE-LOSS-FUNCTION | VARMA vs. VARMAPLUSND | VARMA vs. VARMAPLUSND | VARMA vs. VARMAPLUSND |
| MMD-0801-1812-ABSERR | 0.0013 | 0.27661 | 0.1283 |
| MMD-0801-1812-ERR2 | 0.0046 | 0.2889 | 0.0281 |
| MMD-0801-0908-ABSERR | 0.0238 | 0.1981 | 0.0800 |
| MMD-0801-0908-ERR2 | 0.0349 | 0.4956 | 0.0548 |
| MMD-0801-0908-ENC | 0.0018 | 0.0173 | 0.0120 |
| MMD-0801-1812-ENC | 0.0000 | 0.8061 | 0.0000 |
Table 6.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for intermediate goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
Table 6.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for intermediate goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-INTERM | 0.0216 | 0.0102 | 0.0088 |
| BBLCVDE | 0.0362 | 0.3634 | 0.7236 |
| BBLCVFR | 0.0362 | 0.3634 | 0.8332 |
| BBLCVSP | 0.2184 | 0.3634 | 0.8332 |
| BBTTMI | 0.2184 | 0.5904 | 0.8332 |
| ENHTTMI | 1.0000 | 1.0000 | 1.0000 |
Table 7.
Comparison of the ratios of mean absolute error for models for intermediate goods with an expanding window from 2008:01 to 2018:12.
Table 7.
Comparison of the ratios of mean absolute error for models for intermediate goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| BBLCVDE | 0.4749 | 0.5284 | 0.5672 |
| BBLCVFR | 0.4535 | 0.5181 | 0.5537 |
| BBLCVSP | 0.4431 | 0.5180 | 0.5478 |
| BBTTMI | 0.4304 | 0.5134 | 0.5560 |
| ENHTTMI | 0.4345 | 0.4885 | 0.5362 |
Table 8.
Model confidence set hierarchy loss function is the squared error at the end of the sample for intermediate goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
Table 8.
Model confidence set hierarchy loss function is the squared error at the end of the sample for intermediate goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-INTERM | 0.1490 | 0.1530 | 0.1414 |
| BBLCVDE | 0.1490 | 0.1530 | 0.1414 |
| BBLCVFR | 0.1490 | 0.2798 | 0.3096 |
| BBLCVSP | 0.3568 | 0.2798 | 0.3096 |
| BBTTMI | 0.3568 | 0.2798 | 0.3096 |
| ENHTTMI | 1.0000 | 1.0000 | 1.0000 |
Table 9.
Comparison of the ratios of RMSE for models for intermediate goods with an expanding window from 2008:01 to 2018:12.
Table 9.
Comparison of the ratios of RMSE for models for intermediate goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| BBLCVDE | 0.6603 | 0.7419 | 0.7993 |
| BBLCVFR | 0.6143 | 0.7166 | 0.7496 |
| BBLCVSP | 0.5835 | 0.6698 | 0.7009 |
| BBTTMI | 0.6323 | 0.7344 | 0.7774 |
| ENHTTMI | 0.6296 | 0.6539 | 0.7011 |
Table 10.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for capital goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
Table 10.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for capital goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-CAPITAL | 0.0040 | 0.0036 | 0.0010 |
| BBLCVDE | 0.6618 | 0.0356 | 0.3012 |
| BBLCVFR | 0.8222 | 0.9166 | 0.9820 |
| BBLCVSP | 0.9952 | 0.9328 | 0.9820 |
| BBTMI | 0.9952 | 0.9328 | 0.9820 |
| ENHTTMI | 1.0000 | 1.0000 | 1.0000 |
Table 11.
Comparison of the ratios of absolute error for models for capital goods with an expanding window from 2008:01 to 2018:12.
Table 11.
Comparison of the ratios of absolute error for models for capital goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| BBLCVDE | 0.4508 | 0.4943 | 0.5391 |
| BBLCVFR | 0.4543 | 0.4846 | 0.5327 |
| BBLCVSP | 0.4363 | 0.4924 | 0.5386 |
| BBTTMI | 0.4331 | 0.4907 | 0.5355 |
| ENHTTMI | 0.4344 | 0.5381 | 0.5755 |
Table 12.
Comparison of the ratios of RMSE for models for capital goods with an expanding window from 2008:01 to 2018:12.
Table 12.
Comparison of the ratios of RMSE for models for capital goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| BBLCVDE | 0.5287 | 0.5795 | 0.6065 |
| BBLCVFR | 0.5393 | 0.5690 | 0.5911 |
| BBLCVSP | 0.4606 | 0.5705 | 0.5558 |
| BBTTMI | 0.5350 | 0.5935 | 0.6137 |
| ENHTTMI | 0.5292 | 0.6261 | 0.6586 |
Table 13.
Model Confidence Set Hierarchy Loss function is the squared error at the end of the sample for capital goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
Table 13.
Model Confidence Set Hierarchy Loss function is the squared error at the end of the sample for capital goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-CAPITAL | 0.1412 | 0.0770 | 0.0708 |
| BBLCVDE | 0.7124 | 0.0770 | 0.0708 |
| BBLCVFR | 0.7124 | 0.7062 | 0.6688 |
| BBLCVSP | 0.7124 | 0.7736 | 0.6688 |
| BBTMI | 0.7124 | 0.8882 | 0.6688 |
| ENHTTMI | 1.0000 | 1.0000 | 1.0000 |
Table 14.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for non-durable goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the performance of the model in the row.
Table 14.
Model confidence set hierarchy loss function is the absolute error at the end of the sample for non-durable goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-NDUR | 0.0000 | 0.0000 | 0.0000 |
| BBSNAMINDUSTRIAL | 0.0000 | 0.0000 | 0.0002 |
| ENHSNAMINDUSTRIAL | 1.0000 | 1.0000 | 1.0000 |
Table 15.
Model confidence set hierarchy loss function is the squared error at the end of the sample for non-durable goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
Table 15.
Model confidence set hierarchy loss function is the squared error at the end of the sample for non-durable goods model comparison , number of bootstrap replications = 5000 and block length = 12. The null hypothesis is that the average performance of the model in the row is as small as the minimum average performance across the remaining models. The alternative is that the minimum average loss across the remaining models is smaller than the average performance of the model in the row.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-NDUR | 0.0000 | 0.0000 | 0.0000 |
| BBSNAMINDUSTRIAL | 0.0000 | 0.0000 | 0.0002 |
| ENHSNAMINDUSTRIAL | 1.0000 | 1.0000 | 1.0000 |
Table 16.
Comparison of the ratios of absolute error for models for capital goods with an expanding window from 2008:01 to 2018:12.
Table 16.
Comparison of the ratios of absolute error for models for capital goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-NDUR | 1.0000 | 1.0000 | 1.0000 |
| BBSNAMINDUSTRIAL | 0.6513 | 0.7434 | 0.7251 |
| ENHSNAMINDUSTRIAL | 0.6407 | 0.5787 | 0.5964 |
Table 17.
Comparison of the ratios of RMSE for models for capital goods with an expanding window from 2008:01 to 2018:12.
Table 17.
Comparison of the ratios of RMSE for models for capital goods with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN-NDUR | 1.0000 | 1.0000 | 1.0000 |
| BBSNAMINDUSTRIAL | 0.6292 | 0.7334 | 0.7211 |
| ENHSNAMINDUSTRIAL | 0.6286 | 0.6969 | 0.7053 |
Table 18.
Comparison of the ratios of mean absolute error with an expanding window from 2008:01 to 2018:12.
Table 18.
Comparison of the ratios of mean absolute error with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.4345 | 0.4885 | 0.5362 |
| IPI-CAP | 0.4200 | 0.5265 | 0.5692 |
| IPI-DUR | 0.4976 | 0.5006 | 0.5088 |
| IPI-NDUR | 0.6407 | 0.7196 | 0.7329 |
| IPI-ENERGY | 0.1498 | 0.5145 | 0.5328 |
| IPI-AGG | 0.3503 | 0.4254 | 0.4611 |
| IPI-BENAGG | 1.0019 | 1.0044 | 1.0035 |
Table 19.
Modified Diebold–Mariano statistics for equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
Table 19.
Modified Diebold–Mariano statistics for equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.0000 | 0.0000 | 0.0000 |
| IPI-CAP | 0.0000 | 0.0000 | 0.0000 |
| IPI-DUR | 0.0452 | 0.0539 | 0.0516 |
| IPI-NDUR | 0.0000 | 0.0000 | 0.0000 |
| IPI-ENERGY | 0.0000 | 0.0000 | 0.0000 |
| IPI-AGG | 0.0000 | 0.0000 | 0.0000 |
Table 20.
Comparison of the ratio between mean absolute errors with an expanding window from 2015:01 to 2018:12.
Table 20.
Comparison of the ratio between mean absolute errors with an expanding window from 2015:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.4373 | 0.5935 | 0.6499 |
| IPI-CAP | 0.3890 | 0.4412 | 0.4288 |
| IPI-DUR | 0.8689 | 0.9072 | 0.8852 |
| IPI-NDUR | 0.5974 | 0.6673 | 0.7049 |
| IPI-ENERGY | 0.1603 | 0.6020 | 0.6094 |
| IPI-AGG | 0.3590 | 0.5206 | 0.4957 |
| IPI-BENAGG | 1.0051 | 1.0180 | 1.0170 |
Table 21.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The Loss function is the absolute error.
Table 21.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The Loss function is the absolute error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.0001 | 0.0057 | 0.0179 |
| IPI-CAP | 0.0000 | 0.0000 | 0.0000 |
| IPI-DUR | 0.3469 | 0.4986 | 0.4446 |
| IPI-NDUR | 0.0000 | 0.0000 | 0.0000 |
| IPI-ENERGY | 0.0000 | 0.0081 | 0.0012 |
| IPI-AGG | 0.0000 | 0.0001 | 0.0002 |
Table 22.
Comparison between RMSE ratios with an expanding window from 2008:01 to 2018:12.
Table 22.
Comparison between RMSE ratios with an expanding window from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.6296 | 0.6539 | 0.7011 |
| IPI-CAP | 0.5631 | 0.6695 | 0.7140 |
| IPI-DUR | 0.9298 | 0.9136 | 0.8500 |
| IPI-NDUR | 0.6286 | 0.6969 | 0.7053 |
| IPI-ENERGY | 0.1556 | 0.5361 | 0.5550 |
| IPI-AGG | 0.3917 | 0.4724 | 0.5249 |
| IPI-BENAGG | 0.9982 | 1.0036 | 1.0037 |
Table 23.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
Table 23.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.0389 | 0.0291 | 0.0338 |
| IPI-CAP | 0.0041 | 0.0268 | 0.0252 |
| IPI-DUR | 0.7985 | 0.8010 | 0.9780 |
| IPI-NDUR | 0.0000 | 0.0000 | 0.0000 |
| IPI-ENERGY | 0.0000 | 0.0000 | 0.0000 |
| IPI-AGG | 0.0000 | 0.0000 | 0.0000 |
Table 24.
Comparison of mean ratio between RMSEs with an expanding window from 2015:01 to 2018:12.
Table 24.
Comparison of mean ratio between RMSEs with an expanding window from 2015:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.4517 | 0.6324 | 0.6783 |
| IPI-CAP | 0.4066 | 0.4357 | 0.4306 |
| IPI-DUR | 1.4071 | 1.4748 | 1.4073 |
| IPI-NDUR | 0.5891 | 0.6392 | 0.6439 |
| IPI-ENERGY | 0.1558 | 0.5921 | 0.6161 |
| IPI-AGG | 0.3642 | 0.5176 | 0.4926 |
| IPI-BENAGG | 0.9977 | 1.0048 | 1.0006 |
Table 25.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
Table 25.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-INT | 0.0000 | 0.0003 | 0.0005 |
| IPI-CAP | 0.0003 | 0.0146 | 0.0312 |
| IPI-DUR | 0.0001 | 0.0001 | 0.0001 |
| IPI-NDUR | 0.8694 | 0.7945 | 0.9430 |
| IPI-ENERGY | 0.0000 | 0.0000 | 0.0000 |
| IPI-AGG | 0.0002 | 0.0121 | 0.0053 |
Table 26.
Comparison of ratios between mean absolute errors with an expanding window for electricity from 2008:01 to 2018:12.
Table 26.
Comparison of ratios between mean absolute errors with an expanding window for electricity from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.3910 | 0.4073 | 0.7706 |
| IPI-PETROL | 0.6150 | 0.6712 | 0.7422 |
| IPI-PRODELE | 0.0075 | 0.5686 | 0.6056 |
| IPI-CNG | 0.1543 | 0.2073 | 0.7581 |
| IPI-AGG | 0.1498 | 0.5145 | 0.5328 |
| IPI-BENAGG | 0.9939 | 0.9830 | 0.9836 |
Table 27.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
Table 27.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.0000 | 0.0000 | 0.0094 |
| IPI-PETROL | 0.0000 | 0.0000 | 0.0000 |
| IPI-PRODELE | 0.0000 | 0.0005 | 0.0000 |
| IPI-CNG | 0.0000 | 0.0000 | 0.0004 |
| IPI-AGG | 0.0000 | 0.0000 | 0.0000 |
Table 28.
Comparison of the ratio between mean absolute errors with an expanding window for electricity from 2015:01 to 2018:12.
Table 28.
Comparison of the ratio between mean absolute errors with an expanding window for electricity from 2015:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.3707 | 0.3893 | 0.6791 |
| IPI-PETROL | 0.6763 | 0.7953 | 0.7441 |
| IPI-PRODELE | 0.0054 | 0.6713 | 0.7433 |
| IPI-CNG | 0.0961 | 0.1593 | 0.7501 |
| IPI-AGG | 0.1603 | 0.6020 | 0.6094 |
| IPI-BENAGG | 0.8733 | 0.8573 | 0.8575 |
Table 29.
Modified Diebold–Mariano for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
Table 29.
Modified Diebold–Mariano for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the absolute error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.00000 | 0.00000 | 0.02050 |
| IPI-PETROL | 0.00950 | 0.06220 | 0.20580 |
| IPI-PRODELE | 0.00000 | 0.78530 | 0.03960 |
| IPI-CNG | 0.00000 | 0.00000 | 0.02340 |
| IPI-AGG | 0.00000 | 0.00810 | 0.00120 |
Table 30.
Comparison of the ratio between RMSEs with an expanding window for electricity from 2008:01 to 2018:12.
Table 30.
Comparison of the ratio between RMSEs with an expanding window for electricity from 2008:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.3852 | 0.3967 | 0.8318 |
| IPI-PETROL | 0.6272 | 0.7061 | 0.7946 |
| IPI-PRODELE | 0.0100 | 0.4496 | 0.4778 |
| IPI-CNG | 0.0184 | 0.0235 | 0.0815 |
| IPI-AGG | 0.1556 | 0.5361 | 0.5550 |
| IPI-BENAGG | 1.0012 | 0.9986 | 0.9992 |
Table 31.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
Table 31.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2008:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.0000 | 0.0000 | 0.1298 |
| IPI-PETROL | 0.0000 | 0.0000 | 0.0001 |
| IPI-PRODELE | 0.0000 | 0.0010 | 0.0000 |
| IPI-CNG | 0.0000 | 0.0000 | 0.0003 |
| IPI-AGG | 0.0000 | 0.0000 | 0.0000 |
Table 32.
Comparison of the ratio between RMSEs with an expanding window for electricity from 2015:01 to 2018:12.
Table 32.
Comparison of the ratio between RMSEs with an expanding window for electricity from 2015:01 to 2018:12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.3330 | 0.3524 | 0.6130 |
| IPI-PETROL | 0.7224 | 0.7541 | 0.7532 |
| IPI-PRODELE | 0.0072 | 0.4659 | 0.5101 |
| IPI-CNG | 0.0105 | 0.0180 | 0.0787 |
| IPI-AGG | 0.1558 | 0.5921 | 0.6161 |
| IPI-BENAGG | 0.9129 | 0.9019 | 0.8997 |
Table 33.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
Table 33.
Modified Diebold–Mariano statistics for the equality of forecast accuracy of two forecasts under general assumptions with an expanding window from 2015:01 to 2018:12. The null hypothesis is that the two methods have the same forecast accuracy. The loss function is the squared error.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-EXTRA | 0.0022 | 0.0023 | 0.0164 |
| IPI-PETROL | 0.0212 | 0.1571 | 0.4489 |
| IPI-PRODELE | 0.0017 | 0.5629 | 0.0809 |
| IPI-CNG | 0.0000 | 0.0000 | 0.0163 |
| IPI-AGG | 0.0002 | 0.0121 | 0.0053 |
Table 34.
Model confidence set hierarchy loss function is the absolute error at the end of the sample , number of bootstrap replications = 5000 and block length = 12.
Table 34.
Model confidence set hierarchy loss function is the absolute error at the end of the sample , number of bootstrap replications = 5000 and block length = 12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN | 0.0010 | 0.0000 | 0.0000 |
| IPI-AIRLINELW | 0.0010 | 0.0000 | 0.0000 |
| IPI-VARMABM | 0.0010 | 0.0030 | 0.0010 |
| IPI-VARMABMND | 0.0010 | 0.0150 | 0.0150 |
| IPI-AGG | 1.0000 | 1.0000 | 1.0000 |
Table 35.
Model confidence set hierarchy loss function is squared error at the end of the sample , number of bootstrap replications = 5000 and block length = 12.
Table 35.
Model confidence set hierarchy loss function is squared error at the end of the sample , number of bootstrap replications = 5000 and block length = 12.
| Index | Step 1 | Step 2 | Step 3 |
|---|
| IPI-BEN | 0.0566 | 0.0398 | 0.1012 |
| IPI-AIRLINELW | 0.0566 | 0.0692 | 0.1012 |
| IPI-VARMABM | 0.0566 | 0.0692 | 0.1012 |
| IPI-VARMABMND | 0.0566 | 0.0692 | 0.1012 |
| IPI-AGG | 1.0000 | 1.0000 | 1.0000 |