A Comparison of the Use of Pontryagin’s Maximum Principle and Reinforcement Learning Techniques for the Optimal Charging of Lithium-Ion Batteries
Abstract
1. Introduction
2. Equivalent Circuit Modeling and Criteria for the Energetically Optimal Charging of Lithium-Ion Batteries
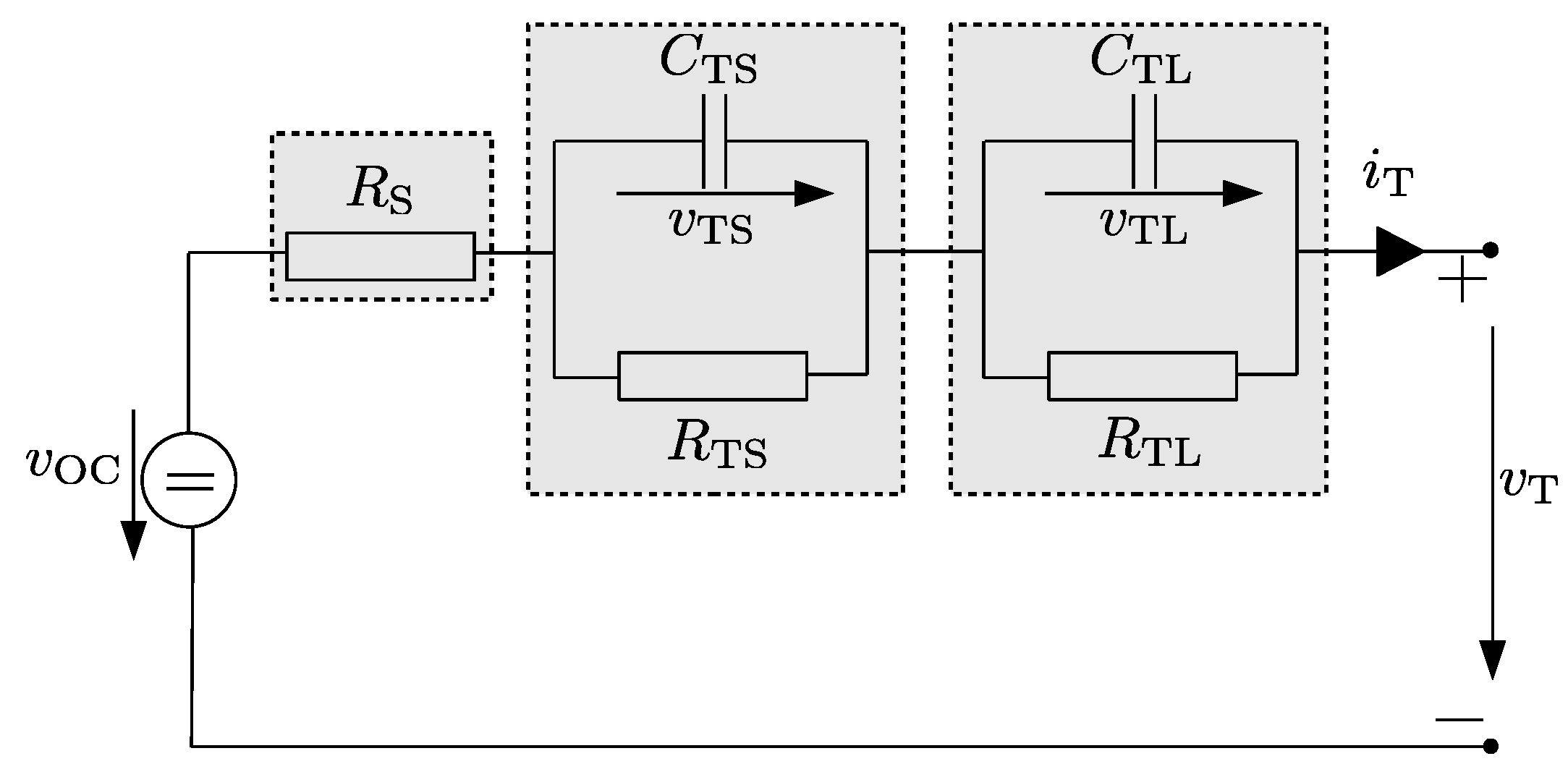
2.1. Equivalent Circuit Modeling
2.2. Quantification of Ohmic Losses
3. Optimal Control Synthesis
3.1. Indirect Optimization Using Pontryagin’s Maximum Principle
3.1.1. Fixed Terminal State
3.1.2. Partially Free Terminal State
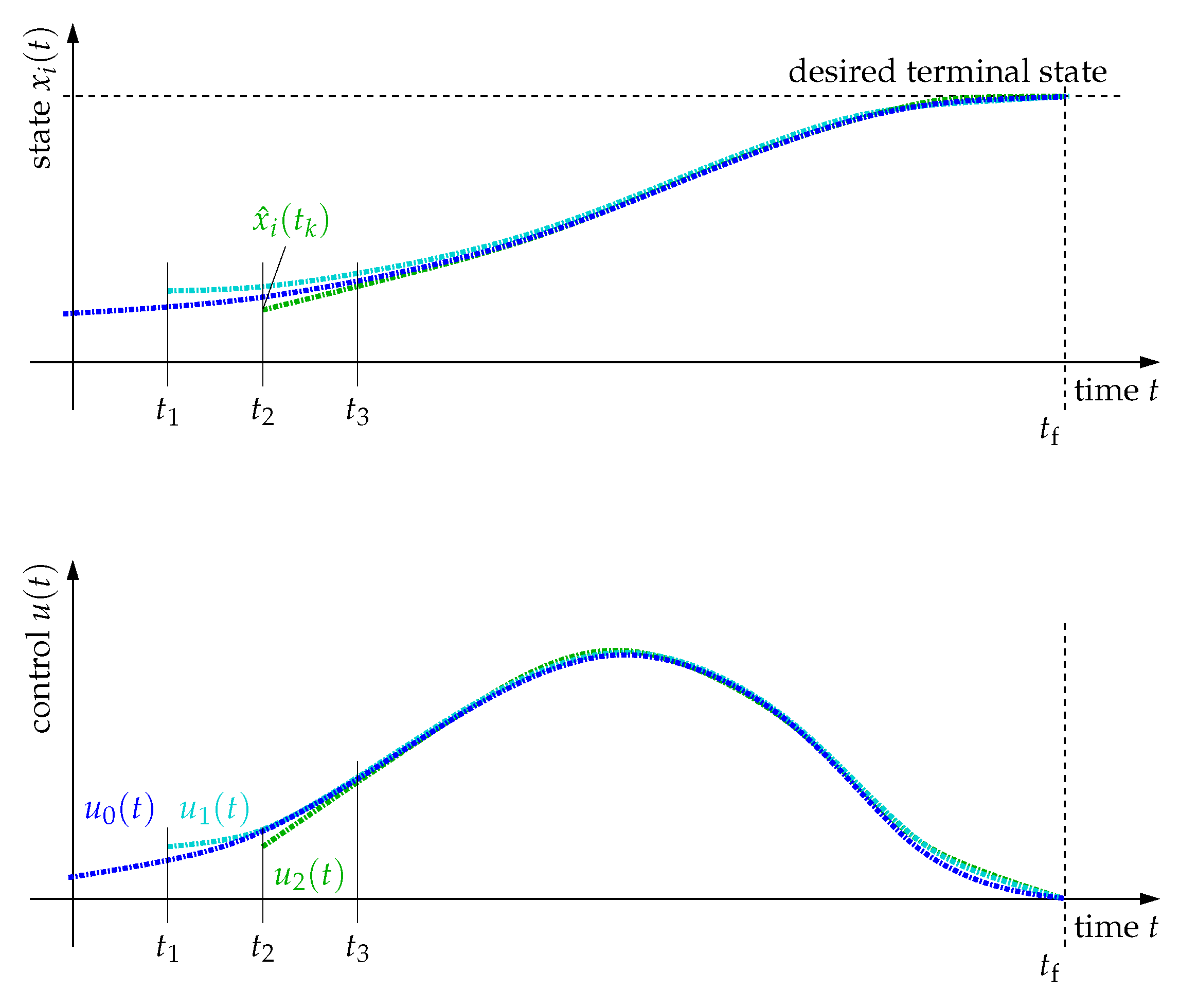
3.2. Conversion into a Model Predictive Control Task
3.3. Relations to Feedback Control Based on a Linear-Quadratic Regulator Design
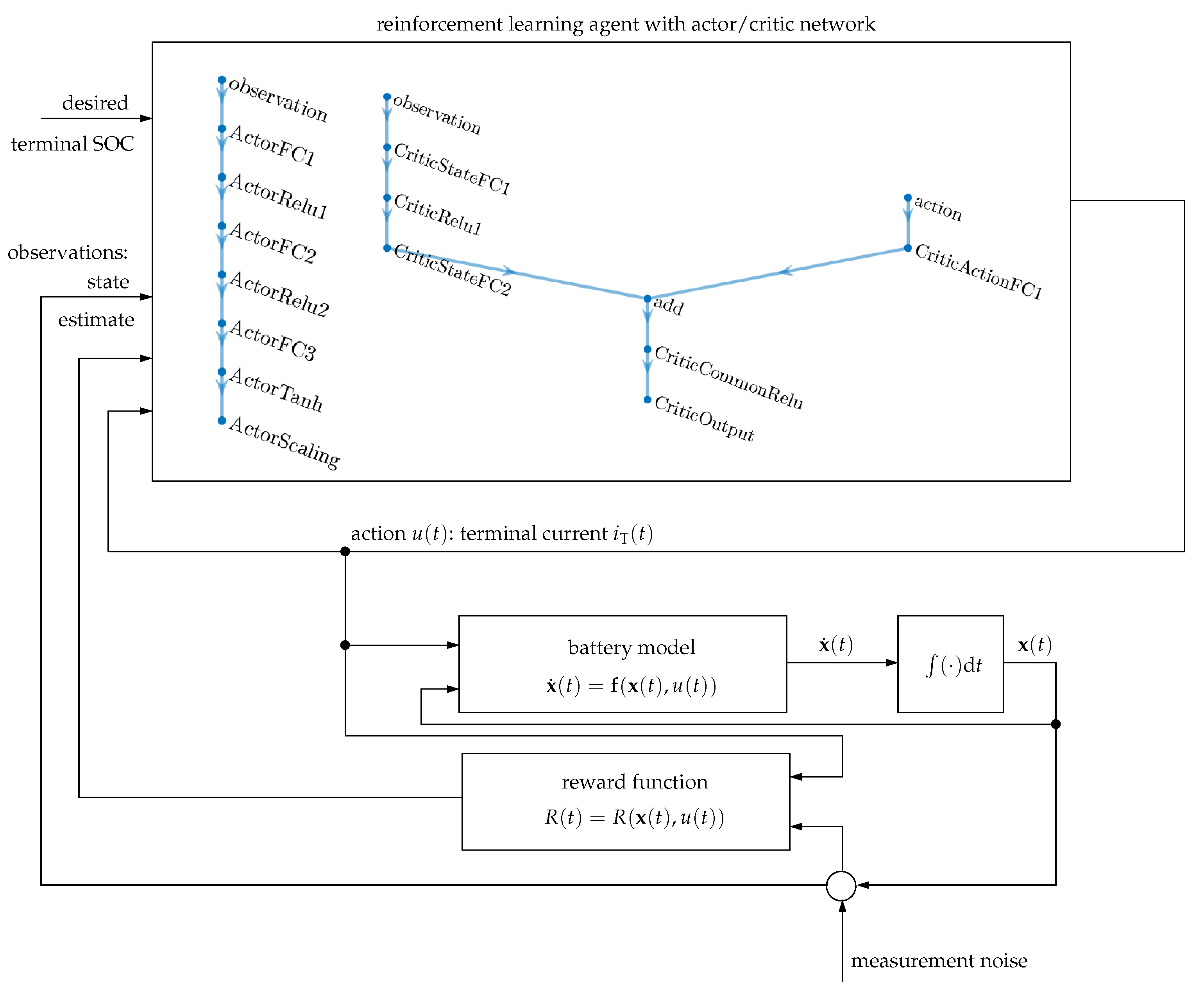
3.4. Direct Optimization by Reinforcement Learning
- The actor network determines the control signal (action) in terms of the observations, where the individual layers in the network according to Figure 4 are fully connected layers denoted by FC and layers with ReLu and tanh activation functions;
- The critic network contains both observations and actions as inputs to determine the reward of the current policy, where the two corresponding input paths are superposed additively, as shown again in Figure 4.
3.5. Summary of the Properties of the Control Approaches
4. Simulation and Optimization Results
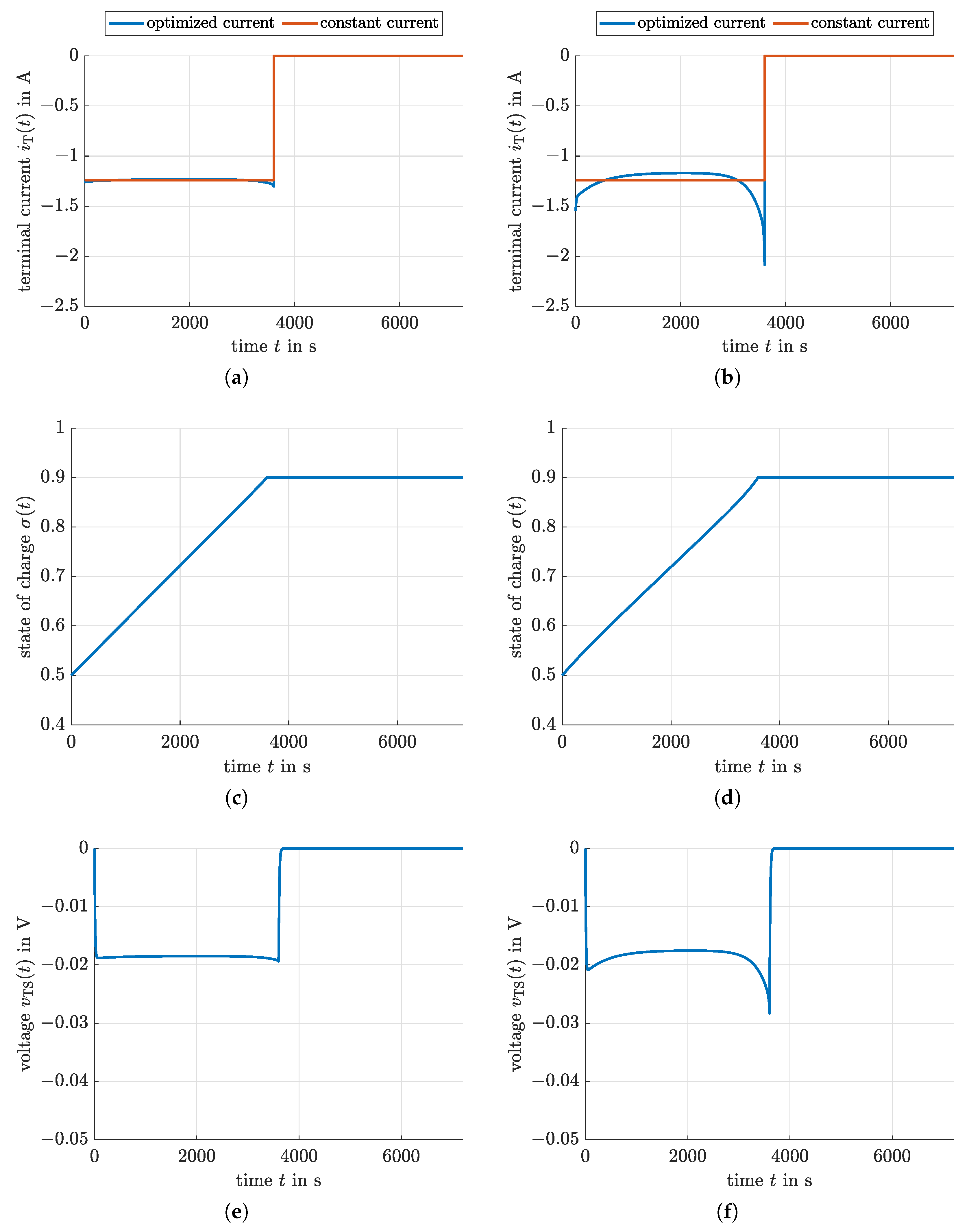
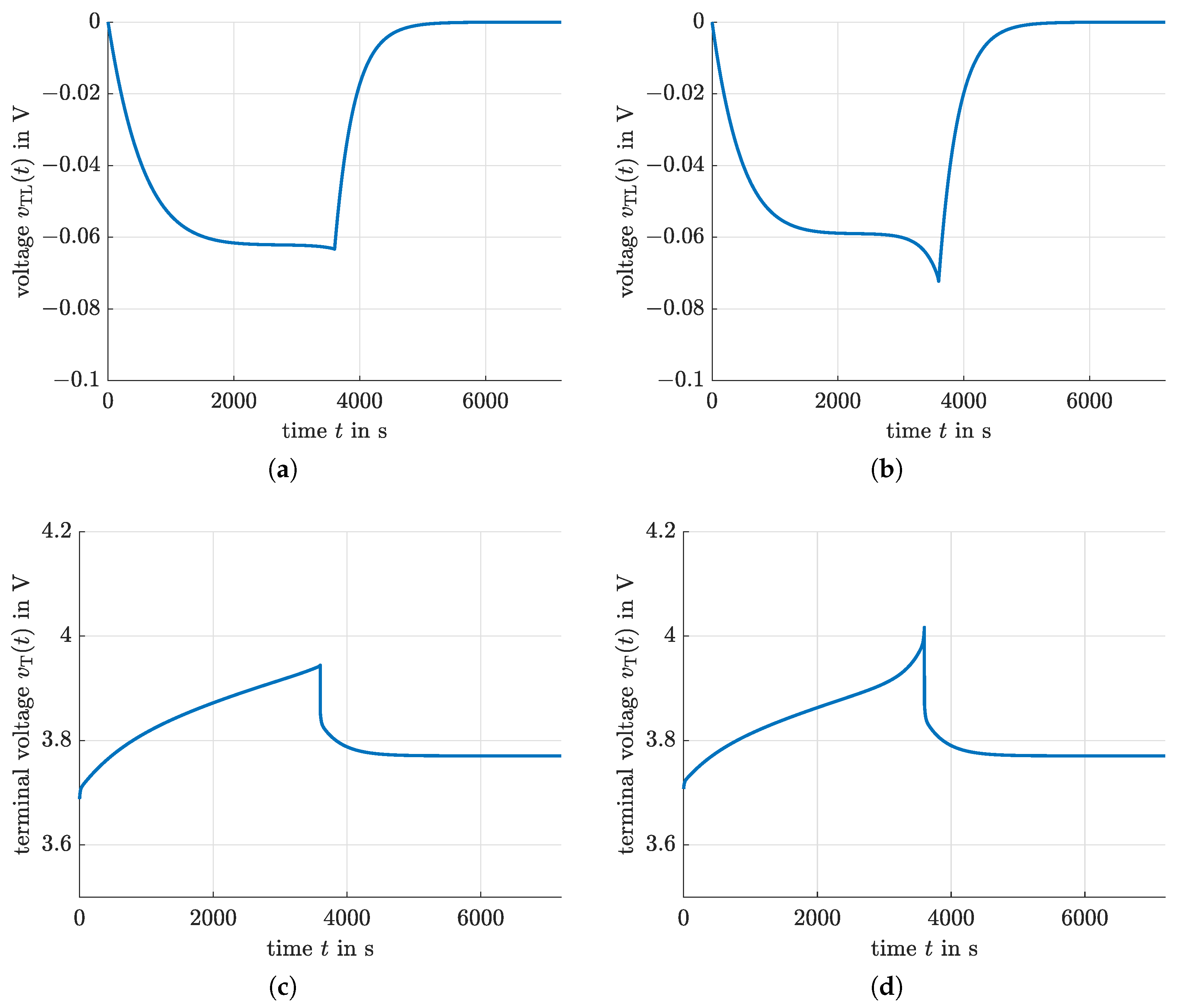
4.1. Indirect Optimization Using Pontryagin’s Maximum Principle
4.2. Model Predictive Control
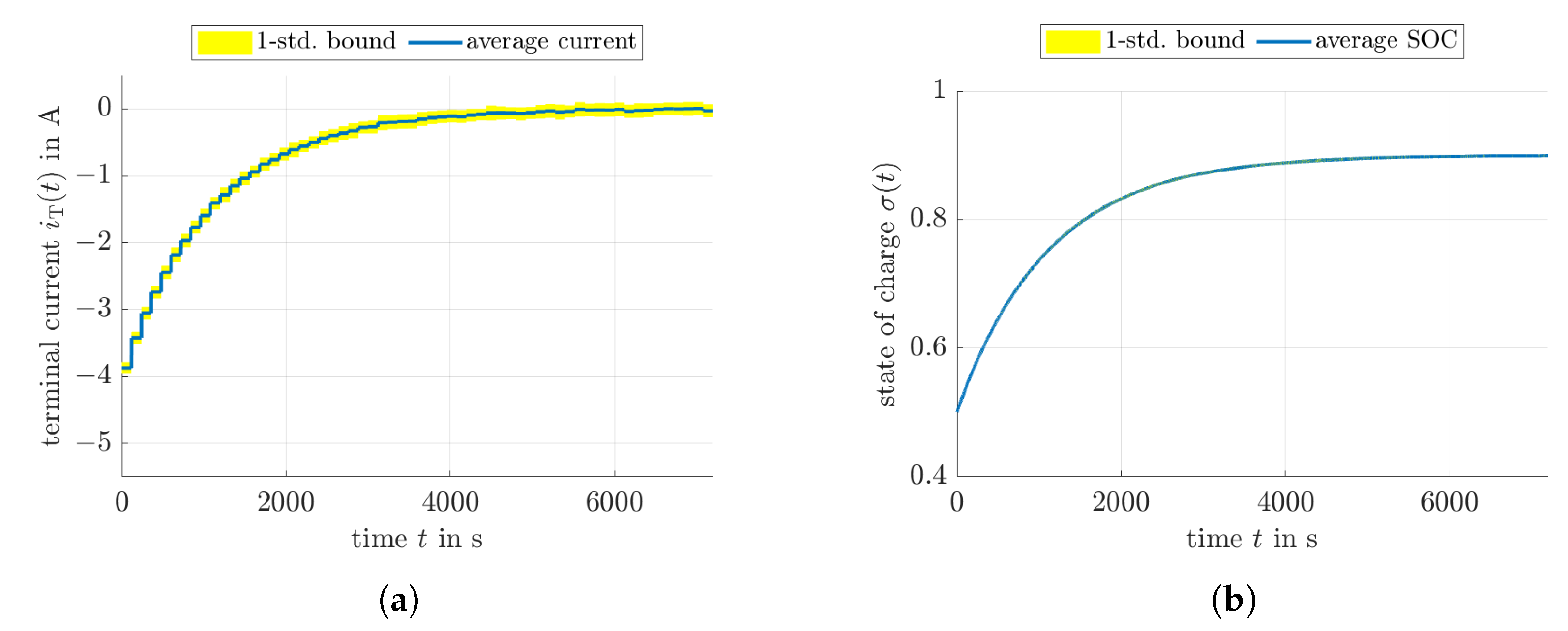
4.3. Feedback Control Based on a Linear-Quadratic Regulator Design
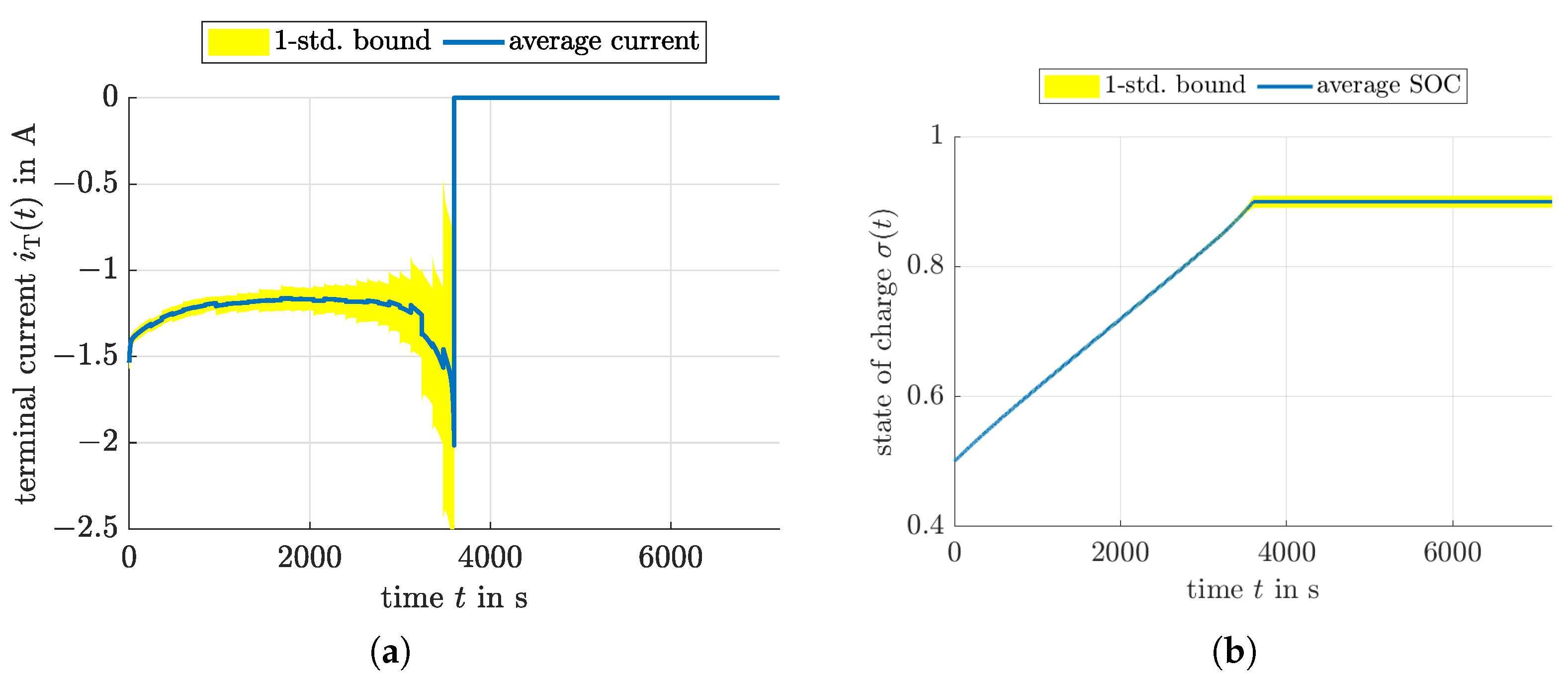
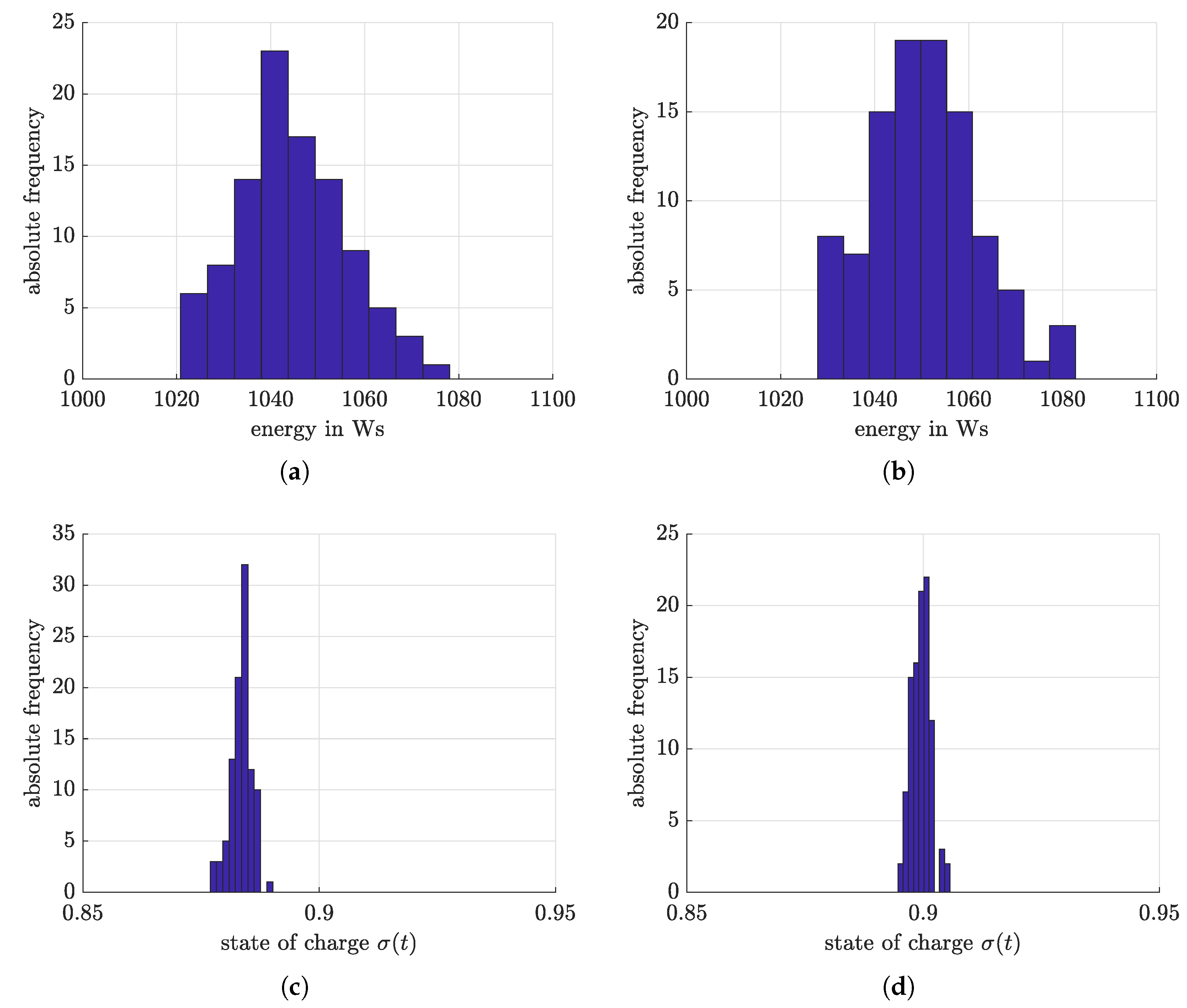
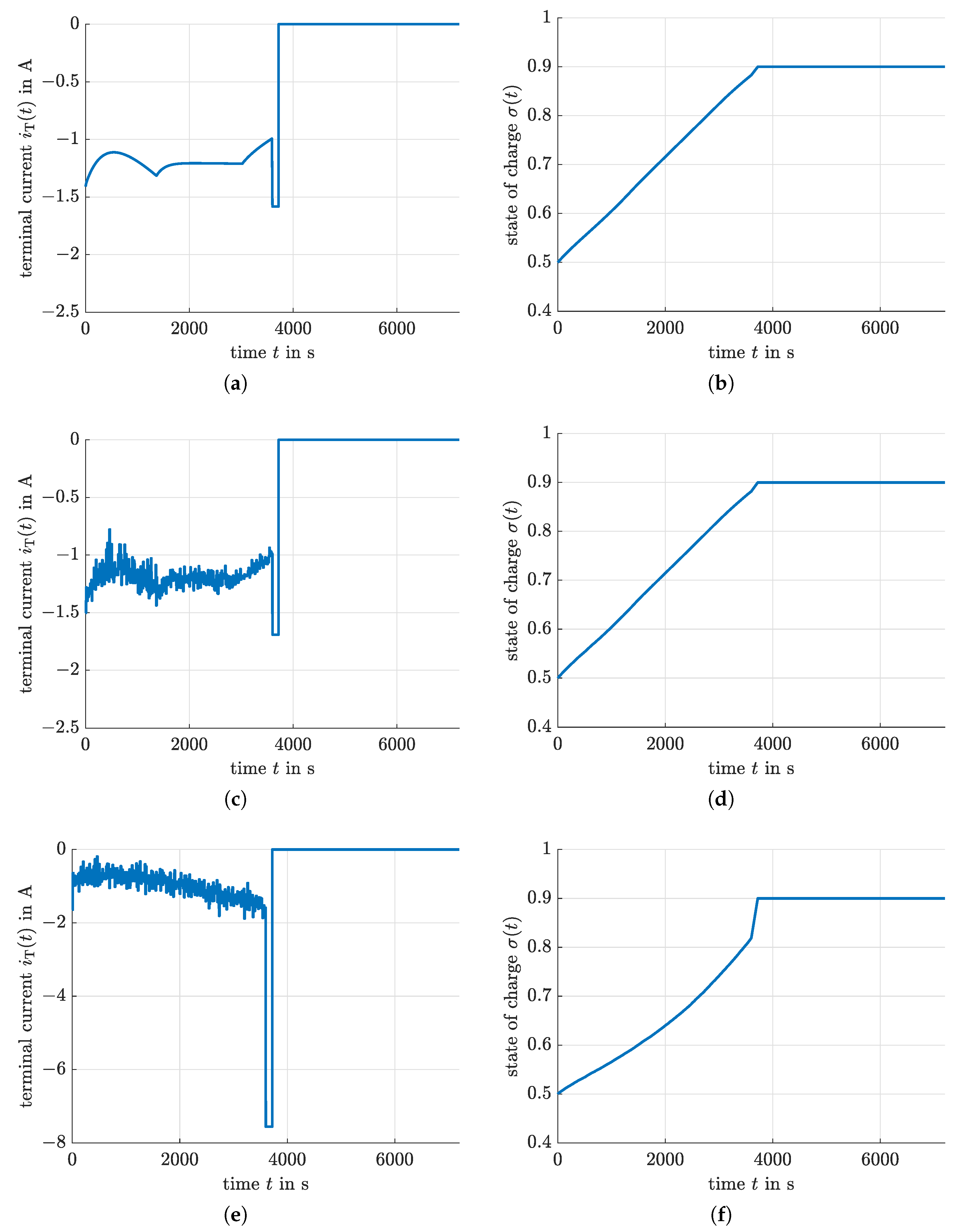
4.4. Optimized Charging Based on Reinforcement Learning
5. Conclusions and Outlook on Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameterization of the Reinforcement Learning Approach
Appendix A.1. Parameterization of the Critic Network
statePath = [ featureInputLayer(numObs,’Normalization’,’none’,’Name’,’observation’) fullyConnectedLayer(200,’Name’,’CriticStateFC1’) reluLayer(’Name’, ’CriticRelu1’) fullyConnectedLayer(150,’Name’,’CriticStateFC2’)]; actionPath = [ featureInputLayer(1,’Normalization’,’none’,’Name’,’action’) fullyConnectedLayer(150,’Name’,’CriticActionFC1’,’BiasLearnRateFactor’,0)]; commonPath = [ additionLayer(2,’Name’,’add’) reluLayer(’Name’,’CriticCommonRelu’) fullyConnectedLayer(1,’Name’,’CriticOutput’)];
Appendix A.2. Parameterization of the Actor Network
actorNetwork = [ featureInputLayer(numObs,’Normalization’,’none’,’Name’,’observation’) fullyConnectedLayer(200,’Name’,’ActorFC1’) reluLayer(’Name’,’ActorRelu1’) fullyConnectedLayer(150,’Name’,’ActorFC2’) reluLayer(’Name’,’ActorRelu2’) fullyConnectedLayer(1,’Name’,’ActorFC3’) tanhLayer(’Name’,’ActorTanh’) scalingLayer(’Name’,’ActorScaling’,’Scale’,max(actInfo.UpperLimit))]; % upper limit = 10
Appendix A.3. Parameterization of the Learning Agent
agentOpts = rlDDPGAgentOptions(... ’SampleTime’,10,... ’TargetSmoothFactor’,1e-3,... ’ExperienceBufferLength’,1e5,... ’NumStepsToLookAhead’,1,... ’DiscountFactor’,0.99,... ’MiniBatchSize’,128); agentOpts.NoiseOptions.Variance = 1e-1; agentOpts.NoiseOptions.VarianceDecayRate = 1e-5;
References
- Xiong, R.; He, H.; Guo, H.; Ding, Y. Modeling for Lithium-Ion Battery used in Electric Vehicles. Procedia Eng. 2011, 15, 2869–2874. [Google Scholar] [CrossRef]
- Kennedy, B.; Patterson, D.; Camilleri, S. Use of Lithium-Ion Batteries in Electric Vehicles. J. Power Sources 2000, 90, 156–162. [Google Scholar] [CrossRef]
- Han, U.; Kang, H.; Song, J.; Oh, J.; Lee, H. Development of Dynamic Battery Thermal Model Integrated with Driving Cycles for EV Applications. Energy Convers. Manag. 2021, 250, 114882. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery Thermal Models for Hybrid Vehicle Simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Liu, Y.C.; Chang, S.B. Design and Implementation of a Smart Lithium-Ion Battery Capacity Estimation System for E-Bike. World Electr. Veh. J. 2011, 4, 370–378. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Pyung, H.; Huynh, T. Computational Analysis on Hybrid Electric Motorcycle with Front Wheel Electric Motor Using Lithium Ion Battery. In Proceedings of the 2017 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 355–359. [Google Scholar]
- Chen, W.; Liang, J.; Yang, Z.; Li, G. A Review of Lithium-Ion Battery for Electric Vehicle Applications and Beyond. Energy Procedia 2019, 158, 4363–4368. [Google Scholar] [CrossRef]
- Misyris, G.S.; Marinopoulos, A.; Doukas, D.I.; Tengnér, T.; Labridis, D.P. On Battery State Estimation Algorithms for Electric Ship Applications. Electr. Power Syst. Res. 2017, 151, 115–124. [Google Scholar] [CrossRef]
- Haji Akhoundzadeh, M.; Panchal, S.; Samadani, E.; Raahemifar, K.; Fowler, M.; Fraser, R. Investigation and Simulation of Electric Train Utilizing Hydrogen Fuel Cell and Lithium-Ion Battery. Sustain. Energy Technol. Assess. 2021, 46, 101234. [Google Scholar] [CrossRef]
- Feehall, T.; Forsyth, A.; Todd, R.; Foster, M.; Gladwin, D.; Stone, D.; Strickland, D. Battery Energy Storage Systems for the Electricity Grid: UK Research Facilities. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 19–21 April 2016; pp. 1–6. [Google Scholar]
- Cao, J.; Schofield, N.; Emadi, A. Battery Balancing Methods: A Comprehensive Review. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar]
- Zhang, X.; Li, L.; Zhang, W. Review of Research about Thermal Runaway and Management of Li-ion Battery Energy Storage Systems. In Proceedings of the 9th IEEE International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 3216–3220. [Google Scholar]
- Wang, Q. State of Charge Equalization Control Strategy of Modular Multilevel Converter with Battery Energy Storage System. In Proceedings of the 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 316–320. [Google Scholar]
- Speltino, C.; Stefanopoulou, A.; Fiengo, G. Cell Equalization in Battery Stacks Through State Of Charge Estimation Polling. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5050–5055. [Google Scholar]
- Raeber, M.; Heinzelmann, A.; Abdeslam, D.O. Analysis of an Active Charge Balancing Method Based on a Single Nonisolated DC/DC Converter. IEEE Trans. Ind. Electron. 2021, 68, 2257–2265. [Google Scholar] [CrossRef]
- Quraan, M.; Abu-Khaizaran, M.; Sa’ed, J.; Hashlamoun, W.; Tricoli, P. Design and Control of Battery Charger for Electric Vehicles Using Modular Multilevel Converters. IET Power Electron. 2021, 14, 140–157. [Google Scholar] [CrossRef]
- Kim, T.; Qiao, W.; Qu, L. Series-Connected Self-Reconfigurable Multicell Battery. In Proceedings of the Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 1382–1387. [Google Scholar]
- Ci, S.; Zhang, J.; Sharif, H.; Alahmad, M. A Novel Design of Adaptive Reconfigurable Multicell Battery for Power-Aware Embedded Networked Sensing Systems. In Proceedings of the IEEE GLOBECOM 2007—IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007; pp. 1043–1047. [Google Scholar]
- Visairo, H.; Kumar, P. A Reconfigurable Battery Pack for Improving Power Conversion Efficiency in Portable Devices. In Proceedings of the 7th International Caribbean Conference on Devices, Circuits and Systems, Cancun, Mexico, 28–30 April 2008; pp. 1–6. [Google Scholar]
- Stengel, R. Optimal Control and Estimation; Dover Publications, Inc.: Mineola, NY, USA, 1994. [Google Scholar]
- Leitmann, G. An Introduction to Optimal Control; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Athans, M.; Falb, P.L. Optimal Control: An Introduction to the Theory and Its Applications; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Pontrjagin, L.S.; Boltjanskij, V.G.; Gamkrelidze, R.V.; Misčenko, E.F. The Mathematical Theory of Optimal Processes; Interscience Publishers: New York, NY, USA, 1962. [Google Scholar]
- Buşoniu, L.; de Bruin, T.; Tolić, D.; Kober, J.; Palunko, I. Reinforcement Learning for Control: Performance, Stability, and Deep Approximators. Annu. Rev. Control 2018, 46, 8–28. [Google Scholar] [CrossRef]
- Gosavi, A. Reinforcement Learning: A Tutorial Survey and Recent Advances. Informs J. Comput. 2009, 21, 178–192. [Google Scholar] [CrossRef]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Maciejowski, J. Predictive Control with Constraints; Prentice Hall: Essex, UK, 2002. [Google Scholar]
- Sontag, E. Mathematical Control Theory—Deterministic Finite Dimensional Systems; Springer: New York, NY, USA, 1998. [Google Scholar]
- Reuter, J.; Mank, E.; Aschemann, H.; Rauh, A. Battery State Observation and Condition Monitoring Using Online Minimization. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 29 August–1 September 2016. [Google Scholar]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A Dynamic Lithium-Ion Battery Model Considering the Effects of Temperature and Capacity Fading. In Proceedings of the International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 383–386. [Google Scholar]
- Rauh, A.; Butt, S.; Aschemann, H. Nonlinear State Observers and Extended Kalman Filters for Battery Systems. Intl. J. Appl. Math. Comput. Sci. AMCS 2013, 23, 539–556. [Google Scholar] [CrossRef]
- Hildebrandt, E.; Kersten, J.; Rauh, A.; Aschemann, H. Robust Interval Observer Design for Fractional-Order Models with Applications to State Estimation of Batteries. In Proceedings of the 21st IFAC World Congress, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- Wang, B.; Liu, Z.; Li, S.; Moura, S.; Peng, H. State-of-Charge Estimation for Lithium-Ion Batteries Based on a Nonlinear Fractional Model. IEEE Trans. Control Syst. Technol. 2017, 25, 3–11. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A Review of Fractional-Order Techniques Applied to Lithium-Ion Batteries, Lead-Acid Batteries, and Supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs—Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs—Part 2. Modeling and Identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs—Part 3. State and Parameter Estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Bo, C.; Zhifeng, B.; Binggang, C. State of Charge Estimation Based on Evolutionary Neural Network. J. Energy Convers. Manag. 2008, 49, 2788–2794. [Google Scholar] [CrossRef]
- Rauh, A.; Chevet, T.; Dinh, T.N.; Marzat, J.; Raïssi, T. Robust Iterative Learning Observers Based on a Combination of Stochastic Estimation Schemes and Ellipsoidal Calculus. In Proceedings of the 25th International Conference on Information Fusion (FUSION), Linkoping, Sweden, 4–7 July 2022; pp. 1–8. [Google Scholar]
- Lahme, M.; Rauh, A. Combination of Stochastic State Estimation with Online Identification of the Open-Circuit Voltage of Lithium-Ion Batteries. In Proceedings of the 1st IFAC Workshop on Control of Complex Systems (COSY 2022), Bologna, Italy, 24–25 November 2022. [Google Scholar]
- Friedland, B. Quasi-Optimum Control and the SDRE Method. In Proceedings of the 17th IFAC Symposium on Automatic Control in Aerospace, Toulouse, France, 25–29 June 2007; pp. 762–767. [Google Scholar]
- Mracek, C.P.; Cloutier, J.R. Control Designs for the Nonlinear Benchmark Problem via the State-Dependent Riccati Equation Method. Int. J. Robust Nonlinear Control 1998, 8, 401–433. [Google Scholar] [CrossRef]
- Çimen, T. State-Dependent Riccati Equation (SDRE) Control: A Survey. In Proceedings of the 17th IFAC World Congress, Seoul, South Korea, 6–11 July 2008; pp. 3761–3775. [Google Scholar]

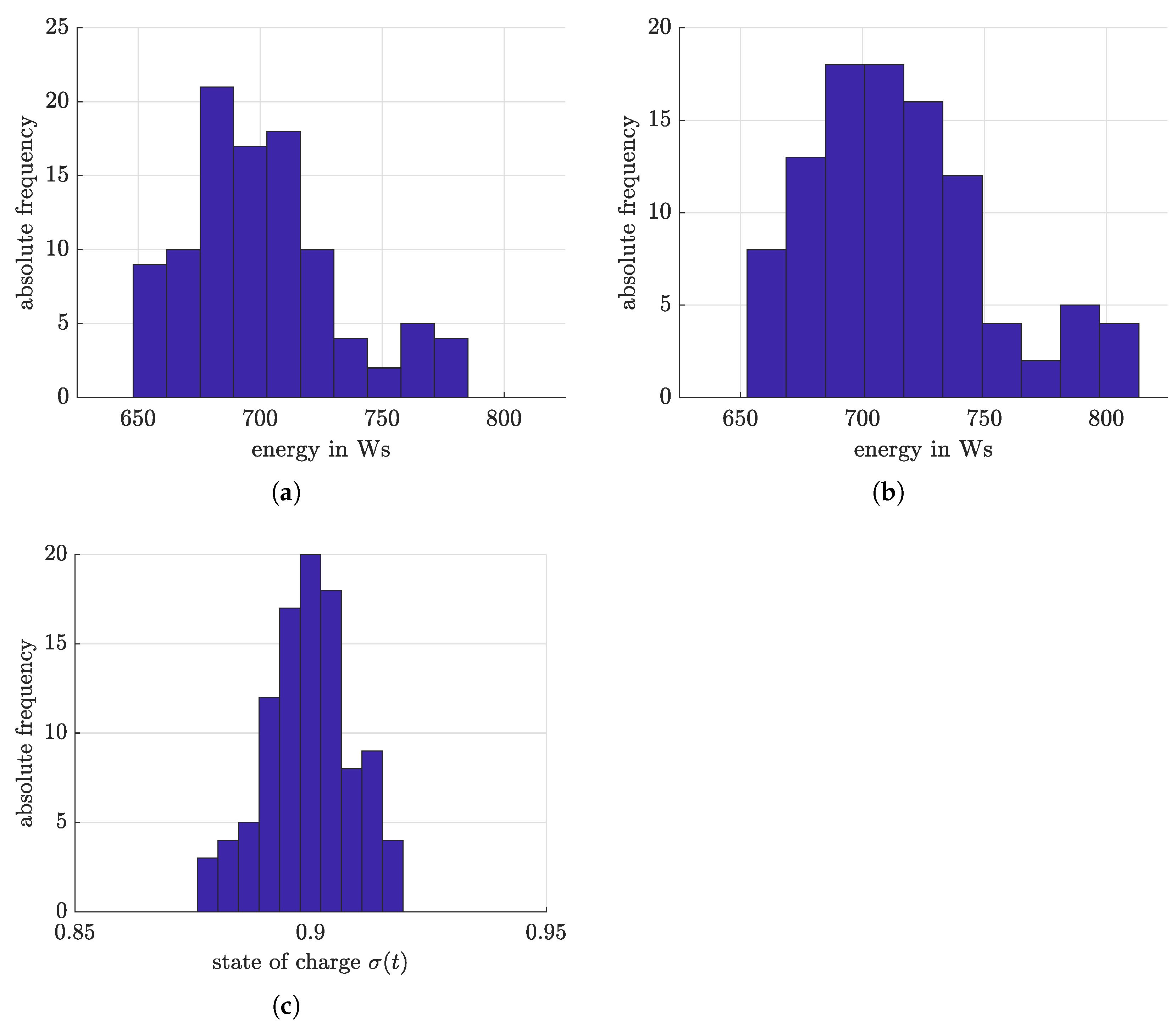
| Approach | Offline Effort | Online Effort | Robustness against Noise | Generalizability with Respect to Initial SOC | Optimization Efficiency |
|---|---|---|---|---|---|
| Maximum principle | medium | low | independent (pure offline solution) | low (recomputation required) | good |
| Predictive control | — | medium–high | depending on cost function parameters | excellent | excellent |
| Linear-quadratic feedback control | low | low | depending on cost function parameters | medium–good | low |
| Reinforcement learning | high | low–medium | high for sufficiently rich training data | good–excellent | excellent |
| Losses during Charging () | Total Losses () | |
|---|---|---|
| 1 | ||
| Losses during Charging () | Total Losses () | |
|---|---|---|
| 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rauh, A.; Lahme, M.; Benzinane, O. A Comparison of the Use of Pontryagin’s Maximum Principle and Reinforcement Learning Techniques for the Optimal Charging of Lithium-Ion Batteries. Clean Technol. 2022, 4, 1269-1289. https://doi.org/10.3390/cleantechnol4040078
Rauh A, Lahme M, Benzinane O. A Comparison of the Use of Pontryagin’s Maximum Principle and Reinforcement Learning Techniques for the Optimal Charging of Lithium-Ion Batteries. Clean Technologies. 2022; 4(4):1269-1289. https://doi.org/10.3390/cleantechnol4040078
Chicago/Turabian StyleRauh, Andreas, Marit Lahme, and Oussama Benzinane. 2022. "A Comparison of the Use of Pontryagin’s Maximum Principle and Reinforcement Learning Techniques for the Optimal Charging of Lithium-Ion Batteries" Clean Technologies 4, no. 4: 1269-1289. https://doi.org/10.3390/cleantechnol4040078
APA StyleRauh, A., Lahme, M., & Benzinane, O. (2022). A Comparison of the Use of Pontryagin’s Maximum Principle and Reinforcement Learning Techniques for the Optimal Charging of Lithium-Ion Batteries. Clean Technologies, 4(4), 1269-1289. https://doi.org/10.3390/cleantechnol4040078






