Assessment of the Accuracy of ISRIC and ESDAC Soil Texture Data Compared to the Soil Map of Greece: A Statistical and Spatial Approach to Identify Sources of Differences †
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Description
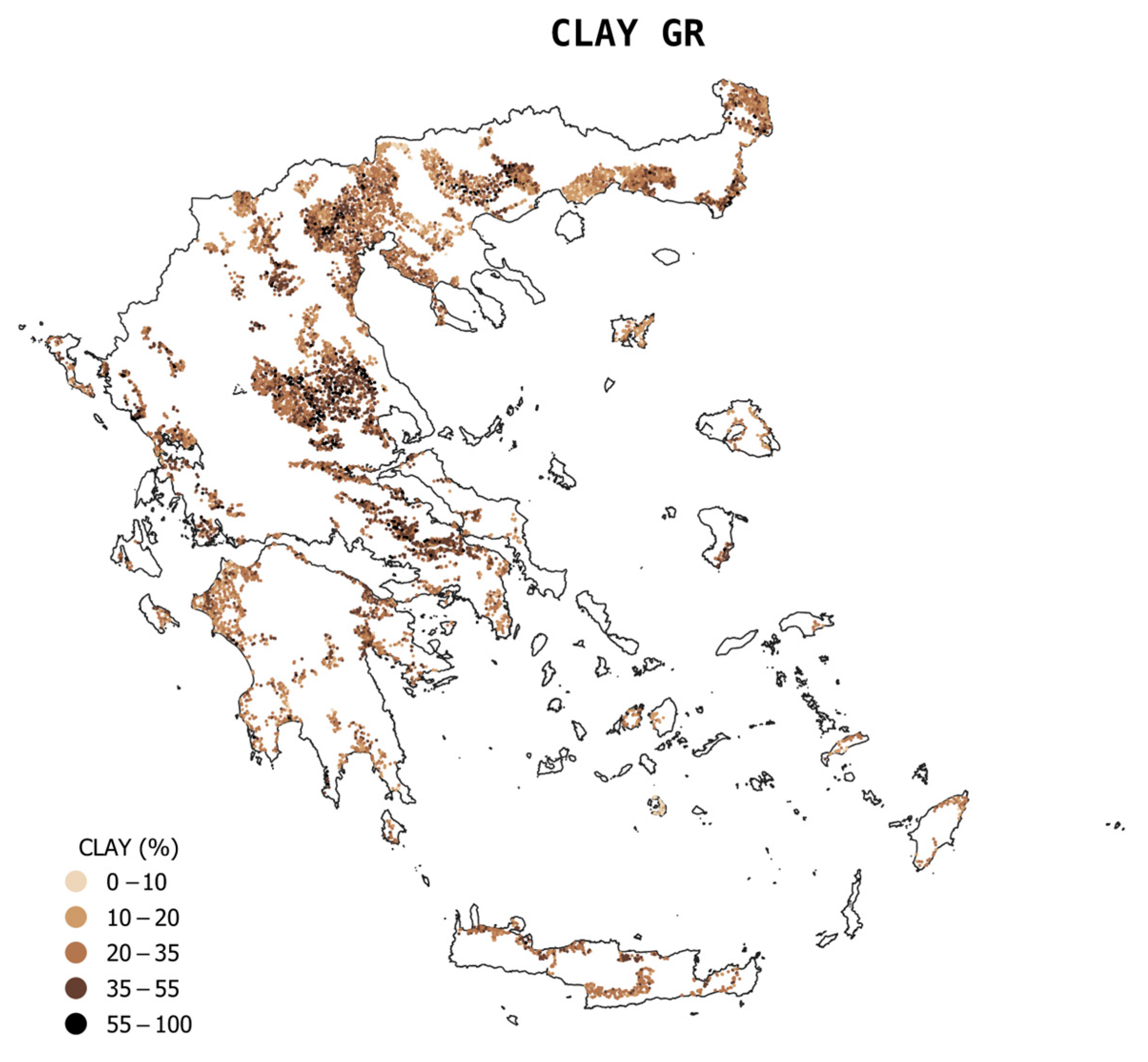
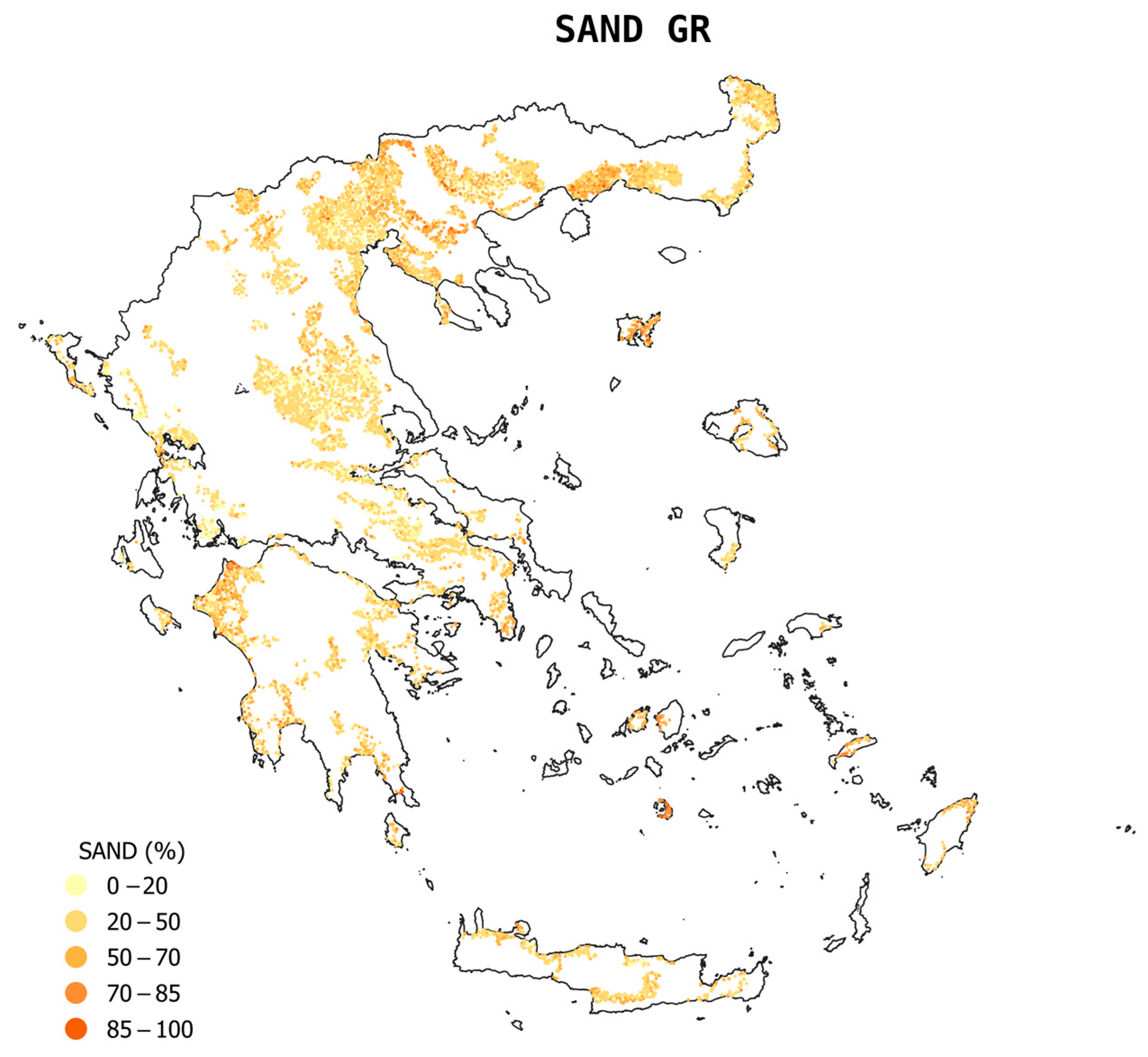
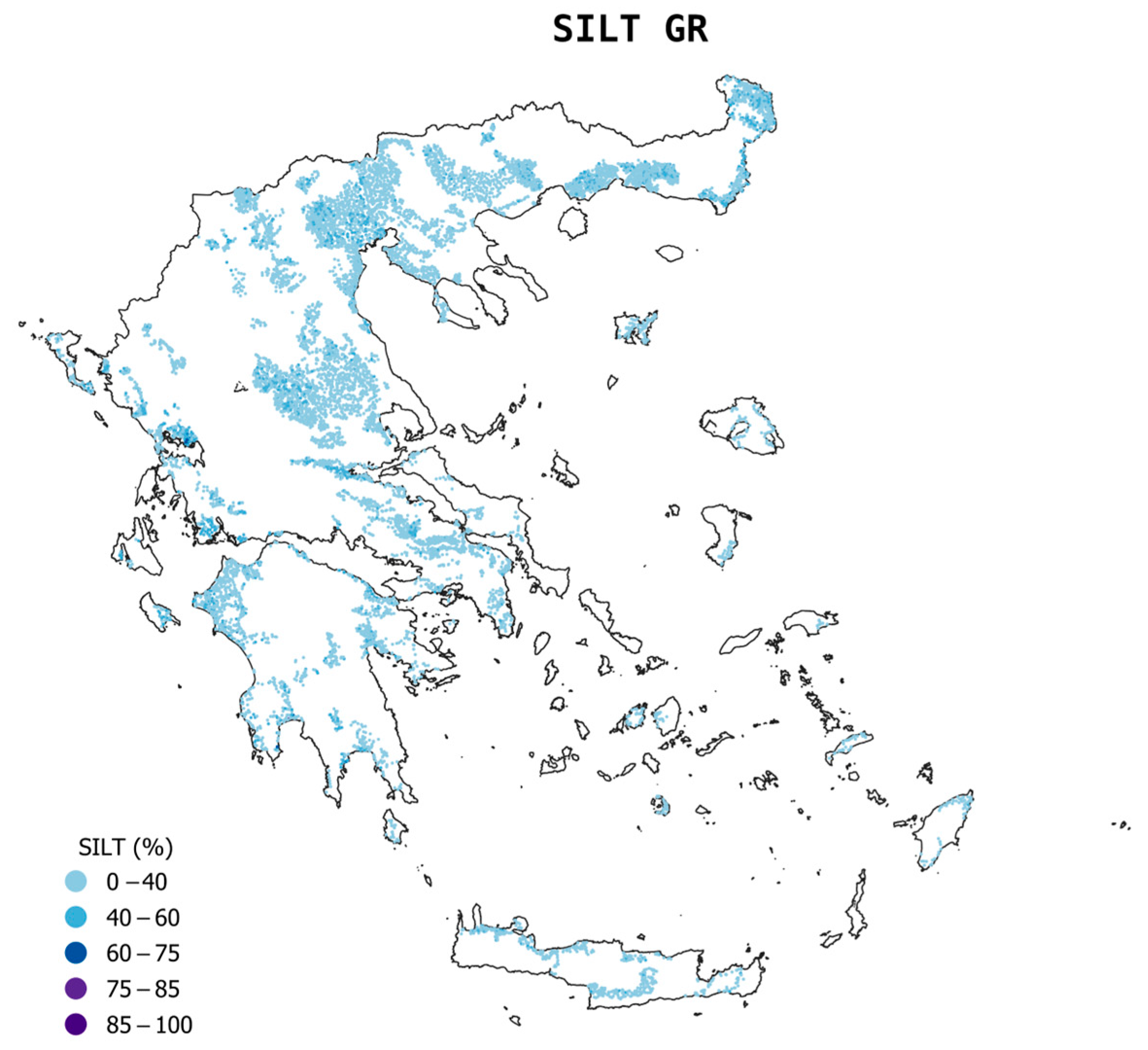
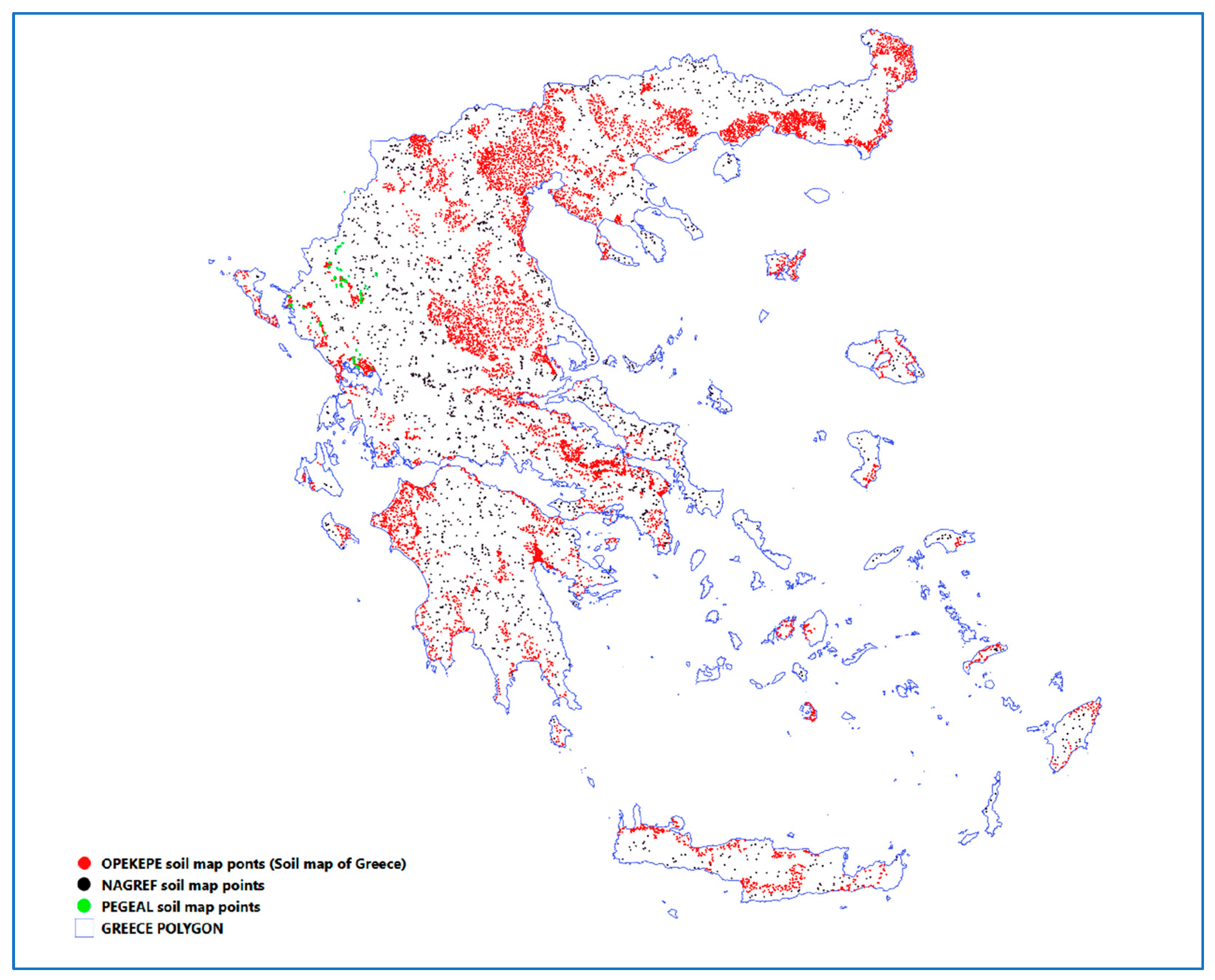
2.2.1. Greek Soil Map
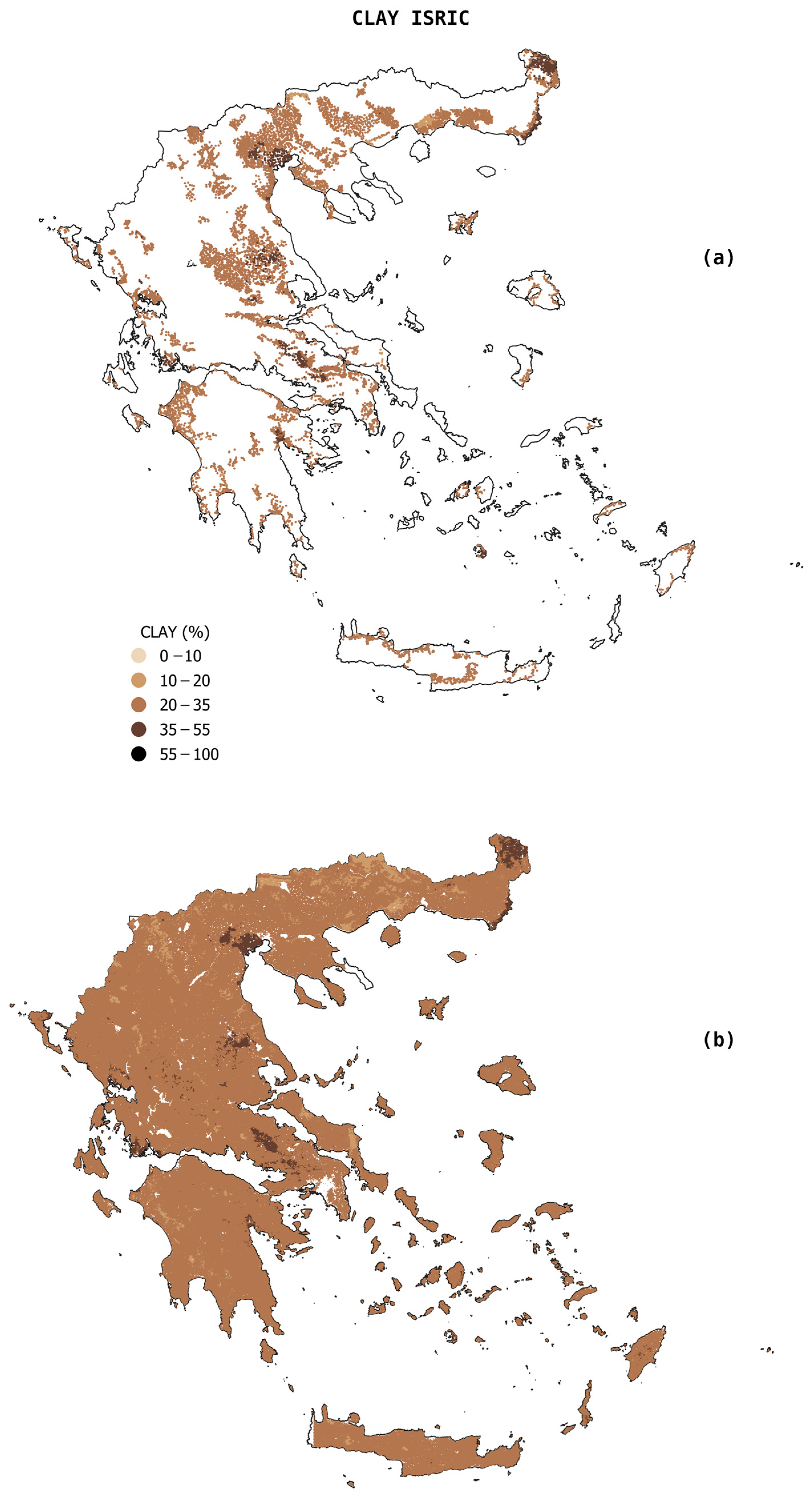
2.2.2. ISRIC Soil Grids
2.2.3. JRC ESDAC Raster Soil Map
2.2.4. Forested Areas Soil Dataset of the NAGREF
2.2.5. Regional Data Sources
2.3. Overall Methodology
2.3.1. Data Acquisition
2.3.2. Raster Processing
2.3.3. Raster Value Extraction Process
2.3.4. Error Calculation
2.3.5. Statistical Analysis
2.3.6. Spatial Variability Analysis
- (i)
- A statistical correlation analysis was performed between the geomorphological variables previously integrated into the attribute table and the prediction errors, aiming to assess the influence of terrain factors on estimation accuracy.
- (ii)
- A clustering analysis of the prediction errors was conducted to identify spatial patterns and areas exhibiting systematic deviations, potentially indicating the influence of localized environmental conditions or limitations in the predictive modeling frameworks.
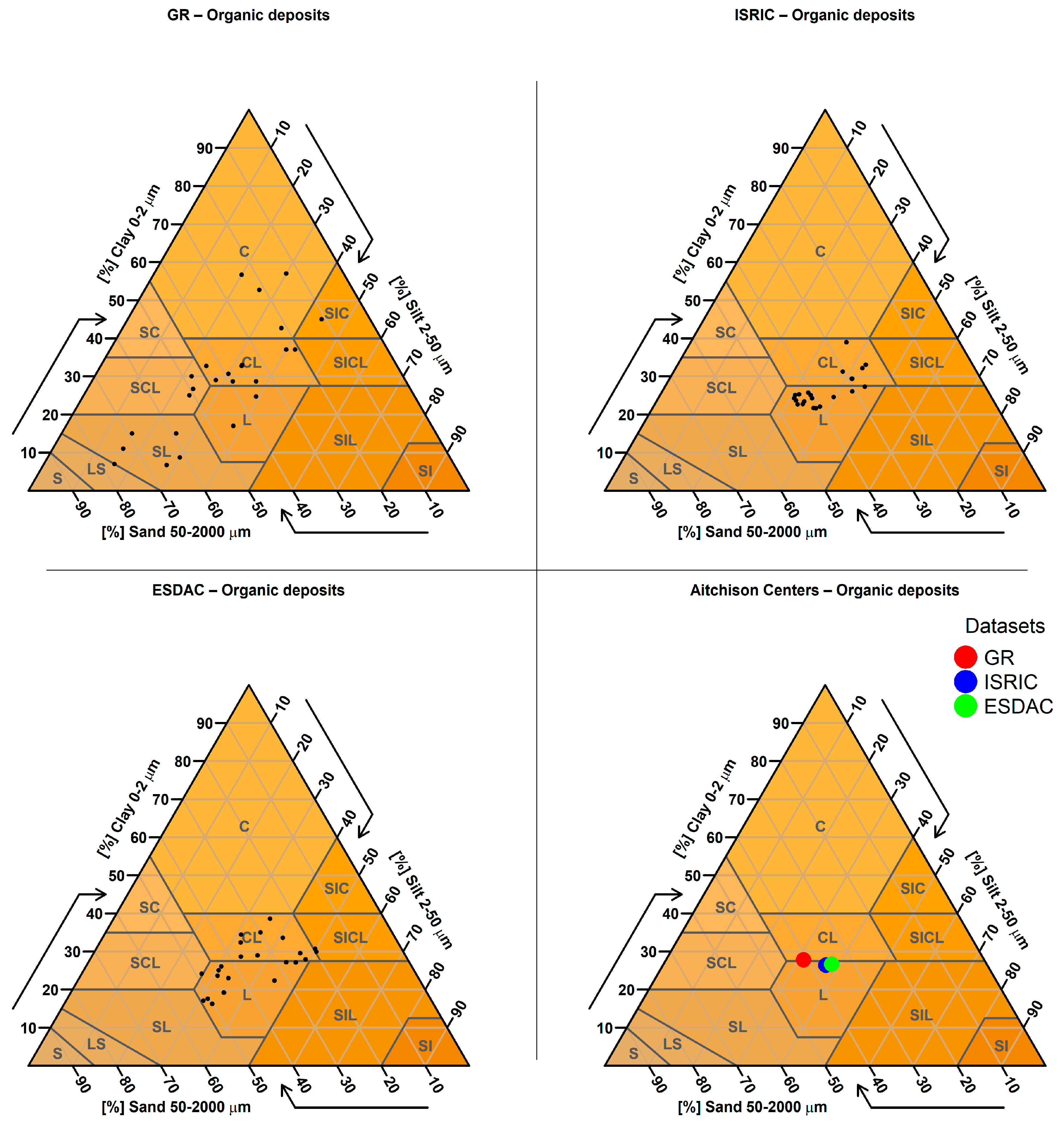
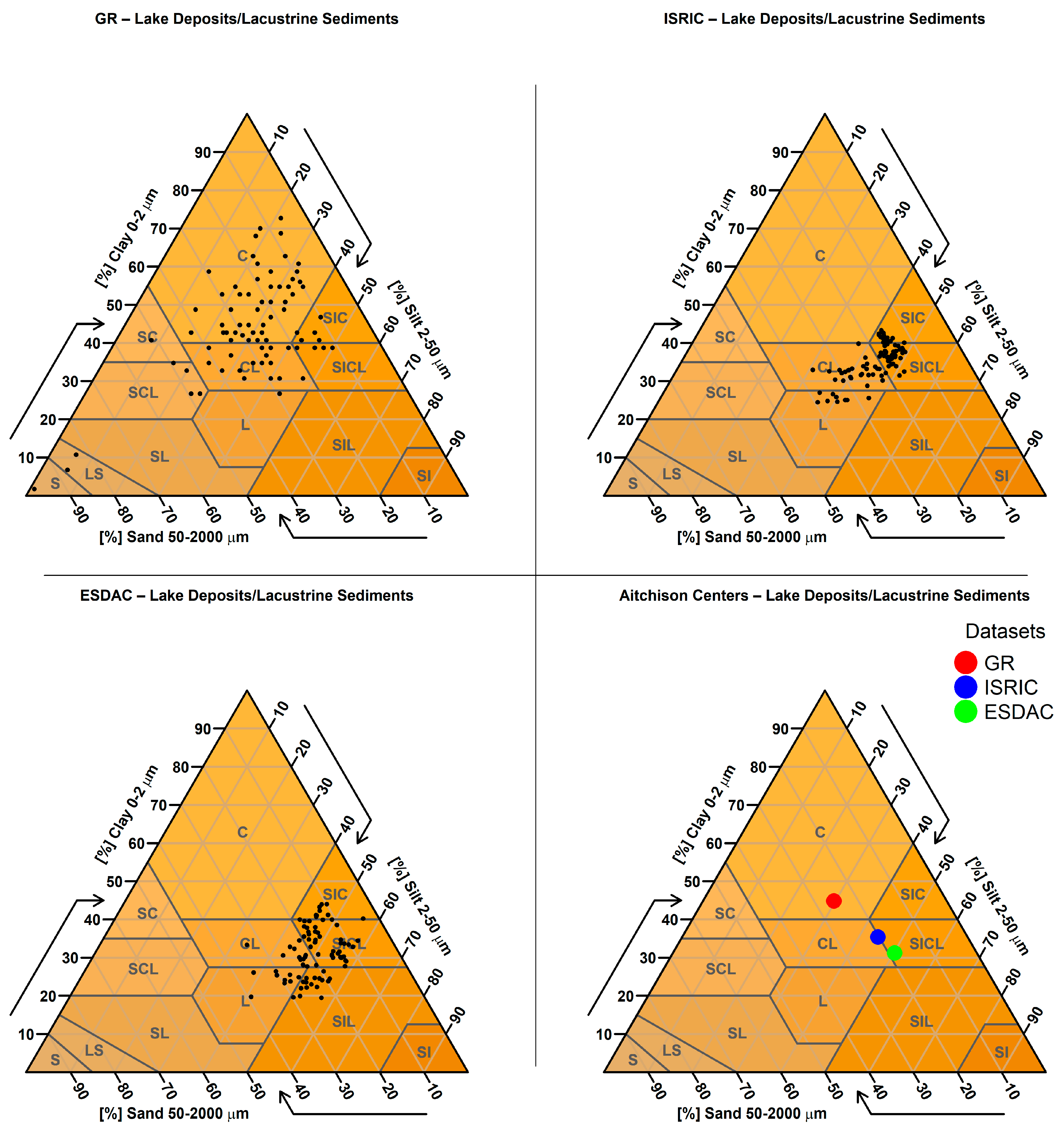
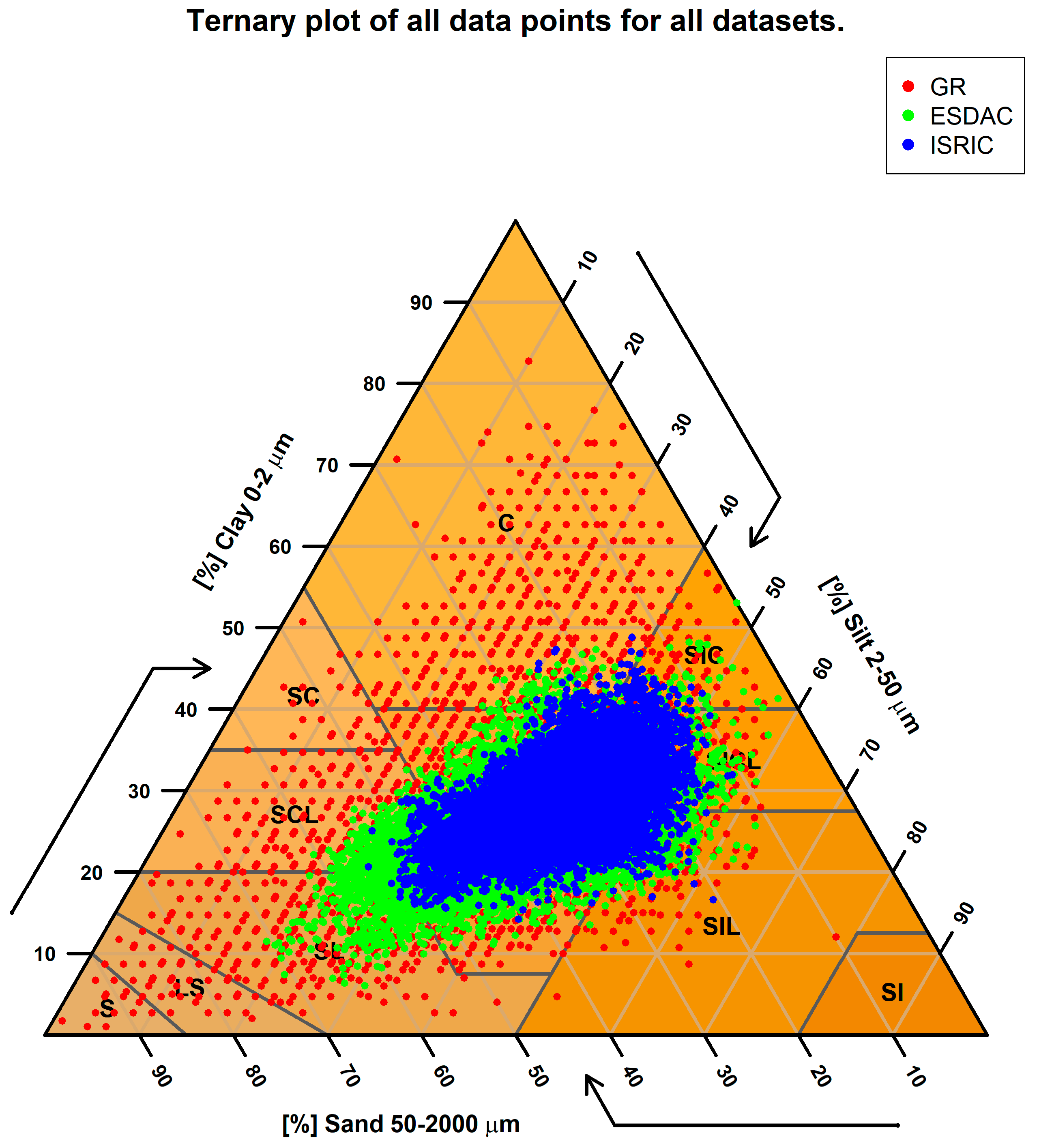
2.3.7. Soil Texture Classification
2.3.8. Categorical Comparison of Soil Texture Classes
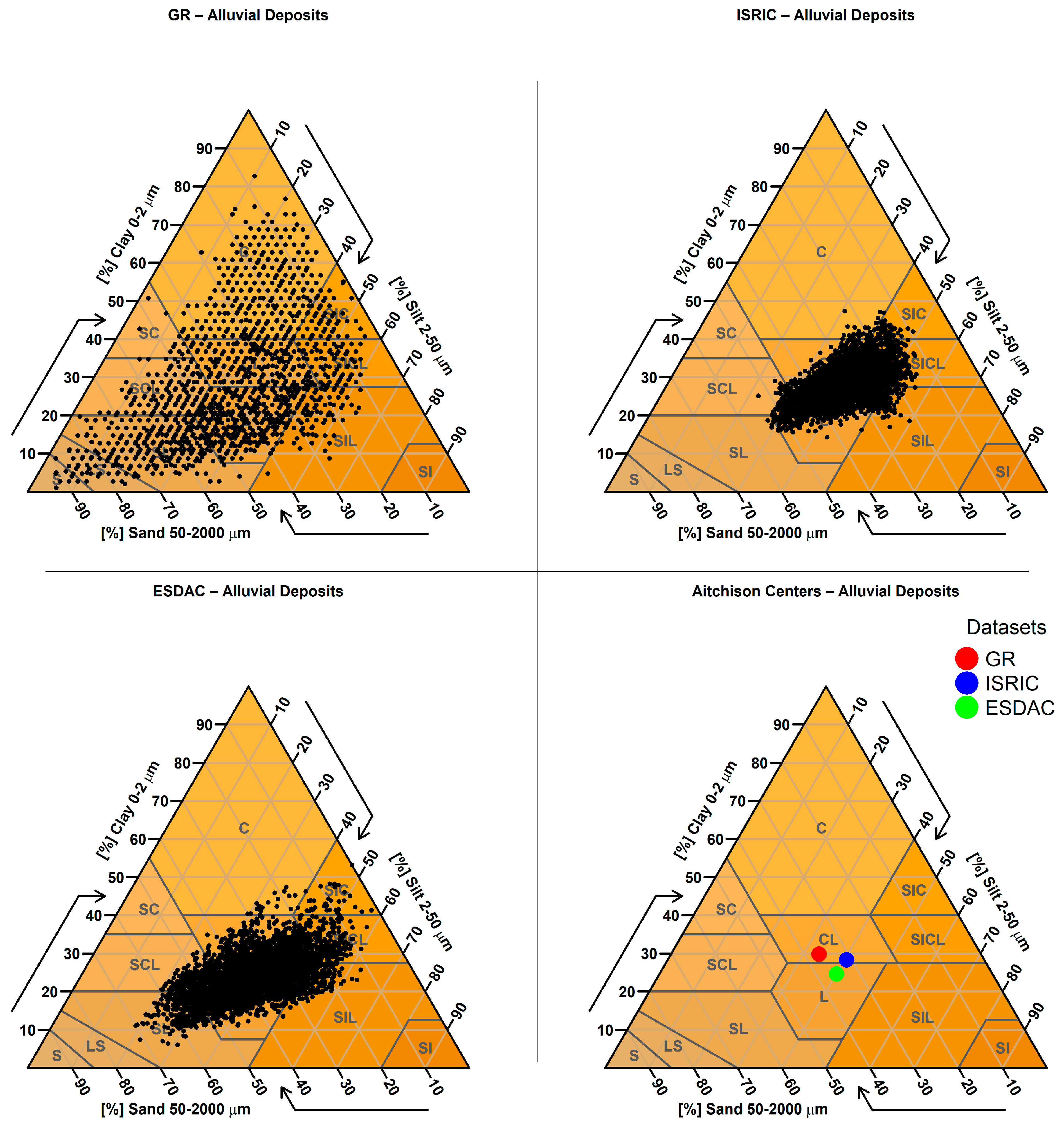
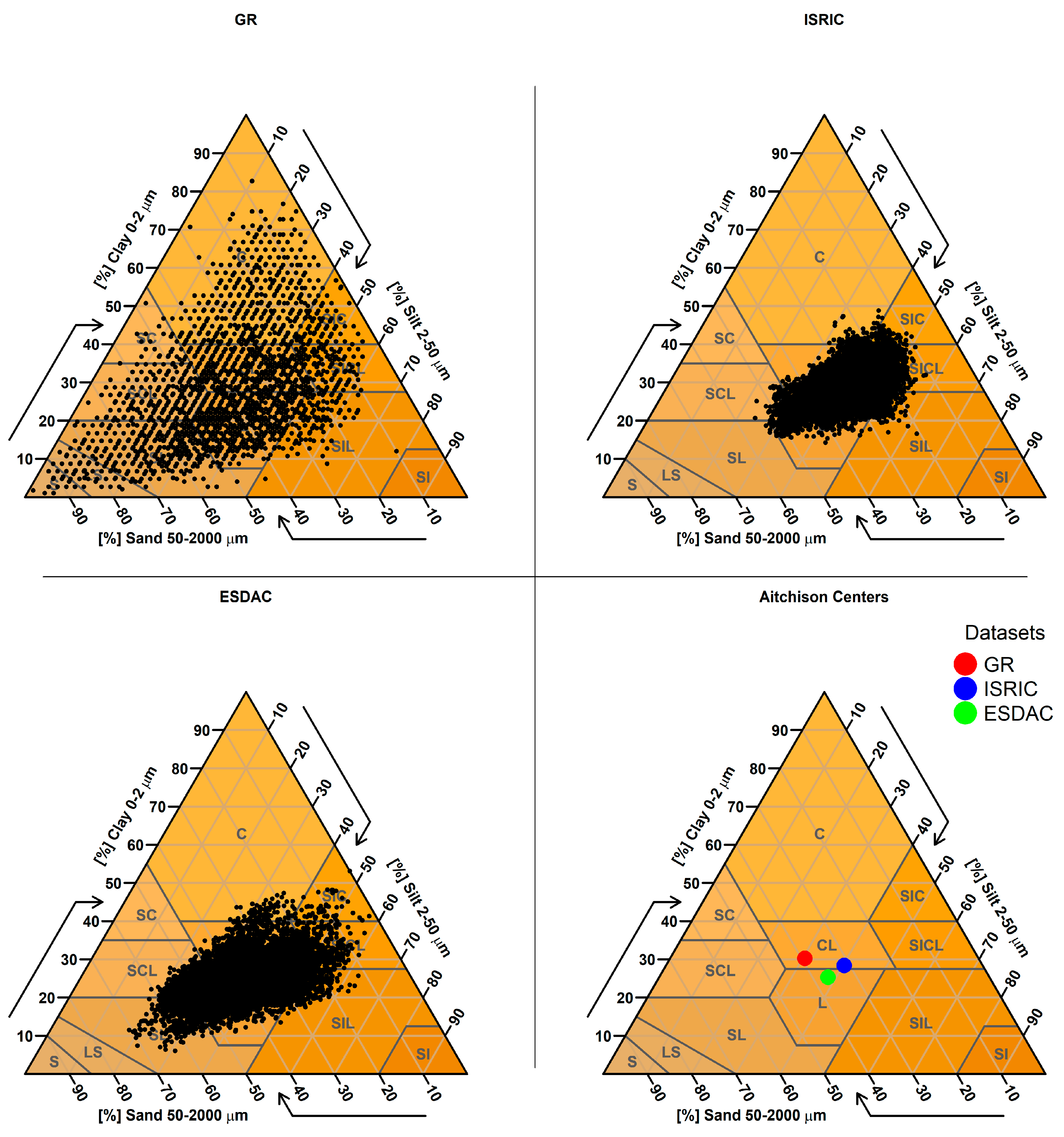
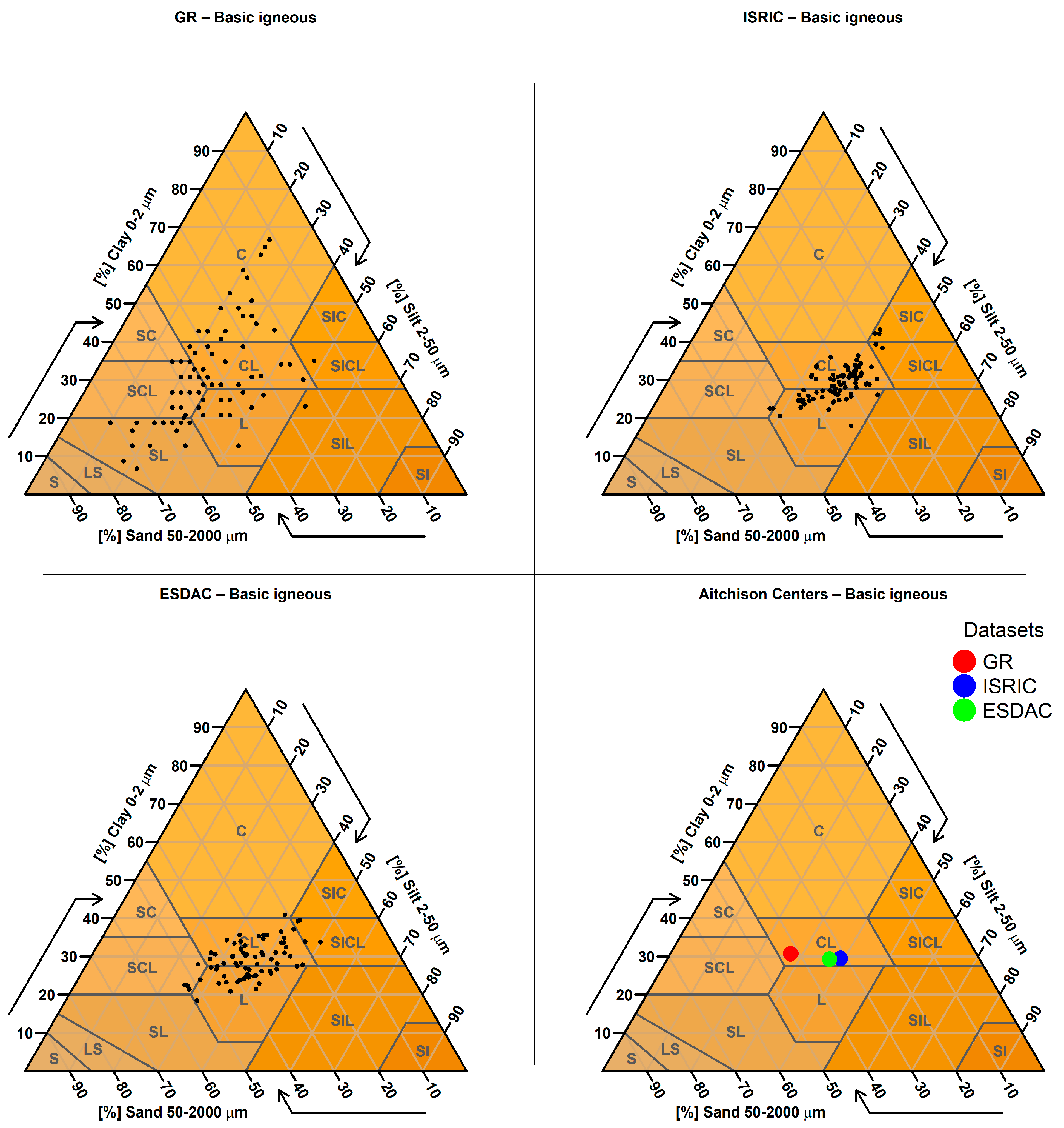
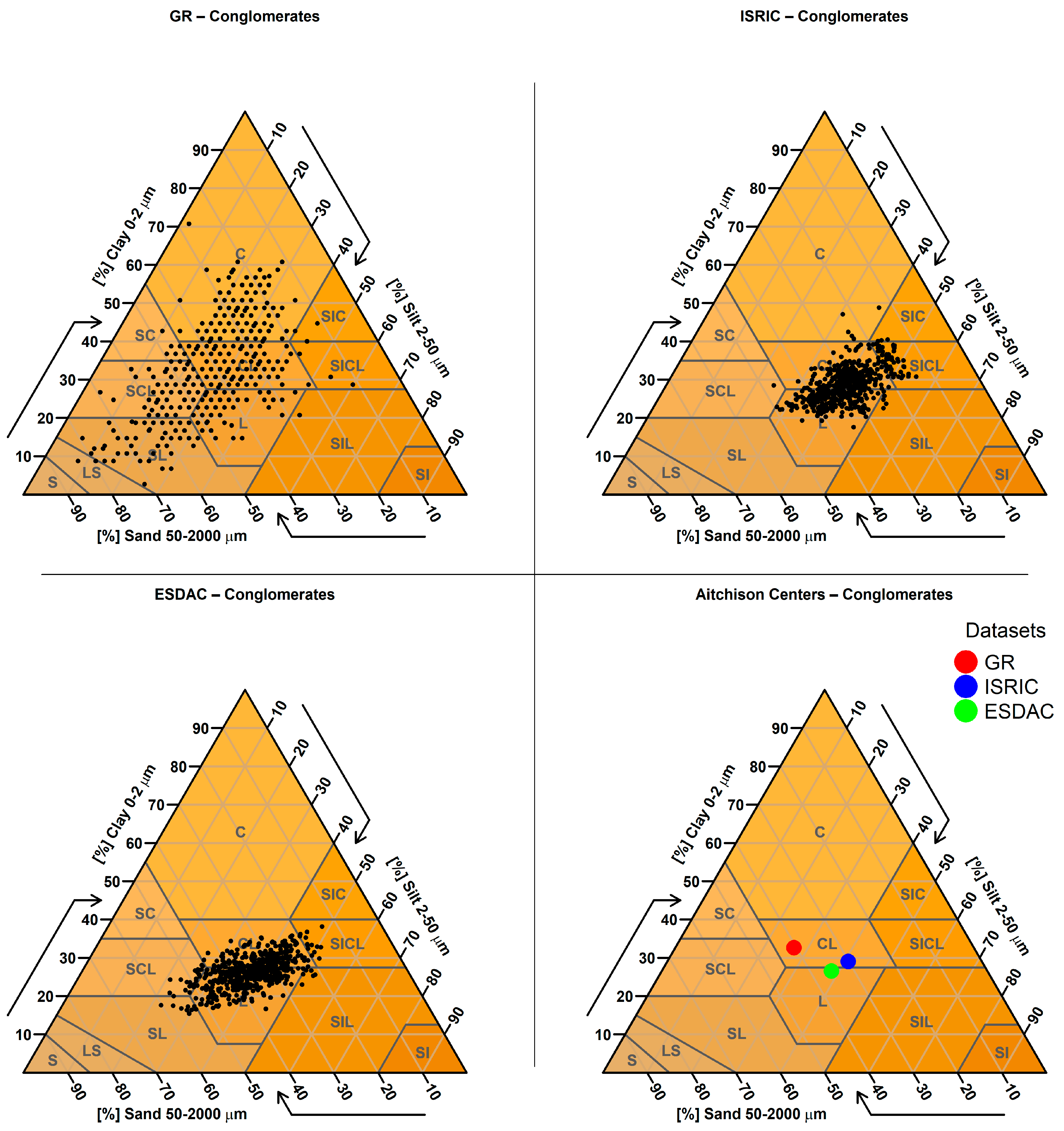
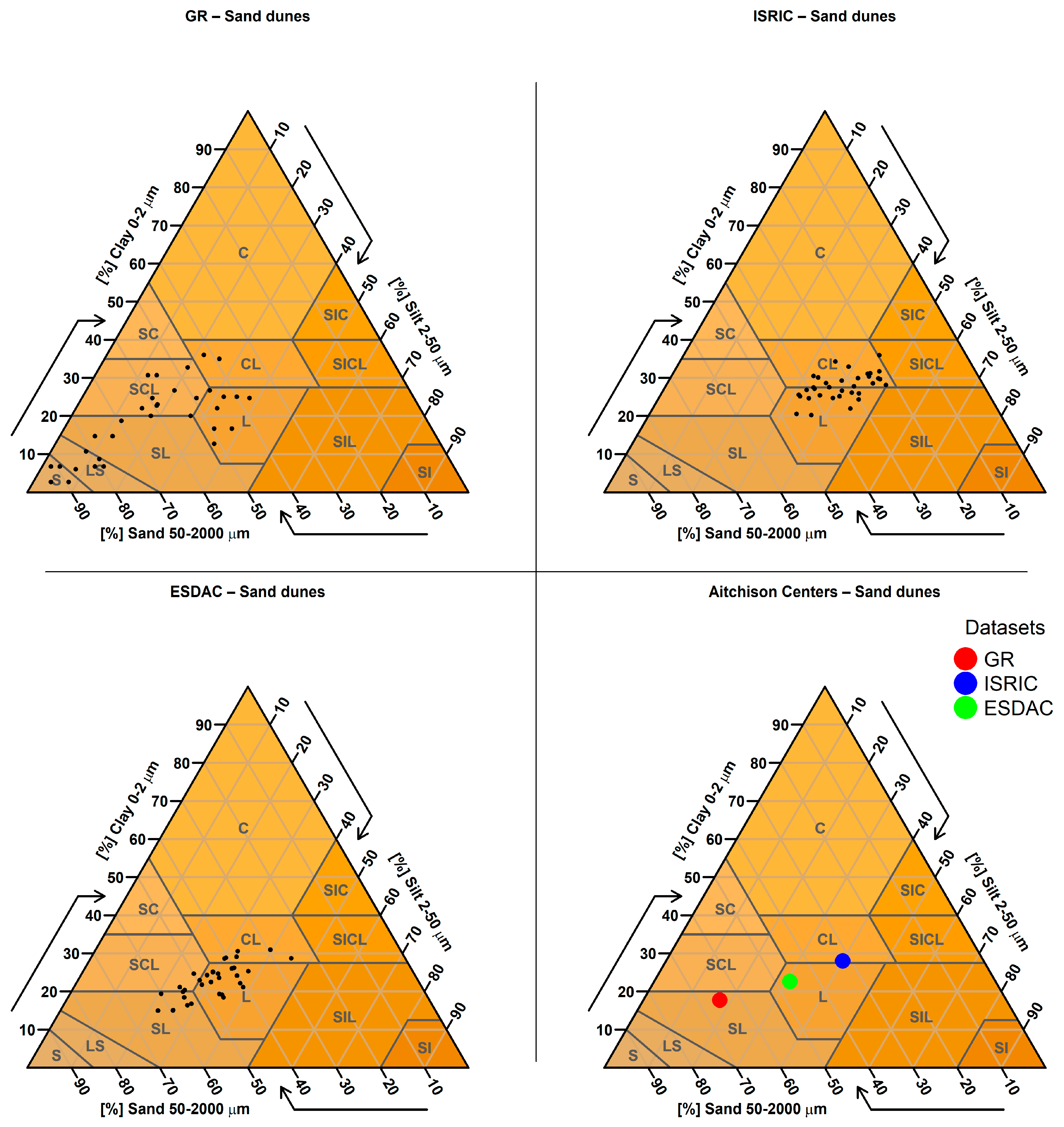
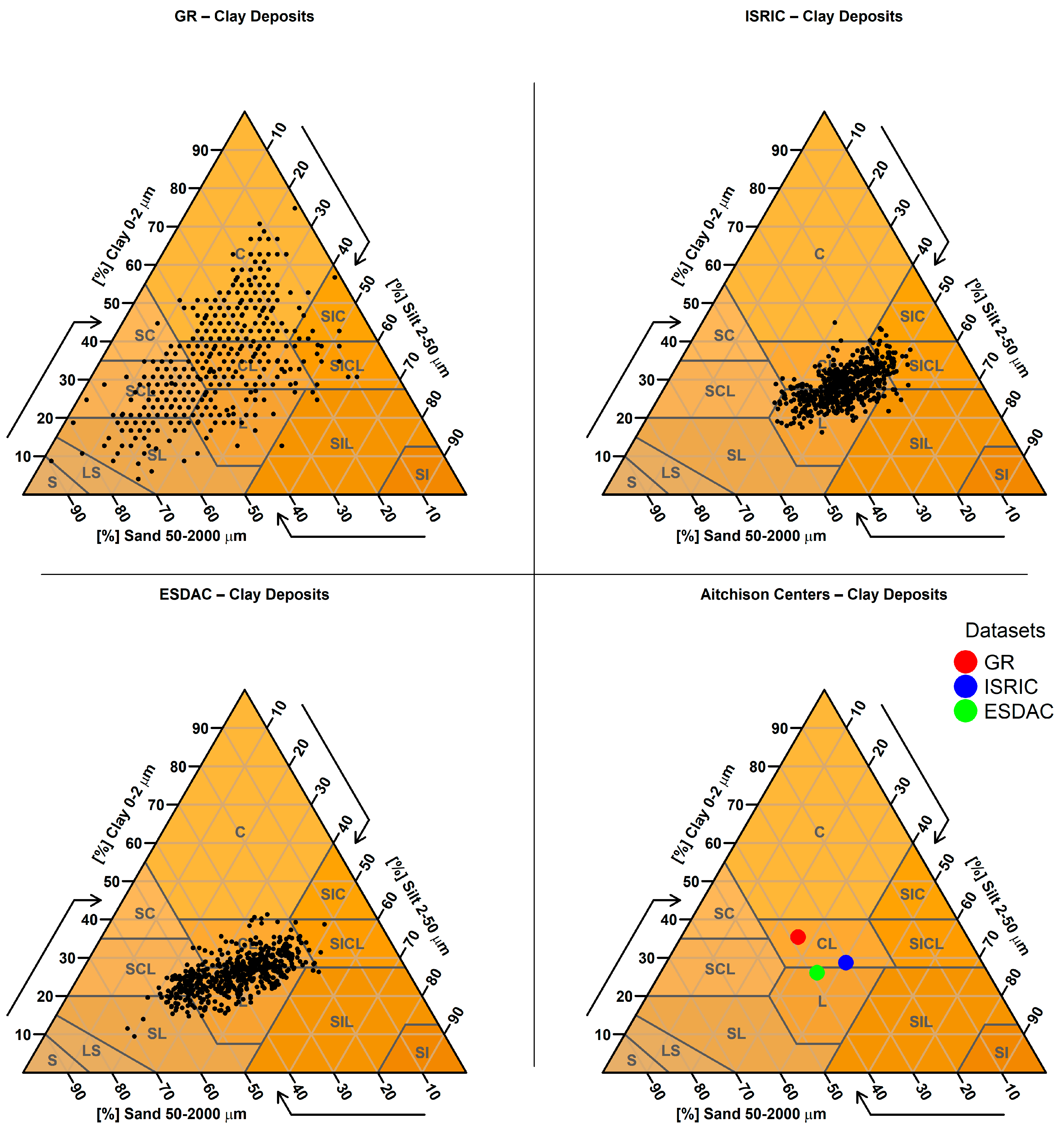
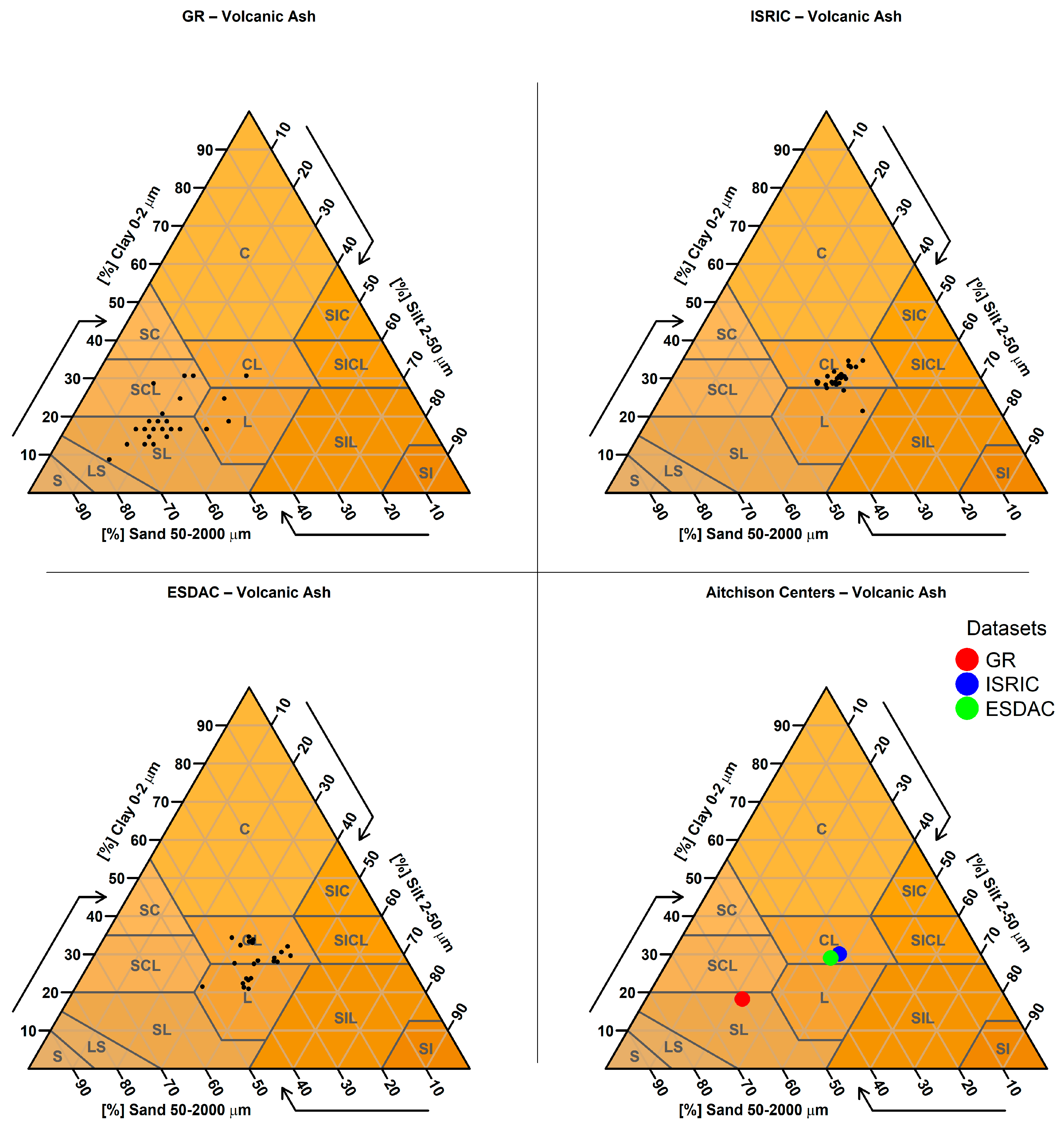
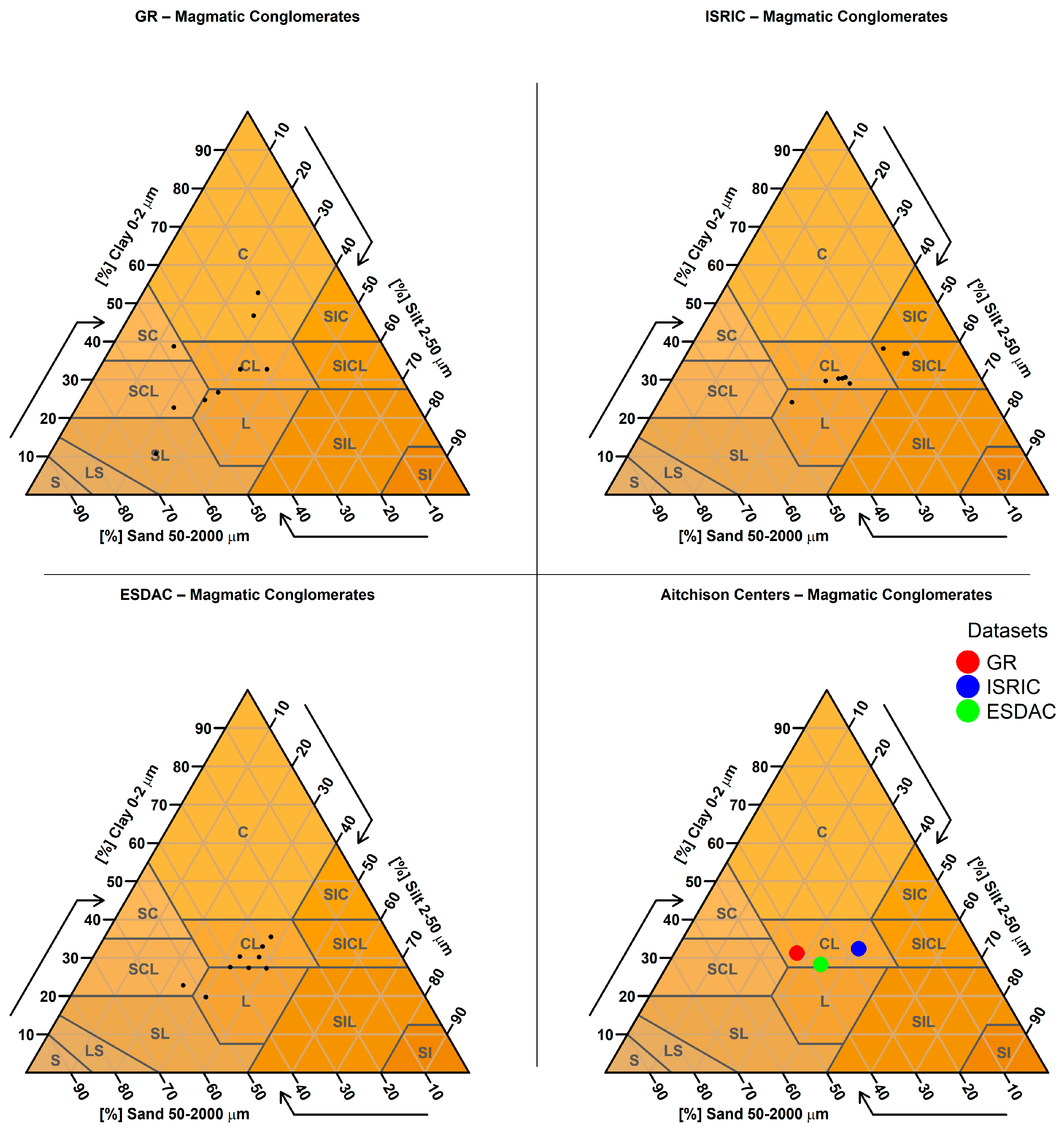
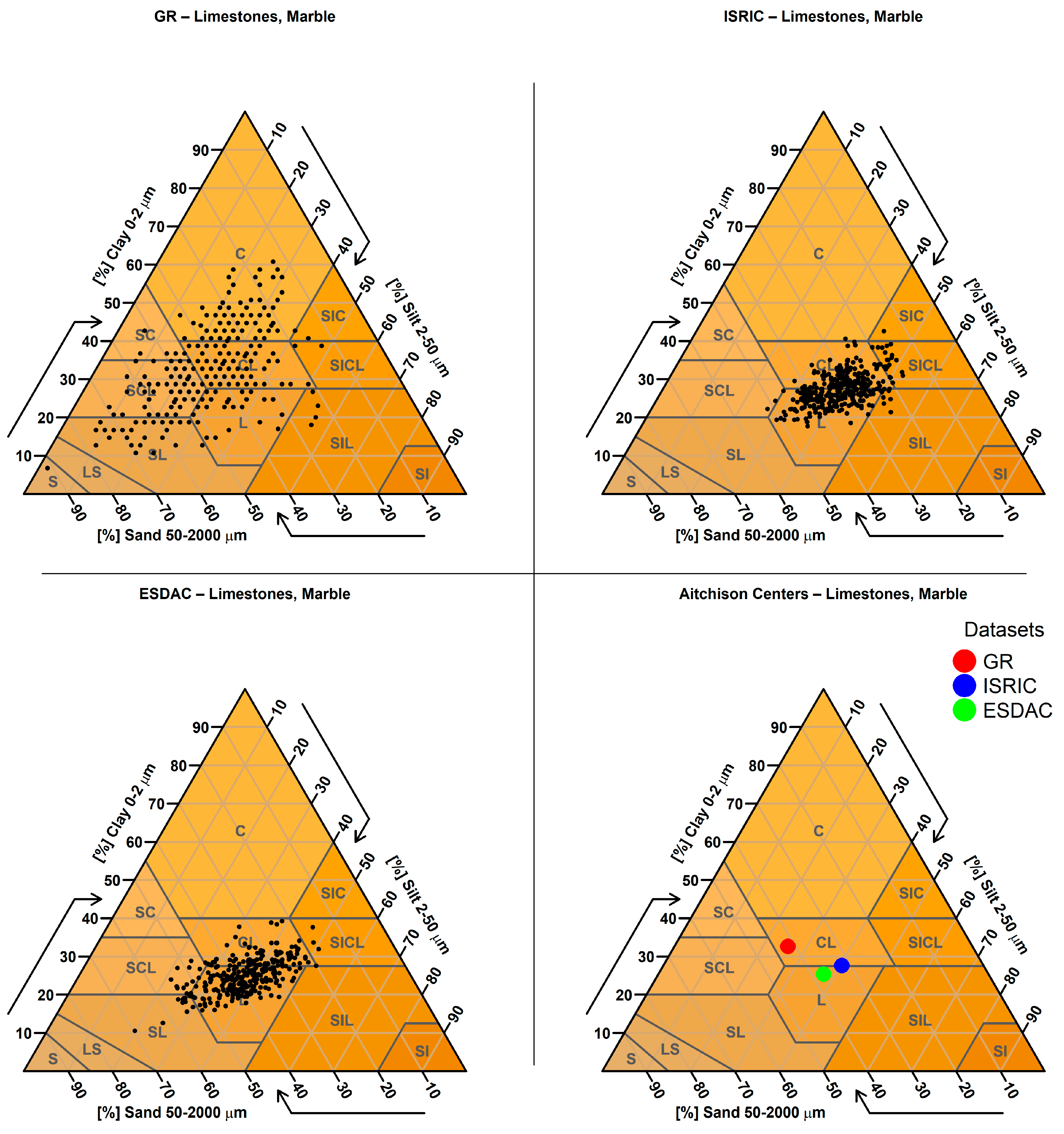
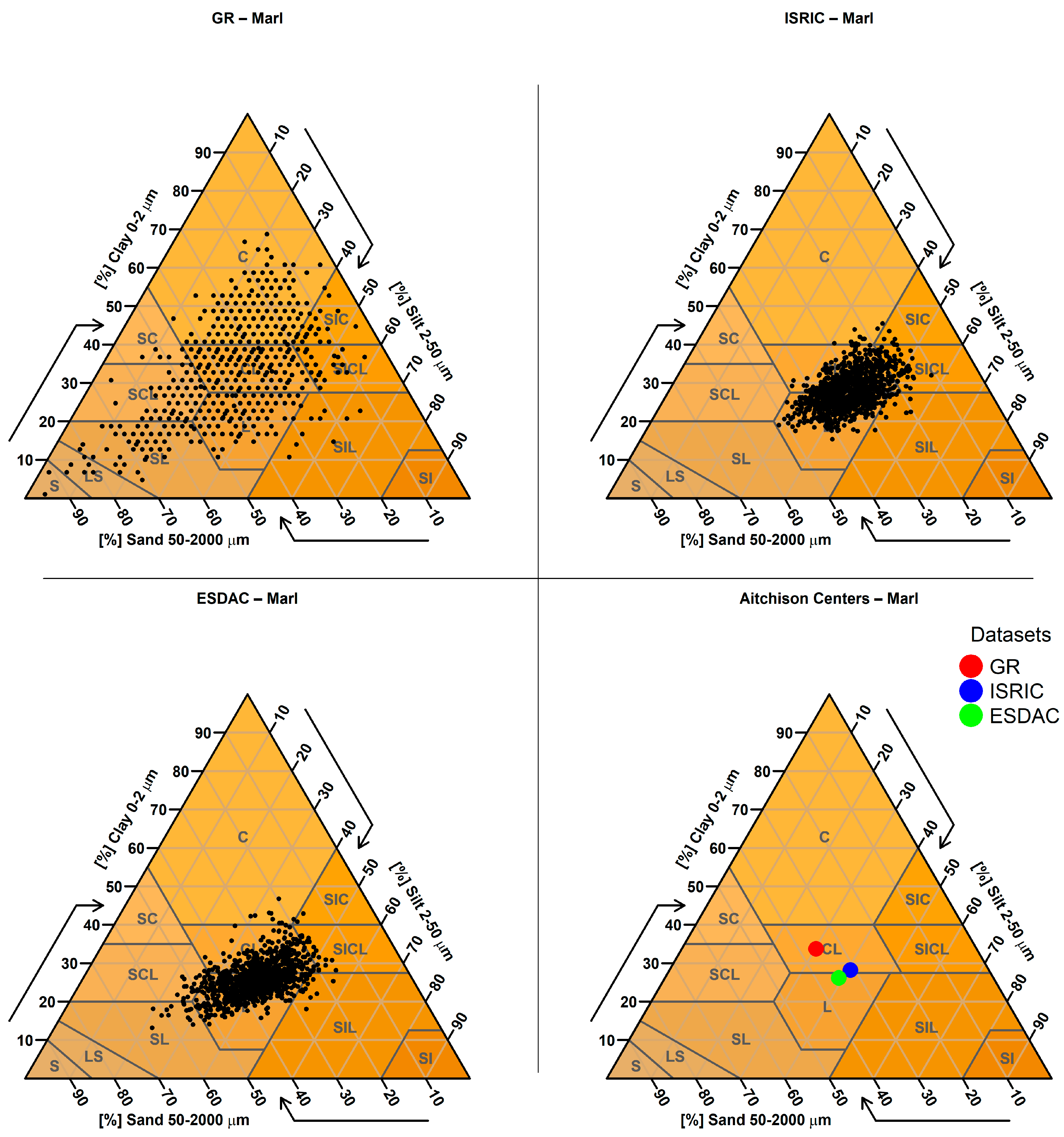
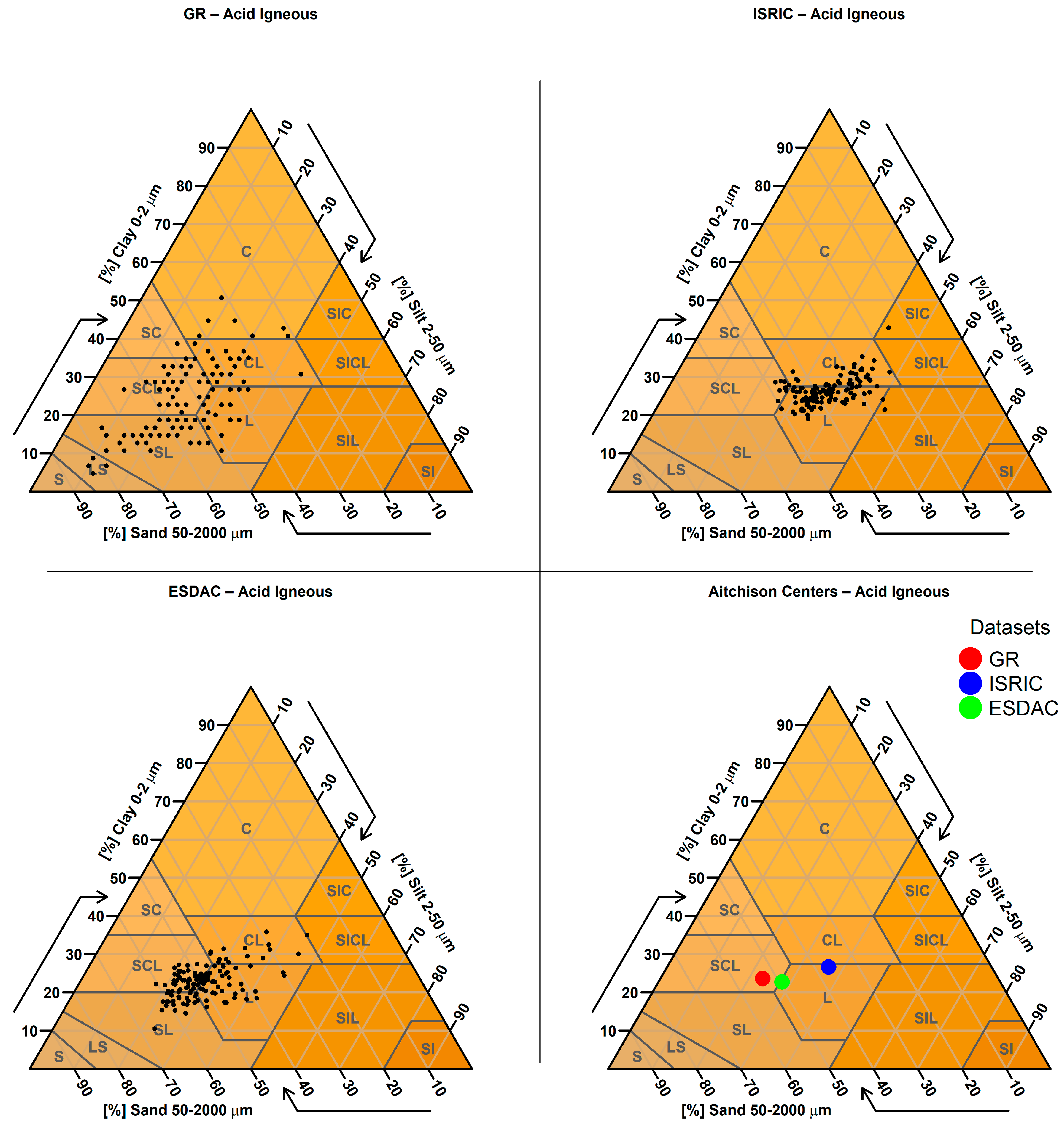
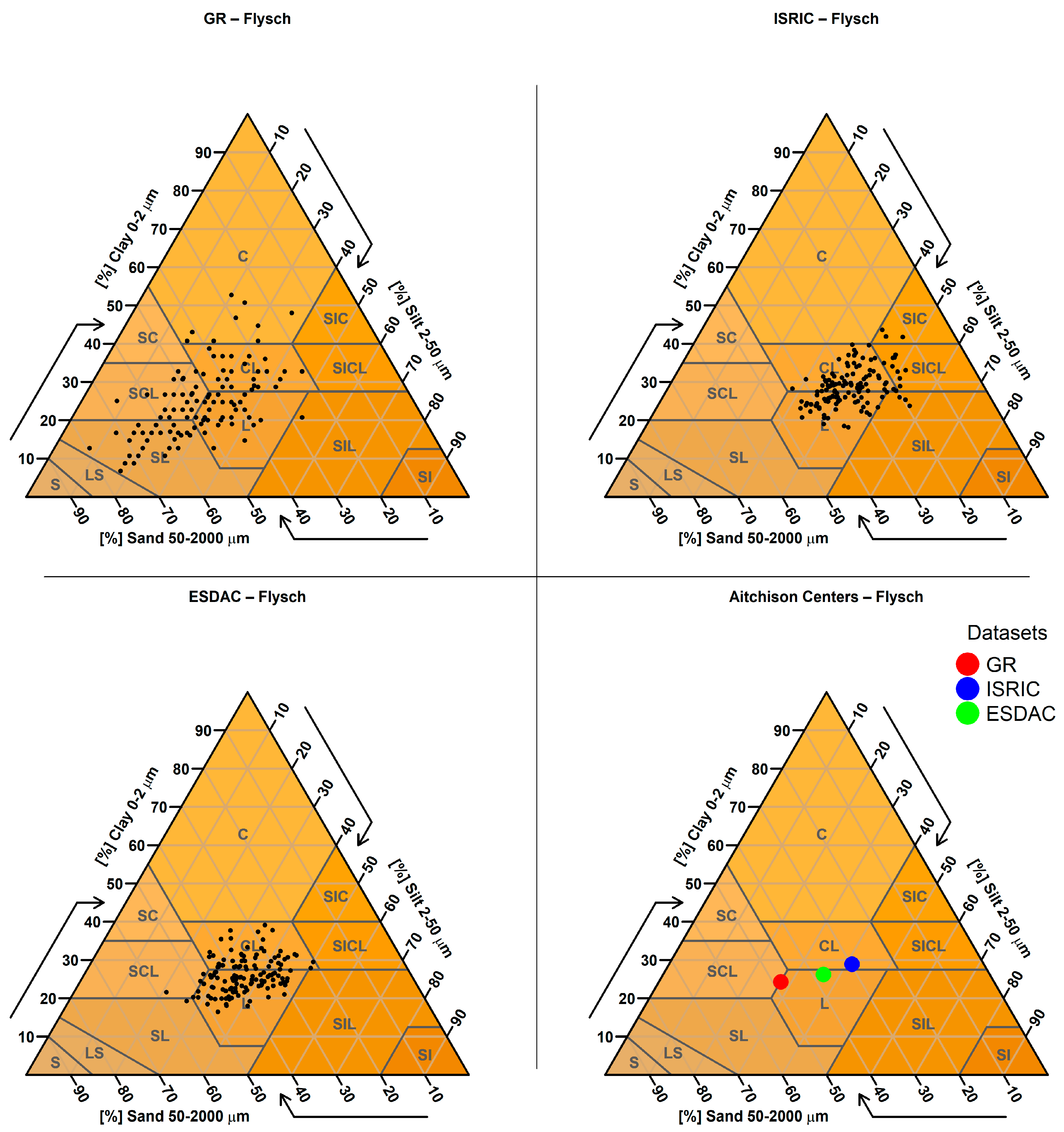
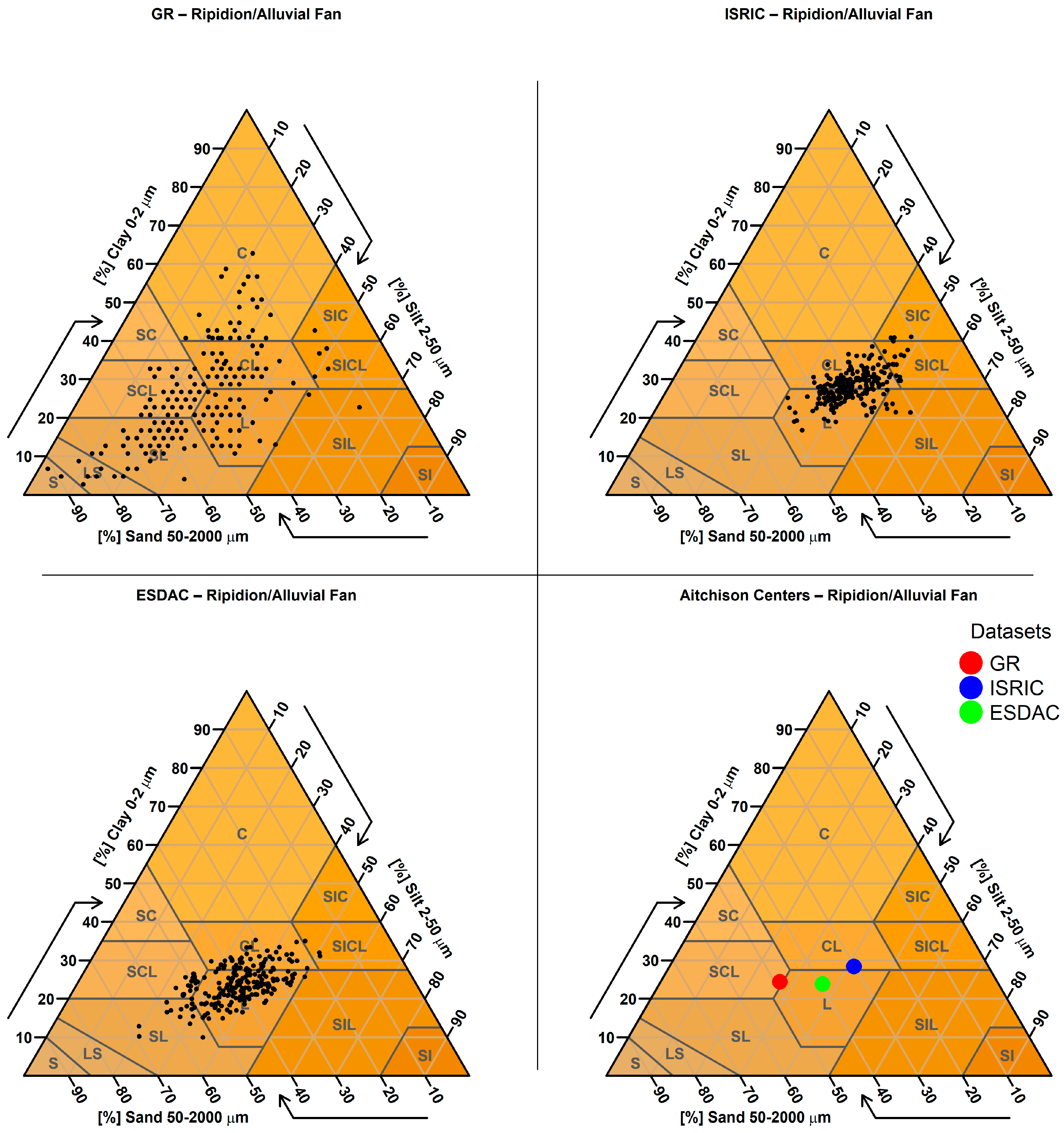
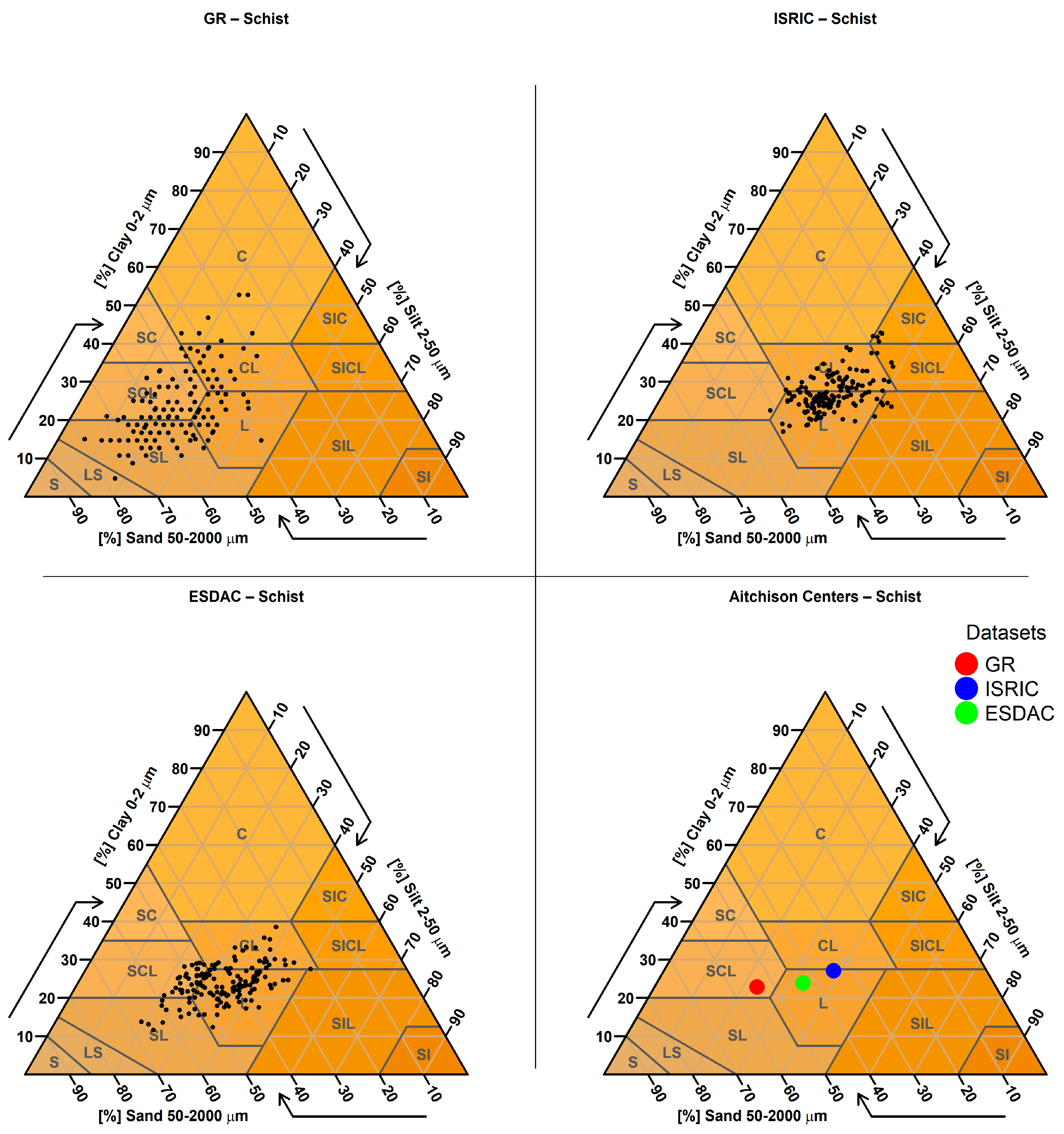
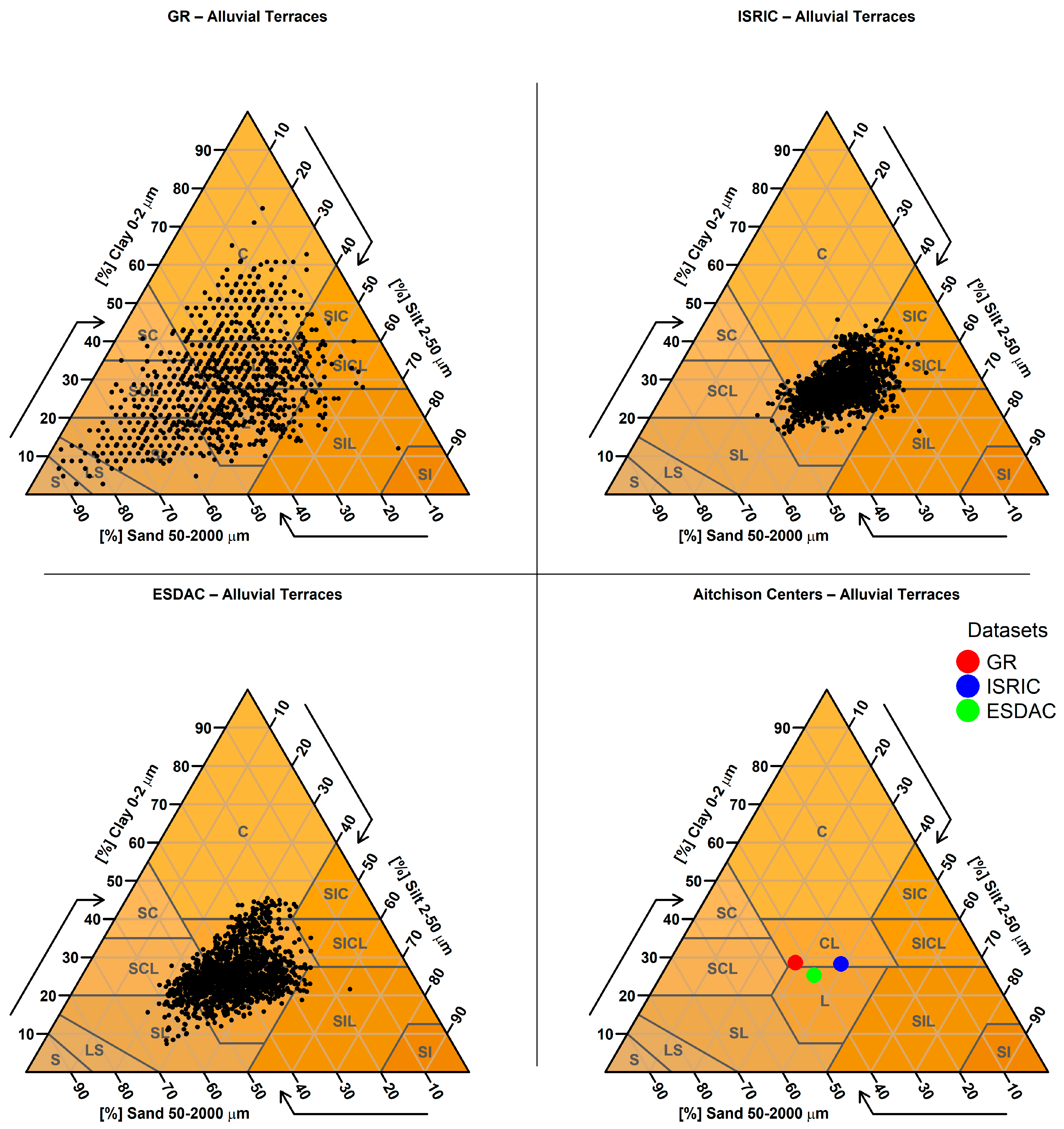
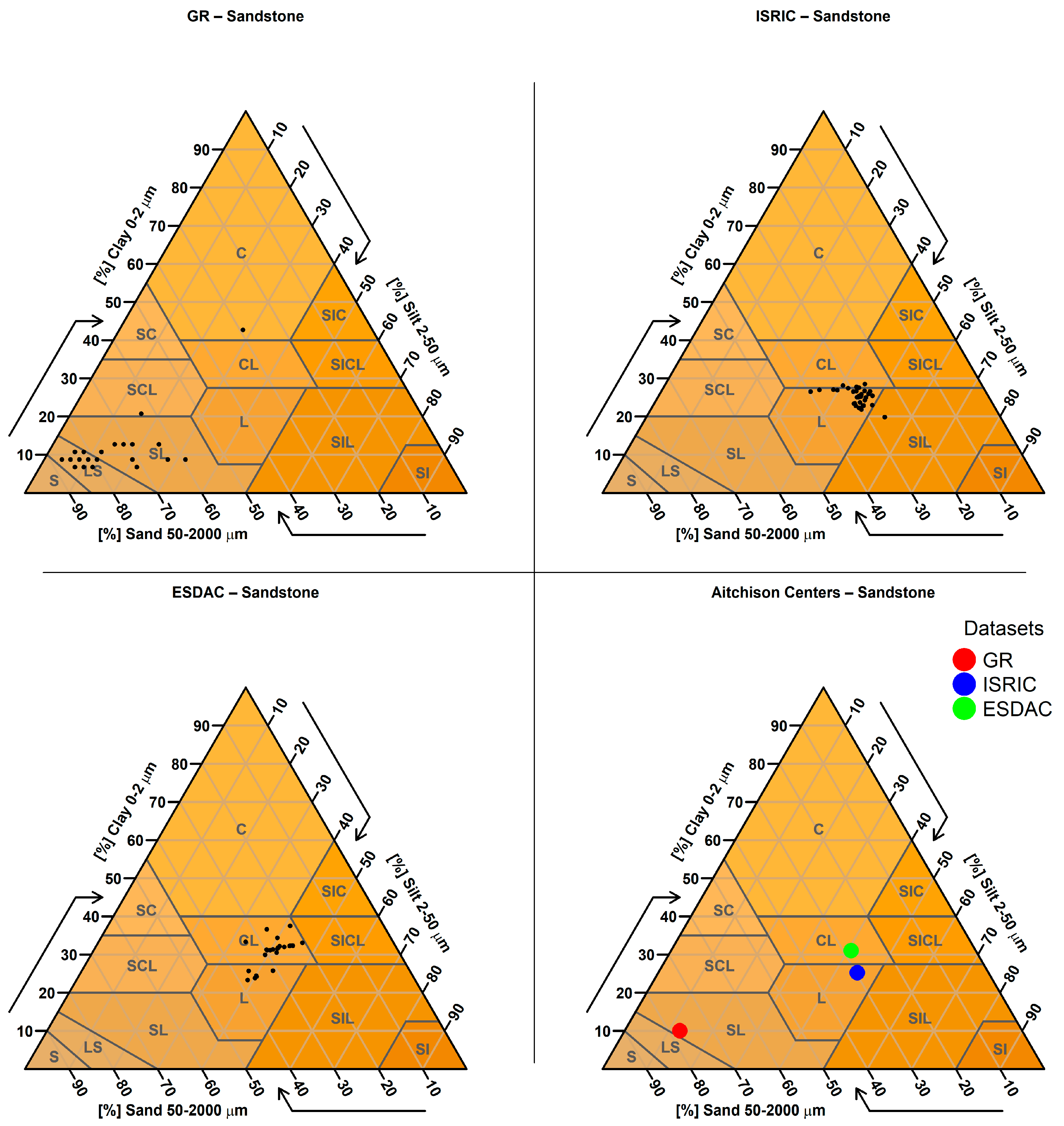
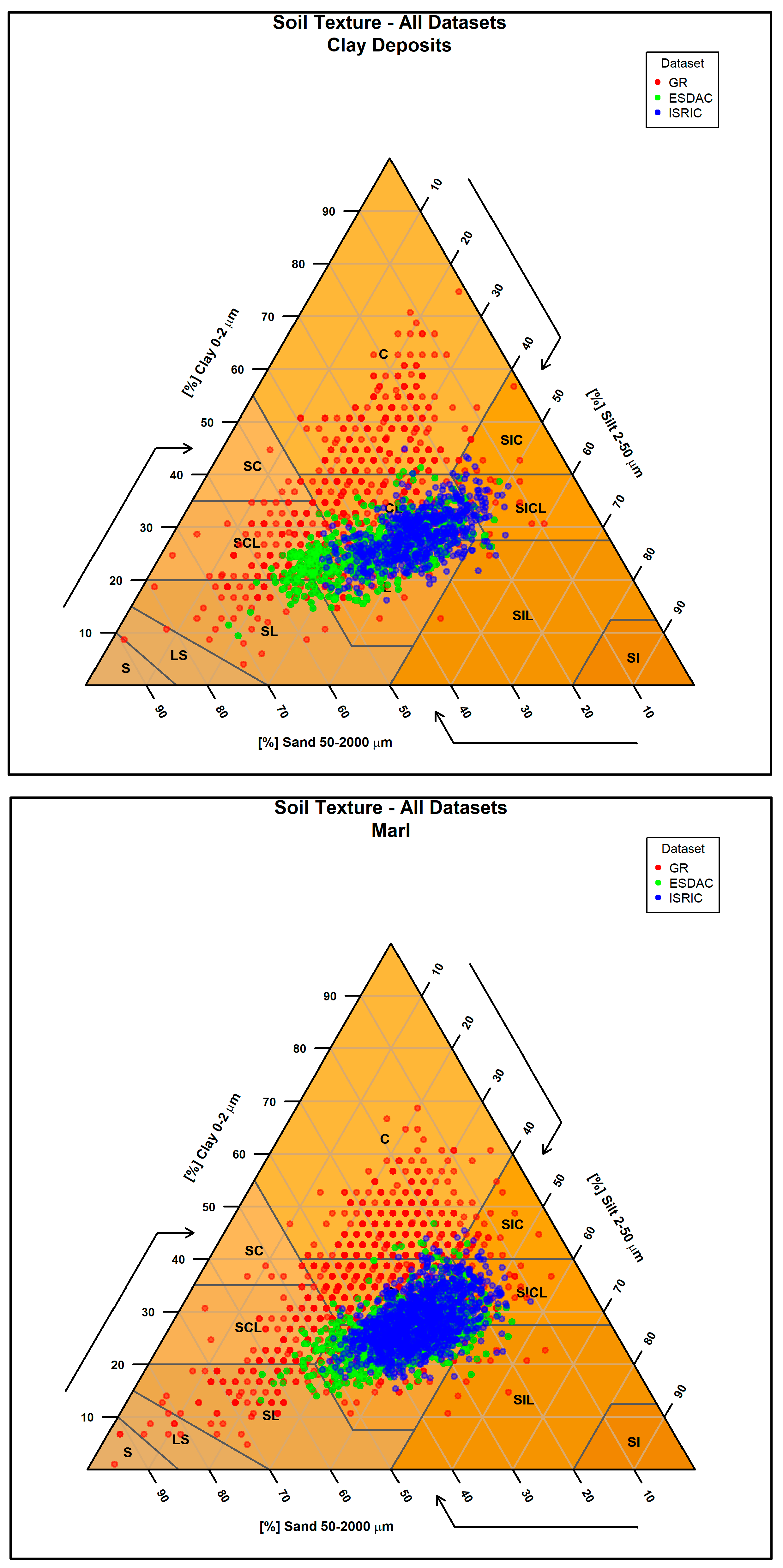
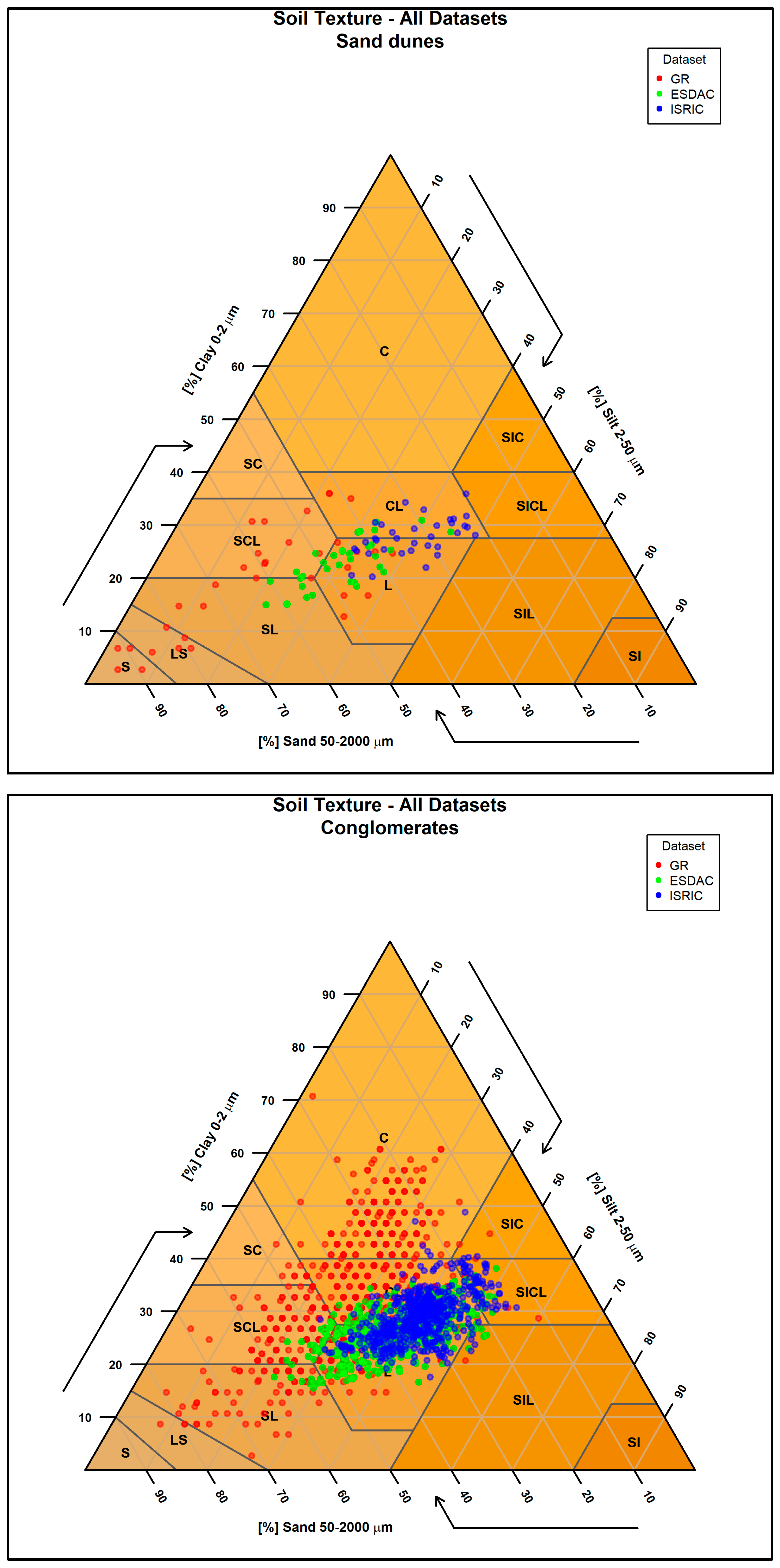
2.3.9. Targeted Analysis Based on Parent Material
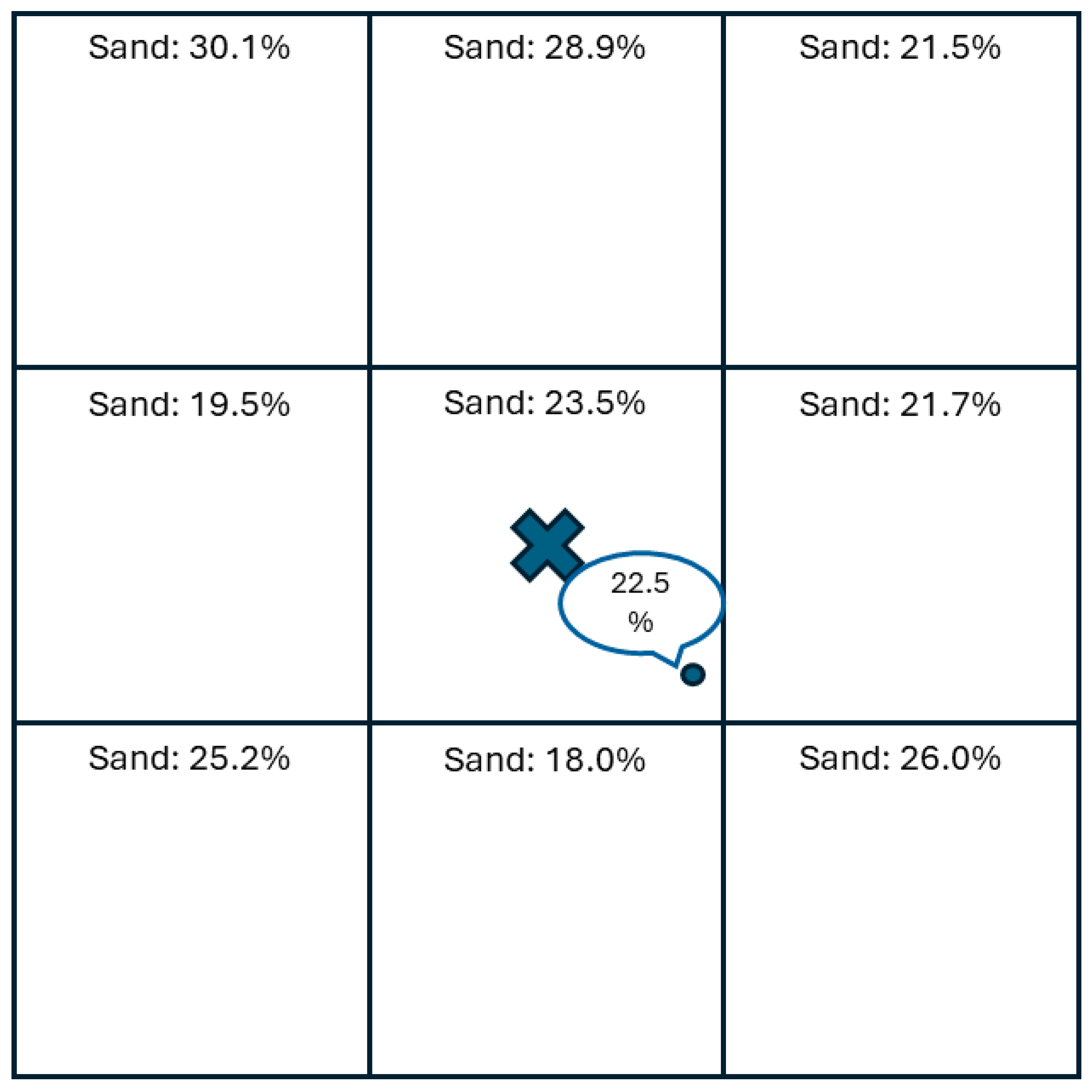
2.3.10. Analysis of Sensitivity Due to Spatial Misalignment
2.3.11. Validation of Results Using Diverse Greek Soil Studies
3. Results
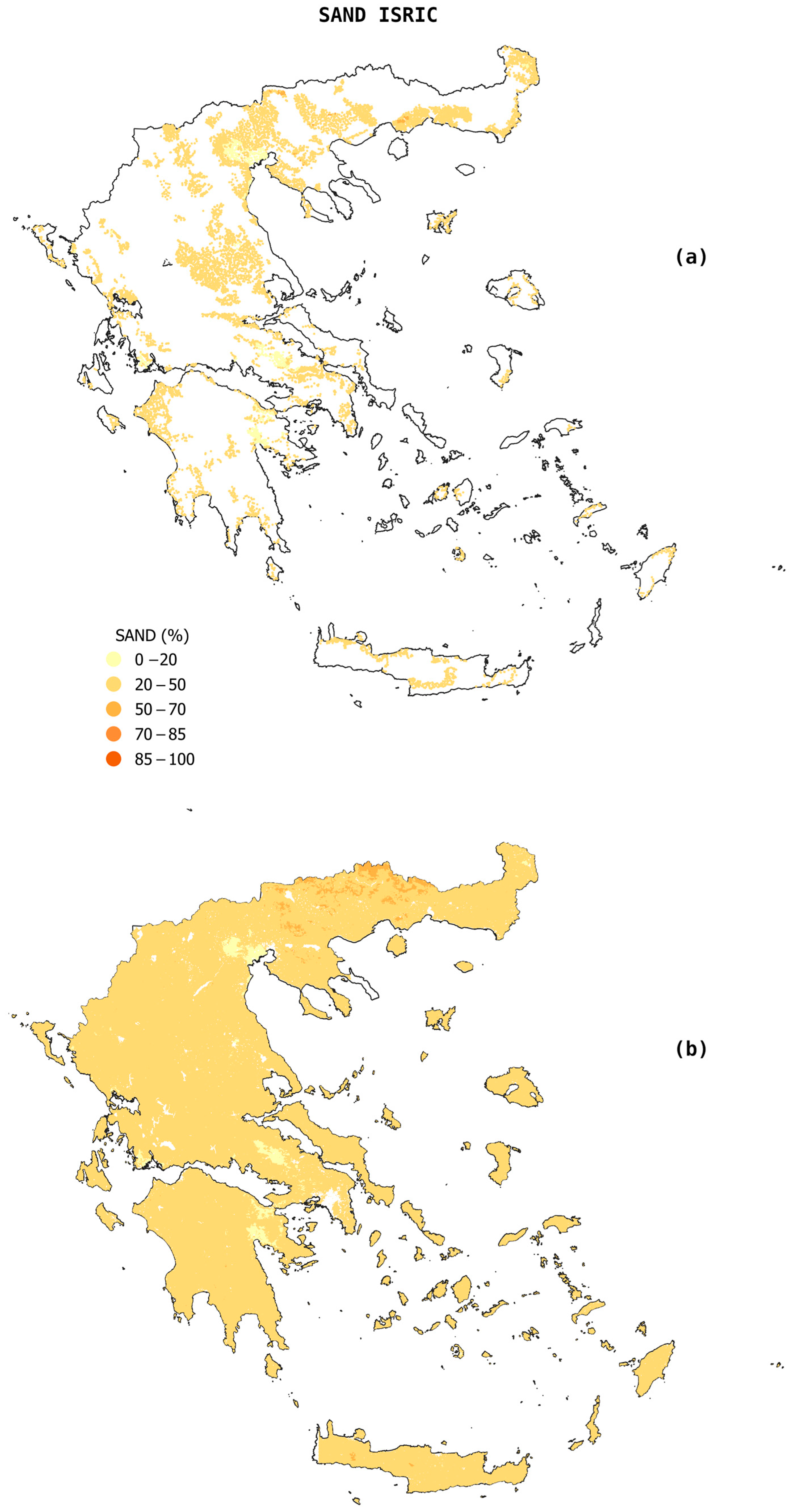
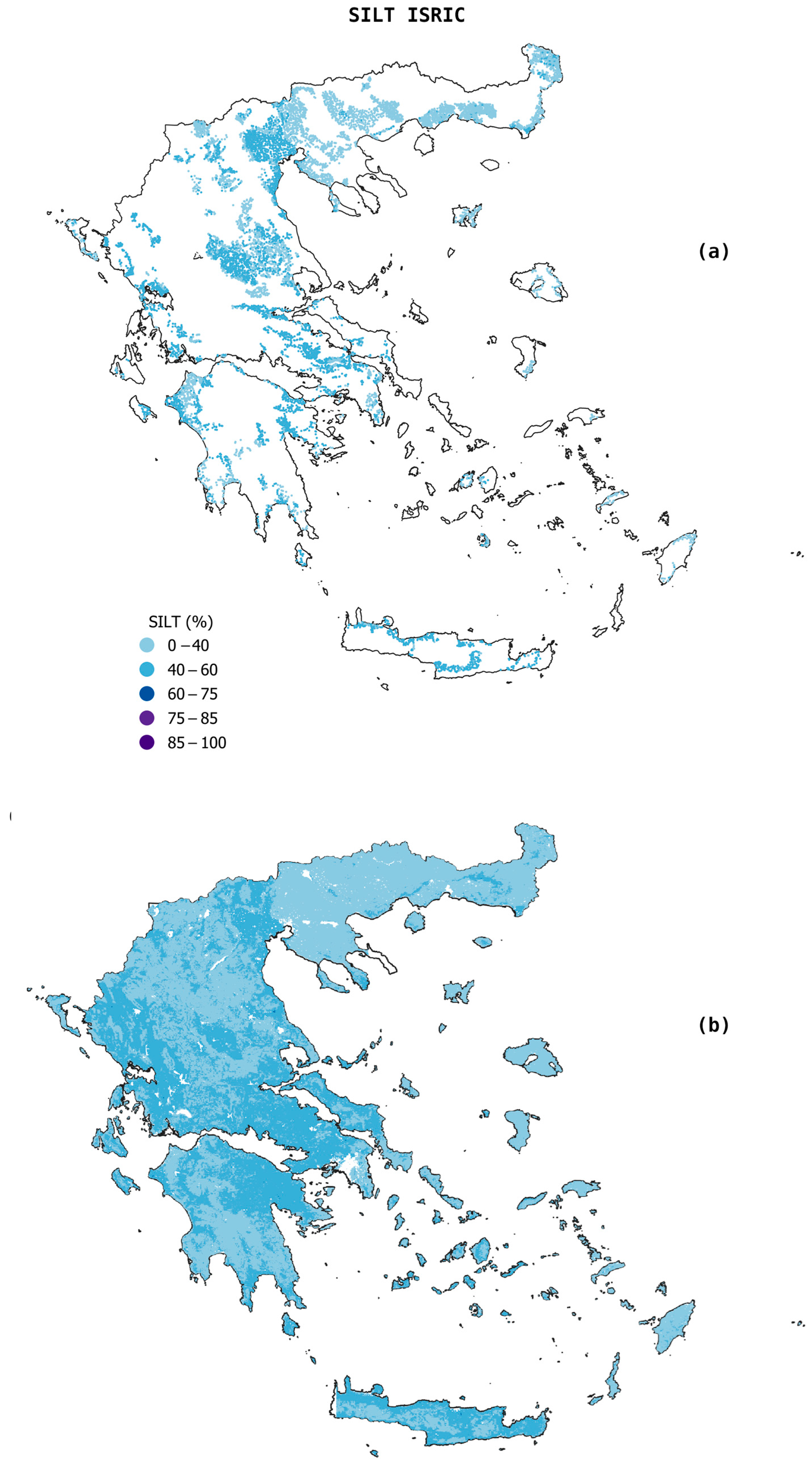
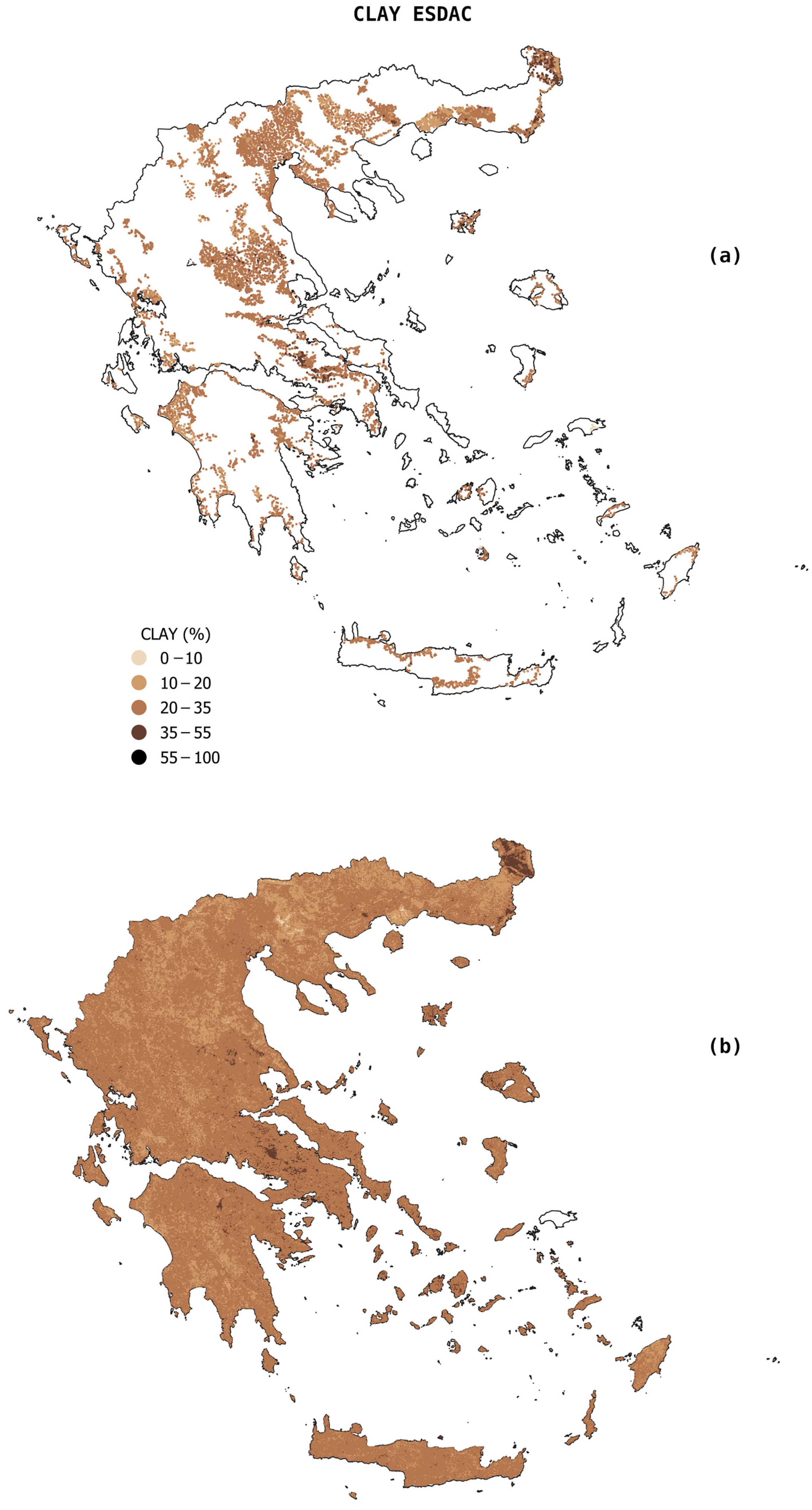
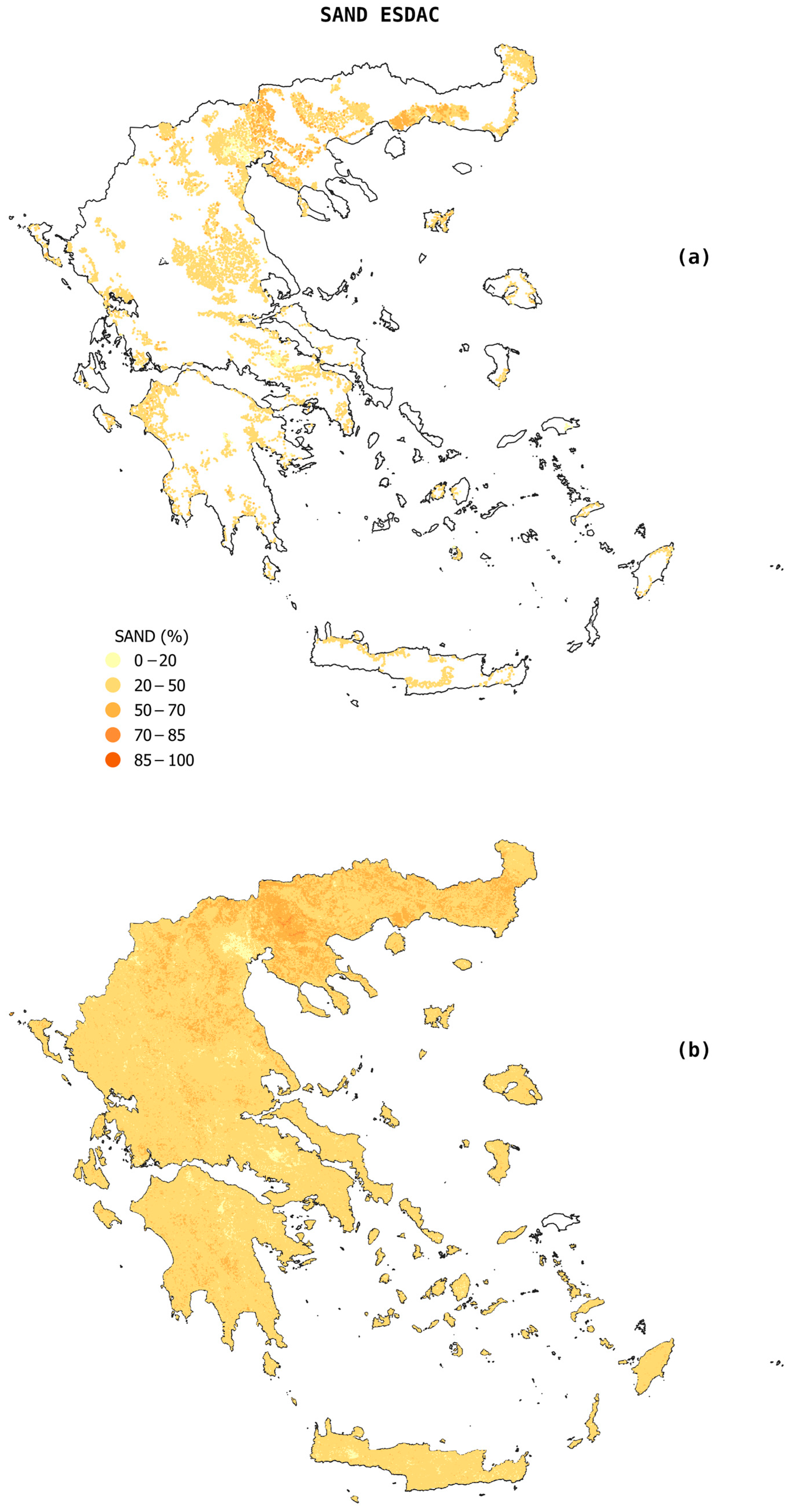
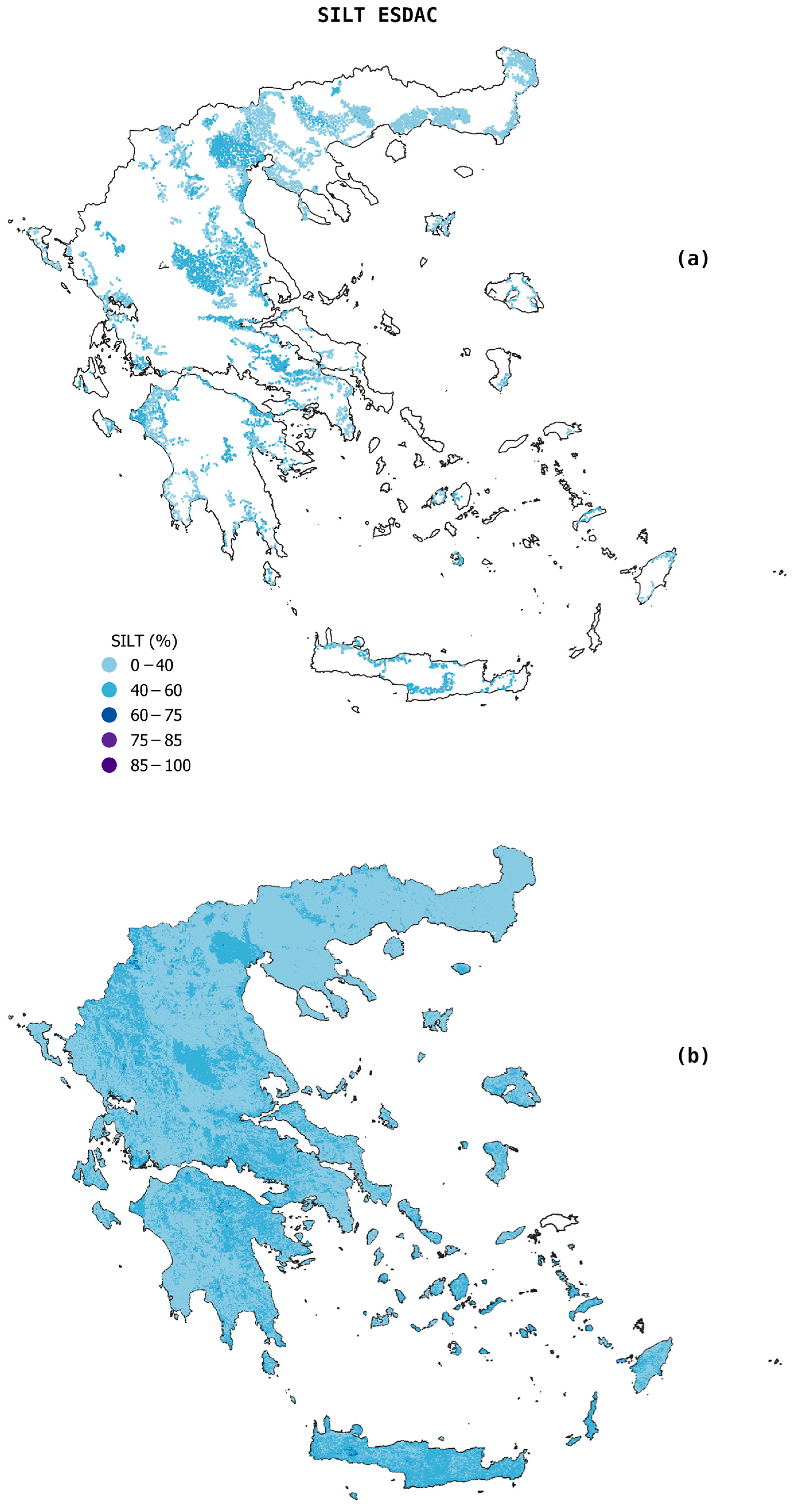
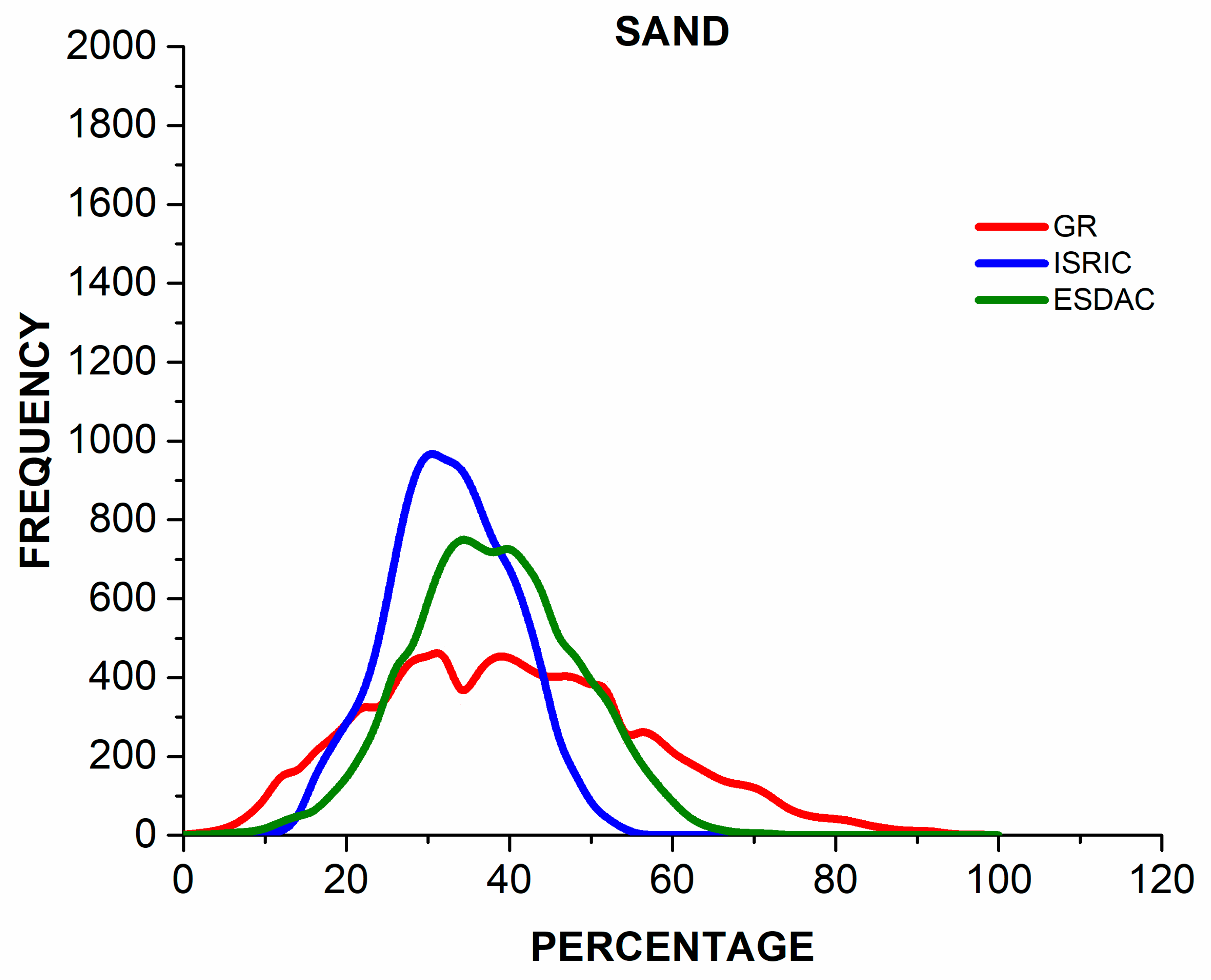
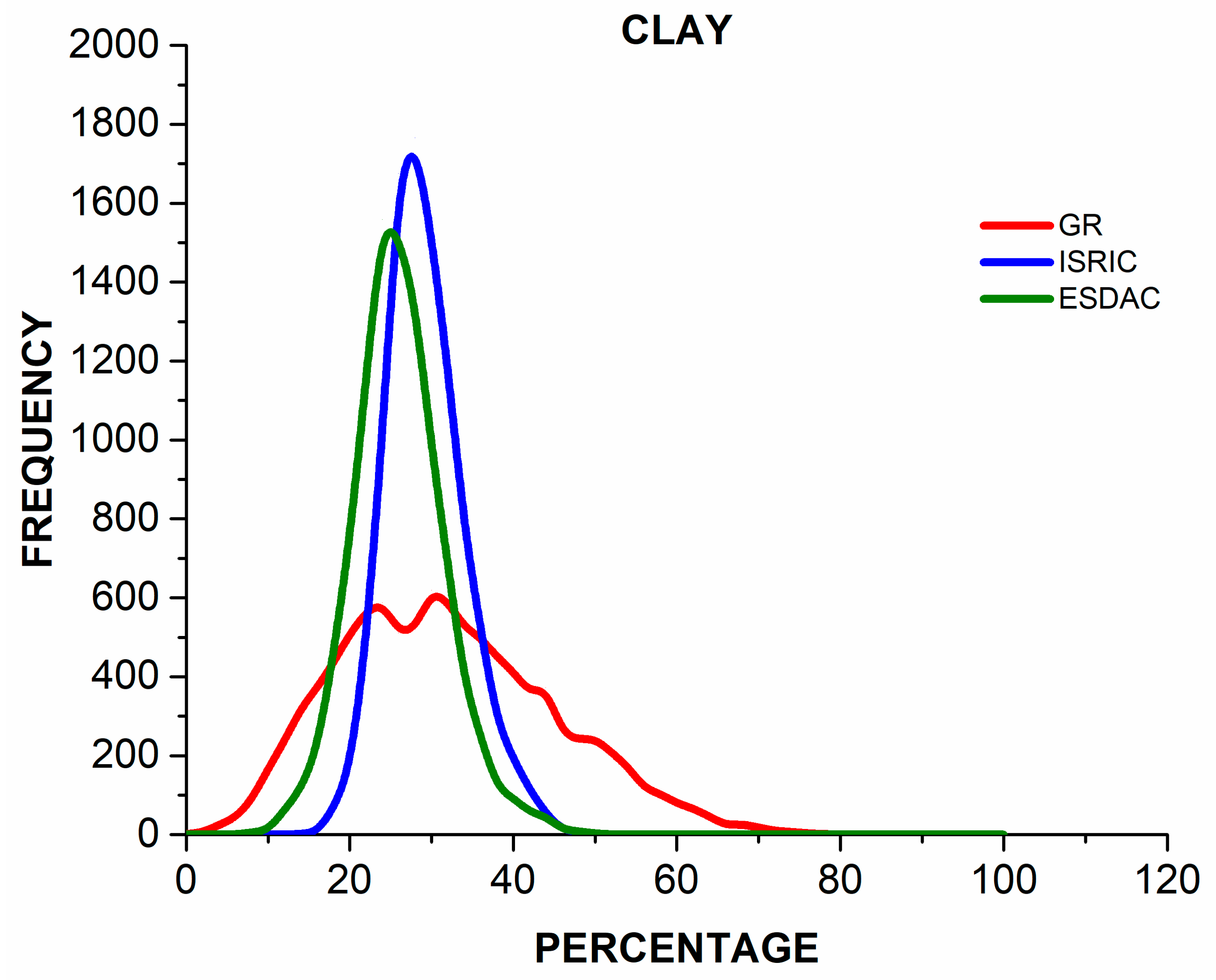
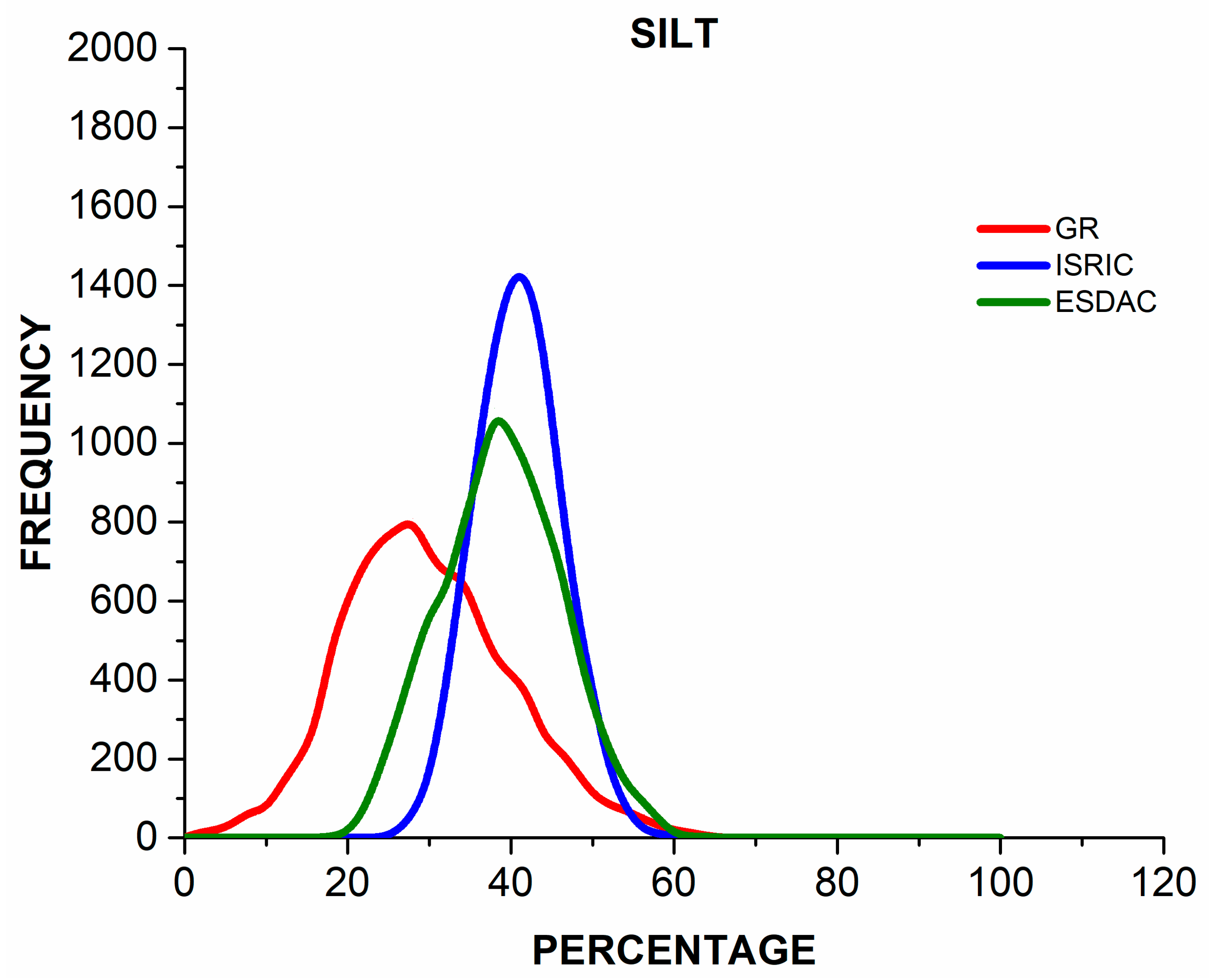
3.1. Descriptive Statistics of the Three Datasets
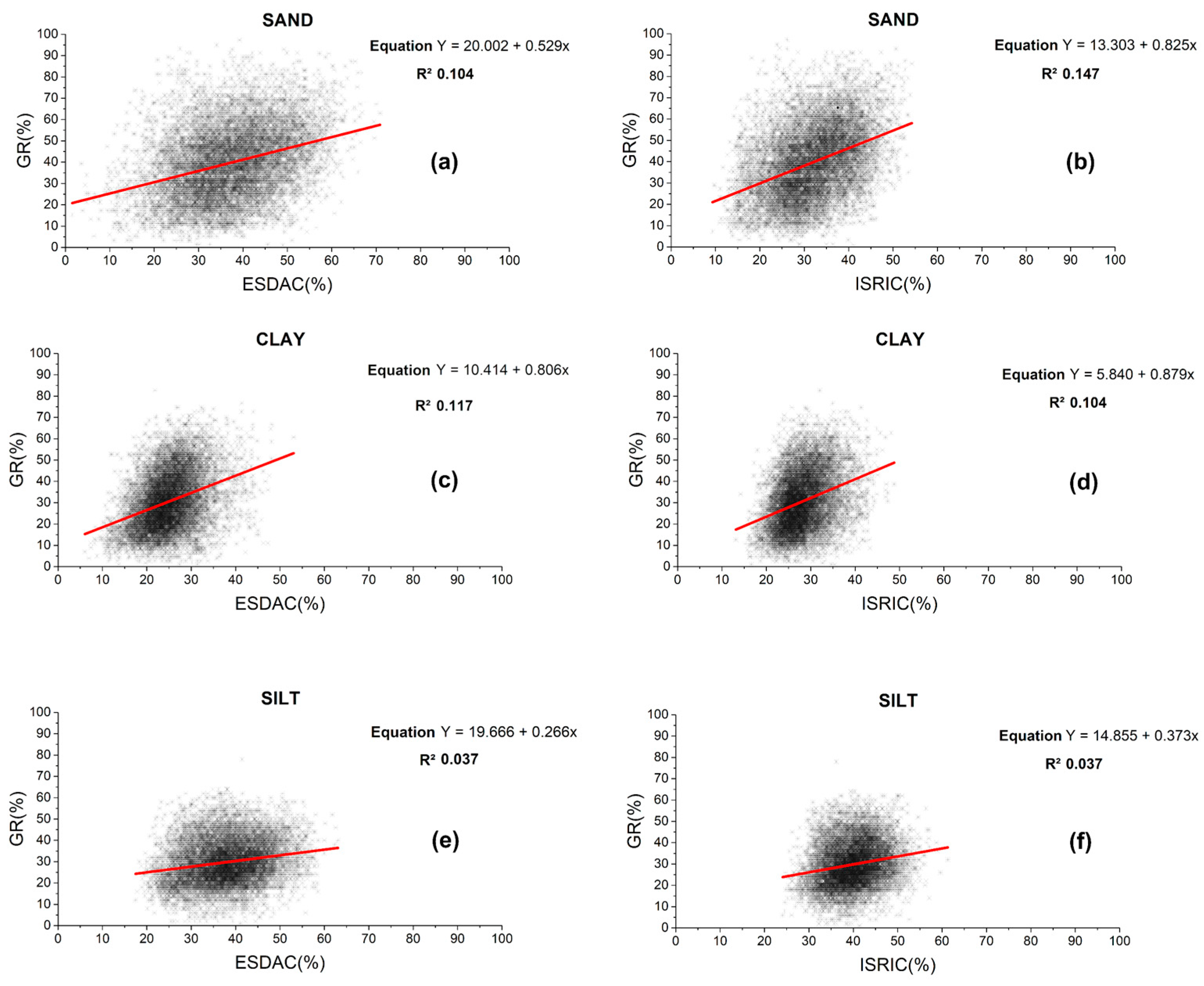
3.2. Differences Between Observed and Estimated Soil Properties Values
3.3. Correlation of Differences with Topographic and Hydrological Factors
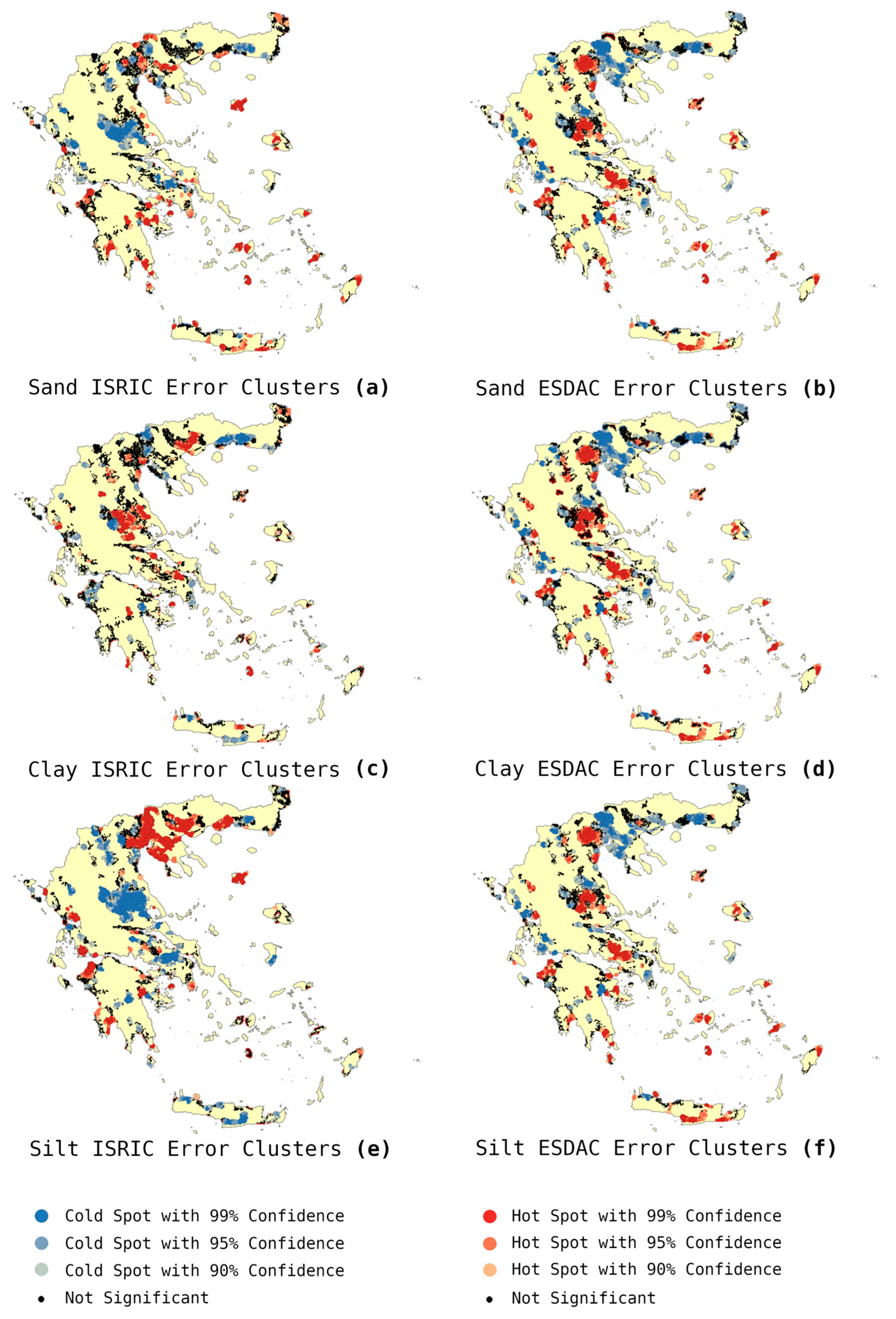
3.4. Hot Spot Analysis
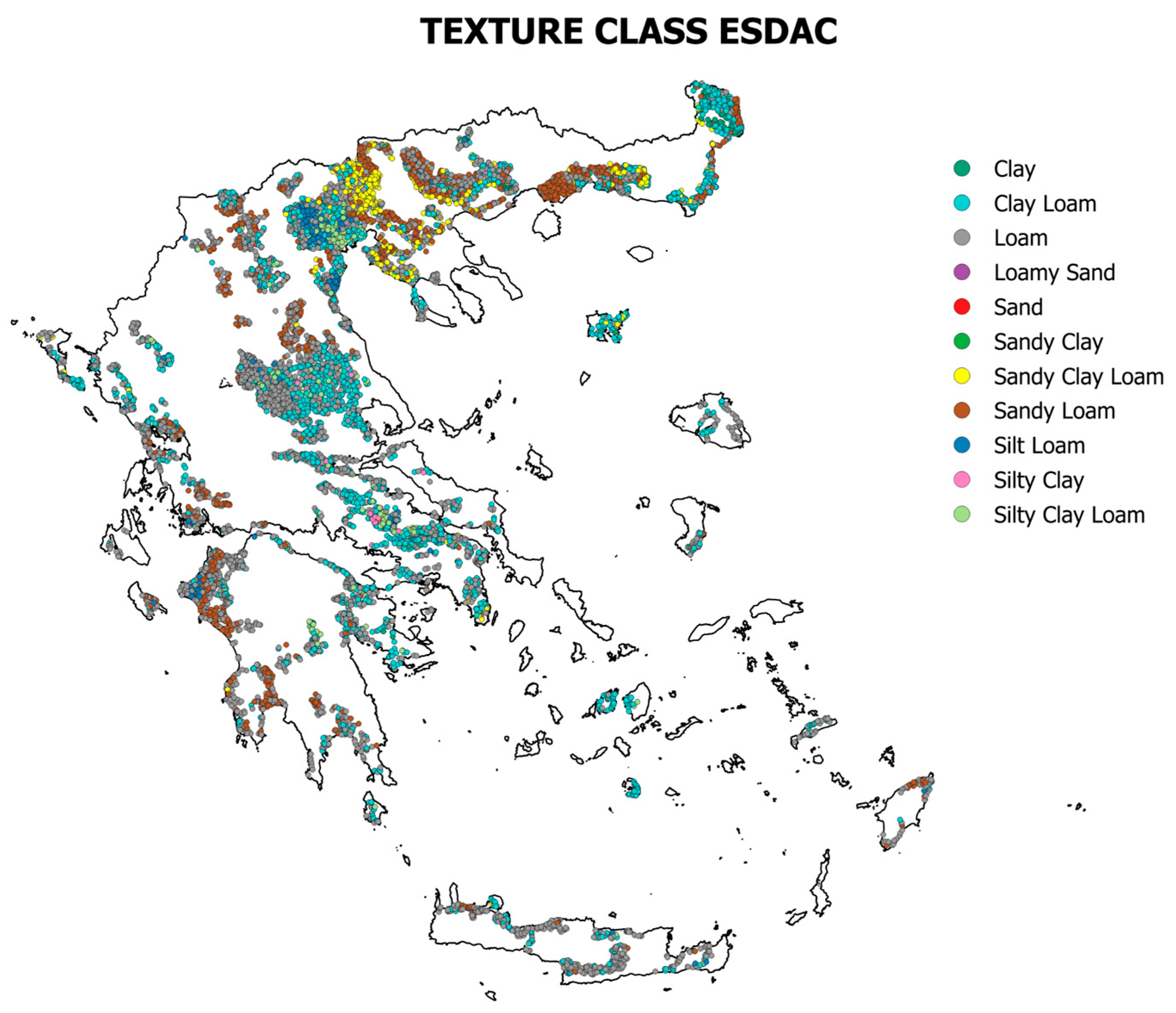
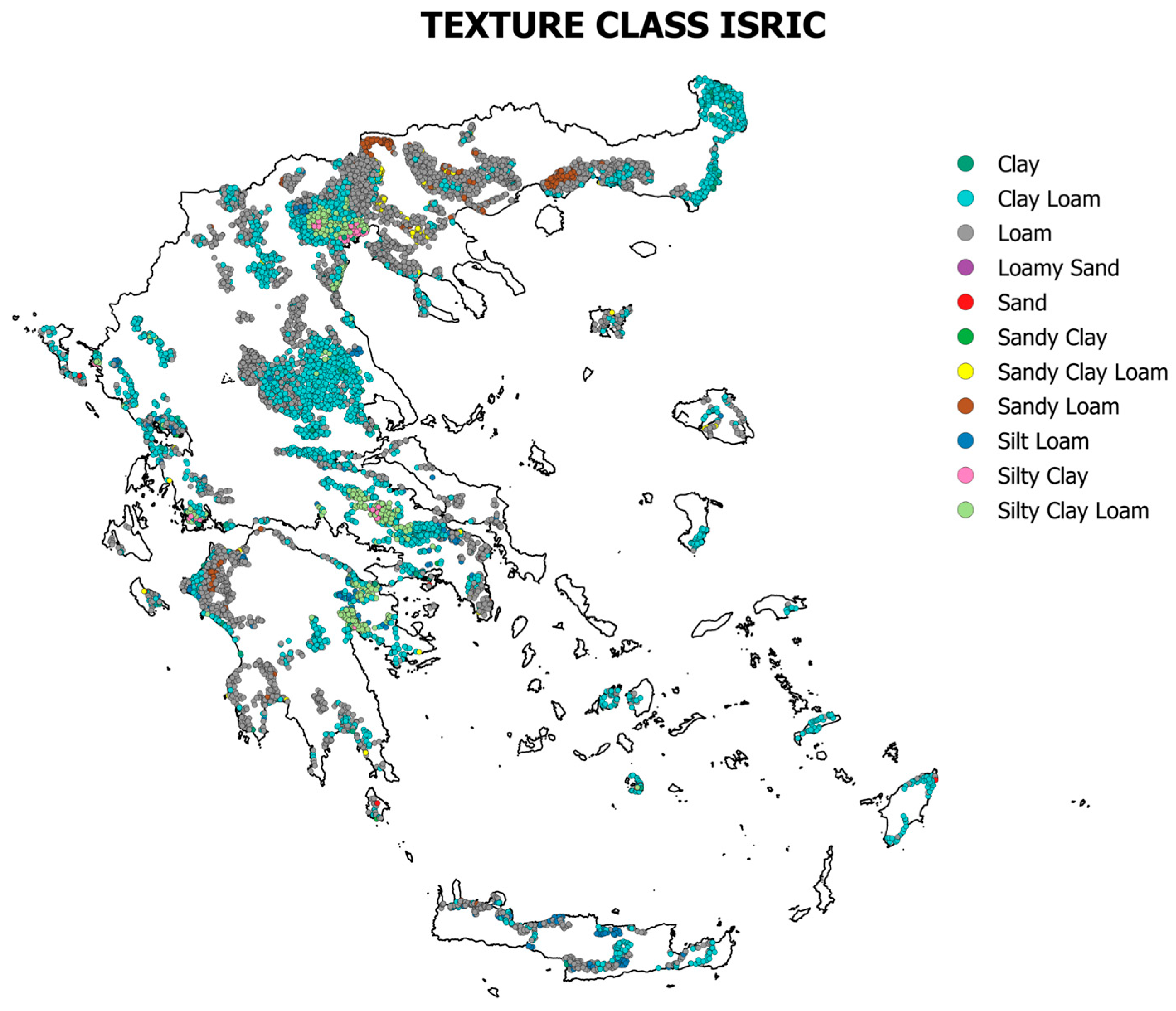
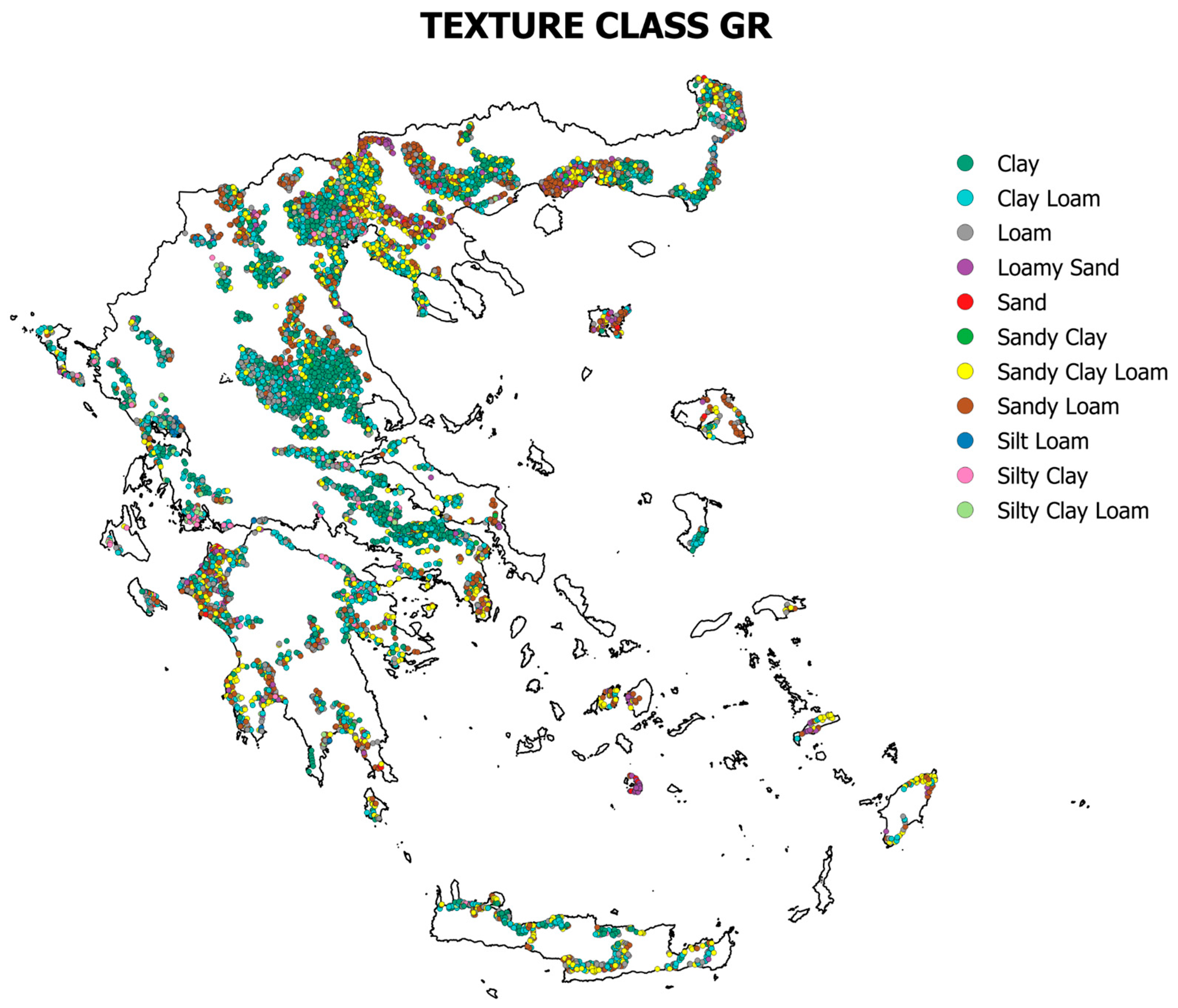
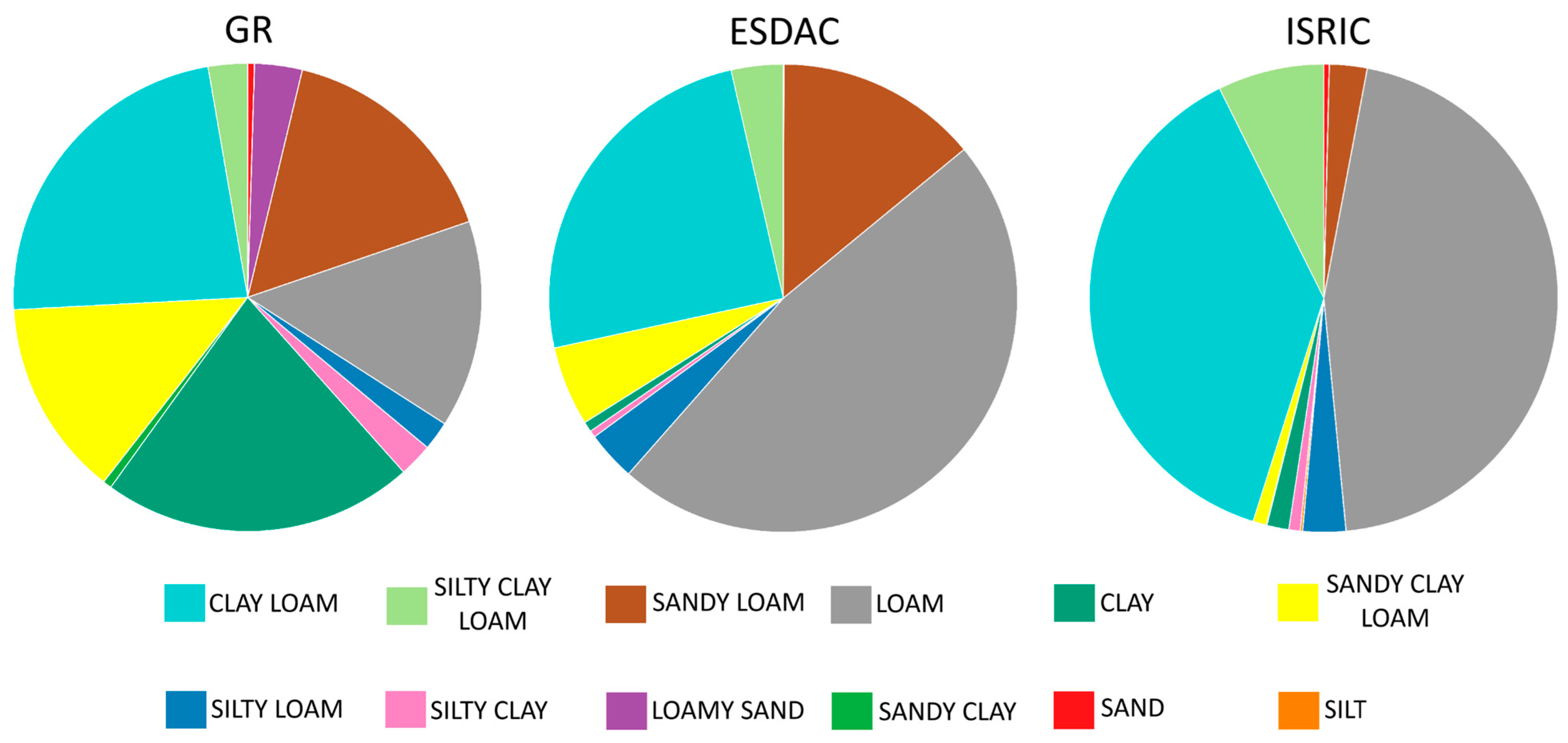
3.5. Soil Texture Class Estimation Errors
3.6. Correlation of Errors with Parent Material
3.7. Sensitivity Due to Spatial Misalignment
3.8. Validation of Obtained Differences Using Diverse Greek Soil Datasets
3.9. Quantification of ISRIC Uncertainty Calibration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ghodrati, M.; Dariane, A.B. Enhancing Hydrological Model Efficiency through Satellite Image Classification. Hydrol. Sci. J. 2024, 69, 2057–2070. [Google Scholar] [CrossRef]
- Isaboke, J.; Osano, O.; Humphrey, O.S.; Dowell, S.M.; Njoroge, R.; Watts, M.J. Influence of Agricultural Land Use Management on Soil Particle Size Distribution and Nutrient Adsorption in Western Kenya. Chem. Afr. 2025, 8, 1599–1610. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Zhao, N.; Li, W.; Wei, X.; Niu, B. Multifractal Dimensions of Soil Particle Size Distribution Reveal the Erodibility and Fertility of Alpine Grassland Soils in the Northern Tibet Plateau. J. Environ. Manag. 2022, 315, 115145. [Google Scholar] [CrossRef] [PubMed]
- Qi, F.; Zhang, R.; Liu, X.; Niu, Y.; Zhang, H.; Li, H.; Li, J.; Wang, B.; Zhang, G. Soil Particle Size Distribution Characteristics of Different Land-Use Types in the Funiu Mountainous Region. Soil Tillage Res. 2018, 184, 45–51. [Google Scholar] [CrossRef]
- OPEKEPE Greek Payment and Control Agency for Guidance and Guarantee Community Aid. Available online: https://www.opekepe.gr/opekepe-organisation-gr/opekepe-e-services-gr/pliroforiaka-systimata/gewpliroforiako-systima-edafologikwn-dedomenwn (accessed on 10 August 2025).
- Karamesouti, M.; Kairis, O.; Gasparatos, D.; Lakes, T. Map-Based Soil Crusting Susceptibility Assessment Using Pedotransfer Rules, CORINE and NDVI: A Preliminary Study in Greece. Ecol. Indic. 2023, 154, 110668. [Google Scholar] [CrossRef]
- Kairis, O.; Karamanos, A.; Voloudakis, D.; Kapsomenakis, J.; Aratzioglou, C.; Zerefos, C.; Kosmas, C. Identifying Degraded and Sensitive to Desertification Agricultural Soils in Thessaly, Greece, under Simulated Future Climate Scenarios. Land 2022, 11, 395. [Google Scholar] [CrossRef]
- Lekka, C.; Petropoulos, G.P.; Triantakonstantis, D.; Detsikas, S.E.; Chalkias, C. Exploring the Spatial Patterns of Soil Salinity and Organic Carbon in Agricultural Areas of Lesvos Island, Greece, Using Geoinformation Technologies. Environ. Monit. Assess 2023, 195, 391. [Google Scholar] [CrossRef]
- Soulis, K.X.; Psomiadis, E.; Londra, P.; Skuras, D. A New Model-Based Approach for the Evaluation of the Net Contribution of the European Union Rural Development Program to the Reduction of Water Abstractions in Agriculture. Sustainability 2020, 12, 7137. [Google Scholar] [CrossRef]
- Ballabio, C.; Panagos, P.; Monatanarella, L. Mapping Topsoil Physical Properties at European Scale Using the LUCAS Database. Geoderma 2016, 261, 110–123. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes De Jesus, J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Kaffas, K.; Pisaturo, G.R.; Premstaller, G.; Hrissanthou, V.; Penna, D.; Righetti, M. Event-Based Soil Erosion and Sediment Yield Modelling for Calculating Long-Term Reservoir Sedimentation in the Alps. Hydrol. Sci. J. 2024, 69, 321–336. [Google Scholar] [CrossRef]
- Kis, A.; Pongrácz, R.; Bartholy, J.; Szabó, J.A. Projection of Runoff Characteristics as a Response to Regional Climate Change in a Central/Eastern European Catchment. Hydrol. Sci. J. 2020, 65, 2256–2273. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS Curve Number Variation Following Forest Fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- Batjes, N.H.; Ribeiro, E.; van Oostrum, A.; Leenaars, J.; Hengl, T.; Mendes de Jesus, J. WoSIS: Providing standardized soil profile data for the world. Earth Syst. Sci. Data 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Poggio, L.; De Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing Soil Information for the Globe with Quantified Spatial Uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Rapčan, I.; Domazetović, F.; Milošević, R.; Plaščak, I. An Independent Validation of SoilGrids Accuracy for Soil Texture Components in Croatia. Land 2023, 12, 1034. [Google Scholar] [CrossRef]
- Dandabathula, G.; Salunkhe, S.S.; Bera, A.K.; Ghosh, K.; Hari, R.; Biradar, P.; Chirala, K.R.; Gaur, M.K. Validation of SoilGrids 2.0 in an Arid Region of India Using In Situ Measurements. Eur. J. Environ. Earth Sci. 2022, 3, 49–58. [Google Scholar] [CrossRef]
- Balla, D.; Varga, O.; Zichar, M. Accuracy Assessment of Different Soil Databases Concerning WRB Reference Soil Groups. Landsc. Environ. 2016, 10, 1–12. [Google Scholar] [CrossRef]
- Lilburne, L.; Helfenstein, A.; Heuvelink, G.B.M.; Eger, A. Interpreting and Evaluating Digital Soil Mapping Prediction Uncertainty: A Case Study Using Texture from SoilGrids. Geoderma 2024, 450, 117052. [Google Scholar] [CrossRef]
- Huang, S.; Eisner, S.; Haddeland, I.; Mengistu, Z.T. Evaluation of two new-generation global soil databases for macro-scale hydrological modelling in Norway. J. Hydrol. 2022, 610, 127895. [Google Scholar] [CrossRef]
- Bodenstein, D.; Clarke, C.; Watson, A.; Miller, J.; van der Westhuizen, S.; Rozanov, A. Evaluation of global and continental scale soil maps for southern Africa using selected soil properties. Catena 2022, 216, 106381. [Google Scholar] [CrossRef]
- Palli Gravani, S.; Gerontidis, S.; Kopanelis, D.; Kairis, O.; Soulis, K.; Kalivas, D. Evaluation of Digital Maps of Top-Soil Properties Compared to Large-Scale Laboratory Soil Data and Synergies towards a Better European Soils’ Delineation. In Proceedings of the EGU General Assembly 2025, Vienna, Austria, 27 April–2 May 2025. [Google Scholar]
- Willoughby, I.; Balandier, P.; Bentsen, N.S.; McCarthy, N.; Claridge, J. Forest Vegetation Management in Europe: Current Practice and Future Requirements; COST Office: Brussels, Belgium, 2009. [Google Scholar]
- Kagkou, E. Agricultural, Fishery, Food and Sustainable Rural Development in Greece. In Les Agricultures Méditerranéennes: Analyses Par Pays; Options Méditerranéennes; Série B. Études et Recherches; CIHEAM: Montpellier, France, 2008; pp. 207–240. [Google Scholar]
- Yassoglou, N.; Tsadilas, C.; Kosmas, C. The Soils of Greece; World Soils Book Series; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-53332-2. [Google Scholar]
- Kostopoulou, E.; Giannakopoulos, C. Projected Changes in Extreme Wet and Dry Conditions in Greece. Climate 2023, 11, 49. [Google Scholar] [CrossRef]
- Regional Laboratory of Agricultural Applications and Fertilizer Analysis of Epirus and Western Macedonia (PEGEAL), Ministry of Rural Development and Food, Greece. Available online: https://www.minagric.gr/xrisimewplirofories-2/syndesmoi/915-p-e-g-e-a-l (accessed on 3 November 2025).
- Bilas, G.; Dionysiou, N.; Karapetsas, N.; Silleos, N.; Kosmas, K.; Misopollinos, N. Development of a National Geodatabase (Greece) for Soil Surveys and Land Evaluation Using Space Technology and GIS. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 1 April 2016; p. EPSC2016-12889. [Google Scholar]
- Alexakis, D.E.; Bathrellos, G.D.; Skilodimou, H.D.; Gamvroula, D.E. Spatial Distribution and Evaluation of Arsenic and Zinc Content in the Soil of a Karst Landscape. Sustainability 2021, 13, 6976. [Google Scholar] [CrossRef]
- Eloi Ribeiro, N.H.B. World Soil Information Service (WoSIS)—Towards the Standardization and Harmonization of World Soil Data. In Procedures Manual 2018; ISRIC—World Soil Information: Wageningen, The Netherlands, 2018. [Google Scholar]
- Batjes, N.H.; Ribeiro, E.; Van Oostrum, A. Standardised Soil Profile Data to Support Global Mapping and Modelling (WoSIS Snapshot 2019). Earth Syst. Sci. Data 2020, 12, 299–320. [Google Scholar] [CrossRef]
- Batjes, N.H.; Calisto, L.; De Sousa, L.M. Providing Quality-Assessed and Standardised Soil Data to Support Global Mapping and Modelling (WoSIS Snapshot 2023). Earth Syst. Sci. Data 2024, 16, 4735–4765. [Google Scholar] [CrossRef]
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Overview; European Commission, Joint Research Centre: Brussels, Belgium, 2013. [Google Scholar]
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European Policy Support and Public Data Requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- ISRIC User Manual. Available online: https://files.isric.org/public/documents/2025_WoSIS_coding_analytical_method_descriptions.pdf (accessed on 3 November 2025).
- Orgiazzi, A.; Ballabio, C.; Panagos, P.; Jones, A.; Fernández-Ugalde, O. LUCAS Soil, the Largest Expandable Soil Dataset for Europe: A Review. Eur. J Soil Sci. 2018, 69, 140–153. [Google Scholar] [CrossRef]
- Yassoglou, N. Soil Survey in Greece. In Soil Resources of Europe; European Soil Bureau Research Report; Office for Official Publications of the European Communities: Luxembourg, 2005. [Google Scholar]
- Spanos, K.A.; Skouteri, A.; Gaitanis, D.; Petrakis, P.V.; Meliadis, I.; Michopoulos, P.; Solomou, A.; Koulelis, P.; Avramidou, E.V. Forests of Greece, Their Multiple Functions and Uses, Sustainable Management and Biodiversity Conservation in the Face of Climate Change. OJE 2021, 11, 374–406. [Google Scholar] [CrossRef]
- Nakos, G. Classification, Mapping and Evaluation of Soils: Technical Specifications; Ministry of Agriculture, Institute of Mediterranean Forest Ecosystems and Forest Products Technology: Athens, Greece, 1991. [Google Scholar]
- ISRIC—World Soil Information SoilGrids Platform. Available online: https://soilgrids.org (accessed on 10 August 2025).
- European Commission, Joint Research Centre European Soil Data Centre. Available online: https://esdac.jrc.ec.europa.eu (accessed on 8 October 2025).
- Copernicus Data Space Ecosystem Digital Elevation Model (DEM) of Greece from Copernicus Data Space Ecosystem. Available online: https://dataspace.copernicus.eu/explore-data/data-collections/copernicus-contributing-missions/collections-description/COP-DEM (accessed on 10 August 2025).
- Aitchison, J. The Statistical Analysis of Compositional Data; Blackburn Press: Surrey, UK, 2003; ISBN 978-1930665781. [Google Scholar]
- van den Boogaart, K.G.; Tolosana-Delgado, R.; Bren, M. Compositions: Compositional Data Analysis, R package version 2.0-9; 2025. Available online: https://CRAN.R-project.org/package=compositions (accessed on 3 November 2025).
- Pawlowsky-Glahn, V.; Buccianti, A. Compositional Data Analysis: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- IBM SPSS Statistics for Windows; Version 25.0 2017; IBM: Armonk, NY, USA, 2017.
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Liu, W.; Ma, L.; Smanov, Z.; Samarkhanov, K.; Abuduwaili, J. Clarifying Soil Texture and Salinity Using Local Spatial Statistics (Getis-Ord Gi* and Moran’s I) in Kazakh–Uzbekistan Border Area, Central Asia. Agronomy 2022, 12, 332. [Google Scholar] [CrossRef]
- Jiang, L.; Qiu, G.; Yu, X. Identification and Spatial Analysis of Land Salinity in China’s Yellow River Delta Using a Land Salinity Monitoring Index from Harmonized UAV-Landsat Imagery. Sensors 2023, 23, 7584. [Google Scholar] [CrossRef]
- Oxoli, D.; Molinari, M.E.; Brovelli, M.A. Hotspot Analysis, an Open Source GIS Tool for Exploratory Spatial Data Analysis: Application to the Study of Soil Consumption in Italy. Rend. Online Della Soc. Geol. Ital. 2018, 46, 82–87. [Google Scholar] [CrossRef]
- Radočaj, D.; Jug, I.; Jurišić, M.; Gašparovic, M. The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland. Agronomy 2021, 11, 2430. [Google Scholar] [CrossRef]
- ESRI. Hot Spot Analysis (Getis-Ord Gi*) (Spatial Statistics). Tool reference. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-statistics/hot-spot-analysis.htm (accessed on 3 November 2025).
- Congalton, R.G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Foody, G.M. Status of Land Cover Classification Accuracy Assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good Practices for Estimating Area and Assessing Accuracy of Land Change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Wilson, M.J. The Importance of Parent Material in Soil Classification: A Review in a Historical Context. CATENA 2019, 182, 104131. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, T.; Lei, L.; Jie, Y. Effects of Parent Material on Soil Hydraulic Properties in Subtropical Hilly Area of Southern China. CATENA 2024, 243, 108210. [Google Scholar] [CrossRef]
- Acosta, J.A.; Martínez-Martínez, S.; Faz, A.; Arocena, J. Accumulations of Major and Trace Elements in Particle Size Fractions of Soils on Eight Different Parent Materials. Geoderma 2011, 161, 30–42. [Google Scholar] [CrossRef]
- Kooijman, A.M.; Jongejans, J.; Sevink, J. Parent Material Effects on Mediterranean Woodland Ecosystems in NE Spain. CATENA 2005, 59, 55–68. [Google Scholar] [CrossRef]
- Gökbulak, F.; Özcan, M. Hydro-Physical Properties of Soils Developed from Different Parent Materials. Geoderma 2008, 145, 376–380. [Google Scholar] [CrossRef]
- Olowolafe, E.A. Soil Parent Materials and Soil Properties in Two Separate Catchment Areas on the Jos Plateau, Nigeria. GeoJournal 2002, 56, 201–212. [Google Scholar] [CrossRef]
- De Kimpe, C.R.; Laverdiere, M.R.; Dejou, J.; Lasalle, P. Effects of Acidic and Basic Parent Materials on Formation of Some Soils in Quebec (Canada). Geoderma 1984, 33, 101–118. [Google Scholar] [CrossRef]
| Step | Description |
|---|---|
| 1. Data Acquisition | Collect raster datasets from ISRIC and ESDAC, and the Greek national soil database. |
| 2. Raster Processing | Subset rasters to topsoil layer (0–30 cm) and clip them to the Greek territory. Project to Greek Grid (EGSA87, ESPG: 2100). |
| 3. Raster value extraction process | Extract values of sand, clay, and silt from raster datasets for each sampling point. |
| 4. Error Calculation | Compute differences between observed (Soil Map of Greece) and predicted (ISRIC and ESDAC) values for each soil property. |
| 5. Statistical Analysis | Perform univariate statistics for each property (sand, clay, silt). |
| 6 Spatial Variability Analysis | Analyze spatial distribution of absolute errors to identify error clustering. |
| 7. Soil Texture Classification | For each sampling point from the Greek Soil Map, the soil texture class was determined based on the calculated sand, clay, and silt percentages using the USDA soil texture classification system. |
| 8. Categorical Comparison of Soil Texture Classes | Predicted soil texture classes from international datasets were compared with the USDA-based classes derived from the Greek Soil Map. Accuracy assessment was performed using producer’s accuracy, user’s accuracy, and overall accuracy—metrics suitable for evaluating agreement between categorical datasets. |
| 9. Targeted Analysis Based on Parent Material | Predicted sand, clay, and silt values were examined for sampling points located on soils derived from parent materials known to produce extreme textural values (e.g., very sandy or clayey soils). A spatial join was performed between the SMUs (containing parent material information) and the sampling points to identify relevant cases. |
| 10. Evaluating the Unbiasedness of the Raster Value Extraction Process | Alternative raster value extraction process method (Step 3) implemented, and the error residuals compared. |
| 11. Validation of Results Using Diverse Greek Soil Studies | Data from diverse datasets were utilized to assess the validity of the results obtained. To this end, steps 1 to 5 were repeated for the additional datasets. |
| SAND (%) | CLAY (%) | SILT (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GR | ESDAC | ISRIC | GR | ESDAC | ISRIC | GR | ESDAC | ISRIC | |
| Mean (%) | 39.69 | 37.06 | 31.76 | 30.6 | 25.08 | 28.26 | 29.7 | 37.86 | 39.98 |
| Aitchison Center Composition (%) | (39.27) ESDAC, (39.05) ISRIC | 36.58 | 31.30 | (30.23) ESDAC, (30.32) ISRIC | 25.19 | 28.37 | (30.50) ESDAC, (30.62) ISRIC | 38.23 | 40.33 |
| Median (%) | 39.30 | 36.80 | 31.57 | 28.7 | 24.79 | 27.73 | 28.00 | 37.86 | 39.93 |
| Variance (%) | 276.25 | 102.50 | 59.19 | 170.18 | 30.86 | 22.95 | 102.14 | 54.44 | 27.25 |
| Min (%) | 1 | 2 | 9 | 0 | 6 | 13 | 0 | 17 | 24 |
| Max (%) | 97 | 71 | 54 | 83 | 53 | 49 | 78 | 63 | 61 |
| Std (%) | 16.62 | 10.12 | 7.694 | 13.04 | 5.55 | 4.79 | 10.10 | 7.37 | 5.22 |
| Kurtosis | −0.28 | −0.16 | −0.391 | −0.23 | 0.83 | 0.42 | 0.05 | −0.32 | −0.15 |
| Skewness | 0.34 | 0.04 | 0.00 | 0.42 | 0.40 | 0.54 | 0.32 | 0.07 | 0.11 |
| Metric | GR-ESDAC | GR-ISRIC |
|---|---|---|
| RMSEA | 0.8132 | 0.8108 |
| MAEA | 0.7071 | 0.7104 |
| SAND | CLAY | SILT | ||||
|---|---|---|---|---|---|---|
| Residuals Statistics | GR–ESDAC | GR–ISRIC | GR–ESDAC | GR–ISRIC | GR–ESDAC | GR–ISRIC |
| Mean | 2.55 | 7.78 | 5.56 | 2.44 | −8.12 | −1.88 |
| Median | 2.00 | 7.00 | 5.00 | 2.00 | −9.00 | −2.00 |
| RMSE (raw) | 17.18 | 18.55 | 13.69 | 13.20 | 14.04 | 14.45 |
| Variance | 269.13 | 235.48 | 151.63 | 153.22 | 127.00 | 193.96 |
| RMSE (backtransformed) | 21.68 | 21.81 | 14.44 | 13.58 | 7.24 | 8.22 |
| MAE (backtransformed) | 17.35 | 17.77 | 11.69 | 11.04 | 5.66 | 6.73 |
| Min | −48.00 | −40.00 | −36.00 | −35.00 | −50.00 | −47.00 |
| Max | 67.00 | 71.000 | 61.00 | 51.00 | 37.00 | 58.00 |
| Std | 16.40 | 15.34 | 12.31 | 12.38 | 11.27 | 13.92 |
| Characteristic | Parameters and Metrics | Sand | Clay | Silt | |||
|---|---|---|---|---|---|---|---|
| GR–ESDAC | GR–ISRIC | GR–ESDAC | GR–ISRIC | GR–ESDAC | GR–ISRIC | ||
| Elevation | Slope | 0.00024 | 0.00221 | 0.00360 | 0.00027 | 0.01061 | 0.01020 |
| Intercept | 1.5919 | 7.4976 | 5.5059 | 1.9932 | −7.0984 | −0.8241 | |
| p-value | 0.000 | 0.108 | 0.131 | 0.000 | 0.000 | 0.000 | |
| R2 | 0.00360 | 0.00027 | 0.00024 | 0.00221 | 0.01061 | 0.01020 | |
| Slope | Slope | 0.17650 | 0.15670 | −0.08420 | 0.0596 | −0.09130 | −0.28000 |
| Intercept | 1.5843 | 6.9861 | 6.0462 | 2.1992 | −7.6318 | −0.6909 | |
| p-value | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | |
| R2 | 0.00449 | 0.00397 | 0.00176 | 0.00090 | 0.00250 | 0.01563 | |
| Sin (Aspect) | Slope | −0.309 | −0.20770 | −0.01560 | −0.11180 | 0.32240 | 0.30720 |
| Intercept | 2.3972 | 7.7066 | 5.6615 | 2.4742 | −8.0557 | −1.9771 | |
| p-value | 0.130 | 0.278 | 0.919 | 0.471 | 0.022 | 0.077 | |
| R2 | 0.00024 | 0.00012 | 0.00000 | 0.00005 | 0.00053 | 0.00032 | |
| Cos (Aspect) | Slope | 0.21440 | 0.27490 | −0.15900 | −0.24670 | −0.05650 | 0.02950 |
| Intercept | 2.3889 | 7.6999 | 5.6625 | 2.474 | −8.0486 | −1.9711 | |
| p-value | 0.286 | 0.145 | 0.296 | 0.107 | 0.684 | 0.863 | |
| R2 | 0.00012 | 0.00022 | 0.00011 | 0.00027 | 0.00002 | 0.00000 | |
| Curvature | Slope | 0.031 | −0.49120 | −0.28940 | 0.27580 | 0.24910 | −0.9092 |
| Intercept | 2.3908 | 7.7032 | 5.6616 | 2.4714 | −8.0495 | −1.9693 | |
| p-value | 0.966 | 0.468 | 0.596 | 0.615 | 0.617 | 0.138 | |
| R2 | 0.00000 | 0.00005 | 0.00003 | 0.00003 | 0.00003 | 0.00023 | |
| TWI | Slope | −0.14780 | −0.0596 | 0.02700 | −0.04700 | 0.11890 | 0.04370 |
| Intercept | 2.5711 | 7.775 | 5.6282 | 2.5292 | −8.194 | −2.0241 | |
| p-value | 0.142 | 0.529 | 0.723 | 0.540 | 0.087 | 0.610 | |
| R2 | 0.00022 | 0.00004 | 0.00001 | 0.00004 | 0.00030 | 0.00003 | |
| Flow Accumulation | Slope | 0.00060 | 0.00100 | −0.00040 | −0.00050 | −0.00010 | −0.00030 |
| Intercept | 2.371 | 7.6702 | 5.6758 | 2.4883 | −8.044 | −1.9624 | |
| p-value | 0.283 | 0.064 | 0.293 | 0.242 | 0.693 | 0.590 | |
| R2 | 0.00012 | 0.00035 | 0.00011 | 0.00014 | 0.00002 | 0.00003 | |
| Class | Producer’s Accuracy | User’s Accuracy | Overall Accuracy | Overall User’s Accuracy | ||||
|---|---|---|---|---|---|---|---|---|
| ISRIC | ESDAC | ISRIC | ESDAC | ISRIC | ESDAC | ISRIC | ESDAC | |
| Clay | 0.016 | 0.007 | 0.311 | 0.228 | 0.188 | 0.204 | 0.188 | 0.205 |
| Clay Loam | 0.410 | 0.260 | 0.248 | 0.243 | - | |||
| Loam | 0.505 | 0.530 | 0.158 | 0.161 | ||||
| Loamy Sand | 0.000 | 0.005 | 0.000 | 0.400 | ||||
| Sand | 0.021 | 0.000 | 0.027 | 0.000 | ||||
| Sandy Clay | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| Sandy Clay Loam | 0.018 | 0.132 | 0.265 | 0.332 | ||||
| Sandy Loam | 0.066 | 0.283 | 0.403 | 0.325 | ||||
| Silt Loam | 0.086 | 0.085 | 0.059 | 0.049 | ||||
| Silty Clay | 0.043 | 0.008 | 0.128 | 0.042 | ||||
| Silty Clay Loam | 0.093 | 0.040 | 0.034 | 0.030 | ||||
| Parent Material (Number of Points) | GR Mean Clay % (Std) | ISRIC Mean Clay % (Std) | ESDAC Mean Clay % (Std) |
|---|---|---|---|
| marl (1105) | 33.6 (11.0) | 26.7 (6.5) | 25.8 (5.2) |
| clay-rich deposits (572) | 70.0 (12.9) | 27.0 (4.9) | 25.0 (5.0) |
| lacustrine sediments (91) | 43.7 (12.5) | 33.1 (6.2) | 30.4 (7.8) |
| flysch formations (138) | 24.7 (8.7) | 24.8 (5.9) | 25.5 (5.9) |
| colluvial materials (ripidion) (236) | 25.6 (11.8) | 25.2 (6.7) | 23.7 (4.9) |
| schist (161) | 23.6 (8.8) | 24.6(5.0) | 23.7 (5.0) |
| Parent Material | Metric | GR vs. ESDAC | GR vs. ISRIC |
|---|---|---|---|
| clay-rich deposits | t-Statistic | 17.641 | 11.797 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 572 | 557 | |
| marl | t-Statistic | 23.700 | 15.450 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 1105 | 1083 | |
| flysch formations | t-Statistic | −0.757 | −4.291 |
| p-Value | 0.450 | 0.000 | |
| Sample Size | 138 | 133 | |
| colluvial materials (ripidion) | t-Statistic | 2.493 | −3.328 |
| p-Value | 0.013 | 0.001 | |
| Sample Size | 236 | 231 | |
| schist | t-Statistic | −0.124 | −4.326 |
| p-Value | 0.902 | 0.000 | |
| Sample Size | 161 | 160 | |
| lacustrine sediments | t-Statistic | 11.206 | 6.286 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 91 | 91 |
| Parent Material (Number of Points) | GR Mean Sand % (Std) | ISRIC Mean Sand % (Std) | ESDAC Mean Sand % (Std) |
|---|---|---|---|
| dunes (34) | 61.0 (17.5) | 36.0 (10.6) | 46.0 (8.6) |
| conglomerates (607) | 40.5 (13.6) | 29.7 (8.6) | 35.3 (8.4) |
| alluvium (4815) | 37.5 (17.4) | 30.0 (9.1) | 35.8 (11.2) |
| basic igneous rocks (85) | 42.0 (14.1) | 32.7 (8.4) | 34.4 (8.4) |
| alluvial terraces (1649) | 42.6 (14.9) | 34.0 (7.6) | 40.0 (8.9) |
| Parent Material | Metric | GR vs. ESDAC | GR vs. ISRIC |
|---|---|---|---|
| alluvium | t-Statistic | 6.722 | 22.501 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 4815 | 4699 | |
| basic igneous rocks | t-Statistic | 4.321 | 6.238 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 85 | 85 | |
| conglomerates | t-Statistic | 9.132 | 15.534 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 607 | 567 | |
| dunes | t-Statistic | 3.687 | 9.049 |
| p-Value | 0.001 | 0.000 | |
| Sample Size | 34 | 34 | |
| alluvial terraces | t-Statistic | 6.518 | 24.056 |
| p-Value | 0.000 | 0.000 | |
| Sample Size | 1649 | 1622 |
| ESDAC | ISRIC | |||
|---|---|---|---|---|
| QGIS Values Assign | Custom Method Values Assign | QGIS Values Assign | Custom Method Values Assign | |
| Sand | 17.18 | 11.72 | 18.55 | 16.17 |
| Clay | 13.69 | 10.59 | 13.20 | 11.69 |
| Silt | 14.04 | 10.34 | 14.45 | 13.42 |
| Metric | GR-ESDAC | GR-ISRIC | NAGREF–ESDAC | NAGREF–ISRIC | PEGEAL–ESDAC | PEGEAL-ISRIC |
|---|---|---|---|---|---|---|
| RMSEA | 0.8132 | 0.8108 | 0.7883 | 0.8311 | 0.7512 | 0.6503 |
| MAEA | 0.7071 | 0.7104 | 0.6793 | 0.7367 | 0.6809 | 0.5703 |
| GR–ISRIC | NAGREF–ISRIC | +/− | GR–ESDAC | NAGREF–ESDAC | +/− | |
|---|---|---|---|---|---|---|
| RMSE (Raw) (%) | ||||||
| Clay | 13.2 | 11.7 | 1.5 | 13.7 | 11.0 | 2.7 |
| Sand | 18.6 | 19.3 | −0.7 | 17.2 | 17.3 | −0.1 |
| Silt | 14.5 | 12.2 | 2.3 | 14.0 | 11.6 | 2.4 |
| RMSE (back-transformed) (%) | ||||||
| Clay | 13.58 | 12.33 | 1.25 | 14.44 | 11.81 | 2.63 |
| Sand | 21.81 | 21.59 | 0.22 | 21.68 | 20.54 | 1.14 |
| Silt | 8.22 | 9.26 | −1.04 | 7.24 | 8.72 | −1.48 |
| MAE (back-transformed) (%) | ||||||
| Clay | 11.04 | 10.05 | 0.99 | 11.69 | 9.39 | 2.3 |
| Sand | 17.77 | 18.24 | −0.47 | 17.35 | 16.69 | 0.66 |
| Silt | 6.73 | 8.19 | −1.46 | 5.66 | 7.31 | −1.65 |
| GR–ISRIC | PEGEAL–ISRIC | +/− | GR–ESDAC | PEGEAL–ESDAC | +/− | |
|---|---|---|---|---|---|---|
| RMSE (Raw) (%) | ||||||
| Clay | 13.2 | 10.5 | 2.7 | 13.7 | 12.9 | 0.8 |
| Sand | 18.6 | 14.3 | 4.3 | 17.2 | 15.9 | 1.3 |
| Silt | 14.5 | 13.2 | 1.3 | 14.0 | 12.7 | 1.3 |
| RMSE (back-transformed) (%) | ||||||
| Clay | 13.58 | 9.9 | 3.68 | 14.44 | 12.78 | 1.66 |
| Sand | 21.81 | 16.45 | 5.36 | 21.68 | 18.33 | 3.35 |
| Silt | 8.22 | 6.55 | 1.67 | 7.24 | 5.55 | 1.69 |
| MAE (back-transformed) (%) | ||||||
| Clay | 11.04 | 8.06 | 2.98 | 11.69 | 10.71 | 0.98 |
| Sand | 17.77 | 13.25 | 4.52 | 17.35 | 15.33 | 2.02 |
| Silt | 6.73 | 5.19 | 1.54 | 5.66 | 4.61 | 1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerontidis, S.; Soulis, K.X.; Stavropoulos, A.; Nikitakis, E.; Kalivas, D.P.; Kairis, O.; Kopanelis, D.; Soulis, X.K.; Palli-Gravani, S. Assessment of the Accuracy of ISRIC and ESDAC Soil Texture Data Compared to the Soil Map of Greece: A Statistical and Spatial Approach to Identify Sources of Differences. Soil Syst. 2025, 9, 133. https://doi.org/10.3390/soilsystems9040133
Gerontidis S, Soulis KX, Stavropoulos A, Nikitakis E, Kalivas DP, Kairis O, Kopanelis D, Soulis XK, Palli-Gravani S. Assessment of the Accuracy of ISRIC and ESDAC Soil Texture Data Compared to the Soil Map of Greece: A Statistical and Spatial Approach to Identify Sources of Differences. Soil Systems. 2025; 9(4):133. https://doi.org/10.3390/soilsystems9040133
Chicago/Turabian StyleGerontidis, Stylianos, Konstantinos X. Soulis, Alexandros Stavropoulos, Evangelos Nikitakis, Dionissios P. Kalivas, Orestis Kairis, Dimitrios Kopanelis, Xenofon K. Soulis, and Stergia Palli-Gravani. 2025. "Assessment of the Accuracy of ISRIC and ESDAC Soil Texture Data Compared to the Soil Map of Greece: A Statistical and Spatial Approach to Identify Sources of Differences" Soil Systems 9, no. 4: 133. https://doi.org/10.3390/soilsystems9040133
APA StyleGerontidis, S., Soulis, K. X., Stavropoulos, A., Nikitakis, E., Kalivas, D. P., Kairis, O., Kopanelis, D., Soulis, X. K., & Palli-Gravani, S. (2025). Assessment of the Accuracy of ISRIC and ESDAC Soil Texture Data Compared to the Soil Map of Greece: A Statistical and Spatial Approach to Identify Sources of Differences. Soil Systems, 9(4), 133. https://doi.org/10.3390/soilsystems9040133










